Supralinear Summation of Synaptic Inputs by an Invertebrate Neuron: Dendritic Gain Is Mediated by an “Inward Rectifier” K⁺ Current

Abstract

Dendritic processing of glutamatergic synaptic inputs was investigated in the anterior pagoda cell of leech. We observed that below spike threshold, the amplitude of individual EPSPs decreased with hyperpolarization and that simultaneous stimulation of pairs of synaptic inputs leads to the supralinear summation of EPSPs. Voltage-clamp measurements revealed a hyperpolarization-activated, Ba²⁺-sensitive, fast, noninactivating K⁺ conductance that depends on the external [K⁺]. These features are those of an “inward rectifier,” Kir. Microsurgery experiments, in combination with electrophysiological measurements, revealed an inhomogeneous spatial distribution of the Kir conductance. Furthermore, on surgical removal of the neurites that contain the Kir conductance, the amplitude of EPSPs from the remaining synaptic inputs increased with hyperpolarization. A model cell, with the Kir conductance as the sole voltage-dependent conductance, reproduced qualitatively the observed voltage dependence of individual EPSPs as well as the supralinear summation of EPSP pairs.

Most neuronal dendrites have various voltage-gated channels (for review, see Midtgaard, 1994; Johnston et al., 1996; Yuste and Tank, 1996; Magee et al., 1998) along with ligand-gated channels that are activated by synaptic inputs from many presynaptic neurons. Understanding the interaction of membrane and synaptic properties is essential for the study of information processing in nervous systems (for review, see Borst and Egelhaaf, 1994; Mel, 1994; Koch, 1999).

When two neighboring regions of a passive dendrite receive simultaneous synaptic inputs of the same type, the resulting postsynaptic potential is less than the linear sum of the potentials generated by each synapse alone. Such sublinear summation is caused by the increase in the membrane conductance attributable to the synaptic conductance, and by the corresponding drop in synaptic driving force by each PSP on the other synapse. Sublinear summation has been demonstrated experimentally (Burke, 1967; Kuno and Miyahara, 1969; Haag et al., 1992, 1995). However, linear summation (Burke, 1967; Langmoen and Andersen, 1983;Skydsgaard and Hounsgaard, 1994; Grabauskas and Bradley, 1996; Cash and Yuste, 1998) and supralinear summation (Margulis and Tang, 1998) have been observed as well, suggesting that the dendrites have voltage-gated channels that counteract the sources of sublinear summation. EPSP amplification has been shown in different neurons to be mediated by various mechanisms: activation of voltage-gated Na⁺ channels (Hirsch and Gilbert, 1991; Schwindt and Crill, 1995; Stuart and Sakmann, 1995; Haag and Borst, 1996; Lipowsky et al., 1996; Margulis and Tang, 1998), activation of voltage-gated Ca²⁺ channels (Deisz et al., 1991; Gillessen and Alzheimer, 1997; Seamans, 1997), and deactivation of the “inward rectifier” potassium channel Kir, (Kandel and Tauc, 1966; Kawaguchi et al., 1989).

We examine dendritic integration in the nervous system of the medicinal leech (Muller et al., 1981). Specifically we have studied inputs from the pressure-sensitive sensory cells (P cell) onto the anterior pagoda (AP) cell (Stewart et al., 1989; Gu, 1991; Wolszon et al., 1995;Melinek and Muller, 1996; Osborn and Zipser, 1996) (Fig.1). The P cells make monosynaptic excitatory inputs onto the AP cell at specific locations in their neurites (Gu, 1991). A spike triggered in a P cell by a short current-pulse injection induces an EPSP in the AP cell (Gu, 1991). There are two P cells on each side, with similar morphology within the central neuropil (Muller and McMahan, 1976). P cells are mirror symmetric across the midline to their contralateral partner. In the intact leech the P cells respond to pressure on the skin and have receptive fields on the dorsal (P_d) and ventral (P_v) ipsilateral side of the skin (Nicholls and Baylor, 1968).

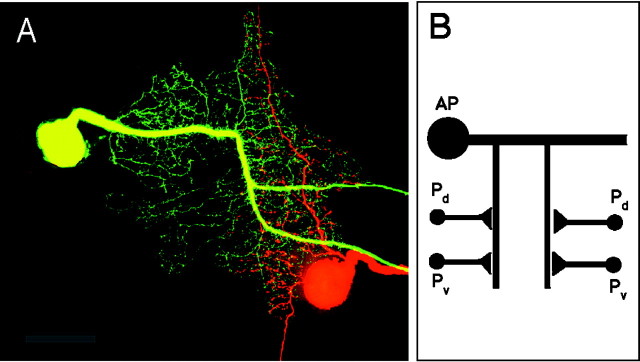
Fig. 1.

Morphology of the AP cell and the contralateral dorsal P cell. A, Light microscopic image of the AP cell (yellow/green, fluorescein-filled) and one of the two contralateral P cells, the dorsal P cell (orange/red, rhodamine-filled). Note the extensive overlap of the AP and P cell neurites contralateral to the AP cell soma. All four P cells have similar morphology and are mirror symmetric across the midline to the P cells on the opposite side. The dim somata result from autofluorescence and serve to show the outline of the ganglion. Anterior is up. Scale bar, 100 μm. B, Schematic of the P-to-AP cell circuit.

In the present study we ask the following questions. (1) What are the characteristics of individual P cell inputs to the AP cell? (2) What is the nature of the interaction among simultaneous P cell inputs? (3) How is such interaction mediated by synaptic or cellular properties?

MATERIALS AND METHODS

Preparation, dissection, and solutions. Leeches (Hirudo medicinalis) were obtained from a commercial supplier (Leeches USA, Westbury, NY) and maintained in artificial pond water at 15°C. Animals were anesthetized in ice-cold saline, and individual ganglia were dissected using surgical methods similar to those described previously (Muller et al., 1981). Ganglia were pinned ventral side up in Sylgard (Dow-Corning, Midland, MI)-lined Petri dishes (bath volume, 10 ml), and the connective tissue sheath over the neuronal somata was removed with fine scissors. For the hemisectioning experiments, the ganglia were cut at the desired location with a scalpel blade, and the AP cell was hyperpolarized below −60 mV with current injection for 30 min. Ganglia were superfused (3 ml/min) with normal leech saline containing (in mm): NaCl 115, KCl 4, CaCl₂ 1.8, MgCl₂ 1.5, glucose 10, Tris-maleate 4.6, Tris-base 5.4, pH 7.4. Equimolar amounts ofN-methyl-d-glucamine replaced Na⁺ in 0 Na⁺ salines. Equimolar amounts of Co²⁺ replaced Ca²⁺ in 0 Ca²⁺ salines. In solutions with increased Ca²⁺ or K⁺ concentration, the Na⁺ concentration was reduced by equal amounts to maintain osmolarity. Experiments were performed at room temperature (20–23°C).

Electrophysiology. Intracellular recordings were made with sharp borosilicate microelectrodes (1 mm outer diameter, 0.75 mm inner diameter, A-M Systems, Carlsborg, WA) pulled on a micropipette puller (P-80, Sutter Instruments, Novato, CA) filled with 3 mK-acetate with resistances of 40–80 mOhm. An Axoprobe 1A (Axon Instruments, Foster City, CA) was used for current-clamp measurements, and an Axoclamp 2B (Axon Instruments) was used for either current-clamp (bridge mode) or two-electrode voltage-clamp (TEVC-mode) measurements. Analog data were low pass-filtered (four-pole Butterworth) at 1 kHz, digitized at 2 kHz, stored, and analyzed on a personal computer equipped with AT-MIO-16E-1 (National Instruments, Austin, TX) and Labview (National Instruments).

The AP cell was impaled with two microelectrodes, one for passing current and one for measuring voltage. P cell somata were impaled and a spike was triggered with a +3 nA, 10 msec current pulse, which in turn produced an EPSP in the AP cell. This EPSP was constant in size and shape for >2 hr when allowing for a 3 min recovery period between trials. For shorter recovery periods, the EPSP peak amplitude decreased. In normal leech saline the EPSP displayed multiple components, indicating the activation of polysynaptic inputs in addition to the monosynaptic input. All polysynaptic inputs were abolished in saline with [Ca²⁺]_oraised from 1.8 to 10 mm, which raises spike threshold, thereby reducing the efficacy of polysynaptic pathways (Nicholls and Purves, 1970; Cohen et al., 1978; Getting, 1981). Raising both [Mg²⁺]_o and [Ca²⁺]_o also abolished polysynaptic pathways, but in addition led to reduced monosynaptic EPSP peak amplitudes (Nicholls and Purves, 1970); therefore this combination was not used. All experiments involving synaptic stimulation were performed in leech saline with [Ca²⁺]_o = 10 mm, similar to previous studies of synaptic interaction in leech (Nicholls and Purves, 1970).

Data are expressed in the text and figures as mean ± SEM.

Histology. To observe pairs of P and AP cells in light microscopy, an AP cell was iontophoretically injected with Fluorescein dextran [5% in H₂O, 3000 molecular weight (MW), Molecular Probes, Eugene, OR], and the P cell was injected with tetramethylrhodamine dextran (5% in H₂O, 3000 MW, Molecular Probes) using sharp electrodes of 10–30 MΩ resistance and pulsed current (−5 ± 2 nA, 10 Hz, 30 min). The ganglia were fixed in 2% paraformaldehyde in 0.1 m phosphate buffer for 2–12 hr, rinsed in PBS, and mounted in a solution of 20% PBS and 80% glycerin. Digital images were taken at 20× magnification with a confocal microscope (Bio-Rad, MRC1024, Hercules, CA) equipped with a krypton/argon laser using the 488 and 563 nm lines for excitation, and the emission filters 540/30 for fluorescein and 585LP for tetramethylrhodamine. Images were adjusted with respect to brightness and contrast using Adobe Photoshop (Adobe Systems, Mountain View, CA).

Numerical simulations. Simulations were programmed in LabVIEW (National Instruments) using the forward Euler method with an integration time-step of 0.01 msec. The capacitance wasC = 0.5 nF. For simplicity, synaptic input was modeled as a pulsed change in conductance from 0 to G_synduring a period of 200 msec. Synapses had a reversal potential,E_syn, of 0 mV. The model included a voltage-independent leak conductance, G_L, and a voltage-dependent inward rectifier conductance,G_Kir, with reversal potentials ofE_L = −45 mV andE_K = −80 mV, respectively. The Kir-channel model was of the form:

$$G_{\text{Kir}}=\frac{G_{max}}{1+exp((V-V_{1/2})/\gamma )}.$$ Equation 1

Because the inward rectifier acts so quickly, it is permissible to neglect any time dependence. To insure consistency with the EPSP measurements, all parameter values were taken from I–Vcurves measured with voltage-clamp in saline with [Ca²⁺]_o raised to 10 mm. The parameter values for the conductances wereG_L = 24 nS,G_max = 28 nS,V_1/2 = −67 mV, and γ = 8 mV. The one-compartment model was of the form:

$$C \frac{\text{dV}}{\text{dt}}=G_{\text{Kir}}(V)(E_K-V)+G_L(E_L-V)+\nu \eta G_{\text{syn}}(E_{\text{syn}}-V)+I_{\text{inj}},$$ Equation 2

with V the membrane potential andI_inj the injected current. The variable η takes the value 1 during the time of synaptic stimulation and is 0 otherwise, and the variable ν specifies the number of synaptic inputs. The difference between the membrane potential before and at the end of the synaptic input was taken as the EPSP peak amplitude.

In the two-compartment model the synaptic conductance, the inward rectifier conductance G_max2, and a leak conductance, G_L2, were placed in the “neurite” compartment that was connected through an axial conductance, G_ax, with the “soma” compartment that contained the leak conductance and the injected current. In this model, the measured leak conductanceG_L is the result of the combined leak conductances from both compartments. Assuming for simplicity the same leak conductance G_L2 in each compartment, Kirchoff’s law yields the relation between the measured leak conductance G_L and the leak conductanceG_L2 in each compartment:G_L = G_L2(G_L2 + 2G_ax)/(G_L2 +G_ax). Similarly, because the Kir conductance was placed in the “neurite” compartment but not in the soma compartment, Kirchoff’s law yields the relation between the measured Kir conductance G_max and the Kir conductance G_max2 in the “neurite” compartment: G_max2 = (G_axG_max)/(G_ax− G_max). For the considered axial conductance of 40 nS, the relations yieldG_L2 = 14 nS andG_max2 = 93 nS. The two-compartment model was of the form:

$$C \frac{{\text{dV}}_{\text{s}}}{\text{dt}}=G_{L2}(E_L-V_S)+G_{\text{ax}}(V_N-V_S)+I_{\text{inj}},$$ Equation 3

for the “soma” compartment and

$$C \frac{{\text{dV}}_N}{\text{dt}}=G_{L2}(E_L-V_N)+G_{\text{ax}}(V_S-V_N)+G_{\text{Kir}2}(V)(E_K-V_N)+\nu \eta G_{\text{syn}}(E_{\text{syn}}-V_N),$$ Equation 4

for the “neurite” compartment, withV_S and V_N the membrane potentials in the “soma” and “neurite” compartments, respectively, and G_Kir2(V) given by Equation 1 with parameters G_max2 = 93 nS, V_1/2 = −67 mV, γ = 11 mV, and G_syn = 9 nS.

RESULTS

AMPA receptors mediating EPSPs

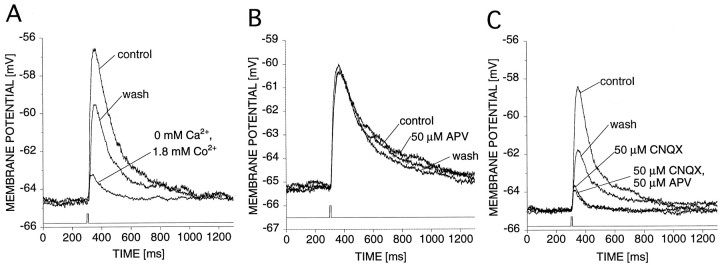
We characterized the P-to-AP monosynaptic inputs under conditions that blocked polysynaptic pathways (see Materials and Methods) and found a major contribution to the EPSP from AMPA receptors and a much smaller fraction from an electrical coupling. When we blocked the presynaptic neurotransmitter release with saline that had its Ca²⁺ replaced by the Ca²⁺ channel blocker Co²⁺ (Simon et al., 1992), the EPSPs were reduced by 87 ± 1% (mean ± SEM, n = 3 cells) (Fig. 2A), suggesting that chemical transmission was the dominant source of the EPSP, with the residue caused by an electrical coupling.

Fig. 2.

Contribution of AMPA receptors to P-to-AP EPSPs.A, Unitary average EPSPs (average of 4 trials) in response to contralateral P_d stimulation at an initial membrane potential of −65 mV in leech saline (10 mmCa²⁺) and in saline with 0 mmCa²⁺ and 1.8 mm Co²⁺, as indicated. B, Unitary average EPSPs (average of 4 trials) in response to contralateral P_d stimulation at an initial membrane potential of −65 mV in leech saline (10 mm Ca²⁺) and in the presence of 50 μm APV, as indicated. C, Unitary average EPSPs (average of 4 trials) in response to contralateral P_dstimulation at an initial membrane potential of −65 mV in leech saline (10 mm Ca²⁺), in the presence of 50 μm CNQX, and in the presence of of 50 μmCNQX and 50 μm APV, as indicated.

The effect of APV was tested at holding potentials of −65 mV, i.e., below the threshold for spiking. The amplitude and time course of the average evoked EPSP were unaffected by the addition of 50 μm APV to the extracellular solution (n = 9 cells) (Fig. 2B). Assuming that APV blocks invertebrate NMDA receptors, this result suggests that NMDA receptors either are absent from the P-to-AP synapses or blocked by extracellular Mg²⁺ in the subthreshold range of membrane potentials. This observation is consistent with previous studies of other leech synapses that also failed to reveal APV-sensitive transmission (Thorogood and Brodfuehrer, 1995).

The EPSP was reduced by 75 ± 2% (n = 12 cells) after addition of 50 μm CNQX to the extracellular solution (Fig. 2C), which suggests that the EPSPs are largely mediated by AMPA receptors. The remaining EPSP was not affected by further addition of 50 μm APV to the extracellular solution (n = 3 cells). Furthermore, this remaining EPSP did not depress in response to a train of 10 spikes at 5 Hz (n = 5 cells; data not shown), thus strengthening the hypothesis that the residue is caused by an electrical coupling as suggested above (Fig. 2A). At a membrane potential of −120 mV the EPSP was reduced by 73 ± 5% (n = 3 cells) after addition of 50 μm CNQX to the extracellular solution (data not shown), which suggests that at this membrane potential the response maintains a chemical component.

Voltage dependence of EPSPs

The amplitude and time course of the P-to-AP EPSPs displayed a voltage dependence that is anomalous for an AMPA response (Fig.3A). Below the threshold for spiking (approximately −50 mV in 10 mmCa²⁺ saline), the EPSP peak amplitude (Fig.3B, thick trace) (n = 9 cells) and duration (Fig. 3C) (n = 9 cells) decreased with hyperpolarization and did not reverse, even at soma membrane potentials well below the potassium equilibrium potentialE_K. The voltage response to a constant current pulse (2000 msec, +0.2 nA) (Fig. 3B, inset) injected into the soma also decreased with hyperpolarization (Fig.3B, thin trace) (n = 10 cells). This voltage dependence is similar to the one of the EPSP peak amplitude, which suggests that the EPSP voltage dependence is caused by a postsynaptic membrane current rather than synaptic properties. The difference between the two voltage dependencies above −80 mV occurs because in the case of the current injection the amplitude of the current is constant, whereas in the case of synaptic stimulation the synaptic current decreases with depolarization attributable to the accompanying reduction in driving force.

Fig. 3.

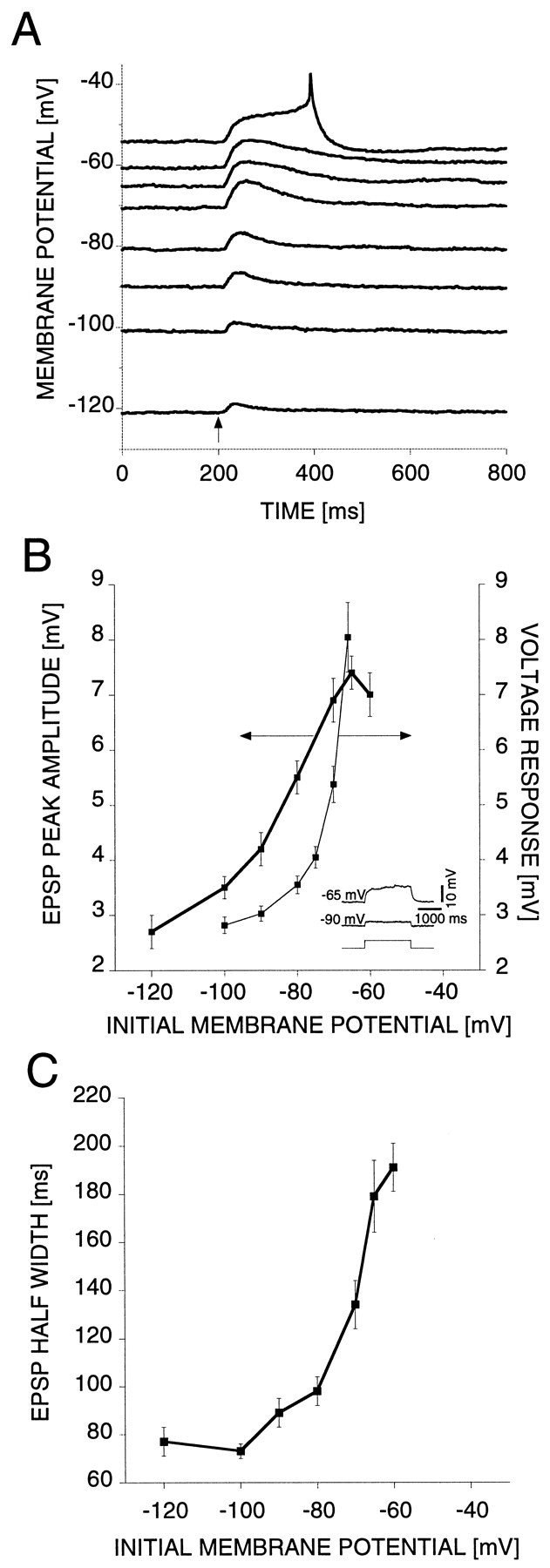
Dendritic gain in AP cells decreases with hyperpolarization in the subthreshold range. A, Response of a representative AP cell to synaptic stimulation via the contralateral dorsal P cell at different membrane potentials in saline with [Ca²⁺]_o elevated to 10 mm. The amplitude and width of the EPSP decrease with hyperpolarization but do not reverse even at soma membrane potentials well below the potassium equilibrium potential. The arrow indicates the timing of the stimulus. B, Plots showing how the EPSP amplitude and the voltage response varied with initial membrane potential.Left axis, EPSP peak amplitude versus initial membrane potential for nine AP cells tested. Right axis, Average steady-state voltage responses to +0.2 nA, 2000 msec current pulses versus initial membrane potential (n = 10 AP cells). Inset, Voltage responses to +0.2 nA, 2000 msec current pulses at different initial membrane potentials.C, EPSP half-width versus initial membrane potential for nine AP cells.

Supralinear summation of synaptic inputs

To investigate synaptic interactions in the AP cell, we stimulated two P cells from the same side of the ganglion, first separately and then simultaneously, and compared the algebraic sum of the separate EPSPs with the EPSP elicited by simultaneous stimulation. Supralinear summation was observed when the initial membrane potential was between −110 and −70 mV (Fig.4A) (average of eight trials). The two bottom traces are the responses from separate ventral (P_v) and dorsal (P_d) contralateral P cell inputs. The gray trace indicates the algebraic sum of the two EPSPs, and the top trace is the response obtained from simultaneous stimulation of both P cells; it is significantly higher than the gray trace. We define a measure of linearity as:

$$\%\text{linearity}\equiv \left(\frac{{\text{peak}}_{\text{simultaneous}}}{{\text{peak}}_{\text{algebraic sum}}}\right)\times 100$$

$$=\left(\frac{V_{\text{PdPv}}-V_{\text{in}}}{(V_{\text{Pd}}-V_{\text{in}})+(V_{\text{Pv}}-V_{\text{in}})}\right)\times 100,$$ Equation 5

with V_in the initial membrane potential,V_PdPv the peak membrane potential after simultaneous activation of P_d and P_v, and V_Pd or V_Pv the peak membrane potential after separate activation of P_d or P_v, respectively. The EPSP peak amplitude for simultaneous stimulation was 122 ± 5% of the algebraic sum of the separate stimulation. For simultaneous stimulation of contralateral (contra/contra; 21 cells) or ipsilateral (ipsi/ipsi; six cells) P cells, we found supralinear summation in the range of initial membrane potential between −110 and −70 mV (average % linearity = 117 ± 2 and 117 ± 5% for contra/contra and ipsi/ipsi, respectively) (Fig. 4B). The EPSP peak amplitude for simultaneous stimulation decreased with hyperpolarization and covered a range between 2 and 16 mV (Fig. 4B,inset). Because EPSPs from ipsilateral stimulation were smaller in general than those from contralateral stimulation, we chose contra/contra stimulation for most experiments. Because of the small size of the EPSPs, we did not explore summation for ipsi/ipsi stimulation below a membrane potential of −90 mV. Synaptic inputs from opposite sides (ipsi/contra, n = 9 cells) summed in a linear manner (average % linearity = 102 ± 2%), suggesting that synaptic inputs from opposite sides are electrically remote from each other. This observation is consistent with the anatomical observation that the processes of a P cell remain largely on the same side as the soma (Fig. 1).

Fig. 4.

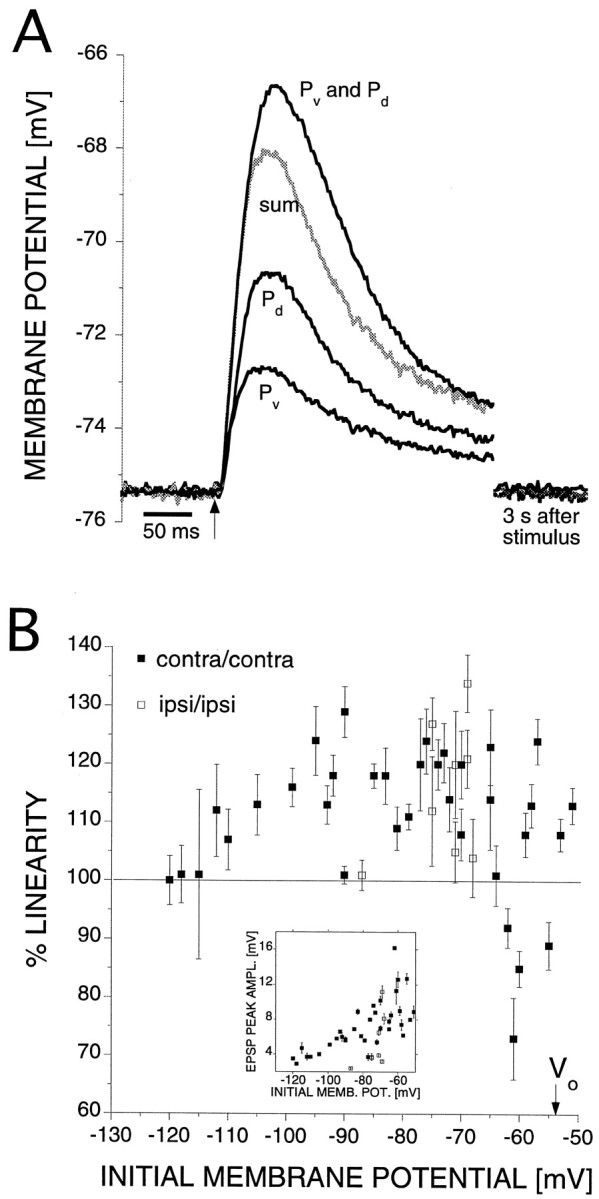
Supralinear summation of synaptic inputs from two sources. A, Averaged results from a representative AP cell (8 trials). The preparation was in a saline with high Ca²⁺ concentration to avoid polysynaptic pathways. The two bottom traces are the responses from individual ventral and dorsal P cell stimulation. The somata of both P cells were contralateral to the AP cell soma. In this case, the EPSP from P_v is smaller than from P_d, although the relative sizes varied in different preparations. The gray trace indicates the algebraic sum of the two EPSPs. Thetop trace is the response to simultaneous stimulation of both P cells; its peak is 122% of the algebraic sum of individual stimulation. B, Peak EPSP from simultaneous stimulation of contralateral dorsal and ventral (▪, 21 cells) or ipsilateral dorsal and ventral (■, 6 cells) P cells expressed as % of algebraic sum at different membrane potentials (mean ± SEM; 5–10 trials). The arrow indicates the zero-current membrane potentialV_o. Inset, EPSP peak amplitude from simultaneous stimulation of dorsal and ventral P cells for the data points shown in the main figure, showing that the EPSP amplitudes decrease with hyperpolarization, as in Figure3B.

Cellular properties: the inward rectifier Kir

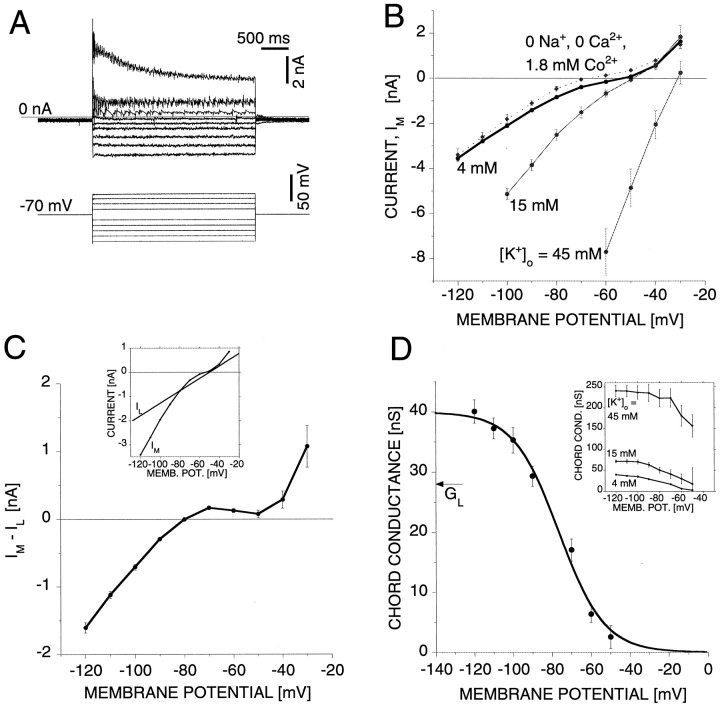
To test the possibility that the voltage dependence and supralinear summation of EPSPs is caused by postsynaptic membrane properties, we used a two-electrode voltage clamp to measure theI–V characteristics of AP cells. We note that the voltage clamp is only assumed to be effective in the AP cell soma. When the cell membrane potential was stepped to test voltages between −120 and −30 mV from a holding potential of −70 mV with the ganglion in normal leech saline, the resulting current showed a strong inward rectification. Furthermore, the current activated in <1 msec, and for test voltages below −50 mV it did not inactivate during the 3 sec voltage steps used in these experiments (Fig.5A). The steady-stateI–V curve measured from the current at the end of the 3 sec voltage step was strongly nonlinear (Fig. 5B, thick trace) (n = 8 cells). In 0 Na⁺, 0 Ca²⁺, 1.8 mm Co²⁺saline, chosen to isolate K⁺ and Cl⁻ currents, the I–V curve was only marginally changed (Fig. 5B, dotted line) (n = 7 cells). The shift of the zero-current potential to a more hyperpolarized level is presumably attributable to the absence of the Na⁺ and Ca²⁺ leak currents. In contrast, an increase of [K⁺]_o to 15 and 45 mm led to a significant increase of the inward current (Fig. 5B,thin lines) (n = 6 cells), strongly suggesting that K⁺ is the dominant current carrier.

Fig. 5.

Evidence for an inward rectifier, Kir.A, Current–response (average of 9 trials) to voltage steps from a holding potential of −70 mV to various test membrane potentials between −120 and −30 mV. B, The current at the end of the 3 sec voltage step plotted versus the test membrane potential in (1) normal leech saline ([K⁺]_o = 4 mm) (average of 8 cells), (2) 0 Na⁺, 0 Ca²⁺, 1.8 mm Co²⁺saline (average of 7 cells), (3) saline with [K⁺]_o elevated to 15 (average of 6 cells), and (4) saline with [K⁺]_oelevated to 45 mm (average of 5 cells). C, Measured current, I_M, in normal saline ([K⁺]_o = 4 mm) minus the non-K⁺ leak current,I_L =G_L(V −E_L). The value of the equilibrium leak potential, E_L, was assumed to be −50 mV, and the non-K⁺ leak conductance was estimated for each cell from the measured current,I_M,EK, at the assumedE_K value of −80 mV:G_L =I_M,EK/(E_K− E_L). The insetshows the measured current and the estimated non-K⁺leak current for one representative cell. D, Potassium chord conductance, G = (I_M −I_L)/(V −E_K). The continuous curve is a least-squares fit of the Boltzmann equation to the data points. The fitting parameters are G_max = 40 nS,V_1/2 = −76 mV, and γ = 12 mV. For comparison the average non-K⁺ leak conductance,G_L = 28 ± 2 nS, is indicated by the horizontal arrow. The inset shows the potassium chord conductance for [K⁺]_o = 15 and 45 mm, estimated as described in the text. For comparison the chord conductance for [K⁺]_o = 4 mm (i.e., the data shown in the graph) is replotted in the inset.

In an attempt to separate the K⁺ current from the measured current I_M, we assumed that the measured current is the sum of the K⁺ currentI_K =G_K(V −E_K), and a non-K⁺ leak current I_L =G_L(V −E_L) (Hagiwara and Yoshii, 1979), with a voltage-independent conductance,G_L, and a reversal potential,E_L = −50 mV, a value assumed close to the zero-current membrane potential that was used previously in modeling studies of leech neurons (Calabrese et al., 1995). At the equilibrium potential for potassium, E_K, the K⁺ current vanishes and thus at V =E_K the measured currentI_M,EK is equal to the non-K⁺leak current, i.e., I_M,EK =I_L,EK =G_L(E_K −E_L). We estimated the non-K⁺ leak conductance for each cell using the relation G_L =I_M,EK/(E_K −E_L).

The value of E_K for leech neurons has been estimated by various methods: extrapolation from the change of membrane potential with [K⁺]_o(E_K = −83 mV) (Nicholls and Kuffler, 1964), flame photometry (E_K = −86 mV) (Nicholls and Kuffler, 1965), and ion exchanger microelectrodes (E_K = −80 mV) (Deitmer and Schlue, 1981;Schlue and Deitmer, 1984). A value of E_K = −80 mV has been used previously in modeling studies in the leech (Calabrese et al., 1995). We took E_K = −80 mV for our data analysis.

With these assumptions in mind, subtracting for each cell the estimated non-K⁺ leak current I_L =G_L(V −E_L) from the measured currentI_M reveals the potassium currentI_K = I_M −I_L for that cell. For illustration, the measured current I_M and the estimated non-K⁺ leak current I_L are shown for one representative AP cell in Figure 5C(inset). Because the leak current varies between cells, we performed this procedure on each cell rather than on the mean to minimize the variation in the estimated potassium current between cells. The average potassium current thus derived from eight cells is shown in Figure 5C. The shape of the potassiumI–V curve with a local minimum at −50 mV suggests that there is only a minor contribution of a potassium leak current to this I–V curve. An upper bound of the potassium leak current is a straight line that crosses the data point atE_K = −80 mV and the data point at the local minimum at −50 mV, yielding a potassium leak conductance of <2.7 nS. Above −50 mV, additional potassium conductances that are activated with depolarization contribute to the current. Thus data points above −50 mV were excluded from the subsequent analysis of the potassium chord conductance.

From the average potassium I–V curveI_K = I_M −I_L, we obtained the potassium chord conductance:

$$G_K=\frac{I_M-I_L}{V-E_K},$$ Equation 6

(Fig. 5D, black dots). The continuous curve is a least-squares fit of a Boltzmann factor:

$$G_K=\frac{G_{max}}{1+exp((V-V_{1/2})/\gamma )},$$ Equation 7

to the calculated data points. The fitting parameters are the maximal conductance, G_max = 40 nS, the membrane potential at which the conductance is half-activated,V_1/2 = −76 mV, and the slope factor, γ = 12 mV. Because γ = kT/ze, wherekT is the thermal energy (25 meV at T = 297 K), e is the elementary electric charge, and z is the number of effective charges of the gating particle, the value of γ = 12 mV yields approximately z = 2.

The observed features of this potassium conductance, i.e., (1) opening with hyperpolarization, (2) activation in <1 msec, and (3) no inactivation, are consistent with the previously described inward rectifier Kir (Hagiwara and Jaffe, 1979; Hagiwara, 1983; Doupnik et al., 1995; Fakler and Ruppersberg, 1996; Isomoto et al., 1997; Nichols and Lopatin, 1997).

In our experiments the chord conductance was best fitted to a Boltzmann expression with a slope factor of γ = 12 mV, corresponding to an effective gating charge of z = 2. Interestingly, the estimated effective gating charge is consistent with the Mg²⁺ block that controls, in part, rectification for Kir channels (Vandenberg, 1987). Inward rectification has previously been fitted to a Boltzman expression with a similar steepness for the voltage dependence: γ = 7 (Hagiwara and Takahashi, 1974); γ = 12–14 (Stanfield et al., 1985); γ = 6–15 (Williams et al., 1988); γ = 10–15 (Lopatin et al., 1994); γ = 12 (Dong and Werblin, 1995); γ = 10 (Aleksandrov et al., 1996).

This Kir conductance has been shown previously to be sensitive to external Ba²⁺ (Hagiwara et al., 1978; Constanti and Galvan, 1983; Tachibana, 1983; Shingai and Christensen, 1986; Williams et al., 1988; Uchimura et al., 1989; Kass et al., 1990; Golard et al., 1992; Kubo et al., 1993; Dong and Werblin, 1995; Holt and Eatock, 1995;Aleksandrov et al., 1996; Döring et al., 1998; Mermelstein et al., 1998; Töpert et al., 1998). For the AP cell, the current, measured in voltage-clamp at a test potential of −120 mV in 15 mm Ba²⁺, was reduced down to 56 ± 5% (mean ± SEM, n = 4 cells) compared with the value from control measurements in 0 Na⁺, 0 Ca²⁺, 1.8 mm Co²⁺saline. The Ba²⁺-sensitive current was similar in its voltage dependence (n = 2 cells; data not shown) to the estimated potassium current (Fig. 5C). Thus this aspect of the conductance is also consistent with the description of the inward rectifier.

[K⁺]_o-dependent gating

It has been noted previously that the gating of the Kir conductance changes with external [K⁺]: with increased [K⁺]_o, the chord conductance shifts to more depolarized levels and the maximal chord conductance increases (Hagiwara and Takahashi, 1974; Hagiwara et al., 1976; Hagiwara and Yoshii, 1979; Leech and Stanfield, 1981; Stanfield et al., 1985; Williams et al., 1988; Uchimura et al., 1989; Dong and Werblin, 1995; Holt and Eatock, 1995; Aleksandrov et al., 1996; Lopatin and Nichols, 1996a,b). To test whether the conductance under investigation displays this property, we measured the I–Vcurve in saline with [K⁺]_o = 4, 15, and 45 mm (Fig. 5B). According to the Nernst equation and assuming that [K⁺]_i= 96 mm (a value consistent with [K⁺]_o = 4 mm andE_K = −80 mV) is independent of [K⁺]_o, the potassium equilibrium potential E_K would be −47, and −19 mV for [K⁺]_o = 15 and 45 mm, respectively. Assuming for simplicity thatE_L and G_L remain constant, we obtained the chord conductance as described above for [K⁺]_o = 15 and 45 mm(Fig. 5D, inset) (n = 6 cells). For comparison, the chord conductance for [K⁺]_o = 4 mm is replotted in the inset. The observed shift to more depolarized levels and the increase of the chord conductance with increasing [K⁺]_o is consistent with the description of the Kir conductance.

Spatial distribution of the Kir channels

Microsurgery experiments, similar to those performed on hippocampal neurons (Benardo et al., 1982), in combination with slope resistance measurements revealed an inhomogeneous spatial distribution of the Kir conductance. Because of the activation of the Kir conductance with hyperpolarization, the observed voltage response to a constant-current pulse (+0.2 nA, 2000 msec) decreased with hyperpolarization in the intact ganglion (Fig.6A, intact,B, gray curve) (n = 10 cells). When the ganglion was cut (see Materials and Methods) between the ipsilateral lateral and the medial packet (Fig. 6A,cut), we observed that the voltage response to a constant-current pulse no longer decreased with hyperpolarization (Fig.6A, cut; Fig. 6B,black curve) (n = 11 cells). This observation indicates that the Kir channels are expressed contralateral but not ipsilateral to the cut, i.e., the border between the ipsilateral lateral and medial packet. Cutting the ganglion down the midline (data not shown) did not separate the soma from the Kir channels.

Fig. 6.

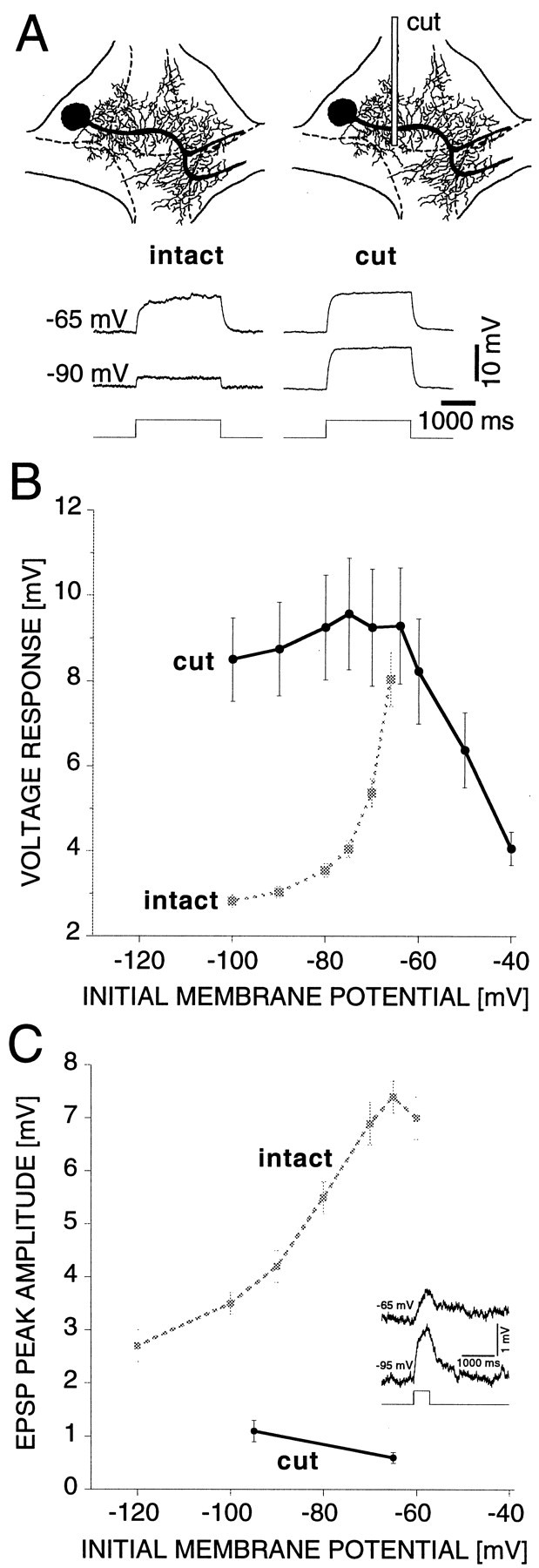
Inhomogeneous spatial distribution of the Kir channels. A, Top, Schematic diagram of the AP cell in an intact (left) and surgically cut (right) ganglion. The location of the cut is indicated by the rectangle. Bottom, Voltage responses to +0.2 nA, 2000 msec current pulses at different initial membrane potentials for the intact (left) and cut (right) AP cell in normal saline. B, Average steady-state voltage responses to +0.2 nA, 2000 msec current pulses versus initial membrane potential for intact (gray, 10 cells) and cut (black, 11 cells) AP cells. The voltage response does not increase with depolarization in the cut cell, indicating a lack of Kir channels ipsilateral to the cut.C, Inset, EPSPs in response to stimulation of the synaptic input remaining after the cut (average of 8 trials alternating between a membrane potential of −65 and −95 mV). The presynaptic ipsilateral P cells were stimulated with +4 nA, 500 msec current pulses initiating an average of 20 spikes.C, Comparison of the voltage dependence of the EPSP peak amplitude in intact (gray, 9 cells) (Fig.2B; 10 mm Ca saline) and cut (black, 6 cells, 10 mm Ca saline) AP cells. In cut AP cells the EPSP peak amplitude decreases with depolarization. In all cases tested the EPSP peak amplitude at −65 mV was smaller than at −95 mV. On average the EPSP peak amplitude at −65 mV was 55 ± 4% of the amplitude at −95 mV.

Although most synaptic inputs were severed by the cut described above, a few synaptic inputs were still present on the neurites proximal to the soma. Stimulation of the ipsilateral P cells with a +4 nA, 500 msec current pulse triggered on average 20 spikes, which evoked measurable EPSPs in the AP cell. In the cut cell the amplitude of the EPSP increased with hyperpolarization (Fig. 6C, insetand black curve) (n = 6 cells), consistent with a passive dendrite, rather than decreased, as was observed in the intact cell (Fig. 6C, gray curve) (n = 9 cells). In all cases tested the EPSP peak amplitude at −65 mV was smaller than at −95 mV. The average EPSP peak amplitude at −65 mV was 55 ± 4% of the amplitude at −95 mV. Thus, when neurites containing the dominant fraction of the Kir conductance had been surgically removed, the EPSP peak amplitude increased with hyperpolarization in a manner consistent with a passive dendrite and a synaptic reversal potential that was more positive than −65 mV.

Despite the drastic surgical procedure, the AP cell soma and proximal neurite under investigation appeared to be healthy. The following observations are taken as evidence of normal functioning of the cut AP cell. (1) The voltage response to a constant-current pulse at a membrane potential of −65 mV is slightly larger than in the intact cell, i.e., the slope resistance increased in the cut cell, indicating that the cut ends sealed rather than remained open; (2) the voltage response to a constant-current pulse decreased with depolarization above −65 mV, indicating that voltage-gated conductances remained active (in the intact cell it was not possible to explore this range of membrane potential because of the occurrence of spikes triggered at the contralateral spike initiating zone); and (3) the cut cell still received synaptic inputs.

Model calculations

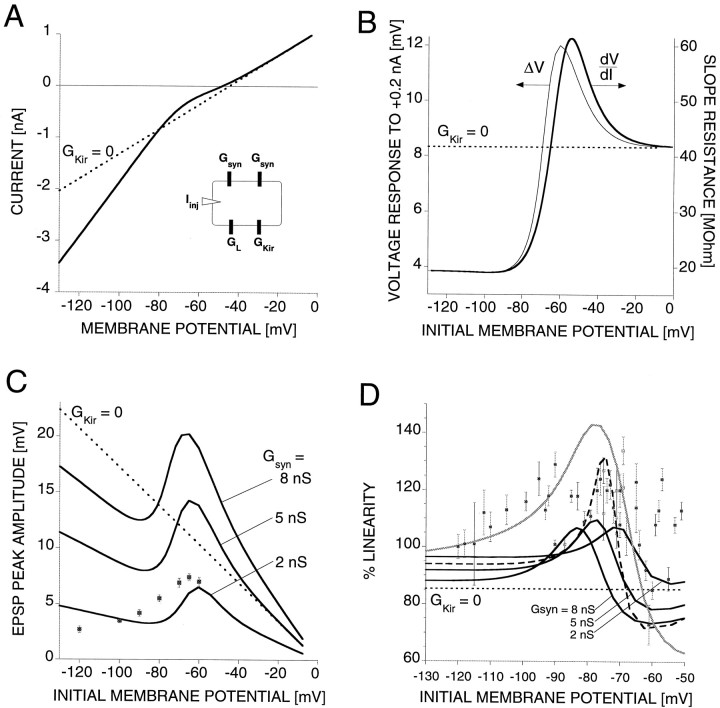
We have used numerical simulations to illustrate how the opposing effects of the reduced synaptic driving force and the deactivation of the inward rectifier with depolarization interact to produce the observed voltage dependence of (1) the EPSP peak amplitude and (2) the summation of pairs of synaptic inputs in the AP cell. The one-compartment model (Fig.7A, inset) contained a leak conductance, G_L, the inward rectifier conductance, G_Kir, two synaptic conductances, G_syn, and an injected current, I_inj. Because all EPSP measurements were taken in saline with [Ca²⁺]_o raised to 10 mm, the parameter values for G_L andG_Kir were taken from I–Vmeasurements in saline with this ion composition (see Materials and Methods for details). To prevent confusion with the effects of the inward rectifier, additional conductances that might be activated, in particular above a membrane potential of −50 mV, were excluded from these simulations. For simplicity the synaptic input was modeled as a chemical synapse, ignoring the electrical component that contributes ∼25% to the EPSP.

Fig. 7.

Model of interactions ofG_Kir with G_L andG_syn. A, I–Vcurve, I =G_Kir(V −E_K) +G_L(V −E_L), with the inward rectifier conductance, G_Kir =G_max/(1 + exp(V− V_1/2)/γ)), the leak conductance,G_L = 24 nS, the leak reversal potential, E_L = −45 mV, the potassium equilibrium potential, E_K = −80 mV, and the parameters of the inward rectifier conductance,G_max = 28 nS,V_1/2 = −67 mV, γ = 8 mV (all parameters from measurements from AP cells in 10 mmCa²⁺ saline). The I–V curve for the model without the inward rectifier is indicated by the dotted line. Inset, Schematic diagram of the model.B, Response characteristics of the model cell.Left axis, Voltage response, ΔV, of the model cell to a +0.2 nA, 200 msec current pulse. Right axis, Slope resistance, dV/dI, of the I–Vcurve in A. The slope resistance for the model without the inward rectifier is indicated by the dotted line.C, Voltage dependence of the EPSP peak amplitude. The synaptic input is modeled by a 200-msec-long pulsed conductance change of different magnitudes: G_syn = 2, 5, and 8 nS, E_syn = 0 mV. The result for the model without the inward rectifier (G_Kir = 0,G_syn = 5 nS) is shown for comparison (dotted line). The data points from Figure3B are replotted for comparison (gray squares). D, Voltage dependence of summing two synaptic inputs of equal conductance change (G_syn = 2, 5, and 8 nS;E_syn = 0 mV). The result for the model without the inward rectifier (G_Kir = 0;G_syn = 5 nS) is shown for comparison (dotted line). The result for the model with increased Kir conductance (G_Kir = 50 nS;G_syn = 5 nS) is shown by thedashed trace. The result for the two-compartment model (see Materials and Methods for details) is shown by the gray trace. The data points from Figure 4B are replotted for comparison (gray squares).

The combined effect of the leak current and the inward rectifier current:

$$I=G_{\text{Kir}}(V-E_K)+G_L(V-E_L)$$ Equation 8

with the inward rectifier conductance:

$$G_{\text{Kir}}=\frac{G_{max}}{1+exp((V-V_{1/2})/\gamma )}$$ Equation 9

leads to an I–V curve with a strong nonlinearity in the subthreshold range of membrane potential (Fig. 7A,thick curve). The leak current alone is shown by the dotted line for comparison. From the monotonously growing I–Vcurve we derive the slope resistance:

$$\frac{\text{dV}}{\text{dI}}={\left(\frac{\text{dI}}{\text{dV}}\right)}^{-1}={\left(\frac{{\text{dG}}_{\text{Kir}}}{\text{dV}}(V-E_K)+G_{\text{Kir}}+G_L\right)}^{-1}.$$ Equation 10

The slope resistance is a measure of the voltage response to an infinitesimal small current pulse and is thus a useful measure to discuss the cell’s response to a synaptic current.

The nonlinear I–V curve yields a slope resistance with a steep voltage dependence in the subthreshold range of membrane potential (Fig. 7B, thick trace). At extremely negative membrane potentials (i.e., below −120 mV), the inward rectifier is fully activated. The slope resistance is 1/(G_L + G_max) and independent of the membrane potential. With less hyperpolarization the Kir conductance is partially deactivated, and the slope resistance increases. Because of the potassium outward current aboveE_K = −80 mV, the slope resistance overshoots the leak resistance 1/G_L (Fig.7B, dotted line), reaches a peak (61 mOhm at −54 mV), and approaches asymptotically 1/G_L from above with further depolarization. The shape of the slope resistance is caused by the interplay of the Kir conductance and the value ofE_K, which results in an outward potassium current with a peak in the subthreshold range of membrane potential. Although the slope resistance represents the voltage response to an infinitesimally small current pulse, we find that it is still a good approximation of the steady-state voltage response of the model cell (see Materials and Methods) to a +0.2 nA current pulse (Fig.7B, thin trace), a level of current expected in the case of synaptic stimulation. This will allow us to discuss the voltage dependence of the EPSP peak amplitude and the summation of synaptic inputs in terms of the interplay between the slope resistance and the synaptic driving force.

First, we consider the voltage response of the model cell (Fig.7A, inset) to a synaptic conductance change (see Materials and Methods). The voltage dependence of the model cell responses to excitatory synaptic inputs follows the slope resistance; however, it is modulated by the counteracting change in the synaptic driving force (Fig. 7C). In particular, in the limit of an infinitesimally small synaptic conductance change, the model cell’s voltage response is determined by a constant slope resistance and driving force: ΔV ≅ (dV/dI)G_syn (V −E_syn). For larger synaptic conductance changes, however, both the slope resistance and the driving force change dynamically. Starting at a membrane potential of −130 mV, the inward rectifier is fully activated, and the slope resistance is independent of voltage. The EPSP peak amplitude decreases with depolarization, as is expected because of the reduced driving force. At less hyperpolarized levels the inward rectifier conductance decreases (compare with Fig. 5D), and the slope resistance increases sharply with increasing depolarization (compare with Fig.7B). The resulting increase of EPSP amplitudes is stronger than the decrease caused by the reduced driving force, which leads to a net increase of EPSP amplitudes with depolarization in the range of membrane potential between approximately −90 and −60 mV (Fig.7C; also compare with Fig. 3B). Because of the reduction of the inward rectifier outward current with depolarization above −70 mV, the slope resistance is larger than the leak resistance and reaches a peak of 61 mOhm at −54 mV (Fig. 7B). As a result the EPSP amplitude reaches values larger than in the case without the inward rectifier (Fig. 7C) (G_syn = 5 nS). Beyond the peak the slope resistance decreases with depolarization, asymptotically reaching the value of the leak resistance. Now the EPSP peak amplitude decreases with depolarization caused by both the reduced slope resistance and the reduced driving force.

Second, we consider the summation of pairs of synaptic inputs. We observe that when two synaptic inputs are stimulated simultaneously and the resulting membrane potential at the peak of the EPSP is in the range where the slope resistance (Fig. 7B) increases with depolarization, the resulting EPSP peak amplitude is larger than the algebraic sum of the EPSPs from individual stimulation, i.e., supralinear summation (Fig. 7D). The membrane potential at the peak of the EPSP is larger than the initial membrane potential. The difference increases with increasing synaptic conductance. Thus the voltage dependence of the supralinearity, expressed as “% linearity” versus initial membrane potential, shifts with the synaptic conductance.

The model explained qualitatively how the Kir conductance can lead to the supralinear summation of synaptic inputs in the considered range of membrane potential. The amplitude and width of the measured % linearity versus membrane potential relation is less well explained by this simple model. However, larger values of supralinearity, similar to those measured, are reproduced in a model with an increased Kir conductance (G_max = 50 nS,G_syn = 5 nS) (Fig. 7C,dashed trace).

Because of the spatial extent of the neuron, the control of the membrane potential at the sites of electrically remote synaptic inputs and Kir conductances is limited. Therefore the sites of synaptic inputs and Kir conductances are sampled over a smaller range of membrane potential around the local resting membrane potential than the somatic recording site is. It is expected that this sampling error leads to a broadening of the % linearity versus membrane potential relation. Such broadening, caused by the limited control of the membrane potential in the neurites, is illustrated using a two-compartment model (Fig.7D, gray trace). In this model the synaptic conductance, the inward rectifier conductance, and a leak conductance were placed in the neurite compartment, which was connected through an axial conductance with the soma compartment that contained the leak conductance and the injected current (see Materials and Methods for details).

Some insight into the numerical results for the summation of synaptic inputs may be found by considering the equation for the one-compartment model in the particular limit of a small synaptic conductance, and with the membrane conductance dominated by G_Kir(V), i.e.,G_S ≪ G_L ≪G_Kir(V). In terms of the % linearity measure, defined in Equation 5, we find (see ):

$$\%\text{linearity}\cong \left\{1+\left[\frac{E_{\text{syn}}-E_K}{\gamma } \frac{e^{(V_{\text{in}}-V_{1/2})/\gamma }}{1+e^{(V_{\text{in}}-V_{1/2})/\gamma }}-1\right]\frac{G_{\text{syn}}}{G_{\text{Kir}}(V_{\text{in}})}\right\}\times 100.$$ Equation 11

This equation shows that the relation between the synaptic reversal potential and the synaptic conductance is not solely multiplicative; in particular, the supralinearity increases with increasing E_syn. At levels ofV_in significantly hyperpolarized toV_1/2, i.e., V_in≪ (V_1/2 − γ), the term in square parentheses becomes negative, yielding sublinear summation. However, at levels of V_in closer toV_1/2 the term turns positive, yielding supralinear summation. At levels of V_indepolarized to V_1/2, the Kir conductanceG_Kir(V) is no longer the dominating membrane conductance and the above approximate relation (Eq.11) no longer holds. For a more general relation, see .

DISCUSSION

Inward rectification is responsible for nonlinear subthreshold summation of synaptic inputs

The major findings of the present experiments are as follows: (1) AP cell neurites express an inhomogeneous spatial distribution of the Kir conductance, (2) activation of the Kir conductance by hyperpolarization decreases the EPSP peak amplitude and half width, and (3) deactivation of the Kir conductance with EPSPs causes supralinear summation of paired excitatory synaptic inputs.

The observed voltage dependence of the EPSP peak amplitude was reversed when the neurites expressing the Kir channel were surgically removed. Both the observed voltage dependence of EPSPs as well as the supralinear summation were reproduced qualitatively in a model with the inward rectifier as the sole voltage-dependent conductance.

The physiological significance of the Kir conductance could be demonstrated experimentally only in the subthreshold range of membrane potential, as a result of the lack of a Na⁺ channel blocker for leech to abolish spikes (Kleinhaus and Angstadt, 1995). However, the extension of the tail end of the activation curve for the Kir conductance into the range of membrane potential above threshold suggests that the physiological significance extends into this range, as demonstrated in the modeling study (Fig. 7). In particular, because the Kir conductances are located in the neurites remote from the soma (Fig. 6), the activation curve, as measured in the soma, represents only a lower estimate of the Kir conductance located in the neurite. Therefore, the Kir conductance in the neurite is likely to be larger than the somatic measurement revealed and thus is expected to contribute significantly to the neurite conductance at zero-current potential.

Comparison with other amplifying mechanisms

The activation of voltage-gated Na⁺conductances (Hirsch and Gilbert, 1991; Schwindt and Crill, 1995;Stuart and Sakmann, 1995; Haag and Borst, 1996; Lipowsky et al., 1996;Margulis and Tang, 1998) or Ca²⁺ conductances (Deisz et al., 1991; Gillessen and Alzheimer, 1997; Seamans, 1997) by EPSPs amplifies the magnitude of the EPSPs en route to other areas of the neuron. Na⁺ conductances mediate supralinear temporal summation in cultured rat hippocampal neurons (Margulis and Tang, 1998). The presence of the hyperpolarization-activated currentI_h in pyramidal cell dendrites (Stuart and Spruston, 1998) decreases EPSP amplitude and duration (Magee, 1998).

The experimental evidence suggests that the Na⁺ and Ca²⁺ currents, as well as the mixed Na⁺/K⁺ H-current, play a minor, if any, role for the observed voltage dependence of the EPSP peak amplitude and supralinear summation in the AP cell in the subthreshold range of membrane potential (less than −55 mV) under investigation. (1) The AP cell I–V curve is only marginally changed in 0 Na⁺, 0 Ca²⁺, 1.8 mmCo²⁺ saline (Fig. 5B) but changes significantly with changes in [K⁺]_o. These observations suggest that the slope resistance (Fig.7B) is dominated by the voltage-dependent potassium conductance. (2) The slope of the voltage dependence of the EPSP peak amplitude as a function of membrane potential was reversed when the neurites expressing the Kir conductance were surgically removed (Fig. 6C). (3) The observed voltage dependence of EPSPs as well as the supralinear summation were reproduced qualitatively in a model with the inward rectifier as the sole voltage-dependent conductance (Fig. 7C,D).

Two kinds of postsynaptic receptors—NMDA or conductance-decrease receptors—could cause, in principle, the observed EPSP voltage dependence. We consider both possibilities unlikely. (1) In the AP cell, the EPSP was not affected by 50 μm APV, a NMDA receptor blocker in vertebrates, whereas most of the EPSP mediated by chemical transmission was blocked by 50 μm CNQX, a blocker of AMPA-type glutamate receptors. (2) If the observed EPSPs were caused by a potassium conductance-decrease EPSP (Kobayashi and Libet, 1968; Weight and Votava, 1970; Krnjevic et al., 1971; Kuba and Koketsu, 1976; Ross, 1989), the binding of a neurotransmitter could lead to a decrease in membrane conductance. Such an EPSP would reverse around E_K = −80 mV, and the EPSP half-width is likely be of the order of seconds. Neither of these features were observed in the P-to-AP EPSP (Fig. 3).

The logical possibility that the CNQX-sensitive glutamate receptor channels are themselves voltage dependent is excluded by the observation that in the truncated preparation without the Kir conductance, the EPSP peak amplitude decreases with depolarization (Fig. 6C), consistent with voltage-independent glutamate receptor channels and a decrease in driving force with depolarization. We were unable to measure the reversal potential of the P-to-AP synapse, because depolarizing the AP cells caused spikes and large decreases of the input resistance. However, previous studies ofl-glutamate excitation in leech Retzius cells have shown that glutamate causes a conductance increase in both sodium and potassium ions (James and Walker, 1979). Extrapolation of the change of the voltage response to glutamate excitation with the membrane potential indicated a reversal potential around −10 mV (Mat Jais et al., 1983), close to the value of 0 mV for mammalian AMPA receptors (Johnston and Wu, 1995).

Generalization to other systems

Kir channels are expressed in various invertebrate (Kandel and Tauc, 1966; Benson and Levitan, 1983) and vertebrate neurons (Constanti and Galvan, 1983; Gaehwiler and Brown, 1985; Stanfield et al., 1985;Faber and Korn, 1986; Lasater, 1986; Shingai and Christensen, 1986;Williams et al., 1988; Kawaguchi et al., 1989; Uchimura et al., 1989;Ueda et al., 1992; Dong and Werblin, 1995; Holt and Eatock, 1995;Krapivinsky et al., 1998; Mermelstein et al., 1998; Töpert et al., 1998). In some cases the Kir conductance contributes significantly to membrane conductance at rest. For instance, for neurons of the nucleus accumbens, the Kir conductance has been estimated to account for ∼40% of the resting conductance (Uchimura et al., 1989). The decrease of the EPSP amplitude and width with hyperpolarization, attributable to the activation of the Kir conductance, has been demonstrated in both invertebrate (Kandel and Tauc, 1966) and vertebrate (Kawaguchi et al., 1989) neurons. Thus we expect that the functional significance of the inward rectifier for dendritic integration of multiple synaptic inputs that we observed in the leech AP cell is important in other systems.

Functional role of the inward rectifier

By conducting outward current in the voltage range a few millivolts positive to E_K, Kir channels help to maintain a resting potential near E_K. However, once other depolarizing influences act on the cell, the Kir channels close down, and the membrane potential is free to change (Hille, 1992). The Kir conductance can also have a major integrative effect on a neuron with an extended spatial structure: the Kir conductance acts like a distributed shunting inhibition, reducing the input resistance, increasing the effective dendritic length, and reducing the time constant, thus decreasing the ability of temporally and/or spatially isolated excitatory synaptic inputs to sum effectively. When a dendrite receives sufficient excitatory input to turn off the Kir conductance, the slope resistance and time constant of the cell will increase, which leads to greater temporal and spatial summation of subsequent excitatory potentials, thereby increasing their potency at the spike initiation zone. In addition, the shortened dendritic electronic length effectively makes the dendrites more compact, which allows distal excitatory inputs to begin to influence each other (Wilson, 1992; Nisenbaum and Wilson, 1995).

The question of whether postsynaptic neurons operate as temporal integrators or coincidence detectors is a much discussed issue in computational neuroscience (Jaslove, 1992; Softky and Koch, 1993;Shadlen and Newsome, 1994, 1995; Softky, 1994, 1995; Koenig et al., 1996; Reyes et al., 1996; Geiger et al., 1997; Agmon-Snir et al., 1998). Interestingly, the Kir channel provides the biophysical basis for both modes of summation. On the one hand, because of the deactivation of the Kir conductance with depolarization, multiple EPSPs occurring on the same branch and within a narrow window of time produce a bigger response than would occur if they were on separate branches or occurred outside this time window. Thus, it may be speculated that the Kir channel provides the nonlinearity that favors coincidence detection. On the other hand, because of the deactivation of the Kir conductance with depolarization, the membrane time constant increases with depolarization, thus increasing the integration time and turning the cell into a temporal integrator. As a result, the cell may readily switch from a coincidence detector at hyperpolarized levels (small time constant) to a temporal integrator at more depolarized levels (large time constant) of membrane potential (Nisenbaum and Wilson, 1995).

This appendix provides details on the derivation of Equation 11. In the steady state with I_inj = 0 the membrane potential of the model cell (Eq. 2) is determined by:

$$V=f(V)=\frac{G_L{E}_L+G_{\text{Kir}}(V)E_K+G_{\text{syn}}{E}_{\text{syn}}}{G_L+G_{\text{Kir}}(V)+G_{\text{syn}}},$$ Equation A1

with G_Kir(V) given by Equation 1. The initial membrane potential V_inis given by the same expression, , withG_syn = 0. For simplicity, we consider the case of identical synaptic inputs and seek to find an analytic expression of the measure of summation (Eq. 5), % linearity ≡L × 100, with:

$$L\equiv \frac{{\text{peak}}_{\text{simultaneous}}}{{\text{peak}}_{\text{algebraic sum}}}=\frac{V_{PP}-V_{\text{in}}}{2(V_P-V_{\text{in}})},$$ Equation A2

as an expansion in the synaptic conductance,G_syn, in the limit thatG_syn ≪ (G_L +G_Kir(V_in)). Our procedure is to expand f(V) to second order in both changes in potential, δV ≡V − V_in, and synaptic conductance, G_syn, to obtain the form:

$$\delta V(G_{\text{syn}})\cong {\text{aG}}_{\text{syn}}+{\text{bG}}_{\text{syn}}^2,$$ Equation A3

from which L is given by Equations EA2 andEA3:

$$L=\frac{1}{2} \frac{\delta V(2G_{\text{syn}})}{\delta V(G_{\text{syn}})}\cong \frac{1}{2} \frac{a(2G_{\text{syn}})+b(2G_{\text{syn}}{)}^2}{{\text{aG}}_{\text{syn}}+{\text{bG}}_{\text{syn}}^2}\cong 1+\frac{b}{a} G_{\text{syn}}$$ Equation A4

To first order in the ratioG_syn/(G_L +G_Kir(V_in)) we find:

$$L\cong 1+\left\{{\left[\frac{\alpha }{1-\alpha \frac{(E_L-E_K)}{\gamma }}\right]}^2\frac{(E_L-E_K)}{\gamma }\left[\frac{G_{\text{Kir}}(V_{\text{in}})}{G_L} \frac{(E_{\text{syn}}-E_K)}{\gamma }+\frac{(E_{\text{syn}}-E_L)}{\gamma }\right]+\frac{\alpha }{1-\alpha \frac{(E_L-E_K)}{\gamma }}\left[\frac{G_{\text{Kir}}(V_{\text{in}})}{G_L} \frac{(E_{\text{syn}}-E_K)}{\gamma }+\frac{(E_{\text{syn}}-E_L)}{\gamma }-\frac{(E_L-E_K)}{\gamma }\right]-1\right\} \frac{G_{\text{syn}}}{G_{\text{Kir}}(V_{\text{in}})+G_L},$$ Equation A5

where α is defined as:

$$\alpha \equiv \frac{G_{\text{Kir}}(V_{\text{in}})G_L}{(G_{\text{Kir}}(V_{\text{in}})+G_L{)}^2} \frac{e^{(V_{\text{in}}-V_{1/2})/\gamma }}{1+e^{(V_{\text{in}}-V_{1/2})/\gamma }}.$$ Equation A6

The function α is positive for all values ofV_in and goes smoothly to 0 with both increased hyperpolarization below V_1/2 and increased depolarization above V_1/2. Therefore, summation of synaptic inputs can be supralinear only for a range of potentials that lie close to V_1/2, otherwise:

$$L\cong 1-\left\{\begin{array}{cc}\frac{G_{\text{syn}}}{G_L}& \text{for} V_{\text{in}}\gg V_{1/2}\\ \frac{G_{\text{syn}}}{G_{\text{Kir}}(V_{\text{in}})+G_L}& \text{for} V_{\text{in}}\ll V_{1/2}\end{array}\right.,$$ Equation A7

and the summation is sublinear.

We consider the zero-order limit of two cases for the analytic expression of L (Eq. EA5). In the limit thatG_Kir(V_in) ≫G_L, with implicit restrictions on the value of V_in relative toV_1/2, we find:

$$\alpha \cong \frac{G_L}{G_{\text{Kir}}(V_{\text{in}})} \frac{e^{(V_{\text{in}}-V_{1/2})/\gamma }}{1+e^{(V_{\text{in}}-V_{1/2})/\gamma }},$$ Equation A8

and the value of L, neglecting terms of orderG_L/G_Kir(V_in) and higher, is:

$$L\cong 1+\left[\frac{(E_{\text{syn}}-E_K)}{\gamma } \frac{e^{(V_{\text{in}}-V_{1/2})/\gamma }}{1+e^{(V_{\text{in}}-V_{1/2})/\gamma }}-1\right]\frac{G_{\text{syn}}}{G_{\text{Kir}}(V)};$$

$$G_{\text{Kir}}(V_{\text{in}})\gg G_L,$$ Equation A9

as reproduced in the main text (Eq. 11) using % linearity ≡ L × 100. In the opposite limit,G_L ≫G_Kir(V_in), with implicit restrictions on the value of V_inrelative to V_1/2, we find that:

$$\alpha \cong \frac{G_{\text{Kir}}(V_{\text{in}})}{G_L} \frac{e^{(V_{\text{in}}-V_{1/2})/\gamma }}{1+e^{(V_{\text{in}}-V_{1/2})/\gamma }},$$ Equation A10

and thus L is always <1, i.e.:

$$L\cong 1-\frac{g_S}{G_L};G_L\gg G_K.$$ Equation A11

In general, there will be a critical value that the ratioG_Kir(V_in)/G_Lmust exceed for supralinear summation to occur. This value will clearly change as a function of potential, V_in, and as shown above (Eq. EA7), outside of a range of potentials nearV_1/2 there will be no supralinearity.