Fine-Grained Provenance for Matching & ETL

Abstract

Data provenance tools capture the steps used to produce analyses. However, scientists must choose among work-flow provenance systems, which allow arbitrary code but only track provenance at the granularity of files; provenance APIs, which provide tuple-level provenance, but incur overhead in all computations; and database provenance tools, which track tuple-level provenance through relational operators and support optimization, but support a limited subset of data science tasks. None of these solutions are well suited for tracing errors introduced during common ETL, record alignment, and matching tasks – for data types such as strings, images, etc. Scientists need new capabilities to identify the sources of errors, find why different code versions produce different results, and identify which parameter values affect output. We propose PROVision, a provenance-driven troubleshooting tool that supports ETL and matching computations and traces extraction of content within data objects. PROVision extends database-style provenance techniques to capture equivalences, support optimizations, and enable selective evaluation. We formalize our extensions, implement them in the PROVision system, and validate their effectiveness and scalability for common ETL and matching tasks.

I. INTRODUCTION

Data science’s need for rigor, consistency, and reproducibility has spurred the development of tools for capturing data provenance. Today, there are three “families” of provenance techniques [7], each making different trade-offs. Workflow provenance [12], [21], [23] techniques handle complex work-flows consisting of arbitrary “black box” modules. Yet they only capture coarse-grained (file-process-file) relationships, which limits their ability to “explain” specific outputs. Provenance API techniques [28] allow programmers to manually instrument code with API calls, thus revealing fine-grained tuple-to-tuple provenance. However, such APIs impose overhead over all computations, and they produce provenance that depends on the order of evaluation of operations. Database-style techniques [2], [7], [11], [18] leverage and extend the provenance semiring model to capture provenance through standard relational operators. Here, (bag-)equivalent query expressions, as produced by a query optimizer, yield equivalent provenance. A variety of middleware [11], [18] and custom query-engine-based [28] solutions have been developed, as have extensions to the relational aspects of Hadoop, Pig, and Spark [1], [16], [17], [20].

A major source of irregularity in data science (encountered in our collaborations with biologists) occurs in information extraction, matching, ranking, and ETL workflows, where data (or features) are pulled from files and objects, records are aligned or mapped against a reference dataset, and results are used for tasks such as OLAP, machine learning, and data visualization. This may involve commercial or open-source ETL tools; dataframe operations in Python or R; or custom scripts and binaries. We develop techniques applicable to all of these settings; our implementation targets scripts and code. Sometimes extraction is done incorrectly, or different workflow executions produce different results due to (undocumented) parameters, or workflow module changes result in inconsistent outputs. Unfortunately, existing techniques do not help troubleshoot such issues. Workflow provenance is too coarse-grained to help troubleshoot issues. Provenance APIs require recompilation of often-large source code bases, incur overhead in recording every derivation in advance, and are sensitive to changes in execution ordering. Database-style techniques hold promise, but do not trace through information extraction-style operations over content within arbitrary datatypes such as strings, binary objects, and images, do not handle user-defined functions, and require that the computation occur in a DBMS or “big data” engine. Moreover, for operations that choose top-k items from within a group, we may need to know both which inputs were selected for the output and which parts of the data were also candidates) in order to create test cases that reproduce behavior.

This paper develops a solution with the optimizability and the potential for on-demand computation provided by database-style techniques, the ability to instrument user-defined code offered by provenance APIs, and general applicability across languages and datatypes used in science. Our work adapts and extends database-style techniques to address a broad class of ETL-style workflows, including record linking, matching against a reference dataset, and data cleaning. Such tasks — in order to scale — rely on relational algebra-like operations, techniques for data partitioning (sharding, blocking), and (typically deterministic) user-defined functions to extract, match, rank, and select. Our PROVision system reproduces fine-grained, record-to-record provenance across a wide variety of ETL and data processing workflows. Our contributions are as follows:

• Extensions to semiring provenance [15] to handle tracking of extraction from a wide variety of structured files and objects — using a single formalism and framework.

• Support for user-defined blocking, transformation, and ranking functions – with datatype-specific optimizations.

• Semantic descriptors based on algebraic operators, to recompute provenance on demand.

• Strategies for optimizing provenance computation, when troubleshooting results, explaining differences, and discovering parameter settings.

• Experimental validation of our techniques’ performance and scalability, versus alternative methods.

Section II highlights prior work. Section III outlines our need to explain differences and detect parameter values in matching and extraction workflows. We propose our operators and provenance model in Section IV, then study optimization in Section V. Section VI uses provenance to troubleshoot differences across workflow versions and recover missing parameters. We evaluate PROVision’s performance in Section VII, and conclude and describe future work in Section VIII.

II. PRIOR WORK

We build upon the literature in the database provenance space [7], particulary provenance semirings [2], [14], [15] that capture fine-grained provenance through relational algebra operators, while preserving the algebraic equivalences used by query optimization. Our novelty is in extending the semiring model to user-defined functions (UDFs), specifically tracking the extraction of sets of values from within user-defined datatypes, and in supporting functions that perform operations such as blocking, approximate matching, and ranking. Like Smoke [25], we develop an implementation, PROVision, based on our own query processing engine — as opposed to using a standard DBMS [11], [18] that is ill-suited to external data and structured scientific file formats, or an instrumented “big data” engine based on Hadoop, Spark, or Pig [1]. Our implementation enables the UDFs to specify what items in an object or a group were “sub-selected,” while also capturing the relationship to the broader object or group. In contrast to SubZero’s [28] or to event logging [22], [22], [27], our model captures equivalences among computations (including equivalences that hold for particular datatypes and UDFs). PROVision’s query optimizer exploits these to “trace” provenance and aid in troubleshooting.

We study finer-grained provenance than scientific work-flow management systems such as Taverna [23], Kepler [21], VisTrails [5], and Galaxy [12]. However, we are limited to relational-style operators augmented by “gray-box” operations, where key functionality is described in tuple- or tuple-group-based user-defined functions.

III. PROBLEM AND APPROACH

Conventional provenance tools do not adequately support detailed reasoning about common ETL-style, matching, and ranking tasks because they are limited to tuple-level operations and they do not support approximate matching or sub-selection. Our study of this problem is motivated by biomedical collaborators who operate a gene sequencing center. Their sequencing machine generates files with lists of text strings representing gene sequence reads. The data is analyzed via a workflow built from open-source tools written in different languages (C, Python, shell scripts). A key stage is sequence alignment: much like a record linking tool, the aligner module reads strings from the sequence machine’s output and compares them against sequences in a reference genome file. It outputs a list of pairs describing the best matching. This gene sequence alignment workflow is specified via a shell script that executes the modules with appropriate command-line parameters, input files, and outputs. Unfortunately, two novel problems arise as the same workflow script is run at collaborating sites.

Version Inconsistency:

As workflow modules or reference datasets are updated, input data gets processed slightly differently. Prior and current workflow versions may produce results that differ in subtly different ways — pointing to a likely bug in one or both versions of the software! This problem requires debugging by a human expert — given a small input test case. Changes in output records can be computed using a standard “diff” tool¹ as in data versioning systems [29] and diff tools [4]. Our goal is to identify sets of inputs that can be used to reproduce those different outputs (assuming the tools are deterministic). In order to deterministically reproduce the exact same ranking and choice among potential outputs, for many matching algorithms our input set must include not only those inputs that directly contributed to the outputs, but other “candidate” inputs that were considered but discarded within the same group, block, or ranking computation.

Missing Parameters:

Many scientific workflows are built from shell scripts, which execute binaries with command-line parameters. It is straightforward to instrument such scripts to capture the majority of provenance information. However, some configuration parameters (e.g. thresholds) are often specified in local configuration files (e.g., in /etc), and these are often missing from the data and provenance shared across a data lake or distributed filesystem. Given output produced by the workflow with unknown parameters, we might be able to reverse engineer which parameter values produced that output. If we understand the operation of the workflow, we can test over a carefully chosen subset of the input data.

A. Reconstructing Provenance Information

Workflow modules for data science take many forms. Our focus is on ETL, content extraction, and approximate matching-style computations, where fine-grained provenance helps diagnose issues. Such computations have been optimized for I/O performance. Our collaborators do not want to incur the significant (factor-of-two or greater) overheads required in recording provenance as computation occurs [28], when they only occasionally need to debug a few answers. Rather than instrumenting individual workflow modules to get fine-grained provenance, we instead develop methods to later recompute provenance rapidly and on-demand, using declaratively specified implementations of the workflow modules that, while not as fast as the original code, allow us to selectively compute only the needed provenance. A PROVision user may (1) trace provenance back to inputs and data sub-objects extracted or matched from the inputs; (2) isolate subsets of inputs that, taken together, produce different outputs across workflows; (3) for certain cases, find parameter values if these were not captured in provenance.

To achieve this, we associate with each workflow module a descriptor. Each descriptor algebraically expresses how the original module extracts structured content from the files; filters, combines, processes, and transforms this content; and/or joins and aggregates results, all with user-defined code. The operations within the descriptor attach provenance information to their outputs (similar in spirit to Smoke [25]).

B. The PROVision System

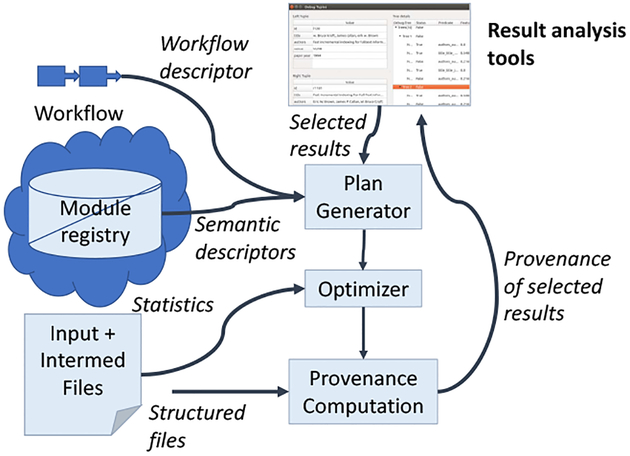
The PROVision system provides tools for reconstructing provenance to improve data consistency. PROVision is given a workflow, input and intermediate files, and records selected by the user. It selectively produces record-level provenance for outputs, subsets of data that produce differences across workflow versions, and values for missing parameters. It is comprised of the modules shown in Figure 1.

Fig. 1:

PROVision system architecture.

Module Registry.

PROVision looks up the workflow modules in a central repository² to find accompanying semantic descriptors. Each descriptor, stored as a JSON file, specifies inputs and data formats, a tree of relational algebra operators (a semantic descriptor, Section IV), and optional user-defined code (or links to code) for the operations.

Plan Generator.

Given the coarse-grained provenance and semantic descriptors from a workflow run, the plan generator builds an initial plan for computing provenance. This query plan makes selected calls to user-defined code for similarity matching, ranking, etc.

Optimizer.

A query rewrite-based [13] optimizer then takes cost information gathered from the original workflow provenance and data, as well as any user selections for results of interest, and generates a more efficient plan. Our optimizer aggressively uses a semijoin-based optimization technique to prune intermediate results (Section V-C).

Provenance Computation.

PROVision executes the query plan using a custom query engine (Section V-B), which works over external files, interfaces with external code, and reproduces workflow results annotated with provenance.

Result Analysis Tools.

Interactive tools (Section VI) enable the user to select records (e.g., those that differ workflow versions) to trace back to their inputs, and to rapidly reconstruct missing parameter values.

IV. SEMANTIC DESCRIPTORS

Workflow modules are arbitrary data-driven programs, invoked with parameter lists, typically operating with structured files as inputs and outputs. Our goal is to describe, using a more tractable specification, the data processing operations being performed within the module — such that we can trace from individual “records” within the output file, back to input “records” in the input file(s). We term this simplified specification a workflow module descriptor.

Key assumptions.

While “re-implementing” workflow modules sounds complex, our task is often easier than full reimplementations like in Smoke or Lipstick. We leverage several factors: (1) many ETL tasks are in fact relational operations; (2) many others are open-source and their “core logic” is already modularized into a function or library, as in our real use cases; (3) many operations within workflow modules, such as those over strings or images, share implementations; (4) workflows share modules. To use PROVision, an expert must instrument key functions such as substring extraction or image clipping, which can be done once per datatype per language; and identify the main code module(s) used to perform key logic such as top-k ranking or approximate matching. This is easy for data-driven code but may be challenging in other settings; we study this in Section VII.

Each workflow module descriptor is specified as a query in an extended relational algebra; operators compute and maintain provenance. We leverage techniques developed for database provenance, but make key innovations in provenance-preserving query operators that invoke user-defined functions to compute new attributes and/or extract multi-valued content embedded within composite (possibly binary, free-text, image, or substring) attributes.

Expressiveness.

We build upon the relational algebra, so our techniques do not capture Turing-complete programs. We target ETL-style operations like extraction of content from data, blocking and binning of records, attribute-to-record transformations, and arbitrary computations over groups of tuples. We develop a unified provenance framework for deterministic extraction, ranking, and transformation operations over many composite datatypes (e.g., strings, images, volumes, trees, binary objects) and collections thereof. We merely assume operations return sets of sub-selected items as fields or records. As formalized in the next section, our only requirement is that each operation can be subdivided into deterministic sub-operations that (a) determine a set of values to be extracted into separate sub-records (e.g., extractions of substrings) and return a set of index markers (“location specifiers” such as bounding boxes) from which the sub-records were extracted; (b) return the sub-records corresponding to individual location specifiers. Our approach can leverage known equivalences that hold for compositions of operations.

Novel requirements.

Our algebra and provenance model build upon the database provenance literature [15], [18], producing results annotated with provenance polynomial expressions in the provenance semiring model. Here, logically equivalent query plans produce algebraically equivalent provenance polynomial expressions. Thus, like Smoke [25], we incorporate SPJU+GROUP operators, but we exploit algebraic equivalences (Section VII-A). Additionally, most ETL and data matching tasks involve user-defined functions, to extract and transform content from composite data (e.g., a nested object in a structured file) or return items from a group (e.g., by choosing top-k items from a set). This requires us to develop a comprehensive treatment for interfacing with user-defined functions, such that we can determine not only what their atomic input values are, but also what we term locations — datatype-specific specifiers of projections, such as subsets, ranges, and bounding boxes — within specific inputs. Importantly, we allow the definition of type- and operation-specific equivalence rules to support optimization.

Insight: Content extraction as a dependent join.

Semiring-style database provenance does not handle “unnesting” or extraction operations over complex datatypes. Yet ETL tasks and scientific workflows operate on JSON/XML, structured files, images, raw text, and even (e.g., in genetics) substrings. We must represent extraction and transforms over any of these formats. To do this, we still assume a tuple-based processing model, possibly of bindings to content (subtrees in XML, faces in an image, or substrings in gene sequences). Now, if input tuples contain (bindings to) objects such as images, objects, trees, or text; a content-specific extraction operation takes one such value at a time, and extracts a set (relation) of values. The input tuples and extracted results are semantically linked by the function call, just as, in data on the web, a parameter to a web service call is linked to the returned results. We propose that the “right” abstraction of this dependency is the dependent join [10], previously used in the data integration literature to represent external function calls. In our case the function returns a set of values for each input: the dependent join is with a relation, not merely a function. This abstraction incorporates table-valued UDFs into the semiring provenance model. This abstraction allows us to formalize the semantics of provenance, but does not reflect how we implement UDFs.

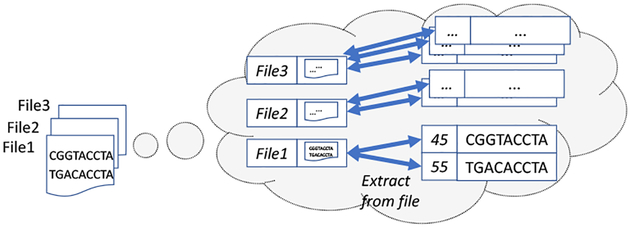
Example 4.1: Figure 2 illustrates extraction of gene sequences. Given a list of (name, content) tuples corresponding to files in the data lake, for each such tuple a file format reader extracts sets of (location, sequence) pairs. We capture this as a dependent join between the input 〈file, object〉 tuples and the set of extracted 〈location, sequence〉 tuples, where the location is relative to the file.

Fig. 2:

Extracting data from structured files: read a sequence of 〈filename, object〉 pairs from the data lake, then join these results with the extracted records within the objects.

A. PROVision Data Model and Algebra

We describe a workflow’s data processing modules using algebraic expression trees that filter, combine, and extract data, starting from raw input data that is stored in files or is remotely accessible via URLs, and resulting in structured outputs.

In a relational DBMS setting, queries (and their provenance) are derived from a set of 1NF base relations. PROVision uses a bag-of-tuples data model with support for binary objects³. Given that PROVision operates in a file-based environment, we instead assume that all of our base data is maintained in a “data lake.” This data lake stores (URL, object) pairs in a single relation $\mathcal{L}(key,value)$. Data values are often composite binary objects (BLOBs), such as structured files, so we make no assumption that our data is in 1NF. As in prior work [14], each tuple in the data lake, $\overline{t}$, is annotated with a provenance token $\text{Prov}〚\overline{t}〛$, a unique, opaque tuple ID.

1). Core Relational Algebra:

PROVision implements bag relational selection, projection, join, union, and distinct (extraction, nesting, and grouping are described later). Selection and join predicates may test attribute equality-by-value and equality-by-reference. For each output tuple $\overline{t}$, each algebra operator creates an annotation, denoted, $\text{Prov}〚\overline{t}〛$, that is a provenance polynomial from the semiring model [15]. Briefly, we assume a unique variable or token associated with each base tuple, which represents any provenance metadata “attached” to that tuple. Each time we derive a new tuple via a relational algebra operation, this new tuple will be annotated with an algebraic, polynomial expression derived from the annotation of the input tuple(s). The expressions are computed as follows:

• For a select expression σ_ϕ (R), for each tuple $\overline{t}\in R$ satisfying $\varphi (\overline{t})$, its provenance expression is $\text{Prov}〚\overline{t}〛$. (Provenance is unchanged by selection.)

• For a (bag) project expression Π_α(R), for each tuple $\overline{t}\in R$, its provenance expression is $\text{Prov}〚\overline{t}\left[\alpha \right]〛$.

• For each output ${\overline{t}}^{\prime }$ from a join expression R ⋈ _θ S, for each tuple pair $t_1^{-}\in R$, $t_2^{-}\in S$ satisfying $\theta \left(t_1^{-},t_2^{-}\right)$, its provenance expression is $\text{Prov}〚t_1^{-}〛\cdot \text{Prov}〚t_2^{-}〛$.

• For a (bag) union expression R ∪ S, for each tuple $\overline{t}\in R\cup S$, its provenance expression is $\text{Prov}〚\overline{t}〛$.

• For a result ${\overline{t}}^{\prime }$ output by a duplicate removal expression, distinct(R), if $t_1^{-},\cdots t_m^{-}\in R$ and all m tuples are equal, $t_1^{-}=\cdots =t_m^{-}$, then $\overline{t^{\prime }}’s$ provenance expression is $\text{Prov}〚{\overline{t}}_1〛+\cdots +\text{Prov}〚{\overline{t}}_m〛$.

Example 4.2: Suppose we have a relational algebra expression distinct(Π_α,y(R ⋈_c=x ϕ_x<5(S))), applied to schema Σ = {R(a, b, c), S(x, y)}, and tuples R(1, 2, 3), R(1, 4, 3), S(3, 4) with provenance tokens p₁, p₂, and p₃, respectively. The result t(1, 4) has provenance Prov[[t]] = p₁ · p₃ + p₂ · p₃, representing that the derived result is generated twice, from the first-and-third and second-and-third base tuples.

2). Novel Operators for User-Defined Functions:

ETL tasks often invoke non-declarative code to extract embedded content within an input object, or to compute a value over some fields of a record. We assume our query plan embeds this logic in the form of a user-defined function (UDF) modeled after the original workflow module, but (as we describe below) that our UDFs additionally provide a limited amount of information about the provenance of any result being computed.

Since some UDFs can be applied to sets of tuples as a result of grouping, and others can be applied to single tuples at a time, we develop separate operators for each (the group-by and compute operations, respectively). We define the operators using the same basic ideas.

Example 4.3: Suppose function fn(x, y) returns a set of pairs (a, b). We model this as a relation from inputs to outputs, R(x^b, y^b, a^f, b^f). We can then represent a function call to f, based on the contents of relation S(u, v) as a dependent join, $S{\bowtie }_{u,v}^{\to }R$, whose results will have the schema (u, v, a, b).

Definition 1 (Scalar UDF operator): The scalar UDF operator, compute, evaluates one tuple $\overline{t}$ at a time, computing a function fn over the fields $\overline{t}\left[\overline{\alpha }\right]$, returning a list of attributes $\overline{\beta }:{\mathit{compute}}_{fn,\overline{\alpha },\overline{\beta }}(R)$. The input parameters to fn must match the arity and types of $R[\overline{\alpha }]$.

The scalar UDF operator is extremely useful for building query plans with extraction functions, and for query optimization. However, we will (in the next 2 sections) need to define the provenance for its outputs. Here it is useful to note that the scalar UDF can be modeled using the dependent join (hence, a standard join for which provenance is well understood), as follows. Let us represent function fn as a relation R_fn, whose schema is $\overline{\alpha }\cup \overline{\beta }$, where $\overline{\alpha }$ are all bound and $\overline{\beta }$ are all free. ${\mathit{compute}}_{fn,\overline{\alpha },\overline{\beta }}\left(R\right)$ can then be rewritten as a dependent join $R{\bowtie }_{\alpha }^{\to }{R}_{fn}$.

Definition 2 (Grouping UDF operator): The grouping UDF operator, group, partitions the input relation R into sets of tuples sharing the same values for grouping fields R[G]. For each set of tuples, it then applies a series of aggregate functions, FN₁ through FN_m over projections ${\overline{\alpha }}_1$ through ${\overline{\alpha }}_m$, respectively; returning values ${\overline{\beta }}_1$ through ${\overline{\beta }}_m$. We denote it as follows:

$$grou{p}_{G,\left(F{N}_1,{\alpha }_1^{-},{\beta }_1^{-}\right),\dots ,\left(F{N}_m,{\alpha }_m^{-},{\beta }_m^{-}\}\right)}\left(R\right)$$

Unlike with the scalar UDF case, aggregate functions are second-order and we cannot capture the full semantics using select/project-join expressions. However, for each set of tuples T ⊆ R belonging to a group (i.e., sharing the same values for all grouping fields G), the output of the grouping operator is a join between the portion of the tuple corresponding to the grouped fields, and the results of applying each function to the set of tuples:

$$distinct(T[G]){\bowtie }_{G}F{N}_1(T)\cdots {\bowtie }_{G}F{N}_m(T)$$

This is similar to the scalar UDF operator, but results in a bag of tuples (namely, a Cartesian product between the grouping tuple and the outputs of each of the m aggregate functions.) Note that each α term consists only of attributes from R so the order of evaluation of the functions does not matter.

Example 4.4: Suppose we are given two aggregate functions, min, which returns the minimum value among a collection of values (and is modeled as relation R_min(x^b, m^f), and the table-valued function top2, which returns the two largest values among a collection of values (modeled as relation R_min(y^b, t^f). Given an SQL query:

SELECT id, average(x), top2(y)
FROM r GROUP BY id

and a table r with values r(1, 2, 3), r(1, 3, 4), r(1, 4, 2) and r(2, 3, 4). The group with id = 1 has three tuples r(1, 2, 3), r(1, 3, 4), and r(1, 4, 2). The grouping tuple will simply be comprised of the grouping attribute: (1). The function average will be called on the values of x, {2, 3, 4} and will return a single unary tuple (3). The function top2 will be called on the values of y, {3, 4, 2} and will return unary relation {(4), (3)}. The ultimate output for this group will be the Cartesian product of these three intermediate relations, which will result in the two tuples (1, 3, 4) and (1, 3, 3).

B. Provenance for Extraction of Nested Content

Unlike the standard relational queries studied in much of the prior work on fine-grained provenance, ETL workloads do not start with records in their fully parsed form. Thus they often take as input a “BLOB” (Binary Large OBject) of binary or string data, and apply an extraction function (or path expression) to the data within that object. For instance, we may extract segments of comma-separated text into different fields, or we may apply an information extraction function to find mentions of dates in an HTML file. These are common use cases for PROVision’s scalar UDF operator, which takes a tuple at a time, applies a user-defined function, and returns a set of tuples representing the extractions. The scalar UDF operator can additionally be useful in allowing a workflow to apply transformations from tuples to tuples (e.g., converting fields from one unit to another) or sets of tuples (e.g., extracting words from lines of text).

Recall that every object in our data lake has a unique provenance token. Every derived SPJU tuple has a provenance semiring polynomial expression in terms of these tokens, as described at the start of this section. We capture the provenance of each tuple as an expression over the provenance of its source tuples. Now, we exploit the observation in the previous section that the scalar UDF operator is a form of a (dependent) join. However, the extraction UDF itself adds a wrinkle: indeed a UDF takes zero or more arguments from an input tuple, and produces a set of results. However, the UDF often only uses a portion of the data in each input tuple’s fields: for instance, it may extract a substring or a sub-region. To precisely capture the provenance in this setting, we need a datatype- and UDF-specific way of capturing the subsets of data used within attributes.

1). Type- and UDF-specific Provenance:

Let us assume the presence of a location specifier and value extractor for a given attribute x and function fn.

Definition 3 (Location specifier): A location specifier L_a,fn, is a datatype- and operation-specific token — typically a range, bounding box, or predicate — for use in extracting a value from a subset of an attribute value a.

This is similar to a provenance token, but deterministically applies to a piece of non-relational data returned by an operation. To more precisely capture this, we factor function fn into the composition of two subfunctions, fn = fn′ ○ v where v is a value extractor function that takes a series of location specifiers (one per input argument to fn), and fn′ is the UDF rewritten based on the outputs of the value extractor.

Definition 4 (Value extractor): A value extractor for function f, $v_{fn,\overline{x}}(\overline{t},\overline{L})$ is an operation that, given a tuple $\overline{t}$ and a vector of location specifiers for each attribute in $\overline{x}$, $\overline{L}$, returns a list of subsets of $\overline{t}[\overline{x}]$ from which $fn(\overline{x})$ can be computed.

The value extractor is akin to a selection operation in the relational algebra: it returns a subset of the input data, which is used by the transformational or computational aspects of UDF f. Together, these allow us to express the provenance of extractions (where each location specifier might represent an index key or projection) or transformations (where each location specifier represents an input). fn(x) which,

Proposition 1: Assume a deterministic UDF for any instance a of attribute(s) x, returns results $fn\left(a\right)\text{=}\left[r_{a,1},\dots ,r_{a,k_a}\right]$. Suppose we can factor fn into composable sub-functions fn′ ○ v, such that given a sequence of location specifiers $L{S}_a=\left[L_{a,1},\dots ,L_{a,k_a}\right]$, fn′(v(LS_a)) = fn(a), for 1 ≤ i ≤ k_a. Then if we can instrument our UDF to produce LS_a for any value of a, our model captures the provenance of fn(x). (Proof is by contradiction.)

Example 4.5: For a CSV string CATGGCCG,alpha, a location specifier might be the interval [0, 7]. The value extractor may simply be the substring function, which takes a string from the CSV file (e.g., CATGGCCG,alpha) and the location specifier, and returns all characters within that interval (CATGGCCG).

We assume our value selector is defined in a way that is independent of any specific input record. Given this, and the ability to compare location specifiers according to a partial ordering on restrictiveness, we can also define a minimal location specifier to be the most restrictive location specifier $L_{a_{min}}$ for a given value a, which still returns the same output f′ (v(a)) = f(a). For instance, the minimal location specifier may represent the smallest substring from which a value is computed, or the minimum bounding box.

2). Composing Provenance:

We also want the provenance of the output of our UDF operators to be the composition of each input tuple’s provenance, along with its location specifiers. Given function fn which takes parameters a₁, … , a_m and returns a set of (zero or more) R_fn(b₁, … , b_q) tuples:

$$fn\left(a_1,\dots ,a_m\right)\mapsto R_{f{n}_{out}}\left(b_1,\dots ,b_q\right)$$

we define the provenance of each output tuple $\overline{t}$ as a provenance function combining the provenance of the base tuple, plus the UDF-specific provenance of the prior section:

$$P_{fn}\left(\text{Prov}〚\overline{t}〛,L_1,L_2,\dots ,L_m\right)$$

where P_fn represents a function symbol in the provenance semiring specific to our function fn. (We later allow for specific algebraic equivalence to be associated with the provenance functions, for query optimization purposes.)

Finally, each output of the scalar UDF function represents the (dependent) join of the input tuple with each output tuple returned from the function, i.e., it is the provenance expression:

$$\text{Prov}〚t〛\cdot P_{fn}\left(\text{Prov}〚\overline{t}〛,L_1,L_2,\dots ,L_m\right)$$

Example 4.6 (Blocking): A key operation in record linking [9] (as well as string and gene sequence alignment) is known as blocking. Given the cost of performing a full comparison between all pairs of tuples, blocking is used to prune the set of comparisons to those with common features. Each tuple is associated with one or more blocks, and all tuples within a block are combined for a similarity comparison. A common blocking function is the n-gram, where all subsets of up to n tokens are returned as candidate blocks. (Each tuple may have multiple blocks, in contrast to a hashing function.)

Given a tuple (′smith′, 123) with provenance token p₀, and a scalar UDF returning all trigrams, fn_3gram, applied to the first attribute, we will get the results and provenance:

block	name	id	provenance
__s	smith	123	p0 . P3gram (p0 , [−2, 0]) p0 . P3gram (p0 , [−1, 1]) p0 . P3gram (p0 , [0, 2]) p0 . P3gram (p0 , [1, 3]) ⋮
_sm	smith	123
smi	smith	123
mit	smith	123
⋮	⋮	⋮

Observe that the provenance column represents the product of the input tuple with a provenance function (for fn_3gram) and a location specifier representing the index positions of a substring. We assume here that index positions that are out of string bounds are filled in with blank ‘_’ characters.

C. Provenance for Aggregates

We now consider another type of user-defined function, which takes a set of tuples as its input. Classically, this is an aggregate function in SQL. However, many types of matching, ranking, and approximate join operations, such as record linking [3], [9], [24], can be captured using a combination of (1) computing, via the scalar UDF function, a set of one or more blocks for each input record, as in our prior example, (2) joining tuples within blocks, forming a Cartesian product among these, (3) and then performing a ranking or thresholding function over the collection of joint tuples within the block to find the most promising matches. The grouping UDF operator is critical to this third step.

To define provenance for each output from the grouping UDF operator, we note that aggregate functions are generally divided into exemplars — input tuples whose output appears in the output — and summaries — where all of the input tuples are combined to produce an output. For summaries, the provenance should clearly be based on the provenance of all of the input tuples. For exemplars, there is a choice between capturing the provenance of all tuples whose values affect the output, and all tuples whose values were considered in producing the output. In either case, we can define a notion of relative provenance, similar to that in Section IV-B. This will represent a combination of the provenance of the input group (e.g., the semiring sum of the provenance expressions of the input tuples) with a notion of type- and operation-specific provenance.

For each aggregate function FN(a₁, … , a_q) applied to a group of tuples T , we get a result tuple whose provenance is:

$$P_{FN}\left(\sum _{\overline{t}\in T}\text{Prov}〚\overline{t}〛,\sum _{t_i^{-}\in T}\langle L_{i,1}\left(t_i\left[a_1\right]\right),\cdots ,L_{i,m}\left(t_i\left[a_q\right]\right)\rangle \right)$$

Recall from Section IV-A2 that we can express the computation done by the grouping UDF operator for each group of tuples T ⊆ R, with multiple functions FN₁ … FN_m, as a series of joins:

$$distinct(T[G]){\bowtie }_{G}F{N}_1(T)\cdots {\bowtie }_{G}F{N}_m(T)$$

Thus, the output provenance for each aggregate tuple, based on a group of tuples T ⊆ R, is a product of the form:

$$\begin{gathered} \sum _{\overline{t}\in T}\text{Prov}〚\overline{t}〛 \\ \cdot P_{F{N}_1}\left(\sum _{\overline{t}\in T}\text{Prov}〚\overline{t}〛,\sum _{t_i^{-}\in T}\langle L_{i,1}\left(t_i\left[a_{y_{1,1}}\right]\right),\cdots ,L_{i,m}\left(t_i\left[a_{y_{1,q}}\right]\right)\rangle \right) \\ \mathrm{\dots } \\ \cdot P_{F{N}_m}\left(\sum _{\overline{t}\in T}\text{Prov}〚\overline{t}〛,\sum _{t_i^{-}\in T}\langle L_{i,1}\left(t_i\left[a_{y_{m,1}}\right]\right),\cdots ,L_{i,m}\left(t_i\left[a_{y_{m,q}}\right]\right)\rangle \right) \end{gathered}$$

Example 4.7 (Aggregation): Suppose we are matching tuples in two relations: A(‘smith′, 123), B(′smythe′, 345), B(′simpson′, 456) with provenance tokens p₀, p₁, p₂, respectively. We use f_3gram to compute a block for each tuple, and we join candidate matches on the block ID.

block	name1	name2	id1	id2	provenance
__s	smith	smythe	123	345	p0 . p1 . P3gram (p0 . p1 , 〈[−2, 0]〉 + 〈[−2, 0]〉) p0 . p2 . P3gram (p0 . p2 , 〈[−2, 0]〉 + 〈[−2, 0]〉) p0 . p1 . P3gram (p0 . p1 , 〈[−1, 1]〉 + 〈[−1, 1]〉) ⋮
__s	smith	simpson	123	456
_sm	smith	smythe	123	345
⋮	⋮	⋮	⋮	⋮

Finally, for each block, we return the highest-scoring pairwise match (top1). We can visualize an intermediate point in the computation. For instance, for block_s, the result would be (‘smith′, ‘smythe′, 123, 345) given that its string edit distance is the lowest in this block. Note that the provenance of the output result would be:

$$\left(p_0\cdot p_1+p_0\cdot p_2\right)\cdot p_{top1}\left(\left(p_0\cdot p_1+p_0\cdot p_2\right),\langle p_0\cdot p_1\cdot p_{3gram}\left(p_0\cdot p_1,\langle \left[-2,0\right]\rangle +\langle \left[-2,0\right]\rangle \right)\rangle \right)$$

D. Algebraic and Provenance Equivalences

Our algebra exhibits all of the standard equivalences for the relational algebra: join associativity and commutativity, selection pushdown, distributivity of join through union, and group-by/join pushdown [6]. Moreover, our UDF operators show certain equivalences, shown in Table I. (We require that UDFs, while effectively black-box, be deterministic.)

TABLE I:

UDF operator equivalences

Commutativity
$\begin{array}{l}{\mathit{group}}_{G,g,{\alpha }_g,{\beta }_g}\left({\mathit{group}}_{G,f,{\alpha }_f,{\beta }_f}(R)\right)\equiv \\ {\mathit{group}}_{G,f,{\alpha }_f,{\beta }_f}\left({\mathit{group}}_{G,g,{\alpha }_g,{\beta }_g}(R)\right)\end{array}$	if αg ∩ βf = ∅˄ αf ∩ βg = ∅
${\mathit{compute}}_{g,{\alpha }_g,{\beta }_g}\left({\mathit{compute}}_{f,{\alpha }_f,{\beta }_f}(R)\right)\equiv {\mathit{compute}}_{f,{\alpha }_f,{\beta }_f}\left({\mathit{compute}}_{g,{\alpha }_g,{\beta }_g}(R)\right)$	if αg ∩ βf = ∅˄ αf ∩ βg = ∅
Compute/Group
${\mathit{compute}}_{g,{\alpha }_g,{\beta }_g}\left({\mathit{group}}_{G,f,{\alpha }_f,{\beta }_f}(R)\right)\equiv {\mathit{group}}_{G\cup {\beta }_q,f,{\alpha }_f,{\beta }_f}\left({\mathit{compute}}_g,{\alpha }_g,{\beta }_g(R)\right)$	if αg ⊆ G, αg ∩ βf = ∅˄ αf ∩ βg = ∅

A virtue of the provenance semiring model is that algebraic equivalences used in query optimization (e.g., commutativity of joins) result in equivalent provenance. We are interested in arbitrary datatypes and UDFs, for which equivalences may or may not hold. Our PROVision system allows an expert to provide type-and-operator-specific equivalence rules. We describe here an important class of datatypes for which we pre-encode equivalence rules for provenance expressions: types with hierarchical containment and operators that project locations. Table II shows some properties that hold for several common cases: namely, strings, images, and trees.

TABLE II:

UDF type/operator provenance equivalences

Strings and substrings
Prov〚substringc,d(substringa,b(S))〛≡ Prov〚substringa+c,a+d(S)〛	if c, d ≤ b − a
Images and Cropping
Prov〚crop(x3,y3),(x4,y4) (crop(x1,y1),(x2,y2)(I))〛≡ Prov〚crop(x1+x3,y1+y3),(x1+x4,y1+y4)(I)〛	If x3, x4 ≤ x2 – x1 ˄y3, y4 ≤ y2 – y1
Trees and simple path expressions
Prov〚pathevalx(pathevaly(T))〛≡ Prov〚pathstepx/y(T)〛

V. PROVENANCE RECONSTRUCTION

We now describe how we implement a query processor for efficiently reconstructing fine-grained provenance.

A. Generating the Initial Execution Plan

As alluded to in Figure 1, PROVision first take the various modules executed in the workflow, looks up each of these in the module registry to retrieve its semantic descriptor. The semantic descriptor specifies the schema and file formats for input and output results. Most importantly, it specifies a tree of algebraic operators (Section IV) for the module — as well as links to any external files and code that must be retrieved to execute any associated user-defined functions. Our implementation supports code written in Python, Java, and C.

B. Engine for Provenance Reconstruction

In our early explorations of the design space for PROVision, we considered building over or extending existing open-source query processors. However, most of the use cases for PROVision are based on data in files, we needed to support user-defined functions in several different languages, and we needed the operators to compute provenance. Hence PROVision has its own custom query engine implemented in Java, built to use pipelined execution over “batches” of tuples, and support for UDFs written in Python, C, and Java. (Our engine uses JNA and Jython to interface with external code.)

The query engine is built using an iterator model, in which tuples are recursively requested from root to child operators. Every tuple carries a unique provenance polynomial expression, itself stored as an in-memory expression (tree) with references. As input tuples are composed within an operator (e.g., a join) to produce output tuples, the output tuples are annotated with polynomial expression trees composed from the inputs (linked by reference, thus avoiding copying). We found that “carrying” the polynomials along with the tuples, produced the best performance within a pipelined query engine; methods for storing the provenance in a separate subsystem added significant overhead due to value copying.

C. Optimizing Provenance Reconstruction

The initial execution plan is optimized based on costs, using rewrite rules. Our query optimizer is built in the style of Volcano [13]: it supports logical-to-logical algebraic transformation rules with optional constraints, as well as logical-to-physical transformation rules with constraints and costs. The search space is internally encoded as an AND/OR DAG, where each node has an associated signature that is the same for logically equivalent expressions. The PROVision framework operates over files, and thus does not have a DBMSs’ sophisticated mechanisms for computing histograms and performing rich cost estimation. However, in fact we have access to the inputs and outputs of each workflow module, since it was previously run and its output materialized, so for many expressions we can directly use the cardinality of the results. Additionally, in our experience most workflow plans have only a few join and aggregation steps, which limits the error that accumulates through cost estimation. We use branch-and-bound pruning to avoid searching plans that are more expensive than the best-known alternative.

Algebraic rewrites.

We implement transformation rules for the algebraic equivalences described in Section IV-D. The optimizer treats the scalar UDF operator as a join with an input binding restriction [10], where one of the inputs must be bound to the UDF’s parameters. It then searches for an optimal ordering among joins and UDF calls.

Pruning with semijoins.

An optimization unique to PROVision exploits the fact that the user typically only wants to reconstruct the provenance for a subset of the output tuples S ⊆ W, where W is the output of the workflow. In effect we want to “trace back” the provenance from the output, but since the provenance does not yet exist, we really need to selectively compute only from those inputs that might relate to the selected results.

We initially model this as computing the query plan for W ⋉ S, i.e., W semijoined with the selected tuples. We then introduce transformation rules for pushing the semijoin. Given a join expression (A ⋈_θ1 B) ⋉_θ2 R, we split θ₂’s predicates to those between the attributes of A and R, resulting in θ₂a; and likewise for B and R; and substitute the expression $\left(A{⋉}_{{\theta }_{2}a}R\right){\bowtie }_{\theta 1}\left(B{⋉}_{\theta 2b}R\right)$. For UDF operators (whether scalar or grouping), a challenge is that many attributes are not necessarily shared between input and output. For any grouping or scalar UDF operator U, given an expression U(A) ⋉_θ R, we can rewrite as U(A ⋉_θ′ (A)) ⋉_θ R. To get θ′ we rewrite θ to DNF, then remove any conjuncts over attributes missing from A. This rewrite may match false positives (some tuples may not actually contribute to the final output) but no false negatives, so it preserves correctness. We later experimentally study when the rewrite actually saves cost and time.

With the semijoin optimization and the input set of selected tuples, PROVision can heavily prune the results it uses during reconstruction, as we shall see in Section VII.

Provenance expression rewrites.

Our query optimizer takes expert-provided type-and-operator-specific rules, including those in Table II, and uses them to simplify provenance.

Primary strategies.

The above optimizations are incorporated into two over-arching strategies to reconstruct provenance. PROVision may eagerly recompute and materialize an entire workflow’s results and provenance, in order to allow future inquiry about the provenance of any intermediate or output result. Alternatively, we may adopt an on-demand strategy where we only recompute the portion of the workflow necessary to produce the provenance of a specific user selection and exploit pruning techniques such as semijoin pushdown during on-demand computation. Here we deploy two strategies: greedy, where we try to pushdown the restrictions as far as we can (maximum pushdown); cost_based, where we pick the best plan based on minimum execution time. Section VII studies the trade-offs between these approaches.

VI. USER ANALYSIS TOOLS

Building upon PROVision’s provenance reconstruction techniques, we consider how to address our motivating problems. Both the version inconsistency and missing parameters problems leverage a provenance-tracing primitive. Algorithm 1, TraceProv, is called with a workflow and intermediate results, WF. It computes the full provenance for the workflow (if selected outputs O_sel = Ø) or the provenance for selected output tuples O_sel (if this is using a semijoin optimization).

A. Version Inconsistency

When workflow module code gets updated, sometimes these changes cause unexpected changes to output. We seek test instances for developers to debug for the output differences. A test case is a small input instance that is guaranteed to

reproduce the behavior and a subset of the different results between (deterministic) module versions. For each output tuple, we must compute those inputs that went into the same block or group that yielded the result. We assume a preprocessing step that executes each version of a module in the workflow, and does a standard diff between the versions’ outputs. PROVision finds the earliest module that results in a difference in outputs: the branching module. It then identifies the output records that differ between the versions, allows the user to sub-select from these, and reconstructs the necessary provenance that went into these outputs. Finally, it outputs the set of input records needed to reproduce the selected output.

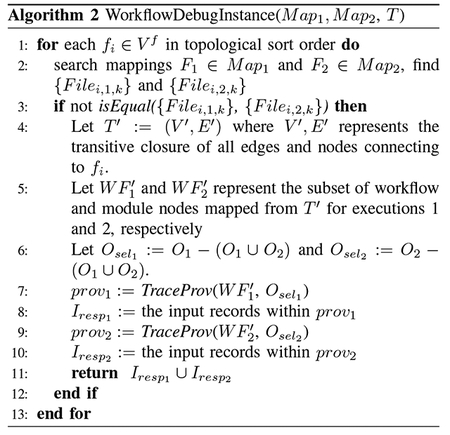
We require the same abstract workflow specification across versions, but the modules and files may differ. The workflow specification is converted into a workflow template DAG, T = (V, E), where nodes V = V^m∪ V ^f represent modules (V^m) and input or output files (V^f); edges E connect from file nodes to module nodes (representing inputs to a program) or from module nodes to file nodes (representing outputs produced by a program). The template T is instantiated each time the workflow is executed. Execution maps each node in T to actual execution instances: in execution run X_j, every module node m_i ∈ V^m is mapped to an executable program (M_j : m_i → Program_i,j); every file node f_i ∈ V^f, f_i is mapped to a set of data files used in the execution (F_j : f_i → {File_i,j,k}, where k = 1, …, q represent multiple(q) files as input or output of a module).

Given template T and mappings of two executions Map₁ = {M₁, F₁} and Map₂ = {M₂, F₂}, Algorithm 2 traces the execution instances. Here the two executions share the same input files, with an overall input set of records I, leading to different output sets of records O₁ and O₂, from which the user selects a subset. We compute the responsible subset of records I_resp ∈ I which leads to the selected output results. The algorithm traverses the file nodes in workflow template T and compares the associated files. From the branching module, we trace provenance back to the input records, for each execution.

B. Missing Parameters

Inconsistency also arises when we re-run a workflow according to its provenance, but we are missing some parameter settings. For instance, consider software with settings in the local /etc directory, where data and provenance are on a shared disk. PROVision “knows” the semantics of the modules and possible parameter values from semantic descriptors: it can run the workflow over carefully chosen subsets of the

data under different parameter settings to quickly isolate “plausible” parameter values. Algorithm 3 searches for the missing parameter values. We take a workflow WF and a search space S = 〈X₁, … , X_m〉, where each set of values X_i represents the possible values for parameter p_i. (The search space is $|S|={\Pi }_{i=1}^m\left|X_i\right|$), and a possible setting for missing parameters is $P^{(i)}=<p_1^{(i)},\dots ,p_m^{(i)}>$, where P⁽ⁱ⁾ ∈ S.

Now we enumerate possible settings for the m parameters, and test (on a subset of the input data) whether these produce results consistent with the original workflow output. Algorithm 3, picks a subset of inputs T ∈ I; this must be done considering which items that are mapped by the algorithm to the same hash bucket or block. We reconstruct the workflow output over input subset I_i with candidate parameter values, producing outputs O_i with provenance prov(O_i). Lines 4–6 validate whether such records appear in the provenance of the original workflow execution, and prunes candidates as appropriate. Finally, we take the (much smaller) candidate parameter settings that passed our tests over data subsets, and return only those that produce consistent output over the full input data (Lines 8–12).

VII. EXPERIMENTAL EVALUATION

We now evaluate the overhead of provenance reconstruction and PROVision’s effectiveness with the version inconsistency and missing-parameter reconstruction problems. We study our different optimization strategies on the space and time overheads of provenance reconstruction. We use workflows and datasets for three types of ETL and scientific tasks.

Gene sequence alignment (Genome).

Scientists often seek to quantify the genes and related proteins from DNA-sequenced tissue. A workflow cleans the sequence records (trim), aligns trimmed sequences against a reference “library” of genes, and finally looks up the genes to determine which proteins are

coded. Our biologist collaborators’ workflow uses modules from the STAR alignment toolkit. Our experiments use 145.5M sequences and three versions of STAR (2.3.0, 2.3.1 and 2.4.0), which each produced subtly different results.

Entity matching (Magellan).

The Magellan [19] entity matching toolkit provides blocking, alignment, and ranking algorithms. Magellan workflows include stages for blocking (comparing subsets of record pairs to find an alignment) and matching (determining which pairs match above a threshold). Building on example workflows provided with Magellan, we seek to link entities between the ACM Digital Library (1813 records) and DBLP (1780 records).

Data cleaning (DuDe).

Another common ETL task involves cleaning records within a data set. The DuDe toolkit [8] is a data cleaning framework, which searches for tuples that represent the same real-world object across data sources (deduplication). Our experiments use a standard DuDe workflow over a compact disc dataset, with 9763 records comprised of 107 (possibly null) attributes.

The three workflows above have simple structure. Moreover, the non-declarative portions of the code — the call the UDF plus any referenced functions (code refd. by UDF in the table) — is proportionally very small. The overall complexity of the semantic descriptors is as follows:

	Genome	Magellan	DuDe
Num. of modules	3	3	2
Num. of operators	12	8	3
Code refd. by UDF	0.3%	2.2%	0.8%

The difficulty of our task (finding and extracting the UDF and instrumenting code) is essentially the same as for instrumenting functionality with API calls, as with SubZero. Experiments were conducted on an Intel Xeon E5–2630 running at 2.20GHz with 24 cores and 64GB of RAM. Our implementation used the Java OpenJDK 1.8.0. Results are averaged over 5 runs and we present 95% confidence intervals.

A. Overhead of Provenance Reconstruction

PROVision does not instrument an existing workflow system; rather, it re-executes certain operations in a workflow (using declarative modules) to derive record-to-record provenance. Thus there is no overhead on the “normal” execution path, but costs are incurred when the user asks for the provenance of selected results. We study execution and space overhead, and then assess the benefits of our optimizations.

We first study three methods for precomputing a complete provenance trace. The naive method recomputes all data and its provenance. The materialized results are comprised of both output data and provenance. The RK method recomputes the provenance as annotations for each tuple, using foreign keys to link the provenance to the data, instead of materializing the full data. The RCS method builds upon RK and additionally simplifies provenance expressions using the equivalences of Section IV-D. Finally, the on-demand method starts with user-selected tuples, and selectively recomputes only the provenance that it needs in order to trace provenance of those tuples.

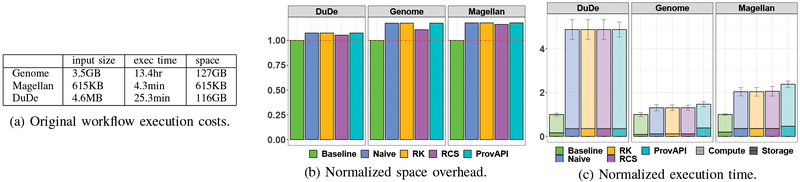
Baseline: original workflow.

The baseline costs, in terms of space and time, are shown for the original data workflows in Figure 3a. The Genome workflow is the most intensive in terms of space and time; the Web entity resolution workflow is small but requires a fair amount of computation per record; the product data cleaning workflow produces combinatorial explosion, but is reasonably fast on a per-record basis.

Fig. 3:

Baselines and overheads for different workloads.

Minimum cost of provenance APIs.

Prior provenance API implementations, such as SubZero [28], are not readily available. To establish a point of comparison, we instrumented the workflow modules’ source code (in C, Java, and Python) to record provenance in-memory. Data was periodically written to disk, forming a “lower bound” on provenance API overhead (since a real implementation is likely to use IPC). We see from Figure 3c that the normalized computation time overheads (vs. the baseline described above) are approximately 30% (Genome) to 480% (DuDe), on every computation. This motivates our selective reconstruction approach.

Full provenance reconstruction.

Figure 3b shows that PROVision adds low space overhead, 7–17%, similar to provenance instrumentation via API. This cost depends on the number of extractions, joins, and aggregations: DuDe only contains two such operators, so adds little overhead; Genome and Magellan have multiple join and aggregation steps so they are larger. The provenance is smaller than the actual data, so the overhead is below 20%. Simplification of provenance expressions (RCS) saves a bit of space; since it adds no CPU cost (Figure 3c), we conclude that compression is beneficial.

Figure 3c shows that CPU overhead varies significantly by workload, based on how many tuple combinations are being considered in the computation and how many calls are made to the UDF. The DuDe implementation essentially performs a Cartesian product on all inputs, hence it adds more than 4x overhead. This could be improved via blocking or pruning techniques; but it is also alleviated by on-demand approaches for computing only the provenance for specific results.

Selective (on-demand) reconstruction.

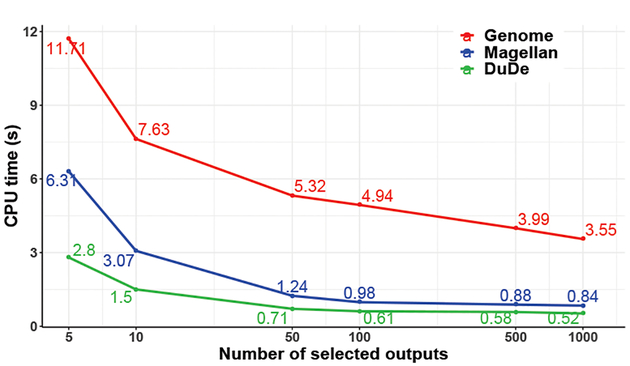
The on-demand approach generally starts with a set of user-selected output records, and PROVision uses semi-join pushdown to limit its computation to relevant results. Table III shows that for small numbers of outputs, greedily using the semijoin (greedy) results in very efficient provenance computations (between 0.7 and 5 sec). In fact, taking costs into effect (cost-based) results in the same query plan, hence the same execution times. Figure 4 shows how the performance speedups gradually drop as we select larger and larger subsets of the output.

TABLE III:

CPU time for tracing 1000 output records.

	Full	Greedy	cost-based
Genome	13.4hr	4.71s	4.71s
Magellan	4.3min	0.995s	0.995s
DuDe	25.3min	0.695s	0.635s

Fig. 4:

Average CPU time for each selected output.

Pruning overhead vs benefits.

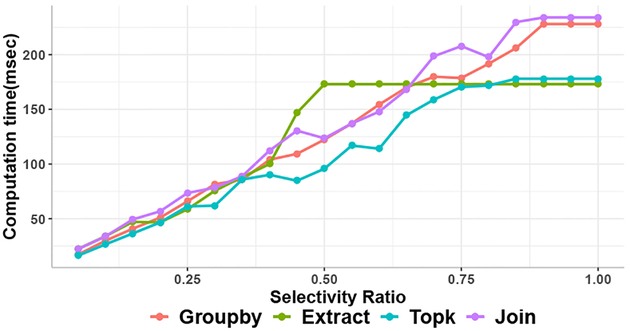
Selective reconstruction relies on semijoins to prune input and intermediate state. A question is how much of the output needs to be of interest before it makes sense to precompute all of the provenance. We measure this for the Genome, Magellan, and DuDe workflows in Figures 5a, 5b, and 5c, respectively. Each figure plots the greedy strategy’s reconstruction time (green line) versus the cost-based strategy (red line) versus the baseline (blue line) and computing all results ahead of time (dashed line). The switchover point between strategies is at around 45–90% of the output results. Our cost-based strategy chooses the best approach in each case. Figure 6 provides greater detail on the potential benefits: using synthetic data, it shows the impact of a semijoin filter’s selectivity vs the performance of a single-operator (group-by, substring extract, top-2, or equijoin) computation. If the semijoin filters 50% of an operator’s input data, there is always a speedup; less-selective semijoins only show speedup for expensive (join, grouping, top-2) operations.

Fig. 5:

Execution time (s) vs proportion of output selected for different workloads.

Fig. 6:

Per-operator selectivity ratio vs running time

B. Enabling Consistency & Reproducibility

PROVision uses provenance to (1) find input test sets that yield inconsistent results across workflow module versions (debugging “version inconsistency”); and (2) find missing parameter values from workflow runs (“parameter finding”).

1). Version Inconsistency:

Our bioinformatics collaborators often face versioning issues. If two versions of a workflow are run over an input, and their results differ according to diff3, PROVision is called. It can “trace back” from the differing outputs, to find an input data subset useful for testing. We took three versions of our collaborators’ workflow modules (v1-v3), compared the outputs to find differences, and then traced back to the input records that contributed to those outputs.

	v1–v2	v2–v3	v1–v3
Prop of outputs differing	0.3%	2.1%	2.1%
Prop of inputs contributing	3.4%	11.6%	12.7%

Relatively few outputs differ between any pair of workflow versions. PROVision can trace back to the specific input records that contributed to those differences — yielding an input set of 3.4–12.7% of the original input set. (Execution costs are identical to Figure 5a and thus not reproduced.) This shows that PROVision helps the user focus on a relatively small set of inputs that directly contribute to differences in answers. In fact, the user can generate even smaller test sets by selecting a few outputs of interest from the “diff” and tracing those in a few seconds (as in Table III).

2). Missing Parameter Discovery:

The Magellan entity matching workflow includes stages for blocking, feature selection, and matching. The blocking stage reduces the number of comparisons needed, whereas the feature selection and matching determine the alignment results. We study how PROVision can recover missing information about the features used in a prior workflow execution.

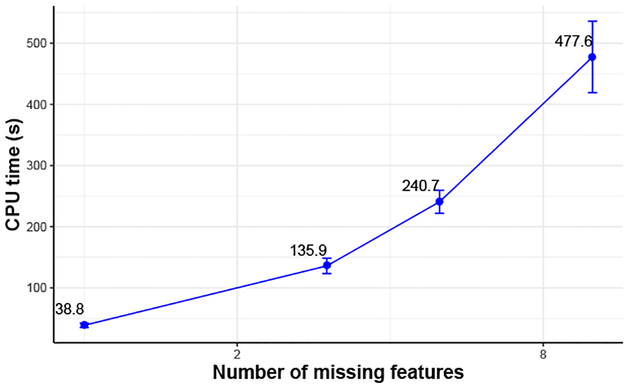
Given a fixed schema, the space of possible features is fixed. The ACM and DBLP tables have 21 candidate features. About half of these are “obvious” features that will always be used, and about half are “tuning” features that need to be adjusted by an expert. Figure 7 shows the cost of exploring the feature space for Magellan to validate which features were used. The cost is exponential in the number of features, but feasible due to PROVision’s ability to test on a subset the data: It takes between half a minute to about 8 minutes for PROVision to find the set of features used to perform entity matching.

Fig. 7:

Provenance computation times to fill in unknown feature values, vs number of missing features.

VIII. CONCLUSIONS AND FUTURE WORK

We proposed novel techniques to reconstruct and reason about fine-grained provenance in data science and ETL work-flows. PROVision uses an extended relational algebra with UDFs that produce provenance annotations. It incorporates type-and-operator-specific equivalence rules and a novel query optimizer and engine to selectively recompute provenance. Using real ETL and scientific workflows, we showed that our methods efficiently trace erroneous results, create test sets for debugging differences in workflow module outputs, and reconstruct missing parameters. Our approach efficiently and retrospectively reconstructs the information necessary to aid in debugging or filling in workflow data. As future work, we are interested in expanding our techniques to a broader class of workloads, including machine learning tasks.

UDFs as joins with binding pattern restrictions.

Borrowing from the data integration literature [26], we model the invocation of a UDF, which takes a set of input parameters, as a dependent join with a relation with binding patterns, of the form $R_f\left(a_1^b,\dots ,a_n^b,b_1^f,\dots ,b_q^f\right)$. Attributes adorned with ^b are bound and those annotated with ^f are free. To retrieve tuples in R_f, we must parameterize (join on) the bound attributes.