Abstract
The ability to visualise blood flow in a vessel-selective manner is of importance in a range of cerebrovascular diseases. Conventional x-ray methods are invasive and carry risks to the patient. Recently, a non-invasive dynamic angiographic MRI-based technique has been proposed using vessel-encoded pseudocontinuous arterial spin labeling (ASL), yielding vessel-selective angiograms of the four main brain-feeding arteries. In this study a novel kinetic model for the signal evolution in such acquisitions is derived and applied to healthy volunteers and to a patient with Moya-Moya disease. The model incorporates bolus dispersion, T1 decay and RF effects and is applicable to other angiographic methods based on continuous or pseudocontinuous ASL. The model fits the data well in all subjects and yields parametric maps relating to blood volume, arrival time and dispersion, changes to which may indicate disease. These maps are also used to generate synthesized images of blood inflow without bias from T1 decay and RF effects, greatly improving collateral vessel visibility in the patient with Moya-Moya disease. Relative volume flow rates in downstream vessels are also quantified, showing the relative importance of each feeding artery. This framework is likely to be of use in assessing collateral blood flow in patient groups.
Keywords: Magnetic Resonance Angiography, Vessel-Encoded Pseudocontinuous Arterial Spin Labeling, Vessel-Selective, Kinetic Model Fitting, Blood Arrival Time, Bolus Dispersion, Collateral Blood Flow, Moya-Moya Disease
Introduction
Vessel-selective information regarding the cerebral vasculature is of interest in a variety of patient groups. For example, in patients with steno-occlusive disease, this information reveals the extent of collateral blood flow, which is important for maintaining the viability of brain tissue when the primary feeding artery is compromised (1). Clinically, such assessments are generally performed using x-ray digital subtraction angiography (DSA) which provides excellent temporal and spatial resolution, but is limited by its invasive nature, the use of ionising radiation and the requirement for catheter repositioning to assess multiple arteries. In addition, these procedures carry a risk of contrast agent reaction, silent ischaemia (2), or even stroke (3). Other angiographic methods, such as conventional time-of-flight (TOF) magnetic resonance angiography (4), lack vessel-selective information.
Non-invasive vessel-selective perfusion mapping methods, such as those based on arterial spin labeling (ASL) (5–10), allow the inference of abnormal flow patterns and have been shown to correlate well with x-ray DSA for the assessment of collateral flow (11, 12). However, the vessel morphology and flow patterns are not visualised directly and in patients with very delayed blood arrival T1 decay may lead to significant signal attenuation before the blood reaches the tissue.
Recently, we proposed a method for vessel-selective dynamic angiography (13) by combining a vessel-encoded pseudocontinuous arterial spin labeling (VEPCASL) preparation (8) with a 2D thick-slab flow-compensated segmented Fast Low Angle Shot (FLASH) readout (14, 15). This technique requires no catheter insertion or contrast agent and provides useful qualitative information on the morphological and functional status of each artery. However, in order to optimise the signal-to-noise ratio (SNR) a long labeling duration was used, so the first acquired image corresponds to a time at which most of the vessels are filled with labeled blood and thus only outflow of the bolus can be observed. The interpretation of these images may also be biased by late arriving blood appearing less intense due to greater T1 decay and signal attenuation induced by the imaging sequence.
In this paper a theoretical kinetic model for the signal evolution in VEPCASL dynamic angiography is presented which is also applicable to similar non-vessel-selective methods. The parameter maps resulting from fitting this model to the data in each voxel provide information relating to blood volume, blood arrival time and bolus dispersion. Changes to these parameters may be indicative of disease in patient groups and the absolute values could be of use to those incorporating dispersion into models of tissue perfusion with arterial spin labeling. These maps also allow the generation of synthesized inflow images in the absence of T1 decay and effects due to the imaging RF pulses with arbitrary temporal resolution, giving an intuitive and unbiased representation of the data. Finally, the maps relating to blood volume can be used to quantify the relative blood volume flow rates in downstream vessels from each of the feeding arteries. Results from the application of this technique in healthy volunteers are presented. To show the potential of this method in patient groups, results are also shown for a patient with Moya-Moya disease, which is characterised by progressive stenosis of some of the cerebral arteries leading to the development of numerous collateral vessels (16).
Theory
Although the VEPCASL dynamic angiography sequence is based upon the principles of arterial spin labeling (ASL), an application of the general ASL kinetic model (17) is not appropriate since there is no exchange between the blood water and tissue in large vessels. Therefore, a novel kinetic model is derived in this section, incorporating effects due to T1 decay, imaging RF pulses and dispersion of the labeled blood as it passes through the vasculature. For clarity the model parameters and their symbols are listed in Table 1.
Table 1.
List of mathematical symbols used for the kinetic model and their meaning.
| Symbol | Description |
|---|---|
| r | Position vector of the voxel of interest |
| t | Time since the start of the VEPCASL pulse train |
| c(r, t) | Normalised concentration of labeled blood |
| d3r | Elemental volume |
| δt(r) | Blood transit time from the labeling plane to the voxel at position r |
| τ | VEPCASL labeling duration |
| κ(r) | Vessel interior flag (1 inside vessels, 0 outside) |
| S(ri, t) | ASL signal intensity in voxel i |
| S0 | Calibration factor giving the ASL signal intensity per unit blood volume |
| td | Time delay caused by dispersion |
| D(r, td) | Dispersion kernel |
| p(r) | Dispersion kernel time to peak |
| s(r) | Dispersion kernel sharpness |
| Г | Gamma function which normalises the dispersion kernel to unit area |
| T(δt, td) | Signal attenuation due to T1 decay |
| T1b | Longitudinal relaxation time of arterial blood |
| R(t, δt, td) | Signal attenuation due to imaging RF pulses |
| TR | Repetition time (i.e. separation of imaging RF pulses) |
| α | Imaging RF pulse flip angle |
| N (r, t, td) | Previous number of RF excitation pulses experienced by the blood |
| t0 | Time at which the first imaging RF pulse is played out |
| δt,min | Time at which labeled blood first arrives in the imaging region |
| v(ri) | Volume of blood within vessels in voxel i |
| A(ri) | Scaling factor proportional to blood volume (A = S0v(ri)) |
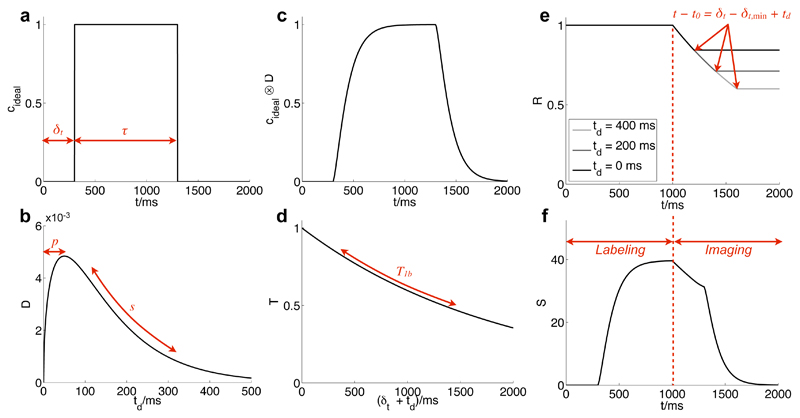
Let c(r, t) be the normalised concentration of labeled blood originating from a particular feeding artery in a small volume, d3r, at a given position, r, and time, t, such that c is equal to one when this small volume is completely filled with labeled blood and zero when outside arteries or in unlabeled blood. Let us first consider the simple case where dispersion, T1 decay and effects due to the imaging RF pulses are neglected and the voxel is supplied by a single feeding artery. Making the assumption that the blood flow is non-pulsatile, c can be written as a simple “rect” function which depends only on the blood transit time from the labeling plane to the position of interest, δt(r), and the VEPCASL labeling duration, τ:
| (1) |
where κ(r) = 1 inside an artery and is zero elsewhere and t = 0 corresponds to the start of the VEPCASL pulse train. cideal is plotted in Fig. 1a along with other factors that affect the final model. In this simple case the ASL signal we expect to measure, S(ri, t), in voxel i at sample time t is proportional to the total volume of labeled blood summed over the voxel volume:
| (2) |
where S0 is a calibration factor describing the ASL signal per unit volume of pure blood in the absence of T1 decay and previous RF excitation pulses. S0 accounts for the equilibrium magnetisation of blood, the excitation flip angle used, the inversion efficiency of the VEPCASL pulse train and the sensitivity of the coil. It is assumed in this discussion that the data have been corrected for non-uniform coil sensitivity profiles in pre-processing, so that S0 is constant across the image.
Figure 1.
Illustration of the various factors which contribute to the final kinetic model describing the ASL signal evolution in a single voxel: the ideal labeled blood concentration is a rect function (a); convolution with a dispersion kernel (b) yields a modified curve (c); account must also be taken of T1 decay (d) and effects due to the RF excitation pulses (e, plotted for three different td values). Note that RF effects are not present before the start of imaging and the curve flattens out to a constant when the time relative to the start of imaging is greater than the time the blood has spent in the imaging region (which varies with td). Combining these effects yields the final model curve (f) which is also scaled by S0 and blood volume. For long labeling durations (τ > δt) only the latter portion of the curve will be observed (as shown in (f)) since imaging cannot commence until the labeling has finished. Parameters used for these plots: A = 50, δt = 300 ms, s=0.01ms-1,p=50ms,δt,min =100ms.
In practice, dispersion of the bolus will cause a smearing out of this “ideal” profile (Fig. 1c), which can be described as a convolution, in a manner similar to Hrabe et al. (18):
| (3) |
| (4) |
where D(r, td) is the convolution kernel describing the fraction of blood arriving at position r which has been delayed by time td due to dispersion, normalised to unit area under the curve. For this study we choose a gamma variate function for the dispersion kernel (Fig. 1b) which has been used previously to model the inflow of an injected bolus of contrast agent (19) or pulsed ASL preparation (20). Here we aim to model the bolus dispersion rather than the entire bolus time-course, but this function has the desirable properties of being causal and the ability to model a long tail, suitable for describing blood flowing in a laminar fashion. We use a parameterisation similar to that described by Rausch et al. (19):
| (5) |
where p(r) describes the time to peak of the distribution, s(r) is the sharpness of the distribution (a low sharpness implies a distribution with a long tail) and Γ is the gamma function which normalises the kernel to unit area:
| (6) |
We have thus far ignored T1 decay and attenuation of the ASL signal caused by previous RF excitation pulses, which can both be described by multiplicative factors that reduce the signal amplitude. T(δt, td) describes the T1 decay experienced by the blood after labeling during its transit to the observation point (Fig. 1d). After labeling it takes the blood a time δt + td to reach the position of interest, so:
| (7) |
where T1b is the longitudinal relaxation time of arterial blood, which is assumed to be equal to 1664 ms in this study (21), corresponding to the value relevant at 3 Tesla.
R(t, δt, td) describes the attenuation of the ASL signal by the excitation RF pulses as the blood passes through the imaged region (Fig. 1e). Assuming all transverse magnetisation is effectively spoiled at the end of every repetition time (TR) period, each RF pulse with flip angle α reduces the longitudinal magnetisation by a factor of cos α. This applies to both the inverted and non-inverted blood and therefore the ASL signal is attenuated by the same factor. Thus:
| (8) |
where N(r, t, td) is the previous number of RF excitation pulses experienced by the blood at position r, time t and time delay td. In the simplest case that the imaging region encompasses everything distal to the labeling plane, then all the labeled blood has experienced all the previous RF pulses so N can be written using a simple expression:
| (9) |
where t0 is the time at which the first imaging pulse is played out and we make a continuous approximation for N for simplicity, in a similar manner to Günther et al. (22). However, it is often the case for transverse acquisitions that there is a gap between the labeling plane and the imaging region within which blood does not experience the imaging pulses. This problem is similar to that faced by standard ASL acquisitions using a Look-Locker readout (22, 23). However, here we must consider RF effects before the blood reaches the voxel of interest and we also account for differences across the dispersed bolus.
If the blood from a given feeding artery takes a time δt,min to reach the imaging plane then the maximum amount of time spent in the imaging region before reaching the voxel of interest is δt − δt,min + td. This equation assumes that the bolus is relatively undispersed upon entry to the imaging region in order to simplify the expression. This maximum time spent in the imaging region limits the number of RF pulses experienced by the blood, so the expression for N becomes:
| (10) |
Putting all this together, the measured signal can therefore be written as:
| (11) |
| (12) |
If we assume that δt, s and p are approximately constant over the dimensions of the voxel (including across the imaging slab in 2D acquisitions) then we arrive at our final model (Fig. 1f):
| (13) |
| (14) |
where v(ri) is the blood volume within vessels in voxel i.
Since S0 is not known a priori it is simpler to combine the factors S0 and v(ri) into a single scaling factor A(ri) = S0v(ri). Thus our final model to fit to the data, incorporating blood volume (A), bolus dispersion (D), T1 decay (T) and RF effects (R) is:
| (15) |
Assuming that the earliest arrival of blood in the imaging region, δt,min, is known (see Methods section), this fit involves four parameters: A, δt, s and p. We have thus far assumed each voxel is fed by a single artery, but this model can be used to fit multiple feeding arteries whose signals have been separated in preprocessing. In this case the fit to the signal from artery j yields Aj (ri) = S0vj (ri) where vj is the volume of blood within the voxel originating from artery j.
Methods
Subjects and Scan Protocol
Six healthy volunteers with no known neurological disease were recruited (4 men, 2 women; age range, 24-39; mean age 32) under a technical development protocol agreed with local ethics and institutional committees. One patient with Moya-Moya disease (male, age 41) was also recruited under a protocol agreed with these committees. All subjects were scanned on a 3 Tesla Siemens MRI scanner (both TIM Verio and TIM Trio, Siemens Healthcare, Erlangen, Germany) using a 12 channel head coil for signal reception and the body coil for transmission. Data from two of the healthy volunteers have been used in a previous publication (13). The scan protocol consisted of a 3D time-of-flight (TOF) sequence used to plan the vessel-encoded acquisitions followed by six-cycle 2D vessel-encoded dynamic angiography (as per (13)) in transverse (50 mm imaging slab) and coronal (100 mm imaging slab) views centred on the circle of Willis. A sagittal acquisition was not performed due to the significant overlap of vessels in this view. The resulting images have an in-plane spatial resolution of 1.1 x 1.1 mm interpolated to 0.54 x 0.54 mm, and a temporal resolution of 55 ms. The scan time for the whole protocol was approximately 25 minutes.
Data Preprocessing
The complex images from each coil were combined using the adaptive combine method of Walsh et al. (24), as described in our previous paper (13). The vascular components present in the resulting combined complex vessel-encoded data were separated using a maximum a posteriori (MAP) Bayesian solution (25) to the general framework for vessel-encoded analysis (26). The signal was separated into contributions from the four main brain feeding arteries: the right and left internal carotid arteries (RICA and LICA) and vertebral arteries (RVA and LVA). The analysis method used allows for rigid body translation and rotation of the arteries between the TOF and vessel-encoded acquisitions, thus attempting to account for the possibility of subject motion between the TOF scan and the subsequent VEPCASL acquisition. Laminar flow with average speed 30 cm/s was assumed in these large feeding arteries to reduce the computational complexity.
The output of the MAP processing is a complex signal value in each voxel at each time point for each vascular component. However, the model described above assumes purely real data. Simply taking the magnitude of the signal could skew the model fit, particularly when the signal is low and noise dominates, since the signal will then always be positive. To overcome this problem a voxelwise phase correction step was performed: the mean phase over time for each vascular component was calculated after weighting by the magnitude of the signal, since the phase of a low magnitude signal is less reliable. This mean phase was subtracted from the phase at each time point before taking the real part of the signal. It is assumed that the phase of the blood signal does not vary significantly over time and any phase variation is due to noise alone. This should be a reasonable assumption since each time frame is acquired 55 ms after the previous frame so the phase variation due to external sources such as B0 drift should be minimal. This was confirmed by comparisons of phase corrected and magnitude images which show negligible differences when not close to the noise level.
The data were corrected for spatial non-uniformity in the coil transmission and reception fields, without the need for additional calibration scans, by using FMRIB’s Automated Segmentation Tool (FAST) (27) on the 3D TOF data. The resulting estimated bias field was transformed into the space of the vessel-encoded data using FMRIB’s Linear Image Registration Tool (FLIRT) (28) (using the known image coordinates, without a search) before being applied.
Determination of Earliest Blood Arrival
The kinetic model described above requires knowledge of the earliest time of arrival of blood in the imaging region (δt,min) from each feeding artery in order to accurately describe the expected signal attenuation due to the imaging RF pulses. In the coronal view the labeling plane was encompassed within the imaging slab and therefore δt,min = 0 for all feeding arteries. However, for the transverse data sets δt,min was unknown and therefore had to be estimated before performing the full fit to the data. This was achieved separately for each feeding artery by fitting the kinetic model to a very restrictive mask containing only the highest intensity voxels corresponding to the large arteries just proximal to the circle of Willis. The mask was created by calculating the mean signal intensity over time for each vascular component and retaining only the 0.1% most intense voxels. For the purposes of this preliminary fitting procedure, δt,min was assumed to be zero, giving an imperfect fit to the data, but allowing reasonably accurate estimation of δt.
Once these initial estimates of δt in the large proximal arteries had been made, the earliest arrival time in the imaging slab could be estimated for each feeding artery separately. One could take the minimum of these δt values, but this is potentially biased by noisy data, so instead the tenth percentile of these values was taken. In initial experiments this process was found to yield values which produced accurate fits to the full kinetic model.
Kinetic Model Fitting
The fitting of the kinetic model (Eq. 15) was performed within a Bayesian framework. This allowed priors to be placed on the parameter values, helping to constrain them to reasonable values in the presence of noisy data. Assuming Gaussian noise on the data and Gaussian priors on each parameter the posterior probability of the parameters, given the data, can be calculated. Maximising this posterior probability corresponds to finding the most likely set of parameters (i.e. the best fit to the data) and the curvature of this function at its maximum relates to the uncertainty on the parameters. This process was performed using a constrained optimisation algorithm (fmincon) within MatlabⓇ (Mathworks™, Natick, Massachusetts, USA). Further details of the fitting procedure can be found in the appendix.
Fitting the kinetic model in voxels which do not contain vessels adds significantly to the computational time. Therefore the fitting procedure was only performed within a mask which was found by calculating the mean signal intensity over time in each voxel, determining the 99th percentile of this value across the whole image (and all vascular components) and then excluding voxels which have mean signal of less than 40% of this value, which are assumed to be non-vascular voxels of no interest.
Inflow Visualisation
For inflow visualisation the parameter estimates from the kinetic model were used to simulate the expected signal at a range of times during blood inflow in the absence of T1 decay and RF effects (i.e. T1b → ∞ and α → 0). An infinite labeling duration was simulated to achieve inflow visualisation in a similar fashion to x-ray DSA.
Relative Volume Flow Rate Quantification
If blood in a downstream vessel is well mixed, then the relative blood volume flow rate due to each feeding artery is equal to the relative blood volume summed over a segment of that vessel. This relative blood volume can be calculated using the A parameter which is proportional to blood volume. In healthy volunteers it is uncommon to expect blood from the major feeding arteries to provide a mixed supply to vessels above the circle of Willis, except in the posterior cerebral arteries (PCAs), so manual masks were drawn over the left and right PCA (P2 segments). The sum of A within each mask for each feeding artery was calculated and used to determine the relative flow rates.
Results
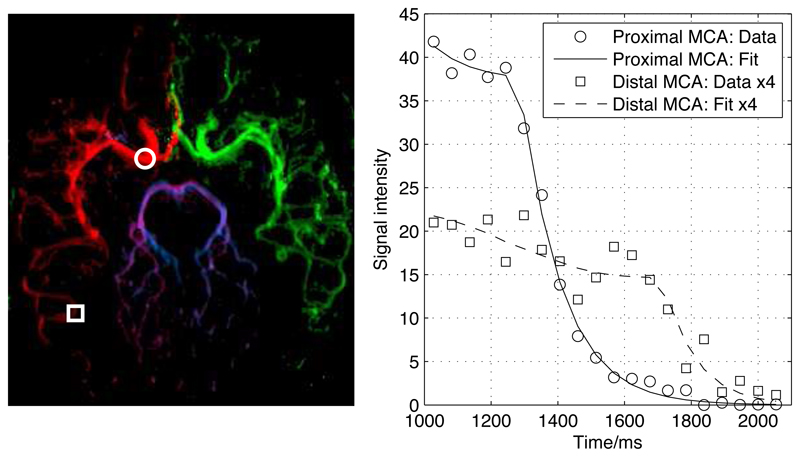
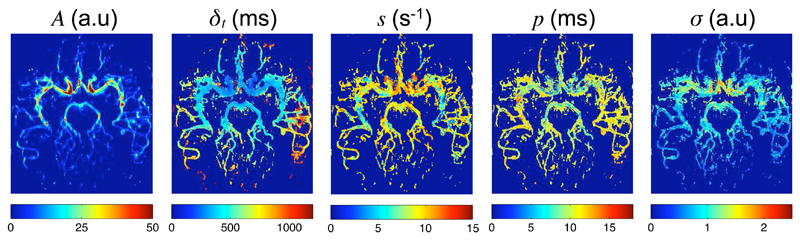
Example fits of the kinetic model to the data are shown in Fig. 2 for one healthy volunteer transverse data set. The model appears to describe the data accurately in both proximal and distal regions, with examples shown here in the right middle cerebral artery (RMCA). The parameter maps generated from the same data set (Fig. 3) show the expected patterns: A, which relates to blood volume, is high in the large proximal vessels, the blood arrival time, δt, is extended in distal vessels and to some extent at the large vessel edges due to the laminar nature of the flow and the dispersion parameters indicate a higher degree of dispersion (low s and high p) in more distal vessels. Note that in some small distal vessels with late blood arrival s and p tend towards the mean values of their prior distributions. This is because less of the tail of the signal curve is present in the acquired data and thus less accurate dispersion parameter estimates can be achieved. The noise estimate, σ, is higher in a region in line with the large proximal vessels. This is probably due to ghosting artefacts across the phase-encode (left-right) direction resulting from the more pulsatile flow in these large vessels. Away from these areas σ is relatively constant as might be expected.
Figure 2.
Examples of the model fit to the data in a healthy volunteer using the transverse view. Two locations in the proximal (circle) and distal (square) right MCA are overlaid on the color coded map of A (left): RICA = red, LICA = green, RVA = blue, LVA = purple. The corresponding time series and model fit at these locations to the right ICA component are also shown (right). The time axis is relative to the start of the VEPCASL pulse train.
Figure 3.
Example parameter maps generated by fitting the kinetic model (Eq. 15) to data from a healthy volunteer in the transverse view, averaged over the vascular components for clarity of presentation.
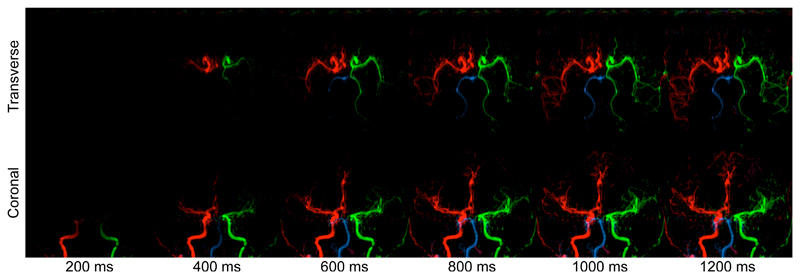
Examples of synthetic blood inflow visualisation using the derived kinetic model parameters are given in Fig. 4, with attenuation due to T1 decay and imaging RF pulses removed. This more intuitive way to display the data shows the expected patterns of inflow into the arterial tree and the later arrival of vertebral blood is clear in these images. Fig. 4 also demonstrates the potential of this method to clearly identify unusual flow patterns within the cerebral vasculature. This subject has little flow in their left vertebral artery and a partial fetal type circle of Willis (29) on the left side. In addition, the left anterior cerebral artery (LACA) is missing the A1 segment, meaning that it is supplied from the RICA via the anterior communicating artery.
Figure 4.
Simulation of blood inflow: example frames in both a transverse and coronal view of the same subject generated using the kinetic model parameter estimates and assuming an infinitely long bolus duration. The simulation time is shown underneath. Note that this subject has non-standard flow patterns around the circle of Willis, including collateral flow from the LICA to the LPCA and absent A1 segment on the left side, meaning that both ACAs are supplied by the RICA.
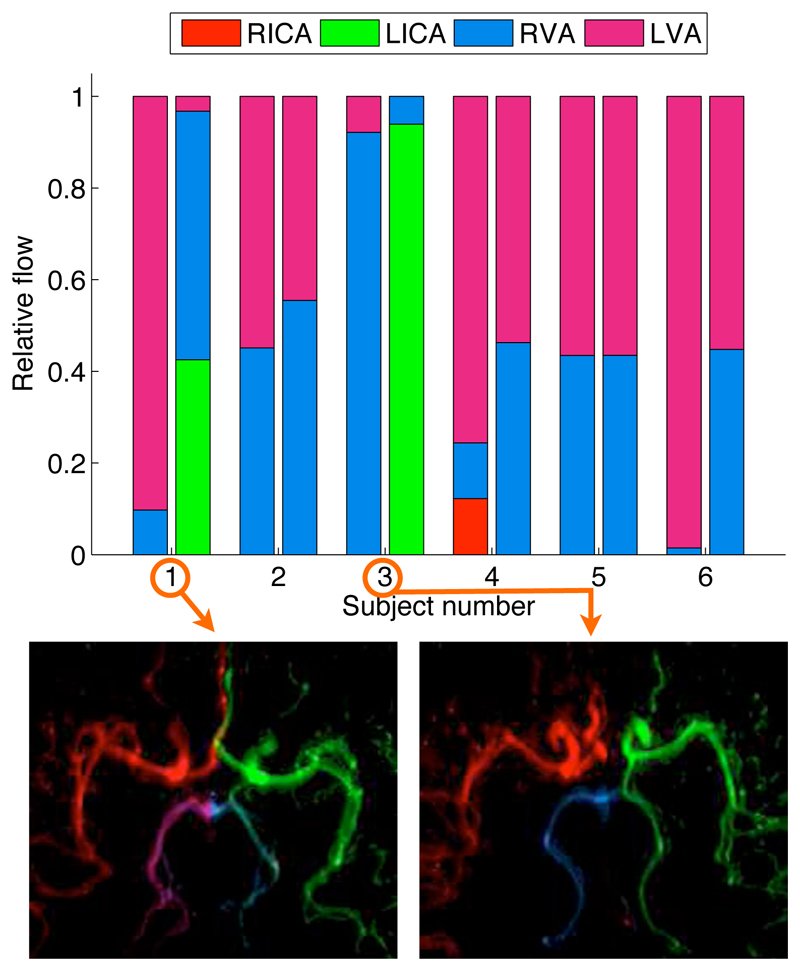
Results from calculations of the relative blood volume flow rates in the PCAs of all healthy volunteers are shown in Fig. 5. Subjects 2, 4, 5 and 6 demonstrate the expected pattern where the majority of blood in each PCA originates approximately equally from the RVA and LVA. Subjects 1 and 3 show a considerable amount of collateral flow from the LICA to the LPCA via the left posterior communicating artery. Interestingly the majority of the blood feeding each PCA for Subject 1 comes from the contralateral VA, as has been shown in a qualitative manner previously (13).
Figure 5.
Relative blood volume flow rate calculations in the PCAs of healthy volunteers in the transverse view. The stacked bar chart shows the relative blood flow contributed by each of the feeding arteries (see legend) in both the RPCA (left bar) and LPCA (right bar) for each subject. For the two subjects (1 and 3) with the greatest degree of collateral flow the corresponding map of A is shown underneath, demonstrating clear filling of the left posterior communicating arteries.
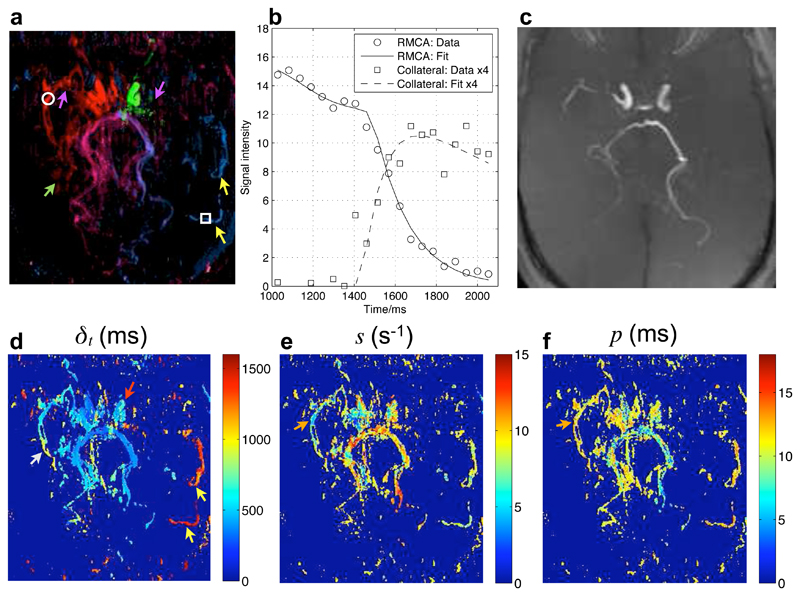
Fig. 6 shows the model fitting results in the patient with Moya-Moya disease. The high degree of stenosis and extensive collateral formation typical of Moya-Moya disease are apparent in these images. These findings agree well with the patient’s x-ray DSA report, which states that high grade stenoses were observed in the right proximal middle cerebral artery and the left distal internal carotid artery along with considerable collateral formation. The model appears to provide an accurate description of the data, even in voxels containing collateral vessels with extremely delayed arrival. The smaller collateral vessels are not visible in the TOF maximum intensity projection (MIP) of the same region and are also difficult to identify in the raw images (not shown). The source of blood to the larger collateral vessels feeding the LMCA territory is clearly visualised with this technique and the extended arrival time is very apparent in the map of δt. Relative flow rate calculations indicate that 99% of the blood in these large collaterals originates in the RVA and only 1% from the LVA, although other small contributions may be present that do not survive the masking procedure. The blood in the RMCA distal to the significant stenosis shows both delayed arrival and a greater degree of dispersion relative to other vessels, suggesting that such parameters may be indicative of upstream disease.
Figure 6.
Model fitting to transverse data from a patient with Moya-Moya disease: a color coded map of A in the transverse view (a) with two voxel locations in the RMCA and a collateral vessel overlaid. The time series of the dominant vascular component and corresponding fit to the model in these locations is plotted in (b), with the collateral data and fit multiplied by four for clarity. The small collateral vessels are not visible in a TOF transverse maximum intensity projection of the same imaging region (c). Other parameter maps (showing only voxels where A > 7 for visual clarity) are also shown (d-f). Points of interest include: high level stenosis in both MCAs (purple arrows), the formation of small branching collateral vessels (green arrow), delayed arrival in the LICA relative to the RICA (red arrow), larger collaterals from the posterior circulation into the LMCA territory with very delayed arrival (yellow arrows) and a higher degree of dispersion (orange arrows) and late arrival (white arrow) in the distal RMCA compared to other vessels.
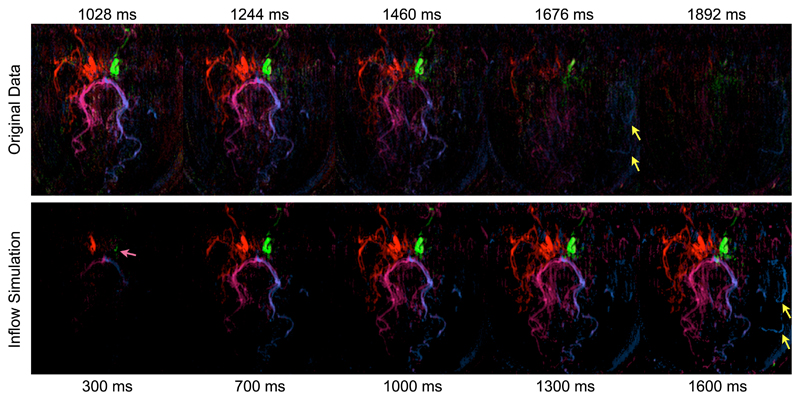
The potential benefits of the inflow visualisation are evident in this patient (Fig. 7) where the extended arrival time in collateral vessels leads to significantly attenuated signal due to T1 decay and the imaging RF pulses. The inflow simulation shows these collateral vessels much more clearly, giving a less biased indication of the volume of blood flowing through each vessel. Differences in arrival time between the two ICAs are also more apparent in the simulation than the original data.
Figure 7.
Comparison between the original unprocessed data (top) and simulated inflow (bottom) which corrects for T1 decay and imaging RF effects in the patient with Moya-Moya disease. Note that different time scales were used to display the full range of information in each data set and the times shown are relative to the start of labeling. The late arrival of blood in collateral vessels is much clearer in the inflow simulation than the original data (yellow arrows) due to compensation for signal attenuation. The slightly later arrival of blood from the LICA compared to the RICA is also more apparent using inflow simulation (pink arrow).
Discussion
In this paper a novel mathematical kinetic model to describe the signal evolution in vessel-encoded arterial spin labeling dynamic angiography acquisitions has been derived, accounting for bolus dispersion, T1 decay and effects due to the imaging RF pulses. This allows the generation of parameter maps relating to blood volume, arrival time and dispersion. In addition, it provides a means to create intuitive inflow visualisation in a similar manner to x-ray DSA without confounding factors that attenuate the ASL signal, and quantification of relative blood volume flow rates from each feeding artery. Although applied to 2D VEPCASL data here, this model is applicable to other angiographic techniques based on continuous or pseudocontinuous ASL, including 3D acquisitions.
Figs 2 and 6 demonstrate that this model accurately describes the angiographic signal in both proximal and distal arteries of healthy volunteers and a patient with Moya-Moya disease. These fits also highlight the importance of accounting properly for the earliest arrival of blood in the imaging region, which causes the early part of these curves to level out to a relatively constant value prior to the bolus washing out of the voxel. Failing to account for this effect would lead to overestimation of the relative blood volume within the voxel.
The derived parameter maps (Fig. 3) show the expected patterns in the healthy volunteers. Differences from these patterns are seen in the patient with Moya-Moya disease (Fig. 6). The delayed arrival of the blood from the LICA relative to the RICA is perhaps due to the greater degree of stenosis in the LMCA than the RMCA, leading to greater resistance to blood flow. The increased level of dispersion in the distal RMCA may also indicate upstream disease. A larger study would be necessary to demonstrate whether these differences are significant, but similar changes in such parameters have been observed in other studies of patients with cerebrovascular disease. For example, the degree of carotid artery stenosis has been shown to be correlated with arrival time differences between hemispheres (30) and flow amplitude and time to peak, a parameter relating to bolus dispersion, in the ipsilateral MCA are altered following carotid endarterectomy (20). Although these studies and others (such as those by van Osch et al. (31) and Okell et al. (13)) have demonstrated maps relating to blood arrival time and/or dispersion, these used empirical approaches or less sophisticated models and most are not appropriate for the VEPCASL preparation used in this study where blood inflow is not observed in many voxels.
It is worth noting that the concentration of labeled blood and its fast passage through large arteries enables a more accurate assessment of the dispersion parameters than may be possible with standard arterial spin labeling methods that focus on tissue perfusion. As mentioned above, dispersion parameters cannot be accurately determined in voxels with late arrival since the tail of the distribution is not visible in the acquired time window. Further experiments using this type of modeling approach and a longer acquisition window could help determine appropriate dispersion parameters in small distal vessels closer to the capillary bed, enabling more accurate quantification of cerebral blood flow or comparison across a range of dispersion models.
The simulated inflow images exemplified in Figs 4 and 7 allow a more intuitive way of visualising the data which is likely to appeal to clinicians who are familiar with x-ray DSA. The removal of effects due to T1 decay and the imaging RF pulses means the signal observed truly relates to the volume of labeled blood present, preventing bias in the image interpretation. This effect is clear from the improved visibility of the collateral vessels with greatly delayed arrival in the patient data shown here. These vessels are poorly visualised using TOF due to the residual signal from overlying tissue (which is subtracted out in the VEPCASL angiographic method) and saturation of slow flowing spins which spend a significant amount of time in the imaging region. Optimisation of the TOF protocol for such patients may result in improved visualisation of these smaller vessels but some level of static tissue signal and in-plane lumen saturation will always remain.
An additional benefit of the inflow visualisation method is reduction in the amount of noise in the data from the smooth nature of the fitted curve, but without the loss of temporal fidelity which would result from time series smoothing. The ability to reconstruct such images at any desired temporal resolution is also advantageous, although ultimately it is limited by the temporal resolution of the acquired data.
The ability to quantify the relative flow rates in distal vessels due to each feeding artery (Fig. 5) is likely to be of use in patient groups, particularly those with stenosis proximal to the circle of Willis. For example, the decision to perform endovascular therapy on such a stenosed artery can be informed by the relative importance of collateral flow from other vessels. The fact that this imaging protocol identified normal variants of flow patterns in healthy volunteers suggests that it may provide useful clinical information in patients with cerebrovascular disease. Van Osch et al. (31) have previously used pulsed ASL angiography to calculate absolute blood volume flow rates in vessel segments distal to the circle of Willis using a measured arterial input function (AIF). In future work we will describe an extension of our modeling approach to achieve comparable absolute blood volume flow rate quantification from each feeding artery without the need for measured AIFs and attempt to validate such methods against more conventional techniques.
However, this study has a number of limitations. The model described here assumes no pulsatility and also assumes that all dispersion occurs between entry into the imaging region and the voxel of interest. This does not appear to adversely affect the fit to the data presented here, although it may lead to small inaccuracies in the fitted parameters and be more significant in other situations where the blood is more pulsatile or the imaging plane is located some distance from the labeling plane.
The need to perform numerical integration to calculate the theoretical signal means that the computational time required to fit the model to these high resolution data sets can be considerable (typically on the order of tens of hours). This could cause difficulties incorporating the processing into a clinical workflow. However, the computational time required could be considerably reduced by optimisation of the fitting procedure and parallelisation of the processing. A simpler model could also be used, although this would potentially lead to bias in the parameter estimates, inflow visualisation and relative flow rate calculations.
The priors used on the parameters were chosen to be Gaussian to simplify the equations and maintain reasonable computational times. This potentially allows for non-physical parameter values (such as negative blood arrival times), although these are avoided by the use of the constrained optimisation procedure. More appropriate priors may benefit this work in the future. In addition, the mean and standard deviation of each prior were chosen empirically and would need to be modified depending on the scanner and coil used for the experiments. A more elegant solution involving scale-free priors for A and σ might be beneficial. However, the use of more sophisticated priors is likely to increase the required computational time. An automatic relevancy determination prior (32) may also help to exclude voxels which do not include vessels, reducing the need for the masking procedure used here.
The synthesized inflow images are sensitive to inaccurate fits of the model to the data, either because of noise, image artefacts or due to an incomplete description of the data by the model. It appears that the Bayesian fitting procedure used in this study prevented spurious fits in the data collected thus far, except in voxels dominated by noise, which are of low signal amplitude and therefore of less significance. However, care should be taken in the interpretation of these images, particularly in the presence of strong artefacts (e.g. due to motion) and the raw data should be reviewed alongside the inflow visualisation to identify potential discrepancies. In future work we plan to incorporate a map showing the “goodness of fit” (such as the sum of squares of the fit residuals) to help highlight areas where the fit is poor. In addition, we plan to compare these simulated inflow images with x-ray DSA data to help validate this approach.
The relative flow rate calculations assume the blood from all feeding arteries is fully mixed, which may not always be the case. Additionally, only contributions large enough to survive the masking procedure are included, meaning that small contributions may be underestimated. These relative values are also not useful for comparing the total volume flow rates between vessels or across subjects. Absolute flow rate measurements would be advantageous and are planned, as mentioned previously.
Finally, although some interesting features appear in the parameter maps and inflow visualisation of the patient with Moya-Moya disease, a larger study is necessary to determine whether such effects are consistently seen.
Conclusions
The kinetic model presented here accurately describes the vessel-encoded arterial spin labeling angiographic signal, yielding maps relating to blood volume, arrival time and dispersion. It has been demonstrated that this information can be used to generate intuitive inflow visualisation of the data and quantify the relative volume flow rates from each feeding artery. Interesting features were observed in a patient with Moya-Moya disease and it is hoped that such information will also be valuable in patients with cerebrovascular diseases. Planned future work includes the application of this method to a range of patient groups, adaption of the model to balanced steady-state free precession (bSSFP) based readouts and an extension to allow the absolute quantification of volume flow rates from each feeding artery in downstream vessels.
Supplementary Material
Table 2.
Chosen values for the prior distributions on each parameter based on some initial experience fitting to 2D VEPCASL angiography data. Note that the prior on A has a mean of zero to prevent large values being estimated in noisy voxels. s is also tightly constrained to discourage very small sharpness fits which approximate a flat curve in noisy voxels. Note that the priors on parameters A and σ depend on the scaling of the images and thus will vary between scanners and coils.
| Parameter (X) | Mean (μX) | Standard Deviation (σX) | Units |
|---|---|---|---|
| A | 0 | 30 | Arbitrary Scanner Units |
| δt | 500 | 500 | ms |
| s | 10 | 2 | s−1 |
| p | 10 | 10 | ms |
| σ | 2 | 0.5 | Arbitrary Scanner Units |
Acknowledgements
The authors would like to thank Dr Jingyi Xie for help with patient data collection and the UK Stroke Association and the Dunhill Medical Trust for funding support. MAC is employed by The Centre of Excellence in Personalised Healthcare funded by the Wellcome Trust and EPSRC under grant number WT088877/Z/09/Z.
References
- [1].Liebeskind DS. Collateral circulation. Stroke. 2003;34:2279–84. doi: 10.1161/01.STR.0000086465.41263.06. [DOI] [PubMed] [Google Scholar]
- [2].Bendszus M, Koltzenburg M, Burger R, Warmuth-Metz M, Hofmann E, Solymosi L. Silent embolism in diagnostic cerebral angiography and neurointerventional procedures: a prospective study. Lancet. 1999;354:1594–7. doi: 10.1016/S0140-6736(99)07083-X. [DOI] [PubMed] [Google Scholar]
- [3].Kaufmann TJ, Huston J, 3rd, Mandrekar JN, Schleck CD, Thielen KR, Kallmes DF. Complications of diagnostic cerebral angiography: evaluation of 19,826 consecutive patients. Radiology. 2007;243:812–9. doi: 10.1148/radiol.2433060536. [DOI] [PubMed] [Google Scholar]
- [4].Masaryk TJ, Modic MT, Ross JS, Ruggieri PM, Laub GA, Lenz GW, Haacke EM, Selman WR, Wiznitzer M, Harik SI. Intracranial circulation: preliminary clinical results with three-dimensional (volume) MR angiography. Radiology. 1989;171:793–9. doi: 10.1148/radiology.171.3.2717754. [DOI] [PubMed] [Google Scholar]
- [5].Hendrikse J, van der Grond J, Lu H, van Zijl PC, Golay X. Flow territory mapping of the cerebral arteries with regional perfusion MRI. Stroke. 2004;35:882–7. doi: 10.1161/01.STR.0000120312.26163.EC. [DOI] [PubMed] [Google Scholar]
- [6].Werner R, Norris DG, Alfke K, Mehdorn HM, Jansen O. Continuous artery-selective spin labeling (CASSL) Magn Reson Med. 2005;53:1006–12. doi: 10.1002/mrm.20475. [DOI] [PubMed] [Google Scholar]
- [7].Günther M. Efficient visualization of vascular territories in the human brain by cycled arterial spin labeling MRI. Magn Reson Med. 2006;56:671–5. doi: 10.1002/mrm.20998. [DOI] [PubMed] [Google Scholar]
- [8].Wong EC. Vessel-encoded arterial spin-labeling using pseudocontinuous tagging. Magn Reson Med. 2007;58:1086–91. doi: 10.1002/mrm.21293. [DOI] [PubMed] [Google Scholar]
- [9].Dai W, Robson PM, Shankaranarayanan A, Alsop DC. Modified pulsed continuous arterial spin labeling for labeling of a single artery. Magn Reson Med. 2010;64:975–82. doi: 10.1002/mrm.22363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Helle M, Norris DG, Rüfer S, Alfke K, Jansen O, van Osch MJP. Superselective pseudocontinuous arterial spin labeling. Magn Reson Med. 2010;64:777–86. doi: 10.1002/mrm.22451. [DOI] [PubMed] [Google Scholar]
- [11].Chng SM, Petersen ET, Zimine I, Sitoh YY, Lim CCT, Golay X. Territorial arterial spin labeling in the assessment of collateral circulation: comparison with digital subtraction angiography. Stroke. 2008;39:3248–54. doi: 10.1161/STROKEAHA.108.520593. [DOI] [PubMed] [Google Scholar]
- [12].Wu B, Wang X, Guo J, Xie S, Wong EC, Zhang J, Jiang X, Fang J. Collateral circulation imaging: MR perfusion territory arterial spin-labeling at 3T. AJNR Am J Neuroradiol. 2008;29:1855–60. doi: 10.3174/ajnr.A1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Okell TW, Chappell MA, Woolrich MW, Günther M, Feinberg DA, Jezzard P. Vessel-encoded dynamic magnetic resonance angiography using arterial spin labeling. Magn Reson Med. 2010;64:698–706. doi: 10.1002/mrm.22458. [DOI] [PubMed] [Google Scholar]
- [14].Günther M, Warmuth C, Zimmer C. Sub-millimeter dynamic spin labeling cerebral 2D-angiography with 40ms temporal resolution. Proceedings of the 10th Annual Meeting of ISMRM; Honolulu, HI. 2002. p. 1100. [Google Scholar]
- [15].Sallustio F, Kern R, Günther M, Szabo K, Griebe M, Meairs S, Hennerici M, Gass A. Assessment of intracranial collateral flow by using dynamic arterial spin labeling MRA and transcranial color-coded duplex ultrasound. Stroke. 2008;39:1894–7. doi: 10.1161/STROKEAHA.107.503482. [DOI] [PubMed] [Google Scholar]
- [16].Vilela P, Goulão A. Ischemic stroke: carotid and vertebral artery disease. Eur Radiol. 2005;15:427–33. doi: 10.1007/s00330-004-2632-6. [DOI] [PubMed] [Google Scholar]
- [17].Buxton RB, Frank LR, Wong EC, Siewert B, Warach S, Edelman RR. A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magn Reson Med. 1998;40:383–96. doi: 10.1002/mrm.1910400308. [DOI] [PubMed] [Google Scholar]
- [18].Hrabe J, Lewis DP. Two analytical solutions for a model of pulsed arterial spin labeling with randomized blood arrival times. J Magn Reson. 2004;167:49–55. doi: 10.1016/j.jmr.2003.11.002. [DOI] [PubMed] [Google Scholar]
- [19].Rausch M, Scheffler K, Rudin M, Radü EW. Analysis of input functions from different arterial branches with gamma variate functions and cluster analysis for quantitative blood volume measurements. Magn Reson Imaging. 2000;18:1235–43. doi: 10.1016/s0730-725x(00)00219-8. [DOI] [PubMed] [Google Scholar]
- [20].MacIntosh BJ, Sideso E, Donahue MJ, Chappell MA, Günther M, Handa A, Kennedy J, Jezzard P. Intracranial hemodynamics is altered by carotid artery disease and after endarterectomy: a dynamic magnetic resonance angiography study. Stroke. 2011;42:979–84. doi: 10.1161/STROKEAHA.110.590786. [DOI] [PubMed] [Google Scholar]
- [21].Lu H, Clingman C, Golay X, van Zijl PC. Determining the longitudinal relaxation time (T1) of blood at 3.0 Tesla. Magn Reson Med. 2004;52:679–82. doi: 10.1002/mrm.20178. [DOI] [PubMed] [Google Scholar]
- [22].Günther M, Bock M, Schad LR. Arterial spin labeling in combination with a Look-Locker sampling strategy: inflow turbo-sampling EPI-FAIR (ITS-FAIR) Magn Reson Med. 2001;46:974–84. doi: 10.1002/mrm.1284. [DOI] [PubMed] [Google Scholar]
- [23].Petersen ET, Lim T, Golay X. Model-free arterial spin labeling quantification approach for perfusion MRI. Magn Reson Med. 2006;55:219–32. doi: 10.1002/mrm.20784. [DOI] [PubMed] [Google Scholar]
- [24].Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med. 2000;43:682–90. doi: 10.1002/(sici)1522-2594(200005)43:5<682::aid-mrm10>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- [25].Chappell MA, Okell TW, Jezzard P, Woolrich MW, Payne SJ. Fast analysis of vessel encoded ASL perfusion and angiographic images for clinical applications. Proceedings 19th Scientific Meeting; Montreal: ISMRM; 2011. p. 366. [Google Scholar]
- [26].Chappell MA, Okell TW, Jezzard P, Woolrich MW. A general framework for the analysis of vessel encoded arterial spin labeling for vascular territory mapping. Magn Reson Med. 2010;64:1529–39. doi: 10.1002/mrm.22524. [DOI] [PubMed] [Google Scholar]
- [27].Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20:45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- [28].Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- [29].van Raamt AF, Mali WPTM, van Laar PJ, van der Graaf Y. The fetal variant of the circle of willis and its influence on the cerebral collateral circulation. Cerebrovasc Dis. 2006;22:217–24. doi: 10.1159/000094007. [DOI] [PubMed] [Google Scholar]
- [30].Warmuth C, Ruping M, Forschler A, Koennecke HC, Valdueza JM, Kauert A, Schreiber SJ, Siekmann R, Zimmer C. Dynamic spin labeling angiography in extracranial carotid artery stenosis. AJNR Am J Neuroradiol. 2005;26:1035–43. [PMC free article] [PubMed] [Google Scholar]
- [31].van Osch MJ, Hendrikse J, Golay X, Bakker CJ, van der Grond J. Non-invasive visualization of collateral blood flow patterns of the circle of willis by dynamic MR angiography. Med Image Anal. 2006;10:59–70. doi: 10.1016/j.media.2005.04.010. [DOI] [PubMed] [Google Scholar]
- [32].MacKay DJC. Probable networks and plausible predictions - a review of practical bayesian methods for supervised neural networks. Network-Computation In Neural Systems. 1995;6:469–505. [Google Scholar]
- [33].MacKay DJC. Information theory, inference, and learning algorithms. Cambridge University Press; Cambridge, UK: 2003. [Google Scholar]
- [34].Yuen KV. Bayesian methods for structural dynamics and civil engineering. John Wiley and Sons; Singapore: 2010. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.