Whole-Cell Models and Simulations in Molecular Detail

Abstract

Comprehensive data about the composition and structure of cellular components has enabled the construction of quantitative whole-cell models. While kinetic network type models have already been established, it is now also becoming possible to build physical, molecular-level models of cellular environments. This review outlines challenges in constructing and simulating such models and discusses near- and long-term opportunities for developing physical whole-cell models that can connect molecular structure with biological function.

INTRODUCTION

At the most fundamental level, biology arises from molecular behavior. Proteins and nucleic acids are the main actors and their dynamics and interactions via molecular recognition and binding are key aspects of virtually any biological function. Atomistic resolution is typically necessary to fully understand these processes. Therefore, a major effort in modern biology has been focused on improving the resolution of macromolecular structures at sub-nanometer scales. As the Protein Data Bank (PDB) (Westbrook et al 2003) continues to grow rapidly, much is known today about the structures of proteins and nucleic acids. In fact, high-resolution experimental structures are available for essentially all major protein types (Vitkup et al 2001, Zhang et al 2006) and an increasing number of macromolecular complexes have been resolved (Marsh & Teichmann 2015). Challenges remain in determining the structures of very large and dynamic complexes, membrane proteins, and ribonucleic acid (RNA) molecules, which may be addressed soon via cryo-electron microscopy (cryo-EM) (Fernandez-Leiro & Scheres 2016). The high-resolution structure of chromosomal deoxyribonucleic acid (DNA) has also remained elusive. However, computational structure prediction is becoming increasingly powerful so that useful models can often be constructed when experimental structures are not available by template-based modeling (Rohl et al 2004, Roy et al 2010, Waterhouse et al 2018) and/or by assisting model-building with lower-resolution experimental data for proteins (Alexander et al 2008, Bowers et al 2000, Li et al 2004) and nucleic acids (Miao et al 2015), including genomic DNA (Bianco et al 2017, Di Stefano et al 2016, Hacker et al 2017, Tiana & Giorgetti 2018, Yildirim & Feig 2017). Both, experiment and modeling continue to see rapid progress. It may therefore be expected that complete structural coverage for all macromolecules in a cell of a specific organism could be within reach.

Structure alone does not fully explain most biological function. Equally important are conformational dynamics within a single molecule and dynamic interactions between molecules. The conformational dynamics of proteins and nucleic acids has been studied extensively via experiment and molecular dynamics (MD) simulations resulting in much insight about the mechanisms of biochemical processes (Hospital et al 2015). However, almost all of these studies, experiment and modeling alike, invoke simplified conditions without considering the high concentrations and physicochemical complexities of cellular environments. In fact, many questions remain about how biological macromolecules behave inside cells and navigate a spectrum of specific and non-specific interactions in the presence of a variety of electrolytes, osmolytes, and other small molecules (Cohen & Pielak 2017, Gnutt & Ebbinghaus 2016, Rivas & Minton 2016). Molecular interactions are essential for enzyme function, signaling, and many other biological processes but interactions can also lead to macromolecular aggregation and the development of diseases (Ross & Poirier 2004). Moreover, interactions between cellular components can stabilize or destabilize biomolecular structures (Wang et al 2012) or lead to the formation of phase separated states (Dumetz et al 2008), thereby further modulating biological function. It is thus becoming increasingly clear that a complete link between molecular structure and biological function requires the integration of structure and conformational dynamics at the atomistic level with dynamics and interactions at the cellular-level under realistic biological conditions.

Experimental techniques can probe many aspects of biomolecular structure and dynamics, but they typically only focus on narrow points in the space-time universe. For example, crystallography and cryoEM can resolve structures in atomistic detail but without any or only very limited time resolution and under artificial conditions that may have little in common with living cells (Drenth 2007, Fernandez-Leiro & Scheres 2016). On the other hand, the best single-molecule fluorescence methods can track the dynamics of molecules in vivo on millisecond time scales but only at spatial resolutions of tens of nanometers (Huang et al 2009). NMR spectroscopy can capture dynamics at atomistic scales under in vitro and in vivo conditions (Inomata et al 2009, Sakakibara et al 2009), but the interpretation of such data especially when collected in heterogeneous environments can be difficult (Pastore & Temussi 2017). Therefore, experiment alone has not been able to provide a unified picture of biomolecular structure, dynamics, and function across the entire range of scales from the molecular to the cellular level. Modeling can fulfill this role via whole-cell models (Trovato & Fumagalli 2017) that incorporate the experimental data and aim to predict how changes at the molecular level propagate to altered function at the systems level.

WHOLE-CELL MODELS

The most successful whole-cell models so far rely on empirical mathematical models that are parameterized based on experimental data and focus on a kinetic view of cellular processes (Guerrier & Holcman 2017, Karr et al 2015, Macklin et al 2014, Szigeti et al 2017, Tomita 2001). These models can access macroscopic time scales and connect directly with biological function. However, spatial resolution is often limited or absent altogether and molecular-level details are rarely if ever considered. As a result, there is no connection to molecular structure and interactions and the physical laws that operate at such level so that predictions of how changes at the molecular level affect the cellular outcome often cannot be made. For example, it would be difficult to predict how the introduction of a new drug candidate perturbs cellular function without making specific assumptions about altered kinetic pathways.

The alternative are physical models that build up by assembling individual molecules based on structures at the atomistic level (Figure 1) (Im et al 2016) and then subjecting such models to computer simulations (Feig et al 2018, Feig et al 2017). Such models connect behavior at the molecular level to cellular function. The wider range of scales – as well as the greater involvement of physical laws - provides, at least in principle, for greater predictive abilities. The main limitation of physical modeling is the computational cost for reaching cellular time and spatial scales with models that retain molecular detail at high resolution. However, as computational methods advance and computer hardware becomes ever more powerful, the physical modeling of cellular environments is becoming possible (Yu et al 2016). This review focuses on the challenges and opportunities of physical models of cellular environments, especially those that connect with molecular structure at atomistic resolution. The main emphasis will be on models of bacterial cells as such systems are beginning to be tractable today, but the general ideas discussed here readily transfer to more complex eukaryotic cells that will become accessible as resources increase and new experimental data will be available.

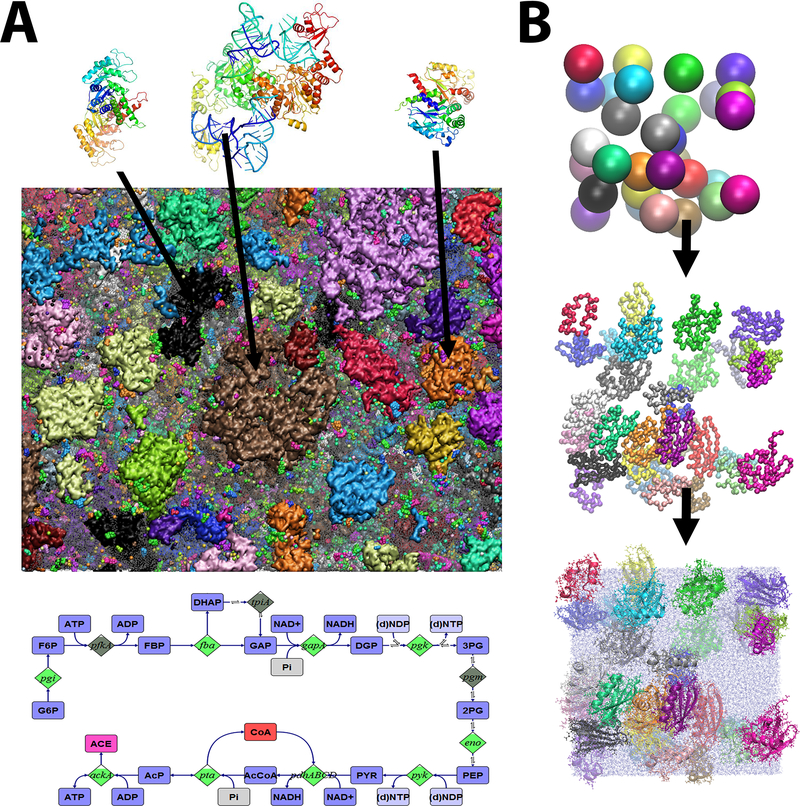
Figure 1:

Construction of cellular systems from atomistic structures of individual molecules based on biochemical pathway reconstruction for the cytoplasm of M. genitalium (A) (Feig et al 2015). Multiscale assembly generation protocol from spherical models to fully solvated atomistic system (B) (Feig et al 2015).

CHALLENGES IN BUILDING PHYSICAL MODELS OF CELLS

Physical models of cellular environments that involve molecular level of detail hold much promise but face a number of challenges which are reviewed in this section. The choice of model resolution is a critical aspect whereas the success of the modeling depends on realistic interaction potentials and the availability of experimental data to construct initial systems. Other challenges revolve around the practical issues of assembling, running, analyzing, and visualizing very large scale molecular systems. These aspects are discussed in more detail in the following.

Model resolution

Physical models of biomolecular systems are typically based on particle-based models at resolutions ranging from atomistic detail to coarse levels where an entire macromolecule may be represented as a single particle. Continuum models are also sometimes employed to represent certain cellular components such as bulk solvent, membranes, DNA, or cytoskeleton components when it is sufficient to capture their macroscopic or overall mechanoelastic properties. The level of resolution determines the accuracy of the models and their ability to project molecular-level effects to the cellular scale, but higher resolution demands increased computational cost and thereby limits what time scales and what size of systems can be investigated with available computer resources.

Atomistic models of biomolecules, where atoms are represented as spherical particles, have been used for decades since they match the resolution of biomolecular structures from experiment. Often, atomistic models are explored via molecular dynamics (MD) simulations to provide insights into the dynamics and energetics of biomolecules that are otherwise difficult to extract from experiments (Huggins et al 2018). Typically, atomistic modeling starts from experimental structures and involves explicit solvent molecules such as water or lipid bilayers for membrane-interacting systems. Because of the high level of detail, a moderate-size single protein surrounded by explicit solvent can easily require 100,000 particles whereas atomistic models of a bacterial cytoplasm reaches 100 M particles for a (100 nm)³ cubic volume that is still only 1/10^th to 1/20^th of the smallest bacterial cell (Feig et al 2015, Yu et al 2016). Such large numbers of particles require substantial computer resources and, therefore, the time scales that can be reached directly are generally limited to sub-millisecond scales, even on the largest computer clusters available today. The accessible time scales can be extended, though, by as much as several orders of magnitude via enhanced sampling methods (Mori et al 2016) and/or by inferring kinetics from Markov State models constructed from shorter simulations (Harrigan et al 2017, Lane et al 2013).

The limitations of atomistic models can be overcome at least in part with coarse-grained (CG) models (Buchete et al 2004, Kar & Feig 2014, Takada et al 2015). Such models combine molecular fragments into single interaction sites to reduce the number of particles and hence the computational cost. The level of resolution may vary from combining just C-H groups into unified particles to models where entire molecule are represented as a single sphere. The reduced degrees of freedom typically come at a price of reduced accuracy and ability to apply physical laws. CG models are typically parameterized based on a combination of data from experiment and higher-resolution modeling such as atomistic simulations. As a result, universal use and transferability is more limited and it is more difficult to derive truly new insights that do not simply recapitulate what is already known from the data or simulations that were used to parameterize the model. However, the simplicity of CG models can be a good choice when questions at larger scales are addressed that do not require atomistic resolution (Ando & Skolnick 2010).

Another strategy for reducing the computational cost is the use of continuum representations for parts of a system where macroscopic properties dominate or where experimental data does not provide sufficient resolution to build high-resolution particle-based models. Continuum models reduce computational costs not just by reducing the degrees of freedom but also by allowing instantaneous relaxation of certain components that are otherwise subject to kinetic barriers due to molecular reorganization. One example is the replacement of explicit aqueous solvent with dielectric-based implicit models (Roux & Simonson 1999). Such models can be extended to lipid bilayers and, in principle, to any heterogeneously varying dielectric environment (Tanizaki & Feig 2005). While implicit solvent models are attractive to capture solvation effects without the need for explicit solvent molecules, it is difficult to capture hydrodynamic interactions accurately within such a framework (Ando et al 2012, Dlugosz et al 2012, Mereghetti & Wade 2012). Continuum models can also be applied to the biomolecules, e.g. in the form of elastic rod models of nucleic acids (Balaeff et al 1999) and cytoskeletal components (Walcott & Sun 2010) to capture bending and twisting flexibility, as elastic models of lipid bilayers to allow deformations in response to interactions with other molecular components (Brown 2008), or as models of flexible globular proteins via fluctuating finite elements that focus on overall shape fluctuations (Solernou et al 2018).

Different resolutions can be applied simultaneously via multi-scale models to limit the use of expensive high-resolution treatments. One strategy is to apply higher resolution models only for selected parts of a system when and where necessary instead of the entire system (Kar & Feig 2017, Renevey & Riniker 2017, Ward et al 2017, Wassenaar et al 2011). In another approach, low-resolution modeling may be used to broadly span conformational sampling before switching to higher resolution to obtain quantitative information of the dynamic landscape of a given system (Harada & Kitao 2012, Tempkin et al 2014, Zhang & Chen 2014). While most multi-scale frameworks focus on bridging spatial scales, it is also possible to bridge time scales. The use of continuum models to avoid kinetic barriers has already been mentioned. Another possibility is to switch kinetically-separated states with a certain probability (Prytkova et al 2016) instead of waiting for simulations to overcome kinetic barriers, similar to what is already in wide use in kinetic network whole-cell models (Bernstein 2005). Multi-scale methods are in principle highly suitable for studying cellular environments where different processes occur on different scales of time and space. However, practical applications have been hindered by technical challenges with coupling models at different levels of resolution and a lack of practical implementations that perform well on high-performance computing platforms.

Interaction potentials

Interaction potentials between the sites of a given model allow the calculation of energies and forces so that simulation can be carried out. The type of interaction potential depends on the level of resolution. At the atomistic level, the potential terms are based on physical laws or designed to approximate physical laws. Chemical bonds and bond angles are typically approximated via harmonic functions while rotations around dihedral torsions are often described via Fourier series terms. Longer-range non-bonded interactions commonly consist of electrostatic Coulomb terms and a Lennard-Jones potential that prevents atom overlap and accounts for van der Waals dispersion attraction forces. The combination of these terms is a classical approximation of what would otherwise be largely quantum mechanical interactions but without allowing bond formation or breakage. Essentially all biomolecular force fields are based on these terms. After many years of development, the latest generation of force fields have arguably reached a high level of accuracy and transferability (Best et al 2012, Galindo-Murillo et al 2016, Harder et al 2016, Huang et al 2017, Klauda et al 2010, Wang et al 2017), including the ability to accurately simulate RNA (Tan et al 2018), intrinsically disordered peptides (Best et al 2014, Huang et al 2017, Robustelli et al 2018), and interacting proteins (Best et al 2014, Nawrocki et al 2017). However, high-quality parameters are still not available for all types of molecules. Especially, available parameters for small molecules have variable accuracy. This impacts the ability to model metabolites or potential drug candidates within cellular environments.

At the CG level, empirical and statistical potentials are used more prominently, sometimes in combination with physical potentials. Often, the empirical potentials are parameterized based on atomistic potentials or certain experimental observables and different CG models tend to focus on specific scientific applications rather than being universally applicable. For example, the widely used MARTINI model (Monticelli et al 2008) was initially developed to reproduce relative hydrophobicities of different amino acids and therefore is well-suited to study water-membrane partitioning, but requires restraints to maintain secondary structures (Monticelli et al 2008). The higher-resolution CG model PRIMO uses mostly physics-based interaction terms to achieve compatibility with atomistic force fields with the drawback of higher computational costs which limit the scale of applications that can be studied (Gopal et al 2010, Kar et al 2013). Structure-based models such as Go models require knowledge of target conformational states but can be useful to study transition pathways (Clementi et al 2000). Some of these higher-resolution CG models may also be suitable for describing protein-protein interactions (Frembgen-Kesner & Elcock 2010, Kmiecik et al 2016). At the very coarse-level, patchy particle models with angle-dependent radial interaction functions have been used for a long time to model the interactions of colloids (Bianchi et al 2011). These types of models can also be applied to biological macromolecules if internal structural and dynamics can be neglected (Bucciarelli et al 2016).

A very recent trend is the use of machine-learning (ML) methods to derive interaction potentials (Chmiela et al 2017, Li et al 2015, von Lilienfeld et al 2015). This can be done at all levels of resolution given suitable training data and, therefore, this approach has the potential to blur the differences between atomistic and CG models. Using ML methods it is possible to generate interaction potentials that match the resolution of the underlying models, especially when ML methods are trained on reproducing energetics rather than fitting parameters for the commonly used standard interaction potential forms.

Input data

Models of cellular environments, or any biological system for that matter, could not be constructed without experimental data. To build models of cellular environments, it is a major effort to assemble the necessary data (Guell et al 2009, Kuhner et al 2009, Singla et al 2018, Yus et al 2009). At the minimum, information about the system composition, the concentration of each species, and structural information is needed. In addition, knowledge about the spatial dimensions and arrangements of cellular components such as membranes, organelles, the cytoskeleton, genomic DNA, and other compartments is also necessary. The structural organization of cells including the distribution of large complexes can be visualized via microscopy or electron tomography (Beck et al 2011). The composition and concentration of cellular components, at least those present in high abundance, can be determined via mass spectrometry (Bantscheff et al 2007) and complemented by insights from metabolic network modeling (Feig et al 2015, Karr et al 2012, Tomita et al 2000). However, complete structural coverage at the molecular level is probably the most significant challenge. Although many high-resolution structures have been resolved, significant structural coverage of the genes in any single organism actually exists only for very few organisms. In fact, for almost all organisms there are none or at best very few structures available in the PDB. Computational structure prediction can fill the gap, and in many cases does so quite well (Modi et al 2016, Waterhouse et al 2018). However, the accuracy of the predicted structures varies and prediction is not always possible when structural templates from related proteins or nucleic acids are not available. Further advances in experimental structural biology are expected to improve the situation but the larger gains will likely have to come from improvements in computational structure prediction methods to provide missing structural information.

System assembly

The assembly of a heterogeneous cellular environments is non-trivial (Figure 1). The initial placement of molecules needs to be consistent with the overall dimensions of a given cellular system and match lower-resolution imaging and tomography data when available. Moreover, the naïve placement of biomolecules at high concentrations leads to significant overlap between different molecules which is difficult to resolve via subsequent minimization or simulation. There are different ways how such complex systems can be built, but two specific approaches appear to be most promising. 1) Instead of assembling a crowded system directly at full resolution, a hierarchical multi-scale scheme may be applied where biomolecules are placed initially at lower resolution to facilitate optimization and relaxation before gradually increasing resolution until the target resolution is reached (Figure 1) (Feig et al 2015). 2) A crowded system can also be built up by packing molecules into pre-defined volumes or shapes. This method is implemented in the CellPACK software, which uses sophisticated packing algorithms to assemble complex systems within short time (Klein et al 2018). Additional challenges arise when systems need to incorporate densely packed genomic DNA (Goodsell et al 2018) or cytoskeletal structures because these elements present obstacles that limit available space for placing other molecules and cannot be approximated well by simple spherical models. Finally, the initial construction of strain-free lipid membranes surrounding cells, organelles, or vesicles is also difficult, especially when lipid compositions are heterogeneous and membrane proteins are embedded (Koldsø & Sansom 2015). More efficient and flexible modeling tools are expected to emerge in the future so that any kind of crowded cellular system can be assembled from molecular components at high levels of resolution.

Simulation methods and software

Subjecting molecular models to simulation or other related computational methods provides insight into dynamics and interactions with other molecules. MD and related techniques such as Brownian and Stokesian dynamics are the most common approach, especially for systems represented at the atomistic level (Brady & Bossis 1988, Ciccotti et al 2014, Ermak & McCammon 1978). Coarse-grained models can also be simulated efficiently via Monte Carlo (MC) techniques (Kmiecik et al 2016). Other computational techniques that focus on dynamics include normal-mode or elastic network methods (Atilgan et al 2001, Case 1994), but these methods are generally limited to studies of conformational dynamics of single molecules and are not well-suited to study interactions in a crowded environment.

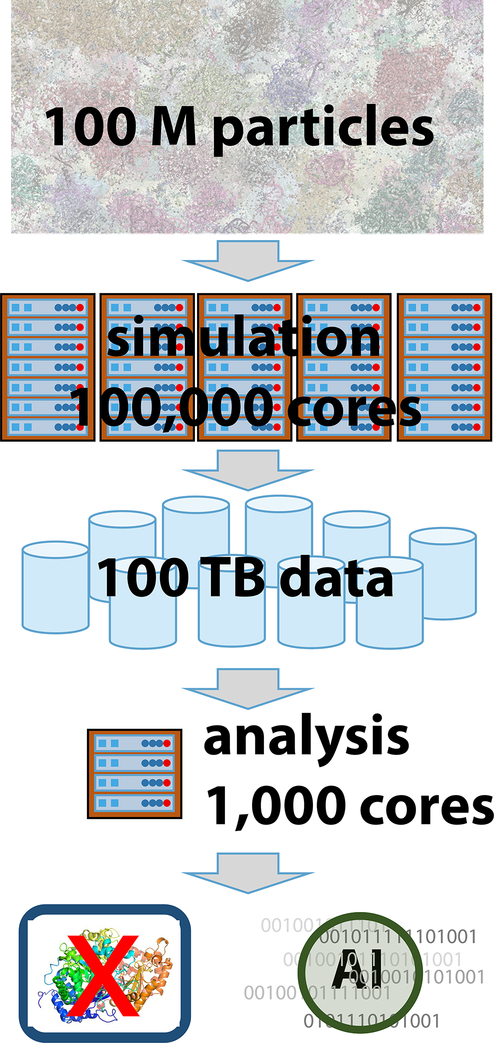
Many highly efficient software packages exist for carrying out MD simulations. Most packages are optimized for the simulation of smaller systems up to 1 M particles, but they are generally not prepared to address the unique challenges when simulating much larger systems. One important practical issue is the handling of input/output and parallel operations which has to be fully distributed for the efficient simulation of systems with 100 M or 1 B atoms because it takes too much time and memory for any single node to read and store the entire system (Figure 2). To our knowledge, this is only supported by some MD software packages so far, most notably GENESIS (Jung et al 2015, Jung et al 2016, Kobayashi et al 2017) and NAMD (Kale et al 1999). Moreover, the high computational cost of large system sizes requires efficient parallelism up to a very large number of cores on conventional clusters or many GPUs on GPU-based clusters, which is also only possible with a few packages (Jung et al 2016, Kale et al 1999) (Hess et al 2008).

Figure 2:

Flowchart of a typical simulation of a large cellular system that involves high-performance computing, data management, and analysis challenges.

Simulations of CG models or of atomistic models with continuum solvent are possible with many packages. It is especially straightforward if the CG model uses interaction potential terms similar to the terms used in standard atomistic force fields, such as with the MARTINI CG model. However, efficient parallel scaling is a significant problem in many CG simulations especially when the number of particles is relatively small. Many CG models do not explicitly consider solvent, which results in uneven particle distributions that create load-balancing issues. Moreover, the complex algorithms underlying continuum solvent and hydrodynamic models, if they are used, are difficult to parallelize. One solution is the use of GPU hardware where many types of CG models can be run very efficiently, especially via openMM (Eastman et al 2017), which allows flexible interaction functions defined at runtime. However, scaling to multiple GPUs is generally difficult with CG models and further software developments are clearly necessary to improve the performance of large-scale CG simulations on conventional and GPU-based clusters.

Analysis and visualization

When cellular models are subjected to simulations, the main outcome are trajectories of particle coordinates as a function of time. Even if coordinate frames are not saved often, the data generated for a cellular system with > 100 M particles can easily reach peta-byte scales (Figure 2). This creates significant challenges for analysis and visualization (Yu et al 2018) and, the analysis itself becomes a high-performance computing challenge that requires significant computing resources and parallel scaling in itself (Yu et al 2018). An even more significant problem is that the very large data sets of complex cellular systems have changed the mode of scientific discovery. While it may be straightforward to visually inspect a single-molecule trajectory via molecular graphics software such as VMD (Humphrey et al 1996) and pyMOL (DeLano 2002), this is not possible anymore for systems of 100 M atoms or more. Apart from the technical challenge of interactively animating such a large number of particles, there is simply too much information for visual analysis of detailed features by humans. Instead, data science methods are desperately needed to automatically inspect large trajectory data sets and identify potentially interesting new scientific aspects. Only with such tools will it be possible to realize the full scientific potential of molecular-level simulations of cellular environments.

OPPORTUNITIES OF PHYSICAL WHOLE-CELL MODELING

Whole-cell modeling largely remains a promise of future scientific impact. This applies to physical models as well as models based on kinetic networks. Network-based models require extensive kinetic data from experiment and complete functional gene annotations which are only available for a few organisms at best. On the other hand, physical models are limited by a lack of structural information and high computational cost. As a result, successful predictive cellular models have so far only been reported for the minimal bacterium Mycoplasma genitalium (Karr et al 2011, Yu et al 2016) and, to a lesser extent, for Escherichia coli (Frembgen-Kesner & Elcock 2013, McGuffee & Elcock 2010). It appears to be certain that models of other and more complex systems will follow as preparations are already underway to develop whole-cell models of systems as large and complex as a human pancreatic β-cell (Singla et al 2018).

The long-term vision of physical whole-cell modeling is that it will be possible to assemble all of the molecules in a given cell in atomistic resolution in a fully consistent fashion with experiment and then subject such an in silico cell to simulations that can reach biological time scales. Assuming that the simulations are sufficiently accurate, the result would be a comprehensive understanding of how molecular structure and function couple at the cellular level in a way that will probably never be measurable via experiments. Moreover, such models could provide a comprehensive understanding of disease and allow the design of new drugs in the full context of the cellular environment.

Many opportunities exist in the short-term to better understand the behavior of biomolecules in cellular environments based on physical models and motivated by recent experiments and simulations as reviewed in detail recently (Feig et al 2017). Fundamental questions remain about how cellular environments affect molecular stability, determine diffusive properties, give rise to non-specific transient interactions and phase transitions, and modulate ligand binding (Figure 3). It is also largely unclear how the presence of genomic DNA and membrane surfaces affects biomolecular structure and dynamics.

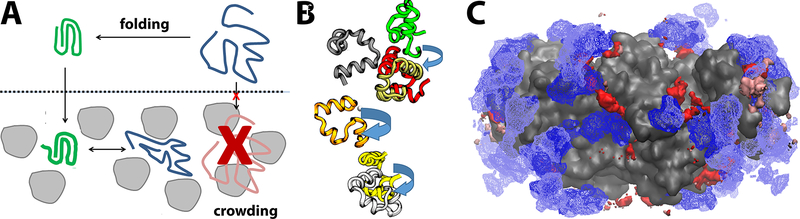
Figure 3:

Effects of cellular environments on stability, dynamics, and binding. Protein stability is altered in crowded cellular environments due to volume exclusion and interactions with crowder molecules (grey) (A) (Harada et al 2013); rotational diffusion in crowded environments depends on transient cluster formation in concentrated villin solutions (B) (Nawrocki et al 2017); binding of ATP (red with crowding, blue without crowding) to acetate kinase (grey) varies in the presence of crowders (C) (Yu et al 2016).

Stability and dynamics of biomolecules

Most biological macromolecules carry out their function in a well-defined native state. If that state becomes destabilized, function is compromised. The question whether crowded cellular environment affect biomolecular stability has been studied for quite some time (Minton & Wilf 1981, Zhou et al 2008, Zimmerman & Minton 1993). Initial studies have identified a largely stabilizing role of the volume exclusion effect under crowded conditions (McPhie et al 2006), but recent experiments suggest that crowding by proteins can have the opposite effect and destabilize native states (Ignatova et al 2007, Miklos et al 2010, Miklos et al 2011). The role of modeling and simulation has been to provide insight into mechanistic details of the experimental observations (Candotti & Orozco 2016, Feig & Sugita 2012, Harada et al 2013, Yu et al 2016) but also to generate new hypotheses for how the stability of biomolecules may be modulated under crowded conditions. One interesting observation from simulation is that metabolites at cellular concentrations appear to be able to induce more compact structures of phosphoglycerate kinase in a manner that otherwise resembles volume exclusion crowding effects (Yu et al 2016). Other studies have begun to examine the effects of cellular environments on nucleic acid structure. One finding is a possible shift between A- and B-DNA forms as a result of cellular environments (Yildirim et al 2014). These examples suggest that cellular environments may impact biomolecular stability in a variety of unanticipated ways. Simulations of biomolecules in cellular environments can in principle identify all of the factors that may be at play and it is likely that much is left to be discovered in that regard.

The conformational dynamics of biomolecules is related to their stability for natively folded proteins but becomes a separate topic for highly dynamic and intrinsically disordered systems (IDPs). Again, the general prediction from volume exclusion effects of crowding is that dynamic ensembles become more compact, but especially IDPs with polymer-like characteristics exhibit behavior that is different from globular proteins (Banks et al 2018, Kang et al 2015, Schuler et al 2016, Soranno et al 2014). Molecular simulations are ideally suited to study the dynamics of biomolecules in cellular environments. Especially IDPs under cellular or crowded conditions present rich opportunities as very few high-resolution simulation studies have been reported to date (Cino et al 2012).

Diffusion of biomolecules

Most biological function involves the encounter of different biomolecules. Therefore, diffusional properties are essential to understand biological function at the cellular level. It is clear that the diffusion of biomolecules is significantly retarded due to crowding (Banks & Fradin 2005, Dauty & Verkman 2004, Li et al 2009, Szymanski et al 2006, Wang et al 2010) but many questions remain about how diffusional properties vary for different molecules, in different local cellular environments, and over different time scales. More generally, it is also still unclear why exactly diffusion is slowed down in cellular environments and how rotational and translational diffusion may be affected differently (Roos et al 2016). Simulations of protein in cellular environments suggest that the propensity to transiently interact non-specifically is a key determinant of diffusional properties (Feig & Sugita 2012, McGuffee & Elcock 2010, Nawrocki et al 2017, Trovato & Tozzini 2014, Yu et al 2016). It appears that translational and rotational diffusion, at least in the short-time regime, can be essentially predicted from transient cluster formation (Nawrocki et al 2017). However, this view is at odds with other studies that ascribe hydrodynamic interactions a significant role (Ando & Skolnick 2010) or simply invoke increased solvent viscosity in crowded environments as the key factor (Ellis 2001). Again, molecular simulations of cellular environments are an ideal tool to dissect the different contributions to diffusion. Especially diffusion on longer time scales, in the presence of larger cellular components, and a better understanding of anisotropic characteristics in crowded systems are good opportunities for future studies.

Phase separation of biomolecules

Biomolecules can be viewed either as globular colloid-like particles or polymers with attractive and repulsive properties that exhibit different phase behavior depending on their interactions and concentration (Zhou & Pang 2018). All biomolecules aggregate into gel-like, amorphous, or crystalline solid phases at concentrations above the solubility limit. At lower concentrations, finite-size clusters (Kowalczyk et al 2011, Stradner et al 2004, Vorontsova et al 2015) or liquid-liquid phase separated states may form (Elbaum-Garfinkle et al 2015, Hyman et al 2014). Biomolecular aggregation is often associated with disease (Ross & Poirier 2004), but recent experiments suggest that phase separations can also have important functional roles (Shin & Brangwynne 2017), e.g. to facilitate the initiation of transcription (Boehning et al 2018). Phase separations in vivo are inherently a cellular-scale phenomenon with a physical origin at the molecular level. Therefore, physical models of cellular environments are well-suited to study such behavior. A major challenge is that it is necessary to describe the formation of macroscopic domains on macroscopic time scales based on molecular interactions at the atomistic level. While this is not feasible today with fully atomistic simulations, a viable strategy is to apply CG models that have been parameterized based on atomistic simulations and tuned based on available experimental data. For globular molecules, simple spherical models can be sufficient as such models have already provided much useful insight in colloid physics (Mani et al 2014, Woldeyes et al 2017, Zhuang & Charbonneau 2016). Phase separations involving IDPs are more challenging as they require higher resolution to capture the characteristics of flexible polymers. As very few studies have straddled the intersection between condensed phase physics and the complexities of biological environments to understand the phase behavior of biomolecules (Nguemaha & Zhou 2018, Qin & Zhou 2017, Woldeyes et al 2017) there is ample room for future modeling studies that can interpret the emerging experimental data.

Interactions with cellular components

Many studies of cellular environments focus on crowding and non-specific interactions within the cytoplasm (Gnutt & Ebbinghaus 2016, Yu et al 2016), neglecting the presence of genomic DNA, plasmids, membranes, organelles, and cytoskeletal elements. These large molecular structures present obstacles to diffusing molecules and present interaction surfaces with unique properties. For example, DNA is highly charged, even after condensation of counterions (Manning 1978) whereas membrane surfaces are ionic or zwitterionic at the water interface and hydrophobic when penetrated. Chromosomal DNA also has a porous structure that allows penetration of other molecules in a size-dependent fashion (Hacker et al 2017, Mondal et al 2011, Yildirim & Feig 2017). Much remains to be discovered about how biomolecules behave in the presence of such structures. For example, diffusion along DNA by DNA-binding proteins has been characterized relatively well (Marcovitz & Levy 2013, Schonhoft et al 2013, Tan et al 2016, Terakawa et al 2012), but much less is known about the diffusion of proteins that do not interact specifically with DNA in the presence of chromosomal DNA (Ando & Skolnick 2014). The interaction of biomolecules with membranes, on the other hand, is also well-explored for proteins that are known to interact with membranes either peripherally or via insertion (Ash et al 2004, Chavent et al 2016, Im & Brooks 2004, Jeon et al 2016, Kirchhoff et al 2008), but relatively little is known about non-specific interactions of biomolecules with membranes that are not known to be membrane-bound (Aisenbrey et al 2008) and effects of crowding on membranes (Guigas & Weiss 2016, Stachowiak et al 2012). There is a clear need for modeling studies to investigate such questions in more detail which will be possible once high-resolution structure of genomic DNA are available and realistic models of biological membranes that include membrane proteins can be constructed.

Ligand binding in cellular environments

The applications of whole-cell models discussed so far focus on fundamental scientific questions. However, the most significant impact may be the ability to study ligand binding in vivo as that would ultimately allow in cellulo rational drug design so that specificity and selectivity can be considered from the very beginning when evaluating potential new drug candidates. While it will be a while before practical methods for in cellulo drug design can be developed, many questions about the binding of ligands in cellular environments can be addressed in the meantime. One key question is whether cellular environments alter ligand binding affinities or pathways. Another question is to what extent ligands interact non-specifically with biomolecules. One possible effect on biomolecular structure has already been mentioned above, but extensive interactions of ligands with biomolecules may also alter solvation properties and solubility. One example is the increase of protein solubility in the presence of ATP (Patel et al 2017). From the ligand perspective, the consequence of extensive non-specific interactions means sequestration that results in an effectively lower concentration and lower average diffusion rates. Experiments as well as simulations have provided some evidence that this may indeed be a significant effect (Duff et al 2012, Yu et al 2016). Substrate channeling between enzymes, although known for a long time (Miles et al 1999), is a related topic that is not well understood in the context of cellular environments. Therefore, it is clear that further studies are needed to gain a better understanding of ligand binding in cellular environments.

CONCLUSIONS AND OUTLOOK

We are entering a time where it is possible to model and simulate cellular environments in full molecular detail. This allows a full connection between structure and systems-level biology and in principle opens up vast predictive abilities for connecting changes at the molecular level to biological function. An important implication is the potential to better understand disease origins and develop new, more effective therapies where side effects are accounted for from the beginning of the design process. On the practical side, although first models of minimal cellular environments in full atomistic detail have emerged (Feig et al 2015, Yu et al 2016), many challenges remain. The simulation of such systems on biologically relevant time scales is the biggest hurdle, but a lack of experimental data, especially for biomolecular structure, hinders progress as well. A viable strategy may be to apply multi-scale modeling strategies where atomistic models are used only to establish shorter-term behavior at the molecular scale and train coarse-grained models that can reach larger scales. Even just at intermediate scales of individual biomolecules exposed to cellular environments, instead of modeling entire cells, there is actually much that remains to be learned in terms of fundamental biophysics and this is probably where physical models of cellular environments can have the greatest impact in the near future. However, as the understanding of biomolecular behavior in cells becomes more comprehensive, physical models could be coupled with kinetic network models to add reactivity and access even longer time scales. Ultimately, only a fully integrated approach that applies different, but connected frameworks across different scales will likely succeed in truly capturing how molecular behavior in cellular environments leads to cellular phenotypes. The focus of this review is on computational modeling, but the role of experiments is essential, not just to provide input data but to validate results from modeling and simulation. This will require advances also on the experimental side which we hope will be stimulated by progress on the modeling side.