Detecting Time-Evolving Phenotypic Topics via Tensor Factorization on Electronic Health Records: Cardiovascular Disease Case Study

Abstract

Objective

Discovering subphenotypes of complex diseases can help characterize disease cohorts for investigative studies aimed at developing better diagnoses and treatments. Recent advances in unsupervised machine learning on electronic health record (EHR) data have enabled researchers to discover phenotypes without input from domain experts. However, most existing studies have ignored time and modeled diseases as discrete events. Uncovering the evolution of phenotypes – how they emerge, evolve and contribute to health outcomes – is essential to define more precise phenotypes and refine the understanding of disease progression. Our objective was to assess the benefits of an unsupervised approach that incorporates time to model diseases as dynamic processes in phenotype discovery.

Methods

In this study, we applied a constrained non-negative tensor-factorization approach to characterize the complexity of cardiovascular disease (CVD) patient cohort based on longitudinal EHR data. Through tensor-factorization, we identified a set of phenotypic topics (i.e., subphenotypes) that these patients established over the 10 years prior to the diagnosis of CVD, and showed the progress pattern. For each identified subphenotype, we examined its association with the risk for adverse cardiovascular outcomes estimated by the American College of Cardiology/American Heart Association Pooled Cohort Risk Equations, a conventional CVD-risk assessment tool frequently used in clinical practice. Furthermore, we compared the subsequent myocardial infarction (MI) rates among the six most prevalent subphenotypes using survival analysis.

Results

From a cohort of 12,380 adult CVD individuals with 1,068 unique PheCodes, we successfully identified 14 subphenotypes. Through the association analysis with estimated CVD risk for each subtype, we found some phenotypic topics such as Vitamin D deficiency and depression, Urinary infections cannot be explained by the conventional risk factors. Through a survival analysis, we found markedly different risks of subsequent MI following the diagnosis of CVD among the six most prevalent topics (p < 0.0001), indicating these topics may capture clinically meaningful subphenotypes of CVD.

Conclusion

This study demonstrates the potential benefits of using tensor-decomposition to model diseases as dynamic processes from longitudinal EHR data. Our results suggest that this data-driven approach may potentially help researchers identify complex and chronic disease subphenotypes in precision medicine research.

Graphical Abstract

Introduction

Chronic diseases such as diabetes, Alzheimer’s disease, and cardiovascular disease (CVD) affect more than 50% of the population, drive up to 90% of healthcare spending in the United States, and are the leading causes of mortality and disability globally.^1–5 Chronic diseases commonly have complex causal mechanisms involving the interplay between genetic, environmental, and lifestyle factors.⁶ Chronic diseases may present with numerous signs and symptoms involving multiple physiologic systems and typically co-occur with other conditions.⁴ For example, CVD patients often present with multiple comorbidities including hyperlipidemia, diabetes, and hypertension.⁷ However, known risk factors (e.g. Framingham study⁷) for CVD may only explain ~75% of major CVD events.⁸ A more precise characterization of complex chronic disease based on different patterns of comorbidities may help identify subpopulations to facilitate prevention, early detection and precise treatment.

Deep phenotyping is a method for identifying disease cohorts that incorporates multiple categories of EHR data. ⁹ Traditional phenotyping algorithms typically require feature engineering and multiple cycles of review from experts to specify inclusion and exclusion criteria on a data set. This does not scale well to large patient cohorts. ^10–12 To address this problem, researchers have developed data-driven approaches to facilitate automated phenotyping. Using a training set including labeled cases and controls (i.e. gold standard), some methods use feature selection techniques ¹¹ or machine learning classifiers ^11,13 to build a phenotyping model.¹⁴ Other methods start with a set of core concepts and use natural language processing to automatically find the occurrence of matched terms in clinical notes, which can be used as input features to build a classifier to predict the target phenotype.^15,16 Most approaches achieve success on a broad range of algorithms through a collaboration among informaticians and clinical experts ¹⁷ However, such supervised methods still need to specify an outcome variable (e.g. a target phenotype) and labeled dataset (e.g. cases or controls). Due to the complexity of the contributing factors of a complex disease and their intricate interactions, such supervised approaches are unsuited to the scenario in which we have limited knowledge to label the phenotypes, and we wish to discover them from the data.¹⁸

Recent advances in unsupervised computational phenotyping have allowed researchers to discover phenotypes from EHR with minimal human guidance.^1,16,18,19 Rather than relying on the pre-defined outcomes, these unsupervised approaches can identify patterns in the entire data source.¹⁸ One such method is topic modeling approach including non-negative matrix factorization (NMF) and Latent Dirichlet Allocation (LDA).^19–21 Researchers have applied these approaches to EHR to identify phenotype candidates –clusters of patients that met with clinical conditions– with no pre-defined phenotype definitions. ^11,20–24 For example, we have previously used NMF to find disease topics (described by clusters of co-occurring symptoms) and study their associations with genetic variants.²⁵ Aside from replicating known signals, we also reported a new correlation between a lipoprotein(a) (LPA) variant (rs10455872) and a topic enriched for lung cancer which was not previously identified via phenome-wide scanning. ²⁵

Nevertheless, these studies typically overlook the valuable information conveyed by a temporal pattern of phenotypes input. The comorbidities and effects of complex chronic diseases like CVD typically evolve and progress over a long time. Thus, incorporating a time effect into phenotyping may help yield more precise phenotypes. Current unsupervised techniques such as LDA and NMF have difficulty capturing the temporal changes of topics²⁶. Others have proposed training separate topic models for each time slice, but accurately measuring the connections of topics from different time slices remains a challenge.^27–29

In this paper, we applied a constrained non-negative tensor-factorization approach to extract phenotypic topics across time scales. This approach models an individual’s medical data as a third-order tensor (i.e., a three-way data array, a cube instead of the matrix) with each order representing phenotypes, time and individuals respectively. By fitting a tensor-factorization model, we can identify a set of topics (i.e., subphenotypes), describe their progress, and obtain patients’ representations in such topics at the same time. Identifying subphenotypes enables us to generate testable hypotheses of how complex diseases differ across patients, such as in temporal disease progression. Furthermore, it may provide insight into differences in the temporal progression of the disease. To demonstrate the feasibility and utility of the approach, we apply this method to EHR data of a large cohort of CVD patients. We identify CVD topics that represent clinically meaningful subphenotypes, some of which are not captured by traditional clinical assessment tools for CVD risk. This approach may improve understanding of disease progression over time, and identify novel subphenotypes that may be used for enhancing precision treatment.

Background and related work

Tensor decomposition (or factorization) can be treated as an extended NMF on high-dimensional data.

Non-negative Matrix Factorization (NMF) for Topic Modeling

NMF assumes that given an n· m sparse data matrix X with n samples (e.g. documents) and m dimensions can be approximated by a small set of k basis vectors – an inner-product of two non-negative matrices W and H such that

$$\Vert X-WH{\Vert }_F^2$$ (1)

is achieved subject to W ≥ 0, H ≥ 0 where || · ||²_F is the Frobenius norm to measure the error between the original data and the approximation. In the context of topic modeling, H is a k × m (k ≤ m) topic – word matrix, indicating m words’ weights corresponding to k topics, and W is an n × k document-topic factor matrix, indicating n documents’ relevance score to k topics. From H, we can order each word’s weights in a particular topic and use the top words to describe topics. Furthermore, W can be used to represent documents for regression and clustering tasks. However, NMF fails to capture the temporal changes of topics.

Tensor decomposition

Tensor decomposition (or factorization), analogous to NMF, can learn latent factors from high dimensional data. After being introduced in 1927 ³⁰, tensor factorization regained popularity in the computer science community in the late 20^th century ^31,32, and until recently, proliferated into many other fields ^33–35. Sun et al. have used PARAFAC2 ³⁶ on automated phenotyping for medically complex children who need intensive medical care due to multisystem dysfunction, technology dependence, or complex medication needs ³⁷. Their extract disease topics, however, may not be independent because they did not impose any orthogonality restraints. Bahargam et al. have utilized tensor factorization in text mining to find dynamic topics from forums. ³⁸ They introduced a method that can add orthogonality or sparsity constraints on each mode. In this study, we used this method to discover the phenotypic topic in longitudinal EHR.

Materials and Method

Data preparation

Study cohort

We used the data from Synthetic Derivative, a database that contains a de-identified copy of the EHR for every patient in the Vanderbilt University Medical Center (VUMC) system (>3 million patients). Our cohort included individuals: 1) phenotype codes (PheCodes) 39 of 411.* or 433.*, i.e., International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) 346.6*(Persistent migraine aura with cerebral infarction), 410–414 (Ischemic Heart Disease), 433–438 (Cerebrovascular Disease, excluded hemorrhage), 996.03 (Mechanical complication due to coronary bypass graft ), V12.54 (Personal history of transient ischemic attack [TIA], V45.81(Aortocoronary bypass status), V45.82 (Percutaneous transluminal coronary angioplasty status), and 2) had ≥ 10 years of EHR data prior to the first diagnosis. For each individual, we defined the baseline date (time 0) as 3 months before their first CVD event date. We extracted the diagnosis codes within the 10-year observation window before their baseline date.

Preprocessing data

From each individual’s records, all distinct ICD-9-CM billing codes within the observation window are captured and grouped into 1821 distinct PheCodes ³⁹. This mapping scheme was developed and validated manually by our group to facilitate high-throughtput phenotypic analysis. ⁴⁰ The phenotype codes have been used in several systematic analyses to successfully replicate previously known gene-disease associations and discover potentially novel pleiotropic associations. ³⁹

We filtered out rare PheCodes (i.e. prevalence <=0.5%) to avoid overfitting and achieved 1068 unique PheCodes. We divided the 10-year observation period into one-year slice windows. For each PheCode, we used a binary value (i.e. 1 or 0) to indicate whether or not a patient had a particular diagnosis each year.

Constructing a tensor from the dataset

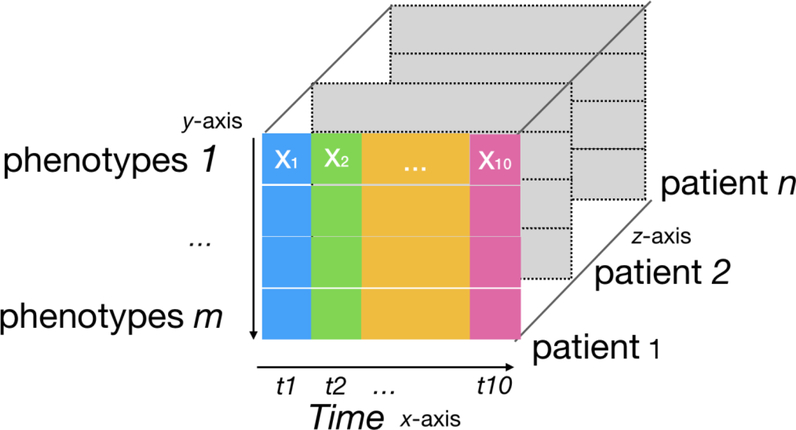
We introduce the following notation for the construction of the data tensors. First, for each patient i ∈ {1,...,n} we constructed a matrix, X_i, of dimensions m × t where m denotes the size of PheCodes, and t is the number of time windows; this matrix X can be treated as a vertical slice of the full tensor T. Then we concatenated each matrix X_i to construct a tensor T of three modes (i.e. axes) corresponding to phenotypes, time windows, and patients. Figure 1. illustrates this construction graphically. Each tensor cell contains a binary value (1 or 0) indicating whether each patient i-th has the PheCode m in t-th window. By slicing the T among different axis, we achieved three modes indicating different views of the data:

Figure 1.

Input data representation for tensor factorization. Each slice along the z-axis is a patient record. In such a slice, each row represents a phenotype (PheCode), and each colored column represents a one-year time interval.

• Phenotype mode (x-z axis): a matrix of a phenotype assigned to all patients across time windows

• Time mode (y-z axis): a matrix of phenotypes from all patients in the specific time window

• Patient mode (x-y axis): a matrix of a patient’s phenotypes across all time windows

Detecting evolving-topics via tensor factorization

Problem formulation

Now that we have described the process of structuring our data in terms of three-dimensional tensors, we describe how to detect time-evolving topics. Given a tensor T, we factorize T into:

$$T={\sum }_{f=1}^k{a}_f\otimes b_f\otimes c_f+e$$ (2)

where a_f, b_f, and c_f correspond to the f-th columns of three-factor matrices: A, B, and C. Specifically, the interpretation for A, B, and C is:

• The factor matrix A corresponds a phenotype – topic matrix of size m × k, where each row denotes phenotypes, and each column represents a topic. Each element a_if represent a weight of i-th phenotype on the f-th topic.

• The factor matrix B corresponds to a time – topic matrix of size t × k, where each row represents a time window and each column represents a topic. The element b_jf represents the f-th topic’s weights or strength in j-th time window.

• The factor matrix C is a patient- topic matrix of size n × k, where each row indicates a patient, and each column represents a topic. The element c_zf represents the z-th patient’s weight on f-th topic.

We normalize each column in the factor matrix (making the length of the column to 1).

The e indicates the error between the original input data T and approximation of the outer product of three factors. We can find A, B, and C that best approximate the input tensor by minimizing the e. Thus, equation (2) can be written as an optimization problem:

$$\underset{A,B,C}{min}\Vert T-{\sum }_{f=1}^k{a}_f\otimes b_f\otimes c_f{\Vert }_F^2$$ (3)

Each factor column a_f, b_f, and c_f corresponds to a disease topic (component) represented in an object in each mode.

To yield clinically interpretable results, we imposed the following constraints:

• Non-negativity: For better interpretability, we restrict the factor matrices A, B, and C to be non-negative: A ≥ 0, B ≥ 0, C ≥ 0.

• Orthogonality: To generate distinct (less overlapped) and independent topics, we imposed orthogonality constraints on the factor matrix (i.e., columns in a factor matrix should be close to orthogonal):

$$\forall i,j\in k,i\ne j,A_i^T{A}_j\le {ϵ}_A,B_i^T{B}_j\le {ϵ}_{B,}{C}_i^T{C}_j\le {ϵ}_c{ϵ}_A,{ϵ}_B,{ϵ}_c\in [0,1]$$

We assumed disease topics to be distinct (less overlapped) and independent. Thus, we imposed strict orthogonality on factor matrix a (i.e., word-topic model) with ∈_A 0.05 (columns in a factor matrix should be close to orthogonal). We relaxed the constraints on B (time-topic) and C (patient-topic) factor matrices by setting ∈_B = 1 and ∈_c= 0.8, because certain topics may have similar time trend, and patients may be inherently similar to others.

• Sparsity: Comparing to the large size of phenotypes, comorbidity or disease may present only a few of them. Similarly, a patient may only have a few comorbidities. Thus, we imposed L1-norm41 on each column in the factor matrix to fortify the sparsity:

$$\forall i\in k,{\Vert A_i\Vert }_1\le {\gamma }_A,{\Vert B_i\Vert }_1\le {\gamma }_B,{\Vert B_i\Vert }_1\le {\gamma }_c;{\gamma }_A,{\gamma }_B,{\gamma }_c\in [0,1]$$

To yield interpretable topics, we used sparsity constraints in this study γ = [0.8,1,1]. Small γ would yield more sparse weights (i.e. a lot of zero weights). We expected PheCode weights in the topic to be sparse for better interpretation. We did not limit sparsity on time and patient factor.

As the equation (2) is not a convex function, we utilized a PARAFAC decomposition with alternating least squares (ALS) to solve it ^42,43. PARAFAC is one of several decomposition methods for multi-way data. Compared with other competitors, such as Tucker3 and unfolding of the multi-way array to a matrix and then performing standard two-way PCA, PARAFAC had fewer parameters and resulted in the most simple and restricted model. ⁴³ Solving PARAFAC required a significant amount of time to run, but fortunately, ALS increased computational efficiency resulting in decreased required clock-time. Also, by iteratively fixing two factors, the equation (2) becomes convex for each intermediate step. We implemented the approach based on Matlab CMTF⁴² and tensor toolbox. The convergence criteria was 10e-5. ⁴⁴

Choosing the number of disease topics

To decide the number of topics (k), we plotted the decay of eigenvalues of the unfolded-input data. The point of inflection can suggest a range of candidate k. To decide the specific k, we considered two metrics: the coherence within a topic (i.e., whether a topic can represent a single theme or similar concept) and the similarity between topics. We first measured topic coherence by using UMass,⁴⁵ which calculates the co-concurrency of the topic descriptors in the original EHR data. Topics with higher UMass are easier to interpret. The similarity between topics can be measured with mean pairwise Jaccard similarity (mean_Jaccard),⁴⁶ or cosine similarity ⁴⁷, reflecting the overlapping degree between topics. We expected the topics should have less similarity. To select the K, we standardized the UMass and the 1/mean_Jaccard and summed these two as the topic quality score. We calculated the topic score for k from 5 to 15. We ranked the topic quality scores in descending order and selected the top 10 highest quality scores. Then we picked the largest K (within the suggestion range), because a larger number of topics may explain more of the input data variation. We involved three reviewers with clinical backgrounds to review the results ⁴⁸. We designed two surveys at the topic and patient levels (Appendix B).

To visualize the topic results, we employed word clouds to present top-ranked phenotypes in a topic. Patients were represented in combined weights of topics (patient-topic factor matrix). We assign a patient to the topic group with the maximum weight. We used t-Distributed Stochastic Neighbor Embedding (t-SNE) to project the patient-topic on a 2-dimensional (2D) map to visualize the similarity between topic groups.

Statistical analysis

Correlation between topics and conventional assessments of CVD risk

For each topic, we examined its association with the risk estimated by the American College of Cardiology/American Heart Association (ACC/AHA) Pooled Cohort Risk Equations ² (ACC/AHA Pooled Equations), which is a widely used clinical tool to estimate 10-year risk of atherosclerotic cardiovascular disease (ASCVD) events - a composite of MI, stroke, or cardiovascular death - based on conventional risk factors, e.g., age, gender, hypertension and smoking status. The goal of the association analysis was to examine the correlation between each topic and the conventional assessed risk of significant cardiovascular outcomes. We hypothesized that our approach would identify subphenotypes where the CVD risk was not adequately captured by a conventional risk assessment tool.

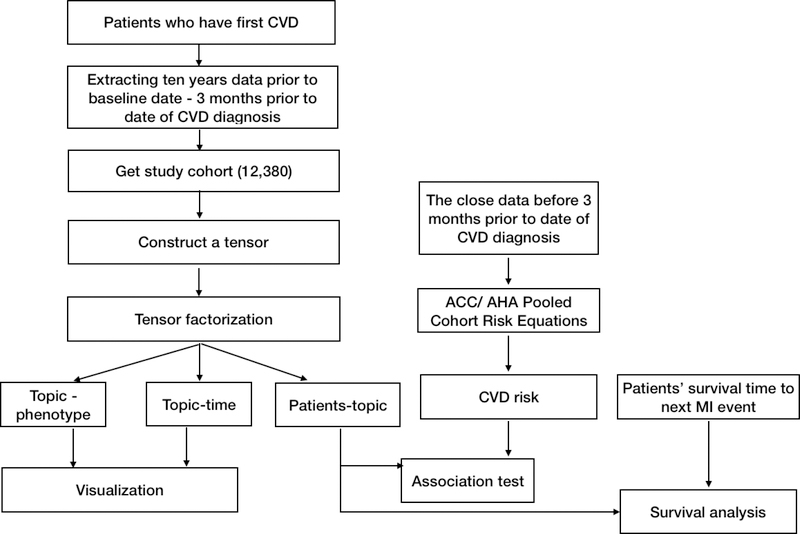
To apply ACC/AHA Pooled Equations to the CVD patients (Figure 2), we collected demographics, hypertension drug usage, smoking status, the most recent physical measurements and lab values (i.e. SBP/DBP and high-density lipoprotein [HDL]- cholesterol level) before the baseline date. We replaced the missing physical or laboratory measures using the median values from the same age, gender and race group. We calculated the ASCVD risk for each individual based on the ACC/AHA Risk Equations.

Figure 2.

Study Design

For each topic, we examined its association with the 10-year CVD risk estimated by ACC/AHA equations using the Pearson correlation coefficient (PCC). The study reported the coefficient and p-value. The level of significance was set at p < 0.05 / number of topics (Bonferroni correction). We further stratified patients into high - (risk probability≥20%) and low - risk (risk probability<7.5%) category ⁵⁰, and plotted the distribution of high/low -risk patients in the top six prevalent topics (Figure A.8). We aimed to find if high or low-risk patients would present any difference in such phenotypic topics.

Risk of subsequent MI among subphenotypes

To demonstrate the clinical importance of the topics, we evaluated the risk of subsequent MI event for topics through survival analysis. We hypothesized that topics would vary in the survival time from their initial diagnosis of CVD to subsequent MI. We first examined Kaplan-Meier plots stratified by topic. The start date of the time outcome (time period 0) was the date of the first CVD diagnosis. The observation time was between time period 0 and the subsequent MI. For patients who had no subsequent MI, we right-censored such patients at the last date they were observed at VUMC. We also applied a Cox proportional hazards regression model using patient’s weights of topics, age, and gender as covariates. We calculated hazard ratios for each topic along with their corresponding confidence intervals and p-values.

Results

Time-evolving disease topics

We identified 12,380 adult CVD patients and extracted 1068 unique PheCodes among them. We applied an unsupervised tensor-factorization on the dataset. In determining the number of topics (k), we tried k from 5 to 20 and set the number of topics as 14 in the study according to the measuring process (Figure A.1–A.3). Three reviewers with clinical practice or medical training background validated the results to ensure clinical relevance (Appendix B). The results showed that at the topic level, the average rating was 1.45 (an ordinal scale of 0–2 [i.e.0-not clinically meaningful;1- possibly clinically meaningful; 2 - clinically meaningful], with a Fleiss’ Kappa ⁵¹ score of 0.41 (moderate agreement). At the patient level, the mean of the three reviewers rating score was 1.16 (an ordinal scale of 0–2 [i.e.0-not relevant;1- relevant; 2- highly relevant], with a Fleiss’ Kappa score of 0.45, suggesting that the topics assigned to each patient were relevant to the patient’s history.

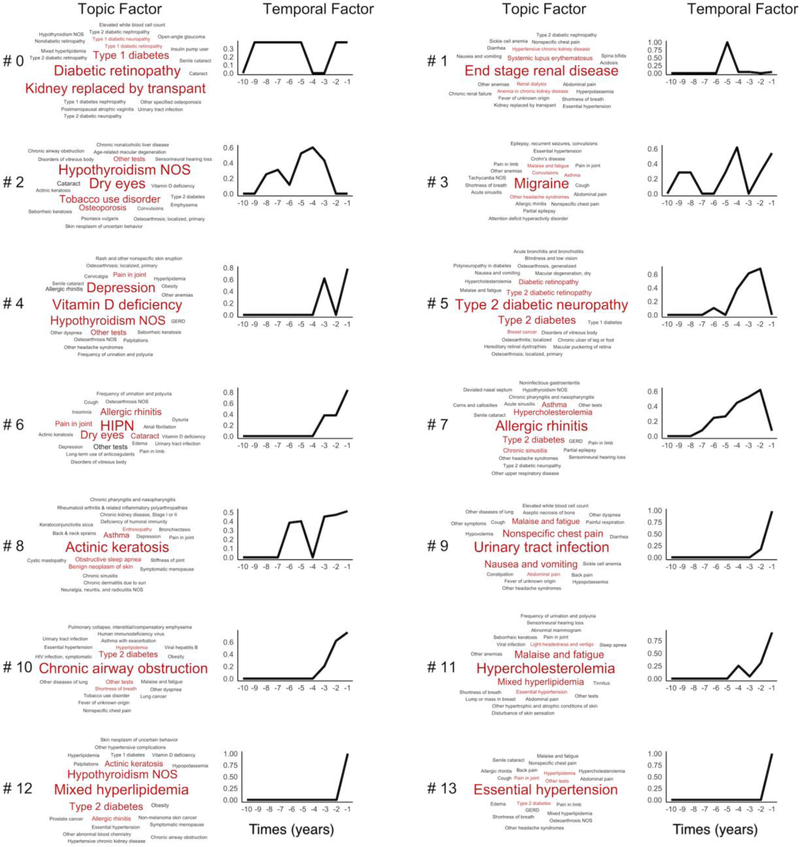
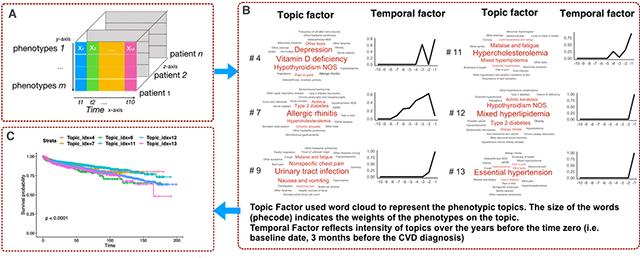
Figure 3 showed the learned 14 topics and the progression pattern over the 10 years prior to the first diagnosis of CVD. Topic #0 and Topic #1 were enriched for serious kidney disease, with more relevance with Type 1 Diabetes in Topic #0 than Topic #1. Topic #4 was enriched for Vitamin D deficiency, Depression, and Hypothyroidism NOS. Topic #5 clustered around complications of Type 2 diabetes, such as Type 2 diabetic neuropathy and Type 2 diabetic retinopathy. Topics #11 and #12 both had lipid disorders as their top diagnoses (Hypercholesterolemia and Mixed Hyperlipidemia, respectively). Yet, they differed substantially in associated diagnoses: Malaise and fatigue, Mixed hyperlipidemia, and Essential hypertension were enriched in Topic #11; while Hypothyroidism NOS and Type 2 diabetes were enriched in Topic #12.

Figure 3.

Tensor factorization on 10 year-diagnoses prior to CVD diagnosis. Each topic contains the topic factor, represented by a word cloud and a time factor showing the time trend. The word size of a PheCode is proportional to its weight (i.e. influence) for the topic (from factor A), e.g. Essential hypertension has a larger influence than GERD within Topic #13. The x-axis on the line charts represent the years prior to the diagnosis of CVD, increasing from 10 years to 1 year prior to CVD. The y-axis represents the mathematical weights (from time factor B) for the respective topics for each year prior to the diagnosis of CVD. HIPN in Topic #6: Hereditary and idiopathic peripheral neuropathy.

The time trend in Figure 3 shows the trajectory of each topic before the first diagnosis of CVD. Specifically, it reflects the changes in the combined intensity of the phenotypes (in the topic) in patients assigned to the topic group from the last 10 years to the first CVD diagnosis. For example, when close to the first CVD, patients in Topic #13 have a sharp increase, which means more Essential hypertension appear in the topic group. Patients in Topic #7 (Allergic rhinitis) increased the events slowly but have a small drop when close to the first CVD.

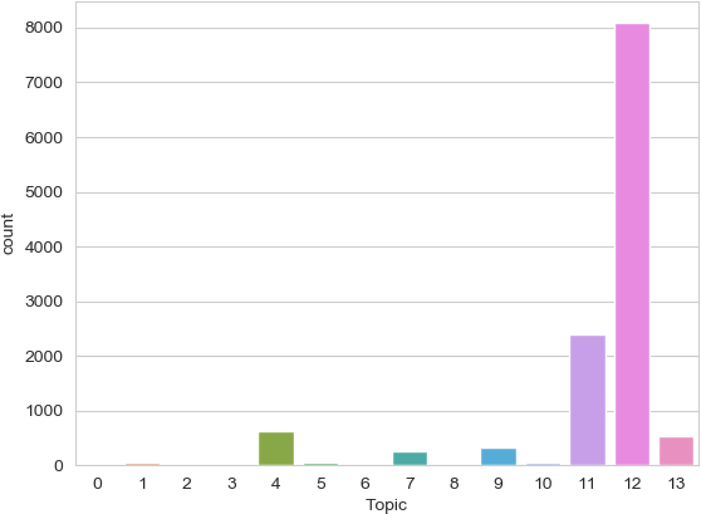
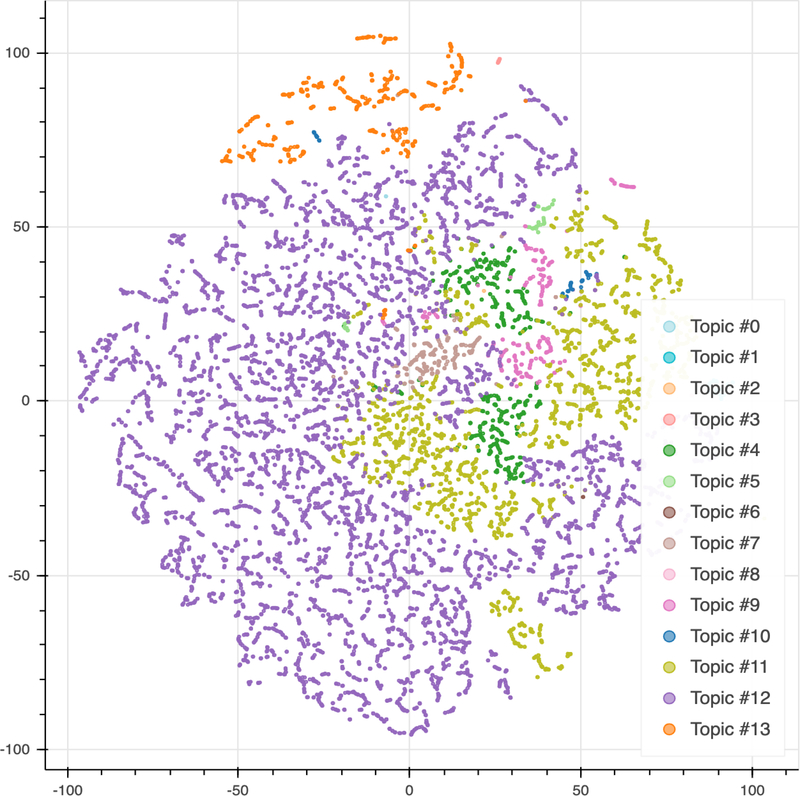
We assigned the patients into their best-fitting topic according to their maximum weights (Fig 4). Topic #12 (Mixed Hyperlipidemia) was the most prevalent topic in the cohort with 8078 patients. Topic #11 (Hypercholesterolemia), Topic #4 (Vitamin D deficiency) and Topic #13 (Essential hypertension) were other prevalent topics in the cohort with 2386, 627, and 541 patients, respectively. Figure 5 showed the visualization of patients-topics in a 2D map using t-Distributed Stochastic Neighbor Embedding (t-SNE). Topic #13 (Essential hypertension) formed a distinct group separate from other groups on the top of the figure.

Figure 4. Topic distribution in the cohort.

To visualize the frequency of each topic in the cohort, we assigned an individual to the topic with the maximum score. The vertical axis represents the number of patients. Topics are plotted on the horizontal axis.

Figure 5. t-SNE visualization of topic clusters.

Each data point represents an individual and the color of each data point represents the topic with the maximum score for that individual. We used principal component analysis (PCA) for t-SNE embedding initialization.

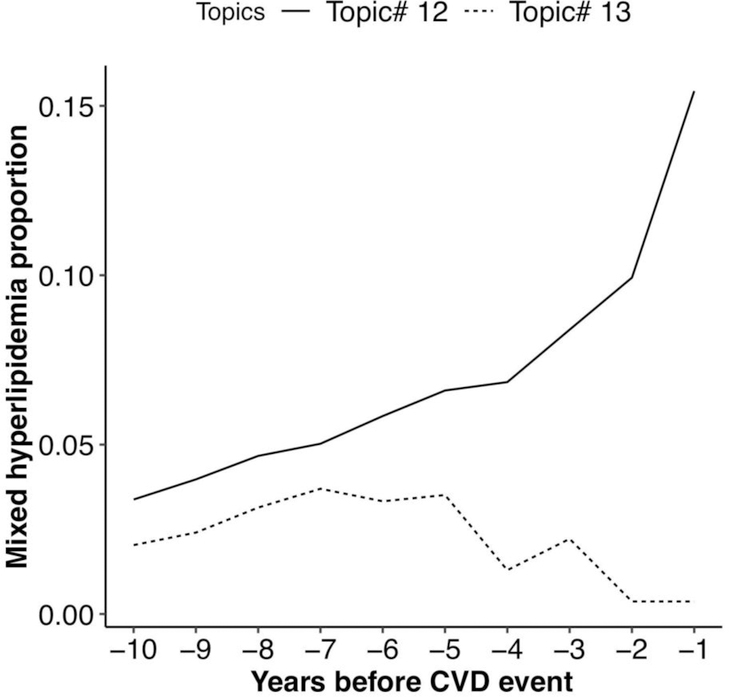
To illustrate the differences in mixed hyperlipidemia between topics, we compared the prevalence of mixed hyperlipidemia between the patients who were assigned with Topic #12 and Topic #13 (Figure 6). Overall, the proportion of patients with Mixed Hyperlipidemia in Topic #13 was smaller than Topic #12. Although the proportion of patients with Mixed Hyperlipidemia was initially similar, the proportions diverged starting at approximately 5 years prior to the CVD event. At that point, the proportion of patients with Mixed Hyperlipidemia in Topic #12 increased substantially, whereas Mixed Hyperlipidemia declined among patients in Topic #13.

Figure 6.

Proportion of patients with mixed hyperlipidemia in patients assigned with Topic #12 (Mixed hyperlipidemia) and Topic #13 (Essential hypertension).

Analysis of correlation between topics and conventional assessments of CVD risk

We applied ACC/AHA Pooled Cohort Risk Equations to calculate the 10-year ASCVD risk for each patient (Table A.1). Table 1 summarizes the association result between topics and the ASCVD risk estimated by ACC/AHA equations. Topics such as #11 (Hypercholesterolemia), Topic #12 (Mixed hyperlipidemia, Type 2 diabetes), and Topic #13 (Essential hypertension) significantly correlated with an increased estimated risk of ASCVD. Among the most prevalent topics, Topic #4 (Vitamin D deficiency, Depression), Topic #7 (Allergic rhinitis), and Topic #9 (Urinary tract infection) have no significant associations between the estimated risk of ASCVD. Figure A.8 further presents the proportion of stratified risk in the top prevalent topics. Topic#11, Topic #12 and Topic #13 contained a higher proportion of high-risk patients than low-risk patients. Both high and low-risk patients present in Topic #9 and Topic #4, with a similar proportion, suggesting that the conventional risk assessment tool did not capture the true risk of CVD for patients in these subphenotypes.

Table 1.

Pearson correlation coefficient testing between topics and estimated ASCVD risk. Significance level after Bonferroni correction is p<0.0036 (0.05/14).

Topic	Top phenotypes	Co-efficient	p-value
#0	Diabetic retinopathy, Kidney replaced by transplant, Type 1 diabetes, Type 1 diabetic retinopathy	−0.004	0.683
#1	End stage renal disease, Systemic lupus erythematosus, Renal dialysis, Anemia in chronic kidney disease	−0.002	0.817
#2	Dry eyes, Hypothyroidism NOS, Tobacco use disorder, Osteoporosis	0.019	0.032
#3	Migraine, Convulsions, Other headache syndromes, Asthma	−0.020	0.025
#4	Vitamin D deficiency, Depression, Hypothyroidism NOS, Other tests	−0.001	0.016
#5	Type 2 diabetic neuropathy, Type 2 diabetes, Type 2 diabetic retinopathy, Diabetic retinopathy	0.016	0.071
#6	Hereditary and idiopathic peripheral neuropathy, Dry eyes, Allergic rhinitis, Cataract	0.016	0.06
#7	Allergic rhinitis, Type 2 diabetes, Hypercholesterolemia, Asthma	0.010	0.267
#8	Actinic keratosis, Asthma, Obstructive sleep apnea, Benign neoplasm of skin	−0.006	0.528
#9	Urinary tract infection, Nonspecific chest pain, Nausea and vomiting, Malaise and fatigue	−0.011	0.197
#10	Chronic airway obstruction, Type 2 diabetes, Other tests, Hyperlipidemia	0.043	1.932e-06
#11	Hypercholesterolemia, Malaise and fatigue, Mixed hyperlipidemia, Essential hypertension	0.035	1.20e-04
#12	Mixed hyperlipidemia, Hypothyroidism NOS, Type 2 diabetes, Actinic keratosis	0.061	1.063e-11
#13	Essential hypertension, Other tests, Type 2 diabetes, Pain in joint	0.054	1.292e-09

Survival analysis

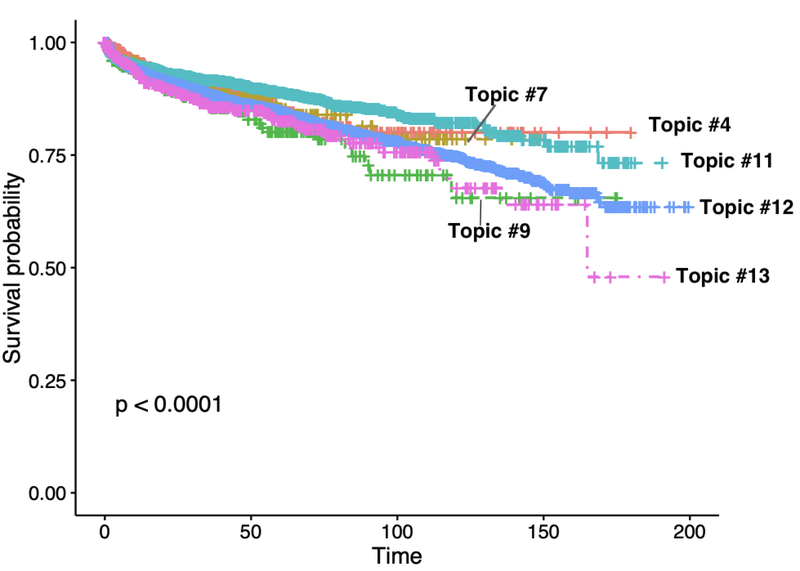
We assessed the risk of subsequent MI following the diagnosis of CVD by using a Kaplan-Meier plot. We stratified patients by the maximum observed weight for each individual among the six most prevalent topics: Topic #4 (Vitamin D deficiency, Depression), Topic #7 (Allergic rhinitis), Topic #9 (Urinary tract infection), Topic #11 (Hypercholesterolemia), Topic #12 (Mixed hyperlipidemia) and Topic #13 (Essential hypertension) We observed a significant difference among these groups (p<0.0001, Figure 7), implying these subgroups may have the differing risk of subsequent MI.

Figure 7.

Associate topic groups (top six prevalent) with the next myocardial infarction (MI) event by fitting a Kaplan-Meier model. The x-axis represents the months between the first diagnosis of CVD and the next MI event. The y-axis represents the probability of an individual surviving past time t with respect to second MI.

We then fit the Cox model with the topic weights as covariates using the lifelines Python package (0.20.0).⁵² Table 2 summarizes the topics that have a significant association with the subsequent MI. We observed that patients who have higher weights in topics #5 (Type 2 diabetic neuropathy, Type 2 diabetes), and Topic #13 (Essential hypertension) had increased the risk for subsequent MI. Patients with Topic #11 (Hypercholesterolemia) had decreased risk for a subsequent MI.

Table 2.

Cox regression models to examine the association between phenotypic topics and the subsequent MI event. We report topics significantly associated with subsequent MI event (statistically significant at the 0.05 level) and provide their corresponding hazard ratio, p-value and 95% confidence interval.

Topic #	Top phenotypes	Hazard ratio (HR)	P	CI
5	Type 2 diabetic neuropathy, Type 2 diabetes, Type 2 diabetic retinopathy, Diabetic retinopathy	29.66	<0.005	(7.6, 127)
11	Hypercholesterolemia, Malaise and fatigue, Mixed hyperlipidemia, Essential hypertension	1.10e-14	0.01	(1.589e-25, 1.132e-03)
13	Essential hypertension, Other tests, Type 2 diabetes, Pain in joint	2.12	0.02	(1.15, 3.86)

Table 2 Cox regression models to examine the association between phenotypic topics and the subsequent MI event. We report topics significantly associated with subsequent MI event (statistically significant at the 0.05 level) and provide their corresponding hazard ratio, p-value and 95% confidence interval.

Discussion

In this study, we leveraged a constrained non-negative tensor-decomposition method to detect time-evolving phenotypes in CVD patients. Compared to previous studies,¹ our approach captures both subphenotypes and their dynamics over time. We examined the association between the phenotypic topics and the estimated ASCVD risk calculated using conventional clinical tools. Results from this analysis showed that some phenotypic topics were not correlated with conventional CVD risk factors, suggesting that individuals with these subphenotypes may be affected by sub phenotypic diseases with different pathophysiologic causes. Furthermore, we observed significant differences in subsequent MI rates between the six most prevalent subphenotypes.

Comparison with traditional NMF

We compared our method with traditional NMF on each time slice of patients’ diagnosis (Appendix F). We measure the stability score (range [0, 1]) between topics of each time slice using Jaccard similarity and Hungarian method.⁴⁹ From the stability plot (Figure A.10), we observed that the similarity between topics in the last first year and last 3 – 10 years were less than 50%, which means the topics changed over 10 years. It would be difficult to read, interpret and trace how topics change using traditional NMF. Further, it lacked a persuasive methodology to combine the weights of topics from each time slice to represent a single patient. Compared to the traditional NMF, our approach provides a solution for data exploration to 1) better show the dynamic changes of the subphenotypes; 2) generate the representations and topic membership for patients to facilitate the analysis.

Choosing the number of factors

Topic modeling and tensor decompositions and related unsupervised learning approaches require pre-specification of topic numbers, k. Choosing the optimal number of topics remains challenging. General approaches include: looking at residuals (e.g. construction errors), plotting the decay of singular values or the percentage of explained variance such as scree-plots and core consistency, and evaluating the interpretability of the factors. Selecting the approaches should consider the characteristics of input data (e.g. data size, sparsity, binary), the goal of the task, and the computing time. In this study, we first plotted the decay of singular values to get suggested candidates of k. As we aimed to yield distinct and interpretable subphenotypes and such metrics, we maximized the topic quality metric (coherence UMass and similarity) to determine the final k. Such approach has been widely used in evaluating the topic model.^24,25,49 We also involved clinicians to validate whether topics were clinically meaningful. Larger k may allow the discovery of deep subphenotypes, but also increases the risk of fracturing meaningful phenotype clusters. Sun et. al applied Core Consistency Diagnostic CONCORDIA), ³⁷ a method that can be used for the PARAFAC model to automatically discover the number of phenotypes. However, through the experiment, we found if we constrained the sparsity and normalized all factors, the core consistency is not accurate. We plotted the core consistency by removing sparsity constraints and only normalizing two factors (Figure A.3). The result showed k=14 achieved the highest core consistency, which matches the number of topics calculated using topic quality metric.

Adding orthogonal and sparsity constraints are important in generating an interpretable phenotype. We showed the topics using PARAFAC model without adding orthogonal and sparsity constraints (Figure A.5–A.6). From Figure A.5–A.6, we observed that it is highly possible to yield overlapped phenotypes.

Clinical relevance

This approach enabled us to obtain meaningful CVD subphenotypes and visualize their progression pattern. Topic #0 and Topic #1 are particularly enriched in individuals with kidney failure but may represent patients with different causes, e.g. uncontrolled Type 1 diabetes ⁵³, and Systemic lupus erythematosus ⁵⁴, respectively. Among the top six most prevalent topics, Topic #11(Hypercholesterolemia, Malaise, and fatigue), Topic #12 (Mixed hyperlipidemia and Type 2 diabetes), and Topic #13 (Essential hypertension) are well-described common comorbidities of CVD. Each of these topics had a time-progression pattern with a sharply increased intensity in the years leading up to the CVD event. Such results confirmed our previous findings in using the longitudinal EHR to predict 10-year CVD, that the most recent years’ value contributes more to the prediction.⁵⁵ In contrast, some prevalent topics demonstrated different time-progressions. For example Topic #4 (Vitamin D Deficiency, Depression)⁵⁶ had a wave change morphology with increased intensity at 3 to 4 years prior to the first diagnosis of CVD, followed by a drop-off, then a final increase in intensity at a year before the event.

As expected, we found statistically significant correlations between ASCVD risk and topics heavily enriched with traditional CVD comorbidities including Topic #11 (Hypercholesterolemia), Topic #12 (Mixed hyperlipidemia and Type 2 diabetes), and Topic #13 (Essential hypertension). Such results were in line with the Framingham study (Table A.1). The main phenotype Chronic airway obstruction in Topic #10, was not included in ACC/AHA ASCVD risk score, but evidence has shown that CVD is more common among patients with Chronic Obstructive Pulmonary Disease (COPD), a major cause of Chronic airway obstruction.⁵⁷ COPD patients also have a higher risk of mortality from complications of CVD.^58–60 Topic #10 had a positive correlation with an estimated risk of ASCVD, mainly because some risk factors of COPD such as age (mean age 69.5 [8.9]), smoking status, weight loss were also known risk factors of CVD. Therefore, ACC/AHA risk equation may still capture many of the important risk factors for CVD in this subphenotype.

We also observed topics such as Topic #4 (Vitamin D deficiency, Depression), and Topic #9 (Urinary tract infection, Nonspecific chest pain, Nausea and vomiting, Malaise and fatigue) had a negative correlation with the traditionally estimated risk. Topic #4 and Topic #9 contained a similar or larger proportion of low-risk patients than high-risk patients. Recent evidence has shown a strong correlation between Urinary tract infections (Topic #9) and cardiovascular events ^61,62 There is also support for moderate to severe Vitamin D deficiency (Topic #4) as a risk factor for developing CVD.⁶³ This suggests that conventional risk assessment tools could not accurately model risk of CVD for patients with these topics.

Topic #5 was not significantly correlated with the estimated risk of ASCVD by the ACC/AHA assessment tool, but it had a high hazard ratio for increased risk of subsequent MI (Table 2). Topic #5 appears to capture a subphenotype of patients with advanced Type 2 diabetes with microvascular complications including diabetic neuropathy and diabetic retinopathy. The presence of microvascular complications of diabetes such as Type 2 diabetic neuropathy portend an increased risk of CVD.⁶⁴ Diabetic autonomic neuropathy is also an independent risk for recurrent CVD events in diabetic patients with a prior history of CVD.⁶⁵ Furthermore, whereas intensive glucose control in patients with newly diagnosed or less advanced Type 2 diabetes may decrease risk of subsequent CVD ⁶⁶; intensive glucose control in patients with long-standing Type 2 diabetes may not reduce the risk of developing CVD.⁶⁷ Therefore, Topic #5 may identify a subphenotype of patients with advanced diabetes as their predominant risk for CVD, where conventional treatment aimed at controlling the risk comorbidity (diabetes) does not mitigate the risk of ultimately developing CVD and subsequent complications like MI.

Essential hypertension (Topic #13) and lipid disorders (Topic #11, Topic #12) are two well-known risk factors of CVD, however; they formed into separate distinct topics (Figure 5), suggesting they may represent distinct subphenotypes. Interestingly, Topic #13 represents a unique group enriched for Essential hypertension but with few hyperlipidemia events across the years (Figure 6). Notably, Topic #13 (Essential hypertension) had significantly increased risk of subsequent MI while high Topic #11 score (Hypercholesterolemia) had decreased risk. This may reflect an increased propensity for Topic #11 patients to receive cholesterol-lowering statin medications, which have a well-understood role in primary prevention of CVD events.^68,69 Although both Topic #11 and Topic #12 contained mixed hyperlipidemia, Topic #12 also had Type 2 diabetes as the key descriptor and had a different evolving trend than Topic #11, indicating two different subphenotypes. The combination of Type 2 diabetes, Mixed Hyperlipidemia, Obesity, and Essential hypertension in the descriptors of Topic #12 capture many features of the metabolic syndrome, a constellation of comorbidities that result from abdominal obesity and insulin resistance.⁷⁰ This suggests that although studies have traditionally treated Hyperlipidemia, Hypertension, and Type 2 diabetes as CVD risk factors, these phenotypes can be treated as different phenotype cohorts, with each having different optimal treatment regimens.

Limitations

This study has several limitations. First, we used binary values to indicate whether an individual received a diagnosis code in each year. A method accounting for disease severity (e.g., using counts of diagnosis codes) could be used in future studies and may improve the identification of subphenotypes. Second, we did not incorporate medications and laboratory tests in this study, which may also improve the identification of meaningful phenotype clusters. Third, although PheCodes are aggregates of ICD codes, there is still overlap among PheCodes, i.e., some distinct PheCodes defined closely related disease (e.g.Type 2 diabetic neuropathy [250.24], Type 2 diabetes [250.2]). Word-embedding models such as Word2Vec⁷¹ may precisely quantify the similarity between related terms. Finally, our study cohort did not include any controls of CVD. If we want to find predictors for CVD, we need to include the negative controls in future work.

Conclusion

This study demonstrated the feasibility of tensor-decomposition for learning time-evolving topics from longitudinal EHRs. The methodology may help identify potentially useful subphenotypes of complex diseases for precision medicine studies.

Highlight.

• Present a method using Tensor Factorization to find subphenotypes from longitudinal EHR.

• We applied this approach to 12380 patients with the diagnosis of CVD.

• We identified 14 subphenotypes that patients established in 10 years prior to CVD, and showed the progress pattern.

• Through an association analysis with estimated CVD risk, we found some topics e.g. Vitamin D deficiency, Urinary infections cannot be explained by conventional risk factors.

• We identified a distinct subphenotype enriched for “Hypertension” with few “hyperlipidemia” that increased the risk of the subsequent MI.