Navigating trials of personalized pain treatments: We’re going to need a bigger boat.

1. Introduction

Personalized or precision treatments are targeted therapies that are particularly effective or have reduced harms for a subgroup of patients within a given condition [3]. This type of targeted therapy has considerable potential benefits, including reduced exposure of patients and study participants to treatments from which they are not likely to benefit and reduced financial resources spent on treatments that are ineffective or potentially harmful for certain individuals. Personalized treatment may be potentially beneficial for chronic pain conditions, in which the percentages of patients who meaningfully improve after initiation of efficacious pharmacologic therapies has been modest [19]. However, the ability of a particular patient characteristic to predict treatment response must be demonstrated in clinical trials before such predictors can be implemented in clinical practice.

Significant advances have occurred in developing a foundation for personalized pain treatment [10, 22]. Phenotypic or genotypic characteristics (e.g., predictive biomarkers [15]) that potentially identify groups of patients that are more likely to respond to a particular treatment have been suggested in multiple studies. For example, quantitative sensory testing (QST) can be used to group patients with similar sensory phenotypes within neuropathic pain conditions and has been shown to predict response to oxcarbazepine. [1, 5, 26]. Patients with specific genetic mutations in receptors that are targeted by certain drugs (e.g., sodium channels [2]) may respond more robustly to those drugs. Psychological characteristics associated with negative affect and pain catastrophizing have been associated with worse outcomes in uncontrolled, prospective studies of single treatments and in studies that qualitatively compare subgroup differences in treatment effects (active vs. placebo) groups [9, 27, 28]. Other potential phenotypic predictors include pain qualities (e.g., neuropathic vs. nociceptive) and sleep quality [10]. The evidence derived from uncontrolled studies is very difficult to interpret because it is possible that the observation of better outcomes in a subgroup might reflect an enhanced placebo effect in that subgroup. For example, increased brain connectivity identified using functional magnetic resonance imaging (fMRI) has been shown to predict placebo response in recent studies [17, 18, 21]. Also, increased variability in baseline pain ratings was shown to predict placebo response in retrospective analyses of data from multiple randomized clinical trials [12, 16].

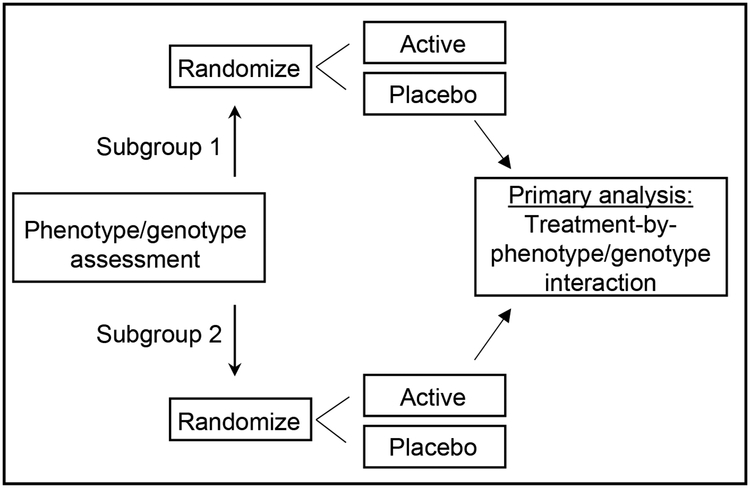
Much of the current literature regarding potential predictors of treatment response, including the studies referenced above, is based on secondary or retrospective analyses of randomized clinical trial (RCT) data that demonstrate a treatment effect in only 1 subgroup [7, 10]. However, the finding that a treatment effect (vs. placebo) yields a significant result in 1 subgroup but not the other is not sufficient to demonstrate that the treatment is more efficacious in 1 subgroup than the other. Concluding that the treatment effect in 1 subgroup is larger than that in another subgroup because the effect is what some authors term “more significant” (i.e., associated with a smaller p-value) in 1 subgroup (e.g., p = 0.001 vs. p=0.045) is also not appropriate [15]. In such a case, differences in statistical significance could be simply due to differences in subgroup sample sizes rather than the magnitude of the treatment effect. Additionally, even if the difference in statistical significance is partially due to differences in the magnitudes of the treatment effect, it does not follow that the magnitudes of the treatment effects for the 2 subgroups are significantly different from each another [15]. In order to demonstrate rigorously the ability of a phenotype or genotype to predict response to active treatment, a RCT with a pre-specified primary analysis that tests the significance of the difference between the effect sizes in the 2 subgroups must be conducted. This is accomplished by testing what is termed the treatment-by-phenotype/genotype interaction. [11, 25] (Figure 1). Demant et al. [5] recently reported such a trial in which the primary analysis was a test of significance of the treatment-by-“irritable nociceptor” phenotype interaction. The trial successfully demonstrated that an “irritable nociceptor” phenotype in patients with peripheral neuropathic pain detected using QST predicted greater response to oxcarbazepine vs. placebo compared with patients who did not have the irritable nociceptor phenotype. Specifically, the estimated standardized effect size (SES) (i.e., (mean_active – mean_placebo)/pooled standard deviation) was 0.73 in the irritable nociceptor group and 0.38 in the non-irritable nociceptor group, and the treatment-by-phenotype interaction was statistically significant (p = 0.047). However, a second trial with a similar design and primary analysis that compared the effects of lidocaine on neuropathic pain between patients with and without the “irritable nociceptor” phenotype did not successfully demonstrate a treatment-by-phenotype interaction [4]. The remainder of this article will discuss sample size determination for prospective randomized clnical trials designed specifically to evaluate treatment-by-phenotype/genotype interactions and the interpretation of such trials. These methods apply to all randomized clinical trials, including those that test pharmacologic, psychological, physical, surgical, and device interventions. Of course, those with the most rigorous blinding possible for the particular intervention will produce the highest quality data.

Figure 1.

Illustrative treatment-by-phenotype/genotype interaction trial schema.

2. Sample size determination for testing interactions

A standard sample size calculation for a parallel group RCT that is designed to compare the means of two groups for a normally distributed outcome variable requires assumptions for the type I error probability (alpha or significance level), power, the minimum group difference in means (treatment effect) that one would like to detect, and the variance of the outcome variable in each group. If the variance is the same in each group, as is often assumed, then one only needs to specify alpha, power, and the ratio of the treatment effect to the standard deviation of the outcome variable (i.e., the SES). For a parallel group RCT that is designed to compare the treatment effects between 2 subgroups (i.e., to evaluate whether the treatment-by-phenotype/genotype interaction is equal to zero), the sample size calculation requires assumptions for alpha, power, the percentages of the randomized sample that will be in each subgroup, and the difference in SES between the 2 phenotype/genotype subgroups that one would like to detect. This assumes that the variance of the outcome variable is the same in each treatment group/subgroup combination, which simplifies the presentation below.

Methods are presented below for determining the sample sizes required for parallel group RCTs and crossover trials that are designed to compare the treatment effects between 2 subgroups (i.e., to evaluate whether the treatment-by-phenotype/genotype interaction is equal to zero).

2.1. Parallel group RCTs

Let μ_ij be the mean outcome in treatment group j (0 = placebo, 1 = treatment) for Subgroup i (i = 1, 2). Let Δ = (μ₂₁ − μ₂₀) – (μ₁₁ − μ₁₀) be the subgroup difference in the treatment effect, where μ₂₁ − μ₂₀ is the treatment effect in Subgroup 2 and μ₁₁ − μ₁₀ is the treatment effect in Subgroup 1. It is of interest to test the null hypothesis that Δ = 0 (i.e., that the treatment effects are the same in each subgroup). Note that the means μ_ij will be estimated by the sample means ${\overline{X}}_{ij}$ and the subgroup difference in the treatment effect will be estimated by $\widehat{\Delta }=\left({\overline{X}}_{21}-{\overline{X}}_{20}\right)-\left({\overline{X}}_{11}-{\overline{X}}_{10}\right)$. Assuming equal variances (σ²) in each treatment group-subgroup combination and that there is equal allocation of treatment and placebo within each subgroup, then it is easy to show that the variance of $\widehat{\Delta }$ is equal to

$$\text{var}\left(\widehat{\Delta }\right)=4{\sigma }^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right),$$

where n₁ and n₂ are the sample sizes for Subgroups 1 and 2, respectively. A formula for the approximate sample size required to provide 100(1 − β)% power to detect a subgroup difference in treatment effect of size Δ, using a t-test and a two-tailed significance level α, is

$$n_2=\frac{r+1}{r}\frac{{\left(Z_{\alpha /2}+Z_{\beta }\right)}^{2}4{\sigma }^2}{{\Delta }^2},n_1=n_{2}r,$$

where r = n₁/n₂ is the ratio of the subgroup sample sizes and Z_υ is the upper 100υ^th percentile of the standard normal distribution (e.g., when α = 0.05 and power = 0.80, Z_0.025 = 1.96 and Z_0.20 = 0.842). The total sample size required is N = n₁ + n₂.

Alternatively, if one has access to software to compute sample size for a two-group comparison of means (using the t-distribution), the required input would be the significance level (α), desired power 100(1 – β)%, subgroup difference in treatment effect (Δ), ratio of the subgroup sample sizes (r), and variance (4σ²). Note here that it is necessary to multiply the variance of the outcome variable by 4 to obtain the required sample size.

2.2. Crossover trials

In a crossover trial, each participant receives both the active treatment and placebo in random order. Let μ_di be the mean treatment – placebo difference (treatment effect) among the n_i participants in Subgroup i, i = 1, 2. Then Δ = μ_d2 − μ_d1 is the subgroup difference in treatment effect, estimated by $\widehat{\Delta }={\overline{X}}_{d2}-{\overline{X}}_{d1}.$ Let ${\sigma }_d^2$ be the variance of the within-participant treatment – placebo difference in outcome, assumed to be the same for each subgroup. Then it is easy to show that the variance of $\widehat{\Delta }$ is equal to

$$\text{var}\left(\widehat{\Delta }\right)={\sigma }_d^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right).$$

A formula for the approximate sample size required to provide 100(1 – β)% power to detect a subgroup difference in treatment effect of size Δ, using a t-test and a two-tailed significance level α, is

$$n_2=\frac{r+1}{r}\frac{{\left(Z_{\alpha /2}+Z_{\beta }\right)}^2{\sigma }_d^2}{{\Delta }^2},n_1=n_{2}r.$$

The total sample size required is N = n₁ + n₂.

As in the case of a parallel group trial, if one has access to software to compute sample size for a two-group comparison of means (using the t-distribution), the required input would be the significance level (α), desired power (1 – β), subgroup difference in treatment effect (Δ), ratio of the subgroup sample sizes (r), and variance $\left({\sigma }_d^2\right).$ It is sometimes the case that there is no information available concerning the variance of the within-participant treatment – placebo difference in outcome, but there is information on the variance of the outcome measured at a single time point (σ²). Assuming that the variance is the same for each treatment condition, the two quantities are related by the formula

$${\sigma }_d^2=2{\sigma }^2\left(1-\rho \right),$$

where ρ is the correlation between the outcomes for the treatment and placebo conditions. If information concerning σ² is all that is available, one would have to make an educated guess regarding the value of ρ to compute the required sample size.

2.3. Results of sample size calculations

Table 1 provides the total sample sizes required to provide either 80% or 90% power to detect specified subgroup differences in treatment effect, using a t-test and a two-tailed significance level of 5%, for various subgroup allocations. The subgroup differences in treatment effect are expressed in terms of the subgroup difference in standardized effect size (SES) Δ/σ. Table 2 provides the sample sizes required to provide either 80% or 90% power to detect specified subgroup differences in treatment effect, using a t-test and a two-tailed significance level of 5%, for various subgroup allocations and values of the correlation ρ. The subgroup differences in treatment effect are again expressed in terms of the subgroup difference in SES. As is usual practice, the above calculations assume that there are no period effects and no treatment-by-period interaction (e.g., no carry-over effects). For both the parallel group and crossover studies, the calculations were performed using R, Version 3.5.1.

Table 1:

Total sample sizes necessary to yield 80% or 90% power to detect a treatment-by-subgroup interaction in parallel group studies

SES	80% Power			90% Power
	Subgroup Allocation
	50:50	34:66	25:75	50:50	34:66	25:75
	Sample Size
1.0	126	142	170	170	189	226
0.9	157	174	209	209	233	277
0.8	198	220	262	265	295	352
0.7	258	286	342	345	383	458
0.6	350	389	466	469	522	625
0.5	505	561	671	674	751	898
0.4	786	876	1049	1053	1172	1402
0.3	1397	1557	1861	1869	2083	2493

SES = Difference in standardized effect size between subgroups

Table 2:

Total sample sizes necessary to yield 80% or 90% power to detect a treatment-by-subgroup interaction in crossover studies.

80% Power
SES	Subgroup Allocation
	50:50					34:66					25:75
	Correlation†
	0.8	0.6	0.5	0.4	0.2	0.8	0.6	0.5	0.4	0.2	0.8	0.6	0.5	0.4	0.2
	Sample Size
1.0	15	27	34	39	54	17	31	37	44	58	19	35	44	53	70
0.9	18	34	42	50	64	20	37	46	55	72	22	43	54	64	86
0.8	22	42	51	62	82	26	46	58	68	90	29	54	67	82	107
0.7	27	54	67	79	106	31	60	74	88	117	37	70	87	106	139
0.6	38	71	90	107	142	41	80	99	120	158	50	94	118	142	188
0.5	54	103	127	154	203	58	114	143	170	226	70	136	171	203	270
0.4	82	159	199	238	315	90	178	221	264	352	107	211	263	316	422
0.3	142	282	351	422	562	158	314	390	469	624	188	374	467	561	747
90% Power
SES	Subgroup Allocation
	50:50					34:66					25:75
	Correlation†
	0.8	0.6	0.5	0.4	0.2	0.8	0.6	0.5	0.4	0.2	0.8	0.6	0.5	0.4	0.2
	Sample Size
1.0	19	35	45	54	70	22	40	49	58	78	26	46	59	70	91
0.9	23	43	54	66	86	26	49	61	73	95	30	59	70	86	114
0.8	30	55	67	82	107	31	61	75	90	120	38	73	91	107	142
0.7	38	71	87	106	139	40	78	98	117	155	48	94	117	139	187
0.6	50	95	119	143	190	55	107	132	158	211	65	126	158	190	251
0.5	70	138	171	203	271	78	152	190	227	302	91	182	227	270	362
0.4	107	214	266	318	423	120	237	296	354	470	142	283	353	422	563
0.3	190	375	470	563	750	211	419	523	627	834	251	501	626	750	998

SES = Difference in standardized effect size between subgroups

^†Correlation between the within-subject outcomes (treatment and placebo conditions)

In both Tables 1 and 2, if an investigator assumes that the SES will be 0.5 in one subgroup and 0.2 in the other subgroup, the sample size for the 0.3 difference in SES (i.e., the treatment-by-subgroup interaction) displayed in the table should be selected. Table 1 expands on the sample size considerations discussed by Vollert et al. [26], who estimate the numbers of patients that need to be screened to identify a sufficient number of patients for adequately powered clinical trials aimed at assessing treatment effects in patients with only a single sensory phenotype. The sample sizes required to have sufficient power to detect a treatment-by-subgroup interaction are typically much higher than that required to detect an overall effect of the treatment. For example, in a parallel group trial, the total sample size required to detect an overall SES of 0.3 with 80% power and a significance level of 5% is approximately 350 patients. If the subgroups are of equal size (50:50 allocation) and the SESs in the subgroups are 0.1 and 0.5, respectively (i.e., an SES of 0.3 for the overall treatment effect), the total sample size required to demonstrate that these subgroups have significantly different treatment effects (i.e., the treatment-by-subgroup interaction, subgroup difference in SES of 0.4) is 786.

Given that larger sample sizes are required to test an interaction, when appropriate and feasible, cross-over designs can be used to reduce the necessary sample sizes. Note that use of the cross-over design can decrease the sample size requirements compared to the parallel group design to varying degrees depending on the assumption regarding the within-patient correlation in outcomes (Tables 1 and 2).

3. Implications and Discussion

In addition to genotypes and phenotypes inherent to patients, the sample size considerations presented here are also applicable to trials aimed at evaluating potentially modifying factors that are assigned at randomization. For example, it has been suggested that the assay sensitivity of clinical trials can be improved by implementing various research design modifications, such as improving the accuracy of pain reporting through patient training programs [6, 20]. However, in order to adequately demonstrate the effects of such efforts, they must be evaluated by testing a treatment-by-training program interaction. The sample size requirements presented in Tables 1 and 2 are also applicable to such trials aimed at evaluating factors that are assigned at randomization. For example, in a clinical trial in which patients are randomized to receive active or placebo treatment and within each treament group are randomized to receive pain rating training or no training, an analysis of the treatment-by-training group interaction will test whether the training increased the effect size of the treatment. These types of trials are necessary to determine the effectiveness of various training methods or other clinical trial design modifications intended to increase assay sensitivity [8, 14, 24]. Such data would be especially important if the methods were expensive to implement or burdensome to patients.

A significant treatment-by-phenotype/genotype interaction indicates that the response to the active treatment relative to placebo is significantly different between groups. In order to understand the potential mechanisms underlying this difference, it can be helpful to examine the magnitude of change over time in each treatment group (i.e., active and placebo) separately in each subgroup and to consider the biological plausability of a differential response to active treatment. This is especially important given the subjective nature of pain ratings and the potential for substantial placebo effects. For example, retrospective analyses suggest that patients with excessively variable baseline pain ratings in RCTs may demonstrate larger placebo responses than those with lower variability in baseline pain ratings, but this difference in response does not seem to occur to the same degree in people receiving the active treatment [12, 16]. It is biologically plausible that patients whose pain ratings are more influenced by their external environment than others will have more variable pain ratings and also be more susceptible to the placebo influences of a clinical trial [23]. Such an interpretation, however, presumes that this placebo-induced response is not added to the true effect of the treatment in this subgroup, but instead largely replaces it. Another example is given by the Demant et al. [5] trial, in which the difference between subgroups in the change over time in subjects receiving oxcarbazepine was large, whereas subjects receiving placebo exhibited almost no change over time in either subgroup. It is also biologically plausible that patients with irritable nociceptors would respond more favorably to oxcarbazepine than those without irritable nociceptors.

4. Conclusions

Continued efforts to develop personalized pain treatments have the potential to accelerate the identification of novel therapies with greater efficacy or safety, or both, for certain subgroups. Proper design of clinical trials with pre-specification of a primary analysis that tests the significance of a treatment-by-phenotype/genotype interaction is necessary to demonstrate the differential efficacy of treatments. Appropriate sample size estimation is needed to ensure that such trials have adequate power to detect minimally important subgroup differences in efficacy. These practices will ensure that personalized pain treatment strategies can be identified in clinical trials as rigorously and efficiently as possible.