Causal inference with interfering units for cluster and population level treatment allocation programs

Abstract

Interference arises when an individual’s potential outcome depends on the individual treatment level, but also on the treatment level of others. A common assumption in the causal inference literature in the presence of interference is partial interference, implying that the population can be partitioned in clusters of individuals whose potential outcomes only depend on the treatment of units within the same cluster. Previous literature has defined average potential outcomes under counterfactual scenarios where treatments are randomly allocated to units within a cluster. However, within clusters there may be units that are more or less likely to receive treatment based on covariates or neighbors’ treatment. We define new estimands that describe average potential outcomes for realistic counterfactual treatment allocation programs, extending existing estimands to take into consideration the units’ covariates and dependence between units’ treatment assignment. We further propose entirely new estimands for population-level interventions over the collection of clusters, which correspond in the motivating setting to regulations at the federal (vs. cluster or regional) level. We discuss these estimands, propose unbiased estimators and derive asymptotic results as the number of clusters grows. For a small number of observed clusters, a bootstrap approach for confidence intervals is proposed. Finally, we estimate effects in a comparative effectiveness study of power plant emission reduction technologies on ambient ozone pollution.

1 |. INTRODUCTION

Most causal inference literature assumes that a unit’s potential outcome depends solely on its treatment, and not on the treatments of other units in the population. However, this assumption is often not reasonable. Perhaps the most classical example arises in vaccination studies (Ali et al., 2005; Hudgens and Halloran, 2008) where a unit’s disease status depends on their own vaccination status but also on the vaccination status of others. The presence of interference can lead to estimated quantities from familiar estimators that are misleading (Sobel, 2006) and lack clear causal interpretation (Tchetgen Tchetgen and VanderWeele, 2012), but can also introduce new estimands of intrinsic scientific interest.

Sobel (2006) defined estimands assuming partial interference referring to situations where the population can be partitioned into clusters (groups) for which a unit’s potential outcomes depend only on the treatment of units within the same cluster. Hudgens and Halloran (2008) formalized causal inference in this setting and in the context of two-stage randomization designs, extended to observational studies by Tchetgen Tchetgen and VanderWeele (2012).

In order to continue development in the context of observational studies, we highlight a key distinction that arises when formulating average potential outcomes in the presence of interference. We use the term treatment allocation strategy to refer to a process giving rise to either observed or hypothesized vectors of treatment assignments. The observed treatment allocation strategy refers to that which gives rise to observed treatments. The counterfactual treatment allocation strategy refers to how treatments may have been assigned in some hypothesized counterfactual world for which causal contrasts are considered. This distinction between observed and counterfactual treatment allocation programs helps illuminate that existing causal estimands are limited to counterfactual treatment allocation programs that remain agnostic with regard to covariate information. These estimands ignore the possible role of unit-level covariates that relate to treatment adoption, implicitly assuming an intervention manipulating each individual unit’s treatment propensity.

In many settings, however, treatment allocations corresponding to unit-level manipulation are difficult to conceive. For example, policy interventions may be designed to increase the regional prevalence of a treatment without direct control over the individual treatment propensity. In such settings, individual treatment adoption might generally depend on unit-level covariates or the treatment status of neighboring units. To address such settings, we develop new causal estimands anchored to counterfactual treatment allocations that correspond to realistic regional interventions. These interventions are conceived at the cluster level, where a particular allocation strategy dictates the cluster-average propensity of receiving treatment without directly specifying individual-level treatment propensities. Note that, in focusing on new estimands for covariate-dependent counterfactual treatment allocation programs, our work has commonalities with independent work in Barkley et al. (2017). Defining estimands for realistic treatment allocations has received limited attention in the causal inference literature with an exemption found in van der Laan and Petersen (2007).

In addition to extending existing estimands to accommodate realistic regional treatment allocations, this work provides entirely novel estimands motivated by the desire to investigate interventions which take place at the population (vs. regional) level. These estimands are useful for evaluating policies that change the distribution of cluster-average propensities of treatment by, for example, providing a population-wide incentive to adopt treatment.

Definition of the new causal estimands described above is accompanied here by new estimators, derivation of corresponding asymptotic properties as the number of clusters grows, and a bootstrap approach to inference when the number of observed clusters is small. Related work can be found in Ferracci et al. (2014), in Liu and Hudgens (2014) where asymptotic results are derived for growing number of clusters or number of individuals within clusters, in Perez-Heydrich et al. (2015) where large sample variance estimators for the estimator of Tchetgen Tchetgen and VanderWeele (2012) are derived, and in Liu et al. (2016) where estimands and estimators are extended to a network where partial interference does not hold, but asymptotic results are derived under the assumption of partial interference.

The motivating context for this work is the evaluation of interventions to limit harmful pollution from power plants. The movement of air pollution through space leads to interference: intervening on one power plant can affect the air pollution surrounding nearby power plants. Importantly, pollution regulations often work by incentivizing regions of power plants to adopt certain technologies without mandating treatment adoption at each individual plant, which, in reality, is heavily influenced by individual power plant characteristics (e.g., size). In addition to regional strategies, federal pollution regulations can provide national incentives for power plants to install technologies, motivating the new population-level estimands.

The new estimators are deployed here to an analysis of U.S. power plants investigating the comparative effectiveness of Selective Catalytic or non-Catalytic Reduction (SCR/SNCR) systems relative to other strategies for reducing ambient ozone pollution. A preliminary investigation of these same data in Papadogeorgou et al. (2018) ignored interference and indicated that these systems causally reduced NO_x emissions (an important precursor to ozone pollution) but estimated an effect on ambient ozone very close to zero. The analysis here to address the possibility of interference produces meaningfully different results that are more consistent with the literature relating NO_x emissions to ambient ozone pollution.

2 |. ESTIMANDS UNDER PARTIAL INTERFERENCE

We adopt the notation used in Tchetgen Tchetgen and VanderWeele (2012). Let N be the number of clusters, and n_i the number of units in cluster i, i ∈ {1, 2, …, N}. Furthermore, let $A_i=\left(A_{i1},A_{i2},\dots ,A_{i{n}_i}\right)\in \mathcal{A}\left(n_i\right)$ denote the cluster treatment vector, and $A_{i,-j}=\left(A_{i1},A_{i2},\dots ,A_{ij-1},A_{ij+1},\dots ,A_{i{n}_i}\right)\in \mathcal{A}\left(n_i-1\right)$ the treatment of all units in cluster i apart from unit j, where $\mathcal{A}(n)={\left\{0,1\right\}}^n$. Furthermore, let L_ij be a vector of individual and cluster-level covariates, and $L_i=\left(L_{i1},L_{i2},\dots ,L_{i{n}_i}\right)$ be the collection of covariates of all units within cluster i. Under the assumption of partial interference, the potential outcome of unit j in cluster i may depend on the treatment of units in cluster i, but not on the treatment of units in different clusters. For every i we postulate the existence of group i’s potential outcomes $Y_i(\cdot )=\left\{Y_i\left(a_i\right),a_i\in \mathcal{A}\left(n_i\right)\right\}$, where $Y_i\left(a_i\right)=\left(Y_{i1}\left(a_i\right),Y_{i2}\left(a_i\right),\dots ,Y_{i{n}_i}\left(a_i\right)\right)$.

2.1 |. Average potential outcome

We define the individual average potential outcome for a counterfactual treatment allocation strategy with two features: (1) treatment assignment for units within a cluster is unlikely to be independent, and (2) individual covariates can be predictive of a unit’s treatment probability. Let P_α,L represent the (arbitrarily specified) counterfactual treatment allocation program, specified intentionally to depend on covariates and/or allow correlated assignments, and whose important features are represented by parameters α. For the purpose of this paper, we consider α to represent the cluster-average propensity of treatment.

The individual average potential outcome for unit j in cluster i is defined as:

$${\overline{Y}}_{ij}^L(a;\alpha )=\sum _{\mathit{s}\in \mathcal{A}\left(n_i-1\right)}{Y}_{ij}\left(A_{ij}=a,{\mathit{A}}_{i,-j}=\mathit{s}\right)\hspace{0.17em}{P}_{\alpha ,L}\left({\mathit{A}}_{i,-j}=\mathit{s}|A_{ij}=a,{\mathit{L}}_i\right),$$ (1)

representing the unit’s expected outcome in the counterfactual world where treatment is assigned according to P_α,L, but treatment of unit j is set to a. The group average potential outcome for cluster i is defined as ${\overline{Y}}_i^L(a;\alpha )=\frac{1}{n_i}\sum _{ni}^{j=1}{\overline{Y}}_{ij}^L(a;\alpha )$. Assuming that clusters are observed from a super-population according to a distribution G₀, the population average potential outcome is defined as ${\overline{Y}}^L(a;\alpha )=E_{G_0}\left\{{\overline{Y}}_i^L(a;\alpha )\right\}$. Note that these estimands are well-defined for any fixed choice of P_α,L. Definitions of the group and population average potential outcomes implicitly require that, when a cluster is observed, data are collected on all the units belonging to that cluster.

In Web Appendix E, we discuss the sample average potential outcome defined in the literature as the (weighted) average of the observed clusters’ group average potential outcomes. There, we provide an argument for a definition (and corresponding estimator) which gives equal-weight to all clusters irrespective of their cluster size.

2.2 |. The counterfactual treatment allocation in existing literature

The above development has left unspecified the term P_α,L in (1) providing relative weights to different cluster treatment vectors in the individual average potential outcomes. Specifying $P_{\alpha ,L}\left(a_i|L_i\right)=\prod _{n_i}^{j=1}{\alpha }^{a_{ij}}{\left(1-\alpha \right)}^{1-a_{ij}}$ would correspond to the estimands in Tchetgen Tchetgen and VanderWeele (2012) and Perez-Heydrich et al. (2015) that give equal probability to all cluster treatment vectors with the same number of treated units, irrespective of which those units are. For this choice of P_α,L, the estimands represent quantities in a counterfactual world where individual treatment propensity can be manipulated and units are assigned to treatment independently and with equal probability α.

2.3 |. Realistic counterfactual treatment allocation program

However, in some situations, counterfactual treatment allocations can only be realistically conceived to depend on covariates or incorporate correlation between treatment of units in the same cluster. In the study of power plant interventions, the decision of whether to “treat” a power plant is at the discretion of the power company and heavily influenced by power plant covariates. Therefore, a hypothesized counterfactual treatment allocation is realistic only when such covariates are incorporated. For example, consider the covariate ‘heat input’, a proxy for the size of the power plant, and let L_ij be the heat input of power plant j in cluster i. One specification of a counterfactual treatment allocation strategy that would acknowledge that different-sized power plants are more or less likely to adopt treatment is:

$$\text{logit\hspace{0.17em}}{P}_{\alpha ,L}\left(A_{ij}=1|L_{ij}\right)={\xi }_i^{\alpha }+\delta L_{ij},$$ (2)

for some fixed value of δ, and ${\xi }_i^{\alpha }$ such that $\left(n_i^{-1}\right)\sum _{j=1}^{ni}\text{expit }\left({\xi }_i^{\alpha }+\delta L_{ij}\right)=\alpha$. The value δ could be specified according to knowledge of how the size of the power plant is expected to impact the propensity to adopt treatment. For δ = 0 the estimands coincide with the ones for independent Bernoulli counterfactual treatment allocations found in Tchetgen Tchetgen and VanderWeele (2012). Note that the covariates included in the counterfactual treatment allocation are at the discretion of the investigator based on judgments about which allocations might correspond to the policies of interest.

Based on (2), the probability of the cluster treatment vector under the counterfactual treatment allocation P_α,L (A_i = a_i|L_i) could be fully specified by hypothesizing that, in the counterfactual world, the A_ij ‘s are conditionally independent given L_i, and A_ij is conditionally independent of L_i,−j given L_ij. Then, $P_{\alpha ,L}\left({\mathit{A}}_i={\mathit{a}}_i|{\mathit{L}}_i\right)=\prod _{j=1}^{n_i}{P}_{\alpha ,L}\left(A_{ij}=a_{ij}|L_{ij}\right)$ which, in turn, specifies P_α,L (A_{i, −j} = s|A_ij = a,L_i) for all $\mathit{s}\in \mathcal{A}\left(n_i-1\right)$ giving relative weights in the specification of the individual average potential outcome (1). Based on this specification of P_α,L, the estimands of interest correspond to quantities in a hypothesized world where treatment within a cluster is assigned independently across units with treatment propensity that depends on L_ij, but is on average equal to α.

Alternatively, a counterfactual treatment allocation strategy could incorporate dependence of treatments of nearby units by, for example, including a spatial random effect in P_α,L. A data-driven way to choose P_α,L is presented in Section 6.

2.4 |. Direct and indirect effects

Contrasts of average potential outcomes can characterize how treatment affects the outcome of interest. For counterfactual allocation strategy P_α,L, direct effects represent contrasts in average potential outcomes when only the individual treatment changes. On the other hand, indirect effects (also known as spillover effects) contrast average potential outcomes for a fixed level of individual treatment, but different specification of the parameter α governing P_α,L. For that reason, indirect effects represent expected changes in potential outcomes for changes only in the “treatment of neighbors”, and they constitute a measure of interference. Based on the average potential outcomes defined above, one can define the individual direct effect as $D{E}_{ij}^L(\alpha )={\overline{Y}}_{ij}^L(1;\alpha )-{\overline{Y}}_{ij}^L(0;\alpha ),$, and the corresponding group and population direct effects as $D{E}_i^L(\alpha )={\overline{Y}}_i^L(1;\alpha )-{\overline{Y}}_i^L(0;\alpha )$, and $D{E}^L(\alpha )={\overline{Y}}^L(1;\alpha )-{\overline{Y}}^L(0;\alpha )=E_{G_0}\left\{D{E}_i^L(\alpha )\right\}$ accordingly. Similarly, the individual indirect effect is specified as $I{E}_{ij}^L\left({\alpha }_1,{\alpha }_2\right)={\overline{Y}}_{ij}^L\left(0;{\alpha }_2\right)-{\overline{Y}}_{ij}^L\left(0;{\alpha }_1\right)$, based on which group and population indirect effects can be defined. Indirect effects could be alternatively specified for individual treatment assignment a = 1, but here our focus is on the effect of neighbors’ treatment in the areas surrounding untreated power plants. Further, total effects can be defined as the sum of direct and indirect effects, while similar development can lead to the definition of overall effects as contrasts of the individual average overall potential outcomes ${\overline{Y}}_{ij}^{L,O}(\alpha )=\sum _{\mathit{s}\in \mathcal{A}\left(n_i\right)}{Y}_{ij}(\mathit{s})P_{\alpha ,L}\left(\mathit{s}|{\mathit{L}}_i\right)$. The overall effects (and corresponding estimators) are discussed in detail in Web Appendix G.

3 |. POPULATION-LEVEL COUNTERFACTUAL DISTRIBUTION OF CLUSTER-AVERAGE PROPENSITY OF TREATMENT

Development in Section 2 pertained to estimands that fix the cluster-average propensity of treatment, α, corresponding to counterfactual worlds were one intervenes at the level of the cluster but units within the cluster choose their own treatment. Here we develop completely new estimands for settings where the cluster average propensity of treatment is not fixed to a specific value α, but arises from a hypothesized distribution of cluster-level propensities.

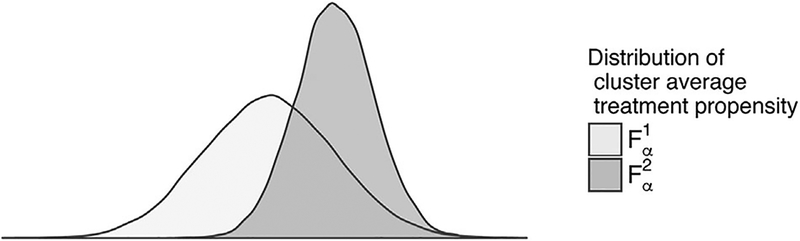
Such estimands correspond to interventions that occur at an administrative level higher than the cluster. For example, a federal regulation targeting all clusters might incentivize increased treatment coverage without enforcing a specific average propensity of treatment for any particular geographic area, leading to an overall shift in the distribution of cluster average propensity of treatment from some distribution $F_{\alpha }^1$ to $F_{\alpha }^2$, like in Figure 1.

FIGURE 1.

Distributions of cluster average propensity of treatment. A federal intervention might target the increase of cluster treatment coverage targeting a shift in the distribution of cluster average treatment propensity from $F_{\alpha }^1$ to $F_{\alpha }^2$.

Let F_α (·) denote a hypothesized distribution of cluster-average propensity of treatment. Then, define the F_α-individual average potential outcome as ${\overline{Y}}_{ij}^L\left(a;F_{\alpha }\right)=\int {\overline{Y}}_{ij}^L(a;\alpha )\text{d}{F}_{\alpha }(\alpha )$. Thus, ${\overline{Y}}_{ij}^L\left(a;F_{\alpha }\right)$ describes the average potential outcome of unit j in cluster i, for cluster average propensity of treatment arising from F_α and individual treatment a. Consequently, the F_α-group and population average potential outcomes are defined as

$${\overline{Y}}_i^L\left(a;F_{\alpha }\right)=\frac{1}{n_i}\sum _{j=1}^{n_i}{\overline{Y}}_{ij}^L\left(a;F_{\alpha }\right),$$ (3)

and

$${\overline{Y}}^L\left(a;F_{\alpha }\right)=E_{G_0}\left\{{\overline{Y}}_i^L\left(a;F_{\alpha }\right)\right\},$$ (4)

accordingly. We focus on the contrast of F_α-population average potential outcomes for hypothesized distributions of cluster-average propensity of treatment $F_{\alpha }^1$ and $F_{\alpha }^2$,

$$I{E}^L\left(F_{\alpha }^1,F_{\alpha }^2\right)={\overline{Y}}^L\left(0;F_{\alpha }^2\right)-{\overline{Y}}^L\left(0;F_{\alpha }^1\right).$$ (5)

Such estimands are of primary interest in the evaluation of air pollution policies, since $I{E}^L\left(F_{\alpha }^1,F_{\alpha }^2\right)$ represents the expected change in air pollution concentration surrounding control units for a federal intervention to increase emission control technology coverage. Direct effect estimands based on the F_α-population average potential outcome could also be defined as $DE\left(F_{\alpha }\right)={\overline{Y}}^L\left(1;F_{\alpha }\right)-{\overline{Y}}^L\left(0;F_{\alpha }\right)$, but are not pursued here.

4 |. ESTIMATING THE POPULATION AVERAGE POTENTIAL OUTCOME

For a fixed choice of P_α,L, we provide estimators of the population average potential outcome ${\overline{Y}}^L(a;\alpha )$, unbiasedness and consistency results, and derive the asymptotic distribution when the number of clusters increases to infinity for a known or estimated (and correctly specified) parametric cluster-propensity score model (defined below). These results are used to derive estimators (and their asymptotic properties) for the estimands in Section 2.4 and the population level estimands in Section 3. Asymptotic results are derived to simplify inference, since analytic finite sample unbiased variance estimators cannot be derived without additional assumptions on the interference structure (Hudgens and Halloran, 2008). For finite sample confidence intervals, we discuss a bootstrap approach. Proofs are in Web Appendix C.

We start by making the consistency of potential outcomes assumption, and cluster-level positivity and conditional ignorability assumptions:

• Assumption 1. Consistency of potential outcomes. Y_ij = Y_ij(A_i) with probability 1.

• Assumption 2. Positivity. There exists ρ > 0 such that the probability of observing cluster treatment vector a_i given cluster covariates L_i, f_A|L,i(A_i = a_i|L_i) > ρ with probability 1. f_A|L,i is the cluster-propensity score.

• Assumption 3. Conditional ignorability. For G₀, A_i ╨ Y_i(·)|L_i.

These assumptions are adaptations of standard assumptions required for causal inference. A crucial difference is that in settings of partial interference these assumptions are made at the level of the cluster, rather than at the level of the individual. Note that the covariates L_i in Assumption 3 do not need to coincide with the ones included in the counterfactual treatment allocation P_α,L.

The inclusion of cluster subscript i in the notation for f_A|L,i depends on the assumed form of the propensity score. In the analysis of clustered data, a cluster-specific random intercept is often included in the propensity score model (as will be discussed in Section 6.1), making the dependence of f_A|L,i on i explicit.

4.1 |. Estimators of the group and population average potential outcome

Let ${\widehat{Y}}_i^L(a;\alpha )=\frac{1}{n_i}\sum _{j=1}^{n_i}\frac{P_{\alpha ,L}\left({\mathit{A}}_{i,-j}|A_{ij}=a,{\mathit{L}}_i\right)}{f_{\mathit{A}|\mathit{L},i}\left({\mathit{A}}_i|{\mathit{L}}_i\right)}I\left(A_{ij}=a\right)Y_{ij}$, and ${\widehat{Y}}^L(a;\alpha )=\frac{1}{N}\sum _{i=1}^N{\widehat{Y}}_i^L(a;\alpha )$. For the true cluster propensity score f_A|L,i(·|L_i) and if Assumptions 2 and 3 hold, ${\widehat{Y}}_i^L(a;\alpha )$ is unbiased for ${\overline{Y}}_i^L(a;\alpha )$. Unbiasedness is derived with respect to the distribution of the observed treatment assignment.

4.2 |. Asymptotic results for population average potential outcome estimators

We derive the asymptotic properties of the estimator ${\widehat{Y}}^L(a;\alpha )$ for an increasing number of clusters N, where G₀ represents the joint distribution of the independent and identically distributed random vectors (Y_i(·), A_i, L_i). (For notational simplicity, n_i is included in L_i.)

We denote the estimator ${\widehat{Y}}^L(a;\alpha )$ based on N clusters as ${\widehat{Y}}_N^L(a;\alpha )$. and derive the asymptotic distribution of ${\widehat{\mu }}_N^{01}(\alpha )={\left({\widehat{Y}}_N^L(0;\alpha ),{\widehat{Y}}_N^L(1;\alpha )\right)}^T$ using the estimated correctly-specified parametric propensity score model. The cluster-propensity score for the observed treatment vector will be denoted by f_{A|L, i}(A_i|L_i; γ) where γ are the propensity score model parameters.

Theorem 1. Let ${\mathit{\mu }}_0^{01}(\alpha )={\left({\overline{Y}}^L(0;\alpha ),{\overline{Y}}^L(1;\alpha )\right)}^T$. Assume that Assumptions 2, 3 hold, the outcome is bounded (there exists M > 0 : |Y_ij| < M with probability 1), the parametric form of the propensity score model indexed by γ, f_A|L,i(a_i|l_i; γ), is correctly specified and differentiable with respect to γ with true parameters γ₀, and ${\widehat{\mu }}_N^{01}(\alpha )$ is calculated using $\widehat{\mathit{\gamma }}$, the MLE of γ. Let ${\mathit{\psi }}_{\gamma }\left(l_i,a_i;\gamma \right)=\frac{\partial }{\partial {\mathit{\gamma }}^T}\text{log}f\left(a_i|l_i;\gamma \right)$ be the score functions. Assume that:

1. γ₀ is in an open subset of the Euclidean space,

2. γ → ψ_γ(l_i, a_i; γ) is twice continuously differentiable ∀(l_i, a_i),

3. $E_{G_0}\Vert {\psi }_{\gamma }\left(L_i,A_i;{\mathit{\gamma }}_0\right){\Vert }_2^2<\infty$,

4. $E_{G_0}\left\{\frac{\partial }{\partial {\mathit{\gamma }}^T}{\mathit{\psi }}_{\gamma }({\mathit{L}}_i,\mathit{\left[}{}_i;\mathit{A}\right)]{|}_{\mathit{\gamma }={\mathit{\gamma }}_0}\right\}$ exists and is non-singular, and

5. ∃ measurable integrable function ${\ddot{\psi }}_{\gamma }\left(l_i,a_i\right)$ fixed such that ${\ddot{\psi }}_{\gamma }$ dominates the second partial derivatives of ψ_γ for all γ in a neighborhood of γ₀.

Then, $\sqrt{N}\left\{{\widehat{\mu }}_N^{01}(\alpha )-{\mu }_0^{01}(\alpha )\right\}\stackrel{d}{\to }N\left(0,W\left({\gamma }_0,{\mu }_0^{01}(\alpha )\right)\right)$, where

$$W(\gamma ,\mathit{\mu })=V(\mathit{\gamma },\mathit{\mu })+A_{21}{B}_{11}^{-1}{A}_{21}^T+A_{21}{B}_{11}^{-1}{B}_{12}+{\left(A_{21}{B}_{11}^{-1}{B}_{12}\right)}^T,$$

$$V(\gamma ,\mathit{\mu })=E_{G_0}\left\{{\psi }_{01,\alpha }\left({\mathit{Y}}_i,{\mathit{L}}_i,{\mathit{A}}_i;\mathit{\mu },\gamma \right){\psi }_{01,\alpha }{\left({\mathit{Y}}_i,{\mathit{L}}_i,{\mathit{A}}_i;\mathit{\mu },\gamma \right)}^T\right\},$$

$${\psi }_{01,\alpha }\left({\mathit{Y}}_i,{\mathit{L}}_i,{\mathit{A}}_i;\mathit{\mu },\gamma \right)={\left({\psi }_{0,\alpha }\left({\mathit{Y}}_i,{\mathit{L}}_i,{\mathit{A}}_i;{\mu }_0,\mathit{\gamma }\right),{\psi }_{1,\alpha }\left({\mathit{Y}}_i,{\mathit{L}}_i,{\mathit{A}}_i;{\mu }_1,\mathit{\gamma }\right)\right)}^T$$

$${\psi }_{a,\alpha }\left(Y_i,L_i,A_i;{\mu }_a,\gamma \right)=\frac{1}{n_i}\sum _{j=1}^{n_i}\frac{P_{\alpha ,L}\left(A_{i,-j}|A_{ij}=a,L_i\right)}{f_{\mathit{A}|\mathit{L},i}\left(A_i|L_i;\gamma \right)}I\left(A_{ij}=a\right)Y_{ij}-{\mu }_a{A}_{21}=A_{21}(\mathit{\gamma },\mu )=E_{G_0}{\{\partial {\psi }_{0,\alpha }\left(Y_i,L_i,A_i;{\mu }_0,\gamma \right)/\partial \mathit{\gamma }\partial {\psi }_{1,\alpha }\left(Y_i,L_i,A_i;{\mu }_1,\gamma \right)/\partial \mathit{\gamma }\}}^T,$$

$$B_{11}=B_{11}(\mathit{\gamma })=E_{G_0}\left\{{\mathit{\psi }}_{\mathit{\gamma }}\left(L_i,A_i;\mathit{\gamma }\right){\mathit{\psi }}_{\gamma }{\left(L_i,A_i;\gamma \right)}^T\right\},$$

$$B_{12}=B_{12}(\mathit{\gamma },\mathit{\mu })=E_{G_0}\{{\psi }_{\gamma }\left(L_i,A_i;\mathit{\gamma }\right){\psi }_{0,\alpha }\left(Y_i,L_i,A_i;{\mu }_0,\gamma \right),{\psi }_{\gamma }\left(L_i,A_i;\mathit{\gamma }\right){\psi }_{1,\alpha }\left(Y_i,L_i,A_i;{\mu }_1,\gamma \right)\},$$

for μ = (μ₀, μ₁).

Even though the MLE $\widehat{\gamma }$ and the score equations were used in Theorem 1, any consistent M-estimator of ψ-type can be used, as long as its objective function ψ_γ(l_i, a_i; γ) satisfies the theorem’s conditions.

For a known propensity score, asymptotic results follow by considering f_A|L,i(A_i|L_i; γ) as fixed with respect to γ, leading to $W\left({\gamma }_0,{\mu }_0^{01}(\alpha )\right)=V\left({\gamma }_0,{\mu }_0^{01}(\alpha )\right)$. In both cases, Theorem 1 leads to the approximation ${\widehat{\mu }}_N^{01}(\alpha )~MV{N}_2\left({\mu }_0^{01}(\alpha ),N^{-1}W\left({\gamma }_0,{\mu }_0^{01}(\alpha )\right)\right)$ for large number of clusters. Even if assumptions about G₀ are made, $W\left({\gamma }_0,{\mu }_0^{01}(\alpha )\right)$ is hard to calculate analytically. Instead, $W\left({\gamma }_0,{\mu }_0^{01}(\alpha )\right)$ can be estimated using $\widehat{W}\left(\widehat{\mathit{\gamma }},{\widehat{\mu }}_N^{01}(\alpha )\right)$, where $\widehat{W}(\mathit{\gamma },\mathit{\mu })$ is the matrix W(γ, μ) where all expectations are substituted with the empirical expectations. For example, ${\widehat{B}}_{11}(\mathit{\gamma })=\frac{1}{N}\sum _{i=1}^N{\mathit{\psi }}_{\gamma }\left(L_i,A_i;\mathit{\gamma }\right){\psi }_{\gamma }{\left(L_i,A_i;\mathit{\gamma }\right)}^T$. Under regularity conditions, discussed in Iverson and Randles (1989), $\widehat{W}\left(\widehat{\mathit{\gamma }},{\widehat{\mu }}_N^{01}(\alpha )\right)$ will be consistent for $W\left({\gamma }_0,{\mu }_0^{01}(\alpha )\right)$. Using Theorem 1, one can obtain the asymptotic distribution of a contrast between ${\widehat{Y}}^L(0;\alpha ),{\widehat{Y}}^L(1;\alpha )$ specifying a direct effect by an application of the multivariate delta method.

Next, we derive the asymptotic distribution for ${\widehat{\mu }}^{IE}\left({\alpha }_0,{\alpha }_1\right)={\left({\widehat{Y}}_N^L\left(0;{\alpha }_0\right),{\widehat{Y}}_N^L\left(0;{\alpha }_1\right)\right)}^T$.

Theorem 2. Let ${\mathit{\mu }}_0^{IE}\left({\alpha }_0,{\alpha }_1\right)={\left({\overline{Y}}^L\left(0;{\alpha }_1\right),{\overline{Y}}^L\left(0;{\alpha }_2\right)\right)}^T$. If the assumptions of Theorem 1 hold, $\sqrt{N}\{{\widehat{\mu }}^{IE}\left({\alpha }_0,{\alpha }_1\right)-{\mathit{\mu }}_0^{IE}\left({\alpha }_0,{\alpha }_1\right)\}\to N\left(0,Q\left({\gamma }_0,{\mathit{\gamma }}_0^{IE}\left({\alpha }_0,{\alpha }_1\right)\right)\right)$, where

$$Q(\gamma ,\mu )=D_{22}(\mathit{\gamma },\mu )+C_{21}{B}_{11}^{-1}{C}_{21}^T+C_{21}{B}_{11}^{-1}{D}_{12}+{\left(C_{21}{B}_{11}^{-1}{D}_{12}\right)}^T$$

$$D_{22}(\mathit{\gamma },\mu )=E_{G_0}\left\{{\psi }_{0,{\alpha }_1,{\alpha }_2}\left(Y_i,L_i,A_i;\mu ,\gamma \right){\psi }_{0,{\alpha }_1,{\alpha }_2}{\left(Y_i,L_i,A_i;\mu ,\gamma \right)}^T\right\}$$

$${\psi }_{0,{\alpha }_1,{\alpha }_2}\left(Y_i,L_i,A_i;\mu ,\gamma \right)={({\psi }_{0,{\alpha }_1}\left(Y_i,L_i,A_i;{\mu }_0,\mathit{\gamma }\right),{\psi }_{0,{\alpha }_2}\left(Y_i,L_i,A_i;{\mu }_0,\gamma \right))}^T$$

$$D_{12}=D_{12}(\mathit{\gamma },\mu )=E_{G_0}\{{\psi }_{\gamma }\left(L_i,A_i;\mathit{\gamma }\right)\times {\psi }_{0,{\alpha }_1}\left(Y_i,L_i,A_i;{\mu }_0,\gamma \right),$$

$${\psi }_{\gamma }\left(L_i,A_i;\mathit{\gamma }\right){\psi }_{0,{\alpha }_2}\left(Y_i,L_i,A_i;{\mu }_0,\mathit{\gamma }\right)\},$$

$$C_{21}=C_{21}(\mathit{\gamma },\mathit{\mu })=E\{\partial {\psi }_{0,{\alpha }_1}\left({\mathit{Y}}_i,{\mathit{L}}_i,{\mathit{A}}_i;{\mu }_0,\mathit{\gamma }\right)/\partial \mathit{\gamma }\hspace{0.17em}\partial {\psi }_{0,{\alpha }_2}\left(Y_i,L_i,A_i;{\mu }_0,\gamma \right)/\partial \mathit{\gamma }\},$$

and B₁₁ as in Theorem 1.

4.3 |. Estimators and asymptotic results for the population-level estimands

Similar arguments lead to estimators of the F_α-group and population average potential outcomes in (3) and (4) as

$${\widehat{Y}}_i^L\left(a;F_{\alpha }\right)=\int {\widehat{Y}}_i^L(a;\alpha )\text{d}{F}_{\alpha }(\alpha )=\frac{1}{n_i}\sum _{j=1}^{n_i}\frac{P_{F_{\alpha },L}\left({\mathit{A}}_{i,-j}|A_{ij}=a,{\mathit{L}}_i\right)}{f_{\mathit{A}|\mathit{L},i}\left({\mathit{A}}_i|{\mathit{L}}_i\right)}I\left(A_{ij}=a\right)Y_{ij},$$

$${\widehat{Y}}^L\left(a;F_{\alpha }\right)=\int {\widehat{Y}}^L(a;\alpha )\text{d}{F}_{\alpha }(\alpha )=\frac{1}{N}\sum _{i=1}^{n_i}{\widehat{Y}}_i^L\left(a;F_{\alpha }\right)$$

accordingly, where $P_{F_{\alpha },L}\left({\mathit{A}}_{i,-j}|A_{ij}\hspace{0.17em}=\hspace{0.17em}a,{\mathit{L}}_i\right)=\int P_{\alpha ,L}\left({\mathit{A}}_{i,-j}|A_{ij}=a,{\mathit{L}}_i\right)\text{d}{F}_{\alpha }(\alpha )$.

Assume that $F_{\alpha }^1$, $F_{\alpha }^2$ are discrete distributions taking values α_k ∈ (0, 1), k = 1, 2, …, K, with probability p_1k and p_2k accordingly, such that $\sum _{k=1}^K{p}_{hk}=1$, h = 1, 2. Then, ${\overline{Y}}^L\left(0;F_{\alpha }^h\right)=\sum _{k=1}^K{p}_{hk}{\overline{Y}}^L\left(0;{\alpha }_k\right)$, $I{E}^L\left(F_{\alpha }^1,F_{\alpha }^2\right)=\sum _{k=1}^K\left(p_{2k}-p_{1k}\right){\overline{Y}}^L\left(0;{\alpha }_k\right)$ and a consistent estimator of $I{E}^L\left(F_{\alpha }^1,F_{\alpha }^2\right)$ is ${\widehat{IE}}^L\left(F_{\alpha }^1,F_{\alpha }^2\right)=\sum _{k=1}^K\left(p_{2k}-p_{1k}\right){\overline{Y}}^L\left(0;{\alpha }_k\right)$. The asymptotic distribution of ${\widehat{IE}}^L\left(F_{\alpha }^1,F_{\alpha }^2\right)$ follows by arguments similar to the ones in Theorem 2 (Web Appendix D).

Although the estimands in Section 3 are well-defined for any distribution F_α, reliable estimation requires sufficiently overlapping support of F_α with the empirical distribution ${\widehat{F}}_{\alpha }$.

4.4 |. Finite sample variance estimator

The asymptotic distributions derived above can be used to compute Wald-type confidence intervals for a sample with a large number of clusters. However, in settings with a small number of observed clusters (as in the study of Section 6 with 50 clusters), a bootstrap (Efron, 1979) approach to finite sample confidence intervals might be preferable.

Note that the population average potential outcome ${\overline{Y}}^L(a;\alpha )$ is defined as the mean of the cluster quantity ${\overline{Y}}_i^L(a;\alpha )$. Thinking of the clusters as the unit of observation, uncertainty around ${\widehat{Y}}^L(a;\alpha )$ can be acquired employing a bootstrap approach commonly used for mean estimators. Here, B new data sets are created, each consisting of the same number of clusters as in the original data, sampled with replacement from the observed ones. Confidence intervals for ${\widehat{Y}}^L(a;\alpha )$ are constructed using the quantiles of the B bootstrap estimates, for large B. Confidence intervals for all estimators discussed here can be obtained similarly.

5 |. SIMULATIONS

Web Appendix A presents a simulation study to evaluate the operating characteristics of the estimators based on the true and estimated propensity score and using the asymptotic variance and bootstrap approach to confidence intervals. We construct a super-population of 2000 clusters, from which N ∈ {50, 300} clusters are sampled randomly. The simulations show that, when the propensity score is known, the estimators are close to unbiased, and the 95% confidence intervals achieve the nominal coverage for both the asymptotic and bootstrap approach. When the propensity score is estimated, 95% confidence intervals based on the asymptotic variance exhibit under-coverage. Bootstrap-based confidence intervals perform favorably achieving close to the 95% level in most cases, with apparent over coverage when estimating the indirect effect with N = 50.

6 |. EVALUATING THE EFFECTIVENESS OF POWER PLANT EMISSIONS CONTROLS FOR REDUCING AMBIENT OZONE POLLUTION

Limited literature exists evaluating U.S. air pollution regulations within a causal inference framework. Power plant regulations for the reduction of NO_x emissions have been predicated on the knowledge that reducing NO_x emissions would lead to a subsequent reduction in ambient ozone. Among various NO_x emission reduction strategies, SCR and SNCR are believed to be the most effective in reducing emissions. While work in Papadogeorgou et al. (2018) corroborated this effectiveness of SCR and SNCR for reducing NO_x emissions, the analysis of ambient ozone pollution in that paper ignores the possibility of interference and estimates an effect on ozone very close to zero. However, interference is a key component in the study of air pollution: ambient pollution concentrations near a power plant will depend on the treatment levels of other nearby power plants.

We use the same data as in Papadogeorgou et al. (2018) to estimate direct and indirect effects of SCR/SNCR against alternatives on ambient ozone under realistic counterfactual programs. The publicly-available data set includes 473 coal or gas burning power generating facilities in the U.S. operating during June, July and August 2004, with covariate information on power plant characteristics, weather and demographic information of the surrounding areas. For every power plant, the value of ozone is calculated as the average of the 4^th highest ozone measurements across EPA monitoring locations within 100km. See Papadogeorgou et al. (2018) for a full description of the data set and linkage. Web Appendix B includes links to the publicly available data set, R package, and R scripts replicating the results.

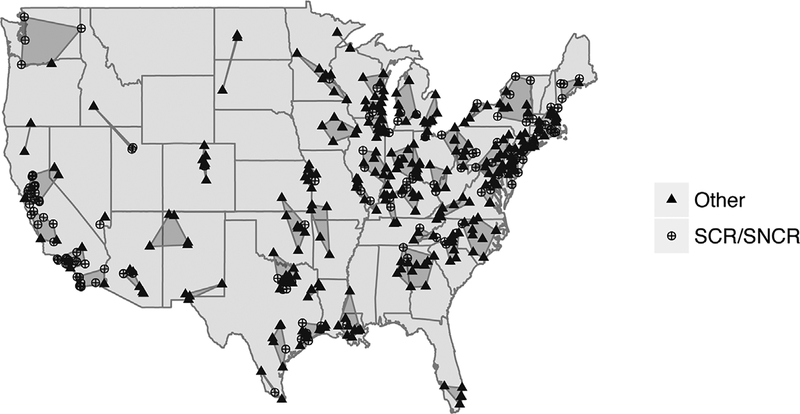
Power plant facilities are grouped according to Ward’s agglomerative hierarchical clustering method (Ward, 1963), which starts by considering every unit as its own cluster and proceeds by merging clusters based on an objective function until all units form a single cluster. Clusters are meant to represent interference groups, so the objective function is based solely on geographic closeness to encourage grouping nearby power plants that are likely to emit over each other. Visual inspection is used to choose 50 clusters of power plants in the sequence of power plant partitions. The grouping and treatment of facilities are depicted in Figure 2.

FIGURE 2.

Treated (SCR/SNCR) and control (Other) power plant facilities during June, July, August of 2004. Shaded areas depict the interference clusters according to the agglomerative clustering method.

6.1 |. Plausibility of the ignorability and positivity assumption

While regulatory programs provide incentives to install emission-control technologies, power plants have latitude to select which (if any) technology to adopt. Such decisions are largely determined by the power plant’s characteristics such as its size and operating capacity, as well as by factors related to local or regional air pollution incentives that are influenced by area-level characteristics such as population density and urbanicity. To capture such factors, 18 covariates are included in the data set describing power plant, weather, and demographic characteristics, based on which ignorability is expected to hold. The variability in the observed proportion of treated power plants across clusters provides an additional indication that the positivity assumption is plausible. The propensity score was modeled as in Papadogeorgou et al. (2018) augmented with a cluster-specific random effect following common practice in the analysis of clustered data:

$$\text{logit\hspace{0.17em}}P\left(A_{ij}=1|L_{ij}\right)={\gamma }_0+{\beta }_i+L_{ij}^T{\mathit{\gamma }}_L,{\beta }_i~N\left(0,{\sigma }_b^2\right),$$ (6)

where $\mathit{\gamma }={\left({\gamma }_0,{\mathit{\gamma }}_L^T,{\sigma }_b^2\right)}^T$ in the notation of Theorem 1. Such model has been shown to perform well in the presence of unmeasured cluster-level confounders (Arpino and Mealli, 2011; Li et al., 2013) providing robustness to violations of the conditional ignorability assumption.

6.2 |. Counterfactual treatment allocation for the installation of SCR/SNCR technologies

To specify counterfactual treatment allocations that reflect realistic relationships between covariates and the propensity to adopt treatment, we specify P_α,L such that the log-odds of treatment installation related to individual covariates are as observed in the propensity score model for the observed treatment in (6). Even though this choice of P_α,L depends on the data through the estimated log-odds, the corresponding estimands are well-defined and the asymptotic results are valid for P_α,L fixed across replications of the sampling or an increasing number of clusters. Note that, in general, the covariates used to specify P_α,L need not be identical to those used in the observed propensity score model.

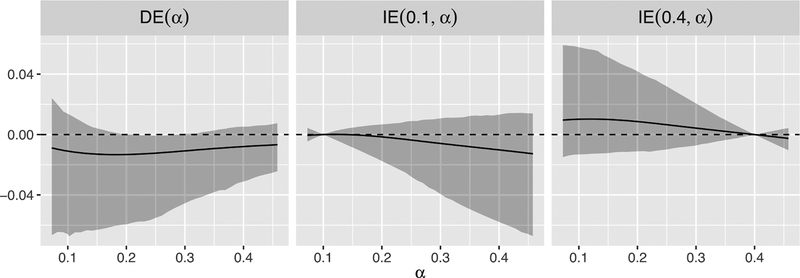
Values of α were considered between the 20^th and 80^th quantiles of the observed cluster treatment proportions, corresponding to α ∈ [0.073, 0.458]. Figure 3 shows the population direct effect DE(α), and population indirect effect IE(α₁, α₂) for a subset of values of α₁ with bootstrap confidence intervals (asymptotic intervals are reported in Web Appendix B). The direct effect is estimated to be negative for all values of α and has a somewhat increasing trend, implying that in a world where the average propensity of SCR/SNCR among power plants in a cluster is fixed, the installation of SCR/SNCR at one power plant is estimated to reduce ozone concentrations in the surrounding area, but these reductions are smaller when the cluster average propensity of treatment is high (larger number of treated neighbors). Using the bootstrap, these reductions are statistically significant for α ∈ (0.22, 0.28), whereas asymptotic confidence intervals indicate significance for almost all values of α considered.

FIGURE 3.

Estimates of the direct effect of SCR/SNCR versus alternative strategies on ozone concentrations as a function of α, and estimates of the indirect effect for values α₁ ∈ {0.1, 0.4}. Shaded areas represent 95% Bootstrap confidence intervals. Ozone is measured in parts per million.

The indirect effect is, in a way, a measure of pollution transport since it quantifies the effect of changes in the cluster average propensity of treatment on ozone concentrations near control power plants. For fixed α₁, IE^L(α₁, α₂) is almost always decreasing in α₂, implying that higher cluster-average SCR/SNCR propensity leads to reductions in ambient ozone concentrations surrounding control power plants. Bootstrap confidence intervals indicate that the indirect effects were not significant. However, based on the asymptotic confidence intervals, the indirect effect is estimated to be significant for values of α₁ > 0.15 and all α₂.

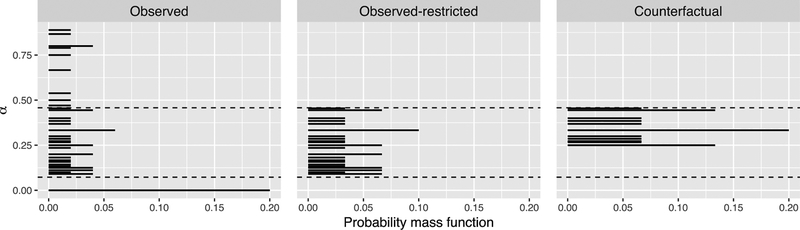
Next, we considered estimating the effect of hypothesized federal regulations that would shift the distribution of cluster-average propensity of treatment. $F_{\alpha }^1\left(F_{\alpha }^2\right)$ was assumed to be a discrete distribution within the 20^th (50^th) and 80^th quantiles of the observed cluster-treatment proportions. In Figure 4, we show the empirical probability mass function, as well as the two counterfactual treatment allocations. $I{E}^L\left(F_{\alpha }^1,F_{\alpha }^2\right)$ was estimated to be −0.0036 parts per million (95% CI: Bootstrap −0.0208 to 0.005, Asymptotic −0.0059 to −0.0013) implying that federal regulations that encourage SCR/SNCR installation enough to bring the cluster average treatment propensity distribution from taking values between the 20^th and 80^th percentiles of the empirical cluster coverage distribution to taking values between the 50^th and 80^th percentiles of the empirical cluster coverage distribution, would lead to ambient ozone concentrations surrounding control power plants that are on average 0.0036 parts per million lower. Compare these estimates against the national ozone air quality standard of 0.07 parts per million.

FIGURE 4.

Observed cluster treatment proportions (“Observed”), and two discrete hypothesized distributions of cluster-average propensity of treatment. One corresponds to the empirical distribution restricted within the 20^th and 80^th quantiles of the observed cluster treatment proportions (“Observed-restricted”), and the other (“Counterfactual”) corresponds to the empirical (or the Observed-restricted) further restricted between the 50^th and 80^th quantiles of the observed cluster treatment proportions.

We explored the sensitivity of the results to the choice of clustering, and saw that the qualitative results for the effectiveness of SCR/SNCR emission reduction technologies are mostly consistent with negative estimated direct effects and decreasing indirect effect curves. The same holds using a propensity score that excluded the cluster-specific random effects. Estimates of the estimands in Tchetgen Tchetgen and VanderWeele (2012) that assume manipulation of individual power-plant treatment propensities indicated similar patterns and magnitudes to those in Figure 3. These results can be found in Web Appendix B.

7 |. DISCUSSION

Analyzing data accounting for interference disentangles the individual treatment effect from one’s neighbors’ treatment effect. We proposed new estimands for counterfactual strategies that depend on covariates and the treatment of one’s neighbors, manipulating treatment at the cluster, or the population of clusters level. Despite the focus on air pollution interventions, similar considerations could be construed in classical interference settings such as vaccine studies, where certain types of community members are more likely to receive the vaccine and vaccine programs are designed to increase coverage at the community, or national level.

For the estimands referring to population level interventions, F_α could be specified to depend on cluster-level covariates acting as predictors of cluster-average propensity of treatment. Alternative estimands can be defined for strategies that manipulate the relationship between covariates and treatment assignment to reflect, for example, interventions for which larger power plants receive higher penalties for over-emission.

Consistent estimators were proposed for which asymptotic distributions were derived. These estimators were employed in the comparative effectiveness of power plant emission control strategies on ambient ozone, returning results that are more in line with subject-matter knowledge than results from a previous study that assumed no interference. While the power plant analysis showed the potential for causal inference methods for interference to lead to important results in air pollution research, the assumption of partial interference– and the existence of distinct clusters– is a simplification since pollution from one power plant can travel long distances. The Web Appendix explores alternative clusterings with comparable results. Ongoing work is oriented towards an account of interference that does not rely on clusters (Forastiere et al., 2018). The existence of between-clusters interference should be viewed in the light of work by Sobel (2006), Tchetgen Tchetgen and VanderWeele (2012), Forastiere et al. (2017), and Sävje et al. (2018), where it is shown that ignoring interference can lead to estimated quantities that lack causal interpretation, unless further assumptions are made. Despite the limitations, the analysis of the air quality data entails a methodological advance for studies of air pollution interventions and formalizes interference in a realm where it has not, to our knowledge, been previously considered in detail.