Spectroscopic X-ray and Mössbauer Characterization of M₆ and M₅ Iron(Molybdenum)-Carbonyl Carbide Clusters: High Carbide-Iron Covalency Enhances Local Iron Site Electron Density Despite Cluster Oxidation

Abstract

The present study employs a suite of spectroscopic techniques to evaluate the electronic and bonding characteristics of the interstitial carbide in a set of iron-carbonyl-carbide clusters, one of which is substituted with a molybdenum atom. The M₆C and M₅C clusters are the dianions (Et₄N)₂[Fe₆(μ₆-C)(μ₂-CO)₂(CO)₁₄] (1), [K(benzo-18-crown-6)]₂[Fe₅(μ₅-C)(μ₂-CO)₁(CO)₁₃] (2), and [K(benzo-18-crown-6)]₂[Fe₅Mo(μ₆-C)(μ₂-CO)₂(CO)₁₅] (3). Because 1 and 2 have the same overall cluster charge (2−) but different numbers of iron sites (1: 6 sites → 2: 5 sites), the metal atoms of 2 are formally oxidized compared to those in 1. Despite this, Mössbauer studies indicate that the iron sites in 2 possess significantly greater electron density (lower spectroscopic oxidation state) compared with those in 1. Iron K-edge X-ray absorption and valence-to-core X-ray emission spectroscopy measurements, paired with density functional theory spectral calculations, revealed the presence of significant metal-to-metal and carbide 2p-based character in the filled valence and low-lying unfilled electronic manifolds. In all of the above experiments, the presence of the molybdenum atom in 3 (Fe₅Mo) results in somewhat unremarkable spectroscopic properties that are essentially a “hybrid” of 1 (Fe₆) and 2 (Fe₅). The overall electronic portrait that emerges illustrates that the central inorganic carbide ligand is essential for distributing charge and maximizing electronic communication throughout the cluster. It is evident that the carbide coordination environment is quite flexible and adaptive: it can drastically modify the covalency of individual Fe–C bonds based on local structural changes and redox manipulation of the clusters. In light of these findings, our data and calculations suggest a potential role for the central carbon atom in FeMoco, which likely performs a similar function in order to maintain cluster integrity through multiple redox and ligand binding events.

Short abstract

An in-depth spectroscopic investigation of a series of iron-carbonyl carbide complexes: [Fe₆C] (1), [Fe₅C] (2), and [Fe₅CMo] (3) is described. Using Mössbauer spectroscopy, valence-to-core X-ray emission spectroscopy, and high-energy-resolution fluorescence-detected X-ray absorption spectroscopy, we detail the ability of the conserved central carbon atom in maintaining cluster stability despite dramatic geometric rearrangements. Our study suggests a potential role for the interstitial carbide in FeMoco as an electronic modulator, allowing for charge and ligand accumulation under turnover conditions.

Introduction

Small-molecule 3d–5d metal clusters that encapsulate light atoms have been of interest to synthetic and catalytic chemistry since their discovery in 1962.¹ Metal–carbonyl and metal-carbonyl-carbide clusters (metal = Ir, Rh, Os, Re, Fe) have been utilized as catalysts in carbon monoxide oxidation, decarbonylation, and hydrogenation reactions. Examples of the carbide-containing complexes have also been implicated as potential models for chemisorbed carbon during heterogeneous catalysis and for Fischer–Tropsch style intermediates.²⁻¹⁰ More recently, clusters containing four-iron frameworks with a variable interstitial light atom (X = carbon or nitrogen) have exhibited hydrogen evolution and CO₂ reduction abilities.¹¹⁻¹⁴

The synthetic flexibility of these polynuclear M_nX compounds has led to the characterization of a wide range of derivatives. Of particular interest are those incorporating modified cage-like core structures, in which 4–6 metal atoms reside at the vertices of an octahedron surrounding a central light atom. Most notable are the 5 and 6 atom clusters of iron, in square pyramidal and octahedral geometries, respectively, which allow for almost modular substitution with Rh and Co atoms.^1,15−17 Recently, Rose and co-workers reported the crystal structure of a substituted six Fe octahedron, in which one axial iron is replaced with molybdenum.¹⁸⁻²⁰ Additionally, Rauchfuss et al. recently published the first report of a synthetic multinuclear iron-carbonyl cluster containing both a totally inorganic carbide and sulfide ligand.²¹

The short Fe–Fe distances in these clusters and a ubiquitous diamagnetic ground state indicate metal–metal bonding and the presence of strong inter-iron antiferromagnetic coupling.²²⁻²⁴ Other multimetallic clusters have previously been shown to exhibit metal-to-metal charge transfer (MMCT) features in X-ray spectroscopy experiments when low-lying and unoccupied 3d orbitals are available.²⁵⁻²⁷ Rees et al. reported that features of this type are found in the spectrum of MoFe at immediately higher energies relative to standard 1s to 3d transitions and have an intensity proportional to the overlap of donor and acceptor atom (both Fe in this case) valence orbitals.

In the present set of complexes (Figure 1), the majority carbonyl ligand sphere allows for significant π-bonding interactions with the core irons and therefore exclusive stabilization of low-spin states. Interestingly, these compounds are capable of reaching multiple oxidation states, with the [Fe₆C] framework in particular able to support two successive 2e^– reductions from the neutral molecule.^28,29 In light of this, we suspect the carbide may play a more significant electronic role than previously considered, especially in the context of diffusing the effects of redox manipulations. A recent study showed that the identity of an interstitial atom (oxygen or fluorine) in a tetranuclear Fe cluster affected the ability of the coordinated irons to translate redox changes and activate terminally bound ligands, lending support to the hypothesis of a more active central atom.^30,31

Figure 1.

Chemical illustrations of 1–3 showing individually labeled iron sites; the bridging carbonyl motifs mimic those found in the crystal structures.

With so many potential avenues of interaction, the electronic structures of these systems are difficult to interrogate and have been the focus of only a few studies. These include the work of Lauher, which provided an in-depth discussion exploring the valence orbitals of these types of systems, but did not elaborate upon the electronic effects of the carbide.³² Moreover, a previous study from Delgado-Jaime et al. reported X-ray absorption (XAS) and valence-to-core X-ray emission spectroscopy (VtC-XES) experiments for the hexa-iron carbide cluster, [Fe₆(μ₆-C)(CO)₁₆]^2–.³³ The study focused on the unique spectroscopic signature of the μ₆ interstitial carbide and compared it with those calculated for other light atom congeners (X = N, O). The study was, at the time, aimed at establishing the VtC-XES fingerprints for pinpointing the light atom in the FeMoco of nitrogenase.³⁴ The subsequent concrete identification of carbon as the interstitial atom of FeMoco^35,36 has since motivated further efforts toward understanding the electronic structure of metal clusters with the interstitial carbide motif. In this context, the present study seeks to holistically (a) delineate fundamental spectroscopic signatures for these complexes and (b) improve the practical and theoretical understanding of metal-carbide bonding motifs. Such advances would enable researchers to better evaluate the role of the carbide in providing stability to the cluster core under turnover conditions.

Herein, we describe an in-depth spectroscopic investigation of a series of iron-carbonyl carbide complexes, including Mössbauer spectroscopy, valence-to-core X-ray emission spectroscopy (VtC-XES), and Kβ high-energy-resolution fluorescence-detected X-ray absorption spectroscopy (HERFD-XAS). First, we compared the structural and electronic characteristics of the aforementioned six-iron cluster (Et₄N)₂[Fe₆(μ₆-C)(μ₂-CO)₄(CO)₁₂] (1) to its five-iron relative [K(benzo-18-crown-6)]₂ [Fe₅(μ₅-C)(μ₂-CO)₂(CO)₁₂] (2) (benzo-18-crown-6 = 2,3-Benzo-1,4,7,10,13,16-hexaoxacyclooctadeca-2-ene). Second, we evaluate 1 and 2 in contrast to the molybdenum substituted M₆ cluster [K(benzo-18-crown-6)]₂[Fe₅Mo(μ₆-C)(μ₂-CO)₃(CO)₁₄] (3). This suite of clusters, pictorially represented in Figure 1, and various analytical methods allow us to assign primary response pathways of iron-carbonyl carbide clusters to geometric and electronic modification.

Experimental Section

Syntheses of Clusters

Each of the clusters, (Et₄N)₂[Fe₆(μ₆-C)(CO)₁₆],²⁸ [K(benzo-18-crown-6)]₂[Fe₅(μ₅-C)(CO)₁₄],¹⁹ and [K(benzo-18-crown-6)]₂[Fe₅Mo(μ₆-C)(CO)₁₇],¹⁹ were prepared as previously reported.

Experimental Spectroscopy

All samples were prepared in an N₂-filled drybox and manipulated under anaerobic conditions.

Mössbauer Spectroscopy

Undiluted crystalline samples of 1–3 were prepared in custom-made sample holders (Delrin and brass). Zero-field Mössbauer spectra were recorded with a ⁵⁷Co source in a Rh matrix using an alternating constant-acceleration Mössbauer spectrometer operated in transmission with a liquid helium cryostat (Oxford Instruments) for measurements at 80 K. The γ-source was kept at room temperature. All isomer shifts are quoted relative to iron metal at 300 K.

Iron XES and XAS

All samples for XAS data collection were collected on duplicate samples diluted to approximately 1% Fe by mass in dry boron nitride and packed into aluminum spacers of 1 mm sample thickness sealed with Kapton tape. Samples for XES were not diluted and packed in the same manner. VtC-XES and HERFD-XAS data were measured at the SOLEIL Synchrotron facility on the GALAXIES beamline (2.75 GeV, 500 mA) equipped with a nitrogen cryostream operated at 90 K.³⁷ Data were collected using a Si(111) double crystal monochromator upstream for energy selection and focusing mirrors to achieve an approximate beam size of 80 (h) × 20 (v) microns. The energy of the incident beam was calibrated by setting the first inflection point of an Fe reference foil to an energy of 7111.2 eV. A 1 m radius Johann spectrometer with a single Ge(620) analyzer crystal in combination with an energy selective silicon-drift detector was utilized for the measurement of X-ray emission. The spectrometer was calibrated by scanning of the elastic lines in the Fe Kβ emission range.

Samples were affixed at a 45° in the beam path and scanned in the vertical direction between acquisition scans for the exposure of fresh sample spots. The incident beam was attenuated by the insertion of variable thickness pieces of aluminum foil so that no radiation damage was observed upon the evaluation of consecutive scans. All presented spectra are the average of a minimum of 15 sample spots. All XES spectra were collected nonresonantly with an incident energy of 7.8 keV. All HERFD-XAS spectra were collected by fixing the Johann spectrometer at the maximum of the Kβ emission energy (∼7056 eV, Figure S26) and scanning the energy of the incident monochromator. Spectra with respective error bars are presented in the Supporting Information (Figures S24–25).

All HERFD-XAS and XES data were processed in MATLAB 2016. HERFD-XAS data were normalized so that the EXAFS region (>100 eV above the edge) was approximately 1. The rising-edge was modeled by an error function and the pre-edge features fit with individual Gaussians. The fits were optimized by a least-squares fitting routine of the squared sum of the residuals. The baseline subtracted VtC-XES data were fit in a similar fashion. The VtC-XES data are scaled to the normalized integrated total spectral intensity (7020–7125 eV).

Density Functional Theory Calculations

All geometry optimizations, Mössbauer, and spectral property calculations were performed in the Orca v4.0 program package developed by Neese and co-workers.³⁸ Initial geometries of 1–3 were extracted from X-ray crystallographic models and optimized using a triple-ζ basis set (def2-tzvp) in conjunction with the B3LYP functional in the gas phase.³⁹⁻⁴¹ These optimizations utilized the resolution of identity approach (RI-J) and chain-of-spheres (COSX) approximation for the Coulomb integral calculations and numerical integration of HF exchange, respectively.^42,43 Closed-shell and broken symmetry solutions of final M_s = 0 states were found for all three clusters, and each approach yielded identical geometry and electronic structures. All property calculations were performed on the final M_s = 0 broken symmetry solutions. Frequency calculations at the same level of theory revealed no imaginary frequencies and confirmed that true energy minima were reached at these geometries.

Mössbauer parameters were calculated as previously described.⁴⁴ Optimized geometries were used with the B3LYP functional and the DKH relativistic approximation, with a combination of the CP(PPP) (Fe only) and def2-tzvp (all other atoms) basis sets.⁴⁵⁻⁴⁷ The angular integration grid was set to Grid5 (FinalGrid 6), with a special integration accuracy of 7 for Fe.

All Fe TDDFT XAS calculations were performed using the B3LYP functional and the same def2-tzvp basis set as described above, paired with the RI-J/COSX approximations. The donor orbitals were Fe 1s, and all virtual orbitals were designated as possible acceptor orbitals. Of up to 250 roots were calculated. 2.0 eV line broadening was applied and calculations were universally shifted by +151.3 eV in order to better align with experiment. Note that atom, molecular orbital, and transition numberings all number begin at 0 within the Orca computational code. Therefore, to retain consistency with Orca computational outputs, the same numbering scheme is maintained throughout this manuscript. Computed excitations were individually analyzed by generating and visualizing transition difference density plots using the ORCA orbital plotting tool (orca_plot) and the UCSF Chimera extensible molecular modeling program. VtC-XES spectra were calculated using a one-electron theoretical protocol in a single-point calculation and shifted the resulting spectra by +144.8 eV.⁴⁸

Results

Crystal Structures and DFT Geometry Optimization

The molecular structures of 1–3 have previously been reported by single crystal X-ray diffraction (XRD), and selected bond metrics are displayed in Table 1. Although the geometries of each have been thoroughly detailed, several structural and electronic features are of particular interest to this study and are thus revisited herein. The XRD structure of 1 consists of two nearly identical subsites, each exhibiting a highly symmetric octahedral μ₆-carbide core “capped” by six irons. The Fe–C distances are contained in a very narrow range (1.88–1.91 Å) with the two longest bonds belonging to Fe₁ and Fe₄, which do not have semibridging carbonyls. Assuming a carbide charge of −4 and neutral carbonyl ligands, all six irons share a delocalized net charge of +2 (based on charge balance with counterions in the crystal), resulting in an average formal iron oxidation state assignment of Fe^0.33.

Table 1. Selected Bond Metrics from the Previously Reported Crystal Structures of 1–3 and DFT Results from the Present Study^a.

	1b - [Fe6C]2–			2b - [Fe5C]2–		3c - [MoFe5C]2–
	crystal site 1	crystal site 2	DFT - b3lyp	crystal	DFT - b3lyp	crystal	DFT - b3lyp
M–C (carbide) (Å)
Mo–C [Ax]						2.113	2.168
Fe0–C	1.876	1.886	1.900	1.882	1.866	1.902	1.918
Fe1–C	1.897	1.906	1.940	1.866	1.902	1.896	1.917
Fe2–C	1.885	1.869	1.908	1.853	1.865	1.881	1.924
Fe3–C	1.896	1.890	1.918	1.863	1.905	1.887	1.928
Fe4–C	1.909	1.901	1.937	1.993	1.992	1.937	1.983
Fe5–C	1.876	1.877	1.913
angles
Fe–C–Fe 1	178.80	178.66	178.53	170.18	177.21	173.33	174.29
Fe–C–Fe 2	178.36	178.08	177.62	167.8	171.72	169.92	170.59
Fe–C–Fe 3	177.04	177.12	175.84
Feapex–Feeq avg				84.82	87.84	93.23	93.3
Mo–C–Feeq avg						86.98	86.9
Mo–C–Feapex						174.18	172.49

^aAll DFT calculated metrics are from the present study.

^bReference (21).

^cReference (19).

Removing one iron and two carbonyl ligands from 1 results in distortion of the remaining scaffold around the now μ₅-carbide, as seen in 2. The axial Fe₄–C distance is elongated by 0.09 Å, and the carbide resides 0.17 Å below the least-squares plane derived from the positions of Fe_0–3. The equatorial irons exhibit Fe–C bonds slightly contracted by ∼0.02 Å to compensate for the lengthened axial bond. Importantly, the net cluster charge of 2 remains unchanged, and thus the average formal iron oxidation state of 2 has increased marginally to Fe^0.4.

Cluster 3 has a similar core structure to 1 but with a Mo atom replacing one of the axial irons. The coordination sphere around the μ₆-carbide core forms a distorted octahedron with a long (2.11 Å) Mo–C bond that is bent toward Fe₂ due to a carbonyl semibridging interaction. The axial Fe₄–C bond (1.94 Å) is intermediate between those of 1 and 2, while the equatorial Fe–C distances have relaxed to values nearly identical to those in 1. Introduction of the Mo⁰ atom maintains the overall cluster charge of −2 and therefore manifests as irons that are formally at the same oxidation state as those in 2– Fe^0.4. The overall stabilities of these iron-carbonyl carbide clusters, in spite of dramatic compositional changes, demonstrate their innate electronic and geometric flexibilities in order to maintain a single cluster redox level.

The optimized geometries of 1–3 were determined by density functional theory (DFT) calculations using the B3LYP/def2-tzvp functional and basis set combination. The optimizations gave structural parameters (shown in Table 1) that generally matched well with those determined by XRD. Relative bond length changes in all three complexes showed good agreement between theory and experiment, though calculated interatomic distances in the iron-carbide core were all elongated by ∼0.02 Å.

Löwdin atomic charges were analyzed for the optimized structures of 1–3 (Table S1). The average charge on each iron was −0.367, −0.399, and −0.392 for 1, 2, and 3, respectively. These were associated with carbide charges of −0.263 (1), −0.190 (2), −0.284 (3). Surprisingly, slight negative charges are predicted for all iron atoms across the suite of complexes, indicating substantial localization of electron density on the core metal scaffold. This is due at least in part to significant charge delocalization of the carbide, which is predicted to be highly oxidized relative to its theoretical −4 formal charge. Cluster 2 exhibits the most oxidized carbide and most reduced iron character, suggesting that the geometric changes and formal oxidation experienced by the cluster may be altering the carbide’s ability to donate charge. In 3, the molybdenum atom holds a relatively oxidized charge of −0.068 and irons that are of intermediate charge relative to 1 and 2, likely because the long Fe–Mo bond lengths and poor orbital overlap obstruct full MMCT electronic dissemination processes. However, addition of an apical metal increases the negative charge of the central carbon atom to an even more reduced state than in 1. This could result from the geometric distortion invoked by the incoming Mo moiety, thus altering the covalency of the remaining iron-carbide scaffold and inhibiting electron density donation from the interstitial atom.

Mössbauer Spectroscopy

Zero-field ⁵⁷Fe Mössbauer spectra for crystalline samples of 1–3 were measured at 80 K and are shown in Figure 2. Complexes 1 and 2 exhibit broad, but well-defined, quadrupole doublets, while the spectrum of 3 contains an asymmetric doublet marked by significant line broadening. Fits to the Mössbauer spectra and the resultant parameters from fits are shown in Figure 2 and delineated in Table 2. Attempts to collect narrower, more resolved Mössbauer spectra by variable-temperature measurements were unsuccessful. Additionally, low-temperature, variable field (up to 7 T, data not shown) did not result in any resolved hyperfine splitting contributions of individual iron-sites to the Mössbauer spectra.

Figure 2.

Zero-field ⁵⁷Fe Mössbauer spectra of crystalline 1–3 obtained at 80 K. Experimental data are shown as black dots and calculated spectral deconvolutions for nonequivalent sites are shown as colored, dashed lines. The overall cumulative fit for each complex is shown as a red line. Mössbauer parameters of nonequivalent sites are displayed next to the corresponding spectra.

Table 2. ⁵⁷Fe Mössbauer Parameters for Crystalline 1–3.

	δ (mm/s)	ΔEq	Γ (mm/s)	area %
1 - [Fe6C]2–
site 1	0.07	0.55	0.39	67
site 2	0.06	0.40	0.32	33
2 - [Fe5C]2–
site 1	0.46	0.59	0.40	42
site 2	0.45	1.00	0.41	40
site 3	0.43	1.46	0.39	18
3 - [Fe5MoC]2–
site 1	0.07	0.85	0.34	40
site 2	0.06	0.50	0.33	40
site 3	0.04	0.16	0.29	20

The solid-state spectrum of 1 agrees well with the solution-state Mössbauer spectrum of 1 reported recently by Kuppuswamy et al., both of which are well-described as two quadrupole doublets with nearly identical parameters in a 2:1 ratio.²⁸ This description matches the XRD structure as previously described, in which there are two crystallographically distinct iron sites in a 4:2 ratio (four irons each with one semibridging carbonyl, two irons with only terminal CO ligands). While 1 may also be fit with a single quadrupole doublet (Figure S27), albeit yielding a slightly poorer goodness of fit, the 4:2 intensity ratio of quadrupole doublets, as reported in Table 2, is also predicted and supported by DFT computations, vide infra.

The Mössbauer spectrum of 2 clearly has distinct iron sites, as a single quadrpole doublet fails to reproduce the data. The spectrum can be modeled by either a two- or three-site fit with intensity ratios of approximately 3:2 and 2:2:1, respectively (see Figure S28). The latter is shown in Figure 2. The three-site model is the statistically favored fit, with the axial iron assigned as the unique isolated site. The observed isomer shift for 2, however, resides at a significantly higher value than that previously reported values of δ = 0.109 and 0.055 mm/s.^15,49,50 This deviation is partially attributed to either the broadened, unresolved spectra or Mössbauer data collection at room temperature.^15,49,50 Nevertheless, such an extreme (+0.38 mm/s) shift corresponding to a seemingly negligible formal oxidation state change (1: Fe^0.33 → 2: Fe^0.4) is curious and merits further discussion. Because of the dramatic change in the zero-field Mössbauer data for 2 compared to 1 and 3, we probed for possible temperature-dependent morphological changes in 2 via a set of variable-temperature powder XRD experiments. PXRD data (Figure S30) did not suggest any significant morphological changes occurring from 100 to 290 K. Additionally, the data were in good agreement with simulated PXRD based on crystal structure data.

It is well established that iron-carbonyls experience a “counter-intuitive” decrease in isomer shift with increasing anionic charge.⁵¹⁻⁵³ This phenomenon is generally explained by an increase in π-back-bonding interactions with ligated CO molecules upon formal Fe reduction, resulting in a metal center that spectroscopically “appears” more oxidized. The CO back-bonding character also leads to an increased Fe K-edge absorption energy for more reduced iron-carbonyl complexes, opposite of standard oxidation assignments in K-edge XAS spectroscopy as discussed vide infra. The Mössbauer spectrum of 3 is previously unreported and nearly resembles that of 1, likely due to their similar coordination geometries. This spectrum can be fit well with overlapping doublets in a 2:2:1 pattern, once again agreeing with the distribution of crystallographically distinct Fe sites. All Mössbauer fits presented are in excellent agreement with the crystallographically distinct iron sites of each complex and the general grouping of similar irons predicted by DFT, vide infra.

Mössbauer parameters for individual iron centers were then computed based on the DFT-optimized geometries for 1–3. Rather than compute absolute isomer shifts, we report values relative to a standard for the purpose of comparing iron centers both within a cluster and between them. The presentation of relative shifts to a single standard alleviates the need for an expansive calibration training set and still retains highly accurate insight as previously demonstrated.⁴⁴ An appropriate standard for 1–3 is the monatomic iron-carbonyl compound, Fe(CO)₅, which has been thoroughly probed by Mössbauer spectroscopy.⁵⁴ The calculations on 1–3 gave δ values for individual iron sites, which were compared to that generated for Fe(CO)₅ as relative isomer shifts [Δδ = δFe_n – δFe(CO)₅], and are plotted in Figure 3. The calculated isomer shift trend observed for the complexes agrees with the “counter-intuitive” trend previously discussed for iron carbonyls, in which the more formally oxidized complex (e.g., 2) has a higher average isomer shift.⁵¹⁻⁵³ The DFT calculated δ parameter for the individual iron sites yields a consistent pattern that allows us to separate them into two groups: those with semibridging (group B) and without bridging CO ligands (group NB). The NB irons are consistently more reduced than B irons, indicating that the geometric distortion induced by a bridging CO allows for more efficient π-backbonding.

Figure 3.

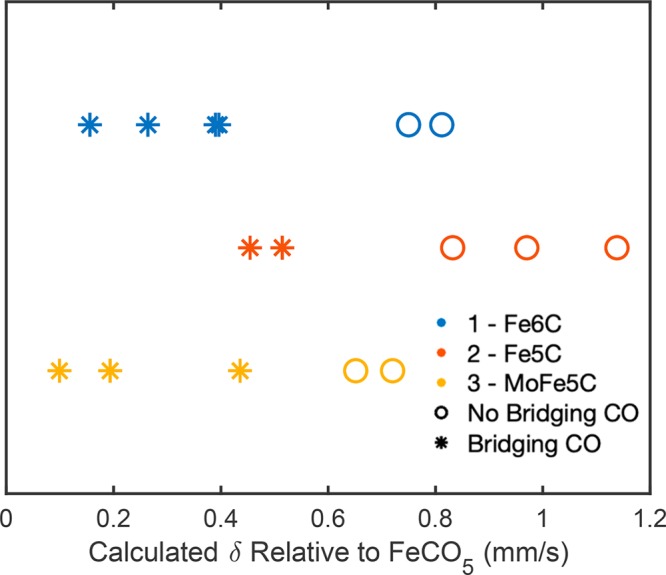
DFT calculated isomer shifts for individual iron sites of 1–3 relative to the standard value calculated for Fe(CO)₅. The Δδ values for 1 are shown in blue, 2 in red, and 3 in yellow. Iron sites that do not have semibridging carbonyl ligands (Group NB) are denoted as open circles, and those that do have a CO bridge (Group B) are shown as stars.

Valence-to-Core X-ray Emission Spectroscopy

Nonresonant VtC-XES was performed on 1–3 to probe the valence orbital character of each complex.⁵⁵ Experimental spectra were compared and analyzed using ground-state DFT calculated valence → 1s core hole transitions (Figure 4).⁴⁸ All three spectra have very similar line shapes that include four primary emission features, the lowest energy of which results from dipole-allowed transitions from the filled CO and carbide valence orbitals (which gain intensity via metal 4p mixing), while the highest energy feature is composed of transitions originating from filled Fe_3d orbitals. Thus, the lower energy range is dominated by Fe_4p → Fe_1s character and is expected to be controlled by changes in the average metal–ligand bond lengths (shorter Fe–L bonds correlate with higher VtC intensity), while the intensity of the high energy region will be sensitive to local site symmetry (resulting from symmetry allowed metal 3d-4p mixing). Both 1 and 2 have overall intensities that are greater than that of 3. Interestingly, out of all three complexes, 2 has the greatest calculated intensity throughout the VtC region. We note that the individual Fe–CO bond lengths vary considerably within and among the three clusters depending on whether they are bridging or terminal. However, the cumulative averages of all Fe–CO bonds in each cluster are comparable, with the average varying only by ±0.002 Å. In contrast, the average Fe–carbide bond length between the three clusters varies more significantly (±0.02 Å) as seen in the mean calculated distanced of 1.92, 1.91, and 1.94 Å for 1–3, respectively.

Figure 4.

VtC-XES spectra of 1–3 paired with the corresponding DFT X → 1s core hole transitions. Experimental spectra are shown on top with solid lines, slightly offset from calculations, denoted by dashed lines. The majority character of the orbitals from which various transitions originate is marked with arrows. In both spectral sets, 1 is shown in blue, 2 in red, and 3 in yellow.

To more thoroughly investigate the electronic origins of the observed features, each spectrum was fit by a linear-least-squares model incorporating multiple pseudo-Voigt lines and examining the corresponding fragment population analysis from DFT calculations. Inspection of the appropriate MOs of individual calculated VtC-XES transitions allows for clear assignments of the donor orbital character. In general, the features of all three complexes have very similar MO-based origins, but vary in intensity. Moving upward beginning at the lowest energy feature around ∼7095 eV, a very weak carbide_2s → Fe_1s transition is observed. This feature is mostly obscured by background and noise in the experimental spectra, but has previously been observed in VtC-XES spectra of 1.³³ The first significant peak at ∼7097 eV is primarily composed of transitions from carbonyl C_2s and O_2sσ* orbitals. At these lower emission energies, the spectral intensities between complexes are very similar, and marked disparities are difficult to identify. More pronounced differences become apparent in the highest intensity peak of the VtC region at ∼7101 eV, composed of majority filled carbonyl C_2p and O_2p π and σ bonding interactions. On the higher energy, falling edge of this peak, the frontier orbitals contribute and a shoulder feature is assigned to a carbide_2p → Fe_1s transition (Figure 4). There is high agreement in this region between calculation and experiment, each showing the feature in 1 as having greater intensity than that of 2 and 3. The depressed emission of 2 relative to 1 at this energy indicates that the carbide_2p orbitals of 2 have experienced a relative loss of electron density, perhaps because of strong σ-donation to the surrounding metal atoms. A higher energy feature at ∼7106.5 eV is ascribed primarily to low-lying, mostly filled Fe_3d orbitals. These transitions are both intra- and inter-iron, with the latter indicating the presence of metal-to-metal charge transfers (MMCT).

Deconvoluting the Valence-to-Core Region

To establish the contributions of the local iron environment on the filled valence manifolds as reflected in VtC-XES, DFT calculations of valence → 1s core hole transitions were performed for each iron in clusters 1–3. The resulting spectra are overlaid for each cluster and displayed in Figure 5. This method essentially represents a site-specific deconvolution of the calculated VtC region. Differences between emission of individual irons are subtle and manifest as slight changes in peak intensity. The most prominent distinctions are consistent across 1–3 and arise between the irons that have CO semibridging interactions (Group B, blue) and those that do not (Group NB, orange). Consistently, Group B irons have lower intensity features associated with transitions from both orbitals previously assigned as majority carbonyl C_2p and O_2p π and σ bonds and those designated as majority Fe_3d. However, Group B irons are also associated with higher intensity features in the energy region assigned to filled carbide_2p orbitals when compared to Group NB irons. These trends fall in line with traditional understanding of the local geometric factors that affect spectral intensities in the VtC region. Namely, the presence of a carbonyl bridge for the Group B irons increases the average Fe–CO bond length around the target atom and correlates with decreased spectral intensity for the carbonyl-based feature at around ∼7101 eV. Additionally, the Fe–carbide bonds for Group B atoms are generally shorter than those of the NB group, leading to a slight increase in the intensity of the carbide-associated VtC shoulder. The DFT calculated Fe–C and Fe–CO bond lengths for individual irons of all three complexes, denoted appropriately as Group B or Group NB are shown in Table 3. While there is some systematic variation between calculation and the crystal structure, bond-length trends remain the same.

Figure 5.

Individual iron atom DFT calculated valence →1s core hole transitions for complexes 1–3. Spectra for individual iron contributions are overlaid to highlight subtle intensity differences for the four primary features previously assigned. Irons that have semibridging carbonyls in their primary coordination sphere (Group B) are denoted as blue lines. Those that only have terminal CO interactions (Group NB) are shown in orange.

Table 3. DFT Calculated Fe–Carbide and Fe–CO Bond-Lengths for Complexes 1–3 Denoted by Appropriate B/NB Identifier.

	DFT - b3lyp
	1 - [Fe6C]2–	2 - [Fe5C]2–	3 - [MoFe5C]2–
M–C (carbide) (Å)
Fe0–C	1.900 (B)	1.866 (B)	1.918 (B)
Fe1–C	1.940 (NB)	1.902 (NB)	1.917 (B)
Fe2–C	1.908 (B)	1.865 (NB)	1.924 (B)
Fe3–C	1.918 (B)	1.905 (B)	1.928 (NB)
Fe4–C	1.937 (NB)	1.992 (NB)	1.983 (NB)
Fe5–C	1.913 (B)
Fe–CO distance (Å)
Fe0–C	1.839 (B)	1.827 (B)	1.837 (B)
Fe1–C	1.775 (NB)	1.776 (NB)	1.802 (B)
Fe2–C	1.830 (B)	1.779 (NB)	1.835 (B)
Fe3–C	1.813 (B)	1.812 (B)	1.778 (NB)
Fe4–C	1.777 (NB)	1.765 (NB)	1.772 (NB)
Fe5–C	1.808 (B)

HERFD-XAS and TDDFT

We utilized Fe Kβ high-energy-resolution fluorescence-detected X-ray absorption spectroscopy (HERFD-XAS) on 1–3 in order to investigate their unoccupied frontier orbital structures. The HERFD-XAS technique suppresses 1s core-hole lifetime broadening of traditional XAS and allows for an improvement in experimental resolution relative to standard techniques and previous studies.^56,57 The obtained spectra are directly compared to time-dependent density functional theory calculations (TDDFT) to allow for detailed assignments of observed spectral features.

The normalized Fe K-edge and expanded pre-edge regions are shown in Figure 6. Observed differences between 1–3 are subtle and composed primarily of slight shifts in the rising edge energy at ∼7122 eV and variable pre-edge intensities. Compared to 1 and 3, the rising edge of 2 is shifted ∼0.5 eV to higher energies. Competing factors notwithstanding, this shift is consistent with the formal oxidation of the iron centers in 2 relative to 1 and 3, which would be expected to manifest most intensely in 1s orbital stabilization to a deeper binding energy.^58,59

Figure 6.

(Left) Normalized Kβ HERFD-XAS rising edges of 1–3. (Right) Magnified pre-edge region with individual pseudo-Voigt deconvolution (displayed as dotted lines) of four select features for each spectrum. In both plots, 1 is shown in blue, 2 in red, and 3 in yellow.

Given the formal oxidation-state assignments of 1–3 (1, 0.33; 2, 0.4; 3, 0.4), one would generally predict that the most oxidized complex, with the lowest site symmetry (e.g., 2) should have the highest pre-edge intensity. This should result from more d-holes and the loss of inversion symmetry, allowing for increased metal 3d-4p mixing. However, the HERFD-XAS of 2 has the least intense pre-edge. To better understand this diversion from elementary principles, the pre-edge regions were fit to the sum of multiple pseudo-Voigt line shapes. This fitting was performed by first subtracting the intensity contribution of the rising edge and optimizing the remaining pre-edge to four peaks with restrained-variable amplitude, full width at half-maximum (fwhm), energy position, and Gaussian/Lorentzian weight parameters. The subcomponents of the fitted pre-edge are shown in Figure 6 (right), and relevant details are delineated in Table 4. The energy and intensity trends of the individual subcomponents are in good qualitative agreement with the TDDFT calculated XAS spectra, shown together in Figure 7. The relative intensity ratios of the pre-edge region (below 7116 eV) and the charge-transfer region (7116–7120 eV) of the HERFD-XAS for each complex appear to change significantly. Each has the same intensity of charge-transfer character, while the formal 1s → 3d pre-edge region is modulated, with 2 possessing the lowest intensity. These relative intensity trends of the two regions are well-reproduced in the TDDFT calculated spectra (Figure 7), allowing for approximate transition assignments.

Table 4. Fitting Parameters for the Pseudo-Voigt Pre-edge Deconvolution of 1–3.

	pre-edge fit parameters
cluster and site	energy (eV)	intensity
1 - [Fe6C]2–
site 1	7113.2	0.181
site 2	7114.6	0.502
site 3	7116.7	0.261
site 4	7118.7	0.152
2 - [Fe5C]2–
site 1	7113.3	0.130
site 2	7114.6	0.289
site 3	7116.5	0.309
site 4	7118.7	0.100
3 - [MoFe5C]2–
site 1	7113.3	0.149
site 2	7114.7	0.403
site 3	7117.0	0.285
site 4	7119.3	0.094

Figure 7.

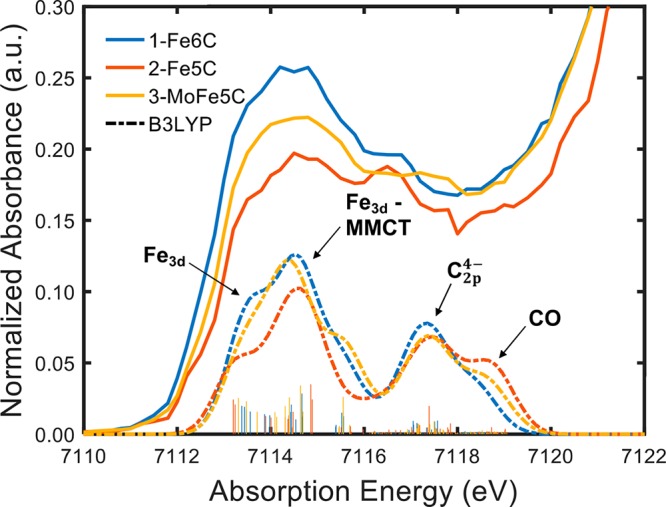
TDDFT calculated spectra of 1–3 (dashed lines) aligned with the corresponding Kβ HERFD-XAS experimental pre-edges (solid line). The dominant character of each feature obtained from transition difference density maps is labeled with a black arrow. Fe_3d refers to 1s → 3d excitations in the absorbing iron, while Fe_3d-MMCT is 1s → 3d transitions from the absorbing atoms to adjacent irons.

Assigning the dominant character of individual features of the TDDFT calculated spectra was performed via analysis of calculated excited states and their corresponding linear combinations of atomic orbitals (LCAOs). It is clear that the pre-edges of 1–3 are dominated by four features of similar character. At lower energies (7112–7115 eV), the pre-edge calculations show a large feature that is divided into a leading shoulder followed by a defined peak. The shoulder can be assigned to local 1s → 3d transitions that incorporate increasing amounts of inter-iron, MMCT character when proceeding to the defined peak at 7115 eV. The lower-intensity, falling shoulder of this feature at ∼7116 eV begins to incorporate orbitals of Fe-CO σ character. At ∼ 7117.5 eV, approximately 5.5 eV above the onset of the pre-edge, a defined peak is seen that can be described as containing excitations into orbitals containing primarily carbide_2p character. A representative example of the transition difference density plot for this “carbide” excitation at ∼7117.5 eV in the spectrum of 2 is displayed in Figure 8. The fact that prominent features are seen in all three complexes at approximately the same energy (Figures S2–S17) which correlates with transitions to the 2p orbitals of the central carbon indicates that description of the light atom as a filled carbide C^4– ion is not entirely correct. Rather, the central atom shares significant electron density with the surrounding metal manifold and thus, we observe significant carbide-based LMCT features. Lastly, at higher energies, near the onset of the rising edge, the acceptor LCAOs are dominated by CO σ* and π* contributions.

Figure 8.

(Left) The HERFD-XAS pre-edge (solid line) spectrum and the TDDFT calculated spectrum (dashed line) for 2; the highlighted slice demarcates the region of examination of vertical excitations and their associated transition difference density plots. (Right) An example of a difference density plot from 2 (isosurface coverage of 0.04); this energy region shows high carbide 2p orbital character.

A molybdenum Kα HERFD-XAS experiment was also performed on 3; the resulting spectrum is shown in Figure S1 and is compared to an oxidized MoCl₃S₃ complex, containing a formal Mo(III) atom.⁶⁰ The Mo edge onset of 3 lies at significantly higher energy than that of the MoCl₃S₃, even though the Mo center of 3 is considered to be Mo(0). This demonstrates the significant back-bonding character of the CO ligands which significantly distorts the ability to utilize the rising-edge as a single spectroscopic probe of oxidation state. The atomic charge analysis of the 3, presented vide supra, is in agreement with a highly reduced Mo(0) assignment. Additionally, the intense pre-edge features of 3 are similar to the intense CO π* pre-edge transitions observed in the Fe K-edge spectra of 1–3.

In Silico Experiments – Deconvoluting the Pre-Edge

With the same aim as our VtC computational deconvolution, a better understanding was sought of how local iron site differences in each cluster affect the character of pre-edge shape and intensity. TDDFT calculations were performed where each individual iron was selected as the lone donor, and the resulting calculated absorption spectra for each cluster are displayed in Figure 9. The transition difference density plots for each individual iron assigned to the appropriate energy ranges for complexes 1–3 are shown in Figures S2–S17. Beginning with 1, the calculated excitations are split into two groups of generally similar line shape: Group B (solid lines) and NB (dotted lines). The members of each group are detailed in Table 3. The primary feature in group B is split by ∼1 eV into peaks containing majority 1s → 3d local-Fe and inter-Fe transitions, respectively. In this region, the NB irons display only a single peak at intermediate energy and of mixed local/inter Fe character. In both cases, the lowest energy intra- and inter-Fe excitations appear to be primarily composed of 1s → 3d_xz/yz character (emphasized in blue). At higher energies, these transitions become distinctly 1s → 3d_z², highlighted in orange. These orbital assignments are consistent with those previously seen by Atkins et al. in calculations of simple iron–carbonyl hydrocarbon molecules.⁶¹ In the same report, it was reported that pure mono-, di-, and trinuclear iron-carbonyls without hydrocarbon ligands showed a reversed orbital trend in the pre-edges. In this set of clusters, it appears that the presence of a bridging carbonyl unit results in the observed magnification of Fe d_xz/yz and d_z² orbital energy splitting, likely resulting from the different coordination geometry induced by a bridging vs terminal carbonyl. A test case using a simple iron-carbonyl dimer with and without bridging ligands was calculated and is shown in Figure S18. Introducing a bridging moiety increases the splitting observed between the two primary pre-edge features, both of which contain orbital character as assigned vide supra. Further support for this hypothesis lies in the unequal sharing of the bridging ligand between each iron in a pair.

Figure 9.

Site-specific TDDFT calculated spectra for the constituent iron atoms of 1–3. Each trace is offset for purposes of comparison. Solid line spectra represent members of Group B and dotted lines designated members of group NB. Energy regions assigned to excitations of predominantly Fe_3d (blue), Fe_3d-MMCT (orange), and carbide (purple) character are denoted by colored vertical bars.

For the B irons of cluster 1, those with the shortest bond distance to the bridging carbon (Fe₃ and Fe₅) have a larger splitting than those with the longer bridge (Fe₀ and Fe₂). The second B pre-edge peak (primarily MMCT character) is also much more intense than the single mixed peak for NB and contains acceptor character that is primarily composed of the Fe atom bridged to the absorber. This likely results, at least in part, from the decreased Fe–Fe distance (average decrease of ∼0.2 Å) upon bridging. It is also important to note that the calculated onset of absorption is generally pushed to slightly higher energies for NB irons, which do not have a split feature. This is an oxidative trend reflected in our previously discussed site-specific Mössbauer calculations. Notably, the carbide feature (∼7117–7118 eV) is shifted to higher energy and is generally lower in intensity for the NB relative to the B irons. Moreover, analysis of the transition difference density plots (Figures S2–S7) in the carbide region reveals that the transitions are directed to orbitals composed primarily of carbide 2p atomic orbitals σ-bonded to the iron, while transitions to MOs of 3d character are almost nonexistent. Other contributing acceptors include the d-orbitals of distal irons not bridged to the absorber.

Next, the pre-edge splitting of 2 mirrors the pattern seen in 1. The difference density plots (Figures S8–S12) also show that carbide acceptor orbitals begin to appear at lower energies than in 1, in the region formally assigned to MMCT (∼7114–7115 eV). Perhaps most surprising, however, is that the 7117–7118 eV “carbide” region shows diminished intensities for all iron absorbers except the apical Fe₄, whose Fe–C bond has been elongated relative to 1. The increase in intensity can partially be attributed to the apical iron site no longer having to “share” the carbide orbitals along the vertical axis. However, the transition acceptor orbitals at this energy have a significantly increased proportion of carbide character, indicating better orbital overlap. The high intensity of this carbide-associated feature at the axial position relative to those in 1 indicates a carbide that has donated significant electron density into the surrounding metal scaffold, leaving comparatively low population on the carbide 2p orbitals.

Finally, the individual absorber pre-edge shapes of 3 follow a pattern that is a “hybrid” of those observed for 1 and 2. Fe₄, which resides trans to the molybdenum atom, displays a carbide-associated feature with decreased intensity similar to that of 1. The transition difference density maps in this region (Figures S13–S17) contain a carbide 2p orbital with qualitatively less isosurface coverage than in 2. It is important to note that due to the geometric distortion produced by the presence of molybdenum, the distribution of the individual contributions to the first pre-edge feature is slightly more disordered (individual excitation features span a larger energy range).

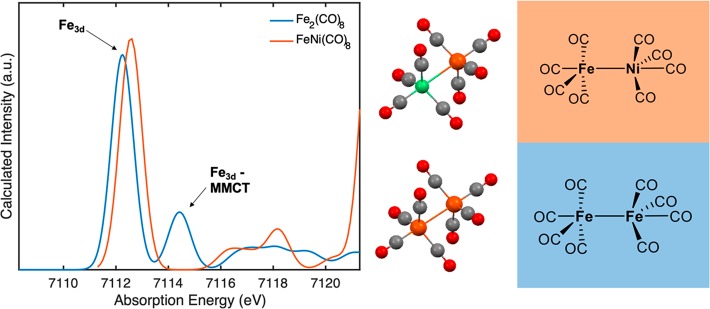
Features of MMCT character were consistently assigned at approximately the same absorption energies across all three clusters. These charge-transfer features are sometimes considered computational artifacts, and thus we sought to confirm our assignments by analyzing similar features in highly simplified, but related models.^62,63 For this purpose, we used an iron-carbonyl dimer with no semibridging (and no carbide) interactions (Figure 10). The TDDFT calculated spectrum of Fe₂(CO)₈ contains two primary peaks in the low energy range representing 1s → 3d local and inter-Fe transitions, respectively. These two peaks are very similar in character to those constituents of the first pre-edge feature in all three carbide complexes. When one of the irons in the dimer is substituted by a closed-shell Ni⁰ atom, the second peak disappears entirely, indicating a complete loss of MMCT transition intensity and confirming the pre-edge assignments in the related clusters 1–3.

Figure 10.

TDDFT XAS calculated spectra for simple model complexes Fe₂(CO)₈ (blue) and FeNi(CO)₈ (orange). The primary orbital contributions to the major features were extracted from transition difference density plots and labeled with black arrows.

In Silico Experiments: Effect of the Carbide

Having gained an understanding of the spectral features arising from different local geometric arrangements and interatomic interactions found in 1–3, we sought to probe the underlying influence of the carbide in these clusters. To begin, absorption spectra for a number of simple model complexes without a bridging carbide moiety were computed by the TDDFT method. By modifying oxidation state, bridging ligands, geometry, and molecular constitution in these “toy complexes”, we aimed to investigate whether the canonical modifiers of pre-edge character manifested in line with traditional understanding when explored using simple iron carbonyls. Varying the local iron oxidation states and geometry in a simple Fe₂(CO)₈ dimer revealed generally well understood pre-edge trends. First, the calculated TDDFT spectra for the [(CO)₄Fe–Fe(CO)₄]^2+/0/2– series, where the local iron oxidation states are Fe(+1), Fe(0), and Fe(−1), respectively, result in diminished intensity of pre-edge features and an increase in the onset energy upon reduction, Figure S19. This shift to higher energies upon reduction is generally not expected, but in these models, it results from increased π back-donation in the more reduced species. This effect is especially interesting considering that the onset of the pre-edge essentially does not shift in energy of clusters 1–3, even under conditions involving formal oxidation, pointing once again to the electronic “leveling” effect of the carbide in 1–3. Additionally, decreasing centrosymmetry (oct → tbp → tet) around the irons resulted in an expected increase in pre-edge intensity due to a greater amount of 3d/4p mixing, Figure S20. These trends are well-known in classic XANES literature, but do not fit the observed pre-edge behavior of compounds 1–3, thus implicating the carbide as playing a critical role in modulating spectroscopic features.^58,64−69

Further investigation into the impact of the carbide on cluster electronics was performed on 1 and 2. The carbide in each cluster was replaced with a point charge (“pc”) equal to the Löwdin atomic charge computed for the optimized geometries (vide supra) yielding the theoretical complexes 1-pc and 2-pc. Atomic population analysis of these modified clusters revealed a change in charge distribution relative to their respective unmodified variants (Table S2). Without the presence of carbide–iron interactions, average iron charges between the complexes are nearly identical between the complexes: −0.258 for 1-pc and −0.252 for 2-pc compared to −0.367 in 1 and −0.399 in 2. Additionally, the average iron charge is distinctly more positive than in both the original optimizations. This exercise serves to highlight the significant covalent bonding and charge donation ability of the interstitial carbide as well as its adaptability to changing iron oxidation states.

The modified clusters 1-pc and 2-pc were examined by DFT and TDDFT calculations to model the XES and XAS spectra, respectively. The resulting spectra of 1-pc, overlaid on the calculations for 1, are displayed in Figure 11. Calculations of the spectra of 2-pc, overlaid on those of 1-pc, are seen in Figure S22. Immediately apparent are the disappearances of features in both spectra ascribed to transitions from/to majority carbide orbitals (at 7095, 7104, and 7117.5 eV) in the unmodified complex as previously described in Figure 7. In the point charge spectra, the absence of these features confirms the previous assignments (vide supra). There are also clear differences between 1 and 1-pc seen in the TDDFT calculated spectra. Most prominently, the two leading peaks of 1-pc have increased in intensity and have spread out over a greater energy range than in 1. To gain insight into which electronic properties were altered upon substitution of the carbide with a point charge, we examined the transition difference density plots for individual vertical excitations in the calculated spectrum of 1-pc. These are highlighted in Figure S23. The first feature at 7112 eV is dominated by clear transitions to the empty Fe_3d manifold of the excited atom. It is important to note that the accepting molecular orbitals in 1-pc are much more localized on individual iron atoms than in 1. Moving to higher energies, the peak at 7115 eV is comprised of more intra-iron excitations paired with a slightly lower density of inter-iron MMCT transitions. The excited atom appears to be distributing electron density primarily to its nearest neighbor, only having very limited MMCT interactions with other irons in the cluster. Again, the fragment population analysis shows much more discrete acceptor orbitals strongly focused around particular iron atoms than in the calculation of1. Lastly, the small peak seen at ∼7118 eV contains vertical transitions comprised mostly of CO π* orbitals.

Figure 11.

Calculated X-ray emission (left) and absorption (right) spectra for the theoretical complex 1-pc in which the central carbon atom has been replaced by a point charge. Calculations for 1-pc are shown in blue and overlaid on calculations for 1, denoted with a dotted orange line.

This experiment underscores our previous judgment that the XAS pre-edges appear to be more sensitive than the VtC-XES to the presence/absence of the carbide and changing cluster oxidation states/geometry. Additionally, we observed that the presence of a central carbon atom rather than a simple point charge produces more delocalized LUMOs, highlighting that the carbide does not serve a pure electrostatic role, but in fact covalently modulates the electronic structure.

Discussion

While the spectroscopic interpretation of iron-carbonyl clusters has historically been dominated by the influence of redox-adaptive π back-bonding interactions between iron and the surrounding CO ligand manifold, we have now shown the significant influence of the interstitial carbide and its ability to significantly alter electronic and structural environments.⁵¹⁻⁵³ In these iron-carbonyl carbide clusters, the extreme σ- and π-donating carbido character takes precedence over these back-bonding effects, and the C^4– moiety becomes the most dominant force in modulating the cluster’s overall electronic structure. Note that the carbide’s π-donating ability arises out of the diversion of these complexes from pure O_h symmetry in which it would be impossible for the carbide 2p orbitals to have any π communication with the iron sites. In reality, the symmetry of the complexes is much lower than O_h due to the CO ligands (evidenced by the substantial iron 3d–4p mixing observed in the XAS pre-edge), allowing for carbide 2p character to arise in the iron π-type d-orbitals. Overall, our spectroscopic analysis of 1–3 reveals trends that do not fall in line with first principle explanations for generic iron-carbonyl compounds, and thus a more in-depth discussion is warranted and provided below.

X-ray Crystallography and Mössbauer Spectroscopy

We must first note the bond flexibility observed in the previously reported crystal structures. Cluster 2 experiences a slight Fe_ax–C bond elongation concomitant with contraction of the equatorial iron plane upon removal of the apical atom from 1. Addition of a Mo atom to form 3 decreases the Fe_ax–C distance, but not quite to the length seen in 1. This Fe–C bond flexibility has been reported in CO inhibited nitrogenase by Scott et al.⁷¹ The latter indicates that the iron-carbide core of nitrogenase may undergo significant distortion following substrate ligation, including an elongation of the substrate-trans Fe–C distance and contraction of the remaining Fe–C bonds. These cooperative bonding effects have also been extensively studied in mononuclear Fe–N₂ model complexes capable of dinitrogen reduction.^70,72,73

Mössbauer spectroscopy on the present set of clusters highlights an exceptional shift (+0.38 mm/s) of 2 to higher δ values relative to 1 and 3. While the direction of the shift is classically nonintuitive for the formal oxidation of the iron sites in 2 compared to the other clusters, such behavior has been previously explained in simple iron-carbonyl systems by the variable nature of π back-bonding with the oxidation state. Generally, one- or two-electron reductions of these simple systems result in relatively small isomer shift changes of around −0.1 and −0.2 mm/s, respectively.⁵¹ Further support for this premise comes from decreased CO stretching frequencies observed by infrared spectroscopy upon reduction of various iron carbonyl complexes, indicating increased π back-bonding and apparently more oxidized irons.⁷⁴ However, parallel Mössbauer behavior has not been observed in iron-carbonyl carbide compounds experiencing discrete redox manipulations. Two-electron oxidations of clusters containing [Fe₄C]^2–, [Fe₅C]^2–, and [Fe₆C]^2– cores have shown decreases in quadrupole doublet isomer shift values by 0.063, 0.03, and 0.04 mm/s, respectively.^15,28,50 These directional shifts are in line with the canonical understanding of oxidations as observed in Mössbauer spectroscopy despite the complexes having significant CO coordination environments. Infrared spectra are only reported for the latter complexes ([Fe₆C]^2–→ [Fe₆C]⁰ and [Fe₅C]^2–→ [Fe₅C]⁰), but indicate respective ∼55 cm^–1 and ∼65 cm^–1 blue-shifts in terminal CO stretching frequencies upon oxidation of the clusters. IR spectroscopy only characterizes the CO character of these iron carbonyl carbide clusters and is traditionally used to estimate the extent of CO back-bonding; in these examples, we see that back-bonding decreases upon oxidation. Mössbauer spectroscopy, on the other hand, probes the iron electronic structure and therefore the extent of charge contribution from both the CO ligands and the interstitial carbide, whose large back-bonding character to the Fe sites have not been thoroughly considered before. In the two-electron oxidations mentioned above, it is clear that the CO manifold is countering changes in the Fe oxidation state, but that this effect is not strong enough to offset the impact of discrete oxidation and therefore results in an expected Mössbauer shift. The fact that we observe the formerly described “counter-intuitive” trend across complexes 1–3 in response to apical atom elimination and substitution indicates that the accompanying minor changes in formal oxidation state are not the main drivers of spectroscopic character, but rather that the geometric manipulations are altering the ability of the carbide to interact with the iron scaffold.

In light of this, it is critical to note that 2 not only possesses a slight increase in formal oxidation compared to 1 but also contains a significant deviation in geometry around the central carbide ligand. In removing an apical Fe, the remaining Fe–C scaffold has adjusted to stabilize the now exposed carbide. It is likely that the change in bonding arrangement has increased orbital overlap between the carbide and the remaining five core irons, formally enhancing the ability of the carbide to donate electron density into the Fe valence manifold through σ-bonding processes. Because the irons in 2 are formally oxidized and have better overlap with the carbide as opposed to those in 1, they accept a greater amount of C^4– electron density and in turn have more heavily populated 3d orbitals. This donation process increases Fe 4s shielding to an extent much greater than would be expected by a simple decrease in π back-bonding upon oxidation, and the isomer shift of a traditionally more “reduced” complex is observed. Carbide ligands are proposed to be excellent σ- and π-donating ligands by multiple computational studies, with the propensity for σ-donation in particular increasing with a decreasing metal oxidation state.^75,76

X-ray Spectroscopy

The HERFD-XAS spectra of 1–3 (Figure 6) exhibit outwardly unorthodox trends that are consistent with the aforementioned carbide σ-donation hypothesis. Although 2 has the lowest local symmetry and is formally oxidized relative to 1 and 3, it has the least intense pre-edge of the group. Removal of an apical iron seems to enhance bonding interactions between the now μ₅-carbide and the surrounding multi-iron framework, consequentially increasing the amount of C^4– σ-donation into the Fe 3d-manifold. This results in—on average—a more occupied valence 3d manifold, appearing as a decrease in pre-edge intensity due to a diminished probability of 1s → 3d transitions. Corroborating this explanation is the deconvolution of the experimental spectra. The pseudo-Voigt absorption line in 2 roughly associated with the “carbide region”, is noticeably higher in intensity and lower in energy than those of 1 and 3, as seen in Figure 6. This change reflects increased carbide σ-donation and metal-orbital overlap due to the carbide, leading to relatively emptier and more stabilized Fe–C bonding orbitals in 1, versus 2 and 3.

The corresponding VtC-XES spectra and calculations (Figure 4) for 1 and 2 reveal a generally greater intensity for 2 except in the region ascribed to the carbide 2p based MOs. This is consistent with the description of 2 as the least symmetric complex, but inconsistent with the formal oxidation of 2 relative to 1 (diminished d-manifold occupancy decreasing the probability of 3d → 1s transitions), such an observation fits into the framework of a more highly σ-donating carbide in 2, resulting in a Fe 3d manifold with greater electron density than that in 1 and 3. Moreover, the diminished carbide feature in the VtC of 2 indicates that C^4– based MOs have decreased occupancy.

Relation to FeMoco

The caged μ₆-carbide structural motif of 1 is generally reminiscent of the iron-carbide core in the molybdenum-containing cofactor (FeMoco) of nitrogenase. It must be noted, however, that direct comparisons between these systems are extremely difficult as a result of the significantly different coordination environments and ground state electronic structures: 1 has a reduced, low-spin iron core coordinated by carbonyls, while FeMoco contains more oxidized, high-spin irons coordinated by bridging sulfides. Nonetheless, the observed electronic and structure-stabilizing behavior of the carbide in 1–3 can provide some context for understanding the unique spectroscopic properties of the carbide-FeMoco assembly in nitrogenase.

DFT calculations on the Mössbauer parameters of the nitrogenate cofactor, which at the time had a yet unidentified interstitial light atom, suggested that the central atom is bound to the surrounding iron cage by highly polarized, ionic-character bonds.⁷⁷ These are claimed to slightly increase electron density on the irons, resulting in relatively high observed isomer shift values. Additionally, this study recognizes the presence of nonbonding Fe–X distances in some of their models, introducing the potential for bond manipulation by the central ligand. More unconventional mechanistic calculations of FeMoco hint at dramatic plasticity in the six-iron core, claiming a variable interstitial atom coordination number between μ₄ and μ₆ under turnover.^78,79 The central ligand is seen as critical for maintaining structural stability during such dramatic cluster rearrangements.

EXAFS and Nuclear resonance vibrational spectroscopy (NRVS) work by Cramer demonstrated significant distortion of the enzymatic Fe–C core structure upon substrate ligation.⁷¹ This observation supports a malleable iron-cage moderated by the interstitial carbide, indicating flexible metal–carbon bonds to the iron sites most closely associated with substrate binding. The notion is supported by a suite of isostructural, mononuclear N₂ activating model complexes synthesized by the Peters group. They feature an axial donor (X = Si, B, C) trans to the bound N₂, with the Fe–X bond experiencing significant elongation upon reduction of the complexes.^72,80 The greatest catalytic competency was observed in the species with the most flexible Fe–X bond (in this case, Fe–B).

In light of these studies, our data and calculations suggest a potential role for the central carbon atom in FeMoco. In the present series of iron–carbonyl carbide clusters 1–3, we observed remarkable electronic and structural adaptability, surmising that cluster stability across different geometries and redox states was directly modulated by the central carbon atom. We also determined that the counter-intuitive character of various spectroscopic features observed by Mössbauer spectroscopy, HERFD-XAS, and VtC-XES were manifestations of strong carbide σ-donation ability responding to changes in cluster geometry. Our TDDFT deconvolutions suggest that the local carbide geometry ideally positions vertex irons to σ-bond with carbide 2p orbitals, which in turn facilitates MMCT processes that disseminate charge during cluster redox events. The interstitial carbon atom of FeMoco likely performs a similar function, maintaining cluster integrity through multiple redox and ligand binding events. In particular, recent studies by Hoffman, Seefeldt, and Dean indicate the buildup of four reducing equivalents and four protons on FeMoco during the E₀ → E₄ conversion prior to N₂ binding where the cluster stores the four electrons as two bridging hydrides.^81,82 Regardless of the exact locations of protonation, reduction, and hydride formation, the iron-core of FeMoco must be able to accommodate significant redox, ligand, and geometric manipulations even in the early stage of the N₂ reduction mechanism. It is possible that the carbide supports the electron and ligand accumulations, disseminating charge through the core via orbital-overlap relaxation pathways, and allows the cluster to reach the catalytically competent redox state.

Conclusion

This study evaluated the electronic and bonding flexibility of the interstitial carbon atom in a series of M₆C and M₅C iron-carbonyl carbide clusters. The compounds under investigation were (Et₄N)₂[Fe₆(μ₆-C)(μ₂-CO)₄(CO)₁₂] (1), [K(benzo-18-crown-6)]₂[Fe₅(μ₅-C)(μ₂-CO)₂(CO)₁₂] (2) and [K(benzo-18-crown-6)]₂[Fe₅Mo(μ₆-C)(μ₂-CO)₃(CO)₁₄] (3). Variation between these clusters manifests as alterations of an Fe₆C carbonyl compound (1) in the elimination of the apical iron site (in 2) and subsequent Mo substitution (in 3)—all the while maintaining a constant overall charge (−2). The primary spectroscopic and theoretical conclusions are as follows:

• (1)⁵⁷Fe Mössbauer studies counter-intuitively indicate that the iron sites in 2 possess greater electron density (lower spectroscopic oxidation state) compared with those in 1 (2: δ_avg ≈ 0.45 mm/s; 1: δ_avg ≈ 0.06 mm/s) despite being formally oxidized compared to the latter.
• (2)Conversely, iron K-edge XAS measurements reveal that the rising-edge of 2 is shifted by ∼0.5 eV to higher energy than that for 1, consistent with the higher formal oxidation states in 2 versus 1.
• (3)TDDFT calculations were used to deconvolute experimental spectra and revealed the presence of significant pre-edge contributions from MMCT and carbide 2p-based transitions. Importantly, the carbide 2p feature in 2 indicates much greater orbital overlap with the axial iron site (2 is square pyramidal around the carbide) and a higher extent of σ-donation from the carbide into the surrounding iron manifold than in 1.
• (4)XES valence-to-core (VtC) measurements show similar character as described above, with less variation between complexes, indicating that formal oxidation and geometric alterations have less of an observable impact on the Fe_3d valence manifold than in the low-lying unfilled orbitals.
• (5)The MMCT and carbide 2p-based assignments were supported by analogous pre-edge calculations with (i) a set of heterometallic clusters that preclude the possibility of MMCT transitions, and (ii) clusters computationally substituted with a point-charge in place of the carbide ion.
• (6)In all of the above experiments, the presence of the molybdenum atom in 3 (Fe₅Mo) results in somewhat unremarkable spectroscopic properties that are essentially a hybrid of those found for 1 (Fe₆) and 2 (Fe₅).
• (7)All of these data highlight the carbide’s ability to electronically respond to changes in geometry and formal oxidation in order to maintain overall cluster stability.

Overall, the central carbide emerges as the essential centerpiece in these clusters, enabling a progression of significant geometric and oxidative modification while consistently providing a stable structural scaffold. Removal of the apical iron from 1 to form 2 results in an overall higher electron density localized on the remaining iron scaffold, likely due to better C_2p and Fe_3d orbital overlap coinciding with geometric adjustment of the carbide. It is apparent that the carbide coordination environment is quite flexible and adaptive: it can drastically modify the covalency of individual Fe–C bonds based on local structural changes (e.g., removal of an iron site, or Mo substitution) and changes in redox state of the clusters. In light of these findings, it is likely that the carbide in the FeMo cofactor of nitrogenase fulfills a similar role, maintaining the electronic and structural stability of the active site despite the multiple reduction and protonation events that occur during the catalytic N₂ reduction cycle.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.inorgchem.9b01870.

• DFT calculated Löwdin atomic charges for 1–3, 1-pc, and 2-pc; molybdenum Kα HERFD-XAS of 3; site-specific TDDFT deconvolution of 1–3 and transition difference density plots; TDDFT pre-edge test cases of simple toy complexes; calculated XAS and XES spectra for 1-pc and 2-pc; calculated XAS pre-edge of 1-pc and transition difference density plots; HERFD-XAS; VtC-XES; Fe Kβ mainline XES spectra; supplemental Mössbauer fits of 1–3; variable temperature powder XRD data of 2; optimized xyz coordinates for 1 (PDF)

The authors declare no competing financial interest.