Cardiologist-Level Arrhythmia Detection and Classification in Ambulatory Electrocardiograms Using a Deep Neural Network

Abstract

Computerized electrocardiogram (ECG) interpretation plays a critical role in the clinical ECG workflow¹. Widely available digital ECG data and the algorithmic paradigm of deep learning² present an opportunity to substantially improve the accuracy and scalability of automated ECG analysis. However, a comprehensive evaluation of an end-to-end deep learning approach for ECG analysis across a wide variety of diagnostic classes has not been previously reported. Here, we develop a deep neural network (DNN) to classify 12 rhythm classes using 91,232 single-lead ECGs from 53,877 patients who used a single-lead ambulatory ECG monitoring device. When validated against an independent test dataset annotated by a consensus committee of board-certified practicing cardiologists, the DNN achieved an average area under the receiver operating characteristic curve (AUC) of 0.97. The average F1 score, which is the harmonic mean of the positive predictive value and sensitivity, for the DNN (0.837) exceeded that of average cardiologists (0.780). With specificity fixed at the average specificity achieved by cardiologists, the sensitivity of the DNN exceeded the average cardiologist sensitivity for all rhythm classes. These findings demonstrate that an end-to-end deep learning approach can classify a broad range of distinct arrhythmias from single-lead ECGs with high diagnostic performance similar to that of cardiologists. If confirmed in clinical settings, this approach could reduce the rate of misdiagnosed computerized ECG interpretations and improve the efficiency of expert-human ECG interpretation by accurately triaging or prioritizing the most urgent conditions.

The electrocardiogram (ECG) is a fundamental tool in the everyday practice of clinical medicine, with more than 300 million ECGs obtained annually worldwide³. The ECG is pivotal for diagnosing a wide spectrum of abnormalities from arrhythmias to acute coronary syndrome⁴. Computer-aided interpretation has become increasingly important in the clinical ECG workflow since its introduction over 50 years ago, serving as a crucial adjunct to physician interpretation in many clinical settings¹. However, existing commercial ECG interpretation algorithms still exhibit substantial rates of misdiagnosis^1,5–7. The combination of widespread digitization of ECG data and the development of algorithmic paradigms that can benefit from large-scale processing of raw data presents an opportunity to re-examine the standard approach to algorithmic ECG analysis and may provide substantial improvements to automated ECG interpretation.

Significant algorithmic advances in the past 5 years have been driven largely by a specific class of models known as DNNs². DNNs are computational models comprised of multiple processing layers, each layer of which can learn increasingly abstract, higher-level representations of the input data as relevant to perform specific tasks. They have dramatically improved the state-of-the-art in speech recognition⁸, image recognition⁹, strategy games such as Go¹⁰, and also in medical applications^11,12. The ability of DNNs to recognize patterns and learn useful features from raw input data without requiring extensive data pre-processing, feature engineering or hand-crafted rules² makes them particularly well suited to interpret ECG data. Furthermore, since DNN performance tends to increase as the amount of training data increases², this approach is well positioned to take advantage of the widespread digitization of ECG data.

A comprehensive evaluation of whether an end-to-end deep learning approach can be used to analyze raw ECG data to classify a broad range of diagnoses remains lacking. Much of the previous work to employ DNNs toward ECG interpretation has focused on single aspects of the ECG processing pipeline, such as noise reduction^13,14 or feature extraction^15,16, or has approached limited diagnostic tasks, detecting only a handful of heartbeat types (normal, ventricular or supraventricular ectopic, fusion etc.)^17–20 or rhythm diagnoses (most commonly atrial fibrillation (AF) or ventricular tachycardia)^21–25. Lack of appropriate data has limited many efforts beyond these applications. Most prior efforts used data from the MIT-BIH Physionet database²⁶ which is limited by the small number of patients and rhythm episodes present in the dataset.

In this study, we constructed a large, novel ECG dataset which underwent expert annotation for a broad range of ECG rhythm classes. We developed a deep neural network to detect 12 rhythm classes from raw single-lead ECG inputs using a training dataset comprised of 91,232 ECG records from 53,549 patients. The DNN was designed to classify 10 arrhythmias as well as sinus rhythm and noise for a total of 12 output rhythm classes (Extended Data Figure 1). ECG data in our dataset was recorded by the Zio® monitor which is an FDA cleared, single-lead, patch-based ambulatory ECG monitor²⁷ that continuously records data from a single vector (modified Lead II) at 200 Hz. Mean and median wear time of the Zio monitor in our dataset was 10.6 days and 13.0 days, respectively. Mean age was 69+/−16 years and 43% were female. We validated the DNN on a test dataset that consisted of 328 ECG records collected from 328 unique patients, and which was annotated by a consensus committee of expert cardiologists (see Methods). Mean age on the test dataset was 70+/−17 years and 38% were female. The mean inter-annotator agreement on the test dataset was 72.8%. Supplementary Table 1 shows the number of unique patients exhibiting each rhythm class.

We first compared the performance of the DNN against the gold standard cardiologist consensus committee diagnoses by calculating the AUC (Table 1a). Since the DNN algorithm was designed to make a rhythm class prediction approximately once per second (see Methods), we report performance both as assessed once every second—which we call “sequence-level” and consists of one rhythm class per interval—and once per record, which we call “set-level” and consists of the group of unique diagnoses present in the record. Sequence-level metrics help capture the duration of an arrhythmia, such as its onset and offset within a record, whereas set-level metrics focus only on the existence of a rhythm class within a record. The DNN achieved an AUC of greater than 0.91 for all rhythm classes; at the sequence-level all but one AUC was above 0.97. The class-weighted average AUC was 0.978 at the sequence-level and 0.977 at the set-level. The model demonstrated high AUCs for arrhythmias of greater clinical significance such as AF, atrio-ventricular block, and ventricular tachycardia. The sequence and set-level results were similar, though sequence-level AUC was higher in the majority of cases. In sensitivity analyses, we calculated multi-class AUC using the method described by Hand and Till²⁸ and results were materially unchanged. Supplementary Table 2 shows the maximum sensitivity achieved by the DNN with specificity >90%, and vice versa. With one exception, all sensitivity and specificity pairs were >90%.

Table 1:

Diagnostic performance of the deep neural network and averaged individual cardiologists compared to the cardiologist committee consensus (n=328). a, Deep Neural Network algorithm area under the receiver operating characteristic curve (AUC) compared to the cardiologist committee consensus. b, Deep Neural Network algorithm and averaged individual cardiologist F1 scores compared to the cardiologist committee consensus.

Table 1a
	Sequence* AUC (95% CI)	Set** AUC (95% CI)
Atrial Fibrillation & Flutter	0.973 (0.966–0.980)	0.965 (0.932–0.998)
Atrio-ventricular Block	0.988 (0.983–0.993)	0.981 (0.953–1.000)
Bigeminy	0.997 (0.991–1.000)	0.996 (0.976–1.000)
Ectopic Atrial Rhythm	0.913 (0.889–0.937)	0.940 (0.870–1.000)
Idioventricular Rhythm	0.995 (0.989–1.000)	0.987 (0.959–1.000)
Junctional Rhythm	0.987 (0.980–0.993)	0.979 (0.946–1.000)
Noise	0.981 (0.973–0.989)	0.947 (0.898–0.996)
Sinus Rhythm	0.975 (0.971–0.979)	0.987 (0.976–0.998)
Supraventricular Tachycardia	0.973 (0.960–0.985)	0.953 (0.903–1.000)
Trigeminy	0.998 (0.995–1.000)	0.997 (0.979–1.000)
Ventricular Tachycardia	0.995 (0.980–1.000)	0.980 (0.934–1.000)
Wenckebach	0.978 (0.967–0.989)	0.977 (0.938–1.000)
Average	0.978	0.977

Table 1b
	Algorithm Sequence-level* F1	Algorithm Set-level** F1	Average Cardiologist Sequence-level F1	Average Cardiologist Set-level F1
Atrial Fibrillation & Flutter	0.801	0.831	0.677	0.686
Atrio-ventricular Block	0.828	0.808	0.772	0.761
Bigeminy	0.847	0.870	0.842	0.853
Ectopic Atrial Rhythm	0.541	0.596	0.482	0.536
Idioventricular Rhythm	0.761	0.818	0.632	0.720
Junctional Rhythm	0.664	0.789	0.692	0.679
Noise	0.844	0.761	0.768	0.685
Sinus Rhythm	0.887	0.933	0.852	0.910
Supraventricular Tachycardia	0.488	0.693	0.451	0.564
Trigeminy	0.907	0.864	0.842	0.812
Ventricular Tachycardia	0.541	0.681	0.566	0.769
Wenckebach	0.702	0.780	0.591	0.738
Average	0.807	0.837	0.753	0.780

^*Sequence-level: describes algorithm predictions that are made once every 256 input samples (approximately every ~1.3 seconds) and are compared against the gold-standard committee consensus at the same intervals.

^**Set-level: describes the unique set of algorithm predictions that are present in the 30-second record. Sequence AUC prediction n=7544; Set AUC prediction n=328.

In addition to a cardiologist consensus committee annotation, each ECG record in the test dataset received annotations from 6 separate individual cardiologists that were not part of the committee (see Methods). Using the committee labels as the gold-standard, we compared the DNN algorithm F1 score to the average individual cardiologist F1 score—which is the harmonic mean of the positive predictive value (precision) and sensitivity (recall) (Table 1b). Cardiologist F1 scores are averaged over 6 individual cardiologists. The trend of the DNN’s F1 scores tended to follow that of the averaged cardiologist F1 scores: both had lower F1 on similar classes such as ventricular tachycardia and ectopic atrial rhythm. The set-level average F1 scores weighted by the frequency of each class for the DNN (0.837) exceeded those for the averaged cardiologist (0.780). We performed multiple sensitivity analyses, all of which were consistent with our main results: both AUC and F1 scores on the 10% development dataset (n=8,761) were materially unchanged from the test dataset results, though were slightly higher (Supplementary Tables 3–4). In addition, we retrained the DNN holding out an additional 10% of the training dataset as a second held-out test dataset (n=8,768), and AUC and F1 scores for all rhythms were materially unchanged (Supplementary Tables 5–6). We note that unlike the primary test dataset which has gold standard annotations from a committee of cardiologists, both sensitivity analysis datasets are annotated by certified ECG technicians.

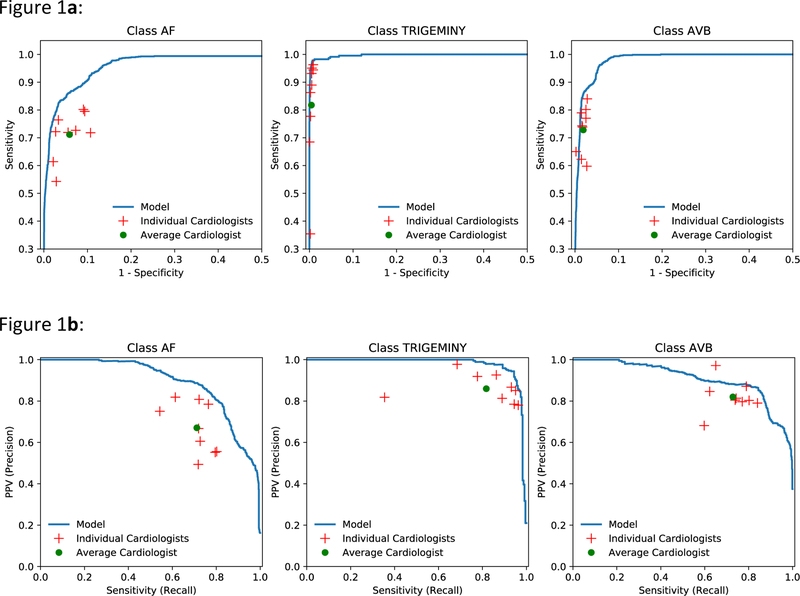
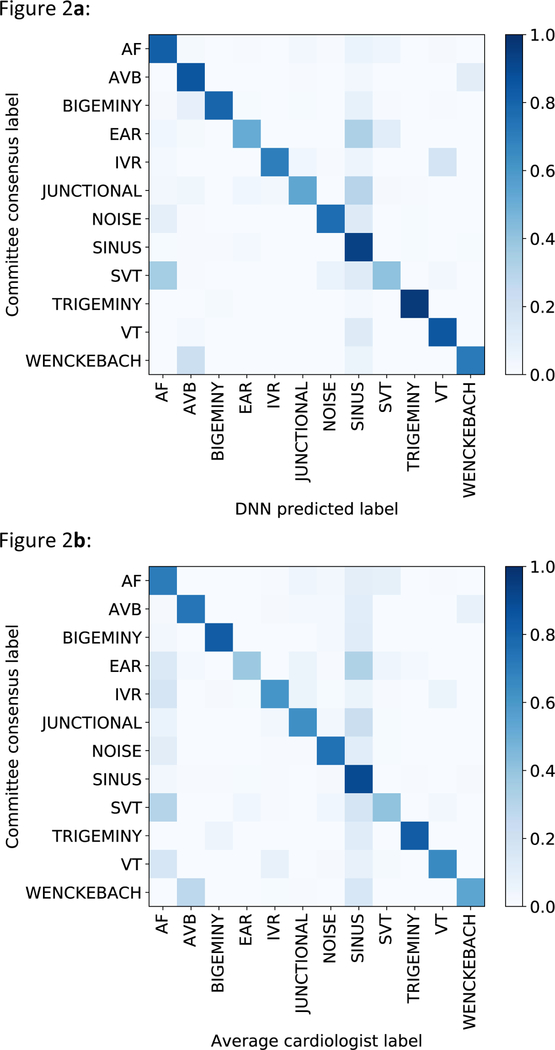
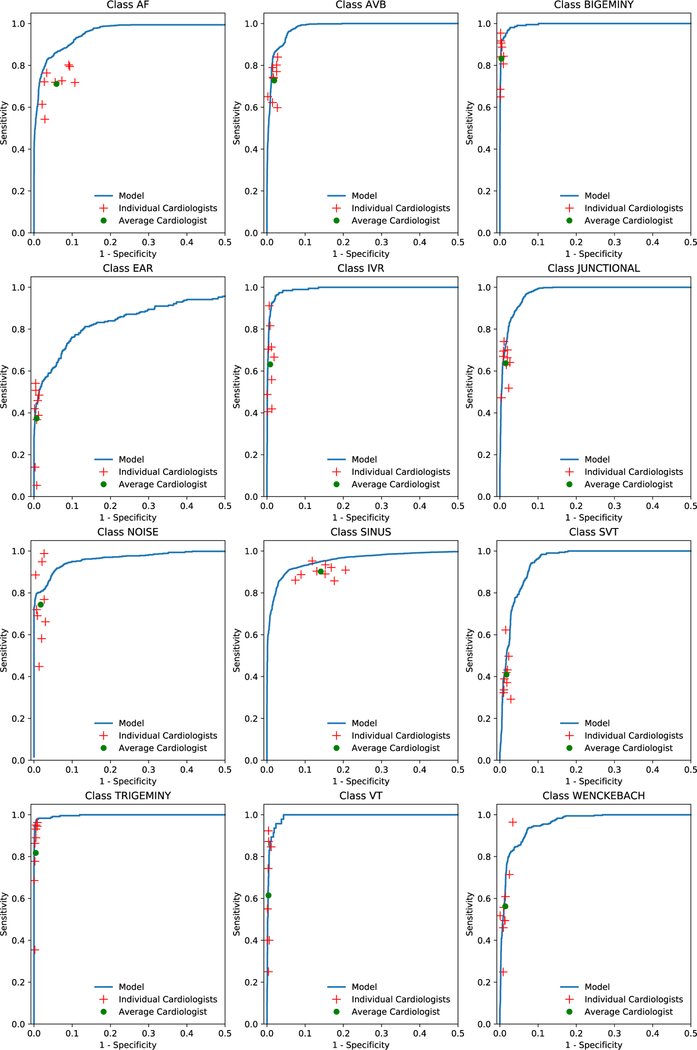
We plotted receiver operating characteristic (ROC) curves and precision-recall curves for sequence-level analyses for three example classes: AF, trigeminy and atrioventricular block (Figures 1a and 1b). Individual cardiologist performances and averaged cardiologist performance are plotted on the same figure. Extended Data Figure 2 presents ROC curves for all classes, showing that the model met or exceeded the averaged cardiologist performance for all rhythm classes. Fixing the specificity at the average specificity level achieved by cardiologists, the sensitivity of the DNN exceeded the average cardiologist sensitivity for all rhythm classes (Table 2). We used confusion matrices to illustrate the discordance between the DNN’s predictions (Figure 2a) or averaged cardiologist predictions (Figure 2b) and the committee consensus. The two confusion matrices exhibit a similar pattern, highlighting those rhythm classes which were generally more problematic to classify (ie. supraventricular tachycardia vs. AF; junctional vs. sinus rhythm; and ectopic atrial rhythm vs. sinus rhythm).

Figure 1:

ROC and precision-recall curves. a, Examples of ROC curves calculated at the sequence level for atrial fibrillation (AF), trigeminy, and AVB. b, Examples of precision-recall curves calculated at the sequence level for atrial fibrillation, trigeminy, and AVB. Individual cardiologist performance is indicated by the red crosses and averaged cardiologist performance is indicated by the green dot. The line represents the ROC (a) or precision-recall curve (b) achieved by the DNN model. n = 7,544 where each of the 328 30-s ECGs received 23 sequence-level predictions.

Table 2:

Deep Neural Network algorithm and cardiologist sensitivity compared to the cardiologist committee consensus, with specificity fixed at the average specificity level achieved by cardiologists.

	Specificity	Average Cardiologist Sensitivity	DNN Algorithm Sensitivity
Atrial Fibrillation & Flutter	0.941	0.710	0.861
Atrio-ventricular Block	0.981	0.731	0.858
Bigeminy	0.996	0.829	0.921
Ectopic Atrial Rhythm	0.993	0.380	0.445
Idioventricular Rhythm	0.991	0.611	0.867
Junctional Rhythm	0.984	0.634	0.729
Noise	0.983	0.749	0.803
Sinus Rhythm	0.859	0.901	0.950
Supraventricular Tachycardia	0.983	0.408	0.487
Trigeminy	0.995	0.832	0.961
Ventricular Tachycardia	0.996	0.652	0.702
Wenckebach	0.986	0.541	0.651

Figure 2:

Confusion matrices. a, Confusion matrix for the predictions of the DNN versus the cardiology committee consensus. b, Confusion matrix for predictions of individual cardiologists versus the cardiology committee consensus. The percentage of all possible records in each category is displayed on a color gradient scale.

Finally, in order to demonstrate the generalizability of our DNN architecture to external data, we applied our DNN to the 2017 Physionet Challenge data (https://physionet.org/challenge/2017/) which contained 4 rhythm classes: sinus rhythm, AF, noise and other. Keeping our DNN architecture fixed and without any other hyper-parameter tuning, we trained our DNN on the publicly available training dataset (n=8,528), holding out a 10% development dataset for early stopping. DNN performance on the hidden test dataset (n=3,658) demonstrated overall F1 scores that were among those of the best performers from the competition (Supplementary Table 7)²⁴, with a class average F1 of 0.83. This demonstrates the ability of our end-to-end DNN-based approach to generalize to a new set of rhythm labels on a different dataset.

Our study is the first comprehensive demonstration of a deep learning approach to perform classification across a broad range of the most common and important ECG rhythm diagnoses. Our DNN had an average class-weighted AUC of 0.97, with higher average F1 scores and sensitivities than cardiologists. These findings demonstrate that an end-to-end DNN approach has the potential to be used to improve the accuracy of algorithmic ECG interpretation. Recent algorithmic and computational advances compel us to revisit the standard approaches to automated ECG interpretation. Furthermore, algorithmic approaches whose performance improves as more data becomes available, such as deep learning², can leverage the widespread digitization of ECG data and provide clear opportunities to bring us closer to the ideal of a learning healthcare system²⁹. We emphasize our use in this study of a dataset large enough to evaluate an end-to-end deep learning approach to predict multiple diagnostic ECG classes, and our validation against the high standard of a cardiologist consensus-committee (most cardiologists were sub-specialized in rhythm abnormalities). We believe this is the most clinically-relevant gold-standard, since cardiologists perform the final ECG diagnosis in nearly all clinical settings.

Our study demonstrates that the paradigm shift represented by end-to-end deep learning may enable a new approach to automated ECG analysis. The standard approach to automated ECG interpretation employs various techniques across a series of steps that includes signal preprocessing, feature extraction, feature selection/reduction and classification³⁰. At each step, hand-engineered heuristics and derivations of the raw ECG data are developed with the ultimate aim to improve classification for a given rhythm, such as AF^31,32. In contrast, DNNs enable an approach that is fundamentally different since a single algorithm can accomplish all of these steps “end-to-end” without requiring class-specific feature extraction—in other words the DNN can accept the raw ECG data as input and output diagnostic probabilities. With sufficient training data, using a DNN in this manner has the potential to learn all of the important previously manually-derived features, along with as-yet unrecognized features, in a data-driven way², and may learn shared features useful in predicting multiple classes. These properties of DNNs can serve to improve prediction performance, particularly since there is ample evidence to suggest that the currently recognized, manually-derived ECG-features represent only a fraction of the informative features for any diagnosis^33,34.

While artificial neural networks were first applied as early as two decades ago toward the interpretation of ECGs^3,35, until recently they only contained several layers and were constrained by algorithmic and computational limitations. More recent studies have employed deeper networks, though some only use DNNs to perform certain steps in the ECG processing pipeline such as feature extraction³³ or classification²⁵. End-to-end DNN approaches have been used more recently showing good performance for a limited set of ECG rhythms such as AF^22,23,36, ventricular arrhythmias²¹, or individual heartbeat classes^20,21,37,38. While these prior efforts demonstrated promising performance for specific rhythms, they do not provide a comprehensive evaluation of whether an end-to-end approach can perform well across a large range of rhythm classes, in a manner similar to that encountered clinically. Our approach is unique in using a 34-layer network in an end-to-end manner to simultaneously output probabilities for a wide range of distinct rhythm diagnoses, all of which is enabled by our dataset that is orders of magnitude larger than most other datasets of its kind²⁶. Distinct from some other recent DNN approaches³⁹, no significant pre-processing of ECG data, such as Fourier or wavelet transforms⁴⁰, is needed to achieve strong classification performance.

Since arrhythmia detection is one of the most problematic tasks for existing ECG algorithms^1,5,6, if validated in clinical settings through clinical trials, our approach has the potential for substantial clinical impact. Paired with properly annotated digital ECG data, our approach has the potential to increase the overall accuracy of preliminary computerized ECG interpretations and can also be used to customize predictions to institution-specific or population-specific applications by additional training on institution-specific data. While expert provider confirmation will likely be appropriate in many clinical settings, the DNN could expand the capability of an expert over-reader in the clinical workflow, for example by triaging urgent conditions or those for which the DNN has the least “confidence.” Since ECG data collected from different clinical applications range in duration from 10 seconds (standard 12-lead ECGs) to multiple days (single-lead ambulatory ECGs), the application of any algorithm, including ours, must ultimately be tailored to the target clinical application. For example, even at the performance characteristics we report, applying our algorithm sequentially across an ECG record of long duration would result in non-trivial false-positive diagnoses. Faced with a similar problem, cardiologists likely incorporate additional mechanisms to improve their diagnostic performance, such as taking advantage of the increased context or knowledge about arrhythmia epidemiology. Similarly, additional algorithmic steps or post-processing heuristics may be important prior to clinical application.

An important finding from our study is that the DNN appears to recapitulate the misclassifications made by individual cardiologists, as demonstrated by the similarity in the confusion matrices for the model and cardiologists. Manual review of the discordances revealed that the DNN misclassifications overall appear very reasonable. In many cases the lack of context, limited signal duration or having a single lead limit the conclusions that can reasonably be drawn from the data, making it difficult to definitively ascertain whether the committee and/or the algorithm was correct. Similar factors, as well as human error, may explain the inter-annotator agreement of 72.8%.

Of the rhythm classes we examined, ventricular tachycardia is a clinically important rhythm for which the model had a lower F1 score than cardiologists, but interestingly had higher sensitivity (94.1%) than the averaged cardiologist (78.4%). Manual review of the 16 records misclassified by the DNN as ventricular tachycardia showed that “mistakes” made by the algorithm were very reasonable. For example, ventricular tachycardia and idioventricular rhythm differ only in the heart rate being above or below 100 beats per minute (bpm), respectively. In 7 of the committee-labeled idioventricular rhythm cases, the record contained periods of heart rate ≥100bpm, making ventricular tachycardia a reasonable classification by the DNN; the remaining 3 committee-labeled idioventricular rhythm records had rates close to 100bpm. Of the 5 cases where the committee-label was AF (4) or supraventricular tachycardia (1), all but one displayed aberrant conduction, resulting in wide QRS complexes with a similar appearance to ventricular tachycardia. If we re-categorize the 7 idioventricular rhythm records with rate ≥100bpm instead as ventricular tachycardia, overall DNN performance on ventricular tachycardia exceeds that of cardiologists by F1 score with a set-level F1 score of 0.82 (vs. 0.77).

This study has several important limitations. Our input dataset is limited to single-lead ECG records obtained from an ambulatory monitor, which provides limited signal compared to a standard 12-lead ECG; it remains to be determined if our algorithm performance would be similar in 12-lead ECGs. However, it may be in applications such as this, which have lower signal-to-noise ratio and where the current standard of care leaves more room for improvement, that approaches such as deep-learning may provide the greatest impact. As we discussed above, a limitation facing this, or any algorithm, before clinical application would be tailoring it to the target application, which may require additional training or post-processing steps. Additionally, systematic differences in the way technicians vs. cardiologists labeled records in our dataset could have decreased DNN performance, though we took precautions to limit this by establishing standard operating protocols for annotation. In addition, as revealed in our manual review of discordant predictions, in some cases there remains uncertainty in the correct label. Given the resource intensive nature of cardiologist committee ECG annotation, our test dataset was limited to records from 328 patients; confidence intervals with our test dataset size were acceptably narrow, as we report in Table 1a, though our ability to perform subgroup analysis (such as by age/gender) is limited. Finally, we also note that in order to obtain a sufficient quantity of rare rhythms in our training and test datasets, we targeted patients exhibiting these rhythms during data extraction. This implies that prevalence-dependent metrics such as the F1 score would not be expected to generalize to the broader population.

In summary, we demonstrate that an end-to-end deep learning approach can classify a broad range of distinct arrhythmias from single-lead ECGs with high diagnostic performance similar to that of cardiologists. If confirmed in clinical settings, this approach has the potential to improve the accuracy, efficiency and scalability of ECG interpretation.

METHODS

Study participants and sampling procedures

Our dataset contained retrospective, de-identified data from adult patients >18 years old who used the Zio® monitor (iRhythm Technologies Inc, San Francisco, CA) from January 2013 to March 2017. All extracted data was de-identified according to the Health Insurance Portability and Accountability Act Safe Harbor. According to iRhythm Technology’s Privacy Policy, fully de-identified patient data may be shared externally for research purposes; patients may opt-out of this sharing. Accordingly, written informed consent was not necessary for this study given that the 30-second ECG samples of both the training and test datasets were appropriately de-identified before use. The study was reviewed and exempted from full review by the Stanford University Institutional Review Board.

We extracted a median of one 30-second record per patient to construct the training dataset. ECG records were extracted based on iRhythm report summaries produced by iRhythm’s clinical workflow which includes a full review by a certified ECG technician of initial annotations from an algorithm which is FDA 510(k) approved for clinical use. We randomly sampled patients exhibiting each rhythm and from these patients selected 30 second records where the rhythm class was present; though the targeted rhythm class was typically present within the record, most records contained a mix of multiple rhythms. To further improve the balance of classes in the training dataset, rare rhythms such as atrio-ventricular block, were intentionally oversampled, with a median of two 30-second records per patient. For the test dataset, 30-second records of each rhythm were sampled in a similar manner to achieve a greater representation of rare rhythms; however, the test dataset included only a single record per patient. The training, development and test datasets had completely disjoint sets of patients.

Annotation Procedures

All ECG records in training and test datasets underwent additional annotation procedures. We used separate procedures to annotate the training and test datasets, reserving the resource-intensive cardiologist annotation for use as the gold-standard in the test dataset. To annotate the training dataset, a group of senior certified ECG technicians reviewed all records and noted the onset and offset of all rhythms on the record. Every record was randomly assigned to be reviewed by a single technician specifically for this task, not for any other purpose. All annotators received specific instructions and training regarding how to annotate transitions between rhythms to improve labeling consistency. We held-out records from a random 10% of the training dataset patients for use as a development dataset to perform DNN hyper-parameter tuning.

Eight board-certified practicing cardiac electrophysiologists and one board-certified practicing cardiologist (all referred to as cardiologists) annotated records in the test dataset. All iRhythm clinical annotations were removed from the test dataset. Cardiologists were divided into three committees of three members each, and each committee annotated a separate one third of the test dataset (112 records). Cardiologist committees discussed records as a group and annotated by consensus, providing the gold-standard for model evaluation. Each of the remaining 6 cardiologists that were not part of the committee for that record also provided individual annotations for that record. These annotations were used to compare the model’s performance to that of the individual cardiologists. In summary, every record in the test dataset received one committee consensus annotation from a group of 3 cardiologists and 6 individual cardiologist annotations.

Many ECG records contained multiple rhythm class diagnoses since the onset and offset of all unique classes were labeled within each 30 second record. The AF class combined AF and atrial flutter. The atrio-ventricular block class combined both type 2 second-degree atrio-ventricular block (Mobitz II) and third-degree atrio-ventricular block. We combined these classes because they have similar clinical consequences. The noise label was selected whenever artifact in the signal precluded accurate interpretation of the underlying rhythm.

Algorithm Development

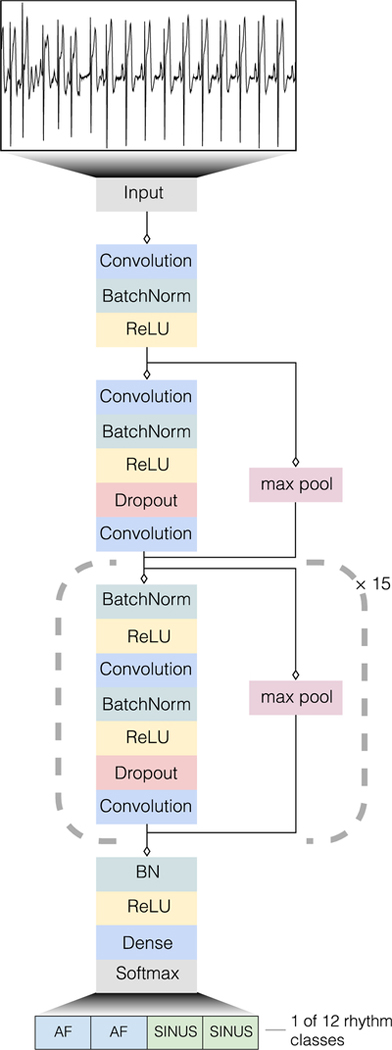
We developed a convolutional DNN to detect arrhythmias (Extended Data Figure 1) which takes as input the raw ECG data (sampled at 200Hz, or 200 samples per second) and outputs one prediction every 256 samples (or every 1.28 seconds), which we call the output interval. The network takes as input only the raw ECG samples and no other patient or ECG related features. The network architecture has 34 layers, and in order to make the optimization of such a network tractable, we employed shortcut connections in a manner similar to the Residual Network architecture⁴¹. The network consists of 16 residual blocks with two convolutional layers per block. The convolutional layers have a filter width of 16 and 32*2^k filters, where k starts at zero and is incremented by one every fourth residual block. Every alternate residual block subsamples its inputs by a factor of two. Before each convolutional layer we applied Batch Normalization⁴² and a rectified linear activation, adopting the pre-activation block design⁴³. The first and last layers of the network are special-cased due to this pre-activation block structure. We also applied Dropout⁴⁴ between the convolutional layers and after the non-linearity with a probability of 0.2. The final fully-connected softmax layer produces a distribution over the 12 output classes.

The network was trained de-novo with random initialization of the weights as described by He et al.⁹ We used the Adam optimizer⁴⁵ with the default parameters $({\beta }_1=0.9\text{and}{\beta }_2=0.999)$ and a minibatch size of 128. We initialized the learning rate to 1e-3 and reduced it by a factor of ten when the development-set loss stopped improving for two consecutive epochs. We chose the model that achieved the lowest error on the development dataset.

In general, the hyper-parameters of the network architecture and optimization algorithm were chosen via a combination of grid-search and manual tuning. For the architecture we searched primarily over the number of convolutional layers, the size and number of the convolutional filters as well as the use of residual connections. We found the residual connections useful once the depth of the model exceeded 8 layers. We also experimented with recurrent layers including long short-term memory cells⁴⁶ and bi-directional recurrence but found no improvement in accuracy and a substantial increase in runtime, thus we abandoned this class of models. We manually tuned the learning rate to achieve fastest convergence.

Algorithm Evaluation

Since the DNN outputs one class prediction every output interval, it makes a series of 23 rhythm predictions for every 30 second record. The cardiologists annotated the start and end point for each rhythm class in the record. We used this to construct a cardiologist label at every output interval by rounding the annotation to the nearest interval boundary. Therefore, model accuracy can be assessed at the level of every output interval—which we call “sequence-level”— or at the record level—which we call “set-level”. To compare model predictions at the sequence-level, the model predictions at each output interval were compared with the corresponding committee consensus labels for that same output interval. At the set-level, the set of unique rhythm classes across a given ECG record that was predicted by the DNN was compared with the set of rhythm classes annotated across the record by the committee consensus. The set-level evaluation, unlike the sequence-level, does not penalize for time-misalignment of a rhythm classification within a record.

Algorithm evaluation at the sequence level allows comparison against the gold standard at every output interval, providing the most comprehensive metric of algorithm performance and which we therefore employ for most metrics. The sequence-level evaluation is also similar to clinical applications for telemetry or Holter monitor analysis, whereby the onset and the offset of rhythms are critical to identify. Evaluation at the set level is a useful abstraction, approximating how the DNN algorithm might be applied to a single ECG record to identify which diagnoses are present in a given record.

To train and evaluate our model on the Physionet challenge data which contains variable length recordings, we made minor modifications to the DNN. Without any change, the DNN can accept as input any record with a length which is a multiple of 256 samples. In order to handle examples which are not a multiple of 256, records were truncated to the nearest multiple. We used the given record label as the label for every ~1.3 second output prediction. In order to produce a single prediction for the variable length record we used a majority vote of the sequence-level predictions.

Statistical Analysis

We calculated ROC analysis and the AUC to assess model discrimination for each rhythm class with a one vs. other strategy^28,47. AUCs for sequence-level and set-level analyses are presented separately. We give a two-sided confidence interval for AUC scores⁴⁸. Sensitivity and specificity were calculated at binary decision thresholds for every rhythm class. We computed the Precision-Recall curve, which shows the relationship between positive predictive value (precision) and sensitivity (recall)⁴⁹. It provides complementary information to the ROC curve, especially with class imbalanced datasets. In order to compare the relative performance of the DNN to the cardiologist committee labels, we calculated the F1 score which is the harmonic mean of the positive predictive value and sensitivity. It ranges from 0 to 1 and rewards algorithms which maximize both positive predictive value and sensitivity simultaneously, rather than favoring one over the other. The F1 score is complementary to the AUC, particularly helpful in the setting of multi-class prediction and less sensitive than AUC in settings of class imbalance⁴⁹. For an aggregate measure of model performance, we computed the class-frequency weighted arithmetic mean for both the F1 score and the AUC. In order to obtain estimates of how the DNN compares to an average cardiologist, cardiologist performance characteristics were averaged across the 6 cardiologists who individually annotated each record. We used confusion matrices to illustrate the specific examples of rhythm classes where the DNN prediction or the individual cardiologist predictions were discordant with the committee consensus at the sequence-level. Among the individual cardiologist annotations in the test dataset, we calculated inter-annotator agreement as the ratio of the number of times two annotators agreed that a rhythm was present at each output interval and the total number of pairwise comparisons.

Extended Data

Extended Data Fig 1:

Deep Neural Network architecture. Our deep neural network consisted of 33 convolutional layers followed by a linear output layer into a softmax. The network accepts raw ECG data as input (sampled at 200 Hz, or 200 samples per second), and outputs a prediction of one out of 12 possible rhythm classes every 256 input samples.

Extended Data Fig 2:

Receiver operating characteristic curves for deep neural network predictions on 12 rhythm classes. Individual cardiologist performance is indicated by the red crosses and averaged cardiologist performance is indicated by the green dot. The line represents the ROC curve of model performance. AF-atrial fibrillation/atrial flutter; AVB-atrioventricular block; EAR-ectopic atrial rhythm; IVR-idioventricular rhythm; SVT-supraventricular tachycardia; VT-ventricular tachycardia. n = 7,544 where each of the 328 30-second ECGs received 23 sequence-level predictions.