The General Anesthetic Propofol Slows Deactivation and Desensitization of GABA_A Receptors

Abstract

Propofol (2,6-di-isopropylphenol) has multiple actions on GABA_A receptor function that act in concert to potentiate GABA-evoked currents. To understand how propofol influences inhibitory IPSCs, we examined the effects of propofol on responses to brief applications of saturating concentrations of GABA (1–30 mm). GABA was applied using a fast perfusion system to nucleated patches excised from hippocampal neurons. In this preparation, propofol (10 μm) had no detectable agonist effect but slowed the decay, increased the charge transfer (62%), and enhanced the peak amplitude (8%) of currents induced by brief pulses (3 msec) of GABA. Longer pulses (500 msec) of GABA induced responses that desensitized with fast (τ_f = 1.5–4.5 msec) and slow (τ_s = 1–3 sec) components and, after the removal of GABA, deactivated exponentially (τ_d = 151 msec). Propofol prolonged this deactivation (τ_d = 255 msec) and reduced the development of both fast and slow desensitization. Recovery from fast desensitization, assessed using pairs of brief pulses of GABA, paralleled the time course of deactivation, indicating that fast desensitization traps GABA on the receptor. With repetitive applications of pulses of GABA (0.33 Hz), the charge transfer per pulse declined exponentially (τ ≈ 15 sec) to a steady-state value equal to ∼40% of the initial response. Despite the increased charge transfer per pulse with propofol, the time course of the decline was unchanged. These experimental data were interpreted using computer simulations and a kinetic model that assumed fast and slow desensitization, as well as channel opening developed in parallel from a pre-open state. Our results suggest that propofol stabilizes the doubly liganded pre-open state without affecting the isomerization rate constants to and from the open state. Also, the rate constants for agonist dissociation and entry into the fast and slow desensitization states were reduced by propofol. The recovery rate constant from fast desensitization was slowed, whereas that from slow desensitization appeared to be unchanged. Taken together, the effects of propofol on GABA_A receptors enhance channel opening, particularly under conditions that promote desensitization.

Many general anesthetics, including propofol (2,6-di-isopropylphenol), prolong the duration of GABAergic IPSCs, and this action is thought to contribute to the behavioral properties of these drugs (MacIver et al., 1991; Orser et al., 1994). Previous studies using conventional multibarrel perfusion systems and whole-cell recordings indicate that propofol has multiple distinct effects on GABA_A receptor (GABA_AR) function, including the potentiation of GABA-evoked currents, direct activation of the receptor, and modulation of desensitization (Hales and Lambert, 1991; Hara et al., 1993; Orser et al., 1994). In those studies, concentration–response relationships were constructed to reflect the interaction between the drug and receptor under near-equilibrium conditions. However, synaptic currents are generated by transient pulses of high concentrations of GABA, and at no time during the response is there equilibrium. It is not certain how the multiple actions of propofol will combine under nonstationary conditions to modify IPSCs.

The shape of IPSCs is determined by several factors, including the concentration and temporal profiles of the neurotransmitter in the synaptic cleft, as well as the kinetic properties of postsynaptic receptors. It is generally believed that a saturating concentration of GABA is released into the synaptic cleft from the presynaptic terminal (Maconochie et al., 1994; Jones and Westbrook, 1995) (but see Frerking et al., 1995). Most of the free GABA is likely cleared from the cleft by the time the IPSC reaches its peak (Jones and Westbrook, 1996;Uteshev and Pennefather, 1996a). Thus, the slow decay of IPSCs primarily reflects receptor gating and the unbinding of agonist rather than diffusion of transmitter within the cleft.

To investigate the physiological and pharmacological properties of the GABA_AR under non-equilibrium conditions (as might occur in the synaptic cleft), several groups have applied high concentrations of agonist (>500 μm) to excised outside-out and nucleated membrane patches (Celentano and Wong, 1994; Maconochie et al., 1994;Jones and Westbrook, 1995; Galarreta and Hestrin, 1997). In these studies, GABA_ARs display a complex pattern of desensitization, which includes a fast component of desensitization (τ_f, <100 msec) that is evident when GABA is applied using fast perfusion systems (open tip exchange time <2 msec). This form of desensitization appears to buffer the channel in an agonist-bound conformation that permits the channel to reopen long after free GABA has been removed. Recovery of the receptor from the desensitized state, through a ligand-bound pre-open state with the opportunity for reopening, contributes to the slow decay of IPSCs (Jones and Westbrook, 1995; Jones et al., 1998). In addition, a slower desensitization process (τ ∼ 3 sec) is evident during longer applications of GABA (Orser et al., 1994; McClellan and Twyman, 1999).

We previously demonstrated, using conventional perfusion systems and whole-cell recording methods, that propofol decreases the rate and extent of slow desensitization (Orser et al., 1994). Here we studied the effects of propofol on GABA_ARs using fast applications of high GABA concentrations to nucleated patches. We discovered that fast desensitization and deactivation are also slowed. To assist with the interpretation of the experimental data, computer simulation was undertaken using a simple kinetic model of GABA_AR gating similar to that proposed by Celentano and Wong (1994). This kinetic model assumes that fast and slow desensitization, as well as channel opening, develop in parallel as absorbing states from a pre-open state. An equal decrease by propofol in the rate of dissociation of GABA from the pre-open state and the rate constants of entry into fast and slow desensitization states adequately accounts for our experimental data. Additionally, propofol reduced the rate of recovery from fast desensitization. Otherwise, the other kinetic parameters can remain unchanged. The slowing of fast desensitization accounts for the observed increase in the amplitudes of the peak and early plateau of the response. Because fast desensitization is slowed but is not greatly reduced, the pronounced effect of propofol on deactivation indicates that propofol must also reduce the rate of dissociation of GABA. In summary, our results suggests that propofol prolongs IPSCs by stabilizing the fully liganded pre-open state of the receptor.

MATERIALS AND METHODS

Cell culture. Cultures of embryonic hippocampal neurons were prepared from Swiss white mice as described previously (MacDonald et al., 1989). Briefly, fetal hippocampi were obtained from mice killed by cervical dislocation. Neurons were dissociated using mechanical trituration and plated on 35 mm collagen-coated culture dishes. Monolayers of cells were formed after 12–16 d in vitro. Before recording, cells were rinsed with a standard extracellular recording solution containing (in mm): 140 NaCl, 1.3 CaCl₂, 5.4 KCl, 2 MgCl₂, 25 HEPES, and 33 glucose, with the pH adjusted to 7.4 with 1 m NaOH. All experiments were conducted at room temperature (22–25°C).

Electrophysiology. Recording pipettes were prepared from borosilicate glass capillaries containing an inner filament (World Precision Instruments, Sarasota, Florida). Electrodes were pulled in two stages using a vertical puller (Narishige PP-83) and had a resistance of 4–7 MΩ when filled with a solution containing (in mm): 120 CsCl, 30 HEPES, 11 EGTA, 2 MgCl₂, 1 CaCl₂, and 4 MgATP, with the pH adjusted to 7.3 with CsOH. The osmolarity of the pipette solution was adjusted to 300–315 mOsm. Voltage-clamp (V_H = −60 mV) whole-cell currents were recorded using a patch-clamp amplifier (Axopatch 1-D, Axon Instruments, Foster City, CA). Currents were recorded simultaneously on a chart recorder (Astro-Med MT8800, West Warwick, RI), a video tape recorder through a converter (VR10, Instrutech, Elmont, NY), and a PC computer using pClamp Software (Axon Instruments).

GABA-induced currents were recorded from nucleated patches formed from cultured hippocampal neurons as described previously (Sather et al., 1992). A double-barrel perfusion pipette made from theta tubing (R&D Scientific Glass Co., Spencerville, MD) was attached to a piezo-electric translator (PZS-100, driven by PZ-150; Burleigh, Fishers, NY). This assembly permitted the rapid switching of the solutions bathing the patches. The open tip solution exchange time was determined by examining the current produced by a change to a dilute extracellular solution (10–20% with water). Under optimum conditions, the open tip exchange time was ∼0.2 msec. The exchange time for solutions bathing the nucleated patch was also determined by measuring the rise time (10–90%) of current associated with an increase in the extracellular concentration of K⁺. The recording electrode was filled with a solution containing (in mm): 140 CsF, 35 CsOH, 10 HEPES, 2 MgCl₂, 1 CaCl₂, 11 EGTA, 2 tetraethylammonium (TEA), and 4 KATP. The pH was adjusted to 7.3 using CsOH. The extracellular concentration of K⁺ was increased from 5 to 50 mm, and the Na⁺ concentration was reduced by 50 mm. The osmolality of the solutions was unchanged. At a holding potential of 0 mV, the inward current associated with the switch to the high K⁺ solution had a rise time (10–90%) of 1.9 ± 0.5 msec (n = 6 patches).

The time interval between the 3 and 500 msec applications of GABA was at least 30 and 120 sec, respectively. Under these conditions, little “rundown” (diminished peak responses with time) was observed for GABA-induced current responses. Patches that displayed a rundown greater than ∼2% per agonist application were discarded.

Propofol was prepared on the day of experiment from Diprivan (Zeneca Pharma, Mississauga, Canada). The effects of propofol on GABA-evoked currents were studied after control recordings were obtained. Propofol was allowed to pre-equilibrate for at least 2 min, and the vehicle Intralipid (KabiVitrium Canada, Toronto, Canada) was included in the control solutions.

Data were expressed as the mean ± SEM, and a paired Student's t test was used to examine the statistical significance of differences between the groups. For multiple groups of data, a two-way ANOVA was used (GraphPad Software, San Diego, CA). A p value <0.01 was considered to be significant.

Simulation. A general simulator program Axon Engineer (Aeon Software, Minneapolis, MN; http://userpages.itis.com/aeonsoft/) was used to simulate the data. This program allows kinetic states to be defined and linked together by rate constants that can be a function of voltage, ion, and drug concentration. The differential equations implicit in the kinetic scheme are then integrated and driven by user-defined stimuli. The distribution of states in time is converted to open probability by assigning conductance weights to the individual states and summating the system at each time point. Given the difficulty in obtaining results with nucleated patches and the relatively high degree of variability of responses between patches, we did not feel that there was sufficient data to warrant an exhaustive parameter optimization effort. Rather, a range of rate constants was deduced by the analysis of a three-state approximation of our kinetic model (see ).

RESULTS

Kinetics of GABA-induced current recorded from nucleated patches

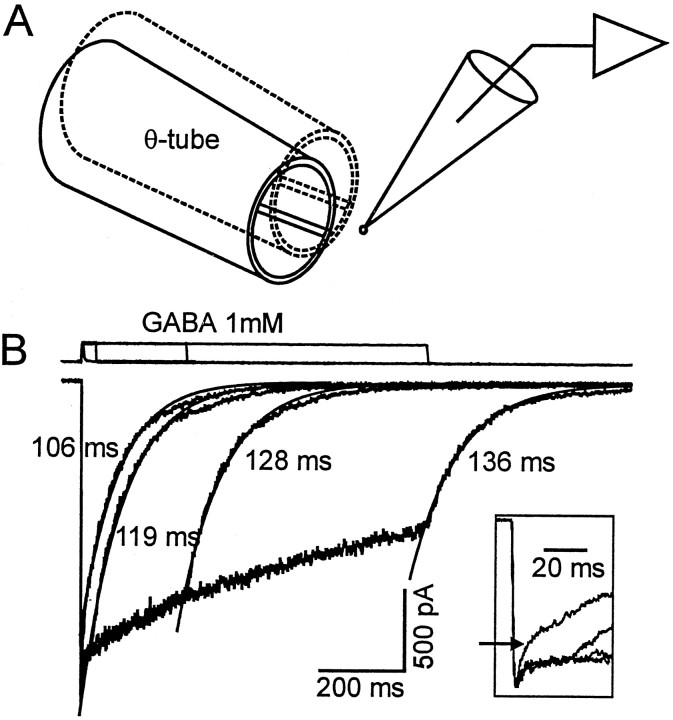
To investigate the mechanisms underlying propofol-induced changes in postsynaptic GABA_A receptor function, currents were activated by rapid applications of GABA (1–30 mm) to nucleated patches. The method used for rapid exchange of extracellular bathing solutions is illustrated in Figure 1A. Responses evoked from a single nucleated patch by applications of 1 mm GABA for 3, 30, 300, and 1000 msec are shown (Fig. 1B). Brief pulses of GABA (3 msec) induced transient currents that peaked with a rapid onset [10–90% rise time (RT) = 2.0 ± 0.2 msec, n = 26], then declined to baseline in a biphasic manner. The time-to-peak for GABA-evoked currents has previously been reported to be ≤1 msec (Maconochie et al., 1994; Puia et al., 1994). We attribute the slower time course observed in our experiments to the slower speed of the agonist application to nucleated patches. The rise time for GABA-evoked responses in nucleated patches was similar to that of the currents associated with an increase in the extracellular concentration of K⁺ (see Materials and Methods). This observation suggests that the binding of GABA to the receptor is fast, and in this preparation the rate of current onset is limited by the rate of solution exchange. The fast component of the decay with the brief 3 msec application of GABA was generally complete within 10 msec (Fig. 1B, inset). The slow component of the decay had a time constant ranging in different cells from 99 to 265 msec.

Longer pulse applications of GABA (30–1000 msec) activated currents that decreased in amplitude during the continued presence of agonist. Fast and slow desensitization processes could be clearly discriminated in most recordings as illustrated in Figure 1. The fast and slow components had time constants estimated to be in the 1.5–4.5 msec and 1–3 sec range, respectively. After the removal of GABA, the currents deactivated with a time course dominated by a single exponential process (τ_d = 151 ± 12 msec, n = 12) (Fig. 1B). Although an additional slower component of deactivation was evident in some records, it represented only a small component of the decay and was not included in the present analysis.

Fig. 1.

Experimental setup and GABA-induced currents recorded from nucleated patch excised from cultured hippocampal neuron. A, The drawing illustrates the rapid solution switching system. The theta tubing with control and GABA-containing solutions flowing through the barrels is rapidly moved in front of the nucleated patch. A rapid step-like change in the concentration of GABA (within 2 msec) occurs as the interface of the solutions is moved across the patch. B, The bottom traces represent superimposed currents recorded from the same nucleated patch. GABA (1 mm) was applied for the various time intervals indicated by the top traces. A brief pulse of GABA (1 mm, 3 msec) induced a transient inward current that increased rapidly, then decayed with a fast and a slow time course (as indicated by thearrow in the inset). The slower component declined monoexponentially with a time constant of 106 msec (smooth line). Longer applications of GABA (30, 300, 1000 msec) induced currents with a similar rising phase and peak amplitude. However, in the continued presence of GABA, currents desensitized with two distinct components that we refer to as fast and slow desensitization (see inset). After the removal of GABA, the responses declined to baseline (defined as deactivation). The major component of deactivation was adequately described by a single exponential function, and the smooth lines superimposed on the experimental data represent an exponential function fit to the data. The time constants are shown. A small slow component is evident but is ignored in our analysis. The inset provides a temporal expansion of the onset and initial decay of the currents activated by brief and longer pulses of GABA. The linesabove the recordings indicate the duration of the agonist application. The transient upward deflection illustrates the junctional current measured after the membrane patch was disrupted.

Effects of propofol on responses to brief (3 msec) application of GABA

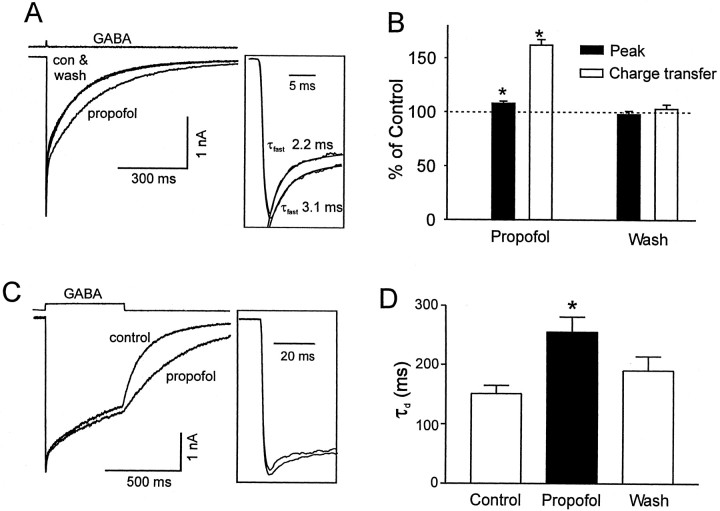
Propofol (10 μm) was added to both control and agonist-containing solutions after stable currents were observed. At this concentration, propofol did not induce any detectable current when applied in the absence of GABA or alter the rise time of GABA-induced currents (RT_control = 1.9 ± 0.2 msec to RT_propofol = 2.0 ± 0.2 msec; p > 0.01, n = 17). However, propofol significantly increased the duration of GABA-induced current from 63 ± 7 to 115 ± 13 msec (measured at 50% of the peak, n = 17, p < 0.01) (Fig. 2A). Similarly, the charge transfer associated with the GABA-induced current was substantially increased by 62 ± 5% (Fig. 2B) (n = 17, p < 0.01). Propofol also reversibly increased the peak amplitude of currents (8 ± 2%, n = 17, p < 0.01) activated by saturating concentrations of GABA (1–30 mm) (Fig. 2B). No significant differences were observed in these parameters with the different concentrations of GABA, so the data were pooled together. Propofol prolonged both the fast and slow component of the decay observed with the brief applications of GABA (Fig. 2A,inset). Recordings that demonstrated a well defined fast component of decay (10 of the 17 patches) were further analyzed by fitting a single exponential function to the response, from the peak to 10 msec after the peak. The initial decay was slowed 1.5-fold by propofol from τ = 5.0 ± 0.7 to 7.2 ± 1 msec (n = 10, p < 0.01). The slow decay measured by fitting an exponential to points 10 msec after the peak response was also prolonged by propofol from τ = 159 ± 17 to τ = 231 ± 24 msec, n = 17 (p < 0.01).

Fig. 2.

Propofol prolonged the deactivation and increased the peak amplitude of GABA-induced current. A, Three superimposed responses to brief pulses of GABA (1 mm) were recorded from the same patch in the absence and presence of 10 μm propofol. Each trace represents the average of two to three individual traces. Propofol increased the peak amplitude and charge transfer associated with the responses, an effect that was reversed after the washout of propofol. The top trace shows the open tip junctional current. The inset illustrates the slowing of the fast decay by propofol. The time constant of the fast component of a biexponential function was increased by propofol from 2.2 to 3.1 msec (solid lines). B, The bar graph summarizes the effects of propofol on the peak amplitude and the charge transfer of currents recorded from 17 patches. Values were normalized to those obtained under control conditions. A consistent increase in peak current amplitude (8 ± 2%, n = 17, p < 0.01; filled bar) and in charge transfer (62 ± 5%, n = 17, p < 0.01; open bar) was observed. C, Superimposed traces of currents activated by longer (500 msec) pulses of GABA (1 mm) in the absence and presence of propofol (10 μm) are shown. Note that the predominant effect of propofol is to prolong the deactivation. Similar to the results obtained for brief pulses of GABA, the peak current amplitude was increased (shown in inset). A temporal expansion of the currents is shown in the inset. Propofol slows the initial decay of the response. D, Thebar graph illustrates that the time constant of deactivation (τ_d) was reversibly increased by propofol.

Propofol modulates GABA_AR deactivation and desensitization

Longer pulses (500 msec) of GABA were used to further investigate the actions of propofol on receptor desensitization and deactivation. As is shown in Figure 2C, clearly the most pronounced effect of propofol (10 μm) was to slow deactivation as evidenced by a slowing of the decay after the removal of GABA. Fitting this decay with a single exponential function revealed that propofol caused 1.7-fold increase in τ_d from 151 ± 14 to 255 ± 26 msec (Fig. 2D) (n = 7, p < 0.01).

Similar to the enhancement observed with the brief pulses of GABA, the peak amplitude of the current activated by 500 msec pulses of GABA was increased by 8 ± 4% (n = 7, p < 0.01). The increase in the peak was associated with a slowing of the decay of the fast component. In five of seven patches in which a fast component was well defined, the initial decline was fit using a single exponential function. The time constant of the decay was slowed by propofol 1.7-fold, from 2.5 ± 0.4 to 4.3 ± 0.7 msec. In the continued presence of agonist, currents decayed slowly, and propofol appeared to reduce this slow desensitization (Fig. 2C).

It is evident in Figure 2C that the slow decline had not reached a steady state by the end of the 500 msec pulse. Therefore, to estimate the rate of onset of slow desensitization, we measured the change in current amplitude from 100 msec (where fast desensitization is complete) to 500 msec (at the end of the agonist pulse). Provided that slow desensitization develops monoexponentially (Mierlak and Farb, 1988; Oh and Dichter, 1992; Orser et al., 1994) and the steady-state response is small, this initial rate of decline allows the time constant of slow desensitization to be estimated. The ratio (amp_500msec/amp_100msec) was 0.75 ± 0.02 under control conditions, indicating a 25% decrement in current over a 400 msec period. This value suggests that the time constant for slow desensitization (τ_slow) equals, at most, 1.4 sec. In the presence of 10 μmpropofol, the ratio amp_500msec/amp_100msec was significantly increased to 0.80 ± 0.02 (n = 11, p < 0.01). A 20% decrement in current amplitude over 400 msec in the presence of propofol is consistent with τ_slow of, at most, 1.8 sec.

Consistent with the 8% increase in the peak current in the presence of propofol, the amplitude at 100 msec was increased 7 ± 4%. This observation suggests that the increase in peak current persisted after the development of fast desensitization. This increase in peak amplitude (despite the application of saturating concentrations of GABA) is consistent with propofol reducing the rate constant of development of fast desensitization (see below). A small increase in channel conductance could also produce a similar change in current amplitude; however, single-channel studies indicate that propofol does not influence channel conductance (Hales and Lambert, 1991; Orser et al., 1994). It is noteworthy that the ratio of current amplitude at 100 msec and the peak amplitude (amp_100msec/amp_peak) was not changed significantly by propofol compared with control (0.75 ± 0.03 and 0.77 ± 0.04, respectively; n = 11, p > 0.01).

Previous studies indicate that recovery from fast desensitization of the GABA_AR underlies the slow deactivation of GABA-induced currents (Jones and Westbrook, 1995; Tia et al., 1996; Galarreta and Hestrin, 1997; Mellor and Randall, 1997; Jones et al., 1998). Therefore, we next examined the relationship between the recovery from fast desensitization and the change in deactivation produced by propofol. Fast desensitization was studied using a previously described double-pulse protocol (Jones and Westbrook, 1995; Tia et al., 1996). With this method, a second test pulse of GABA delivered at various time intervals after the conditioning pulse examines the recovery from desensitization induced by the conditioning pulse.

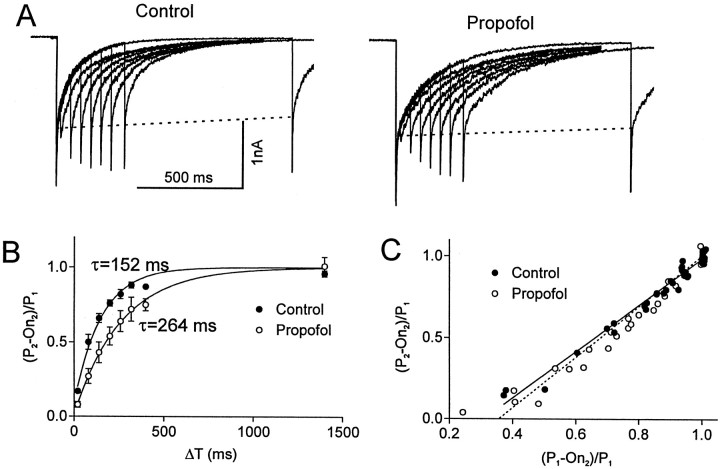
As illustrated in Figure 3, the peak current induced by a brief test pulse of GABA (3 mm for 3 msec) produced little additional current when applied 20 msec after the conditioning pulse. As the interval between these pulses was increased, the amplitude of the test response gradually increased to a level similar but not quite equal to that of the conditioning pulse. The time course of recovery from desensitization was examined by plotting the amplitude of the test response (P₂) after subtracting the amount of current remaining at the end of the first pulse (On₂). This value was normalized to the control response (P₁), i.e., (P₂ − On₂)/P₁. The normalized value was then plotted against the time interval betweenP₁ and P₂ (ΔT) as illustrated in Figure 3B, and the time course was fit by a single exponential function. Because saturating concentrations of GABA were applied, (P₂ −On₂)/P₁ measures the proportion of receptors that are no longer associated with GABA and have returned to a resting and “activatable” state. If there was no fast desensitization and the biexponential decay simply reflected two modes of deactivation, P₂ should be the same as P₁. Under these conditions, the measure (P₂ − On₂)/P₁ would increase with a rate constant equal to the deactivation time constant. However, if the receptors desensitize and the process recovers through a pathway that is different from that of deactivation, then this difference will be apparent in the recovery time course. If there is a common state through which both activated and desensitized receptors recover, the measure should start at zero and approach 1 with a time constant that is the same as the deactivation rate.

Fig. 3.

Recovery from fast desensitization was slowed by propofol. A, Superimposed currents evoked by paired pulses of GABA (3 mm, 3 msec) are illustrated. Desensitization produced by the conditioning pulse was investigated by applying a second test pulse. The test pulse produced negligible additional current when the time interval between the pulses was 20 msec. As the interval between the pulses increased, the amplitude of the test response gradually increased to a level that was similar but not quite equal to that of the conditioning pulse. The reduction in the amplitude of the test response was primarily caused by loss of the fast component that occurred within the first 10 msec. The dashed lines indicate that the slow component of the decay is relatively stable. The time course of recovery from desensitization was slowed by propofol (10 μm). B, The ratio of the amplitude of test pulse and the conditioning pulse [(P₂ − On₂)/P₁)] is plotted versus the time interval between the two pulses (Δt). To control for rundown of the response during the recordings, the amplitude of the conditioning response was normalized to the initial value of P₁. The data pointsrepresent the average values for currents recorded from three difference patches in the absence (filled circle) and presence of propofol (open circles). The time course of the recovery was best fit by a single exponential function (τ_control = 152 msec, τ_propofol = 264 msec). C, The relationship between the fraction of receptor population that has recovered from desensitization (P₂ − On₂)/P₁ and the extent of deactivation (P₁ − On₂)/P₁ is shown. Note that the plots can be superimposed in the absence and presence of propofol, suggesting that deactivation parallels desensitization and propofol does not influence this relationship.

We found that this measure of recovery appeared to follow a single exponential process with a time constant τ = 152 msec (Fig. 3B). When propofol (10 μm) was added to the perfusion solution, the recovery from desensitization was slower: τ = 264 msec (Fig. 3B). These values are similar to the deactivation time constants in the presence and absence of propofol (see above).

The reduction in peak amplitude of the test pulse primarily resulted from a decrease in the fast component of decay. As the interval between the two pulses was increased, the amplitude of the fast component rapidly recovered, whereas the slower component remained relatively unchanged (Fig. 3A, dashed line). When the fast component of the second pulse (defined as P₂ − response at 10 msec after P₂) was plotted against ΔT, propofol slowed the time constant of this recovery from 107 to 181 msec (data not shown).

The correlation between the recovery from desensitization and deactivation is illustrated in Figure 3C. The parallel time course in the absence and presence of propofol is now illustrated by plotting fast desensitization (P₂ − On₂)/P₁ as a function of extent of deactivation (P₁ − On₂)/P₁. Note that (P₁ − On₂)/P₁ = 1 when the current is fully deactivated. These plots superimpose in the presence and absence of propofol, indicating that the prolongation of deactivation by propofol does not change the relationship between deactivation and desensitization. These observations are consistent with a model whereby fast desensitization leads to trapping of the agonist on the receptor, enabling those receptors to reopen after the free GABA has been washed away (Jones and Westbrook, 1995; Jones et al., 1998).

The onset but not recovery from slow desensitization is modulated by propofol

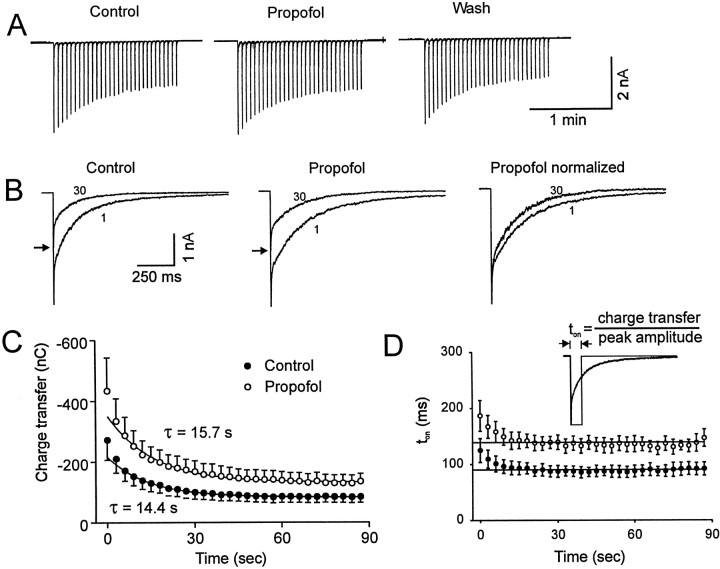
The slow component of desensitization is difficult to characterize accurately because it takes several seconds to reach a steady state (Celentano and Wong, 1994; McClellan and Twyman, 1999). We observed that it is technically difficult to produce stable currents with prolonged (>500 msec) applications of agonist to nucleated patches. Therefore, we adopted an approach of phasic stimulation to investigate the slower kinetic processes (Jassar et al., 1993). Thirty brief (3 msec) pulses of GABA were administered at a rate of 0.33 Hz (Fig.4). The evoked charge transfer declined with each pulse of GABA until a new steady-state value was reached within 15 pulses (Fig. 4C).

Fig. 4.

Propofol reduces slow desensitization. A, Current traces illustrate the response to repetitive applications of brief (3 msec) pulses of GABA (30 pulses administered at a rate of 1 per 3 sec). Under control conditions, the peak amplitude of the current gradually declined to a steady-state level. Propofol reversibly increased the duration of each response and also increased the amplitude of each of the 30 responses to a similar extent. B, A temporal expansion of currents evoked by the 1st and 30th application of GABA is shown. Responses are superimposed, and thearrows indicate the peak amplitude of the 30th response. Note that in the absence or presence of propofol, the decay of the 30th response was accelerated compared with the initial response. This effect is further illustrated in the panel to theright where the peak amplitude is normalized to the maximum response. C, The charge transfer associated with each response during the repetitive applications of GABA is shown. Data points are the average values obtained from seven different patches. After the first two pulses, in the absence of propofol (filled circle), the charge transfer declined monoexponentially with a time constant of 14.4 sec to a steady-state value 39% of the initial response. In the presence of propofol (open circle), the time constant was 15.7 sec, and the steady-state value was 38% of the initial value. The first two data points were not included in the exponential fit. Propofol significantly increased the charge transfer of all 30 pulses to a similar extent (two-way ANOVA, p < 0.01). D, The decline in t_on (charge transfer/amplitude) for the 30 pulses activated by GABA is shown. Propofol increased t_on of GABA-evoked currents (two-way ANOVA, p < 0.01). The straight line plotted through the last 28 data points represents a linear regression with the slope restricted to zero. The intercept of this line for t_on was 90 and 142 msec for currents recorded in the absence and presence of propofol, respectively. Theinset illustrates the calculation of t_on.

To analyze the build up of slow desensitization during the phasic stimulation, we applied a previously described form of analysis (Starmer, 1986; MacDonald et al., 1991; Jassar et al., 1993). The assumptions implicit to this analysis have been previously summarized (Jassar et al., 1993; Starmer, 1986). This analysis assumes that receptors are saturated during the brief response and that the rate constant of recovery from slow desensitization (r_s) is slow relative to the time intervals between pulses. Here, the transient currents are considered to be equivalent to a theoretical square pulse of activated receptors (Fig. 4D, inset). Channels activated by the actual response to a transient application of agonist have the same opportunity for slow desensitization as a theoretical square pulse of activated receptors with a duration of t_on, where t_on = charge transfer (Q) /peak amplitude of the response (P). A mathematically more sophisticated analysis of phasic stimulation is also possible (Uteshev and Pennefather, 1996b) but provides little additional information in the present case. It is evident in Figure 4D that after the first several pulses, t_on is constant. The values for t_on in the absence and presence of propofol were 90 and 142 msec, respectively.

The apparent rate constant for the development of slow desensitization (d′_s) during phasic stimulation can be estimated using the calculated values for t_onand the fractional decrement of change transfer per pulse (λ). The actual rate constant (d_s) will dependent on the proportion of doubly liganded receptors in the state that lead to slow desensitization. By defining the time during which receptors are not activated as t_off(t_off = pulse interval −t_on), then one can demonstrate that λ =d′_s ∗ t_on + r_s ∗ t_off, and the relative fractional amplitude of the steady-state response observed during continued phasic stimulation is such that (1 − Q_steady-state/ Q_initial) = d′_s ∗ t_on/λ and Q_steady-state/ Q_initial= r_s ∗ t_off/λ (Starmer, 1986). A fraction of the available receptors enter the desensitized state with each pulse, and the steady-state value reflects the product of the rate of recovery from slow desensitization (R_s) and t_off.

Using the data summarized in Figure 4 and considering the steady-state response, we note that propofol decreases the rate of entry into the slow desensitized state such that d′_s is reduced from d′_s = 1.37 sec⁻¹ under control conditions to d′_s = 0.85 sec⁻¹in the presence of propofol. This decrease in d′_s reflects the fact that λ and the steady-state response are relatively unchanged despite the increase in t_on by propofol. We also estimate that r_s = 0.025 sec⁻¹ in the presence and 0.028 sec⁻¹ in the absence of propofol. These estimated values ignore the possibility of the multiple desensitized states. Alternatively, multiple receptor subtypes with different kinetic properties could account for the initial deviation of the t_on as well as the biphasic time course of recovery from desensitization reported previously (Orser et al., 1994). Nevertheless, these values produce a reasonable simulation of our experimental results when used in conjunction with our model (see below).

Propofol thus appears to slow the onset of slow desensitization to the same extent that it reduces the deactivation rate. This observation suggests that propofol slows both of these transitions out of the pre-open state to the same extent. Our results are consistent with previous data that indicate propofol slows the entry into the slowly developing state of desensitization but has little effect on the recovery process (Orser et al., 1994). The results predict that propofol will increase the steady-state response observed during a prolonged application of saturating GABA, after slow desensitization has been allowed to equilibrate (Orser et al., 1994). Indeed, slow desensitization will be decreased to the same extent as the response is prolonged after a brief application of GABA (∼1.85-fold).

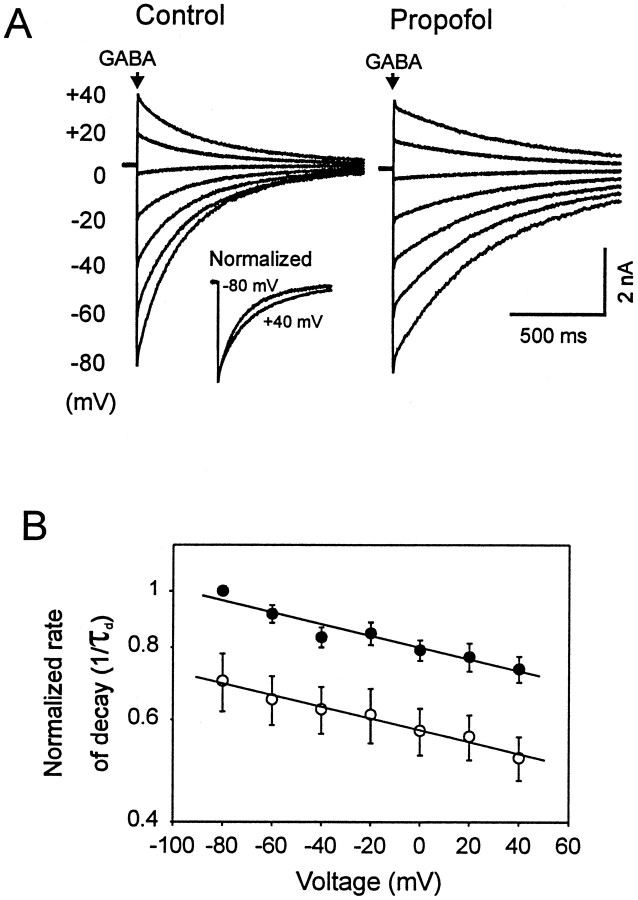
Propofol's action is not voltage-dependent

We next tested whether the membrane potential influences the action of propofol on deactivation of GABA-induced current. In the absence of propofol, membrane hyperpolarization (+40 to −80 mV) was associated with an increase in the rate of current decay (Fig. 5A). The rate of deactivation (1/τ_d) decreased with increasing membrane potentials at a rate of e-fold/420 mV. Propofol increased τ_d by ∼60% at all holding potentials tested (Fig. 5B). Therefore, the slope of the linear regression line for the relationship between log 1/τ_d and voltage was not influenced by propofol. In addition, propofol did not alter the reversal potential of GABA-induced current (data not shown).

Fig. 5.

Slowing of deactivation by propofol is voltage-independent. A, Currents evoked by GABA (3 mm, 3 msec) at various holding potentials are superimposed. The rate of decay (1/τ_d) was increased at hyperpolarizing potentials. The inset illustrates the superimposed currents obtained at holding potentials of +40 mV (inverted) and −80 mV normalized to the peak amplitude for responses. The decay was increased by propofol at all holding potentials. B, Data obtained from five different patches were averaged and plotted versus 1/τ_d (log scale). A linear relationship was observed between 1/τ_d and holding potential (voltage) under control conditions (filled circle) and in the presence of propofol (open circles). Propofol produced a similar decrease in the rate of current decay at all holding potentials as indicated by the slope of the lines (n = 5, two-way ANOVA, p < 0.01).

Simulations

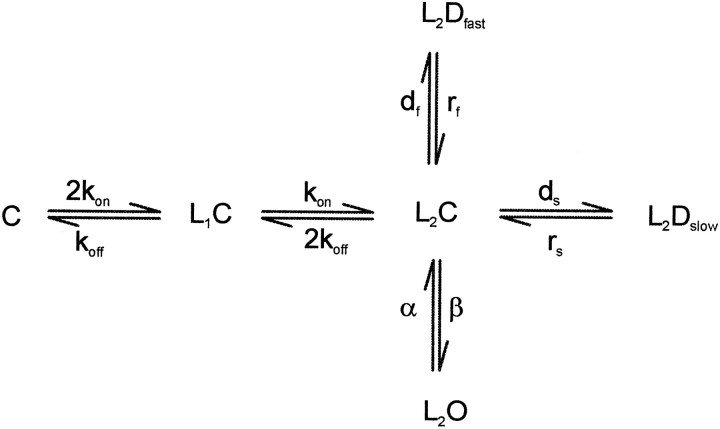
To simulate the actions of propofol, we consider a simple parallel model (reproduced below) similar to that proposed by Celantano and Wong (1994). However, only two components of desensitization are considered. C represents the closed state, L depicts the agonist ligand, and D and O represent the desensitized and open states, respectively.

This model assumes that there are two equivalent ligand binding sites with the binding and unbinding rates k_on and k_off, respectively. These rates (Table1) are multiplied by statistical factors that take into account that two equivalent agonist sites are available. Occupation of these two binding sites by agonist generates the pre-open state, (L₂C). The receptor can either rapidly isomerize into an open state (L₂O) with a rate constant β or rapidly convert into a desensitized state (L₂D_for L₂D_fast) with a rate constant d_f. Closing of the channel occurs with a rate α, and recovery from L₂D_f occurs with a rate constant r_f. In this model, GABA cannot readily dissociate from the L₂D_f or L₂O states, so after the removal of GABA, deactivation will be limited by the unbinding of GABA from the closed but double-liganded receptor state L₂C. For simplicity we have allowed slow desensitization to proceed only from the L₂C state with a rate constant d_s. Recovery from slow desensitization (L₂D_s or L₂D_slow) occurs as the reverse of this process through the L₂C state with a rate constant r_s.

Table 1.

The values of rate constants used in the kinetic scheme

Rates (sec−1)	Control	Propofol	Control/propofol
kon	106× M−1	106 × M−1	1.00
koff	103	56	1.85
β	6000	6000	1.00
α	400	400	1.00
df	3000	1620	1.85
rf	200	120	1.70
rs	0.027	0.027	1.00
ds	26	14	1.85

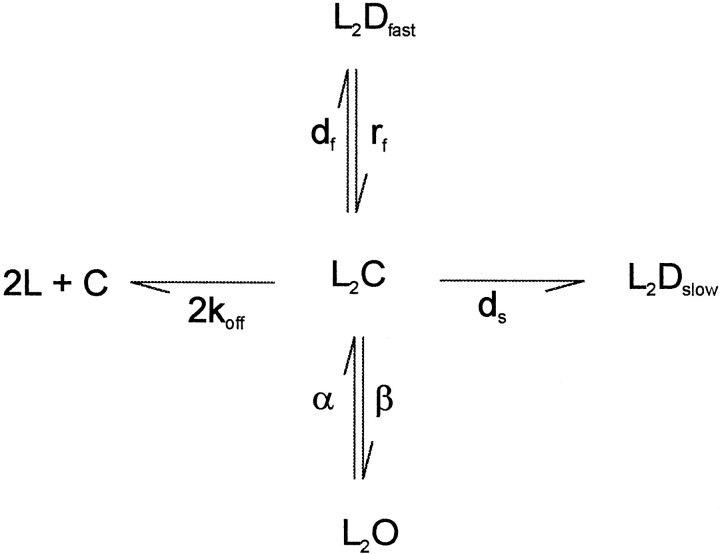
Scheme FS1 can be simplified to a three-state system for which analytical solutions are possible. If we assume that binding is fast, then after the application of a saturating concentration of GABA all of the receptors will rapidly convert into L₂C, and the rising phase of the response is determined primarily by the isomerization to L₂O and L₂D_f. Thus, at time zero all of the receptors are in the L₂C state (SchemeFS2 in the ). Using this assumption, we chose to deduce the parameters by analysis of a three-state approximation of our model rather than fit each of our recordings to the model using optimization techniques.

Fig. FS1.

Fig. FS2.

In the we show how the kinetics of the response to GABA observed here permit further simplifications of these analytical equations such that quite simple relations can be derived that relate model rate constants to the observed kinetic components of the response. For example in Equation EA10a we show that if β and d_f are fast compared with k_off, then the deactivation rate (1/τ_d) will be approximated by:

$$1/{\tau }_{\text{d}}\approx 2k_{\text{of\hspace{0.5em}f}}/(1+\beta /\alpha +d_{\text{f}}/r_{\text{f}})$$ Equation 1

The denominator reflects the relative proportions of L₂C, L₂O, and L₂D_fastpresent during the deactivation phase. Thus, the rate of deactivation will be slowed to the extent that GABA is trapped on L₂O and L₂D_f. Likewise, it can be shown (Eq.EA17) that under these conditions, the amplitude of the response after fast desensitization has developed, but before extensive slow desensitization has developed (the initial plateau response or ∼10 msec after the peak) it will be:

$$L_{2}O(\text{pl})/L_{2}C(\text{o})\approx 1/\{1+(\alpha /\beta )(1+d_{\text{f}}/r_{\text{f}})\}\text{or}$$ Equation 2

$$1/\{1+(\alpha /\beta )(d_{\text{f}}/r_{\text{f}})\},\text{when} \alpha /\beta \text{is small}.$$ Equation 2a

For situations where the rising phase is dominated by β and where α/β is small, the initial fast decay time constant τ_f (Eq. EA16) will be approximated by:

$$1/{\tau }_{\text{f}}=r_{\text{f}}\{1+(\alpha /\beta )(d_{\text{f}}/r_{\text{f}})\}.$$ Equation 3

To assign parameters to our more complicated model (Scheme FS1), we first set β as large as was consistent with experimental observation (6/msec) (Maconochie et al., 1994). Previous measurements (Orser et al., 1994) constrain α at 0.4/msec. Thus, β/α = 15 and α/β is ≪1. On the basis of preliminary simulations, we decided to consider the condition where d_f/ r_f = β/α and therefore (α/β)(d_f/ r_f) = 1. Thus, at the initial plateau phase the distribution between opening and fast desensitization will be 50:50 and L₂O (pl)/ L₂C(o) = 0.5. With long pulses, we estimated that τ_f = 2.5 msec (see above). Therefore, using Equation 3 and our estimate of (α/β)(d_f/ r_f) = 1, we set r_f = 0.20/msec and d_f = 3/msec. Using Equation 1 we set 2k_off = 31/151 msec = 0.206/msec. For k_on, we use the value of 1 mm/msec, which gives an EC₅₀ value for the peak response of 25 μm. However, because we are using saturating concentrations of GABA, this value is not critical to our simulations. For the slow desensitization parameters, we use a rough estimate of r_s = 2.7 × 10⁻⁵/msec that was derived from the analysis of phasic activation with brief pulses (Fig. 4). If d_s is set at 0.026/msec, then Scheme FS1reproduces the results obtained with phasic activation for a two-state scheme where d′_s = 1.37/sec, r_s = 2.7 × 10⁻⁵/msec, and t_on = 90 msec (see above).

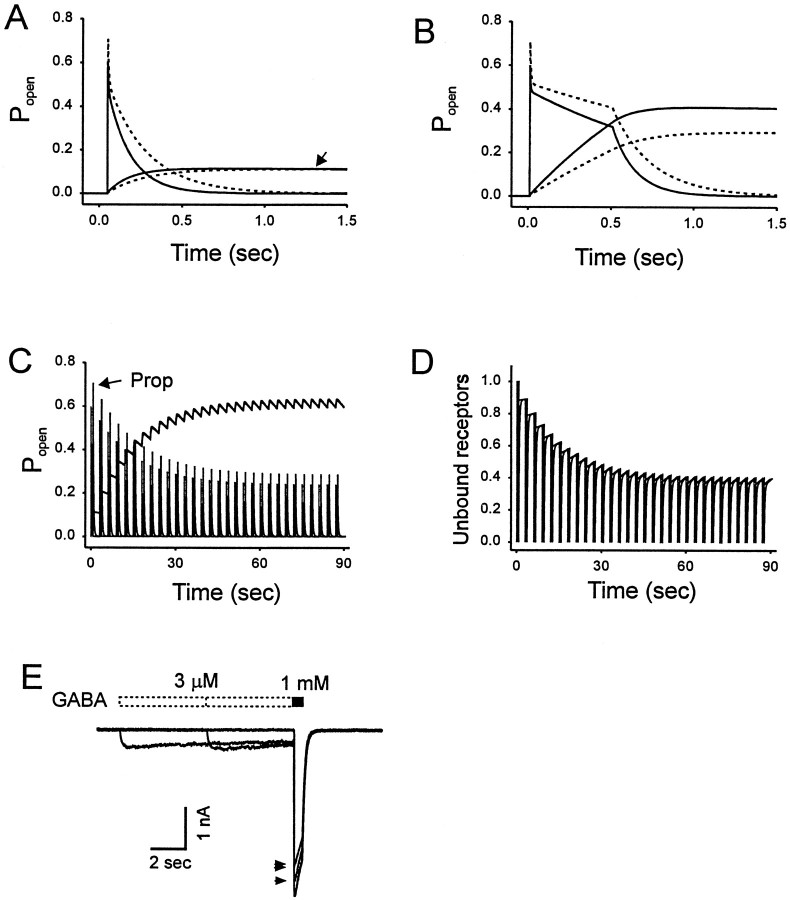
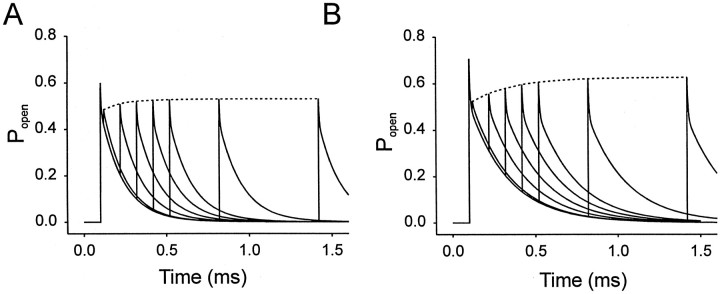
Simulations of the brief pulses of GABA (Fig. 6A) indicate that the proposed parameters generate a peak response where 59% of available receptors are in the open state. All receptors are occupied, however, with 37% of receptors in the fast desensitized state and 4% in the pre-open state. Simulation of the longer pulses of GABA (Fig. 6B) indicates that the fraction of activated receptors quickly declines to a value of 49% as the equilibration between the L₂O and states L₂D_f gives rise to a pseudo-equilibrium within a 10 msec period.

Fig. 6.

Simulations of the effects of propofol on GABA-induced current and predesensitization of GABA currents. A, Simulations of GABA_AR-mediated activity after the application of brief pulses of GABA (3 mm, 3 msec). P_open represents fraction of channels in open state. The solid declining line depicts the rapid decrease in open probability. Superimposed is a plot of the probability of slow desensitization (L₂D_slow) in the absence (solid line) or presence (dashed line) of propofol. The slower buildup of the L₂D_slow state under control conditions is indicated by the solid inclining line(arrow). Propofol causes an increase in the open probability and a small decrease in slow desensitization as indicated by thedotted lines. B, Simulations of the longer (500 msec) pulses of GABA is shown. Again, superimposed is a plot of L₂D_slow. Note the increase in open probability and slower buildup of L₂D_slow in the presence of propofol (dashed lines). Propofol (10 μm) increased the probability of channel opening and reduced slow desensitization. C, Simulation of the application of 30 brief pulses of GABA at 30 pulses administered at a rate of 1 per 3 sec in the absence and presence of propofol. The buildup of the L₂D_slow state was extensive in the absence and presence of propofol. D, Simulation of the same experiment as in C only now monitoring the level of unbound receptors (C). E, Experimental data illustrate that the preapplication of 3 μm GABA decreased the amplitude of current evoked by a saturating concentration of GABA (1 mm), but this effect is far from equilibrium even with longer applications. Increasing the duration of the preapplication from 5 sec (arrow) to 10 sec (double arrows) doubled the effect from an 8% decrease to a 17% decrease. However, our model parameters predict that at equilibrium, 3 μm GABA will reduce the test response by 16 and 24% in the absence and presence of propofol, respectively. Thus, a 10 sec predesensitization period will underestimate the affinity of the slow desensitized state for GABA because the IC₅₀ for predesensitization is 3 μm at equilibrium.

Propofol reduces the rate of onset of fast desensitization ∼1.7-fold, whereas the initial plateau is only changed by 7%. Therefore, from Equations 2a and 3 we can estimate that r_f is reduced 1.7-fold to 0.12/msec. The plateau is enhanced by propofol so that d_f must be reduced by a slightly greater extent than r_f. The 7% increase in the plateau is reproduced if d_f is reduced 1.85-fold to 1.62/msec. If d_f is reduced to exactly the same extent as r_f, then Equation 2 would predict that the response at 100 msec with long pulses would not be changed at all by propofol because the ratio of d_f/ r_f would remain the same. These reductions in d_f and r_f predicts a 17% increase in the amplitude of the response (Fig. 6A), whereas an increase of 8% was observed.

According to previous models (Jones and Westbrook, 1995), the slight reduction in the extent of fast desensitization, if anything, should increase the rate of deactivation in the presence of propofol. Because previous results suggest that propofol does not affect α and the rise time is also unchanged by propofol, we conclude that propofol has little effect on the opening/closing isomerization. Therefore, using Equation 1 we can estimate that 2k_off is reduced 1.85-fold by 10 μm propofol.

For slow desensitization, we accept that propofol has no effect on recovery from slow desensitization (see above) and set r_s at 0.027/sec. We then adjust d_s until Scheme FS1 gives a steady-state level of desensitization of 60% during phasic stimulation (Fig. 4). The resulting value of d_s = 0.014/msec is also 1.85-fold lower than the control value. Thus, our analysis suggests that propofol stabilizes the pre-open state and increases the energy barrier for transitions to fast and slow desensitized states as well as for agonist dissociation to similar extents.

Because saturating concentrations of GABA are used in the current experiments, the time course of desensitization from the single bound state (L₁C) makes little difference to the simulations. However, the assumption of equivalent binding sites in our model means that with low agonist concentrations, as well as during deactivation, a significant fraction of receptors will be in the L₁C state. Furthermore, with our model, propofol will potentiate this state because it decreases k_off. In preliminary experiments, we observed that slow desensitization requires minutes to develop at low agonist concentrations in this preparation (Fig. 6E). This result is not consistent with the development of significant slow desensitization from L₁C. This observation may also explain the unexpected finding of Orser et al. (1994) where the GABA IC₅₀ value for predesensitization was similar to the GABA EC₅₀ for activation of GABA_A receptor. In the previous study, GABA was applied for only 10 sec to predesensitize the receptors. If slow desensitization can only develop from an L₂C state at the rates deduced here, a 10 sec time period is inadequate to reach equilibrium at low agonist concentrations.

Our model parameters predict that at equilibrium, the IC₅₀for slow desensitization is 3 μm GABA, whereas the EC₅₀ for peak responses is ∼25 μm. This value could be confirmed using predesensitization protocols in which sufficient time is allowed for a true equilibrium to develop. In our previous model (Orser et al., 1994) we included an additional binding step for the induction of slow desensitization so that predesensitization and activation could be allowed to occur over a similar range of concentrations.

It is noteworthy that although the model predicts that propofol will potentiate the GABA response and therefore reduce the EC₅₀value for GABA-evoked currents, the IC₅₀ for predesensitization will be changed to a lesser extent. Desensitization is reduced by an amount similar to the enhancement of the response. Thus, potentiation of background current (Bai et al., 1998) will have a smaller effect on resting desensitization and the concomitant reduction in the amplitude of spontaneous miniature IPSCs (mIPSCs).

The process of slow desensitization is highlighted by the phasic stimulation protocol. We simulated the experimental results as illustrated in Figure 6C. However, the model did not predict the acceleration of deactivation observed during the first few responses in the train (Fig. 4B, right panel, D). In our simulations, the time course of the first and the last response can be superimposed once responses are normalized to the peak amplitude (data not shown). This acceleration of the decay may reflect the desensitization of two populations of GABA_AR that are present in the nucleated patches.

The effect of slowing recovery from fast desensitization is shown in Figure 7. The model accurately reproduces the results obtained with the paired-pulse protocol. Recovery from fast desensitization and deactivation occurred in parallel, and the small amount of slow desensitization that develops per pulse is reflected by the incomplete recovery of the amplitude of the second pulse (Fig.3).

Fig. 7.

Simulation of the recovery from desensitization. Using our proposed model, we simulated the currents activated by paired pulses of GABA. GABA (3 mm for 3 msec) was applied at intervals of 20, 120, 220, 320, 420, 720, 1320, and 1920 msec. Thedotted line represents the fit of a monoexponential equation to the peak amplitude of the second pulse. B, Simulated currents for responses activated in the presence of propofol (10 μm).

DISCUSSION

We examined the actions of propofol on GABAergic currents under nonequilibrium conditions. The most prominent effect of propofol on responses to brief applications of GABA is to cause a voltage-independent prolongation of deactivation. Consistent with an earlier report (Orser et al., 1994), propofol also reduces slow desensitization, as evidenced by changes in the time course of responses to 500 msec pulses of GABA. Slow desensitization was also indicated by the decline in peak amplitude of currents evoked by repeated brief applications of GABA. Propofol increased t_on by prolonging the deactivation of individual responses. However, the fractional decline (λ) in peak amplitude per pulse in a train was unchanged despite this enhanced response, suggesting that propofol must also reduce the rate of development of slow desensitization.

A fast component of desensitization could be resolved using our fast perfusion system with saturating concentrations of GABA. Propofol increased the amplitude of the peak current, an effect that is consistent with propofol causing a decrease in the kinetics of fast desensitization. An increase in current amplitude attributable to a redistribution of the receptors between activated and fast desensitized states may explain how some compounds increase the amplitude of mIPSCs despite receptor saturation. Hence, an increase in peak amplitude cannot be used as evidence (Frerking et al., 1995) that receptors contributing to mIPSCs are not saturated.

The rise time of GABA-induced current in this study was ∼2 msec (10–90%). This value is similar to that reported by Jones and Westbrook (1995) for hippocampal neurons but slower than that reported for cerebellar granule cells (Maconochie et al., 1994; Zhu and Vicini, 1997), cortical neurons (Galarreta and Hestrin, 1997), or basket cells of the dentate gyrus (Berger et al., 1998). The slower rise time reported in the present study could be attributed, in part, to the accessibility of agonist to receptors present in the nucleated patch because the exchange time for the K⁺ current recorded under similar experimental conditions was 1.9 msec. The slower rise time of GABA currents might also be determined by the subunit composition of the receptor (Haas and Macdonald, 1999; McClellan and Twyman, 1999).

Actions of propofol on GABA-evoked currents in nucleated patches of hippocampal neurons mimic its effect on mIPSCs

The action of propofol to slow deactivation of GABA-evoked currents qualitatively resembles the effects of propofol on mIPSCs (Orser et al., 1994). Propofol causes a concentration-dependent increase in the duration of synaptic currents. However, the decay of mIPSCs recorded in cultured hippocampal neurons is two to four times faster than deactivation of GABA-evoked responses (Jones and Westbrook, 1997; Mozrzymas et al., 1999; our data). Using our kinetic model, the rapid decay of mIPSCs could not be mimicked by simply altering the duration or the concentration of GABA (data not shown). However, a simple increase in the rate of dissociation of GABA (k_off) from synaptic receptors permits our model to simulate the more rapid decay of mIPSCs. This observation is consistent with the suggestion that the inherent binding and gating properties of postsynaptic GABA_AR differ from receptors present in excised patches (Nusser et al., 1995; Brickley et al., 1999). For example, synaptic GABA_ARs may not trap GABA as extensively on the desensitized states. The subunit composition of the receptors (Tia et al., 1996; Haas and Macdonald, 1999; McClellan and Twyman, 1999) or post-translational modification by second messenger systems (Jones and Westbrook, 1997; Mozrzymas and Cherubini, 1998) or regulatory cytoskeletal proteins might also contribute to the differences between synaptic receptors and those present in the excised patches. Nevertheless, the action of propofol on the duration of IPSCs could be explained if propofol slows k_off at synaptic receptors to the same extent as it slows dissociation of GABA from extrasynaptic receptors.

Alterations of GABAergic currents by pharmacological agents depend on the time course and concentration of GABA

GABA_ARs undergo multiple conformational changes after the binding of agonist, and the pharmacological properties of these conformational states can differ. Thus, the time course and magnitude of receptor activation by the GABA influences the pharmacological sensitivity of a population of receptors (Quastel and Pennefather, 1983; Mozrzymas et al., 1999). This may account, in part, for differences between drug modulation of synaptic currents and GABA-evoked currents that have been demonstrated for various compounds, including barbiturates (Hill et al., 1998), benzodiazepines (Lavoie and Twyman, 1996; Mellor and Randall, 1997; Perrais and Ropert, 1999), neurosteroids (Harrison et al., 1987; Zhu and Vicini, 1997), phenothiazine (Mozrzymas et al., 1999), and lanthanum (Zhu et al., 1998).

Recently, a tonic form of GABAergic inhibition has been described whereby GABA_ARs are activated by persistent low ambient concentrations of transmitter (Valeyev et al., 1993; Brickley et al., 1996). An important prediction of our kinetic model is that drugs such as benzodiazepines and propofol that have different actions on slow desensitization will have discordant effects on the tonic current and IPSCs. For example, diazepam-like benzodiazepines increase the frequency of single-channel opening (Rogers et al., 1994) and prolong deactivation (Orser et al., 1999) but do not reduce the rate of onset of slow desensitization. On the other hand, propofol increases the frequency of channel opening (Orser et al., 1994), slows deactivation of macroscopic current, and decreases slow desensitization (this study). According to our model, midazolam applied to receptors persistently activated by low concentrations of GABA will facilitate the accumulation of the receptors into the slow desensitized state. Absorption of receptors into this nonconducting state will counter the enhancement of current caused by slowed deactivation. In contrast, for propofol our model predicts that for the same degree of prolongation of mIPSCs, there will be a larger effect on the sustained background response to ambient GABA. Consistent with these predictions, preliminary evidence indicates that low concentrations of propofol enhanced the tonic current recorded from cultured hippocampal neurons to a greater extent than midazolam, whereas propofol and midzolam produced similar changes to the time course and charge transfer associated with mIPSCs (Bai et al., 1998). Thus, our kinetic model predicts that drugs with differing actions on slow desensitization will have different effects on the enhancement of currents activated by low concentrations of GABA under near-equilibrium conditions compared with currents evoked by saturating concentrations of agonist under nonequilibrium conditions.

In summary, we demonstrate that the prominent effect of propofol on GABA-evoked currents is to slow deactivation. We attribute this effect to a stabilization of the ligand-bound pre-open state and suggest that it accounts for the prolongation of synaptic currents by propofol. The action of propofol to slow the onset of desensitization would not contribute appreciably to changes in synaptic currents activated at a low frequency but would enhance charge transfer during high-frequency stimulation. Propofol would also reduce desensitization of GABAergic currents activated by persistent low concentrations of agonist and enhance the steady-state amplitude of that current.

ANALYSIS OF THREE-STATE SIMPLIFICATION OF SCHEME 1

Scheme FS2 is a three-state simplification of Scheme FS1, which assumes that binding of GABA is instantaneous and isomerization is rate limiting. Thus, an instantaneous application of a saturating concentration of GABA will rapidly drive all the available receptors to an initial level of L₂C(o) at time zero. The time course of the response will reflect build up and then decline of L₂D_f and L₂O modified by the decay of L₂C to C and L₂D_s.

If s O, s C, and s D are the Laplace transforms of the differential equations dL₂O/dt, dL₂C/dt, and dL₂D/dt, respectively, then the kinetic Scheme FS2 predicts that the following equations hold (Gibraldi and Perrier, 1992). To simplify the nomenclature we set k = 2k_off:

$$s\overline{O}=\beta \overline{C}-\alpha \overline{O},$$ Equation A1

$$s\overline{C}=L_{2}C(o)-(\beta +d_{\text{f}}+k+d_{\text{s}})\overline{C}+r_{\text{f}}\overline{D}+\alpha \overline{O},$$ Equation A2

$$s\overline{D}=d_{\text{f}}\overline{C}-r_{\text{f}}\overline{D},$$ Equation A3

from Equation EA1,

$$\frac{\overline{O}}{L_{2}C(o)}=\beta \frac{\overline{C}}{L_{2}C(o)(s+\alpha )},$$ Equation A4

combining equations A1, A2, A3 with Equation EA4,

$$\frac{\overline{C}}{L_2{C}_0(s+\alpha )}=\frac{(s+r_{\text{f}})}{\begin{array}{c}(s+\alpha )(s+r_{\text{f}})(s+\beta +d_{\text{f}}+k+d_{\text{s}})-s(r_{\text{f}}{d}_{\text{f}}+\alpha \beta \\ \hfill -\alpha r_{\text{f}}(d_{\text{f}}+\beta )\hfill \end{array}}$$ Equation A5

$$=\frac{(s+r_{\text{f}})}{\begin{array}{c}{s}^3+s^2(s+\alpha +\beta +d_{\text{f}}+r_{\text{f}}+k+d_{\text{s}})+s(\alpha (d_{\text{f}}+k+d_{\text{s}})\\ \hfill +r_{\text{f}}(\alpha +{\beta }_{\text{f}}+k+d_{\text{s}})\hfill \\ \hfill +r_{\text{f}}\alpha (k+d_{\text{s}})\hfill \end{array}},$$

combining Equations EA4 and EA5,

$$\frac{\overline{O}}{L_2{C}_0}=\frac{\beta (s+r_{\text{f}})}{\begin{array}{c}{s}^3+s^2(s+\alpha +\beta +d_{\text{f}}+r_{\text{f}}+k+d_{\text{s}})\\ \hfill +s(\alpha (d_{\text{f}}+k+d_{\text{s}})+r_{\text{f}}(\alpha +{\beta }_{\text{f}}+k+d_{\text{s}}))\hfill \\ \hfill +r_{\text{f}}\alpha (k+d_{\text{s}})\hfill \end{array}},$$ Equation A6

$$\frac{\overline{D}}{L_{2}C(o)}=\frac{d_{\text{f}}(s+\alpha )}{\begin{array}{c}{s}^3+s^2(s+\alpha +\beta +d_{\text{f}}+r_{\text{f}}+k+d_{\text{s}})\\ \hfill +s(\alpha (d_{\text{f}}+k+d_{\text{s}})+r_{\text{f}}(\alpha +{\beta }_{\text{f}}+k+d_{\text{s}}))\hfill \\ \hfill +r_{\text{f}}\alpha (k+d_{\text{s}})\hfill \end{array}},$$ Equation A7

The transforms in Equations EA6 and EA7 have the form (As + B)/{(s + a)(s + b)(s + c)} and therefore define a function with three exponential components with rate constants a, b, c. If a > b > c then a will define a rising phase, and b and c will define the fast and slow component of the decay phase (Gibraldi and Perrier, 1992). The inverse transforms are:

$$\frac{L_{2}O(t)}{L_{2}C(o)}=-\frac{\beta (a-r_{\text{f}})exp[-\text{at}]}{(a-b)(a-c)}+\frac{\beta (b-r_{\text{f}})exp[-\text{bt}]}{(a-b)(b-c)}+\frac{\beta (r_{\text{f}}-c)exp[-\text{ct}]}{(a-c)(b-c)},$$ Equation A8

$$\frac{L_{2}D(t)}{L_{2}C(o)}=-\frac{d_{\text{f}}(a-\alpha )exp[-\text{at}]}{(a-b)(a-c)}+\frac{d_{\text{f}}(b-\alpha )exp[-\text{bt}]}{(a-b)(b-c)}+\frac{d_{\text{f}}(\alpha -c)exp[-\text{ct}]}{(a-c)(b-c)}.$$ Equation A9

The fast rise and fast initial decline followed by a slower final decay of the response to brief applications of GABA implies that a > b ≫ c, and the following approximations can be made:

$$(a-b)(b-c)(a-c)\approx (a-b)\text{ab}$$

$$a+b+c=r_{\text{f}}+d_{\text{f}}+\alpha +\beta +k+d_{\text{s}}\approx a+b$$

$$\text{ab}+c(a+b)=(\alpha +\beta +k+d_{\text{s}})r_{\text{f}}+\alpha (d_{\text{f}}+k+d_{\text{s}})\approx \text{ab}$$

$$\text{abc}=r_{\text{f}}\alpha (k+d_{\text{s}}).$$

Therefore,

$$c=\frac{\text{abc}}{\text{ab}}\approx \frac{k+d_{\text{s}}}{1+\frac{\beta +k+d_{\text{s}}}{\alpha }+\frac{d_{\text{f}}+k+d_{\text{s}}}{r_{\text{f}}}}.$$ Equation A10

This will be true regardless of whether L₂O (t) or L₂D (t) is monitored. When β, d_f ≫ k + d_s and k ≫ d_s, then:

$$c\approx \frac{k}{1+\frac{\beta }{\alpha }+\frac{d_{\text{f}}}{r_{\text{f}}}}=\frac{2k_{\text{of}}}{1+\frac{\beta }{\alpha }+\frac{d_{\text{f}}}{r_{\text{f}}}}.$$ Equation A10a

Note, that at equilibrium and pseudo-equilibrium,

$$\frac{L_{2}C}{L_{2}C+L_{2}O+L_2{D}_{\text{f}}}=\frac{k}{1+\frac{\beta }{\alpha }+\frac{d_{\text{f}}}{r_{\text{f}}}}.$$

Thus, the deactivation rate c reflects the actual rate of dissociation of GABA from its receptor and the proportion of receptors in the L₂C state.

Now consider a time where GABA is still present such that the L₂C is continuously replaced and where d_s is too slow to have generated much loss. Such a situation will hold during the first 20 msec of a long application of GABA. Fast desensitization is complete within this time, whereas slow desensitization takes seconds to develop even with saturating concentrations of GABA. Under these conditions k and d_s can be set to 0 and Equations EA6 and EA7become:

$$\frac{\overline{O}}{L_{2}C(o)}=\frac{\beta (s+r_{\text{f}})}{s(s^2+s(s+\alpha +\beta +d_{\text{f}}+r_{\text{f}})+r_{\text{f}}(\alpha +\beta )+\alpha d_{\text{f}})},$$ Equation A11

$$\frac{\overline{D}}{L_{2}C(o)}=\frac{d_{\text{f}}(s+\alpha )}{s(s^2+s(s+\alpha +\beta +d_{\text{f}}+r_{\text{f}})+r_{\text{f}}(\alpha +\beta )+\alpha d_{\text{f}})}.$$ Equation A12

The functions corresponding to the Laplace transforms in EquationsEA11 and EA12 describe a rising phase from 0 followed by a falling phase to a steady-state value such that:

$$\frac{L_{2}O(t)}{L_{2}C(o)}=-\frac{\beta (a-r_{\text{f}})exp[-\text{at}]}{(a-b)}+\frac{\beta (b-r_{\text{f}})exp[-\text{bt}]}{(a-b)}+\frac{\beta r_{\text{f}}}{\text{ab}},$$ Equation A13

$$\frac{L_{2}D(t)}{L_2{C}_0}=-\frac{d_{\text{f}}(a-\alpha )exp[-\text{at}]}{(a-b)}+\frac{d_{\text{f}}(b-\alpha )exp[-\text{bt}]}{(a-b)}+\frac{\alpha d_{\text{f}}}{\text{ab}},$$ Equation A14

where:

$$\hspace{1em}\text{ab}=(\alpha +\beta )r_{\text{f}}+\alpha d_{\text{f}}=\beta r_{\text{f}}\{1+\alpha /\beta (1+d_{\text{f}}/r_{\text{f}})\},$$ Equation A15

$$=\beta r_{\text{f}}\{1+(\alpha /\beta )(d_{\text{f}}/r_{\text{f}})\}\text{when} 1\gg \alpha /\beta .$$ Equation A15a

When β is large it will approach the rise rate, a, and under that condition:

$$1/{\tau }_{\text{f}}=b=r_{\text{f}}\{1+(\alpha /\beta )(d_{\text{f}}/r_{\text{f}})\}.$$ Equation A16

If pl is a time (i.e., 20 msec) where the plateau is established, then Equations EA13 and EA14 predict that:

$$L_{2}O(\text{pl})/L_{2}C(\text{o})=\beta {\text{r}}_{\text{f}}/\text{ab}=1/\{1+(\alpha /\beta )(1+d_{\text{f}}/r_{\text{f}})\},$$ Equation A17

$$L_{2}D(\text{pl})/L_{2}C(\text{o})=d_{\text{f}}\alpha /\text{ab}=1/\{1+(\beta /\alpha )(1+r_{\text{f}}/d_{\text{f}})\},$$ Equation A18

and,

$$\frac{L_{2}O(\text{pl})}{L_{2}O(\text{pl})+L_2{D}_{\text{f}}(\text{pl})}=\frac{\beta r_{\text{f}}}{\beta r_{\text{f}}+\alpha d_{\text{f}}}=\frac{1}{1+(\alpha /\beta )(d_{\text{f}}/r_{\text{f}})}.$$ Equation A19