Abstract
Hypolimnetic oxygen depletion in lakes is a widespread problem and is mainly controlled by the sediment oxygen uptake (SOU) and flux of reduced substances out of the sediments (Fred). Especially in eutrophic lakes, Fred may constitute a major fraction of the areal hypolimnetic mineralization rate, but its size and source is often poorly understood. Using a diagenetic reaction-transport model supported by a large data set of sediment porewater concentrations, bulk sediment core data and lake monitoring data, the behavior of Fred was simulated in eutrophic Lake Baldegg. Transient boundary conditions for the gross sedimentation of total organic carbon and for hypolimnetic O2 concentrations were applied to simulate the eutrophication and re-oligotrophication history of the lake. According to the model, Fred is dominated by methanogenesis, where up to70% to the total CH4 is produced from sediments older than 20 years deposited during the time of permanent anoxia between 1890 and 1982. An implementation of simplified seasonal variations of the upper boundary conditions showed that their consideration is not necessary for the assessment of annual average fluxes in long-term simulations. Four lake management scenarios were then implemented to investigate the future development of Fred and SOU until 2050 under different boundary conditions. A comparison of three trophic scenarios showed that further reduction of the lake productivity to at least a mesotrophic state is required to significantly decrease Fred and SOU from the present state. Conversely, a termination of artificial aeration at the present trophic state would result in high rates of organic matter deposition and a long-term increase of Fred from the sediments of Lake Baldegg.
Introduction
O2 depletion in the hypolimnion of productive lakes and reservoirs still poses a challenge for their management. The sediment oxygen demand (SOD) combines the two main sinks, the sediment oxygen uptake (SOU, i.e. the diffusion-controlled flux of O2 to the sediment-water interface and its consumption within the top sediment layer) and the flux of reduced substances out of the sediment (Fred) [1–3]. The SOU is dominated by the rapid aerobic mineralization of freshly deposited organic matter (OM) and contributions from the oxidation of reduced substances such as CH4 and NH4+. In lakes with a high nutrient load, O2 levels usually decrease to zero within the first millimeters of the sediment [4], while in oligotrophic lakes the O2 penetration depth can reach up to several centimeters [5]. The ensuing anaerobic degradation processes generate reduced substances such as CH4, NH4+, Mn(II), Fe(II) and S(-II), which once in contact with O2, will be oxidized. Hence, the combined fluxes of reduced substances (Fred) from the sediment can be regarded as a negative O2 flux. Especially in the hypolimnion of shallow lakes, Fred can constitute the main sink for ambient O2 with up to 80% of the total hypolimnetic O2 consumption [2, 3].
Artificial aeration systems were installed in many anoxic lakes to increase hypolimnetic O2 levels. Surprisingly, SOD increased in the pursuit of artificial aeration, presumably because the additional O2 was consumed to mineralize large parts of recently deposited OM and to oxidize Fred generated by “legacy” OM [3, 6], which was largely buried during hypolimnetic anoxia. This phenomenon where sediments continue to be a major sink for DO, in spite of decades of artificial aeration, is called “sediment memory effect” [7]. However, it is still unclear under which circumstances hypolimnetic O2 depletion rates will start to decrease as the relative importance of SOU and Fred and their possible resilience to re-oligotrophication measures are poorly understood. To better understand these feedbacks and to navigate re-oligotrophication campaigns and aeration systems, a multi component early diagenesis model has been developed on the basis of the Van Cappellen and Wang [8], Couture, Shafei [9] and Dittrich, Wehrli [10] models. The model uses kinetic rate constants for biogeochemical reactions and processes coupled with a one-dimensional transport model using parameters mostly universal for the aquatic environment. This type of reaction network reflects the current state of the art of modeling [9–11] and enables the investigation of both O2 sinks, Fred and SOU. The model also allows simulations of the transient behavior of the O2 fluxes under varying boundary conditions due to seasonal variations or long-term trends such as eutrophication, re-oligotrophication or climate change.
This paper investigates the controls of long-term O2 depletion in the hypolimnion of the Swiss eutrophic Lake Baldegg. To this end, we model SOD of four scenarios for variations in total organic carbon (TOC) gross sedimentation rate and O2 concentrations, and depict the resulting fluxes of reduced substances out of the sediment and the flux of O2 into the sediments. The different modeling scenarios are based on sediment and sediment porewater data from Lake Baldegg. Lake monitoring data from Lake Baldegg was used to define the upper boundary conditions for the “Status Quo” (SQ) and “No artificial aeration” (NoAa) scenarios. Data from neighboring mesotrophic Lake Hallwil and from oligotrophic Lake Aegeri were utilized for the “Mesotrophic” and the “Oligotrophic” scenario, respectively.
In a first step, a model with constant boundary conditions was applied to reproduce average sediment porewater concentration. As SOD is governed by the quality and quantity of TOC deposited at the sediment surface and the overlying O2 concentrations [1, 2, 12], the different transient input parameters of the modeling scenarios show changes in SOD and help identifying lake restoration goals. Hence, in a second step, as lake primary production and other parameters such as hypolimnetic O2, NO3- and SO42- concentrations and concentrations of reduced substances at the sediment-water interface (NH4+, Mn(II), Fe(II)) can show seasonal variations [13], their respective upper boundary concentrations were modeled with simplified cosine functions to assess the possible impact of seasonal variations on long term O2 depletion.
Materials and methods
Study site
The study was conducted with data from eutrophic Lake Baldegg located on the Swiss plateau. The lake with an area of 5.2 km2 has a maximum depth of 66 m, a mean hypolimnion depth of 27.6 m and water residence time of 4.3 years [14]. The catchment of 73 km2 is dominated by intensive agriculture and pig farms with a high surplus of manure. In 1982, the total phosphorus (TP) concentration reached 520 μgP L-1. The lake is still eutrophic today but has recovered to ∼25 μgP L-1. In spite of artificial aeration with O2 during the stratified season and forced circulation in winter, the bottom waters become sub- to anoxic towards the end of summer stagnation. Although P loads and TP concentrations have dramatically decreased over the last 35 years, primary production and TOC gross sedimentation rate did not show a downward trend [3]. At the deepest point, anoxic conditions as evidenced by the formation of varves occurred from 1885 until the start of the artificial aeration system in 1982 [15].
Sediment data
We used a sediment porewater data set collected during two years of extensive field campaigns in 2014 and 2015. Sixteen sediment cores were retrieved for sediment porewater analysis (CH4, NH4+, Mn(II), Fe(II), SO42-, NO3-, NO2-, dissolved inorganic phosphorus (DIP)) and several additional cores were taken for bulk sediment analysis such as dating (210Pb, 137Cs, varve counting), TOC content, total nitrogen (TN) total phosphorus (TP), and total sulfur and physical parameters such as water content and porosity [2]. The sediment cores were taken at the deepest part of the lake at 64 m water depth (47° 11´ 53´´ N, 8°15´36´´ E), four times during a course of a year (March, June, September, November). Details of the sediment core retrieval and analytical procedures are given in Steinsberger, Schmid [2].
Total Fe and Mn contents of the sediment were taken from Schaller, Moor [16]. Sediment trap material was collected bi-weekly and was analyzed for TN, TP and TOC gross sedimentation rates.
Model formulation
The general model approach is outlined in Van Cappellen and Wang [8] and Couture, Shafei [9]. A system of partial differential equations corresponding to early diagenesis equations is automatically generated in MATLAB and solved by MATLAB’s built-in solver pdepe. The general, one-dimensional partial differential equation for the approximation of the temporal variations of the concentrations of soluble and solid substances in the sediments was used based on deposition, molecular diffusion, bioturbation and transformation processes [17]:
| Eq 1 |
Here, Ci is the concentration of solid (μmol g-1) or solute (μmol cm-3) i, x is the positive downward position along the 1-D vertical domain (x = 0 corresponding to the sediment water interface (SWI)), and t is time. ∑εri (z,t,Ci, …) the sum of the sources and sinks of all species i, including the rates of all biogeochemical reactions producing or consuming species, as well as the non-local transport processes that remove or add dissolved species, most notably bioturbation. ε = φ for solutes and ε = 1- φ for solids with φ defined as the sediment porosity. For solids, Di is the bioturbation coefficient Db (cm2 yr-1). For solutes, Di is calculated as Db + Dsed with Dsed = Dmo /(1-log(φ2) the tortuosity corrected molecular diffusion coefficient (Dmol) at in situ temperature and salinity [18]. For solids and solutes, ϑequals to the burial velocity of the sediments (cm yr-1).
The upper boundary condition for solutes at the SWI (x = 0) is given by the flux through the diffusive boundary layer (DBL) above the SWI:
| Eq 2 |
Here, Bi(t) is the concentration of the solute in the bottom boundary layer of the water column, and can be time-dependent in non-steady state simulations to reflect long-term or seasonal changes in bottom water concentrations with dDBL as the thickness of the DBL. Potential geochemical reactions in the DBL are neglected.
For solid-bound species (e.g. total organic carbon or Fe/Mn solid species), the flux continuity condition at x = 0 is:
| Eq 3 |
Where Ji(t) is the (transient) depositional flux of any given solid-bound species. ρb(1-φ) is the denominator ensuring consistency among the units of Ji(t) (μmol cm-2 yr-1) and Ci (μmol g-1 for solid species) with ρb dry density (g cm-3).The depth dependence of the bioturbation coefficient Db was approximated from Katsev and Dittrich [19]:
| Eq 4 |
is the value at the SWI, τb shows the characteristic depth half interval in which most of the reduction of Db occurs, while H is the depth of the steepest gradient of Db in the sediment [20]. Dbmin is added to account for very small disturbances in the sediment and to increase numerical stability, however with a very low value (0.01 cm-2 yr-1).
At the lower boundary xL, zero gradients (equivalent to zero diffusive fluxes) are imposed for all solute and solid species:
| Eq 5 |
The grid points between the sediment surface and the maximum simulated sediment depth (here 50 cm) were calculated using a curvature function. This function increases the number of grid points in the upper sediment where production/consumption rates are highest. In the top centimeter the resolution varied between 0.04 mm and 0.13 mm. In deeper less reactive sediments, fewer grid points were used to increase simulation speed with a resolution reaching 2.9 mm at 30 cm sediment depth and 4.8 mm at 50 cm sediment depth. Modeled time steps are automatically chosen by MATLABs PDE solver according to the chosen process rates, species concentrations and tolerance levels. The system of PDEs (partial differential equations) defined in section 2.3 is solved in Matlab using the function pdepe within the temporal to < t < tf and spatial (xo < x < xf) domains. The pdepe function is designed to solve initial-boundary value problems consisting of systems of parabolic and elliptic PDEs in space and time. The numerical method is based on a piecewise nonlinear Petrov-Galerkin method with second-order accuracy. This method solves the ordinary differential equations (ODE) from the spatial discretization of the PDEs, using the built-in Matlab ODE solver to obtain approximated solutions at specific times within a defined time interval. Furthermore, the Matlab code evaluates the boundary values at each time step separately and therefore enables transient boundary conditions. This feature becomes particularly useful when simulating the fate of compounds whose inputs are or can be changed by anthropogenic activity like artificial aeration or re-oligotrophication efforts e.g. a change in TOC gross sedimentation rate.
Modeled species
Twelve solute and ten solid species are modeled as listed in Table 1. SOU is calculated as the flux of O2 into the sediment and Fred as the sum of the fluxes of reduced substances out of the sediment (NH4+, CH4, Mn(II), Fe(II), S(-II)). Based on the respective redox stoichiometry, the fluxes of reduced compounds (Jx) were converted to fluxes of O2 equivalents and denoted in gO2 m-2 d-1 (Eq 6).
Table 1. Upper boundary conditions used for the simulated soluble and solid species in the various scenarios defined in section 2.8.
For solutes, these are the concentrations in the bottom boundary layer above the DBL, for solids the depositional fluxes. Between the dates given here, values were linearly interpolated.
| Time-dependent Input Parameters | 1860 | 1890 | 1900 | 1982 | 1985 | 2018 | SQ (2030) | M (2030) | O (2030) | NoAa (2030) |
|---|---|---|---|---|---|---|---|---|---|---|
| O2 (μmol cm-3) | 0.180 | 10−5 | 10−5 | 10−5 | 0.1 | 0.1 | 0.1 | 0.15 | 0.2 | 10−5 (from 2020) |
| NO3 (μmol cm-3) | 0.030 | 0.030 | 10−5 | 10−5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.100 | 10−5 |
| SO4 (μmol cm-3) | 0.035 | 0.035 | 10−5 | 10−5 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 | 10−5 |
| NH4 (μmol cm-3) | 10−4 | 10−4 | 0.15 | 0.5 | 0.1 | 0.1 | 0.1 | 0.05 | 10−4 | 0.3 |
| Mn(II) (μmol cm-3) | 10−10 | 10−10 | 0.08 | 0.08 | 0.01 | 0.01 | 0.01 | 0.005 | 10−10 | 0.08 |
| Fe(II) (μmol cm-3) | 10−10 | 10−10 | 0.08 | 0.08 | 0.01 | 0.01 | 0.01 | 0.005 | 10−10 | 0.08 |
| S(-II) (μmol cm-3) | 10−10 | 10−10 | 0.03 | 0.034 | 10−10 | 10−10 | 10−10 | 10−10 | 10−10 | 0.03 |
| CH4 (μmol cm-3) | 10−10 | 10−10 | 0.1 | 0.8 | 0.05 | 0.05 | 0.05 | 0.05 | 10−10 | 100 |
| OM1 (μmol cm-2 yr-1) | 192.5 | 407.75 | 479.5 | 623 (from 1950) | 623 | 623 | 623 | 350 | 210 | 623 |
| OM2 (μmol cm-2 yr-1) | 82.5 | 174.75 | 205.5 | 267 (from 1950) | 267 | 267 | 267 | 150 | 90 | 267 |
| Mo1 (μmol cm-2 yr-1) | 7 | 7 | 7 | 10 | 10 | 10 | 10 | 8 | 7 | 7 |
| Mo2(μmol cm-2 yr-1) | 1 | 1 | 1 | 1.25 | 1.25 | 1.25 | 1.25 | 1.25 | 1 | 1 |
| Foh1 (μmol cm-2 yr-1) | 18 | 18 | 18 | 23 | 23 | 23 | 23 | 20 | 18 | 18 |
| Foh2(μmol cm-2 yr-1) | 3.3 | 3.3 | 3.3 | 3.6 | 3.6 | 3.6 | 3.6 | 3.4 | 3.3 | 3.3 |
| Dbo (Bioturbation) | 1 | 1 | 0 | 0 | 0.2 | 0.7 | 0.7 | 1 | 1 | 0 |
| Sedimentation rate (cm yr-1) | 0.15 | 0.15 | 0.18 | 0.33 (from 1950) | 0.33 | 0.33 | 0.33 | 0.22 | 0.15 | 0.33 |
| Constant Input Parameters | ||||||||||
| CO2 (μmol cm-3) | 0.01 | |||||||||
| HCO3 (μmol cm-3) | 1 | |||||||||
| N2 (μmol cm-3) | 0.1 | |||||||||
| HPO4 (μmol cm-3) | 0.001 | |||||||||
| FeS (μmol cm-2 yr-1) | 10−10 | |||||||||
| Pyrite (μmol cm-2 yr-1) | 10−10 | |||||||||
| Vivianite (μmol cm-2 yr-1) | 10−5 | |||||||||
| Eq 6 |
| Eq 7 |
| Eq 8 |
Both measured and modeled porewater fluxes were calculated from the vertical porewater concentration gradients by Fick’s first law. Measured porewater fluxes were further evaluated by a one-dimensional reaction-transport model [21] that was adapted from Epping and Helder [22].
Although many studies use three OM pools (reactive, slow reactive and non-reactive) [10, 19], this model uses only two OM pools (OM1, reactive; and OM2, non-reactive). While the total amount of settled organic matter or TOC can be accurately determined, the ratio of reactive to non-reactive TOC is not known. After setting the main reaction rates, the ratio of reactive to non-reactive TOC was determined by comparing simulated and measured CH4, NH4,TOC and TN concentrations. Best results were found for 2/3 reactive and 1/3 non-reactive TOC. Similarly, the boundary conditions of total Fe and Mn were estimated from sediment trap analyses assuming that the predominant fraction of these metals is reactive (Foh1, 82% of total Fe; and Mo1 63% of total Mn), while a smaller part is less reactive (Foh2, 13% of total Fe; and Mo2 8% of total Mn) with the remaining fraction being non-reactive and consequently not modeled. The relative fractions of reactive and non-reactive Fe and Mn were calibrated to match the measured Fe(II) and Mn(II) porewater profiles and total solid Fe and Mn sediment profiles measured by Schaller, Moor [23]
The input of both organic matter pools is characterized by the measured elemental C (cx1): N (cy1): P (cz1): S (cs1) ratio of 106: 8: 0.5: 0.5. Other elements contained in the OM are discarded. Hence, by the turnover of one OM1 106 carbon (cx1), 8 nitrogen (cy1), 0.5 phosphorous (cz1) and 0.5 sulfur (cs1) are liberated (see S1 Table).
Seasonal modeling
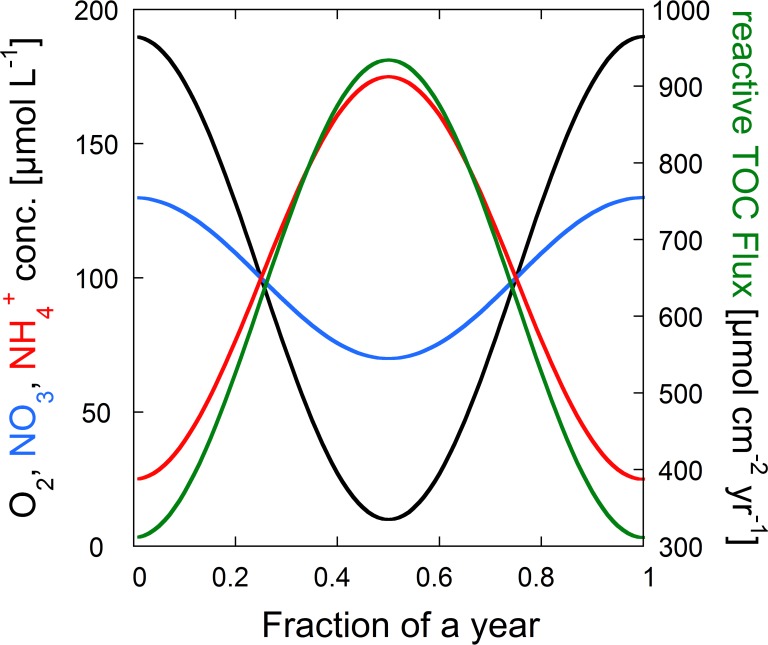
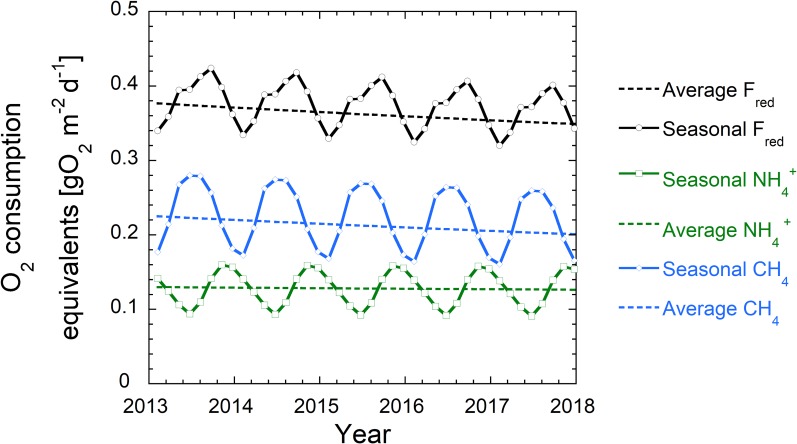
Seasonal changes of TOC gross sedimentation rate and concentrations in O2, NO3-, SO42-, NH4+, CH4, Fe(II), Mn(II) were observed during the two year-long field campaign [2]. These naturally occurring seasonal variations could influence the hypolimnetic O2 depletion rate. As the model allows for temporally varying upper boundary conditions, seasonal variations can be readily appended. However, direct data inputs of e.g. highly fluctuating TOC gross sedimentation rates captured in a daily and/or biweekly basis, result in numerical instability. Instead, the boundary conditions were multiplied with cosine functions with different amplitudes and phase shifts as simple approximations for the measured seasonal fluctuations (see Fig 1 and Table 2)[10]. The same cosines functions were applied to all scenarios leading to slight overestimations of hypolimnetic O2 levels in the “oligotrophic scenario”.
Fig 1. Simplified seasonal variations in the boundary concentrations of the “status quo” scenario shown for selected TEAs, the reactive TOC flux and NH4+.
Table 2. Seasonal variations in boundary concentration for a list of modeled species calculated by various cosines functions.
For the seasonal model, the boundary conditions from in Table 1 were multiplied with the seasonal functions given here. t is the time in years.
| Changing Input Parameters | Seasonal variation function |
|---|---|
| O2 | 1+0.9xcos(2xπxt) |
| NO3 | 1+0.3xcos(2xπxt) |
| SO4 | 1+0.1xcos(2xπxt) |
| NH4, Mn(II), Fe(II), CH4 | 1–0.75xcos(2xπxt) |
| OM1, OM2, Mo1, Mo2, Foh1, Foh2 | 1–0.5xcos(2xπxt) |
Biogeochemical reactions
All biogeochemical reactions are listed in S2 Table. The mineralization processes are calculated with the stoichiometric coefficients of the OM cx1 (C), cy1 (N), cz1 (P) and cs1 (S). The biogeochemical degradation of OM is cascading according to the standard electron acceptor utilization (O2, NO3-, Mn-oxides, Fe-(hydr)oxides, SO42-, and terminal methanogenesis) based on the available Gibbs Free energy [24]. Hence, the decomposition of the OM1 pool and availability of terminal electron acceptors (TEA) fundamentally drive all reactions considered in this model.
For this study, the concentrations and fluxes of O2 and NH4+, CH4, Mn(II), Fe(II) and S(-II) are of particular importance as they compose SOU and Fred. Other secondary reactions and mineral precipitation and dissolution reactions are included and act as sources or sinks for reduced substances. NH4+ is released in each primary mineralization. Once O2 concentrations decline sufficiently, denitrification becomes the dominant mineralization process, where N2 is produced and lost to the overlying water and is not further modeled. Once NO3 is sufficiently depleted, Mn-oxides, Fe-(hydr)oxides and SO42-are utilized as electron acceptors and reduced to Fe(II), Mn(II) and S(-II). During the final methanogenesis, NH4+, CH4 and CO2 are produced. All reduced substances are prone to aerobic oxidation by secondary reactions e.g. nitrification or anaerobic oxidations such as anaerobic methane oxidation (AMO) or oxidation by other oxides such as ferric iron. Further, various more stable forms of Fe- and Mn-containing mineral phases are formed such as iron sulfides, pyrite, vivianite, and manganese carbonates.
Simulated scenarios
The model and the respective modeling scenarios are based on historic observations, lake monitoring data, bulk sediment parameters and sediment porewater data of Lake Baldegg [2, 23, 25, 26]. To calculate the different scenarios, two other lakes of comparable size and morphometry were chosen where complete limnological data sets were available. Similar to Lake Baldegg, neighboring Lake Hallwil was aerated since the 1980s but already shows decreased primary production and was therefore chosen as representative for the mesotrophic scenario. Lake Aegeri, where total phosphors concentrations are below 10 μg L-1 due to the low fraction of agriculture in its catchment, was chosen as representative for the oligotrophic scenario. The initial conditions were set to match the presumed natural oligotrophic state of the lake with average DO concentrations of 5.76 mg O2 L-1 available at the sediment water interface and low TOC gross sedimentation rate and were modeled for 350 years. All boundary conditions can be found in Table 1 and all reaction rates in Table 3. The transient boundary conditions of the model were then used to simulate the advancing eutrophication of Lake Baldegg starting in 1860 with decreasing O2 concentrations until permanent anoxic conditions were reached in 1890. These anoxic conditions are preserved in the sediments by the onset of sediment varves [15, 25]. The anoxic phase in the hypolimnion of Lake Baldegg lasted at least from 1890 until 1982 and was only reversed by the initiation of artificial aeration. During the anoxic phase, the boundary conditions of all reduced substances, especially for NH4+, rose as they started accumulating in the hypolimnetic waters and became an increasing environmental problem. Furthermore, this condition led to enhanced geochemical focusing as more reduced manganese and iron were exported to the sediments of the hypolimnion [27]. Based on the available lake O2 monitoring data, following the onset of aeration boundary O2 concentrations were set to 3.2 mg O2 L-1 between 1982 and 2018. The simulations were then continued from 2018 to 2050 with four scenarios with different upper boundary conditions to represent different trophic and oxic conditions in Lake Baldegg until the year 2050:
Table 3. Model parameters used in the model.
The reaction rates and corresponding reactions are defined in the S1 and S2 Tables. The asterisks are used to distinguish between calibrated (*), literature (**) or measured (+) parameters.
| Parameter | Description | Value | Units | Literature values. | Refs. |
|---|---|---|---|---|---|
| Simulated sediment depth (+) | 50 | cm | |||
| Sediment density (+) | 2.48 | g cm-3 | 2.5 | [19] | |
| Sedimentation rate (*) | 0.15 | cm yr-1 | |||
| Bioturbation coeff. () (**) | 1 | cm2 yr-1 | 0.1–5 | [19] | |
| Hbio (**) | Depth of max. bioturbation gradient | 0.5 | cm | [19] | |
| τbio (**) | Bioturbation depth attenuation | 1.43 | cm | 1–3 | [19] |
| Dbl (**) | Diffusive boundary layer thickness | 0.082 | cm | 0.082 | [1, 3] |
| Porosity(*) | 0.84 | ||||
| (**) | Oxic respiration | 9.1 | yr-1 | 9.13 | [10] |
| (**) | Denitrification | 7.3 | yr-1 | 7.31 | [10] |
| (*) | MnO2 reduction | 1.08 x 10−2 | yr-1 | 3.65 x 10−2 | [10] |
| kdeg,FeOOH (*) | FeOOH reduction | 1.08 x 10−2 | yr-1 | 1.83 x 10−4 | [10] |
| (*) | Sulfate reduction | 1.44 | yr-1 | 3.65 x 10−2 | [10] |
| (*) | Methanogenesis | 5.28 x 10−2 | yr-1 | 5.84 x 10−3 | [10] |
| (*) | Rate inhibition concentrations | 1 x 10−3 | μmol cm-3 | 10−4–10−2 | [8, 19] |
| (*) | 1 x 10−3 | μmol cm-3 | 10−3–10−1 | [19, 29] | |
| (*) | 16 | μmol g-1 | 16–200 | [8, 19] | |
| kdeg,FeOOH,inh (*) | 100 | μmol g-1 | 3–2000 | [8, 19] | |
| (*) | 0.1 | μ mol cm-3 | 0.06–1 | [19] | |
| knhox (*) | NH4 oxidation by O2 | 500 | cm3 μmol-1 yr-1 | 5000 | [19] |
| kmox (*) | Mn(II) oxidation by O2 | 7500 | cm3 μmol-1 yr-1 | 800–2000 | [8] |
| kfox (*) | Fe(II) oxidation by O2 | 1 x 104 | cm3 μmol-1 yr-1 | 3.5 x 104 | [19] |
| ksox (*) | S(-II) oxidation by O2 | 160 | cm3 μmol-1 yr-1 | 160–16000 | [19] |
| kchox (*) | CH4 oxidation by O2 | 3 x 105 | cm3 μmol-1 yr-1 | 1 x 107 | [8] |
| knhmo (*) | NH4 oxidation by reactive MnO2 | 7.5 x 10−4 | cm3 μmol-1 yr-1 | 0 | [19] |
| knhmx (*) | NH4 oxidation by less-reactive MnO2 | 7.5 x 10−5 | cm3 μmol-1 yr-1 | ||
| knhfo (*) | NH4 oxidation by reactive FeOOH | 9.45 x 10−4 | cm3 μmol-1 yr-1 | ||
| knhfx (*) | NH4 oxidation by less-reactive FeOOH | 9.45 x 10−5 | cm3 μmol-1 yr-1 | ||
| kfmo (*) | Fe(II) oxidation by reactive MnO2 | 1.5 x 10−2 | cm3 μmol-1 yr-1 | 1–3000 | [19] |
| kfmx (*) | Fe(II) oxidation by less-reactive MnO2 | 1.5 x 10−3 | cm3 μmol-1 yr-1 | ||
| ksmo (*) | S(-II) oxidation by reactive MnO2 | 1 | cm3 μmol-1 yr-1 | 10–20 | [8, 19] |
| ksmx (*) | S(-II) oxidation by less-reactive MnO2 | 0.1 | cm3 μmol-1 yr-1 | ||
| ksfo (*) | S(-II) oxidation by reactive FeOOH | 2.5 | cm3 μmol-1 yr-1 | 10−2–102 | [8, 19] |
| ksfx (*) | S(-II) oxidation by less-reactive FeOOH | 0.25 | cm3 μmol-1 yr-1 | ||
| kchso (*) | CH4 oxidation by sulfate | 0.5 | cm3 μmol-1 yr-1 | 10 | [8] |
| kmoN (*) | Mn(II) oxidation by nitrate | 1 x 103 | cm3 μmol-1 yr-1 | ||
| kvivpre (**) | Vivianite precipitation | 2.72 x 10−5 | μmol g-1 yr-1 | 10−4–1.7 x 10−3 | [19, 20] |
| kvivdis (**) | Vivianite dissolution | 1 | yr-1 | 1 | [19] |
| kEqViv (**) | 3 x 10−20 | 3 x 10−20 | [19] | ||
| ksviv (**) | Vivianite dissolution by S(-II) | 10 | cm3 μmol-1 yr-1 | 10–100 | [19] |
| kIronSulfidePre (**) | FeS precipitation | 0.1 | μmol g-1 yr-1 | 0.1–100 | [19] |
| kIronSulfideDis (**) | FeS dissolution | 2 x 10−3 | yr-1 | 1 x 10−3 | [19] |
| kEqIronsulfide (**) | 6.3096 | [19] | |||
| kpyrpre (**) | FeS2 precipitation | 4 | cm3 μmol-1 yr-1 | 10−3–103 | [19, 20] |
| kMnCarbonatePre (*) | MnCO3 precipitation | 0.01064 | μmol g-1 yr-1 | 10–10000 | [19] |
| (**) | 2375 x 10−8 | ||||
| kEqMnCarbonate (**) | 0.022 | 0.022 | [19] | ||
| H+ (pH) (**) | 10−7 | ||||
| L (*) | Rate limiting constant | 10−8 |
Status Quo (SQ) scenario, in which O2 concentrations (average 3.2 mg O2 L-1) and TOC gross sedimentation rates (107 g C m-2 yr-1) remain constant at current levels.
Mesotrophic production (M) scenario based on lake monitoring data from neighboring mesotrophic Lake Hallwil [2], which has been undergoing a re-oligotrophication phase since the early 1980s. Similar to Lake Baldegg, lake TP concentrations in Lake Hallwil decreased from 235 μg P L-1 in 1976 to 90 μg P L-1 in the 1990s and further to 12 μg P L-1 in 2015. However in Lake Hallwil, this change was accompanied by a drastic decrease of primary production and hence TOC gross sedimentation from over 100 g C m-2 yr-1 [28] to around 60 g C m-2 yr-1 [2]. Hence, for the M scenario the TOC gross sedimentation rate was reduced by 44% of the present day value and O2 concentrations were increased to an annual average of 4.8 mg O2 L-1.as observed in Lake Hallwil.
Oligotrophic production (O) scenario: Here we assume that TP concentrations rapidly decline over a 12-year period to a low productive state with low TOC gross sedimentations rates. Sediment trap data (TOC gross sedimentation) and O2 measurements from oligotrophic Lake Aegeri were used as proxy values for Lake Baldegg in a low productive state. In 2013 and 2014, in Lake Aegeri TOC gross sedimentation rates were 36 g C m-2 yr-1 [2] and hence the TOC flux in this scenario is reduced to 33% of the present day value. The O2 concentration value was set to an annual average of 6.4 mg O2 L-1.
-
No artificial aeration scenario (NoAa): As artificial aeration systems are expensive due to maintenance costs, the reduction of maintenance costs or termination of the aeration systems are regularly debated. However, it is highly likely that without artificial aeration Lake Baldegg would rapidly turn anoxic during summer stagnation, and depending on the intensity of winter mixing, most probably become permanently anoxic within a few years, similar to its status before the onset of artificial aeration in 1982. Therefore, the O2 concentration is set to 0 mg L-1. Similarly, NO3- and SO42- concentrations are decreased. The TOC gross sedimentation is assumed to be not affected by this and is kept constant at the present-day level. Furthermore, the boundary conditions of the reduced substances NH4+, CH4, Fe(II), Mn(II) and S(-II) are increased to 300 μmol L-1, 100 μmol L-1, 80 μmol L-1, 80 μmol L-1and 30 μmol L-1, respectively, to account for their likely accumulation in the hypolimnion (see Table 1).
The underlying premise of the SQ, M and O scenarios is that artificial aeration remains active to supply sufficient hypolimnetic DO. The detailed boundary conditions for each scenario are given in Table 1. Finally, all scenarios were modeled with simplified seasonal variations of the TOC gross sedimentation rate, the boundary concentration of all TEAs (O2, NO3-, Mn(IV)-oxides, Fe(III)-hydroxides, SO42-) and the boundary concentrations of all reduced substances.
Results and discussion
Model calibration
The values of the model parameters (Table 3) were initially set either based on literature values or field observations. Boundary conditions were subsequently modified during the calibration process, using a manual trial-and-error approach (Table 1). Further, reaction rates taken from similar model studies by Van Cappellen and Wang [8], Dittrich, Wehrli [10] and Katsev and Dittrich [19] were used as initial rates. First, by using these initial rates, relative fractions of reactive to non-reactive pools of OM, Fe, and Mn were determined by visually comparing the modeled and measured porewater and sediment profiles. Then, process rates were calibrated to further improve, reproduce and match the measured porewater concentration profiles and sediment concentrations without using numerical fitting procedures (see asterisks Table 3).
The sensitivity of the model results to individual process rates was assessed by step-wise increasing/decreasing (±1%) the respective rate and comparing the resulting AHM to that from the baseline run. Sensitivities in the following are expressed as relative change in the model output divided by relative change of the model parameter. The sensitivity of O2 consumption and Fred production to most of the process rates was low (below <0.01), but adjusting these rates was required for reproducing the observed concentrations of individual species e.g Fe(II) oxidation rate for total solid Fe or the Fe(II) profile. The highest sensitivities of AHM were found for the deposition rate of OM1 (1.04) and the rate of the main carbon mineralization pathway methanogenesis (kdeg,CH4) with 0.25. Oxic degradation (kdeg,O2) showed a surprisingly low sensitivity of ~0.20. The other main carbon mineralization pathways showed lower sensitivities with denitrification (kdeg,NO3) ~0.04, FeOOH reduction (kdeg,FeOOH) <0.01, MnO2 reduction (kdeg,MnO2) <0.01 and sulfate reduction (kdeg,SO4) <0.01.
Based on the fluxes across the sediment-water interface, the total mass within the sediment and the amounts leaving the modeled sediment depth range at the bottom, the total mass balance of each element species was calculated. Mass balances of all species were preserved. Carbon and nitrogen mass balances are shown in S1 Fig.
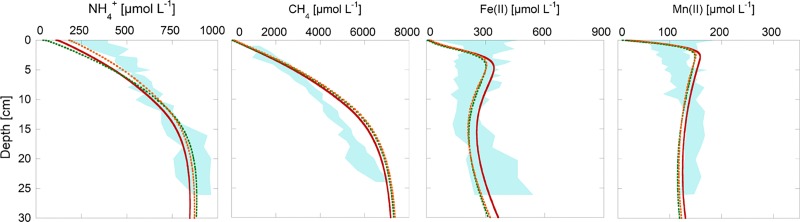
The first goal of the calibration was to reproduce observed porewater profiles of the most important species contributing to Fred and their respective fluxes from the sediment to the water column. The measured and modeled results for NH4+, CH4, Fe(II) and Mn(II) are shown in Fig 2.
Fig 2. All measured porewater concentrations for the years 2014 and 2015 and modeled porewater concentrations of 2015.
The blue shaded area indicates the seasonal porewater variations encountered in the field campaign. The red line is the modeled porewater concentration using average input parameters. The dotted lines represent seasonal modeled concentrations during the middle of the year (mid-June, orange) and the end of the year (mid-December, green).
Porewater profiles
In agreement with sediment porewater measurements [2], modeled porewater concentrations of NH4+ and CH4 increased with increasing sediment depth. This was mainly a result of the aerobic mineralization at the top of the sediment and the dominating process of methanogenesis in the deeper parts of the sediment. While modeled and measured CH4 concentrations were similar in the top few of centimeters, the deviation increased with increasing sediment depth. Reproduction of the observed shape of the CH4 profiles required an additional CH4 sink below the oxic zone or changes of the C/N ratio in the OM pool. Several anaerobic oxidation processes of CH4 such as oxidation by ferric iron oxides [30], Mn(IV)-oxides [31] or humic compounds [32] might play a role here but are not implemented in the reaction network.
Modeled and measured porewater profiles of Fe(II) and Mn(II) were also in reasonable agreement, despite their complex shapes due to various precipitation and dissolution reactions. The Fe(II) peak is caused by the initial reduction of iron (hydr-)oxides. The resulting ferrous iron diffuses towards the sediment surface where it is rapidly re-oxidized to various forms of ferric (hydr-)oxides creating an iron redox cycle. Although the major reactions for Fe(III) and Mn(IV) precipitation and reductive dissolution were included in the model, we acknowledge that without simultaneous pH calculations their significance remains limited. However, as Fe(II) and Mn(II) concentrations and hence fluxes only contributed a very small fraction to the total Fred [3, 7], their values had a negligible effect on the overall picture.
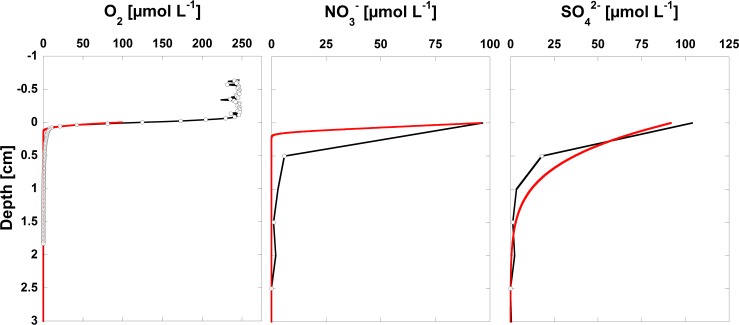
Measured and modeled sediment porewater concentrations of O2, NO3- and SO42- are shown in Fig 3. O2 measurements were taken during winter overturn with highest O2 concentrations of around 245 μmol L-1 in the sediment overlying water and decreasing to zero within 2 mm below the diffusive boundary layer. Similar rapid drops in porewater concentrations were observed for NO3- and SO42-, where porewater concentrations decrease to zero within 5 mm and 15 mm, respectively.
Fig 3. Modeled (red line) and measured (black line) porewater concentrations of the terminal electron acceptors O2, NO3- and SO42-.
Direct O2 measurements were taken only once during winter overturn.
Fluxes of reduced substances (Fred)
The porewater fluxes were estimated from measured porewater concentration profiles using Fick’s first law of diffusion. The fluxes where then expressed as O2 equivalents according to their oxidation stoichiometry and summed up to Fred [3]. The Fred flux resulting from the sediment model for 2015 was 0.36 gO2 m-2 d-1. The modeled value is close to the value determined with the steady-state 1-D model by Epping and Helder [22] of 0.49±0.09 gO2 m-2 d-1 in 2015 [2]. Likewise modeled and measured CH4 fluxes were in perfect agreement with 0.22 and 0.25±0.06 gO2 m-2 d-1 respectively. Similarly, modeled and measured NH4 fluxes were in good agreement with 0.13 and 0.18±0.07 gO2 m-2 d-1 respectively. Modeled CH4 and NH4+ fluxes contributed 61.1% and 34.7% to Fred, respectively, while measured CH4 and NH4+ fluxes contributed 55.1±5.6% and 41.7±5.7% to Fred. Modeled and measured Fe(II) and Mn(II) fluxes were 2x10-3 and 3±1x10-3 gO2 m-2 d-1 and 6x10-3 and 1±1x10-3 gO2 m-2 d-1, respectively. Modeled Mn(II) and Fe(II) fluxes contributed 1.7% and 0.5% to Fred, observed values were 0.7±0.5% and 1.8±0.3%, respectively.
Modeled sulfide (S-II) fluxes accounted for 3.3% of Fred, although dissolved S(-II) has not been detected in the field.
Sediment TOC
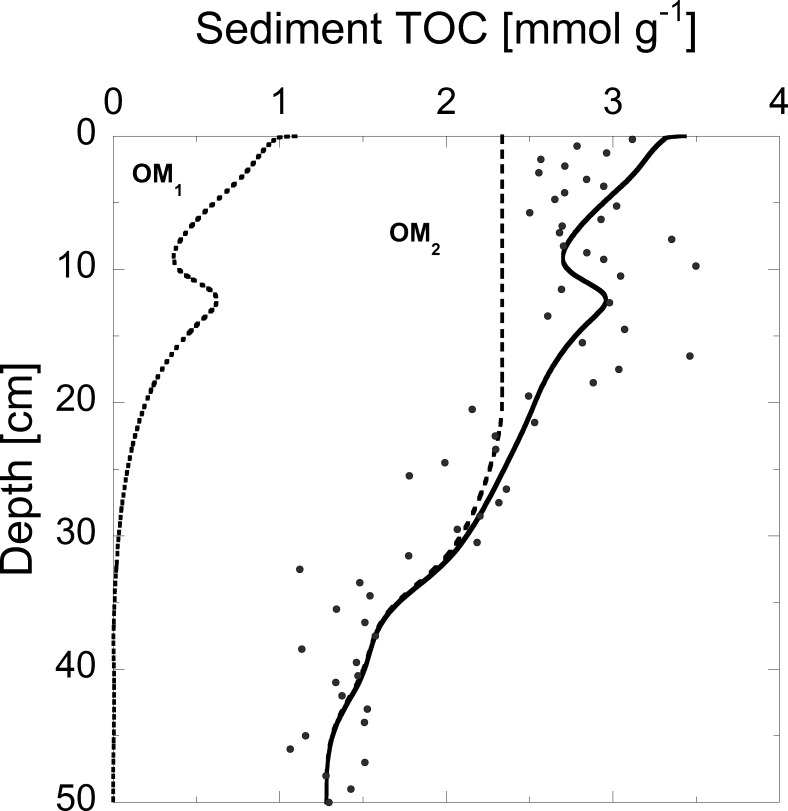
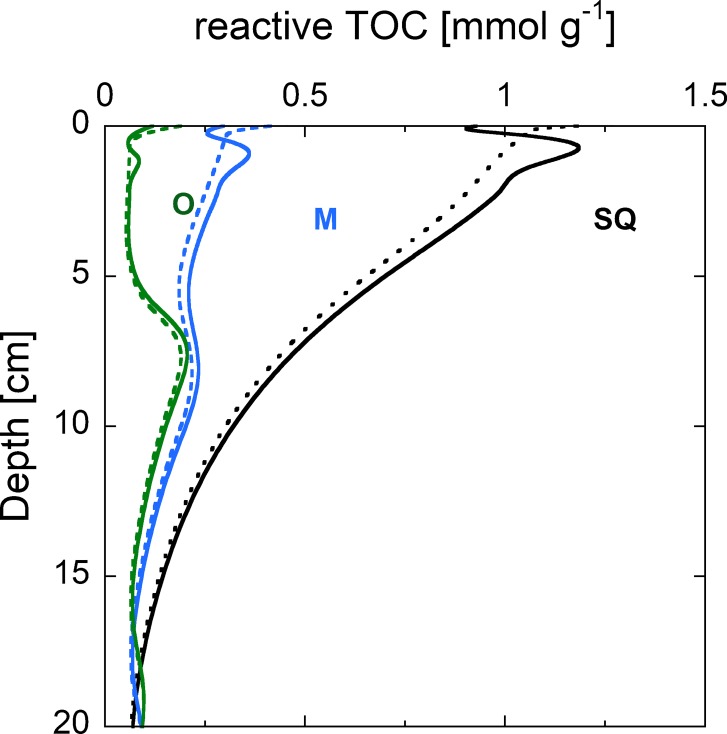
To reproduce the observed vertical profiles of TOC in the sediment, we calibrated the ratio between reactive and non-reactive OM. A good agreement between simulated and observed TOC was reached under the assumption that two thirds of the total TOC gross sedimentation are reactive with an absolute error of ~ 7.5% between the measured and modeled TOC values (Fig 4). This assumption seems reasonable for a highly productive lake such as Lake Baldegg. A large fraction of the reactive TOC pool (OM1) was mineralized directly at the sediment surface, and decreased by about 50% within the top 10 centimeters of the sediment. Deeper in the sediment, the largest TOC pool consisted of non-reactive TOC, and no reactive TOC was left below 33 cm.
Fig 4. Vertical profiles of measured (dots) and simulated (line) TOC concentrations (2015).
Simulated concentrations are further split up into reactive OM1 (dotted) and non-reactive OM2 (dashed) TOC pools. The “bump” in the modeled TOC concentration between 10 and 15 cm depth is caused by the onset of artificial aeration in 1982.
Simulated scenarios
The calibrated model is an excellent tool for assessing the future development of the O2 consumption rate in the lake applying different management strategies. The transient boundary conditions of the model were adjusted to simulate four different scenarios up to the year 2050. Each setup started with the same initial conditions in 1850, and boundary conditions were only changed after 2018 to account for the four abovementioned scenarios: “Status Quo” (SQ), Mesotrophic production (M), “Oligotrophic production” (O) and “No artificial aeration” (NoAa). The underlying premise for all settings (except NoAa) is that artificial aeration remains active to supply sufficient hypolimnetic O2. Furthermore, all scenarios were modeled twice, once with no seasonal variations and once with simplified seasonal variations of the changing input parameters described in Table 1.
SQ scenario (Status quo continued)
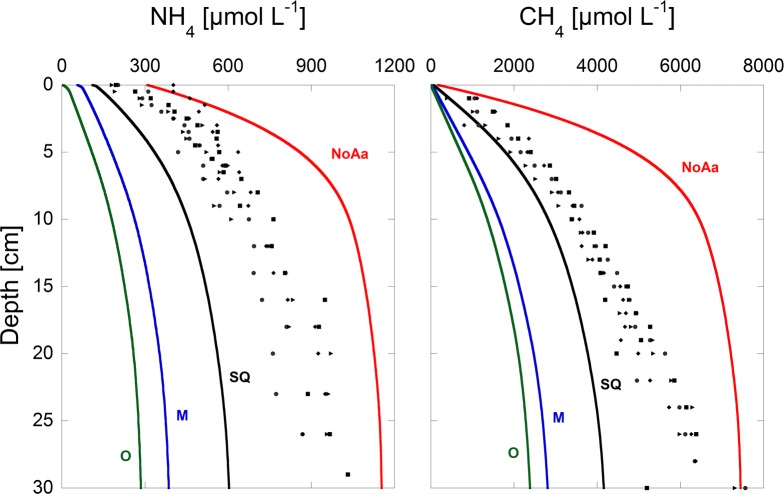
The modeled concentration profiles of NH4+ and CH4 for the year 2050 in the various scenarios are shown in Fig 5.
Fig 5. Modeled CH4 and NH4 porewater concentrations for the year 2050.
The colored lines represent results for the different scenarios: red (no artificial aeration), black (status quo), blue (mesotrophic) and green (oligotrophic). In comparison, the porewater concentrations measured in the year 2015 are plotted with black dots.
In the SQ scenario, NH4+ fluxes are projected to decrease by 8.6% from 2015 to 2050. In contrast, CH4 fluxes (37%) decline more rapidly until 2050. NH4+ is produced during each mineralization step of organic matter, while CH4 is solely the result of methanogenesis, which occurs deeper in the sediment and is fueled by the buried reactive TOC (see Fig 6).
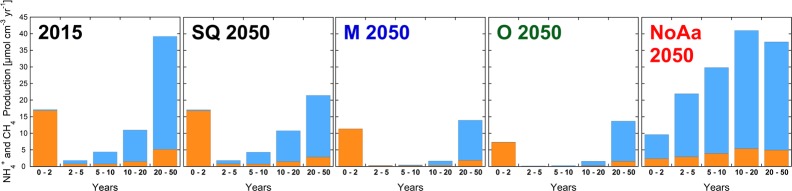
Fig 6. NH4+ (orange) and CH4 (blue) production rates (in μmol cm-3 yr-1) at different sediment depths (split up in layers corresponding to different ages since sediment deposition) for the year 2015, and for the year 2050 in the SQ, M, O and the NoAa scenario.
Note that as the scenarios have different sedimentation rates, the age of the layers at a certain depth differs between the scenarios.
In 2015, the methanogenesis in sediments older than 20 years contributed ~20% of NH4+ production but ~70% of the CH4 production. In contrast, 68% of the NH4+ released from the sediments originate from OM deposited during the last two years and, therefore, its contribution indirectly reflects the current primary production.
By 2050, the contribution to NH4+ and CH4 production by sediments older than 20 years will decrease by ~55%, whereas almost no change in sediments younger than 20 years occurs (see Fig 6). This suggests that the upper sediment strata will remain in quasi steady state with the current TOC gross sedimentation and O2 concentration, while the stock of buried reactive TOC from the era of hypertrophy and anoxia decreases over time (see Fig 7). The SQ assumption shows that the present share of NH4+ and CH4 production from sediments older than 20 years is 53% and will decrease to 39% by the year 2050 (Fig 6) These results are in agreement with previous studies. Matzinger, Müller [7] calculated that in Türlersee and Pfäffikersee, deep buried organic rich sediments (>20 years) contributed up to 29% of the CH4 and NH4+ fluxes from the sediment.
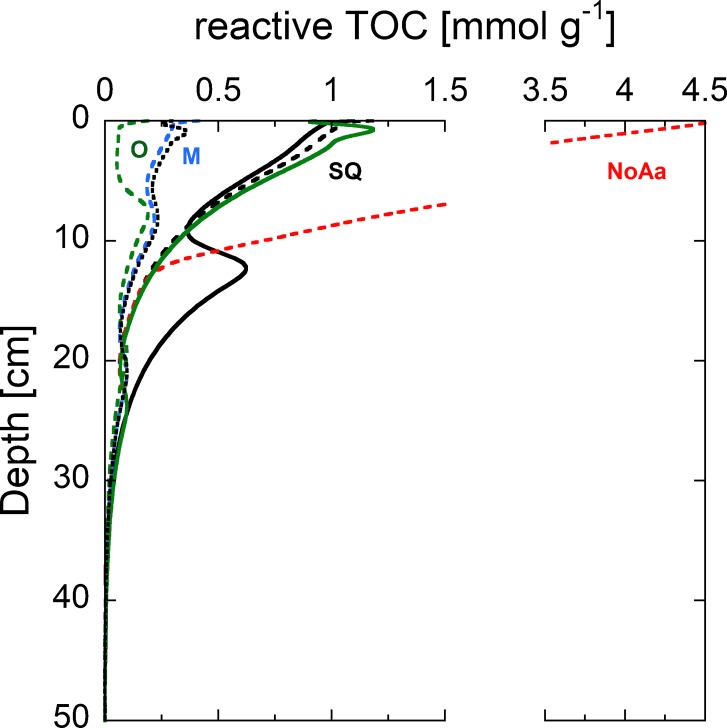
Fig 7. Modeled concentrations of reactive TOC in the different scenarios in 2050 (dashed lines).
The large accumulation of reactive TOC in the NoAa scenario (red dashed) is due to anoxic conditions. The solid black line represents modeled reactive TOC concentrations in 2015 for comparison.
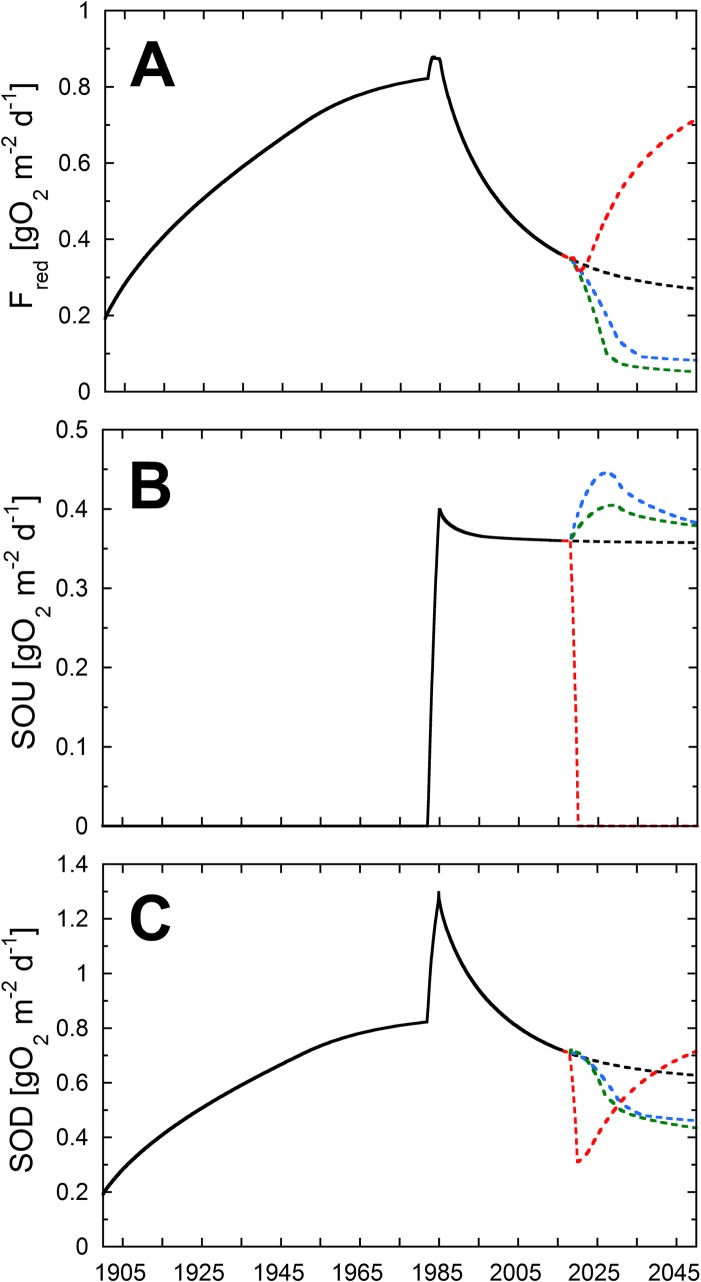
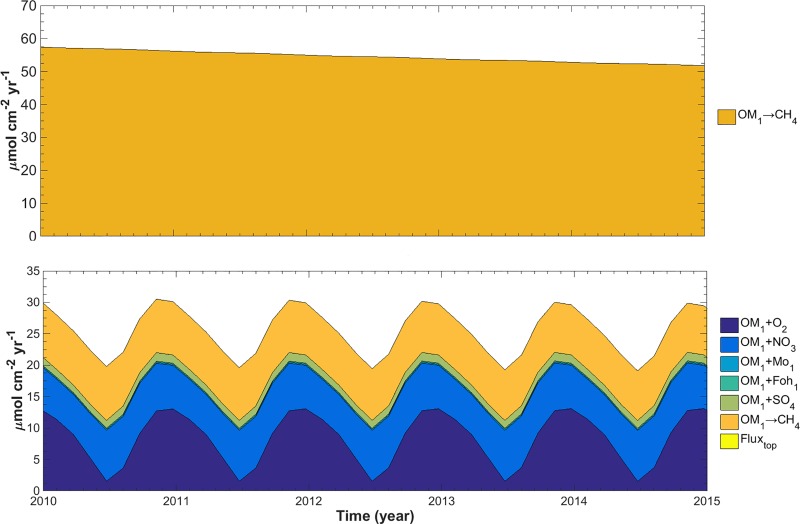
Total Fred will decrease by 23% from 0.35 gO2 m-2 d-1 (2015) to 0.27 gO2 m-2 d-1 (2050) until 2050 (Fig 8A), while SOU remains unchanged at 0.36 gO2 m-2 d-1 (Fig 8B). Hence, SOD will decrease only by 13% until 2050 (see Fig 8C), largely as a consequence of the diminishing pool of reactive TOC.
Fig 8.
(C) O2 consumption by the two O2 sinks Fred (A) and SOU (B) in gO2 m-2 d-1. The solid black line shows the modeled values until 2018. The dashed lines indicate the different modeling scenarios: SQ (black), M (blue), O (green) and NoAa (red).
Reoligotrophication scenarios
The mesotrophic (M) and oligotrophic (O) scenarios consider the potential decrease of DO consumption if further measures for reoligotrophication are implemented in the lake and its catchment. We assumed the TOC flux to be reduced to 60 gC m-2 yr-1 for the M scenario and to 36 gC m-2 yr-1 for the O scenario. Simultaneously, average O2 concentrations are increased from 3.2 mgO2 L-1 (in SQ) to 4.8 mgO2 L-1 (in M) and to 6.4 mgO2 L-1 (in O) over a 12-year period from 2018 to 2030. These changes lead to decreased NH4+ and CH4 production rates in the sediments (Fig 6). Sediment CH4 production decreases by ~58% for both the M and O scenarios compared to the SQ scenario. Interestingly, the eventual CH4 production is not smaller for the O than for the M scenario, probably because already in the mesotrophic state, TEA concentrations are sufficient to mineralize enough TOC and thus minimize the supply for methanogenesis. In contrast to the present state and the SQ scenario, mineralization of reactive TOC is largely completed within the top few centimeters and only a small fraction of reactive TOC is available for methanogenesis deeper in the sediment (see Figs 6 and 7). In both reoligotrophication scenarios, the main fraction of CH4 (88%) originates from sediments older than 20 years. NH4+ production decreases by 38% in the M scenario and by 59% in the O scenario. In contrast to CH4 production, the largest decrease in NH4+ production occurs in the top two centimeters of the sediment and reflects the decreased deposition and increased initial mineralization of OM (see Fig 6).
The NH4+ flux decreases by 43% in the M scenario and by 62% in the O scenario. The CH4 flux decreases to zero in both scenarios, as all upward diffusing CH4 is oxidized within a small oxic layer of the sediment. Consequently, the relative O2 consumption by CH4 oxidation increases from 20% in the SQ to 50% in M scenario to 70% in the O scenario. Although a higher O2 concentration was chosen in the O scenario, the elevated O2 concentration does not increase the SOU rate (see Fig 8B). In fact, SOU rates in the M and O scenarios converge with growing influence of CH4 oxidation as a major O2 sink. Further, the O2 penetration depth (O2 concentration >0.1 μmol L-1) increases from 0.95 mm in the SQ scenario to 4 mm in the O scenario.
While SOU is predicted to increase from 0.36 gO2 m-2 d-1 in 2015 to 0.38 gO2 m-2 d-1 by 2050, Fred decreases from 0.36 gO2 m-2 d-1 to only 0.08 gO2 m-2 d-1 in the M scenario, to 0.05 gO2 m-2 d-1 in the O scenario and only contributes 12% and 18% to SOD, respectively (see Fig 8A and 8B). Hence, in the reoligotrophication scenarios SOD decreases by over 36% and is mainly controlled by SOU and, therefore, by the lake’s current primary production.
No artificial aeration scenario (NoAa)
Without measures to reduce primary production and without artificial hypolimnetic aeration promoting aerobic mineralization of TOC, large amounts of reactive TOC would be buried in the sediments of Lake Baldegg (see Fig 7). Under the resulting anoxic conditions bioturbation rapidly decreases (see Table 1). The high deposition of reactive TOC (see Fig 6) increases the production of NH4+ and CH4 in all sediment depths (see Fig 5). As a result, methanogenesis dominates TOC mineralization in 2050 with up to 93% in contrast to only about 30% in 2015. Furthermore, fluxes of NH4+ and CH4 increase by 23% and 191%. In total, Fred doubles from 0.36 gO2 m-2 d-1 to 0.72 gO2 m-2 d-1 by 2050 (see Fig 8A). The projected increase of the NH4+ flux from the sediments is rather modest due to the increasing concentration of NH4+ in the bottom water (300 μmol L-1). The boundary condition for CH4 was set to 100 μmol L-1, however, we acknowledge that much higher concentrations might be possible. In Lake Rotsee, a highly productive and eutrophic lake, CH4 concentrations reach the gas saturation concentration directly below the sediment surface during summer stagnation, and CH4 is therefore additionally lost to the hypolimnion by bubble formation [33]. SOU obviously is zero during permanent anoxia (see Fig 8B), and SOD consists only of Fred (0.72 gO2 m-2 d-1). However, once aeration is restarted, a large spike in SOD, similar to the spike following the begin of aeration in 1982, is expected to occur. The large TOC pool buried during the anoxic phase (2020–2050) would cause high Fred values for decades (similar to the reactive TOC pool buried during the anoxic phase between 1890 to 1982). This would impede any efforts of ensuing re-oligotrophication measures and artificial aeration.
Seasonal modeling
In the seasonal models, concentrations and fluxes of TOC, NH4+, CH4, Mn(II) and Fe(II) increased during summer stratification, while concentrations of O2, NO3- and SO42- decreased (see Fig 1). Consequently, during the time of the highest TOC deposition rate, the lowest concentrations of TEAs occurred. This resulted in the highest fluxes of Fred at the end of summer stratification (Fig 9) as increasingly more material is degraded anaerobically at that time. Lowest Fred values occurred during winter overturn, where highest O2 concentrations and lowest TOC gross sedimentation prevailed. Hence, during winter overturn the deposited TOC is increasingly exposed to and mineralized by O2 thereby diminishing the storage of OM in the sediment.
Fig 9. Modeled seasonal and average fluxes of CH4 and NH4+ expressed in O2 consumption equivalents (Fred).
While CH4 fluxes (blue) decreased over time as less buried TOC was available for methanogenesis, NH4+ fluxes (green) remained almost constant as they were dominated by the initial steps of anaerobic degradation. Seasonal fluxes of CH4 and NH4+ oscillated due to the seasonally changing prevalence of aerobic and anaerobic degradation.
Since most of the CH4 was produced in the deeper parts of the sediment, its rate was independent of seasonal variations (Fig 10). It decreased only when old deposits of reactive TOC were exhausted. However, seasonal variations of CH4 fluxes are induced by varying O2 penetration depths (see Fig 8). In contrast to CH4, only ~30% of the NH4+ is produced during methanogenesis (Fig 10). Aerobic mineralization of OM (≤ 37%) and dissimilatory reduction of nitrate to ammonium (≤ 27%) together produce up to 64% of NH4+. As O2 concentrations in the hypolimnion decrease during stratification, the production of NH4+ via aerobic mineralization diminishes likewise. The seasonal impact of other TEAs such as NO3-, Fe(III)-(hydr)oxides, Mn(IV)-oxides and SO42- on the overall NH4+ production is negligible. Conversely, the fraction of aerobically degraded TOC increases at the end of each year. In contrast to CH4, both the production and fluxes of NH4+ show distinct seasonal variations (Fig 10).
Fig 10.
Production of CH4 (top) and NH4+ (bottom) for the seasonal SQ model from 2010 to 2015. The colors indicate the pathway of production.
Seasonal variations of fluxes of reduced substances were observed in several lakes [2, 7, 34]. The coincidence of highest TOC gross accumulation and lowest TEA concentrations in the middle of any given year leads to higher accumulation rates of reactive TOC and thus to increased burial of reactive TOC in the sediments (see Fig 11) [12]. However, this effect is only apparent in the seasonal models.
Fig 11. Content of reactive TOC in the sediments in 2050 modeled with average boundary conditions (dotted) and seasonally varying conditions (solid lines) for three different scenarios: SQ (black), M (blue) and O (green) in the middle of the year.
As more reactive TOC is buried, slightly higher fluxes of Fred are encountered in the seasonal models compared to non-seasonal models (see Fig 9). The average Fred modeled for the year 2015 is 0.36 gO2 m-2 d-1 in the SQ scenario, and 0.38±0.03 gO2 m-2 d-1 for the seasonal model. Caused by the seasonal changes in O2 concentrations and aerobic degradation, SOU and consequently SOD show higher variability. Averaged SOD values between 2030 and 2050 in the non-seasonal SQ model are 0.64±0.01 gO2 m-2 d-1, comparable to the 0.63±0.17 gO2 m-2 d-1 of the seasonal SQ model.
In conclusion, simplified seasonal variations of the upper boundary condition cause seasonal variations in the NH4+ production, slightly higher accumulation rates of reactive TOC, variations in Fred, increased SOU and consequently, slightly higher O2 depletion rates. Although the overall impact of seasonal boundary variation is negligible, they are important to explain observed porewater profiles of species such as NH4+, Fe(II) and Mn(II), which have been shown to vary seasonally, especially in the top five centimeters of the sediments (see Fig 2)[2].
Conclusion
A multicomponent early diagenesis model with transient boundary conditions was developed and calibrated using historic observations, monitoring data and recent state of the art porewater data from the eutrophic and artificially aerated Lake Baldegg. The model was applied to simulate four different management scenarios, including a continuation of the status quo, two re-oligotrophication scenarios, and a scenario where lake aeration is stopped. Simulations with seasonal boundary conditions yielded similar O2 depletion rates as the non-seasonal model, implying that it is not necessary to consider seasonality and thus increase computation time for long-term projections of sediment oxygen demand.
All modeled scenarios show the direct impact of the TOC gross sedimentation rate and the bottom water O2 concentration on the hypolimnetic O2 depletion rates. While the upper boundary O2 concentration is doubled between the scenarios (SQ to O), the sediment oxygen uptake (SOU) differs only slightly. However, less reactive TOC is buried which significantly decreases Fred. Although older sediments (deposited during the hypertrophic and anoxic period) dominate Fred due to methanogenesis, this “sediment memory effect” [7] or “legacy carbon effect” [6] is overcome once primary production decreases. This is shown in both reoligotrophication scenarios, where SOD is mostly controlled by SOU. Interestingly, already a change to mesotrophic production yields a SOD rate comparable to a low productive state. Hence, with an adequate O2 concentration, a return to mesotrophic productivity could be sufficient for a long-term decline of SOD. In contrast, a termination of the aeration program without measures to decrease TOC gross sedimentation would yield long-lasting damaging effects on the O2 consumption in the hypolimnion of Lake Baldegg as large amounts of buried reactive TOC would lead to a high production of CH4 and NH4+ and eventually to hypolimnetic conditions similar to the anoxic phase between 1885 and 1982.
Supporting information
Mass balances of carbon (top) and nitrogen (bottom). The individual fluxes into the sediment are calculated through their respective upper boundary conditions. The fluxes out of the sediment at bottom are defined as the sediment strata that is moved out of the active modelled area.
(TIF)
(DOCX)
Please note that for each transformed om1, the Redfield ratio equivalent of 106 carbons are liberated. L is used as a rate limitation constant in each reaction.
(DOCX)
Acknowledgments
We thank Robert Lovas (Environment and Energy, Canton of Lucerne) for providing data of Lake Baldegg. Arno Stöckli (Dept. for the Environment, Canton of Aargau) is acknowledged for providing monitoring data of Lake Hallwil. We thank the reviewers for improving the manuscript. This work was financially supported by SNF Grant 200021_146234.
Data Availability
All files for the model are uploaded at the Eawag Page (https://www.eawag.ch/fileadmin/Domain1/Abteilungen/surf/projekte/medialab/medialab.zip) While the data for the model can be found here: https://doi.org/10.6084/m9.figshare.5170687.
Funding Statement
The study was funded by supported by Swiss National Fund (SNF) Grant 200021_146234. The funder provided support in the form of salaries for authors Dr. Thomas Steinsberger, Dr. Babak Shafei and Dr. Christoph Gerber, but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The specific roles of these authors are articulated in the ‘author contributions’ section. AquaRNG did not play a role in the funding or conception nor handling of the project.
References
- 1.Schwefel R, Steinsberger T, Bouffard D, Bryant LD, Müller B, Wüest A. Using small-scale measurements to estimate hypolimnetic oxygen depletion in a deep lake. Limnol Oceanogr. 2018;63(S1):S54–S67. 10.1002/lno.10723. [DOI] [Google Scholar]
- 2.Steinsberger T, Schmid M, Wüest A, Schwefel R, Wehrli B, Müller B. Organic carbon mass accumulation rate regulates the flux of reduced substances from the sediments of deep lakes. Biogeosciences. 2017;14(13):3275–85. 10.5194/bg-14-3275-2017. [DOI] [Google Scholar]
- 3.Müller B, Bryant LD, Matzinger A, Wüest A. Hypolimnetic oxygen depletion in eutrophic lakes. Environ Sci Technol. 2012;46(18):9964–71. 10.1021/es301422r [DOI] [PubMed] [Google Scholar]
- 4.Sweerts J-PR, Baer-Gilissen MJ, Cornelese AA, Cappenberg TE. Oxygen-consuming processes at the profundal and littoral sediment-water interface of a small meso-eutrophic lake(Lake Vechten, The Netherlands). Limnol Oceanogr. 1991;36(6):1124–33. 10.4319/lo.1991.36.6.1124. [DOI] [Google Scholar]
- 5.Martin P, Goddeeris B, Martens K. Oxygen concentration profiles in soft sediment of Lake Baikal (Russia) near the Selenga delta. Freshwat Biol. 1993;29(3):343–9. 10.1111/j.1365-2427.1993.tb00768.x. [DOI] [Google Scholar]
- 6.Carey CC, Doubek JP, McClure RP, Hanson PC. Oxygen dynamics control the burial of organic carbon in a eutrophic reservoir. Limnology and Oceanography Letters. 2018. 10.1002/lol2.10057. [DOI] [Google Scholar]
- 7.Matzinger A, Müller B, Niederhauser P, Schmid M, Wüest A. Hypolimnetic oxygen consumption by sediment-based reduced substances in former eutrophic lakes. Limnol Oceanogr. 2010;55(5):2073–84. 10.4319/lo.2010.55.5.2073. [DOI] [Google Scholar]
- 8.Van Cappellen P, Wang Y. Cycling of iron and manganese in surface sediments; a general theory for the coupled transport and reaction of carbon, oxygen, nitrogen, sulfur, iron, and manganese. Am J Sci. 1996;296(3):197–243. 10.2475/ajs.296.3.197 [DOI] [Google Scholar]
- 9.Couture R-M, Shafei B, Van Cappellen P, Tessier A, Gobeil C. Non-Steady State Modeling of Arsenic Diagenesis in Lake Sediments. Environ Sci Technol. 2010;44(1):197–203. 10.1021/es902077q [DOI] [PubMed] [Google Scholar]
- 10.Dittrich M, Wehrli B, Reichert P. Lake sediments during the transient eutrophication period: Reactive-transport model and identifiability study. Ecol Model. 2009;220(20):2751–69. 10.1016/j.ecolmodel.2009.07.015. [DOI] [Google Scholar]
- 11.Couture R-M, Fischer R, Van Cappellen P, Gobeil C. Non-steady state diagenesis of organic and inorganic sulfur in lake sediments. Geochim Cosmochim Acta. 2016;194:15–33. 10.1016/j.gca.2016.08.029. [DOI] [Google Scholar]
- 12.Sobek S, Durisch-Kaiser E, Zurbrügg R, Wongfun N, Wessels M, Pasche N, et al. Organic carbon burial efficiency in lake sediments controlled by oxygen exposure time and sediment source. Limnol Oceanogr. 2009;54(6):2243–54. 10.4319/lo.2009.54.6.2243. [DOI] [Google Scholar]
- 13.Koretsky CM, Haas JR, Miller D, Ndenga NT. Seasonal variations in pore water and sediment geochemistry of littoral lake sediments(Asylum Lake, MI, USA). Geochem Trans. 2006;7(11). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Moosmann L, Gächter R, Müller B, Wüest A. Is phosphorus retention in autochthonous lake sediments controlled by oxygen or phosphorus? Limnol Oceanogr. 2006;51(1):763–71. [Google Scholar]
- 15.Lotter AF, Sturm M, Teranes JL, Wehrli B. Varve formation since 1885 and high-resolution varve analyses in hypertrophic Baldeggersee (Switzerland). Aquat Sci. 1997;59(4):304–25. 10.1007/bf02522361. [DOI] [Google Scholar]
- 16.Schaller T, Moor HC, Wehrli B. Sedimentary profiles of Fe, Mn, V, Cr, As and Mo as indicators of benthic redox conditions in Baldeggersee. Aquat Sci. 1997;59(4):345–61. 10.1007/BF02522363. [DOI] [Google Scholar]
- 17.Aguilera DR, Jourabchi P, Spiteri C, Regnier P. A knowledge‐based reactive transport approach for the simulation of biogeochemical dynamics in Earth systems. Geochem Geophys Geosyst. 2005;6(7). 10.1029/2004GC000899. [DOI] [Google Scholar]
- 18.Boudreau BP. Diagenetic models and their implementation: modelling transport and reactions in aquatic sediments: Springer, New York; 1997. [Google Scholar]
- 19.Katsev S, Dittrich M. Modeling of decadal scale phosphorus retention in lake sediment under varying redox conditions. Ecol Model. 2013;251:246–59. 10.1016/j.ecolmodel.2012.12.008. [DOI] [Google Scholar]
- 20.Katsev S, Tsandev I, L'Heureux I, Rancourt DG. Factors controlling long-term phosphorus efflux from lake sediments: Exploratory reactive-transport modeling. Chem Geol. 2006;234(1):127–47. 10.1016/j.chemgeo.2006.05.001. [DOI] [Google Scholar]
- 21.Müller B, Wang Y, Dittrich M, Wehrli B. Influence of organic carbon decomposition on calcite dissolution in surficial sediments of a freshwater lake. Water Res. 2003;37(18):4524–32. 10.1016/S0043-1354(03)00381-6 [DOI] [PubMed] [Google Scholar]
- 22.Epping EH, Helder W. Oxygen budgets calculated from in situ oxygen microprofiles for Northern Adriatic sediments. Cont Shelf Res. 1997;17(14):1737–64. 10.1016/S0278-4343(97)00039-3. [DOI] [Google Scholar]
- 23.Schaller T, Moor HC, Wehrli B. Reconstructing the iron cycle from the horizontal distribution of metals in the sediment of Baldeggersee. Aquat Sci. 1997;59(4):326–44. 10.1007/BF02522362. [Google Scholar]
- 24.Canfield DE, Thamdrup B. Towards a consistent classification scheme for geochemical environments, or, why we wish the term ‘suboxic’ would go away. Geobiology. 2009;7(4):385–92. 10.1111/j.1472-4669.2009.00214.x [DOI] [PubMed] [Google Scholar]
- 25.Wehrli B, Lotter A, Schaller T, Sturm M. High-resolution varve studies in Baldeggersee (Switzerland): project overview and limnological background data. Aquat Sci. 1997;59(4):285–94. 10.1007/BF02522359. [DOI] [Google Scholar]
- 26.Gächter R, Wehrli B. Ten years of artificial mixing and oxygenation: no effect on the internal phosphorus loading of two eutrophic lakes. Environ Sci Technol. 1998;32(23):3659–65. [Google Scholar]
- 27.Schaller T, Wehrli B. Geochemical-focusing of manganese in lake sediments—An indicator of deep-water oxygen conditions. Aquatic Geochemistry. 1996;2(4):359–78. 10.1007/BF00115977. [DOI] [Google Scholar]
- 28.Bloesch J, Uehlinger U. Horizontal sedimentation differences in a eutrophic Swiss lake. Limnol Oceanogr. 1986;31(5):1094–109. 10.4319/lo.1986.31.5.1094. [DOI] [Google Scholar]
- 29.Berg P, Rysgaard S, Thamdrup B. Dynamic modeling of early diagenesis and nutrient cycling. A case study in an artic marine sediment. Am J Sci. 2003;303(10):905–55. 10.2475/ajs.303.10.905 [Google Scholar]
- 30.Norði Kà, Thamdrup B, Schubert CJ. Anaerobic oxidation of methane in an iron-rich Danish freshwater lake sediment. Limnol Oceanogr. 2013;58(2):546–54. 10.4319/lo.2013.58.2.0546. [DOI] [Google Scholar]
- 31.Beal EJ, House CH, Orphan VJ. Manganese- and Iron-Dependent Marine Methane Oxidation. Science. 2009;325(5937):184–7. 10.1126/science.1169984 [DOI] [PubMed] [Google Scholar]
- 32.Smemo KA, Yavitt JB. Evidence for Anaerobic CH 4 Oxidation in Freshwater Peatlands. Geomicrobiol J. 2007;24(7–8):583–97. 10.1080/01490450701672083. [DOI] [Google Scholar]
- 33.Schubert CJ, Diem T, Eugster W. Methane Emissions from a Small Wind Shielded Lake Determined by Eddy Covariance, Flux Chambers, Anchored Funnels, and Boundary Model Calculations: A Comparison. Environ Sci Technol. 2012;46(8):4515–22. 10.1021/es203465x [DOI] [PubMed] [Google Scholar]
- 34.Urban NR, Dinkel C, Wehrli B. Solute transfer across the sediment surface of a eutrophic lake: I. Porewater profiles from dialysis samplers. Aquat Sci. 1997;59(1):1–25. 10.1007/BF02522546. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Mass balances of carbon (top) and nitrogen (bottom). The individual fluxes into the sediment are calculated through their respective upper boundary conditions. The fluxes out of the sediment at bottom are defined as the sediment strata that is moved out of the active modelled area.
(TIF)
(DOCX)
Please note that for each transformed om1, the Redfield ratio equivalent of 106 carbons are liberated. L is used as a rate limitation constant in each reaction.
(DOCX)
Data Availability Statement
All files for the model are uploaded at the Eawag Page (https://www.eawag.ch/fileadmin/Domain1/Abteilungen/surf/projekte/medialab/medialab.zip) While the data for the model can be found here: https://doi.org/10.6084/m9.figshare.5170687.