Changes in the relationship between zooplankton and phytoplankton biomasses across a eutrophication gradient

Abstract

The relationship between zooplankton biomass and phytoplankton biomass can provide insight into the structure and function of lake biological communities. We used a Bayesian network model to analyze a continental-scale data dataset to estimate changes in the relationship between zooplankton (Z) and phytoplankton (P) biomasses along a eutrophication gradient. The Bayesian network model allowed us to combine two different measurements of phytoplankton biomass (chlorophyll a concentration and directly observed biovolume) to improve the precision of estimates of true biomass within each sample. The model also allowed us to estimate separate relationships between P and zooplankton abundance and between P and mean individual zooplankton biomass and then to combine these two relationships into an estimate of seasonal mean zooplankton biomass. The resulting analysis indicated that seasonal mean zooplankton biomass increased proportionally with phytoplankton biomass in oligotrophic lakes, yielding a constant ratio between Z and P and suggested that bottom-up forces determined zooplankton biomass in these systems. In eutrophic lakes, seasonal mean zooplankton biomass was nearly constant with increases in phytoplankton biomass, yielding a decrease in the ratio between Z and P with increasing eutrophication. Bottom-up forces, as quantified by an increase in the proportion of cyanobacteria, accounted for approximately one fifth of the residual variance in the model as the relationship between Z and P changed from direct proportionality in oligotrophic lakes to the nearly constant value of Z observed in eutrophic lakes, suggesting that a combination of both top-down and bottom-up forces likely determined zooplankton biomass in eutrophic lakes.

Introduction

Quantifying biomass ratios between different trophic levels (Elton 1927) and understanding the mechanisms that determine these ratios may help determine other important ecosystem attributes (e.g., Duffy 2003) and potentially quantify the effects of human activities on ecosystem function. For example, human activities can often remove top predators from an ecosystem, and the cascading effects of the loss in the biomass of apex predators can differ among ecosystems depending on the characteristics of the food web (e.g., Ripple et al. 2014; Rizzari et al. 2015). A number of studies have explored the factors that influence biomass ratios within and among different ecosystems. For example, some researchers have suggested that the consistency of relationships between heterotroph and autotroph biomasses among different ecosystems along productivity gradients reflects the same basic underlying processes (Hatton et al. 2015). Conversely, others have observed that differences in the relationships between heterotroph and autotroph biomasses among ecosystems can be attributed to differences in the nutritional quality of producers (Cebrian et al. 2009). The shape of biomass pyramids have also been discussed in the context of size spectra and metabolic scaling theory (Trebilco et al. 2013).

Studies of biomass ratios are common in lakes, where ratios between zooplankton and phytoplankton biomasses (Z:P) have been observed to decrease along a eutrophication gradient (e.g., Leibold et al. 1997), similar to observations in marine systems (Gasol et al. 1997). The reasons for this change have been debated but most mechanisms can be described in terms of the either top-down or bottom-up forces (Leroux and Loreau 2015). Bottom-up forces include changes in resource levels, such as nutrients, that change phytoplankton biomass, whereas top-down forces describe predation pressure from higher trophic levels. For zooplankton in particular, bottom-up forces include changes in the quantity and quality of the phytoplankton assemblage (Filstrup et al. 2014), and top-down forces include the effects of planktivore fish on zooplankton biomass (Jeppesen et al. 2003). Because eutrophication is one of the main effects of human activities on lakes, a clear understanding of how this critical link between phytoplankton and zooplankton changes along the eutrophication gradient is important for informing environmental management decisions.

Underlying these discussions is the empirical quantification of Z:P from field data and the specific analysis used to estimate changes in Z:P along the eutrophication gradient. In particular, existing observations that Z:P decreases along the eutrophication gradient may not fully appreciate subtle changes in this relationship that may occur along the gradient owing to at least two factors. First, field data sets that have been used to quantify Z:P have spanned different sections of the eutrophication gradient, such as data collected primarily in eutrophic lakes (Heathcote et al. 2016) or data collected primarily in oligotrophic lakes (del Giorgio and Gasol 1995; Hessen et al. 2006). Some data sets have been assembled from different surveys (McCauley and Kalff 1981; Hanson and Peters 1984; Leibold et al. 1997; Jeppesen et al. 2003), but a single data set collected with consistent sampling protocols with a sufficient sampling density to examine relationships across the full eutrophication gradient has thus far not been available. Second, estimates of Z:P are complicated by the fact that substantial uncertainty accompanies measurements of both zooplankton and phytoplankton biomass. Some analyses have accounted for this uncertainty by using type II regression to estimate the relationship between Z and P while accounting for uncertainty in both predictor and response variables (McCauley and Kalff 1981; Heathcote et al. 2016). Regardless of the estimation method, though, the uncertainty in the measurements may have restricted analyses to only estimating linear relationships between log-transformed Z and P. These linear models have precluded the possibility of observing changes in this relationship along the eutrophication gradient.

Here, we describe a hierarchical Bayesian analysis of a continental scale data set of zooplankton and phytoplankton biomasses. These data were collected from lakes and reservoirs across the conterminous United States by the 2012 National Lakes Assessment (NLA). The broad spatial extent of the sampling frame ensured that lakes spanning the eutrophication gradient were included in the analysis, while the Bayesian models provided the means of accounting for and propagating the effects of measurement errors consistently through the analysis. In conducting this analysis, we attempt to answer the question of whether the functional form of Z:P changes over the eutrophication gradient, and whether these changes are consistent with current understanding regarding the relative strength of bottom-up effects on zooplankton biomass.

Methods and Materials

Data

We analyzed data collected by the NLA in the summer (May-September) of 2012. The NLA consists of a random sample of lakes from the continental United States. Lakes greater than 1 ha were selected from the contiguous United States using a stratified randomized sampling design (US EPA 2011). The final data set was supplemented by approximately 100 hand-picked lakes and reservoirs that were identified a priori as being less disturbed by human activities. These additional lakes were included to increase the number of least-disturbed lakes for which data were available and to help ensure that the full range of conditions was sampled. The overall sampling design of the NLA was synoptic, but 10% of sampled lakes were randomly selected and resampled on a different day after the initial visit. The timing of the second visit varied among lakes, but on average, the second sample was collected approximately 46 days after the first.

During each visit to a selected lake, an extensive set of abiotic and biological variables was measured. Only brief details on sampling protocols are provided here regarding the parameters used in the analysis; more extensive descriptions of sampling methodologies are available (US EPA 2011). At each lake, a sampling location was established in open water at the deepest point of each lake (up to a maximum depth of 50 m) or in the mid-point of reservoirs. An additional sampling location for collection of phytoplankton and chl a data was established in the littoral zone approximately 10 m out from a randomly selected point on the shoreline.

At the open water site, a water sample was collected using a vertical, depth-integrated methodology that collected water from the photic zone of the lake (to a maximum depth of 2 m). Multiple sample draws were combined in a rinsed, 4 liter (L) Cubitainer, which when full, was gently inverted to mix the water. A 1L aliquot of this water was poured off for the phytoplankton sample. A 2L subsample was poured into a rinsed brown bottle for a chl a sample. Chl a samples were filtered on glass fiber filters in the field and sent to a centralized lab, where samples were processed in a 90% acetone extraction analysis with fluorometry (US EPA 2012). Two zooplankton samples were also collected from the same open water location with vertical tows for a cumulative tow length of 5 m using fine (50 μm) and coarse (150 μm) mesh Wisconsin nets. In lakes that were at least 7 m deep, one 5 m deep tow was collected with each mesh. In shallower lakes, vertical tows over shorter depths were combined to reach the cumulative tow length of 5 m. At the littoral zone site, grab water samples were collected 0.3 m below the surface at a depth of at least 1 m, where a chl a sample was collected in a 2L brown bottle and a phytoplankton sample was collected in a 1L bottle. These grab samples were used to quantify chl a concentration and phytoplankton biovolume in the littoral zone.

Phytoplankton biovolume was measured from the field samples in the laboratory. Samples collected from both open water and littoral zone locations where examined by taxonomists, who identified at least 400 natural algal units to species under 1000× magnification. Observations were aggregated and abundance was calculated as cells per mL. In each sample, the dimensions of the taxa that accounted for the largest proportions of the observed assemblage were measured and used to estimate biovolume. Biovolumes of the most abundant taxa were based on the average of measurements from at least 10 individuals, while biovolumes for less abundant taxa were based on somewhat fewer measurements. The biovolume was reported as μm³/mL (US EPA 2012), which we converted to mm³/L. Approximately 5% of the phytoplankton samples were randomly selected and re-identified and measured by a second taxonomy lab. These re-identified samples provided a basis for estimating lab measurement error.

Zooplankton samples from the coarse and fine mesh net tows were processed separately. In each sample, zooplankton specimens were examined and counted under 100 – 1000× magnification, in discrete subsamples until at least 400 individuals were identified. In the coarse mesh net samples, all taxa were identified and enumerated. In the fine mesh net, only “small” taxa were identified and enumerated (Cladocera < 0.2 mm long, copepods < 0.6 mm long, rotifers, and nauplii). Zooplankton abundance was estimated based on the volume of sampled lake water that was used to identify the targeted count of 400 individuals. Measurements of at least 20 individuals were collected for dominant taxa (i.e., taxa encountered at least 40 times in the subsample), at least 10 individuals were measured for taxa that were encountered from 20 – 40 times, and at least 5 individuals were measured for rare taxa (encountered less than 20 times in the subsample). Zooplankton biomass estimates were based on existing length and width relationships (Dumont et al. 1975; McCauley 1984; Lawrence et al. 1987). Estimates from the coarse and fine mesh samples were combined to yield a single zooplankton sample per lake visit that was used in this analysis.

Lake physical characteristics were estimated from mapped data. These characteristics included lake surface area, geographic location (latitude and longitude), elevation, lake catchment area, and lake perimeter. From these characteristics, the following composite variables were calculated: (1) the shoreline development (SLD), which is defined as the ratio between the perimeter of the lake and the perimeter of a circle with the same area as the lake and characterizes the geometric complexity of the lake shore; and (2) the lake geometry ratio, which is defined as Area^0.25/Depth, or the ratio between fetch and lake maximum depth, and has been shown to differentiate lakes that stratify seasonally (low values of the geometry ratio) from lakes that are polymictic (Gorham and Boyce 1989). Variables quantifying the mean annual precipitation (Precip) and mean annual air temperature at the lake location were extracted from 30-year averaged climatic data (Daly et al. 2008).

Statistical analysis

We focused our analysis on deep lakes (defined here as lakes with maximum depth greater than 4 m, Padisák and Reynolds 2003) because of differences in how we expected zooplankton and phytoplankton relationships to manifest in shallow lakes owing to potentially stronger linkages between the benthic and pelagic communities (Vadeboncoeur et al. 2002; Benndorf et al. 2002; Scheffer and van Nes 2007).

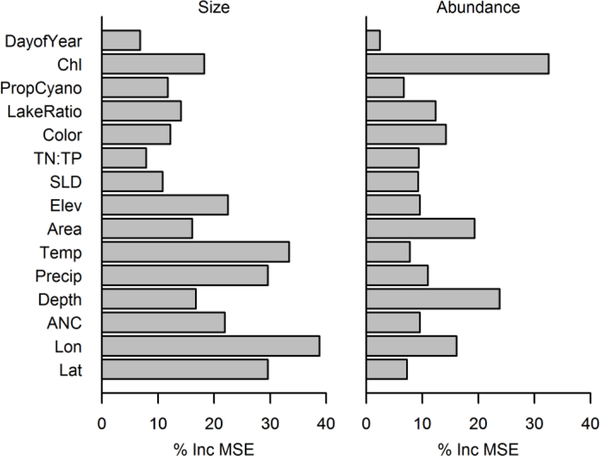
We first identified variables that were most strongly associated with zooplankton mean individual size and abundance using a random forest model (Breiman 2001). For this initial exploratory analysis, we calculated mean values of these two measures of zooplankton over all available samples collected at each lake, and then matched these summary measures to candidate predictors. Predictors included sampling day, lake geographic location (latitude and longitude, and elevation), morphology (i.e., depth, surface area, shoreline development, and lake geometry ratio), climate (i.e., mean annual temperature and precipitation), color, alkalinity, and phytoplankton biomass (quantified initially here as chl a concentration). For simplicity in this exploratory analysis chl a concentration was used as a proxy for phytoplankton biovolume, whereas both phytoplankton biovolume measurements and chl a were used in the final model to estimate true phytoplankton (see below). A random forest model was then fit using these predictors for each of the zooplankton measurements. Variable importance (defined as the increase in mean squared prediction error observed when a variable was randomly permuted) then provided insights into which of the candidate predictors best accounted for observed variability in the two zooplankton measurements.

Based on the insights from exploratory analysis, we specified a Bayesian network model to estimate the relationship between phytoplankton and zooplankton biomass (Figure 1). A Bayesian network provides a unified framework for modeling the cascading relationships between different measurements and propagates estimation errors and model uncertainty correctly throughout the model. Different components of the network model addressed different challenges inherent in the data. First, the model estimated mean phytoplankton biomass based on both chl a concentration and measurements of phytoplankton biomass. These two measurements provided independent estimates of phytoplankton biomass, each with different sources of error. Chl a is measured precisely from field samples, but the chl a content of phytoplankton can vary depending on environmental conditions and species composition (Kasprzak et al. 2008), such that a measured chl a concentration in one sample may indicate a slightly different phytoplankton biomass from the same chl a measured in another sample. Hence, we modeled chl a concentration as being directly proportional to the true phytoplankton biomass in the sample (P_samp), but allowed the constant of proportionality, b, (i.e., the chl a content of phytoplankton in a sample) to vary among samples. The log-transformed version of this model equation is as follows:

$$\log \left(ch{l}_i\right)=\log \left(P_{samp,i}\right)+\log \left(b_i\right)$$

$$\log \left(b_i\right)=Normal\left({\mu }_b, {\sigma }_b\right)$$

Where we assume that the value of b_i for each sample, i, is drawn from a single log-normal distribution characterized by a mean, μ_b, and a standard deviation, σ_b. This multilevel expression of the model equation allows the mean chl a content of phytoplankton cells for each sample to vary, but imposes the constraint that the estimates of phytoplankton chl a content for each sample must be drawn from a common log-normal distribution (Gelman and Hill 2007).

Figure 1.

Schematic representation of Bayesian network model. Shaded ovals indicate available measurements. Rectangles indicate model-estimated variables.

Direct measurements of phytoplankton biomass provide an unbiased estimate of true phytoplankton biomass. However, these direct measurements are acquired by summing contributions from measurements taken from many different phytoplankton specimens, each of which includes measurement error. Hence, the summed estimate of total biomass includes a substantial amount of measurement error. We modeled this measurement error explicitly, expressing a second estimate of the true phytoplankton biomass in a sample as follows:

$$\log \left(P_{obs,i}\right)=\log \left(P_{samp,i}\right)+e_{1,i}$$

Where P_obs,i is the observed phytoplankton biomass in sample i and e_1,i is drawn from a log-normally distributed measurement error with a mean value of zero. The standard deviation of the values of e_1,i are quantified using lab replicate measurements of phytoplankton biomass. Final model estimates of P_samp,i are then consistent with both chl a and observed phytoplankton biovolume, and by combining these two measurements, we maximized the accuracy of this final estimate.

P_samp,i estimates phytoplankton biomass within a single sample, but to model the relationship between phytoplankton and zooplankton biomass, we were interested in seasonal mean values of phytoplankton biomass for each lake. To estimate seasonal mean phytoplankton biomass, we used model estimates of P_samp,i corresponding to measurements collected at the same lake on different days and corresponding to measurements collected on the same day in the littoral zone and in the middle of the lake to provide a final estimate of the combined magnitude of temporal and sampling variability. Seasonal mean phytoplankton (P) can then be expressed as follows:

$$\log \left(P_{samp,i}\right)=\log \left(P_{j\left[i\right]}\right)+e_{2,j}$$

$$\log \left(P_j\right)=Normal\left({\mu }_P, {\sigma }_P\right)$$

Where j indexed different lakes, e_2,j is drawn from a log-normally distributed error term representing temporal and sampling variations in P_samp,i about the seasonal mean value. The distribution of seasonal mean phytoplankton concentrations among all sites was then modeled as a log-normal distribution with mean, μ_P, and standard deviation, σ_P.

To model seasonal mean zooplankton biomass, we first expressed biomass as the product of sample mean individual zooplankton size (S) and zooplankton abundance (A):

$$\log \left(Z_j\right)=\log \left(S_j\right)+\text{log}\left(A_j\right)$$

Where j again indexes different lakes. We then modeled seasonal mean individual zooplankton size and abundance as different functions of phytoplankton biomass:

$$\log \left(S_j\right)=d_1+d_2\log \left(P_j\right)+e_{3,j}$$

$$\log \left(A_j\right)=g\left(P_j\right)+e_{4,j}$$

Where, based on exploratory analysis, log-transformed seasonal mean zooplankton size is modeled as a linear function of log-transformed seasonal mean phytoplankton. In contrast, exploratory analysis suggested that zooplankton abundance was best modeled with a “bent-cable” model, represented here as g(.), in which two linear segments are connected by a quadratic section that smoothly blends with the slopes of the linear sections where they meet (Chiu et al. 2006). The random errors, e_3,j and e_4,j are drawn from log-normal distributions and quantify uncertainty in the modeled relationships between mean phytoplankton biovolume and zooplankton size and between phytoplankton biovolume and zooplankton abundance.

Observed values of zooplankton abundance and biomass are then related to the estimated mean values:

$$\log \left(A_{obs,i}\right)=\log \left(A_{j\left[i\right]}\right)+e_{5,i}$$

$$\log \left(Z_{obs,i}\right)=\log \left(Z_{j\left[i\right]}\right)+e_{6,i}$$

Similar to the model equations for phytoplankton, variability in the observations of zooplankton abundance and biomass relative to estimated mean values are quantified with log-normally distributed error terms (e₅ and e₆). These error terms included contributions from temporal, sampling, and measurement error.

All of the model equations were fit simultaneously to data collected at each lake, including revisits on different days, littoral and mid-lake samples, and lab replicates of phytoplankton measurements using Stan (Stan Development Team 2016). Weakly informative priors were specified for all model parameters (Gelman 2006).

Results

Data from 621 lakes that were at least 4 m deep were available with both zooplankton and phytoplankton measurements. Of these, 55 lakes were resampled on a different day. Chl a concentrations and observed phytoplankton biovolume were measured in samples collected at both the center of the lake and at the littoral site during each visit, so 1341 measurements were available. An additional 71 lab replicate measurements of phytoplankton biovolume were available to quantify measurement error. Summaries of the observed data are shown in Table 1.

Table 1.

Summary statistics for NLA observations.

	5th %tile	25th %tile	Median	75th %tile	95th %tile
Zooplankton biomass (μg/L)	6.55	27.8	79.2	160.0	583.9
Zooplankton abundance (ind/L)	32	127	284	603	1768
Phytoplankton biovolume (mm3/L)	0.10	0.50	1.39	4.00	19.9
Chl a (μg/L)	0.7	2.1	4.8	13.1	53.9

Different predictor variables were identified as important by random forest models for zooplankton mean individual biomass and for zooplankton abundance (Figure 2). Zooplankton abundance was most strongly predicted by chl a concentration, followed by lake depth. In contrast, the mean biomass of zooplankton individuals was best predicted by physical lake characteristics such as geographic location, mean annual temperature, mean annual precipitation, elevation, and acid neutralizing capacity.

Figure 2.

Importance of different variables in predicting zooplankton size (mean individual biomass) and abundance. Abbreviations for variables are as follows: LakeRatio: lake geometry ratio, SLD: shoreline development ratio, Elev: elevation, Area: lake surface area, Temp: mean annual air temperature, Precip: mean annual precipitation, ANC: acid neutralizing capacity, Lon: longitude, Lat: latitude, DayofYear: sampling day of year, Chl: chlorophyll a concentration, PropCyano: proportion cyanobacteria.

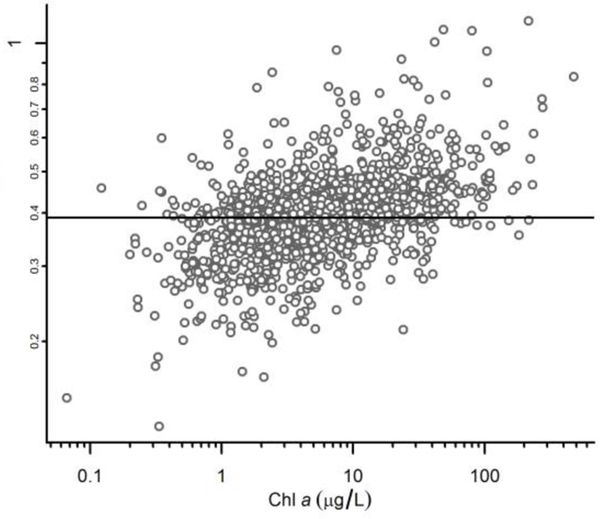
Results from the Bayesian model indicated that estimated true phytoplankton biovolume within each sample was much more strongly associated with chl a concentration than with observed phytoplankton biovolume, owing to the high measurement error associated with measured phytoplankton biovolume (Figure 3). Variance in laboratory replicate measurements accounted for 38% of the total variance in observed phytoplankton biovolume, a percentage that was somewhat less than the variance attributed to differences in seasonal means among sites (56%) and much greater than the percentage of variance attributed to temporal and sampling variability (6%). For simplicity, we estimated phytoplankton biomass by using a conversion factor of 1 g/mL biovolume, similar to recommended value of 1.1 (Holmes et al. 1969). Based on this conversion, the median chl a content in phytoplankton was 0.39%. 90% of the estimates of chl a content for different samples were between 0.20% and 0.77%. Estimated chl a content in phytoplankton increased systematically along the eutrophication gradient (Figure 4). The combination of low measurement error and a relatively low range of mean phytoplankton chl a content yielded a more precise predictor of true phytoplankton biovolume than the direct observations of phytoplankton biovolume.

Figure 3.

Estimated true phytoplankton biovolume versus chl a and observed phytoplankton biovolume. Solid line in left panel shows mean relationship between chl a and true phytoplankton biovolume. Solid line in right panel shows 1:1 relationship.

Figure 4.

Estimated mean sample chlacontent of phytoplankton versus chlaconcentration. Horizontal line shows the overall mean chlacontent of 0.39%.

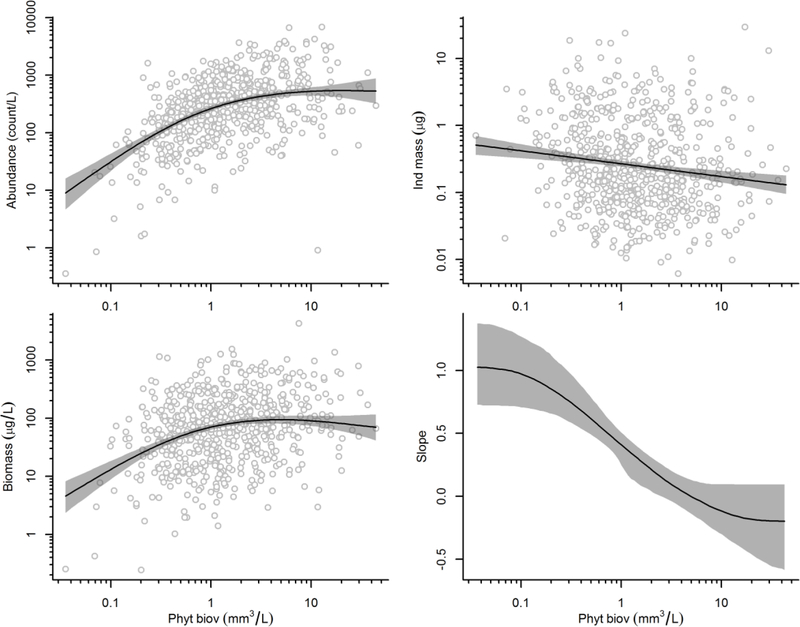
Zooplankton abundance increased with increasing phytoplankton biovolume, but at biovolumes exceeding | 3 mm³/L, only minimal increases in zooplankton abundance were observed (Figure 5). Mean individual zooplankton biomass decreased weakly with increasing phytoplankton biovolume. Zooplankton biomass mirrored the patterns observed with abundance, increasing at low levels of phytoplankton biovolume, but leveling out to a nearly constant value at high levels of phytoplankton biovolume. Another approach to considering changes between zooplankton biomass and phytoplankton biovolume is to examine the estimated slope of the relationship. The estimated slope of the relationship between zooplankton biomass and phytoplankton biovolume changed from approximately 1 at low levels of phytoplankton biovolume to slightly less than zero at high levels of phytoplankton biovolume.

Figure 5.

Zooplankton abundance, mean individual size, and biomass versus phytoplankton biovolume. Observed data shown as open circles, mean relationships shown as solid lines, 90% confidence intervals on mean relationships shown as shaded grey areas.

Model results can also be displayed by plotting log(Z:P) as a function of phytoplankton biovolume (Figure 6). In this format, at low levels of phytoplankton biovolume, log(Z:P) is nearly constant. As phytoplankton biomass increases, log(Z:P) decreases, eventually approaching a line with a slope equal to negative log(P). For reference, boundaries between different trophic states are noted with vertical lines. The locations of these lines correspond to trophic states defined by chl a in which chl a ≤ 2 μg/L is classified as oligotrophic, 2 < chl a ≤ 7 μg/L is mesotrophic, 7 < chl a ≤ 30 μg/L is eutrophic, and chl a > 30 μg/L is hypereutrophic (US EPA 2017). Chl a thresholds were converted to phytoplankton biovolume using the model parameters described above. Trophic boundaries based on phytoplankton standing stock such as these may not represent the full potential for productivity that may be captured by measurements of nutrient concentrations. However, at the large spatial scales of this data, we expect that plots of Z:P versus other correlates to phytoplankton biovolume (e.g., total P, chl a) would have a similar form.

Figure 6.

Zooplankton to phytoplankton biomass ratio (Z:P) versus phytoplankton biovolume. Solid line: fitted relationship, open circles: estimated seasonal mean Z:P at different sites.

Discussion

We have observed that in deep lakes, at the continental spatial scale of these data, the zooplankton and phytoplankton components of a biomass pyramid change to become progressively more bottom-heavy with position along the eutrophication gradient, as defined by phytoplankton biomass. We also observed that the rate of change in Z:P varied with position along the eutrophication gradient. In oligotrophic lakes, Z:P was constant with increases in phytoplankton biomass, whereas in eutrophic lakes, zooplankton biomass was nearly constant with changes in phytoplankton biomass, so Z:P decreased with increasing phytoplankton. We first discuss the performance of the Bayesian network model, and then discuss the trends observed in Z:P.

The Bayesian network model provided a statistically consistent means of combining several different measurements and maximized our ability to extract patterns from the data. Bayesian network models have been used extensively with discrete probabilities (see, for example, Allan et al. 2012), but recent advances in Bayesian software (Stan Development Team 2016) have made it possible to fit complex, continuous Bayesian networks that quantify the full probability distribution of different parameters (Qian and Miltner 2015). In the present application, the Bayesian network provided a means of using two different measurements of phytoplankton biovolume to improve estimates of true sample biovolume, provided the means to account for temporal and sampling variability, and provided the means to separately estimate relationships between zooplankton individual biomass and abundance with phytoplankton biovolume and to combine these two relationships to estimate a final relationship with sample biomass.

The results for the model for phytoplankton biovolume were consistent with those reported in the literature. The estimated mean chl a content per unit of phytoplankton biomass was 0.39%, a value that is very similar to the median value of 0.447% estimated from a survey of published values, and the range of possible values was also similar (Kasprzak et al. 2008). Similarly, in data collected from lakes in Florida, median chl a content was estimated as 0.20%, with a wide range of values (Canfield et al. 1985). Others have also noted as we have that chl a provides more precise estimates of phytoplankton biomass (Hessen et al. 2006). In our model, we assumed that both measured phytoplankton biovolume and chl a provided unbiased estimates of true sample biovolume, but systematic changes in estimated chl a content along the eutrophication gradient (Figure 4) suggest that this assumption was not fully met. Our model allowed for variations in chl a content and so accounted for this relationship, but in future models, it may be useful to explicitly account for the systematic changes in chl a content. Measurements of phytoplankton biovolume in highly oligotrophic lakes may also underestimate the contribution from picoplankton (Hessen et al. 2003), a phenomenon that may contribute to some of trends we observed in chl a content in the present analysis.

Phytoplankton and zooplankton biomass can vary substantially over the course of a sampling season (e.g., Lampert et al. 1986), and the data used here is composed primarily of single samples collected at each lake. Compared to other similar studies (e.g., del Giorgio and Gasol 1995), the number of samples collected from each lake is small, and in any single lake, these single measurements would provide relatively uncertain estimates of their seasonal mean values. However, the design of the current study prioritizes the goal of providing data from many different lakes over providing detailed information from a much smaller set of lakes, and hence, the data span a wider range of conditions than other available datasets. Furthermore, two factors increase our ability to extract meaningful relationship from these data. First, repeat samples in time at a subset of the sites provided a means of estimating the magnitude of temporal variability for each of the parameters. Also, two samples of phytoplankton biovolume were available from each visit, providing a means of estimating sampling variability within each lake. These estimates of temporal and sampling variability were incorporated into estimates of seasonal mean values in the Bayesian model such that the contribution from each lake to the final model is a distribution of possible seasonal mean values rather than a single value (Kamarainen et al. 2008; Cha and Stow 2014). Therefore, uncertainty in estimated seasonal mean values were reflected in the final estimated relationships. Second, our interest in estimating a mean relationship among different lakes allows us to leverage the large number of distinct samples to further average out much of the uncertainty in individual measurements (Yuan 2007).

The intent of this analysis was not to broadly examine the effects of different environmental factors on zooplankton biomass, and the random forest results presented here merely reflect our initial exploration of the data to guide the subsequent model development. Random forest analyses provide insights into which factors, at the large spatial scale of this data, most strongly affected zooplankton abundance and mean individual biomass. Our observation that average individual zooplankton biomass was only weakly related to the eutrophication gradient, whereas zooplankton abundance was strongly related (Figure 2) motivated the specification of separate models for individual zooplankton biomass and abundance. The weakness of the effect of lake productivity on the biomass of individual zooplankton has been observed in other studies (Pace 1986; Barnes et al. 2010). Instead, location of the lake, as characterized by latitude, longitude, and elevation, as well as mean temperature, annual precipitation, and ANC explained the vast majority of variation in average individual zooplankton biomass. These relationships may arise from biogeographical effects on zooplankton composition (Carter et al. 1980; Shaw and Kelso 1992), water temperature effects on zooplankton size (Gillooly and Dodson 2000; Havens et al. 2015), or arise from biogeographical effects on fish assemblage composition (Mazaris et al. 2010), which then influences the zooplankton size distribution (Mills et al. 1987). The magnitude of predation effects was not quantified in this study, but likely contributed to changes in individual zooplankton biomass as well (Hart and Bychek 2011). In contrast, as discussed below, zooplankton abundance and biomass have been consistently associated with phytoplankton biovolume and chl a in numerous studies.

In the Bayesian model, we did observe that mean individual size of zooplankton decreased slightly along the eutrophication gradient. This change is consistent with the idea that planktivore abundance increases with eutrophication, and selectively feed on larger zooplankton (Brooks and Dodson 1965; Jeppesen et al. 2002; Iglesias et al. 2011). Others have also observed that zooplankton size decreases with increased abundance of cyanobacteria because shifts in the edibility of phytoplankton alters the competitive relationship among different zooplankton (Gliwicz and Lampert 1990). Overall, though, the magnitude of the change in individual zooplankton size was substantially less than the change observed in zooplankton abundance across the eutrophication gradient (Figure 5), similar to what we observed in the random forest model.

We observed distinct patterns in the relationship between Z:P and phytoplankton biovolume corresponding to different locations along the eutrophication gradient. The constant value of Z:P observed in oligotrophic lakes suggests that bottom-up forces drive zooplankton biomass in these systems. That is, any unit increase in phytoplankton biomass was associated with the same fractional increase in zooplankton biomass, characteristic of a resource-dependent biomass pyramid. Our observation that bottom-up effects likely control zooplankton biomass in oligotrophic lakes is consistent with trends observed in other datasets collected in oligotrophic lakes. For example, in data collected from oligotrophic lakes in Quebec, the Type II regression slope between zooplankton and phytoplankton biomass was indistinguishable from 1 (del Giorgio and Gasol 1995). Similarly, the slope estimated between zooplankton and phytoplankton biomass in oligotrophic Norway lakes was 1 (Rognerud and Kjellberg 1984).

In eutrophic lakes, zooplankton biomass was nearly constant with changes in phytoplankton biomass. Other analyses of data collected from eutrophic lakes have observed that the slope of log(Z) as a function of log(P) is substantially less than 1 (e.g., Heathcote et al. 2016), a finding that is consistent with fitting a straight line to data that spans a section of the eutrophication gradient in which the relationship transitions gradually from a slope near one to a slope near zero. Others have observed the flattening of the relationship between log(Z) and log(P) and attempted to fit an asymptotic relationship (Hessen et al. 2006). Furthermore, the flattening of the relationship at higher levels of eutrophication can be seen in the distribution of points in the plotted data from other studies (McCauley and Kalff 1981; Leibold et al. 1997; Jackson et al. 2007).

Reasons for the generally decreasing trend in Z:P along the eutrophication gradient have been the subject of some debate, much of which centers on the relative importance of top-down versus bottom-up effects. One bottom-up mechanism that is often cited is the possible decrease in the edibility of the phytoplankton assemblage, and in particular, the increased dominance of cyanobacteria, with increasing levels of eutrophication. Laboratory studies suggest that the lack of highly unsaturated fatty acids in the cyanobacteria that tend to dominate in eutrophic lakes negatively affects the growth rates of Daphnia (Demott and Müller-Navarra 1997; Persson et al. 2007), and field observations (Müller-Navarra et al. 2000) and microcosm experiments (Park et al. 2003) have added further support for this hypothesis. Many cyanobacteria also present physical challenges to grazers, collecting in colonies or filaments that are too large to be consumed (Bednarska and Dawidowicz 2007), or surrounding themselves with gelatinous sheaths (Vanni 1987). The stoichiometric quality of phytoplankton under different levels of eutrophication may also influence zooplankton biomass (Hessen 2008). Finally, some species of zooplankton may be sensitive to the toxins that are often produced by cyanobacteria, although meta-analyses of experimental evidence have provided only weak support for this hypothesis (Wilson et al. 2006; Tillmanns et al. 2008).

Empirical analysis suggests that modeling zooplankton biomass as a function of only the edible portion of phytoplankton may explain some of the decrease in Z:P (Heathcote et al. 2016), and similar conclusions have been drawn from exploratory analysis of similar data (Filstrup et al. 2014). Following these efforts, we conducted an analysis to directly quantify the effects of increased cyanobacteria dominance. In our model, the deviation from the nearly constant value of Z:P observed in oligotrophic lakes to the observed functional relationship along the eutrophication gradient can be seen more clearly by extrapolating the linear relationship estimated in oligotrophic lakes to higher biovolumes (line A in left panel of Figure 7). This extrapolated line then provides the basis for estimating the degree to which increased cyanobacteria dominance accounts for the shift away from resource-control. More specifically, we computed the difference between the seasonal mean zooplankton biomass at each site and the corresponding predicted value based on the model described by line A. We then modeled this difference as a function of the seasonal mean proportion of cyanobacteria at that same site (right panel Figure 7). The mean square error associated with predicting seasonal mean zooplankton with line A was 0.28. The proportion of cyanobacteria at each site accounted for a statistically significant fraction of this error, reducing it to 0.25. However, the mean square error associated with predicting seasonal mean zooplankton with line B was only 0.14. Hence, the increased dominance of cyanobacteria along the eutrophication gradient accounted for approximately 21% of the deviation of the observed mean relationship from the resource controlled model observed in oligotrophic lakes. This estimate may be biased low because of measurement errors associated with quantifying the proportion of cyanobacteria, but nonetheless, the current analysis suggests that while increased cyanobacteria does account for a significant decrease in zooplankton biomass, other mechanisms are necessary to fully explain the shift in zooplankton biomass from resource control.

Figure 7.

Left panel: Comparison of the resource-controlled model for zooplankton biomass extrapolated to all phytoplankton biovolumes (A) versus the estimated mean relationship (B). Open circles: estimated seasonal mean zooplankton biomass. Right panel: Deviation of seasonal mean zooplankton biomass from model described by line A versus proportion cyanobacteria. Solid line: linear fit to the relationship.

The primary top-down mechanism affecting zooplankton biomass is the increase in planktivore abundance with position along the eutrophication gradient, which reduces the biomass of zooplankton. Fish data were not available in the data set analyzed here, so we could not quantitatively compare the magnitudes of top-down and bottom-up effects. Nonetheless, a rich body of literature exists that explores top-down effects on phytoplankton and zooplankton biomass, and we can qualitatively compare trends observed here with those predicted in the literature. A number of observational studies have identified significantly lower zooplankton biomass in lakes with planktivores compared to lakes without planktivores (Jeppesen et al. 1997). In some of these studies, regression models also indicated that planktivore abundance, but not cyanobacteria abundance, was significantly associated with changes in Z:P, providing evidence confirming the relative importance of top-down forces (Jeppesen et al. 2003). A similar absence of an effect of cyanobacteria was observed in data collected from shallow lakes in Denmark (Jeppesen et al. 1997). Manipulative studies have also observed strong changes in zooplankton abundance when piscivores were selectively removed from a lake because planktivore abundance increased in the absence of predators and zooplankton abundance decreased (Carpenter et al. 2001). However, another analysis of combined data from whole-lake manipulations suggested that the presence of planktivores accounted only for the variation in zooplankton biomass within the trends observed across the eutrophication gradient (Leibold et al. 1997). Our finding that mean individual biomass of zooplankton decreased over the eutrophication gradient was consistent with increased fish predation pressure (Brooks and Dodson 1965). Also, given that estimated effects of cyanobacteria dominance only accounted for a portion of the reduction in zooplankton abundance, it seems reasonable to infer that planktivory also accounted for additional decreases in zooplankton biomass.

The finding from the current study that is perhaps more important than the general decrease in Z:P with eutrophication is our observation that zooplankton biomass was virtually unrelated to phytoplankton biovolume in eutrophic lakes. The absence of an association between these two factors is consistent with predictions from simple food chain models with three trophic levels (Oksanen et al. 1981; Leibold et al. 1997), but application of these types of models to data collected from such a broad variety of lakes is difficult, given variations in the number of trophic levels and differences in the composition of assemblages at different trophic levels (Abrams 1993). More simply, though, this finding suggests that on average, the mechanisms that determine zooplankton biomass in eutrophic lakes are weakly related to changes phytoplankton biovolume, possibly because the mechanisms are several causal steps removed from phytoplankton biovolume. For example, we found that cyanobacteria dominance is associated with decreases of zooplankton biomass from a resource-controlled model, but the proportion of cyanobacteria is only correlated with phytoplankton biovolume at r = 0.40. When the uncertainty in the linkage between phytoplankton biovolume and cyanobacterial dominance is compounded with the uncertainty in the linkage between cyanobacterial dominance and changes in zooplankton biomass, the combined effect is an overall weak correlation between zooplankton biomass and phytoplankton biomass. The correlation we observed between cyanobacterial dominance and phytoplankton biovolume was somewhat weaker than observed in other studies (Downing et al. 2001), due possibly to the measurement uncertainty associated with single samples of phytoplankton and the broader variety of lakes sampled. However, even with a stronger relationship between phytoplankton biomass and cyanobacteria dominance, we suggest that the diversity of factors that can affect different steps in the causal path would weaken the relationship between zooplankton and phytoplankton biomass in eutrophic lakes (Reynolds 2008).

A similar rationale applies to fish effects on zooplankton biomass. Fish assemblage composition has been observed to vary along the eutrophication gradient in favor of higher abundances planktivores (Persson et al. 1991). However, other factors such as lake morphology can also strongly affect fish composition (Mehner et al. 2005, 2007). We suggest that in the lakes sampled in this study, fish composition is likely related to the eutrophication gradient, but the weakness of this relationship and the compounded uncertainty of fish predation effects on zooplankton yield a weak relationship between zooplankton and phytoplankton. Note though, that the weak relationship observed here among many eutrophic lakes does not preclude strong effects on a site-specific basis. Indeed, the high variability of zooplankton biomass at different levels of phytoplankton biovolume admits a wide range of possible responses within individual lakes (Leibold et al. 1997).

The weakness of the relationship between Z and P in eutrophic lakes may also inform efforts to synthesize findings from different manipulative studies. Relationships between changes in phytoplankton and zooplankton biomass observed from mesocosm and whole-lake manipulations differ substantially from the overall trends observed from survey data (Leibold et al. 1997). Different hypotheses have been proposed to explain these differences, but our observation of a weak association between phytoplankton and zooplankton provides an alternate explanation, in that on average, a weaker, multi-step causal relationship exists between P and Z in eutrophic lakes. Hence, manipulative studies would be expected to yield a diversity of responses because other environmental factors have a greater potential for influencing different steps in the causal path. In contrast, our finding of a constant ratio between phytoplankton and zooplankton biomass in oligotrophic lakes is more indicative a direct causal relationship, and hence, this result is more likely to be observed consistently in manipulative studies.

Case studies of biomanipulation provide another set of whole-lake experiments to compare with the present results, and in a review of these studies, the success of top-down control of phytoplankton biomass varies according to lake depth (i.e., shallow versus deep), trophic status, and time-scale of the experiment (Benndorf et al. 2002). In long-term experiments in deep lakes, top-down control of phytoplankton in mesotrophic to eutrophic lakes was possible, when the magnitude of nutrient loading to the lake was below a prescribed threshold. These findings are consistent with our current model in which we still observed a relationship between phytoplankton and zooplankton biomass in the transition zone between oligotrophic and eutrophic lakes. Similarly, in biomanipulations conducted in eutrophic or hypereutrophic lakes, top-down control of phytoplankton was not common, as would be expected based on our current results, where zooplankton was unrelated to phytoplankton. Finally, biomanipulation studies applied to oligotrophic lakes suggested that phytoplankton in these lakes are controlled primarily by bottom-up forces, as we have found in our current study.

We recognize additional potential shortcomings of this study are that field sampling methods may have missed some large, migrating zooplankton and deep chlorophyll maxima. The NLA zooplankton collection method focuses on sampling in the upper 5 m of the water column. For this reason, cladocera and some copepods that perform diel migration may not have been reflected in these samples. Diel migration seems to be influenced by several factors including the presence of predators, ultraviolet radiation, temperature, and food availability (Williamson et al. 2011), but more importantly, diel migration has been observed in lakes spanning the eutrophication gradient. Therefore, the potential effects of diel migration on the current results likely contributed a similar amount of additional random variability to observations across the eutrophication gradient, and did not bias our results. Nevertheless, while outside of the scope of this analysis, the impact of migration dynamics on Z:P relationships among lakes could be an interesting topic for future investigations.

The NLA phytoplankton and chlorophyll sampling protocol collected water from the upper 2 m of the lake, and so, any deep water chlorophyll maximum would not have been observed. Because these deep water maximum typically occur in high transparency, oligotrophic lakes (Hamilton et al. 2010), our estimates of phytoplankton biomass in these systems may be biased low. Hence, the current observations of the relationship between zooplankton and phytoplankton biomasses reflect relationships in the epilimnion of the lake, and in some lakes, would not represent interactions occurring in the deeper waters. As noted earlier, though, substantial variability in Z:P in individual lakes exists within the mean trends observed in the present analysis.

Although the Bayesian network model allowed us to estimate a relationship between zooplankton and phytoplankton biomass, the magnitude of the residual variance in zooplankton biomass observations about this estimated mean relationship was large. Because zooplankton biomass was calculated as the sum of measurements of individual specimens (similar to the phytoplankton biovolume measurement), we expect the measurement error to be large, which likely accounts for a substantial proportion of the residual variance. However, other environmental factors such as lake depth and surface area (Figure 2) likely introduce additional residual variability. The influence of these factors may be reduced by taking them into account in the analysis. As an example, we divided the data set into two equally sized groups, based on lake depth (4 < depth < 8 m, and depth > 8 m), and refit the models, allowing for different relationships between zooplankton abundance and phytoplankton biovolume in each of the two groups (see Supplemental Information). This new, classified model yielded a slight, 5%, reduction in the residual variance. Consideration of other covariates may further reduce the residual variance of the models, but considering methods to reduce the measurement error of zooplankton biomass (e.g., averaging multiple measurements) may be a more effective way of improving the precision of the estimated relationships. Moreover, we encourage additional research to explore patterns between environmental factors and variability in zooplankton size and abundance among lakes.

From a management perspective, the findings from this analysis may help direct future efforts in using biomanipulation to reduce phytoplankton biomass in different lakes by further reinforcing the emerging consensus regarding the types of lakes in which changes to higher trophic levels are likely to cascade down to phytoplankton abundance. Conversely, these insights may also help identify lakes in which reductions in nutrient loads are more likely to yield changes in lake conditions. Finally, thresholds at which the relationship between Z and P changes may provide useful points of reference to assess and compare the status of different lakes.