A Solid-State NMR and MD Study of the Structure of the Statherin Mutant SNa15 on Mineral Surfaces

Abstract

Elucidation of the structure and interactions of proteins at native mineral interfaces is key to understanding how biological systems regulate the formation of hard tissue structures. In addition, understanding how these same proteins interact with non-native mineral surfaces has important implications for the design of medical and dental implants, chromatographic supports, diagnostic tools, and a host of other applications. Here, we combine solid-state NMR spectroscopy, isotherm measurements, and molecular dynamics simulations to study how SNa15, a peptide derived from the hydroxyapatite (HAP) recognition domain of the biomineralization protein statherin, interacts with HAP, silica (SiO₂) and titania (TiO₂) mineral surfaces. Adsorption isotherms are used to characterize the binding affinity of SNa15 to HAP, SiO₂, and TiO₂. We also apply 1D ¹³C CP MAS, 1D ¹⁵N CP MAS, and 2D ¹³C-¹³C DARR experiments to SNa15 samples with uniformly ¹³C- and ¹⁵N- enriched residues to determine backbone and side-chain chemical shifts. Different computational tools, namely TALOS-N and molecular dynamics simulations, are used to deduce secondary structure from backbone and side-chain chemical shift data. Our results show that SNa15 adopts an α-helical conformation when adsorbed to HAP and TiO₂, but the helix largely unravels upon adsorption to SiO₂. Interactions with HAP are mediated in general by acidic and some basic amino acids, although the specific amino acids involved in direct surface interaction vary with surface. The integrated experimental and computational approach used in this study is able to provide high-resolution insights into adsorption of proteins on interfaces.

INTRODUCTION

Several organisms produce hard structures such as bone, teeth, shells, and exoskeletons from inorganic materials (i.e. calcite, silica, and hydroxyapatite) through a process known as biomineralization. These organisms use specialized proteins that interact with these inorganic materials thereby accelerating¹ or inhibiting^2,3 the growth of mineral solids, or even altering mineral morphology.^4–10 Detailed atomic-level insight of how of proteins interact with these minerals is required to better understand the role that proteins play in biomineralization and to thereafter exploit it for materials synthesis. This requires the resolution of the secondary and tertiary structure of proteins adsorbed on surfaces, the identification of both the residues that are crucial for protein-surface interaction and the nature of protein-surface interactions.

To date, only a handful of experimentally confirmed structural models of proteins interacting with their native mineral surfaces have been reported.^11–18 These protein-surface systems include either small extracellular matrix (ECM) proteins or ECM protein domains that are adsorbed onto hydroxyapatite (HAP) crystals.^14,19–29 These studies suggest that protein secondary structure can change when adsorbed to surfaces. They also hypothesize that the interaction of amino acid side-chains with inorganic surfaces are dependent on the secondary structures of adsorbed proteins.^{20,22,24,25,27,30} Thus, all components of protein-surface interaction can be determined only when the structure of the adsorbed protein is resolved.

Salivary statherin is a 43-residue ECM protein (DpSpSEEKFLRRIGRFGYGYGPYQPVPEQPLYPQPYQPQYQQYTF) that regulates HAP nucleation at enamel surfaces. The structure of statherin adsorbed onto HAP has been resolved.^29,31–33 Statherin has been studied by calorimetric methods^12,25, adsorption isotherms,^31,34 solution NMR,^35,36 solid-state NMR (ssNMR),^{19–21,23,24,26,27,29,32,33,37,38} and circular dichroism.^31,39 These studies indicate that statherin is unstructured in solution but structures when adsorbed onto HAP surfaces. Notably, the 15-residue long N-terminus adopts a distorted α-helical conformation and the C-terminus also becomes partly helical upon adsorption to HAP.^33,40,41

These studies also identify specific residues in statherin that interact with HAP. For example, acidic side-chains exhibit strong affinity for calcium phosphate surfaces.³¹ Consequently, the N-terminus of statherin, which containing acidic residues like phosphoserine (pS), aspartic acid (D), and glutamic acid (E), has been shown to be essential for HAP binding.³¹ Similarly, the interaction of basic residues with HAP have also been studied. When Goobes et al. mutated selected basic residues to alanine, the protein displayed lower the binding affinity to the surface but did not affect the surface coverage or the adsorption enthalpy.²⁹ In contrast, when all the basic residues (K6, R9, R10, and R13) were replaced with alanine, there was a significant change in the adsorption enthalpy and surface coverage. Therefore, they hypothesized that the nature of basic residues is not as important to binding as the presence of a number of basic residues.²⁹ In contrast to acidic and basic residues, the role of non-polar residues in protein-surface interactions is less clear. The HAP-binding domain of statherin has four types of nonpolar residues (L, I, G, and F) but only F14 was found to be in proximity with the HAP surface.^20,23

There are limited studies that model the interaction of statherin and HAP. Notably, Rosetta and RosettaSurface modeling programs have been used for this.^22,32,42 However, these all-atom models of the protein include simplifying assumptions that make calculations faster, like freezing the surface, restraining the protein backbone, and not accounting for waters and ions. Thus, they might exclude important interactions that affect protein structures. MD simulations, which can explicitly model the surface, protein, and solvent, include these interactions. In fact, recent advances in the use of advanced MD-based simulation methods like metadynamics^43,44 have been shown to be highly effective in simulating the structure and binding of peptides at surfaces⁴⁵. Furthermore, owing to the ease with which NMR chemical shifts can be directly estimated from classical simulations,^46,47 the metadynamic metainference approach^48,49 has been developed as part of a growing integrative structural biological toolkit⁵⁰ for pairing enhanced sampling MD simulations with experimental structural restraints.

Metainference⁴⁹ is a quantitative and rigorous mathematical framework based on Bayesian inference. In this approach, a structural ensemble of the protein or peptide is generated by a multi-replica MD simulation guided by a hybrid energy function, which combines physico-chemical information (the atomistic force field) with additional conformational restraints aimed at enforcing agreement of the structural ensemble of the peptide with the available experimental data. Furthermore, to accelerate sampling since structural states might be separated by huge energy barriers, metainference is combined with metadynamics (the Parallel-Bias (PBMetaD) flavor)⁴⁸. In this combined approach, an additional, time-dependent bias potential is added to each replica and shared among all of them, in the spirit of the multiple-walkers⁵¹ approach. Metadynamic metainference addresses two of the major challenges in molecular simulations – (1) the limited accuracy of empirical force fields, which is improved by the introduction of experimental information, and (2) the time-scale limitations of standard MD, which is accelerated by the use of PBMetaD.

In this study, we make use of the N-terminal domain of statherin, SN15 (DpSpSEEKFLRRIGRFG, where pS indicates a phosphorylated serine), which is often used as a model for statherin since it has nearly the same binding affinity for HAP as statherin²⁶. Importantly, the binding of SN15 to HAP is greatly diminished if the serines are not phosphorylated. Remarkably, this binding affinity can be restored when the serine residues are replaced by aspartic acid³¹, leading to the model peptide SNa15 (DDDEEKFLRRIGRFG). We study the adsorption of SNa15 to different inorganic surfaces, namely HAP, silica (SiO₂), and titania (TiO₂). We explore the surface-bound structure of the peptide, identify the binding residues, and investigate the changes in binding upon changing the mineral substrate to which the peptide binds. For this, we use an integrative experimental and simulation approach, similar to recent studies,^14,19,52, especially using NMR data as structural restraints in the molecular dynamics step to predict binding motifs of peptides on surfaces.^48,53

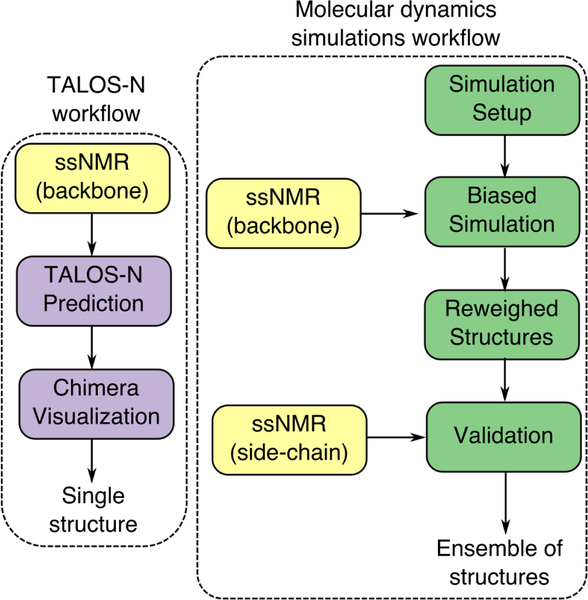
To characterize binding experimentally, we use both adsorption isotherms and 1D ¹³C CP MAS, 1D ¹⁵N CP MAS, and 2D ¹³C-¹³C DARR experiments. These experiments provide chemical shifts for the backbone and side-chain which can resolve the peptide structure with high fidelity. Further, we use two modeling approaches – TALOS-N and molecular dynamics (MD) simulations. TALOS-N utilizes a protein database to predict the most likely structure of the peptide given the database and the experimentally-determined chemical shift data.⁴⁵ However, since peptides often present an equilibrium ensemble of many structures with similar free-energies, even when bound to a surface, a single snapshot derived from TALOS-N might not provide a complete picture.^49,54 Thus, we use MD simulations to generate an ensemble of surface-bound conformations consistent with experimental data. We use a recently proposed method named metadynamic metainference^48,49 which uses Bayesian inference to incorporate structural restraints derived from experimental data, while accounting for errors in both the experimental data and simulation models. This integrated approach allows us to resolve the peptide structure with higher fidelity than possible with a single structure prediction, allows us to zoom in on the specificity of the side-chains to the surface. Measured side-chain chemical shifts are not used in the molecular simulation step but kept aside for validation as illustrated in Schematic 1.

RESULTS

Adsorption Isotherms

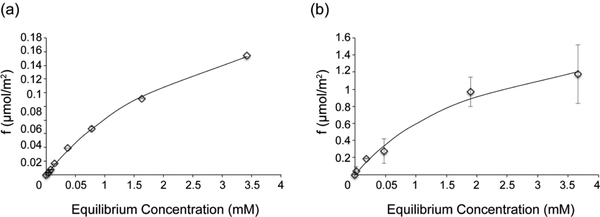
To determine how SNa15 interacts with the SiO₂ and TiO₂ surfaces, Langmuir adsorption isotherm curves were measured (Figure 1). Isotherms for SNa15 interacting with HAP can be found in the literature.³¹ The curves were fit with Equation 1

$$f=\text{A}\frac{\left[\text{SNa}15\right]}{\left[\text{SNa}15\right]+{\text{K}}_{\text{d}}}$$ (1)

where K_d is the disassociation constant (mM), f is the fractional saturation, A is a scaling factor (unitless), and [SNa15] is the concentration of free SNa15 in equilibrium (mM). The K_d obtained from these data were 2.98 mM and 2.30 mM for SNa15 adsorbing onto SiO₂ and TiO₂, respectively. The maximum amounts of SNa15 adsorbed were 0.2 μmol/m² and 1.2 μmol/m² for SiO₂ and TiO₂, respectively.

Figure 1.

Adsorption isotherms for SNa15 interacting with (a) SiO₂ and (b) TiO₂. Data are a mean from two independent repeats, and the standard deviation is shown. The disassociation constants obtained from the fitting are: K_d = 2.98 mM for SiO₂ and K_d = 2.30 mM for TiO₂.

Chemical Shift Assignments

Further, to obtain site-specific chemical shift assignments, 1D ¹⁵N CP MAS and 1D ¹³C CP MAS experiments were performed in conjunction with 2D ¹³C-¹³C DARR experiments. We resolved and assigned most of the ¹³C spins and the side-chain ¹⁵N spins in SNa15 containing up to two uniformly ¹³C- and ¹⁵N-enriched amino acids. To assign the chemical shifts for the entire peptide, seven isotopically enriched samples were analyzed, as shown in Table 1. The only amino acids not assigned by this study are L8, I11, and the C-terminal G15.

Table 1.

SNa15 peptides synthesized in this study. (*) Indicates that the preceding amino acid is uniformly ¹³C and ¹⁵N enriched.

Sample Name	Label Position
D2R9	DD*DEEKFLR*RIGRFG
D3R10	DDD*EEKFLRR*IGRFG
E4F7	DDDE*EKF*LRRIGRFG
E5F14	DDDEE*KFLRRIGRF*G
K6	DDDEEK*FLRRIGRFG
G12	DDDEEKFLRRIG*RFG
R13	DDDEEKFLRRIGR*FG

An example of the data collected for each sample is shown in Figure 2. A 1D ¹⁵N CP MAS (Fig. 2a), 1D ¹³C CP MAS (Fig. 2b), and 2D ¹³C-¹³C DARR (Fig. 2c) spectrum was collected for each sample in order to make complete, unambiguous chemical shift assignments. Since the ¹⁵N amide spins had too much overlap, they could not be assigned unambiguously. Therefore, only the ¹⁵N side-chain spins were assigned.

Figure 2.

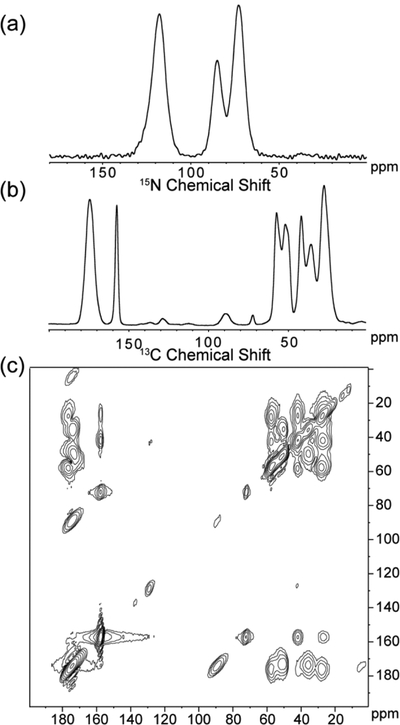
Representative set of the data collected for each labeled SNa15 peptide in each of the studied phases: neat and adsorbed on HAP, SiO₂, and TiO₂. The data shown are for D2R9 and are the following: (a) ¹⁵N CP MAS, (b) ¹³C CP MAS, and (c) ¹³C-¹³C DARR.

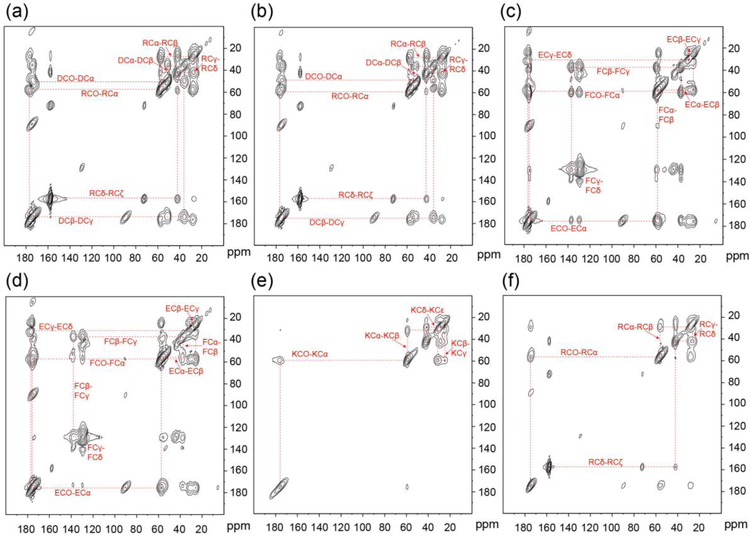
Figure 3 illustrates how all chemical shift assignments are made for the entire neat SNa15 peptide. The cross-peak interactions are highlighted by the dashed red lines and labeled with the corresponding ¹³C spins. These correlations allow for the assignment of unique chemical shifts. All ¹³C chemical shift assignments were made via this method for the entire SNa15 peptide in the four phases studied: neat, adsorbed on HAP, adsorbed on SiO₂, and adsorbed on TiO₂. Due to the broad nature of the ¹³C lineshapes and the overlap in both carbonyl and aliphatic regions, as evident in Figure 2, 2D spectroscopy was deemed unnecessary to further resolve these assignments.

Figure 3.

¹³C-¹³C DARR spectra of neat (a) D2R9, (b) D3R10, (c) E4F7, (d) E5F14, (e) K6, and (f) R13. The dashed lines show the correlation of spins.

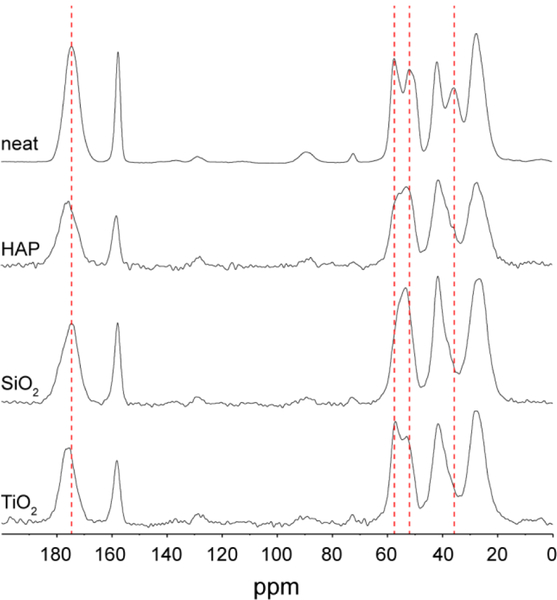
Additionally, changes in the chemical shifts (ΔCS) of the adsorbed peptide with reference to the peptide in water can provide information about (a) the structural changes of the peptide and (b) changes in local environment upon adsorption of the peptide to the surface. Figure 4 shows the chemical shifts of D2R9 in water and adsorbed to the three inorganic interfaces. The dashed lines emphasize positions of significant differences between these spectra. Notably, the resolution in the aliphatic region significantly decreases upon the adsorption of the peptide, necessitating the use of 2D spectroscopy.

Figure 4.

¹³C CP MAS spectra of D2R9 in four phases: neat, adsorbed to HAP, adsorbed to SiO₂, and adsorbed to TiO₂. The dashed lines highlight some of the more obvious chemical shift differences between the four spectra.

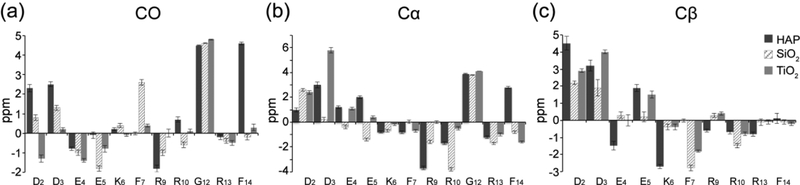
ΔCS values for the backbone of SNa15 at different surfaces are plotted in Figure 5. These values are obtained by subtracting the chemical shift of the ¹³C spin in neat SNa15 from the corresponding ¹³C spin in the adsorbed SNa15 peptide. A positive ΔCS indicates a downfield perturbation of the chemical shift (higher ppm, less shielded), while a negative ΔCS indicates an upfield perturbation of the chemical shift (lower ppm, more shielded).

Figure 5.

Backbone ΔCS plots showing chemical shift perturbations for (a) ¹³CO shifts, (b) ¹³Cα shifts, and (c) ¹³Cβ shifts. ΔCS for SNa15 on HAP (black), SiO₂ (hatched), and TiO₂ (gray) are in reference to neat SNa15. Positive changes indicate a downfield shift while negative changes indicate an upfield shift relative to the neat peptide.

From Figure 5, it is evident that some chemical shift trends are common for all three mineral systems. For the case of the ΔCS for ¹³CO, E4 exhibits upfield shifts and G12 exhibits downfield shifts. Similarly, all three adsorbed phases experience large downfield shifts for the ¹³Cα spins of G12 and D2. Additionally, they all experience a pronounced downfield shift for the ¹³Cβ spins of D2 and D3 while there is a pronounced upfield shift for the ¹³Cα spins of R13 and the ¹³Cβ spins of R10. The fact that ΔCS of these residues have the same trend at all interfaces indicates that these regions in the peptide display similar structural changes when adsorbed to any of these surfaces. Specifically, the N-terminus (D2-E4) and the C-terminus (R10, G12, and R13) experience similar conformational changes upon adsorption to HAP, SiO₂, and TiO₂. Additionally, there are pronounced backbone ΔCS changes for SNa15 that are unique to each mineral phase and might be useful in highlighting the unique conformation of SNa15 adsorbed to each mineral phase, which we further explore with MD simulations.

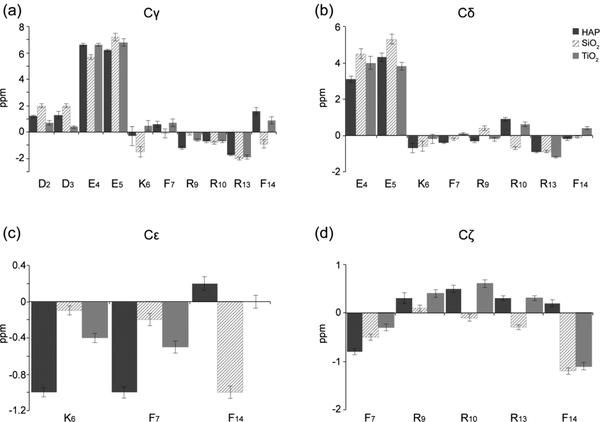
ΔCS values for the side-chains of SNa15 at different surfaces are plotted in Figure 6. SNa15 experiences downfield shifts for the ¹³Cγ of D2 and D3 and the ¹³Cδ of E4 and E5 across all mineral surfaces. These spins correspond to the side-chain carboxyl groups in the aspartic acid and glutamic acid residues in the N-terminus of SNa15, respectively. The ¹³CO shifts of E4 and E5 are also accompanied by large downfield shifts of the ¹³Cγ spins for SNa15 upon adsorption to all three mineral surfaces. The basic residues of SNa15 (K6, R9, R10, and R13) generally experience less pronounced and less consistent perturbations across the three surfaces. There is a consistent upfield shift for both the ¹³Cγ and ¹³Cδ spins of R13 in SNa15. Additionally, there is an upfield shift of the ¹³Cε spin of K6 upon adsorption to HAP and TiO₂, although not SiO₂. Typically, upfield shifts of lysine ¹³Cε spins indicate proximity to a negatively-charged mineral surface.⁵⁵

Figure 6.

Side-chain ΔCS plots showing chemical shift perturbations for (a) ¹³Cγ shifts, (b) ¹³Cδ shifts, (c) ¹³Cε shifts, and (d) ¹³Cζ ΔCS. ΔCS for SNa15 on HAP (black), SiO₂ (hatched), and TiO₂ (gray) are in reference to neat SNa15. Positive changes indicate a downfield shift while negative changes indicate an upfield shift relative to the neat peptide.

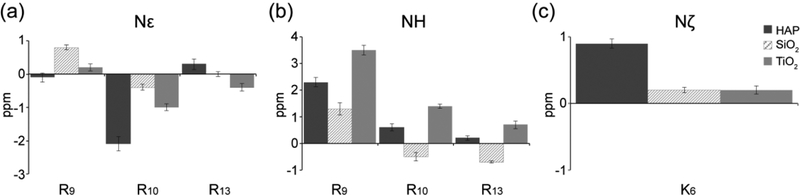
Figure 7 shows the ¹⁵N side-chain ΔCS values for different surfaces. Downfield perturbations are observed for R9 ¹⁵N shifts upon adsorption to HAP (2.3 ppm), SiO₂ (1.3 ppm), and TiO₂ (3.5 ppm), indicating interactions with the phosphate buffer and/or the surfaces. The K6 ¹⁵Nζ spin also experiences a downfield perturbation, albeit less pronounced, upon adsorption to HAP (0.9 ppm), SiO₂ (0.2 ppm), and TiO₂ (0.2 ppm).

Figure 7.

Side-chain ΔCS plots showing chemical shift perturbations for (a) ¹⁵Nε, (b) ¹⁵NH, and (c) ¹⁵Nζ. ΔCS for SNa15 on HAP (black), SiO₂ (hatched), and TiO₂ (gray) are in reference to neat SNa15. Positive changes indicate a downfield shift while negative changes indicate an upfield shift relative to the neat peptide.

SNa15 Secondary Structure Predictions from TALOS-N

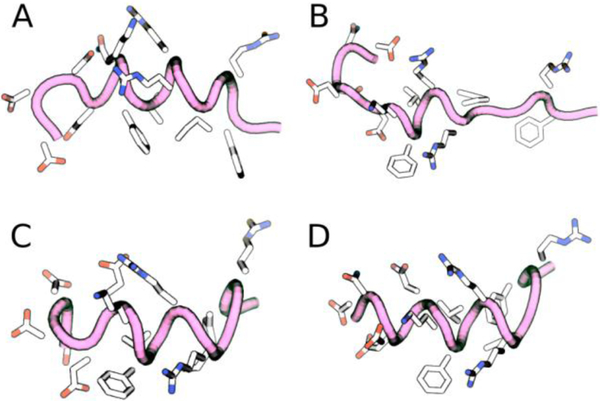
Following the conventional practice for structure prediction from ssNMR data, the backbone ¹³C chemical shifts for SNa15 were input to the TALOS-N⁵² program, that predicts the ϕ/ψ torsion angles (Supplementary Information). Chimera⁵⁶ was used to visualize the structure that corresponds to these predicted torsional angles (Figure 8 and Figure 9). Figure 8 shows that SNa15 has some α-helical structure in each surface-bound state and that SNa15 is largely unstructured when adsorbed to SiO₂. For neat SNa15, the ϕ/ψ torsion angles for E4-I11 are clustered around the accepted α-helical values (−57/−47), while the ϕ/ψ torsion angles for R13 and F14 are clustered around (−80/+150), indicating a loss of helicity at the C-terminus and a more extended secondary structure. Largely, the torsion angles upon adsorption to HAP are similar to those in the hydrated solid state, as evident by the similarity in structures of A and C (Figure 8). In the case of HAP, residues E5-I11 exhibit α-helical character, while residues in the N-terminus (D2-E4), and C-terminus (R13-F14) exhibit more extended structures. In contrast, upon adsorption on TiO₂, the α-helix is extended farther into the N-terminus; the ϕ/ψ angles for D2-I11 are all clustered around α-helical values, although the C-terminus remains extended, as seen in HAP. Remarkably, the structure of SNa15 differs greatly upon adsorption to SiO₂, when compared to the other systems. The helical region of SNa15-SiO₂ is limited to K6-R9.

Figure 8.

Chimera⁵⁶-generated models of (a) SNa15-neat, (b) SNa15-SiO₂, (c) SNA15-HAP, and (d) SNa15-TiO₂ using TALOS-N⁵²-predicted torsion angles from experimentally obtained chemical shifts. Each peptide is shown from N-terminus to C-terminus right-to-left.

Figure 9.

End-view of (a) SNa15-neat, (b) SNa15-SiO2, (c) SNA15-HAP, and (d) SNa15-TiO₂ with each residue labeled. Structures are visualized with Chimera⁵⁶ using torsion angles predicted by TALOS-N.⁵²

The end-view of each predicted structures is visualized in Figure 9 to highlight helical content and the relative orientation of the side-chains. In the mineral systems, F7 and F14 are pointing in different directions. This is consistent with chemical shift data, relaxation dynamics (T₁/T_1ρ)^20,27, ¹³C{³¹P} REDOR²⁰, ²H ssNMR²⁷, and NEXAFS²⁴ data, which all conclude that F7 is far from the HAP surface (at least 7 Å) while F14 is close to (within 4 Å) and interacting with the surface. The ΔCS values in this study support this theory, since there are significant perturbations for F14 (¹³Cγ, ¹³Cδ, ¹³Cε, and ¹³Cζ data), yet much smaller perturbations for the same shifts of F7. Further, it has been posited that F14 is in a near-parallel orientation to HAP, thus exposing the delocalized electrons in the phenyl ring.⁵⁷

SNa15 Secondary Structure Predictions of Adsorbed Peptides from MD Simulations

Further, MD is used to generate an ensemble of conformations of the peptide consistent with the experimentally measured chemical shifts. The backbone ¹³CO, ¹³Cα, and ¹³Cβ chemical shift data for SNa15-HAP, SNa15-SiO₂, and SNa15-TiO₂ were used to restrain an ensemble of configurations using the metadynamic metainference approach⁴⁸ (See Methods). The restraints are applied to the average chemical shifts across many simulation replicas, thereby limiting the average deviation of the backbone chemical shift to be within the error predicted by experiments. The calculated side-chain chemical shifts are not directly used in the simulations or analysis of the clusters and provide a posteriori validation of our approach. Root mean squared errors (RMSE) of the backbone (training error) and side chain (validation error) for the surface adsorbed peptides are provided in Table 2. We see that the error in both the backbone and side chain chemical shifts are between 1.48 – 2.25 ppm, which denotes agreement with experimental data (experimental error ~2 ppm), providing strong evidence that the ensemble of peptide conformations generated by the metadynamic metainference simulation are consistent with the experimental data.

Table 2.

The root-mean squared error of the backbone and side-chain.

Simulation	RMSE of backbone	RMSE of side-chains
SNa15-HAP	2.17	1.59
SNa15-SiO2	2.25	1.75
SNa15-TiO2	1.91	1.48

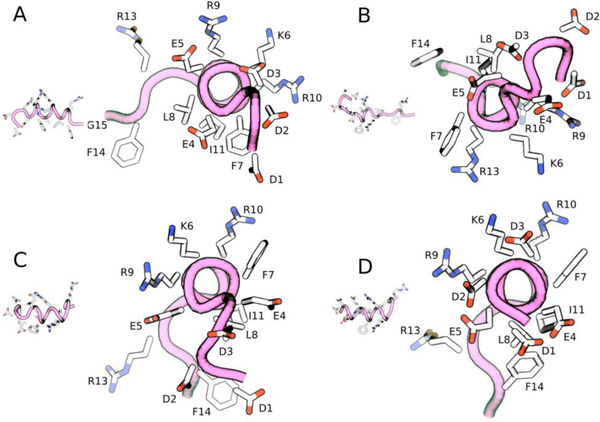
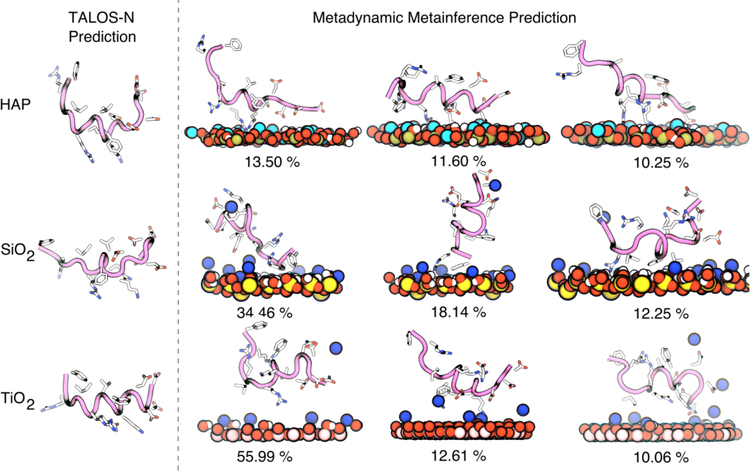
We next determined the most likely conformations of the peptide generated by the MD simulation by performing a clustering (See Methods). The center of the top three most likely clusters of peptide backbone conformations (and their weights determined from post-processing of the metadynamics simulations) along with the representative structure from TALOS-N are shown in Figure 10. For the case of SiO₂, all conformations are random coils with a helical middle section. Noticeably, the structure predicted by TALOS-N has the same structural motif. The MD-predicted structures of SNa15 on HAP show similar amounts of secondary structure, with more variance in the number of helical turns in the center. For both TiO₂ and HAP surfaces, the TALOS-N predicted structure displays a greater level of helicity (with unstructured ends) than the MD-predicted structure. However, the top three peptide structures encompass the helical components present in the TALOS-N structures. This demonstrates the need to view the structure of SNa15 on mineral oxide surfaces as an ‘ensemble’ and not a single entity. We note that in all cases, the exact structure predicted by TALOS-N can be found within the biased MD simulations, although it does not appear in the top three reweighted cluster centers shown here.

Figure 10.

TALOS-N prediction and metadynamics metainference predictions of the structures of SNa15 on HAP (top), SiO₂ (center), and TiO₂ (bottom) surfaces. The peptide backbone is shown in mauve with tube structure. Surface atoms are colored blue for sodium ions, light blue for calcium, red for oxygen, yellow for silicon. The heavy side-chain atoms on the protein are rendered with licorice and colored blue for nitrogen, red for oxygen, and white for carbon. The percentages of the MD configurations refer to the weight of that cluster within the structural ensemble.

Further, to ascertain which residues are interacting with the surface, the top three clusters were placed near the respective surface and simulated for 50 ns (with the backbone restrained using an RMSD restraint on the Cα atoms) (see Figure S4–7). For the case of the HAP surface (Figure S4), SNa15 is anchored to the interface by a mixture of basic (R9, K6, and R10) and acidic (D1, D2, and E5) residues. Since the surface is neutral overall, and has local pockets of positive and negative charge, it is understandable that the peptide needs both types of binding residues to bind to the surface. The TiO₂ surface is a negatively charged surface. Consequently, basic residues (R10, and K6) allow SNa15 to bind to the the surface (Figure S5). Acidic residues (D1, D2, and D3) interact with mobile sodium ions. Similar to the TiO₂ surface, the SiO₂ surface is also negatively charged and neutralized with mobile, displaceable sodium ions. Therefore, SNa15 is also anchored with basic residues only (R13 and R9) (Figure S6). Notably, neutral, hydrophobic residues like F14, F7, and I11 also approach the surface. On approach, F14 and F7 lay flat on the surface.

Additionally, the contact profile of individual residues with the surface is explored. Several residues show a bimodal distribution of contacts on the SiO₂ the surface (D2, D3, K6, F7, R9, and F14) (Figure S7). Further, most N-terminus residues of SNa15 are closer to the surface on SiO₂ and TiO₂ than they are on the HAP surface (Figure S7). Notably, all SNa15 residues are in closer contact with the SiO₂ surface than the other surfaces. We hypothesize that greater contact with the surface might promote the SNa15 residues to unfold more, thus SNa15 has much lesser helical content on the SiO₂ surface.

Finally, the distribution of secondary structure elements along the peptide is determined (Figure S8). The results indicate helical structures in the middle residues of SNa15 peptide on all three mineral surfaces. However, the peptide is more likely to be helical on the TiO₂ surface, as also seen in the TALOS-N predictions. SNa15 has significant random coil structure on the HAP surface. Finally, SNa15 shows distinct bends on the SiO₂ surface, which is also evident in the TALOS-N prediction.

DISCUSSION

Both the structure of the protein and the interaction of its side-chains with the surface are integral to the process of recognition of biomineral surfaces by proteins. Expectedly, the foundational goals in this field are centered around the determination of protein secondary structure, the evaluation of changes in structure upon adsorption, and the estimation of the proximity or orientation of amino acids to the surface. To further these goals, we have chosen the model peptide SNa15 and elucidated its structure upon binding to three naturally occurring mineral surfaces (HAP, SiO₂, and TiO₂). In fact, we have demonstrated an integrated approach that pairs experimental data with MD simulations to make more robust predictions about the ensemble of surface adsorbed structures. Experimentally, we used 1D and 2D ssNMR techniques to determine the secondary structure of SNa15 in the pure, i.e. unadsorbed solid state, and when adsorbed to HAP, SiO₂, and TiO₂ surfaces. On the modeling front, we used the structure prediction software TALOS-N, and classical all-atom MD simulations (with metadynamic metainference enhanced sampling) to generate an ensemble of conformations of the peptide on the surface, which are consistent with the experimental data.

Overall, the backbone (¹³CO, ¹³Cα, and ¹³Cβ) chemical shift data and subsequent TALOS-N⁵² predictions indicate that SNa15 is helical (with unraveling at the termini) in water, and when adsorbed to HAP and TiO₂. In contrast, the peptide is predicted to be largely unfolded on the SiO₂ surface. The picture, when viewed from the perspective of integrated MD+ssNMR is more nuanced, with a need to explore in more detail the full conformational ensemble.

Further, we explore the interaction of various amino-acid side-chains with the surface via the ΔCS for the side-chain ¹³C spins. Notably, large downfield perturbations in the ΔCS of E4, E5, and F14 (in all cases) suggest that they are interacting with each surface. There are large downfield perturbations for the side-chain ¹³Cγ and ¹³Cδ spins of E4 and E5 (Fig. 6a–b). In fact, this CS perturbation is attributed to the decreased shielding of the carboxyl group due to its interaction with the surface.⁵⁵ Fernandez et al.⁵⁵ also noted similar downfield shifts in ¹³Cδ spins (~ 2 ppm) in their study of poly-L-glutamic acid adsorbed on HAP and SiO₂. In our study, these downfield shifts range from 3–5.3 ppm indicating a stronger effect than that seen by Fernandez et al.⁵⁵ Moreover, since the perturbations are roughly the same magnitude within error for both residues, this suggests a similar degree of contact with the surface. This contrasts with the predicted behavior of SN15 and statherin on HAP, where only E5 was proposed to interact with HAP.²³ In fact, MD simulations predict that E4 and E5 have a much higher degree of conformational flexibility (Figure S7) on HAP compared to SiO2 and TiO2. Notably, NMR-derived side-chain constraints were not included in the MD simulation, therefore some deviations in the side-chain behavior is expected.

Amongst the aromatic groups, we observe that F14 is also interacting significantly with the surface. The role of phenylalanine residues in the binding of statherin to HAP has been studied extensively.^20,24,27 Gibson and coworkers²⁰ studied the role of F7 and F14 in SN15 adsorption to HAP through isotropic chemical shift perturbations, ¹³C{³¹P} REDOR, and T_1ρ relaxation measurements. They found that when compared to F7, F14 is closer to the surface and is more dynamically constrained. In fact, F7 is observed to be oriented away from the HAP surface.²⁰ The study by Weidner and coworkers²⁴ used NEXAFS and SFG also corroborates this observation. Correspondingly, in this study, we note large ΔCS for F14 and minimal ΔCS for F7 (Fig. 5–6). MD simulations also predict the interaction of F14 with SiO₂. In fact, the ¹³CO and ¹³Cα chemical shift data also show that F14 behaves differently in HAP than the other two surfaces.

In the case of basic residues, there are negligible perturbations for most of the side-chain ¹³C spins for K6, R9, and R10. MD simulations also show that other basics residues (K6, R9, and R10) are away from the surface (Figure S7). This suggests that these residues do not specifically adsorb to or identify any of these surfaces. In fact, previous studies where the 4 basic residues (K6, R9, R10, R13) of statherin were mutated to alanine have shown that individually, none of these residues are crucial to binding.²⁹ However, as a group they act to decrease the overall charge of statherin, thus reducing repulsive protein-protein interactions and promoting a higher surface affinity and coverage.²⁹

In contrast, the R13 ¹³Cγ and ¹³Cδ spins experience significant perturbations in the range of −0.9 to −2 ppm. This suggests that R13 interacts with the surfaces while the remaining basic residues do not. From the end-view of TALOS-N predicted structures (Figure 9), it is evident that the R13 side-chain is oriented on the same face of SNa15 as E4, E5, and F14 (the residues that are hypothesized to interact with the surfaces). The behavior of R13 is corroborated with MD simulations only in the case SiO₂.

Finally, we observe that D2 and D3 are also crucial to the recognition of surfaces. In the case of HAP, D2 and D3 are oriented along the hypothesized binding face of SNa15. These residues experience a downfield shift of 1.2 and 1.3 ppm, respectively, upon adsorption. This is also true for adsorption on SiO₂, since D2 and D3 both experience a downfield shift of 2 ppm. However, in the case of TiO₂, only D2 is oriented along the binding face (predicted by a significant ΔCS in D2 only). From MD simulations, we see that D2 contribute to the binding of SNa15 to all surfaces (Figure S7) while D3 contributes to the binding to SiO₂ and TiO₂.

Based on the information above, we hypothesize that the binding domain of SNa15 consists of some residues from N-terminus (D2-E5) and C-terminus (R13 and F14) residues for binding to HAP and SiO₂. For the case of TiO₂, D3-E5, R13, and F14 residues contribute to binding. MD simulations predict that SNa15 binds from the N-terminus on the HAP and TiO₂ surfaces, and from the C-terminus on the SiO₂. The residues composing the hypothesized binding domain are all oriented on the same face of SNa15 and all experience significant chemical shift perturbations upon adsorption. In fact, the lack of α-helical character in the N-terminus allows consecutive acidic residues to be positioned along the same face and interact completely with the surface.

Since SNa15 is comparable to other model peptides (SN15) and its parent protein statherin, it is possible to compare the behavior of SNa15 with previously reported observation about the other peptides. In fact, prior studies of statherin and SN15 on HAP were based on distance measurements obtained from dipolar couplings between ¹³C and ¹⁵N spins within the peptides and between ¹³C spins in peptide side chains and ³¹P spins in the HAP surface. Since these studies and the current studies results in predictions of the peptide structure, it is useful to compare these results, albeit qualitatively. For example, the distorted helical structure obtained for SNa15 on HAP, obtained by analysis of the ¹³CO, ¹³Cα, and ¹³Cβ chemical shifts via TALOS and MD simulations, is in agreement with earlier dipolar coupling-based studies of the structure of SN15 and statherin on HAP.^15,31,37 Our present study of SNa15 and prior studies of statherin and SN15 find that the acidic N-termini of SNa15 and SN15 interact strongly with the HAP surface, but details of exactly which side chains are involved in surface interactions differ. Downfield changes to the chemical shifts of the γ and δ carboxyl ¹³C spins in SNa15’s D₂D₃E₄E₅ moiety observed upon adsorption to HAP indicate interactions with the HAP surface. Relaxation and chemical shift line shape studies of pS2 and pS3 in SN15 on HAP similarly find that these N-terminal amino acids are anchored to the surface³⁶, but a ¹³C{³¹P} REDOR study finds that the ¹³Cδ spin of E5 is much closer to the HAP surface than the carboxyl group of E4.¹⁹ Based on ¹³Cζ upfield chemical shift changes upon adsorption to HAP, only R13 is assumed to interact with the HAP surface in SNa15, while a ¹³C{³¹P} REDOR study of statherin on HAP finds that the¹³Cε spin of K6 and ¹³Cζ spins of R9 and R10 are close to the HAP surface. Some of these differences may result from variations in local secondary structure, where for example the substitution of D for pS at positions 2 and 3 in SNa15 may perturb the local helical structure making it possible to simultaneously expose E4 and E5 in SNa15 to the surface. The apparent differences between exposure of basic amino acids in SN15 and SNa15 to the HAP surface may similarly result from structural changes in the acidic portion of the N-terminus that perturb the surface orientation of the basic amino acids.

Another factor to consider is the effect that the orientation of the side chain has on ΔCS values. In a study of SK rich peptides in SiO₂ and TiO₂ composites, density functional theory (DFT) calculations showed that the chemical shift of ¹³Cε spins in lysine side chains has a large upfield ΔCS when the side chain is oriented perpendicular to the surface, but the ΔCS is greatly diminished for ¹³Cε when the side chain is oriented parallel to the surface.⁵⁸ Also, for lysine ¹³Cε spins ΔCS values drop off rapidly as a function of the distance between the amine group and the surface. For example, when the distance from the lysine side chain amine to the SiO₂ surface exceeds 3 Angstroms ΔCS perturbations are comparable to experimental error.

Some of the results obtained in our study of SNa15-mineral interactions are similar to results reported in other studies of statherin-mineral interactions. For example structural dispersion of SN15 on HAP was observed in a solid state NMR study by Chan et al⁸¹ Those workers observed two sets of cross peaks for K6 in the 1D ¹³C-¹³C correlated spectrum.. The ¹³Cα chemical shift of the major component (66%) was close to that observed for free (i.e. helically structured) SN15 while the minor component chemical shift was close to random coil. A study of differential adsorption of statherin and the statherin peptide SN21 on HAP and silica by ellipsometry⁸²showed higher adsorption levels for both peptides on HAP versus hydrophilic silica. This observation was attributed by the authors in part to repulsion between the negatively changed surface and the negatively charged side chains at the N-terminus.

However, a significant result of our study is that differential adsorption of Sna15 on TiO₂ and HAP versus SiO₂, is accompanied by differential structuring on these surfaces, i.e. more helical structuring on TiO₂ and HAP versus SiO₂.. If this differential structuring effect can be demonstrated for other proteins on mineral surfaces, then the detailed surface structure of the protein and the arraying of side chains is an important component of its surface interactions and may, for example, explain in part the affinity of tissue cells for particular implant coatings It has long been known that interactions between tissue-generating cells and implant surfaces are mediated by a proteinaceous layer.^83–85 Ideally a layer of specifically adsorbed proteins promotes cell adhesion to the implant surface and normal cellular response, leading ultimately to integration of the implant with the surrounding tissue. Non-specific adsorption of proteins or the presence of proteins in an unstructured or otherwise unrecognized state may result in a foreign body response and implant failure. It has been observed that osteoblasts differentiation is enhanced on TiO2 coatings versus SiO2 coating.⁸⁶ Although further studies protein surface structures are required to support a general explanation, the ability of TiO₂ to support a layer of structured adhesion proteins may contribute to its ability to support osteoblast differentiation.

CONCLUSION

This study of the adsorption of SNa15 onto HAP, SiO₂, and TiO₂ surfaces demonstrates an integrated approach that pairs ssNMR with advanced MD simulations as a means to predict ensembles of surface-bound peptide structures. Measured adsorption isotherms and companion structure predictions from the software TALOS-N provide additional characterization of the systems. In contrast to using TALOS-N to predict a single set of dihedral angles, the integrated approach allows for structure prediction of an entire conformational ensemble with average backbone chemical shifts constrained to the measured experimental values. This approach is thus a promising way to estimate not only the conformational ensemble, but also the key binding residues to the surface and orientation of the adsorbed biomolecule.

Although this method can be applied to many peptide/surface systems in the future to study biomineralization processes, the approach has potential areas for future investigation. First, there is a continued need to improve surface potentials and representation of accurate surface chemistries for use in MD simulations of peptide adsorption, even with metadynamic metainference approach to help overcome systematic errors. Second, DFT can be used to provide accurate estimates of the surface response of amino acids such as those shown here and to help provide an assessment of the accuracy of using the SHIFTX and CAMSHIFT methods for peptides on surfaces.

METHODS

Peptide Synthesis

All natural and uniformly labeled ¹³C and ¹⁵N amino acids were purchased from Sigma Aldrich (St. Louis, MO). Preloaded Fmoc-protected Wang resin was purchased from EMD Millipore (Billerica, MA). All other reagents were purchased from Sigma Aldrich (St. Louis, MO) and used without purification. Peptides were synthesized on a CEM Liberty Blue peptide synthesizer using a standard 9-fluorenylmethoxycarbonyl (FMOC) and tert-butyl protection scheme. Preloaded Fmoc-protected Wang resin was used for solid phase synthesis. Peptides were cleaved from the resin in a 10 mL solution of 95:2.5:2.5 trifluoroacetic acid: triisopropylsilane (TRIS): water mixture per 1.0 gram of peptide/resin. The resulting filtrate was added dropwise into cold tert-butyl methyl ether, followed by centrifugation and three rinses of the resulting solids with 40 mL of cold tert-butyl methyl ether. Peptides were purified using RP-HPLC (Varian ProStar HPLC, Alltima WP C4 column, 5 mL/min, eluent A: water with 0.2% TFA, eluent B: acetonitrile with 0.2% TFA), using a gradient of 15–50% B over 40 minutes. Chromatograms were generated by observing the UV absorbance at 254 nm, and the analyte was verified by mass spectrometry. The fractions were then lyophilized, resulting in the pure peptide.

Surface Area Determination

HAP (product number 677418; a synthetic, crystalline nanopowder with a reported particle size <200 nm), SiO₂ (product number 637246; a spherical, porous nanopowder with a reported particle size of 5–20 nm), and TiO₂ (product number 637262; a rutile titanium (IV) oxide nanopowder with a reported particle size <100 nm) nanoparticles were purchased from Sigma Aldrich (St. Louis, MO) and used without purification. The surface area of the HAP, SiO₂, and TiO₂ nanoparticles was determined using a Nova 4200e Surface Area and Pore Size Analyzer from Quantachrome Instruments. BET measurements showed a surface area of 34.4 m²/g for HAP, 331.9 m²/g for SiO₂, and 28.6 m²/g for TiO₂ nanoparticles.

Adsorption Isotherms

Known concentrations of SNa15 (1ml) were equilibrated with 10 mg of HAP, SiO₂, or TiO₂ nanoparticles for 4 hours in phosphate buffer (100mM, pH=7.4). After adsorption, the solid nanoparticles were separated from the mixture via centrifugation at 13000 x g for 15 minutes. The peptide concentrations in the supernatant solutions were measured using an Agilent 8453 Diode Array UV-Vis Spectrophotometer and compared with the initial concentrations.

ssNMR Sample Preparation

SNa15 (2mM, 5ml) was equilibrated with 60 mg of mineral nanoparticle for 4 hours in phosphate buffer (100mM, pH=7.4). After adsorption, the solid was separated from the mixture via centrifugation at 13000 x g for 15 minutes. The supernatant was discarded, and the remaining solid was dried in vacuo.

ssNMR

All solid-state NMR experiments were conducted using a 16.4 T magnetic field (proton resonant field of 700.18 MHz) on a Bruker Avance III spectrometer fitted with a ¹H {¹³C,¹⁵N} 3.2 mm MAS probe. The spinning speed for all experiments is 15 kHz ± 5Hz, and is regulated by a Bruker MAS controller unit. All experiments were run at room temperature. 1D ¹³C CP MAS experiments were collected using a 4 μs proton π/2 pulse, a contact time of 1.2 ms, and a recycle delay of 2 s. Neat samples required 2k scans while adsorbed samples required 8k scans. 1D ¹⁵N CP MAS experiments were collected using a 4 μs proton π/2 pulse, a contact time of 2 ms, and a recycle delay of 2 s. Neat samples required 4k scans while adsorbed samples required 32 k scans. All ¹³C chemical shifts reported were indirectly referenced to tetramethylsilane (TMS) in the solid-state using adamantane (δ=38.48 ppm).⁵⁹ All ¹⁵N chemical shifts reported were indirectly referenced to NH₃⁺ in the solid-state using glycine (δ=33.4 ppm).⁶⁰ 2D ¹³C-¹³C DARR experiments were collected with a 1.2 ms contact time, a 4 μs proton π/2 pulse, and a 4 μs ¹³C π/2 pulse. Mixing times were 60 ms. For neat samples, there were 256 points in the indirectly detected dimension (F1) and 1k points in the directly detected dimension (F2). For adsorbed samples, there were 128 points in F1 and 1k points in F2. Again, the chemical shifts reported were indirectly referenced to TMS in the solid-state using adamantane (δ=38.48 ppm).⁵⁹

Molecular Dynamics Simulations

System Setup

The structure of SNa15 peptide when adsorbed onto HAP, SiO₂, and TiO₂ surfaces was probed using classical all-atom molecular dynamics simulations. The peptide was modeled using the AMBER99SB-ILDN force field.⁶¹ Water was modeled using SPC/E water model.⁶² HAP and SiO₂ were modeled using the INTERFACE force field,⁶³ while the TiO₂ was modeled using the force field by Predota et al.⁶⁴ (details about surface construction in SI). These models were chosen according to previously published studies of peptide and surfaces.^65–69 The HAP surfacs was neutral, whereas the negatively-charged TiO₂ and SiO₂ surfaces was neutralized by 72 and 80 Na⁺ ions, respectively. The peptide had a net negative charge of −1 which was neutralized by a single Na⁺ ion.

For each peptide-surface system, a slab of the inorganic surface was created, and the peptide was placed near the surface. This system was then solvated with water (7935 waters for HAP, 8273 water for SiO₂, and 8134 waters for TiO₂). Unfavorable contacts during this packing were removed by using a steepest descent algorithm that minimized the energy of the system. The pressure of the system was equilibrated to 1 bar by propagating the system in the NPT ensemble (Temperature = 300 K; Pressure = 1 bar) for 1 ns. The semi-isotropic version of Berendsen barostat⁷⁰ (tau =1.0 ps) was used so that only the z-axis of the box changed to correct the pressure of the system. The Bussi-Donadio-Parrinello thermostat⁷¹ (tau = 0.1 ps) was used to maintain the temperature at 300 K. For the production run, the system was propagated in the NVT ensemble (300 K) for a total of 2 microseconds with 4 replicas (500ns/replica). For all simulations, long-range electrostatics were treated with particle-mesh Ewald summation.⁷² A cut-off of 1.0 nm was used for Lennard-jones and coulombic interactions. All bonds between hydrogens and heavy atoms were constrained using the LINCS algorithm⁷³ allowing for a simulation time step of 2 fs. All simulations were conducted using GROMACS 2016.⁷⁴

Biasing Scheme

We used the parallel bias metadynamics⁷⁵ scheme which allows for efficient sampling of such high-dimensional free energy landscapes. To ensure that all binding conformations of the peptide were explored, we biased 4 collective variable – 3 for structural elements of the peptide (radius of gyration, alpha-helical and 3₁₀-helix coordination numbers) and 1 for the distance of the peptide from the surface. The radius of gyration was calculated using all alpha carbon atoms. Coordination numbers were calculated using carbonyl oxygen and amide hydrogen contacts within 0.30 nm of the i^th and i+4^th residues for the alpha-helix and i^th and i+3^th residues for the 3₁₀-helix. The distance was calculated by using the z-distance between the center of mass of all alpha-carbon atoms and a reference surface atom. The peptide was restrained to explore only distances below 2 nm so that the peptide only explores surface-bound structures. The parameters for the bias were – initial hill height of 1.2552 kJ/mol, hill deposition pace of 1 hill/500 steps, biasfactor of 10, and temperature 300 K. The collective variables had hill widths of 0.5 nm (radius of gyration and distance), and 0.1 (alpha-helical and 3₁₀-helix coordination numbers).

The combination of classical MD with an enhanced sampling scheme promotes the exploration of multiple conformation states of the peptide. However, the prevalence of specific conformations can be over-predicted or under-predicted according to the accuracy of the force field used.⁷⁶ To correct for these inaccuracies and ensure that experimentally relevant conformations are correctly represented in the simulation, we combined the parallel bias enhanced sampling method with metainference.^48,49 Using Bayesian inference, this approach allows for the NMR chemical shifts to be used as restraints on the predicted chemical shifts averaged over an ensemble of peptide conformations. Chemical shifts were calculated on-the-fly using CAMSHIFT⁴⁷ (as implemented in the PLUMED 2.4⁷⁷ library). Our criteria for assessing convergence, and demonstration of convergence of the calculations are discussed in the SI (Figures S8–10).

Validation of Peptide Structures

After the production simulations are completed, the simulation trajectories are analyzed to find the most representative structures of the surface-bound peptide. Since the trajectories are large, every 50^th frame is used for analysis, resulting in 20000 frames. Further, some frames were excluded from the trajectory as mentioned in Section 1 in the SI. Finally, the chemical shifts calculated at every frame. Backbone chemical shifts were calculated on the fly using CAMSHIFT⁴⁷ as implemented in PLUMED, whereas side-chain chemical shifts were calculated using SHIFTX⁴⁶ since CAMSHIFT does not provide side chain chemical shifts.

At the end of the simulation, we can use the accumulated bias potential as weights to calculate the free energy with respect to another variable (separate from the variables biased in the original simulation).⁷⁸ A weight (=$e^{\frac{V}{kT}}$, where kT = 2.5 kJ/mol at 300 K, V is the bias at each frame) is assigned to each frame using the bias potential as a quasi-static bias potential. These weights were used to calculate the weighted average chemical shift from the trajectory, following the protocol of Torrie and Valleau.⁷⁹ The root-mean-squared error of the backbone and side-chain chemical shifts, with reference to the experimentally determined values, were calculated using the formula:

$$RMSE={\left(\sum _{i=1}^N{\left({\text{CS}}_{i,predicted}-{\text{CS}}_{i,exp}\right)}^2\right)}^{0.5}$$

Detection of Top-weighted Peptide Conformations

The structures of the peptide in the trajectory are identified and clustered using the gromos⁸⁰ method (RMSD calculation using alpha-carbon atoms with cut-off of 0.20 nm). Then, the cluster number assigned to each frame of the trajectory is reweighted with the above-mentioned weights.

Detection of Top-weighted Peptide Orientations

To study relaxation of the sidechains and orientation of the peptides on the surfaces, the top three weighted conformations for each surface were extracted and simulated for 50 ns in the NVT ensemble (300 K). The backbone was held rigid during the simulation using a restraint on the RMSD of the C-alpha carbons using a harmonic restraining potential (Value = 0.15 nm; Kappa = 10000.0). No other bias was added during these simulations. The trajectories were viewed in VMD to identify the residues that interact with each surface (shown in Figure S4–6). For a quantitative analysis of contacting residues, the normal surface distance of side-chain atoms (Cγ, Cδ, Cε, and Cζ) from a reference surface atom was calculated for the whole trajectory. The probability of the occurrence of the side-chain atom at a certain distance from the surface was calculated using the kernel density estimation technique (shown in Figure S7).

Detection of the secondary structure of each residue

A secondary structure was assigned to each residue of SNa15 in each frame of the trajectory using the do_dssp functionality of the GROMACS simulation engine. The probability of each residue being in a certain secondary structure was calculated using the reweighting procedure mentioned above.

Scheme 1.

Schematic of the modeling and simulation workflows used in this study