Abstract
Background:
The objective of this study was to compare cortical thickness of rib specimens scanned with clinical computed tomography (clinical-CT) at 0.5 and 1.0 mm slice thickness versus micro-CT at 0.05 mm slice thickness. Cortical thickness variation and accuracy was explored by anatomical region (anterior vs. lateral) and cross-sectional quadrants (superior, interior, inferior, and exterior).
Methods:
A validated cortical thickness algorithm was applied to clinical-CT and micro-CT scans of 17 rib specimens from six male post mortem human subjects aged 42–81 years. Each rib specimen was segmented and the thickness measurements were partitioned into cross-sectional quadrants in the anterior and lateral regions of the rib. Within each rib quadrant, the following were calculated: average thickness ± standard deviation, mean thickness difference between clinical-CT and micro-CT, and a thickness ratio between clinical-CT and micro-CT. Correlations from linear regression and paired-t tests were determined for paired clinical-CT and micro-CT results.
Results:
On average, the 0.5 mm clinical-CT underestimated the micro-CT thickness by 0.005 mm, while the 1.0 mm clinical-CT overestimated the micro-CT thickness by 0.149 mm. Thickness derived from 0.5 mm clinical-CT showed greater significant linear correlations (p < 0.05) with micro-CT thickness compared to 1.0 mm clinical-CT.
Conclusions:
The small mean differences and thickness ratios near 1 show validation for the cortical thickness algorithm when applied to rib clinical-CT scans. Using clinical-CT scans as way to accurately measure rib cortical thickness offers a non-invasive way to analyze millions of CT scans collected each year from males and females of all ages.
Keywords: Thorax, Ribs, Cortical thickness, Age, Computed tomography, Micro-CT
1. Introduction
Rib fractures are a common injury following motor vehicle crashes (MVCs), falls, and lung radiation therapy [1–9]. Rib fractures have been linked to reductions in bone strength, bone mineral density, and cortical thickness changes that can occur with age [10,11] or radiation treatment [12]. Rib fractures in older adults pose almost double the risk of mortality and morbidity compared to younger adults and result in a greater economic burden [13–15]. Accurate measurement of rib cortical thickness for men and women of all ages could lead to enhanced tools and models for predicting [16–22] and surgically repairing [23–25] rib fractures in individual patients and the population. Finite element (FE) human body models have been developed to better understand the injury mechanisms leading to rib fractures [19,20]. Several age-specific thoracic FE models incorporate material properties and geometries representing young adults versus older adults [16,18,21,22]. Most FE models use simplified cortical shells with constant thickness even though rib cortical thickness varies by anatomical region (anterior, lateral, and posterior) and cross-sectional quadrant (superior, interior, inferior, and exterior) [26–35]. Incorporating region-specific rib cortical thickness variations in FE models could improve biofidelity and injury prediction accuracy.
FE model geometry is often developed from computed tomography (CT) images, but the resolution of CT scans collected in clinical care limits the level of detail. Rib cortical thickness ranges from approximately 0.5 mm–2 mm [36,37], and clinical-CT scan resolution is on the order of 0.6 mm/pixel to 1 mm/pixel, making it difficult to distinguish cortical bone boundaries. Micro-CT images provide higher resolution, but the small-bore size and higher radiation exposure limit use to post mortem human subjects (PMHS). Most PMHS tested in experiments are older and generally have a thinner rib cortex compared to the general population. An algorithm developed by Treece et al. has been used to estimate cortical bone thickness from clinical-CT images [38]. This algorithm has been validated on the femoral head and neck, hip, and skull [39–41] and recently on the ribs [42] and will be referred to as the cortical density method (CDM). Prior validation of the CDM algorithm (version 1; v1) achieved an error prediction of −0.05 ± 0.22 mm from clinical-CT scans of 34 rib specimens collected from a single PMHS subject (54 years old). However, comparison has not yet been done on the more recent version 2 (v2) of the CDM algorithm or extended to PMHS specimens of varying ages. Further, comparison data has not been reported for the ribs on a regional basis (e.g. anterior versus lateral; cross-sectional quadrants). Thus, the objective of this study is to measure local rib cortical thickness variation in cross-sectional quadrants of the anterior and lateral rib regions of six male PMHS scanned with clinical-CT scans at two resolutions (0.5 mm and 1.0 mm) using the CDM v2, and to compare these measurements to those obtained from micro-CT scans of the same specimens. Further validation of this algorithm will support future use of clinical-CT scans to non-invasively measure rib cortical thickness variation from males and females of various ages.
2. Methods
2.1. Scan collection and image segmentation
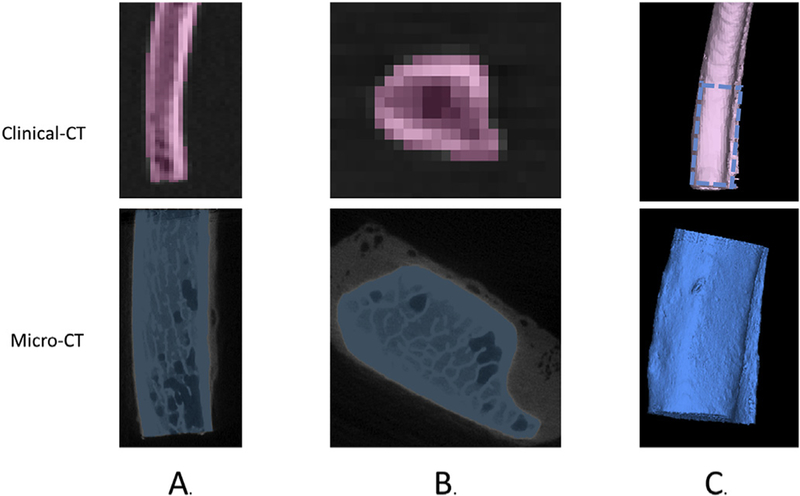
Seventeen rib specimens were obtained from three-point bending tests performed by Kemper et al. [26]. These rib specimens were previously fractured and consisted of anterior and lateral regions of left ribs 4 through 7 of six male PMHS ranging from 42 to 81 years old (Table 1). Although the specimens had been previously fractured, the fractured part of the rib was excluded from the scan. Each specimen was scanned using micro-CT (slice thickness 0.05 mm) and clinical-CT (slice thickness 0.50 mm and 1.0 mm) with the centerline of rib specimen oriented to be parallel to the scanner bed and the superior and inferior surfaces of the specimen oriented as defined in Fig. 1. By carefully documenting the orientation of each specimen scanned with clinical-CT and micro-CT, homologous regions on each specimen could be identified to directly compare cortical thickness between the two scanning methods. The clinical-CT specimens were embedded in gelatin to simulate soft tissue (Fig. 1A). The micro-CT specimens were scanned in air, but a fixture was used to suspend the specimens so they were not laying against a surface (Fig. 1B). This was done because the partial volume effects of the surrounding soft tissue would matter more for the clinical-CT scans due to the lower resolution. The ribs of each subject were segmented individually using a semi-automated technique in Mimics (Materialise, Leuven, Belgium). Segmentation of the ribs involved automated bone thresholding based on Hounsfield units for cortical bone to create a mask. Next, region growing was used to select the connected voxels in the cortical bone mask that belonged to the specimen. Hole filling was then used to fill the interior of the cortical bone mask. Finally, manual editing was conducted to fill in any missing voxels or exclude any that should not have been in the segmentation mask of the specimen. Each segmented rib was exported as an individual stereolithography (STL) geometry model (Fig. 2).
Table 1.
Specimen ID, age, rib analyzed, and anatomical region.
| Specimen ID | Age | Left Rib Level | Anatomical Region |
|---|---|---|---|
| 37 | 56 | 7 | Anterior |
| 5 | Lateral | ||
| 40 | 66 | 4 | Anterior |
| Lateral | |||
| 48 | 45 | 6 | Lateral |
| 7 | |||
| 50 | 72 | 4 | Lateral |
| 5 | |||
| 6 | |||
| 7 | |||
| 52 | 42 | 7 | Anterior |
| 4 | Lateral | ||
| 59 | 81 | 4 | Anterior |
| 5 | Lateral | ||
| 6 | Anterior | ||
| Lateral | |||
| 7 | Lateral |
Fig. 1.
Rib orientation in clinical-CT (A) and micro-CT (B) scans to ensure proper in-vivo orientation was mapped to segmentation and thickness analysis. Definitions of the cross-sectional quadrants are shown below the box.
Fig. 2.
Rib specimen segmentation from the 0.50 mm slice thickness clinical-CT (pink) and micro-CT (blue) scans showing the sagittal view (A), axial view (B), and 3-D reconstruction of the micro-CT (blue) and clinical-CT (pink) with the region scanned with both modalities designated by dashed blue lines (C).
2.2. Cortical thickness measurement
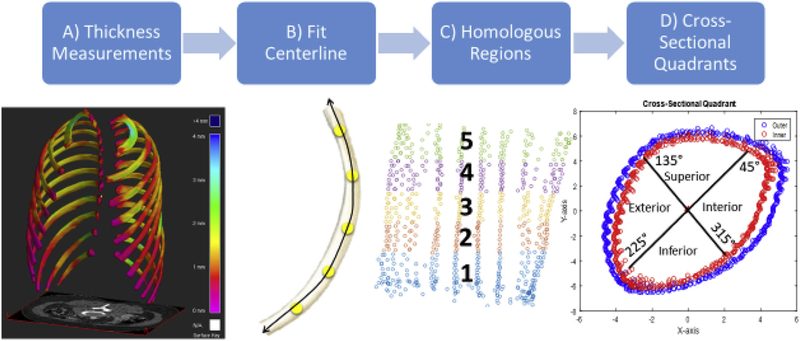
The STL model of each segmented specimen was imported as a 3D surface model along with the subject’s corresponding clinical-CT or micro-CT scan into the open source software, Stradwin, published by Treece et al. [38,40,43]. The CDM v2 method was applied to clinical-CT scans of the 17 rib specimens to estimate cortical thickness [44]. The CDM algorithm uses the bone and surrounding soft tissue greyscale values to estimate the thickness of the cortical bone at each of the STL vertices. The algorithm identifies the inner and outer cortical surface of the bone and calculates the thickness as the distance between the inner and outer surfaces (Fig. 3A). To improve the cortical thickness estimation used by the CDM v1, an improvement was made to incorporate a local estimation of the cortical density as described in Treece et al., 2015 [44]. This method, known as CDM v2, was applied to all clinical-CT scans in this study. The full width at half maximum model-based fit implemented in Stradwin was used to measure cortical thickness from the micro-CT scans. The full width at half maximum technique is considered the “gold standard” when there is a high resolution, unblurred CT scan (such as a micro-CT scan) [40]. Outputs from Stradwin included inner and outer cortical surface point clouds defined by Cartesian coordinates, as well as the cortical thickness for each point (measured as the distance between the inner and outer surface). Approximately 2500 and 300,000 cortical thickness measurements were obtained per specimen for the clinical-CT and micro-CT scans, respectively.
Fig. 3.
Partitioning the rib specimen into homologous regions.
2.3. Registering Clinical-CT and Micro-CT outputs
Each specimen’s STL models in the clinical-CT and micro-CT co-ordinate systems were registered in Geomagic Studio (3D Systems, Rock Hill, SC). The best-fit alignment tool was used to rigidly register the STL models using a rotation and translation matrix, and the clinical-CT specimens were then cropped to match the micro-CT samples (Fig. 4). This ensured that the specimens were registered for direct comparison of clinical-CT and micro-CT derived cortical thicknesses in the different anatomical regions (anterior versus lateral) and cross-sectional quadrants.
Fig. 4.
Geomagic Studio best fit alignment tool used to align the micro-CT segmentation (blue) with the 0.50 mm slice thickness clinical-CT segmentation (orange) to allow for direct comparison of regions within the specimen.
2.4. Partitioning cortical thickness measurements into homologous regions
To analyze local thickness variation on each rib, the point clouds from each specimen were partitioned into homologous regions using MATLAB (The MathWorks, Natick, MA). The first step involved fitting a centerline consisting of equidistant points spanning the rib specimen (Fig. 3B). Perpendicular planes along the centerline were then placed to partition the rib specimen into five homologous regions and a centroid was calculated for each homologous region (Fig. 3C). Each homologous region, including the centerline through the region, was centered about its centroid. Several rotation matrices were applied to orient the points correctly in the x-y plane and a polar coordinate system was used to define the angular location “θ” of each point in the rib cross-section. For each rib cross-section, the superior-most point was identified according to the in-vivo scan orientation since all specimens were scanned in the same orientation. The superior most point was then located at θ = 90, in the polar coordinate system, which was defined at the positive y-location corresponding to x = 0, with the centerline of the homologous region positioned at the origin. The superior, interior, inferior, and exterior quadrants of the cross-section were then defined (Fig. 3D). Cortical thickness measurements were analyzed in each cross-sectional quadrant of the anterior and lateral rib specimens. The following measurements were computed for each rib specimen using both clinical-CT and micro-CT scan data:
The mean rib thickness and standard deviation in the anterior and lateral regions and cross-sectional quadrants in each modality; For each cross-sectional quadrant, there were over 500 clinical-CT thickness measurements and 70,000 micro-CT thickness measurements per specimen from which an average and standard deviation were calculated.
The rib thickness ratio: (clinical CT thickness)/(micro CT thickness), where the thicknesses used in the ratio are the mean rib thicknessfrom clinical-CT and micro-CT calculated in #1 above;
The rib thickness mean difference: (clinical CT thickness) − (micro CT thickness), where the thicknesses used in the difference calculation are the mean rib thickness from clinical-CT and micro-CT calculated in #1 above
A coefficient of determination (R2) from linear regression between the paired clinical-CT and micro-CT rib thicknesses.
A paired t-test for both the 1.0 mm clinical-CT vs the micro-CT and the 0.5 mm clinical-CT vs the micro-CT.
3. Results
The mean difference between the rib thicknesses derived from clinical-CT versus micro-CT data was compared to gain insight on the accuracy of the CDM v2 method and to compare to published results from CDM v1 [42]. Thickness ratios greater than 1 and a positive mean difference indicate the CDM v2 algorithm is overestimating the thickness, and thickness ratios under one or a negative mean difference indicate an underestimation of thickness. Fig. 5 shows good qualitative agreement of micro-CT and clinical-CT derived thickness mapped onto the rib specimens. Individual specimen results for all regions and quadrants can be found in Appendix A and B.
Fig. 5.
Example illustrating good agreement between cortical thickness measurements for the micro-CT and clinical-CT scans of the same rib specimen. Interior (A) and exterior (B) views shown as well as the thickness difference for a 2-D cross section of the clinical-CT with cross-sectional quadrants illustrated (C).
The average thickness ± standard deviation amongst the anterior rib specimens analyzed was 0.99 ± 0.39 mm (0.5 mm clinical-CT), 1.12 ± 0.43 mm (1.0 mm clinical-CT), and 1.00 ± 0.38 mm (micro-CT). The average thickness ± standard deviation amongst the lateral rib specimens analyzed was 1.14 ± 0.43 mm (0.5 mm clinical-CT), 1.30 ± 0.48 mm (1.0 mm clinical-CT), and 1.14 ± 0.46 mm (micro-CT). Within cross-sectional quadrants, lateral rib thickness was greater than anterior rib thickness in both the clinical-CT and micro-CT scans, except in the exterior quadrant for the micro-CT (Fig. 6).
Fig. 6.
Average anterior quadrant thickness (A) and lateral quadrant (B) with standard deviations for rib specimens.
When comparing 0.5 mm clinical-CT to micro-CT, the range of rib thickness ratios was 0.91–1.00 (anteriorly) and 0.95–1.12 (laterally), indicating good agreement between clinical-CT and micro-CT (Fig. 7). Anterior thickness was underestimated in all quadrants (0.91–1.00). Lateral thickness was underestimated in the inferior and superior quadrants (0.95, 0.98), but overestimated in the interior and exterior quadrants (1.02, 1.12). When comparing 1.0 mm clinical-CT to micro-CT, the range of rib thickness ratios was 1.07–1.19 (anteriorly) and 1.04–1.38 (laterally), further indicating good agreement between the clinical-CT and micro-CT (Fig. 7). Anterior thickness was overestimated in all quadrants with ratios ranging from 1.07 (interior) to 1.19 (exterior). Lateral thickness was also overestimated in all quadrants with ratios ranging from 1.04 (interior) to 1.38 (exterior). Overall, the thickness ratios indicate the rib thickness estimated from 0.5 mm clinical-CT is within 0% (perfect) to 12% of the micro-CT thickness, with an average 2% overestimation. For 1.0 mm clinical-CT, the estimated rib thickness is within 4–19% of the micro-CT thickness (except in the lateral-exterior quadrant), with an average 17% overestimation.
Fig. 7.
Clinical-CT/micro-CT thickness ratios in the anterior (A) and lateral (B) quadrants of the rib specimens.
Small mean differences were observed when comparing rib thicknesses derived from clinical-CT versus micro-CT (Table 2). When comparing 0.5 mm clinical-CT to micro-CT, mean differences averaged −0.016 mm (anteriorly) and −0.001 mm (laterally). When comparing 1.0 mm clinical-CT to micro-CT, mean differences averaged −0.124 mm (anteriorly) and 0.158 mm (laterally). Overall, rib thicknesses were underestimated by 0.005 mm for 0.5 mm clinical-CT and overestimated by 0.149 mm for 1.0 mm clinical-CT (Appendix A and B).
able 2.
Average mean differences (clinical CT – micro CT ) for each anterior and lateral cross-sectional quadrant.
| Clinical-CT Slice Thickness | Anatomical Region | All Quadrants (mm) | Superior (mm) | Interior (mm) | Inferior (mm) | Exterior (mm) |
|---|---|---|---|---|---|---|
| 0.5 mm | Anterior | −0.016 | −0.088 | 0.024 | −0.002 | 0.258 |
| Lateral | −0.001 | −0.008 | 0.029 | −0.083 | 0.066 | |
| 1.0 mm | Anterior | 0.124 | 0.090 | 0.122 | 0.162 | 0.223 |
| Lateral | 0.158 | 0.107 | 0.060 | 0.165 | 0.412 |
Table 3 shows the R2 coefficients and the p-values from the linear regression and the paired t-test of the rib thicknesses derived from clinical-CT versus micro-CT. For the 0.5 mm clinical-CT, all regressions were significant (p < 0.05) except for the anterior-superior quadrant. For the 1.0 mm clinical-CT, regressions were significant when grouping all quadrants, and for the anterior-inferior, anterior-exterior, lateral-superior, and lateral-exterior quadrants (p < 0.05). Scatterplots of the rib thicknesses derived from clinical-CT versus micro-CT show clustering around the equivalency line, further indicating the accuracy of the CDM v2 method used to obtain cortical thickness (Fig. 8). Furthermore, the paired t-test for the 0.5 mm clinical-CT showed no statistically significant differences compared to micro-CT thicknesses across all cross-sectional quadrants of the anterior and lateral regions. For the 1.0 mm clinical-CT scans, thickness was significantly different from micro-CT in the exterior and inferior quadrants of the anterior and lateral regions, and the all quadrant measure of the lateral region.
Table 3.
Linear regression of paired clinical-CT and micro-CT thickness measurements with R2 and p-values for the anterior and lateral cross-sectional quadrants (pr) and p-values for the paired t-test between clinical-CT and micro-CT thickness measurements (pt).
| Clinical-CT Slice Thickness | Anatomical Region | All Quadrants | Superior Quadrant | Interior Quadrant | Inferior Quadrant | Exterior Quadrant |
|---|---|---|---|---|---|---|
| 0.5mm | Anterior | R2 = 0.36 pr = 0.01* pt = 0.90 |
R2 = <0.01 pr=0.90 pt = 0.32 | R2 = 0.33 pr < 0.01* pt = 0.97 |
R2 = 0.23 pr = 0.02* pt = 0.98 |
R2 = 0.65 pr < 0.01* pt = 0.86 |
| Lateral | R2 = 0.76 pr < 0.01* pt = 0.99 |
R2 = 0.58 pr < 0.01* pt = 0.90 |
R2 = 0.77 pr < 0.01* pt = 0.26 |
R2 = 0.14 pr < 0.01* pt = 0.44 |
R2 = 0.46 pr < 0.01* pt=0.11 |
|
| 1.0mm | Anterior | R2=0.51 pr < 0.01* pt = 0.09 |
R2 = 0.01 pr = 0.74 pt=0.36 |
R2 = 0.06 pr = 0.25 pt = 0.53 |
R2 = 0.23 pr = 0.02* pt = 0.05* |
R2=0.34 pr < 0.01* pt = 0.01* |
| Lateral | R2 = 0.52 pr < 0.01* pt < 0.01* |
R2 = 0.23 pr < 0.01* pt = 0.10 |
R2 = 0.02 pr = 0.32 pt = 0.18 |
R2 = <0.01 pr = 0.65 pt = 0.01* |
R2 = 0.17 pr < 0.01* pt < 0.01* |
Fig. 8.
Rib thicknesses derived from 0.5 mm clinical-CT (A) and 1.0 mm clinical-CT (B) plotted versus micro-CT thickness. Thicknesses are plotted for all quadrants analyzed in the anterior and lateral rib specimens.
4. Discussion
The CDM v2 method applied to clinical-CT scans obtained cortical thickness estimates similar to thickness measured from micro-CT using the full width at half maximum technique. Rib thicknesses measured in clinical-CT scans obtained at 0.5 mm slice thickness more closely matched micro-CT measurements, compared to clinical-CT scans obtained at 1.0 mm slice thickness (Fig. 6; Table 2). Rib thicknesses derived from 0.5 mm clinical-CT had a roughly equal distribution of underprediction and overprediction errors, whereas 1.0 mm clinical-CT consistently overpredicted thickness (Fig. 6). The results indicated that the lateral regions of the ribs are thicker than the anterior regions. A possible explanation for this difference could be the width-to-height ratio found in previous studies. The ribs are almost two times as high as they are wide in the anterior region and the superior and inferior regions are thinner than the interior and exterior regions. These findings are in agreement with literature values [26,37]. A slightly wider range of rib thicknesses was computed from clinical-CT compared to micro-CT (Fig. 7). However, the standard deviations of the thicknesses derived from clinical-CT and micro-CT were similar (Fig. 6), and the thicknesses fall within the range of published literature values [26,45].
Comparing to published values by Holcombe et al. [42] with a mean difference between clinical-CT and micro-CT of −0.03 mm (0.37 mm resolution CT) and −0.05 mm (0.98 mm resolution CT) for the CDM v1, the CDM v2 algorithm shows improvement for clinical-CT resolutions in this range (−0.005 mean difference for 0.5 mm clinical-CT), possibly due to the use of local density calculations to estimate cortical thickness. However, our study found an average 0.149 mm overestimation of rib thickness in 1.0 mm clinical-CT, which may indicate reduced accuracy compared to the CDMv1. However, direct comparison is challenging since the CDMv1 was previously validated using rib specimens from a single 54 year old PMHS [42], and our results may reflect the CDM algorithm’s accuracy when applied to 1.0 mm clinical-CT scans of subjects of varying ages. The overestimation may be attributed to the thicker slice thickness that the scans were collected at (1.0 mm compared to the more accurate 0.5 mm slice thickness).
This study allowed for analysis of cortical thickness at precise locations throughout the rib specimens by identifying cross-sectional quadrants within homologous regions of the specimen. Using clinical-CT scans and the CDM v2 algorithm as an alternative to micro-CT scans allows for future in vivo collection of cortical thickness data from a large population of subjects. This is highly encouraging because accurate cortical thickness measurements can be collected in a timely manner from patients as well as from existing databases. An FE modeling application would take information from these databases using this technique to develop more biofidelic models of the thorax that incorporate age- and sex-specific variations in cortical thickness. Previous studies have shown that FE models with variable cortical shell thickness more accurately simulate fracture and the force-displacement relationship in the rib [34,45]. With the application of this technique, detailed human body models can be constructed and validated to improve the accuracy of injury prediction in computational simulation of thoracic trauma. Specific age-based models that have been developed can be improved by incorporating accurate rib cortical thickness data collected from clinical-CT scans [16,18,21,22,46]. A clinical application of the CDM algorithm would be to apply the methods presented to a wide range of ages and regress rib cortical thickness with age and use the results to improve existing age-based regression functions in the literature [47]. Normative data on rib cortical thickness with age and sex would be valuable to surgical device design (e.g. rib fixation), and the identification of patients who may be at high risk for rib fractures due to osteoporosis or radiation-induced bone loss. Rib fixation devices require screws that are usually 12–16 mm thick and the plate thickness is 1–3.5 mm [48]. The 0.149 mm overestimation by the 1.0 mm clinical-CT scans falls well below the minimum thickness criteria for the screws and plate and would not have negative clinical outcomes. This over-estimation is also negligible compared to the thickness change necessary to induce fracture risk based on findings of one study showing that patients receiving stereotactic body radiation therapy experienced rib fractures at the treatment site following a 15% decrease (0.25–0.3 mm change) in rib thickness [12]. The CDM v2 algorithm offers a non-invasive method to opportunistically mine the millions of CT scans collected each year around the world in order to quantify rib cortical thickness from males and females of varying ages [49].
4.1. Limitations
The sample size of rib specimens analyzed is small (17) and was not split evenly between anterior (5) and lateral (12) regions. Despite the limited sample size, different anatomical regions of the ribs were analyzed as well as cross-sectional quadrants. Another limitation is the averaging of both the clinical-CT and micro-CT data. For each cross-sectional quadrant, there were over 500 clinical-CT thickness measurements and 70,000 micro-CT thickness measurements per specimen that were averaged. This captured the overall thickness within a cross-sectional quadrant but does not characterize variability in thickness within that quadrant. Furthermore, more analysis needs to be done to improve upon the 0.149 average overestimation for the 1.0 mm clinical-CT scans. However, the standard deviations reported give some indication of the per-subject variability in thickness in each cross-sectional quadrant. Furthermore, there are also changes in material properties, gross geometry, and cross-sectional changes that will alter the strength and injury tolerance of the ribs that were not measured in this study.
5. Conclusions
This study compared rib cortical bone thickness for 17 rib specimens gathered from six PMHS subjects spanning ages 42–81 using clinical-CT scans and micro-CT scans. The study took a novel approach by adapting a cortical thickness algorithm developed originally for the femur, and applying it to quantify its accuracy in estimating cortical thickness in homologous regions of the ribs. Compared to the micro-CT, the CDM v2 algorithm found similar clinical-CT derived rib cortical thicknesses in the anterior and lateral cross-sectional quadrants. The results also show an improvement in overall accuracy when using a smaller slice thickness (0.5 mm compared to 1.0 mm). Accurately characterizing the cortical bone thickness variations in the ribs with age will allow for more biofidelic models of the ribcage to be developed for use in simulating thoracic trauma, designing rib fracture devices, and detecting osteoporosis or radiation-induced cortical thinning of the ribs.
6. Summary
The objective of this study was to compare rib cortical thickness measured in anterior and lateral cross-sectional quadrants of rib specimens scanned with clinical computed tomography (clinical-CT) at 0.5 and 1.0 mm slice thickness versus micro-CT at 0.05 mm slice thickness. Rib cortical thickness variation and accuracy was explored by anatomical region (anterior vs. lateral) and cross-sectional quadrant (superior, interior, inferior, and exterior) across middle age to older adults.
A cortical thickness algorithm validated for sub-millimeter thickness estimation was applied to clinical-CT and micro-CT scans of 17 rib specimens taken from six male post mortem human subjects aged 42–81 years. Each rib specimen scanned with clinical-CT (at two different resolutions) and micro-CT was segmented and the rib thickness measurements were partitioned into superior, interior, inferior, and exterior quadrants in the anterior and lateral regions of the rib. This grouped the clinical-CT and micro-CT derived thicknesses into homologous (i.e. comparable) regions across all specimens. Within each rib quadrant, the following were calculated: average rib thickness ± standard deviation (SD) in each modality, the mean rib thickness difference between clinical-CT and micro-CT, and a rib thickness ratio between clinical-CT and micro-CT. Correlations were determined from linear regression of paired clinical-CT and micro-CT results.
The average thickness measured using clinical-CT and micro-CT was very similar. On average, the 0.5 mm clinical-CT slightly underestimated the micro-CT thickness (−0.016 and −0.001 mm mean difference in the anterior and lateral regions respectively; 0.98 and 0.99 clinical-CT:micro-CT thickness ratio in the anterior and lateral regions respectively), while the 1.0 mm clinical-CT slightly overestimated the micro-CT thickness (0.124 and 0.158 mm mean difference in the anterior and lateral regions respectively; 1.13 and 1.14 thickness ratio in the anterior and lateral regions). Thickness derived from clinical-CT was linearly correlated with micro-CT thickness for all region-quadrants (p < 0.05), except for the anterior-superior quadrant (0.5 mm clinical-CT), and the anterior-superior, anterior-interior, lateral-interior, and lateral-inferior quadrants (1.0 mm clinical-CT).
The small mean differences and thickness ratios near 1 show validation for the cortical thickness algorithm when applied to rib clinical-CT scans. Results indicate the algorithm can detect cortical thickness variation in the anterior and lateral regions and within cross-sectional quadrants. Accuracy was improved in clinical-CT scans acquired at 0.5 mm compared to 1.0 mm slice thickness. Using clinical-CT scans as way to accurately measure rib cortical thickness offers a non-invasive way to opportunistically mine the millions of CT scans collected each year from males and females of all ages.
Acknowledgements
We gratefully acknowledge Dr. Andrew Kemper for providing the rib specimens used in this study as well as Xin Ye, Sarah Lynch, and Jennifer Dawkins for their assistance with data collection and analysis. Funding: This study was funded by the National Highway Traffic Safety Administration under Cooperative Agreement Number DTN22-09-H-00242. Views expressed are those of the authors and do not represent the views of NHTSA.
APPENDIX A
Table A1.
Measured thickness (in mm) from all anterior rib specimens. Abbreviations: Ant (Anterior); Sup (Superior); Int (Interior); Inf (Inferior); Ext (Exterior).
| Specimen-Rib | Measure | All Quadrants | Ant-Sup Quadrant | Ant-Int Quadrant | Ant-Inf Quadrant | Ant-Ext Quadrant |
|---|---|---|---|---|---|---|
| 37–7 | Avg ± SD (CT 0.5 mm) | 1.38 ± 0.57 | 0.91 ± 0.41 | 1.62 ± 0.24 | 1.10 ± 0.36 | 2.09 ± 0.31 |
| Avg ± SD (CT 1.0 mm) | 1.38 ± 0.48 | 1.17 ± 0.41 | 1.67 ± 0.29 | 1.28 ± 0.47 | 1.69 ± 0.54 | |
| Avg ± SD (mCT) | 1.06 ± 0.41 | 0.84 ± 0.40 | 1.14 ± 0.28 | 0.91 ± 0.33 | 1.44 ± 0.32 | |
| Ratio: CT 0.5 mm/mCT | 1.30 | 1.07 | 1.42 | 1.20 | 1.45 | |
| Ratio: CT 1.0 mm/mCT | 1.30 | 1.38 | 1.47 | 1.40 | 1.17 | |
| Mean Diff. 0.5 mm-mCT | 0.32 | 0.07 | 0.48 | 0.19 | 0.65 | |
| Mean Diff. 1.0 mm-mCT | 0.32 | 0.33 | 0.53 | 0.37 | 0.25 | |
| 40–4 | Avg ± SD (CT 0.5 mm) | 0.70 ± 0.25 | 0.62 ± 0.31 | 0.63 ± 0.17 | 0.75 ± 0.19 | 0.85 ± 0.20 |
| Avg ± SD (CT 1.0 mm) | 0.90 ± 0.37 | 0.75 ± 0.42 | 0.74 ± 0.27 | 1.00 ± 0.27 | 1.16 ± 0.31 | |
| Avg ± SD (mCT) | 0.90 ± 0.33 | 0.94 ± 0.41 | 0.93 ± 0.24 | 0.81 ± 0.26 | 0.99 ± 0.31 | |
| Ratio: CT 0.5 mm/mCT | 0.78 | 0.66 | 0.67 | 0.93 | 0.86 | |
| Ratio: CT 1.0 mm/mCT | 1.00 | 0.80 | 0.80 | 1.23 | 1.17 | |
| Mean Diff. 0.5 mm-mCT | −0.20 | −0.32 | −0.30 | −0.06 | 1.00 | |
| Mean Diff. 1.0 mm-mCT | 0.00 | −0.19 | −0.19 | 0.19 | 0.17 | |
| 52–7 | Avg ± SD (CT 0.5 mm) | 1.03 ± 0.48 | 0.76 ± 0.39 | 1.23 ± 0.32 | 0.92 ± 0.50 | 1.48 ± 0.28 |
| Avg ± SD (CT 1.0 mm) | 1.24 ± 0.51 | 0.98 ± 0.41 | 1.38 ± 0.31 | 1.15 ± 0.58 | 1.72 ± 0.27 | |
| Avg ± SD (mCT) | 1.20 ± 0.43 | 0.98 ± 0.40 | 1.32 ± 0.25 | 1.12 ± 0.46 | 1.53 ± 0.31 | |
| Ratio: CT 0.5 mm/mCT | 0.85 | 0.78 | 0.93 | 0.82 | 0.96 | |
| Ratio: CT 1.0 mm/mCT | 1.03 | 1.00 | 1.04 | 1.02 | 1.12 | |
| Mean Diff. 0.5 mm-mCT | −0.17 | −0.22 | −0.09 | −0.20 | −0.05 | |
| Mean Diff. 1.0 mm-mCT | 0.04 | 0.00 | 0.06 | 0.03 | 0.19 | |
| 59–4 | Avg ± SD (CT 0.5 mm) | 0.82 ± 0.32 | 0.73 ± 0.33 | 1.15 ± 0.33 | 0.81 ± 0.26 | 0.76 ± 0.23 |
| Avg ± SD (CT 1.0 mm) | 0.99 ± 0.40 | 0.90 ± 0.33 | 1.16 ± 0.45 | 0.93 ± 0.32 | 1.24 ± 0.54 | |
| Avg ± SD (mCT) | 0.84 ± 0.33 | 0.74 ± 0.30 | 1.12 ± 0.32 | 0.83 ± 0.32 | 0.85 ± 0.28 | |
| Ratio: CT 0.5 mm/mCT | 0.97 | 0.98 | 1.02 | 0.97 | 0.89 | |
| Ratio: CT 1.0 mm/mCT | 1.17 | 1.21 | 1.03 | 1.11 | 1.46 | |
| Mean Diff. 0.5 mm-mCT | −0.02 | −0.01 | 0.03 | −0.02 | −0.09 | |
| Mean Diff. 1.0 mm-mCT | 0.15 | 0.16 | 0.04 | 0.10 | 0.39 | |
| 59–6 | Avg ± SD (CT 0.5 mm) | 1.00 ± 0.34 | 0.94 ± 0.33 | 1.29 ± 0.22 | 1.00 ± 0.37 | 0.89 ± 0.19 |
| Avg ± SD (CT 1.0 mm) | 1.11 ± 0.40 | 1.05 ± 0.38 | 1.35 ± 0.29 | 1.04 ± 0.39 | 1.23 ± 0.50 | |
| Avg ± SD (mCT) | 0.99 ± 0.37 | 0.90 ± 0.35 | 1.38 ± 0.23 | 0.92 ± 0.36 | 1.11 ± 0.30 | |
| Ratio: CT 0.5 mm/mCT | 1.01 | 1.04 | 0.94 | 1.09 | 0.80 | |
| Ratio: CT 1.0 mm/mCT | 1.12 | 1.16 | 0.98 | 1.14 | 1.11 | |
| Mean Diff. 0.5 mm-mCT | −0.01 | 0.04 | 0.00 | 0.08 | −0.22 | |
| Mean Diff. 1.0 mm-mCT | 0.11 | 0.15 | 0.17 | 0.12 | 0.12 | |
| All Specimens | Avg ± SD (CT 0.5 mm) | 0.99 ± 0.39 | 0.79 ± 0.35 | 1.18 ± 0.26 | 0.92 ± 0.34 | 1.21 ± 0.24 |
| Avg ± SD (CT 1.0 mm) | 1.12 ± 0.43 | 0.97 ± 0.39 | 1.26 ± 0.32 | 1.08 ± 0.41 | 1.41 ± 0.43 | |
| Avg ± SD (mCT) | 1.00 ± 0.38 | 0.88 ± 0.37 | 1.18 ± 0.26 | 0.92 ± 0.35 | 1.18 ± 0.30 | |
| Ratio: CT 0.5 mm/mCT | 0.98 | 0.91 | 1.00 | 1.00 | 0.99 | |
| Ratio: CT 1.0 mm/mCT | 1.13 | 1.10 | 1.07 | 1.17 | 1.19 | |
| Mean Diff. 0.5 mm-mCT | −0.02 | −0.09 | 0.02 | 0.00 | 0.26 | |
| Mean Diff. 1.0 mm-mCT | 0.12 | 0.09 | 0.12 | 0.16 | 0.22 |
APPENDIX B
Table B1.
Measured thickness (in mm) from all lateral rib specimens. Abbreviations: Lat (Lateral); Sup (Superior); Int (Interior); Inf (Inferior); Ext (Exterior).
| Specimen-Rib | Measure | All Quadrants | Lat-Sup Quadrant | Lat-Int Quadrant | Lat-Inf Quadrant | Lat-Ext Quadrant |
|---|---|---|---|---|---|---|
| 37–5 | Avg ± SD (CT 0.5 mm) | 1.37 ± 0.36 | 1.43 ± 0.30 | 1.73 ± 0.34 | 1.10 ± 0.24 | 1.41 ± 0.22 |
| Avg ± SD (CT 1.0 mm) | 1.36 ± 0.47 | 1.17 ± 0.50 | 1.51 ± 0.41 | 1.36 ± 0.41 | 1.48 ± 0.45 | |
| Avg ± SD (mCT) | 1.20 ± 0.49 | 1.12 ± 0.40 | 1.68 ± 0.39 | 0.93 ± 0.45 | 1.17 ± 0.36 | |
| Ratio: CT 0.5 mm/mCT | 1.14 | 1.27 | 1.03 | 1.18 | 1.21 | |
| Ratio: CT 1.0 mm/mCT | 1.13 | 1.05 | 0.90 | 1.46 | 1.27 | |
| Mean Diff. 0.5 mm-mCT | 0.17 | 0.31 | 0.05 | 0.17 | 0.24 | |
| Mean Diff. 1.0 mm-mCT | 0.16 | 0.05 | −0.17 | 0.43 | 0.31 | |
| 40–4 | Avg ± SD (CT 0.5 mm) | 1.36 ± 0.57 | 1.49 ± 0.63 | 1.07 ± 0.49 | 1.26 ± 0.48 | 1.68 ± 0.49 |
| Avg ± SD (CT 1.0 mm) | 1.44 ± 0.51 | 1.32 ± 0.47 | 1.15 ± 0.55 | 1.52 ± 0.38 | 1.75 ± 0.47 | |
| Avg ± SD (mCT) | 1.23 ± 0.51 | 1.49 ± 0.52 | 1.00 ± 0.47 | 1.14 ± 0.41 | 1.29 ± 0.52 | |
| Ratio: CT 0.5 mm/mCT | 1.11 | 1.00 | 1.07 | 1.11 | 1.30 | |
| Ratio: CT 1.0 mm/mCT | 1.17 | 0.89 | 1.16 | 1.33 | 1.35 | |
| Mean Diff. 0.5 mm-mCT | 0.13 | 0 | 0.07 | 0.12 | 0.39 | |
| Mean Diff. 1.0 mm-mCT | 0.21 | −0.17 | 0.15 | 0.38 | 0.46 | |
| 48–6 | Avg ± SD (CT 0.5 mm) | 0.97 ± 0.37 | 0.98 ± 0.34 | 1.32 ± 0.20 | 0.71 ± 0.33 | 1.10 ± 0.20 |
| Avg ± SD (CT 1.0 mm) | 1.34 ± 0.49 | 1.33 ± 0.46 | 1.63 ± 0.36 | 1.10 ± 0.51 | 1.46 ± 0.39 | |
| Avg ± SD (mCT) | 1.11 ± 0.44 | 0.99 ± 0.39 | 1.34 ± 0.29 | 1.09 ± 0.54 | 1.14 ± 0.31 | |
| Ratio: CT 0.5 mm/mCT | 0.87 | 0.99 | 0.98 | 0.65 | 0.97 | |
| Ratio: CT 1.0 mm/mCT | 1.20 | 1.35 | 1.21 | 1.00 | 1.28 | |
| Mean Diff. 0.5 mm-mCT | −0.13 | −0.01 | −0.02 | −0.38 | −0.04 | |
| Mean Diff. 1.0 mm-mCT | 0.24 | 0.34 | 0.29 | 0.01 | 0.32 | |
| 48–7 | Avg ± SD (CT 0.5 mm) | 0.97 ± 0.39 | 1.10 ± 0.28 | 1.25 ± 0.34 | 0.62 ± 0.30 | 1.02 ± 0.31 |
| Avg ± SD (CT 1.0 mm) | 1.16 ± 0.46 | 1.24 ± 0.41 | 1.36 ± 0.30 | 0.93 ± 0.50 | 1.31 ± 0.38 | |
| Avg ± SD (mCT) | 1.10 ± 0.43 | 1.07 ± 0.39 | 1.20 ± 0.28 | 1.10 ± 0.54 | 1.07 ± 0.33 | |
| Ratio: CT 0.5 mm/mCT | 0.88 | 1.03 | 1.04 | 0.57 | 0.95 | |
| Ratio: CT 1.0 mm/mCT | 1.06 | 1.16 | 1.13 | 0.85 | 1.23 | |
| Mean Diff. 0.5 mm-mCT | −0.13 | 0.03 | 0.05 | −0.48 | −0.05 | |
| Mean Diff. 1.0 mm-mCT | 0.06 | 0.17 | 0.16 | −0.17 | 0.24 | |
| 50–4 | Avg ± SD (CT 0.5 mm) | 0.81 ± 0.38 | 0.66 ± 0.29 | 1.26 ± 0.38 | 0.77 ± 0.20 | 0.68 ± 0.35 |
| Avg ± SD (CT 1.0 mm) | 0.99 ± 0.41 | 0.86 ± 0.41 | 1.24 ± 0.42 | 0.96 ± 0.28 | 0.98 ± 0.47 | |
| Avg ± SD (mCT) | 1.04 ± 0.43 | 1.01 ± 0.45 | 1.26 ± 0.38 | 0.94 ± 0.38 | 0.92 ± 0.43 | |
| Ratio: CT 0.5 mm/mCT | 0.78 | 0.66 | 1.00 | 0.81 | 0.74 | |
| Ratio: CT 1.0 mm/mCT | 0.95 | 0.85 | 0.98 | 1.02 | 1.06 | |
| Mean Diff. 0.5 mm-mCT | −0.23 | −0.35 | 0 | −0.17 | −0.24 | |
| Mean Diff. 1.0 mm-mCT | −0.06 | −0.15 | −0.02 | 0.02 | 0.06 | |
| 50–5 | Avg ± SD (CT 0.5 mm) | 1.17 ± 0.42 | 0.89 ± 0.33 | 1.55 ± 0.37 | 1.07 ± 0.35 | 1.39 ± 0.23 |
| Avg ± SD (CT 1.0 mm) | 1.30 ± 0.55 | 1.17 ± 0.56 | 1.54 ± 0.38 | 1.11 ± 0.50 | 1.76 ± 0.51 | |
| Avg ± SD (mCT) | 1.06 ± 0.46 | 0.94 ± 0.41 | 1.45 ± 0.39 | 0.88 ± 0.39 | 1.04 ± 0.40 | |
| Ratio: CT 0.5 mm/mCT | 1.10 | 0.94 | 1.07 | 1.21 | 1.33 | |
| Ratio: CT 1.0 mm/mCT | 1.22 | 1.24 | 1.07 | 1.26 | 1.70 | |
| Mean Diff. 0.5 mm-mCT | 0.11 | −0.05 | 0.1 | −0.11 | −0.09 | |
| Mean Diff. 1.0 mm-mCT | 0.24 | 0.23 | 0.09 | 0.16 | 0.78 | |
| 50–6 | Avg ± SD (CT 0.5 mm) | 1.05 ± 0.45 | 0.93 ± 0.33 | 1.68 ± 0.47 | 0.84 ± 0.25 | 0.89 ± 0.22 |
| Avg ± SD (CT 1.0 mm) | 1.27 ± 0.44 | 1.21 ± 0.46 | 1.57 ± 0.42 | 1.13 ± 0.37 | 1.28 ± 0.41 | |
| Avg ± SD (mCT) | 1.11 ± 0.48 | 0.98 ± 0.39 | 1.58 ± 0.45 | 0.95 ± 0.38 | 0.98 ± 0.42 | |
| Ratio: CT 0.5 mm/mCT | 0.94 | 0.94 | 1.06 | 0.88 | 0.91 | |
| Ratio: CT 1.0 mm/mCT | 1.14 | 1.23 | 1.00 | 1.19 | 1.31 | |
| Mean Diff. 0.5 mm-mCT | −0.06 | −0.05 | 0.1 | −0.11 | −0.09 | |
| Mean Diff. 1.0 mm-mCT | 0.16 | 0.23 | −0.01 | 0.18 | 0.30 | |
| 50–7 | Avg ± SD (CT 0.5 mm) | 0.90 ± 0.44 | 0.91 ± 0.49 | 1.25 ± 0.37 | 0.65 ± 0.29 | 0.95 ± 0.36 |
| Avg ± SD (CT 1.0 mm) | 1.09 ± 0.49 | 1.13 ± 0.52 | 1.33 ± 0.33 | 0.82 ± 0.42 | 1.27 ± 0.46 | |
| Avg ± SD (mCT) | 1.05 ± 0.49 | 1.15 ± 0.52 | 1.22 ± 0.41 | 0.86 ± 0.47 | 1.01 ± 0.45 | |
| Ratio: CT 0.5 mm/mCT | 0.85 | 0.79 | 1.03 | 0.75 | 0.94 | |
| Ratio: CT 1.0 mm/mCT | 1.04 | 0.98 | 1.09 | 0.95 | 1.26 | |
| Mean Diff. 0.5 mm-mCT | −0.15 | −0.24 | 0.03 | −0.21 | −0.06 | |
| Mean Diff. 1.0 mm-mCT | 0.04 | −0.02 | 0.11 | −0.04 | 0.26 | |
| 52–4 | Avg ± SD (CT 0.5 mm) | 0.86 ± 0.38 | 0.70 ± 0.34 | 0.95 ± 0.33 | 0.93 ± 0.35 | 0.84 ± 0.43 |
| Avg ± SD (CT 1.0 mm) | 1.16 ± 0.52 | 0.86 ± 0.42 | 1.29 ± 0.38 | 1.32 ± 0.49 | 1.17 ± 0.66 | |
| Avg ± SD (mCT) | 0.99 ± 0.38 | 1.08 ± 0.41 | 1.06 ± 0.32 | 0.95 ± 0.37 | 0.83 ± 0.34 | |
| Ratio: CT 0.5 mm/mCT | 0.86 | 0.65 | 0.90 | 0.98 | 1.01 | |
| Ratio: CT 1.0 mm/mCT | 1.17 | 0.79 | 1.22 | 1.39 | 1.41 | |
| Mean Diff. 0.5 mm-mCT | −0.13 | −0.38 | −0.11 | −0.02 | 0.01 | |
| Mean Diff. 1.0 mm-mCT | 0.17 | −0.22 | 0.23 | 0.37 | 0.34 | |
| 59–5 | Avg ± SD (CT 0.5 mm) | 1.62 ± 0.44 | 1.68 ± 0.40 | 1.81 ± 0.29 | 1.38 ± 0.49 | 1.76 ± 0.30 |
| Avg ± SD (CT 1.0 mm) | 1.57 ± 0.45 | 1.63 ± 0.46 | 1.61 ± 0.38 | 1.35 ± 0.40 | 1.87 ± 0.37 | |
| Avg ± SD (mCT) | 1.36 ± 0.46 | 1.30 ± 0.47 | 1.79 ± 0.32 | 1.13 ± 0.33 | 1.19 ± 0.36 | |
| Ratio: CT 0.5 mm/mCT | 1.19 | 1.30 | 1.01 | 1.22 | 1.48 | |
| Ratio: CT 1.0 mm/mCT | 1.15 | 1.26 | 0.90 | 1.20 | 1.56 | |
| Mean Diff. 0.5 mm-mCT | 0.26 | 0.38 | 0.02 | 0.25 | 0.57 | |
| Mean Diff. 1.0 mm-mCT | 0.21 | 0.33 | −0.18 | 0.22 | 0.68 | |
| 59–6 | Avg ± SD (CT 0.5 mm) | 1.34 ± 0.42 | 1.56 ± 0.43 | 1.57 ± 0.29 | 1.00 ± 0.25 | 1.27 ± 0.34 |
| Avg ± SD (CT 1.0 mm) | 1.43 ± 0.43 | 1.59 ± 0.44 | 1.46 ± 0.36 | 1.15 ± 0.36 | 1.57 ± 0.37 | |
| Avg ± SD (mCT) | 1.26 ± 0.44 | 1.41 ± 0.45 | 1.39 ± 0.36 | 1.00 ± 0.36 | 1.26 ± 0.45 | |
| Ratio: CT 0.5 mm/mCT | 1.07 | 1.10 | 1.13 | 1.00 | 1.01 | |
| Ratio: CT 1.0 mm/mCT | 1.14 | 1.13 | 1.05 | 1.15 | 1.24 | |
| Mean Diff. 0.5 mm-mCT | 0.08 | 0.15 | 0.18 | 0 | 0.01 | |
| Mean Diff. 1.0 mm-mCT | 0.17 | 0.18 | 0.07 | 0.15 | 0.31 | |
| 59–7 | Avg ± SD (CT 0.5 mm) | 1.25 ± 0.49 | 1.29 ± 0.52 | 1.43 ± 0.31 | 0.95 ± 0.39 | 1.70 ± 0.36 |
| Avg ± SD (CT 1.0 mm) | 1.48 ± 0.52 | 1.50 ± 0.58 | 1.56 ± 0.31 | 1.26 ± 0.47 | 1.97 ± 0.37 | |
| Avg ± SD (mCT) | 1.17 ± 0.46 | 1.18 ± 0.51 | 1.55 ± 0.30 | 0.94 ± 0.39 | 1.08 ± 0.30 | |
| Ratio: CT 0.5 mm/mCT | 1.07 | 1.09 | 0.92 | 1.01 | 1.58 | |
| Ratio: CT 1.0 mm/mCT | 1.27 | 1.27 | 1.00 | 1.34 | 1.83 | |
| Mean Diff. 0.5 mm-mCT | 0.08 | 0.11 | −0.12 | −0.05 | 0.14 | |
| Mean Diff. 1.0 mm-mCT | 0.31 | 0.32 | 0.01 | 0.27 | 0.89 | |
| All Specimens | Avg ± SD (CT 0.5 mm) | 1.14 ± 0.43 | 1.13 ± 0.44 | 1.41 ± 0.36 | 0.94 ± 0.42 | 1.22 ± 0.39 |
| Avg ± SD (CT 1.0 mm) | 1.30 ± 0.48 | 1.25 ± 0.47 | 1.44 ± 0.38 | 1.17 ± 0.42 | 1.49 ± 0.44 | |
| Avg ± SD (mCT) | 1.14 ± 0.46 | 1.14 ± 0.44 | 1.38 ± 0.36 | 0.99 ± 0.42 | 1.08 ± 0.39 | |
| Ratio: CT 0.5 mm/mCT | 0.99 | 0.98 | 1.02 | 0.95 | 1.12 | |
| Ratio: CT 1.0 mm/mCT | 1.14 | 1.09 | 1.04 | 1.18 | 1.38 | |
| Mean Diff. 0.5 mm-mCT | −0.00 | −0.01 | 0.03 | −0.08 | 0.07 | |
| Mean Diff. 1.0 mm-mCT | 0.16 | 0.11 | 0.06 | 0.17 | 0.41 |
References
- [1].ArajÄrvi E, Santavirta S, Chest injuries sustained in severe traffic accidents by seatbelt wearers, J. Trauma Acute Care Surg 29 (1) (1989) 38–42. [PubMed] [Google Scholar]
- [2].Ruan J, et al. , Prediction and analysis of human thoracic impact responses and injuries in cadaver impacts using a full human body finite element model, Stapp. Car Crash J 47 (2003) 299. [DOI] [PubMed] [Google Scholar]
- [3].Viano DC, Ridella S, Significance of Intersection Crashes for Older Drivers, (1996) (SAE Technical paper).
- [4].Aoki M, et al. , Radiation-induced rib fracture after stereotactic body radiotherapy with a total dose of 54–56 Gy given in 9–7 fractions for patients with peripheral lung tumor: impact of maximum dose and fraction size, Radiat. Oncol 10 (1) (2015) 99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Kim SS, et al. , Clinical prognostic factors and grading system for rib fracture following stereotactic body radiation therapy (SBRT) in patients with peripheral lung tumors, Lung Cancer 79 (2) (2013) 161–166. [DOI] [PubMed] [Google Scholar]
- [6].Mutter RW, et al. , Dose–volume parameters predict for the development of chest wall pain after stereotactic body radiation for lung cancer, Int. J. Radiat. Oncol. Biol. Phys 82 (5) (2012) 1783–1790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Amini A, et al. , Stereotactic body radiation therapy (SBRT) for lung cancer patients previously treated with conventional radiotherapy: a review, Radiat. Oncol 9 (1) (2014) 210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Reyngold M, et al. , Toxicity and outcomes of thoracic re-irradiation using stereotactic body radiation therapy (SBRT), Radiat. Oncol 8 (1) (2013) 99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Taremi M, et al. , Stereotactic body radiotherapy for medically inoperable lung cancer: prospective, single-center study of 108 consecutive patients, Int. J. Radiat. Oncol. Biol. Phys 82 (2) (2012) 967–973. [DOI] [PubMed] [Google Scholar]
- [10].Barrett-Connor E, et al. , Epidemiology of rib fractures in older men: osteoporotic Fractures in Men (MrOS) prospective cohort study, BMJ 340 (2010) c1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Wuermser L-A, et al. , What accounts for rib fractures in older adults? J. Osteoporos 2011 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Okoukoni C, et al. , A cortical thickness and radiation dose mapping approach identifies early thinning of ribs after stereotactic body radiation therapy, Radiother. Oncol 119 (3) (2016) 449–453. [DOI] [PubMed] [Google Scholar]
- [13].Bergeron E, et al. , Elderly trauma patients with rib fractures are at greater risk of death and pneumonia, J. Trauma Acute Care Surg 54 (3) (2003) 478–485. [DOI] [PubMed] [Google Scholar]
- [14].Burns ER, Stevens JA, Lee R, The direct costs of fatal and non-fatal falls among older adults—United States, J. Saf. Res 58 (2016) 99–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Bulger EM, et al. , Rib fractures in the elderly, J. Trauma Acute Care Surg 48 (6) (2000) 1040–1047. [DOI] [PubMed] [Google Scholar]
- [16].Ito O, Dokko Y, Ohashi K, Development of Adult and Elderly FE Thorax Skeletal Models, (2009) (SAE Technical Paper).
- [17].Kemper AR, et al. , Material Properties of Human Rib Cortical Bone from Dynamic Tension Coupon Testing, SAE Technical Paper, 2005. [DOI] [PubMed]
- [18].Kent R, et al. , Structural and material changes in the aging thorax and their role in crash protection for older occupants, Stapp. Car Crash J 49 (2005) 231–249. [DOI] [PubMed] [Google Scholar]
- [19].Kindig M, et al. , Effect of intercostal muscle and costovertebral joint material properties on human ribcage stiffness and kinematics, Comput. Methods Biomech. Biomed. Eng 18 (5) (2015) 556–570. [DOI] [PubMed] [Google Scholar]
- [20].Lizee E, et al. , Development of a 3D Finite Element Model of the Human Body, SAE Technical Paper, 1998.
- [21].Schoell SL, et al. , Development and validation of an older occupant finite element model of a mid-sized male for investigation of age-related injury risk, Stapp. Car Crash J 59 (2015) 359. [DOI] [PubMed] [Google Scholar]
- [22].Schoell SL, et al. , Age-and sex-specific thorax finite element model development and simulation, Traffic Inj. Prev 16 (sup1) (2015) S57–S65. [DOI] [PubMed] [Google Scholar]
- [23].Billè A, et al. , Experience with titanium devices for rib fixation and coverage of chest wall defects, Interact. Cardiovasc. Thorac. Surg 15 (4) (2012) 588–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Piper ML, Delrosario L, Hoffman WY, Distraction osteogenesis of multiple ribs for the treatment of acquired thoracic dystrophy, Pediatrics 137 (3) (2016) e20152053. [DOI] [PubMed] [Google Scholar]
- [25].Vu K-C, et al. , Reduction of rib fractures with a bioresorbable plating system: preliminary observations, J. Trauma Acute Care Surg 64 (5) (2008) 1264–1269. [DOI] [PubMed] [Google Scholar]
- [26].Kemper AR, et al. , The biomechanics of human ribs: material and structural properties from dynamic tension and bending tests, Stapp. Car Crash J 51 (2007) 235–273. [DOI] [PubMed] [Google Scholar]
- [27].Holcombe SA, Wang SC, Grotberg JB, Modeling female and male rib geometry with logarithmic spirals, J. Biomech 49 (13) (2016) 2995–3003. [DOI] [PubMed] [Google Scholar]
- [28].Holcombe SA, Wang SC, Grotberg JB, The Effect of Rib Shape on Stiffness, SAE Technical Paper, 2016. [DOI] [PubMed]
- [29].Holcombe S, et al. , Ribcage characterization for FE using automatic CT processing, 2008 5th IEEE International Symposium on Biomedical Imaging: from Nano to Macro, IEEE, 2008. [Google Scholar]
- [30].Holcombe SA, Wang SC, Grotberg JB, Age-related changes in thoracic skeletal geometry of elderly females, Traffic Inj. Prev 18 (sup1) (2017) S122–S128. [DOI] [PubMed] [Google Scholar]
- [31].Holcombe SA, Wang SC, Grotberg JB, The effect of age and demographics on rib shape, J. Anat 231 (2) (2017) 229–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Agnew AM, et al. , The effect of age on the structural properties of human ribs, J. Mech. Behav. Biomed. Mater 41 (2015) 302–314. [DOI] [PubMed] [Google Scholar]
- [33].Agnew AM, et al. , Age-related changes in stiffness in human ribs, Proceedings of IRCOBI Conference, 2013. [Google Scholar]
- [34].Albert DL, et al. , A comparison of rib structural and material properties from matched whole rib bending and tension coupon tests, IRCOBI Conference Proceedings, 2017. [Google Scholar]
- [35].Kent R, et al. , Age-related changes in the effective stiffness of the human thorax using four loading conditions, The International Conference on the Biomechanics of Impact, IRCOBI), 2003. [Google Scholar]
- [36].CHOI H-Y, KWAK D-S, Morphologic characteristics of Korean elderly rib, Small 1 (2011) 0. [Google Scholar]
- [37].Mohr M, et al. , Geometry of human ribs pertinent to orthopedic chest-wall reconstruction, J. Biomech 40 (6) (2007) 1310–1317. [DOI] [PubMed] [Google Scholar]
- [38].Treece GM, et al. , High resolution cortical bone thickness measurement from clinical CT data, Med. Image Anal 14 (3) (2010) 276–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Poole KE, et al. , Cortical thickness mapping to identify focal osteoporosis in patients with hip fracture, PLoS One 7 (6) (2012) e38466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Treece GM, Poole K, Gee AH, Imaging the femoral cortex: thickness, density and mass from clinical CT, Med. Image Anal 16 (5) (2012) 952–965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Lillie EM, et al. , Estimation of skull table thickness with clinical CT and validation with micro CT, J. Anat 226 (1) (2015) 73–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Holcombe SA, et al. , Measuring Rib Cortical Bone Thickness and Cross Section from CT, Medical Image Analysis, 2018. [DOI] [PubMed]
- [43].Treece G, Gee A, Cortical Bone Mapping: Measurement and Statistical Analysis of Localised Skeletal Changes, Current osteoporosis reports, 2018, pp. 1–9. [DOI] [PMC free article] [PubMed]
- [44].Treece GM, Gee AH, Independent measurement of femoral cortical thickness and cortical bone density using clinical CT, Med. Image Anal 20 (1) (2015) 249–264. [DOI] [PubMed] [Google Scholar]
- [45].Agnew AM, et al. , The response of pediatric ribs to quasi-static loading: mechanical properties and microstructure, Ann. Biomed. Eng 41 (12) (2013) 2501–2514. [DOI] [PubMed] [Google Scholar]
- [46].Murach MM, et al. , Rib geometry explains variation in dynamic structural response: potential implications for frontal impact fracture risk, Ann. Biomed. Eng 45 (9) (2017) 2159–2173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Dokko Y, Ito O, Ohashi K, Development of Human Lower Limb and Pelvis Fe Models for Adult and the Elderly, (2009) (SAE Technical Paper).
- [48].I.M.I. Division, CT Market Outlook Report, (2017), p. 140 2017.