Functionally Independent Components of the Late Positive Event-Related Potential during Visual Spatial Attention

Abstract

Human event-related potentials (ERPs) were recorded from 10 subjects presented with visual target and nontarget stimuli at five screen locations and responding to targets presented at one of the locations. The late positive response complexes of 25–75 ERP average waveforms from the two task conditions were simultaneously analyzed with Independent Component Analysis, a new computational method for blindly separating linearly mixed signals. Three spatially fixed, temporally independent, behaviorally relevant, and physiologically plausible components were identified without reference to peaks in single-channel waveforms. A novel frontoparietal component (P3f) began at ∼140 msec and peaked, in faster responders, at the onset of the motor command. The scalp distribution of P3f appeared consistent with brain regions activated during spatial orienting in functional imaging experiments. A longer-latency large component (P3b), positive over parietal cortex, was followed by a postmotor potential (Pmp) component that peaked 200 msec after the button press and reversed polarity near the central sulcus. A fourth component associated with a left frontocentral nontarget positivity (Pnt) was evoked primarily by target-like distractors presented in the attended location. When no distractors were presented, responses of five faster-responding subjects contained largest P3f and smallest Pmp components; when distractors were included, a Pmp component appeared only in responses of the five slower-responding subjects. Direct relationships between component amplitudes, latencies, and behavioral responses, plus similarities between component scalp distributions and regional activations reported in functional brain imaging experiments suggest that P3f, Pmp, and Pnt measure the time course and strength of functionally distinct brain processes.

Late positive event-related potentials (ERPs) (300–1000 msec) dominated by a vertex-positive response, called P300, occur in response to stimuli perceived as belonging to an infrequently presented category (Sutton et al., 1965). Although similar late positive responses are reliably evoked by visual, auditory, or somatosensory stimuli in a variety of tasks, they may not be unitary (Squires et al., 1975; Ruchkin et al., 1990). Their amplitudes and peak latencies are affected by several task variables, including attention and novelty, and their scalp distributions vary both within and across responses. Results of lesion studies (Halgren et al., 1980; Knight et al., 1989) and functional imaging experiments (Ford et al., 1994; Ebmeier et al., 1995) also suggest that late positive responses are complexes of components generated in more than one brain region.

Scalp-recorded late positive complexes (LPCs) cannot be easily decomposed into components, because their time courses and scalp projections generally overlap. LPC components are commonly identified with single response peaks in single-channel waveforms. By this procedure, Squires et al. (1975) reported that auditory target responses in some subjects contained three components. Others have attempted to identify components with peaks in difference waves between LPCs evoked in simple and choice response tasks (Hohnsbein et al., 1991; Falkenstein et al., 1995). However, none of these studies adequately assessed the spatial stationarity of the response near the identified peaks. Thus, they could not be sure that each peak was composed of only one spatially fixed component. Peak-based methods also cannot be used when response components do not produce separate peaks. Nor can they determine other details of the component time courses. Independent Component Analysis (ICA), a new approach to linear decomposition (Bell and Sejnowski, 1995; Makeig et al., 1996a, 1997), can overcome some of these limitations. ICA is compatible with the assumption that an ERP is the sum of brief, coherent activations occurring in a small number of brain regions whose spatial projections on the scalp are fixed across time and task conditions.

Nearly all visual LPC studies have used simple tasks involving the presentation of two or three stimulus types in pseudorandom order at a single spatial location. Most ERP studies of spatial selective attention, in contrast, have focused on early visual response features whose amplitudes are augmented or suppressed in response to stimuli presented at attended or nonattended locations (Hillyard et al., 1995). Here, we present results of applying ICA to 31-channel ERP recordings of ERPs evoked in two visual selective attention tasks. We demonstrate that LPCs evoked in these tasks can be robustly decomposed into four components with distinct time courses and relationships to behavior. Two of these components varied in amplitude and peak latency between faster- and slower-responding subjects, suggesting that intersubject differences in visual response speed may be accounted for by differences in the degree to which independent components of the scalp-recorded LPC are activated. In particular, a new frontoparietal component (P3f) appears to reflect brain activity involved in rapidly responding to stimuli presented at an attended location.

MATERIALS AND METHODS

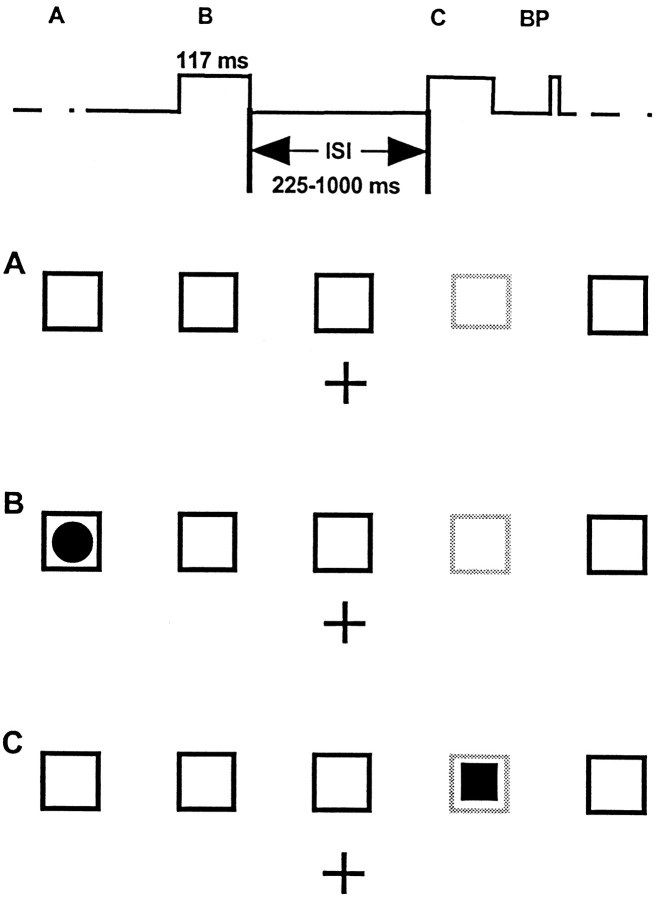
Task design. ERPs were recorded from subjects who attended to randomized sequences of filled round or square disks appearing briefly inside one of five empty squares that were constantly displayed 0.8 cm above a central fixation cross (Fig.1A). The 1.6 cm square outlines were displayed on a black background at horizontal visual angles of 0, ±2.7, and ±5.5° from fixation. During each 76 sec block of trials, one of the five outlines was colored green, and the other four were blue. The green square marked the location to be attended. This location was counterbalanced across blocks. One hundred single stimuli (filled white circles in one condition, filled circles and squaresin a second) were displayed for 117 msec within one of the five empty squares in a pseudorandom sequence with interstimulus intervals of 250–1000 msec (in four equiprobable 250 msec steps).

Fig. 1.

Schematic view of the task. The top trace shows the time line of a typical trial.BP, Button press. A, Screen before stimulation. The cross is the fixation point, and thelightly shaded box is the attended location during the ensuing 76 sec block. B, Appearance of a filled circle stimulus at an unattended location; no response required. C, Appearance of a filled square at the attended location in the discrimination task; button press required. See Materials and Methods.

Ten right-handed volunteers (two women, eight men; ages 22–40 years) with normal or corrected to normal vision participated in the experiment. Subjects were instructed to maintain fixation on the central cross while responding only to stimuli presented in the green-colored (attended) square. In the “detection” task condition, all stimuli were filled circles, and subjects were required to press a right-hand held thumb button as soon as possible after stimuli presented in the attended location (Fig. 1B). Thirty blocks of trials were collected from each subject, yielding 120 target and 480 nontarget trials at each location. Subjects were given 1 min breaks between blocks.

In the “discrimination” task condition, 75% of the presented stimuli were filled circles, the other 25% filled squares. Subjects were required to press the response button only in response to filled squares appearing in the attended location (Fig. 1C) and to ignore filled circles. In this condition, thirty-five blocks of trials were collected from each subject, seven blocks at each of the five possible attended locations. Each block included 35 target squares and 105 distractor (or “nogo”) circles presented at the attended location, plus 560 circles and squares presented at the four unattended locations.

These experiments were designed and run to study the attentional enhancement of early visual components P1 and N1 (positive and negative peaks occurring between 100 and 200 msec) evoked by stimuli presented in different parts of the visual field (Townsend et al., 1996). Analyses of those data will be reported elsewhere. Here we report an analysis of brain responses to the target stimuli presented at attended locations in the same experiments.

Evoked responses. EEG data were collected from 29 scalp electrodes mounted in a standard electrode cap (Electrocap) at locations based on a modified International 10–20 system and from two periocular electrodes placed below the right eye and at the left outer canthus. All channels were referenced to the right mastoid with input impedance <5 kΩ. Data were sampled at 512 Hz within an analog pass band of 0.01–50 Hz. To further minimize line noise artifacts, responses were digitally low-pass filtered below 40 Hz before analysis. After rejecting trials containing electrooculographic (EOG) potentials >70 μV, brain responses to circle and square stimuli presented at each location in each attention condition were averaged separately using the ERPSS (Event-Related Potential Software System, J. S. Hansen, Event-Related Potential Laboratory, University of California San Diego, La Jolla, CA, 1993) software package, producing a total of 75 512-point ERPs for each subject in the two tasks. Responses to target stimuli were considered correct and averaged only when subjects responded between 150 and 1000 msec. Most studies of the LPC or P300 have used a simple “oddball” paradigm, presenting stimuli in only two classes (standard, rare), although similar-appearing late positive components are evoked by infrequently presented stimuli in a wide range of evoked-response experiments. We hypothesized that data from these five-location selective-attention tasks might be better suited than simple oddball paradigms for decomposing LPCs by ICA because it included a relatively large number (75) of target and nontarget classes.

Independent component analysis. The “infomax” ICA algorithm we used (Bell and Sejnowski, 1995, 1996) is one of a family of algorithms that exploits temporal independence to perform blind separation. Recently, Lee et al. (1999a) have shown that all these algorithms have a common information theoretic basis, differing chiefly in the form of distribution assumed for the sources, which may not be critical (Amari, 1998). Infomax ICA finds a square “unmixing” matrix by gradient ascent that maximizes the joint entropy (Cover and Thomas, 1991; Linsker, 1992; Nadal and Parga, 1994) of a nonlinearly transformed ensemble of zero-mean input vectors (see for further details). Logistic infomax can accurately decompose mixtures of component processes having symmetric or skewed distributions, even without using nonlinearities specifically tailored to them.

The algorithm can be used practically on data from a 100 or more channels. The number of time points required for training may be as few as several times the number of variables (the square of the number of channels). In turn, the number of channels must be at least equal to the number of components to be separated. As confirmed by simulations (Makeig et al., 1996b), when training data consists of a mixture of fewer large source components than channels, plus many more small source components, as might be expected in actual EEG data, large source components are accurately separated into separate output components, with the remaining output components consisting of mixtures of smaller source components. In this sense, performance of the infomax ICA algorithm degrades gracefully as the amount of “noise” in the data increases.

ICA outputs. At the end of training, multiplying the input data matrix by the unmixing matrix gives a new matrix whose rows, called the component activations, are the time courses of relative strengths or activity levels of the respective independent components across conditions. ICA component activations are similar to the factor weights produced by spatial principal component analysis (PCA). The columns of the inverse of the unmixing matrix give the relative projection strengths of the respective components onto each of the scalp sensors. These may be interpolated to show the scalp map associated with each component. ICA scalp maps are similar to spatial PCA eigenvectors or factor loadings. Unlike components produced by PCA and Varimax, however, component scalp maps found by ICA are not constrained to be orthogonal and thus are free to accurately reflect the actual projections of functionally separate sources, if they are successfully separated.

The projection of the ith independent component onto the original data channels is given by the outer product of theith row of the component activation matrix with theith column of the inverse unmixing matrix, and is in the original units (e.g., microvolts). Neither the scalp maps nor the activation time series found by the infomax ICA algorithm are normalized. In this case, scaling information is distributed between them, and the true size of a component is given only by the size of its projection. Because ICA decomposition is a novel technique, we now present a brief overview of the assumptions underlying the application of ICA to electrophysiological data (more information and a collection of MATLAB routines for performing and visualizing the analysis are available at http://www.cnl.salk.edu/∼scott/ica.html).

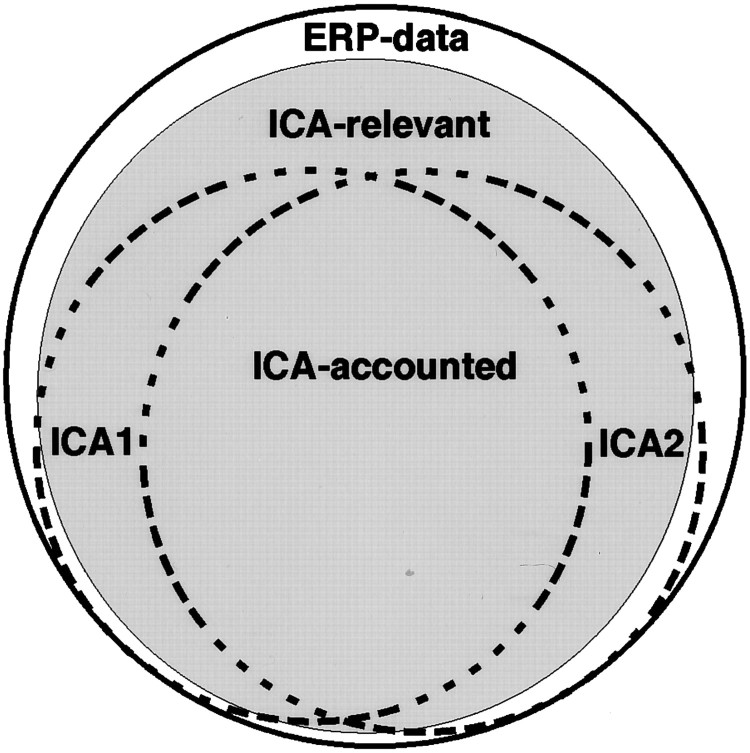
ICA limitations. Figure 2gives a highly schematic overview of possible limitations of ICA as applied to event-related brain responses. Of all the processes contributing to a set of recorded ERP data phenomena (outer circle), ICA can only successfully separate “ICA-relevant”’ processes (gray circle) whose activities satisfy several assumptions used in ICA (see below). Although ICA algorithms typically give quite comparable results when applied to simulated model data precisely fitting these assumptions, results obtained using different ICA algorithms applied to actual brain response data (dashed circles labeled ICA1, ICA2), although agreeing in large part (region labeledICA-accounted), may also differ in their details. ICA analysis of ERP data must therefore be viewed as exploratory, and care must be taken to test the functional distinctness of the resulting ICA components. Simply demonstrating their replicability across subjects and experimental conditions is not sufficient to ensure their physiological unity. In particular, ICA may account for a single brain component by more than one ICA component. In addition, one must attempt to establish relationships between component activations and independent experimental variables such as subject performance and behavior, as well as considering their physiological plausibility.

Fig. 2.

Schematic overview of ICA applied to ERP data. ICA methods (dotted circles) may account for somewhat different portions of ERP phenomena (outer circle) that match the assumptions of ICA (shaded area). See Materials and Methods.

ICA assumptions. Four main assumptions underlie ICA decomposition of ERP data: (1) signal conduction times are equal, and summation of currents at the scalp electrodes is linear, both reasonable assumptions for currents carried to the scalp electrodes by volume conduction at EEG frequencies (Nunez, 1981); (2) spatial projections of components are fixed across time and conditions; (3) source activations are temporally independent of one another across the input data; and (4) statistical distributions of the component activation values are not Gaussian (in contrast, PCA assumes that the sources have a Gaussian distribution).

Spatial stationarity. Spatial stationarity of the component scalp maps, assumed in ICA, is compatible with the observation made in large numbers of functional imaging reports that performance of particular tasks increases blood flow within small (several cubic centimeters), discrete brain regions (Friston, 1998). ERP sources reflecting task-related information processing are generally assumed to sum activity from spatially stationary generators, although stationarity may not apply to some spontaneously generated EEG phenomena such as spreading depression or sleep spindles (Werth et al., 1997).

Temporal independence. To fulfill the temporal independence assumption used by ICA, response components must be activated with temporally independent time courses. In the case of event-related brain components with temporally overlapping active periods, this may be accomplished or approximated by, first, sufficiently and systematically varying the experimental stimulus and task conditions, and, next, training the algorithm on the concatenated collection of resulting event-related response averages. However, simply varying stimuli and tasks does not guarantee that all the spatiotemporally overlapping response components appearing in the averaged responses are independently activated in the ensemble of input data.

Fortunately, the first goal of experimental design, to attain independent control of the relevant output variables, is compatible with the ICA requirement that the activations of the relevant data components be independent. Unfortunately, however, independent control of temporally overlapping components may be difficult or impossible to achieve. Examples of processes unlikely to be separated by ICA are parallel activations of both auditory cortices by auditory stimuli. In this case, ICA must fuse both activations into a single component, unless appropriate experimental interventions are developed to block or delay each activation independently in one or more of the input conditions.

Decomposing subaverages. For ICA decomposition of ERP data, there may be a performance trade-off between (1) first averaging together large numbers of trials and/or conditions and then decomposing the few resulting averages, or (2) decomposing a larger number of subaverages of the same data. Response averages or subaverages summing fewer trials normally contain larger remnants of spontaneous EEG processes and nonbrain artifacts that are, moreover, superimposed by the averaging process, decreasing their chance of being temporally independent. Decomposing a few averages obtained by summing large numbers of trials and conditions, on the other hand, may minimize the contributions of neural and artifactual processes not reliably time- and phase-locked to experimental events, but may also remove evidence of the temporal independence of overlapping components that might be exhibited in the different subaverages. The group-mean data, whose analysis we report here, consisted of between 25 and 75 1-sec averages from different task and/or stimulus conditions, each summing a relatively large number of single trials (250–7000). Elsewhere, we explore use of an alternative approach, decomposing the unaveraged single trials (T.-P. Jung, S. Makeig, M. A. Westerfield, J. Townsend, E. Courchesne, and T. J. Sejnowski, unpublished observations).

Dependence on source distribution. Because of the central limit theorem, even when mixtures of many processes appear to be normally distributed, this does not mean that the processes themselves are Gaussian. In theory, multiple Gaussian processes cannot be separated by ICA, although in practice even small deviations from normality can suffice to give good results. Also, not all ICA algorithms are capable of unmixing independent components with sub-Gaussian (negative-kurtosis) distributions. Intuitively, sub-Gaussian processes are relatively “active” more of the time than the best-fitting Gaussian process. Examples include sinusoids and uniformly distributed noise.

In particular, the infomax ICA algorithm using the logistic nonlinearity is biased toward finding super-Gaussian (sparsely activated) independent components (i.e., sources with positive kurtosis). Super-Gaussian sources, which are relatively “inactive” more often than the best-fitting Gaussian process, recur in speech and many other natural sounds and visual images (Bell and Sejnowski, 1996, 1997). The assumption of super-Gaussian source distributions is compatible with the physiologically plausible assumption that ERPs are composed of one or more overlapping series of relatively brief activations within spatially fixed brain areas performing separable stages of stimulus information processing.

Nonetheless, some sub-Gaussian independent components have been demonstrated in EEG data (Jung et al., 1998), chiefly line noise. Because our data were low-pass filtered below 40 Hz, their power at the line frequency (60 Hz) was negligible. To insure that some other sub-Gaussian component or components were not present in the data, we also decomposed some of the data by two different ICA algorithms capable of detecting and separating sub-Gaussian components, extended infomax and Joint Approximate Diagonalization of Eigen-matrices (JADE; see ). For comparison with previously proposed linear decomposition methods, we also decomposed these same data using PCA, and rotated the largest seven PCA components using Varimax and Promax (see ). We compared the closest resulting PCA-based components with the ICA-derived components for stability across subjects and degree of relationship to performance.

Evoked-response decomposition. The logistic infomax ICA algorithm was applied to sets of 25–75 averaged ERP epochs (31 channels, 512 time points) time locked from 100 msec before to 900 msec after onsets of target and nontarget stimuli presented at each of the five stimulus locations in the five spatial attention conditions in the two tasks (detection, discrimination). Initial decompositions were performed on grand averages of data from all 10 subjects. Subsequently, data from subject subgroups selected on the basis of response speed, and from single subjects, were decomposed separately as detailed below. ICA decomposition was performed using routines running under Matlab 5.01 (the Mathworks) on a Dec Alpha 300 MHz processor. The learning batch size was 65–110, depending on input data length. Initial learning rate started at ∼0.004 and was gradually reduced to 10⁻⁶ during 50–100 training iterations that required ∼5 min of computer time. Results of the analysis were relatively insensitive to the exact choice or learning rate or batch size. For further details, see .

Single-trial artifact removal. In most evoked response research, the possibility that neural activity is expressed in periocular data channels is usually ignored for fear of mislabeling eye activity artifacts as brain activity. Some of the ICA components of EEG records can be identified as accounting primarily for eye movements, line or muscle noise, or other artifacts (Makeig et al., 1996a;Vigario, 1997). Subtracting the projections of artifactual components from averaged or single-trial data can eliminate or reduce these artifacts while preserving the remaining nonartifactual EEG phenomena in all of the data channels (Jung et al., 1998). ICA thus makes it possible, for the first time, to examine periocular neural activity.

To examine the between-trial distribution of periocular components observed in the target response averages, all single target trials in the detection task for two subjects were decomposed using ICA, and projections of 16 of the resulting 31 components were removed from the single-trial data. The removed components were those that either (1) accounted predominantly for eye movements or muscle activity, or (2) whose projections appeared to contribute only very small amounts of noise to the averaged response. We identified eye and muscle artifact components on the basis of their scalp maps and activation time courses. Eye movement components had dominant periocular and frontal projections and slow, sporadic activations; muscle–noise components had localized scalp patterns and were dominated by broadband 20–50 Hz activity. The remaining 15 single-trial components were projected together back onto the scalp channels. For further details of this procedure, see Jung et al. (1998).

RESULTS

Target-evoked response

Performance levels on both the detection task and the discrimination task were high [detection task: 94.8% hits = correct 150–1000 msec response times (RTs), 0.6% false alarms, median RT 353 ± 41 msec; discrimination task: 91.4% hits, 0.6% false alarms, median RT 455 msec]. Responses evoked by target stimuli (their grand mean shown in Fig.3A, colored traces) contained a prominent LPC peaking after expected early visual response peaks P1, N1, P2, and N2. In the grand-mean detection-task response, no single-channel waveform contained more than one large positive peak between 300 and 700 msec. However, during this period the scalp topography of the response varied continuously (Fig.3A, scalp maps).

Fig. 3.

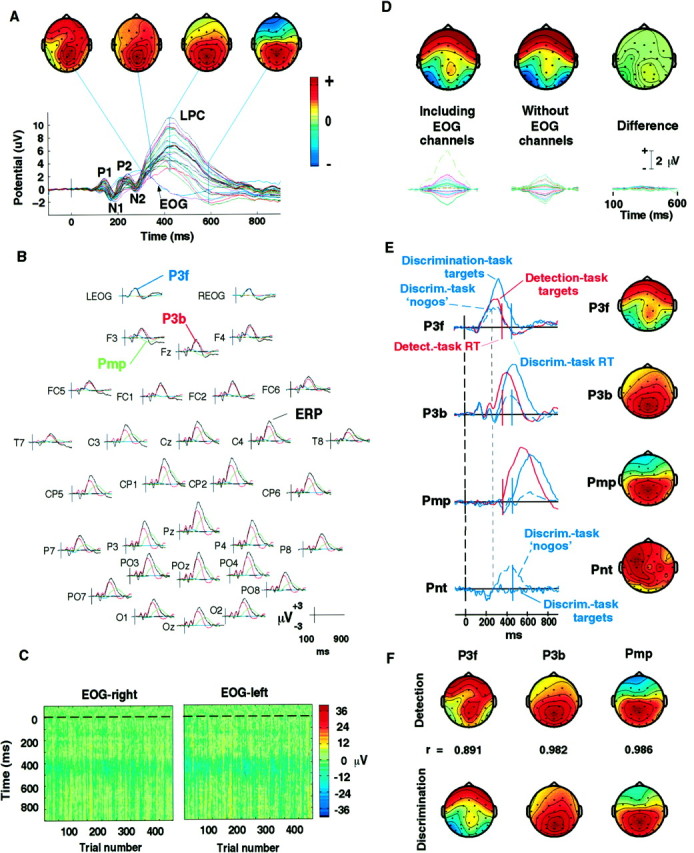
A, The scalp distribution of the LPC evoked by attended visual stimuli is not spatially fixed. Grand mean evoked response to detected target stimuli in the detection task (average of responses from 10 subjects and five attended locations). Response waveform at all 29 scalp channels and two periocular channels (EOG) are plotted on a common axis. Topographic plots of the scalp distribution of the response at four indicated latencies show that the LPC topography is labile, presumably reflecting the summation at the electrodes of potentials generated by temporally overlapping activations in several brain areas, each having broad but topographically fixed projections to the scalp. All scalp maps are shown individually scaled to increase color contrast with polarities at their maximum projection, as indicated in the color bar.B, Separate projections of the three major LPC components (colored traces) overplotted on the grand mean target response (black traces) for the detection task. Note the large projection of the P3f component (blue trace) at the two periocular electrodes (top traces) and its smaller projection at Pz and the polarity reversal of component Pmp (green traces) between central and frontal channels. C, Single target-response trials at the periocular electrodes (see Materials and Methods) for one subject in the detection task (all five locations), plotted asvertical colored lines (color code onright). Before plotting, noise and movement artifacts were removed from each trial by subtracting ICA components accounting for eye artifact, line, and muscle noise from a 31-channel decomposition of the single-trial data (Jung et al., 1998). An early broad positivity (yellow band) appeared between 200 and 350 msec in most trials, with near constant amplitude, latency, and duration. D, Separation of P3f was not affected by omitting the two periocular channels. Separate ICA decompositions of 25 grand-mean (figure legend continues) detection-task ERPs (10 subjects) using first (left) all 31 channels, and then (center) 29 scalp channels alone, identified nearly identical P3f components (right). Scalp maps plotted on the same relative scale, with polarities as in A (bottom traces). Projections of the P3f component and their difference (bottom right) on the same microvolt scale. E,Activation time courses and scalp maps of the four LPC components produced by the ICA algorithm applied to 75 1 sec grand-mean (10-Ss) responses from both tasks. Map scaling as inA. Because microvolt scaling information for each ICA component is divided between its activation and its scalp map, units are not indicated (see Results). The thick dotted line(left) indicates stimulus onset. Mean subject-median RTs in the detection task (red) and discrimination task (blue) are indicated by solid vertical bars. Three independent components (P3f, P3b, Pmp) accounted for 95–98% of LPC variance in both tasks. In both tasks, median RT coincided with Pmp onset. Pnt, a fourth, left-frontocentral component, was evoked mainly after nogo nontargets presented in the attended location in the discrimination task. The faint vertical dotted line at ∼250 msec shows the temporal relationship between the onsets of Pnt and P3b and the divergence of the P3f activations after target and nogo stimuli in the discrimination task. F,Separate ICA decompositions of ERPs from the detection and discrimination tasks gave similar LPC components. For all three components, both the scalp maps (shown) and periods of activation (data not shown) were nearly equivalent. Correlations between the respective component scalp maps are indicated. Maps individually scaled as inA.

Note that both periocular channels (Fig. 3A, EOG) contained a small (∼3 μV), broad positive potential peaking at ∼300 msec. Grand mean target responses from each of the 10 subjects (e.g., means of response averages for all five attended locations) contained a positive deviation with similar time course near-equal in amplitude in the two channels. Examination of artifact-corrected single trials (derived as described in the Methods) showed that this potential was evoked in most or all single trials of every attended-location condition (Fig. 3C). Most likely these potentials were not produced by eye movements, because only small, slow, diagonal eye movements reliably and precisely time-locked to stimulus onsets could have produced them.

Joint decomposition

ICA was applied to all 75 31-channel responses from both tasks (1 sec ERPs from 25 detection-task and 50 discrimination-task conditions) producing 31 temporally independent components. Of these, just three accounted for 95–98% of the variance in the ten target responses from both tasks. A parsimonious decomposition was achieved, although data for the two conditions for each subject were obtained on separate days and thus might have included small between-session differences in electrode placements, which were reduced by averaging across subjects. Figure 3B shows the projections of the three components [labeled for convenience as P3f, P3b, and postmotor potential (Pmp)] in response to targets in the detection task at all 31 electrode sites (colored traces) superimposed on the grand mean response at the same sites (black traces). Component P3f (blue traces) became active near the N1 peak. Its active period continued through the P2 and N2 peaks and the upward slope of the LPC. That is, P3f accounted for a slow shift beginning before LPC onset, positive at periocular and frontal channels and weakly negative at lateral parietal sites (top rows).

A near-exact P3f analog (projection, r = 0.95) was also recovered from a decomposition of the 25 detection-task ERPs at the 29 scalp channels alone, omitting the two periocular channels (Fig.3D). Component P3b (Fig. 3B, red traces) accounted for nearly all of the LPC at frontocentral channels and for most of its peak amplitude at posterior channels. Component Pmp (Fig. 3B, green traces) accounted for part of the frontal negative-going slow wave after the LPC as well as for the longer duration of the LPC at central and posterior sites.

All three ICA components were active near the LPC peak, thus producing an apparently continuously varying scalp distribution. Although P3b accounted for most of the LPC peak distribution and resembled components with the same term in earlier literature (Squires et al., 1975), the scalp distribution of P3f appeared to be more strongly frontal and markedly less central than the “novelty P3”, a large central LPC evoked by rare, novel stimuli (Courchesne et al., 1975) and other components labeled “P3a” (Katayama and Polich, 1998). Although the label P3f was chosen to reflect the relatively frontal projection of this component, P3f also contained a consistent local maximum near Pz and weak bilateral negativities at inferior parietal sites.

Smaller activations of the same three components, plus a fourth left frontocentral component, together accounted for 80–86% of the variance of the five smaller LPCs evoked by nogo stimuli (nontarget circles presented in the attended location) in the discrimination task. Responses to most other stimuli did not contain the four LPC components; nontarget stimuli that weakly activated them were invariably presented at or near the attended location. Analysis of these nontarget activations will be presented elsewhere.

The four LPC components

Figure 3E shows the scalp maps and time courses of activation of the four LPC components in both tasks. To illustrate the outputs of the algorithm and to allow easy comparison between the time courses of the different components, the raw activations and scalp maps are presented. Relative sizes of the components are indicated in Figure3B. Two vertical lines in each panel mark mean subject-median RT, which was 102 msec longer (455 msec) in the discrimination task than in the detection task (353 msec).

Component P3f

P3f was evoked principally by targets in both tasks, with largest amplitudes in the discrimination task. Onset was at ∼140 msec, and offset followed median RT by ∼60 msec. Peak root-mean square (RMS)-projected amplitude in the grand-mean target response was 1.5 μV. When detection-task responses from each of the 10 subjects were decomposed separately, seven of the ten decompositions contained P3f analogs, defined as components whose projections at all channels were correlated (r > 0.5) with the grand-mean component projection. Each of these seven P3f components included a weak central parietal positivity that in six of the seven subjects had a maximum slightly right of midline. The three decompositions not containing a P3f analog were of responses from three of the four subjects with the longest median RTs. The scalp projection of P3f was largest at the periocular electrodes (Fig. 3B, top sites). P3f also was also evoked with smaller amplitudes by discrimination-task nogo stimuli and by target stimuli presented in the central location during noncentral discrimination-task attention conditions.

Component P3b

In single-subject decompositions of detection-task data, clear P3b analogs (projection, r > 0.75) were returned for all ten subjects. Peak P3b RMS-projected amplitude in the grand-mean target response was 6.1 μV, and P3b peak latency covaried with median RT in the two tasks. The P3b scalp map resembled peak P300 scalp distributions reported for experiments in which subjects simply counted or attended to rare stimuli instead of pressing a response button (seeAlexander et al., 1995 and Fig.4A).

Fig. 4.

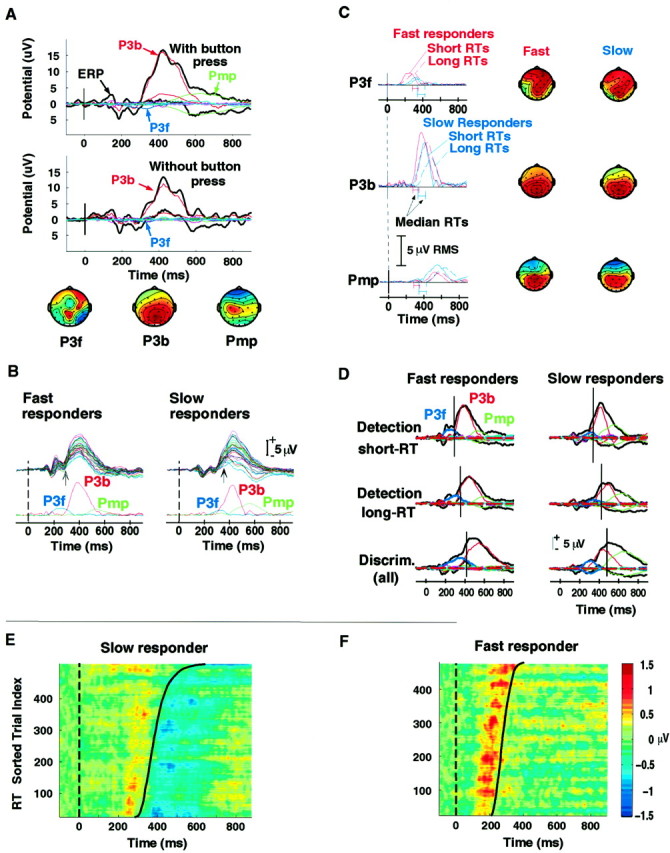
A, Component Pmp is linked to button presses. Results of a control experiment on one slow responder whose target LPC was decomposed by ICA into clear group P3f, P3b, and Pmp component analogs. In a second detection-task session, the subject was asked only to mentally note target stimuli without pressing the response button. Data from both sessions were decomposed together by ICA. The two panels plot the “envelopes” (the minimum and maximum values, at each time point, over the 29 scalp channels) of the responses (black traces) and of the scalp projections of the three major ICA components (colored traces). The scalp maps of the three components (below, individually scaled as in Fig. 3A) resembled those of the group decompositions (Fig. 3F). The grand-mean target response in the button-press condition (top panel) contained all three LPC (figure legend continues) components; the grand-mean response to targets presented in the no-button press condition (bottom panel) evoked only P3b plus a small P3f, but no Pmp, strongly suggesting that that Pmp was directly related to the button press in the first session. B, Comparison of the raw target ERPs with the time courses of the three LPC components. Target responses in shorter-RT detection-task target trials (five attended locations; subaverages for five faster and five slower responders, respectively). Responses at 29 scalp channels are shown on a common time base above the time courses of projected RMS amplitude of the three LPC components (microvolt scaling as shown, top right). Arrows show median RT for each group. The activation period for component P3f encompasses a slow positive shift in the data that begins earlier (near peak N1) and grows larger in the fast-responder response (bottom left, blue trace). The larger and later-peaking in the slow-responder average Pmp (bottom right, green trace) accounts for the larger bipolar spread of activity at ∼600 msec in the slow-responder data (top right). C, Separate ICA decompositions of grand-mean detection-task responses from the five faster- and slower-responding subjects gave comparable LPC components. Scalp maps (individually scaled as in Fig. 3A) and time courses of projected RMS amplitude (microvolt scaling indicated) of the three target-response LPC components, from separate decompositions of 20 nontarget responses plus 10 target responses (short-RTs, long-RTs at five locations) for the five faster- and five slower-responding subjects, respectively. Correlations between scalp maps indicated. See Results. D, Comparison of data and projected component envelopes with median RT (short vertical bar). Envelopes of the scalp projections of all 31 ICA components (in microvolts, see bar) superimposed on the envelopes of the grand-mean target responses (all 31 channels) for faster- and slower-responding subgroups in the detection task (top rows) and discrimination task (bottom row). Results from all four decompositions (task by subgroup) gave three major LPC components whose amplitudes and peak latencies varied systematically with RT in different ways for the two subgroups. Note the small size of the projections of the remaining 28 components (thick red bundles). See Results. E, F, Detection-task target responses at the left periocular electrode for one slower responder and one faster responder. Responses plotted as horizontal colored lines (see color bar) after sorting by RT (thick black lines) and then smoothing with a 30-trial moving-average. Stimulus onsets occurred at dashed lines (left). In the response of the slower responder (left panel), note the relatively weak and fixed-latency pre-response positivity at ∼250 msec and the strong post-response (Pmp-related) negativity. For the faster responder (right panel), peak latency of the strong (P3f-related) positivity immediately preceded RT in all trials, and the post-response (Pmp-related) negativity was absent.

The P3b component also accounted for some early response activity. This appeared to reflect a tendency of the algorithm to make very large components “spill over” into periods of weak activity with related scalp distributions. Subsequent decompositions of the detect-task data by PCA, Varimax, and Promax (see below) produced P3b analogs in which this spillover was stronger than for ICA (compare Fig.5B). However, separate ICA decomposition of the first 300 msec after stimulus onset (to be reported elsewhere) gave a parsimonious decomposition of the early response components P1 and N1 into one or more components none of which resembled P3b, whereas a separate decomposition of the latter portion of the epochs (300–900 msec) reproduced the whole-epoch P3b (scalp map, r = 0.999).

Fig. 5.

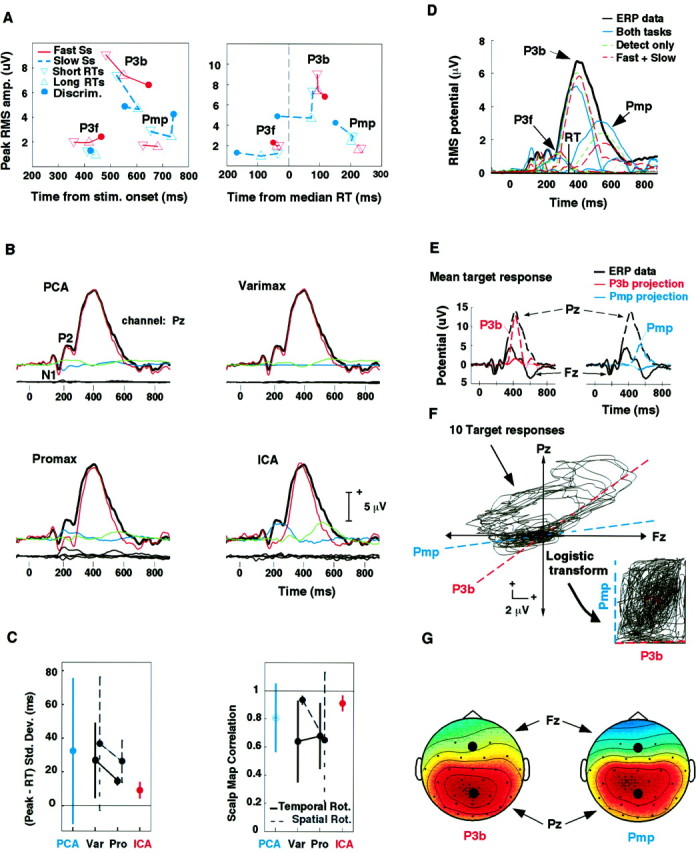
A, LPC component peak amplitudes and latencies plotted relative to target stimulus onset (left panel) and to median RT (right panel). Peak latencies of all three LPC components were tied to RT in the fast-responder averages only. B,Comparison of ICA and PCA-based decompositions. Sets of 30 fast-responder and slow-responder detection-task response averages (compare Fig. 4) were separately decomposed using PCA (top left). The largest seven principal components were then rotated by Varimax (top right) and Promax (bottom left) applied either to their activation time courses (shown here) or to their spatial maps (eigenvectors) (data not shown). The figure shows envelopes of the grand-average short-RT target response for the fast responders (black traces) with envelopes of the respective component projections (colored traces) superimposed. The temporal Varimax and Promax rotations, shown here, appear to approach the ICA decomposition, although the ICA decomposition appears most parsimonious. See Results. C,ICA components were more stable and more tightly linked to behavior than analogous PCA-based components. The left panelshows means and SDs of the RMS millisecond difference between component peak latency and median RT (averaged across two subgroup decompositions and three LPC components and two RT-separated data subsets). Theright panel shows mean and SD scalp map correlations between analogous (figure legend continues) component pairs in the fast-responder and slow-responder response decompositions (averaged across the three LPC components). ICA component latencies were more tightly linked to behavior, and their scalp maps better correlated between subject groups, than the PCA-based components. D, Relative stability of the ICA decomposition. Comparison of the envelopes of the projections of the three LPC components of the grand-mean (all 10 subjects) detection-task target response derived by three ICA decompositions involving this data. Although each decomposition was dominated by three LPC components, relative component peak latencies were more stable between decompositions than peak amplitudes. Vertical bars: median RT. See Results. E–G, ICA identifies spatially periods of fixed scalp topography. Decomposition of 30 detection-task response means for the slow-responder subgroup produced two large LPC components, P3b and Pmp. F, A scatter plot of the short-RT and long-RT target responses (separately at five attended locations) (middle panel) at two scalp electrodes, Fz and Pz, contains two strongly radial (i.e., spatially fixed) features. The dashed lines show the directions associated with components P3b and Pmp in these data, as determined by (G) the values of their respective component scalp maps (black dots). Thus, ICA separated out two important spatially fixed components of the input data using its (nonGaussian) higher-order statistics. E, Projections of components P3b and Pmp of the grand mean target response onto the same two scalp channels (top panel, colored traces), overplotted on the grand-mean response waveforms (black traces), indicate that the two components, P3b and Pmp, dominate the central and late portions of the LPC, respectively. Infomax ICA found the two component directions by maximizing joint entropy (i.e., the evenness of the density distribution) of a nonlinear transform of the (31-channel) unmixed data (center right insert). See .

Component Pmp

Although components P3f and P3b were evoked by discrimination-task nogo nontargets (Fig. 5A, dashed lines) at approximately half the strength of their activation by discrimination-task targets (Fig. 5A, solid lines), neither these nor any other stimuli not followed by a button press strongly activated Pmp. In both tasks, Pmp onset nearly coincided with median RT, and its scalp map reversed polarity near the central sulcus. Peak RMS-projected amplitude in the grand-average target response was 3.09 μV. Pmp appears to be an analog of the response positivity also known to peak ∼200 msec after infrequent voluntary button presses (Makeig et al., 1996c).

In single-subject decompositions, Pmp analogs (projection,r > 0.6) were found for eight of the 10 subjects, the exceptions being two of the four subjects with the fastest median RTs. The scalp maps of Pmp analogs in individual subjects strongly resembled those recently published for a somewhat earlier (80 msec postmovement) measure of the voluntary postmovement positivity also peaking at ∼200 msec after movement (Boetzel et al., 1997). In seven of the eight Pmp-analog scalp maps, the posterior positive peak was over the left hemisphere. Decompositions of responses from three additional left-handed subjects not included in this study each contained a Pmp analog with a positive maximum over the right hemisphere.

Component Pnt

Component Pnt (for nontarget positivity) was evoked chiefly by nogo nontargets in the discrimination task (Fig. 5, dotted trace) and by targets (Fig. 5, solid trace). Its scalp map was most positive over left dorsolateral prefrontal and central cortex (maximum RMS-projected amplitude in the grand-mean target response, 0.9 μV) with negligible projection to the periocular electrodes. Pnt analogs were found in five of the 10 individual subject decompositions. Its onset (∼260 msec) coincided with the divergence of the nogo and target P3f activations, and its period of activation paralleled that of P3b. The ICA decomposition thus explained the more anterior distribution of the nogo LPCs in the discrimination task as resulting from the addition of Pnt to the small P3b evoked in the same time period by nogo stimuli, accompanied by a blunted P3f activation. The divergence of P3f activations after targets and nogo stimuli respectively began at the onset of Pnt at ∼250 msec (Fig. 5,faint dotted line). Pnt was activated more strongly when the attended location was in the right visual field.

Absence of sub-Gaussian components

To test for the presence of independent components with subGaussian distributions, the same grand-average data for all ten subjects in both tasks (75 responses in all) were decomposed using two ICA algorithms capable of separating sub-Gaussian components, extended infomax, and JADE (see ). The resulting decompositions resembled that produced by logistic infomax. In particular, none of the 31 components derived by either method had a sub-Gaussian distribution.

Cross-task reliability

Next, logistic infomax ICA decomposition was applied separately to the 25 responses from the detection task and to the 50 responses from the discrimination task. Both decompositions produced three components accounting for 96–98% of the variance in the grand mean LPCs (300–700 msec) at the five locations (Fig. 3F). The periods of activation of the three component pairs were equivalent, and their scalp distributions were highly correlated (89–98.6%), suggesting that despite the 102 msec difference in median RT, the target LPCs in the two tasks could arise from three spatially fixed brain systems or sets of concurrently activated networks.

Within-task reliability

To test the reliability of convergence of the algorithm, the detection-task data (25 1 sec responses) were decomposed 20 times in succession. The 31 component scalp maps returned from each of the decompositions were correlated with the 31 component maps returned by the original decomposition. Next, the highest-correlated pair of component maps was determined and removed from further consideration. In the same manner, 30 more successively best-correlated map pairs were drawn from the two sets of component maps, and the absolute correlations between the successive best-correlated pairs were noted. In all 20 decompositions, the scalp maps of >10 returned components were nearly identical (r > 0.995) to maps of analogous components in the original decomposition, and at least 21 component map pairs were correlated (r > 0.95). Maps for the three LPC components (ranking 1, 2, and 7 by size in the original decomposition) were near-perfectly replicated (mean of the map correlations: P3b, 0.9995; Pmp, 0.9985; P3f, 0.9937).

Relative montage independence

To test the dependence of the results on the choice of electrode sites, 20 randomly selected subsets of the 31 data channels were selected for analysis, leaving out the remaining 11 channels. Correlations between the activation time courses of resulting ICA components were computed and rank-ordered as above. On average, the three best-correlated activation pairs were correlated;r > 0.94. The three LPC component maps were accurately recovered (submap correlations: 0.998, P3b; 0.993, Pmp; 0.964, P3f).

Attend-only control experiment

One of the 10 subjects participated in a second session of the detection-task control experiment in which he was asked simply to “mentally note” targets without making motor responses to them. ICA decomposition was then performed on all 50 responses from both detection-task sessions for this subject. Figure 4A(top panel) shows the envelopes (the most positive and most negative single-channel data values, across the 29 scalp channels, at each time point) of the projections of all 31 components of the grand mean target response in the button-press condition, superimposed on the envelope of the ERP data (black traces). Envelope plots allow the time courses, strengths, latencies, and predominant polarities of several ICA components to be visualized in relation to the data envelope in a single figure.

The LPC was again decomposed into three spatially fixed components clearly analogous in time course and scalp map to the group P3f, P3b, and Pmp. In this right-handed subject, the Pmp analog had a clear left-central scalp projection. The grand mean target response in the no-button-press condition (Fig. 4A, middle panel) was comprised chiefly of P3b and included a small P3f, but no Pmp, further confirming that Pmp reflected brain processes induced by the response movement and/or resulting tactile feedback. In this condition, the subject’s LPC was dominated by a single spatially fixed component, P3b.

Note that the most-positive traces of the ERP data envelopes for both sessions (Fig. 4A, top black traces) contain three positive peaks occurring at ∼100 msec intervals during the LPC. These, however, were not accounted for by activity of the three LPC components. Instead, the decomposition explained these three peaks as being produced by one or more α-band components summing with the LPC and having scalp topographies different from the three LPC components. In this case, that is, an LPC apparently containing three positive peaks was decomposed by ICA primarily into a single LPC component (P3b) plus residual α activity.

Component differences between faster and slower responders

In the detection task, subject’s median RTs ranged between 287 and 396 msec. Examination of single-subject decompositions suggested that responses of some faster and slower responders differed not only in latency but also in the relative amplitudes of the LPC components. To assess these differences more clearly, subjects were divided by median RT into two subgroups of five subjects dubbed “fast responders” and “slow responders”, respectively. In the detection task, median RTs of fast responders were all shorter than 355 msec (mean ± SD, 321 ± 32 msec), whereas median RTs of slow responders were all longer than 380 msec (mean ± SD, 386 ± 7 msec). The five fastest and five slowest responders in the discrimination task (420 ± 28 and 489 ± 33 msec, respectively) were the same as in the detection task. Target response rates for the fast-responder and slow-responder subgroups did not differ statistically, although fast responders tended to make more false alarms (0.77 vs 0.4%, both tasks; F_(1,8)= 10.36; p = .012).

To determine whether the observed ERP differences were stable across relatively short-RT and long-RT trials, separate subaverages were computed of responses to correctly detected targets in the detection task for which RT was shorter or longer than the subject median. These five short-RT and five long-RT target response averages (one each for each attended location) were then averaged across subjects in the fast- and slow-responder subgroups, giving four (fast-responder/slow-responder by short-RT/long-RT) target response subaverages at each of the five stimulus locations. Grand average discrimination-task target responses were also computed for each subgroup. Because there were far fewer targets presented in the discrimination task, these target responses were not further separated by response times.

Next, for each subgroup an ICA decomposition was performed on 30 1 sec detection-task ERP ensembles consisting of 20 average responses to nontarget stimuli (i.e., those presented in the four unattended locations in each of the five attended-location conditions), plus the five short-RT and five long-RT target responses. For both subgroups, ICA again recovered three dominant LPC components. Figure4B shows both short-RT subaverages at the 29 scalp channels above the time courses of projected RMS amplitude of the three component projections. Plotting RMS-projected amplitude displays the true scalp energy ratios of the various components but ignores their polarity differences. Component P3f accounted for the slow positive shift in the responses encompassing the N2/P2 peaks and part of the LPC onset, and could not, therefore, have been derived by decomposition methods that treated each peak as a separate component. The larger component Pmp in the slow-responder average accounted for the larger bipolar spread in the scalp distribution of the response at ∼600 msec.

Figure 4C compares the scalp maps and time courses of projected RMS amplitude for the three target-LPC components. Although the responses analyzed came from two separate subject subgroups and response decompositions, the component scalp maps for the two groups were again highly similar (scalp maps). P3f onset and peak latencies (top left) were earlier in the fast-responder average, and the projected P3f amplitude was larger. Its frontal scalp distribution appeared somewhat more left-sided in the slow-responder group response decomposition, although the component map values at the two periocular electrodes (data not shown) were near equal for both groups. In single-subject responses as well as in the group subaverages, P3b peak latency (r = 0.724;F_(1,8) = 8.8; p = 0.019) covaried with RT. In all subjects, P3b peak amplitude (12.2 ± 5.7 vs 8.4 ± 4.4 μV; t₍₉₎ = 6.27;p < 0.0001) and RMS-projected amplitude (3.2 ± 1.5 vs 2.2 ± 1.2 μV; t₍₉₎ = 5.95;p < 0.0002) were larger in short-RT trial averages,. This association of P3b and RT is consistent with early reports on late LPC features (Roth et al., 1978).

Component Pmp was larger in the slow-responder group subaverages. For both groups, neither P3f nor Pmp amplitudes varied markedly with RT subset. Examination of individual decompositions suggested that the subgroup amplitude differences in these two components arose mainly from the absence or near-absence of P3f in responses of three of the slow responders and of Pmp analogs in responses of two of the fast responders. Very similar or more pronounced subject group differences in amplitudes and time courses of P3f and Pmp were produced by a single decomposition of all 50 concatenated detection-task responses from the two groups (data not shown).

Between-task response differences

Sets of 50 grand mean discrimination-task ERPs for the fast- and slow-responder subgroups were decomposed separately. Figure4D shows the envelopes of the target responses and all of their 31 constituent ICA components for the three detection-task and discrimination-task subaverages. Examination of P3b analogs in decompositions of all 75 detection- and discrimination-task responses from nine subjects separately (omitting one subject with very small responses) showed that P3b peak RMS-projected amplitude was not significantly larger in the detection-task responses (probability of rejecting the null hypothesis by two-tailed t test,p = 0.31). Note that in both discrimination-task decompositions, the envelope peak latency of the P3b component differs from the response peak latency. In the slow-responder averages (right column) P3f peak latency was similar in the three response conditions, irrespective of RT differences. All three subaverages for the fast responders (left column), on the other hand, contained a P3f with a larger envelope that peaked 30–40 msec before median RT.

Subsequent to this analysis, detection-task data were collected from 12 more normal subjects. Initial analysis of grand averaged data from the five fastest responders (median RTs, 261–363 msec) and five slowest responders (median RTs, 381–429 msec) supported the differences in P3f amplitudes shown in Figure 4D. A large P3f component, highly correlated with the fast-responder P3f (scalp map,r = 0.857), was found for the new group of faster responders, whereas no equivalent prominent or spatially correlated component was derived from the response averages of the new slower responders. Further results of the enlarged subject group comparisons will be reported elsewhere.

The slow-responder target response in the discrimination task (Fig.4D, bottom right) contained a prominent component Pmp that peaked, as in the other two subaverages, ∼200 msec after median RT. In individual decompositions, Pmp analogs of all five slow responders had larger peak RMS-projected amplitude in the discrimination task. However, in the discrimination task neither the fast-responder subgroup subaverage (Fig.4D, bottom left) nor any of the five individual fast-responder discrimination-task target response decompositions contained a Pmp analog. Note that the group differences in relative sizes of P3f and Pmp were maintained in the decompositions of the long-RT subaverage for fast responders (Fig.4D, middle left) and the short-RT subaverage for slow responders (Fig. 4D, top right), although the median RTs for these trial subsets were nearly identical (356 and 346 msec, respectively). Clear Pnt analogs (data not shown), present in both group decompositions, were somewhat earlier and larger in the fast-responder group average.

Figure 4, E and F, shows all detection-task target responses at the left periocular electrode for one of the fast responders and one of the slow responders, with single trials sorted (left to right) in order of increasing RT (black traces) and then smoothed with a 30-trial moving average in a style we call an “ERP image” (Jung, Makeig, Westerfield, Townsend, Courchesne, and Sejnowski, unpublished observations). In the faster responder, RT followed the P3f peak immediately in all but the few longest-RT trials, whereas in longer-RT trials of the slower responder, RT lagged behind the P3f peak by 200 msec or more. The figure also shows the prominent post-RT frontal negativity in the slower responder accounted for by Pmp, which was absent from the responses of all five fast responders.

Figure 5A plots the peak LPC component amplitudes of the subgroup averages (whose envelopes were shown in Fig.4D) against their latencies relative to stimulus onset (left panel) and median RT (right panel). In the fast-responder averages (red solid lines), peak latencies of all three components were time locked to median RT (right panel, red symbols), whereas in the slow-responder averages (blue dashed lines), P3f peak latency was time locked to stimulus onset (left panel, bottom left). The response-locked latency of the P3f peak in the slow-responder averages matched that of fast-responders only in the detection-task short-RT trial subaverage (right panel, bottom left).

Timing of the motor command

To more closely assess the relationship between P3f peak latency and RT, a control experiment was performed in which the subject pressed the response button to targets in a single-location variant of the detection task with her right thumb while electromyographic (EMG) activity was recorded from the thumb muscle (extensor pollis brevis). The EMG record (data not shown) clearly indicated that EMG activity began at ∼25 msec before the switch closure used to compute RTs in these experiments. Estimating the travel time from the brainstem to the thumb muscle at 16 msec (0.8 m at 50 m/sec), the P3f peak and the motor command appear to have been nearly simultaneous for the faster responders in all three response conditions.

Comparison with other linear decomposition methods

Detection-task data consisting of 10 long-RT and short-RT target response averages plus 20 nontarget response averages were decomposed separately for the fast-responder and slow-responder groups using spatial PCA. Each data set had four eigenvalues larger than unity (with three larger than 2). Because PCA, like ICA, is a linear decomposition, PCA and ICA components can be plotted using identical methods. Figure5B shows the grand-mean short-RT target response (all five attended locations) for the fast responders at centroparietal scalp site Pz (black traces), with the projections of the three largest principal components at the same channel superimposed (colored traces), with the projection waveforms of the next four (relatively small) principal components shown below it.

PCA maximized the variance of the first principal component projection (Fig. 5B, red), thereby accounting for most of the (ICA) P3b plus some of the Pmp and P3f. The second-largest component (Fig. 5B, green), constrained by PCA to be spatially and temporally orthogonal to the first, also accounted for early and late activity assigned separately by ICA to Pmp and P3f. Orthogonal Varimax rotation of the activations of the seven largest principal components (Fig.5B, top right) somewhat reduced the temporal spread of the second (Fig. 5B,green) component, consistent with its goal of rotation toward “simple structure.” Further oblique rotation of the resulting Varimax component activations using the Promax algorithm (Fig.5B, bottom left) further focused the activation of this (Fig. 5B,green) component to the Pmp time period and partly separated P3b from the early LPC. The scalp map (data not shown) of the largest Promax component active during the early LPC resembled that of P3f. Time courses of the largest components produced by spatial Varimax (data not shown) generally resembled those for temporal Varimax. Spatial Promax (data not shown) fractionated P3b into five components with similar time courses.

Projections of the three ICA components are shown for comparison (Fig.5B, bottom right). Note the relative parsimony of the ICA component structure, with nearly all of the variance accounted for by three components having compact periods of activation. The spillover of P3b activity (Fig. 5B,red) into the N1 and P2 response peaks is smaller in the ICA decomposition than in the other three decompositions.

To test the reliability of the ICA components relative to those derived by PCA-based methods, we measured differences in the four response conditions (fast- and slow-responder subgroups by short- and long-RT trial subsets) between median reaction time and peak latencies of the three large components most analogous in time course to the ICA P3f, P3b, and Pmp. Figure 5C (left panel) shows the means and SDs of this RMS latency difference, averaged across all three components and four subject and response subsets. The covariation of the component peaks with median RT was tightest for ICA (red) (RMS difference, <10 msec), and was tighter for temporal Varimax and Promax rotations (solid lines) than for spatial rotations (dashed lines).

The right panel of Figure 5C shows means and SDs of the correlations between scalp maps (data not shown) of the three ICA component-analogs from the fast- and slow-responder decompositions, respectively (averaged over the three LPC components). The subgroup scalp map correlations were more invariant for ICA (red) (r > 0.9). These results strongly suggest that, applied to these data, ICA decomposition had more simple structure, was more consistent across subject subgroups, and was more tightly linked to performance than decompositions produced by PCA-based methods.

Degree of stability of the decomposition

Although the decomposition produced by ICA is linear, ICA training is nonlinear. Therefore, the projection of an ICA component derived from the mean of two responses may differ from the mean of analogous component projections drawn from separate decompositions of the same responses. Figure 5D shows the time courses of RMS amplitude of the three LPC component projections for the grand-mean detection-task target response (all 10 subjects and five locations) as given by the three ICA decompositions described above: (1) simultaneous decomposition of 75 10-subject response averages from both tasks; (2) separate decomposition of the 25 grand-mean detection-task responses only; and (3) the average of separate detection-task projections for the fast-responder and slow-responder groups, respectively. All three decompositions produced LPC components with similar scalp distributions (compare Figs. 3F, 4C), peak latencies, and time courses. However, as their peak amplitudes vary, projected ICA-component amplitudes are best compared within rather than between decompositions.

ICA identifies independent periods of spatial stationarity

Geometric insight into how the ICA algorithm decomposes ERP is suggested by Figure 5F, which shows all 10 mean short- and long-RT detection-task target responses for the slow-responder group at two midline scalp electrodes (Fz and Pz). In this scatter plot format (middle panel), the data traces follow a cyclic trajectory, although time is not represented explicitly. Amplitude changes in spatially fixed response components are represented by movements in radial directions away from or toward the origin. This plot shows (dashed lines) the two radial directions corresponding to the two largest ICA components (P3b, Pmp) as defined by the relative strengths of these components at the two locations in their scalp maps (e.g., Fig. 5G, black dots). The two component directions are aligned with the most nearly radial portions of the data (Fig. 5F), which represent periods when the scalp distribution of the response was unchanging at the two channels and were accordingly dominated by single ICA components (Fig. 5E).

The spatial structure of the data scatter plot (Fig.5F) resembles an oblique parallelogram rather than a Gaussian cloud. ICA decomposition, by identifying its natural boundaries, finds its periods of strongest spatial stationarity, and in so doing finds the axes and bias offsets that transform the irregular shape of the input data scatter plot into a near-evenly filled square (right plot insert), thereby maximizing its entropy. In contrast, PCA would in effect fit a Gaussian distribution to the data, returning only its major and minor axes. In this case, the first principal component (data not shown) would point in a direction resembling but not matching that of P3b, and the second principal component, orthogonal to it, would ignore the sizable stationarity accounted for by Pmp, because the two ICA component scalp maps are well correlated (r = 0.888), but PCA maps must be orthogonal. ICA identified important nonGaussian features of the input data by means of higher-order (e.g., nonGaussian) statistics implicitly involved in its training (see ).

DISCUSSION

The results reported here using ICA confirm and clarify the evidence from early ERP studies that target LPCs are composed primarily of three components. In addition, a left-frontal LPC component was evoked by nogo stimuli that required subjects to refrain from responding. These four ICA components had distinctly different scalp distributions, and their dynamics covaried in orderly ways with the task, subject, and response time differences. The decomposition provided information about the effects of dependent variables on spatially and temporally overlapping components that would have been difficult or impossible to obtain from separate measurements on single-channel waveforms.

The novel P3f component

First, an early frontoparietal positivity (with bilateral lateral parietal negativities), called here P3f, was active from the N1 peak through the first portion of the LPC. In the subaverages of faster responders, its peak latency was nearly simultaneous with the subcortical motor command, whereas for five slower responders its peak latency matched RT only for short-RT trials in the simpler detection task condition. In nearly all decompositions, the topography of P3f combined a frontal/periocular positivity with a focal, slightly right-of-center parietal positivity whose peak was slightly anterior to the P3b extremum. Because the P3f amplitude was near-equal at both periocular sites and occurred in nearly every trial with similar (∼3 μV) amplitude and latency, it is unlikely that its periocular projection was generated by eye movements. Instead, P3f likely derives from stimulus-evoked activity in a frontoparietal system concerned with orienting to spatial stimuli. Recently, Corbetta et al. (1998) have shown that two tasks, one involving voluntary covert shifts of spatial attention (eyes fixated) and the other, voluntary overt attention shifts (saccadic eye movements to attended locations), produced fMRI signal activations in bilateral frontal and parietal areas considered to be analogs of monkey frontal eye field, superior eye field, and lateral intraparietal sulcus areas, respectively (Gaymard et al., 1998). This set of areas is compatible with the scalp distribution of P3f.

The selective evocation of P3f by targets (and partially by nogo near-targets), its frontoparietal topography, and its close association with response production in faster responders all suggest that P3f may also reflect activity in brain systems associated with speeded manual responding. The combination of periocular, frontal, and bilateral parietal scalp features in P3f suggests coordinated activity in brain regions underlying frontal and bilateral parietal sites involved in speeded manual responses, particularly in faster responders. These possibly include human homologs of the superior parietal “reach region” (Snyder et al., 1997) and frontal eye fields (Schlag et al., 1998) in monkey orbitofrontal cortex, shown to be activated by alarming stimuli and sudden auditory events (Cottraux et al., 1996; Johnsrude et al., 1997), and prefrontal cortex (Rao et al., 1997). More experiments will be required to determine the relative importance of speeded responding, selective attention, and/or spatial orienting for P3f generation.

Novel stimuli presented during focused attention to a stream of known stimuli or rare stimuli presented during passive attention can produce a relatively early, large centrofrontal LPC feature (Courchesne et al., 1975). The scalp distributions of this novelty or P3a component (Katayama and Polich, 1998) appear different from the P3f, but further studies will be required to evaluate possible differences between them.

The P3b component and P300

The largest of the three independent LPC components, P3b, had a central parietal maximum and a right-frontal bias, like the LPC peak itself. In the detection task, its peak amplitude appeared inversely related to median RT. In the discrimination task, the ∼90 msec delay between RT and the P3b peak observed in the detection task was reproduced only in the fast-responder response. These characteristics of the central LPC component (P3b) identified by ICA appear consistent with those of the LPC peak in the detection task, often called P300. However, in the discrimination-task subaverages (Fig.4D) the LPC and P3b peaks did not coincide. Thus, ICA decomposition may greatly increase the precision of studies that use P3b amplitude and latency measures as covariates to explore the nature and progression of psychiatric and neurological conditions such as aging (Friedman et al., 1997), schizophrenia (Turetsky et al., 1998), and autism (Courchesne et al., 1990).

The motor-related Pmp component

The third LPC component, Pmp, was activated only after a button press. Its posterior maximum was contralateral to response hand, and its latency and topographic variability across subjects strongly resembled that of the 200 msec postmovement positivity in the voluntary motor response (Makeig et al., 1996c; Boetzel et al., 1997). However, in the discrimination task no Pmp was present in target responses of the five faster responders. Most probably, Pmp accounts for a component originally called SW (slow wave) whose peak covaried with RT (Simson et al., 1977; Roth et al., 1978). Makeig et al. (1997; their Fig. 4) also found an ICA component strongly resembling Pmp in a task requiring button presses after indistinct auditory targets.

The Pnt component and response inhibition

A fourth LPC component, labeled Pnt, was activated in parallel with P3b after nogo nontarget distractors presented in the attended location in the discrimination task. The scalp distribution of Pnt explains the more anterior LPC distribution consistently observed in responses to nogo compared with go stimuli (Fallgatter et al., 1997), but not previously dissociated from the concurrent residual P3b also evoked by these stimuli (Fig. 3E). The scalp distribution of Pnt appears consistent with activation of left dorsolateral prefrontal brain areas repeatedly found in lesion and imaging studies to be involved in response inhibition (Taylor et al., 1997; Jonides et al., 1998; McKeown et al., 1998a). In particular, a homologous left frontal activation was found by Ebmeier et al. (1995) in a positron emission topography experiment in which a three-stimulus oddball paradigm including rare nogo nontargets was compared with a standard two-stimulus oddball paradigm.

Faster and slower responders

Jokeit and Makeig (1994) reported that subjects in a speeded auditory response experiment were split neatly into two equal groups of faster- and slower-responding subjects by the time courses of EEG power near 40 Hz before and after the imperative stimuli. They tentatively interpreted this result as supporting a theory advanced by early psychophysiologists, including Wundt (1913), that faster responders can respond in speeded response tasks without waiting for a clear and conscious perception of the stimulus, whereas slower responders inhibit their response until they recognize the target event and make a conscious decision to respond to it. Our results suggest that the relatively early responses of faster responders may be triggered by P3f, which appears to comprise concurrent activations in more than one brain region. Possibly, the larger Pmp in slower responders might index their greater tendency to attend to somatosensory feedback from their button press, a hypothesis compatible with Wundt’s characterization.

The analytic power of ICA

Although the ICA technique is relatively new, and its effectiveness in separating ERPs into components that reflect underlying brain processes has not yet been established, the results reported here are encouraging. They demonstrate, first, that ICA can parsimoniously decompose ERP data sets comprised of many scalp channels, stimulus types, and task conditions into temporally independent, spatially fixed, and physiologically plausible components without necessarily requiring the presence of multiple local response peaks to separate meaningful response components. Second, the apparent consonance of the identified scalp distributions for P3f, Pmp, and Pnt with fMRI activations reported for related task paradigms suggests use of these methods may lead to increased convergence between results of cognitive ERP and fMRI experiments. Third, the LPC components identified here had distinct scalp distributions, and their dynamics covaried in orderly ways with task, subject, and response time. Furthermore, they provided more information about the relationships of spatially and temporally overlapping components to subject performance than either PCA, Varimax, or Promax, information that would be difficult or impossible to obtain from separate measurements of single-channel waveforms. ICA has also been applied successfully to analysis of fMRI data (McKeown et al., 1998b) and optical recording data using voltage-sensitive dyes (Brown et al., 1998).

Conclusions

Responses to visual stimuli analyzed with ICA have revealed three major components to the LPC, in accord with the results of early ERP studies on auditory target LPCs. Motor responses of faster responders were triggered at the peak of an early component, P3f, that begins at ∼140 msec and includes concurrent frontal and bilateral parietal scalp foci. The second component, P3b, resembled the P300 response reported in simple oddball experiments not involving motor responses. The third component, Pmp, tended to follow responses of slower responders and matched the 200 msec postmovement positivity in voluntary button press responses in both latency and scalp distribution. Subject group differences linked to median RT appeared to be equally expressed in subaverages of subjects short- and long-RT trials, suggesting they may be robust to changes in instructions and strategy, although this has not yet been tested. The methods demonstrated here might be used with normal or clinical subjects to assess cognitive function. They provide a valuable new window into the relative strengths and time courses of underlying brain processes.

Lee et al. (1999a) have shown that the major algorithms proposed for ICA can be derived from an information theoretic framework, differing mainly in the distributions they assume for the activation values of the separate components (Jutten and Herault, 1991;Cichocki et al., 1994; Comon, 1994; Bell and Sejnowski, 1995; Amari et al., 1996; Cardoso and LaHeld, 1996; Perlmutter and Parra, 1996;Karhunen et al., 1997; Lewicki and Sejnowski, 1998; Lee et al., 1999b). The infomax ICA algorithm of Bell and Sejnowski (1995), when implemented using a sigmoid nonlinearity, is capable of separating arbitrary full-rank mixtures of component processes having temporally independent activations, with super-Gaussian (positive-kurtosis) distributions.

Independence of two or more variables implies not only that they are uncorrelated, a condition on the second-order moments, but also that all the higher-order joint moments are zero. Thus, decorrelation is a weaker restriction than independence. Independence is equivalent to minimizing the mutual information between a set of signals, which can be accomplished under certain conditions by maximizing their joint entropy (Bell and Sejnowski, 1995). Entropy is a measure of the amount of disorder in a system; its maximum occurs when the joint, multidimensional probability distribution of the system is uniform.

The infomax ICA algorithm

Each input vector, x(t), represents a set of EEG voltages recorded from all the input channels at time t. Joint entropy maximization is performed on the (randomly time-ordered) input data after they are linearly transformed and then compressed by a nonlinear sigmoidal function:

$$y(t)=g(u(t)),\text{where} u(t)=\text{Wx}(t)+W_0$$ Equation 1

The sigmoidal nonlinearity, g(), provides necessary higher-order statistical information to guide the entropy maximization. Optional sphering of the input data before training:

$$x_s(t)=\text{Sx}(t),\text{where} S=2\langle {\text{xx}}^T{\rangle }^{-½}$$ Equation 2

where < > is the average taken over the data, removes secondorder correlations between channels and may speed up convergence (Bell and Sejnowski, 1996).

Before training, W is initialized to the identity matrix,I (or else, if the data are not sphered, to the sphering matrix, S) and W₀ to 0, and then W and W₀ are iteratively adjusted using small batches of randomly selected data vectors (normally 10 or more) drawn from {x} without substitution, according to:

$$\mathrm{\Delta }W=\epsilon \left(\frac{\partial H(y)}{\partial W}\right)W^{T}W=\epsilon (I+\varphi u(t{)}^T)W$$ Equation 3

$$\mathrm{\Delta }{W}_0=\epsilon \varphi (t)$$ Equation 4

Here, H(y) is the joint entropy of y, ε is the learning rate (normally <0.01), and the function ϕ() has elements:

$${\varphi }_i(t)=\frac{\partial }{\partial u_i(t)}ln\left(\frac{\partial y(t)}{\partial u_i(t)}\right)$$ Equation 5

The “natural gradient” termW^TW in the update equation (Amari et al., 1996; Cardoso and Laheld, 1996) avoids matrix inversions and greatly speeds convergence (Amari, 1998). The logistic nonlinearity:

$$y_i(t)=g(u_i)=1/(1+e^{-u_i})$$ Equation 6

gives

$${\varphi }_i(t)=1-2y_i(t)$$ Equation 7

and a simple update rule,

$$W_{0i}(t)\to \epsilon (1-2y_i(t))$$ Equation 8

that biases the algorithm toward finding sparsely activated (super-Gaussian) independent components with positive kurtosis, compatible with the assumption that ERPs are composed of one or more overlapping series of brief activations within spatially fixed brain systems performing separable stages of stimulus information processing.

The number of time points needed for the method may be as few as several times the number of recording channels, which in turn must be at least equal to the number of components to be separated. The columns of the inverse matrix, W⁻¹, or(WS)⁻¹ if the data are sphered, give the projection strengths of the respective components onto the scalp sensors. These may be interpolated to give a scalp mapassociated with each component. The projection of the ith component activation into the original data space is given by the outer product of the ith row of the component activation matrix with the ith column of the inverse unmixing matrix. As scaling information and polarity are distributed between the activation waveforms and the maps (unless one or the other are normalized), the strengths of different components should be compared through the strengths of their projections, which are scaled in the original data units (microvolts) (Makeig et al., 1997).

Infomax training

The infomax algorithm reported here used an initial learning rate near ε = 0.004 and computed updates based on batches of ∼25 time points chosen at random without substitution from the input data set. After each pass through all the data points, an angle representing the difference in direction between the update vectors in the current and previous passes was computed. Whenever this angle was >60°, the learning rate was reduced by 10%. Training was halted when the learning rate decreased below 0.000001 [Stand-alone and Matlab routines used are available via the world wide web (S. Makeig, MATLAB toolbox for electrophysiological data analysis, version 3.2, WWW Site, Computational Neurobiology Laboratory, Salk Institute, La Jolla CA, http://www.cnl.salk.edu/∼scott/ica.html {World Wide Web Publication}, 1998)]. Repeated testing showed that the decomposition so derived was little affected by the exact choice of training, annealing, or stopping parameters. As expected, the absolute values of correlations, {r}, between component activations (across all the input data) were low (SD of  r  < 0.029).

Extended-infomax

The infomax algorithm learning rule can be generalized to separate sources with either sub-Gaussian (negative-kurtosis) or super-Gaussian (positive-kurtosis) distributions by approximating the estimated probability density function in the form of a fourth-order Edgeworth approximation (Girolami and Fyfe, 1997). The algorithm becomes:

$$\mathrm{\Delta }W=\epsilon [I-K \text{tanh}(u)u^T-{\text{uu}}^T]W$$ Equation 9

where K is an n-dimensional diagonal matrix whose elements are

$${\text{k}}_{\text{i}}=+1 \text{for super}­\text{Gaussian sources}$$

$${\text{k}}_{\text{i}}=-1 \text{for sub}­\text{Gaussian sources}$$

The k_is can be estimated from the generic stability analysis of separating solutions. This yields the choice of k_is used by Lee et al., (1999b):

$$k_i=\text{sign}(E\{sec{h}^2(u_i)\}E\{u_i^2\}-E\{\text{tanh}(u_i)u_i\})$$ Equation 10

which ensures stability of the learning rule.

JADE

The JADE algorithm (Cardoso and Laheld, 1996) also performs ICA based on joint diagonalization of cumulant matrices involving all cumulants of orders two and four. It can separate both sub-Gaussian and super-Gaussian sources. The JADE software release (J.-F. Cardoso, JADE code for real-valued signals, version 1.5, WWW Site, CRNS, Paris, France, http://sig.enst.fr:80/∼cardoso/{World Wide Web Publication}, 1997) requires no parameter tuning. The current implementation limits the number of data channels (and separated sources) that can be practically separated to ∼50 on current computers.

PCA-based decomposition methods

A second class of proposed LPC decompositions have involved PCA (Donchin, 1966; Glaser and Ruchkin, 1976; Friedman, 1984; Dien et al., 1997). Although PCA can efficiently characterize Gaussian-distributed data, actual ERP data are not Gaussian (compare Fig.5F). Because of this, these researchers have explored the possible usefulness of several orthogonal and oblique component vector rotation methods for finding simple structure in high-dimensional data. Advantages and shortcomings of these approaches have been extensively discussed (Wood and McCarthy, 1984; Mocks and Verleger, 1986; Chapman and McCrary, 1995).

Varimax and Promax

Varimax and Promax are two methods for rotating components such as those derived by PCA toward simple structure. Applied to rotation of components obtained by spatial PCA, the principle of simple structure implies that the variance in the original data accounted for by each component is concentrated into relatively few scalp channels or into relatively few time points, depending on whether the rotation is applied to the time courses of activation of the PCA components or to their scalp maps (eigenvectors). Spatial rotation toward simple structure attempts to minimize the number of scalp channels accounted for by each component, thereby generally biasing components to account for the activity of superficial brain sources. Often, in practice, only the largest principal components are rotated.

Varimax (Kaiser, 1958) is an orthogonal rotation method and does not strictly require initialization by transformation of the data into a principal component subspace (Mocks and Verleger, 1986). Because it produces an orthogonal rotation, Varimax components derived from PCA eigenvectors cannot account for activity from functionally separate brain sources whose spatial projections to the scalp are nonorthogonal (Donchin et al., 1986). Promax (Hendrickson and White, 1964) is an iterative nonlinear method that performs a highly constrained oblique rotation to further intensify the orthogonal “rotation to simple structure” produced by Varimax. In Promax, the unrotated data and the data accounted for by each component are first raised to a positive power (often the fourth), retaining their original sign and emphasizing their peak values, and the component filters are rotated so as to minimize the least-square distance between their projections and the distorted data. We applied both temporal and spatial Varimax and Promax rotation to the largest seven principal components of the data (Fig.5B,C). Promax training was halted when the relative distance measure stopped decreasing (after 1–3 iterations).