Abstract
The purpose of this investigation was to determine the differences between halves in the most demanding passages of play in football players according to playing position and duration-specific activity. Global positioning system data were collected from twenty-three football players from a reserve squad of the Spanish La Liga. A total of 265 individual match half data were analysed across the competitive season. Players were categorised based on positional groups: full-back (FB), central defender (CD), midfielder (MF), offensive midfielder (OMF) and forwards (FW). The most demanding passage of match play was analysed using a rolling average method, where maximal values were calculated for five different time durations (1, 3, 5, 10 min and half completed) using distance (m·min-1), high metabolic load distance (HMLD; m·min-1) and average metabolic power (AMP; W·kg-1) as variables of interest. The differences between the first and second half increased as the rolling duration increased, reaching the greatest difference between halves in the complete half (45 min) in all the variables studied (ES = 0.54 ± 0.15, 0.75 ± 0.15 and 0.76 ± 0.15 in distance, HMLD and AMP). The CDs were the players that presented the greatest differences, and it was in the AMP variable where the greatest differences between the first and second half were found. Large decreases in AMP were found for CD (ES = -1.30 ± 0.36) and moderate decreases were found in AMP for FB (ES = -0.84 ± 0.30) and OMF (ES = -0.78 ± 0.37). These results provide insight into the most demanding passages of play to inform training practices for specific football playing positions.
Keywords: Team sports, Match demands, Peak intensity, Global position system
INTRODUCTION
The analysis of soccer competition is one of the most common research topics in the last decades [1–2]. One of the purposes of time-motion analyses is to provide information that allows appropriate management of training intensity. Thus, match-play activity can serve as a guide or reference when proposing training activities [3–4].
The comparison of activity between the first and second half of a competition has been performed in different research studies [5–6]. Previous studies [5–7] have reported that greater distance is covered during the first half of the match compared to the second half, although the results are not entirely consistent [8–9]. These inconsistent findings may reflect the interaction of other variables such as research designs, instruments, analytic techniques [10] or particular contextual dynamics (e.g. due to situational variables) of each game [1–11].
Although the most common time-motion analysis has been the study of the average demands imposed on the soccer player, in recent years attention has been devoted to the most demanding passage of match play [12–13]. Studies initially examined periods of fixed durations [8–15] but have more recently examined moving averages [16–17]. The application of the moving average duration method has been used to study the most demanding phases of competition in different team sports such as Gaelic Football [18], Rugby League [16], Australian Football [19] and European football [20]. The objective of these studies was to compare the demands imposed on players according to position [13–20], the relative demands of training and competition [21–22], and relating the activity of players during these periods with their physical attributes [23].
The most demanding passage of training tasks have been studied for different playing positions [21], but it is unknown whether there are differences among playing positions for the most demanding passage of match play, or if different activity durations and locomotor variables or the results alter across the course of a match (e.g. between the first and the second half).
The purpose of this study was to investigate the most demanding passages of match play in a football competition according to playing position, variable criteria and using varying moving average durations. We also examined whether the most demanding passages of match play differed between the first and second half. The results of the study will provide insight into the most demanding passages of football match play in order to develop appropriate training strategies to adequately prepare players for competition.
MATERIALS AND METHODS
Experimental Approach to the Problem
In order to establish the differences between halves and among playing positions for the most demanding passage of match play, global positioning system (GPS) data were collected during the 2016–2017 competitive season. Different GPS variables were used, along with different moving average durations. Prior to the commencement of the study, all subjects were informed of the aims and requirements of the research, and informed consent was obtained. The study conformed to the recommendations of the Declaration of Helsinki [24].
Subjects
Twenty-three professional football players participated in this study (age: 20.8 ± 1.8 years, mass: 70.5 ± 6.7 kg and stature: 1.78 ± 0.67 m). Players belonged to a reserve squad of a Spanish La Liga club that also competed in the Union of European Football Associations (UEFA) Champions League. Data were collected throughout 37 competitive matches of the 2016–2017 competitive season (13 wins, 15 losses, 9 draws, final position 11th). Each match was 90 min in duration (two 45–min halves). Players were grouped according to their playing position, as central defenders (CD: n=3; 49 records), fullbacks (FB: n=5; 65 records), midfielders (MF: n = 3; 44 records), offensive midfielders (OMF: n= 5; 48 records) and forwards (FW: n=7; 59 records). The mean (± SD) number of observations per player was 11.5 ± 6.4. A total of 265 observations were recorded from each half.
Activity Profile
The activity profile of players was monitored during each official match using a portable 10 Hz GPS unit (Viper Pod, 50 g, 88 x 33 mm, Statsports Viper, Northern Ireland) as used in previous studies [25–26]. The accuracy of these devices has been studied recently, with 2.53 ± 6.03% estimation error for distance covered, with accuracy (%) improving as the distance covered increased and the speed of movement decreased [27]. In order to avoid interunit error, each player trained with the same GPS device during the whole study period [28–29]. The GPS model used in this study was worn in a purpose-designed vest, inside a mini pocket positioned in the centre area of the upper back, just above the shoulder blades, and thus not affecting mobility of the upper limbs and torso.
Upon completion of each match, GPS data were extracted using the appropriate proprietary software (Viper, Statsports, Ireland). The team systematically played in a 1–4–3–3 formation, with a goalkeeper, two FB, two CD, a MF, two OMF and three FW. Goalkeepers were not included in the analysis.
Procedures
The STATSports software (Version 1.2) was used for the computation of a moving average over each variable of interest (distance, high metabolic load distance [HMLD] and average metabolic power [AMP]), using five different durations (1, 3, 5, 10 min and half completed) recording the maximum value for each duration. As a result, for each match, maximum values using three variables of interest were calculated for each of the 5 moving average durations (1, 3, 5, 10 minutes and half completed) for each half of the match completed. These four different durations were analysed because they correspond to the usual duration of the training drills in the team studied. Descriptive statistics and analysis were then calculated based on positions of play. These data were then averaged across all observations per position for between-group analysis.
This method allowed the computation of a number of output variables for each player, including distance (m·min-1), high metabolic load distance (HMLD; m·min-1) and average metabolic power (AMP; W·kg-1). Distance was representative of the traditional model, where accelerated running is ignored [16]. Composite variables combining multiple physical factors were also considered. The high metabolic load distance (HMLD) sums up high-speed running distance (>14.4 km·h-1) and also includes the distance covered when the player is involved in high acceleration/deceleration activities (set by the manufacturer at >2 m·s-2 by default). HMLD represents the distance covered (m) by a player when their metabolic power (energy consumption per kilogram per second) is above the value of 25.5 W·kg-1. It can provide additional information on the total high-intensity activities of players who are not regularly involved in high-speed running but which include short accelerations and braking [30]. The average metabolic power (AMP) represents a theoretical approximation of the energy cost of team sports where in addition to the speed of running, the energetic cost of accelerating and decelerating is considered [31]. This variable is an estimate of the metabolic demands of running only (i.e. not kicking or jumping). This indicator presents some controversy in the literature [31–32], although it has been validated in different studies [31–33].
Statistical Analysis
The data are presented as means and standard deviations (mean ±SD). Magnitude-based inferences and precision of estimation were used to analyse the data [34]. Prior to the comparisons, all processed variables were log-transformed to reduce the non-uniformity of error. Differences between halves (1st half and 2nd half) were assessed via standardized mean differences (Cohen’s d) and respective 90% confidence limits. Threshold values for standardized differences were >0.2 (small), >0.6 (moderate), >1.2 (large) and very large (>2.0) [35].
RESULTS
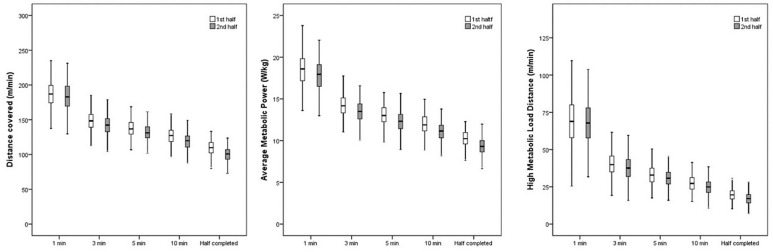
Figure 1 shows the mean ± SD distance (m·min-1), HMLD (m·min-1) and AMP (W·kg-1) values for pooled soccer players in the five analyzed periods of time (1, 3, 5, 10 and half completed). The distance covered showed small differences between halves for 3 min (ES=-0.35; 90% confidence limits ± 0.15), 5 min (ES=-0.36 ± 0.15) and 10 min (ES= -0.53 ± 0.15) durations, while the differences in the half completed were moderate (ES= -0.75 ± 0.15). Small differences were found in HMLD between halves for 3 min (ES= -0.29 ± 0.15), 5 min (ES= -0.27 ± 0.15), 10 min (ES= -0.38 ± 0.15) and half completed (ES=-0.54 ± 0.15). In addition, small differences were found in AMP between halves for 3 min (ES= -0.44 ± 0.15), 5 min (ES= -0.50 ± 0.15), 10 min (ES= -0.60 ± 0.015) and half completed (ES= -0.54 ± 0.15).
FIG. 1.
Distance (m·min-1), HMLD (m·min-1) and AMP (W·kg-1) values for pooled soccer players in the five analyzed periods of time (1, 3, 5, 10 and half completed).
Table 1 shows the mean ± SD distance (m·min-1) values for the specific positions in the game, including the standardized differences and magnitude-based inferences in the five analyzed periods of time (1, 3, 5, 10 min and half completed). A large reduction in distance covered occurred in the second half in the CD (ES = -1.43 ± 0.36), while in the rest of the positions the distance covered during the second half was moderately reduced (ES = -0.62 to 1.10). The differences between halves in the 1–minute periods were small in all positions (ES = -0.06 to -0.25). Only the CD showed moderate differences between halves in the 3 min (ES = -0.74 ± 0.36) and 5 min periods (-0.80 ± 0.36), while moderate differences between halves in the 10 min period were found in the CD (ES = -1.14 ± 0.36), FB (ES = -0.82 ± 0.30) and OMF (ES = -0.84 ± 0.36).
TABLE 1.
Comparison of the first and second halves for the most demanding passage of match play for each playing position using distance (m·min-1) for five different time durations (1, 3, 5, 10 min and half completed).
| Duration | 1st half | 2nd half | Difference (%) | Difference standardized (Cohen) | Chances | Qualitative | |
|---|---|---|---|---|---|---|---|
| CD | 1 min | 177.1 ± 14.0 (48) | 175.6 ± 12.4 (46) | -0.8 ± 2.7 | -0.10 (SD 0.37) (-0.47/0.26) | 9/58/33 | Unclear |
| 3 min | 141.7 ± 8.5 (48) | 135.2 ± 9.2 (45) | -4.6 ± 2.2 | -0.74 (SD 0.36) (-1.10/-0.38) | 0/1/99 | Very Likely | |
| 5 min | 130.8 ± 7.6 (48) | 124.4 ± 8.2 (43) | -4.9 ± 2.1 | -0.80 (SD 0.36) (-1.15/-0.44) | 0/0/100 | Most Likely | |
| 10 min | 121.5 ± 6.9 (48) | 113.8 ± 6.7 (45) | -6.4 ± 2.0 | -1.14 (SD 0.36) (-1.50/-0.78) | 0/0/100 | Most Likely | |
| Half completed | 105.9 ± 6.9 (49) | 96.7 ± 6.0 (49) | -8.7 ± 2.1 | -1.43 (SD 0.36) (-1.79/-1.08) | 0/0/100 | Most Likely | |
| FB | 1 min | 189.5 ± 16.3 (59) | 185.5 ± 21.4 (59) | -2.6 ± 3.4 | -0.23 (SD 0.30) (-0.53/0.08) | 1/43/56 | Possibly |
| 3 min | 149.0 ± 11.1 (64) | 143.0 ± 9.9 (65) | -4.0 ± 2.1 | -0.55 (SD 0.30) (-0.85/-0.25) | 0/3/97 | Very likely | |
| 5 min | 137.4 ± 9.3 (65) | 132.2 ± 8.6 (65) | -3.7 ± 1.9 | -0.56 (SD 0.30) (-0.86/0.26) | 0/2/98 | Very Likely | |
| 10 min | 126.6 ± 9.5 (65) | 119.1 ± 7.9 (65) | -5.9 ± 2.1 | -0.82 (SD 0.30) (-1.12/-0.52) | 0/0/100 | Most Likely | |
| Half completed | 108.6 ± 8.0 (64) | 99.5 ± 9.4 (64) | -8.6 ± 2.8 | -0.88 (SD 0.30) (-1.17/-0.58) | 0/0/100 | Most likely | |
| MF | 1 min | 196.4 ± 21.6 (32) | 190.2 ± 20.2 (32) | -3.0 ± 4.3 | -0.25 (SD 0.36) (-0.61/0.11) | 2/39/59 | Possibly |
| 3 min | 155.5 ± 17.2 (32) | 150.1 ± 15.0 (31) | -7.6 ± 4.4 | -0.26 (SD 0.36) (-0.62/0.10) | 2/37/61 | Possibly | |
| 5 min | 144.9 ± 14.8 (32) | 139.6 ± 14.2 (32) | -3.6 ± 4.4 | -0.29 (SD 0.36) (-0.65/0.07) | 1/32/66 | Possibly | |
| 10 min | 134.7 ± 14.7 (31) | 127.3 ± 13.9 (32) | -5.5 ± 4.7 | -0.41 (SD 0.36) (-0.78/-0.05) | 0/16/83 | Likely | |
| Half completed | 118.0 ± 12.7 (32) | 107.2 ± 13.7 (32) | -9.4 ± 4.8 | -0.67 (SD 0.36) (-1.03/-0.32) | 0/2/98 | Very Likely | |
| OMF | 1 min | 194.6 ± 25.9 (47) | 192.0 ± 22.7 (44) | -0.9 ± 5.5 | -0.06 (SD 0.36) (-0.42/0.30) | 12/62/26 | Unclear |
| 3 min | 156.6 ± 13.0 (48) | 150.8 ± 13.5 (42) | -3.7 ± 3.0 | -0.43 (SD 0.36) (-0.79/-0.07) | 0/14/85 | Likely | |
| 5 min | 146.4 ± 12.2 (45) | 140.5 ± 12.3 (44) | -4.1 ± 3.0 | -0.49 (SD 0.36) (-0.85/-0.13) | 0/9/91 | Likely | |
| 10 min | 136.7 ± 11.7 (42) | 127.4 ± 10.6 (40) | -6.9 ± 2.9 | -0.84 (SD 0.36) (-1.20/-0.47) | 0/0/100 | Most Likely | |
| Half completed | 118.3 ± 9.9 (48) | 106.3 ± 11.8 (48) | -10.4 ± 3.3 | -1.10 (SD 0.36) (-1.46/-0.73) | 0/0/100 | Most Likely | |
| FW | 1 min | 174.9 ± 22.8 (57) | 170.6 ± 25.1 (57) | -2.7 ± 4.8 | -0.17 (SD 0.31) (-0.48/0.14) | 2/54/44 | Possibly |
| 3 min | 136.2 ± 16.5 (59) | 131.5 ± 16.5 (56) | -3.7 ± 3.8 | -0.29 (SD 0.31) (-0.60/0.02) | 0/31/69 | Possibly | |
| 5 min | 125.5 ± 14.5 (59) | 121.6 ± 13.8 (57) | -4.3 ± 3.7 | -0.35 (SD 0.31) (-0.66/-0.04) | 0/21/79 | Likely | |
| 10 min | 115.8 ± 13.6 (57) | 110.2 ± 13.5 (57) | -4.6 ± 3.6 | -0.40 (SD 0.31) (-0.71/-0.09) | 0/14/86 | Likely | |
| Half completed | 100.6 ± 12.0 (58) | 93.0 ± 12.4 (58) | -7.7 ± 3.7 | -0.62 (SD 0.31) (-0.92/-0.31) | 0/1/99 | Very Likely | |
| AVG | 1 min | 186.0 ± 22.2 (243) | 182.0 ± 22.6 (238) | -2.2 ± 2.0 | -0.16 (SD 0.15) (-0.31/-0.01) | 0/66/34 | Possibly |
| 3 min | 147.2 ± 16.0 (251) | 141.4 ± 15.2 (239) | -3.9 ± 1.6 | -0.35 (SD 0.15) (-0.50/-0.21) | 0/4/96 | Very Likely | |
| 5 min | 136.4 ± 11.3 (249) | 131.0 ± 13.7 (241) | -3.9 ± 1.6 | -0.36 (SD 0.15) (-0.51/-0.21) | 0/4/96 | Very Likely | |
| 10 min | 126.3 ± 13.9 (243) | 118.8 ± 12.8 (239) | -5.9 ± 1.6 | -0.53 (SD 0.15) (-0.68/-0.38) | 0/0/100 | Most Likely | |
| Half completed | 109.6 ± 12.1 (251) | 100.0 ± 12.1 (251) | -8.9 ± 1.7 | -0.75 (SD 0.15) (-0.90/-0.60) | 0/0/100 | Most Likely | |
CD = central defender; FW = forward; MF = midfielder; OMF = offensive midfielder; FB = full back.
Table 2 presents the mean ± SD values for HMLD (m·min-1). The HMLD in the second half was moderately lower in the CD than the first half (ES = -0.91 ± 0.36), while in the rest of the positions the HMLD during the second half represented small reductions (ES = -0.54 to -0.49). MF exhibited small reductions (ES = -0.21 ± 0.37) between halves in the 1 min period, with no meaningful differences observed in the other positions. In the 3 min and 5 min periods, the differences between halves were small in all positions, except for the MF in the 5 min period, where no differences were observed. Only the CD showed moderate differences between halves in the 10 min period (ES = 0.63 ± 0.36).
TABLE 2.
Comparison of the first and second halves for the most demanding passage of match play for each playing position using high metabolic load distance (HMLD; m·min-1) for five different time durations (1, 3, 5, 10 min and half completed).
| Duration | 1st half | 2nd half | Difference (%) | Difference standardized (Cohen) | Chances | Qualitative | |
|---|---|---|---|---|---|---|---|
| CD | 1 min | 62.4 ± 11.9 (48) | 64.5 ± 11.7 (48) | 3.5 ± 6.9 | 0.19 (SD 0.36) (-0.17/0.55) | 47/49/4 | Possibly |
| 3 min | 35.7 ± 6.6 (49) | 33.7 ± 6.2 (48) | -5.9 ± 6.8 | -0.30 (SD 0.36) (-0.67/0.06) | 1/30/68 | Possibly | |
| 5 min | 28.5 ± 4.3 (48) | 27.5 ± 4.2 (49) | -3.7 ± 5.2 | -0.25 (SD 0.36) (-0.60/0.11) | 2/39/59 | Possibly | |
| 10 min | 23.5 ± 3.0 (48) | 21.6 ± 3.1 (48) | -8.3 ± 4.5 | -0.63 (SD 0.36) (-0.99/-0.27) | 0/2/98 | Very Likely | |
| Half completed | 16.9 ± 2.2 (49) | 14.9 ± 2.1 (49) | -11.8 ± 4.3 | -0.91 (SD 0.36) (-1.27/-0.56) | 0/0/100 | Most Likely | |
| FB | 1 min | 73.5 ± 16.5 (62) | 72.6 ± 15.9 (58) | -1.3 ± 6.6 | -0.06 (SD 0.30) (-0.36/0.24) | 8/70/22 | Unclear |
| 3 min | 42.2 ± 7.2 (64) | 39.9 ± 7.9 (59) | -5.9 ± 5.5 | -0.31 (SD 0.30) (-0.60/0.01) | 0/28/72 | Possibly | |
| 5 min | 35.1 ± 5.9 (64) | 33.0 ± 5.5 (60) | -5.7 ± 4.8 | -0.34 (SD 0.30) (-0.64/-0.05) | 0/21/79 | Likely | |
| 10 min | 29.1 ± 5.0 (62) | 26.6 ± 4.5 (58) | -8.5 ± 4.9 | -0.50 (SD 0.30) (-0.80/-0.20) | 0/5/95 | Very Likely | |
| Half completed | 20.2 ± 3.7 (64) | 18.1 ± 3.4 (64) | -10.8 ± 5.3 | -0.56 (SD 0.29) (-0.86/-0.27) | 0/2/98 | Very Likely | |
| MF | 1 min | 69.6 ± 15.1 (32) | 66.1 ± 15.4 (32) | -5.0 ± 8.7 | -0.21 (SD 0.37) (-0.57/0.16) | 3/46/51 | Possibly |
| 3 min | 38.6 ± 7.8 (32) | 36.7 ± 8.1 (33) | -4.9 ± 8.3 | -0.21 (SD 0.36) (-0.56/0.15) | 3/46/51 | Possibly | |
| 5 min | 32.5 ± 6.9 (32) | 30.7 ± 5.8 (31) | -4.6 ± 8.3 | -0.19 (SD 0.36) (-0.55/0.16) | 3/48/49 | Possibly | |
| 10 min | 27.0 ± 5.6 (32) | 24.8 ± 5.2 (31) | -8.0 ± 8.4 | -0.33 (SD 0.36) (-0.69/0.03) | ww1/27/72 | Possibly | |
| Half completed | 20.0 ± 4.2 (32) | 16.9 ± 4.0 (32) | -15.5 ± 8.9 | -0.57 (SD 0.36) (-0.93/-0.21) | 0/4/96 | Very Likely | |
| OMF | 1 min | 74.3 ± 14.9 (45) | 73.5 ± 13.5 (42) | -1.0 ± 7.3 | -0.05 (SD 0.36) (-0.41/0.32) | 13/63/25 | Unclear |
| 3 min | 44.8 ± 9.1 (48) | 41.6 ± 7.4 (42) | -6.7 ± 7.0 | -0.33 (SD 0.36) (-0.69/0.03) | 1/26/73 | Possibly | |
| 5 min | 37.1 ± 7.9 (48) | 34.7 ± 7.2 (46) | -6.0 ± 7.5 | -0.28 (SD 0.36) (-0.64/0.08) | 2/34/64 | Possibly | |
| 10 min | 31.5 ± 7.1 (48) | 28.4 ± 5.3 (44) | -9.0 ± 7.7 | -0.40 (SD 0.36) (-0.77/-0.04) | 0/17/82 | Likely | |
| Half completed | 23.1 ± 5.5 (48) | 19.7 ± 5.2 (48) | -15.0 ± 9.2 | -0.54 (SD 0.36) (-0.90/-0.18) | 0/6/94 | Likely | |
| FW | 1 min | 67.3 ± 16.6 (57) | 64.5 ± 14.9 (57) | -3.7 ± 7.6 | -0.15 (SD 0.31) (-0.46/0.16) | 3/58/39 | Possibly |
| 3 min | 38.9 ± 8.2 (58) | 36.1 ± 9.4 (56) | -8.5 ± 7.2 | -0.35 (SD 0.31) (-0.66/0.04) | 0/21/79 | Likely | |
| 5 min | 32.1 ± 6.9 (58) | 29.8 ± 6.9 (58) | -7.8 ± 6.8 | -0.34 (SD 0.31) (-0.64/-0.03) | 0/23/77 | Likely | |
| 10 min | 25.7 ± 6.1 (57) | 23.8 ± 6.1 (57) | -8.0 ± 7.4 | -0.32 (SD 0.31) (-0.63/0.01) | 0/26/74 | Possibly | |
| Half completed | 18.4 ± 4.8 (58) | 16.0 ± 5.0 (58) | -14.3 ± 8.2 | -0.49 (SD 0.31) (-0.80/-0.19) | 0/6/94 | Likely | |
| AVG | 1 min | 69.6 ± 15.7 (244) | 68.2 ± 14.9 (237) | -1.8 ± 3.4 | -0.08 (SD 0.15) (-0.23/0.07) | 0/91/9 | Likely |
| 3 min | 40.0 ± 7.8 (251) | 37.7 ± 7.8 (238) | -6.4 ± 6.9 | -0.29 (SD 0.15) (-0.44/-0.14) | 0/15/85 | Likely | |
| 5 min | 33.2 ± 7.0 (250) | 31.2 ± 6.5 (244) | -5.9 ± 6.5 | -0.27 (SD 0.15) (-0.42/-0.13) | 0/21/79 | Likely | |
| 10 min | 27.4 ± 5.4 (247) | 25.0 ± 4.8 (238) | -8.4 ± 6.6 | -0.38 (SD 0.15) (-0.53/-0.23) | 0/2/98 | Very Likely | |
| Half completed | 19.7 ± 4.6 (251) | 17.1 ± 4.3 (251) | -13.5 ± 3.5 | -0.54 (SD 0.15)(-0.68/-0.39) | 0/0/100 | Most Likely | |
CD = central defender; FW = forward; MF = midfielder; OMF = offensive midfielder; FB = full back.
Table 3 shows the mean ± SD values for AMP (W·kg-1) for the specific positions in the match. The AMP in the second half was lower in the CD in the half completed (ES = -1.50 ± 0.36), while in the rest of the positions the AMP during the second half was moderately smaller (ES = -0.60 to -1.09).The differences between halves in the 1 min period were small in all positions (ES = -0.49 to -0.26). Only the CD showed moderate differences between halves in the 3 min period (ES = -0.85 ± 0.36) while moderate differences between halves in the 5 min period were found in the CD (ES = -1.10 ± 0.36) and FB (ES = -0.63 ± 0.30). Large decreases between halves were observed in CD (ES = -1.30 ± 0.36) and moderate decreases were found in FB (ES = -0.84 ± 0.30) and OMF (ES = -0.78 ± 0.37).
TABLE 3.
Comparison of the first and second halves for the most demanding passage of match play for each playing position using average metabolic power (AMP; W·kg-1) for five different time durations (1, 3, 5, 10 min and half completed).
| Duration | 1st half | 2nd half | Difference (%) | Difference standardized (Cohen) | Chances | Qualitative | |
|---|---|---|---|---|---|---|---|
| CD | 1 min | 17.5 ± 1.3 (48) | 16.9 ± 1.4 (48) | -3.1 ± 2.8 | -0.40 (SD 0.37) (-0.76/0.03) | 0/18/82 | Likely |
| 3 min | 13.4 ± 0.9 (49) | 12.7 ± 0.9 (48) | -5.4 ± 2.2 | -0.85 (SD 0.36) (-1.20/-0.49) | 0/0/100 | Most Likely | |
| 5 min | 12.3 ± 0.7 (48) | 11.6 ± 0.8 (49) | -6.4 ± 2.0 | -1.10 (SD 0.36) (-1.46/-0.74) | 0/0/100 | Most Likely | |
| 10 min | 11.4 ± 0.6 (48) | 10.5 ± 0.7 (48) | -7.7 ± 2.1 | -1.30 (SD 0.36) (-1.66/-0.93) | 0/0/100 | Most Likely | |
| Half completed | 9.7 ± 0.6 (49) | 8.8 ± 0.6 (49) | -9.1 ± 2.1 | -1.50 (SD 0.36) (-1.14/0.36) | 0/0/100 | Most Likely | |
| FB | 1 min | 19.0 ± 1.7 (62) | 18.5 ± 1.9 (58) | -2.8 ± 2.8 | -0.30 (SD 0.30) (-0.60/0.01) | 0/30/70 | Possibly |
| 3 min | 14.4 ± 1.2 (64) | 13.7 ± 1.0 (59) | -4.5 ± 2.2 | -0.58 (SD 0.29) (-0.87/-0.28) | 0/2/98 | Very Likely | |
| 5 min | 13.2 ± 1.0 (64) | 12.6 ± 0.9 (60) | -4.7 ± 2.2 | -0.63 (SD 0.30) (-0.93/-0.33) | 0/1/99 | Very Likely | |
| 10 min | 12.1 ± 1.0 (62) | 11.3 ± 0.8 (58) | -6.8 ± 2.3 | -0.84 (SD 0.30) (-1.14/-0.55) | 0/0/100 | Most Likely | |
| Half completed | 10.2 ± 0.8 (64) | 9.4 ± 0.7 (64) | -7.7 ± 2.1 | -1.03 (SD 0.29) (-1.32/-0.73) | 0/0/100 | Most Likely | |
| MF | 1 min | 18.9 ± 1.8 (32) | 17.9 ± 2.0 (32) | -5.6 ± 4.1 | 0.49 (SD 0.37) (-0.86/-0.13) | 0/9/91 | Likely |
| 3 min | 14.6 ± 1.5 (32) | 13.8 ± 1.5 (33) | -5.1 ± 4.3 | -0.42 (SD 0.36) (-0.77/-0.06) | 0/16/84 | Likely | |
| 5 min | 13.6 ± 1.3 (32) | 12.8 ± 1.4 (31) | -6.1 ± 4.2 | -0.51 (SD 0.36) (-0.87/-0.15) | 0/8/92 | Likely | |
| 10 min | 12.5 ± 1.3 (32) | 11.6 ± 1.3 (31) | -7.1 ± 4.5 | -0.55 (SD 0.36) (-0.92/-0.19) | 0/5/95 | Likely | |
| Half completed | 10.8 ± 1.2 (32) | 9.9 ± 1.1 (32) | -8.6 ± 4.4 | -0.66 (SD 0.36) (-1.02/-0.31) | 0/2/98 | Very Likely | |
| OMF | 1 min | 19.3 ± 1.8 (45) | 18.6 ± 1.9 (42) | -3.8 ± 3.8 | -0.36 (SD 0.37) (-0.73/0.01) | 1/23/77 | Likely |
| 3 min | 14.9 ± 1.3 (48) | 14.2 ± 1.4 (42) | -4.6 ± 3.3 | -0.49 (SD 0.36) (-0.85/-0.13) | 0/9/91 | Likely | |
| 5 min | 13.8 ± 1.2 (48) | 13.1 ± 1.4 (46) | -5.0 ± 3.5 | -0.52 (SD 0.37) (-0.89/-0.14) | 0/8/92 | Likely | |
| 10 min | 12.8 ± 1.2 (48) | 11.9 ± 1.1 (44) | -7.3 ± 3.3 | -0.78 (SD 0.37) (-1.15/-0.41) | 0/1/99 | Very Likely | |
| Half completed | 11.0 ± 1.0 (48) | 9.8 ± 1.2 (48) | -11.4 ± 3.5 | -1.09 (SD 0.36) (-1.45/-0.73) | 0/0/100 | Most Likely | |
| FW | 1 min | 17.5 ± 2.4 (57) | 16.9 ± 2.4 (57) | -3.7 ± 4.3 | -0.26 (SD 0.31) (-0.57/0.05) | 1/36/63 | Possibly |
| 3 min | 13.2 ± 1.7 (58) | 12.6 ± 1.7 (56) | -4.4 ± 3.9 | -0.34 (SD 0.31) (-0.65/0.03) | 0/22/78 | Likely | |
| 5 min | 12.1 ± 1.5 (58) | 11.5 ± 1.5 (58) | -4.7 ± 3.8 | -0.37 (SD 0.31) (-0.68/-0.06) | 0/18/82 | Likely | |
| 10 min | 10.9 ± 1.4 (57) | 10.3 ± 1.4 (57) | -5.7 ± 4.0 | -0.43 (SD 0.31) (-0.74/-0.12) | 0/11/89 | Likely | |
| Half completed | 9.4 ± 1.2 (58) | 8.6 ± 1.3 (58) | -8.3 ± 4.0 | -0.60 (SD 0.31) (-0.91/-0.30) | 0/2/98 | Very Likely | |
| AVG | 1 min | 18.4 ± 2.0 (244) | 17.7 ± 2.1 (237) | -3.9 ± 1.7 | -0.33 (SD 0.15) (-0.48/0.18) | 0/7/93 | Likely |
| 3 min | 14.1 ± 1.5 (251) | 13.4 ± 1.5 (238) | -4.9 ± 1.6 | -0.44 (SD 0.15) (-0.59/-0.29) | 0/0/100 | Most Likely | |
| 5 min | 12.9 ± 1.4 (250) | 12.2 ± 1.3 (244) | -5.5 ± 1.6 | -0.50 (SD 0.15) (-0.65/-0.35) | 0/0/100 | Most Likely | |
| 10 min | 11.9 ± 1.3 (247) | 11.1 ± 1.3 (238) | -7.0 ± 1.7 | -0.60 (SD 0.15) (-0.75/-0.45) | 0/0/100 | Most Likely | |
| Half completed | 10.2 ± 1.1 (251) | 9.3 ± 1.1 (251) | -9.0 ± 1.7 | -0.76 (SD 0.15) (-0.91/-0.61) | 0/0/100 | Most Likely | |
CD = central defender; FW = forward; MF = midfielder; OMF = offensive midfielder; FB = full back.
DISCUSSION
This study compared the most demanding passage of match play performed by football players during the first and second half, taking into account playing position, the duration of the time window and the variable studied. Our findings show that irrespective of playing position and the variable studied, as the duration of intervals increase, differences between the first and second half also increase.
To our knowledge, no study has made the comparison between the most demanding passages of match play in different halves of football competition. The results indicate that during the second half of matches, the most demanding passage of play is reduced during 1 min durations regardless of playing position. Specifically, the differences are small and unclear in the variable of HMLD and distance covered, while they are possible/likely small in the AMP variable.
As the duration of the temporal window increases, the differences between the activity of the first and the second half also increase. Several factors could affect such results, such as effective playing time, the time in which the ball is in play excluding regulatory infractions and when the ball goes outside the limits of the playing field [11–36]. These, and possibly other contextual factors could all affect locomotor activity of the players as observed previously in different game formats [37]. Fatigue may cause a decrease in activity over longer periods of time, but would be expected to have less effect on short yet demanding passages of play. That is, the possible fatigue and effective playing time could have a greater impact on the activity of the player as the time window is extended, without affecting the periods of short duration (1 minute).
Traditionally the activity of players has been studied across both halves or the entire match, with the knowledge that this activity is position-dependent [1–2]. More recently, it has also been observed that the activity of players during the periods of maximum demand of different duration and with different variables of interest also presents significant differences depending on the position of the player [20]. The results of our study indicate that the changes that occur in activity between the most demanding passage of the first and second half are also position-dependent, with greater differences in the CD. It seems therefore that the CD, despite having lower activity during the periods of maximum demand [20], show a greater decrease in activity during the second half. Perhaps a lower level of fitness or aspects related to the team game model could explain these results.
Numerous studies have found a decrease in activity during the second half of football matches [5–38]. However, in the previous studies carried out in football, the variables studied have always been distance variables (e.g. total distance and distances covered in different speed ranges) [39]. However, distances covered may not accurately reflect the activity of football players, as accelerations and decelerations are not considered in these variables. The inclusion of variables that consider the metabolic demands derived from moving at a certain speed while accelerating or decelerating could be useful variables in the evaluation of the player's activity during the match 31]. Therefore, the study of the temporal dynamics of variables that consider the intensity of both accelerations and decelerations could be an alternative for future studies. However, the results of our study indicate that the exclusive study of HMLD actions (HMLD) detects only small decreases (ES <0.6) in the second half compared to the first, while for distance covered and AMP, moderate decreases (ES = 0.6 to -1.2) were found. In the case of CD, large reductions (ES = -1.50 ± 0.36 in AMP and ES = -1.43 ± 0.36 in distance covered) were reported. Consistent with previous studies in Gaelic football, it seems that AMP decreases in the second half [17].
Regarding the different variables studied in the maximum demand period, we observed that AMP was the variable that presented the greatest number of moderate and large reductions, while HMLD had the fewest reductions. Although more specific studies are required in this regard, the findings of our study suggest that AMP could be a variable sensitive to the decreases in activity that occur during football match play. Having specific knowledge of the variable and time duration most affected by fatigue would allow strength and conditioning coaches to implement training strategies to optimize performance and establish appropriate protocols to facilitate recovery [40–41].
A limitation of our study is that we are unable to provide kinematic information on how each of the values was achieved. Since in football the activity of the player is multidirectional, multidimensional and iterative, a detailed description of the activity performed by players, and the context [42], during these most demanding passage of match play would be of interest to managers, fitness coaches and team medical staff. For example, two players could obtain the same AMP (W·kg-1) values over a given period of time, but the activity performed by the players may be very different (in one case, based on actions performed at high speed, and in another case by acceleration and deceleration actions). An understanding of the scenarios that create the maximum demands may provide greater insight into the possible causes of transient fatigue that occurs during match play.
CONCLUSIONS
The activities that a football player performs are multidimensional; it is therefore necessary to consider the activities that comprise the most demanding passages of match play for specific playing positions. Although the differences between the most demanding passages are trivial or unclear when short time windows are considered (e.g., 1 and 3 min), as the activity duration becomes larger, larger differences emerge between the first second half.
PRACTICAL APPLICATIONS
Our data should help coaches to design training situations, such as specific Small-Sided Games (SSG) , that replicate and even surpass the most demanding passages of match play, that is, proposing constraints to SSG in order to achieve desired intensities [43,44], while also respecting the nature and specificity of the sport. This should allow the coaching staff to consider the need to implement interventions in training that prevent this decline in performance.
ACKNOWLEDGMENTS
The authors thank all the athletes who participated in the study. The authors gratefully acknowledge the support of the Spanish government subproject Mixed method approach on performance analysis (in training and competition) in elite and academy sport [PGC2018–098742–B-C33] (Ministerio de Ciencia, Innovación y Universidades, Programa Estatal de Generación de Conocimiento y Fortalecimiento Científico y Tecnológico del Sistema I+D+i), which is part of the coordinated project New approach of research in physical activity and sport from mixed methods perspective (NARPAS_MM) [SPGC201800X098742CV0].
Conflict of interest
The authors did not report any potential conflicts of interest.
REFERENCES
- 1.Carling C. Interpreting physical performance in professional soccer match-play: Should we be more pragmatic in our approach? Sports Med. 2013;43(8):655–663. doi: 10.1007/s40279-013-0055-8. [DOI] [PubMed] [Google Scholar]
- 2.Castellano J, Alvarez-Pastor D, Bradley PS. Evaluation of research using computerised tracking systems (Amisco and Prozone) to analyse physical performance in elite soccer: A systematic review. Sports Med. 2014;44(5):701–712. doi: 10.1007/s40279-014-0144-3. [DOI] [PubMed] [Google Scholar]
- 3.Owen AL, Djaoui L, Newton M, Malone S, Mendes B. A contemporary multi-modal mechanical approach to training monitoring in elite professional soccer. Sci Med Football. 2017;1(3):216–221. doi: 10.1080/24733938.2021.1942539. [DOI] [PubMed] [Google Scholar]
- 4.Stevens TG, de Ruiter CJ, Twisk JW, Savelsbergh GJ, Beek PJ. Quantification of in-season training load relative to match load in professional Dutch Eredivisie football players. Sci Med in Football. 2017;1(2):117–125. [Google Scholar]
- 5.Barros RML, Misuta MS, Menezes RP, Figueroa PJ, Moura FA, Cunha SA, Anido R, Leite NJ. Analysis of the distances covered by first division Brazilian soccer players obtained with an automatic tracking method. J Sports Sci Med. 2007;6(2):233–242. [PMC free article] [PubMed] [Google Scholar]
- 6.Di Salvo V, Baron R, Tschan H, Montero F. C, Bachl N, Pigozzi F. Performance characteristics according to playing position in elite soccer. Int J Sports Med. 2007;28(03):222–227. doi: 10.1055/s-2006-924294. [DOI] [PubMed] [Google Scholar]
- 7.Rampinini E, Coutts AJ, Castagna C, Sassi R, Impellizzeri FM. Variation in top level soccer match performance. Int J Sports Med. 2007;28(12):1018–1024. doi: 10.1055/s-2007-965158. [DOI] [PubMed] [Google Scholar]
- 8.Bradley PS, Sheldon W, Wooster B, Olsen P, Boanas P, Krustrup P. High-intensity running in English FA Premier League soccer matches. J Sport Sci. 2009;27(2):159–168. doi: 10.1080/02640410802512775. [DOI] [PubMed] [Google Scholar]
- 9.Di Salvo V, Baron R, Cardinale M. Time motion analysis of elite footballers in European cup competitions. J Sports Sci Med. 2007;6(10):14–15. [Google Scholar]
- 10.Randers MB, Mujika I, Hewitt A, Santisteban J, Bischoff R, Solano R, Zubillaga A, Peltola E, Krustrup P, Mohr M. Application of four different football match analysis systems: A comparative study. J Sports Sci. 2010;28(2):171–182. doi: 10.1080/02640410903428525. [DOI] [PubMed] [Google Scholar]
- 11.Castellano J, Blanco-Villaseñor A, Álvarez D. Contextual variables and time-motion analysis in soccer. Int J Sports Med. 2011;32(6):415–421. doi: 10.1055/s-0031-1271771. [DOI] [PubMed] [Google Scholar]
- 12.Gabbett TJ, Kennelly S, Sheehan J, Hawkins R, Milsom J, King E, Whiteley R, Ekstrand J. If overuse injury is a ‘training load error’, should undertraining be viewed the same way? Br J Sports Med. 2016;50(17):1017–1018. doi: 10.1136/bjsports-2016-096308. [DOI] [PubMed] [Google Scholar]
- 13.Martín-García A, Casamichana D, Díaz AG, Cos F, Gabbett TJ. Positional Differences in the Most Demanding Passages of Play in Football Competition. J Sports Sci Med. 2018;17(4):563. [PMC free article] [PubMed] [Google Scholar]
- 14.Carling C, Bloomfield J, Nelsen L, Reilly T. The role of motion analysis in elite soccer: contemporary performance measurement techniques and work rate data. Sports Med. 2008;38(10):839–962. doi: 10.2165/00007256-200838100-00004. [DOI] [PubMed] [Google Scholar]
- 15.Di Mascio M, Bradley PS. Evaluation of the most intense high-intensity running period in English FA premier league soccer matches. J Strength Cond Res. 2013;27(4):909–915. doi: 10.1519/JSC.0b013e31825ff099. [DOI] [PubMed] [Google Scholar]
- 16.Delaney JA, Duthie GM, Thornton HR, Scott TJ, Gay D, Dascombe BJ. Acceleration-Based Running Inensities of Professional Rugby League Match Play. Int J Sports Physiol Perform. 2016;11(6):802–809. doi: 10.1123/ijspp.2015-0424. [DOI] [PubMed] [Google Scholar]
- 17.Malone S, Solan B, Hughes B, Collins K. Duration specific running performance in elite Gaelic football. J Strength Cond Res. 2017 doi: 10.1519/JSC.0000000000001972. Epub ahead of print. [DOI] [PubMed] [Google Scholar]
- 18.Malone S, Solan B, Collins K, Doran D. The metabolic power and energetic demands of elite Gaelic football match play. J Sports Med Phys Fitness. 2017;57(5):543–549. doi: 10.23736/S0022-4707.16.06233-2. [DOI] [PubMed] [Google Scholar]
- 19.Delaney JA, Thornton HR, Burgess DJ, Dascombe BJ, Duthie GM. Duration-specific running intensities of Australian Football match-play. J Sports Sci Med. 2017;20(7):689–694. doi: 10.1016/j.jsams.2016.11.009. [DOI] [PubMed] [Google Scholar]
- 20.Delaney JA, Thornton HR, Rowell AE, Dascombe BJ, Aughey RJ, Duthie GM. Modelling the decrement in running intensity within professional soccer players. Sci Med in Football. 2018;2(2):86–92. [Google Scholar]
- 21.Lacome M, Simpson BM, Cholley Y, Lambert P, Buchheit M. Small-sided games in elite soccer: Does one size fits all? Int J Sports Physiol Perform. 2018;13(5):568–576. doi: 10.1123/ijspp.2017-0214. [DOI] [PubMed] [Google Scholar]
- 22.Abbott W, Brickley G, Smeeton NJ. Positional differences in GPS outputs and perceived exertion during soccer training games and competition. J Strength Cond Res. 2018;32(11):3222–3231. doi: 10.1519/JSC.0000000000002387. [DOI] [PubMed] [Google Scholar]
- 23.Black GM, Gabbett TJ, Johnston RD, Cole MH, Naughton G, Dawson B. Physical fitness and peak running periods during female Australian football match-play. Sci Med in Football. 2018:1–6. [Google Scholar]
- 24.Winter EM, Maughan RJ. Requirements for ethics approvals. J Sports Sci. 2009;27(10):985. doi: 10.1080/02640410903178344. [DOI] [PubMed] [Google Scholar]
- 25.Bowen L, Gross AS, Gimpel M, Li FX. Accumulated workloads and the acute: chronic workload ratio relate to injury risk in elite youth football players. Br J Sports Med. 2016;51(5):452–459. doi: 10.1136/bjsports-2015-095820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fox R, Patterson SD, Waldron M. The relationship between heart rate recovery and temporary fatigue of kinematic and energetic indices among soccer players. Sci Med in Football. 2017;1(2):132–138. [Google Scholar]
- 27.Beato M, Bartolini D, Ghia G, Zamparo P. Accuracy of a 10 Hz GPS unit in measuring shuttle velocity performed at different speeds and distances (5–20 M) J Hum Kinet. 2016;54(1):15–22. doi: 10.1515/hukin-2016-0031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Buchheit M, Simpson B, Mendez-Villanueva A. Repeated high-speed activities during youth soccer games in relation to changes in maximal sprinting and aerobic speeds. Int J Sports Med. 2013;34(1):40–48. doi: 10.1055/s-0032-1316363. [DOI] [PubMed] [Google Scholar]
- 29.Castellano J, Casamichana D, Calleja-Gonzalez J, San Roman J, Ostojic SM. Reliability and accuracy of 10 Hz GPS devices for short-distance exercise. J Sports Sci Med. 2011;10(1):233. [PMC free article] [PubMed] [Google Scholar]
- 30.Silva P, Santos ED, Grishin M, Rocha JM. Validity of heart rate-based indices to measure training load and intensity in elite football players. J Strength Cond Res. 2017;32(8):2340–2347. doi: 10.1519/JSC.0000000000002057. [DOI] [PubMed] [Google Scholar]
- 31.Osgnach C, Poser S, Bernardini R, Rinaldo R, Di Prampero PE. Energy cost and metabolic power in elite soccer: A new match analysis approach. Med Sci Sports Exerc. 2010;42(1):170–178. doi: 10.1249/MSS.0b013e3181ae5cfd. [DOI] [PubMed] [Google Scholar]
- 32.Buchheit M, Manouvrier C, Cassirame J, Morin JB. Monitoring locomotor load in soccer: is metabolic power, powerful? Int J Sports Med. 2015;36(14):1149–1155. doi: 10.1055/s-0035-1555927. [DOI] [PubMed] [Google Scholar]
- 33.di Prampero PE, Fusi S, Sepulcri L, Morin JB, Belli A, Antonutto G. Sprint running: A new energetic approach. J Exp Biol. 2005;208(14):2809–2816. doi: 10.1242/jeb.01700. [DOI] [PubMed] [Google Scholar]
- 34.Batterham AM, Hopkins WG. Making meaningful inferences about magnitudes. Int J Sports Physiol Perform. 2006;1(1):50–57. [PubMed] [Google Scholar]
- 35.Hopkins WG, Marshall SW, Batterham AM, Hanin J. Progressive statistics for studies in sports medicine and exercise science. Med Sci Sports Exerc. 2009;41(1):3–13. doi: 10.1249/MSS.0b013e31818cb278. [DOI] [PubMed] [Google Scholar]
- 36.Bradley PS, Noakes T. Match running performance fluctuations in elite soccer: Indicative of fatigue, pacing or situational influences? J Sports Sci. 2013;31(15):1627–1638. doi: 10.1080/02640414.2013.796062. [DOI] [PubMed] [Google Scholar]
- 37.Casamichana D, Castellano J. Time–motion, heart rate, perceptual and motor behaviour demands in small-sides soccer games: Effects of pitch size. J Sports Sci. 2010;28(14):1615–1623. doi: 10.1080/02640414.2010.521168. [DOI] [PubMed] [Google Scholar]
- 38.Burgess DJ, Naughton G, Norton KI. Profile of movement demands of national football players in Australia. J Sci Med Sport. 2006;9(4):334–341. doi: 10.1016/j.jsams.2006.01.005. [DOI] [PubMed] [Google Scholar]
- 39.Buchheit M, Simpson BM. Player-tracking technology: Halffull or half-empty glass? Int J Sports Physiol Perform. 2017;12(S2):35. doi: 10.1123/ijspp.2016-0499. [DOI] [PubMed] [Google Scholar]
- 40.Carling C, Dupont G. Are declines in physical performance associated with a reduction in skill-related performance during professional soccer match-play? J Sports Sci Med. 2011;29(1):63–71. doi: 10.1080/02640414.2010.521945. [DOI] [PubMed] [Google Scholar]
- 41.Carling C, Lacome M, McCall A, Dupont G, Le Gall F, Simpson B, Buchheit M. Monitoring of Post-match Fatigue in Professional Soccer: Welcome to the Real World. Sports Med. 2018:1–8. doi: 10.1007/s40279-018-0935-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bradley PS, Ade JD. Are current physical match performance metrics in elite soccer fit for purpose or is the adoption of an integrated approach needed? Int J Sports Physiol Perform. 2018;13(1):656–664. doi: 10.1123/ijspp.2017-0433. [DOI] [PubMed] [Google Scholar]
- 43.Halouani J, Chtourou H, Dellal A, Chaouachi A, Chamari K. Soccer small-sided games in young players: rule modification to induce higher physiological responses. Biol Sport. 2017;34(2):163–168. doi: 10.5114/biolsport.2017.64590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Halouani J, Chtourou H, Dellal A, Chaouachi A, Chamari K. The effects of game types on intensity of small-sided games among pre-adolescent youth football players. Biol Sport. 2017;34(2):157–162. doi: 10.5114/biolsport.2017.64589. [DOI] [PMC free article] [PubMed] [Google Scholar]