Differential Tuning to Visual Motion Allows Robust Encoding of Optic Flow in the Dragonfly

Abstract

Visual cues provide an important means for aerial creatures to ascertain their self-motion through the environment. In many insects, including flies, moths, and bees, wide-field motion-sensitive neurons in the third optic ganglion are thought to underlie such motion encoding; however, these neurons can only respond robustly over limited speed ranges. The task is more complicated for some species of dragonflies that switch between extended periods of hovering flight and fast-moving pursuit of prey and conspecifics, requiring motion detection over a broad range of velocities. Since little is known about motion processing in these insects, we performed intracellular recordings from hawking, emerald dragonflies (Hemicordulia spp.) and identified a diverse group of motion-sensitive neurons that we named lobula tangential cells (LTCs). Following prolonged visual stimulation with drifting gratings, we observed significant differences in both temporal and spatial tuning of LTCs. Cluster analysis of these changes confirmed several groups of LTCs with distinctive spatiotemporal tuning. These differences were associated with variation in velocity tuning in response to translated, natural scenes. LTCs with differences in velocity tuning ranges and optima may underlie how a broad range of motion velocities are encoded. In the hawking dragonfly, changes in LTC tuning over time are therefore likely to support their extensive range of behaviors, from hovering to fast-speed pursuits.

SIGNIFICANCE STATEMENT Understanding how animals navigate the world is an inherently difficult and interesting problem. Insects are useful models for understanding neuronal mechanisms underlying these activities, with neurons that encode wide-field motion previously identified in insects, such as flies, hawkmoths, and butterflies. Like some Dipteran flies, dragonflies exhibit complex aerobatic behaviors, such as hovering, patrolling, and aerial combat. However, dragonflies lack halteres that support such diverse behavior in flies. To understand how dragonflies might address this problem using only visual cues, we recorded from their wide-field motion-sensitive neurons. We found these differ strongly in the ways they respond to sustained motion, allowing them collectively to encode the very broad range of velocities experienced during diverse behavior.

Introduction

Flying insects live in complex and varied 3D environments and display diverse flight behavior, from near stationary hovering, to territorial patrolling and rapid pursuits of prey or conspecifics. Encoding both fast and slow motion places extensive demands on the neuronal networks underlying self-motion detection. Neurons that respond robustly to patterns of wide-field motion have been studied in several insect groups, including Dipteran flies (Hausen, 1982; Hausen and Egelhaaf, 1989), moths (Wicklein and Varju, 1999; Theobald et al., 2010; Stöckl et al., 2016), and bees (DeVoe et al., 1982; Ibbotson, 1991; Mertes et al., 2014). Typified by lobula plate tangential cells (LPTCs) of Dipteran flies, these neurons take input from local elementary motion detection (EMD) elements located in the medulla (Borst et al., 2010) and use local correlation of spatially separated inputs with asymmetric delay mechanisms, consistent with influential computational motion models (Hassenstein and Reichardt, 1956; Barlow and Levick, 1965; Gruntman et al., 2018). Such neurons are tuned to specific spatial and temporal frequency ranges by their underlying spatial sampling and temporal delay filters. Because this places fundamental limitations on the range of velocities that neurons can individually encode, insects have evolved strategies for motion analysis that match their distinctive behavior. For example, diurnal and nocturnal hawkmoths are precise hoverers when flower feeding and use wide-field motion-sensitive neurons specialized for such slow velocities (O'Carroll et al., 1996, 1997; Wicklein and Varju, 1999; Theobald et al., 2010; Stöckl et al., 2016). By contrast, fast flying butterflies and bees show tuning to higher image speeds (Ibbotson, 1991; O'Carroll et al., 1996).

In Dipteran flies, diverse flight modes involve switches between slow-speed hovering to high-speed pursuit flight. These are in part met by multimodal integration of fast input to descending visual pathways from the ocelli (Parsons et al., 2006) and specialized hindwing mechanosensory organs (halteres) that detect rapid accelerations, allowing visual neurons (the LPTCs) to encode slower motion (Hengstenberg, 1991). Although dragonflies have recently emerged as an important model for studying visual target tracking, their neural tuning to wide-field motion remains largely unknown. Dragonflies exhibit a similarly diverse behavioral repertoire, but have a lower wingbeat frequency, and lack specialized halteres for detecting gyroscopic forces. As a predominantly visual creature, how do dragonflies encode the large-velocity ranges demanded by their behavior? One potential strategy is to process the same retinal input using parallel pathways using spatiotemporal filters tuned to different speed ranges, as seen in mammals (Movshon and Newsome, 1996; Nassi and Callaway, 2009). In many insects, however, replicating such parallel pathways may be constrained by their size and weight. Indeed, in species studied to date, motion tuning at a behavioral level appears to reflect a single common EMD mechanism (Buchner, 1976). Nevertheless, we hypothesize that parallel processing may be viable for dragonflies, with among the largest eyes and brain of extant insects. Alternatively, useful coding of different speed ranges may result from additional downstream processing. Motion adaptation, for example, can improve velocity contrast via relief from saturation (Maddess and Laughlin, 1985; Barnett et al., 2010) and on a timescale similar to the stimulus response (Nordström et al., 2011). It also improves velocity encoding of natural images (Shoemaker et al., 2005; Straw et al., 2008; Barnett et al., 2010) and enhances differentiation between foreground and background features (Li et al., 2017).

We tested these two alternative strategies by recording from wide-field motion-sensitive neurons in the dragonfly lobula. We found evidence of significant variation in the tuning properties of these motion-sensitive neurons, not observed in other species. Our data suggest that these neurons likely share common early visual pathways (i.e., using the same EMD inputs) but differ radically in how their responses evolve over time to sustained image motion. These differences in how neurons respond over time, tune otherwise similar neurons to significantly different velocity ranges, providing very robust encoding of natural image motion over several decades of image speed.

Materials and Methods

Electrophysiology.

Seventy wild-caught, dragonflies (Hemicordulia tau, 61 male, 1 female; Hemicordulia australiae, 7 male, 1 female) were immobilized with a 1:1 beeswax and rosin mixture and fixed to an articulated magnetic stand with the head tilted forward to access the posterior surface. A hole was cut above the brain to gain access to the lobula and lateral midbrain, but the preparation was otherwise left with the perineural sheath and overlying hemolymph sacs intact. We penetrated the sheath and recorded intracellularly using aluminosilicate micropipettes (OD = 1, ID = 0.58), pulled on a Sutter Instruments P-97 puller, and backfilled either with KCl (2 m, electrode tip resistance typically 50–150 mΩ) or 4% Lucifer yellow solution in 0.1 m LiCl. Electrodes were placed in the medial portion of the lobula complex and stepped through the brain from the posterior to anterior lobula complex using a piezoelectric stepper (Marzhauser-Wetzlar, PM-10). Intracellular responses were digitized at 5 kHz with a 16-bit A/D converter (National Instruments) for offline analysis.

Visual stimuli.

We presented stimuli on high-definition LCD monitors (120–165 Hz frame rate). The animal was placed 20 cm away and centered on the visual midline. Contrast stimuli were presented at screen center (i.e., at the dragonflies' visual midline) to minimize off-axis artifacts. The display projection was distorted using OpenGL to ensure each 1° onscreen was 1° from the animal's perspective. The visual field was 104° (−52° to 52° azimuth) by 58.5° (20.75° to 79.25° elevation from equator). All temporal frequencies tested were limited to one-fourth of the monitor's frame rate. Stimulus scripts were written using Psychtoolbox version 3 (Brainard, 1997) for MATLAB and integrated into the data acquisition system.

To classify neurons as wide-field motion-sensitive, an initial sequence of characterizing stimuli was presented to the dragonfly. These included a randomly generated texel pattern (1°), which filled the entire FOV and was translated in a circular pattern (without rotation), gray to black and gray to white full screen flicker (white represents 338 cd/m²; black represents 0.5 cd/m²), moving edges (up, down, left and right, 25°/s), moving bars (2° width, up, down, left and right, 25°/s), and a square-wave grating pattern moving up, down left and right (0.025 cycles/°, 6.25 Hz). Neurons were categorized as wide-field motion-sensitive based on robust responses to the gyrated texel pattern and square-wave gratings with limited responses to small stimuli, such as moving targets. Subsequently, sinusoidal gratings were presented to dragonflies that had a linear increase in contrast for 1 s (0 to 0.25, Michelson) followed by a 1 s exponential rise (0.25 to 1). Between experiments, a gray screen was presented to the dragonfly.

Natural images were generated according to methods detailed by Brinkworth and O'Carroll (2009). These images were stretched to subtend the full vertical FOV (58.5°) without changing the aspect ratio of the images.

Neuroanatomy.

The morphology of wide-field motion-sensitive neurons were visualized by intracellular labeling with Lucifer yellow (see Fig. 1A–C). Iontophoresis was achieved by passing 1 nA negative current through electrodes tip-filled with Lucifer yellow for 12 min. Brains were carefully dissected under PBS, fixed overnight in 4% PFA at 4°C. We processed the brains in accordance with published protocols (Gonzalez-Bellido and Wardill, 2012). Brains were rinsed (3 × 10 min) in PBS, before permeabilization in 80/20 DMSO/methanol solution for 55 min. They were then rinsed (3 × 30 min) in PBT, and preincubated in 5% NGS in PBT for 3 h at room temperature under gentle agitation. Afterward, brains were incubated in 1:50 dilution of primary antibody (anti-Lucifer yellow, RRID:AB_2536190) in universal antibody dilution solution (Sigma-Aldrich) for 3 d at 4°C under gentle agitation. They were then rinsed (3 × 30 min) in 10% NGS, before incubation with a 1:50 dilution of NeutraAvadin DyLight 633 for 3 d at 4°C under gentle agitation. The labeled sample was dehydrated in ethanol series (70%, 90%, 100%, 100%), cleared in methyl salicylate, and mounted using Permount on a slide using three spacer rings and covered with a coverslip for imaging. The mounted sample was then scanned using a confocal microscope using a 10× objective and the 3D slices reconstructed using NeuTube.

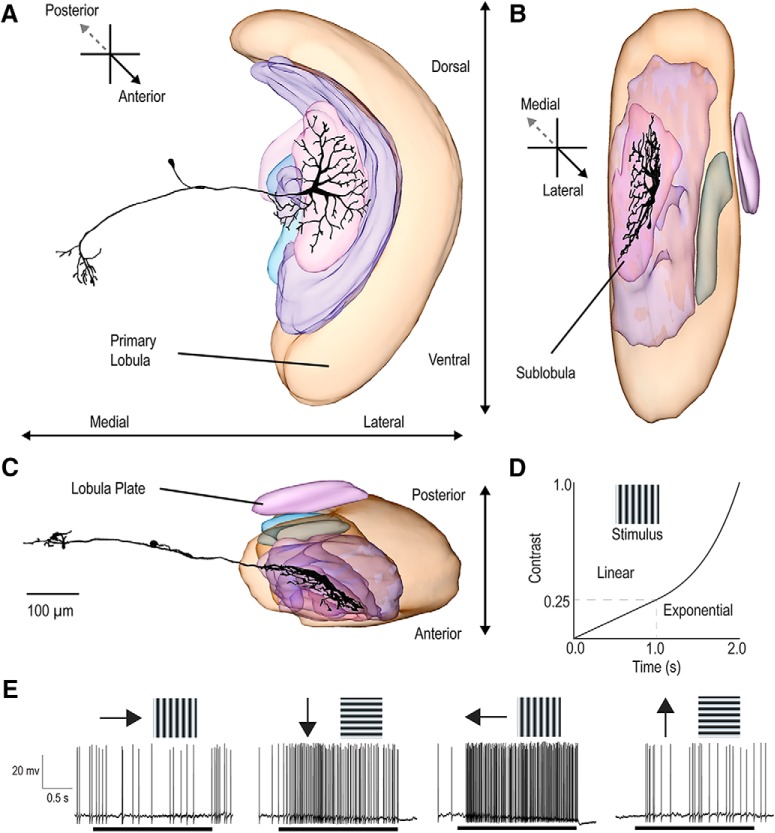
Figure 1.

Neuroanatomy and directional responses of LTCs. Anterior (A), longitudinal (B), and horizontal (C) projections for a 3D model reconstruction of a dragonfly LTC. The morphology is similar to that observed in Dipteran LPTCs; however, this example neuron has tangential inputs in the sublobula. D, A drifting grating that ramps in contrast is used to characterize response tuning and contrast sensitivity in LTC neurons. At cessation of a prestimulus period, the contrast rises linearly for 1 s from 0 to 0.25 (Michelson). The contrast then rises exponentially over 1 s, from 0.25 to 1.0. E, An example of a direction-opponent LTC response to sinusoidal gratings moved in four directions. Black bars represent the duration of the 2 s contrast ramp. Direction-opponent neurons are inhibited by motion in the “antipreferred” direction (left) while responding strongly when stimulated by the opposite direction of motion (third from left).

Experimental design and statistical analysis.

All analysis was completed in MATLAB (The MathWorks). Spike-counting was done using a custom-written spike-counting script. Curve fits used MATLAB's built-in curve-fitting tools. Spontaneous activity was defined as the mean spike rate in response to 1 s of a gray screen. Variation in spontaneous activity was defined by the spike-rate variation in 50 ms bins taken during this same period. To find peaks of tuning curves, repeated measures were averaged followed by the application of a 5 point moving average filter to smooth data before finding the maximum. All statistical tests were two-sample nonparametric tests (Mann–Whitney U test, for unpaired data) with appropriate multiple-comparison corrections (Bonferroni) or sample nonparametric tests (Kruskal–Wallis with post hoc correction). All means are calculated from biological replicates (i.e., repeated measurements from neurons in different animals). Each biological replicate represents the mean of between 1 and 5 technical replicates. p values are reported as raw numbers in text if significant (unmarked otherwise) or as < 0.0001 if sufficiently small. Box-and-whisker plots represent the 75th, 50th, and 25th quartiles (lines) with raw data shown.

Clustering analysis was completed with k-means and the gap statistic (Tibshirani et al., 2001) using MATLAB's built-in implementation.

Results

Neuroanatomical characterization

We stained a total of three of these neurons, two of which had morphology similar to that shown in Figure 1. This confirms a similar general organization to that in Diptera and several other insect orders (Hausen, 1982; Egelhaaf and Borst, 1989), where optic flow is integrated within specialized subregions of the third optic ganglion (the lobula complex) by a set of tangential neurons, the well-studied wide-field motion-sensitive LPTCs (Hausen, 1982). These neurons have input dendrites that integrate tangentially across arrays of retinotopically organized inputs from underlying local motion detectors (presumptive EMDs) at earlier stages of visual processing.

Figure 1A–C shows the reconstructed morphology of a dragonfly neuron that exhibited wide-field motion sensitivity. The overall morphology of these neurons strongly resembles their Dipteran counterparts, with tree-like input arborizations within the lobula complex, and outputs in the lateral midbrain. However, as with this individual example, several neurons described in this study have their inputs originating solely from a deep neuropil on the anterior side of the lobula, similar to the “sublobula” identified in bees (Devoe et al., 1982; Strausfeld, 2005; Strausfeld et al., 2006), rather than from a posterior lobula plate. Until the homologies between these different lobula subregions with their counterparts in other insect groups are more clearly identified, we label these neurons more generally as lobula tangential cells (LTCs).

Direction selectivity and opponency

We tested the motion sensitivity of LTCs using sinusoidal gratings drifted in eight directions (presented randomly in 45° increments). Each grating was displayed as a “contrast ramp” with a nonlinear increase in contrast from zero over a 2 s period (Fig. 1D). This ramp stimulus avoids onset-transients inherent with step changes in contrast. The ramp also weights more time around important threshold (low) contrast values while still providing a stimulus that contains the entire contrast range (O'Carroll et al., 1996, 1997).

Figure 1E shows an individual neuron's spiking response to four directions of motion. This LTC response exhibits clear direction opponency, with excitation in response to preferred direction motion and inhibition to the opposite (antipreferred) direction of motion (leftward and rightwards motion, respectively). The response time courses of our recordings typically show high initial sensitivity to low contrast, indicated by a rapid rise in firing rate, although this was not universal among neurons.

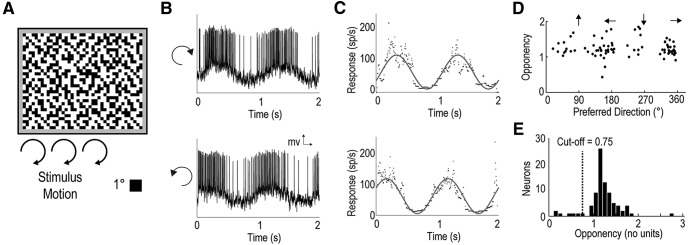
We measured LTC directionality by presenting a gyrated random (binary) texel pattern (where each “texel” measured 1° across), which filled the whole screen (Fig. 2A). This continuous stimulus is composed of a broad range of spatial and temporal frequencies and permits precise calculation of direction selectivity. The full-screen texture was gyrated (see Materials and Methods) in a clockwise and counterclockwise direction for two complete cycles. In direction opponent neurons, this elicits a sinusoidal pattern of excitation and inhibition (Fig. 2B). We thus fitted a sinusoid (Fig. 2C) to the instantaneous spike rate (inverse interspike interval). Responses to clockwise and counterclockwise rotations were then averaged to eliminate any phase-lag due to response latency (Krapp and Hengstenberg, 1996). The maximum and minimum values of the fitted sinusoid were taken as the neuron's preferred (R_p) and antipreferred (R_a) responses. We then defined a direction opponency metric relative to the spontaneous activity level (R_s) as follows:

We used this basic stimulus to characterize the direction selectivity in 93 neurons (recorded from the dragonfly lobula complex) that gave strong responses to wide-field motion (Fig. 2D). These opponent LTCs exhibit both vertical and horizontal preferred directions, clustering around all four cardinal directions (i.e., left, right, up, and down). A similar alignment of neuronal sensitivity to the different directional components of ego-motion is also observed in the frontal visual fields of LPTCs in other insect species (Strausfeld and Lee, 1991; Krapp and Hengstenberg, 1996).

Figure 2.

DO in a subset of LTCs. A, Moving patterns (1° texels) at a constant orientation were presented (full screen) to the dragonfly while recording from wide-field motion-sensitive neurons. The pattern was gyrated (translated in a constantly changing direction) twice in a clockwise circle (not rotated) and then twice counterclockwise at 50°/s. B, An example of spiking activity in response to the stimulus shows a periodicity corresponding to the texel pattern's direction of motion. C, The derived inverse interspike interval is fitted with a sinusoidal curve for both a clockwise (top) and counterclockwise (bottom) texel gyration. These curve fits provide both the peak response phase (i.e., preferred direction) and response strength at the preferred and antipreferred direction used to calculate the neuron's DO. D, Each point indicates the neuron's preferred direction and DO, revealing preferences for four directions (left, right, upward, downward). E, Histogram represents the direction selectivity of all wide-field motion-sensitive neurons. We further investigated neurons with strong LPTC-like direction opponency (DO >0.75).

This selection of neurons was likely biased by repeated recordings from stereotyped locations, where we had previously located direction-selective neurons. Hence, the resulting distribution of directional opponency (DO) values may underestimate the number of neurons that are not direction-selective (this also applies to observations of preferred direction). Nevertheless, while the recorded neurons displayed a large range of DO (from near 0 to 2.8), a histogram of DO reveals a clear peak in the distribution >1.0, indicating that most of the neurons were strongly direction opponent (Fig. 2E). Strong direction selectivity and opponency are characteristic of many of the LPTC neurons seen in other taxa, so the role of weakly directional neurons from this group in optic flow analysis is unclear at this stage. We therefore limit our subsequent analysis in this paper to a subset of the recorded neurons with strong direction selectivity (DO > 0.75), which are more likely to be analogs or homologs of the LPTC-like neurons in other species (Fig. 2E).

Spatiotemporal tuning

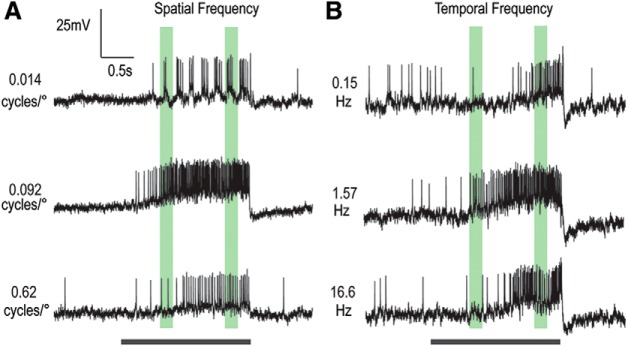
In many animals, motion-sensitive neurons exhibit distinctive tuning to both the spatial and temporal frequency of drifted gratings (Devoe et al., 1982; Hausen, 1982; Arenz et al., 2017), providing insight into the underlying mechanisms of motion detection (O'Carroll et al., 1996). Here we established LTC spatiotemporal tuning by presenting two series of sinusoidal gratings. To establish spatial tuning, we used a sequence of 30 different gratings with spatial frequencies logarithmically spaced between 0.01 and 1 cycles/°, presented in random order at a fixed temporal frequency (5 Hz). To establish temporal tuning, we presented an equivalent series with varying temporal frequencies logarithmically spaced between 0.1 and 30 Hz, at a fixed spatial frequency (0.1 cycles/°). In each case, the grating stimulus was a ramp of contrast as previously described (Fig. 1D).

Figure 3 shows data for a single neuron that exemplifies a subset of LTCs that show consistency in their spatial (Fig. 3A) and temporal (Fig. 3B) tuning across time, and thus to increasing contrast as the ramp stimulus progresses. This particular neuron gave mixed-mode responses, with spikes that ride on graded depolarization when the stimulus was excitatory. Separate quantitative analysis of such mixed-mode responses revealed general consistency between the graded and spiking responses across a wide range of stimulus conditions. Other neurons showed only biphasic (axonal) action potentials (e.g., Fig. 1). At very low spatial frequencies, responses are often phase-locked to the first harmonic of the stimulus waveform (i.e., the original 5 Hz frequency), particularly at high contrast (e.g., Fig. 3A, top). This phase-locking is not evident, however, at higher spatial frequencies. Stimulus conditions that elicit the strongest responses during presentation of the grating also lead to a strong rebound response on motion cessation (i.e., a motion aftereffect) (Anstis et al., 1998; Nordström and O'Carroll, 2009) very evident in the graded response, but also in a reduction in spike firing rate in the poststimulus period.

Figure 3.

Responses of an individual LPTC to select spatial and temporal frequencies (contrast ramped drifting gratings). An example LTC shows strong consistency in spatial and temporal tuning over increasing contrast and time. Black bar represents stimulus duration. Green regions represent early and late analysis windows. A, Raw responses to gratings with 3 spatial frequencies (0.014, 0.092, and 0.62 cycles/°) at a temporal frequency of 5 Hz. Responses reveal phase locking at low frequencies and are most robust at the middle spatial frequency. B, Raw responses to 3 temporal frequencies (0.15, 1.57, and 16.6 Hz) at a constant spatial frequency of 0.1 cycles/°. For this example LTC, responses are most robust at the middle temporal frequency, and this preference is sustained throughout the stimulus duration.

Spatiotemporal tuning in response to contrast ramps

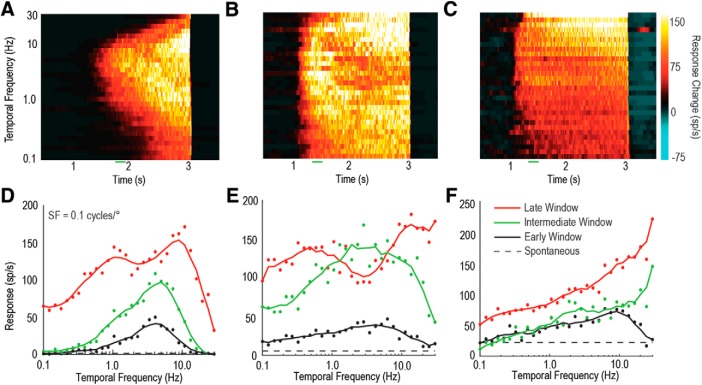
Are the temporal tuning properties across LTCs homogeneous? To best illustrate the differences between the tuning properties of LTCs, we produced 3D plots of the response to contrast-ramp sinusoidal gratings of differing temporal frequencies over time. As can be seen from the three different neurons shown in Figure 4A–C (color map represents change from spontaneous activity), the temporal tuning properties of LTCs differ markedly, especially in their response to changing contrast over time. To compare early with later responses, we derived tuning curves (Fig. 4D–F) based on two 200 ms duration analysis windows (Fig. 3, green regions). The early window (black line) starts when responses exceed the spontaneous activity by 2 SDs. A late window (red line) begins 250 ms before the end of the ramp stimulus, thus avoiding offset transients. For these three individual neurons, we also show an intermediate window (green line), 300 ms after the early window, further illustrating the progression of temporal tuning over time. Figure 4A, D depicts an LTC that exhibits properties similar to wide-field motion-sensitive neurons seen in other species, such as Dipteran LPTCs (Hausen, 1982; Harris et al., 1999). This neuron shows both stronger response (including some saturation) and broadening of tuning (reflecting recruitment activity for less optimal stimuli) in response to the increased contrast at both the intermediate and late windows. Any change in response over time is not dependent on temporal frequencies, resulting in a tuning response curve that is a relatively uniform shape with increased contrast.

Figure 4.

Individual LTCs show varied patterns of tuning at different temporal frequencies. A–C, 3D color maps of the change in spike rate over time (from spontaneous) when presented with contrast ramps at 30 different temporal frequencies (spatial frequency of 0.1 cycles/°). These examples reveal three LTCs with different tuning properties. D–F, LTC temporal tuning curves are derived by averaging neuronal responses within analysis windows (200 ms) early in the ramp (low contrast, black line), intermediate (300 ms after low contrast, green line), or late (high contrast, red line).

Figure 4B, E depicts an LTC with markedly different tuning properties. First, the neuron's contrast sensitivity is much higher with a near-maximal response within 500 ms of stimulus onset (green line). Initial responses are strongest at intermediate frequencies (2–5 Hz, black and green lines). As contrast increases, neuronal responses increase nonuniformly across the temporal frequencies tested. At higher (20 Hz) and lower (0.5 Hz) temporal frequencies, the response increases more than at intermediate frequencies, resulting in the formation of two peaks and a characteristic trough. Interestingly, the trough is deepest at the original optimal temporal frequency.

Figure 4C, F shows responses from an LTC that exhibits an asymmetric response to the range of temporal frequencies, which is most pronounced at high temporal frequencies. In the early window, the response is tuned similarly to the previous two neurons (compare the early window of Fig. 4C with that of Fig. 4A,B). However, over time, the preferred temporal frequency shifts to higher frequencies, even exceeding the frequency limits of our display (30 Hz, i.e., one-fourth of 120 Hz). This change in temporal tuning occurs rapidly, as shown by the intermediate analysis window (green line, ∼300 ms after stimulus onset). This is particularly unusual as the proposed underlying mechanism of motion detection (i.e., a Hassenstein–Reichardt correlator or Barlow–Levick correlator) tends to bias transient responses at onset toward high-frequency stimuli rather than after prolonged stimulation. Despite the neurons' temporal frequency tuning changes, their direction selectivity was maintained across frequencies (data not shown).

Clustering of LTC response properties

To examine the differences between neurons in this LTC group, we quantified both their temporal and spatial tuning properties, using both the tuning peaks and their change over time.

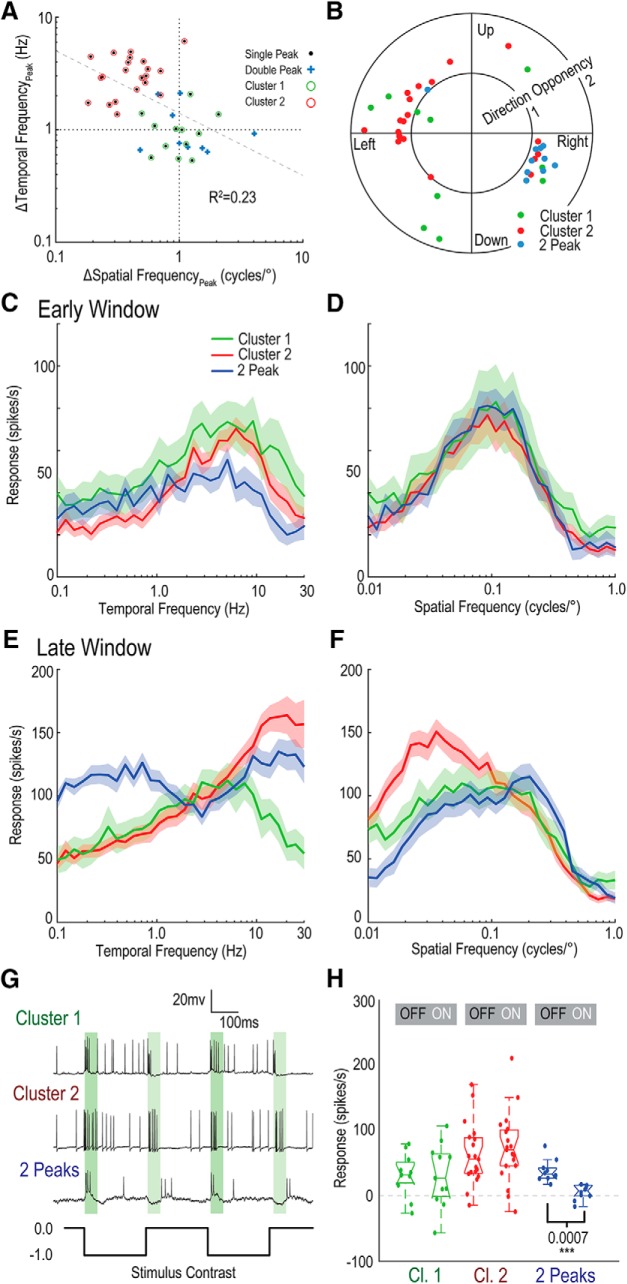
For each neuron, the temporal and spatial frequency optima were calculated in the early and late windows (as in Fig. 4D–F), and then the late window was divided by the early window (geometric rather than arithmetic comparisons best represent these logarithmic distributions). This produced a value nominally centered at ∼1.0 for no peak shift. Neurons that exhibited two obvious peaks (as in Fig. 4B,E) in the late window were excluded from this analysis (12 neurons). Because it was not possible to determine the frequency of the central peak accurately in this group of neurons, we instead plot an estimation of the peak derived from the bottom of the trough.

Figure 5A reveals that, whereas some neurons exhibited minimal change in their spatial and temporal optima, others exhibit strong shifts. In most LTCs, an upward shift of peak temporal frequency tuning corresponded with a downward shift in peak spatial frequency tuning. We performed regression analysis (dotted gray line), indicating an association between spatial frequency and temporal frequency peak change (R² = 0.23). Then, we tested for the clustering tendency of the data using the Hopkins statistic, which showed that the data were neither uniformly, nor randomly, distributed and exceeded the required threshold (0.5) for clustering (H = 0.544) (Hopkins, 1954). We then applied k-means using the gap statistic (Tibshirani et al., 2001) to determine both the number and distributions of the clusters.

Figure 5.

LTCs exhibit clustering when observing changes in their spatial and temporal frequency tuning over time. A, Scatter plot depicting the shift in temporal and spatial frequency optimum of LTC neurons between early and late windows. 2-Peak neurons are plotted (blue crosses) at the location of the minimum between peaks (rather than the maximum peak). Correlation analysis reveals an association between temporal and spatial frequency peak shift (R² = 0.23). With 2-Peak neurons excluded, k-means clustering indicates the presence of 2 clusters (red, green). B, Polar plot of direction tuning (peak angle) plotted against direction opponency (magnitude, where DO > 0.75; see Fig. 2). 2-Peak neurons appear to only code horizontal motion. C, Average temporal tuning for LTC groups (Cluster 1, Cluster 2, and 2-Peak) in the early response window (mean line and shaded SE). In the early window, all three neuron groups show comparatively similar shape and peak tuning. D, Average spatial frequency tuning in the early window. There is little difference between neuron groups. E, Temporal tuning of the three neuron groups in the late analysis window. Each of the three groups shows a large difference in response at the end of the contrast ramp. Cluster 1 (green) exhibits little change from the early window responses, whereas Cluster 2 (red) shows a large increase in response to high temporal frequencies. 2-Peak neurons show the consistent “notch” at the early window, peak frequency (∼3–5 Hz). F, Spatial frequency tuning in the late window. Cluster 1 tuning is similar to the early window, although with a slight increase at low spatial frequencies and flattening of the peak. Cluster 2 neurons show a marked shift to low spatial frequencies. 2-Peak neurons show little evidence of two peaks in the spatial domain, though still quite broad in tuning. G, Raw traces of individual LTCs from each group, when stimulated by full-screen flicker (gray to black, 0.0 to −0.99 Weber contrast). Green bars represent analysis window (20–70 ms). The Cluster 1 and Cluster 2 neurons exhibit full-wave rectification (increased responses to both ON and OFF luminance changes), whereas 2-Peak neurons were inhibited to ON flicker. H, Boxplot distributions of responses to ON and OFF components of full screen flicker. 2-Peak neurons show minimal response to ON flicker, whereas Cluster 1 and Cluster 2 neurons show responses to both ON and OFF components.

Using the inbuilt MATLAB implementation (k-means++), which uses random initialization, the analysis supported two clusters as shown in red and green in Figure 5A (random initialization, run 10 times). This analysis indicates differences in response properties between LTC groups (Clusters 1 and 2), as typified by the individual neuronal responses observed in Figure 4A,C.

While it is not possible to determine the central peak frequency of the 2-Peak neurons, the distribution (based on the location of the “trough” minimum) broadly aligned with those in Cluster 1 (Fig. 5A, green).

We examined whether the clustered changes in tuning corresponded to the neurons' directional preference (Fig. 5B); however, we found no significant association. We did note that all 2-Peak neurons showed preference for horizontal motion, with either leftward or rightward preferred directions (Fig. 5B).

Following the proposed grouping of LTCs (Cluster 1, no shift; Cluster 2, large shift and 2-Peaks), we looked for differences in their temporal and spatial tuning properties. Figure 5C–F shows the mean temporal and spatial tuning of LTC groups for both the early and late windows (shaded area represents SE). Importantly, we note that the early window (both spatial and temporal tuning) is similar across all three groups. The optimal temporal frequency is centered at ∼5 Hz (Fig. 5C) and the optimal spatial frequency at ∼0.1 cycles/° (Fig. 5D). The early temporal tuning is broad across all groups showing some response above spontaneous levels at all temporal frequencies measured. A spatial tuning roll-off by 0.5 cycles/° is theoretically predicted from the interommatidial angle (Buchner, 1976), which is a little less than 1° for this species (Horridge, 1978). Consistent with this prediction, there is broad tuning to spatial frequencies with a return to spontaneous levels (data not shown) by ∼0.5 cycles/° in all three groups and strong phase-locking at low spatial frequencies.

However, in the late window, the groups differ markedly. Cluster 1 (green, n = 12) shows a highly conserved shape (though with stronger overall amplitude) in the late window (Fig. 5E), whereas Cluster 2 (red, n = 21) shows a marked shift to higher temporal frequencies in the late window, despite the relatively similar shape in the early window. The 2-Peak LTCs (blue, n = 9) show robust responses across the entire temporal frequency range measured (0.1–30 Hz), with the characteristic “trough” approximately located at the early window's optimal temporal tuning. The overall temporal tuning curve is remarkably flat, revealing strong responses at all frequencies (mean spontaneous activity ∼20 spikes/s). Indeed, most individual neurons showed >50% of the maximum response at all the frequencies measured (accounting for spontaneous activity).

With respect to spatial frequencies, Cluster 2 (red) shows a threefold decrease in the peak during the late window (Fig. 5F). Interestingly, the large trough exhibited in 2-Peak neurons (blue) in the temporal frequency domain is not replicated in the spatial frequency domain, although there is some flattening of response. This flattening occurs despite higher responses seen in the temporal frequency curves indicating that this flattening is unlikely due to saturation effects. The Cluster 1 spatial frequency tuning (Fig. 5F, green) also shows flattening, but this occurs at a similar spike rate to the peak of the Cluster 1 temporal frequency curve, more indicative of saturation.

In Dipteran LPTCs, ON and OFF channels are processed separately (Joesch et al., 2010), with recent work supporting a model that integrates inputs to local motion detectors from ON and OFF pathways originating in early visual processing (Borst and Helmstaedter, 2015). In dragonflies, we previously showed separation of ON and OFF channels in the target-detection pathway (Wiederman et al., 2013). Although LTCs give robust motion responses, like their Dipteran counterparts, they also respond transiently to full-screen flicker (i.e., square wave on and off luminance changes) at low temporal frequencies (Fig. 5G). In comparison, our prior work shows that the target pathway (same dragonfly species) is strongly selective for the OFF pathway (Wiederman and O'Carroll, 2011). Do we see differences in responses to the ON and OFF flicker components between LTC clusters? Figure 5G shows example data traces of individual LTCs in response to a 2 Hz full-screen flicker. We analyzed response windows 20–70 ms after the onset of each ON and OFF phase (shaded green regions) for the LTC clusters (Fig. 5H). Overall, both Cluster 1 and Cluster 2 provide spiking responses to both ON and OFF phases of the full screen flicker (full-wave rectification) whereas the 2-Peak neurons responded more strongly to the OFF component, with little or no response to the ON phase (luminance increment).

Temporal adaptation in response to contrast steps

Although a contrast ramp stimulus avoids an onset flicker transient, it does confound stimulus contrast and time. Therefore, differences observed between clusters may be due to variation in contrast sensitivity. We quantified contrast sensitivity by calculating when neuronal responses exceeded 2× the SD of spontaneous activity and determined the corresponding Michelson contrast value (in time). We took the inverse of this threshold value as the contrast sensitivity, a method equivalent to the detectability criterion used in previous insect studies (Dvorak et al., 1980). All three neuron groups showed high-contrast sensitivity (Fig. 6A), with median values of 24 (Cluster 1), 35 (Cluster 2), and 40 (2-Peak). These values are similar to those reported for other insect species (O'Carroll and Wiederman, 2014). Peak contrast sensitivity was significantly lower in Cluster 1 (no-shift) than in the other two groups (Cluster 1, n = 12; Cluster 2, n = 23; 2-Peak, n = 12; Kruskal–Wallis with multiple comparisons).

Figure 6.

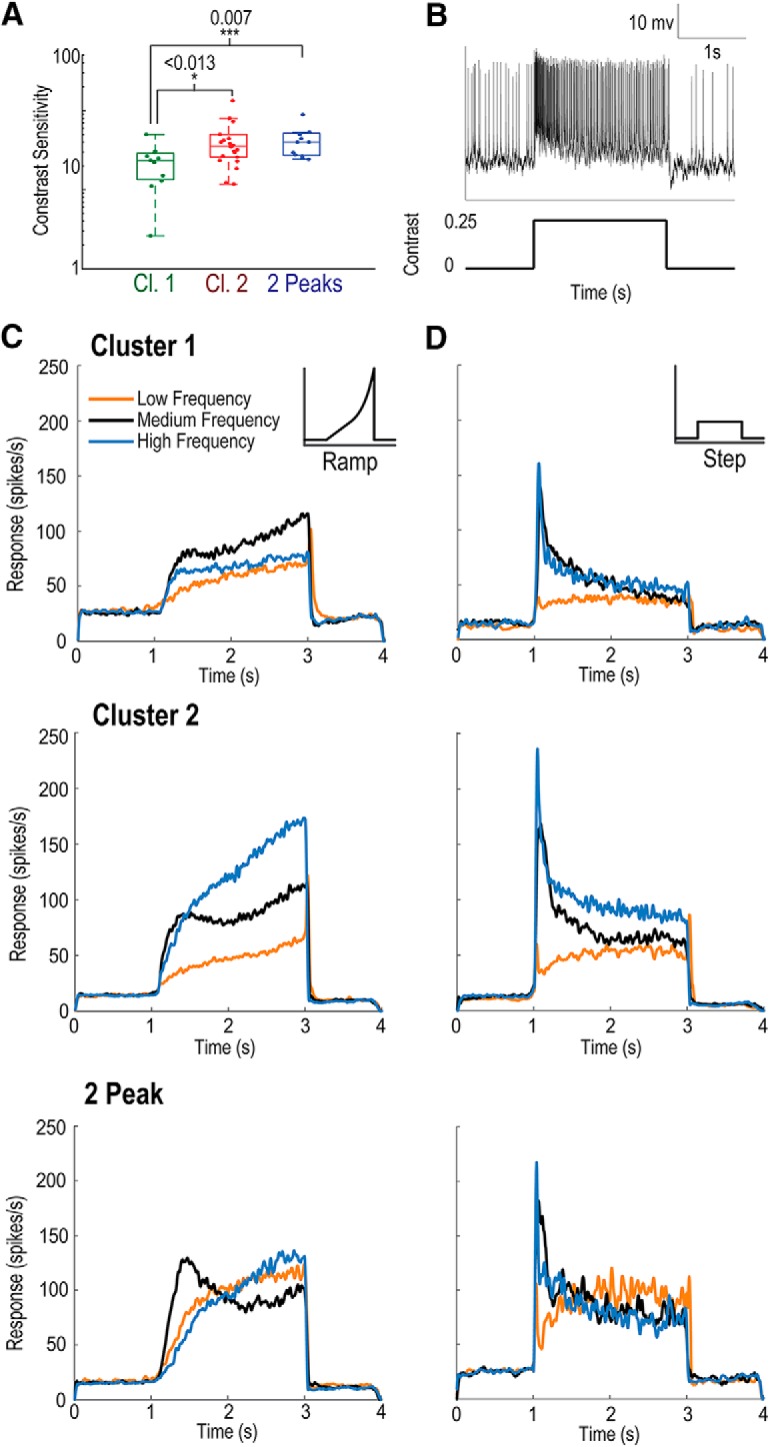
LTCs exhibit temporal adaptation. A, Boxplot distributions of LTC contrast sensitivity (to a drifting grating) derived from the contrast required to evoke a neuronal response (2× the SD of the spontaneous activity). Cluster 1 neurons exhibit significantly lower peak contrast sensitivity than the other two groups (Mann–Whitney U test; Cluster 1, n = 11; Cluster 2, n = 21; 2-Peak, n = 12). B, Individual raw spike trace in response to a contrast step. Neurons are exposed to 2 s of a constant contrast (0.25_Michelson) grating after 1 s of a gray screen. C, Mean response over time taken for contrast ramps from the average of three temporal frequency ranges (low, 0.27–0.4 Hz, orange; medium, 3.4–5.1 Hz, black; high, 13.7–20.2 Hz, blue) for each of the three LTC groups (top, Cluster 1; middle, Cluster 2; bottom, 2-Peak). Cluster 1 LTCs exhibit a stronger response to medium frequencies, which temporarily flatten 300 ms after ramp onset, then slowly rise with increased contrast. Cluster 2 LTCs exhibit an early strong response at medium frequencies before significant adaptation and flattening of the response. At high temporal frequencies, no such flattening occurs with responses increasing strongly with contrast. Responses to low frequencies are uniformly low and only rise slowly with time (and contrast). 2-Peak LTCs exhibit a strong early response to medium frequencies before weakening over time, whereas responses to low and high frequencies slowly and steadily increase. D, Same as in C, but in response to contrast steps. All groups show large onset transients, most pronounced at medium and high temporal frequencies. We observe sustained temporal adaptation over the stimulus duration. Cluster 2 neurons maintain stronger responses to high temporal frequencies over the entire time course. 2-Peak neurons quickly reach similar responses from all temporal frequencies, with low temporal frequencies having the strongest response late in stimulus duration.

To further disambiguate the effects of contrast and time, in a subset of recordings, we used additional trials comprised of a moderate contrast “step,” that is, where the 2 s stimulus stepped from contrast (Michelson) 0 to 0.25 (Fig. 6B). We recorded far fewer neuronal responses to this step stimulus (Cluster 1, n = 4; Cluster 2, n = 8; 2-Peak, n = 3). While generally inferior to the ramp stimulus (which provides an estimate of contrast sensitivity and also removes the effect of onset flicker transients that may artifactually change early window analysis), this stimulus should confirm whether temporal adaptation, rather than an effect of contrast is the cause of the observed differences between clusters. For comparison, contrast ramp responses (Fig. 6C) are plotted alongside contrast step responses (Fig. 6D). For each group of neurons (top, Cluster 1; middle, Cluster 2; bottom, 2-Peak), we plot three lines representing the mean response across neurons for three frequency ranges (low, 0.27–0.4 Hz; medium, 3.4–5.1 Hz; high, 13.7–20.2 Hz) represented by the orange, black, and blue lines, respectively.

Responses to the ramp stimulus (Fig. 6C) match those previously described for the individual neurons (Fig. 4A–C). In the period immediately after stimulus onset, all three LTC groups show maximal response to intermediate frequencies. This response rapidly increases with increasing contrast before plateauing despite increasing contrast. All three groups show some further increase in response toward the end of the ramp when the contrast increase is most rapid due its exponential rise.

In Cluster 1 LTCs (n = 12), the medium frequencies (black line) remain the strongest throughout the stimulus with both high and low temporal frequencies showing smaller responses. These responses reiterate the consistent optima of temporal tuning in Cluster 1 LTCs with increasing contrast over time (Fig. 4C).

Cluster 2 LTCs (n = 21) have a similarly strong early response to intermediate frequencies (black line); however, the high temporal frequency responses (blue line) increase strongly over the course of the stimulus. The response to low temporal frequencies (yellow line) rises, but not to levels observed for either medium or high frequencies. These results reiterate the shift to higher temporal frequencies (early vs late windows), previously described in Figure 5.

The 2-Peak LTCs (n = 12) show an initially strong response to the intermediate frequencies (black line) before decreasing to levels below that of either the high- or low-frequency ranges. Again, these results indicate that response changes appear to affect different temporal frequencies unevenly, with intermediate frequencies decreasing strongly compared with high and low frequencies.

How does this compare with the contrast step stimulus? Despite the moderate contrast of the contrast step stimuli (0.25), responses strongly decrease for medium and high frequencies in all three neuron groups. This temporal adaptation (i.e., a decrease in neuronal response over time to a constant stimulus) is still in effect long after the initial transient responses (due to full screen flicker effects) have resolved. Moreover, in Cluster 2 LTCs (n = 8), the ordering of frequency responses is preserved (i.e., high, medium, low, Fig. 6D, middle) congruent with the ramp stimulus observations. Our comparison demonstrates the difficulty of using contrast steps to estimate temporal tuning because the flicker onset transients mask the early intermediate frequency preference of Cluster 2 LTCs before temporal adaptation but would not be present in real-world scenarios. Nevertheless, while step-onsets tend to bias tuning to higher frequencies in correlation-based motion detection (Borst and Bahde, 1988), the sustained preference for high temporal frequencies we observed lasts for seconds, far longer than the timeframe of onset biases. Thus, the shift in preferred temporal frequency observed in Cluster 2 LTCs is not a consequence of the ramped change in contrast.

Velocity coding by LTCs for natural scenes

Our analysis of response tuning using narrow-band sinusoidal gratings suggests that all three LTC groups have similar spatial and temporal tuning in their underlying motion detectors at low contrast before any adaptation. This is evidenced by their similar spatial and temporal tuning in the early window. In other insects, such optima for sinusoidal patterns provide robust predictions for the velocity range over which the same neurons respond to broad-band images, including natural scenes (Dror et al., 2000; Barnett et al., 2010). However, as the contrast ramps progress, the large response differences to the stronger motion stimuli among different LTC groups may have a substantial influence on responses to moving natural patterns.

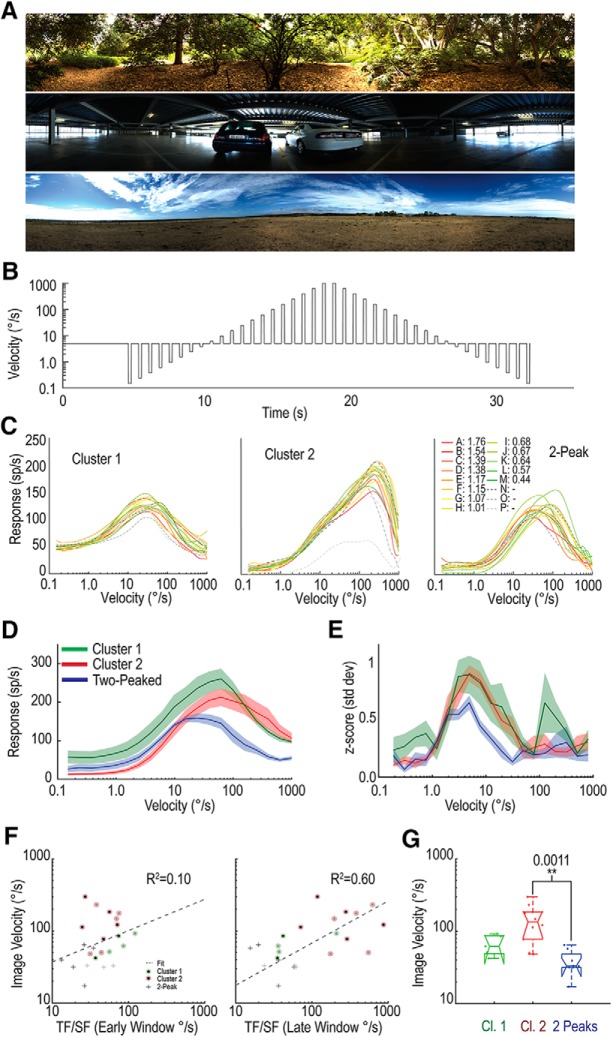
To test this, we estimated velocity tuning using prolonged exposure to motion for a suite of either six or an extended set of 16 natural image panoramas, depending on the experiment recording duration (Fig. 7A). We also modified the initial starting phase of the image (minimum 2 phases) to avoid phase-locked behavior. The stimulus comprised a sequence of brief periods of test motion across a wide range of velocities, interleaved with a constant adapting stimulus (Straw et al., 2008), but always moved continuously in the preferred direction for the neuron (Fig. 7B). The adapting periods are longer than the brief test speeds (500 ms vs 200 ms) to ensure that the adaptation state is kept reasonably constant at the start of each test period. The test velocities cycle through an ascending and descending order to evaluate any hysteresis that may reflect differential adaptation to the test pulses themselves.

Figure 7.

Velocity tuning of LTCs in response to moving, natural scenes. A, Three examples from the set of 16 panoramas used as natural image stimuli. B, The velocity for each panoramic image is modulated over time, translated horizontally on the screen oriented in the preferred direction of the neuron. Following an initial 4 s period, brief test periods (200 ms) of varying velocities were interleaved with longer (500 ms) periods of the adapting speed (5°/s). C, Individual examples from three different LTC groups, with each line a velocity tuning profile for a different natural image. C_A-C_P, Color-coded in order of their image contrast (Straw et al., 2008). These LTCs exhibit consistency between images despite large changes in image contrast. In particular, note the consistency across images over decades of velocity for the example Cluster 2. D, Average responses of the three LTC groups (mean line and shaded SE) to the test portion of the modulated velocity shown in B, 50 ms after the velocity change (100 ms window). Each group exhibits a different velocity tuning profile, with 2-Peak LTCs exhibiting a particularly low velocity peak (24.5°/s) compared with either Cluster 1 or Cluster 2 (62°/s). E, Plot represents the z scores (a measurement of information content; see Materials and Methods) at each velocity for each group. 2-Peak LTCs show the largest interimage variation and therefore the lowest z score. F, Scatter plot represents velocity tuning estimates (from grating data) against velocity tuning measurements (from natural image data) for early (left) and late (right) windows of the grating recordings. Estimates defined as the peak temporal tuning divided by the peak spatial tuning. Early windows show little correlation (R² = 0.1), whereas late windows show a far stronger correlation (R² = 0.6), indicating that the later grating responses are more representative of velocity tuning. G, Box plot showing the distributions of velocity tuning optima for different LTC groups. p values indicate significantly lower optima in the 2-Peak LTCs than the Cluster 2 LTCs (Mann–Whitney U). Therefore, differential changes result in variable velocity tuning between LTC groups, with the following peak tuning: Cluster 1, 62°/s; Cluster 2, 135°/s; and 2-Peak, 33°/s.

For each neuron, we calculated the spike rate in a 100 ms analysis window, starting 50 ms after the stimulus velocity change. This timing accounts for neuronal response latency, while limiting the degree of adaptation to the changed velocity. We then calculated the mean response across all image phases and produced a velocity-tuning curve for each background image. Figure 7C shows responses to 16 different natural images for an individual neuron of each group (left, Cluster 1; middle, Cluster 2; right, 2-Peak). All three examples show very little variation between images despite significant changes in contrast. The Cluster 2 neuron in particular (Fig. 7C, middle) shows remarkable velocity constancy over a large range. Such a velocity tuning curve, with constancy between radically varying images, is the ideal result when developing computational models for motion-sensitive neurons (Shoemaker et al., 2005; Evans et al., 2016). For each neuron, we then averaged the responses across images and separated the responses by group. We plotted the mean and SE for each group (Fig. 7; Cluster 1, n = 5; Cluster 2, n = 10; 2-Peak, n = 8). The tuning differences we earlier described (Fig. 6) manifest themselves as differences in the optimal velocity tuning for each of the LTC groups. While all three begin responding to the moving background at ∼1°/s, their responses to faster velocities are markedly different. 2-Peak neurons (blue line) exhibit the lowest velocity peak, occurring at 24.5°/s. Both Cluster 1 (green line) and Cluster 2 (red line) peaked at ∼60°/s; however, Cluster 2 showed a broader tuning around this peak.

We also analyzed the velocity constancy (i.e., the degree of variation in the response to different images). Surprisingly small variation was already evident within single-neuron recordings (Fig. 7C), despite the large contrast differences between the images in this set. This suggests that, like LPTCs in Diptera (Straw et al., 2008; Barnett et al., 2010), LTCs in dragonflies exhibit strong velocity constancy. To quantify this further, we calculated the z score at each velocity. The z score captures the response variation between different velocities (i.e., the useful information) compared with the response variation at a single velocity due to the change in background image. The change in mean response between successive velocities is divided by the variation between images for a single velocity pair. This value is then normalized by a factor (k) to account for the number of velocity samples per decade of velocity (higher resolution samples show smaller mean differences between subsequent velocity measures). This final measure (z score) gives an indication of which velocity ranges LTCs convey the most information (i.e., their dynamic range). Figure 7E shows that Cluster 1 and Cluster 2 neurons exhibit a much higher z score at their peaks than the 2-Peak neurons. This indicates that they convey more information about velocity, potentially improving the precision of the velocity estimate. Given that the 2-Peak neurons show such flat temporal frequency tuning, this is an expected result. With a flat temporal tuning curve, the velocity tuning will become dominated by the frequency statistics of the background being encoded, biasing the response to lower frequencies due to the larger power content of natural images at low spatial frequencies (Field, 1987; Tolhurst et al., 1992).

How do the changes in velocity tuning relate to the corresponding temporal and spatial tuning? One short-hand method for approximating velocity tuning is to divide the temporal frequency tuning by its corresponding spatial tuning (O'Carroll et al., 1997). We tested this comparison using both the early and late window from our temporal frequency tuning curves and plotted them against our velocity tuning peak estimates (Fig. 7F, left, early; right, late). We performed correlation analysis (taking into account the logarithmic transform) and found only a weak relationship between the velocity tuning curve and early spatial and temporal tuning (R² = 0.10). However, using the late window revealed a strong correlation (R² = 0.60), indicating that the adapted spatiotemporal tuning for gratings appears to better reflect the velocity tuning in the adapted state, even when the adapting velocity is very different from the test velocity, as one might observe during prolonged patrol flights.

Finally, we tested whether there were differences between the peaks of the velocity tuning of each group of neurons (Kruskal–Wallis, multiple comparisons, Fig. 7G). We found a significant difference in the velocity tuning of Cluster 2 and 2-Peak neurons (p = 0.0011), indicating that these neurons are tuned for different velocities. It is apparent that the differential changes in spatiotemporal tuning exhibited by the different groups of LTCs strongly influence their velocity tuning to natural scenes.

Discussion

Effect of adaptation on velocity tuning

Overall, our results elucidate the variety of spatial, temporal, and velocity tuning of dragonfly LTCs, but also several intriguing properties thus far unique to dragonflies. In Dipteran LPTCs (e.g., the blowfly H1 neuron), exposure to high temporal frequencies (20 Hz) leads to a rapid decay in response; whereas at low-frequency (1 Hz), responses are sustained for many seconds (Jung et al., 2011). We observe the opposite effect in the dragonfly, with the strongest recruitment of responses by the end of the stimulus at the highest temporal frequency tested. Does this apparent shift of maximal sensitivity to high temporal and low spatial frequencies reflect an adaptation mechanism that shifts maximal sensitivity from very low speed to very high speed? A similar mechanism has been proposed to explain motion adaptation in different species, including humans (Clifford et al., 1997). Contrary to predictions of that model, however, estimates of temporal tuning before and after adaptation to a constant motion stimulus (typically a fast-moving pattern) showed that the time constant of the underlying delay filter responsible for temporal tuning is not altered in Dipteran LPTCs. Rather, decreased contrast gain primarily explains these reductions (Harris et al., 1999, 2000).

In Cluster 2 neurons, very weak responses at low temporal frequencies late in the ramp, but very strong responses at high frequencies, certainly suggest a differential adaptation mechanism more strongly recruited by slowly changing patterns in these neurons: a form of potent, nonlinear high-pass filtering recruited by high contrasts. However, because our adapter is not constant in each trial, we cannot infer any change in the delay time constant of the underlying motion detector. Nevertheless, since dragonflies experience prolonged exposure to motion across a large range of velocities within high-contrast natural scenes during natural behavior, it is interesting to consider how this complex adaptation interacts with underlying spatiotemporal tuning to shape velocity tuning during natural image motion. While the higher velocity optimum for Cluster 2 neurons with natural scenes (Fig. 7F) would at first seem consistent with adaptation shifting optima to higher temporal and lower spatial frequencies, more careful evaluation of the theoretical relationship between responses to narrow band sinusoids and broad band natural scenes suggests otherwise. The spatial and temporal optima from the early window in ramp data at ∼0.1 cycles/° and 6 Hz, respectively, for Cluster 2 neurons predict an optimum speed of ∼60°/s for narrow band sinusoids. Natural scenes, however, have their highest contrast at low spatial frequencies, with declining power at higher frequencies: the famous 1/fⁿ characteristic (Field, 1987; Tolhurst et al., 1992). This results in velocity optima at approximately twice those predicted by sinusoidal stimuli (Dror et al., 2000). Hence, our observed velocity optimum for the Cluster 2 neurons during prolonged exposure to high-contrast natural images (∼135°/s) is actually a good match for predictions based on the spatial and temporal optima from the unadapted (early) window sinusoid data (Fig. 7G). Indeed, both the sinusoid and natural scene responses for these dragonfly neurons are similar to those observed in LPTCs of male hoverflies (Straw et al., 2008; Barnett et al., 2010).

Hence, it is the very slow velocity optima for natural scenes of the 2-Peak groups (approximately one-third that of the Cluster 2 neurons) that is surprising. These optima are inconsistent with the predictions based on their responses to low contrast sinusoids, despite the latter being similar across all three groups. This suggests that adaptation or other nonlinear processing during prolonged exposure to motion of natural scenes leads to suppression of responses to higher velocities, which otherwise ought to be a more potent stimulus for these two LTC groups. For 2-Peak neurons at least, this conclusion is consistent with the appearance of the “notch” that we observe in the temporal frequency tuning for initially optimal patterns. Full resolution of this issue will require extensive future work using a rigorous test-adapt-test approach to examine how different components of adaptation previously identified in Dipteran LPTCs (Harris et al., 1999) are differentially recruited by different adapting stimuli.

Mechanisms underlying adaptation

Previous studies have demonstrated that differences in initial versus sustained responses to motion at different temporal frequencies can be altered by the behavioral state of the animal (e.g., during tethered flight vs restrained states) (Chiappe et al., 2010; Longden and Krapp, 2010; Maimon et al., 2010; Lüders and Kurtz, 2015). Many features of this differential adaptation to prolonged stimuli can also be induced in restrained animal preparations by exogenous application of agonists for the neuromodulator octopamine, leading to apparent shifts in temporal tuning of Dipteran LPTCs (Jung et al., 2011; Suver et al., 2012; Arenz et al., 2017). Could differences in octopaminergic modulation of the different groups of dragonfly LTCs potentially explain some of the differences we observe in their response time courses? Although we did not test this directly, it seems an unlikely explanation for the unusual tuning shift we observe in Cluster 2 neurons, for several reasons. First, in prolonged (>4 h) individual recordings, the temporal tuning was repeatedly measured with no apparent change in response shape. Second, we recorded data for two or more groups of LTC in the same animal on several occasions exhibiting very different tuning responses. Both observations argue against global changes in octopaminergic activity. Finally, increased locomotor activity or octopamine agonists primarily downregulate LPTC response reduction at high temporal frequencies during prolonged motion exposure (Jung et al., 2011). Hence, the higher gain following application of octopamine agonists in Dipteran LTPCs results primarily from less adaptation to sustained motion at high temporal frequencies. By contrast, Cluster 2 neurons already give sustained, vigorous responses at the highest temporal frequencies tested, despite our animals being fully restrained. Instead, we see selectively weaker responses at lower temporal frequencies and high spatial frequencies: both are more consistent with some form of powerful redundancy reduction in signals at the motion detector inputs.

Strong temporal and spatial (center surround) antagonism have both been observed in dragonfly lamina monopolar cells (Laughlin, 1974). Although linear spatial filtering ought to equally affect the early response window of our ramp stimuli, it would hardly be surprising if potent antagonism, either spatial or temporal, were recruited nonlinearly as contrast increases (e.g., via additional voltage gated or inactivating conductances in feedforward synapses). Indeed, such a mechanism may be required for a system with high-contrast sensitivity (as observed here) to regulate gain of local motion detectors and limit saturation in the real world, where average contrasts are high. Hence, differences we see between LTC groups may potentially arise from differences in which classes of lamina cells (or their postsynaptic targets) lie on the inputs to underlying motion detectors, an observation further supported by the differences we see in their transient responses to flicker (Fig. 5G). Both strong antagonism and nonlinear temporal high pass filtering are key components of models proposed to explain spatiotemporal tuning of local motion detecting elements for the small target motion detector pathway involved in target tracking in the lobula in these same dragonflies (Wiederman et al., 2008; Wiederman and O'Carroll, 2011), so it is possible that some LTCs take their primary inputs from the same local motion detectors as these feature-detecting neurons.

Velocity constancy for natural scenes

In all three LTC groups, we observed a high degree of consistency of responses to the movement of natural images. The majority of the curves peak at a similar optimal velocity, and the gain in response to different velocities is similar despite very large differences in the global contrast among this image set (Brinkworth and O'Carroll, 2009; Barnett et al., 2010). Such “velocity constancy” for highly variable natural scenes in Dipteran LPTCs has previously been shown to derive from a number of dynamic nonlinear processing stages in biological vision, commencing with fast temporal adaptation in the photoreceptors and second-order neurons, but also with a strong contribution from dynamic gain control within local motion detectors (Shoemaker et al., 2005; Brinkworth and O'Carroll, 2009). Whatever the underlying mechanisms responsible for this impressive velocity constancy, some neurons recorded (particularly neurons from Cluster 2) come closer to being ideal velocity estimators than anything previously described at a single neuron level, in any animal, giving a progressive monotonic rise in response over more than a 100-fold range of velocities (Fig. 7C).

Behavioral implications

Hemicordulia dragonflies exhibit numerous distinct behaviors, including hawking, patrolling, and aerobatic conspecific engagements. Each task places different constraints on any system encoding optic-flow information, and this would provide selective pressure for dragonflies to either adopt an extremely flexible motion-detection system or one specialized for different tasks. Our data suggest that differences in the tuning among different LTC groups are matched to different behavioral tasks. During hovering and hawking behavior, the detection and cancelling of subtle perturbations due to airflow require a motion system capable of detecting slow velocities. 2-Peak LTCs exhibit a surprisingly robust response to grating patterns, even the slowest patterns we tested. Such neurons would appear to be well suited in a system designed to detect the slow-sustained shifts in optic flow that might occur during hawking behaviors. Meanwhile, Cluster 2 LTCs exhibit extremely robust responses to fast motion and are better suited to fast moving tasks, such as patrolling or rapid conspecific pursuit encounters. Finally, Cluster 1 LTCs exhibit similar properties to Dipteran LPTCs, which have been linked to turning behaviors, such as the optomotor response (Haikala et al., 2013). In concert with Cluster 2 LTCs, they may extend the velocity ranges over which Hemicordulia can operate by providing parallel pathways tuned to both slow and fast motion.