Abstract
Background:
Developing efficient procedures of model calibration, which entails matching model predictions to observed outcomes, has gained increasing attention. With faithful but complex simulation models established for cancer diseases, key parameters of cancer natural history can be investigated for possible fits, which can subsequently inform optimal prevention and treatment strategies. When multiple calibration targets exist, one approach to identifying optimal parameters relies on the Pareto frontier. However, computational burdens associated with higher-dimensional parameter spaces require a metamodeling approach. The goal of this work is to explore multiobjective calibration using Gaussian process regression (GPR) with an eye towards how multiple goodness-of-fit (GOF) criteria identify Pareto-optimal parameters.
Methods:
We applied GPR, a metamodeling technique, to estimate colorectal cancer (CRC) related prevalence rates simulated from a microsimulation model of CRC natural history known as the Colon Modeling Open Source Tool (CMOST). We embedded GPR metamodels within a Pareto optimization framework to identify best-fitting parameters for age-, adenoma-, ademona-staging dependent transition probabilities and risk factors. The Pareto frontier approach is demonstrated using genetic algorithms with both sum-of-squared errors (SSE) and Poisson deviance GOF criteria.
Results:
The GPR metamodel is able to approximate CMOST outputs accurately on two separate parameter sets. Both GOF criteria are able to identify different best-fitting parameter sets on the Pareto frontier. The SSE criterion emphasizes the importance of age-specific adenoma progression parameters, while the Poisson criterion prioritizes adenoma-specific progression parameters.
Conclusion:
Different GOF criteria assert different components of the CRC natural history. The combination of multiobjective optimization and nonparametric regression, along with diverse GOF criteria, can advance the calibration process by identifying optimal regions of the underlying parameter landscape.
Keywords: cancer simulation, calibration, Gaussian process, regression, Pareto frontier, goodness-of-fit criterion, microsimulation
Introduction
Decision makers in the healthcare policy realm are increasingly relying on the predictive power of disease simulation models Stout et al. (2009); Caro et al. (2012). These models explore the medical and economic impacts of diseases by simulating their progression. Parameters within the model, which describe the natural history of the target disease, can be varied to simulate disparate health outcomes and forecast the effect of possible interventions.
Existing clinical data can fail to estimate model parameters reliably, rendering them unobservable. Moreover, information on these unobservable model parameters may be sparse or nonexistent. Calibration enables estimation of the model parameters by varying simulated model outputs to match existing data Stout et al. (2009); Kong et al. (2009); Vanni et al. (2011); Erenay et al. (2011); Briggs et al. (2012). The necessary elements for calibration include: (1) target parameters for calibration, (2) existing clinical data, (3) a goodness-of-fit (GOF) criterion, (4) a parameter search algorithm, (5) acceptable parameter values, and (6) an effective stopping criterion Vanni et al. (2011).
Given multiple calibration targets, or multiobjective calibration, identifying a best-fitting parameter set is often reduced to optimizing a singular weighted sum measure Vanni et al. (2011). However, consensus or validation on the choice of weights is rarely found. An appealing alternative is to consider the notion of Pareto optimality, whereby a set of nondominated model parameters can be determined that fit all calibration targets relatively equally Enns et al. (2015). No one parameter combination improves on, or dominates, all other parameter combinations in all calibration targets. Pareto-optimal parameter combinations were also found to contain higher variance than weighted-sum parameter combinations, suggesting a more realistic snapshot of parameter uncertainty untainted by user biases on objective-function weights.
Another essential feature of the calibration problem is the GOF criterion. A comparative study of various GOF criteria revealed likelihood-based criteria minimized the deviation between estimated and true parameter values when inferring parameter values for a microsimulation model in multiple calibration scenarios van der Steen et al. (2016). Clearly, in the absence of consensus on what constitutes an effective individual GOF criterion, evaluating multiple GOF criteria will improve the quality of calibration.
The difficulty of calibration is further exacerbated by the number of unobservable parameters and their corresponding ranges, as well as the computational effort needed to evaluate each parameter combination via the simulation model. Lengthy computation times, when especially exacerbated by complex individually based microsimulations, necessitate the efficient use of accurate metamodels to adequately summarize model outputs. Under often restrained computational budgets, these metamodels can be used to produce new insights into calibrating the original simulation models. Gaussian process regression (GPR) is a viable metamodeling technique to encapsulate simulation model behavior for medical decision making. No prior functional or parametric relationship need be assumed between input and output.
The cost-effectiveness of osteoporosis treatments has been modeled as a function of the relative risks of bone fracture using GPR Stevenson et al. (2004). The use of GPR has reduced the computation time for estimating the impact of these interventions by more than 99%. GPR has also been applied to estimate intensive care unit discharge times, and then compared to predictions made by established authorities Meyfroidt et al. (2011). The resulting regressor outperforms existing scoring systems and intensive care clinicians. Postoperative outcomes of patients with spinal cord disorders have also been modeled using GPR, surpassing linear regression, support vector regression, and k-nearest neighbor regression in terms of mean absolute difference on a test dataset Lee et al. (2016). When GPR approximates noisy patient vital signs for use in early warning systems at hospitals, it can provide reduced mean-squared error estimates of heart and breathing rates compared to conventional signal-smoothing techniques Clifton et al. (2012). Signal-smoothing techniques substitute incomplete data with the corresponding mean value of the vital sign from either the entire patient population or an individual patient. A probabilistic model like GPR has the advantage of forecasting the distribution of missing data, rather than producing a single point estimate. Furthermore, GPR has been able to predict anomalous patient behavior before the conventional signal smoothing techniques by at least 9 hours when trained on manual observational data prior to a critical event that would benefit from an early warning system. The expected value of learning certain parameters in health economic decision models entails computationally intensive calculations requiring nested calls to the underlying patient-level simulation model. Conducting this value of information analysis with GPR reduces the computational burden by replacing the simulation model Rojnik and Naveršnik (2008); Strong et al. (2014). When compared against alternative models for value of information analysis, the GPR model is more accurate than linear regression and similar in accuracy to general additive models.
The objective of this study is to perform multiobjective calibration of disease prevalence data using GPR. Our contributions are (1) demonstrating the viability of GPR as a metamodeling technique for computationally expensive disease simulation models; and (2) providing insights into the use of different GOF criteria in calibrating Pareto-optimal parameters for multiple simulation outcomes.
For demonstration purposes, we adapt the Colon Modeling Open Source Tool (CMOST) model, a microsimulation model of the natural history of colorectal cancer (CRC) Prakash et al. (2017). CRC is the third most common cancer worldwide and the fourth leading cause of cancer-related death Ferlay et al. (2015). For the calibration, we focus on an individually based state-transition stochastic model for the colorectal adenoma-carcinoma sequence. Adenoma is the most common precancerous colon polyp, which is believed to be the precursor for about 80% of CRC Heitman et al. (2009). By training a GPR metamodel on training instances generated by CMOST, we perform multiobjective optimization using an established multiobjective genetic algorithm and multiple GOF criteria to identify a multidimensional Pareto front by interrogating the surrogate model in place of the original simulator, exerting significantly less computational effort. After confirming the accuracy of the regression model, we proceed to construct the Pareto frontier. Results demonstrate the efficacy of our approach in generating an informative set of nondominated points in the multiobjective space with an accurate metamodel.
The remainder of this paper is organized as follows. The Methods section will introduce the modeling approaches used in this work. The Results section will present the findings from our investigation into multiobjective calibration using Gaussian processes. Finally, the Discussion section will summarize our work and present future extensions.
Methods
Adapted CMOST Simulation Model
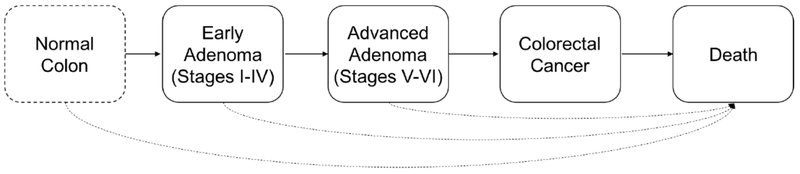
We calibrate a set of CRC-related prevalence outcomes via an adapted version of CMOST, an open-source Matlab-based framework for microsimulation of CRC natural history and screening strategies Prakash et al. (2017). In principle, a microsimulation model simulates each individual patient from some hypothetical cohort for an extended period of time (e.g., from birth to death), during which the patient can experience different stages of the disease. CMOST contains assumptions underlying the natural history of CRC. These assumptions reflect various clinical hypotheses on incidence and growth along different CRC pathways, including the adenoma-carcinoma sequence (Figure 1), the process by which normal colorectal epithelium evolves to cancer Leslie et al. (2002).
Figure 1.
Structure of the adapted CMOST model
With the adapted model, we focus on a set of 3-month transition probabilities in the calibration. These risks govern individually based state transitions along the adenoma-carcinoma sequence (i.e., adenoma initiation and stage-wise progression), which are generated to take place in a probabilistic fashion. The adenoma initiation rate (state-transition probability from normal to stage I adenoma) is age-dependent and modeled with a sigmoidal function containing three parameters (i.e., θ1; θ2; θ3). The adenoma-carcinoma sequence comprises six stages differentiated in part by adenoma size. Early adenomas constitute the first four stages with adenoma sizes below 1 cm, whereas advanced adenomas constitute the last two stages with adenoma sizes exceeding 1 cm. In CMOST and our adapted model, early and advanced stage-specific progression rates (3-month instantaneous transition probabilities) in the baseline case are assumed to be constant throughout lifetime of each individual and to any adenoma. The baseline progression rates are thus parameterized by θ4 – θ9. Furthermore, for each adenoma, these transition probabilities are adjusted by age and adenoma-specific risk factors that are differentiated by the stage the individual adenoma is at (early versus advanced). For convenient exploration, visualization, and reproduction, determination of these risk factors assumes concise functional forms. Adenoma-specific progression risk factors are modeled with exponential functions and parameterized with two sets of scalars (i.e., θ10 and θ11; θ12 and θ13). Age-dependent progression risk factors are modeled with Gaussian functions and parameterized with two sets of scalars (i.e., θ14 – θ16; θ17 – θ19). In addition, adenoma-specific risk adjustment are confounded by a risk factor associated with the individual having the adenoma (e.g., gender, family history, etc.). The risk, denoted by p, is presented in percentiles, and assumed to be given in our calibration. In summary, stage-wise adenoma progression (early or advanced) is based on the baseline stage-wise adenoma progression rate, adjusted by age-dependent and adenoma-specific progression risk factors. Finally, for ease of showing the viability of our calibration methodology, we consider possible mortality from any stage to maintain sufficient calibration freedom and collapse the pre-clinical and clinical stages of CRC to focus the calibration on the adenoma-carcinoma sequence. In total, we estimate 19 model parameters via calibration. For a summary of the parameters/scales, please refer to Table 1.
Table 1.
Random variates of interest in the adapted model from CMOST Prakash et al. (2017). Age (in years) is denoted by a and risk percentile is denoted by p.
| Random Variates of Interest | Properties | Functional Form (where applicable) |
|---|---|---|
| Age-specific adenoma initiation rate | Defined by a sigmoidal funciton w.r.t. θ1, θ2, θ3 | |
| Baseline adenoma stage-specific progression rate | ||
| Early stages | Constant. Stage I – IV, parameterized by θ4–θ7 | |
| Advanced stages | Constant. Stage V, VI, parameterized by θ8, θ9 | |
| Adenoma-specific progression risk factor | ||
| Early stages | Defined by an exponential function, w.r.t. θ10, θ11 | θ10 exp(θ11p) |
| Advanced stages | Defined by an expotential function, w.r.t. θ12, θ13 | θ12 exp(θ13p) |
| Age-specific progression risk factor | ||
| Early stages | Defined by a Gaussian function, w.r.t. θ14, θ15, θ16 | θ14 exp (–(θ15a – θ16)2) |
| Advanced stages | Defined by a Gaussian function, w.r.t. θ17, θ18, θ19 | θ17 exp(–(θ18a – θ19)2) |
Calibration Targets
We calibrate the adapted CMOST simulation model to clinical data reported from a German observational cohort study with nearly 3.6 million participants aged 55-79, from 2003-2010 Brenner et al. (2013). The objective of the study was to derive annual transition rates from early to advanced adenoma and from advanced adenoma to CRC. Transition rates described the proportion of people who would progress to the next state of the disease after one year. Since these transition rates could not be observed directly (i.e., adenomas are removed upon detection), data from the German national screening colonoscopy registry was used to infer sex- and age-specific transition rates. A birth cohort analysis partitioned the cohort by birth year and sex into ten 5-year age groups, five for each sex. Transition rates were then calculated by observing the increase in prevalence after one year for each age group. The study found that transition rates from advanced adenoma to CRC were similar across sex, but increased with age.
For our calibration, we make use of the male prevalence data reported in the German cohort study. We define our calibration targets (Table 2) by averaging the prevalence data for the three states of colorectal neoplasia (i.e., detected with 1. only early or non-advanced adenomas, 2. advanced adenomas, and 3. colorectal cancer) over all male participating subjects. Thus, our model outputs are age-averaged over all male subjects.
Table 2.
Calibration targets derived from Brenner et al. (2013). Prevalence rates are age-averaged prevalence rates for males only.
| Calibration target | Prevalence rate | (%) |
|---|---|---|
| y1 | Early adenoma | 17.88 |
| y2 | Advanced adenoma | 8.86 |
| y3 | CRC | 1.46 |
GOF Criteria
By simulating the CMOST model with the aforementioned parameter combinations (i.e., specific realizations of θ1 to θ19), we obtain a set of age-averaged prevalence rates for the three states. These simulated outcomes can then be compared to the corresponding calibration targets reported by Brenner et al. (2013). With the three calibration targets, we formulated a 3-objective calibration problem. Mathematically, the calibration problem is stated as:
| (1) |
where fi(θ), is the calibration objective indexed by i. We consider two GOF criteria to compare our simulation outcomes with the calibration targets. One is the commonly used sum-of-squared errors (SSE) criterion:
| (2) |
where is simulated outcome i with parameter set , and yi is the observed data, or target value, of outcome i, listed in Table 2.
The second criterion is the Poisson deviance function:
| (3) |
The Poisson deviance function was found to possess the lowest prediction error amongst all GOF criteria studied between its estimated parameters and the ground truth van der Steen et al. (2016).
Gaussian Process Regression (GPR)
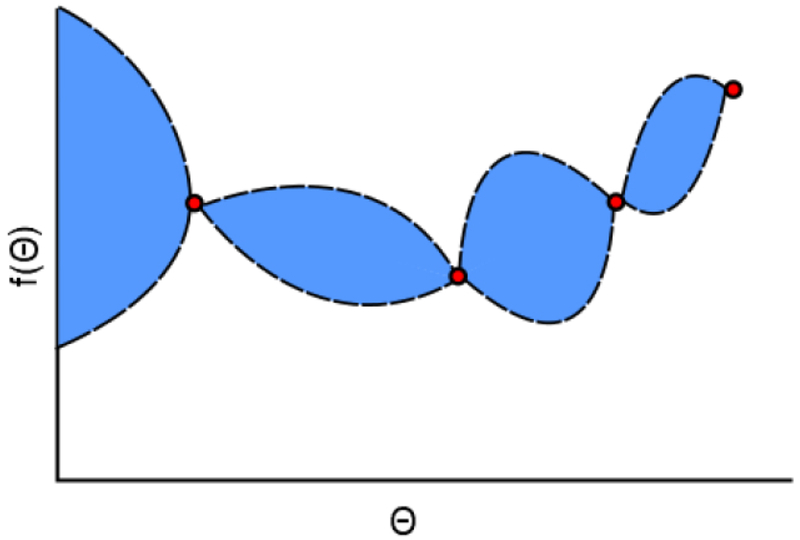
Gaussian process regression is a nonparametric, kernel-based, supervised learning algorithm that exploits Gaussian processes, continuous stochastic processes defined by multivariate Gaussian distributions Rasmussen and WilliamTs (2006). A posterior probability distribution is formed by conditioning an initial prior distribution on newly observed data. After fitting to this observed data, the resulting regressor can approximately interpolate the observed parameter combinations, while providing predictions constrained by confidence intervals for previously unseen parameter combinations. An example of GPR modeling is shown in Figure 2. Predictions between adjacent data points tend to contain uncertainty in their values. The quantification of prediction uncertainty is valuable for microsimulation models, wherein the same parameter combination may produce slightly different outputs. The covariance function of a GPR model specifies its shape and smoothness by quantifying the similarity between two parameter combinations, the assumption being that similar parameter values are highly correlated. In Figure 2, this assumption is demonstrated by the tapering of uncertainty around the observations, which are assumed to be well known. GPR explains an output by introducing random variables from a Gaussian process, and explicit basis functions h(θ), with coefficients β:
| (4) |
Figure 2.
An example of Gaussian process regression in two dimensions, where prediction uncertainty (blue region) exists between observations (red dots).
With a combination of both parametric (h(θ)Tβ) and nonparametric (g(θ)) forms, an improved estimate of yi can be obtained.
Multiobjective Optimization using Genetic Algorithms
To perform multiobjective optimization for the CRC calibration problem, we rely on a genetic algorithm-based implementation, encoded in the Matlab function gamultiobj. This function determines a Pareto front by propagating and transforming a set of candidate solutions using a series of genetic operators. It is a controlled elitist genetic algorithm derived from the genetic algorithm NSGA-II Deb et al. (2002). It balances the search for solutions with better fitness values, or ranks, against solutions that are widely distributed across the search space at greater distances. Rank and distance measures are assigned to each solution, or parameter combination, to quantify their fitness for selection for the next generation, or iteration, of the algorithm. The rank of a parameter combination indicates its propensity to lie on the Pareto front, while the distance measure signifies the dispersion among parameter combinations with equal rank. The genetic algorithm favors nondominated parameter (lower rank) combinations that are evenly distributed across the Pareto front (greater distance) for the next generation.
The algorithm initiates with an initial population satisfying the bound constraints of 0 being created. Then the selection of parents commences with random pairwise comparisons between parameter combinations on the basis of rank and distance. The better parameter combination is then selected for breeding. Child parameter combinations from these “parents” are then created by applying genetic operators such as crossover and mutation. An augmented population consisting of the current parameter combinations and their children are then culled to the maximum population size by retaining the best-performing parameter combinations from each rank. The algorithm terminates once the maximum number of generations is reached, or when movement in the Pareto front between successive iterations falls below a certain threshold.
Overall Model Calibration Algorithm
Our proposed multiobjective calibration algorithm relies on multiobjective optimization of two GOF criteria comparing three actual CRC prevalence rates, assumed to be our calibration targets, with emulated outputs produced from a Gaussian process metamodel. We train separate regressors for each CRC state. To properly deploy the GPR technique, appropriate model settings, or hyperparameters, must be selected. Once these hyperparameters are optimized, the resulting models can then be evaluated for accuracy performance on different datasets. The GPR models approximate CMOST outputs at selected points in the parameter space.
Multiobjective optimization via gamultiobj identifies Pareto-optimal parameter combination in the 3-dimensional objective space. A population of 5000 parameter combinations are generated and maintained through a maximum of 200 generations, or iterations, of the algorithm. The genetic algorithm consults the (fully trained) GPR models each time a parameter combination must be evaluated to generate prevalence rates. These estimated prevalence rates can then be compared against the calibration targets to yield three objective function values using the GOF criteria. The lower and upper bounds of the overall parameter space Θ are determined by multiplying the published values in the CMOST model for parameters θ1,…,θ19 by and 2, respectively.
We select a cohort size of 100,000 patients as input into the CMOST simulator. This cohort size is of comparable size to the cohort studied by Brenner et al. Brenner et al. (2013), and is computationally reasonable to simulate for the number of parameter combinations desired. The overall algorithm is implemented on Matlab R2016b executed on a computer with a 3.8 GHz processor and 8 GB RAM running Windows 10.
Results
GPR Model Accuracy
GPR Model Hyperparameter Optimization For GPR, we must specify the basis functions h(θ), coefficients β, and kernel function k(θ,θ′) Selecting these model hyperparameters properly is critical to model training and predictive accuracy. As opposed to manual, grid, or random search procedures for appropriate hyperparameter values, we make use of a sequential model-based Bayesian hyperparameter optimization algorithm. Bayesian optimization improves the hyperparameter tuning process by revising its understanding of the hyperparameter space after each sample Snoek et al. (2012). The objective function being minimized is the mean-squared error on a subset of the training set, known as the validation set. Initially, a few points in the hyperparameter space are sampled, the objective function is evaluated, and then future points are selected that maximize a metric known as the acquisition function, which suggests points that are expected to improve upon the current optima the most.
Table 3 shows the hyperparameters selected for each GPR model. The regressors for early and advanced adenoma use a Matern kernel function, which is commonly used due to its properties of stationarity and isotropy Rasmussen and Williams (2006). Both regressors differ in their choice of basis functions, as well as the value for the signal standard deviation σf The regressor for CRC uses a rational quadratic kernel function, also a standard kernel for GPR models. This kernel is equivalent to multiple radial basis function kernels with differing length scales Rasmussen and Williams (2006). The kernel functions for all three regressors are generalizations of the commonly used radial basis function kernel.
Table 3.
Hyperparameter settings for Gaussian process regressors from Bayesian optimization, is weighted Euclidean distance between parameters θ and θ′.
| Regressor | Type of Basis Function | Kernel Function |
|---|---|---|
| Linear |
|
|
| Constant | ||
| Constant |
GPR Model Performance
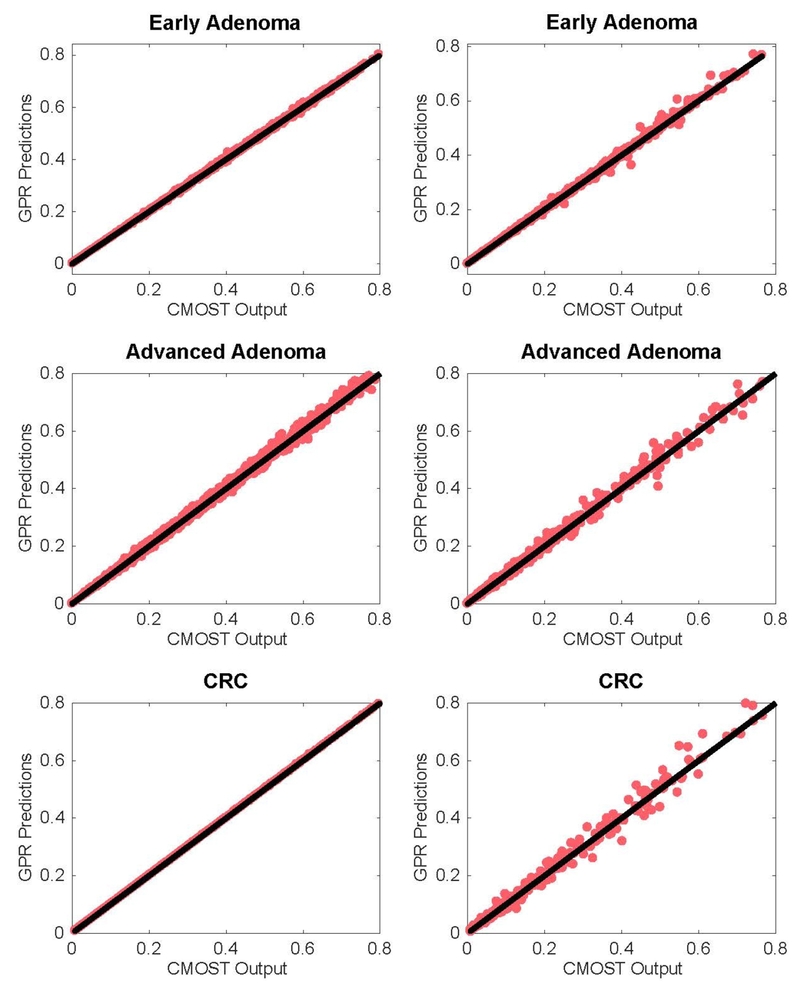
To evaluate the overall performance of the GPR models, we train them using 5000 parameter combinations sampled from 0 using Latin Hypercube Sampling (LHS) McKay et al. (1979). These 5000 parameter combinations are then inputted into the CMOST simulator to output “true” prevalence rates. We label these 5000 parameter combinations and their true prevalence rates the training set. Each simulation run entails input of a single parameter combination with the specified cohort size. We then test the models on unseen data by sampling an additional 1000 parameter combinations via LHS, and simulated their true prevalence rates; these combinations and their prevalence rates are labeled the test set. The GPR model predictions are then compared against the CMOST simulator output, for both training and test sets. These results are visualized in Figure 3, with a solid black reference line that indicates perfect prediction. Deviation from this line indicates some error on the part of the regressor. There is good agreement between the original and surrogate models as most GPR predictions do not stray away from their intended values. In particular, the GPR models for early adenoma and CRC appear well-trained. Prediction performance improves near the calibration targets for the test set, across all regressors.
Figure 3.
CMOST simulator outputs and Gaussian process predictions for the prevalence rates of each CRC state, in both training (left) and test (right) sets. Black solid line inserted for reference.
Identification of the Pareto Frontier
The multiobjective optimization procedure initiates with the training set being chosen as the initial population, for convenience, using gamultiobj. 10 replications of multiobjective optimization are completed using each GOF criterion. Figure 4 displays histograms for the values of each of the 19 parameters from the parameter combinations deemed Pareto-optimal, for both GOF criteria, resulting from all 10 replications. Certain parameter distributions seem normally distributed, while others appear skewed. Left-skewed (θ4, θ14 for SSE, θ2, θ7, θ17 for Poisson) and right-skewed (θ1, θ3 for SSE, θ5, θ11, θ19 for Poisson) parameter distributions emerge, yet both distributions display significant overlap. We also conduct a 2-sample Kolmogorov-Smirnov test (α = 0.05) in order to determine if the parameter samples presented in Figure 4 for both criteria come from the same underlying distribution for each of the 19 parameters. Each pairwise test concludes that the samples indeed originate from different continuous distributions (p < 0.001).
Figure 4.
Pareto-optimal parameter distributions resulting from all 10 replications performed, grouped by the GOF criterion.
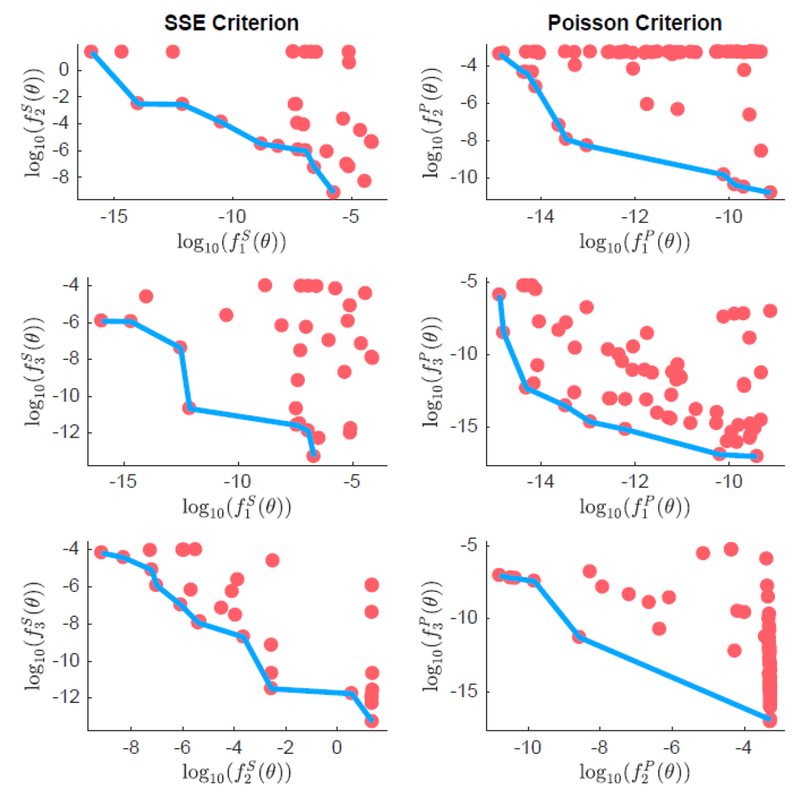
Figure 5 shows the Pareto-optimal points in the objective function space, and a visualization of the Pareto frontier formed by the nondominated parameter combinations, with each GOF criterion, for one replication. Both criteria perform well in identifying points that calibrate the model well to data, with objective values mostly less than 1. There is clear evidence of a Pareto frontier when visualizing each of the objectives in logarithmic space. Some of the two-dimensional projections of the frontier appear with gaps along the frontier, like vs for the SSE criterion, and vs , vs for the Poisson criterion. These gaps span three or four orders of magnitude in the objective values. Furthermore, there is evidence of oversampling of points that contain very similar values of for the Poisson criterion, visualized in the top right and bottom right plots. The plots of vs possesses a Pareto frontier with a set of well-distributed points.
Figure 5.
Pareto frontier (blue line) plotted against Pareto-optimal parameter combinations (red dots) in two-dimension projections. Axes represent objective function values plotted in logarithmic scale.
To provide some further comparison between both criteria, we observe the average number of generations and the spread of solutions on the corresponding frontiers, across replications. 80% and 60% of replications for the SSE and Poisson GOF criteria, respectively, converge prematurely before the maximum number of generations is reached due to little or no change in the Pareto front. Both GOF criteria identify their Pareto fronts in approximately 160 generations, on average. The spread metric we use measures the homogeneity of the distribution of points along the frontier and the change in extreme objective function values across iterations. Across the 10 replications, we compute a mean spread value of 3.5 and 4.2 for the SSE and Poisson GOF criteria, respectively, suggesting that the SSE criterion leads to a slightly better spread of solutions than the Poisson criterion.
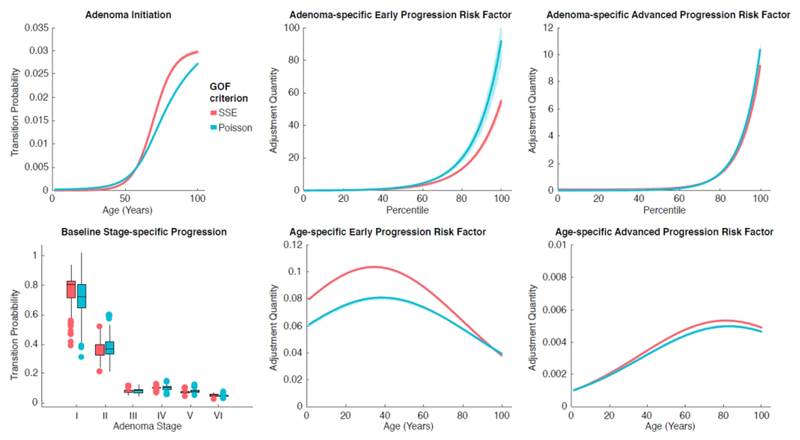
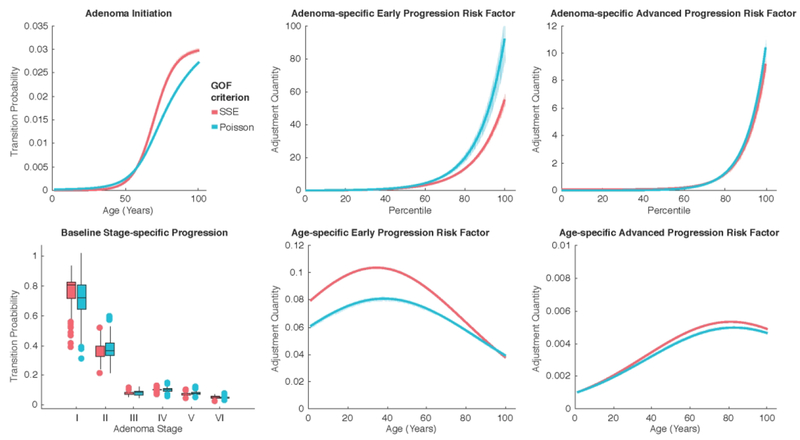
Visualizing the Risk Distributions
Using all Pareto-optimal parameter combinations we obtain from each of the GOF criteria, we visualize the corresponding transition probabilities and risk distributions for the age-, adenoma-, and stage-specific risk factors. Figure 6 shows the various distributions for each of the GOF criteria. Three clear trends are evident upon analysis. First, the Poisson criterion tends to have increased adenoma-specific risk factors relative to the SSE criterion. The other trend is that the SSE criterion tends to have elevated age-specific risk factors relative to the Poisson criterion. Finally, all early progression risk factors exceed their advanced progression counterparts.
Figure 6.
Risk distributions determined by Pareto front parameters, indicated by age, individual adenoma, and adenoma stage.
Adenoma initiation rates for both criteria are nearly equal until about age 60, at which point the SSE risk begins to exceed the Poisson risk. The baseline adenoma stage-specific progression rates preserve the rank ordering of the stages presented by the original parameter values θ4,…,θ9. Both criteria tend to overlap in their interquartile ranges for these rates. The Poisson criterion outpaces the SSE criterion for the adenoma-specific progression risk factors. The top centiles for both risk factors contain vastly increased values that are higher for the Poisson criterion. Again, Figure 4 shows how θ10, θ12, and θ13 for the Poisson criterion are shifted slightly to the right of the SSE criterion; these parameters define the adenoma-specific progression risk factors.
The age-specific early and advanced progression risk factors, modeled as Gaussian functions, peak at distinctive age groups. The early progression risk factor peaks between ages 35-40, while the advanced progression risk factor peaks between ages 80-85. This trend can be explained by the parameter distributions whose values specify the age-specific progression risk factors (θ14 -- θ19 in Figure 4), as the SSE distribution displays a slight left skew relative to its Poisson counterpart.
Discussion
Our work implements multiobjective optimization using Gaussian process regression-based metamodeling to perform and improve model calibration on a microsimulation model of CRC. Gaussian process regression represents a suitable technique for individually based state-transition stochastic models or even hybrid micorsimulations. It is appropriate when simulation model evaluations are difficult or timeconsuming and the parameter space of interest is of moderate to high dimension. A significant amount of time can be saved by referring to the metamodel (< 1 second) rather than the original simulator (90 seconds), for a single model evaluation run. Our results demonstrate that multiobjective calibration using two different goodness-of-fit criteria can fit observed adenoma prevalence data by identifying different adenoma progression mechanisms. Our approach can be extended to other contexts where cheap statistical modeling can alleviate the computational burden in successively evaluating disease simulation models to identify tradeoffs among multiple, competing objectives using diverse calibration criteria.
The results suggest a feasible means by which to determine Pareto-optimal points that conform to observed data at the simulation level. Either elevated age-specific (SSE) or adenoma-specific (Poisson) risk factors are sufficient to obtain simulated outcomes approaching the observed prevalence data. The risk of early progression of an adenoma, whether it be indexed by age, adenoma stage, or individual adenoma, is significantly higher than the corresponding advanced progression risk, by a factor of approximately 10. This conclusion is consistent with clinical observations Brenner et al. (2013) and existing CRC disease model calibration work in the literature Prakash et al. (2017). These observations can facilitate fast deployment of complex CRC disease model calibration prior to testing cost-effectiveness of screening methods and strategies in different settings.
The simulation model we rely on for producing our prevalence estimates is the Colon Modeling Open Source Tool (CMOST). The advantages of CMOST include its ability to characterize adenoma risk distributions parametrically, its transparent and adaptable open-source concept, and its incorporation of multiple, simultaneous adenomas per patient. However, in using CMOST, we consider fewer parameters for calibration than are available to us. Additional parameters that may be of interest in future calibrations are those pertaining to cancer regression (reversion of adenomas in severity), direct cancer (cancers without adenomatous precursors typically difficult or impossible to detect), and fast cancer (cancers evolving from non-Stage VI adenomas) Prakash et al. (2017). In addition, assumptions about adenoma dwell time, which were found to produce indistinguishable model predictions Prakash et al. (2017), may also need to be examined. We configure CMOST to US data for mortality, screening and treatment calculations, which may not be ideal for data obtained from a German cohort study. Above all, the parameter values we obtain through multiobjective optimization are greater than the default values available in CMOST.
Exploration and exploitation of an available parameter space is critical to identifying acceptable parameter combinations. We propose a conservative parameter range Θ that expands below and above the default values available in the CMOST simulation model. However, more suitable parameters values may lie outside this space. Revisiting Θ and including fast, direct, gender-specific, and location-specific cancer parameters in the parameter space may provide additional degrees of specificity to the target cohort. Moreover, we have examined a limited set of calibration targets that are age-averaged and sex-specific. Enumerating the calibration targets by age and gender separately can enable dynamic analysis of the acceptable parameter values as different patient categories are considered. The benefits of comparative analysis across age and gender would be invaluable to characterizing CRC natural history with greater precision.
Comparison of multiple calibration objectives using the Pareto frontier approach forgoes the often arduous task of assigning preferential weights to certain objectives that may bias performance of the calibration algorithm subject to certain GOF criteria Enns et al. (2015). However, ineffective searches of the parameter space may impair the ability to form a well-distributed Pareto frontier. We characterize the relative ability of each GOF criterion in producing well-spaced points on the Pareto frontier through the spread metric. We acknowledge that additional metrics to evaluate the performance of multiobjective evolutionary algorithms exist Yen and He (2013). Furthermore, we assume that the three objectives could be pursued independently of one another, an assumption that likely does not hold (i.e., CRC prevalence can be influenced by early and advanced adenoma prevalences), and may actually underestimate parameter uncertainty Alarid-Escudero et al. (2018). Finally, even though our parameter combinations are selected off the Pareto fronts, the construction of the Pareto fronts is based on the surrogate models. So we want to note the readers for special caution when addressing the practical implications of the selected parameter combinations for ensuing health economic modeling.
Genetic algorithms guide a population of prospective solutions towards the best attainable solution. Evolution of these solutions towards the optima is accomplished with genetic operators, such as selection, crossover, and mutation, which perturb parameter values in the attempt to improve existing optima. The Matlab function gamultiobj adapts this stochastic, derivative-free optimization method to multiobjective optimization. Multiple calibration runs (i.e., multiple calls to gamultiobj using the trained GPR models) minimize any potential bias experienced with a single run. One caveat to this technique, however, is that gamultiobj may produce local Pareto fronts, in which Pareto optimal points are nondominated with respect to their nearby neighborhood, but are inferior with respect to distant points.
Our GOF criteria follow a previous comparative study of GOF criteria in calibrating microsimulation models van der Steen et al. (2016), although the number of calibration targets and input parameters we consider are greater. In that study, the SSE criterion was found to require the most computation time, and was sensitive to variations in scale among calibration targets. Fortunately, the biases of the SSE criterion do not affect the calibration process in this work since the multiobjective problem is pursued. By considering two different GOF criteria, we allow for Pareto-optimal parameters to be selected according to each criterion’s own definition of best fit, preventing direct comparisons. Furthermore, unlike the comparative study, we have no “ground truth” parameter values by which we could compare the convergence of the two GOF criteria. Nevertheless, we demonstrate through analyses of Figures 3 and 5 that both criteria derive statistically different Pareto-optimal parameter distributions that emphasize different aspects of adenoma progression to explain the calibration targets. Both criteria prove capable of forming tradeoffs among multiple objectives, expressed in log space.
Closely related to the calibration problem is the issue of nonidentifiability. When nonidentifiability persists, different parameter combinations may yield the same level of fit to the chosen calibration targets, as was the case here, rendering uncertainty as to the downstream decision-making that would be undertaken as a result of these parameter values. The reasons cited for nonidentiability include an insufficient number (or type) of calibration targets, an excessive number of unknown model parameters, a large parameter space, or an inappropriate GOF criterion Alarid-Escudero et al. (2018). We have attempted to mitigate nonidentifiability in this work by presenting a multiobjective approach that eliminates the possibility of a single GOF criterion, and a conservative parameter range 0. Additionally, we note that heuristics proposed to assess nonidentifiability, such as the collinearity index, are available Alarid-Escudero et al. (2018).
The use of Gaussian process regression allows for unrestricted interrogation of a metamodel that can output approximate values quicker than an original model can output precise ones. Each training set of instances can uniquely specify a regressor for use in prediction. Gaussian processes can both predict model outputs and quantify the uncertainty in those predictions. We demonstrate how well our regressors perform on both training and test sets. The advantage to having a metamodel estimate model outputs for multiobjective searches is invaluable. However, by delineating the boundaries of the parameter space, we are unable to apply an unconstrained search algorithm like the Nelder-Mead simplex method Nelder and Mead (1965); Lagarias et al. (1998). While the regressors’ outputs are expectations taken over the space of all possible functions, a future algorithm could sample additional parameter combinations in regions of the parameter space where the GPR models may contain higher amounts of prediction uncertainty. This information may provide additional confidence to model predictions.
Overall, we present an effective multiobjective calibration procedure for disease microsimulation models through development of GPR-based metamodels and integration of GOF criteria into the Pareto optimization framework. Future work will focus on modifying the algorithm presented here to enhance the calibration process. Different multiobjective optimization algorithms, coupled with different metamodeling approaches, may reveal insights not uncovered with the methodologies presented here. Bayesian calibration and active learning, which have been cited as viable approaches to calibrating cancer simulation models, can contribute to calibrating cancer simulation models by updating its knowledge of the parameter space as more parameter combinations are selected Cevik et al. (2016); Whyte et al. (2011). In the future, we will also test how well the calibration performs against age-stratified outcomes. If this is unsuccessful, we will identify age groups where the simulation error cannot be ignored for each outcome. Based on these age group and outcome pairs, we will adapt a holistic viewpoint to examine the effects of perturbing certain parameter values and improve the calibration performance in the multiobjective context.
Reference
- Alarid-Escudero F, MacLehose RF, Peralta Y, Kuntz KM, Enns EA. Nonidentifiability in model calibration and implications for medical decision making. Med Decis Making 2018. October;38(7):810–21. doi: 10.1177/0272989X18792283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner H, Altenhofen L, Stock C, Hoffmeister M. Natural history of colorectal adenomas: birth cohort analysis among 3.6 million participants of screening colonoscopy. Cancer Epidemiol Biomarkers Prev. 2013. June;22(6):1043–51. doi: 10.1158/1055-9965.EPI-13-0162. [DOI] [PubMed] [Google Scholar]
- Briggs AH, Weinstein MC, Fenwick EA, Karnon J, Sculpher MJ, Paltiel AD; ISPOR-SMDM Modeling Good Research Practices Task Force. Model parameter estimation and uncertainty: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force--6. Value Health. 2012. Sep-Oct;15(6): 835–42. doi: 10.1016/j.jval.2012.04.014. [DOI] [PubMed] [Google Scholar]
- Caro JJ, Briggs AH, Siebert U, Kuntz KM; ISPOR-SMDM Modeling Good Research Practices Task Force. Modeling good research practices--overview: a report of the ISPOR-SMDM modeling good research practices task force--1. Value Health. 2012. Sep-Oct;15(6):796–803. doi: 10.1016/jjval.2012.06.012. [DOI] [PubMed] [Google Scholar]
- Cevik M, Ergun MA, Stout NK, Trentham-Dietz A, Craven M, Alagoz O. Using active learning for speeding up calibration in simulation models. Med Decis Making. 2016. July;36(5):581–93. doi: 10.1177/0272989X15611359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clifton L, Clifton DA, Pimentel MA, Watkinson PJ, Tarassenko L. Gaussian process regression in vital-sign early warning systems. Conf Proc IEEE Eng in Med Biol Soc. 2012;2012:6161–4. doi: 10.1109/EMBC.2012.6347400. [DOI] [PubMed] [Google Scholar]
- Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation. 2002;6(2):182–7. doi: 10.1109/4235.996017. [DOI] [Google Scholar]
- Enns EA, Cipriano LE, Simons CT, Kong CY. Identifying best-fitting inputs in health-economic model calibration: a Pareto frontier approach. Med Decis Making. 2015. February;35(2):170–82. doi: 10.1177/0272989X14528382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erenay FS, Alagoz O, Banerjee R, Cima RR. Estimating the unknown parameters of the natural history of metachronous colorectal cancer using discrete-event simulation. Med Decis Making. 2011. Jul-Aug;31(4): 611–24. doi: 10.1177/0272989X10391809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferlay J, Soerjomataram I, Dikshit R, Eser S, Mathers C, Rebelo M, Parkin DM, Forman D, Bray F. Cancer incidence and mortality worldwide: sources, methods and major patterns in GLOBOCAN 2012. Int J Cancer. 2015. March 1;136(5):E359–86. doi: 10.1002/ijc.29210. [DOI] [PubMed] [Google Scholar]
- Heitman SJ, Ronksley PE, Hilsden RJ, Manns BJ, Rostom A, Hemmelgarn BR Prevalence of adenomas and colorectal cancer in average risk individuals: a systematic review and meta-analysis. Clin Gastroenterol Hepatol. 2009. December;7(12):1272–8. doi: 10.1016/j.cgh.2009.05.032. [DOI] [PubMed] [Google Scholar]
- Kong CY, McMahon PM, Gazelle GS. Calibration of disease simulation model using an engineering approach. Value Health. 2009. June;12(4):521–9. doi: 10.1111/j.1524-4733.2008.00484.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIOPT. 1998;9(1):112–47. doi: 10.1137/S1052623496303470. [DOI] [Google Scholar]
- Lee SI, Mortazav B, Hoffman HA, Lu DS, Li C, Paak BH, Garst JH, Razaghy M, Espinal M, Park E, Lu DC, Sarrafzadeh M. A prediction model for functional outcomes in spinal cord disorder patients using Gaussian process regression. J-BHI. 2016;20(1):91–9. doi: 10.1109/JBHI.2014.2372777. [DOI] [PubMed] [Google Scholar]
- Leslie A, Carey FA, Pratt NR, Steele RJ. The colorectal adenoma-carcinoma sequence. Br J Surg. 2002. November;89(7):845–60. doi: 10.1046/j.1365-2168.2002.02120.x. [DOI] [PubMed] [Google Scholar]
- McKay MD, Beckman RJ, Conover WJ. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics. 1979;21(2):239. doi: 10.2307/1268522. [DOI] [Google Scholar]
- Meyfroidt G, Guiza F, Cottem D, De Becker W, Van Loon K, Aerts JM, Berckmans D, Ramon J, Bruynooghe M, Van den Berghe G. Computerized prediction of intensive care unit discharge after cardiac surgery: development and validation of a Gaussian processes model. BMC Med Inform Decis Mak. 2011. October;11:64. doi: 10.1186/1472-6947-11-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. TCJ. 1965;7(4):308–13. doi: 10.1093/comjnl/7.4.308. [DOI] [Google Scholar]
- Prakash MK, Lang B, Heinrich H, Valli PV, Bauerfeind P, Sonnenberg A, Beerenwinkel N, Misselwitz B. CMOST: an open-source framework for the microsimulation of colorectal cancer screening strategies. BMC Med Inform Decis Mak. 2017. June;17(1):80. doi: 10.1186/s12911-017-0458-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen CE, Williams CKI. Gaussian Processes for Machine Learning Adaptive Computation and Machine Learning Series. Cambridge, MA: The MIT Press; 2006. doi: 10.1142/S0129065704001899. [DOI] [Google Scholar]
- Rojnik K, Naveršnik K. Gaussian process metamodeling in Bayesian value of information analysis: a case of the complex health economic model for breast cancer screening. Value Health. 2008. Mar-Apr;11(2): 240–50. doi: 10.1111/j.1524-4733.2007.00244.x. [DOI] [PubMed] [Google Scholar]
- Snoek J, Larochelle H, Adams RP. Practical Bayesian optimization of machine learning algorithms. Adv Neural Inf Process Syst. 2012;25:2960–8. [Google Scholar]
- Stevenson MD, Oakley J, Chilcott JB. Gaussian process modeling in conjunction with individual patient simulation modeling: a case study describing the calculation of cost-effectiveness ratios for the treatment of established osteoporosis. Med Decis Mak. 2004. Jan-Feb;24(1):89–100. doi: 10.1177/0272989X03261561. [DOI] [PubMed] [Google Scholar]
- Stout NK, Knudsen AB, Kong CY, McMahon PM, Gazelle GS. Calibration methods used in cancer simulation models and suggested reporting guidelines. Pharmacoeconomics. 2009;27(7):533–45. doi: 10.2165/11314830-000000000-00000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strong M, Oakley JE, Brennan A. Estimating multiparameter partial expected value of perfect information from a probabilistic sensitivity analysis sample: a nonparametric regression approach. Med Decis Mak. 2014. April;34(3):311–26. doi: 10.1177/0272989X13505910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Steen A, van Rosmalen J, Kroep S, van Hees F, Steyerberg EW, de Koning HJ, van Ballegooijen M, Lansdorp-Vogelaar I. Calibrating parameters for microsimulation disease models: a review and comparison of different goodness-of-fit criteria. Med Decis Mak. 2016. July;36(5):652–65. doi: 10.1177/0272989X16636851. [DOI] [PubMed] [Google Scholar]
- Vanni T, Karnon J, Madan J, White RG, Edmunds WJ, Foss AM, Legood R. Calibrating models in economic evaluation: a seven-step approach. Pharmacoeconomics. 2011. January;29(1):35–49. doi: 10.2165/11584600-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Whyte S, Walsh C, Chilcott J. Bayesian calibration of a natural history model with application to a population model for colorectal cancer. Med Decis Mak. 2011. Jul-Aug;31(4):625–41. doi: 10.1177/0272989X10384738. [DOI] [PubMed] [Google Scholar]
- Yen G, He Z. Performance metrics ensemble for multiobjective evolutionary algorithms. IEEE T EVOLUT COMPUT 2013;18(1):131–44. doi: 10.1109/TEVC.2013.2240687. [DOI] [Google Scholar]