Quantifying Interpersonal Dynamics for Studying Socio-Emotional Processes and Adverse Health Behaviors

Abstract

Objective:

We introduce a new statistical software R package, rties, that simplifies the use of dynamic models for investigating interpersonal emotional processes. We demonstrate the package by using it to test whether emotional dynamics in romantic couples can predict, or are predicted by, shared unhealthy behaviors.

Methods:

We use data from 74 romantic couples discussing their health behaviors. The conversations were video-taped and rated for evidence that the couples engaged in unhealthy behaviors that benefitted the relationship in some way (e.g., increasing closeness). Participants also provided video-prompted continuous recall of their emotional experience during the conversation. We use the rties package to estimate the parameters for Inertia-Coordination and Coupled-Oscillator models of the couples’ emotional experience. Those parameter estimates are then used as predictors and outcomes of the couple’s shared unhealthy behavior.

Results:

The Coupled-Oscillator model accounted for 17% of the variance in unhealthy behavior, with both partner’s amplification predicting higher unhealthy behavior (Women: B = 0.95, S.E. = 0.31, t(63) = 3.06, p. = .003, 95% C.I.: 0.25 – 1.45; Men: B = 0.9, S.E. = 0.29, t(63) = 3.09, p. = .003, 95% C.I.: 0.32 – 1.47). These results suggest that co-dysregulation, an unstable interpersonal pattern of amplified emotional oscillations is associated with more shared unhealthy behaviors. In contrast, the dynamics assessed with Inertia-Coordination were not associated with behavior.

Conclusions:

The new rties package provides a set of relatively easy to use statistical models for representing and testing theories about interpersonal emotional dynamics. Our results suggest that emotional co-dysregulation may be a particularly detrimental pattern for health.

It is well established that the quantity and quality of people’s social relationships are associated with health (1,2). It is also becoming increasingly apparent that emotional processes may partially explain these associations (3). Suboptimal emotional functioning can impact health through physiological pathways, such as contributing to autonomic imbalance (4), and through behavioral pathways, such as motivating a person to eat unhealthy food (5). Conversely, the health status of family members can have a major impact on the socio-emotional functioning of the individuals involved (6,7). Thus interpersonal emotional processes may be both a contributor to health and an outcome of it. Importantly, most emotional skills can be learned (8), which makes them a tractable target for public health promotion and intervention. The situation is complicated, however, by the fact that emotional processes are not bounded by the individual, but extend outwards through close relationships and social networks. Emotional processes are also not static, but play out over time, both within- and between- people (9). The result is that to understand socio-emotional processes and health, we are faced with trying to understand temporal interpersonal emotion systems (TIES; 7–9).

Understanding TIES from a scientific perspective requires being able to represent them in mathematical form. More specifically, we need mathematical models that represent both within- and between-person temporal processes. For example, partner’s emotions can be tightly connected or disconnected, they can rise and fall together, and they can be stable or chaotic. A number of potentially important interpersonal emotional patterns have been identified and appropriate methods have been developed to investigate them (12). It is currently unclear, however, whether these patterns are good, bad or irrelevant for health due to a lack of cumulative empirical work. One reason for this lack of scientific momentum may be the relatively high level of statistical expertise required. To address this challenge, we introduce a new R package (rties, available at GitHub, https://github.com/ebmtnprof/rties (13)) that simplifies testing whether a set of interpersonal emotional patterns either predict, or are predicted by, health indicators (or any other variable of interest).

Models of Temporal Interpersonal Emotion Systems (TIES)

A growing body of work suggests that interpersonal emotional dynamics are associated with important health variables, including (but not limited to) body weight (6), depression and anxiety (14–16), regulation of the hypothalamic pituitary adrenal axis (17–19) and immune functioning (20). There are also theoretical grounds for going beyond studying associations between individual differences and health, most centrally that the static study of individual differences does not tell us about more proximal causes. We may be able to account for a lot of variance in some health outcome with a model that includes distal factors such as personality, age, and social support, but we will not have learned anything about mechanism. Doing so requires identifying the active ingredients that explain these associations, which in turn requires investigating sequences of relevant variables as they unfold over time (21). For example, explaining why perceived social support is associated with health requires a plausible biopsychosocial chain of events that links the perception of support to some identifiable health outcome, or conversely, connects some measure of health back to quality of support (22). Such chains cannot be investigated with a cross-sectional approach.

In the present paper we focus on emotional dynamics as potential mechanisms for explaining bidirectional associations between relationship variables and health, but the models we present are agnostic with respect to the processes represented. For example, our approach would be equally appropriate for studying within-person dynamics across different biological sub-systems, such as the interplay of the sympathetic and parasympathetic branches of the autonomic system. Or on a larger scale, they could be used to study dynamics across social networks, such as changes in the content of Facebook posts over time and indicators of depressive symptoms in the friends viewing them. In short, the models we present are appropriate for any situation where two variables are assessed over time. The number of time points required depends upon the model, with the simplest needing only about 5 and the most complex requiring about 20 at a minimum. This issue and other methodological considerations are extensively documented on the rties website. In the present paper we focus on two models that have been used the most in prior work, which we refer to as the Inertia-Coordination model and a Coupled-Oscillator model.

The Inertia-Coordination model.

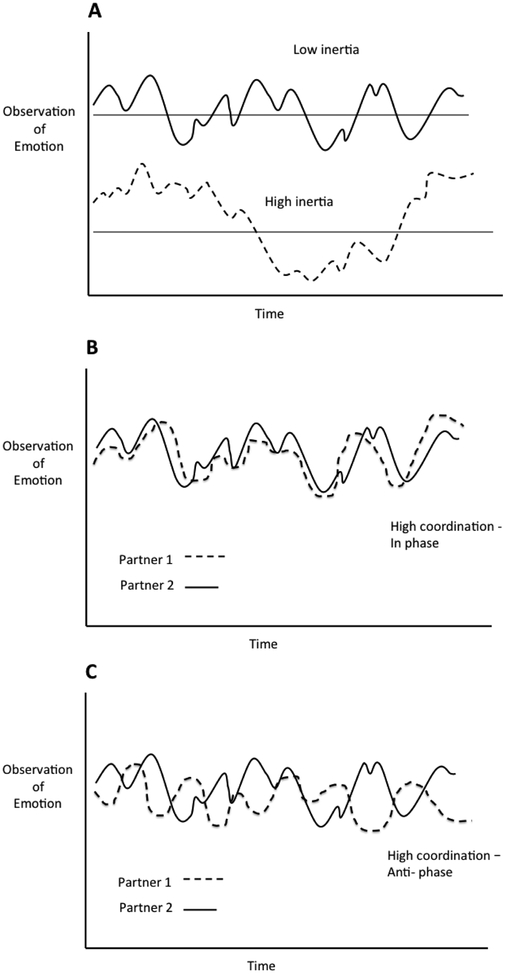
Variations of the Inertia-Coordination model have been used fairly extensively under different names, including Stability-Influence (23), vector auto-regression (24–26), and cross-lagged panel models (27). The model represents two emotional processes: 1) within-person inertia, defined as the extent to which a person’s emotional state can be predicted from his or her own state at a prior time point, and 2) between-person coordination, defined as the extent to which one partner’s emotion can be predicted from their partner’s emotion either concurrently or time-lagged (28). Figure 1 provides an illustration of inertia and coordination. Higher inertia implies slower within-person fluctuations in emotional responding. For coordination, a positive between-person parameter implies an in-phase pattern, such that when one partner is high on the measure of emotion, so is their partner, while a negative parameter implies an anti-phase pattern, such that when one partner is high the other partner is low (20,28,29).

Figure 1.

Patterns represented by the Inertia-Coordination model. Panel A shows the interpretation of low versus high positive inertia parameter estimates. Panels B and C show the interpretation of positive and negative coordination parameter estimates respectively.

Inertia has been used to represent within-person stability or regulatory processes, while coordination has been used to represent between-person influence or co-regulatory processes (23,27). The model also allows for asymmetric coordination (e.g., the parameter for one partner is larger or smaller than the parameter for the other partner), which has been taken as evidence that one person is influencing the other more than vice versa (23). A caveat is required, however. Imagine two strangers watching the same emotionally evocative film at the same time in two different cities. We should expect relatively low inertia, because their emotions would depend on the film, not processes internal to the individuals. In contrast, we should expect a strong correlation between the peoples’ emotions due to the shared stimuli, even though they have nothing to do with each other. In summary, although the Inertia-Coordination model can be useful for investigating interpersonal regulation and influence, careful interpretation is necessary.

It is also unclear whether emotional inertia or coordination are related to health. Higher inertia could represent emotional “stability” (presumably good for health) or “rigidity” (presumably bad for health). Both alternatives are reflected in the empirical literature. Although higher inertia has often been associated with internalizing symptoms (16), one study found that higher inertia predicted greater romantic relationship stability (30). Even less is known about between-partner coordination, because in-phase and anti-phase patterns have rarely been distinguished (31). In addition, emotional coordination has not typically been studied with respect to health variables, although it has been associated with relationship quality in romantic couples and therapeutic dyads (27,32–34) and in one study with heightened inflammation (20).

The Coupled-Oscillator model.

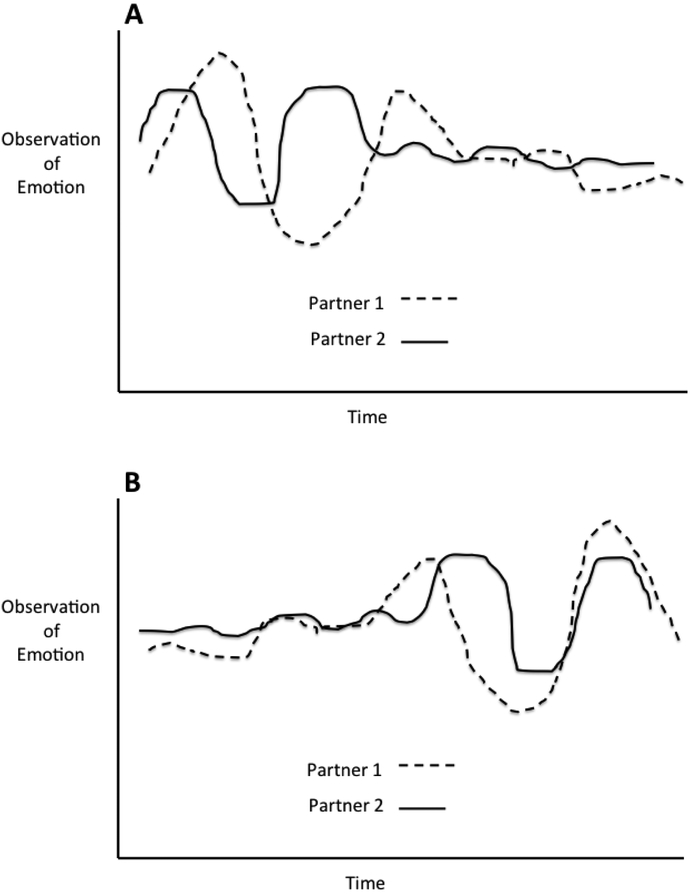
Variations of coupled-oscillator models have also been used relatively often in the literature (11,22,23,33–37). In general, they are based on differential equations and represent oscillatory phenomena. When applied to emotions, they can represent the frequency of each partner’s emotional oscillations, the damping or amplification of their oscillations (e.g., whether the oscillations are diminishing and becoming more stable, or growing larger and less stable), and the coupling between partners (e.g., mutual influence). The ability to represent damping versus amplification is particularly important because it is central to defining co-regulation, whereby partner’s mutual influence has a homeostatic effect, resulting in both partners returning to a stable set-point following some disruption to the system, versus co-dysregulation, whereby partner’s mutual influence results in increasingly volatile fluctuations away from a set-point (6,10). These patterns are shown in Figure 2.

Figure 2.

Patterns represented by the Coupled-Oscillator model. Panel A shows mutual partner damping, which suggests co-regulation. Panel B shows mutual partner amplification, which suggests co-dysregulation.

As with the Inertia-Coordination model, coupled-oscillator models have not generally been investigated with respect to health. The closest studies we are aware of showed that: 1) emotion-focused social coping predicted quicker damping of negative emotion following bereavement (41), and 2) couples with an overweight female partner, but healthy weight male, showed co-dysregulation, while those with an overweight male partner, but healthy weight female, showed co-regulation (6). Other work has shown that attachment style likely moderates these dynamics, but the results tend to be complex and sometimes contradictory (37,39). As with the Inertia-Coordination model, we hope that providing the tools to use one version of a coupled-oscillator model with relative ease will contribute to more cumulative knowledge about social dynamics and health.

The Present Study: Interpersonal Dynamics and Unhealthy Behaviors

We demonstrate the use of rties by testing hypotheses about interpersonal emotional dynamics as both predictors and outcomes of shared unhealthy behavior in romantic relationships. Our goal is to demonstrate the approach, rather than to delve into the details. We refer the reader to the rties website where we provide extensive guidance in the form of vignettes, including the sequence of analytic steps, interpretation of output, and discussion of important methodological decisions, such as required sample sizes for the models. In addition, because rties is a live package that will grow and change over time, we also provide a separate archival package, qid (for Quantifying Interpersonal Dynamics) that holds the data and documentation for the present analyses, along with the version of rties that we used to produce the present results (available at https://github.com/ebmtnprof/qid).

For the present study, we investigated whether interpersonal emotional dynamics can predict, or be predicted by, a pattern of behavior that has been called symptom-system fit (SSF) (42,43). SSF is defined as a problematic or unhealthy behavior being perpetuated in the context of a close relationship because it contributes to positive relationship quality, at least in the short run. For example, smoking (the “symptom”) together as a couple has been shown to “fit” within the “system” of the romantic relationship by increasing positive emotion and interpersonal emotional synchrony (42,43). In keeping with prior research (42–44), we operationalize SSF by assessing unhealthy behaviors that may act as “symptoms,” specifically behaviors that romantic couples either engage in together, or one person encourages the other person to do, because of associated relational benefits (e.g., increased closeness). We refer to these as shared unhealthy behaviors (SUB).

From a family-systems perspective, SUB implies weak interpersonal boundaries, where one partner is easily pulled into the other’s unhealthy behavior. SUB is also an avoidant form of emotion regulation, whereby emotions are altered with behaviors such as eating sugary food or distracting oneself with sedentary activities, rather than engaging directly with the emotional content. Prior research suggests that such avoidant tactics tend to be ineffective in the long run and can exacerbate the problem (45–47). Taken together, we theorized that these characteristics of SUB would result in it being both a predictor and an outcome of: 1) tighter intermingling of partners’ emotions (e.g., higher coordination as assessed by the Inertia-Coordination model), and 2) volatile, unstable interpersonal emotional oscillations (e.g., evidence of co-dysregulation as assessed by the Coupled-Oscillator model).

Methods

Sample and Procedures

The data come from a larger study of health behavior and weight change across 6 months in heterosexual romantic couples during the first year of cohabiting. Data collection took place between May, 2012 and August, 2014. The complete study included a baseline questionnaire, eating/activity interviews at baseline and 6 months, a laboratory session, a daily diary portion and a follow-up questionnaire at 6 months. All procedures were approved by the University of Arizona Institutional Review Board. A total of 192 people (92 dyads and 8 individuals) provided their consent to participate and completed some portion of the study. The data for the present analyses come from the laboratory session and includes the 74 couples who had usable data from both partners on all relevant measures.

During the laboratory session couples discussed a series of topics while being videotaped. The topics included the importance of a healthy lifestyle, things the partners do that help or hinder each other to be healthy, things they would like the other person to change, and something for which they would like more support from their partner. They were given 5 minutes to discuss each topic, but could move on if they finished with a topic sooner. Conversations ranged in length from 7.2 minutes to 22.6 minutes (M = 16.5 minutes, SD = 4.3 minutes). Following the conversations, the partners separately watched the videotape of their conversation and used a rating-dial to indicate how they remembered feeling (ranging from positive = 5 to negative = 0) on a moment-by-moment basis during the conversation. These continuous self-reports of emotional experience were aggregated into 2-second units and provide the variables for assessing system dynamics in the present analyses (M = 3.0, SD = 1.1, Range = .02 – 4.8)

The variable to be used as either the predictor or outcome of the emotional-experience dynamics is an observational measure of partner’s shared unhealthy behaviors (SUB). Two trained research assistants, blind to the purpose of the study, rated the videotapes in 20 second increments for evidence of unhealthy behaviors that both partners shared, or one partner encouraged or facilitated the other person to do, due to the behavior providing some relational benefit (inter-rater reliability = .96). In other words, SUB was coded as present if one or both partners discussed an unhealthy behavior and the discussion was about facilitating, encouraging, or the relational benefit of that behavior. The participants spontaneously discussed many different adverse health behaviors, including (but not limited to) poor diet, inadequate sleep, excessive alcohol use, lack of physical activity, and smoking. Since conversations varied in length, the measure used for analyses is the percentage of the total conversation time during which evidence of SUB was rated as being present (M = 3%, SD = 1.9%, Range = 0 to 7.8%). This variable was fairly normally distributed (skew = 0.56, kurtosis = −0.09), making it an appropriate outcome variable for Gaussian linear models.

Overview of Modeling

Studying interpersonal emotional dynamics requires repeated measures over time of some aspect of emotion from both partners in relationships. We focus on two person relationships (dyads), and so far rties only supports analyses of distinguishable dyads (see (48)), but the methods presented could be extended to non-distinguishable partners or larger groups. Such data violate the assumptions of the General Linear Model because the observations, and hence the residuals, are unlikely to be independent (49). Rather, repeated observations are likely to be correlated with each other from one time to the next (autocorrelation) and observations from relationship partners are also likely to be correlated. The most common way to approach this interdependence is to use multilevel modeling (a.k.a. random coefficient or hierarchical linear modeling), which models the interdependence as part of the error structure. In other words, the interdependence is put in the background and treated largely as a nuisance. Theories about how socio-emotional processes impact health, however, recognize that over-time and between-person dependencies should be the focus of our inquiry. Thus we take a different approach and put the dependencies explicitly in the foreground, using them as either predictors or outcomes of other variables of interest.

The first step in our method is to choose an observed variable that is assumed to be a valid indicator of emotion, assessed repeatedly over time for both partners in a sample of dyads. The number of observations required, both in terms of number of time points and number of dyads, depends upon the model. Guidelines for sample size at both levels are provided in the rties documentation. The temporal unit of observation (e.g., seconds, minutes, days) depends on theory about the emotional process of interest, As described above, in the present analyses we focus on emotional experience assessed in 2-second increments from romantic partners during conversations about their health behaviors. In the language of dynamic systems, the pair of observed responses are indicative of the underlying (latent) states of the system across time. In rties we refer to the two time-series of observed emotional responses as the “state” variables, and seek to represent their dynamics with a mathematical model.

The second step is to choose a mathematical model that represents theoretically relevant aspects of the system that characterizes the observed state variables. For example, imagine a very simple model that has only intercepts and linear slopes for each partner’s emotional experience (e.g., we theorize that the system can be characterized by two independent lines, which is clearly over-simplified and not “interpersonal” at all, but useful for understanding our general approach). We then estimate the parameters for that model separately for each dyad. So, in this example each dyad would have two intercept and two slope parameter estimates, one for each partner.

In the final step we use the parameter estimates for each dyad as either predictors or outcomes of some variable of interest. We refer to these predictor/outcome variables as “system” variables because they are theoretically related to the system being studied, but change slower than the state variables used to assess the dynamics. The system variable can be assessed at either the dyad level (e.g., both partners have the same score, as for relationship length) or at the individual level (e.g., partners can have different scores, as for a personality measure). In the first case (dyad level), a regular regression model is appropriate for predicting the system variable, since both partner’s have the same score on the dependent variable. In the second case (an individual level system variable), we use a multilevel model to account for the potential interdependence of partner’s dependent variables. In both cases, when the dynamic parameters are the dependent variables, we use multivariate multilevel models to account for the nesting of parameters within dyads. In our example, we focus on couples’ health behaviors as described above (a dyad level variable, so the prediction models are regular regressions) and test whether the parameter estimates from the two models representing emotional dynamics can either predict, or be predicted by, those behaviors (for examples of other research groups using similar approaches see: 9–11,11–13).

Model Descriptions

The Inertia-Coordination model.

We estimate inertia and coordination using a multiple regression model, applied to one dyad at a time, with the temporal and interpersonal dependencies accounted for by the predictors. Specifically, the time-series emotional experience variable is predicted by: 1) separate intercepts for each partner (e.g., the emotional experience for the man and the woman at time zero), 2) each person’s own state variable at a prior time point, which gives two “inertia” estimates, one for each partner, and 3) the person’s partner’s state variable at the same prior time point, which gives two “coordination” estimates, again one for each partner.

One complexity in using the Inertia-Coordination model is that the results are highly dependent upon the chosen lag length. This dependence on the lag makes interpretation problematic unless one has a strong theory about the temporal processes at work. If the state variables are oscillating at all, the inertia and coordination parameter estimates will also oscillate depending on lag. Thus choosing the lag relies on a combination of theory, prior research, and how quickly you expect the phenomenon of interest to be changing (see (23), for additional discussion). To help inform this decision, the rties package makes it easy to try different lag lengths and to observe the impact on the results.

The Coupled-Oscillator model.

One challenge of using coupled-oscillator models is that they rely on derivatives. The typical approach in social science is to estimate those derivatives from the data, which has limitations but is tractable, and this is the approach we use in rties (for a discussion see (55)). We make use of a Local Linear Approximation suggested and implemented by S. Boker (35,56). The rties version of a coupled-oscillator model uses a multiple regression model to predict the second derivative of the observed state variable from: 1) a person’s own state variable, which is related to the frequency of oscillations, 2) a person’s own first derivative of the state variable, which indicates damping/amplification, 3) a person’s partner’s state variable, which indicates coupling with respect to frequency, and 4) a person’s partner’s first derivative of the state variable, which indicates coupling with respect to damping/amplification. The model includes separate estimates for both partner types (e.g., men and women), resulting in a total of 8 parameters.

Results

Participants

Participants were on average 27 years old (men’s M = 28.0, SD = 9.4; women’s M = 26.4, SD = 8.9). They had been in a romantic relationship together for an average of 2 years (SD = 1.3 years; range = 1 month to 6 years), were predominantly not married (85%), had no children (95%) and were very satisfied with their relationship (men’s M = 2.4, SD = 1.1; women’s M = 2.7, SD = 0.8, scale ranged from −3 to +3). The majority of the sample self-identified as either European American or Non-Hispanic White (77% of women; 70% of men), or Other (15% of women; 24% of men). In addition, 22% of the women and 26% of the men self-identified as Hispanic. Most participant’s body mass index was on the cut off between healthy and overweight (men’s M = 26.7, SD = 5.0; women’s M = 24.2, SD = 5.5), but they generally had a healthy percentage of body fat (men’s M = 21.2, SD = 10.1; women’s M = 29.4, SD = 9.1).

Inertia-Coordination

One analytic step that is often neglected is to consider whether a model provides a reasonable description of the data. In other words, do model predicted scores for the state variables (e.g., time-series of emotional experience) bear any resemblance to the actual observed time series data? This step is critical for ensuring valid conclusions and is built into the rties package by providing adjusted R^2 values for the model fit to each dyad’s data, along with plots of the model predicted scores overlaid on the observed scores. The Inertia-Coordination model fit the data fairly well, with a mean adjusted R^2 of .40 (Range = .02 to .74). The mean inertia estimate was .54 for women and .49 for men (combined Range = −.04 to .87), while the mean coordination estimate was .17 for women and .16 men (combined Range = −.26 to .56). Thus emotional experience was typically fairly stable and synchronized in-phase between partners, but there was substantial between-dyad variance in the estimates.

The next step in the analysis was to predict the system variable (e.g., SUB) from the parameter estimates for each dyad for three variants of the inertia-coordination model: 1) inertia only, 2) coordination only, and 3) the full model. Specifically, multiple regression models assessed whether the system variable could be predicted from just the two inertia estimates, or just the two coordination estimates, or the four estimates from the full model. Due to the outcome being a dyad-level variable (e.g., the measure of the SUB was with respect to the dyad as a whole), results for men and women are identical in this case.

Adjusted R^2 values for the three models show that none of them account for much variance in SUB, but of these the coordination-only model accounts for the most (inertia R^2 = .00, coordination R^2 = .03, inertia-coordination R^2 = .01). In addition, the coordination-only model showed a positive association between the men’s coordination and SUB (B = 0.04, S.E. = 0.02, t(71) = 2.13, p. = .037, 95% C.I.: .002 - .074). As predicted, couples in which the man’s emotional experience was more coordinated in-phase with his female partner’s emotional experience showed higher evidence of SUB. However, since the model did not account for a significant amount of variance in SUB (F(2,71) =2.31, p. = .107), this result needs to be considered with caution and represents at best a very small effect.

Finally, we turn the analysis around and ask whether SUB can predict any of the dynamic parameters. Here we compare a baseline “intercept-only” multivariate model that predicts the dynamic parameters from just their means to one in which SUB is included as a predictor of each dynamic parameter. The baseline model accounted for 49% of the variance in the parameter estimates, while the model including SUB accounted for 50%, showing clearly that the dynamics could not be predicted from SUB.

Coupled-Oscillator

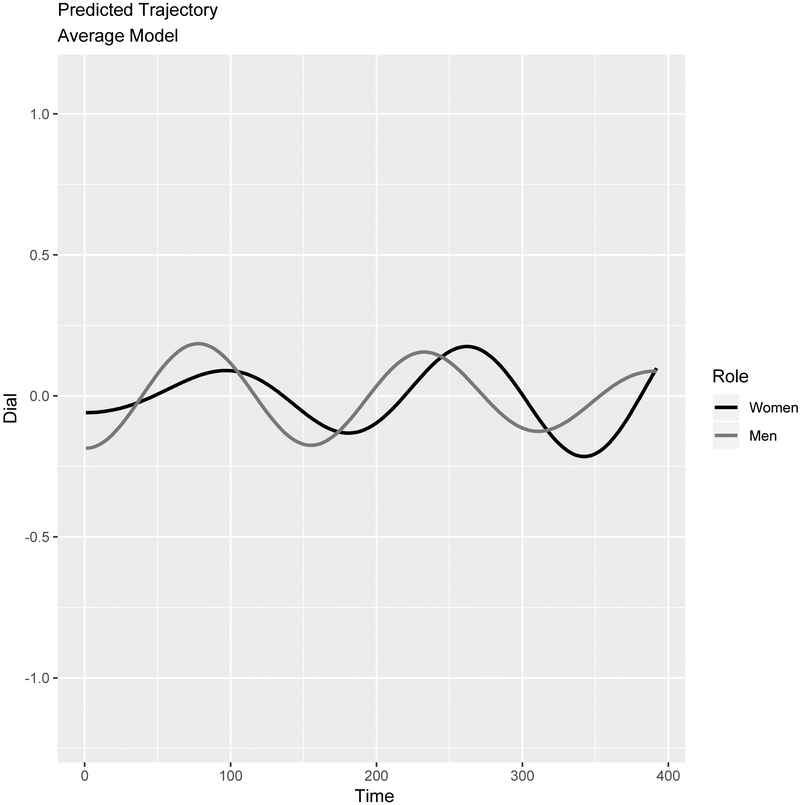
The Coupled-Oscillator model also provided a good fit to the time-series emotional experience data, with an average adjusted R^2 of .65 (Range = .46 to .91). The average oscillation period was 5.6 minutes, which means that couples completed about 2 to 3 oscillations over the course of the approximately 15 minute conversation. Unlike the Inertia-Coordination model, the parameters of the Coupled-Oscillator are not easily interpreted in isolation from each other, due to working together as a set to predict non-linear trajectories. We therefore provide the average model-predicted trajectory in Figure 3, which shows that the typical couple had low amplitude in-phase emotional oscillations over time.

Figure 3.

Model predicted trajectories of emotional experience at sample average values of the coupled-oscillator parameters.

Again we compare variants of the model for predicting SUB, with the models being uncoupled versus coupled oscillators. The adjusted R^2 showed that the full Coupled-Oscillator accounted for 17% of the variance in SUB (F(8,63) =2.79, p. = .010), which is a medium effect size, while the Uncoupled-Oscillator only accounted for 9%. The predictive power of the coupled oscillator was driven by the fact that both partners’ damping/amplification parameters predicted higher SUB (Women: B = 0.95, S.E. = 0.31, t(63) = 3.06, p. = .003, 95% C.I.: 0.25 – 1.45; Men: B = 0.9, S.E. = 0.29, t(63) = 3.09, p. = .003, 95% C.I.: 0.32 – 1.47).

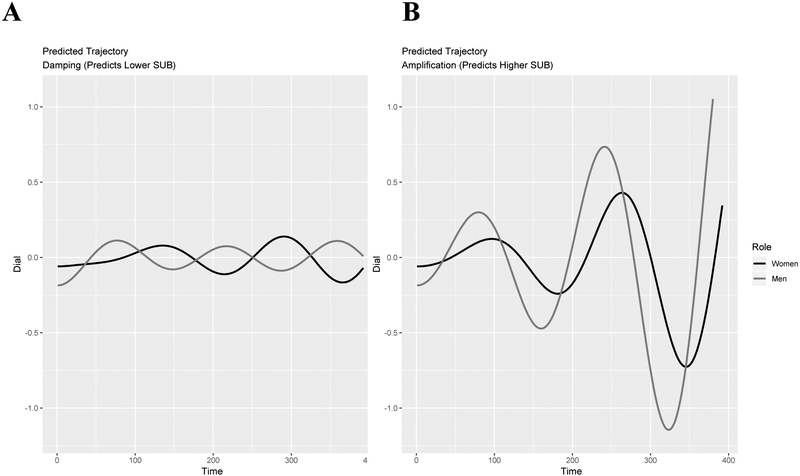
As a set, these results suggest that interpersonal amplification of emotional oscillations was associated with higher levels of SUB. Figure 4 shows model predicted trajectories of emotional experience if both partner’s had low damping/amplification parameters (Panel A; the pattern associated with low SUB), compared to if both had high damping/amplification parameters (Panel B; the pattern associated with high SUB). The former could be considered a form of co-regulation, in that the emotional oscillations are low amplitude and take a balanced anti-phase pattern, while the latter is indicative of co-dysregulation, with increasingly volatile emotional fluctuations occurring over time.

Figure 4.

Model predicted trajectories of emotional experience when all damping/amplification parameters are negative, indicative of damping (Panel A, which was the pattern associated with lower shared unhealthy behaviors) and when all damping/amplification parameters are positive, indicative of amplification (Panel B, which was the pattern associated with higher shared unhealthy behaviors).

Finally, we test whether SUB can predict any of the Coupled-Oscillator parameters. We again compare a baseline “intercept-only” multivariate model to one in which SUB is included as a predictor of each dynamic parameter. The baseline model accounted for 4% of the variance in the parameter estimates, while the model including SUB accounted for 6%, showing that the dynamics could not be predicted from SUB.

Including Covariates

Although we found no evidence of associations between the dynamics assessed with the Inertia-Coordination model and SUB, we did find that the Coupled-Oscillator parameters accounted for a notable amount of variance in SUB. It could be asked, however, whether the dynamics are accounting for unique variance, or if we could explain SUB just as well with simpler cross-sectional variables such as body mass index, length of relationship, etc. To test this we examined zero-order correlations amongst all the major variables in our data set (n = 51 variables) and found that the largest correlation between SUB and another variable was for self-reported acute stress (r = .20). We therefore re-ran the Coupled-Oscillator analysis including stress as a covariate. We found that stress was not a significant predictor of SUB in the full model, while the results for the Coupled-Oscillator parameters were virtually unchanged, suggesting that the dynamics accounted for unique variance in health behaviors.

Discussion

Our emotional reactions involve most of our being, including biology, psychology and behavior (57). Thus emotions can impact health via biological and behavioral pathways. In turn, how healthy we are colors our emotional responding. For example, systemic inflammation is closely connected to depressive mood (58,59). If we understood these bidirectional feedback loops it might offer novel targets for health intervention and prevention. Two factors that make this challenging are that health and emotion are both emergent states that evolve over time and extend beyond the individual, encompassing social networks. Thus studying them demands statistical tools capable of representing dynamic interpersonal systems. The new rties package provides such tools.

Interpersonal Emotional Dynamics and Health Behavior

The present investigation used rties to investigate bidirectional associations between emotional dynamics and couple-shared unhealthy behaviors (SUB). We hypothesized that SUB would be both a predictor and outcome of emotional dynamics indicative of: 1) blurred interpersonal boundaries, represented by higher between-partner in-phase coordination as assessed by the Inertia-Coordination model, and 2) co-dysregulation, represented by strongly coupled unstable emotional oscillations as assessed by the Coupled-Oscillator model. We found minimal support for our first hypothesis. SUB did not predict the Inertia-Coordination parameters and although higher men’s emotional coordination was “significantly” associated with higher SUB as predicted, the effect size was very small. We hasten to point out, however, that the procedures implemented in rties made it impossible for us to ignore this fact. By focusing on effect sizes and model comparison, the user cannot help but notice when effects are too small to be relevant to applied goals, although they may still contribute to theory.

In contrast, we found stronger support for our second hypothesis. Although SUB did not predict the Coupled-Oscillator parameters, we did find evidence that emotional dynamics predicted SUB. Specifically, couples with dynamics consistent with co-regulation (e.g., between-partner coupling of low amplitude, stable emotional oscillations) showed less evidence of SUB, while couples showing a pattern consistent with co-dysregulation (e.g., between-partner coupling of increasing amplitude, unstable emotional oscillations) showed more evidence of SUB. Furthermore, this was a medium sized effect, which is notable given the lack of shared method variance (e.g., the dynamic parameters came from modeling continuous self-reports of emotional experience from both partners, while health behaviors were rated by observers). In addition, the results were undiminished when we included stress as a covariate, which had the highest first-order correlation with SUB out of all the variables in our data.

The present results also fit with our prior work, where we found emotional co-regulation in romantic couples discussing their health behaviors when the male partner was an unhealthy weight, but co-dysregulation when the female partner was an unhealthy weight (6). We had predicted these findings on the basis that mixed-weight status in romantic relationships (e.g., one partner is a healthy weight and the other is overweight) appears to be more problematic when it is the female partner who is heavier (46,60–62). Although in the present study SUB did not predict the dynamics, taken together with our prior work the results suggest a potentially circular system in which indicators of health status, such as body weight, contribute to interpersonal emotional dynamics, which in turn potentiate behaviors that feedback into health status.

Modeling Interpersonal Emotional Dynamics

At a general level of abstraction, questions about interpersonal dynamics and health involve questions about coordination, defined as the way processes change together over time (63). The Inertia-Coordination and Coupled-Oscillator models are both useful for representing key components of coordination including between-partner coupling, phase patterns (e.g., symmetric or asymmetric changes) and stability versus instability over time. The Coupled-Oscillator model is appropriate for assessing these processes when the variables of interest actually oscillate, meaning that they swing back and forth around a central tendency with some degree of systematic repetition. In contrast, the Inertia-Coordination model is appropriate when the variables are changing together, but do not show systematic oscillations. Both models make it possible to address endless new questions, such as how, when and with what health consequences different coordination patterns emerge in close relationships? What factors determine whether one partner is asymmetrically driving the dynamics? What patterns of coordination are common and what are their associations with health? Are interpersonal coordination at the physiological, behavioral and experiential level related to health in similar or different ways? By removing some of the methodological challenges, rties will allow researchers to be limited primarily by their imagination when it comes to investigating interpersonal dynamics and health.

Another question that we hope rties will contribute to answering is whether there is added value in investigating complex interpersonal dynamics in connection to health. In short, even if rties does make it easier, is it worth the trouble to assess interpersonal dynamics, or do simpler methods suffice for understanding health outcomes? Theoretical arguments suggest that the added complexity of studying dynamics will be offset by the advantage of getting closer to mechanisms. Nevertheless, most researchers studying health have not been able to address the question because they are limited by methodology. We hope rties will reduce this barrier.

Limitations and Future Directions

The essence of the rties approach is to estimate parameters representing interpersonal system dynamics one dyad at a time and then use those within-dyad parameter estimates as predictors and outcomes of other between-dyad variables of interest. One strength is that this makes use of both ideographic (e.g., dyad specific) and nomothetic (e.g. generalizing across dyads) information. It also lends itself to simple interpretation despite the fact that the dynamics represented can be very complex. One potential limitation of the current implementation of rties, however, involves the second step of the analysis. When the dynamics are the predictors, the General Linear Model (e.g., variations of multiple regression) appears to work well. In contrast, when the dynamics are the outcomes it is less clear. Currently rties uses multivariate models to predict the parameters as a set, but such a model does not take into account how the parameters might work together to generate actual dynamic patterns. We believe this may explain our null findings with respect to SUB as a predictor of dynamics. In future work we will consider alternate approaches for this portion of the analysis.

Having a sensitive model for predicting dynamics from other variables of interest will be especially important for advancing experimental work. The present study was limited by assessing both emotional dynamics and SUB during the same 10 to 15 minute time window. Future work using experimental and longitudinal designs will be critical for unpacking the direction of effects linking emotional dynamics and health. The current version of rties provides initial tools for this purpose, but it is a high priority to test and refine models for the situation where the dynamics are the outcomes.

We have many additional plans to extend rties, including more models for representing other aspects of interpersonal dynamics, cross-validation for model selection, and a pseudo-couples comparison (randomly pairing data from individuals) for a better test of when interpersonal dependencies are meaningful. Despite these limitations, the version that exists provides a relatively easy to use, yet powerful tool, for quantifying interpersonal emotional dynamics and studying connections between social relationships and health.

Abbreviations:

SUB

Shared unhealthy behavior

TIES

Temporal interpersonal emotion systems

SSF

Symptom-System Fit