Abstract
Potentially suspicious breast neoplasms could be masked by high tissue density, thus increasing the probability of a false-negative diagnosis. Furthermore, differentiating breast tissue type enables patient pre-screening stratification and risk assessment. In this study, we propose and evaluate advanced machine learning methodologies aiming at an objective and reliable method for breast density scoring from routine mammographic images. The proposed image analysis pipeline incorporates texture [Gabor filters and local binary pattern (LBP)] and gradient-based features [histogram of oriented gradients (HOG) as well as speeded-up robust features (SURF)]. Additionally, transfer learning approaches with ImageNet trained weights were also used for comparison, as well as a convolutional neural network (CNN). The proposed CNN model was fully trained on two open mammography datasets and was found to be the optimal performing methodology (AUC up to 87.3%). Thus, the findings of this study indicate that automated density scoring in mammograms can aid clinical diagnosis by introducing artificial intelligence-powered decision-support systems and contribute to the ‘democratization’ of healthcare by overcoming limitations, such as the geographic location of patients or the lack of expert radiologists.
Keywords: machine learning, deep learning, transfer learning, convolutional neural network, breast density scoring
Introduction
In a variety of recent publications, a strong independent predictor of breast cancer is reported to be mammographic density (1–3). From the middle of the 1990s it was found that women with a mammographic breast density (MBD) >75% had an almost 5-fold increased risk of presenting with breast cancer (4). To this end, an objective computer system for MBD classification is of paramount importance for cancer screening and monitoring. Such computer systems are usually evaluated against the actual breast density scoring from expert radiologists using the BI-RADS reporting system of the American College of Radiology (ACR) (5). As of 2013, the BI-RADS descriptors classify breast density content as ‘entirely fat’, ‘scattered areas of fibroglandular density’, ‘heterogeneously dense’ and ‘extremely dense’.
This classification problem is usually handled by machine and deep learning techniques. Published studies concerning feature-based methods have incorporated several approaches. In particular, Bovis (6) proposed image analysis with spatial gray level dependence (SGLD) matrices as a texture feature extractor, dimensionality reduction with principal component analysis (PCA) and two-/four-class density scoring using artificial neural networks (ANN). Tzikopoulos et al (7) examined statistical and differential feature extraction methods for MBD classification by decision trees. Oliver et al (8) utilized the fuzzy C-means algorithm paired with both k-NN and ID3 decision trees for scoring mammographic data.
On the other hand, a deep learning framework was previously applied by Fonseca et al (9) with a three-layer CNN for feature extraction and a Support Vector Machine (SVM) for a four-class classification according to the American College of Radiology (ACR) density characterization. Petersen et al (10) investigated both learnable segmentation and patch-based CNN classification based on scoring of percentage mammographic density (PMD). Kallenberg et al (11) proposed a merged unsupervised segmentation and feature extraction process with an external classifier for PMD scoring. The performance metrics of the relevant literature is summarized in Table I.
Table I.
Breast density scoring.
| Methodology or study, authors (Refs.) | mini-MIAS (2-class) ACC/AUC (%) | mini-MIAS (3-class) ACC (%) | DDSM (2-class) ACC/AUC (%) | DDSM (3-class) ACC (%) | DDSM (4-class) ACC (%) | No. of images |
|---|---|---|---|---|---|---|
| Machine learning | ||||||
| HOG | 71.8/52.3 | 53.1 | – | – | – | Full |
| LBP | 83.3/78.0 | 74.2 | 67.1/71.4 | 55.1 | 36.6 | Full |
| SURF | 82.6/77.6 | 68.3 | 79.3/84.2 | 67.5 | 46.8 | Full |
| Gabor + LBP | 76.7/68.4 | 61.7 | 62.8/67.1 | 52.1 | 35.8 | Full |
| Selected HOG | 69.0/48.7 | 53.1 | – | – | – | Full |
| Selected LBP | 77.9/71.1 | 70.2 | 73.7/79.2 | 64.5 | 40.7 | Full |
| Selected SURF | 83.8/77.6 | 73.6 | 75.6/81.5 | 62.9 | 46.8 | Full |
| Selected Gabor + LBP | 64.9/60.9 | 50.9 | 62.1/67.7 | 55.4 | 37.7 | Full |
| Bovis et al (6) | – | – | 96.6/ - | – | 71.4 | 377 |
| Tzikopoulos et al (7) | – | 70.3 | – | – | – | Full |
| Oliver et al (8) | – | – | – | – | 40.3–47 | 300 |
| Deep learning | ||||||
| Proposed architecture | 84.2/87.3 | 79.8 | 75.2/82.7 | 68.6 | 54.8 | Full |
| Inception 3 | 73.6/75.7 | 70.8 | 72.7/79.1 | 49.5 | 48.8 | Full |
| VGG19 | 68.6/67.8 | 72.4 | 72.1/79.3 | 62 | 36.8 | Full |
| InceptionResNetV2 | 69.9/63.7 | 73.1 | 72.7/79.2 | 55.6 | 37.3 | Full |
| DenseNet201 | 75.5/79.6 | 77.9 | 73.1/80.5 | 61.7 | 36.5 | Full |
| NASNetLarge | 66.5/66.3 | 72.8 | 72.3/78.7 | 61.4 | 37.8 | Full |
The table presents a 5-fold cross-validation averages for the examined methodologies. HOG, histogram of oriented gradients; LBP, local binary pattern; SURF, speeded-up robust features. Values in bold font indicate the optimal performing methodologies.
This study constitutes an extensive analysis of MBD classification using two publicly available datasets incorporating various feature extraction methods, such as histogram of oriented gradients (HOG) (12), speeded-up robust features (SURF) (13), local binary pattern (LBP) (14), Gabor filters (15) and deeper end-to-end convolutional neural networks (CNNs) fully trained or off-the-shelf models trained on the ImageNet dataset (16).
The main aim of this study was to present and discuss the results of modern machine learning techniques combining the aforementioned feature extraction methods alongside with more robust CNN schemes presented in the bibliography. In the following section, the mammographic datasets and the proposed workflow are presented.
Patients and methods
Patient cohort
The patient population used in this study is based on two publicly available datasets, the Mammographic Image Analysis Society Digital Mammogram (mini-MIAS) and the Digital Database for Screening Mammography (DDSM). Further information regarding each dataset is presented below:
Mini-MIAS
The mini-MIAS (http://peipa.essex.ac.uk/info/mias.html) is a free scientific database for research and consists of 161 patients with 322 mammograms. The database is digitized at 50-micron pixel edge. Image labels are categorized by their breast density from expert radiologists, using 3 classes: Fatty (F) (106 images), fatty-glandular (G) (104 images) and dense-glandular (D) (112 images).
DDSM
The DDSM (http://www.eng.usf.edu/cvprg/Mammography/Database.html) database consists of approximately 2,500 patients with 10,239 multi-view images including benign, malignant and normal cases. Image resolution varies from 42 to 50 microns. Breast density labels for this dataset are categorized using four classes: Fatty, glandural, dense and extremely dense.
Dataset stratification
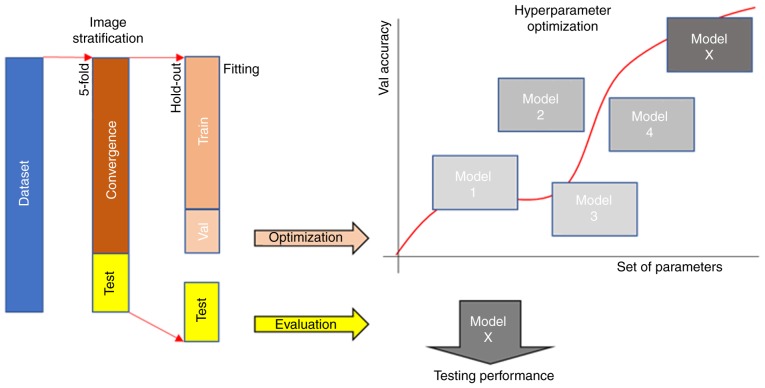
Medical imaging databases usually consist of limited patient cohorts, such as the aforementioned datasets restricting the learning capacity of deep models. Therefore, to avoid biases related to the low sample number, an exhaustive k-fold cross-validation was performed for splitting the dataset into the multiple convergence and testing set. Additionally, the corresponding convergence set was split into the training and validation set by a shuffle hold-out process as presented in Fig. 1. In particular, the performance metrics on mini-MIAS were acquired by 64 testing images and the fitting process on 258 images (208 training, 50 validation) per fold. Similarly, the same stratification procedure was applied on the whole patient cohort of the DDSM dataset but only the cranio-caudal images were used (approximately 5,000). Every examined image analysis methodology including deep and feature-based models were adapted on the same convergence set and evaluated on same unseen testing set to establish a fair assessment among the resulted models.
Figure 1.
The data stratification methodology for model fitting, hyperparameter optimization and transparent performance evaluation across every examined image analysis process.
Pre-processing
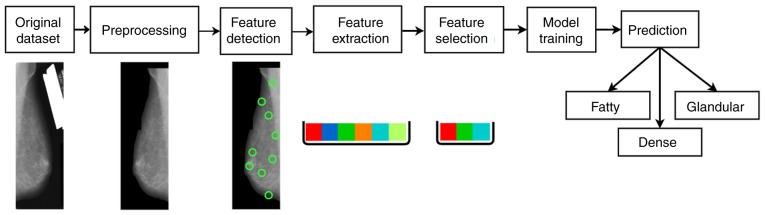
In order to ensure reliable image quality without artefacts, and limit background noise that may potentially affect the feature extraction analysis, both mini-MIAS and DDSM images were pre-processed as follows. Initially, the threshold selection method described in the study by Otsu (17) was applied as a method for background removal. Moreover, boundary detection (18) was performed for the elimination of these areas (labels with a patient's personal information, as illustrated in Fig. 2, ‘Original Dataset’). Image cropping in addition to bicubic interpolation for resizing was applied to reduce computational complexity for the MBD analysis and ensure consistent image size across the studied cohorts.
Figure 2.
Graphical representation of the machine learning workflow illustrating the three-class breast density mammogram classification case.
Machine learning workflow
Feature extraction
Distinguishing key points in imaging structures is a crucial step to capture essential abstractions, pixel intensity variations and local dependencies for differentiating between tissue classes. Mammography images usually include different structures, including muscle, breast tissue and benign/malignant lesions. To address this variability in tissue content, a number of algorithms with diverse mathematical backgrounds were employed for extracting discriminative compact representations, including gradient-based features, such as HOG, SURF and texture features, such as LBP and Gabor filters combined with LBP.
Feature selection
This step has been established in the proposed methodology for reducing the high-dimensional raw features to the most significant components resulting in an improved computational complexity and improved performance. The selection was enacted with the use of the neighborhood component analysis (NCA) (19).
Classification
Linear discriminant analysis (20) was used for the classification of the annotated feature vectors following the NCA selection process by modeling the differences among the examined classes and searching for linear combinations of the most statistical significant features. A graphical representation of the proposed machine learning methodology is provided in Fig. 2.
Deep learning-fully trained CNN methodology
Deep learning analytics introduce a fully automated analysis pipeline with data-driven learnable parameters providing a domain-specific modelling methodology. The main objective of these deep learning architectures, such as CNNs is to learn hierarchical representations of the examined domain across several layers by convolving and propagating features maps of the initial input in an end-to-end and automatic manner. This is formulated as a convex optimization where the model adapts its weights through backwards propagation. To address the clinical question of this study, several pre-trained deep learning models were evaluated for feature extraction such as inception networks, VGG19 (http://www.robots.ox.ac.uk/~vgg/research/very_deep/), DenseNet (https://ai-pool.com/m/densenet-1556378134) and NASNet (https://ai-pool.com/m/nasnet-1556378807). Additionally, a custom end-to-end 2D CNN architecture trained on the studied datasets was developed.
Data augmentation
This process represents an artificial method of increasing the training set and simultaneously promote the generalization ability of the models by offering alternative variants of the original image. The added noise of image transformations, including rotation, flipping, elastic deformation and mirroring amplifies model properties, such as translation, rotational and scale invariance.
Proposed architecture
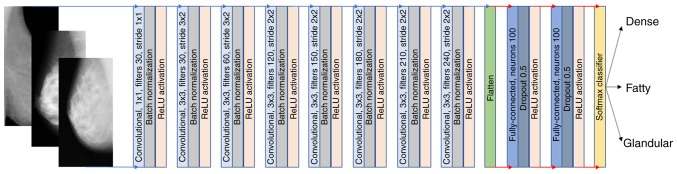
The fully trained 2D CNN architecture consists of 15 layers, including the image input of shape 725×234×1, 6 convolutional layers each followed by a batch-normalization layer, 2 fully-connected layers with 100 neurons each and finally a softmax classification layer as depicted in Fig. 3. ReLU was selected as the activation function of the convolutional layers with 30 to 240 kernels per layer and a 3×3 receptive field. Additionally, 20% chance of dropout was applied to the fully-connected neurons. Glorot methodology was utilized for weight initialization. The complete source code and the final hyperparameters of the custom 2D architecture are available online (https://github.com/trivizakis/breast-density-analysis).
Figure 3.
Overview of the proposed architecture (fully-trained CNN), including the network layout and layer parameters, such as the receptive field, number of filters, convolutional stride, activation function, number of neurons, dropout and classifier. CNN, convolutional neural network.
Hyperparameter optimization
The fitting process of a deep architecture poses a challenging task of searching the optimal parameters in order to discover the best performing model. The validation set as part of the convergence set was used to perform this task in a transparent and unbiased way on a limiting database, as depicted in Fig. 1. In particular, overlaying the training and validation loss curve reveal details about the fitting status of the model and assists in the parameter selection process. Adjusting the number of learnable parameters, such as layers, kernels and neurons can minimize the memorization of the dataset from the model therefore preventing overfitting. Additionally, early-stopping was performed after maximizing the validation accuracy to provide the best fitted models, avoiding overtraining and refraining from unnecessary time-consuming convergence cycles.
Deep learning based on pre-trained models
Models
Transfer learning is a powerful research methodology used in the data science community particularly for overcoming the limitations arising in highly-specialized but small datasets. In particular, the contribution of an ‘off-the-shelf’ model in terms of performance was evaluated by an external classifier as a feature extraction component. The selected pre-trained models compute different type of deep features since they integrate diverse architecture elements, such as residual connections, connectivity between successive layers, number of layers and number of parameters.
Deep feature extraction
The pre-trained models with ImageNet weights were employed for this purpose from the open source Keras library (21). During feature extraction, the input layer and the neural part of the trained network were discarded. This was a necessary step considering the differences in the ImageNet versus the mini-MIAS image size. Only the weights of the convolutional part were retained for extracting deep features from the last convolutional layer of each pre-trained model.
Classification
SVMs are popular classifiers widely used in a variety of image analysis problems demonstrating robust performance. Taking into account the different types of feature-based and deep features calculated by the corresponding proposed methodologies, SVM was selected for the evaluation of the classification performance among the feature extraction processes in a meaningful and direct manner. In particular, the selected kernels for the studied SVMs were the following: Radial basis function for the multiclass and linear for the binary MBD classification. Finally, input feature vectors were generated from the original 5-fold splits of the corresponding model to guarantee a fair evaluation.
Performance evaluation metrics
The studied binary classification models were evaluated mainly in terms of the area under curve (AUC) score, which is a widely used performance metric of class separability. The multi-class analyses were evaluated with the following accuracy (ACC) metric:
where TP, TN, FP, and FN stand for true-positive, true-negative, false-positive and false-negative respectively.
Results
All studied models were fitted on the same stratified hold-out convergence (training/validation) set and evaluated on identical testing folds of cross-validation to ensure a fair and transparent comparison. This resulted in 64.6% training, 15.4% validation and 20% testing mammography images from the mini-MIAS and 63.9% training, 16.1% validation and 20% testing from the DDSM database, respectively.
Different algorithms and annotation strategies were performed on the two studied datasets to identify the optimal feature space representation. Accuracies in the mini-MIAS dataset ranged from 50.9% (GABOR + LBP selected features) to 74.2% (LBP) for three-class classification, while for binary classification, the AUC scores varied from 48.7% (HOG selected features) to 78.0% (LBP). Similarly, the previously described methodology was applied on the full DDSM dataset for predicting the MBD scoring in a binary and multi-class annotation scheme. The optimal score (ACC 79.3% and AUC 84.2%) for the feature-based techniques was observed in binary (non-dense versus dense mammograms) analysis with the SURF method. The full performance metrics of the proposed machine learning analyses are presented in Table I along with results from relevant studies in the literature.
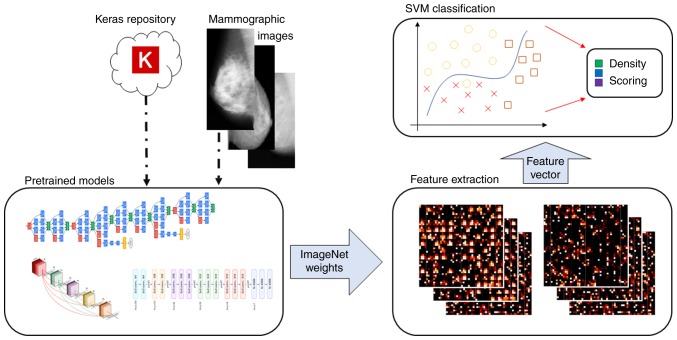
The proposed 2D CNN, as depicted in Fig. 3, is a custom architecture with hyperparameters tuned on the studied databases. Data augmentation was applied on the training set to artificially increase the total number of samples up to a factor of 10 with targeted transformations, leading to models that are less prone to overfitting, as mentioned above (please see subsection entitled ‘Data augmentation’ in the section entitled ‘Deep learning-fully trained CNN methodology’). This increased the validation accuracy by 4% on average. The convergence process was performed on an Nvidia GTX 1070 with approximately 7 sec per epoch on the mini-MIAS and 34 sec per epoch on DDSM. The pre-trained models with ImageNet weights were downloaded from the Keras library and were utilized as ‘off-the-shelf’ feature extractors with a new input and no fully connected layers. Only the convolutional kernels with weights trained on ImageNet were transferred to the new pipeline, where a feature vector was extracted from the last convolutional layer of the model and an SVM was trained on the same cross validation folds as the previous methodologies. A complete pipeline overview of this methodology is provided in Fig. 4. An empirical comparison of the average cross-validation performance metrics reveals the superiority of the data-driven custom CNN against the other methodologies employed in this study. In addition, the proposed CNN exhibit a greater efficiency than those reported in relevant studies on datasets of similar sizes as presented above in the Introduction section, apart from the methodology reported by Bovis and Singh (6), achieving up-to 96.9% accuracy, but on a selected subset of DDSM dataset consisting of 377 images as opposed to this study with >2.500 patients. The proposed architecture demonstrates the highest performance in density scoring with AUC performance of up to 87.3% for the binary classification task and up to a 79.8% accuracy for the multi-class models. A complete comparison of the metrics across every methodology and the corresponding literature is provided in Table I.
Figure 4.
The examined pipeline for feature extraction and classification using ‘off-the-shelf’ pre-trained methods.
Discussion
In the present study, modern machine and deep learning techniques for MBD classification were developed and evaluated on two open datasets. A variety of texture and gradient-based features were investigated in the context of breast density scoring classification. Additionally, end-to-end image analysis architectures including fully trained CNN and ‘off-the-shelf’ deep learning models were also employed with the goal to increase accuracy in the automated breast tissue density classification.
The examined classification clinical tasks were selected based on the current literature regarding mammography image analysis and classification. The majority of similar published works incorporate binary tissue type analysis (non-dense versus dense). This was achieved by merging the fatty and glandular into the ‘non-dense’ class for binary classification in the mini-MIAS dataset. The DDSM can also be examined as a two-class set by merging fatty-glandular and dense-extremely dense, or as a three-class problem with fatty, glandular and a unified dense-extremely dense and finally a four-class analysis based on the BI-RADS criteria for tissue characterization.
The reported results in Table I confirm that deep learning architectures outperform feature-based methods by a wide margin, exhibiting increased performance regardless of the number of classes in the classifications tasks. The integration of the NCA feature selection process in the feature-based analysis did not improve the performance in most scenarios. It is noticeable that the performance of all the examined methods is reduced in the DDSM comparing to the MIAS database providing a robust and objective benchmark for performance evaluation mainly considering the larger patient cohort. As discussed in the previous section, according to the study by Bovis and Singh (6), the authors reported the optimal performance method concerning the DDSM database, but using only a limited set of images of the DDSM database. As regards the findings of this study, the custom CNN achieved an AUC performance of up to 87.3%, the pre-trained ‘off-the-shelf’ models up to 79.6% and the best feature-based model up to 70.6%, all for the MIAS database and the binary classification case. It is worth mentioning that the transfer learning technique seems promising, particularly as regards the investigation of fine-tuning of the trained weights to better model the target domain by adapting additional neural and classification layers.
This study mainly focused on the medium-size database setting. As regards the presented deep-learning framework, other published studies using databases of similar sizes, have reported an AUC from 59 to 73% for binary MBD classification. In particular, Kallenberg et al (11) reported an AUC of 59%, while Fonseca et al (9) and Petersen et al (10) reported an ACC of 73% and AUC 68%, respectively. Driven from the results of this study, the deep learning methodology outperforms the aforementioned publications as shown in Table I.
Recently, in the literature, deep learning architectures for MBD classification have achieved greater performances than this study; however, these were with databases that are not publicly available and the sample sizes were in the order of tens of thousands of images. In particular, Lehman et al (22) claimed an accuracy of 86–94% on >40,000 examinations; however, some issues were raised regarding the density annotation by the expert radiologists. Similarly, Mohamed et al (23) reported an AUC of 92.6–98.8% from a cohort of 1,427 patients, but with >20,000 images. Ma et al (24) also reported an accuracy of 80.7–89% with 2,581 cases. It is important to note that the proposed methodology is not comparable with these studies due to the lack of performance metrics on benchmark open databases, such as the examined DDSM, the vastly different database size and the different, unknown data-curation curation strategies.
The high dimensionality of extracted features and the challenging feature selection process can be a limiting factor in feature-based methods. Selecting the optimal extraction algorithm and reduction strategy requires a domain expert in both clinical field and statistics. In particular, the extraction of HOG features could not be completed due to the high demand in computational time and memory resources for the analysis of a large dataset like DDSM. By contrast, deep architectures converge to better models with large databases, but require specialized high throughput computing (HTC) and a complex hyperparameter search to ensure a generalizable analysis. This can be partially resolved by utilizing pre-trained models with the only drawback being the potential need for fine-tuning for domain adaptation.
A dense breast could possibly mask suspicious neoplasms difficult to differentiate in routine mammographic images; thus, a computer-based decision support can add valuable, objective information in support of the clinicians' assessment. To this end, MDB classification is a challenging and important task and the results of this study call for further research in this field, as well as for the further testing of new methodologies, particularly in the smaller dataset setting.
To facilitate future research, a meta-model analysis on multiple feature extraction methods, sophisticated selection algorithms and machine learning classifiers fused by a higher-level decision component, such as logistic regression, AdaBoost, weighted average or even voting could provide richer compact representations of the mammographic data improving the inference confidence. As regards the pre-trained models, fine-tuning could introduce domain-specific analysis improvements allowing an end-to-end fully automated inference and consequently offering substantial performance gains. Finally, the integration of both cranio-caudal and medio-lateral mammographic images either in a unified model or by combining different methods, features and models derived from both views, may further enhance the prediction power of such automated breast density classification systems.
Acknowledgements
Not applicable.
Funding
GSI acknowledges the support by the Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT), under the HFRI PhD Fellowship grant (GA. no. 31430). ET was financially supported by the Stavros Niarchos Foundation within the framework of the project ARCHERS (‘Advancing Young Researchers’ Human Capital in Cutting Edge Technologies in the Preservation of Cultural Heritage and the Tackling of Societal Challenges’).
Availability of data and materials
All data generated or analyzed within this study are included in this published article.
Authors' contributions
ET, GSI, VDM and KM conceived and designed the study. GZP, AT and DAS researched the literature, performed the analysis of the data and contributed to the drafting of the manuscript. ET, GSI, VDM, GZP, AT, DAS and KM critically revised the article for important intellectual content. All authors have read and approved the final manuscript.
Ethics approval and consent to participate
All patient data were obtained from publicly available datasets. Thus, no approval was required.
Patient consent for publication
Not applicable.
Competing interests
DAS is the Editor-in-Chief for the journal, but had no personal involvement in the reviewing process, or any influence in terms of adjudicating on the final decision, for this article. All the authors declare that they have not competing interests.
References
- 1.Duffy SW, Morrish OWE, Allgood PC, Black R, Gillan MGC, Willsher P, Cooke J, Duncan KA, Michell MJ, Dobson HM, et al. Mammographic density and breast cancer risk in breast screening assessment cases and women with a family history of breast cancer. Eur J Cancer. 2018;88:48–56. doi: 10.1016/j.ejca.2017.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Titus-Ernstoff L, Tosteson AN, Kasales C, Weiss J, Goodrich M, Hatch EE, Carney PA. Breast cancer risk factors in relation to breast density (United States) Cancer Causes Control. 2006;17:1281–1290. doi: 10.1007/s10552-006-0071-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Checka CM, Chun JE, Schnabel FR, Lee J, Toth H. The relationship of mammographic density and age: Implications for breast cancer screening. AJR Am J Roentgenol. 2012;198:W292–W295. doi: 10.2214/AJR.10.6049. [DOI] [PubMed] [Google Scholar]
- 4.Byrne C, Schairer C, Wolfe J, Parekh N, Salane M, Brinton LA, Hoover R, Haile R. Mammographic features and breast cancer risk: Effects with time, age, and menopause status. J Natl Cancer Inst. 1995;87:1622–1629. doi: 10.1093/jnci/87.21.1622. [DOI] [PubMed] [Google Scholar]
- 5.D'Orsi CJ, Sickles EA, Mendelson EB, Morris EA, et al. Reston, VA: American College of Radiology; 2013. ACR BI-RADS® Atlas, Breast Imaging Reporting and Data System. [Google Scholar]
- 6.Bovis K, Singh S. Classification of mammographic breast density using a combined classifier paradigm. Proceedings of the 4th International Workshop on Digital Mammography. 2002:177–180. [Google Scholar]
- 7.Tzikopoulos S, Georgiou H, Mavroforakis M, Theodoridis S. A fully automated scheme for breast density estimation and asymmetry detection of mammograms. Eur Signal Process Conf. 2009:1869–1873. [Google Scholar]
- 8.Oliver A, Freixenet J, Zwiggelaar R. Proceedings of the IEEE International Conference on Image Processing. IEEE; 2005. Automatic classification of breast density; pp. II–1258. [Google Scholar]
- 9.Fonseca P, Mendoza J, Wainer J, Ferrer J, Pinto J, Guerrero J, Castaneda B. Proceedings of the Medical Imaging 2015. Vol. 9414. SPIE Medical Imaging; Orlando, FL: 2015. Automatic breast density classification using a convolutional neural network architecture search procedure. Computer-Aided Diagnosis. [Google Scholar]
- 10.Petersen K, Chernoff K, Nielsen M, Ng AY. Breast density scoring with multiscale denoising autoencoders. Proceedings of the MICCAI Workshop on Sparsity Techniques in Medical Imaging. 2012 [Google Scholar]
- 11.Kallenberg M, Petersen K, Nielsen M, Ng AY, Pengfei Diao, Igel C, Vachon CM, Holland K, Winkel RR, Karssemeijer N, Lillholm M. Unsupervised deep learning applied to breast density segmentation and mammographic risk scoring. IEEE Trans Med Imaging. 2016;35:1322–1331. doi: 10.1109/TMI.2016.2532122. [DOI] [PubMed] [Google Scholar]
- 12.Dalal N, Triggs B. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05) Vol. 1. IEEE; 2005. Histograms of Oriented Gradients for Human Detection; pp. 886–893. [DOI] [Google Scholar]
- 13.Bay H, Tuytelaars T, Van Gool L. Springer; Berlin, Heidelberg: 2006. SURF: Speeded Up Robust Features; pp. 404–417. [Google Scholar]
- 14.Ojala T, Pietikainen M, Harwood D. Proceedings of 12th International Conference on Pattern Recognition. Vol. 1. IEEE; 1994. Performance evaluation of texture measures with classification based on Kullback discrimination of distributions; pp. 582–585. [DOI] [Google Scholar]
- 15.Fogel I, Sagi D. Gabor filters as texture discriminator. Biol Cybern. 1989;61:103–113. doi: 10.1007/BF00204594. [DOI] [Google Scholar]
- 16.Deng J, Dong W, Socher R, Li LJ, Li K, Fei-Fei L. Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition. IEEE; 2009. ImageNet: A Large-Scale Hierarchical Image Database. [DOI] [Google Scholar]
- 17.Otsu N. A Threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern. 1979;9:62–66. doi: 10.1109/TSMC.1979.4310076. [DOI] [Google Scholar]
- 18.Ma WY, Manjunath BS. EdgeFlow: A technique for boundary detection and image segmentation. IEEE Trans Image Process. 2000;9:1375–1388. doi: 10.1109/83.855433. [DOI] [PubMed] [Google Scholar]
- 19.Yang W, Wang K, Zuo W. Fast neighborhood component analysis. Neurocomput. 2012;83:31–37. doi: 10.1016/j.neucom.2011.10.021. [DOI] [Google Scholar]
- 20.Zhao W, Chellappa R, Phillips PJ. Center for Automation Research University of Maryland; College Park, MD: 1999. Subspace Linear Discriminant Analysis for Face Recognition (Technical Report CAR-TR-914) [Google Scholar]
- 21.Chollet F. Keras. GitHub Repository. 2015 [Google Scholar]
- 22.Lehman CD, Yala A, Schuster T, Dontchos B, Bahl M, Swanson K, Barzilay R. Mammographic breast density assessment using deep learning: Clinical implementation. Radiology. 2019;290:52–58. doi: 10.1148/radiol.2018180694. [DOI] [PubMed] [Google Scholar]
- 23.Mohamed AA, Berg WA, Peng H, Luo Y, Jankowitz RC, Wu S. A deep learning method for classifying mammographic breast density categories. Med Phys. 2018;45:314–321. doi: 10.1002/mp.12683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ma X, Fisher CE, Wei J, et al. Proceedings of the Medical Imaging 2019. Vol. 10950. SPIE Medical Imaging; 2019. Multi-path deep learning model for automated mammographic density categorization; p. 86. Computer-Aided Diagnosis. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analyzed within this study are included in this published article.