Small separation frequency-domain near-infrared spectroscopy for the recovery of tissue optical properties at millimeter depths

Abstract

Millimeter-depth sensitivity with frequency domain near-infrared spectroscopy has been challenging due to the breakdown of the diffusion equation for source-detection separations < 1cm. To overcome this challenge, we employ a Monte-Carlo lookup table-based inverse algorithm to fit small separation (3-6 mm) frequency-domain near-infrared spectroscopy (FDNIRS) data for absorption and reduced scattering coefficients. We verify this small separation FDNIRS method through a series of in vitro and in vivo studies. In vitro, we observed a root mean squared percent error (RMSE) in estimation of the reduced scattering coefficient and absorption coefficient of 2.8% and 7.6%, respectively, in liquid phantoms consisting of Intralipid and Indian ink, and a RMSE in estimation of oxygen saturation and total hemoglobin concentrations of 7.8 and 11.2%, respectively, in blood-mixed liquid phantoms. Next, we demonstrate one particularly valuable in vivo application of this technique wherein we non-invasively measure the optical properties of the mouse brain (n = 4). We find that the measured resting state cerebral oxygen saturation and hemoglobin concentration are consistent with literature reported values, and we observe expected trends during a hyper-/hypoxia challenge that qualitatively mimic changes in partial pressure of oxygen (pO₂) measured simultaneously with an invasive pO₂ sensor. Further, through simulations of the mouse head geometry, we demonstrate that the skull and scalp exert minimal influence on the estimate oxygen saturation, while leading to small but systematic underestimation of total hemoglobin concentration. In total, these results demonstrate the robustness of small separation FDNIRS to assess tissue optical properties at millimeter depth resolution.

1. Introduction

Frequency domain near-infrared spectroscopy (FDNIRS) is a non-invasive optical technique used to estimate the optical properties of human tissue, namely the wavelength-dependent absorption and reduced scattering coefficients (μ _a and μ_s′, respectively). Typically, FDNIRS measurements are made in a reflection geometry at large source-detector separations (i.e., >> 3/(μ_s′ + μ _a)). In this configuration, the diffusion approximation to the radiative transfer equation can be readily applied to estimate bulk optical properties of the interrogated tissue from the measured change in amplitude attenuation and phase shift as a function of either source-detector separation or modulation frequency. However, the diffusion approximation breaks down at source-detector separations < 1 cm. Alternative analytical strategies are required for applications of FDNIRS that require millimeter depth penetration.

A handful of studies have successfully developed approaches to extract optical properties with FDNIRS at source-detector separations < 1 cm by employing multiple modulation frequencies. Chen et al. [1] used Monte Carlo simulations combined with an artificial neural network-based inverse algorithm approach to estimate optical properties with multi-frequency FDNIRS at separations < 3 mm. Willmann et al. [2,3] developed a time-integrated “modified microscopic Beer Lambert law” approach to FDNIRS that estimates μ _a from changes in amplitude attenuation and phase shift as a function of modulation frequency. Tseng et al. [4,5] developed a clever small separation FDNIRS approach wherein a diffusing layer is placed between the source/detector and the sample of interest such that a modified two-layer diffusion model can be employed to recover optical properties of the bottom layer. All of these studies require an FDNIRS device that operates at multiple modulation frequencies to extract optical properties. To our knowledge, small separation FDNIRS at a single modulation frequency has not been demonstrated to date.

In 1997, Kienle and Patterson [6] posed a theoretical approach to estimate optical properties with small source-detector separation FDNIRS using a single modulation frequency. Using a Monte Carlo-based inverse algorithm, the authors demonstrated that a unique solution for μ _a and μ_s′ can be determined when using the ratio between the AC amplitudes and the difference between the phases measured from 2 unique small source-detection separations (< 1cm). However, this approach was not experimentally validated at the time due to limitations in the phase noise of existing FDNIRS instrumentation. Today, commercially available FDNIRS devices have relatively low phase noise (< 1°) and minimal amplitude/phase crosstalk, allowing Kienle and Patterson’s small separation FDNIRS approach to be put into experimental practice. Herein we experimentally validate this small separation FDNIRS approach in vitro using liquid phantoms. Moreover, we demonstrate one particularly valuable in vivo application of this technique wherein we non-invasively measure the optical properties of the mouse brain during a gas challenge. We validate these measurements against an invasive partial pressure of oxygen sensor, and we computationally characterize the influence of skull and scalp layers for our source-detector geometry.

2. Materials and methods

2.1. Small separation FDNIRS Monte Carlo lookup table

To construct a Monte Carlo (MC) lookup table of small separation FDNIRS data, time-domain MC simulations [7,8] were performed on a total of 70 semi-infinite, homogenous tissue models of varying optical properties. The input absorption coefficient, μ _a, ranged from 0.05 to 0.45 cm^-1 with a step size of 0.05 cm^-1 and the reduced scattering coefficient, μ_s′, ranged from 2 to 14 cm^-1 with a step size of 2 cm^-1. For each simulation, 2×10⁸ photons were launched from a 1 mm source fiber with a numerical aperture (NA) of 0.39. The scattering angle was determined by the Henyey-Greenstein phase function with an anisotropy factor, g, of 0.5. This value for g was chosen because the difference in amplitude ratio and phase difference as g varies 0.5 and 0.9 is less than 1.4% and 0.08°, respectively, and because computation is significantly faster for smaller values of g. The re-emitted photons were collected by two 400 μm, 0.39 NA detection fibers spaced 3 and 6 mm away from the source. To minimize discretization errors and ensure sufficient SNR for the Fourier transform to the frequency domain [9], the time-resolved reflectance was recorded for up to 1ns with a temporal resolution of 2 ps. Further, the semi-infinite solution to the time-resolved photon diffusion equation [10] was used to calculate reflectance for 1 ns < t < 5 ns, as Kienle and Patterson previously demonstrated that Monte Carlo data closely matches the diffusion approximation for t > 500 ps [10]. Finally, the simulated time-resolved reflectance (0 – 1ns) was combined with the diffusion approximated time-resolved reflectance (1-5 ns), and a fast Fourier transform was used to calculate the amplitude (AC) and phase shift (ϕ) at 110 MHz for each source-detector separation.

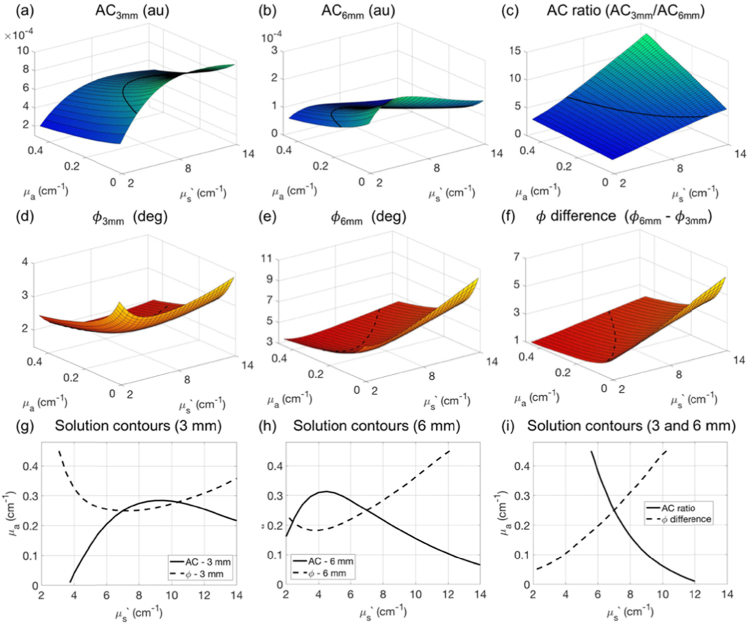
Figure 1 shows the resulting MC lookup tables for AC amplitude and phase shift at source-detector separations (ρ) of 3 and 6 mm as a function of the absorption and reduced scattering coefficients. For a single separation, a unique solution for μ _a and μ_s′ to the inverse problem does not always exist, as demonstrated by the multiple intersections of representative iso-amplitude (black solid) and iso-phase lines (black dashed) in Fig. 1(g)-1(h). To overcome this problem of non-uniqueness, we employ the AC ratio (AC_ratio = AC_3mm/AC_6mm, Fig. 1(c)) and phase difference (ϕ_diff = ϕ_6mm – ϕ_3mm, Fig. 1(f)) between the 3 and 6 mm separations. In contrast to a single separation, both AC_ratio and ϕ_diff change monotonically as a function of μ _a and μ_s′ ; thus, the iso-amplitude ratio and iso-phase difference lines always intersect at a unique solution for μ _a and μ_s′ as exemplified in Fig. 1(i). The final MC lookup tables used for all subsequent data analysis consisted of AC_ratio and ϕ_diff interpolated with spline for a finer μ _a and μ_s′ resolution of 0.01 and 0.5 cm^-1, respectively.

Fig. 1.

Monte Carlo-based lookup table for small separation FDNIRS. Monte Carlo simulated AC amplitude at ρ = 3 mm (a), ρ = 6 mm (b), and the ratio of AC at 3 versus 6mm (c), as well as phase shift (ϕ) at ρ = 3 mm (d), ρ = 6 mm (e), and the phase difference between 3 and 6 mm (f) as a function of absorption and reduced scattering coefficient of the tissue (μ _a and μ_s′, respectively). The black lines in (a-f) depict representative isolines of AC (solid) and phase (dashed) that we project onto the μ_s′-μ_a axis in (g-i). The iso-phase and iso-amplitude lines from a single separation (g,h) intersect at multiple points, whereas the iso-AC ratio and iso-phase difference contour lines form a unique intersection point (i).

2.2. FDNIRS instrumentation

For all experiments described herein, we employed a commercially-available frequency-domain near-infrared spectroscopy system with a custom wavelength modification (Imagent, ISS, Urbana Champaign, IL). The system utilizes 6 near-infrared laser diode sources with wavelengths of 690, 730, 750, 785, 800, and 830 nm modulated at 110 MHz and four photomultiplier tube (PMT) detectors with gain modulation of 110.005 MHz to achieve heterodyne detection at 5 kHz. The lasers were rapidly multiplexed, allowing fast data acquisition at 20 Hz.

2.3. In vitro liquid phantom verification

Liquid phantoms were first used to test the accuracy of μ _a(λ) and μ_s′(λ) measured with small separation FDNIRS. Phantoms consisted of 20% Intralipid (Fresenius Kabi, Baxter Healthcare, Deerfield, IL) and India ink (Higgins, Chartpak, MA) as scattering and absorption agents, respectively. Three sets of scattering base (μ_s′(λ = 785nm) = 5, 7.5 and 10 cm^-1) were each titrated with India ink to achieve desired μ _a(λ = 785nm) = 0.08, 0.15, 0.22, and 0.29 cm^-1. Experiments were performed in a 279 × 168 × 137 mm (2.2 L) container to ensure a semi-infinite medium. The reference optical properties of each phantom were obtained by fitting AC and phase measured at 15, 20, 25 and 30 mm to the semi-infinite solution of the photon diffusion equation [11,12]. For the remainder of this manuscript, we refer to this approach for obtaining reference optical properties as “large-separation FDNIRS”.

For each phantom measurement, a black 3D printed fiber holder was secured to the air-liquid boundary. A single 1 mm multimode detector fiber (FT1000EMT, Thorlabs, Newton, NJ) was sequentially positioned 3 and 6 mm away from a 1 mm multimode source fiber (FT1000EMT, Thorlabs). Data was acquired for 3 seconds at each separation; measurements were repeated three times per each phantom.

2.4. In vitro blood phantom verification

To further verify the accuracy of small separation FDNIRS estimates of oxygen saturation and hemoglobin concentration, blood phantoms were used. These phantoms consisted of pooled bovine blood (Item #828574, Carolina Biological Supply Company, Burlington, NC), 20% Intralipid, phosphate-buffered saline (pH = 7.4, ThermoFisher Scientific, Waltham, MA), and sodium bicarbonate buffer 8.4% (SBB, 1 mmol/ml, S5761, Sigma-Aldrich, St. Louis, MO) [13]. Each phantom was contained in a cylindrical baking pan (152-mm diameter and 102-mm deep) on a hot plate to maintain temperature at 36 - 37°C. Initially, the blood phantom was fully oxygenated (i.e., SO₂ = 100%). Glucose 50% (G8270, Sigma Aldrich) and baker’s yeast were added to gradually deoxygenate the blood over ∼40 minutes. A magnetic stir bar was used to ensure homogenously distributed oxygen consumption (100 revolutions/min). SBB was added as needed to maintain pH > 7.4.

Two blood phantoms with different scattering bases of μ_s′(λ = 785nm) = 6 and 10 cm^-1 were each titrated with blood to achieve a desired total hemoglobin concentration (HbT) of 40 and 60 μM. After the 40 μM phantom was fully deoxygenated, blood was added to increase HbT to 60 μM and oxygen was bubbled in to re-oxygenate the phantom. While the phantom was being deoxygenated, small-separation (3 and 6 mm) and large-separation (15, 20 and 25 mm) FDNIRS data was sequentially acquired by translating the detector fiber within the 3D printed fiber holder at the tissue interface. The time difference between small and large-separation measurements was < 30 s such that two methods measured approximately the same oxygenation status.

2.5. In vivo mice validation

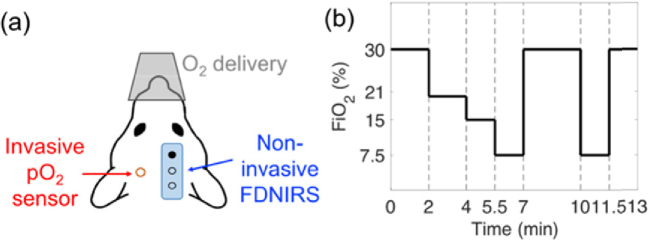
Next, we validated small separation FDNIRS method in vivo in mice during a graded hyper-/hypoxia challenge while concurrently monitoring tissue partial pressure of oxygen (pO₂) with an invasive sensor (Fig. 2). Ten-week old adult male C57BL/6 mice were used in all experiments. All animal procedures were approved by the Institutional Animal Care and Use Committee (IACUC) at Emory University and conform to the National Institute of Health Guide for Care and Use of Laboratory Animals. Anesthesia was induced with 4.5% isoflurane in a 70:30 N₂O:O₂ mixture (1L/min) for 45s and then maintained for the duration of the experiment at 1.5 ∼ 2.5%. Rectal temperature was kept at 37 °C using a thermostatically controlled heating pad (TCAT-2LV, Physitemp Instruments, Clifton, NJ). Heart rate, arterial oxygen saturation (SpO₂) and breath rate were continuously monitored (MouseOx Plus, Starr Life Sciences, Oakmont, PA). After stabilization, the mouse was secured in a stereotaxic head mount (Model 900, David Kopf Instrument, Tujunga, CA), a 3 × 3 mm portion of the left scalp was retracted, and a burr hole (diameter < 1 mm) was made in skull over the left hemisphere for pO₂ sensor placement. The pO₂ sensor (NX-BF/OT/E, Oxford Optronix, tip diameter = 350 µm) was inserted 1 mm into the cortex (3 mm posterior and 2 mm lateral to bregma) using a micromanipulator with 0.1 mm resolution. Depth of implantation was confirmed via post-mortem histological assessment using Evans blue stain. A small separation (3 and 6 mm) FDNIRS sensor was placed onto the intact scalp over the right hemisphere. No interference between pO₂ and FDNIRS measurements was observed.

Fig. 2.

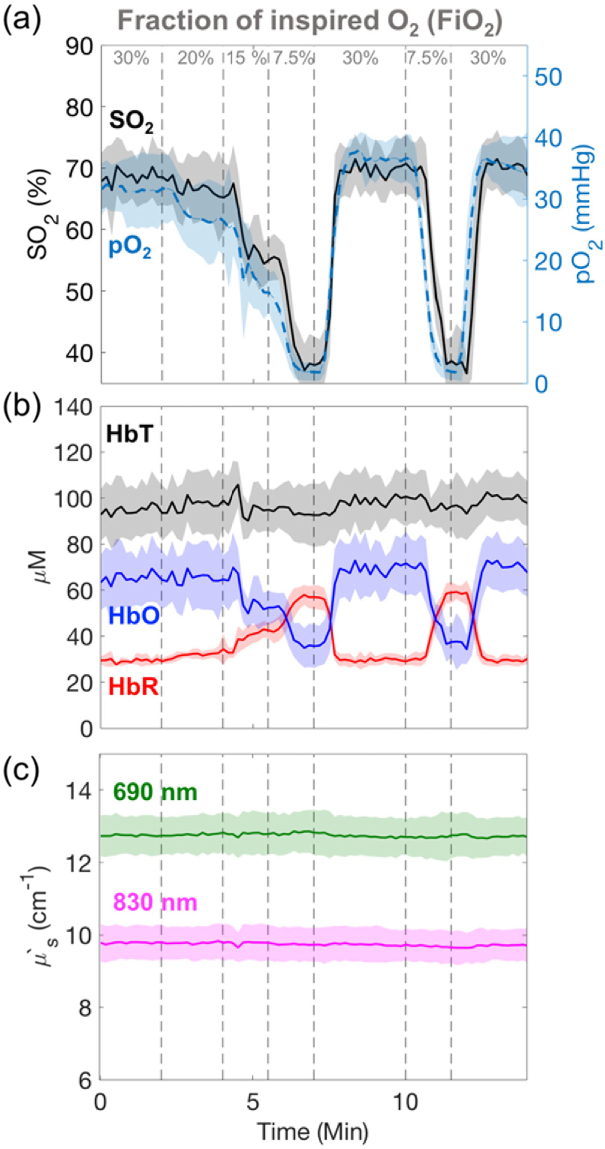
Experimental setup for in vivo mice validation. (a) An invasive oxygen partial pressure (pO₂) sensor was implanted into the cortex (red), and non-invasive FDNIRS measurements at 3 and 6 mm source-detector separation were made on the contralateral hemisphere over the intact scalp (blue) (b) For each mouse measurement, the fraction of inspired oxygen (FiO₂) was manipulated from 30 to 7.5%.

To perturb oxygen content to the brain, the fraction of inspired oxygen (FiO­­₂) was manipulated from 30 to 7.5% at regular intervals, as depicted in Fig. 2(b). This graded hyper-/hypoxia gas challenge lasted 13 minutes and was repeated twice for a total of 26 minutes of monitoring. FDNIRS data was acquired continuously (20 Hz) throughout the procedure.

2.6. In silico verification of mouse results using a multi-layered MC model

Finally, to investigate the effect of the extracerebral layers on small separation FDNIRS measurements that assume a semi-infinite geometry, we ran MC simulations on a three-layered slab model to simulate mouse scalp, skull, and brain. The scattering coefficient, refractive index (n), and anisotropy (g) of each layer were obtained from literature values and remained fixed for all simulations (Table 1). The thickness of the scalp and skull were assumed to be 0.65 and 0.35 mm, respectively, based on post mortem analysis of a representative adult male C57BL/6 mouse. The scalp was assumed to have a fixed oxygen saturation of 70% and total hemoglobin concentration of 55 μM; the absorption coefficient of skull was assumed to be 0.25 cm^-1 for all wavelengths. For the brain layer, we assumed combinations of 5 different values for HbT (40, 55, 70, 85 and 100 μM) and 3 different levels of SO₂ (40, 55 and 70%), for a total of 15 simulations.

Table 1. Optical properties used for three-layered MC simulation.

	Thickness	n	g	Scattering	Absorption
Scalp	0.65 mm	1.38 [14]	0.8 [14]	μs′ = 0.11λ-4 + 1.61λ0.22 [15]	HbT = 55 μM, SO2 = 70% [16]
Skull	0.35 mm	1.55 [17]	0.92 [18]	μs′ = 1.72λ-0.65 [15]	0.25 cm-1 for all wavelengths [18]
Brain	Infinite	1.37 [19]	0.9 [14]	μs′ = 14.9λ-1.07 [20]	HbT = [100 85 70 55 40] μM, SO2 = [70 55 40] %

Per each brain HbT and SO₂ combination, simulated AC_ratio and ϕ_diff at 6 wavelengths (690, 730, 750, 785, 800, and 830 nm) were fit to the MC lookup table built using a semi-infinite geometry (Section 2.1) to estimate a bulk average μ_s′(λ) and μ _a(λ) of the interrogated tissue. The estimated μ _a(λ) were further processed to calculate HbT and SO₂.

2.7. Data analysis

For all experiments, measured data was averaged for 3s (phantoms) or 1s (mice) to improve SNR. Data was discarded if the standard deviation of phase across this time interval was > 2° or if the ratio of the AC standard deviation to the AC mean was > 0.05. All measured AC_ratio and ϕ_diff data was calibrated to a reference phantom with known optical properties to correct for system responses (e.g., phase-amplitude crosstalk, varying detector efficiency).

To estimate μ _a(λ) and μ_s′(λ), we fit the measured AC_ratio(λ) and ϕ_diff(λ) to the MC lookup table. In this inversion process, the initially-seeded μ_s′ and μ _a were iteratively updated using fmincon (MATLAB R2018b, MathWorks) to minimize the following cost function, χ²,

$${\chi }^2={\left(\frac{A{C}_{ratio}^{MC}-A{C}_{ratio}^{Measured}}{A{C}_{ratio}^{Measured}}\right)}^2+{\left(\frac{{\varphi }_{\mathit{\text{diff}}}^{MC}-{\varphi }_{\mathit{\text{diff}}}^{Measured}}{{\varphi }_{\mathit{\text{diff}}}^{Measured}}\right)}^2.$$ (1)

When appropriate, oxy- and deoxy- hemoglobin concentration (HbO and HbR, respectively) were derived by fitting the measured μ_a(λ) to the hemoglobin spectra and assuming a water concentration of 99.6% for the blood phantom and 80% for in vivo study [21]. To ensure a good fit to the hemoglobin spectra, data were discarded if the Pearson’s correlation coefficient between the measured versus best fit μ_a across all wavelengths at a given time point had an associated p-value < 0.05. Moreover, because the wavelength-dependence of μ_s′ in biological tissue should obey a power law model [14], data were discarded if the associated p-value for Pearson’s correlation coefficient between μ_s′ (λ) versus wavelength was > 0.05. Total hemoglobin concentration and tissue oxygen saturation were computed as HbT = HbR + HbO and SO₂ = HbO/HbT×100%, respectively.

Pearson’s correlation (r) and Lin’s concordance correlation coefficient (CCC) [22] were used to assess the relationship between small separation FDNIRS measures and expected values. Bland-Altman analysis [23,24] was also performed when applicable. Further, the root mean square percent error (RMSE) in measured FDNIRS values was computed as

$$RMSE=\sqrt{\frac{1}{N}{\sum _{}^N\left(\frac{Measured-Known}{Known}\right)}^2}\times 100(\mathrm{\%}),$$ (2)

where N is a total number of estimations.

3. Results

3.1. In vitro liquid phantom verification

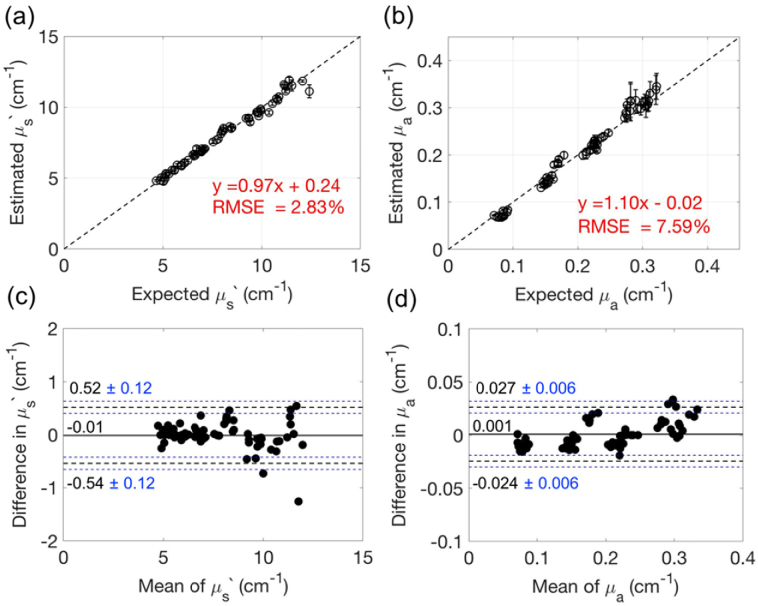
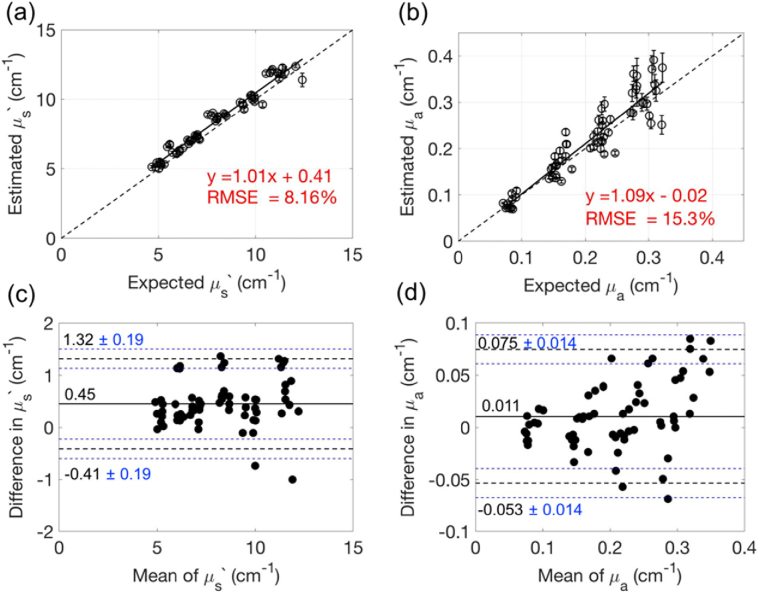
The estimated μ_s′ and μ_a of the liquid Intralipid/ink phantoms using small separation FDNIRS show excellent agreement with the expected μ_s′ and μ_a measured with large-separation FDNIRS (Fig. 3). Note data from one phantom (target μ_s′(785nm) = 5 cm^-1, μ_a(785nm) = 0.07 cm^-1) was discarded due to poor data quality caused by debris on the source fiber discovered after data collection. Across all other phantoms, we observed a strong linear correlation between the measured and expected values of μ_s′ (slope = 0.97 [CI: 0.94–0.99], intercept = 0.24 [CI: 0.03–0.45], r = 0.99, p < 0.001, CCC = 0.99 [CI: 0.99–1.00]) and μ_a (slope = 1.10 [CI: 1.07–1.13], intercept = -0.02 [CI: - 0.03 – -0.01], r = 0.99, p < 0.001, CCC = 0.99 [CI: 0.98–0.99]) as shown in Fig. 3(a) and (b). The RMSEs were 2.8% for μ_s′ and 7.6% for μ_a. In the Bland-Altman analysis, the mean difference between measured and expected μ_s′ and μ_a are close to zero (-0.01 cm^-1 for μ_s′, 0.001 cm^-1 for μ_a, Fig. 3(c),(d)). The 95% limits of agreement between two methods are within ± 6.7% and ± 12.4% of the mean of two methods for μ_s′ and μ_a, respectively.

Fig. 3.

Intralipid/ink phantom verification of small separation FDNIRS. (a, b) Expected vs. estimated μ_s′ (a) and μ_a (b) across all Intralipid/ink liquid phantoms. Here estimated μ′_s and μ_a were obtained using small separation FDNIRS and expected μ′_s and μ_a were obtained with large-separation FDNIRS. The dashed lines represent the line of unity. Error bars indicate the standard deviation of three repetitions at each phantom. (c, d) Bland-Altman plots of the difference between estimated and excepted μ_s′ (c) and μ_a (d) versus the mean of two methods. The solid horizontal line indicates the mean difference between the two methods. The black dotted lines indicate 95% limits for agreement. The blue dotted lines indicate 95% confidence interval of the limit of agreement.

3.2. In vitro blood phantom verification

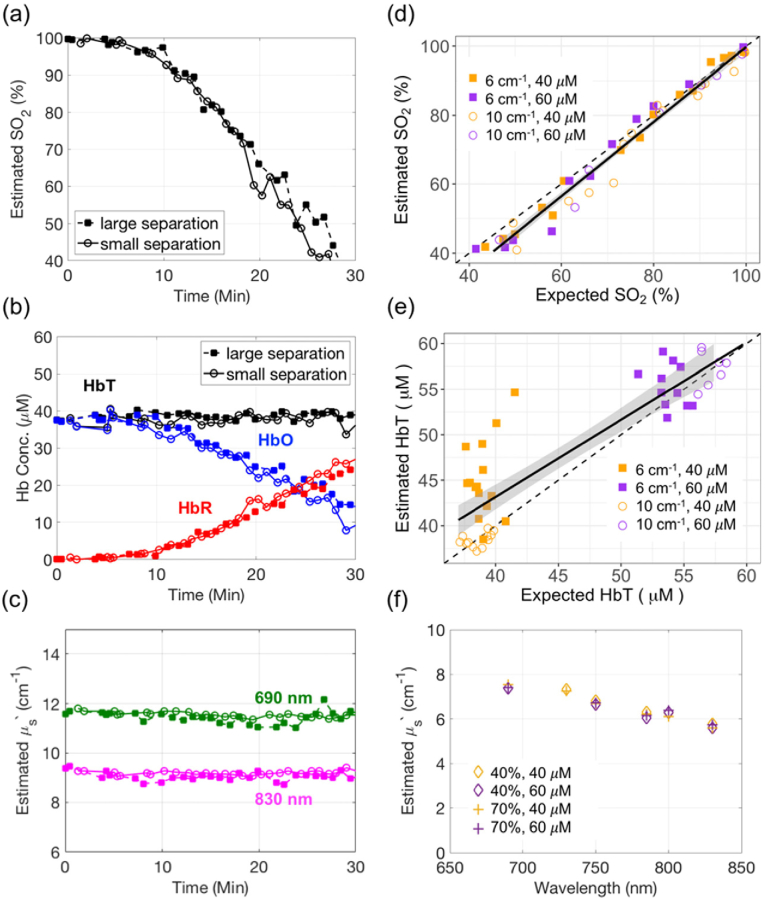
A total of 4 blood phantoms were measured during deoxygenation. The majority of data passed our rigorous quality control criteria, although ∼9% was discarded due to poor linearity between the estimated μ_a(λ) and the expected hemoglobin spectra. In general, adding yeast/glucose to a fully oxygenated blood phantom led to transient increases in deoxy-hemoglobin along with decreases in oxy-hemoglobin and oxygen saturation, as seen in the representative SO₂ time series measured by both small and our “gold standard” large separation FDNIRS (Fig. 4(a),(b)). Both total hemoglobin concentration and the reduced scattering coefficient remained constant during deoxygenation (Fig. 4(b),(c)). Across all blood phantoms, the estimated SO₂ using small separation FDNIRS agreed well with the expected SO₂ measured by large-separation FDNIRS (slope = 1.07 [CI: 1.02–1.12], intercept = -7.44 [CI: -11.28 – -3.60], r = 0.99, p < 0.001, CCC = 0.98 [CI: 0.96–0.99], RMSE = 7.8%, Fig. 4(d)). Further, total hemoglobin concentration agreed well between two methods (slope = 0.95[CI: 0.80–1.10], intercept = 4.51 [CI: -2.28–11.30], r = 0.88, p < 0.001, CCC = 0.85 [CI: 0.75–0.91], RMSE = 11.2%, Fig. 4(e)). Moreover, the wavelength-dependence of μ_s′ measured by small separation FDNIRS remained constant as the oxygenation state and hemoglobin concentration of the phantom changes, suggesting minimal absorption/scattering crosstalk (Fig. 4(c),(f)).

Fig. 4.

Blood-mixed liquid phantom verification (a-c) Representative time traces of oxyhemoglobin (HbO, red), deoxyhemoglobin (HbR, blue), total hemoglobin (HbT, black), oxygen saturation (SO₂) and reduced scattering coefficients at 690 (green) and 830nm (magenta) estimated by small separation FDNIRS (solid rectangle) and by large separation FDNIRS (hollow circles) during blood phantom deoxygenation. (d-e) Comparison of small separation FDNIRS with expected large-separation FDNIRS HbT (d) and SO₂ (e) across four blood phantoms with target HbT of 40 μM (orange) or 60 μM (purple) and target μ_s′(785 nm) of 6 cm^-1 (solid rectangles) or 10 cm^-1(hollow circles). The black dotted lines in (d,e) denote the line of unity, the black solid lines denotes the line of best linear fit, and the grey shaded regions denotes the confidence interval of the linear fit. (f) Four representative μ_s′ spectra measured by small separation FDNIRS on a blood phantom (target μ_s′(785 nm) of 6 cm^-1) where HbT was varied from 40 to 60μM (orange and purple, respectively) and SO₂ was varied from 40 to 70% (diamond and cross, respectively).

3.3. In vivo mouse validation

A total of four mice were each subject to 2 trials of the graded hyper/hypoxia challenge. One trial was excluded because of unreliable pO₂ sensor readings. Approximately 17% of the data was discarded due to poor linearity (p > 0.05) between the estimated μ_a(λ) and the expected hemoglobin spectra. Figure 5(a) shows the average response of cerebral oxygen saturation (SO₂) measured noninvasively by small separation FDNIRS along with cortical tissue pO₂ measured invasively across 7 trials in 4 mice. Both SO₂ and pO₂ respond rapidly to changes in FiO₂ and exhibit similar dynamic trends. SO₂ and pO₂ decrease to an average of 37.9% and 2.1 mmHg, respectively, during hypoxia (FiO₂ = 7.5%) and recover to an average of 68.5% and 36.0 mmHg at FiO₂ = 30%. These responses were consistent across trials and between animals, as indicated by tight standard deviations (color-shaded area) in the group averaged time series.

Fig. 5.

In vivo validation during an inspired gas challenge. (a) Temporal changes in cerebral oxygen saturation (SO₂, black) measured with non-invasive small separation FDNIRS along with concomitant changes in partial oxygen pressure (pO₂, blue) measured invasively with an implanted sensor. Measurements were made during a graded hyper/hypoxia challenge wherein the fraction of inspired oxygen (FiO₂) was manipulated from 30 to 7.5%. (b) Temporal changes in oxy- (HbO, blue), deoxy- (HbR, red) and total (HbT, black) hemoglobin concentration during the gas challenge. (c) Reduced scattering coefficient (μ_s′) at 690 nm (green) and 830 nm (magenta) during the gas challenge. In all plots, the solid lines (shaded regions) denote the mean (standard deviation) across 7 measurements in 4 mice. For visualization of these mean values, all data have been downsampled to 0.1Hz. Vertical dotted grey lines denote changes in fraction of inspired oxygen.

Both HbO and HbR change dynamically with changes in FiO₂ (Fig. 5(b)); HbO decreases by ∼ 28.8 μM, and HbR increases by ∼ 28.7 μM during hypoxia while HbT remains constant at 96.8 ± 3.1 μM. The reduced scattering coefficients are consistent across animals (12.8 ± 0.6 cm^-1 at 690 nm, 9.7 ± 0.5 cm^-1 at 830 nm) and remain constant as FiO₂ changes (Fig. 5(c)).

3.4. In silico verification

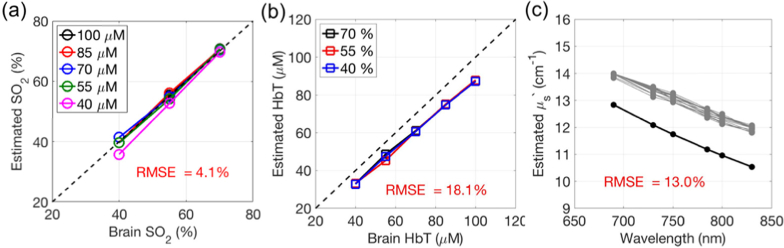
Finally, we explored the influence of extracerebral layers on small separation FDNIRS in the mouse using a set of MC simulated data generated from a 3-layer model that emulated the mouse head geometry. The SO₂ measured with small separation FDNIRS shows excellent agreement with the brain SO₂ across a wide range of brain HbT (CCC = 0.99 [CI: 0.98–1.00], Fig. 6(a)) with an average RMSE across all 15 simulations of 4.1%. In contrast, HbT measured with small separation FDNIRS systematically underestimates brain HbT with a RMSE of 18.1% (r = 0.99, p < 0.001, Fig. 6(b)). Similarly, the measured μ_s′(λ) systematically overestimates expected brain μ_s′(λ) by an average of 13.0% (Fig. 6(c)).

Fig. 6.

Influence of extracerebral layers. Results of fitting simulated 3-layer data to our small separation FDNIRS algorithm that assumes a semi-infinite homogenous medium. The x-axis in (a) and (b) denotes the simulated brain (bottom layer) oxygen saturation (SO₂) and total hemoglobin concentration (HbT), respectively, while the y-axis denotes the small separation FDNIRS estimated obtained assuming a semi-infinite geometry. The dashed line in (a) and (b) represents an ideal estimation. (c) Simulated brain μ_s′(λ) (black) and μ_s′(λ) measured by small separation FDNIRS (grey) as a function of wavelength for 15 total simulations (5 brain HbT x 3 brain SO₂).

4. Discussion

Herein we present experimental validation of small separation frequency domain near-infrared spectroscopy for estimation of tissue optical properties. Although diffusion theory can be used to estimate optical properties with FDNIRS at large source-detector separations, this approximation breaks down for separations < 1 cm. Certainly, alternative techniques exist to estimate optical properties at millimeter depths, including visible steady-state reflectance spectroscopy, which works for source-detector separations < 3 mm [25], and spatial frequency domain imaging [26], which is sensitive to depths of 2-6 mm [27]. However, to our knowledge, this is the first work that employs single-modulation-frequency FDNIRS to recover optical properties at sub-centimeter source-detector separations.

The liquid phantom results demonstrate excellent agreement between small separation FDNIRS and our “gold standard” large separation FDNIRS results (Fig. 3 and 4). In both the Intralipid/ink phantom and blood phantom, the RMSE was < 10% across a wide range of physiologically-relevant optical properties. Further, minimal crosstalk was observed between absorption and scattering (exemplified by Fig. 4(c),(f)). Interestingly, calibrating the AC ratio and phase difference data to a known reference phantom significantly improved accuracy, with a reduction of RMSE in both μ_a and μ_s′ of ∼50% (Appendix 1). We posit that calibration helps negate the influence of amplitude-phase crosstalk [28,29], which is on the order of 1°/OD in our system. Although small, this crosstalk can be significant, as the expected phase difference between 3 and 6 mm at 110 MHz is < 5° (Fig. 1(d),(e)). Thus, we recommend using a reference phantom with known optical properties for calibration of all small separation FDNIRS measurements.

In addition to validating this technique in vitro, we also demonstrate a promising in vivo application to non-invasively assess oxygen saturation and hemoglobin concentration in the mouse brain. The small size of the mouse brain (∼5×10×10 mm) necessitates the use of small (< 7 mm) source detector separations to avoid significant contamination from extracerebral tissue. Our resting state values of cerebral SO₂, HbT, and μ_s′ in the mice are consistent with literature reported values [20], and the gas challenge induced expected changes in SO₂ with minimal changes in HbT and μ_s′ (Fig. 5) [30]. Moreover, trends in SO₂ qualitatively mimic changes in pO₂ measured invasively, although we note that direct comparison between SO₂ and pO₂ was not possible because the necessary parameters to convert pO₂ to SO₂ via the oxygen dissociation curve (i.e., pH, temperature) were difficult to obtain in vivo [31]. Finally, our in silico multilayered simulations suggest that extracerebral layers exert a small but significant influence on small separation FDNIRS (which assumes a semi-infinite geometry) such that the measured HbT consistently underestimated brain HbT by ∼20% and brain μ_s′ was consistently overestimated by ∼10% (Fig. 6). However, extracerebral layers appear to have minimal effects on the estimation of brain SO₂, with a RMSE of < 5%. In studies where estimation of HbT and/or μ_s′ requires improved precision, multi-layered Monte Carlo look up tables may be used to improve quantification.

Mouse models are invaluable in brain research given the wide range of genetically modified strains and injury models available, and relatively low-cost compared to other large animal models. Non-invasive quantification of oxygen saturation and blood volume in small animals has the potential to elucidate mechanism driving changes in these parameters in various brain injuries and diseases (e.g., sickle cell disease [32], stroke [33], or traumatic brain injury [34]), and to investigate efficacy of novel therapeutic strategies in normalizing these parameters. Further, small separation FDNIRS measures of oxygen saturation combined with the recently validated small separation diffuse correlation spectroscopy (DCS) measures of cerebral blood flow [35] can be used to non-invasively assess an index of absolute cerebral metabolic rate of oxygen (CMRO₂) using Fick’s law [36]. Thus, a hybrid small separation FDNIRS/DCS system may serve as a relatively low-cost, non-invasive tool to monitor a battery of hemodynamic and metabolic biomarkers (oxygen saturation, blood volume, blood flow, and oxygen metabolism) in small animal models.

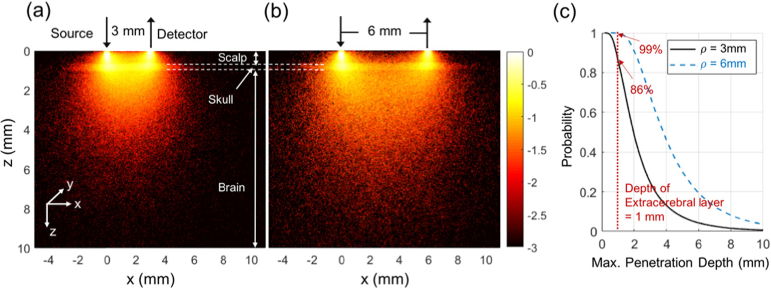
We note several limitations of this study. First, the choice of source detector separations (3 and 6 mm) was somewhat empirical. However, we theoretically confirm in our photon path analysis using MC simulation on a layered brain model that a majority of detected photons at these separations (86% at 3 mm and 97% at 6 mm) reach the brain before detection at the tissue surface (see Appendix 2). Future systematic computational and experimental tests are needed to determine the optimal source detector separation for a given application. Second, in the liquid phantoms, although our MC lookup table was created assuming a 400 μm detector fiber, we experimentally employed a 1000 μm detector to maximize SNR. We confirmed through a handful of simulated μ_a/μ_s′ values that the choice of detector diameter minimally influences the amplitude ratio and phase difference, and the strength of the agreement between our estimations and the expected values confirms this assertion. Nevertheless, recovery of optical properties with small separation FDNIRS could be further improved if the MC lookup table is generated to exactly mimic each experimental setup. Third, in the blood phantom validation, we sequentially translated a single detection fiber for both small and large separation FDNIRS measurements. Although the time difference between the two methods was small compared to the deoxygenation speed, this experimental limitation may contribute to the small discrepancy between two estimations, particularly in the lower oxygenation range where deoxygenation process was accelerated. We expect that the agreement would improve if concurrent measures were obtained.

Finally, we emphasize that while we focus the latter half of this work on application to mouse brain, this method could be applied to any biological tissue in which millimeter depth penetration is desired. One interesting application would be characterizing the optical properties of the extracerebral layers (skull/scalp) in human brain studies in order to improve estimations of cerebral blood flow with multi-layered DCS [37]. Other applications include longitudinal monitoring of preclinical tumor models for hypoxia [38] and skin grafts for recovery of blood volume and oxygenation [39].

5. Conclusion

Herein we present experimental validation of frequency domain near-infrared spectroscopy at small (<1 cm) source-detector separations using a Monte Carlo-based inverse algorithm. We verify in vitro that the technique can accurately estimate absorption and scattering coefficients to within 10% error. Further, we demonstrate the feasibility of an attractive application of this non-invasive technique, namely estimation of oxygen saturation and hemoglobin concentration in the mouse brain. Using a hyper-/hypoxia challenge, we show that we are sensitive to expected trends in cerebral oxygen saturation with minimal absorption/scattering crosstalk. These results suggest that small separation single-frequency FDNIRS can provide accurate estimation of tissue optical properties for applications requiring millimeter depth penetration.

Appendix 1. Uncalibrated data analysis of Intralipid/ink phantom

Without calibration, we observed a strong positive linear correlation between the estimated and expected values of μ_s′ (slope = 1.01 [CI: 0.96–1.04], intercept = 0.41 [CI: 0.06–0.76], r = 0.98, p < 0.001, CCC = 0.96 [CI: 0.94–0.97]) and μ_a (slope = 1.09 [CI: 1.00–1.18], intercept = -0.02 [CI: - 0.03–-0.01], r = 0.93, p < 0.001, CCC = 0.91 [CI: 0.87–0.94]) as shown in Fig. 7(a),(b)

Fig. 7.

Intralipid/ink phantom verification of small separation FDNIRS without calibration. (a, b) Expected vs. estimated μ_s′ (a) and μ_a (b) across all Intralipid/ink liquid phantoms. Here estimated μ_s′ and μ_a were obtained using small separation FDNIRS and expected μ_s′ and μ_a were obtained with large-separation FDNIRS. The solid black lines represent the best linear fit and the dashed lines represent the line of unity. Error bars indicate the standard deviation of three repetitions at each phantom. (c, d) Bland-Altman plots of the difference between estimated and excepted μ_s′ (c) and μ_a (d) versus the mean of two methods. The solid horizontal line indicates the mean difference between the two methods. The dotted lines indicate the 95% limits for agreement. The blue dotted lines indicate 95% confidence intervals of the limits of agreement.

. The RMSEs increases to 8.2% for μ′_s and 15.3% for μ_a. Bland-Altman analysis reveals that the mean differences between two methods are 0.45 and 0.01 cm^-1 for μ_s′ and μ_a, respectively (Fig. 7(c),(d)). The 95% limits of agreement between two methods are 1.32 and -0.41 cm^-1 for μ′_s, and 0.075 and -0.053 cm^-1 for μ_a. These limits (±0.86 and ± 0.064) are ± 10.4% and ± 30.9% compared to the mean of two methods for μ_s′ (8.22 cm^-1) and μ_a (0.207 cm^-1), respectively. Notably, the difference in the expected versus measured μ_a increases as the mean increases (Fig. 7(d)).

Appendix 2. Photon tissue interaction density visualization

To visualize the probed tissue area, we used the Monte Carlo results from the 3-layered mouse head model described in Section 2.6 with brain HbT = 70 μM and SO₂ = 70%. For these simulations, a photon packet is launched from the source with a weight of 1, and the weight is attenuated at each scattering event by $e^{-{\mu }_a\ell }$, where $\ell$ is the pathlength. For each detected photon, the weight of each scattering step was binned into a voxel field with cubic voxels of side length 0.025 mm. We defined the interaction density [3] in the n^th voxel (S_n) as the sum of the photon weights, i.e.,

$$S_N=\sum _{i=1}^N{w}_{n,j},$$ (3)

where w_n,i is the weight of the i_th detected photon in the n^th voxel, and N is a total number of detected photons that experienced scattering events within the n^th voxel. Figures 8(a) and (b)

Fig. 8.

Photon interaction density for small separation FDNIRS. MC simulation was performed on a three-layer model simulating mouse scalp, skull and brain. (a,b) Each pixel in these images represents the interaction density, S_n, normalized to the maximum S within the x-z plane. Pixels with weights less than three-orders of magnitude relative to the maximum were set to black. The color bar indicates a base 10 logarithm of the normalized S_n. (c) Probability distribution of the maximum z-coordinate of each detected photon at 3 (solid line) and 6 mm (dotted line). The vertical red line denotes the typical thickness of extracerebral layers for an adult C57BL/6 mouse. For the 3 mm separation, >86% of detected photons reach a depth > 1 mm. Similarly, for 6 mm, >99% of detected photons reach a depth > 1 mm.

display the normalized interaction density within a slice from the x-z plane for source-detector separations of 3 and 6 mm, respectively. Here we have normalized to the maximum S_n within this 2D slice and visualized interaction density using a logarithmic scale. Typical “banana” shaped patterns are observed, with greater than 86% and 99% of detected photons at separations of 3 and 6 mm, respectively, penetrating to the bottom (brain) layer.

Funding

National Heart, Lung, and Blood Institute10.13039/100000050 (R21-HL138062); National Institute of Neurological Disorders and Stroke10.13039/100000065 (R21-NS104801); Children's Healthcare of Atlanta10.13039/100012423 (Junior Faculty Award); American Heart Association10.13039/100000968 (19POST34380337).

Disclosures

The authors declare no conflicts of interest.