Polarization-sensitive optical coherence elastography

Abstract

Polarization-sensitive optical coherence elastography (PS-OCE) is developed for improved tissue discrimination. It integrates Jones matrix-based PS-optical coherence tomography (PS-OCT) with compression OCE. The method simultaneously measures the OCT intensity, attenuation coefficient, birefringence, and microstructural deformation (MSD) induced by tissue compression. Ex vivo porcine aorta and esophagus tissues were investigated by PS-OCE and histological imaging. The tissue properties measured by PS-OCE are shown as cross-sectional images and a three-dimensional (3-D) depth-trajectory plot. In this trajectory plot, the average attenuation coefficient, birefringence, and MSD were computed at each depth, and the trajectory in the depth direction was plotted in a 3-D feature space of these three properties. The tissue boundaries in a histological image corresponded with the depth-trajectory inflection points. Histogram analysis and t-distributed stochastic neighbour embedding (t-SNE) visualization of the three tissue properties indicated that the PS-OCE measurements provide sufficient information to discriminate porcine esophagus tissues.

1. Introduction

Optical coherence tomography (OCT) visualizes tissue structures noninvasively with micrometer-scale resolution [1]. The contrast of OCT is based on the back scattering intensity. However, the back scattering intensity is a property of the probe beam and not a property of the tissue itself. Therefore, OCT only indirectly visualizes the tissue properties. However, investigation of tissue properties is important for assessment of tissue abnormalities. Several extensions of OCT have thus been investigated for measurement of tissue properties.

The depth-resolved attenuation coefficient of the OCT signal reflects the scattering and absorption properties of the tissue. Recently, Vermeer et al. established a model-based attenuation coefficient measurement method that has been successfully applied to the investigation of ocular tissue properties [2]. Because the attenuation coefficient directly reflects the tissue properties, it is useful in tissue classification. Azuma et al. used the attenuation coefficient for segmentation of ocular tissues, including the retinal pigment epithelium and choroidal stroma [3]. Kasaragod et al. used the attenuation coefficient for segmentation and quantification of the lamina cribrosa [4]. In addition to the model-based method, there are several attenuation coefficient computation methods, and they were used to investigate several types of tissues, including cerebral tissue [5], coronary artery tissue [6,7], and burn scar tissue [8].

Birefringence is another example of an optical property of tissue that can be measured using an extended version of OCT called polarization sensitive-OCT (PS-OCT). Early PS-OCT devices measured the cumulative phase retardation [9,10]. Both the birefringence and the phase retardation are sensitive to fibrous tissues, such as tissues with collagenous ultrastructures and/or tissues with fibrosis. Phase retardation measurements have thus been used to investigate burnt tissue [11], fibrous tissues in the retina [12,13] and the anterior eye [14,15], the sclera [16–18], and cancer tissue [19]. The phase retardation is defined as the phase difference between two beams with the two eigen-polarization states of the sample. As indicated by this definition, the cumulative phase retardation only represents the tissue properties indirectly [20]. Recently, several modified PS-OCT methods have been proposed for measurement of local (i.e., noncumulative) phase retardation, or equivalently, birefringence [21–26]. Because the birefringence is a direct property of the tissue, it can visualize tissue abnormalities more directly than the cumulative phase retardation [20]. Atherosclerotic plaques in human aorta have been visualized and quantitatively analyzed using PS-OCT [27,28].

The mechanical properties of tissue can also be measured using an extended version of OCT called optical coherence elastography (OCE) [29,30]. OCE applies mechanical stimulation to the tissue under study by direct compression [31], acoustic radiation force [32], or other methods [33,34]. The microscopic displacement induced by this mechanical stimulation is then measured by OCT. The microscopic displacement visualizes the mechanical properties of the tissue [35], while more quantitative elastographic information, such as the Young’s modulus [31] or shear modulus [36], can be obtained by combining the displacement information with the mechanical stimulation information. OCE has been used to investigate the mechanical properties of cornea [37], breast cancer tissue [38], and several other tissues [39–42]. The combined use of OCE and PS-OCT has also been demonstrated [43].

Because the attenuation coefficient imaging, PS-OCT, and OCE visualize different types of tissue properties, it seems only natural to believe that use of a combination of the three will provide better discrimination of tissues and better visualization of the tissue structures. In this paper, we demonstrate a Jones matrix OCE system, which represents a unification of Jones matrix-based PS-OCT and compression OCE. This system is referred to as polarization-sensitive OCE (PS-OCE). The system simultaneously measures OCT, the attenuation coefficient, the birefringence, and the microstructural deformation [44] induced by tissue compression. A new method for visualization of multiple tissue properties, the depth-trajectory plot in a three-dimensional (3-D) tissue property space, is presented. The PS-OCE and the 3-D depth-trajectory visualization methods are then examined by applying them to ex vivo porcine tissues, including the aorta and esophagus. The high tissue discrimination ability of PS-OCE is demonstrated by comparison with corresponding histologies.

2. Methods and subjects

2.1. Polarization-sensitive optical coherence elastography

2.1.1. System configuration

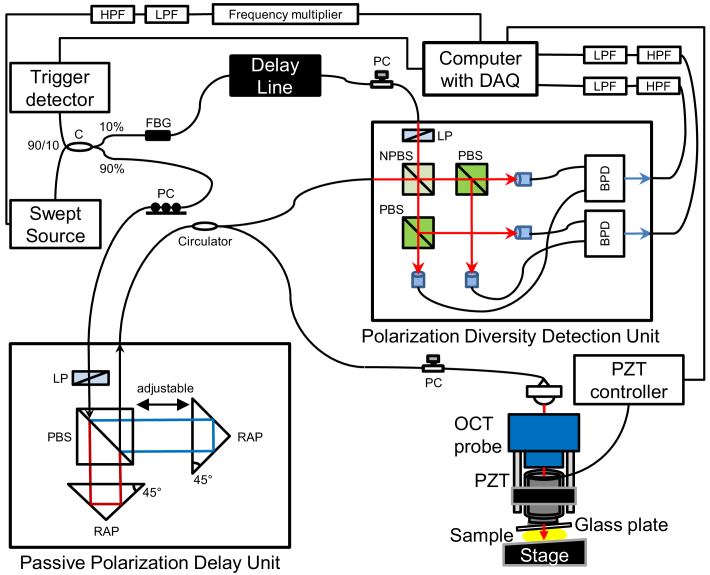
The PS-OCE system is newly developed. PS-OCE is a Jones matrix-based PS-OCT (JM-OCT) [45] equipped with a tissue compression probe to perform OCE measurements (such as that in Fig. 2(a) of Ref. [29]). The JM-OCT is implemented using a single-mode-fiber interferometer with a nonfiber passive polarization delay and polarization diversity detection [20,46–49]. The tissue compression probe is built using a piezoelectric (PZT) ring actuator.

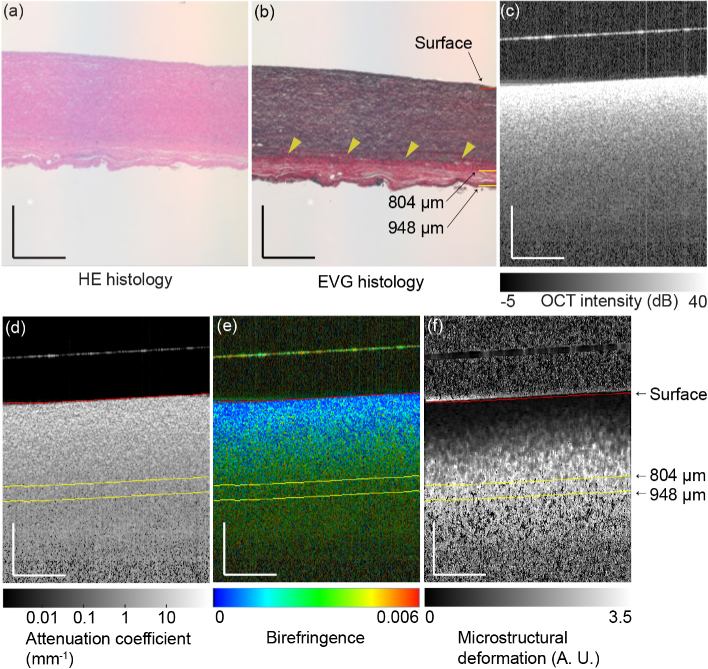
Fig. 2.

(a) H&E and (b) EVG histologies of the aorta. (c) OCT intensity, (d) attenuatin coefficient, (e) birefringence, and (f) MSD images of the aorta. The scale bars represent 0.5 mm × 0.5 mm. Arrow heads indicate the interface between the tunica media and the tunica externa. The surface of the glass plate appears as a hyperreflective line above the tissue surface in (c), (d), (e) and (f).

More specifically, the light source is a microelectromechanical systems (MEMS)-based wavelength sweeping laser source (AXP50124-8, Axun Technologies, MA) with a center wavelength of 1,310 nm, a coherence length of 40 mm, and a scanning rate of 50 kHz. The incident beam is split into reference and probe beams using a 90/10 coupler, with 90% for the probe. The incident beam is further split into two orthogonal independent polarizations and different delays are applied to each polarization using a compact encased passive polarization delay module (DE-G043-13, Optohub Co., Ltd, Saitama, Japan). This mutual delay results in depth-multiplexing of the two incident polarizations. The probe beam is collimated using a fiber-tip collimator (3.49 mm beam diameter; PAF-X-18-C, Thorlabs), steered using a two-axis galvanometric scanner (6220H, Cambridge Technology Inc., MA), and focused on the sample using an OCT objective (effective focal length = 54 mm; working distance = 42.3 mm; LSM04, Thorlabs) through a glass window (0.4 mm thickness) that is mounted on a ring-PZT actuator (HPSt 150/20-15/12 VS35 SG, Piezomechanik GmbH, Germany). The glass windows contact at the sample surfaces and apply a compression force for OCE measurement. This configuration is similar to that reported in Ref. [50].

The light that is backscattered from the sample is sent to a polarization diversity detection module (DE-G036-13, Optohub). In this module, the reference and probe beams are combined to generate an interference signal. The interference signal is then split into two polarization components and these polarization components are detected independently using two balanced photodetectors.

For signal acquisition, A-line acquisition triggers are generated using a fiber Bragg grating (≥80% reflectivity at 1354 nm; FBG-SMF-1354-80-0.2-A-(2)60F/E, Tatsuta Electric Wire and Cable Co., Ltd., Osaka, Japan). The built-in k-clock of the light source was cleaned up by low-pass (pass band: DC-158 MHz; ZX75LP-158-S+, Mini-Circuits, NY) and high-pass filters (pass band: 140-2000 MHz; ZX75HP-73-S+, Mini-Circuits, NY), and frequency-doubled using a frequency multiplier (multiplication factor of 2, 0.05-150 MHz input, 0.1-300 MHz output; MK-3, Mini-Circuits, NY) to obtain more sampling points to ensure a sufficiently large depth measurement range. And it is fed to the data acquisition board (0.5 GS/s maximum; ATS9350, Alazar Technologies Inc., Quebec, Canada) to act as a sampling clock. The k-linear spectral interference signals are thus detected, and an extended depth-measurement range of 9.9 mm in air (or 7.2 mm in tissue with a refractive index of 1.38) is achieved using the frequency-doubling approach.

It should be noted here that the two OCT images of the two incident polarizations are multiplexed at different depths. Therefore, the depth measurement range for each incident polarization channel is 3.6 mm in tissue, which is approximately half the extended measurement range. Because of the use of polarization diversity detection in addition to incident polarization multiplexing, this PS-OCE system provides four complex OCT images from a single scan and it forms a cumulative Jones matrix that is mathematically similar to the round trip Jones matrix of the sample.

The power incident on the sample is approximately 14 mW. The sensitivity was measured to be 104 dB for each of the four polarization channels. The stability of phase shift measurement was experimentally determined as 44.1 mrad with a static polyvinyl chloride sample (plastic eraser). In addition, the stability of displacement measurement was evaluated in the second paragraph of page 4 in Ref. [44]. The lateral resolution (1/e²-width) was 19 µm. The depth resolution (full width at half-maximum) was 19 µm in air (14 µm in tissue), while the depth-pixel separation was 10 µm in air (7.24 µm in tissue).

The JM-OCT and PS-OCE hardware is described in more detail in Refs. [44,49]. A schematic of the system is shown in Fig. 1 .

Fig. 1.

Schematic of the system. C: coupler; FBG: fiber Bragg grating; PC: polarization controller; LP: linear polarizer; PBS: polarizing beam splitter; RAP: right angle prism; NPBS: non-polarization beam splitter; BPD: balanced photodetetor; LPF: low-pass filter; HPF: high-pass filter.

2.1.2. Measurement protocol

The samples are measured using the following scanning protocol. Each B-scan consists of 512 A-lines and covers a 2.0 mm transversal line, i.e., 3.9 µm A-line interval. Since the optical lateral resolution is 19 µm, this scanning configuration results in 4.9-fold over sampling. This oversampling is necessary for digital-shifting-complex-correlation method used in Section 2.1.5 [51]. 512 B-scans were acquired sequentially at a single location. The PZT actuator increased the compression during the sequential B-scan acquisition process. A moderate amount of silicone oil (AK 35, Wacker Silicones, Munich, Germany) was used to lubricate the tissue-glass-plate interface. The overall compression during the 512 B-scan acquisition process was 12 µm, so the compression difference between each pair of adjacent B-scans was 0.023 µm. This measurement protocol ultimately provides a data cube composed of 512 pixel (depth) times 512 pixel (transversal) times 512 compression states. Each pixel consists of four complex OCT signals that form a cumulative Jones matrix.

The attenuation coefficient, the birefringence, and the microstructural deformation index are then computed from the Jones matrix, as described in Sections 2.1.3, 2.1.4, and 2.1.5, respectively.

2.1.3. Attenuation coefficient imaging

To compute the attenuation coefficient, we first computed a polarization-insensitive OCT intensity image. This polarization-insensitive image is the average of the absolute-squared intensities of four Jones matrix entries, i.e., four OCT signals corresponding to four polarization channels. The pixel-by-pixel depth-resolved attenuation coefficient is then computed using the method described by Eq. (18) in Ref. [2]. Here, the signal roll-off by the coherence length of the light source and the signal attenuation caused by confocal gating are not corrected.

In general, the scattering will be more dominant than the absorption in the tissue if the tissue contains less blood. Therefore, we consider the attenuation coefficient here as mainly representing the scattering property of the tissue.

2.1.4. Birefringence measurement

The sample birefringence, which is defined as local phase retardation, is computed using the measured Jones matrix. First, the depth-localized Jones matrix (the local Jones matrix) is computed from two Jones matrices that have a small depth separation [22]. In this study, the depth separation is 8 pixels (57.9 µm in tissue). The local phase retardation is then computed from the two eigenvalues of the local Jones matrix and is linearly scaled with respect to the birefringence using Eq. (2) from Ref. [26].

The birefringence is then processed further using a maximum a posteriori (MAP) birefringence estimator [26] to enhance its accuracy. In this study, the MAP estimator uses a 2 × 2-pixel (7.8 µm × 14.5-µm, transversal times depth) spatial kernel to estimate the birefringence value for each pixel. The MAP estimator also provides the reliability metric of the estimation for each pixel. A pseudo-color birefringence image is created for subjective observation by combining the OCT intensity, the birefringence, and the estimation reliability, as described in Section 3.4 of Ref. [26]. To form the pseudo-color image, the OCT intensity, the birefringence, and the reliability are used as the pixel brightness, the color hue, and the color saturation, respectively.

2.1.5. Microstructural-deformation elastographic imaging.

The mechanical properties of the sample are computed using the same method that was described in our previous publication [44]. Briefly, we used the digital-shifting-complex-correlation [52] based OCE method [44,53]. This method computes noise-corrected local correlation coefficient maps [54] between a target B-scan and a reference B-scan. These correlation maps were computed not only with the original reference B-scan but also with four digitally shifted versions of the B-scan, so a total of five correlation maps were obtained. These five correlation maps then provide five simultaneous equations [Eqs. (1)–(5) in Ref. [52]]. In-plane depth and lateral displacement maps, depth and lateral OCT resolution maps, and microstructural deformation (MSD) map are obtained by solving this set of simultaneous equations.

The MSD map represents the deformation of the microscopic tissue structures, which is smaller than the spatial resolution of the OCE (see Section 4.3 for a description of the OCE resolution). In this study, the MSD is used to represent the mechanical properties of the sample. Because the JM-OCT used four OCT images that corresponded to four polarization channels, four MSD maps were subsequently obtained. The final MSD map was obtained by weighted averaging of these four maps, where the weights used were the OCT intensities of each channel.

In this study, the target and reference B-scans were extracted from a B-scan sequence that was obtained as described in Section 2.1.2 with an interval of 40 frames (compression difference of 0.9 µm). The MSD map thus visualizes the MSD caused by this 0.9 µm compression. Here, we selected the 40-frame interval to ensure the displacement was linear to the compression within this interval. The linearity was computed by using phase sensitive axial displacement measurement method similar to Ref. [31]. The local correlation was computed using a 7 × 7-pixel [27.3 µm (transversal) × 50.7 µm (depth)] kernel. The MSD map that is used for subjective observation and further analysis is the average of 20 MSD maps that were computed from the B-scan sequence. The averaging range was selected based on the linearity of displacement to the compression. The details of the determination of the averaging range and its rationality is discussed extensively in Ref. [44].

2.1.6. Depth-trajectory plot

To provide a more intuitive understanding of the tissue properties, we plotted the tissue properties along the depth direction as a trajectory in a 3-D feature space. The three features of this feature space are the attenuation coefficient, the birefringence, and the MSD.

In this visualization procedure, the tissue surface is first segmented. (See Appendix A. for details of the segmentation procedure.) For each relative depth from the surface, each tissue property value, i.e., each feature, is averaged over the transversal field, except for the six pixels at each of the left and right ends. These left- and right-end pixels were excluded because the MSD values were computed using 7 × 7-pixel kernel and the MSD values at the ends were thus unreliable.

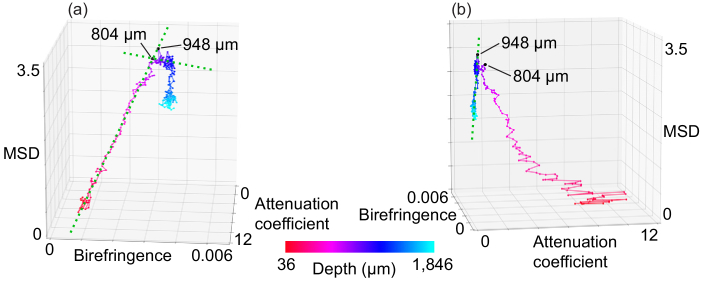
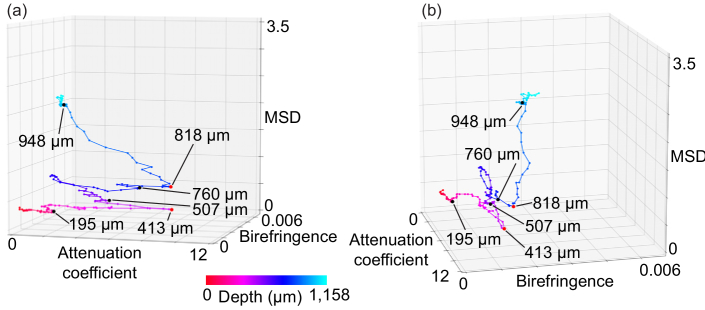
The depth-oriented alterations in the averaged tissue properties are then plotted in the 3-D feature space as a trajectory. We call this visualization a “depth-trajectory plot.” Examples of depth-trajectory plots are presented later in Figs. 4(a), 4(b), 6(a), and 6(b).

Fig. 4.

(a), (b) Depth-trajectory plots for the aorta from various angles (see also Visualization 1 ^{(2.4MB, mp4)} ).

Fig. 6.

(a), (b) Depth-trajectory plots of esophagus from various angles (see also Visualization 2 ^{(2.3MB, mp4)} ).

2.2. Sample preparation

We measured ex vivo porcine aorta and esophagus samples that were obtained from an abattoir (Tokyo Shibaura Zouki, Tokyo, Japan). The aorta was opened along the longitudinal direction. For the PS-OCE measurements, the sample was placed on a metal stage with the internal surface facing upward and contacting the glass plate for the OCE compression. The B-scan was then acquired along the longitudinal direction. The total thickness of the aorta was approximately 1 mm.

The esophagus was also opened along the longitudinal direction. The sample was then placed on a metal plate for the JM-OCE measurements with the internal surface contacting the glass plate. The B-scan was acquired along the circumferential direction. The total thickness of the esophagus was approximately 2 mm.

Both samples were also examined by bright field microscopy, as will be described in the next section (Section 2.3).

2.3. Histological imaging

Two types of histologies were obtained from both samples. To collocate the histology with the PS-OCE measurements, burn marks were imprinted on the sample as landmarks using a hot poker (i.e., an electric soldering iron tip) before the PS-OCE measurements. After the PS-OCE measurements, the samples were fixed using 10% formalin (Mildform 10N, Wako Pure Chemical, Osaka, Japan). The samples were then embedded in paraffin, and then tissue sections with 2-µm thickness were prepared for hematoxylin and eosin (H&E) and Elastica van Gieson (EVG) staining.

In the H&E-stained images, cytoplasm is observed as red, muscles are dark red, collagen is pale pink, and nuclei are either blue or purple. In the EVG-stained images, collagen appears as red, elastin is black, muscles are yellow, and cytoplasm also appears as yellow.

3. Results

3.1. Porcine aorta

3.1.1. Cross-sectional observation

The H&E- and EVG-stained histologies of the porcine aorta are shown in Figs. 2(a) and (b) , respectively. The EVG-stained histology [Fig. 2(b)] clearly shows the interface between the tunica media and the tunica externa (arrow heads), while the interface is unclear in the H&E-stained histology [Fig. 2(a)]. The tunica media contains a significant amount of elastin, so it appears in black in the EVG-stained histology. In contrast, the tunica externa is a collagenous tissue, so it appears in red.

Figure 2(c)–(f) show several types of OCT images, including the standard OCT intensity, attenuation coefficient, birefringence, and MSD images of the same aorta sample, respectively. Note that the depth scales of the OCT images and the histological images are identical here. Therefore, the same thickness in the image represents the same tissue thickness, given that the shrinkage of the histology is negligible.

The OCT intensity decreases monotonically along the depth direction and no specific boundary can be observed [see Fig. 2(c)]. It should be noted that there are some OCT signals in the region below the posterior boundary of the tissue. These signals may originate from multiply-scattered photons.

Similar to the OCT intensity, the attenuation coefficient decreases gradually along the depth direction [Fig. 2(d)] and no clear boundary between the tunica media and the tunica externa was observed.

The birefringence changes along the depth direction [Fig. 2(e)]. By comparing the birefringence with the histology [Figs. 2(a) and (b)], it is found that this change occurs even in the same tissue, i.e., the tunica media, which mainly consists of elastin. This birefringence change within the tunica media may be explained by depth-dependent microstructural variations. The high-magnification EVG histology is shown in Fig. 3 . The microstructure is well aligned in the shallow region [Fig. 3(b)] but becomes wavy in the deeper regions [Figs. 3(c) and (d)]. While this structure is too large to be the direct source of the structural birefringence, it may indicate that the finer fibrous structure may also vary along the depth. These variation in the finer fibrous structure can account for the birefringence change.

Fig. 3.

High-definition image of EVG histology of aorta. (b), (c), and (d) show enlarged images of the yellow windows in (a). The scale bars represent 0.5 mm × 0.5 mm.

Figure 2(f) shows the MSD map of the aorta. The MSD increases monotonically along the depth direction. This change may also be explained by the microstructural variation described above. The interface between the tunica media and the tunica externa is again not observed clearly.

3.1.2. Depth-trajectory analysis

Figures 4(a) and (b) show the depth-trajectory plots for the porcine aorta (see also Media-1). The first five points corresponding to the first five pixels from the segmented surface are not shown in this plot because they were strongly affected by segmentation errors. Two evident inflection points are observed in the trajectory at depth of 804 µm and 948 µm. Although the inflection points exist in a deep tissue region, the OCT signal intensity is still higher than the noise level at these points. The green dashed lines in Figs. 4(a) and (b) were drawn manually to indicate the direction of the trajectory and thus emphasize the inflection points. Comparison of the depth trajectories and the cross-sectional images shows that the 804 µm inflection point corresponds to the interface between the tunica media and the tunica externa. The 948 µm inflection point may indicate the posterior end of the sample. While the lines corresponding to these inflection points are not clear in the OCT images [Figs. 2(c)–(f)], they are easily recognized in the depth-trajectory plot. This may indicate that the depth-trajectory analysis provides improved tissue discrimination.

3.2. Porcine esophagus

3.2.1. Cross-sectional observation

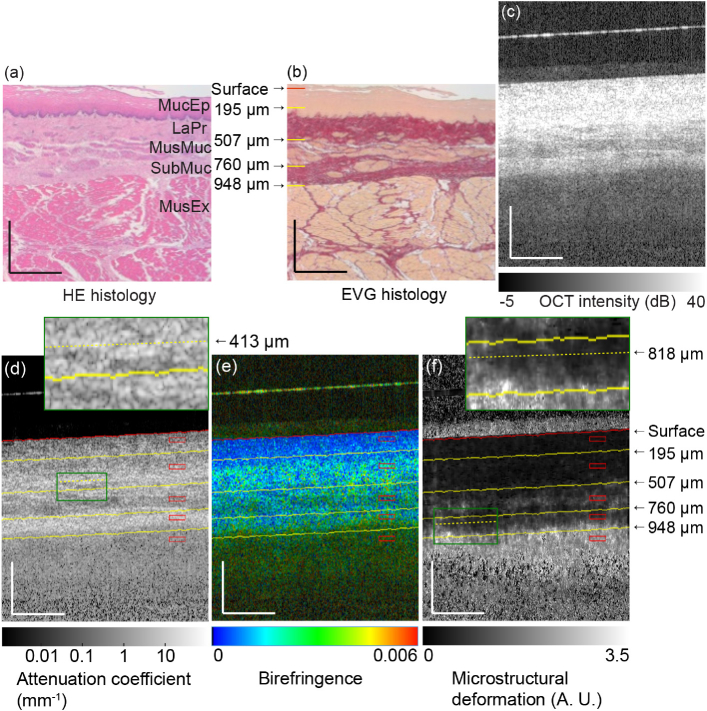
As shown in Fig. 5 , both the H&E- [Fig. 5(a)] and EVG- [Fig. 5(b)] stained histologies clearly show the layered tissue structure. The EVG histology in particular shows a stark contrast between the connective tissues (the lamina propria and submucosa) and the muscular tissues (the muscularis mucosa and muscularis externa). The connective tissues here appear in red because they are collagenous. The muscular tissues appear in yellow because they consist of smooth muscle. The mucosal epithelium consists of cytoplasm and also appears in yellow.

Fig. 5.

(a) H&E and (b) EVG histologies of esophagus. (c) OCT intensity, (d) attenuation coefficient, (e) birefringence, and (f) MSD images of esophagus. The scale bars represent 0.5 mm × 0.5 mm. MucEp: mucosal epithelium; LaPr: lamina propria; MusMuc: muscularis mucosa; SubMuc: submucosa; MusEx: muscularis externa. The surface of the glass plate appears as a hyperreflective line above the tissue surface in (c), (d), (e) and (f).

Figure 5(c) shows a cross-sectional OCT intensity image. The layered structure can again be observed, although it is not as clear as that in the histological images. The attenuation coefficient cross-section [Fig. 5(d)] shows the layered structures more clearly and is very similar to the EVG-stained histology. The connective tissues (the lamina propria and submucosa) appear as high-attenuation layers, while the muscular tissues (the muscularis mucosa and muscularis externa) appear as low-attenuation layers. These high- and low-attenuations probably correspond to high and low levels of scattering, respectively.

The mucosal epithelium appears as nonbirefringent tissue (blue) in Fig. 5(e). In contrast, the connective tissues show mild to moderate birefringence (green to yellow colors) because they consist of collagen. This result is consistent with Ref. [55].

The MSD image shows higher decorrelation (white) in the muscular tissues than the connective tissues in Fig. 5(f). This indicates that higher MSD was occurred in the muscular tissues during tissue compression than in the connective tissues.

3.2.2. Depth-trajectory analysis

Figures 6(a) and (b) show the depth-trajectory plots for the porcine esophagus, where both figures present the same plot but shown from different viewpoints (see also Media-2). To interpret these trajectory plots by comparing their inflections and tissue layers, we identified the depths of the tissue interfaces manually. For identification, the tissue surface was initially identified automatically (see Section A. for details), as indicated by the red lines in Figs. 5(d)–(f). Then, each interface among the tissue layers was identified manually in terms of its relative depth from the surface, as indicated by in the yellow lines. The interface between the mucosal epithelium and the lamina propria was identified in the birefringence image [Fig. 5(e)] as being 195 µm from the surface, where the birefringence clearly transitions from low (blue) to moderate (green). The other interfaces were identified in the attenuation coefficient image [Fig. 5(d)] as being 507, 760, and 948 µm from the surface based on their contrast differences. These landmark depths are indicated also on the EVG histology [Fig. 5(b)].

Clear correspondences between the inflection points in the depth trajectory and the tissue interface were found as follows. The interface between the mucosal epithelium and the lamina propria was found at 195 µm in the birefringence image. The corresponding inflection was found in the depth-trajectory plot.

The interface between the lamina propria and the muscularis mucosa was found 507 µm from the surface in the attenuation-coefficient image, and the corresponding inflection was clearly observed in the depth-trajectory plot. Another clear inflection was found at 413 µm, which is located within the lamina propria layer. At the corresponding depth in the attenuation-coefficient image [Fig. 5(d)], low-attenuation (dark) regions can be observed as indicated by the green box [see the inset of Fig. 5(d)]. The EVG histology [Fig. 5(b)] indicates that these are likely to be stray smooth muscle tissues in the lamina propria. Therefore, the area from 413 µm to 507 µm can be regarded as a transitional zone between the lamina propria and the muscularis mucosa and would account for the inflection occurring at 413 µm. Showing consistency with this proposal, the MSD begins to increase from the depth of 413 µm, as shown in Fig. 6(a).

The interface between the muscularis mucosa and the submucosa (at 760 µm) also shows a clear inflection in the depth-trajectory plot.

The segmented boundary between the submucosa and the muscularis externa occurred at the depth of 948 µm. However, no clear inflection was visible at the 948 µm depth, while a clear inflection was found instead at 818 µm. In the depth-trajectory plot, the MSD increases along the depth direction in the region deeper than 818 µm. The corresponding region in the MSD map [inset of Fig. 5(f)] shows an inhomogeneous appearance, i.e., some of the regions show high MSD while others show low MSD. Note here that the segmented tissue boundary was not actually a direct segmentation of the submucosa-muscularis externa interface, but was in fact an equal-depth line from the tissue surface and its accuracy was thus not high. We therefore suppose that the 818 µm depth represents the starting point of the transitional area from the submucosa to the muscularis externa.

In the deeper region, the changes in all the parameters become very low, and the trajectory becomes a tangle. This may be caused by the OCT signal being too low in the deep region.

4. Discussion

4.1. Interpretation of the attenuation coefficient, birefringence, and MSD

In this study, we used the attenuation coefficient, the birefringence, and the MSD as features that reflect the tissue’s properties. These features can be interpreted in terms of the tissue properties as follows.

The attenuation coefficient is a combination of the absorption and scattering coefficients of the tissue [2]. Because higher tissue density would cause higher scattering, the attenuation coefficient may reflect the tissue density. In a previous acoustic investigation, it was reported that connective tissues show higher tissue density and higher attenuation than muscle tissues [56]. Our optical results are consistent with these acoustic results.

It is known that collagenous tissues have birefringence [57]. In addition, the birefringence measured by PS-OCT is affected by both the collagen density and the orientation of the collagen fiber [58]. Therefore, the birefringence can be interpreted as an indicator of the presence of collagenous microstructures. In Fig. 2(e), the birefringence is shown to increase along the depth direction. This depth-oriented monotonic change in the birefringence may be caused by the gradual change in the microstructural orientation visualized in the EVG-stained histology (Fig. 3).

The microstructural deformation or MSD describes deformation of the tissue structure that is smaller than the imaging resolution. The imaging resolution is determined not only by the optical resolution but also by the computational kernel used to calculate the MSD (see Section 4.3 for details). It is natural to think that greater MSD will occur in softer tissue. It is also plausible to believe that tissues of lower density are likely to be softer. Therefore, we hypothesize that the high MSD, the softness property of the tissue, low tissue density, and a low attenuation coefficiet are interrelated.

In our results for the porcine esophagus [Fig. 5(f)], the MSD was higher in the muscular tissue than in the connective tissue. This result is consistent with the fact that the muscular tissue showed a lower attenuation coefficient [Fig. 5(d)].

4.2. Tissue discrimination capability of PS-OCE

We used three tissue parameters, which were denoted as features, including the attenuation coefficient, the birefringence, and the MSD to observe and discriminate between the tissues. Here, we use the esophagus case as an example and discuss its tissue discrimination capability. First, we discuss the appearance characteristics of each feature at each tissue layer (Section 4.2.1) and then we discuss the contributions of these features to the tissue discrimination performance (Sections 4.2.2 and 4.2.3).

4.2.1. Characteristics of features in esophageal tissues

The appearance characteristics of the features in the esophagus tissue (Sections 3.2.1 and 3.2.2) are summarized in Table 1 . In this table, MucEp is the mucosal epithelium, LaPr is the lamina propria, MusMuc is the muscularis mucosa, SubMuc is the submucosa, and MusEx is the muscularis externa. These abbreviations are used also in the later sections.

Table 1. Appearance characteristics of features for each of the tissue layers. MucEp: mucosal epithelium; LaPr: lamina propria; MusMuc: muscularis mucosa; SubMuc: submucosa; MusEx: muscularis externa.

	MucEp	LaPr	MusMuc	SubMuc	MusEx
Attenuation coefficient	Low	High	Low	High	Low
Birefringence	Low	Moderate	Moderate	Moderate	Moderate
MSD	Low	Low	High	Low	High

The attenuation coefficient is high in the connective tissues but low in the muscular tissues. The birefringence is moderate in all tissues other than the mucosal epithelium, where it is low. The MSD indicates low deformation in the connective tissues, but it was high in the muscular tissues. As evident from Table 1, the adjacent tissue layers have different characteristics for these features. It may thus be possible to discriminate between the layers using these features.

This tissue discrimination capability is discussed more quantitatively in the following sections (Sections 4.2.2 and 4.2.3).

4.2.2. Histogram distance for each layer

The tissue discrimination capabilities of each of the features are evaluated in a more quantitative manner by computing the histogram distance between each pair of tissue layers. The histograms were obtained from manually selected regions of interest (ROIs) in each layer, where small ROIs were used to avoid inclusion of other tissue types such as stray smooth muscles [indicated by the red boxes in Figs. 5(d)–(f), where each ROI consists of 240 points] and the Bhattacharyya distance [59] was used as the histogram distance. The Bhattacharyya distance represents the similarity distance between two histograms, i.e., the Bhattacharyya distance becomes zero if the histograms are identical, while it becomes larger as the difference between the histograms increases. It finally reaches a value of 1 if there is no overlap between the histograms.

The Bhattacharyya distances for each of the features among the tissue layers are summarized in Tables 2 (for the attenuation coefficient), 3 (for the birefringence), and 4 (for the MSD).

Table 2. Bhattacharyya distances for the attenuation coefficient among the tissue layers. MucEp: mucosal epithelium; LaPr: lamina propria; MusMuc: muscularis mucosa; SubMuc: submucosa; MusEx: muscularis externa. Red font indicates distances less than 0.700.

	MucEp	LaPr	MusMuc	SubMuc	MusEx
MucEp	0.000	0.751	0.495	0.930	0.530
LaPr	-	0.000	0.624	0.598	0.603
MusMuc	-	-	0.000	0.861	0.437
SubMuc	-	-	-	0.000	0.850
MucEx	-	-	-	-	0.000

Table 3. Bhattacharyya distances for the birefringence among the tissue layers. MucEp: mucosal epithelium; LaPr: lamina propria; MusMuc: muscularis mucosa; SubMuc: submucosa; MusEx: muscularis externa. Red font indicates distances less than 0.700.

	MucEp	LaPr	MusMuc	SubMuc	MusEx
MucEp	0.000	0.786	0.697	0.874	0.937
LaPr	-	0.000	0.598	0.575	0.777
MusMuc	-	-	0.000	0.620	0.743
SubMuc	-	-	-	0.000	0.733
MusEx	-	-	-	-	0.000

Table 4. Bhattacharyya distances for MSD among the tissue layers. MucEp: mucosal epithelium; LaPr: lamina propria; MusMuc: muscularis mucosa; SubMuc: submucosa; MusEx: muscularis externa. Red font indicates distance less than 0.700.

	MucEp	LaPr	MusMuc	SubMuc	MusEx
MucEp	0.000	0.278	1.000	0.971	1.000
LaPr	-	0.000	1.000	0.954	1.000
MusMuc	-	-	0.000	0.605	0.998
SubMuc	-	-	-	0.000	1.000
MusEx	-	-	-	-	0.000

In these tables, the Bhattacharyya distance was written in red font if it is smaller than 0.700. This represents an indicator of lower discrimination ability between the two tissue types. Therefore, some of the features only show low discrimination ability for some combinations of the tissues. The mean and minimum Bhattacharyya distances are 0.668 (mean) and 0.437 (minimum) for the attenuation coefficient, 0.734 (mean) and 0.575 (minimum) for the birefringence, and 0.881 (mean) and 0.278 (minimum) for the MSD.

The overall tissue discrimination abilities of these three features can be represented by the maximum distance among the features. Table 5 shows the maxima of the three Bhattacharyya distances for the three features. The table shows that all combinations of the tissue have large Bhattacharyya distances, where even its minimum is 0.786 (between the mucosal epithelium and the lamina propria), and the mean distance is 0.957. This indiates that each combination of the tissue layers showed large differences in at least one of the three features.

Table 5. Maximum Bhattacharyya distances among the birefringence, attenuation coefficient, and MSD. MucEp: mucosal epithelium; LaPr: lamina propria; MusMuc: muscularis mucosa; SubMuc: submucosa; MusEx: muscularis externa. No combination of the tissue layers shows a Bhattacharyya distance of less than 0.700.

	MucEp	LaPr	MusMuc	SubMuc	MusEx
MucEp	0.000	0.786	1.000	0.971	1.000
LaPr	-	0.000	1.000	0.954	1.000
MusMuc	-	-	0.000	0.861	0.998
SubMuc	-	-	-	0.000	1.000
MusEx	-	-	-	-	0.000

4.2.3. Tissue discrimination in dimension-reduced feature space

The previous section (Section 4.2.2) indicated that simultaneous usage of the three features will provide a good discrimination capability. This tissue discrimination capability can be understood intuitively by visualizing the data points for each tissue layer in a low-dimensional reduced feature space.

Here, we used t-distributed stochastic neighbor embedding (t-SNE) [60] to reduce the dimensionality. Here, we used t-SNE rather than other dimensionality reduction method, such as principal component analysis (PCA), spectral-embedding, or isomap. Because, PCA and isomap were found not to separate the five tissue types. Spectral-embedding was found to work somehow. However, t-SNE gave clearer visualization than the spectral-embedding. The data points from the same ROIs studied in Section 4.2.2 [red boxes in Figs. 5(d)–(f)] were processed using t-SNE. Because each ROI consists of 240 points and five ROIs (corresponding to five tissue layers) were used, 1,200 points were processed in total using t-SNE.

In Fig. 7(a) , the data points are plotted in a reduced 2-D feature space, where each axis represents the first and second quantities obtained by t-SNE, which are denoted by t-SNE1 and t-SNE2. Here, the data points of the different layers were visualized using different colors; the mucosal epithelium is orange, the lamina propria is blue, the muscularis mucosa is green, the submucosa is yellow, and the muscularis externa is red. It is evident from the figure that the muscularis externa (red) is clearly distinguishable from the other tissues. The mucosal epithelium (orange) also forms a nearly independent cluster. We can thus conclude that these two tissues can be discriminated from each other and also from the other tissues.

Fig. 7.

Distributions of (a) five ROIs and (b) three ROIs of porcine esophagus when visualized using t-SNE.

The lamina propria (blue), the submucosa (yellow), and the muscularis mucosa (green) are not clearly separated in this 2-D feature space. We therefore applied t-SNE again to the data sets, but only for these three tissues (720 points in total). Figure 7(b) shows the results of this second t-SNE process. Note that the axes in the plot represent the first and second t-SNE features but they are not the same quantities as used in the first t-SNE process. In this plot, it is found that the three tissues are readily distinguishable.

These results indicate that a combination of three features, i.e., the attenuation coefficient, the birefringence, and the MSD, and the two-step dimensionality reduction step by t-SNE enable discrimination of the five tissue types of the porcine esophagus. For the simplest example, the mucosal epithelium (orange) and the muscularis externa (red) can be discriminated or equivalently segmented by applying a machine learning-based discrimination algorithm such as a support vector machine in the feature space of t-SNE1 and t-SNE2 shown in Fig. 7(a). Then, the other three tissues can be discriminated (segmented) from each other in the second reduced feature space shown in Fig. 7(b) using the same discrimination algorithm.

4.2.4. Summary of tissue discrimination results

The findings in Section 4.2 can be summarized as follows. The appearance characteristics of each tissue layer (Section 4.2.1) suggested qualitatively that each adjacent tissue layer could be distinguished from each other, i.e., tissue boundaries can be found using the three features of the attenuation coefficient, the birefringence, and the MSD. This is consistent with the findings from the depth-trajectory visualization process [Fig. 6].

The histogram distance analysis (Section 4.2.2) indirectly suggests that the five tissue layers can be distinguished using these three features. Note that the findings presented in Section 4.2.1 indicate that only adjacent tissue layers can be distinguished, while the histogram analysis indicates that any combination of the tissues can be distinguished.

Finally, the t-SNE based dimensionality reduction process (Section 4.2.3) showed direct evidence to indicate that the five tissues can be distinguished using the three features of PS-OCE. Notably, this tissue discrimination (segmentation) can be performed without spatial or structural information while using the feature values alone. This suggests that this segmentation method would be able to discriminate not only clearly layered tissues but also stray tissues, such as the stray muscle that was discussed in Section 3.2.2.

4.3. Resolutions

The spatial resolutions of the attenuation coefficient map were defined by two independent factors. The first is the optical resolution of the OCT and the second is the depth-pixel separation because the attenuation coefficient was calculated using pixel-by-pixel differences in intensity along the depth direction. The OCT imaging resolution was defined by both the optical resolution and the pixel separation. In the PS-OCE system used in this work, the optical resolutions were 19 µm (lateral) and 14 µm (depth in tissue), while the pixel separations were 3.9 µm (lateral) and 7.2 µm (depth in tissue). Therefore, the lateral and depth OCT image resolutions were dominated by the optical resolution, with values of $\mathrm{\Delta }{x}_{\text{oct}}$ = 19 µm (lateral) and $\mathrm{\Delta }{z}_{\text{oct}}$ = 14 µm (depth in tissue). The depth-pixel separation is, as noted above, $\mathrm{\Delta }{z}_{\text{ps}}$ = 7.2 µm (depth in tissue). The overall resolution of the attenuation coefficient map was defined via the convolution of these two factors and it was roughly estimated to be $\mathrm{\Delta }{x}_{\text{ac}}$ = $\mathrm{\Delta }{x}_{\text{oct}}$ = 19 µm (lateral) and $\mathrm{\Delta }{z}_{\text{ac}}$ = $\mathrm{\Delta }{z}_{\text{oct}}$ + $\mathrm{\Delta }{z}_{\text{ps}}$ = 21 µm (depth in tissue).

The spatial resolutions of the birefringence images were defined by three independent factors, including the optical resolution of the OCT, the depth separation for the birefringence calculations (depth-size of the local Jones matrix) [22], and the kernel size of the MAP birefringence estimator [26]. The first factor, the optical resolution, is identical to that in the discussion above. The second factor, the depth separation for the birefringence calculation, is the size of the local area in which a local phase retardation, or equivalently the birefringence, is computed. In the PS-OCE system used in this work, this depth-size is $\mathrm{\Delta }{z}_{\text{bds}}$ = 8 pixels (57.9 µm depth in tissue). The third factor, the birefringence estimation kernel size, was 2 × 2 pixels. Therefore, the kernel occupied $\mathrm{\Delta }{x}_{\text{bek}}$ = 7.8 µm (lateral) and $\mathrm{\Delta }{z}_{\text{bek}}$ = 14.5 µm (depth in tissue). The overall resolution of the birefringence measurements was defined via the convolution of these factors. Therefore, the rsolution was roughly estimated to be $\mathrm{\Delta }{x}_{\text{biref}}$ = $\mathrm{\Delta }{x}_{\text{oct}}$ + $\mathrm{\Delta }{x}_{\text{bek}}$ = 27 µm (lateral) and $\mathrm{\Delta }{z}_{\text{biref}}$ = $\mathrm{\Delta }{z}_{\text{oct}}$ + $\mathrm{\Delta }{z}_{\text{bds}}$ + $\mathrm{\Delta }{z}_{\text{bek}}$ = 86 µm (depth in tissue).

The spatial resolutions of the MSD were defined by three independent factors, including the optical resolution of the OCT, the kernel size of the correlation computation, and the digital shifts in the reference B-scan. The latter two factors were associated with the digital-shifting-complex-correlation-based OCE method [44,52]. The first factor, the optical resolution, is identical to that in the previous discussions above. The second factor, the correlation kernel size, was 7 × 7 pixels, so the kernel occupied $\mathrm{\Delta }{x}_{\text{ck}}$ = 27.3 µm (lateral) and $\mathrm{\Delta }{z}_{\text{ck}}$ = 50.7 µm (depth in tissue). The third factor, the digital image shift, was ± 1 pixel. This corresponded to $\mathrm{\Delta }{x}_{\text{ds}}$ = 7.8 µm (lateral) and $\mathrm{\Delta }{z}_{\text{ds}}$ = 14.5 µm (depth in tissue). The overall resolution of the MSD was defined via the convolution of these factors. Therefore, the resolution was roughly estimated to be $\mathrm{\Delta }{x}_{\text{msd}}$ = $\mathrm{\Delta }{x}_{\text{oct}}$ + $\mathrm{\Delta }{x}_{\text{ds}}$ = 54 µm (lateral) and $\mathrm{\Delta }{z}_{\text{msd}}$ = $\mathrm{\Delta }{z}_{\text{oct}}$ + $\mathrm{\Delta }{z}_{\text{ck}}$ + $\mathrm{\Delta }{z}_{\text{ds}}$ = 79 µm (depth in tissue). It is noteworthy that Hepburn et al. showed that the resolution simulated with a similar convolution model well corresponded to that obtained by experiments [61].

5. Conclusions

We have constructed a PS-OCE system that is capable of measuring the optical and mechanical properties of tissue samples simultaneously. This PS-OCE system was applied to ex vivo porcine esophagus and aorta tissues, and simultaneous measurements of the attenuation coefficient, the birefringence and the MSD of these tissues was demonstrated. The PS-OCE images and the depth-trajectory plots were carefully compared with the histological cross-sections of the tissues and it was found that the tissue boundaries in the histological images appeared as inflection points in the depth-trajectory plots. Therefore, the PS-OCE images contain comparable quantities of information to that in the EVG-stained histology to enable identification of the tissue boundaries. The tissue discrimination ability was further investigated through histogram analysis and t-SNE visualizations of the attenuation coefficient, birefringence, and MSD of the esophagus. The results of these analyses indicated that the PS-OCE measurements acquire sufficient information to distinguish all tissue layers found in the EVG histology. We thus conclude that PS-OCE is highly capable of performing noninvasive tissue classification processes.

A. Surface segmentation method

Surface segmentation of the B-scan images was performed using the Fiji distribution of ImageJ [62].

First, a Gaussian filter (sigma = 2) followed by a Sobel filter were applied to an OCT intensity image to perform edge detection. The image was then converted into a binary mask by applying a threshold that was determined using Otsu’s method. The binary mask was then skeletonized and a morphological closing operation (a dilation followed by an erosion with a 3 × 3 square structuring element) was applied. In this map, the pixels that correspond to a clear interface in the image, such as a tissue surface, are given a value of 1 (true); otherwise, the pixels are given a value of 0 (false). To remove any erroneous true pixels, clusters of true pixels with a size of less than 100 pixels were removed. A continuous surface curve can now be observed in the binary image but it still contains some minor stray true pixels. These minor stray pixels can correctly be ignored in the following step.

The final estimation of the tissue surface is then performed as follows. First, we manually select a starting point, i.e., a starting A-line and a starting depth, which must be deeper than the surface, and there must be no stray true pixels within the region between the starting depth and the surface. Next, on the starting A-line, the nearest true pixel from the starting point is selected as a surface pixel. Then, the true pixels within a ±3-pixel depth on an adjacent A-line are selected, and the deepest pixel among these selected pixels is then selected as the surface pixel for this A-line. Surface pixels in all the A-lines are selected sequentially for both the right and left directions in the same manner. After this process is applied to all the B-scans, a 2-D surface map consisting of 1D surface arrays of all the B-scans is obtained. A 2-D median filter (a circular kernel with a 3-pixel radius) is used to remove spikes from the surface map.

The entire process, with the exception of selection of the starting point for surface detection (where the same starting point is used in all B-scans), was performed automatically.

Funding

Japan Science and Technology Agency10.13039/501100002241 (JPMJMI18G8); Japan Society for the Promotion of Science10.13039/501100001691 (15K13371, 18H01893, 18J13841); Otsuka Toshimi Scholarship Foundation.

Disclosures

AM, EL: Kao Corp. (F), Yokogawa Electric Corp. (F), Topcon (F), Tomey Corp (F), Nidek (F). SM, YY: Kao Corp. (F), Yokogawa Electric Corp. (F), Topcon (F), Tomey Corp (F, P), Nidek (F). KY, MK, SS: (E) Kao Corp.