Abstract
Laser Doppler holography was introduced as a full-field imaging technique to measure blood flow in the retina and choroid with an as yet unrivaled temporal resolution. We here investigate separating the different contributions to the power Doppler signal in order to isolate the flow waveforms of vessels in the posterior pole of the human eye. Distinct flow behaviors are found in retinal arteries and veins with seemingly interrelated waveforms. We demonstrate a full field mapping of the local resistivity index, and the possibility to perform unambiguous identification of retinal arteries and veins on the basis of their systolodiastolic variations. Finally we investigate the arterial flow waveforms in the retina and choroid and find synchronous and similar waveforms, although with a lower pulsatility in choroidal arteries. This work demonstrates the potential held by laser Doppler holography to study ocular hemodynamics in healthy and diseased eyes.
1. Introduction
The ocular circulation is of major interest for the study of increasingly prevalent diseases such as diabetic retinopathy, glaucoma, and hypertension. Other fundus diseases such as retinal vein occlusion and central serous chorioretinopathy are even more directly linked with the fundus perfusion. For the purposes of screening these diseases early on, understanding their pathophysiologies, and monitoring the efficiency of administrated treatments, measuring blood flow in the retina and choroid is of great importance. In the last decade, the irruption and development of optical coherence tomography (OCT) and subsequently of OCT-angiography (OCT-A) has allowed for a comprehensive study of the relationship between diseases affecting the eye and the fundus vasculature anatomy by its ability to resolve the retinal microvasculature [1,2], and the thickness of the vascular choroidal compartment [3]. Another approach to investigate the ocular circulation is the study of the blood flow dynamics, which requires a temporal resolution currently not in the reach of present day OCT-A systems [4]. First, blood flow monitoring is important to evidence retinal hypoperfusion inherent to many ocular diseases. For example laser speckle flowgraphy can measure abnormal perfusion in some types of glaucoma [5,6], and Doppler ultrasound is able to detect decrease of the ocular circulation [7]. Going further into the study of blood flow dynamics, a time-resolved analysis of blood flow changes contains a wealth of information as the arterial waveform profile is influenced by the arterial compliance and peripheral resistance [8–10]. Several approaches are used to investigate the Doppler waveform profiles such as the study of the arterial peak systolic and end diastolic blood flow velocity [11,12], which can be combined to produce indices to characterize the pulsatility [13]. Another approach is to derive mathematical metrics from the pulse waveform curve such as skew, blowout time, rising rate and falling rate [14–16]. A wave decomposition analysis of ultrasonic Doppler flow velocity waveforms has also proven able to identify microvascular hemodynamic abnormalities in the ophthalmic and carotid artery in cases of diabetic retinopathy [17]. Another factor to take into consideration for the shape and amplitude of the arterial flow profile is the site of measurement of the waveform. As reflection flow and pressure waves superimpose with the forward waves, they modify the incident arterial flow profile on a predictable basis with ageing and diseases [18–20]. Reflection waves are rapidly dissipated when propagating, thus it would be of great interest to measure the flow waveforms as close as possible from the arteriolar branching as it is considered to be the main sites of wave reflections [21]. This flow waveform is all the more interesting as measurements of an impaired pulsatile arterial flow could provide more information regarding potential microvascular damages provoked by an overly high perfusion pressure.
For the purpose of measuring blood flow directly in the retina, optic nerve head (ONH), and choroid, laser Doppler flowmetry (LDF) makes use of the time profile characteristics of the Doppler power spectrum density (DPSD) [22–24]. Determining the Doppler broadening induced by the distribution of velocities and scattering angles allows to measure blood flow parameters such as volume and velocity. A short-time Fourier transform method is carried out to analyze the self-interfering light backscattered by the fundus, and blood flow variations are measured with a temporal resolution sufficient to observe the DPSD changes transient to cardiac cycles. However, this technique is performed only at a single location, and although full-field alternatives have been proposed [25], they have not been implemented in the retina as they require more illumination than permissible. Scanning implementation with the aim of imaging a two dimensional (2-D) field of view face a dilemma between temporal resolution and the spatial extent of the investigated area. Thus so far flying spot and line-scanning LDF have not demonstrated hemodynamic measurements over a 2-D field of view [26, 27]. Laser Doppler holography (LDH) is a digital holographic method that relies on measuring the DPSD from the interference between a Doppler broadened beam and a holographic reference beam, allowing to extract a blood flow contrast similar to LDF [28–30]. The additional reference beam is a plane or spherical wave and provides two advantages: it allows to use a higher camera frame rate by simply increasing the reference beam power, and it opens the door to all sorts of numerical manipulation of the wave field, such as numerical refocusing and digital adaptive optics [31,32], or synthetic subaperture Doppler measurements [33–35]. This way it becomes possible to perform a pixel wise parallel estimation of the DPSD in the human retina, which leads to simultaneous measurements of Doppler broadening over the 2-D field of view. We have previously used LDH to make full-field non-directional blood flow measurements in the retina with a few milliseconds of temporal resolution [36]. We have then shown that the depth of field of a few hundreds microns provided by LDH allows to encompass both the retinal and choroidal vessels in a single imaging plane, and LDH is able to reveal non-invasively the choroidal vasculature while providing quantitative Doppler frequency shift measurements [37]. We have used this feature to show the large differences of blood flow existing between arteries and veins in the choroid, and proposed an arteriovenous differentiation of choroidal vessels based on a flow analysis. In this article, we more carefully examine the waveform profiles that can be measured in retinal arteries and veins after spatio-temporal filtering, and show that the flow behavior is very different according to the vessel type. We then demonstrate the use of indices to characterize power Doppler waveforms: 2-D maps of the local vascular resistivity index (RI) and coefficient of variation (CV) are shown. These metrics can be calculated over a few cardiac cycles and provide clear discrimination of arterial and venous flow in the retina. Finally, we analyze the dynamic flow in the choroid and demonstrate that the spatially averaged baseline signal (dominant signal) in laser Doppler measurements is close to the choroidal arterial waveform.
2. Methods
2.1. Optical setup
We use the laser Doppler holographic setup presented in [36]. Briefly, it consists of a fiber Mach-Zehnder optical interferometer where the light source is a 45 mW and 785 nm single frequency laser diode (Newport SWL-7513-H-P). It is an external cavity laser diode that is spatially and temporally coherent, with a 200 kHz spectral linewidth which is favorable for laser speckle contrast measurements [38]. The power of the laser beam incident at the cornea is 1.5 mW of constant exposure and covers the retina over a disk with a radius of 3 to 4 mm. This irradiation level is compliant with the exposure levels of the international standard for ophthalmic instruments ISO 15004-2:2007. Informed consent was obtained from the subjects, experimental procedures adhered to the tenets of the Declaration of Helsinki, and study authorization was sought from the appropriate local ethics review boards (CPP and ANSM, IDRCB number: 2019-A00942-5). The results shown were obtained from 7 eyes of 5 different subjects, with ages ranging from 24 to 33.
The wave backscattered by the retina is combined with the reference wave using a non-polarizing beamsplitter cube. The polarization of the reference wave is adjusted with a half-wave plate and a polarizer to optimize fringe contrast. The interferograms formed in the sensor plane are recorded using a CMOS camera (Ametek - Phantom V2511, quantum efficiency 40%, 12-bit pixel depth, pixel size 28 μm) with a frame rate fS of typically 60 or 75 kHz in a 512 × 512 format. The diffracted speckle pattern is numerically propagated to the retinal plane using the angular spectrum propagation method [39]. The configuration is on-axis and the reconstruction distance is large enough so that the holographic twin image energy is spread over the reconstructed hologram and has no appreciable effect on the resulting image. The following data processing consists of measuring the local optical temporal fluctuations of the holograms cross-beating terms in order to make quantitative measurements from the DPSD.
2.2. Doppler processing
After numerical propagation of the recorded interferograms, the beat frequency spectrum of the reconstructed holograms is analyzed pixel-wise by short-time Fourier transform:
| (1) |
Where H(x, y, τ) is the hologram complex amplitude at pixel indexes (x,y) and time τ, and twin is the integration time of the sliding window which determines the temporal resolution of the system. In order to optimize the trade-off between signal-to-noise ratio (SNR) and temporal resolution (twin), we typically use a short-time window with 512 images (6.8 ms with a 75 kHz frame rate) and an overlap between two consecutive windows of 256 images.
The Doppler spectrum contains a lot of hemodynamic information that can be retrieved through the changes over time of amplitude and frequency of the spectrum. In the conventional data processing for optical [22], and ultrasound Doppler measurements [40,41], the zeroth moment, first moment, and normalized first moment of the DPSD reveal local blood volume, blood flow, and blood velocity, respectively. The zeroth and first moment of the DPSD are here denoted M0(x, y, tn) and M1(x, y, tn), and are calculated in the following way:
| (2) |
| (3) |
In the rest of the article, the zeroth moment is also referred to as “power Doppler”; it is computed as the area under the power spectrum curve so it represents the number of scatterers traveling at any speed above the frequency threshold. Consequently it depends on the quantity of moving red blood cells, i.e. the blood volume in a given pixel. The frequency content of the spectrum reflects the velocity of the sampled area; it is analyzed using the normalization of the first moment by the zeroth moment, which mathematically yields the mean Doppler frequency shift:
| (4) |
We have empirically determined that for fmean the best results were obtained when removing the first term of the Fourier spectrum, i.e. with a frequency range of [0.5 kHz – fS/2]. The interferometric zero-order term is naturally removed by the spectrum analysis which gives more weight to higher frequencies. As for M0, the upper integration boundary is also generally set to fS/2, but a higher low cut-off frequency is used so as to remove bulk motion noise. This low cut-off frequency is typically set to 6 kHz to obtain a power Doppler image where smaller vessels can be revealed, or 10 kHz if the aim is to measure a waveform without any contribution from ocular movement in the signal (except for micro-saccades). The result of this high-pass filtering is that M0 not only depends on blood volume but also on blood velocity as when the flow speed increases, a part of the spectrum reaches the frequency threshold and becomes integrated in M0. This effect is analyzed in section 3.2.
Finally M0(x, y, tn) and M1(x, y, tn) images are compensated for the non-uniform illumination of the retina and vignetting. To do so, each image is divided by its spatially filtered (blurred) self. A conservation of the image energy (calculated as the sum of all pixel intensity) is used so that each image has the same energy before and after division. Only the spatial distribution of energy is changed while the total energy is conserved.
2.3. Indices to characterize the Doppler waveform
Several indices quantitatively characterizing Doppler waveform profiles have been introduced so as to study circulatory parameters [13]. In this approach, the vascular circulation is described as an alternative current circuit, where the blood flow in the arterial system is a pulsatile phenomenon driven by periodic myocardiac contractions, and whose waveform profile is shaped by both upstream and downstream circulatory parameters [42,43]. The higher compliance at the level of the large elastic arteries helps buffering the intermittent inflow in order to convert it into a steadier flow. The end of the vascular tree also plays an important role by offering a vascular resistance to the incoming flow at the arteriolar level. The opposition to blood flow due to friction on the vessel walls encompasses parameters such as blood viscosity, vessel length, and total cross-sectional area of the arterial bed. In the analogy with electrical circuits, the arterial compliance plays a capacitive role and the downstream opposition to flow acts as a resistance. Therefore, the flow wave is shaped by fundamental properties of the vasculature, and analyzing the Doppler waveform is of great interest as a surrogate means to assess these properties. The indices used for the purpose of studying the hemodynamic modulation of the Doppler waveform have various discriminatory performances and abilities to reflect different circulatory parameters; their use has become standard in Doppler ultrasound [13,44,45]. In this work, we used two of these metrics: the first one is known as the Pourcelot or resistivity index (RI) [46]. For a given function g, the RI is calculated pixel-wise using the following formula:
| (5) |
Where g(x, y, t)syst and g(x, y, t)diast are the values of the function g at the peak systolic and end diastolic time points, which are manually determined. In a compliant vasculature, the resisitivity index increases with the vascular resistance peripheral to the measurement site [47–49]. However it is also subject to changes of arterial compliance as a reduced upstream arterial compliance produces an impaired pulsatile flow with abnormally high systolic flow and lower than normal diastolic flow. Therefore it has been suggested to name it impedance index instead [47,50]. The second metric we used is a simple estimation of the local coefficient of variation of the power Doppler temporal fluctuations, calculated as the local standard deviation normalized by the local average.
| (6) |
Where σg(x,y) and μg(x,y) denote the standard deviation and average of temporal fluctuations calculated pixel-wise over a few cardiac cycles. With both the RI and CV metrics, the areas where the systolodiastolic variations are greater come out with greater values, whereas areas with lower variations have lower values.
3. Results in the retina
3.1. Pulsatile flow in retinal arteries and veins
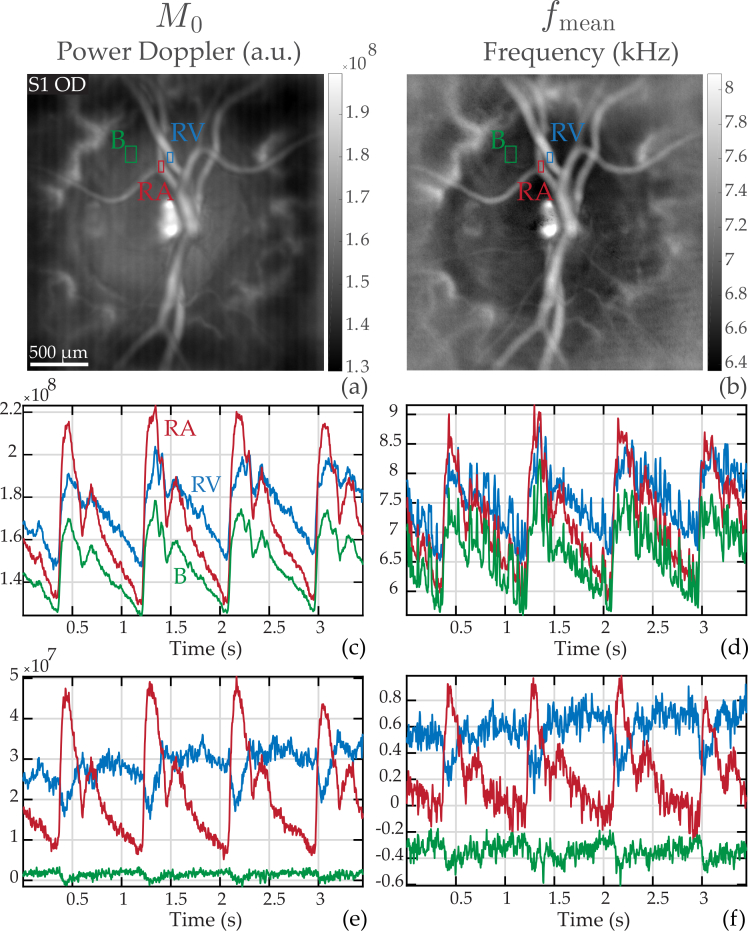
In Fig. 1, we analyze the temporal changes in power Doppler M0(x, y, tn) and mean Doppler frequency shift fmean(x, y, tn) in different regions of interest (ROIs). The LDH acquisition was performed close to the optic nerve head, at 75 kHz, and M0 was integrated over the frequency range [10–37 kHz] to fulfill Nyquist requirement, while we used the frequency range [0.5–37 kHz] for the calculation of fmean. In Fig. 1(a) and (b), we show the power Doppler, and mean Doppler frequency shift images averaged over time. In Fig. 1(a–b) are shown the ROIs used to measure the local pulsatile flow; the red, blue, and green boxes mark an artery, a vein, and an area in the background devoid of any large vessels. In Fig. 1(c) and (d), we have plotted the local dynamic power Doppler and mean frequency shift variations in the depicted ROIs and found very similar variations in all areas. So, in Fig. 1(e) and (f), the baseline signal (spatially averaged over the entire field of view, also referred to as dominant signal), is subtracted from the same measurements, i.e. we measure M0 − 〈M0〉x,y, and fmean − 〈fmean〉x,y. The difference between the raw movie and the movie corrected from the spatial average are shown in Visualization 1 (23.8MB, avi) and Visualization 2 (41.4MB, avi) , for M0 and fmean.
Fig. 1.
Analysis of the dynamic changes in power Doppler signal and mean Doppler frequency shift, which supposedly yield volume and velocity, respectively. (a) and (b): power Doppler image M0(x, y) and mean frequency shift fmean(x, y) temporally averaged; the red, blue, and green ROIs mark a retinal artery (RA), a retinal vein (RV), and the background (B), respectively. (c) and (d) temporal traces of M0 and fmean in the depicted ROIs. (e) and (f): temporal traces in the same ROIs when subtracting the spatially averaged signal over the entire image, i.e. M0 − 〈M0〉x,y, and fmean − 〈fmean〉x,y. See Visualization 1 (23.8MB, avi) and Visualization 2 (41.4MB, avi) for the juxtaposed movies of M0 and fmean corrected and not-corrected from the spatial average. Removing the spatial average allows to reveal the retinal flow waveforms.
The power Doppler and mean Doppler frequency shift images are similar but some difference of contrast can be noticed in certain features, especially the optic disc appears darker with the mean frequency image than with the power Doppler image. As mentioned in section 2, the power Doppler supposedly reflects the local blood volume while the mean frequency shift is related to the local blood velocity; fmean is measured in absolute frequency units (kHz) whereas M0 is measured in arbitrary units (a.u.). A first observation on the signal dynamic changes that can be made from Fig. 1(c) and (d), is that the raw measurements performed with LDH are very correlated between all the ROIs. For both the power Doppler and mean frequency shift, all measured waveforms have very similar profiles. The systolic and diastolic times are very well visible, and the dicrotic notch is also noticable, in the artery, vein and background. When subtracting 〈M0〉x,y and 〈fmean〉x,y from the dynamic signal as shown in Fig. 1(e) and (f), significantly different behaviors can be observed accordingly with the probed feature. Indeed, with this process, the signal in the retinal artery shows considerably larger systolodiastolic variations whereas the signal in the retinal vein appears to be more constant, almost cycloidal; the dicrotic notch becomes clearly visible only in the artery and not in the vein. In the arterial profile, the systolic upward slope is very steep while the diastolic downward slope is gentle. Finally, for both the power Doppler and mean frequency shift, the arterial systolic peak maximum coincides with the minimum of flow in the retinal vein.
Subtracting the baseline signal allows to reveal flow behaviors specific to the probed features. This operations aims at removing the contribution of underneath features such as multiple scattering from the choroid. The spatially averaged signal subtracted from the dynamic data also has an effect on the images by adding an offset value to the power and mean frequency shift maps. A calibration should be done to derive the actual physical units [22]. The variations over time measured in terms of power Doppler and mean frequency shift are quite similar, although fmean is more noisy. This is because unlike for M0, the low frequency range [0.5–10 kHz] is used in the calculations of fmean, and this frequency range carries a contribution from global eye movements. However the time-averaged mean frequency image seems of slightly better quality than the power Doppler image. In the rest of the article we represent images mostly with the mean frequency shift metric, and temporal line plots of the hemodynamic with the power Doppler metric.
3.2. Dependence of the waveform profile upon the frequency range
In Fig. 2, we analyze the arterial waveform profile as a function of the frequency range used for the power Doppler calculation. Figure 2(a) and (b) show the dynamic raw power Doppler and power Doppler corrected from the spatial average in an artery for three frequency ranges: 6–10 kHz in the pink solid line, 10–20 kHz in the red dashed line, and 20–37 kHz in the deep red dotted line. In Fig. 2(c) and (d), we show the corresponding waveform profiles averaged over three cardiac cycles with variation normalized between 0 and 1.
Fig. 2.
Dependence of the retinal arterial waveform profile upon the Doppler frequency range. All curves are obtained from the same LDH measurements, only with different processing. (a) and (b): dynamic raw power Doppler and power Doppler corrected from the spatial average for three frequency ranges: 6–10 kHz in the pink solid line, 10–20 kHz in the red dashed line, and 20–37 kHz in the deep red dotted line. (c) and (d): waveform profile averaged over three cardiac cycle with variations normalized between 0 and 1. The waveform profile calculated with the frequency band 6–10 kHz shows a pulsatile signal tainted by bulk motion (attributed by unexpected oscillations); the normalized arterial waveform calculated with the very high frequency range appears steeper due to the velocity thresholding effect.
A first observation is that the waveform profile calculated with frequencies under 10 kHz resembles the pulse waveform, but with additional noise. This is presumably because this lowest frequency range contains a mix of spectral contributions from bulk motion and pulsatile blood flow. Thus even though a part of the investigated flow signal lies in the frequency range 6–10 kHz, it seems best not to use this frequency range because it is tainted by global eye movements. In order to obtain a waveform purely representative of pulsatile blood flow, in the rest of the article we work with a 10 kHz lower frequency threshold for the calculation of M0. The second observation is that the very high Doppler frequency shifts normalized arterial waveform exhibits a steeper profile as visible from the difference between the 10–20 and 20–37 kHz profiles in Fig. 2(d). This is the result of the high-pass frequency filtering which acts as a velocity threshold. This thresholding removes the contribution of the lower speed constant flow as the velocity limit is exceeded mostly during systole and dicrotic notch. This leads to a sharper peak during systole and dicrotic notch, which amplifies the pulsatile shape of the blood flow waveform.
3.3. Phase relationship between the arterial and venous waveforms
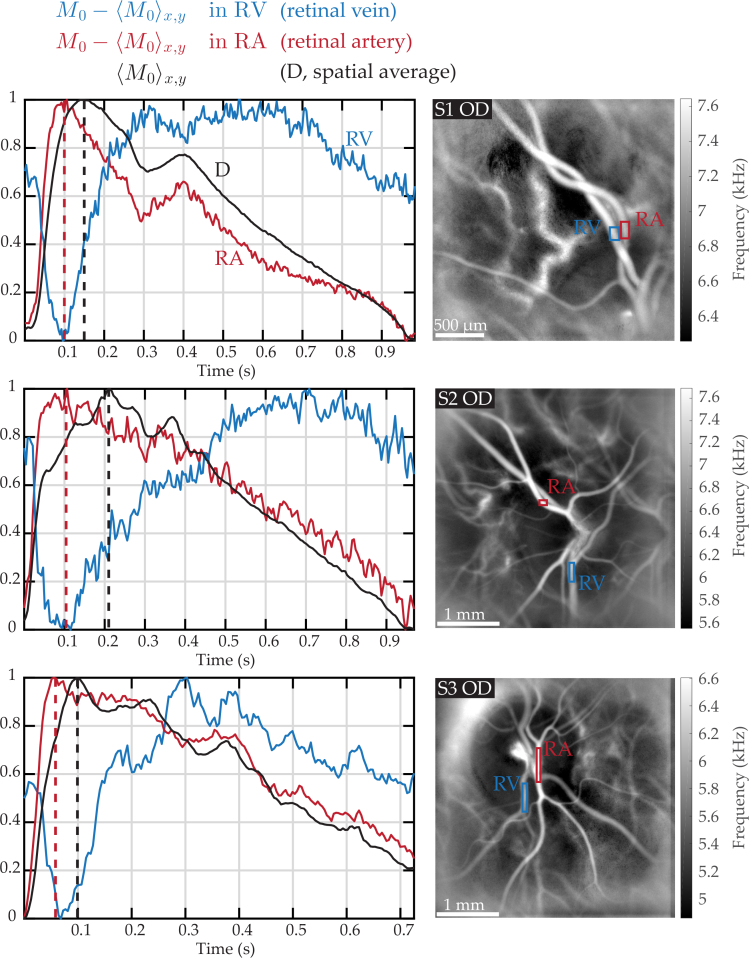
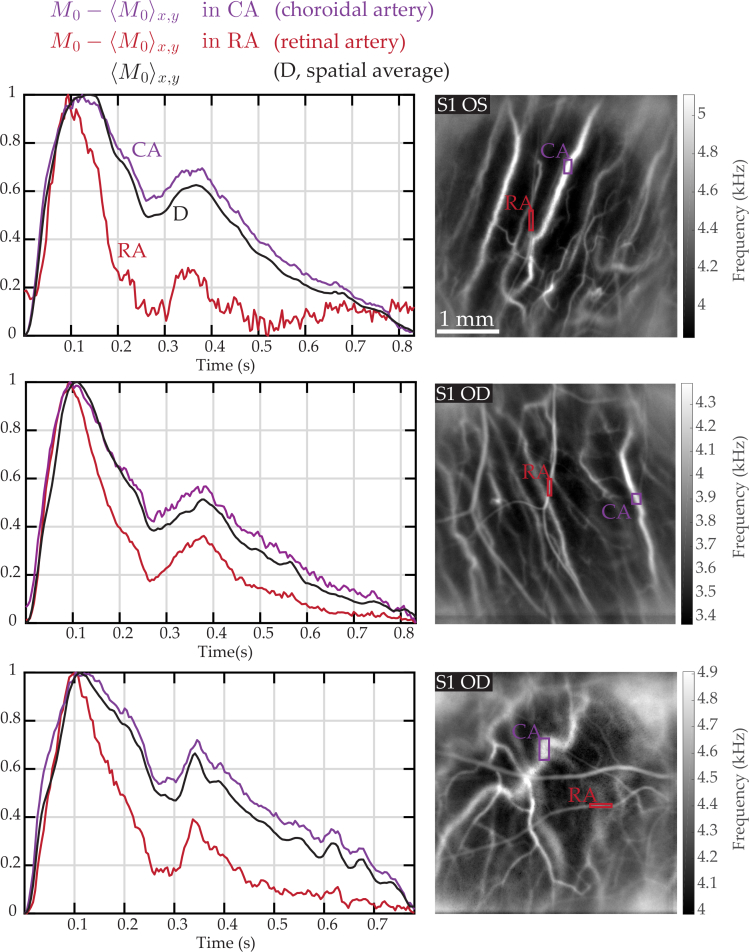
We applied the waveform normalization process in Fig. 3 to investigate how the retinal arterial and venous waveform timings are linked. To this end, we compare waveform profiles normalized between 0 and 1, and corrected from the spatial average in a retinal artery ’RA’ (red) and a retinal vein ’RV’(blue), and the normalized waveform of the spatially averaged dominant signal ’D’ (black). It should be kept in mind that the amplitude of venous flow variations is in reality considerably lower than the amplitude of arterial flow variations, as was shown in Fig. 1. The measurements were performed in three different subjects, and averaged over two to four cardiac cycles.
Fig. 3.
Venous and arterial retinal waveforms compared to the spatial average in three examples close to the ONH. Left column: normalized waveform in a retinal vein and artery (’RV’ in blue, and ’RA’ in red), and normalized waveform of the spatial average (over the entire image) in black. As seen from the red and black dashed lines indicating the end of systole, the venous minimum is more contemporary with the retinal arterial flow maximum than with the maximum of the spatial average. See Visualization 3 (14.8MB, avi) and Visualization 4 (68.3MB, avi) .
In all the examples shown in Fig. 3, the spatially averaged power Doppler and the power Doppler in the retinal artery follow similar variations, but the systolic peak is earlier by a few tens of milliseconds in the retinal artery with a few inter-individual variations. The arterial and venous waveforms also vary from one person to another but some common features can be observed: right before the systolic peak, a venous drop is synchronous with a rapid arterial increase up to the arterial systolic peak which coincides with the venous minimum flow. After the systole, the arterial flow drops then increases a little at the dicrotic notch (when present), and then slowly decreases until the end of diastole. For its part the venous flow increases after the systole and reaches its maximum a few hundreds milliseconds after the systole, then slowly decreases till the diastole end. When looking more closely, it can be seen that the venous minimum is more contemporary with the arterial maximum than with the dominant signal maximum. In the first example shown in Visualization 3 (14.8MB, avi) , it can also be observed that the arterial increase is contemporary with a venous decrease during the dicrotic notch. In Visualization 4 (68.3MB, avi) , the lower hemivein swells and retracts in a timing consistent with the power Doppler curve: the vessel retracts until the flow is minimum, and reaches its maximum swelling when the measured power Doppler is maximum.
The dominant signal is subtracted from the dynamic signal, thus it is possible that there is an overcompensation of this signal which could introduce artifacts in the shape of the venous profile. However it seems that the venous minimum contemporary of the arterial maximum is not an artifact. Indeed in case of an overcompensation, the venous minimum would have been synchronous with the maximum of the dominant signal ’D’. The fact that it is instead synchronous with the arterial signal indicates that it likely truthfully reflects the retinal venous blood flow waveform. Moreover, the caliber of the vein in Visualization 4 (68.3MB, avi) changes in a pattern consistent with the flow measurements. This vein’s behavior may be particular to that subject due to a specific vascular branching, as one of the vein branches makes an acute angle with the larger vein which might complicate the convergence of venous inflow. Nonetheless, the arterial and venous waveforms measured in these vessels are representative of those we measured in all other eyes.
3.4. Blood flow resistivity mapping
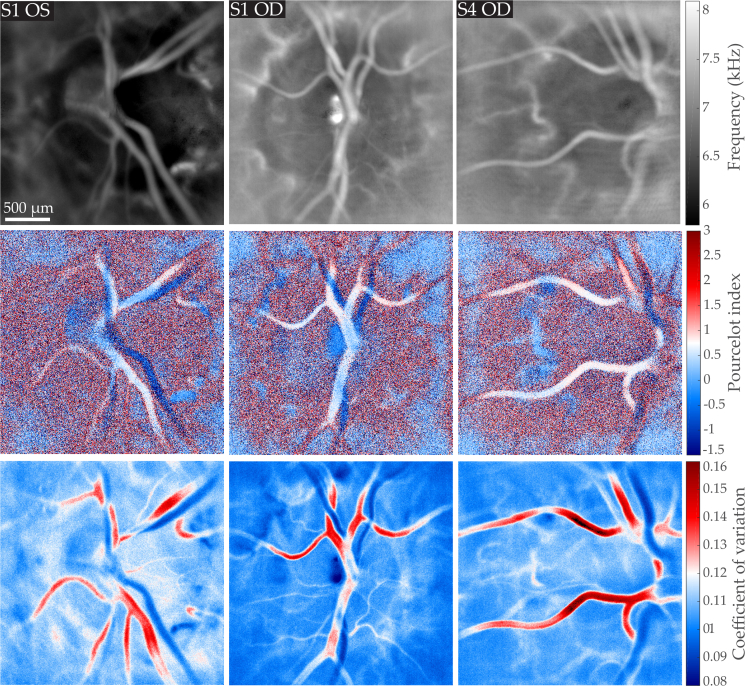
In Fig. 4, we show in three different eyes examples of mapping of the local blood velocity, RI, and CV indices. For each eye, the measurement was performed in the vicinity of the optic disc, and the camera sampling frequency was set to fS = 75kHz. The first row of Fig. 4 shows the local mean Doppler frequency shift fmean(x, y) calculated over the frequency range [0.5–37 kHz]. The second row shows the resistivity map calculated according to the Pourcelot index RIM0−〈M0〉x,y from power Doppler movies corrected from the background. Finally, the third row shows the local coefficient of variation CVM0 calculated from the raw power Doppler variations.
Fig. 4.
Mapping in three different eyes of the local blood velocity, RI, and CV indices; all images are displayed on the same gray/color scale. First row: mean Doppler frequency shift fmean(x, y). Second row: resistivity map calculated according to the Pourcelot index on the flow variations corrected from the baseline signal RIM0−〈M0〉x,y ; the RI value in the arteries is around 0.7. Third row: coefficient of variation map of the raw signal CVM0.
On the time-averaged frequency maps fmean(x, y), the mean Doppler frequency shift is greater in greater vessels: the value measured within large retinal vessels is around 7–8 kHz, and 6–6.5 kHz in the optic disc where there are no visible vessels but there should be unresolved capillaries. All fmean images were averaged over 3.5s, so it is not possible to distinguish arteries from veins based on the value of the mean frequency shift because when averaged over cardiac cycles these values are too similar in the two types of vessels. With the resistivity maps shown below in Fig. 4, a difference of contrast between veins and arteries appears: with the Pourcelot index, it is possible to see large retinal arteries in white, and large retinal veins in blue. The resisitivity index value measured in these examples is approximately 0.7 for arteries, which is consistent with the values measured with Doppler sonography in the central retinal artery [44]. The coefficient of variations maps calculated on the raw power Doppler signal show similar contrast but with a much better signal to noise ratio. Arteries come out in red with values around 0.12 – 0.16, veins come out in blue with values in the range of 0.08 – 0.11, and the value in the background is around 0.10.
This difference of contrast between veins and arteries in the RI and CV maps can be easily understood in the light of the information shown in Fig. 1. Whether the maps are computed using the raw signals or on the signal corrected from the spatial average, the amplitude of systolodiastolic variations is larger in arteries than in veins, thus a difference of contrast appears. The systolodiastolic variations are slightly greater in the veins than in the background, but the variations normalized by the mean value are greater in the background. Consequently the veins come out as the features with the lowest RI and CV values. The most striking difference between CVM0 and RIM0−〈M0〉x,y is an improvement of the SNR, which is due to the fact that the coefficient of variation calculation uses all the data points of the cardiac cycles, whereas the Pourcelot index is solely based on two time measurements made at peak systolic and end diastolic time points. Only the Pourcelot index holds a real physical sense, as the values of the coefficient of variations are based on raw power Doppler which are figurative of the background signal variations. However as these two types of maps yield similar contrasts, we used the coefficient of variation in the rest of the manuscript to provide high SNR arteriovenous mapping. Interestingly, with the LDH technique we used in this work, the Doppler contrast is not quite equally sensitive to in-plane motion as it is to out of plane motion [36]. This may result in overestimation of blood volume and velocity in out of plane vessels. The resistivity maps are predicted to be relatively independent of the flow geometry given that the angular Doppler sensitivity is expected to be compensated in the ratio. Finally it can be noticed that resistivity values in arteries are corrupted when there is a vein beneath. This is due to the relative transparency of blood vessels and the large depth of field of the instrument; it can be also be noticed on flow images that when vessels overlap their intensity is cumulated.
3.5. Comparative CV mapping with fmean and M0
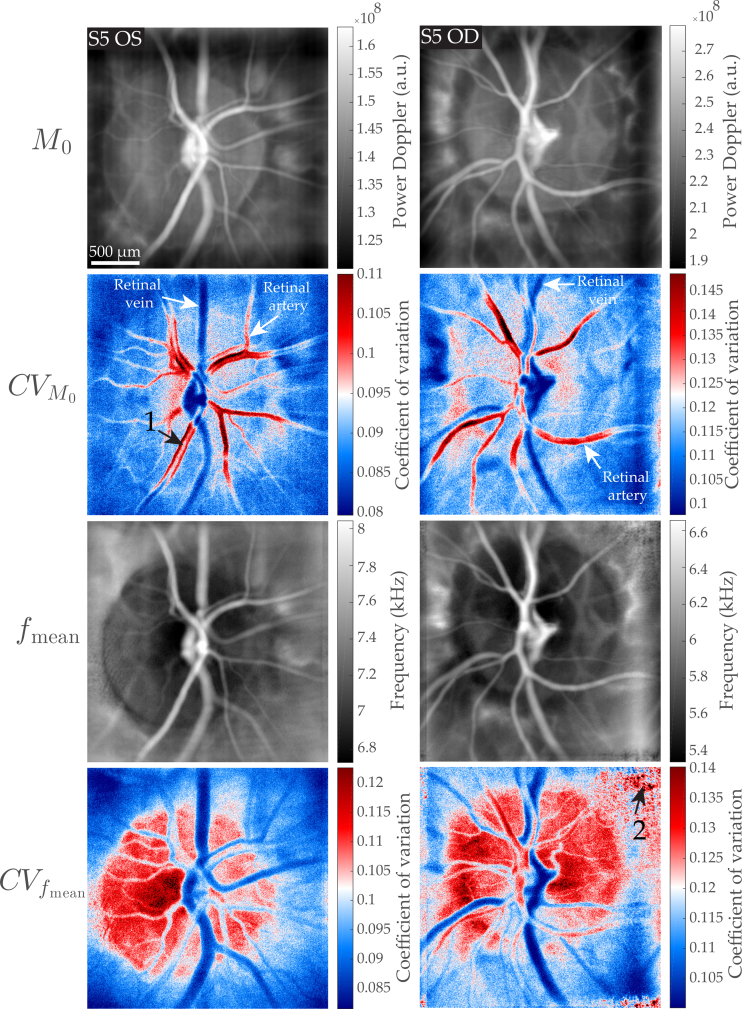
In Fig. 5, we compare the coefficient of variation maps that can be obtained on the basis of the pixel-wise variations of fmean, and compare them to the maps calculated from the variations of M0 as those that were shown in Fig. 4. The two corresponding maps are denoted CVfmean(x, y) and CVM0(x, y). The two columns in Fig. 5 show these images for the right and left eye of the same subject; both measurements were performed with a camera frame rate of 60 kHz. The frequency ranges used for the calculations of fmean and M0 are 0.5–30 kHz and 6–30 kHz, respectively.
Fig. 5.
Comparison of CV maps obtained from the variation of M0 and fmean in the right and left eye of the same subject. From top to down: M0(x, y), CVM0(x, y), fmean(x, y), and CVfmean(x, y). The coefficient of variation in the optic disc differs significantly between the two methods. The arrow ’1’ and ’2’ point to areas where the Doppler broadening is undersampled and to low frequency noise, respectively.
With both the CVfmean and CVM0 maps, a difference of contrast is visible between arteries and veins, and the values found in CVM0(x, y) are very close to those of CVfmean(x, y). The most visible difference is that in CVfmean(x, y) maps, the coefficient of variation is greater in the optic disc than in almost any other feature, except for arteries in the optic disc because they benefit from the signal of the optic disc underneath. As a result, unlike with the CVM0(x, y) map, retinal arteries are not the structures where the coefficient of variation is the greatest. Compared to the rest of the visible features, the optic disc area appears darker with fmean(x, y) than with M0(x, y). As CVfmean(x, y) is calculated as the division of the standard deviation image by the time-averaged image, this explains why this region appears redder than the rest of the image in the coefficient of variation maps. As for the retinal veins, they are the structures with the lowest coefficient of variation with the two types of maps. It can also be noticed that the apparent diameter of retinal vessels is larger with images based on fmean than with images based on M0. A likely explanation is that because the 0.5–6 kHz frequency range is not used in M0 images, the contribution of higher frequencies (which reveal greater blood flow) is more important, so vessels show a weaker signal closer to the edges.
It can be noted than the lumen of some large retinal arteries in CVM0(x, y) (arrow ’1’) has a lower coefficient of variation than closer to the vessel walls. As we fail to see any physical explanation of this phenomenon, we suppose it is caused by an aliasing of the Doppler spectrum during systole in the area where the velocity is the greatest, which would result in a lower than normal systolic power Doppler flow measurement, and thus in lower systolodiastolic variations. We had already noticed that at 60 kHz this sort of Doppler undersampling could occur in branches of the central retinal artery [36]. An interesting feature of CVfmean(x, y) maps, is that as fmean itself, they are more prone to low frequency noise (arrow ’2’), and require a careful instrumentation that minimizes specular reflections.
4. Results in the choroid
The blood flow supply to the retina is carried out by two independent vasculatures originating from the ophthalmic artery that differ in organization and function. The retinal vessels are branches of the central retinal artery and supply the neural retina and the prelaminar region of the ONH, whereas the choroidal vessels originate from the posterior ciliary arteries (PCAs) which supply the photoreceptor and epithelial cells. These two vascular systems especially differ at the capillary bed level as choroidal capillaries are considerably bigger than retinal capillaries [51], resulting in a lower vascular resistance in the choroid. Therefore, because they share a common inflow source but differ in outflow, the retinal and choroidal circulation are interesting to study the ocular circulation. The difficulty about the choroid is that it lies beneath the photoreceptor and RPE layers which have a non-trivial effect on the light. We previously demonstrated that LDH is able to reveal the deep choroidal vasculature, and that this difference of organization allows to discriminate arteries from veins in the choroid on the basis of the flow they carry [37]. Here we investigate the blood flow dynamics in the choroid.
4.1. Choroidal arterial waveform in different regions
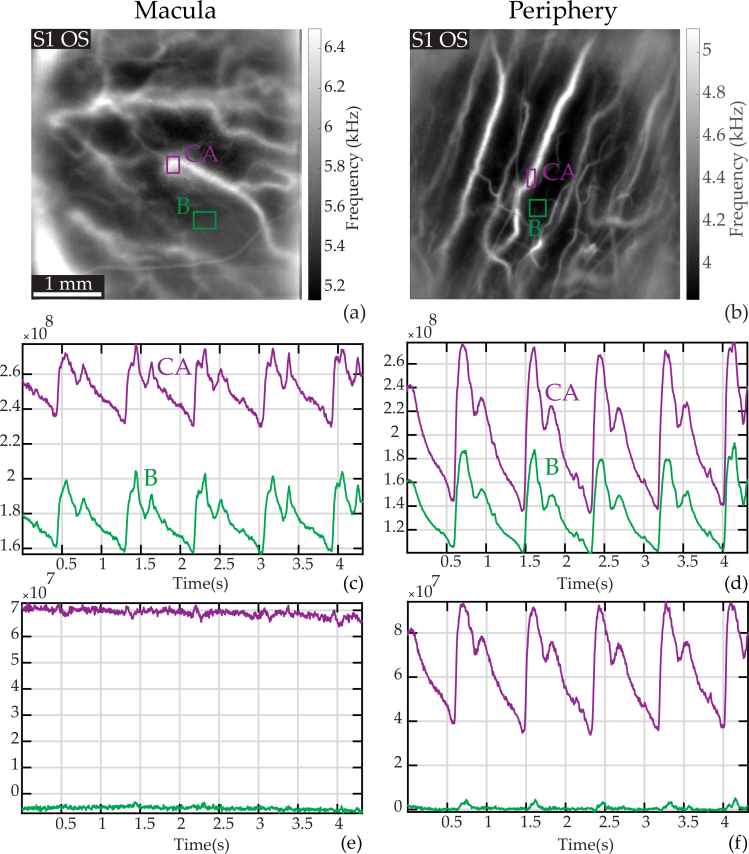
In Fig. 6, we explore how the photoreceptor density affects the laser Doppler measurements in choroidal arteries. To that end, we imaged two areas in the fundus, in the macular region and in a peripheral region at approximately 40 degrees of foveal eccentricity where the density of photoceptor and RPE cells is expected to be considerably lower. In Fig. 6(a) and (b), we show the mean frequency images of the two imaged areas, and the ROIs placed on a choroidal artery (’CA’, purple) and an area devoid of any large vessels (’B’, green). In Fig. 6(c) and (d), we show the raw power Doppler measured in the ROIs, i.e. M0. Then in Fig. 6(e) and (f), we show the power Doppler in the same ROIs when subtracting the spatially averaged dynamic signal, i.e. M0 − 〈M0〉x,y.
Fig. 6.
Laser Doppler measurements in choroidal arteries in the macular and peripheral regions. (a) and (b): Mean frequency images with ROIs on a large choroidal artery (’CA’, purple) and the background (’B’, green). (c) and (d): Raw power Doppler signal M0 in the ROIs. (e) and (f): Power Doppler signal in the same ROIs when subtracting the spatially averaged dynamic value, i.e., M0 − 〈M0〉x,y. In the peripheral region the power Doppler signal in ’CA’ corrected from the dominant signal yields a arterial-like waveform whereas the power Doppler signal measured in ’CA’ in the macular region shows only noise. This is probably because of the higher photoreceptors/RPE density, and because the dynamic signal measured in ’CA’ in the macula is exactly like the spatial average signal.
Similarly to the results shown in Fig. 1, the raw power Doppler variations in the two ROIs have very correlated variations. When subtracting the baseline dynamic value, a pulsatile arterial signal remains in the choroidal artery in the peripheral region, whereas in the macular region the signal measured in the choroidal artery only shows noise. We presume it is the higher density of photoreceptor and RPE cells in the macular region that prevents us from making measurements in choroidal arteries in the same way as in the periphery. A plausible explanation is that the choroidal arterial signal in the macular region is exactly the dominant signal, which explains why it is totally suppressed when subtracting the spatially averaged signal. This particularity had already been demonstrated in laser Doppler flowmetry as the absence of retinal vasculature in the fovea was already used to make choroidal blood flow measurements [23].
4.2. Simultaneous blood flow measurements in the retina and choroid
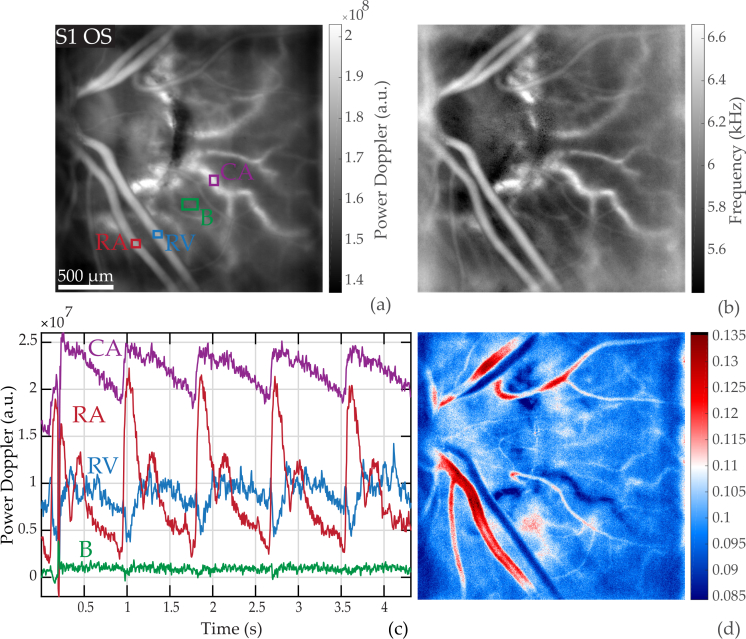
In Fig. 7, we provide an example of a CV map in an area close to the ONH with visible choroidal arteries that are branches of paraoptic short PCAs. The camera sampling frequency was set to 60 kHz. In Fig. 7(a) and (b) are respectively shown the time-averaged power Doppler image M0(x, y) and mean Doppler frequency shift image fmean(x, y). The power Doppler waveforms in the ROIs corrected from the spatial average are plotted in Fig. 7(c), and finally Fig. 7(d) shows the coefficient of variation map CVM0(x, y). The corresponding power Doppler movie corrected from the spatial average is shown in Visualization 5 (46.6MB, avi) .
Fig. 7.
Pulsatile flow in the retina and choroid. (a) Power Doppler image M0(x, y) indicating the ROIs; the red, blue, green, purple boxes mark a retinal artery and vein, the background, and a choroidal artery, respectively. (b) Mean frequency shift image fmean(x, y). (c) Waveform of M0 − 〈M0〉x,y in the ROIs. (d) Coefficient of variation map CVM0(x, y): the choroidal artery has a coefficient of variation close to the values found in retinal veins, despite exhibiting an arterial waveform profile. See the power Doppler movie in Visualization 5 (46.6MB, avi) .
We see here the same distinct flow behaviors in the retinal artery and vein as before, leading to similar contrast on the CV map. The choroid artery ’CA’ appears on the power Doppler and mean frequency images with a Doppler signal greater than in any other feature. The blood flow measured in this vessel in Fig. 7(c) exhibits an arterial-like waveform with very reduced systolodiastolic variations compared to the retinal artery, and slightly more noisy; it seems to have an offset value compared to the retinal vessel. It is apparent in Visualization 5 (46.6MB, avi) that the measured pulsatility in the choroidal artery is very reduced compared to that of the retinal artery. Finally in the CV map displayed in Fig. 7(d), the choroidal artery ’CA’ can be seen with a similar contrast to that of retinal veins.
This lower modulation depth combined with the high average value explains why this choroidal artery appears in blue in the coefficient of variation map. Although reduced systolodiastolic variations are expected in the choroid because of the lower vascular resistance compared to the retina, the photoreceptor and RPE could also be playing a role in reducing the amplitude due the multiple scattering and absorption they introduce. This makes it impossible to compare the raw power Doppler value between the retinal and choroidal layers. To circumvent this issue, we here limit the study to the comparisons of shapes and timings of choroidal and retinal arteries flow waveforms in Fig. 8 by normalizing the waveform profiles.
Fig. 8.
Retinal and choroidal arterial waveforms compared to the spatial average in three examples in peripheral regions. Left column: normalized waveform of power Doppler corrected from the spatial average in a retinal and a choroidal artery (’RA’ in red, and ’CA’ in purple), and normalized waveform of the Doppler signal spatially averaged over the entire image (’D’ in black). The dominant signal waveform has an arterial waveform, which strongly resembles that of choroidal arteries.
4.3. Comparison of the waveform of retinal arteries, choroidal arteries, and of the spatial average
In Fig. 8, we compare the waveform profiles of retinal and choroidal arteries, and of the dominant signal. In three examples, we measured the power Doppler signal corrected from the spatial average in a retinal and a choroidal artery (’RA’ and ’CA’), and averaged the waveform profiles over several cardiac cycles (typically 2 to 4). We then compared these waveforms to the spatial average waveform ’D’, i.e. to 〈M0〉x,y. All waveforms were normalized to have variations between 0 and 1. For each example, we show the ROIs on the mean frequency shift image on the right, and the corresponding curves on the left. The retinal artery is marked ’RA’ in red, and the choroidal artery ’CA’ in purple.
In the three examples, all waveforms exhibit an arterial profile: the systolic, diastolic, and dicrotic times are visible. No difference of synchronicity for the start of the systole and dicrotic notch can be observed between the different waveforms, but the systolic peak is slightly delayed in ’D’ and ’CA’. A dominant contribution to the spatial average of light scattered in the choroid seems likely.
4.4. Arteriovenous differentiation in the retina and choroid
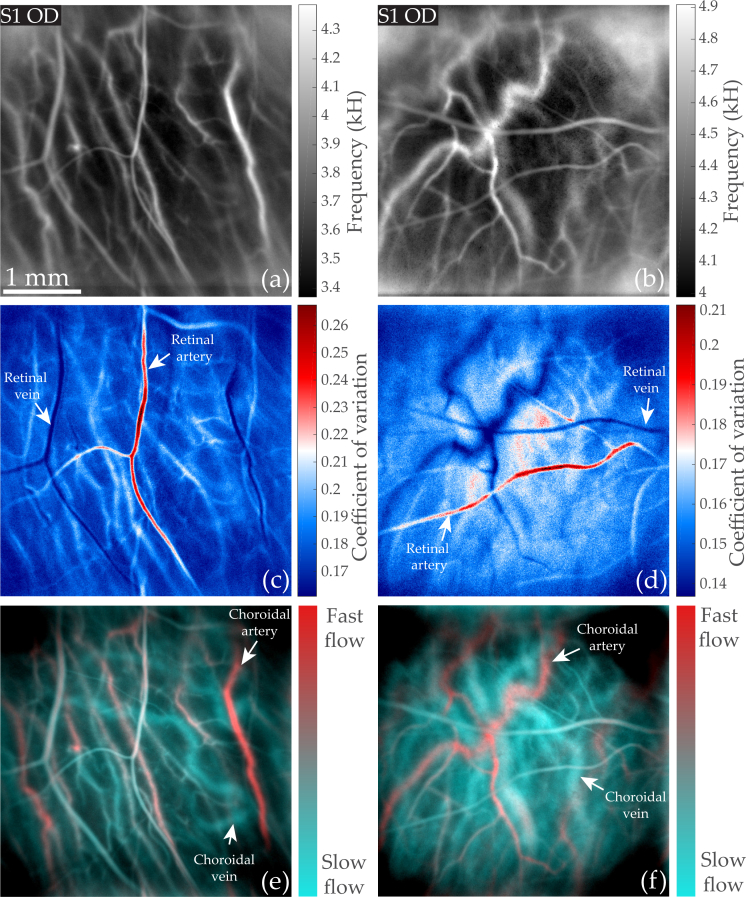
In Fig. 9, we demonstrate the ability of LDH to perform an arteriovenous differentiation in the retina and choroid using a method adapted to each vasculature. In Fig. 9(a) and (b) we show images of the local mean Doppler frequency shift fmean(x, y). Then in Fig. 9(c) and (d), we show the mapping of the local coefficient of variation CVM0(x, y). Finally, in Fig. 9(e) and (f), we show the composite color images obtained by merging low and high frequency power Doppler images (calculated with the frequency ranges 2.5–6, and 10–30 kHz, respectively) in cyan and red, following the process we previously demonstrated [37].
Fig. 9.
Arteriovenous differentiation in the retina and choroid. (a) and (b): mean Doppler frequency fmean(x, y). (c) and (d): coefficient of variation CVM0 revealing retinal arteries and veins. (e) and (f): color composite images obtained by merging low frequency and high (2.5–6 kHz, 10–30 kHz) power Doppler images in cyan and red, allowing identification of choroidal arteries and veins (colorbars are only indicative).
In the mean frequency shift images, all vessels from both the retinal and choroidal layers are visible except the choroidal veins. Although one can distinguish the retinal from the choroidal vessels as the latter are slightly larger, identifying the type of each vessel on the basis on the mean frequency shift is not possible. In the coefficient of variation maps, a difference of contrast appears between retinal arteries and veins and they can be clearly identified: as we have shown before, arteries come out in bright red and veins in deep blue. However on CV maps, the vessels of the choroid cannot be clearly identified: choroidal arteries have the same contrast as retinal veins, and choroidal veins have the same contrast as the background. Finally in the composite color images, while the retinal vessels appear with a neutral contrast, large differences can be noticed among choroidal vessels: choroidal arteries clearly stand out in red because they carry a larger flow, while choroidal veins can be seen in cyan. A final observation regarding Fig. 9, is that in these peripheral regions, the mean frequency shift is lower than in regions close to the ONH, while the average coefficient of variation index is greater.
LDH is able to carry out an arteriovenous differentiation of all vessels because it is able to make quantitative measurements of power Doppler in both the retina and choroid, and this quantity is related to the flow. For the retinal vasculature the discrimination is made on the basis of the respective hemodynamics of arteries and veins using CV maps. In the choroid, the arteriovenous segregation relies on the ability to analyze the flow in choroidal vessels. Choroidal venous vessels are the hardest vessels to image in laser Doppler because they carry a smaller flow. We had found that in regions of eccentricity smaller than approximately 30–40 degrees, the Doppler broadening due to blood flow in choroidal veins lies in the frequency range 2.5–6 kHz [37]. However in this same range of frequency there are strong contributions of involuntary eye movements and fundus pulsations, which prevents us from measuring a dynamic signal. This is why so far we have not managed to measure the blood flow waveform in choroidal veins.
5. Discussion and conclusion
Our results indicate that the choroid constitutes the predominant contribution to the high frequency laser Doppler signal in all reported areas of the fundus. It is however possible to circumvent its influence by subtracting the spatially averaged baseline signal. Similar conclusions have been reached with other blood flow monitoring methods. In laser speckle flowgraphy, the spatially averaged value of MBR (mean blur rate) which is used to assess blood flow is subtracted in order to correct for the background pulsatile signal due to the choroid [52–54]. In scanning LDF, it was found that the measured perfusion maps did not give an accurate description of the retinal circulation alone as they failed to predict retinal hypoperfusion where expected [55]. The conclusion reached was that despite confocal gating, laser Doppler measurements represented the combined circulations of the retina and choriocapillaris. The ability to make full-field laser Doppler measurements thus appears as crucial as it allows to filter this dominant contribution from the choroid through the subtraction of the spatial average. This overall signal is most likely due to the scattering of the light backscattered by the choroid by the intermediate layers, with a likely Doppler broadening contribution from the choroidal precapillary sphincter or choriocapillaris that would explain why the spatially averaged signal reaches its systolic peak later than the retinal arteries.
In Fig. 8, we observed different waveform profiles in retinal and choroidal vessels. These measurements could potentially reflect a difference of arterial waveforms between these two vasculatures, but the important bias introduced by the high-pass frequency filtering of the power Doppler prevents any direct conclusion. As we saw in Fig. 2, the spectral contribution of global eye movements overlaps with the Doppler broadening due to pulsatile blood flow in the 6–10 kHz frequency range, especially in the periphery where retinal vessels are smaller and carry slower flows. We performed these measurements shown in Fig. 8 in the periphery to make measurement in choroidal vessels with a higher SNR, but the retinal arteries are smaller thus strongly impacted by the high-pass Doppler frequency filter set at 10 kHz. The frequency thresholding acts as a high-pass velocity filter which leads to a sharper waveform profile as the contribution of the constant flow is removed. Thus the pulsatile shape of the retinal arteries waveform profiles in Fig. 8 is amplified. Another doubt can be retained regarding the exactitude of the measured choroidal arterial waveform as it is possible that there remains a residual contribution of the dominant signal. Thus any interpretation based on the comparison of retinal and choroidal arterial waveforms should be made cautiously. Nonetheless these results stand in good agreement with the profiles measured with Doppler sonography measurements [44,56], as it was found that the flow in PCAs exhibits lower systolodiastolic variations than in the central retinal artery, as it is typical in case of a lower downstream vascular resistance. LDH may be a useful technique to further study how the distal vascular resistance alters the arterial waveform.
We observed pulsatile blood flow changes in retinal veins in all investigated eyes. Visualization 4 (68.3MB, avi) shows spontaneous retinal venous pulsation (SRVP). This is commonly observed in normal veins close to the disc, and probably results from interactions between intraocular and intracranial pressure (ICP), although the exact mechanism is uncertain [57, 58]. Our data suggests that the peak venous diameter is associated with the maximum of flow. Given the interest of such phenomenon for probing ICP, further research are warranted to better understand the flow behavior in cases of SRVP. Venous pulsation is rather uncommon in the human body, and there has been controversial reports regarding the phase of the flow and caliber pulsatile behavior of retinal veins [59–62]. In this work we have found the arterial blood flow systolic peak to be coincident with the venous minimum flow in all investigated eyes. In the past decades, several modern ophthalmic instruments have experimentally confirmed the coincidence of arterial maximum flow and venous minimum flow such as Doppler-OCT [63,64], Doppler sonography [44,65], or dynamic angiography in cases of retinal vein occlusion [66].
In conclusion, we have shown that thanks to its high temporal resolution and full-field imaging capability, LDH is able to measure blood flow in retinal arteries and veins, and exhibit their specifically interrelated waveforms. Further we show that despite the absence of sectioning ability in LDH which results in having the retinal and choroidal layers reconstructed in a single plane, by spatio-temporal filtering it seems possible to isolate the contributions of each vasculature. We also demonstrate the use of the resistivity index which leads to a clear arteriovenous differentiation in the retina that complements the ability of LDH to differentiate arteries from veins in the choroid that we had previously demonstrated. The ability to characterize retinal and choroidal hemodynamic in the normal physiological state with LDH lays the foundation for studying altered blood flow in pathological conditions.
Acknowledgments
The authors would like to thank Sarah Mrejen, and Philippe Bonnin for helpful discussions, Kate Grieve for language corrections and her help in obtaining safety authorizations, and reviewers for their helpful comments.
The Titan Xp used for this research was donated by the NVIDIA Corporation.
Funding
LABEX WIFI (Laboratory of Excellence ANR-10-LABX-24) within the French Program Investments for the Future (ANR-10-IDEX-0001-02 PSL); European Research Council (ERC Synergy HELMHOLTZ, #610110).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Kashani A. H., Chen C.-L., Gahm J. K., Zheng F., Richter G. M., Rosenfeld P. J., Shi Y., Wang R. K., “Optical coherence tomography angiography: A comprehensive review of current methods and clinical applications,” Prog. Retin. Eye Res., 7, 2 (2017). 10.1016/j.preteyeres.2017.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chua J., Chin C. W. L., Hong J., Chee M. L., Le T.-T., Ting D. S. W., Wong T. Y., Schmetterer L., “Impact of hypertension on retinal capillary microvasculature using optical coherence tomographic angiography,” J. Hypertens. 37, 572–580 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mrejen S., Spaide R. F., “Optical coherence tomography: imaging of the choroid and beyond,” Surv. Ophthalmol. 58, 387–429 (2013). 10.1016/j.survophthal.2012.12.001 [DOI] [PubMed] [Google Scholar]
- 4.Rosenfeld P. J., Durbin M. K., Roisman L., Zheng F., Miller A., Robbins G., Schaal K. B., Gregori G., “Zeiss angioplex spectral domain optical coherence tomography angiography: technical aspects,” in OCT Angiography in Retinal and Macular Diseases, vol. 56 (Karger Publishers, 2016), pp. 18–29. 10.1159/000442773 [DOI] [PubMed] [Google Scholar]
- 5.Shiga Y., Kunikata H., Aizawa N., Kiyota N., Maiya Y., Yokoyama Y., Omodaka K., Takahashi H., Yasui T., Kato K., et al. , “Optic nerve head blood flow, as measured by laser speckle flowgraphy, is significantly reduced in preperimetric glaucoma,” Curr. Eye Res. 41, 1447–1453 (2016). 10.3109/02713683.2015.1127974 [DOI] [PubMed] [Google Scholar]
- 6.Mursch-Edlmayr A. S., Luft N., Podkowinski D., Ring M., Schmetterer L., Bolz M., “Laser speckle flowgraphy derived characteristics of optic nerve head perfusion in normal tension glaucoma and healthy individuals: a pilot study,” Sci. Reports 8, 5343 (2018). 10.1038/s41598-018-23149-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bonnin P., Pournaras J.-A. C., Makowiecka K., Krivosic V., Kedra A. W., Le Gargasson J.-F., Gaudric A., Levy B. I., Cohen Y. S., Tadayoni R., et al. , “Ultrasound assessment of ocular vascular effects of repeated intravitreal injections of ranibizumab for wet age-related macular degeneration,” Acta Ophthalmol. 92, e382–e387 (2014). 10.1111/aos.12356 [DOI] [PubMed] [Google Scholar]
- 8.McVeigh G. E., Bank A. J., Cohn J. N., “Arterial compliance,” in Cardiovascular Medicine, (Springer, 2007), pp. 1811–1831. 10.1007/978-1-84628-715-2_88 [DOI] [Google Scholar]
- 9.Avolio A. P., Butlin M., Walsh A., “Arterial blood pressure measurement and pulse wave analysis: their role in enhancing cardiovascular assessment,” Physiol. Meas. 31, R1 (2009). 10.1088/0967-3334/31/1/R01 [DOI] [PubMed] [Google Scholar]
- 10.Rosenbaum D., Kachenoura N., Koch E., Paques M., Cluzel P., Redheuil A., Girerd X., “Relationships between retinal arteriole anatomy and aortic geometry and function and peripheral resistance in hypertensives,” Hypertens. Res. 39, 536 (2016). 10.1038/hr.2016.26 [DOI] [PubMed] [Google Scholar]
- 11.Brar H. S., Platt L. D., “Reverse end-diastolic flow velocity on umbilical artery velocimetry in high-risk pregnancies: an ominous finding with adverse pregnancy outcome,” Am. J. Obstet. Gynecol. 159, 559–561 (1988). 10.1016/S0002-9378(88)80007-3 [DOI] [PubMed] [Google Scholar]
- 12.Nichols W. W., Edwards D. G., “Arterial elastance and wave reflection augmentation of systolic blood pressure: deleterious effects and implications for therapy,” J. Cardiovasc. Pharmacol. Ther. 6, 5–21 (2001). 10.1177/107424840100600102 [DOI] [PubMed] [Google Scholar]
- 13.Maulik D., “Spectral Doppler sonography: waveform analysis and hemodynamic interpretation,” in Doppler Ultrasound in Obstetrics and Gynecology (Springer, 2005), pp. 35–56. 10.1007/3-540-28903-8_4 [DOI] [Google Scholar]
- 14.Tsuda S., Kunikata H., Shimura M., Aizawa N., Omodaka K., Shiga Y., Yasuda M., Yokoyama Y., Nakazawa T., “Pulse-waveform analysis of normal population using laser speckle flowgraphy,” Curr. Eye Res. 39, 1207–1215 (2014). 10.3109/02713683.2014.905608 [DOI] [PubMed] [Google Scholar]
- 15.Luft N., Wozniak P. A., Aschinger G. C., Fondi K., Bata A. M., Werkmeister R. M., Schmidl D., Witkowska K. J., Bolz M., Garhöfer G., et al. , “Ocular blood flow measurements in healthy white subjects using laser speckle flowgraphy,” PLoS One 11, e0168190 (2016). 10.1371/journal.pone.0168190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gu B., Wang X., Twa M. D., Tam J., Girkin C. A., Zhang Y., “Non-invasive in vivo characterization of erythrocyte motion in human retinal capillaries using high-speed adaptive optics near-confocal imaging,” Biomed. Opt. Express 9, 3653–3677 (2018). 10.1364/BOE.9.003653 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Plumb R. D., Hamilton P. K., Rea D. J., Wright S. A., Hughes S. M., McGivern R. C., McVeigh G. E., “Wave reflection signatures: identifying early microvascular abnormalities in type 2 diabetes,” The Br. J. Diabetes & Vasc. Dis. 11, 243–248 (2011). 10.1177/1474651411422650 [DOI] [Google Scholar]
- 18.McVeigh G. E., Hamilton P. K., Morgan D. R., “Evaluation of mechanical arterial properties: clinical, experimental and therapeutic aspects,” Clin. Sci. 102, 51–67 (2002). 10.1042/cs1020051 [DOI] [PubMed] [Google Scholar]
- 19.Laurent S., Cockcroft J., Van Bortel L., Boutouyrie P., Giannattasio C., Hayoz D., Pannier B., Vlachopoulos C., Wilkinson I., Struijker-Boudier H., “Expert consensus document on arterial stiffness: methodological issues and clinical applications,” Eur. Hear. J. 27, 2588–2605 (2006). 10.1093/eurheartj/ehl254 [DOI] [PubMed] [Google Scholar]
- 20.Safar M. E., “Arterial stiffness as a risk factor for clinical hypertension,” Nat. Rev. Cardiol. 15, 97 (2018). 10.1038/nrcardio.2017.155 [DOI] [PubMed] [Google Scholar]
- 21.Safar M. E., Lacolley P., “Disturbance of macro-and microcirculation: relations with pulse pressure and cardiac organ damage,” Am. J. Physiol. Circ. Physiol. 293, H1–H7 (2007). 10.1152/ajpheart.00063.2007 [DOI] [PubMed] [Google Scholar]
- 22.Bonner R. F., Nossal R., “Principles of laser-Doppler flowmetry,” in Laser-Doppler Blood Flowmetry, (Springer, 1990), pp. 17–45. 10.1007/978-1-4757-2083-9_2 [DOI] [Google Scholar]
- 23.Riva C., Cranstoun S., Grunwald J., Petrig B., “Choroidal blood flow in the foveal region of the human ocular fundus,” Invest. Ophthalmol. Vis. Sci. 35, 4273–4281 (1994). [PubMed] [Google Scholar]
- 24.Riva C. E., Geiser M., Petrig B. L., “Ocular blood flow assessment using continuous laser Doppler flowmetry,” Acta Ophthalmol. 88, 622–629 (2010). 10.1111/j.1755-3768.2009.01621.x [DOI] [PubMed] [Google Scholar]
- 25.Serov A., Lasser T., “High-speed laser Doppler perfusion imaging using an integrating CMOS image sensor,” Opt. Express 13, 6416–6428 (2005). 10.1364/OPEX.13.006416 [DOI] [PubMed] [Google Scholar]
- 26.Michelson G., Schmauss B., Langhans M., Harazny J., Groh M., “Principle, validity, and reliability of scanning laser Doppler flowmetry,” J. Glaucoma. 5, 99–105 (1996). 10.1097/00061198-199604000-00004 [DOI] [PubMed] [Google Scholar]
- 27.Mujat M., Lu Y., Maguluri G., Zhao Y., Iftimia N., Ferguson R. D., “Visualizing the vasculature of the entire human eye posterior hemisphere without a contrast agent,” Biomed. Opt. Express 10, 167–180 (2019). 10.1364/BOE.10.000167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Magnain C., Castel A., Boucneau T., Simonutti M., Ferezou I., Rancillac A., Vitalis T., Sahel J.-A., Paques M., Atlan M., “Holographic laser Doppler imaging of microvascular blood flow,” JOSA A 31, 2723–2735 (2014). 10.1364/JOSAA.31.002723 [DOI] [PubMed] [Google Scholar]
- 29.Pellizzari M., Simonutti M., Degardin J., Sahel J.-A., Fink M., Paques M., Atlan M., “High speed optical holography of retinal blood flow,” Opt. Lett. 41, 3503–3506 (2016). 10.1364/OL.41.003503 [DOI] [PubMed] [Google Scholar]
- 30.Donnarumma D., Brodoline A., Alexandre D., Gross M., “4d holographic microscopy of zebrafish larvae microcirculation,” Opt. Express 24, 26887–26900 (2016). 10.1364/OE.24.026887 [DOI] [PubMed] [Google Scholar]
- 31.Hillmann D., Spahr H., Hain C., Sudkamp H., Franke G., Pfäffle C., Winter C., Hüttmann G., “Aberration-free volumetric high-speed imaging of in vivo retina,” Sci. reports 6, 35209 (2016). 10.1038/srep35209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ginner L., Schmoll T., Kumar A., Salas M., Pricoupenko N., Wurster L. M., Leitgeb R. A., “Holographic line field en-face OCT with digital adaptive optics in the retina in vivo,” Biomed. Opt. Express 9, 472–485 (2018). 10.1364/BOE.9.000472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Spahr H., Pfäffle C., Koch P., Sudkamp H., Hüttmann G., Hillmann D., “Interferometric detection of 3Dmotion using computational subapertures in optical coherence tomography,” Opt. express 26, 18803–18816 (2018). 10.1364/OE.26.018803 [DOI] [PubMed] [Google Scholar]
- 34.Ginner L., Wartak A., Salas M., Augustin M., Niederleithner M., Wurster L. M., Leitgeb R. A., “Synthetic subaperture-based angle-independent Doppler flow measurements using single-beam line field optical coherence tomography in vivo,” Opt. Lett. 44, 967–970 (2019). 10.1364/OL.44.000967 [DOI] [PubMed] [Google Scholar]
- 35.Brodoline A., Rawat N., Alexandre D., Cubedo N., Gross M., “4d compressive sensing holographic microscopy imaging of small moving objects,” Opt. Lett. 44, 2827–2830 (2019). 10.1364/OL.44.002827 [DOI] [PubMed] [Google Scholar]
- 36.Puyo L., Paques M., Fink M., Sahel J.-A., Atlan M., “In vivo laser Doppler holography of the human retina,” Biomed. Opt. Express 9, 4113–4129 (2018). 10.1364/BOE.9.004113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Puyo L., Paques M., Fink M., Sahel J.-A., Atlan M., “Choroidal vasculature imaging with laser Doppler holography,” Biomed. Opt. Express 10, 995–1012 (2019). 10.1364/BOE.10.000995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Postnov D. D., Cheng X., Erdener S. E., Boas D. A., “Choosing a laser for laser speckle contrast imaging,” Sci. Reports 9, 2542 (2019). 10.1038/s41598-019-39137-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Goodman J. W., Introduction to Fourier Optics (Roberts and Company Publishers, 2005). [Google Scholar]
- 40.Evans D. H., Doppler Ultrasound: Physics, Instrumentation, and Clinical Applications (John Wiley & Sons, 1989). [Google Scholar]
- 41.Macé E., Montaldo G., Cohen I., Baulac M., Fink M., Tanter M., “Functional ultrasound imaging of the brain,” Nat. Methods 8, 662 (2011). 10.1038/nmeth.1641 [DOI] [PubMed] [Google Scholar]
- 42.Nichols W., Pepine C., Geiser E., Conti C., “Vascular load defined by the aortic input impedance spectrum,” in Federation Proceedings, vol. 39 (1980), pp. 196–201. [PubMed] [Google Scholar]
- 43.Toy S. M., Melbin J., Noordergraaf A., “Reduced models of arterial systems,” IEEE Transactions on Biomed. Eng. 1985 174–176 (1985). 10.1109/TBME.1985.325439 [DOI] [PubMed] [Google Scholar]
- 44.Tranquart F., Bergès O., Koskas P., Arsene S., Rossazza C., Pisella P.-J., Pourcelot L., “Color Doppler imaging of orbital vessels: personal experience and literature review,” J. Clin. Ultrasound 31, 258–273 (2003). 10.1002/jcu.10169 [DOI] [PubMed] [Google Scholar]
- 45.Demené C., Pernot M., Biran V., Alison M., Fink M., Baud O., Tanter M., “Ultrafast Doppler reveals the mapping of cerebral vascular resistivity in neonates,” J. Cereb. Blood Flow & Metab. 34, 1009–1017 (2014). 10.1038/jcbfm.2014.49 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pourcelot L., “Applications cliniques de l’examen Doppler transcutane,” Velocim. Ultrason. Doppler 34, 780–785 (1974). [Google Scholar]
- 47.Bude R. O., Rubin J. M., “Relationship between the resistive index and vascular compliance and resistance,” Radiology 211, 411–417 (1999). 10.1148/radiology.211.2.r99ma48411 [DOI] [PubMed] [Google Scholar]
- 48.Bude R. O., Rubin J. M., “Effect of downstream cross-sectional area of an arterial bed on the resistive index and the early systolic acceleration,” Radiology 212, 732–738 (1999). 10.1148/radiology.212.3.r99se13732 [DOI] [PubMed] [Google Scholar]
- 49.Halpern E. J., Merton D. A., Forsberg F., “Effect of distal resistance on Doppler US flow patterns,” Radiology 206, 761–766 (1998). 10.1148/radiology.206.3.9494498 [DOI] [PubMed] [Google Scholar]
- 50.Polska E., Kircher K., Ehrlich P., Vecsei P. V., Schmetterer L., “RI in central retinal artery as assessed by CDI does not correspond to retinal vascular resistance,” Am. J. Physiol. Circ. Physiol. 280, H1442–H1447 (2001). 10.1152/ajpheart.2001.280.4.H1442 [DOI] [PubMed] [Google Scholar]
- 51.Network C. V., “Developmental anatomy of the retinal and choroidal vasculature,” The Retin. Its Disord. 179 (2011). [Google Scholar]
- 52.Isono H., Kishi S., Kimura Y., Hagiwara N., Konishi N., Fujii H., “Observation of choroidal circulation using index of erythrocytic velocity,” Arch. Ophthalmol. 121, 225–231 (2003). 10.1001/archopht.121.2.225 [DOI] [PubMed] [Google Scholar]
- 53.Iwase T., Yamamoto K., Ra E., Murotani K., Matsui S., Terasaki H., “Diurnal variations in blood flow at optic nerve head and choroid in healthy eyes: diurnal variations in blood flow,” Medicine 94, 519 (2015). 10.1097/MD.0000000000000519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Fondi K., Bata A. M., Luft N., Witkowska K. J., Werkmeister R. M., Schmidl D., Bolz M., Schmetterer L., Garhöfer G., “Evaluation of flicker induced hyperemia in the retina and optic nerve head measured by laser speckle flowgraphy,” PloS One 13, e0207525 (2018). 10.1371/journal.pone.0207525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Squirrell D., Watts A., Evans D., Mody C., Talbot J., “A prospective evaluation of the heidelberg retina flowmeter in diagnosing ischaemia following branch retinal vein occlusion: a masked, controlled comparison with fluorescein angiography,” Eye 15, 261 (2001). 10.1038/eye.2001.91 [DOI] [PubMed] [Google Scholar]
- 56.Lieb W. E., Cohen S. M., Merton D. A., Shields J. A., Mitchell D. G., Goldberg B. B., “Color Doppler imaging of the eye and orbit: technique and normal vascular anatomy,” Arch. Ophthalmol. 109, 527–531 (1991). 10.1001/archopht.1991.01080040095036 [DOI] [PubMed] [Google Scholar]
- 57.Morgan W. H., Hazelton M. L., Yu D.-Y., “Retinal venous pulsation: Expanding our understanding and use of this enigmatic phenomenon,” Prog. In Retin. And Eye Res. 55, 82–107 (2016). 10.1016/j.preteyeres.2016.06.003 [DOI] [PubMed] [Google Scholar]
- 58.Wartak A., Beer F., Desissaire S., Baumann B., Pircher M., Hitzenberger C. K., “Investigating spontaneous retinal venous pulsation using Doppler optical coherence tomography,” Sci. Reports 9, 4237 (2019). 10.1038/s41598-019-40961-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kain S., Morgan W. H., Yu D.-Y., “New observations concerning the nature of central retinal vein pulsation,” Br. J. Ophthalmol. 94, 854–857 (2010). 10.1136/bjo.2009.169813 [DOI] [PubMed] [Google Scholar]
- 60.Morgan W. H., Lind C. R., Kain S., Fatehee N., Bala A., Yu D.-Y., “Retinal vein pulsation is in phase with intracranial pressure and not intraocular pressure,” Investig. Ophthalmol. & Vis. Sci. 53, 4676–4681 (2012). 10.1167/iovs.12-9837 [DOI] [PubMed] [Google Scholar]
- 61.Morgan W. H., Hazelton M. L., Betz-Stablein B. D., Yu D.-Y., Lind C. R., Ravichandran V., House P. H., “Photoplethysmographic measurement of various retinal vascular pulsation parameters and measurement of the venous phase delay,” Investig. Ophthalmol. & Vis. Sci. 55, 5998–6006 (2014). 10.1167/iovs.14-15104 [DOI] [PubMed] [Google Scholar]
- 62.Moret F., Reiff C. M., Lagreze W. A., Bach M., “Quantitative analysis of fundus-image sequences reveals phase of spontaneous venous pulsations,” Transl. Vis. Sci. & Technol. 4, 3 (2015). 10.1167/tvst.4.5.3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tan O., Liu G., Liang L., Gao S. S., Pechauer A. D., Jia Y., Huang D., “En face Doppler total retinal blood flow measurement with 70 khz spectral optical coherence tomography,” J. Of Biomed. Opt. 20, 066004 (2015). 10.1117/1.JBO.20.6.066004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Doblhoff-Dier V., Schmetterer L., Vilser W., Garhöfer G., Gröschl M., Leitgeb R. A., Werkmeister R. M., “Measurement of the total retinal blood flow using dual beam fourier-domain Doppler optical coherence tomography with orthogonal detection planes,” Biomed. Opt. Express 5, 630–642 (2014). 10.1364/BOE.5.000630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Michelson G., Harazny J., “Relationship between ocular pulse pressures and retinal vessel velocities,” Ophthalmology 104, 664–671 (1997). 10.1016/S0161-6420(97)30254-1 [DOI] [PubMed] [Google Scholar]
- 66.Paques M., Baillart O., Genevois O., Gaudric A., Lévy B., Sahel J., “Systolodiastolic variations of blood flow during central retinal vein occlusion: exploration by dynamic angiography,” Br. J. Ophthalmol. 89, 1036–1040 (2005). 10.1136/bjo.2004.061275 [DOI] [PMC free article] [PubMed] [Google Scholar]