Deep learning based topology guaranteed surface and MME segmentation of multiple sclerosis subjects from retinal OCT

Abstract

Optical coherence tomography (OCT) is a noninvasive imaging modality that can be used to obtain depth images of the retina. Patients with multiple sclerosis (MS) have thinning retinal nerve fiber and ganglion cell layers, and approximately 5% of MS patients will develop microcystic macular edema (MME) within the retina. Segmentation of both the retinal layers and MME can provide important information to help monitor MS progression. Graph-based segmentation with machine learning preprocessing is the leading method for retinal layer segmentation, providing accurate surface delineations with the correct topological ordering. However, graph methods are time-consuming and they do not optimally incorporate joint MME segmentation. This paper presents a deep network that extracts continuous, smooth, and topology-guaranteed surfaces and MMEs. The network learns shape priors automatically during training rather than being hard-coded as in graph methods. In this new approach, retinal surfaces and MMEs are segmented together with two cascaded deep networks in a single feed forward propagation. The proposed framework obtains retinal surfaces (separating the layers) with sub-pixel surface accuracy comparable to the best existing graph methods and MMEs with better accuracy than the state-of-the-art method. The full segmentation operation takes only ten seconds for a 3D volume.

1. Introduction

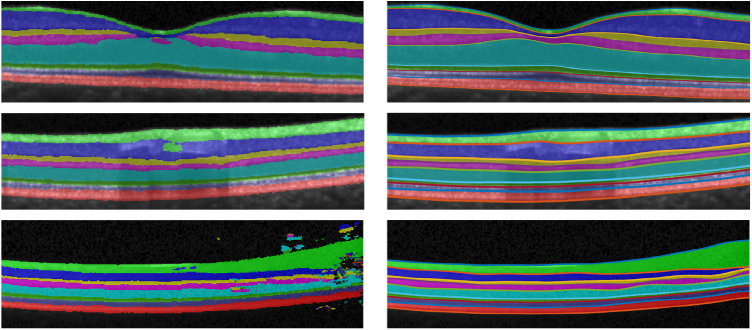
Optical coherence tomography (OCT) is a widely used non-invasive and non-ionizing modality which can obtain 3D retinal images rapidly [1]. The retinal depth information obtained from OCT enables measurements of layer thicknesses, which are known to change with certain diseases [2]. Multiple sclerosis (MS) is a disease of the central nervous system that is characterized by inflammation and neuroaxonal degeneration in both gray matter and white matter. However, OCT has emerged as a complementary tool to magnetic resonance imaging and can track neurodegeneration in MS [3,4], as well as predict disability [5]. Specifically, OCT-derived measures of peripapillary retinal nerve fibre layer (p-RNFL) and ganglion cell plus inner plexiform layer (GCIP) thickness reflect global aspects of the MS disease process [6–8]. With GCIP thicknesses having greater utility than p-RNFL due to the reliability and reproducibility, and lower susceptibility to swelling during optic nerve inflammation [9]. Additionally, GCIP thickness correlates better with both visual function and EDSS scores than p-RNFL thickness [3]. Moreover, GCIP atrophy is well correlated with grey matter atrophy over time in the brain [8]. Approximately 5% [10] of MS subjects can also develop microcystic macular edema (MME), which has been shown to be correlated with MS disease severity. The presence of MME at baseline has been shown to predict clinical and radiological inflammatory activity [11]. Thus, our ability to accurately quantify both retinal layer thicknesses and MMEs in MS subjects is important for both clinical monitoring and the development of disease therapies. An example OCT image with pseudocysts caused by MME is shown in Fig. 1. Physiologically, retinal layers have a strict ordering from inner to outer layers (top to bottom in conventional B-scans), and maintaining the correct topological structure is important for segmentation algorithms and also in surface based registration methods [12]. Fast automated retinal layer and MME segmentation tools are crucial for large MS cohort studies.

Fig. 1.

B-scan with MME (left) and manual labels (right). The MME pseudocysts are denoted in red (right).

Automated retinal layer segmentation has been well explored [13–19]. To achieve topologically correct layers, level set methods [13,14,20] have been proposed. However, the multiple object level set methods are computationally expensive, with reported run times of hours. Graph based methods [15,16] have been widely used and combined with machine learning methods [17,18]. State-of-the-art methods use machine learning (e.g., random forest, or deep learning) for coarse pixel-wise labeling and graph methods to extract the final surfaces with the correct topology. These approaches are limited by the need for manually selected features and parameters for the graph. To build the graph, boundary distances and smoothness constraints, which are spatially varying, are usually experimentally assigned, and application to new patient groups requires tuning [21]. These manually-selected features and fine-tuned graph parameters limit the application of these methods across pathologies and scanner platforms [22].

Recently, deep learning has shown promising results on OCT segmentation tasks. Fang et al. [17] used deep networks to predict the label of the central pixel of a given image patch and then, with this information, used a graph method to extract boundary surfaces. The method used one image patch per pixel, which is time consuming and computationally redundant. Fully convolutional networks (FCNs) [23] have been used to design highly successful segmentation methods in many applications. An FCN outputs a label map instead of a set of single pixel classifications, which is much more computationally efficient. FCNs have been used for the segmentation of retinal layers [24,25], macular cysts [26,27], and both together [28]. However, these FCN methods for retinal layer segmentation have two major drawbacks. First, there is no explicit consideration of the proper shape and topological arrangement of the retinal layers; a naive application of an FCN will typically produce results that violate the known ordering of the retinal layers (see Fig. 8). Second, only pixel-wise label maps are obtained, so the final retinal surfaces must be extracted using a post-processing approach such as a graph or level set method.

Fig. 8.

In the left column are S-Net results showing incorrect segmentations and topology defects. The right column shows the corrected segmentation generated by SR-Net.

Previous researchers have proposed deep segmentation networks that address shape and topology requirements [25,29,30]. BenTaieb et al. [29] proposed to explicitly integrate topology priors into the loss function during training. Ravishankar et al. [30] and He et al. [25] used a second auto-encoder network to learn the segmentation shape prior. These methods can improve the shape and topology of the segmentation results, but none guarantees the output to provide a correct ordering of the segmented layers due to the pixel-wise labeling nature of FCNs.

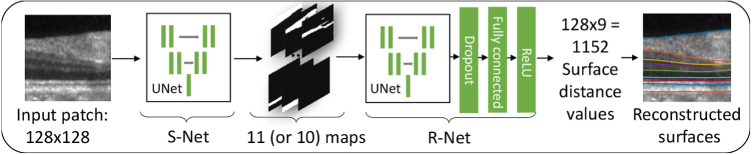
In this paper, we present a deep learning framework for MME and topology-guaranteed retinal surfaces segmentation. Our framework includes two parts, as illustrated in Fig. 2. The first part is a modified U-Net [31] segmentation network that we call S-Net. It outputs segmentation probability maps for the input image; these results conform well to the data but may not have the correct layer ordering on every A-scan. We therefore use a second network, a regression network that we call R-Net, which computes feasible surface positions that approximate the probability maps and use prior shape information. To guarantee correct layer ordering, we make a conceptual change to the approach in Shah et al. [32] which directly outputs multiple surface positions by estimating relative distances between adjacent surfaces and by using ReLU [33] as the final output layer activation function. The resultant non-negativity of these relative distances guarantees topological correctness of layer ordering throughout the volume. An effective training scheme, wherein we train S-Net and R-Net separately, is also proposed. S-Net is trained to learn intensity features whereas R-Net is trained to learn the shape priors like the boundary smoothness and layer thicknesses (as implicit latent variables within the network). By decoupling the training of S-Net and R-Net, it is much easier to build data augmentation methods for training R-Net, as noted in [30]. Another benefit of our approach over the direct regression method of Shah et al. [32], is that we obtain MME pseudocyst masks directly from S-Net. Our approach offers three distinct advantages over the previous publicly available state-of-the-art graph based methods [18]: 1) it is an order of magnitude faster; 2) it provides both layer and MME segmentation; and 3) it is the first deep learning approach to guarantee the correct layer segmentation topology and output surface positions directly.

Fig. 2.

Architecture of the proposed method. A 128×128 patch extracted from a flattened B-scan is segmented by S-Net. S-Net outputs an 11 (or 10)×128×128 segmentation probability map. R-Net takes the S-Net outputs and generates 128×9 outputs corresponding to the nine surface distances across the 128 A-scans.

2. Methods

2.1. Topologically correct segmentation

Consider a B-scan of size $h\times w$, where $w$ is the number of A-scans and $h$ is the number of pixels per A-scan. We assume that all nine layer surfaces appear in every A-scan. If this is not the case—i.e., if the retina is cut off or lesion corrupts layer surfaces—then the algorithm will still provide an answer, but the surfaces and layers in these places will not be accurately estimated. Typically, it is possible to discern 8 retinal layers; therefore, there are 9 boundary surfaces that define these layers. We define a real-valued matrix $B$ of size $9\times w$ wherein each column corresponds to an A-scan and the values of $B$ in its rows from 1–9 define the depths (from the top of the B-scan) of the 9 boundaries in order from top to bottom (inner to outer retina). Correct topological ordering of the retinal layers requires that the entries in any column of $B$ are non-decreasing and fall in the interval $[0,h]$. Formally, we say that $B\in \mathcal{B}$, where $\mathcal{B}$ is the set of $9\times w$ matrices satisfying the above properties.

A segmentation map $S$ is an $h\times w$ matrix with integer values in the interval $[1,11]$ that labels the vitreous (label 1), 8 retinal layers (from inner to outer retina) (labels 2–9), choroid (label 10), and MME (label 11). We do not assume a topological relationship between MME and the retinal layers, but we do want the layer ordering to remain correct. Therefore, to guarantee that $S$ is topologically correct, its values (excluding label 11) must be non-decreasing within each column (from row 1 to row $h$). Formally, we say that $S\in \mathcal{S}$ where $\mathcal{S}$ is the set of all $h\times w$ matrices satisfying the above properties.

Let $S_M$ be a binary MME segmentation map—i.e., $S_M$ is a matrix of size $h\times w$ with the value one where a pseudocyst is estimated and zero otherwise. Then $B$ and $S_M$ together can uniquely generate $S=\varphi (B,S_M)$ where

$$S_{i,j}=\{\begin{array}{ll}1,& \text{if}i<B_{1,j}\text{and}{S}_{M_{i,j}}=0\\ 10,& \text{if}i\ge B_{9,j}\text{and}{S}_{M_{i,j}}=0\\ 11,& \text{if}{S}_{M_{i,j}}=1\\ l+1,& \text{if}{B}_{l,j}\le i<B_{l+1,j}\end{array}$$ (1)

Because of the finite physical spacing of the pixels within an A-scan and the fact that $B$ is capable of representing sub-voxel accuracy, $B$ is not uniquely determined by $S$. So we view $S_M$ and $B$ as the main outputs of our macular segmentation strategy. We note that if a pseudocyst cuts through a layer boundary (a rare occurrence), then $B$ will still provide a topologically valid surface that goes under, over, or through the pseudocyst.

The overall strategy of our segmentation algorithm can now be described. We start with S-Net, a fairly standard FCN, which finds a pixel labeling $\tilde{S}$ of the input B-scan. This result is unlikely to be topologically correct, but it does provide underlying probability maps representing likely locations of the 8 retinal layers and the vitreous, choroid, and MME. We use these probability maps as input to R-Net, which finds a feasible segmentation $B\in \mathcal{B}$. From $B$, a variety of retinal layer thicknesses, averaged over the whole macula or within macular regions, can be computed. Given $B$ and $S_M$ from $\tilde{S}$, a feasible hard segmentation can be produced using $S=\varphi (B,S_M)$, which provides a visualization of the result. We now describe these steps in more detail.

2.2. Preprocessing

We follow the preprocessing steps in the AURA toolkit [18]. The OCT image (496×1024×49 voxels) is first intensity normalized and flattened to an estimate of Bruch’s membrane (BM), found using intensity gradient based methods. We then crop the B-scans to 128×1024 pixels, which preserves the retina and removes unnecessary portions of the choroid and vitreous. Twenty 128×128 pixels patches per B-scan, overlapping horizontally, are then extracted for training. In testing, the B-scan images are similarly processed into 128×128 pixel patches for inference and the results are reconstructed back to the original image size, as described below.

2.3. Segmentation network (S-Net)

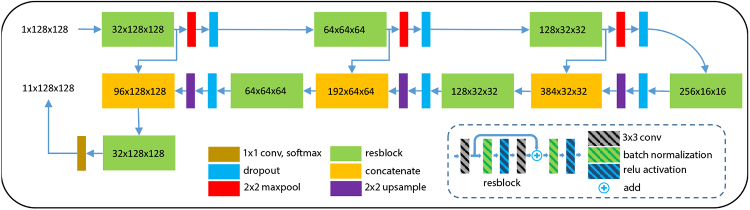
Our segmentation FCN (S-Net) is a modification of the U-Net [31]. We use residual blocks (resblocks) [34] with 3×3 convolutions, batch normalizations, ReLU activations, and skip connections in our network, as shown in Fig. 3. The number of channels after the first resblock is 32 and we double the number of channels after each resblock in the encoder portion of the network. 2×2 max-pooling and 2×2 up-sampling (implemented by simply repeating values) are used to transition between the various scales. The input to the network is a 128×128 pixel patch and the outputs are eleven 128×128 pixel probability maps, one for each of eight retina layers, two backgrounds (vitreous and choroid), and the MME. S-Net training is described below.

Fig. 3.

A schematic of our S-Net, based on U-Net [31].

2.4. Regression net (R-Net)

The objective of R-Net is to estimate a surface position matrix $B\in \mathcal{B}$ from a segmentation map $\tilde{S}$ (which most likely has topology defects). Each A-scan (column) of the image intersects all 9 surfaces and these 9 depth positions must be non-decreasing. Instead of directly estimating these depth positions, R-Net estimates the depth positions of surface 1, the distance from surface 1 to surface 2, the distance from surface 2 to surface 3, and so on. ReLU activation [35] is used as the final layer, so the output from R-Net is guaranteed to be non-negative and thus the surface ordering is guaranteed.

R-Net consists of two parts: an FCN (U-Net) identical to S-Net except that it has a different number of input and output channels and a fully connected final layer. The U-Net encoder maps the 11×128×128 S-Net result $\tilde{S}$ into a latent shape space which we hypothesize will not be significantly affected by defects and will be close to the latent representation of the ground truth $S$ [30]. The U-Net decoder takes the latent representation and produces a high resolution 10×128×128 feature map. The skip connections that are present in the U-Net help to preserve fine details. Dropout with rate 0.2 is applied to the final activations in order to improve generalization. These features are then flattened into a 1D vector which is sent to the fully connected layer with ReLU activation. The output from the R-Net is a $128\times 9=1152$ 1D vector representing 9 surface distances for 128 A-scans. This result is reshaped and summed column-wise to obtain nine surface positions $B\in \mathcal{B}$ and to generate $S=\varphi (B,S_M)\in \mathcal{S}$ where $S_M$ is the binary MME segmentation mask generated from $\tilde{S}$ using argmax on label 11. By using R-Net, we obtain a topologically correct segmentation.

2.5. Training

S-Net and R-Net are trained separately. S-Net is trained with a common pixel-wise label training scheme to learn the intensity features and their relationships to the 11 labels. R-Net is trained with an augmented ground truth layer and MME masks to learn about the expected layer shapes, topology, and the mapping to boundary positions. We now describe the two training strategies in detail.

2.5.1. S-Net training

The negative mean smoothed Dice loss is used for training S-Net. The smoothed Dice coefficient is calculated for all objects and the negative mean value is used as the training loss,

$${\mathcal{L}}_{\text{S-Net}}=-\frac{1}{N}\sum _{i=1}^N\frac{ϵ+\sum _{\mathit{x}\in {\mathrm{\Omega }}_i}2g_i(\mathit{x})p_i(\mathit{x})}{ϵ+\sum _{\mathit{x}\in {\mathrm{\Omega }}_i}(g_i(\mathit{x})+p_i(\mathit{x}))}.$$ (2)

Here, ${\mathrm{\Omega }}_i$ is the set of all pixels in the segmentation map of object $i$, $g_i(\mathit{x})$ and $p_i(\mathit{x})$ are the probabilities that pixel $x$ belongs to object $i$ in the ground truth and S-Net prediction, respectively, and $ϵ$ is a smoothing constant ($ϵ=0.001$ here). We have manual delineations of the nine surface positions and the MME masks, as shown in Fig. 1. We have converted the surface positions into segmentation masks; thus, in conjunction with the MME masks, every pixel has one of eleven labels—either MME or one of the following: vitreous, RNFL, GCIP, INL, OPL, ONL, IS, OS, RPE, or choroid. We train the S-Net based on these segmentation masks as ground truth.

The network is initialized with the “He normal” [36] method and trained with the Adam optimizer with an initial learning rate of ${10}^{-4}$ until convergence. For each training batch, we perform the following data augmentations with probability 0.5: 1) flip the image horizontally and 2) scale the image vertically with a random ratio between $0.8$ and $min(1.2,s)$, where $s$ is the maximum scaling ratio so that the retina is not thicker than the input image height. We then crop the scaled image to the original image size.

2.5.2. R-Net training

To learn a latent representation that is not affected by topology defects, we use the strategy of [37] wherein topology defects are artificially introduced in the ground truth segmentation masks and the network must still find the true surface positions. To produce correctly-ordered surfaces, we modify what was done in [37] by directly seeking only the position of the first boundary and thereafter seek the difference between the boundaries (which is enforced to be non-negative through the use of ReLU as the final step). Other improvements over [37] are described below.

The loss function for R-Net is the mean squared error between the ground truth surface positions and the reconstructed surface positions from R-Net,

$${\mathcal{L}}_{\text{R-Net}}=\frac{1}{9w}\sum _{i=1}^9\sum _{j=1}^w{(h_i(j)-r_i(j))}^2.$$ (3)

Here, $h_i(j)$ and $r_i(j)$ are the ground truth and the predicted surface position of surface $i$ (by summing up the predicted surface distances above surface $i$) on A-scan $j$, respectively. The segmentation masks converted from the manual surfaces and MME (see 3.1) are augmented with topology defects and are used as input to the R-Net, whose output ground truth are the nine manual surface positions. We augment each training mini-batch with probability 0.5 by flipping the ground truth surface position and MME masks horizontally and translate them vertically with random offsets (while making sure the retina is within the image). Scaling augmentation is not used, as we want to learn the shape information of retina layer thicknesses. Eleven segmentation masks are generated based on the augmented manual surfaces and MME masks.

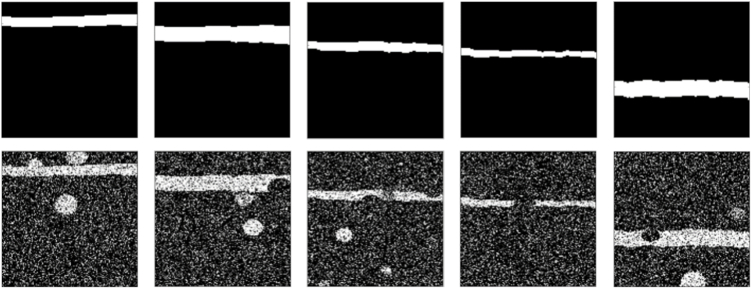
We then augment each mini-batch of generated segmentation masks above with probability 0.5 by adding Gaussian noise and simulated defects. This is a common strategy to help networks learn shape completion [25,30]. The defects are ellipse-shaped masks with pixel values uniformly distributed from $-1.5$ to $1.5$. So if an ellipse mask with negative magnitude is added to a ground truth mask, a hole defect will be introduced. The number, center, and semi-major/minor axis of ellipses added to each layer mask are randomly generated. Softmax is used to normalize the masks with added defects before adding Gaussian noise. Examples of the simulated input maps to R-Net are shown in Fig. 4. The convolution layer in R-Net is initialized with the “He normal” [36] method and the initial bias for the fully connected layer are set to one which is important for letting the gradient flow through the ReLU in the beginning. R-Net is trained with the Adam optimizer with an initial learning rate of ${10}^{-4}$ until convergence.

Fig. 4.

Shown in the top row are masks generated from ground truth surface positions before the addition of simulated defects. On the bottom row, we see the affects of the addition/subtraction of ellipses and additive Gaussian noise to the ground truth masks. The pairs of ground truth surface position and simulated masks with defects are used to train R-Net.

2.6. Patch Concatenation

Ideally, after training is complete (see next section), we would process an entire B-scan at once. However, because of GPU memory limitations, R-Net, which has a fully connected layer, can only process input image patches with a fixed size. We therefore extract and process $128\times 128$ pixel patches one at a time. Because of the convolution operation and the use of zero padding for values outside a patch, the predictions near patch boundaries are not accurate. To address this problem, we use overlapping patches and combine predictions in the overlapping regions (the maximum overlapping width is smaller than half of the patch width). We assume that the closer a pixel is to the patch boundary, the more unreliable the prediction is and use a linear weighting scheme to combine the patches found by S-Net. In particular, prior to passing the S-Net probability maps to R-Net we make the following correction. Suppose pixel $\mathit{x}$ at A-scan $j$ within a given B-scan is contained in the overlap region of patches $A$ and $B$ (see Fig. 5).

Fig. 5.

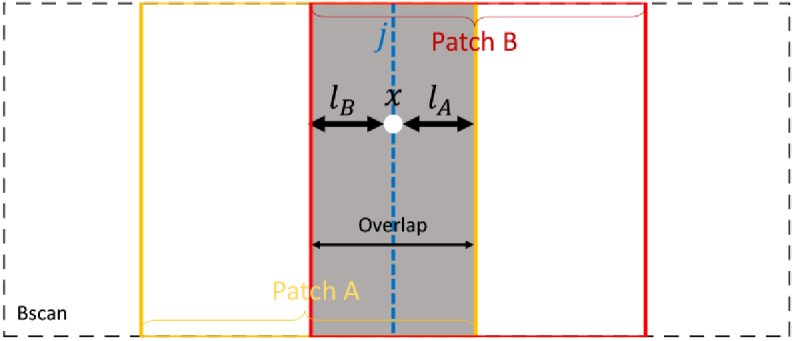
A schematic of the patch concatenation.

Let the distances from A-scan $j$ to the nearest boundaries of patches $A$ and $B$ be $l_A$ and $l_B$, respectively. We adjust the S-Net prediction $p(\mathit{x})$ to be a linear combination of prediction $p_A(\mathit{x})$ and $p_B(\mathit{x})$ from patches $A$ and $B$ as follows,

$$p(\mathit{x})=\frac{p_A(\mathit{x})\times l_A+p_B(\mathit{x})\times l_B}{l_A+l_B}.$$ (4)

The surface depth position $d_A(j),d_B(j)$ from R-Net for each patch at column $j$ are concatenated into the whole B-scan using

$$d(j)=\frac{d_A(j)\times l_A+d_B(j)\times l_B}{l_A+l_B},$$ (5)

which is the same linear weighting scheme as in Eq. 4. This weighting scheme alleviates the patch boundary inaccuracy caused by the invalid convolutions and the inconsistency of the prediction in the overlapping areas.

3. Experiments

To validate our method, we compared it to publicly available state-of-the-art algorithms that had been actively used in clinical research for segmenting retinal surfaces and MME. We first compared it to the AURA toolkit [18], which is a random forest and graph-based method for segmentation of nine retinal surfaces. Tian et al. [38] compared six state-of-the-art publicly available retina surface segmentation methods including the IOWA reference algorithm [39], and the AURA toolkit achieved the best surface accuracy. We also compared to a state-of-the-art deep learning method called RelayNet [28]. RelayNet only outputs layer maps without any topology guarantee but we can obtain the surface positions by summing up the layer maps in each column. The AURA toolkit is only able to segment surfaces, so we compared our MME segmentation results with another state-of-the-art random forest based methods proposed by Lang et al. [40]. A benchmark study of intra-retina cysts segmentation by Girish et al. [41] compared seven cysts segmentation algorithms, and the method of Lang et al. [40] achieved the top ranking. Since the AURA toolkit [18] is not able to segment MMEs and Lang’s MME method [40] has no retinal surface segmentation method, we compared our surface segmentation accuracy with the AURA toolkit and our MME segmentation accuracy with Lang’s MME method using two separate data sets. In order to compare with RelayNet, we retrained it on our training data until convergence using the author’s pytorch implementation. The optimizer parameters and augmentation strategy for RelayNet training are the same as that used for S-Net.

Our proposed method is the cascade of S-Net and R-Net, trained separately, which we denote as SR-Net. As mentioned in Section 3.1. and [32], S-Net and R-Net can be trained together as a pure regression net without training S-Net first, and we denote the resulting network as SR-Net-T.

3.1. Retina layer surface evaluation

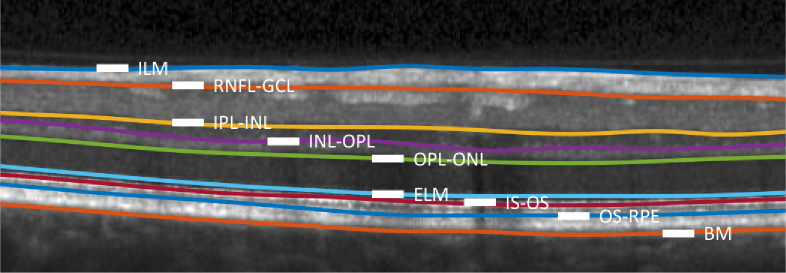
Our first data set includes 35 macular OCT scans, publicly available from [42], acquired from a Spectralis OCT system (Heidelberg Engineering, Heidelberg, Germany). Twenty-one of the scans are diagnosed with multiple sclerosis (MS) and the remaining fourteen are healthy controls (HC). Each scan contains 49 B-scans of size 496×1024. The lateral and axial resolution and the B-scan separation are 5.8$\mu$m, 3.9$\mu$m, and 123.6$\mu$m, respectively. Nine surfaces were manually delineated for each B-scan in all 35 subjects. An example of the delineated boundaries, also defining the layer abbreviations, is shown in Fig. 6. Note that because the boundary between the GCL and IPL is often indistinct, this boundary is not estimated; the layer defined by the RNFL-GCL and IPL-INL boundaries is referred to as GCL+IPL in the following.

Fig. 6.

An example B-scan with manually delineated boundaries separating the following retinal layers: the retinal nerve fiber layer (RNFL), the ganglion cell layer (GCL); the inner plexiform layer (IPL); the inner nuclear layer (INL); the outer plexiform layer (OPL); the outer nuclear layer (ONL), the inner segment (IS); the outer segment (OS); and the retinal pigment epithelium (RPE). Boundaries (surfaces) between these layers are identified by hyphenating their acronyms. The named boundaries are: the inner limiting membrane (ILM); the external limiting membrane (ELM); and Bruch’s Membrane (BM).

We used the last six of the HC scans and the last nine of the MS scans for training both the deep networks and the AURA toolkit (which requires training of the random forest that it uses); the remaining 20 scans were used for testing. This data set includes both HC and MS patients but does not have manual delineations for MME. For a fair comparison with the AURA toolkit, we redesigned the S-Net output to include only the 10 surface segmentation maps (and to exclude the MME map). The S-Net in the experiment has four max-pooling layers and is trained for 30 epochs until convergence and R-Net is trained for 300 epochs since it is trained with numerous simulated datasets and has lower risk for over-fitting. We trained SR-Net-T for 300 epochs, and the input training image is augmented as mentioned in 3.1.

We present results for both SR-Net-T and SR-Net in Tables. 1 and 2. We also present the following results: S-Net, the first part of our proposed SR-Net; Aura toolkit [18] (downloaded from https://www.nitrc.org/projects/aura_tools/) which is a state-of-the-art graph method and the winner of a recent comparison [38]; and ReLayNet [28] a state-of-the-art deep learning method.

Table 1. Dice scores for each tested method compared to manual delineation. Larger values are better and the best result in each column is denoted in bold font.

Layer	RNFL	GCL+IPL	INL	OPL	ONL	IS	OS	RPE	Overall
AURA	0.938	0.945	0.874	0.899	0.947	0.874	0.875	0.916	0.908
ReLayNet	0.936	0.947	0.877	0.899	0.948	0.871	0.875	0.914	0.908
SR-Net-T	0.928	0.940	0.853	0.875	0.930	0.804	0.820	0.875	0.878
S-Net	0.928	0.942	0.862	0.886	0.939	0.838	0.847	0.905	0.893
SR-Net	0.937	0.951	0.883	0.902	0.950	0.872	0.872	0.907	0.909

Table 2. Mean absolute distance (MAD) and rooted mean square error (RMSE) evaluated on 20 manually delineated scans for four of the tested methods. Smaller values are better and the best value for both MAD and RMSE are shown in bold font.

	MAD ($\mathit{\mu }\mathit{m}$)				RMSE ($\mathit{\mu }\mathit{m}$)
Boundary	AURA	SR-Net-T	ReLayNet	SR-Net	AURA	SR-Net-T	ReLayNet	SR-Net
ILM	2.37 (0.36)	2.96 (0.78)	3.17 (0.61)	2.38 (0.36)	3.08 (0.51)	4.22 (2.50)	4.11 (1.06)	3.20 (0.99)
RNFL-GCL	3.09 (0.64)	3.55 (0.55)	3.75 (0.84)	3.10 (0.55)	4.58 (1.03)	5.52 (2.07)	5.65 (1.57)	4.64 (1.19)
IPL-INL	3.43 (0.53)	3.71 (0.82)	3.42 (0.45)	2.89 (0.42)	4.57 (0.79)	5.08 (1.47)	4.59 (0.75)	3.91 (0.57)
INL-OPL	3.25 (0.48)	3.80 (0.69)	3.65 (0.34)	3.15 (0.56)	4.29 (0.58)	4.94 (0.96)	4.75 (0.56)	4.10 (0.71)
OPL-ONL	2.96 (0.55)	3.87 (0.78)	3.28 (0.63)	2.76 (0.59)	4.36 (1.05)	5.11 (1.06)	4.57 (1.24)	3.99 (1.12)
ELM	2.69 (0.44)	3.72 (1.26)	3.04 (0.43)	2.65 (0.66)	3.38 (0.54)	4.52 (1.34)	3.78 (0.52)	3.38 (0.81)
IS-OS	2.07 (0.81)	3.57 (1.28)	2.73 (0.45)	2.10 (0.75)	2.62 (0.91)	4.23 (1.27)	3.31 (0.46)	2.73 (0.89)
OS-RPE	3.77 (0.94)	4.72 (1.12)	4.22 (1.48)	3.81 (1.17)	4.94 (1.14)	5.80 (1.25)	5.31 (1.66)	4.89 (1.42)
BM	2.89 (2.18)	5.44 (2.98)	3.09 (1.35)	3.71 (2.27)	3.61 (2.26)	6.21 (2.96)	3.87 (1.47)	4.41 (2.34)
Overall	2.95 (1.04)	3.93 (1.47)	3.37 (0.92)	2.95 (1.10)	3.94 (1.31)	5.07 (1.86)	4.44 (1.31)	3.92 (1.37)

Table. 1 shows that direct application of S-Net, a direct pixel-wise labeling method, yields good Dice scores. However, these results are not topologically correct, as shown in Fig. 8. R-Net, which is trained on simulated data with defects, corrects the defects in S-Net and outputs surfaces with the correct topology. As a result, SR-Net achieves better results than S-Net in all layers (see Table. 1) and guarantees the correct topology. Layer topology is guaranteed in AURA toolkit as well because of its graph design and surface distance constraints. SR-Net is comparable in performance to the AURA toolkit, is much faster, and does not require any hard-coded surface distance constraints for different retinal regions. The Dice scores of RelayNet are also similar to SR-Net, but the implied surface positions of RelayNet (see Table. 2) are not as good as our method or the AURA toolkit. This is likely due to topological defects in the layer masks of RelayNet that may not greatly affect Dice coefficients but will yield inaccurate surface positions.

Given that the depth resolution is 3.9 $\mu$m, Table. 2 shows that AURA toolkit, ReLayNet, and our proposed SR-Net all have sub-pixel error on average. Statistical testing was done between SR-Net and AURA using a Wilcoxon rank sum test. Two boundaries reached significance ($\alpha$ level of $0.05$) for MAD and RMSE: IPL-INL ($p$-values are both $0$ for MAE and RMSE) and BM ($p$-values are both $0.02$), but shows no statistical significance for overall surface segmentation accuracy ($p$-values are $0.97$ and $0.86$). When comparing against SR-Net-T, SR-Net is statistically better in all surfaces and AURA is better for all surfaces except the IPL-INL. As for Dice scores, AURA and SR-Net shows no statistical difference. SR-Net is statistically better than S-Net in all layers and overall performance expect for the RPE. SR-Net is significantly better than SR-Net-T, which implies that decoupling the network training improves results.

For qualitative comparison, an example result is shown in Fig. 7 . We observe that AURA toolkit, SR-Net, and SR-Net-T provide visually acceptable results on this B-scan. To illustrate a key difference between SR-Net and SR-Net-T, we show the intermediate feature maps from the S-Net parts of SR-Net and SR-Net-T in Figs. 7(e) and 7(f), respectively. We can see that the feature map makes intuitive (interpretable) sense for SR-Net (as it appears to be a good labeling of the retinal layers) while it does not make intuitive sense in SR-Net-T.

Fig. 7.

Shown overlaid on a B-scan are the delineations from the (a) manual delineation, (b) AURA toolkit, (c) SR-Net, (d) SR-Net-T. (e) is the S-Net result overlaid with SR-Net surface result and (f) is the intermediate S-Net result of SR-Net-T overlaid with the SR-Net-T surface result.

Figure 8shows three examples (the three rows) from challenging B-scans where S-Net (separately trained within SR-Net) yields topologically incorrect results. The left-hand column shows feature maps from S-Net where the layer segmentation map became discontinuous due to the thinning layers around the fovea (top row), has an incorrect prediction due to blood vessels (middle row), and has numerous defects due to poor image quality (bottom row). The right-hand column shows the result of SR-Net, where R-Net used the S-Net results (left column) and learned shape information encoded in the learned network weights to generate surfaces that look acceptable (and are guaranteed to have the correct topology).

Our proposed method takes 10 seconds to segment a $496\times 1024\times 49$ scan (preprocessing and reconstruction included), of which the deep network inference takes 5.85 s on an NVIDIA GeForce 6 GB 1060 graphics processing unit (GPU). The segmentation is performed with Python 3.6 and the preprocessing is performed using Matlab R2016b called directly from the Python environment. The AURA toolkit takes a total segmentation time of 100 s in Matlab R2016b, of which the random forest classification takes 62 s and the graph method takes 20 s on an Intel i7-6700HQ central processing unit. The speed of our method is beneficial for large cohort studies of MS patients.

3.2. MME evaluation

The AURA toolkit is not able to segment MMEs; thus, we compared our method with Lang et al.’s MME segmentation method [40], which won a recent benchmark study on retinal cyst segmentation [41]. Our MME cohort consists of twelve MS subjects, each of whom had a 3D macular OCT acquired on a Spectralis system, with each 3D scan containing 49 B-scans. Each of the 49 B-scans in all twelve subjects had their MMEs delineated [43,44]. Additionally, they had their retinal surfaces delineated on 12 B-scans in each of the 3D volumes. The subjects were divided into two folds for cross-validation with each fold containing a cross-section of MME load—from high to low. We retrained S-Net and R-Net on one fold and tested on the other, then repeated this by swapping the training and testing folds. In this two-fold experiment, both networks were trained until the losses converged. In the case of the S-Net, this took 110 epochs, while the R-net required 200 epochs. For evaluation of MME segmentation, in each fold we tested on all 49 B-scans of the six testing subjects—i.e., 294 B-scans. Thus across the two folds, we evaluated MME segmentation performance on 588 B-scans.

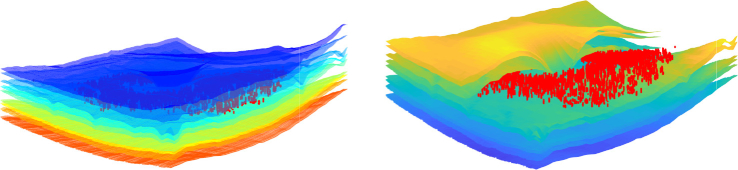
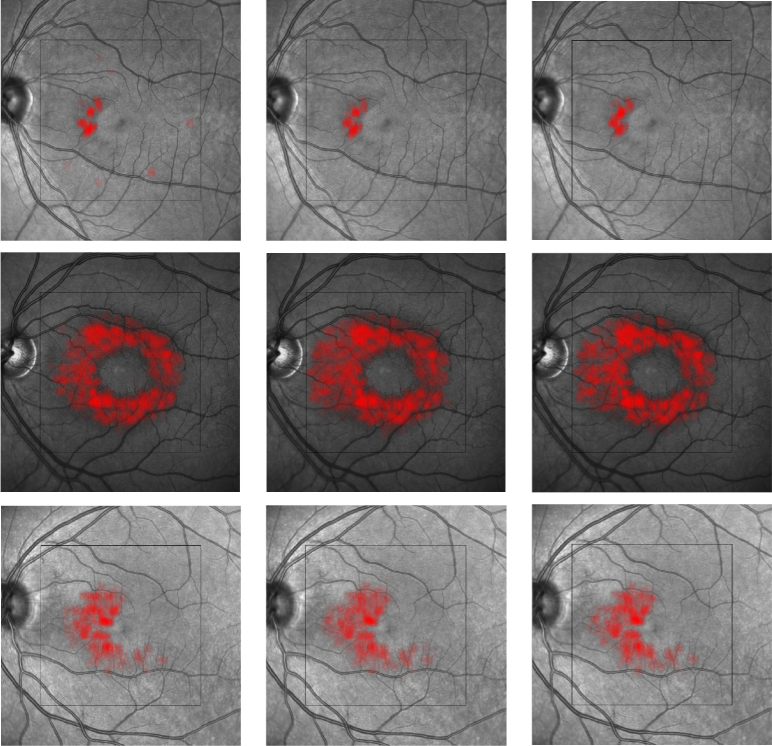
The MME volume Dice score was evaluated on all volume scans. The results are shown in Table. 4 with ground truth MME total pixel numbers also listed. From the table, our method achieved better results than the state-of-the-art baseline method [40] in ten of the twelve subjects. Subject #4 is an outlier, as part of the retina is shadowed and has poor SNR. The true number of MME pixels for Subject #4 is only 81; thus, any noise causes a large Dice score drop-off. However, the RF method, with its hand-crafted features, has no issue as the features (SNR and fundus image used) were designed specifically for edge cases like Subject #4. This deficiency could eventually be solved in our method, if more training data were available (currently we only have 72 B-Scans for training). The MAE and RMSE for MME surface segmentation was also evaluated on all 144 B-scans (12 subjects, 12 B-scans each) and the results are shown in Table. 3. The depth resolution is 3.9 $\mu m$ and thus the overall MAE is still below one pixel. Example segmentation results are shown in Figs. 9. Figure 10 provides a 3D visualization of both the retinal surface and MME from our segmentation and Fig. 11 shows MME fundus projection images. From the figures, we can see that the proposed method can learn the relationship between MMEs and retinal surfaces automatically and perform a good segmentation.

Table 4. Dice scores, against manual delineations, for MME cyst comparison for our proposed method and the state-of-the-art Lang et al. [40]. Higher values are better, with the best result in each column denoted in bold. We also list the total number of cyst pixels for each subject.

Subject	1	2	3	4	5	6	7	8	9	10	11	12	Mean
Our Method	0.73	0.62	0.65	0.00	0.81	0.80	0.39	0.80	0.51	0.73	0.80	0.76	0.64
Lang et al.	0.66	0.41	0.50	0.76	0.80	0.76	0.49	0.80	0.13	0.61	0.70	0.70	0.61
True # MME pixels	3342	442	246	81	28621	7858	79	16793	121	374	5081	1578	5384

Table 3. Mean absolute distance (MAD) and rooted mean square error (RMSE) evaluated on 12 subjects (12 B-scans per subject) with our proposed SR-Net on subjects with MME.

Boundary	ILM	RNFL-GCL	IPL-INL	INL-OPL	OPL-ONL	ELM	IS-OS	OS-RPE	BM	Overall
MAD	2.91 (0.67)	3.28 (0.71)	4.10 (0.94)	3.81 (0.58)	3.78 (0.93)	3.14 (0.63)	3.18 (0.89)	4.52 (1.64)	4.43 (0.80)	3.68 (1.04)
RMSE	3.88 (1.25)	4.69 (1.55)	5.07 (0.99)	4.71 (0.56)	5.14 (1.83)	3.73 (0.60)	3.68 (0.84)	5.48 (1.80)	5.17 (0.81)	4.62 (1.35)

Fig. 9.

Results of surface and MME segmentation. Shown are (a) the ground truth, (b) our proposed deep network, and (c) the MME segmentation generated by Lang et al.’s [40] random forest approach.

Fig. 10.

Visualization of MME (red) and surfaces (left) and the cross-section (right).

Fig. 11.

MME projection on the fundus image. Each row is one example scan. From left to right: Lang et al.’s method [40], our method, and the manual delineation.

4. Discussion

Characterizing neurological disease through retinal imaging is a powerful recent development facilitated by OCT imaging and image analysis. Accelerating the performance of retinal layer segmentation and providing MME segmentation—without compromising the accuracy of layer segmentation—is an important step forward in the use of this technology. Since our approach is purely data-driven—an advantage of the deep learning framework—we expect that it will be readily applicable to a broader range of cohorts without the need for the extensive manual tuning needed by graph methods [45]. Manual delineations are needed for training, of course, but this is also the case for graph methods.

It is often claimed that end-to-end training of deep networks is preferable [46]. However, in our case, we demonstrate that use of separate training is more effective. The simultaneously trained SR-Net-T learns a regression from intensity image to surface distances directly. Thus it does not explicitly rely on boundary evidence from the images. The intermediate result from SR-Net-T in Fig. 7 cannot be explained easily, whereas the meaning of the S-Net result from SR-Net is clear, and we can also use it to output MME masks. The poor performance of SR-Net-T can be explained by the fact that only surface distance values at each column are used in the loss function whereas S-Net is trained with weighted Dice loss. This means that the classification error of every pixel in the training data was back-propagated [47] and therefore provides more training samples. The decoupling of S-Net and R-Net training also makes the data augmentation for training R-Net easier since we can generate masks with defects easily. An alternative way to train R-Net is to take the S-Net output as input and output the ground truth surface distances. Since S-Net output does not equal the ground truth mask, the training masks and output surface distances are not perfectly paired which will bias and over-fit R-Net.

The R-Net is composed of a U-Net and a fully connected layer. The encoder of this U-Net encodes the segmentation from S-Net into a latent shape space and the decoder maps it back to the high dimensional space and the fully connected layer with ReLU activation output surfaces with guaranteed topology. For less parameters, we would like to replace this fully connected layers with convolution layers (and ReLU activation). The basic convolution layer to convert the $11\times 128\times 128$ S-Net output to a $9\times 128$ surface position could be applying a $128\times 16$ convolution kernel with zero pixel vertical padding, eight pixels horizontal padding, eleven input channels and nine output channels. We replace the fully connected layer with this convolution layer and tried with different settings (kernel sizes, layer numbers) but the results are substantially worse than the fully connected layer. Thus, we chose to keep the fully connected layer in our R-Net. S-Net is used to produce pixel-wise labeling results without explicitly using topology constraints. This is beneficial for lesion segmentation, since the spatial distribution and shapes of some lesions are not fixed. We do not assume topology constraints for MME lesions and thus the MME segmentation maps from S-Net are what we need.

Recent work using deep networks for segmentation has automated the feature selection process and achieved high quality results [28,48]. However, many such methods have stopped after completing the pixel-wise labeling. Such deep network segmentation results do not have the correct topology and therefore the desired surfaces are not obtained. Other works use graph (or level set) methods to incorporate shape and topology priors and extract boundaries from the initial segmentation probability maps [17,49]. However, manually designing the shape model becomes difficult in the presence of pathology, and the inference for a graph or a deformable model cannot be easily integrated into the deep learning framework (thus off-the-shelf GPU support may not be available).

Instead of a manually designed shape model, we use a second network (R-Net) to learn the shape and topology priors and transform the problem into a surface distance regression problem. By using the ReLU activation as the final layer, the output is guaranteed to be non-negative and thus guarantees the reconstructed surface topology.

As in our algorithm, the AURA algorithm was originally designed for healthy controls and MS subjects. It has also been shown to be capable of adaptation to other diseases (see [45]). However, such adaptation has required careful hand-tuning of the underlying graph constraints. Given that our approach is data-driven, we expect that adaptation to other diseases will only require new training data and subsequent retraining (ideally starting with the current weights). Proof of this conjecture is left to future work.

5. Conclusion

In this paper, we proposed the first topology guaranteed deep learning methods for retinal surface segmentation that does not use graph methods or level sets for post-processing. The cascaded deep network structure with decoupled training permits effective learning of both the pixel properties for accurate pixel-labeling and shape priors for correction of topological defects. A novel regression framework in the second network guarantees topological correctness of the estimated retinal boundary surfaces. The resultant deep network has a single feed forward propagation path and is computationally faster than the best competing methods. The network was developed to simultaneously segment both retinal layers and the MMEs that are sometimes observed in MS patients, which shows its applicability in pathological cases.

Funding

National Eye Institute10.13039/100000053 (R01-EY024655 (PI: J.L. Prince)); National Institute of Neurological Disorders and Stroke10.13039/100000065 (R01-NS082347 (PI: P.A. Calabresi)).

Disclosures

The authors declare that there are no conflicts of interest related to this article.