Generation of the configurational ensemble of an intrinsically disordered protein from unbiased molecular dynamics simulation

Significance

A major challenge in biology is characterizing the structural flexibility of intrinsically disordered proteins (IDPs). Ensemble-averaged experimental data do not provide the underlying protein structures. Here, we performed independently small-angle neutron and X-ray scattering experiments and unbiased molecular dynamics simulations to probe the solution structure of an IDP. We report that enhancing the sampling of the simulations can generate an ensemble of IDP structures in quantitative agreement with scattering and NMR, without the need for biasing the simulation or reweighting the results. The demonstration of established simulation technology that produces accurate physical models of flexible biosystems may pave the way to relating conformational flexibility to biological function.

Abstract

Intrinsically disordered proteins (IDPs) are abundant in eukaryotic proteomes, play a major role in cell signaling, and are associated with human diseases. To understand IDP function it is critical to determine their configurational ensemble, i.e., the collection of 3-dimensional structures they adopt, and this remains an immense challenge in structural biology. Attempts to determine this ensemble computationally have been hitherto hampered by the necessity of reweighting molecular dynamics (MD) results or biasing simulation in order to match ensemble-averaged experimental observables, operations that reduce the precision of the generated model because different structural ensembles may yield the same experimental observable. Here, by employing enhanced sampling MD we reproduce the experimental small-angle neutron and X-ray scattering profiles and the NMR chemical shifts of the disordered N terminal (SH4UD) of c-Src kinase without reweighting or constraining the simulations. The unbiased simulation results reveal a weakly funneled and rugged free energy landscape of SH4UD, which gives rise to a heterogeneous ensemble of structures that cannot be described by simple polymer theory. SH4UD adopts transient helices, which are found away from known phosphorylation sites and could play a key role in the stabilization of structural regions necessary for phosphorylation. Our findings indicate that adequately sampled molecular simulations can be performed to provide accurate physical models of flexible biosystems, thus rationalizing their biological function.

Intrinsically disordered proteins (IDPs) are structurally flexible and lack stable secondary structures in physiological conditions. They play a critical role in many cellular functions, such as signal transduction, transcriptional regulation, cell growth, binding, gene expression, and homeostasis (1–5). IDPs are also associated with multiple diseases, such as cancers (6, 7), amyloidosis, diabetes, cardiovascular problems, and neurodegenerative disorders (8, 9).

To understand the disorder–function relationship IDPs present and to elucidate the mechanism by which their pathological mutations lead to human diseases (2), we need to determine their configurational ensemble: the collection of 3-dimensional (3D) structures they adopt (10). Several experimental techniques have been applied to study the structures of IDPs, including NMR spectroscopy (6, 11–18), single-molecule Förster resonance energy transfer (sm-FRET) (17, 19, 20), cryoelectron microscopy (21, 22), and small-angle X-ray and neutron scattering (SAXS and SANS) (6, 15, 17, 23–28). However, the information obtainable from these experiments is limited and they cannot provide a high-resolution description of IDP ensembles (29–34). Further, most techniques employed to study IDPs suffer from a conundrum: The experimental observables represent an average over the conformational ensemble, but the ensemble itself cannot be unequivocally inferred from the experiments (10, 29, 35). For SAXS and SANS, unambiguous structural interpretation is made more difficult by the inherent orientational averaging.

Molecular dynamics (MD) simulation can, in principle, provide the structural ensemble of biomolecules. However, MD faces 2 distinct, yet related, challenges when applied to IDPs: the accuracy of the physics-based molecular mechanics force fields that model the interactions in the system and the need for adequate sampling of the large configurational space of an IDP and its associated solvent. Recent progress has considerably improved molecular mechanics force fields for IDPs (36–43). Nevertheless, the accuracy of simulations, as assessed by comparison to experiments, was found to depend on the specific IDP, the employed force field, and configurational sampling in a weakly funneled energy landscape (36–38, 40, 42).

The current state-of-the-art approach to structurally characterizing IDPs at atomic detail requires either restraining the MD or reweighting (44–50) the MD-generated ensemble to match the experimental data (35, 51). This creates overfitting issues and makes it difficult to judge the accuracy of the models because of a degeneracy problem: Different ensembles may yield the same experimental observable (29, 52, 53). Despite recent successes of Bayesian methods when refining MD-derived structures against SAXS data (54, 55), reproducing experiments without the need to modifying simulation results presents one of the most important challenges in structural biology of IDPs. Addressing this challenge would lead to increased confidence that the obtained models accurately describe the physical behavior of the systems.

Here, we combine MD simulation with SAXS, SANS, and NMR experiments to elucidate the conformational ensemble of the 95-residue intrinsically disordered N terminus of the proto-oncogene nonreceptor human tyrosine kinase c-Src, which contains the Src homology 4 (SH4) and unique domains. c-Src plays a major role in cellular transduction pathways such as cell growth, differentiation, transcription, proliferation, adhesion, and survival (12, 56) and is associated with a variety of human cancers (57). SH4 regulates c-Src kinase localization in response to cellular stimulation (56) by binding/anchoring to the cell membrane, whereas the unique domain (UD) mediates the interaction of Src with lipids, specific receptor and protein targets (12, 13, 58).

In the present work a heterogeneous ensemble of structures of SH4UD was generated by enhancing the sampling of unbiased atomistic simulations in an explicit solvent by using Hamiltonian replica exchange MD (HREMD) (59–61). Critically, the SAXS, SANS, and NMR observables of SH4UD thus generated are found to be in excellent agreement with the experimental data without the need for biasing or reweighting. The use of HREMD is critical in achieving this agreement. The simulations reveal a weakly funneled and rugged free energy landscape and predict 3 transient helical regions that do not coincide with the known phosphorylation sites but are proximal to a lipid-binding region. We hypothesize that such transient structures act as a molecular recognition feature for phosphorylation-mediated regulator of enzyme activity and for membrane binding.

Results

Agreement between Experiments and Simulations.

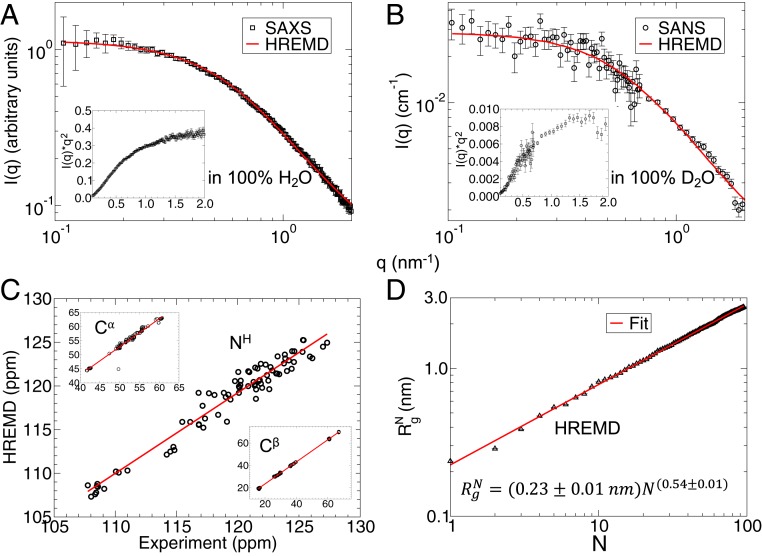
We conducted SAXS (Fig. 1A) and SANS (Fig. 1B) experiments of SH4UD. The Guinier [ln(I) vs. q²] and Zimm [1/I(q) vs. q²] plots follow a linear behavior at low q, as expected for monodisperse samples (SI Appendix, Fig. S1). The upturn at high q in the Kratky plot (Fig. 1, Insets) confirms the disordered nature of SH4UD. The distribution of atom-pair distances, P(r), is asymmetric with an extended shoulder at distances r ≥ 6 nm (SI Appendix, Fig. S2). This suggests the average shape of SH4UD is elongated, where the interpretation is consistent with previous studies (62, 63).

Fig. 1.

(A and B) Experimental (A) SAXS in 100% H₂O and (B) SANS in 100% D₂O profiles are shown in black squares and circles, respectively. Experimental Kratky plots, I(q) × q² vs. q shown in the Insets confirm the unfolded structure of SH4UD. The ensemble-averaged profiles calculated from ∼510-ns HREMD trajectory are shown as a red line. (C) Comparison between experimental and calculated (HREMD) NMR chemical shifts, expressed in parts per million (ppm), of the backbone N^H, C^α, and C^β atoms. The NMR experimental data are taken from Biological Magnetic Resonance Data Bank entry 15563 (12) and the theoretical chemical shifts were calculated using SHIFTX2 from ∼51,000 structures (122). (D) Radius of gyration $\left(R_g^N\right)$ of a protein segment consisting of N residues calculated from the HREMD simulation. The red line is a fit of Eq. 1 to the data.

SANS and SAXS provide different information because the 2 techniques are sensitive to different atomic properties: neutrons interact with atomic nuclei, whereas X-rays interact with electron clouds. For example, there is significantly different contrast between a protein and its hydration shell in SAXS and SANS (64–66). This is illustrated in our data when obtaining the radius of gyration (R_g) by taking the second moment of the P(r). We obtain $R_g^{SANS}$ = 2.52 ± 0.10 nm for SANS and $R_g^{SAXS}$ = 2.71 ± 0.04 nm for SAXS of the same sample. The difference in R_g between SAXS and SANS reported here is consistent with scattering measurements from globular proteins, in which R_g determined from SANS in 100% D₂O is smaller than that obtained from SAXS data of the same sample in 100% H₂O (65, 67).

The ensemble-averaged SAXS and SAXS profiles calculated directly from the trajectory of the lowest-rank replica of the HREMD simulation are found to be in excellent agreement with experiment: ${\chi }^2=1.2$ for SAXS and ${\chi }^2=1.3$ for SANS (see Eq. 2) (Fig. 1 and SI Appendix, Figs. S3, S5, and S6). This agreement is obtained by an unbiased/unrestrained simulation, free from reweighting and using explicit water molecules when calculating SAXS/SANS curves, thus avoiding the need for optimized free parameters to account for the contribution of the hydration shell.

We also calculated the ensemble average NMR chemical shifts of the backbone atoms (N^H, C^α, and C^β) of SH4UD from the HREMD simulation and compared them to previously published experimental values (12). The excellent agreement between NMR and HREMD is reflected by the regression coefficients R² > 0.93 (Fig. 1C and SI Appendix, Fig. S7).

The unbiased HREMD simulations are thus consistent with 3 independent experimental probes of global and local protein structure: SAXS, SANS, and NMR. The underlying conformational ensemble contains all of the structures from the ∼510-ns-long trajectory and has a broad distribution of R_g, as reflected in the density plot of the theoretical I(q) (SI Appendix, Fig. S3). The use of HREMD is critical in obtaining good agreement with scattering and NMR experiments (SI Appendix, Figs. S3 and S7). The convergence of the calculations is shown in detail in SI Appendix, Figs. S5–S9.

Chain Statistics.

The degree of compaction of a polypeptide chain in aqueous solution can be quantified by the Flory exponent, ν, which is determined by the relative strengths of the protein–solvent and intraprotein interactions (17, 24, 25, 68). Polymer theory predicts only 3 values of ν for polymers: When intraprotein interactions are favorable, ν = 0.333 and the protein adopts a collapsed conformation, for balanced interactions, ν = 0.5 and the protein is a Gaussian random coil, whereas for favorable protein–solvent interactions ν = 0.588 and the protein adopts a self-avoiding random coil conformation (24).

Here, the Flory exponent was calculated from the atomic coordinates using the relation (24, 69, 70),

$$R_g^N\hspace{0.17em}=\hspace{0.17em}{R}_0{N}^{\upsilon },$$ [1]

where $R_g^N$ is the radius of gyration of a protein segment consisting of N residues and R₀ is a constant. Fitting Eq. 1 to the simulation data (Fig. 1D) gives ν = 0.54 ± 0.01, suggesting the overall SH4UD–water interaction is favorable and SH4UD chain statistics lie between Gaussian and self-avoiding random coil behavior. Several studies have indicated similar chain statistics of other IDPs (17, 24, 25, 68).

Weakly Funneled Free Energy Landscape.

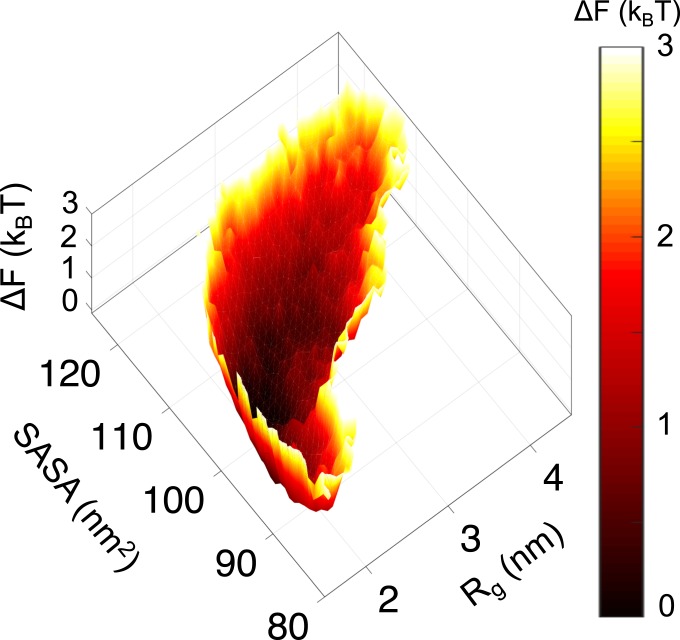
R_g and the solvent-accessible surface area (SASA) quantify important global protein characteristics: the overall size and solvent exposure, respectively. As such, they are used here as collective variables for describing the conformations of SH4UD by projecting the free energy onto them. SH4UD depicts a weakly funneled and rugged free energy landscape (Fig. 2). We note that barrier heights derived from 2D histogram analysis of HREMD simulations may carry large errors. The multiple shallow minima indicate the large number of conformational substates demonstrating a conformational heterogeneity. This structural heterogeneity is one of the distinctive characteristics of IDPs (25, 71–73).

Fig. 2.

Free energy landscape of SH4UD as a function of its R_g and SASA from HREMD simulations showing a large number of the conformational substates sampled in the simulation.

Secondary Structure Propensity.

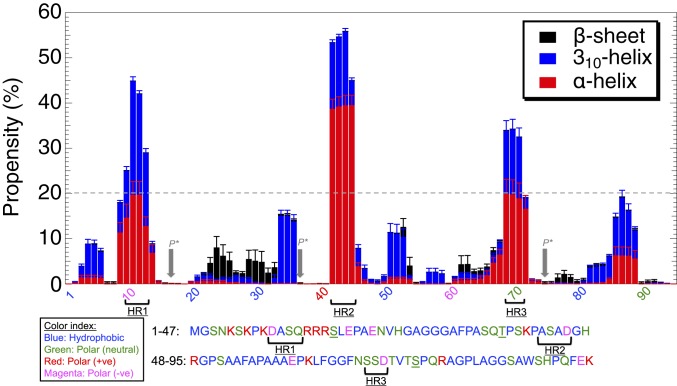
The propensity of residues to form secondary structure, calculated from the HREMD, indicates that SH4UD mainly adopts coil structures with almost negligible beta-sheet content, in agreement with NMR experiments (12). However, 3 short sequence segments that display occasional helical structures were found, defined here as having helical propensity higher than 20% (Fig. 3): helical region 1 (HR1), residues D10-A11-S12-Q13; HR2, A42-S43-A44-D45; and HR3, S69-S70-D71.

Fig. 3.

Propensity of each residue to form secondary structures calculated from the HREMD using DSSP (119). Arrows at underlined polar (neutral) residues S17, T37, and S75 are the known phosphorylation sites (P*) located between the predicted transient helical regions (HR1, HR2, and HR3).

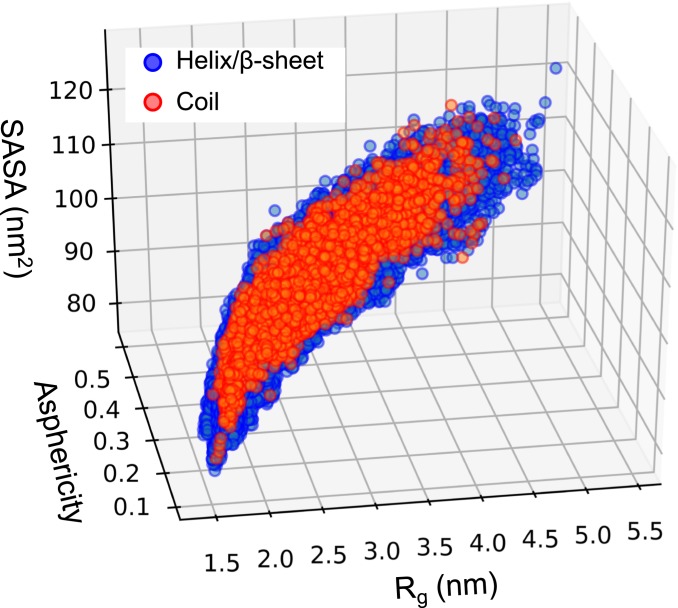
The conformations sampled by HREMD are of varying degree of compactness and asphericity (70) (Fig. 4). The broad distribution of R_g, SASA, and asphericity indicate the continuous and heterogeneous nature of the structures comprising the ensemble. Coil conformations with no secondary structure represent only ∼6% of the HREMD trajectory and are evenly distributed in the (R_g, asphericity, SASA) space (SI Appendix, Fig. S10). The chain statistics (Eq. 1) of the coil structures are similar to those of the entire ensemble and yield a ν = 0.54 ± 0.01 Flory exponent (SI Appendix, Fig. S10).

Fig. 4.

SH4UD structures projected on R_g, SASA, and asphericity. Frames are separated into those that have only coil (red) and those that have at least 1 helix or beta-sheet (blue) in their sequence.

Hydration Shell Structure.

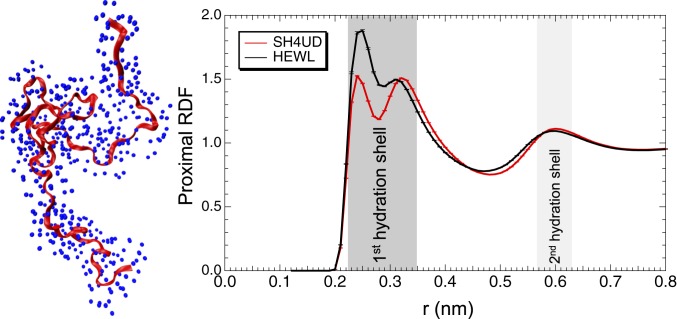
The hydration shell structure was quantified by calculating the proximal radial distribution function (pRDF) (74, 75) of water oxygen atoms around the nonhydrogen atoms of protein (Fig. 5). The 2 peaks of the pRDF at a distance r ∼ 0.30 nm from the protein surface correspond to the first hydration shell, which is found here to have a higher density than the bulk. The peak at r ∼ 0.25 nm arises from correlation distances involving protein oxygen and nitrogen atoms with water oxygen atom, whereas the peak at r ∼ 0.30 nm corresponds to carbon atoms (SI Appendix, Fig. S11).

Fig. 5.

(Left) A snapshot of SH4UD (red) and water oxygen atoms (blue) within a distance of 0.3 nm from protein’s surface. (Right) The pRDF as a function of the distance r between an oxygen atom of water and the nonhydrogen atoms of HEWL (black dashed curve) and SH4UD (solid red curve) proteins.

We compare the pRDFs of hydration water around SH4UD and hen egg white lysozyme, HEWL, a globular folded protein. While the pRDFs are similar for distances >0.35 nm, the first hydration shell is less dense for SH4UD than for HEWL, as shown by the lower peak heights, especially for the water oxygen–protein nitrogen interactions (SI Appendix, Fig. S11). This result indicates that the IDP hydration shell is more similar to bulk than for folded proteins. A smaller fraction of hydrophobic residues on the surface of HEWL compared to SH4UD were found that might explain the smaller hydration shell density of SH4UD (SI Appendix, Tables S1 and S2).

Discussion

The biological significance of IDPs and their abundance in many genomes have been increasingly realized (3). IDPs represent ∼30% of the human genome, play important cellular functions, and are associated with many diseases. Understanding their biological function in detail requires resolving the heterogeneous 3D ensembles of their structures, which remains a challenge because of the ensemble-averaged nature of most experimental data.

To determine IDP ensembles MD simulation is frequently combined with SAXS experiments (6, 24, 76, 77). However, it has hitherto been necessary to bias the populations of conformations obtained by MD to produce agreement with experiment (35, 46). In the present work we conducted unbiased HREMD simulations and obtained SAXS, SANS, and NMR observables in quantitative agreement with experiment. We calculated theoretical SAXS and SANS profiles considering explicitly water molecules in the simulation, avoiding the use of fitting parameters to account implicitly for the hydration shell (49). Critically, we overcame the need to reweight the simulation trajectories by enhancing the configurational sampling using HREMD. The sampling provided by HREMD, as compared to 10 μs of standard MD simulation, was crucial for obtaining good agreement with experiment (SI Appendix, Fig. S3).

The generation of a configurational ensemble in agreement with experiment suggests that details of the generated ensemble can be examined with some confidence. SH4UD is found to occupy numerous conformational substates in a weakly funneled and rugged free energy landscape (Fig. 2), which differentiates it from the strongly funneled free energy landscape of folded globular proteins (18, 71–73).

Low mean hydrophobicity and high mean net charge are considered as characteristics of IDPs (78–82). However, SH4UD has an abundance of hydrophobic residues that make its sequence more similar to folded globular proteins. Indeed, SH4UD lies near the border line of the charge-hydrophobicity plot commonly used to identify IDP propensity (78, 80, 81) (SI Appendix, Fig. S12). Based on the fraction of positively and negatively charged residues (SI Appendix, Fig. S13), SH4UD would be predicted to adopt collapsed structures (68, 83). However, perhaps somewhat surprisingly, SH4UD is found to adopt extended conformations. This is understood to occur from the distribution (“mixing”) of charged and polar residues across the entire sequence of SH4UD (68) (Fig. 3). The extended coil conformation of SH4UD is consistent with the finding that many hydrophobic IDPs are expanded in water (24).

The Flory exponent we obtained for SH4UD (ν = 0.54; Fig. 1D) lies in between the 2 values predicted for coils from polymer theory: ν = 0.5 for a Gaussian ideal coil and ν = 0.588 for a self-avoiding random coil. The value of ν = 0.54 has been reported for other IDPs studied with SAXS and sm-FRET (19, 24, 68). Thus, SH4UD cannot be accurately described by polymer theory. The Flory exponent of ν = 0.54 is found both for SH4UD structures that contain transient secondary structure elements and for pure coils (SI Appendix, Fig. S10).

SH4UD contains 3 known phosphorylation sites (residues S17, T37, and S75) that regulate Src activity (84, 85) and that do not coincide with the 3 transient helical regions we identified (HR1, HR2, and HR3). The present findings suggest that the higher solvent accessibility of the phosphorylation sites afforded by the absence of secondary structure may facilitate their modification by kinases. Further, we hypothesize that the transient helices provide an inherent stability near phosphorylation sites in SH4UD, consistent with the finding of short and transient helical structures near the phosphorylation sites of the (unphosphorylated) disordered region of the sodium protein exchanger 1 (86).

A recent NMR study found SH4UD has lipid-binding regions that include residues S51, A53, and A55 (13), which have ∼10% helical propensity in the HREMD (Fig. 3). We speculate that the transient helices might facilitate binding of c-Src to the cell membrane. Similar molecular recognition and stabilization due to the presence of transient secondary structures have been reported for other IDPs (16, 77, 86–94).

The hydration shells of IDPs have been studied less than those of folded proteins (65, 95–97). We found the hydration water around SH4UD to be less dense compared to folded HEWL. This result contrasts with previous simulation studies of 2 IDPs, alpha-synuclein and beta-amyloid (98), which, however, employed the Amber ff99SB and TIP3P force fields that may not accurately account for the interactions of IDPs and water (37, 38, 99–101).

Conclusions

We have obtained an accurate, atomic-detail physical model of the heterogeneous ensemble of structures of the intrinsically disordered SH4UD terminus of c-Src kinase. The model is based on structures generated by unbiased enhanced sampling MD simulations and is validated by calculation of SAXS, SANS, and NMR observables and comparison to experiment without constraining or reweighting the simulations. This physical model cannot be obtained alone by experiment, which provides either sparse or low-resolution information. We show that SH4UD explores heterogeneous conformational substates, from extended to partially collapsed in a weakly funneled and rugged free energy landscape. The conformations of SH4UD do not obey simple polymer theory. Transient helices are located away from known phosphorylation sites. We suggest that the transient helices are preconfigured structures, which localize c-Src by binding to the cell membrane and may facilitate phosphorylation-mediated regulation of c-Src. Our results suggest accurate physical models of flexible biomolecular systems, such as IDPs and proteins consisting of multiple domains connected by linkers, are within reach, and may pave the way to relating conformational flexibility to biological function.

Materials and Methods

Sample Preparation.

A gene encoding a 95-amino acid SH4UD construct with the sequence MGSNKSKPKDASQRRRSLEPAENVHGAGGGAFPASQTPSKPASADGHRGPSAAFAPAAAEPKLFGGFNSSDTVTSPQRAGPLAGGSAWSHPQFEK that included a C-terminal Strep tag (SAWSHPQFEK) was cloned into the pET-14b vector with NcoI and BamHI sites. Briefly, the SH4UD was expressed overnight in Escherichia coli Rosetta BL21 (DE3) at 20 °C and the cells were lysed by sonication in 100 mM Tris and 150 mM NaCl, pH 8.0. The lysate was passed over a strepavidin Sepharose column, washed with 20 column volumes of 100 mM Tris and 150 mm NaCl, pH 8.0, and eluted with 10 mM desthiobiotin. The eluted protein was then concentrated and purified to homogeneity using size-exclusion chromatography (Superdex 75; GE Healthcare).

SAXS.

The peak fraction of SH4UD obtained after size-exclusion chromatography, as described above, was analyzed using SAXS. The SAXS experiments were conducted on a Rigaku BioSAXS 2000 instrument equipped with a Pilatus 100 K detector (Rigaku Americas). The sample-to-detector distance and beam center were calibrated using a silver behenate standard. The samples were automatically loaded into a Julabo temperature-controlled flow cell from a Julabo temperature-controlled 96-well plate. SAXS data of SH4UD were collected at a concentration of 1.5 mg/mL at room temperature. The data were reduced using instrument reduction software to obtain the scattering intensity, I(q), as a function of wave vector, q [= 4π sin(θ)/λ, where 2θ is the scattering angle and λ is the wavelength], for sample and buffer. Subsequently, the buffer background was subtracted, and the resulting sample scattering profile was employed for further data analysis. The pair distance distribution function [P(r)] was calculated from the indirect Fourier transform of I(q) using GNOM/ATSAS (102).

SANS.

SANS measurements were performed at the EQ-SANS instrument in the facility Spallation Neutron Source located at the Oak Ridge National Laboratory (103). The spallation source was operating at 60 Hz. A sample aperture of 10 mm was used for beam collimation. Two different configurations were used to obtain a large q-range, to cover a combined q-range of 0.05 nm⁻¹ < q < 7 nm⁻¹ · q = (4π/λ) sin(θ) is the magnitude of the scattering vector, where 2θ is the scattering angle. For these 2 configurations, the sample-to-detector distances were 2.5 m and 4 m with a minimum neutron wavelengths of 2.5 Å and 10 Å, respectively. Data reduction with I(q) vs. q as output was performed according to standard procedures implemented in the Mantid software (104), and the reduced intensities were placed on an absolute scale using a calibrated porous silica standard with a scattering intensity of 450 cm⁻¹ at very small q. All SANS data were measured at low temperatures (∼10 °C) using 1-mm-thick banjo Hellma cells. For a spatially homogenous temperature over the sample area, these Hellma cells were loaded into titanium sample holders using the banjo cell adaptors.

Atomistic Model.

MD simulations were performed on the same 95-amino acid residue SH4UD protein sequence (discussed above) that was analyzed using SAXS and SANS. The initial disordered 3D structure was obtained using I-TASSER (105) and a starting structure was chosen after equilibrating with MD simulation. The protein was solvated in a cubic box of 12.6-nm edge, and 4 chlorine ions were added to neutralize the system, which contained a total of ∼250,000 atoms. The Amber ff03ws (39, 106) protein force field and the TIP4P/2005s water model (107) were employed in all of the simulations.

MD Simulations.

We performed unbiased MD simulations using GROMACS 5.1.2 (108–113). All bonds involving hydrogen atoms were constrained using LINCS algorithm (114). The Verlet leapfrog algorithm was used to numerically integrate the equation of motions with a time step of 2 fs. A cutoff of 1.2 nm was used for short-range electrostatic and Lenard-Jones interactions. Long-range electrostatic interactions were calculated by particle-mesh Ewald (115) summation with a fourth-order interpolation and a grid spacing of 0.16 nm. The solute and solvent were coupled separately to a temperature bath of 300 K using a modified Berendsen thermostat with a relaxation time of 0.1 ps. The pressure coupling was fixed at 1 bar using the Parrinello–Rahman algorithm (116) with a relaxation time of 2 ps and isothermal compressibility of 4.5 × 10⁻⁵ bar⁻¹. The energy of each system was minimized using the 1,000 steepest decent steps followed by 1-ns equilibration at NVT ensemble. The production runs were carried out in the NPT ensemble.

HREMD Simulations.

To enhance the conformational sampling, replica exchange with solute tempering 2 (REST2) (59, 60), a HREMD method, was employed. In HREMD, interaction potentials of part of the system can be scaled so as to promote large-scale conformational change. REST2 was chosen because it is computationally cheaper than temperature REMD and because it has been shown to efficiently explore conformational space in proteins (59–61, 117). This method scales intraprotein interactions by a factor λ, and the protein–water interaction by √λ, while water–water interactions are unaltered. Here, λ = T_eff,0/T_eff,i, where T_i is the effective temperature of i^th replica and lowest temperature replica has order 0. Using λ_max = 1 and λ_min = 0.75, 20 replicas were simulated (SI Appendix), each for ∼510 ns, with protein snapshots saved every 10 ps. Exchange of configurations between neighboring replicas was attempted every 400 MD steps, with an average exchange probability of 0.6. The trajectory from the lowest rank replica (i.e., T = 300 K) was used for analysis. REST2 was implemented in GROMACS 5.1.4 (108–113) patched with PLUMED 2.3.4 (118). More details on the HREMD simulation are provided in SI Appendix. The analysis of MD trajectories was performed using GROMACS. The secondary structure prediction was calculated with DSSP (119). The asphericity was determined by calculating the gyration tensor of the protein (70). Convergence of the HREMD is discussed in detail in SI Appendix.

Calculation of Scattering Profiles.

The theoretical SAXS profiles were calculated from the HREMD trajectory using SWAXS (120), which considers the protein hydration shell explicitly. The theoretical SANS profiles were calculated using SASSENA (121), a program that takes explicitly into account the solvent molecules in the simulation. The water and protein exchangeable hydrogen atoms were assigned the deuterium scattering length density, while the protein nonexchangeable hydrogen atoms were assigned that of hydrogen. As such, the hydration shell density and thickness are determined directly from the simulation, avoiding overfitting issues encountered in implicit hydration shell methods (36).

The agreement between experiment and simulation was evaluated with the following χ² score:

$${\chi }^2=\frac{1}{N-1}{{\displaystyle \sum _{i=1}^N\{\frac{\left[<\hspace{0.17em}{I}_{expt}\left(q_i\right)>-\left(c<I_{sim}\left(q_i\right)>+bgd\right)\right]}{{\sigma }_{expt}\left(q_i\right)}\}}}^2,$$ [2]

where <I_expt(q)> and <I_sim(q)> are the ensemble averaged experimental and theoretical SAXS or SANS data, respectively, N is the number of experimental q points, c is a scaling factor, bgd is a constant background, and σ_expt is the experimental error.

The 2 fitting parameters in Eq. 2 are almost inevitably used when comparing experiment and theory. The scaling factor c is required because experimental data are often expressed in arbitrary or absolute units (depending on the data normalization method at the instrument), making it necessary to scale the theoretical SAXS/SANS data to the same units as experiments. c has no effect on the shape of SAXS/SANS profiles. A background (bgd) term is required to incorporate the uncertainty due to mismatch in buffer subtraction at higher q-values (24).