Cerebellar Control of Reach Kinematics for Endpoint Precision

SUMMARY

The cerebellum is well appreciated to impart speed, smoothness, and precision to skilled movements such as reaching. How these functions are executed by the final output stage of the cerebellum, the cerebellar nuclei, remains unknown. Here, we identify a causal relationship between cerebellar output and mouse reach kinematics and show how that relationship is leveraged endogenously to enhance reach precision. Activity in the anterior interposed nucleus (IntA) was remarkably well aligned to reach endpoint, scaling with the magnitude of limb deceleration. Closed-loop optogenetic modulation of IntA activity, triggered on reach, supported a causal role for this activity in controlling reach velocity in real time. Relating endogenous neural variability to kinematic variability, we found that IntA endpoint activity is adaptively engaged relative to variations in initial reach velocity, supporting endpoint precision. Taken together, these results provide a framework for understanding the physiology and pathophysiology of the intermediate cerebellum during precise skilled movements.

In Brief

Reaching movements are dysmetric following cerebellar damage, with unclear etiology. Using closed-loop optogenetic manipulations and single-unit recordings in mice, Becker and Person show that the cerebellar interposed nucleus adaptively decelerates the limb to support reach endpoint precision and accuracy.

INTRODUCTION

A hallmark of cerebellar damage is a unique decomposition of reaching movements, termed dysmetria (Holmes, 1917). During movement, people with cerebellar damage exhibit a tremor-like oscillation of the limb, especially noticeable as over- and undershooting of target endpoint (Bonnefoi-Kyriacou et al., 1998). These kinematic features resemble a control system lacking the ability to predictively guide the limb to the target, relying instead on slow sensory feedback, thus producing oscillatory movements. The striking features of dysmetria, combined with decades of research identifying associative learning mechanisms in the cerebellar cortex, support a view of the cerebellum as an essential predictive modulator of movement (Ohyama et al., 2003; Wolpert et al., 1998). However, the mechanisms translating these predictions into motor control are matters of significant debate, especially for the sole output regions of the cerebellum, the cerebellar nuclei. More specifically, the contribution of cerebellar nuclear activity to reaching movements remains obscure.

The cerebellum exhibits broad functional topography, with intermediate regions being clearly involved in limb control. Inactivation or lesion of the anterior interposed nucleus (IntA), an output structure of the intermediate cerebellum, recapitulates some aspects of dysmetria seen in cerebellar patients (Cooper et al., 2000; Low et al., 2018; Martin et al., 2000; Mason et al., 1998; Milak et al., 1997; Monzée et al., 2004). Furthermore, early studies in decorticate preparations revealed limb movement in response to electrical stimulation of the intermediate cerebellum, with a general bias toward flexor activation (Magoun et al., 1935; Miller and Laughton, 1928; Sprague and Chambers, 1953). However, these and more contemporary studies note complex dependencies on limb state, even observing antagonistic effects (e.g., extensor versus flexor activation) under different baseline conditions (Ekerot et al., 1995). Moreover, significant disagreement exists over the basic question of whether cerebellar stimulation has reduced or enhanced effects during movement compared with quiescence, with some authors reporting increased but variable effects during movement (Krauzlis and Miles, 1998) and others reporting an absence of effect during movement (Hoogland et al., 2015; Rispal-Padel et al., 1982). The variability of effects of IntA stimulation reported across contexts leaves open the question of the causal role of IntA in shaping reach kinematics, motivating experiments that modulate nuclear activity specifically during reach.

Recordings from neurons in the intermediate cerebellum also support a specific role during active limb control. Purkinje neurons in the intermediate cerebellar cortex exhibit strong encoding of limb movement kinematics, mirroring results in other motor behaviors, including eye, whisker, and eyelid movements (Chen et al., 2016; Halverson et al., 2015; Herzfeld et al., 2015; Hewitt et al., 2011, 2015; Pasalar et al., 2006). In contrast, IntA neurons exhibit large rate fluctuations specifically during reach-to-grasp movements (as opposed to single-joint movements or control of manipulanda) (Gibson et al., 1996; van Kan et al., 1993, 1994), but no clear functional consensus has emerged from analyses of their encoding properties or relationships to muscle activation (Burton and Onoda, 1977; Gibson et al., 1996; Goodkin and Thach, 2003; Thach, 1978). Anatomically, IntA projection neurons heavily target motor cortex (via thalamus) and the red nucleus (Eccles et al., 1967; Houck and Person, 2015; Low et al., 2018), both important motor control centers for reach behavior (Denny-Brown, 1950; Houk, 1991). Thus, fluctuations in IntA activity during reach likely influence ongoing control, yet the rules governing this interaction remain uncharacterized. One intriguing hypothesis given observations of dysmetria following IntA damage is that IntA may act as a “brake” during reach, signaling limb endpoint, although this theory is only indirectly supported (Ekerot et al., 1997; Hore et al., 1991). Importantly, the nature of the functional relationship between IntA neural activity and limb movement during reaching, including its sign, strength, and context dependence, remains unknown. Without any clear description of the causal relationship between IntA activity and the kinematic parameters of reach, functional interpretations of reach-associated IntA activity remain necessarily incomplete.

In this study, we sought to identify causal relationships between IntA activity and reach kinematics and relate those findings to recordings of endogenous activity during reach behavior. Using a novel kinematic closed-loop system for optogenetic manipulation of IntA during reach, we found that IntA activity exerts monotonic, directional control over reach kinematics across a wide range of activity levels. Recordings of IntA neurons during unstimulated reaches revealed that this causal relationship is leveraged endogenously to slow the limb near endpoint and is scaled to modulate deceleration relative to early reach velocity, illustrating online contributions of IntA to reach endpoint precision. Taken together, these results identify the existence and utility of a directional, scalable motor controller for reach kinematics in IntA. We relate these observations to those made in cerebellar control of other effectors, highlighting shared principles of cerebellar control across movements with differing degrees of freedom and skill.

RESULTS

IntA Neurons Are Modulated Near Reach Endpoint

Several studies in cats and monkeys report rate fluctuations in IntA neurons during limb movement, yet these investigations of encoding properties have resulted in little consensus about IntA function (Armstrong and Edgley, 1984; Burton and Onoda, 1977; Fortier et al., 1989; Thach, 1978). One consistent observation is that IntA neurons are particularly modulated by reach-to-grasp movements (Gibson et al., 1996; van Kan et al., 1993, 1994), though a lack of quantitative movement tracking prevented direct comparisons with specific kinematic features of reach. In this study, we combine quantitative measurement of reaching movements with in vivo recording and manipulations of IntA activity in order to further elucidate the mechanisms of reach control implemented by IntA. We therefore leveraged machine vision motion capture technology to accurately track the spatiotemporal trajectories of reaching movements in mice, which have recently become a model system for studying the neural mechanisms underlying skilled reach behavior (Azim et al., 2014; Guo et al., 2015; Whishaw, 1996). We trained mice on a self-initiated reach task in which freely behaving animals retrieve small food pellets from a pedestal (peak success rate 56% ± 3%, N = 18 mice). We then recorded single-unit IntA activity with tetrodes (n = 84 neurons, N = 4 mice) while simultaneously tracking three-dimensional (3D) paw position during reaching behavior (Figure 1A; Figure S1; Video S1; n = 7,039 reaches, spatial resolution 150 μm, frame rate 120 Hz).

Figure 1. IntA Neurons Are Modulated Near Reach Endpoint.

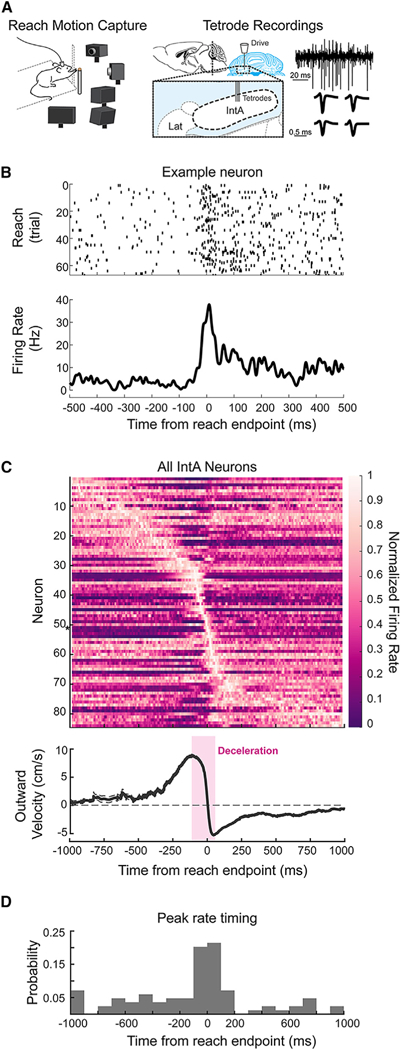
(A) Schematic of in vivo electrophysiological recording mouse reach paradigm. A tetrode drive was targeted to IntA (right). Example extracellular voltage trace from a single lead and average spike waveforms across tetrode leads for a single cell (far right).

(B) Raster (top) and peri-event time histogram (PETH; bottom) of an example IntA neuron aligned to reach endpoint.

(C) Population PETH including all cells recorded in IntA(n = 84) aligned to reach endpoint and sorted by time of peak mean firing rate (top). Firing rate is normalized to maximum on a per cell basis. Asterisk indicates example neuron in (B). Average (±SE) reach velocity in the outward direction, aligned to reach endpoint (bottom). The deceleration phase of the outreach is highlighted in magenta; endpoint is defined as time when outward reach velocity crosses zero (dashed line).

(D) Histogram of the timing of peak mean firing rates relative to reach endpoint for all cells.

We first confirmed that IntA neurons are modulated during reaching movements in mice. IntA neurons had a baseline firing rate of 39.1 ± 23.7 Hz (mean ± SD), with most neurons exhibiting modulation during reach (average peak rate 66.0 ± 56.4 Hz; p < 0.0001, Wilcoxon signed rank test). Aligning activity to reach start, as has been done previously (van Kan et al., 1993), we observed a broad tiling of activity during the reach (Figures S2A and S2B). However, because the hallmark deficit of IntA lesions, dysmetria, is most prominent around reach endpoint (Holmes, 1917), we hypothesized that IntA activity might exhibit unique patterning at or near this kinematic landmark. We therefore aligned IntA neural activity to reach endpoint and calculated average neural responses on a per cell basis (Figure 1B). Across the population of IntA neurons, endpoint alignment revealed a striking organization of peak activation times near reach endpoint (Figure 1C, top panel). The clear clustering of activity increases that occurred specifically during the deceleration phase of the outreach argued for a reach phase-specific role for many neurons in IntA (Figures 1C and 1D; n = 35 of 84 neurons, peak mean firing rate within 100 ms of endpoint; 2,000 ms analysis window). Peak mean firing rate times were significantly more clustered around endpoint than reach start (Figure 1D; Figure S2C; p < 0.0001, chi-square test; n = 11 of 84 neurons, peak activity within 100 ms of reach start). Moreover, firing rates were also less variable over trials when aligned to reach endpoint versus reach start (mean Fano factor, reach start [FFs], 2.2 ± 0.2; mean Fano factor, reach endpoint [FFe], 1.7 ± 0.1; p <0.0001, Wilcoxon signed rank; FFs > FFe for 61 of 84 neurons). This selective engagement of IntA neurons near reach endpoint raised the question of whether this activity is causally related to reach kinematics.

Closed-Loop Activation of IntA during Reach Reduces Outward Velocity

Endpoint-aligned activity in IntA could be contributing directly to limb deceleration, in congruence with the ongoing reach kinematics at that phase of movement. Alternatively, IntA activation near endpoint could be functionally resisting limb deceleration, counterbalancing decelerative commands generated elsewhere. Previous causal experiments that recapitulate the dysmetric phenotype seen in cerebellar patients, including lesion or inactivation of the IntA (Cooper et al., 2000; Low et al., 2018; Martin et al., 2000; Mason et al., 1998; Milak et al., 1997), do not distinguish these possibilities. Because those manipulations lasted orders of magnitude longer than a single reaching movement, IntA’s precise temporal contribution throughout reach behavior has remained obscure.

To circumvent these limitations, we designed a kinematic closed-loop system to drive optogenetic manipulations tied directly to reaching movements. By tracking and analyzing the 3D trajectories of mouse reaching movements in real time, our system facilitates brief optogenetic stimulation of IntA at specific, experimenter-defined kinematic landmarks (Figure 2A). As the total closed-loop latency (9.5 ms) is ~30-fold shorter than the duration of trained reaches (309 ± 40 ms, outreach only; Figure S3), we were able to manipulate IntA activity at specific phases of the reaching movement. We introduced ChR2 into IntA either by injecting trained animals with AAV-hSyn-hChR2-mCh (N = 6) or by crossing Ntsr1-Cre mice with FLEX-ChR2 transgenic mice, which limited expression to cerebellar premotor output neurons (N = 3; Houck and Person, 2015). An optical fiber was then implanted in IntA ipsilateral to the arm used for reaching (Figure S4). When mice reached for the pellet, we delivered a 50 ms train of blue light pulses (2 ms, 100 Hz) in closed loop at a kinematic landmark near the position of maximal reach velocity (Figure S3), stimulating on a random 25% of reaches to avoid anticipation. This positional landmark, a vertical plane located near the opening of the behavior box that the animals reach through (see STAR Methods), was consistently applied across all animals tested, unless otherwise noted.

Figure 2. Brief, Closed-Loop Activation of IntA during Reach Reduces Outward Velocity and Causes Hypometric Reaches.

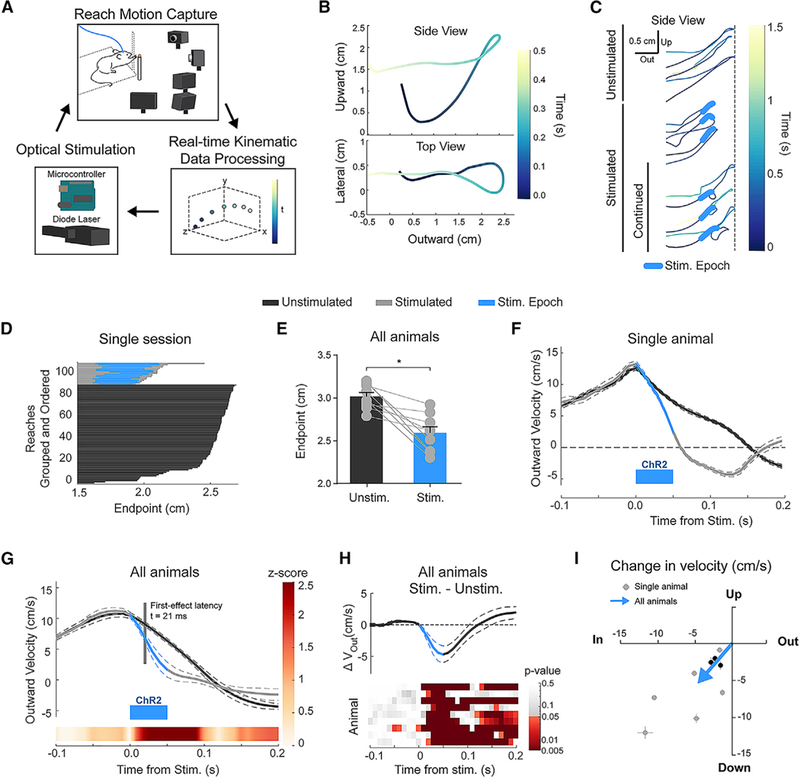
(A) Schematic of kinematic closed-loop system, in which real-time tracking of mouse reach kinematics is used to trigger optogenetic stimulation.

(B) Example mouse 3D reach trajectory tracked in real time. “Upward,” “lateral,” and “outward” represent the three spatial dimensions monitored, with “outward” being in the direction toward the food pellet target.

(C) Examples of complete unstimulated reach trajectories (top 3) that extend fully to the target location (dashed line), stimulated reach trajectories that return fully after stimulation (middle 3), and stimulated reaches that continue out toward the target following the initial direction reversal (“continued,” bottom 3).

(D) Reach trajectories from a single behavioral session at their initial maximum extent in the outward direction (endpoint). Reaches are grouped by type (unstimulated or stimulated) and ordered for visual clarity.

(E) Average (±SE) initial endpoint of unstimulated and stimulated reaches (p = 0.0039).

(F) Example (single animal) of average outward velocity of unstimulated and stimulated reaches aligned to time of stimulation. Blue bar indicates the stimulation epoch (50 ms, 2 ms pulses, 100 Hz). All velocity profiles display mean (solid line) ± SE (dashed lines).

(G) Population average of outward velocity profiles across animals. The linearly interpolated Z score (color bar) shows the time course of statistical divergence between the unstimulated and stimulated reach velocities, with the latency to first effect marked and labeled in gray (inset; see STAR Methods).

(H) Difference (Stim. – Unstim.) of population average velocity profiles plotted in (G) (top). Heatmap of p values associated with Wilcoxon rank-sum tests conducted for each animal (rows) at 10 ms intervals (columns).

(I) Two-dimensional (2D) plot of average change in outward (x axis) and upward (y axis) velocity for each animal (Stim. – Unstim.; gray dots and lines indicate mean and SE, respectively). Values at the origin would indicate no difference between stimulated and unstimulated reaches. The three NTSR1-Cre/FLEX-ChR2 animals tested are indicated in black. The average 2D effect size across animals is indicated by the tip of the blue arrow (p = 0.0039 for both outward and upward directions).

Using this method, we found that brief excitation of IntA during outreach resulted in clear and consistent kinematic effects (N = 9 animals, n = 2,897 reaches). Stimulated reaches showed a short-latency reversal in outward trajectory, resulting in reaches with premature endpoints (Figure 2C; latency from Stim.: mean 82 ± 10 ms; Videos S2, S3, and S4). Although some reaches were truncated in the outward direction after stimulation, a majority (75% ± 9% of stimulated reaches) continued toward the target after the initial direction reversal, arguing against non-specific behavioral disengagement (“continued reaches,” Figure 2C; latency from Stim.: mean 211 ± 33 ms; N = 4; Video S3). Across all animals and across days, stimulation consistently resulted in shorter reaches in the outward and upward direction, with no significant effect on endpoint variability (Figures 2D and 2E; Figure S5E; Video S4; p = 0.0039, Wilcoxon rank-sum test). Even allowing for continued reaches, success rates were significantly impaired by IntA excitation (stimulated [Stim.] – unstimulated [Unstim.], −6.5% ± 2.2%; p = 0.020, paired t test). These effects were not a consequence of light distracting the mouse, as identical experiments in animals not expressing ChR2 had no effect on reach kinematics (N = 4; Figures S5F–S5H).

To better characterize the temporal and directional properties of IntA activity on reach kinematics, we analyzed effects of IntA excitation on reach velocity in three dimensions. Unstimulated reaches possessed a characteristic bell-shaped outward velocity profile (Flash and Hogan, 1985) (Figure 2F, black trace). As implied by the positional effects, IntA excitation slowed the limb in the outward direction (Figure 2F, gray trace; Figure S5B). Average unstimulated and stimulated outward velocity trajectories were indistinguishable up to the point of stimulation, at which point they quickly diverged as stimulated reaches slowed prematurely (Figures 2G and 2H). The excitation-induced decrease in outward velocity was rapid, diverging from control velocity within 21 ± 3 ms on average (first effect latency; see STAR Methods). In all animals tested, excitation of IntA during outreach decreased outward and upward velocity relative to unstimulated reaches (Figure 2I; Figure S5C; Stim. – Unstim.: outward, −4.7 ± 1.3 cm/s [p = 0.0039, Wilcoxon signed rank test]; upward, −5.4 ± 1.3 cm/s [p = 0.0039, Wilcoxon signed rank test]), with inconsistent changes in lateral velocity (see Figure 6D). IntA excitation in wild-type and Ntsr1-Cre/FLEX-ChR2 animals exhibited the same pattern of kinematic effects, decreasing the outward and upward velocity of the limb during reach (Figure 2I, black dots), supporting the view that IntA premotor output neurons mediate the kinematic effects we observe in response to IntA excitation generally.

Figure 6. Effects of IntA Activation Are Gated by Behavioral Context.

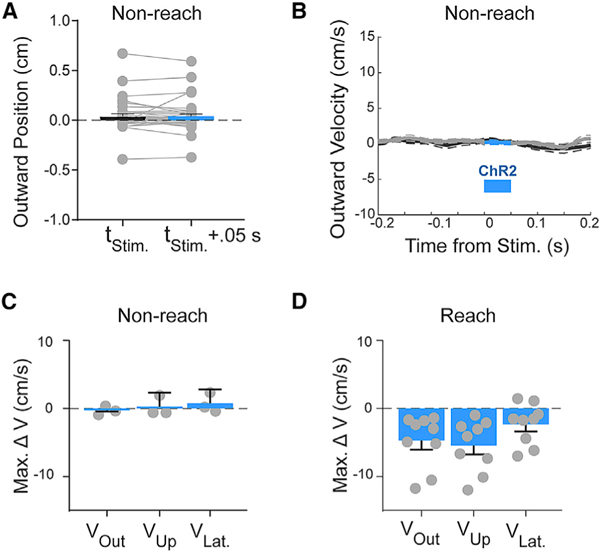
(A) Example of the effect of optogenetic stimulation outside of reach behavior (e.g., standing, feeding; see STAR Methods) on average (±SE) paw position (p > 0.05). Each paired point represents the outward position before and after stimulation, reflecting the lack of dependence on initial starting position.

(B) Example of the effect of optogenetic stimulation during non-reach behavior on average (±SE) paw velocity (p > 0.05).

(C) Summary of average (±SE) maximum velocity effect magnitudes of stimulation during non-reach (Stim. – Unstimulated; outward, three of three animals, p > 0.05; upward, two of three animals, p > 0.05) in each of the three spatial dimensions across subjects (gray dots).

(D) For comparison with (C). Replotted summary of average (±SE) maximum velocity effect magnitudes of stimulation during reach (Stim. – Unstim.; outward, nine of nine animals, p < 0.05; upward, nine of nine animals, p < 0.05) in each of the three spatial dimensions across subjects (gray dots).

The Magnitude and Timing of IntA Activation Scales Reach Kinematics

If the magnitude of IntA activity modulation contributes to the control of reach kinematics to enable movement precision and accuracy, we would predict that graded fluctuations of IntA activity should result in proportional changes in reach velocity. IntA activity modulation was graded by varying light power levels ranging from 0.5 to 5 mW, increasing rates by 53.9%–152.3% on average (Figure S6). We leveraged this experimental control by stimulating ChR2-expressing neurons in IntA with a range of optical powers during reach (N = 3 animals, n = 1,669 reaches). Consistent with graded control of reach kinematics, the magnitude of kinematic change scaled with optical power in all animals tested, with the maximum difference between average unstimulated and stimulated velocities decreasing as the light power dropped (Figures 3A and 3C; Figure S7A; Stim. – Unstim., outward: 1.0 mW, −9.4 ± 0.7 cm/s; 0.5 mW, −7.9 ± 0.1 cm/s; 0.25 mW, −7.5 ± 0.2 cm/s; 0.1 mW, −1.3 ± 0.1 cm/s). This was not due to a change in the frequency of an all-or-none effect, as reach velocity values exhibited a clear merging of unstimulated and stimulated distributions (Figure 3B; see STAR Methods; Figure S7A). Importantly, these graded effects on reach velocity were accompanied by concomitant shifts in endpoint: the larger the excitation amplitude, the more hypometric reaches became (Figure 3D), implying that IntA activity levels could be leveraged to control endpoint position.

Figure 3. The Magnitude of IntA Activation Scales Reach Kinematics.

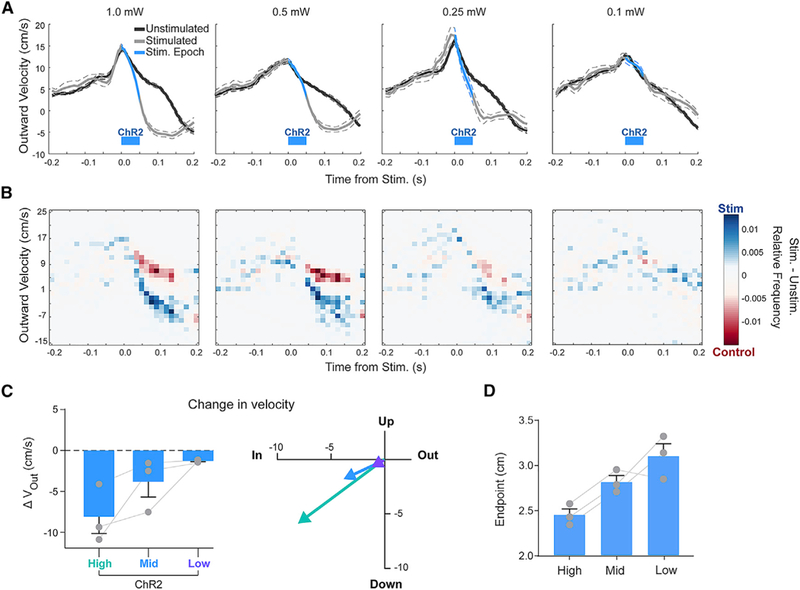
(A) Average (±SE) outward velocity of unstimulated and stimulated reaches with decreasing optical power of optogenetic stimulation (“ChR2”)from high (1.0 mW; far left) to low (0.1 mW; far right).

(B) Heatmap of relative frequency of unstimulated and stimulated reach velocity values from data in (A). Individual frequency heatmaps for unstimulated reaches and stimulated reaches were normalized and subtracted (stimulated – unstimulated) to view the relative prevalence of reach velocity values in each distribution.

(C) Summary of the magnitude (left) and direction (right) of average changes in outward reach velocity (Stim. – Unstim.; mean ± SE) in response to graded levels of excitation.

(D) Average (±SE) initial endpoint of stimulated reaches in response to graded levels of excitation.

We next reasoned that if the magnitude of IntA activity can scale the kinematic parameters of reach, then different IntA activation timings might also differentially control reach kinematics. However, because the biomechanical state of the limb changes continuously throughout a single reaching movement, IntA activation at different reach phases might be expected to have qualitatively different kinematic effects. We therefore added two additional closed-loop landmarks flanking our original stimulation location, each comprising a unique initial position and velocity (Figure 4A; N = 3 animals, n = 906 reaches; p < 0.0001, Kruskal-Wallis test; called “early,” “middle,” and “late”). IntA excitation slowed outward and upward velocity with short latency regardless of the position or velocity of the paw at the time of stimulation (Figures 4B and 4C; Stim. – Unstim., outward: early, −7.5 ± 3.0 cm/s; middle, −6.4 ± 3.0 cm/s; late, −2.8 ± 2.3 cm/s; upward: early, −5.6 ±1.5 cm/s; middle, −6.8 ±1.2 cm/s; late, −2.8 ±1.7 cm/s; mean first effect latency: early, 17 ms; middle, 13 ms; late, 17 ms). The magnitude of deceleration was correlated with the starting velocity (Figure S7B). This relationship held true for unstimulated reaches as well, measured from the same time points as stimulation would have occurred. Thus, these results illustrate that IntA excitation at diverse times during reach consistently reduces outward and upward limb velocity.

Figure 4. The Timing of IntA Activation Does Not Alter Directionality.

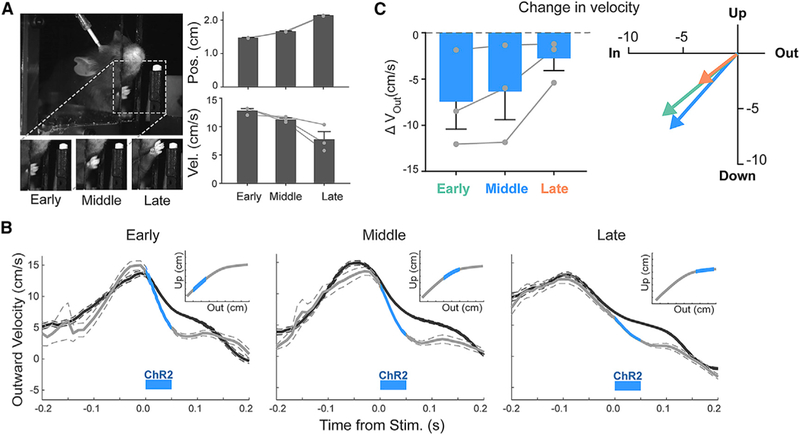
(A) Images of paw at three kinematic landmarks used to trigger IntA stimulation (left) and the associated positional and velocity characteristics at each landmark (mean ± SE; right).

(B) Average (±SE) outward velocity of reaches stimulated with ChR2 at the kinematic landmarks in (A), overlaid with unstimulated reaches. Insets: schematic of stimulation trigger points.

(C) Summary of the magnitude (left) and direction (right) of average changes in outward reach velocity (Stim. – Unstim.; mean ± SE) in response to stimulation at different kinematic landmarks during reach.

IntA Exerts Directional Control on Reach Kinematics

The observation that IntA excitation consistently reduces outward limb velocity is consistent with two opposing modes of influence, specifically speed control and velocity control. First, IntA could act as a gain controller, influencing the speed of ongoing movement generated elsewhere, as has been suggested previously for both the cerebellum and basal ganglia (MacKay and Murphy, 1979; Optican and Robinson, 1980; Yttri and Dudman, 2016). Alternatively, it could act as a directional controller, imparting a consistent velocity change (speed in a given direction) independent of ongoing movement direction (Noda et al., 1988). These models make opposite predictions about the effects of IntA excitation during the outreach and return phases of reach. If IntA controls gain, IntA excitation should slow the limb during return, as observed during outreach; if, on the other hand, IntA control is directional, excitation should cause decreased outward velocity, speeding the limb during return (Figure 5A). We therefore stimulated IntA during the return phase of reach, after the animal had already obtained the pellet (N = 3 animals, n = 346 reaches). IntA excitation during the return phase of reach caused the limb to move inward faster than in the unstimulated condition (Figures 5B and 5C; Stim. – Unstim. −2.9 ± 1.5 cm/s; three of three animals; p < 0.01, Wilcoxon rank-sum test). Taken together, these results demonstrate that excitation of IntA exerts directional control, pulling the limb inward regardless of reach phase.

Figure 5. IntA Exerts Directional Control on Reach Kinematics.

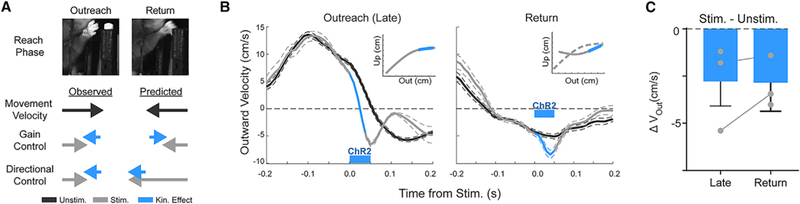
(A) Schematic of observed and predicted effects of IntA excitation under the directional control and gain control hypotheses. Images of paw position during outreach and return (top). The observed stimulation effects on movement velocity during outreach are consistent with either gain or directional control, but the two hypotheses make opposite predictions for the direction of kinematic effects (blue arrows) in response to stimulation during the return phase of reach (bottom, right-hand column). For a gain controller, decreased return velocity is predicted (shorter gray arrow); for a directional controller, increased return velocity is predicted (longer gray arrow).

(B) Average (±SE) outward velocity of reaches stimulated during the outreach phase (left) or return phase of reach (right). Insets: schematic of stimulation trigger points.

(C) Summary of the magnitude of average changes in outward reach velocity (Stim. – Unstim.; mean ± SE) in response to stimulation during the outreach and return phases of reach. “Late” data are replotted from Figure 4C for comparison with “return.” Paired data are indicated with a connecting line; one animal was unpaired each for late and return experiments.

Effects of IntA Activation Are Gated by Behavioral Context

Next, we tested the specificity of IntA motor control to reach behavior. IntA lesion studies and recording data consistently identify reach-to-grasp behavior as a particularly salient behavioral context for IntA function (Cooper et al., 2000; van Kan et al., 1993), an observation that is supported by the strong kinematic effects we report here. Nevertheless, the nature of the effect (the paw moving back toward the body) prompted concern that the underlying mechanism was off target to reach control or related to an aversive response. Although the existence of “continued” reaches argues against this concern (Figure 2C; Video S3), we also performed control experiments in which the same optogenetic stimulation protocol was applied during periods of non-reach behavior (i.e., feeding and standing; see STAR Methods). Interestingly, stimulation outside of the context of active reaching had little or no effect on paw position or velocity (Figures 6A–6C; Video S5; outward direction velocity, three of three animals [p > 0.05, Wilcoxon rank-sum test]; upward direction, two of three animals [p > 0.05, Wilcoxon rank-sum test]). This observation was consistent across a range of paw states, including when the paw the placed down, lifted, or held the food pellet during eating (Figure S7C). Although stronger IntA excitation is able to cause non-purposive limb movements at rest, consistent with previous observations (Lee et al., 2015; Witter et al., 2013) (data not shown), our results nevertheless demonstrate increased kinematic sensitivity of the limb to cerebellar modulation during active reach (Figures 6C and 6D). These data are consistent with the view that the motor system has higher sensitivity to IntA activity during purposive limb movement.

Brief Inhibition of IntA Increases Outward Velocity and Causes Hypermetric Reaches

If the endogenous IntA firing rate increases we observed during reaching (Figure 1) slow outward velocity, then inhibition of IntA during reach would be predicted to have the opposite kinematic effect compared with excitation, namely, increasing outward velocity. To test this prediction, we performed closed-loop inhibition of IntA using the inhibitory opsin Arch (AAV-hSyn-Arch3.0-YFP; N = 9 animals, n = 2,223 reaches), which in control recordings significantly inhibited IntA neurons, albeit with varying degrees of efficacy depending on the recording condition (Figure S6) (Chow et al., 2010; Mattis et al., 2011). Consistent with the idea that IntA can bidirectionally control reach kinematics, IntA inhibition significantly increased outward and upward reach velocity (Figures 7A–7D; Figure S8; Stim. – Unstim.: outward, 1.7 ± 0.2 cm/s [p = 0.0039, Wilcoxon signed rank test]; upward, 1.0 ± 0.2 cm/s [p = 0.0078, Wilcoxon signed rank test]). Moreover, IntA-inhibited reaches traveled farther and showed significantly hypermetric reach endpoints compared with unstimulated reaches (Figures 7E and 7F; p = 0.023, paired t test; endpoint difference 0.04 ± 0.01 cm). Although this positional effect was relatively small, stimulated reaches had a lower success rate than unstimulated reaches, demonstrating an importance of this level of accuracy to behavioral performance (Figure S8C; Stim. – Unstim. −4.9% ± 1.7%; p = 0.023, paired t test). In summary, we found a directional, monotonic relationship between IntA activity and real-time control of limb velocity: excitation of IntA decreased outward and upward velocity, while inhibition of IntA increased outward and upward velocity.

Figure 7. Brief Inhibition of IntA Increases Outward Velocity and Causes Hypermetric Reaches.

(A) Example (single animal) of average (±SE) outward velocity of unstimulated and stimulated reaches aligned to time of stimulation. Green bar Indicates the stimulation epoch (50 ms).

(B) Population average (±SE) of outward velocity profiles across animals, with linearly interpolated Z score (color bar) displaying the time course of statistical divergence between the unstimulated and stimulated reach velocities.

(C) Difference (Stim. – Unstim.) of population average (±SE) velocity profiles plotted in (B) (top). Heatmap of p values associated with Wilcoxon rank-sum tests conducted for each animal (rows) at 10 ms intervals (columns).

(D) Two-dimensional (2D) plot of average change in outward (x axis) and upward (y axis) velocity for each animal (Stim. – Unstim.; gray dots and lines indicate mean and SE, respectively). The average 2D effect size across animals is indicated by the tip of the green arrow (outward, p = 0.0039; upward, p = 0.0078).

(E) Average (±SE) distance traveled over time following stimulation for both stimulated and unstimulated reaches (70 ms time point; p = 0.0002, paired t test).

(F) Average (±SE) initial endpoint of unstimulated and stimulated reaches (p = 0.023, paired t test).

Endogenous IntA Activity Is Scaled to Enhance Endpoint Precision

The causal experiments described above imply that IntA population activity could be leveraged endogenously to control the kinematics of reaching movements in real time by modulating the amplitude and timing of rate changes. To interrogate this idea, we returned to the recording data from IntA neurons during reach and analyzed the relationship between activity levels and reach kinematics in neurons with peak activity near reach endpoint (n = 35; peak mean firing rate within 100 ms of reach endpoint; see STAR Methods). We made the prediction that the properties we observed in the causal data–including directionality, scalability, and behavioral context dependence–would be observable at the level of single neurons.

We first tested whether endogenous increases in IntA activity were associated with decreases in outward velocity. To do so, we performed a burst-triggered average, aligning reach kinematics to time points of significantly high instantaneous neural firing rates (“bursts”) on a per cell basis (Figure 8A; n = 35 cells; Z score ≥ 2.5 for a minimum of 5 ms; see STAR Methods). This alignment revealed that endogenous increases in IntA neural activity are correlated with significant decreases in outward paw velocity, both for single cells and across the population of endpoint-activated cells (Figures 8B and 8C; change in velocity, 0–45 ms: −1.1 ± 0.3 cm/s; p = 0.0051, Wilcoxon signed rank test). Choosing random times for alignment revealed no significant kinematic structure (Figure 8D; 0.0 cm/s; p = 0.99, Wilcoxon signed rank test). Furthermore, we found that endogenous increases in IntA activity outside of reach behavior (i.e., between reaches) had almost no structured relationship to paw kinematics (Figure 8D; −0.1 cm/s; p = 0.43, Wilcoxon signed rank test), consistent with the context-dependent gating of IntA excitation we observed previously (Figure 6).

Figure 8. Endogenous IntA Activity Is Scaled to Enhance Endpoint Precision.

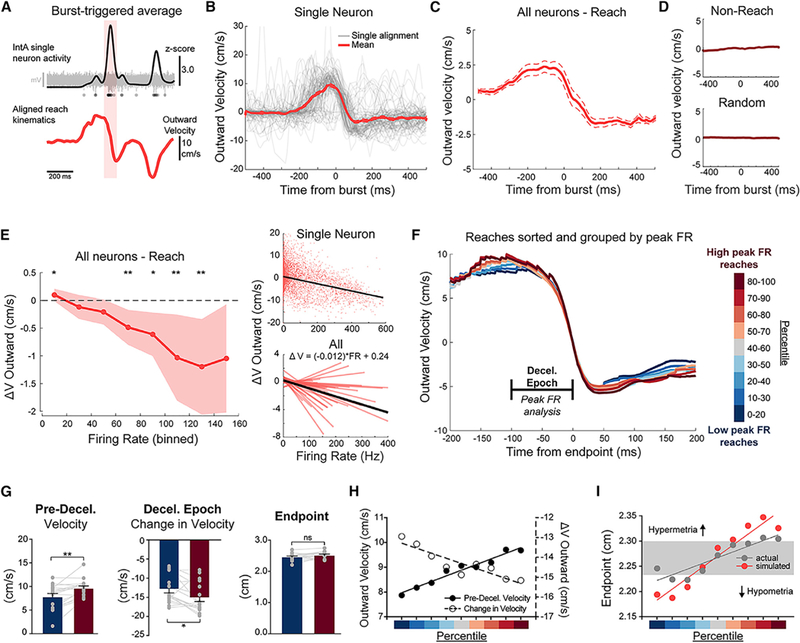
(A) Schematic of the protocol for burst-triggered average analysis. The timing of IntA bursts (Z score ≥ 2.5 for 5 ms) was identified and used to align paw kinematics. Red shading indicates burst identification example. Raw extracellular voltage trace of an example burst is displayed in gray, with detected spikes marked below.

(B) Example of individual (gray) and average (±SE) (red) burst-aligned kinematics for a single IntA neuron for bursts occurring during the reach epoch.

(C) Population average (±SE) (all “endpoint” neurons, n = 35; see STAR Methods) of burst-aligned kinematics during reach.

(D) Population average (±SE) of burst-aligned kinematics during non-reach (top) and for random alignments (bottom).

(E) Left: binned instantaneous firing rates (x axis) and the average (±SE) change in outward reach velocity (y axis) for all neurons during the reach epoch (*p < 0.05 and **p < 0.01, Wilcoxon signed rank test; H₀: no change). Right: linear regression relating instantaneous firing rate and change in outward velocity for an example neuron (top) and for the population (bottom). The grand mean of regression coefficients is plotted in black (bottom) with its associated equation.

(F) Grand mean outward reach velocity profiles aligned to endpoint for reaches grouped by activity level in IntA neurons (deceleration [decel.] epoch neurons, n = 17; see STAR Methods). Reaches were sorted per cell on the basis of peak instantaneous firing rate within the deceleration epoch, segregated into sliding quintiles (see color bar, right) and averaged and then combined across cells to generate grand means. The “deceleration epoch” was the analysis window for peak instantaneous firing rates.

(G) Kinematic comparison between high peak instantaneous firing rate reaches (red) and low peak instantaneous firing rate reaches (blue) for each cell (gray dots) and the population (bars). Comparisons include the difference in pre-deceleration velocity (left; p = 0.015), the change in outward velocity during the deceleration epoch (middle; p = 0.002), and the final endpoint distance (right; p = 0.071). Bars indicate ±SE.

(H) Inverse relationship between pre-deceleration velocity (left axis, filled circles) and change in velocity (right axis, open circles) across quintile groups, as separated across the range of low to high peak instantaneous firing rates (percentile color scale as in F). Linear regressions in (H) and (I) are for display.

(I) Calculated endpoints on the basis of kinematic parameters at the beginning of the deceleration epoch (100 ms prior to endpoint) across quintile groups, as separated across the range of low to high peak instantaneous firing rates. Endpoints were calculated from grand mean kinematic data for each quintile using either the actual deceleration for that quintile (“actual”) or the average deceleration across all reaches (“simulated”). Gray bar indicates the SE of endpoints across quintiles for “actual” endpoints.

This relationship between endogenous IntA activity and change in velocity extended beyond the largest bursts, suggesting graded control. To test this, we binned reach-associated instantaneous firing rates across a wide range of activity levels and measured the subsequent average change in outward velocity. This analysis revealed a monotonic relationship between neural activity level and the average change in outward velocity, supporting the idea that graded levels of IntA activity cause graded changes in reach kinematics (Figure 8E). Importantly, the observation extended to decreased activity relative to baseline: we found that the lowest rates of IntA neural activity were associated with significant increases in outward reach velocity, consistent with our results from IntA inhibition (change in velocity 0.10 ± 0.05 cm/s; p = 0.022, Wilcoxon signed rank test). We also performed correlation analyses, relating instantaneous firing rates with changes in limb velocity. At the individual neuron level, the vast majority of cells (29 of 35) exhibited significant negative correlations between instantaneous firing rate and subsequent outward velocity change (Figure 8E, right). Taken together, this analysis defines an endogenous relationship between IntA neural activity and reach kinematics that matches our results from causal experiments.

The above analyses lend support to the idea that endogenous IntA activity exerts real-time control of reach kinematics. Because the cerebellum is known to enhance motor control, we asked whether variation in IntA activity might contribute to endpoint precision or accuracy. To test this idea, we exploited the natural variability in both neural recordings and reach kinematics to ask whether reaches associated with relatively high IntA activity were different than reaches associated with relatively low IntA activity. We examined neurons that had peak mean firing rates during the deceleration epoch leading up to reach endpoint (−100 to 0 ms aligned to endpoint; n = 17), reasoning that these neurons could causally contribute to endpoint location. Per cell, we then sorted reach trials into nine sliding quintiles on the basis of the amplitude of peak instantaneous firing rate during the deceleration epoch. Consistent with previous observations, reaches with high IntA activity exhibited faster decelerations in the outward direction (Figures 8F and 8G, middle; high – low, difference in velocity change, −2.2 ± 0.8 cm/s; p = 0.015, Wilcoxon rank-sum test). Interestingly, we found that reach velocity prior to the deceleration epoch (and thus prior to peak neural activity) was significantly higher compared with trials with the lowest levels of IntA activity (Figures 8F and 8G, left; high – low, difference in velocity, 1.8 ± 0.5 cm/s; p = 0.002, Wilcoxon rank-sum test). Thus, stronger IntA activity caused larger decelerations of faster reaches; conversely, weaker IntA activity caused smaller decelerations of slower reaches (Figure 8H). Remarkably, despite variable peak velocities, reach endpoints associated with high IntA activity were not different from reaches associated with low IntA activity (Figures 8F and 8G, right; p = 0.071, Wilcoxon rank-sum test). In other words, IntA activity levels were reciprocally matched to preceding reach velocity, such that endpoint accuracy was maintained for both slow and fast reaches. To demonstrate the importance of this observed variable deceleration to endpoint precision, we simulated the expected endpoints of reaches from each quintile using the mean deceleration across all reaches, rather than variable deceleration across groups. Without the observed reciprocal matching between starting velocity and magnitude of deceleration, slow reaches became more hypometric, and fast reaches became more hypermetric, resulting in significantly more variable endpoints (Figure 8I; p = 0.019, Levene’s test). By adaptively scaling IntA activity, the cerebellum therefore enhances the accuracy of single reaches and, over the course of many reaches, improves precision. This process is consistent with an online corrective mechanism reducing motor variability.

DISCUSSION

Although the cerebellum is known to mediate motor learning in service of improved performance, the neural mechanisms supporting real-time sculpting of multijoint movements are obscure. Here, we identified causal limb control signals in a major output pathway from the cerebellum during reaching movements: a complex multijoint behavior dependent on cerebellar control for precision (Holmes, 1917; Low et al., 2018; Martin et al., 2000; Mason et al., 1998; Milak et al., 1997). Neuronal activity in the cerebellar IntA was well aligned to limb deceleration, and optogenetic activation of this region in closed loop with reach produced short latency deceleration of the limb, which is supportive of a causal role. Converse closed-loop inhibition of IntA accelerated the limb, leading to limb overshoot. Overall, these data point to a principle of cerebellar output in mediating predictive endpoint control despite the complexity of many degrees of freedom afforded by multijoint movements.

The cerebellum is known to enhance movement precision and accuracy. In the present study, we provide mechanistic insight into this aspect of cerebellar function in control of reach endpoints. We found that the largest increases in IntA firing rates, whether caused by optogenetic stimulation or endogenous rate changes, were associated with the largest decelerations of the limb. This relationship was bidirectional, extending to rate decreases, with both optogenetic inhibition and endogenous rate decreases preceding limb acceleration. The monotonic, graded control we observed raised the question of whether IntA could be adaptively engaged to enhance endpoint precision on a reach-by-reach basis. We found that the strongest endpoint-aligned firing rate changes correlated with the fastest limb decelerations and, remarkably, followed faster than average outward velocities. These activity patterns are suggestive of online, predictive control of reach velocity by IntA in service of endpoint stability, illustrating how variable output from the cerebellum is engaged to reduce movement variability. Dysmetric reaches would be predicted to stem from maladaptively timed or scaled cerebellar output relative to the preceding reach kinematics, such that endpoint precision is eroded rather than enhanced (Flament and Hore, 1986). If dysfunctional IntA activity were biased to higher or lower rates, we would predict consistently hypo- or hypermetric reaches, respectively, affecting endpoint accuracy as well. This perspective could explain the common finding in dysmetric movements that antagonist muscle activation is mistimed, thus reducing reach accuracy (Hore et al., 1991).

Although previous studies of IntA have provided little consensus on its role in limb movements, one hypothesis that has received sustained interest is the idea that it could act as a “braking” signal (Ekerot et al., 1997; Hore et al., 1991). This idea leaves ambiguous the details of whether IntA regulates the speed of movements, akin to roles proposed for basal ganglia (Yttri and Dudman, 2016), or alternatively, introduces a directional “command” that integrates with commands generated elsewhere (Noda et al., 1988). Indeed, previous studies in eye movements have proposed conflicting models in which cerebellar output could regulate the gain of downstream signals or act akin to a command (MacKay and Murphy, 1979; Optican and Robinson, 1980). We show here that stimulation during either outreach or return causes identical vectors of velocity change, supporting a model in which cerebellar output issues a directional command irrespective of ongoing movement direction. Importantly, these experiments were limited to testing the net effect of IntA excitation along a single axis of movement, leaving open the possibility of different movement directions being controlled by unique IntA subpopulations (Fortier et al., 1989). We also observed that endpoint-aligned population activity in IntA spanned the entire outward decelerative phase of the reach, including both slowing of outreach and acceleration of return. Thus, although activity in IntA appears to regulate limb slowing to target, akin to a “brake,” it also participates in accelerating the limb back to the body after the endpoint. Such an observation may account for some of the more complicated aspects of movement decomposition with cerebellar damage (e.g., dyssynergia), where multiphase movements such as reaching-to-grasp become labored sequences. Thus, the patterns of IntA activity observed here lend insight into mechanisms that could lead to seamless progression of complex movements.

Our understanding of cerebellar contributions to limb control has lagged behind that of other effectors because of the complexities of multijointed movements. The present study identifies surprising shared themes and also highlights differences. Clear analogy extends to cerebellar control of eye saccades, where bursts of activity in the caudal fastigial nucleus (cFN) occur near the endpoint of ipsiversive eye movements and correlate with deceleration (Fuchs et al., 1993; Ohtsuka and Noda, 1991). However, disagreement exists over whether cFN burst properties regulate saccade kinematics and, if so, whether single-trial cFN activity is scaled to adaptively ensure endpoint precision (Robinson and Fuchs, 2001; Sun et al., 2016). Our data contribute to this discussion by identifying correlated variance in endpoint-associated IntA activity and preceding reach kinematics, arguing that the magnitude of population activity in IntA can be scaled to improve endpoint precision. The homology of IntA reach control demonstrated here to cFN eye control implies that predictive modulation of directional controllers could be a broader organizational feature of cerebellar output.

Previous work describing IntA’s functional influence often focused on patterns of muscle activation, sometimes to the exclusion of kinematic measures. Although the general theme of limb flexor predominance is often observed, there exists significant disagreement about the level of organization. Early studies argued that IntA activation can control single muscles (Harvey et al., 1979; Perciavalle et al., 1978a, 1978b; Thach, 1978), with later studies observing coordinated movements across limb segments or even across the body (Ekerot et al., 1995; Rispal-Padel et al., 1982). The present study focused on quantifying end-effector kinematics, leaving untested the patterns of muscle activation that enable such kinematics. In addition, because our causal experiments necessarily modulate a population of IntA neurons, it remains likely that the kinematic effects we observe are due to the concerted action of neurons with diverse tuning and muscle control properties. However, the properties of IntA kinematic control we identified–including directionality, scalability, and behavioral context dependence–extended to electrophysiological analysis of single cells. Moreover, we never observed different directions of kinematic effects across animals or light power levels, arguing against a functionally segregated topography in IntA for limb control. Nevertheless, distinct neuronal modules may exist within IntA and across cerebellar nuclei that influence diverse behaviors, such as conditioned eyelid closures, gait, and grasping, as identified by previous studies (Armstrong and Edgley, 1984; Gibson et al., 1996; Heiney et al., 2014; Sarnaik and Raman, 2018; Sauerbrei et al., 2015).

Although the present work was not designed to interrogate all possible kinematic consequences of IntA stimulation across the entire body, it was not apparent that activation drove movement of other effectors. Interestingly, we observed strong context dependence of both optogenetic stimulation and endogenous firing rate changes on limb kinematics, suggesting downstream gating of cerebellar influence on movement. Such gating could occur at diverse targets, including cerebral cortex, brainstem, and spinal cord, to modulate the complexity of cerebellar influence on subsequent movement, including which muscle groups are responsive. Indeed, contextual gating could account for the diversity of observed effects of IntA electrical stimulation previously reported, which almost exclusively stimulated during rest (Ekerot et al., 1995; Hare et al., 1936; Lee et al., 2015; Miller and Laughton, 1928; Perciavalle et al., 1978b; Sprague and Chambers, 1953; Witter et al., 2013). In the rare exception, stimulation during movement was noted to have had no effect but was not investigated systematically (Hoogland et al., 2015; Rispal-Padel et al., 1982). These differences raise the important point that cerebellar contributions to complex skilled movements may depend upon the evolving state of the downstream motor system.

Our finding that IntA activity levels are reciprocally matched to preceding reach kinematics begs the question of how such a code might be modified over the course of motor learning. The cerebellar cortex is widely appreciated as an associative learning machine, capable of adapting movements according to newly experienced sensorimotor contingencies, likely through the generation of forward models of the body (Albus, 1971; Marr, 1969; Ohyama et al., 2003; Wolpert et al., 1998). In reaching, the cerebellum has been shown to be essential for sensorimotor remapping (Chen et al., 2006; Martin et al., 1996), and Purkinje cells in limb-associated regions of cerebellar cortex modify their activity patterns throughout the course of adaptation (Gilbert and Thach, 1977; Hewitt et al., 2015). The translation of learned predictions of Purkinje cells into adaptive regulation of movement at the level of the cerebellar nuclei has remained obscure. Our work provides an essential stepping stone linking the well-developed algorithmic theories of cerebellar cortical function with basic causal relationships actuating motor control. The mechanisms that enforce precise temporal patterning of IntA activity in the face of significant kinematic variability, both during peak performance and throughout motor learning, likely share homology with other control modules across the cerebellum. At a minimum, we argue that patterned IntA activity may not simply be the result of cancelling forward model predictions but rather exists as a dynamic substrate from which alterations in activity parameters can correct motor errors.

STAR★METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Abigail Person (abigail.person@ucdenver.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Behavioral and recording data were collected from 22 adult (P70-P365) mice of either sex (20 females, 2 males), including the following genotypes: (1) ‘wild-type’ C57/Bl6 (N = 19); (2) ‘Neurotensin receptor1-Crex FLEX-ChR2′ (N = 3; Ntsr1-Cre: Mutant Mouse Regional Resource Center; Tg(Ntsr1-cre)GN220Gsat/ Mmucd; Flex-ChR2: RCL-ChR2(H134R)/EYFP; Jackson Labs Stock No: 024109). Ntsr1-Cre / FLEX-ChR2 animals were only used for behavioral experiments. There was no a priori expectation of sex differences in cerebellar motor control, thus the study was not powered to examine such potential differences. Animals were housed on a 12:12 light-dark cycle with ad libitum access to food and water except during behavioral training and experimentation (described below), and maintained bodyweights above 80% for the entirety of the study. Animals were group housed with like genotypes until surgery, at which point they were singly housed with a running wheel. All procedures were in accordance with NIH guidelines for the care and use of laboratory animals and were approved by the University of Colorado Anschutz Institutional Animal Care and Use Committee and Institutional Biosafety Committee.

METHOD DETAILS

Behavior

Animals were trained on a skilled reach task described previously (Azim et al., 2014; Whishaw, 1996). Briefly, animals were food restricted to 80%–90% their initial body weight and monitored daily for weight gain or loss as well as signs of distress. They were then accommodated to the behavioral arena, and subsequently trained to reach for 20 mg pellets of food (BioServ #F0163). The behavioral arena consisted of a custom plexiglass box with a 0.9 cm opening providing access to a cylindrical pedestal that held a food pellet 1 cm away, 2 cm from the bottom of the behavioral arena and slightly left-of-center to encourage reaching with the right hand. The pellet pedestal (0.5 cm diameter) was designed to avoid physical interference with outreach or return limb reach trajectories and required the animals to skillfully grab the pellet to retrieve it. On training day 1, the pellet location was moved close enough to the arena opening to be retrieved with the tongue, and was slowly moved farther away on subsequent days to encourage reaching with the limb. All animals learned to accomplish the task using the right hand (n = 22; range of 1 to 10 days of training). Sessions lasted until 30 pellets were successfully retrieved or 20 min were spent in the arena, whichever came first. Success was defined as bringing the pellet into the behavioral arena. Animals were considered ‘trained’ and ready for experimentation when they could successfully retrieve 30 pellets in a 20 min behavioral session.

Real-time kinematic tracking and closed-loop system

Paw position was monitored by an infrared-based real-time motion-capture system consisting of five 120 frames-per-second cameras (Optitrack Slim3U Camera board with Motive), each with a 10 mm focal length lens (Edmund Optics). Custom built camera mounts allowed stable camera positioning day-to-day and three-degree-of-freedom control over positioning. Cameras were mounted with infrared LED ring arrays and light level was controlled via digital power supply (Hewlett Packard). Camera position and orientation was optimized to capture the mouse’s paw movement throughout the extent of the reach, resulting in a capture volume of approximately 4 cm³. Four cameras were used for online kinematic tracking, and one was used for reference video. 1.5 mm diameter retroreflective markers (B&L Engineering) were used for both camera calibration and tracking of mouse reach kinematics. Camera calibration was conducted in Optitrack Motive software with a custom built calibration wand (4 and 8 mm marker spacing) and ground plane (10 and 15 mm marker spacing). The spatial origin of the reach capture volume was located approximately 1.6 cm inside the behavioral arena, measured from the front plexiglass wall, and approximately 2.0 mm left-of-center from the reach opening (in line with the pellet target location). The front wall of the behavioral arena defined the ‘upward’ and ‘lateral’ dimensions, with the ‘outward’ dimension defined perpendicularly from that plane toward the pellet. Calibration procedures were identical throughout the study, and the system was recalibrated as necessary to maintain accurate detection. After calibration, Motive reported mean spatial triangulation errors of less than 0.05 mm throughout all experimental sessions.

For kinematic tracking, marker detection thresholds were set to minimize spurious detection of non-marker objects (e.g., the mouse’s eye or snout). Real-time tracking of paw position was conducted by Motive and streamed into MATLAB (R2015b; RRID: SCR_001622) for processing, with a tracking latency of less than 1 ms. A custom-written MATLAB program detected when the paw crossed a user-defined boundary and sent a ‘go’ signal to an Arduino microcontroller, pre-programed to drive a laser via TTL pulses. We modified an open-source C++ dynamic link library (Stavropoulos, 2015; https://github.com/tstavropoulos/TestArduino) to facilitate low-latency communication between MATLAB and Arduino (0.5 ± 0.1 ms (mean ± standard deviation) reflection latency). Combined with the camera frame rate (120 Hz), this system supports a closed-loop latency of 9.5 ms. The three-dimensional reach position data were saved in MATLAB along with the time of stimulation and reach success. Reach success was monitored manually by the experimenter through a keypress function in MATLAB.

Surgical procedures and histology

All surgical procedures were conducted under Ketamine/Xylazine anesthesia. The stereotaxic location of anterior interposed nucleus (IntA) was targeted as −1.95 mm posterior, 1.6 mm lateral, and 2.3 mm ventral from lambda. Pressure viral injections were performed with a pulled glass pipette. Approximately 150 nL of virus was injected unilaterally into the right IntA, ipsilateral to the paw used for reaching, over the course of approximately 1 min. A minimum of four weeks was allowed for expression before optogenetic stimulation experiments. For ‘ChR2′ experiments, we used AAV2-hSyn-hChR2(H134R)-mCherry; for ‘Arch’ experiments, we used AAV2-hSyn-eArch3.0-EYFP (UNC Vector Core). Optical fibers (105 μm core diameter, ThorLabs) attached to a ceramic ferrule (1.25 mm, ThorLabs), polished to efficiency >90%, were implanted so that the tip of the optical fiber rested 0.1 mm above the injection site. The ceramic ferrule was affixed to the skull using luting (3M) and dental acrylic (Teet’s cold cure). After behavioral experiments were completed, animals were sacrificed according to standard procedures via pentobarbital overdose, transcardially perfused with 4% paraformaldehyde, and processed for histological analysis as described previously (Beitzel et al., 2017). Injection sites and fiber implant tracts were visually inspected on an upright epifluorescent microscope (Zeiss) by two independent observers. For spatial quantification of opsin expression (Figure S4), images were taken of the section of interest and were processed with a 100 pixel width Gaussian filter and thresholded using a contour function to find the region of brightest expression. Thresholds were selected independently for each animal.

Optogenetics

Stimulation for ChR2 experiments was obtained via activation of a 470 nm diode laser (Opto Engine LLC) with 2 ms pulses at 100 Hz, 50 ms pulse train duration. During kinematic closed-loop experiments, a custom-built patch cord (approx. 1.0 m) connected the laser to the implanted ferrule and was secured with a ceramic sleeve connector (ThorLabs). For ChR2 experiments, power was set to between 0.5–1.0 mW, measured at the end of the patch cord. For experiments that use light power as an experimental variable, powers between 0.05–2.0 mW were used, with ranges varying individually between animals. Stimulation for Arch experiments was obtained via activation of a 561 nm diode laser (SLOC) with a single 50 ms pulse with light power at 5.0 mW. Light power levels were calibrated daily. The irradiance at the tip of the 105 μm diameter optical fiber ranged from approximately 5.0 mW/mm² (0.05 mW) to 230 mW/mm² (2.0 mW) for ChR2 experiments, and was 580 mW/mm² (5.0 mW) for Arch experiments. Light spread analysis was modeled using a Monte-Carlo simulation (Stujenske et al., 2015).

Stimulation occurred on a pseudorandom 25 percent of reaches to avoid anticipation. Stimulation occurred in closed-loop based on a kinematic landmark defined prior to the experimental session. All experiments used a positional threshold in the outward direction near the point of maximum outward reach velocity as the kinematic landmark (Figure S3), unless otherwise noted in experiments directly manipulating stimulation location. This main kinematic landmark was a vertical plane 1.6 cm from the ‘origin point’, defined during calibration, which corresponds to the opening in the front acrylic wall of the behavioral arena. The ‘Early’ kinematic landmark was located 1.4 cm from the origin, while the ‘Late’ kinematic landmark was located 2.1 cm from the origin. Stimulation during return was performed at the position of the ‘Late’ kinematic landmark following completion of outreach, as measured by a direction reversal. Stimulation outside of the context of active reach behavior occurred during standing and/or feeding used identical stimulation parameters, except that stimulation was triggered every 10 s as the animals rested or ate food pellets placed inside the behavioral arena. Non-reach stimulation data were further divided via visual inspection into one of three ‘paw states’ that occurred during these sessions (Figure S7C): ‘paw down’, in which the animal was standing still with the paw placed against the floor of the behavioral arena; ‘paw lifted’, in which the animal was standing still or walking with the paw lifted at the time of stimulation (i.e., resting on hindpaws); and ‘eating’, in which the animal was actively eating a food pellet, which involved grasping the pellet in both paws.

Kinematic analysis

Data were analyzed with custom-written functions in MATLAB. Time-stamped three-dimensional paw position data (reported as values relative to the spatial origin set during calibration) were processed in several stages to segment data into individual reaches. First, we corrected for spurious object detection (< 3% of data frames detected more than one marker) by conducting a nearest-neighbor analysis, linking marker positions across frames to differentiate the marker from other objects. Next, we filtered continuous kinematic data captured throughout the behavioral session, including while the animal freely moved in the behavioral arena and performed reaches. Between reaches, the marker could become hidden from view, thus to avoid artifacts from erroneously linking distant marker data, we linearly interpolated missing points prior to filtering. After applying a 2^nd order 10 Hz cutoff Butterworth filter (Yu et al., 1999), we removed the interpolated frames, which resulted in continuous filtered marker position of data captured during the experiment.

To segment reaches from the continuously collected kinematic data, we extracted marker positions beyond a positional threshold unique to reaching, located just beyond the reach opening of the arena. To ensure that we captured the entirety of the reach, we included marker data that continuously moved in the outward direction prior to the paw reaching the positional threshold. The inverse criterion was applied to the end of the reach to obtain full reach trajectories.

Reach velocity was calculated as the numerical gradient of reach position data in each dimension. We defined the endpoint of the reach as the first local maximum in the outward direction. The ‘outreach’ and ‘return’ phases were split by the endpoint. All quantification of endpoint distance included both outward and upward components as a distance from the origin point set during calibration (2-dimensional Euclidean distance). To produce average reach velocity profiles for unstimulated or stimulated reaches, we first time-interpolated the velocity data at 10 ms intervals over a 400 ms window aligned to time of stimulation. For unstimulated reaches, the alignment point was chosen as the point at which stimulation would have occurred during that behavioral session. Average velocity at each time point is reported as the mean of the population of reaches under consideration (minimum of 20 reaches). Since the reach data traces could have different lengths, standard error was calculated on a point-by-point basis for each average. Two-dimensional plots of velocity effects were generated by plotting the maximum difference between mean unstimulated and stimulated velocity profiles in each dimension, agnostic to effect direction. We calculated the latency to maximum effect on a per animal basis by finding the peak Euclidean difference in average velocity between stimulated and unstimulated reaches. The amplitude of the effect was reported for each animal at its calculated latency of maximum effect observed in the means. Difference plots were generated by subtracting the population average unstimulated velocity profile the from stimulated velocity profile (Figures 2H and 7C). p value heatmaps were generated for each animal by conducting a Wilcoxon rank sum test comparing unstimulated and stimulated velocity values in 10 ms intervals across the analysis epoch. Distance traveled overtime was calculated relative to the position of the paw at the time of stimulation (t = 0).

To analyze the distribution of velocity values within the population of unstimulated or stimulated reaches, as in the graded stimulation experiments, we generated a two-dimensional histogram over the range of possible velocity values over the 400 ms time window. These histograms were normalized to the total number of data points per condition to obtain a relative ‘prevalence’ of velocity values in each bin. These values were then subtracted on a bin-by-bin basis (Stimulated – Unstimulated) to visualize differences in the likelihood of velocity measurements between unstimulated and stimulated reaches as populations, displayed as heatmaps. To determine graded kinematic effects with graded stimulation powers, we analyzed the distribution of velocity differences (relative to average unstimulated velocity profiles) across power levels within each animal (Figure S7A). Distributions were taken at a unique time point for each animal corresponding to the maximum effect latency in the means at the lowest stimulation power strength. To investigate determinates of the amplitude of kinematic effects of stimulation at different positional landmarks, we correlated velocity at the time of stimulation to change in velocity over the next 50 ms across conditions (stimulated and unstimulated) for each animal (Figure S7B). Linear regression was performed for both unstimulated and stimulated reaches.

To visualize continuous z-scores for average velocity profiles, a Wilcoxon rank-sum test was conducted on the time interpolated averages at each time point. The first time point to surpass a z-score of 2.5 was defined as the ‘first-effect latency’ signifying divergence of the two velocity averages. For visualization of statistical divergence over time, the absolute value of the z-score is interpolated and plotted as a color bar.

Recordings

Mice injected with AAV2-hSyn-hChR2(H134R)-mCherry or AAV2-hSyn-eArch3.0-EYFP to the cerebellar nuclei were implanted with an optetrode drive (Anikeeva et al., 2011). Four 0.012 mm NiCr wire tetrodes affixed to a 105 μm core optical fiber were attached to an electrode interface board (Neuralynx) and 3D-printed movable drive. Tetrodes were electrochemically plated with gold solution to an impedance of 250 kΩ. Tetrodes were positioned 0.5 mm below the tip of the optical fiber. The optical fiber/tetrode bundle was implanted 0.3 mm above IntA (−1.95 mm posterior, 1.6 mm lateral, and 2.0 mm ventral from lambda) and affixed to the skull using luting (3M) and dental acrylic (Teet’s cold cure). For control experiments measuring the effect of optogenetic stimulation, neurons were recorded as the animal rested or ate food pellets placed inside the behavioral arena, and optogenetic stimulation was applied as described for behavioral experiments (ChR2: 0.5–5.0 mW, 100 Hz, 2 ms pulses, 50 ms train; Arch: 5.0 mW, 50–200 ms pulse). For recordings of reach-associated activity, behavioral procedures were applied as described above. The drive was incrementally lowered by 0.05 mm the day before each recording session. Recordings were conducted with a Cereplex M digital headstage connected to a Cereplex Direct acquisition system (Blackrock Microsystems), which also monitored optical stimulation timing via TTL. Blackrock Offline Spike Sorter software was utilized to filter data (250 Hz high-pass Butterworth), detect spikes (> 4.0 factor of noise root mean square values), and sort individual units from noise. No more than one cell per tetrode per recording day was used to avoid over-counting neurons. Spike times were subsequently imported into MATLAB for analysis and alignment to stimulation or reach behavioral events as necessary.

For slice recordings, mice injected with AAV2-hSyn-eArch3.0-EYFP to the cerebellar nuclei (> 4 months old) were deeply anaesthetized with isofluorane and transcardially perfused with warm (36°C) ACSF containing (in mM): 123 NaCl, 3.5 KCl, 26 NaHCO₃,1.25 NaH₂PO₄,1.5 CaCl₂,1 MgCl₂,10 glucose and equilibrated with 95/5% O₂/CO₂. Mice were then rapidly decapitated and the brains removed into ACSF (36°C). Slices (300 μm thick) were cut on a Vibratome (Leica VT100S) and incubated in warmed (37°C), oxygenated ACSF for at least 1 h before recording. Cerebellar slices were transferred to a recording chamber perfused continuously with warmed (30–32°C), oxygenated ACSF at a flow rate of 2–4 ml/min. Slices were visualized with infrared differential interference contrast microscopy and fluorescence (Zeiss AxioExaminer) and recordings were made from neurons expressing GFP. Borosilicate patch pipettes were pulled to tip resistances of 4 MΩ and filled with an internal solution containing (mM): 130 K-gluconate, 2 Na-gluconate, 6 NaCl, 10 HEPES, 2 MgCl2, 0.1 or 1 EGTA, 14 Tris-creatine phosphate, 4 MgATP, 0.3 Tris-GTP and 10 sucrose. A 105 um core optical fiber was positioned over the slice and coupled to a 561 nm diode laser (SLOC). Recordings were made in the on-cell configuration to monitor spontaneous firing. 50 ms light pulses were delivered 1/s after achieving a recording collecting over 100 sweeps/neuron.

Analysis of recording data

Extracellular recording data were imported into MATLAB for analysis using Blackrock Microsystems NPMK 4.4.2.0. Custom scripts were written to analyze and display features of single unit activity. Single-lead voltage signals were filtered (250 Hz high-pass Butterworth) for display in figures. For statistical quantification of neural responses to optogenetic stimulation, we tested paired single-trial spike counts during the 75 ms before and after the start of stimulation. For reach behavior experiments, mean firing rates aligned to a behavioral event (e.g., endpoint) were calculated by trial averaging spike counts in 1 ms bins and then smoothing with a 5 ms Gaussian. To test for significant rate modulation during reach, baseline rate was taken as the mean rate from 300–100 ms before reach start (defined above), and peak firing rate was within 100 ms of reach endpoint (i.e., a 200 ms window centered on reach endpoint). To display alignment of neural activity to reach start or reach endpoint across the population (population peri-event time histogram, PETH), mean firing rates were normalized to their maximum rate (2000 ms analysis window) on a per-cell basis. To test for differences in alignment of neural activity to endpoint versus reach start, we constructed histograms (100 ms bins) of the timing of peak mean firing rate relative to these different alignments across the population of neurons. We then performed a Chi-square test on the number of neurons that showed peak mean firing rate within 100 ms of reach endpoint versus reach start. To test the reliability of neural responses around reach start and reach endpoint, we calculated the Fano Factor of spike counts in the same window in the two different alignments. These analyses were performed on all 84 cells.

Subsequent analysis relating single neuron instantaneous firing rate to reach kinematics (Figure 8) were performed on a subset of ‘endpoint’ cells, which had maximum mean firing rates within 100 ms before or after reach endpoint (n = 35 cells).To calculate instantaneous firing rate for single-trial analyses, we took the inverse of each inter-spike-interval digitized at 1 kHz and smoothed with a 20 ms Gaussian. The reach epoch was defined as described above (see ‘Kinematic analysis‘). For the “burst-triggered” average of kinematics, instantaneous firing rates were z-score normalized (baseline mean and standard deviation defined outside of reach, with a 100 ms shoulder) and bursts were defined as z-scores greater than 2.5 for a minimum of 5 ms. Kinematic data were then aligned to the time of peak burst activity for each event. Random alignments were generated using a pseudorandom process in MATLAB, controlling for the average number of reach-associated events for each cell.

To calculate the average difference in outward velocity corresponding to a range of IntA activity levels, we binned firing rates and averaged kinematic data on a per cell basis. To calculate change in velocity, we subtracted the velocity 45 ms in the future from the velocity at the time point of each instantaneous firing rate value. 45 ms was chosen because it corresponds to the average maximum kinematic effect latency we observed during causal experiments. We then grouped and averaged these change-in-velocity data based on their corresponding firing rate bin. We restricted this analysis to time points that occurred during the reach epoch as defined above. We then averaged across all cells to obtain the population average of change in velocity across firing rate bins. To compute the correlation between instantaneous firing rate and change in outward velocity during the reach epoch for each cell, we regressed all instantaneous firing rates during the reach epoch with the change in velocity over 45 ms from each rate measurement. The grand mean linear regression was computed by averaging regression coefficients across the population.

To analyze how variability in reach kinematics was correlated with variability in recording data (Figures 8F–8I), we separated reaches into sliding quintiles based on peak instantaneous firing rate for each cell, (top quintile: ‘High’; bottom quintile: ‘Low’). On a per-reach basis, we found the maximum instantaneous firing rate in a 100 ms window centered on the time (relative to endpoint) of mean peak firing rate for that particular cell. We then sorted reaches by peak instantaneous firing rate and averaged the kinematics, computing reach velocity profiles for each cell for each sliding quintile based on peak instantaneous firing rate. To demonstrate robustness of kinematic results across the range of activity levels, we created nine sliding quintiles that incremented by 10 percent (0–20, 10–30, 20–40. etc.). We limited this analysis to cells that had their peak mean firing rate within the 100 ms before reach endpoint (n = 17) in order to exclude cells whose peak modulations occurred after the endpoint, since we were concerned with investigating causal control of endpoints. Finally, reach velocity profiles were group averaged within quintiles to produce the final comparison between reaches with High and Low peak firing rates across the population of cells. The net change in velocity during deceleration was calculated from 100 ms before endpoint to 50 ms after endpoint. The pre-deceleration velocity measurements were taken at a time point 134 ms before endpoint, which represented the time of peak difference between the highest and lowest activity quintiles.

To simulate how variable deceleration contributes to endpoint precision (Figure 8I), we utilized a fundamental equation of motion,

$$\frac{V_f^2-V_0^2}{2a}=S-S_0$$

where S represents displacement, V represents velocity, a represents acceleration, and f and ₀ indicate final and initial conditions respectively. We took measured values of average starting position and velocity 100 ms prior to endpoint across all quintiles (defined above, Figure 8F). We then computed displacement using the actual deceleration associated with that quintile (labeled ‘actual’) or the average deceleration of all reaches grouped together (‘simulated’). The resulting endpoints were calculated, and variance across quintile groups was calculated as a statistical measure of endpoint precision for both ‘actual’ and ‘simulated’ endpoints.

QUANTIFICATION AND STATISTICAL ANALYSIS

Two-tailed nonparametric statistical tests were used for all analyses unless otherwise noted. All data subjected to parametric analyses were first tested using D’Agostino and Pearson normality test. All data are displayed as mean ± standard error unless otherwise noted. Statistical tests and results are stated in the text, along with population sizes for animals (N), reaches (n), and cells (n). Alpha was 0.05. Statistical displays such as continuous z-score were never used to establish significance, precluding multiple comparisons confounds. Time series data were tested for statistical divergence by finding the latency of maximum difference between group means and conducting post hoc significance tests at that latency.

DATA AND SOFTWARE AVAILABILITY

Data analyzed and code generated in this study are available upon written request to corresponding author.

Supplementary Material

1

Figure S1. Related to Figure 1. Extracellular recordings of IntA neurons.

A. Example extracellularly-recorded voltage traces from a single tetrode lead on individual reach trials across a recording session (left; traces are aligned and centered on reach endpoint). Detected spikes are indicated by black dots. Corresponding single reach velocity profiles in the outward direction (right).

B. Four additional example rasters (top) and peri-event time histograms (bottom) of neurons recorded from IntA, aligned to reach endpoint. Insets display raw voltage traces high-pass filtered (250 Hz) for each neuron.

Figure S2. Related to Figure 1. IntA population activity aligned to reach start.

A. Raster (top) and PETH (bottom) of an example IntA neuron (same neuron as Figure 1B) aligned to reach start.

B. Population PETH including all cells recorded in IntA (n = 84) aligned to reach start and sorted by time of maximum firing rate (top). Firing rate is normalized to maximum on a per-cell basis. The reach epoch is highlighted in magenta (from reach start to average outreach duration of 313 ms).

C. Histogram of the timing of peak firing rates relative to reach start for all cells.

Figure S3. Related to Figure 2. Kinematic closed-loop system enables short-latency optogenetic stimulation at a precise kinematic landmark.

A. Performance latency of closed-loop reflection test between Matlab and Arduino for short latency communication.

B. Histogram of outreach duration for a single behavioral session (n = 82 reaches) compared to total latency of kinematic closed-loop stimulation system (9.5 ms).

C. Mean outreach duration for each animal (n = 18; black dots) and grand mean across the population of animals (bar).

D. Reach velocity (colorbar) as a function of outward position during 50 reaches from a single behavioral session. The consistent location of maximum outward velocity was chosen as the main kinematic landmark (1.6 cm from origin).

Figure S4. Related to Figures 2 through 7. Histological analysis of injection location, optical fiber placement, and drive placement in IntA.

A. Location of expression determined with confocal microscopy (contours) and fiber placement (black lines) in IntA for ChR2 animals. The contour for expression is displayed in a unique color for each animal.

B. Same as in A for experiments in which Arch is expressed.

C. Optetrode drive placements in IntA determined from post-hoc histological analysis.

D. Light spread analysis for highest optical power used in ChR2 experiments (2.0 mW; left) and Arch experiments (5.0 mW; rights). Contours illustrating 10% and 1% of maximum irradiance are indicated by white lines. Light spread falls off to 10% within 0.5 mm from fiber tip.

E. Example histological section. The specimen with the most off-target expression in the cerebellar cortex is displayed; no expression was noted in Purkinje neurons. Inset: mCh expression is largely confined to IntA, and optical fiber tip extends to just above the nucleus.

Figure S5. Related to Figure 2. Extended analyses of IntA excitation results and control experiments.

A. Average distance travelled over time following the stimulation trigger location for both stimulated (grey) and unstimulated reaches (black). Time of stimulation is indicated in blue.

B. Outward velocity over time for all unstimulated and stimulated individual reaches for a single animal (same data as Figure 2F).

C. Difference (Stim. – Unstim.) of velocity profiles for the population average (black) and all individual animals (colors). Heatmap of p-values associated with Wilcoxon rank sum tests conducted for each animal (rows) at 10 ms intervals (columns). Same data as Figure 2H.

D. Average success rates for each animal (grey dots) and the group mean (large black and blue dots) for IntA excitation with ChR2, compared to unstimulated reaches (paired t-test, p = 0.02). These data are for stimulation at the standard kinematic location and optical power only. Note that this definition of success rate included successful pellet retrieval on ‘continued reaches’ (see Figure 2C).

E. Average endpoint variance (standard deviation) for each animal (grey dots) and the group mean (large black and blue dots) for IntA excitation with ChR2, compared to unstimulated reaches (paired t-test, p = 0.67).

F. Population average of average outward velocity of unstimulated and stimulated reaches aligned to time of stimulation for mice with no opsin expressed in IntA (N = 4 animals). Blue indicates the stimulation epoch (50 ms, 2 ms pulses, 100 Hz). No significant difference was noted at any timepoint ( p > 0.05) for any individual animal or for the population mean (N = 4 animals).

G. Summary of average maximum velocity effect magnitudes of stimulation in each of the three spatial dimensions across subjects (grey dots) and as a whole (bars) for ‘no opsin’ animals (Wilcoxon signed-rank, p = 0.13).

H. Average initial endpoint of unstimulated and stimulated reaches for ‘no opsin’ animals (paired t-test; p = 0.97).

Figure S6. Related to Figure 3 and Figure 7. Recordings of IntA neurons during optogenetic stimulation.

A. Average firing rate of IntA neurons (n = 59) during baseline and ChR2 stimulation epochs at varying optical powers (**** p < 0.0001).

B. Average firing rate of IntA neurons recorded in vivo (left; individual neurons, grey; mean, black/green) and in slice (right) in response to Arch stimulation (in vivo: n = 4, * p = 0.012; in slice: n = 5, * p = .049).

C. Example raster and PSTH of ChR2-expressing neuron in response to 470 nm light stimulation (2.0 mW) using standard parameters used in this study (100 Hz, 2 ms pulses, 50 ms train).

D. Example raster and PSTH of Arch-expressing neuron in response to 561 nm light stimulation (5.0 mW) recorded in vivo.

E. Comparison of the distribution of firing rates under the strongest optical power tested (5.0 mW) with peak endogenous firing rates recorded during reach (‘Endog.’). Similar ranges of firing rates were observed in these conditions.

Figure S7. Related to Figures 3, 4, and 6. Extended kinematic analyses of various IntA stimulation conditions.

A. Distributions of velocity difference values (Stim. – Unstim.) at a specific latency for each of three optical powers (High, Middle, Low) for each animal tested. Within each animal, distributions were significantly different (Kolmogorov-Smirnov, p < 0.05), and means were significantly different (Wilcoxon rank sum, p < 0.05) across all pairs of neighboring conditions. Same data as Figure 3.

B. Relationship between outward velocity at the time of stimulation (time 0, x-axis) and subsequent change in velocity over the next 50 ms (y-axis) for unstimulated (grey) and stimulated (blue) reaches. All reaches that were recorded across different stimulation locations are plotted (Early, Middle, Late; same data as Figure 4). For Animals 1 and 2, regression lines had statistically indistinguishable slopes between unstimulated and stimulated reaches (p > 0.05), but significantly different y-intercepts (p < 0.0001), while the slope of the relationship decreased significantly for stimulated reaches in Animal 3 (p < 0.0001).

C. Outward velocity aligned to the time of stimulation for stimulated (grey lines; stim. epoch in blue) and unstimulated epochs, outside the context of active reaching behavior (N = 2 animals; n = 138 trials). Unstimulated epochs were drawn randomly from the continuous tracking data. Paw states (paw down, eating, and paw lifted) are described in Methods. No significant differences were measured in any context. Same data as Figure 6B.

Figure S8. Related to Figure 7. Extended analyses and experiments for IntA inhibition

A. Outward velocity over time for all unstimulated and stimulated individual reaches for a single animal (same data as Figure 7A).

B. Difference (Stim. – Unstim.) of velocity profiles for the population average (black) and all individual animals (colors). Heatmap of p-values associated with Wilcoxon rank sum tests conducted for each animal (rows) at 10 ms intervals (columns). Same data as Figure 2H.

C. Average success rates for each animal (grey dots) and the group mean (large black and green dots) for IntA inhibition with Arch, compared to unstimulated reaches (paired t-test, p = 0.02).

D. Average outward velocity of unstimulated and stimulated reaches aligned to time of stimulation, using standard stimulation parameters (50 ms, standard kinematic landmark).

E. Representative example of average outward velocity of unstimulated and stimulated reaches aligned to time of stimulation (N = 3 animals), using longer duration stimulation (100 ms, standard kinematic landmark). Note that the magnitude of the effect is larger.

F. Representative example of average outward velocity of unstimulated and stimulated reaches aligned to time of stimulation (N = 2 animals), using the ‘Late’ kinematic landmark described in Figure 4 (50 ms, ‘Late’ kinematic landmark). Note that the location of the kinematic effect follows the location of stimulation.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
AAV2-hSyn-hChR2(H134R)-mCherry	UNC Vector Core	N/A
AAV2-hSyn-eArch3.0-EYFP	UNC Vector Core	N/A
Experimental Models: Organisms/Strains
Mouse: C57BL/6J	The Jackson Laboratory	000664
Mouse: Tg(Ntsr1-cre)GN220Gsat/ Mmucd	Mutant Mouse Regional Resource Center	017266-UCD
Gt(ROSA)26Sortm32(CAG-COP4*H134R/EYFP)Hze	The Jackson Laboratory	024109
Software and Algorithms
MATLAB (versions: 2015b, 2018a)	MathWorks	https://www.mathworks.com/
Motive 1.9.0	Optitrack	https://optitrack.com/products/motive/
Prism 7	GraphPad	https://www.graphpad.com/
Arduino IDE 1.6.5	Arduino	https://www.arduino.cc/en/main/software
TestArduino	T. Stavropoulos	https://github.com/tstavropoulos/TestArduino
Other
1.5 mm retroreflective markers	B&L Engineering	MKR-1.5
Food pellets: 20 mg, grain-based	BioServ	F0163
Camera lens, 10 mm focal length	Edmund Optics	58204
Digital Power Supply	Hewlett Packard	E3630A
Optical fiber, 0.125 mm	ThorLabs	FG105LCA
Ceramic ferrule, 1.25 mm	ThorLabs	CFLC128
Laser, 470 nm	Opto Engine LLC	MDL-III-470–100mW
Laser, 561 nm	SLOC	YL561T8–050FC
Electrode interface board, 16 channel	Neuralynx	EIB-16
Digital headstage	Blackrock Microsystems	Cereplex M
Data acquisition system	Blackrock Microsystems	Cereplex Direct

Highlights.

• Cerebellar anterior interposed nucleus (IntA) neurons are modulated near reach endpoint

• Closed-loop optogenetic manipulation of IntA adjusts reach kinematics in real time

• IntA activity is variably engaged to enhance reach endpoint precision

• Data provide a mechanistic insight into reach dysmetria