Abstract
Introduction
The increasing use of large sample sizes for population and personalized medicine requires high‐throughput tools for imaging processing that can handle large amounts of data with diverse image modalities, perform a biologically meaningful information reduction, and result in comprehensive quantification. Exploring the reproducibility of these tools reveals the specific strengths and weaknesses that heavily influence the interpretation of results, contributing to transparence in science.
Methods
We tested–retested the reproducibility of MRICloud, a free automated method for whole‐brain, multimodal MRI segmentation and quantification, on two public, independent datasets of healthy adults.
Results
The reproducibility was extremely high for T1‐volumetric analysis, high for diffusion tensor images (DTI) (however, regionally variable), and low for resting‐state fMRI.
Conclusion
In general, the reproducibility of the different modalities was slightly superior to that of widely used software. This analysis serves as a normative reference for planning samples and for the interpretation of structure‐based MRI studies.
Keywords: automated segmentation, multimodality brain MRI, reproducibility, test–retest
Addressing the methodological reproducibility of imaging postprocessing is essential for planning and data interpretation. MRICloud showed reproducible results for whole‐brain, multimodal, structure‐based quantification. Structural analyses (volumetric and DTI) show higher reproducibility than rsfMRI analysis.

1. HIGHLIGHTS
Addressing the methodological reproducibility of imaging postprocessing is essential for planning and data interpretation.
MRICloud showed reproducible results for whole‐brain, multimodal, structure‐based quantification.
Structural analyses (volumetric and diffusion tensor images) show higher reproducibility than rsfMRI analysis.
2. INTRODUCTION
Integrative analysis of multiple MRI contrasts is increasingly popular because the power to discriminate populations with a single modality is often limited. Typically, diseases are characterized by changes with small effect size in multiple domains; rarely, a single specific/sensitive feature fully characterizes individuals. While analyzing multiple MRI features potentially increases the power of phenotypic characterization, it aggravates statistical problems related to multiple comparisons. Methodologies designed to reduce the dimensions of information are imperative. A well‐known strategy is to aggregate voxels that represent a given structure in regions of interest (ROIs), resulting in a biologically comprehensive quantification. As manually drawing ROIs creates practical challenges (Tae, Kim, Lee, Nam, & Kim, 2008), automated methods for imaging segmentation of multiple contrasts represent a viable strategy (Faria, Liang, Miller, & Mori, 2017; Miller, Faria, Oishi, & Mori, 2013; Mori, Oishi, Faria, & Miller, 2013).
MRICloud (http://www.MRICloud.org) (Mori et al., 2016) is a recently developed web‐based tool with which to perform automated segmentation and quantification of multiple MRI modalities. MRICloud provides a platform to characterize anatomy (using T1 high‐resolution‐weighted images for volumetric analysis), white matter (using diffusion tensor images [DTI]), and resting‐state functional connectivity, built on structure‐based analysis. MRICloud can analyze all these modalities in the same anatomical framework, thus facilitating the integration of information from multiple domains in a biologically meaningful set of structures. In addition, MRICloud is a widely available tool, which is free online, completely automated and, therefore, meets the requirements for a neuroimaging tool that is widely applicable to large‐scale multimodal processing.
The reliability and accuracy of MRICloud for whole‐brain segmentation, based on DTI or T1‐WIs, have been extensively tested and validated (Ceritoglu et al., 2009; Liang et al., 2015; Oishi et al., 2008, 2009; Tang et al., 2015; Wu et al., 2016). A few other software that perform high‐resolution T1‐based automated segmentation, including FreeSurfer (Fischl, 2012), FSL (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012), SPM (Penny, Friston, Ashburner, Kiebel, & Nichols, 2007), ANTS (Avants et al., 2011), also underwent detailed reliability analysis, including testing the robustness of the respective pipelines to technical factors and artifacts (Ceritoglu et al., 2009; Han et al., 2006; Jovicich et al., 2009; Tustison et al., 2014; Ye et al., 2018). Most of these segmentation tools perform admirably when compared with the “gold standard” manual segmentation of selected structures, particularly when tested by the developers, in healthy subjects. A different aspect, less often reported, is the reproducibility of such technologies, over the entire brain, particularly when applied to DTI and resting‐state fMRI measurements, which has raised concerns about the interpretation of the results of these methods in the past (Huang et al., 2012; Morey et al., 2010; Shou et al., 2013; Vollmar et al., 2010).
Here, we assess the test–retest reproducibility of MRICloud structural quantification for different MRI modalities (T1‐based volumetric analysis, DTI for automated quantification of fractional anisotropy [FA] and mean diffusivity [MD], and resting‐state fMRI [rsfMRI] synchrony). We compare the MRICloud reproducibility with that of other well‐established methods, such as FreeSurfer and CONN‐SPM. Relevant information about biomarkers, particularly in longitudinal studies focused on subtle conditions, can be provided only by reliable neuroimaging tools and reproducible pipelines. It is the responsibility of the developers to provide users with the level of reproducibility of their tools, as the unknown reproducibility hinders the validation and the interpretation of the results.
3. MATERIALS AND METHODS
3.1. Participants and images
We used the two independent and public datasets to measure the reproducibility of MRICloud multimodality results:
Kirby21, the “multimodal MRI reproducibility resource” (Landman et al., 2011). Kirby21 is a public dataset available in the Neuroimaging Informatics Tools and Resources Clearinghouse (http://www.nitrc.org). This database consists of 21 healthy volunteers with no history of neurologic diseases (11 male, 22–61 years old), scanned twice in a day, on a 3T Phillips Achieva Scanner. One subject (#8) was excluded because the original DTI scan was not available. A brief description of the image protocol follows: (a) T1‐weighted images: sagittal orientation, matrix 240 × 256 mm, voxel size 1 × 1 × 1.2 mm3, TR/TE/TI 6,300/3.1/842 ms, flip angle 8°; (b) diffusion tensor images (DTI): spin echo sequence, reconstructed matrix 256 × 256 mm, voxel size (interpolated to) 2.2 × 2.2 × 2.2 mm3, 65 slices, TE/TR 67/6,181 ms, flip angle 90°, 32 gradient directions, b‐factor = 700 s/mm2; (c) resting‐state functional MRI (rsfMRI): EPI sequence, voxel size 3 × 3 × 3 mm3, slice gap 1 mm, TR/TE 2,000/30 ms, flip angle 75°, voxel matrix 80 × 80 × 37, 210 frames per run.
Human Connectome Project (HCP) test–retest dataset, which is a subset of the 1,200 individual MRIs, made public by HCP (Van Essen et al., 2013). It includes MRI test–retest MRIs of 45 healthy individuals (13 male, 22–35 years old), scanned in 3T machines, in variable intervals (4.7 ± 2 months interval, minimum = 1 month, maximum = 11 months). Two individuals have no rest–retest DTI. Note that the long retest interval increases likelihood of biological influences in the test–retest analysis, although these effects are presumably small in young healthy individuals. A brief description of the image protocol follows: (a) T1‐WI: axial orientation, FOV = 224 × 224 mm, voxel size 0.7 mm3 (isotropic), TR/TE/TI 2,400/2.14/1,000 ms, flip angle 8°; (b) DTI: 18 b0 images, 90 gradient directions, b = 3,000 s/mm2, TE/TR 89/5,520 ms, 1.25 mm voxel (isotropic); (c) rsfMRI: EPI sequence, voxel 2 mm3 (isotropic), TR/TE 720/33.1 ms, flip angle 52°, 72 slices, 1,200 frames per run.
3.2. Image processing
3.2.1. Multimodality processing with MRICloud
The images were automatically postprocessed, segmented, and quantified in MRICloud (http://www.MRICloud.org) (Mori et al., 2016). Briefly, the process for segmenting the T1‐WI, used for volumetric analysis, involves orientation and homogeneity correction; two‐level brain segmentation (skull‐stripping, then whole brain); image mapping based on a sequence of linear, nonlinear algorithms, and large deformation diffeomorphic mapping (LDDMM); and a final step of multi‐atlas labeling fusion (MALF) (Tang et al., 2013), adjusted by PICSL (Wang & Yushkevich, 2013). Please read (Tang et al., 2015; Wu et al., 2016) for technical details. As for the multi‐atlas library, we chose “Adult_22_55yrs_283Labels_26atlases_M2_252_V9B” under MRICloud atlas choices. This atlaset contains 26 healthy individuals, 22–55 years old, demographically close to our cohort, as recommended for atlas mapping (Ye et al., 2018).
For the DTI, the tensor reconstruction and quality control followed the algorithm used by DtiStudio (http://www.MRIStudio.org). The automated DTI segmentation was similar to that used for T1‐WIs, except for the use of complementary contrasts (mean diffusivity [MD], fractional anisotropy [FA], and eigenvector [fiber orientation]) and a diffeomorphic likelihood fusion algorithm (Tang et al., 2014) for multi‐atlas mapping. Please read (Ceritoglu et al., 2009) for technical details. We used the only atlas library available for DTI mapping in MRICloud: “Adults_168labels_12atlases_V1,” which contains 12 healthy individuals, 20–50 years old.
For the rsfMRI postprocessing (Faria et al., 2012), the T1‐WI and the respective segmentations obtained as described above were coregistered to the motion and slice timing‐corrected, resting‐state dynamics. Time courses were extracted from all the cortical and subcortical gray matter regions defined in the atlases and detrended, regressed for motion and physiological nuisance (Behzadi, Restom, Liau, Liu, 2007). Intensity and motion “outliers” were extracted with ART (https://www.nitrc.org/projects/artifact_detect). Seed‐by‐seed correlation matrices were obtained from the “nuisance‐corrected” time courses, and z‐transformed by the Fisher's method.
After the multimodal brain segmentation and quantification, each individual, in each session, was represented by a vector of image features. The image features considered in this study were 226 structural volumes from T1‐WIs processing (listed in Table 1), 97 white matter structural FA, and 97 white matter structural MD measures from DTI processing (listed in Table 2), and 1,431 pairwise, resting‐state z‐correlations between 54 gray matter seeds from rsfMRI (listed in Table 3).
Table 1.
Regional intraclass correlation coefficients (ICCs) for the T1‐based volumetric analysis, outputted from MRICloud (using Kirby21 and Human Connectome Project [HCP]) and FreeSurfer (using Kirby21)
| Mricloud | Kirby 21 | Connectome | Kirby 21 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | R | White matter beneath | L | R | White matter beneath | Freesurfer | L | R | ||||
| L | R | L | R | |||||||||
| Cortex | Superior frontal gyrus | 0.964 | 0.981 | 0.985 | 0.973 | 0.978 | 0.981 | 0.981 | 0.986 | Superior frontal gyrus | 0.947 | 0.954 |
| Superior frontal gyrus/pole | 0.967 | 0.987 | 0.916 | 0.945 | 0.960 | 0.980 | 0.938 | 0.957 | ||||
| Superior frontal gyrus/prefrontal cortex | 0.985 | 0.992 | 0.992 | 0.991 | 0.983 | 0.983 | 0.989 | 0.992 | ||||
| Middle frontal gyrus | 0.986 | 0.987 | 0.970 | 0.979 | 0.988 | 0.979 | 0.994 | 0.987 | Middle frontal gyrus | 0.968 | 0.930 | |
| Middle frontal gyrus/dorsolateral prefrontal cortex | 0.989 | 0.993 | 0.984 | 0.988 | 0.985 | 0.992 | 0.982 | 0.984 | ||||
| Inferior frontal gyrus/pars opercularis | 0.985 | 0.972 | 0.985 | 0.982 | 0.983 | 0.977 | 0.981 | 0.989 | Opercular part of the inferior frontal gyrus | 0.949 | 0.954 | |
| Inferior frontal gyrus/pars orbitalis | 0.986 | 0.994 | 0.977 | 0.980 | 0.979 | 0.989 | 0.967 | 0.978 | Orbital part of the inferior frontal gyrus | 0.612 | 0.646 | |
| Inferior frontal gyrus/pars triangularis | 0.989 | 0.978 | 0.983 | 0.987 | 0.979 | 0.982 | 0.984 | 0.989 | Triangular part of the inferior frontal gyrus | 0.961 | 0.878 | |
| Rectus gyrus | 0.973 | 0.975 | 0.955 | 0.964 | 0.990 | 0.990 | 0.954 | 0.977 | Straight gyrus, gyrus rectus | 0.654 | 0.833 | |
| Middle fronto‐orbital gyrus | 0.982 | 0.966 | 0.97 | 0.970 | 0.939 | 0.977 | 0.969 | 0.952 | ||||
| Lateral fronto‐orbital gyrus | 0.978 | 0.989 | 0.986 | 0.951 | 0.987 | 0.984 | 0.981 | 0.980 | Orbital gyri | 0.922 | 0.958 | |
| Postcentral gyrus | 0.969 | 0.989 | 0.973 | 0.973 | 0.990 | 0.983 | 0.991 | 0.978 | Postcentral gyrus | 0.939 | 0.944 | |
| Precentral gyrus | 0.991 | 0.995 | 0.979 | 0.979 | 0.986 | 0.992 | 0.986 | 0.993 | Precentral gyrus | 0.950 | 0.942 | |
| Superior parietal lobule | 0.983 | 0.985 | 0.982 | 0.986 | 0.985 | 0.988 | 0.989 | 0.991 | Superior parietal lobule | 0.961 | 0.923 | |
| Supramarginal gyrus | 0.983 | 0.991 | 0.978 | 0.954 | 0.992 | 0.987 | 0.990 | 0.965 | Supramarginal gyrus | 0.958 | 0.787 | |
| Angular gyrus | 0.991 | 0.989 | 0.991 | 0.985 | 0.980 | 0.980 | 0.985 | 0.974 | Angular gyrus | 0.859 | 0.948 | |
| Precuneus | 0.985 | 0.985 | 0.98 | 0.979 | 0.985 | 0.984 | 0.975 | 0.979 | Precuneus | 0.914 | 0.924 | |
| Cuneus | 0.975 | 0.986 | 0.993 | 0.992 | 0.990 | 0.990 | 0.987 | 0.992 | Cuneus | 0.950 | 0.936 | |
| Fusiform gyrus | 0.989 | 0.987 | 0.990 | 0.987 | 0.995 | 0.990 | 0.989 | 0.990 | Lateral occipito‐temporal gyrus (fusiform gyrus) | 0.925 | 0.943 | |
| Superior occipital gyrus | 0.982 | 0.959 | 0.938 | 0.981 | 0.980 | 0.980 | 0.980 | 0.984 | Superior occipital gyrus | 0.939 | 0.912 | |
| Middle occipital gyrus | 0.993 | 0.991 | 0.987 | 0.995 | 0.996 | 0.992 | 0.992 | 0.992 | Middle occipital gyrus | 0.897 | 0.947 | |
| Inferior occipital gyrus | 0.992 | 0.987 | 0.971 | 0.972 | 0.988 | 0.982 | 0.972 | 0.981 | Inferior occipital gyrus and sulcus | 0.960 | 0.823 | |
| Occipital pole | 0.941 | 0.898 | ||||||||||
| Lingual gyrus | 0.981 | 0.979 | 0.991 | 0.990 | 0.990 | 0.990 | 0.989 | 0.992 | Lingual gyrus, ligual part of the medial occipito‐temporal gyrus | 0.979 | 0.962 | |
| Superior temporal gyrus | 0.989 | 0.99 | 0.978 | 0.986 | 0.995 | 0.991 | 0.993 | 0.990 | Lateral aspect of the superior temporal gyrus | 0.965 | 0.959 | |
| Planum temporale or temporal plane of the superior temporal gyrus | 0.887 | 0.879 | ||||||||||
| Middle temporal gyrus | 0.983 | 0.983 | 0.988 | 0.994 | 0.995 | 0.995 | 0.991 | 0.994 | Middle temporal gyrus | 0.939 | 0.961 | |
| Anterior transverse temporal gyrus (of heschl) | 0.823 | 0.871 | ||||||||||
| Middle temporal gyrus/pole | 0.987 | 0.986 | 0.982 | 0.982 | 0.972 | 0.982 | 0.976 | 0.981 | Temporal pole | 0.760 | 0.659 | |
| Superior temporal gyrus/pole | 0.974 | 0.977 | 0.966 | 0.972 | 0.984 | 0.981 | 0.943 | 0.973 | ||||
| Inferior temporal gyrus | 0.983 | 0.989 | 0.980 | 0.979 | 0.990 | 0.987 | 0.987 | 0.989 | Inferior temporal gyrus | 0.870 | 0.923 | |
| Rostral anterior cingulate | 0.977 | 0.986 | 0.984 | 0.970 | Anterior part of the cingulate gyrus and sulcus | 0.911 | 0.939 | |||||
| Subcallosal anterior cingulate | 0.936 | 0.919 | 0.937 | 0.945 | ||||||||
| Dorsal anterior cingulate | 0.985 | 0.994 | 0.950 | 0.905 | 0.986 | 0.979 | 0.974 | 0.947 | Middle‐anterior part of the cingulate gyrus and sulcus | 0.863 | 0.915 | |
| Subgenual anterior cingulate | 0.953 | 0.918 | 0.964 | 0.965 | ||||||||
| Posterior cingulate | 0.992 | 0.990 | 0.973 | 0.986 | 0.990 | 0.990 | 0.987 | 0.986 | Middle‐posterior part of the cingulate gyrus and sulcus | 0.940 | 0.887 | |
| Posterior‐dorsal part of the cingulate gyrus | 0.924 | 0.928 | ||||||||||
| Isthmus of the cingulate | 0.966 | 0.960 | 0.966 | 0.960 | Isthmus of the cingulate gyrus | 0.715 | 0.935 | |||||
| Insula | 0.985 | 0.976 | 0.989 | 0.994 | Short insular gyri | 0.938 | 0.881 | |||||
| Entorhinal area | 0.919 | 0.869 | 0.916 | 0.838 | ||||||||
| Amygdala | 0.960 | 0.961 | 0.974 | 0.973 | Amygdala | 0.846 | 0.902 | |||||
| Parahippocampal gyrus | 0.966 | 0.914 | 0.955 | 0.943 | Parahippocampal gyrus, parahippocampal part of the medial occipito‐temporal gyrus | 0.882 | 0.821 | |||||
| Hippocampus | 0.983 | 0.974 | 0.983 | 0.983 | Hippocampus | 0.927 | 0.960 | |||||
| Body of the lateral ventricle | 0.999 | 0.999 | 0.998 | 0.998 | Lateral ventricle | 0.997 | 0.999 | |||||
| Frontal horn of the lateral ventricle | 0.997 | 0.999 | 0.995 | 0.994 | ||||||||
| Lateral ventricle, atrium part | 1.000 | 0.999 | 0.995 | 0.997 | ||||||||
| Occipital horn of the lateral ventricle | 0.991 | 0.977 | 0.982 | 0.951 | ||||||||
| Inferior horn of the lateral ventricle | 0.973 | 0.985 | 0.974 | 0.984 | Inferior lateral ventricle | 0.945 | 0.954 | |||||
| Ventricles and sulci | Sulci of the frontal lobe | 0.99 | 0.976 | 0.990 | 0.991 | Superior frontal sulcus | 0.684 | 0.952 | ||||
| Middle frontal sulcus | 0.787 | 0.860 | ||||||||||
| Inferior frontal sulcus | 0.945 | 0.812 | ||||||||||
| Orbital sulcus (h‐shaped sulci) | 0.798 | 0.891 | ||||||||||
| Medial orbital sulcus (olfactory sulcus) | 0.827 | 0.662 | ||||||||||
| Lateral orbital sulcus | 0.701 | 0.551 | ||||||||||
| Fronto‐marginal gyrus (of wernicke) and sulcus | 0.895 | 0.810 | ||||||||||
| Suborbital sulcus (sulcus rostrales, supraorbital sulcus) | 0.658 | 0.670 | ||||||||||
| Transverse frontopolar gyri and sulci | 0.808 | 0.831 | ||||||||||
| Central sulcus | 0.983 | 0.989 | 0.974 | 0.955 | Central sulcus | 0.958 | 0.922 | |||||
| Inferior part of the precentral sulcus | 0.937 | 0.871 | ||||||||||
| Paracentral lobule and sulcus | 0.900 | 0.911 | ||||||||||
| Postcentral sulcus | 0.892 | 0.886 | ||||||||||
| Sulcus intermedius primus (of jensen) | 0.702 | 0.839 | ||||||||||
| Superior part of the precentral sulcus | 0.786 | 0.963 | ||||||||||
| Subcentral gyrus (central operculum) and sulci | 0.829 | 0.953 | ||||||||||
| Sulci of the parietal lobe | 0.989 | 0.980 | 0.989 | 0.988 | Subparietal sulcus | 0.893 | 0.947 | |||||
| Intraparietal sulcus (interparietal sulcus) and transverse parietal sulci | 0.852 | 0.87 | ||||||||||
| Parieto‐occipital sulcus (or fissure) | 0.908 | 0.889 | ||||||||||
| Sulci of the occipital lobe | 0.988 | 0.988 | 0.965 | 0.966 | Middle occipital sulcus and lunatus sulcus | 0.851 | 0.819 | |||||
| Anterior occipital sulcus and preoccipital notch (temporo‐occipital incisure) | 0.743 | 0.644 | ||||||||||
| Superior occipital sulcus and transverse occipital sulcus | 0.956 | 0.779 | ||||||||||
| Calcarine sulcus | 0.892 | 0.702 | ||||||||||
| Lateral occipito‐temporal sulcus | 0.883 | 0.888 | ||||||||||
| Medial occipito‐temporal sulcus (collateral sulcus) and lingual sulcus | 0.849 | 0.907 | ||||||||||
| Sulci of the temporal lobe | 0.986 | 0.972 | 0.951 | 0.933 | Inferior temporal sulcus | 0.841 | 0.697 | |||||
| Superior temporal sulcus (parallel sulcus) | 0.963 | 0.862 | ||||||||||
| Transverse temporal sulcus | 0.775 | 0.746 | ||||||||||
| Posterior transverse collateral sulcus | 0.750 | 0.664 | ||||||||||
| Anterior transverse collateral sulcus | 0.897 | 0.945 | ||||||||||
| Horizontal ramus of the anterior segment of the lateral sulcus (or fissure) | 0.710 | 0.816 | ||||||||||
| Posterior ramus (or segment) of the lateral sulcus (or fissure) | 0.925 | 0.861 | ||||||||||
| Vertical ramus of the anterior segment of the lateral sulcus (or fissure) | 0.694 | 0.874 | ||||||||||
| Sulci of the cingulate gyrus | 0.985 | 0.977 | 0.939 | 0.927 | Marginal branch of the cingulate sulcus | 0.693 | 0.844 | |||||
| Pericallosal sulcus (of corpus callosum) | 0.599 | 0.827 | ||||||||||
| Sylvian fissure and anterior insular sulcus | 0.988 | 0.984 | 0.968 | 0.964 | Anterior segment of the circular sulcus of the insula | 0.814 | 0.854 | |||||
| Inferior segment of the circular sulcus of the insula | 0.944 | 0.878 | ||||||||||
| Superior segment of the circular sulcus of the insula | 0.910 | 0.841 | ||||||||||
| Sylvian fissure and posterior insular sulcus | 0.978 | 0.980 | 0.917 | 0.887 | Long insular gyrus and central sulcus of the insula | 0.735 | 0.558 | |||||
| Deep nucleae | Caudate nucleus | 0.986 | 0.991 | 0.990 | 0.994 | Caudate nucleus | 0.988 | 0.966 | ||||
| Globus pallidus | 0.928 | 0.943 | 0.960 | 0.970 | Pallidum | 0.863 | 0.868 | |||||
| Putamen | 0.973 | 0.975 | 0.990 | 0.993 | Putamen | 0.781 | 0.969 | |||||
| Thalamus | 0.959 | 0.953 | 0.990 | 0.985 | Thalamus | 0.901 | 0.851 | |||||
| Deep white matter | Genu of corpus callosum | 0.981 | 0.981 | 0.986 | 0.982 | Anterior corpus callosum | 0.87 | |||||
| Middle anterior corpus callosum | 0.975 | |||||||||||
| Body of corpus callosum | 0.990 | 0.982 | 0.989 | 0.986 | Central corpus callosum | 0.974 | ||||||
| Splenium of corpus callosum | 0.972 | 0.990 | 0.996 | 0.997 | Posterior corpus callosum | 0.849 | ||||||
| Middle posterior corpus callosum | 0.969 | |||||||||||
| Anterior limb of internal capsule | 0.963 | 0.962 | 0.987 | 0.974 | ||||||||
| Posterior limb of internal capsule | 0.930 | 0.937 | 0.971 | 0.981 | ||||||||
| Retrolenticular part of internal capsule | 0.946 | 0.940 | 0.968 | 0.967 | ||||||||
| External capsule | 0.934 | 0.955 | 0.980 | 0.980 | ||||||||
| Claustrum | 0.852 | 0.468 | 0.800 | 0.800 | ||||||||
| Posterior thalamic radiation | 0.936 | 0.965 | 0.996 | 0.992 | ||||||||
| Sagittal stratum | 0.970 | 0.959 | 0.100 | 0.990 | ||||||||
| Superior fronto‐occipital fasciculus | 0.766 | 0.766 | 0.816 | 0.776 | ||||||||
| Superior longitudinal fasciculus | 0.94 | 0.971 | 0.990 | 0.990 | ||||||||
| Inferior fronto‐occipital fasciculus | 0.937 | 0.948 | 0.960 | 0.967 | ||||||||
| Anterior corona radiata | 0.971 | 0.972 | 0.993 | 0.994 | ||||||||
| Posterior corona radiata | 0.910 | 0.939 | 0.978 | 0.985 | ||||||||
| Superior corona radiata | 0.912 | 0.932 | 0.990 | 0.985 | ||||||||
| Corticospinal tract | 0.927 | 0.932 | 0.919 | 0.918 | ||||||||
| Cerebral peduncle | 0.935 | 0.940 | 0.970 | 0.980 | ||||||||
| Lateral part of the periventricular white matter | 0.953 | 0.978 | 0.967 | 0.967 | ||||||||
| Fornix | 0.912 | 0.894 | 0.900 | 0.880 | ||||||||
| Fornix/stria terminalis | 0.939 | 0.787 | 0.942 | 0.953 | ||||||||
| Inferior cerebellar peduncle | 0.858 | 0.922 | 0.950 | 0.920 | ||||||||
| Middle cerebellar peduncle | 0.974 | 0.959 | 0.975 | 0.979 | ||||||||
| Superior cerebellar peduncle | 0.917 | 0.868 | 0.942 | 0.920 | ||||||||
| Pontine crossing tract | 0.735 | 0.803 | 0.869 | 0.888 | ||||||||
| Cerebellum gray matter | 0.997 | 0.997 | 0.954 | 0.906 | Cerebellum cortex | 0.944 | 0.959 | |||||
| Cerebellum white matter | 0.978 | 0.969 | 0.983 | 0.983 | Cerebellum white matter | 0.942 | 0.929 | |||||
Table 2.
ICCs for regional fractional anisotropy (FA) and mean diffusivity (MD), outputted by MRICloud, using Kirby21 and HCP
| MRICloud | Kirby 21 | HCP | ||||||
|---|---|---|---|---|---|---|---|---|
| ICC for FA | ICC for MD | ICC for FA | ICC for MD | |||||
| L | R | L | R | L | R | L | R | |
| Superior parietal gyrusa | 0.885 | 0.880 | 0.812 | 0.885 | 0.753 | 0.725 | 0.696 | 0.811 |
| Cingulate gyrusa | 0.808 | 0.709 | 0.878 | 0.938 | 0.804 | 0.796 | 0.800 | 0.824 |
| Superior frontal gyrusa | 0.925 | 0.850 | 0.901 | 0.856 | 0.796 | 0.669 | 0.489 | 0.474 |
| Middle frontal gyrusa | 0.842 | 0.809 | 0.883 | 0.788 | 0.798 | 0.635 | 0.432 | 0.625 |
| Inferior frontal gyrusa | 0.861 | 0.902 | 0.785 | 0.757 | 0.873 | 0.649 | 0.411 | 0.624 |
| Precentral gyrusa | 0.887 | 0.865 | 0.804 | 0.902 | 0.872 | 0.767 | 0.815 | 0.783 |
| Postcentral gyrusa | 0.959 | 0.928 | 0.918 | 0.894 | 0.712 | 0.735 | 0.774 | 0.816 |
| angular gyrusa | 0.774 | 0.863 | 0.726 | 0.883 | 0.732 | 0.710 | 0.691 | 0.773 |
| Precuneusa | 0.869 | 0.799 | 0.883 | 0.914 | 0.814 | 0.782 | 0.802 | 0.851 |
| Cuneusa | 0.907 | 0.764 | 0.832 | 0.777 | 0.851 | 0.756 | 0.795 | 0.822 |
| Lingual gyrusa | 0.625 | 0.691 | 0.655 | 0.753 | 0.762 | 0.715 | 0.615 | 0.744 |
| Fusiform gyrusa | 0.819 | 0.725 | 0.676 | 0.681 | 0.727 | 0.656 | 0.782 | 0.765 |
| Superior occipital gyrusa | 0.908 | 0.875 | 0.892 | 0.844 | 0.842 | 0.840 | 0.897 | 0.856 |
| Inferior occipital gyrusa | 0.825 | 0.839 | 0.506 | 0.740 | 0.825 | 0.707 | 0.855 | 0.769 |
| Middle occipital gyrusa | 0.888 | 0.841 | 0.785 | 0.795 | 0.821 | 0.723 | 0.869 | 0.829 |
| Superior temporal gyrusa | 0.416 | 0.604 | 0.623 | 0.727 | 0.851 | 0.714 | 0.775 | 0.776 |
| Inferior temporal gyrusa | 0.724 | 0.648 | 0.491 | 0.558 | 0.821 | 0.892 | 0.802 | 0.811 |
| Middle temporal gyrusa | 0.895 | 0.798 | 0.770 | 0.763 | 0.784 | 0.763 | 0.774 | 0.758 |
| Lateral fronto‐orbital gyrusa | 0.884 | 0.865 | 0.681 | 0.617 | 0.868 | 0.602 | 0.612 | 0.695 |
| Middle fronto‐orbital gyrusa | 0.786 | 0.787 | 0.512 | 0.406 | 0.713 | 0.785 | 0.687 | 0.635 |
| Supramarginal gyrusa | 0.896 | 0.937 | 0.875 | 0.885 | 0.876 | 0.770 | 0.766 | 0.794 |
| rectus gyrusa | 0.746 | 0.753 | 0.823 | 0.716 | 0.635 | 0.744 | 0.675 | 0.602 |
| Insulaa | 0.847 | 0.887 | 0.964 | 0.671 | 0.804 | 0.796 | 0.777 | 0.734 |
| Cerebellum | 0.790 | 0.901 | 0.936 | 0.901 | 0.813 | 0.750 | 0.733 | 0.751 |
| Corticospinal tract | 0.897 | 0.858 | 0.741 | 0.659 | 0.886 | 0.897 | 0.886 | 0.893 |
| Inferior cerebellar peduncle | 0.436 | 0.649 | 0.478 | 0.588 | 0.800 | 0.853 | 0.836 | 0.819 |
| Medial lemniscus | 0.735 | 0.626 | 0.621 | 0.595 | 0.927 | 0.912 | 0.831 | 0.749 |
| Superior cerebellar peduncle | 0.642 | 0.781 | 0.605 | 0.607 | 0.797 | 0.756 | 0.791 | 0.775 |
| Cerebral peduncle | 0.817 | 0.814 | 0.785 | 0.404 | 0.921 | 0.935 | 0.714 | 0.880 |
| Anterior limb internal capsule | 0.755 | 0.659 | 0.653 | 0.616 | 0.891 | 0.803 | 0.552 | 0.797 |
| Posterior limb internal capsule | 0.818 | 0.846 | 0.427 | 0.716 | 0.868 | 0.895 | 0.641 | 0.814 |
| Retro lenticular internal capsule | 0.790 | 0.875 | 0.525 | 0.811 | 0.897 | 0.831 | 0.711 | 0.739 |
| Posterior thalamic radiation | 0.848 | 0.863 | 0.692 | 0.869 | 0.892 | 0.907 | 0.829 | 0.758 |
| Anterior corona radiata | 0.952 | 0.902 | 0.774 | 0.625 | 0.873 | 0.810 | 0.424 | 0.634 |
| Superior corona radiata | 0.910 | 0.941 | 0.715 | 0.861 | 0.924 | 0.875 | 0.683 | 0.729 |
| Posterior corona radiata | 0.928 | 0.886 | 0.647 | 0.838 | 0.867 | 0.950 | 0.828 | 0.894 |
| Cingulum | 0.915 | 0.907 | 0.750 | 0.730 | 0.878 | 0.810 | 0.679 | 0.859 |
| Fornix stria terminalis | 0.805 | 0.843 | 0.808 | 0.707 | 0.841 | 0.818 | 0.677 | 0.815 |
| Superior longitudinal fasciculus | 0.879 | 0.926 | 0.544 | 0.772 | 0.879 | 0.876 | 0.586 | 0.707 |
| Superior fronto‐occipital fasciculus | 0.760 | 0.851 | 0.822 | 0.872 | 0.760 | 0.677 | 0.822 | 0.453 |
| Inferior fronto‐occipital fasciculus | 0.828 | 0.912 | 0.641 | 0.453 | 0.891 | 0.848 | 0.710 | 0.720 |
| Sagittal stratum | 0.889 | 0.861 | 0.588 | 0.823 | 0.819 | 0.786 | 0.665 | 0.756 |
| External capsule | 0.802 | 0.860 | 0.455 | 0.710 | 0.854 | 0.758 | 0.477 | 0.684 |
| Uncinated fasciculus | 0.638 | 0.936 | 0.696 | 0.767 | 0.807 | 0.881 | 0.785 | 0.811 |
| Pontine crossing tract | 0.723 | 0.882 | 0.693 | 0.602 | 0.881 | 0.905 | 0.858 | 0.866 |
| Middle cerebellar peduncle | 0.677 | 0.775 | 0.312 | 0.284 | 0.829 | 0.757 | 0.845 | 0.864 |
| Fornix | 0.893 | 0.718 | 0.946 | 0.703 | 0.774 | 0.875 | 0.602 | 0.676 |
| Genu corpus callosum | 0.896 | 0.923 | 0.574 | 0.617 | 0.901 | 0.850 | 0.554 | 0.641 |
| Body of the corpus callosum | 0.878 | 0.914 | 0.922 | 0.830 | 0.898 | 0.900 | 0.598 | 0.828 |
| Splenium corpus callosum | 0.880 | 0.919 | 0.736 | 0.894 | 0.866 | 0.920 | 0.686 | 0.770 |
Abbreviations: HCP, Human Connectome Project; ICC, intraclass correlation coefficients.
White matter labels beneath the gray matter.
Table 3.
Averaged ICCs of seed‐by‐seed correlations outputted by the rsfMRI processed with MRICloud (using Kirby21 and HCP) and SPM CONN (using Kirby21)
| Structure | ICC for Mricloud | ICC for SPM CONN | ||||
|---|---|---|---|---|---|---|
| Kirby 21 | HCP | Kirby 21 | ||||
| L | R | L | R | L | R | |
| Angular gyrus | 0.387 | 0.376 | 0.482 | 0.527 | 0.155 | 0.264 |
| Cuneus | 0.433 | 0.438 | 0.392 | 0.417 | 0.153 | 0.080 |
| Fusiform gyrus | 0.342 | 0.419 | 0.253 | 0.339 | 0.163 | 0.249 |
| Rectus gyrus | 0.384 | 0.340 | 0.444 | 0.458 | 0.150 | 0.077 |
| Inferior frontal gyrus/pars opercularis | 0.243 | 0.369 | 0.470 | 0.432 | 0.228 | 0.238 |
| Inferior frontal gyrus/pars orbitalis | 0.283 | 0.413 | 0.417 | 0.449 | 0.092 | 0.208 |
| Inferior frontal gyrus/pars triangularis | 0.302 | 0.367 | 0.350 | 0.442 | 0.183 | 0.103 |
| Inferior occipital gyrus | 0.356 | 0.355 | 0.381 | 0.396 | 0.156 | 0.282 |
| Inferior temporal gyrus | 0.329 | 0.387 | 0.362 | 0.446 | 0.130 | 0.107 |
| Lingual gyrus | 0.374 | 0.394 | 0.334 | 0.304 | 0.219 | 0.150 |
| Middle frontal gyrus | 0.317 | 0.418 | 0.435 | 0.532 | 0.270 | 0.216 |
| Middle frontal gyrus (dorsolateral prefrontal cortex) | 0.258 | 0.378 | 0.421 | 0.460 | 0.124 | 0.216 |
| Middle occipital gyrus | 0.332 | 0.447 | 0.342 | 0.338 | 0.189 | 0.246 |
| Middle temporal gyrus | 0.323 | 0.400 | 0.443 | 0.446 | 0.276 | 0.129 |
| Middle temporal gyrus/pole | 0.402 | 0.337 | 0.465 | 0.397 | 0.116 | 0.025 |
| Postcentral gyrus | 0.388 | 0.380 | 0.327 | 0.366 | 0.176 | 0.166 |
| Posterior cingulate cortex | 0.363 | 0.364 | 0.385 | 0.189 | 0.147 | 0.213 |
| Precentral gyrus | 0.424 | 0.378 | 0.333 | 0.393 | 0.223 | 0.164 |
| Precuneus | 0.425 | 0.443 | 0.412 | 0.386 | 0.135 | 0.270 |
| Superior frontal gyrus | 0.372 | 0.406 | 0.415 | 0.444 | 0.133 | 0.185 |
| Superior frontal gyrus/pole | 0.413 | 0.416 | 0.280 | 0.388 | 0.012 | 0.000 |
| Superior frontal gyrus/prefrontal cortex | 0.356 | 0.328 | 0.431 | 0.469 | 0.195 | 0.202 |
| Superior occipital gyrus | 0.425 | 0.434 | 0.030 | 0.188 | 0.253 | 0.204 |
| Superior parietal lobule | 0.284 | 0.261 | 0.387 | 0.366 | 0.229 | 0.128 |
| Superior temporal gyrus | 0.364 | 0.350 | 0.333 | 0.383 | 0.240 | 0.178 |
| Superior temporal gyrus/pole | 0.413 | 0.391 | 0.456 | 0.399 | 0.171 | 0.185 |
| Supramarginal gyrus | 0.316 | 0.382 | 0.445 | 0.437 | 0.233 | 0.178 |
Abbreviations: HCP, Human Connectome Project; ICC, intraclass correlation coefficients.
3.2.2. T1‐WIs volumetric analysis with FreeSurfer
Volumes of Kirby21 cortical labels and the deep gray matter were obtained from FreeSurfer v.5.3, for further comparison of reliability with MRICloud. Briefly, images are aligned to the Talairach and Tournoux atlas, corrected for magnetic field inhomogeneity, skull‐stripped, and the tissues are classified as gray matter, white matter, or CSF. Next, the white surface (the interface between gray and white matter) and the pial surfaces are estimated by triangle meshes and smoothed with a Gaussian filter of 10 mm FWHM (Fischl & Dale, 2000). Cortical thickness is calculated as the shortest distance between the pial and white surface at each vertex across the cortical mantle. The cortical volume is the multiplication of cortical thickness and surface area. The volumes for subcortical regions are calculated as well (Fischl et al., 2002). For comparison of reliability, we determined the correspondence between MRICloud and FreeSurfer labels (listed in Table 1), which is feasible since both methods label according to structural anatomy.
3.2.3. rsfMRI analysis with SPM CONN toolbox
We used the SPM CONN toolbox, version 17e, to preprocess and perform first‐level statistics of Kirby21 rsfMRI data, and further compared the reliability of these results with those from MRICloud. The CONN toolbox is the most widely used tool for processing rsfMRI and uses a combination of SPM12 and native‐implemented functions. The preprocessing was attuned to keep the rsfMRI in the native space and used the default CONN parameters for slice‐time correction and realignment. As in the MRICloud pipeline, ART identified the outlier scans (97th percentiles in a normative sample). The effect of the rest model and its first‐order derivative were used as first‐level covariates (individual regressors). Sequentially, the processed functional images were detrended and band‐pass‐filtered (0.008–0.09 Hz). After tissue segmentation and skull‐stripping, the T1‐WIs and the respective parcellation maps obtained from MRICloud were brought to the rsfMRI space. The use of the same anatomic labels enabled a direct comparison between SPM CONN and MRICloud seed‐by‐seed correlations.
Although there are descriptions of automated white matter parcellations using cortical‐parcellation‐based strategies and fiber clustering parcellation (Zhang et al., 2019), to the best of our knowledge, MRICloud is the only automated pipeline available for whole‐brain, DTI structure‐based analysis. Therefore, the reproducibility of DTI regional quantification outputted from MRICloud was not directly compared with that from other software.
3.3. Statistical analysis
3.3.1. Test–retest reproducibility
To assess the test–retest reliability of the different metrics in each region of interest, we used the intraclass correlation coefficient (ICC) (Shrout & Fleiss, 1979). To access a global measure of the reproducibility for a given modality, we used the image intraclass correlation coefficient (I2C2) (Shou et al., 2013), which takes in account the total variability of the data. Because I2C2 is less sensitive to regions with low variability, it tends to be lower, and more realistic, than the average of regional ICCs.
A problem that cannot be intuitively solved by looking at I2C2 or ICCs is whether the global individual pattern of image features is reproducible. This “fingerprint” problem has recently been explored in neuroimaging (Finn et al., 2015; Liu, Liao, Xia, & He, 2018; Mars et al., 2018). Assuming that the MRI data itself are reproducible (which is a valid assumption for structural data, such as T1‐based volumes), if the postprocessing and quantification tool is reliable, a given individual will be closer to him/herself rather than to someone else in the space of the image features.
In order to explore this idea, we used principal component analysis (PCA) to reduce the dimensionality of the data in each modality. The first three principal components, which are linear combinations of the features in question, are those that explain most of the data variability. The distances across different subjects in the 3D PCA plots (indicated by circles with different colors in our figures) reflect anatomical variability among normal brains, as well as the measurement variability. Through the test–retest pairs (indicated by circles of same colors in our figures), one can estimate the size of the measurement variability, that is, the precision of the measurement, with respect to the anatomical variability of the population. We also ranked the Euclidean distance among subjects in the three‐dimensional PCA space. The lowest rank of 1 represents a pair of individuals that are closest in the feature space (i.e., a pair with the lowest variability). If the measurement variability is lower than the anatomical variability, a test–retest pair has a low score, ideally, 1. We judged “correct classification” when the two closest neighbors were the first and second scans of the same subject (the “test–retest” pair), and “misclassification” otherwise.
Finally, we checked for significant differences in the diverse metrics between groups (test and retest) using Wilcoxon, corrected for multiple comparisons with false discovery rate. We also calculated the percentage of difference between the test and retest metrics, as ([test metric + retest metric]/test metric) * 100. Furthermore, although this study is not designed to test the reliability of the segmentation itself, we calculated the Dice index between each pair (test–retest) of parcels obtained by the T1 and DTI processing in MRICloud, as a sanity check. Note that the Dice was the only metric calculated not in the native space, but in a MNI space, to ameliorate differences in the head position between the test–retest scans.
3.3.2. Power analysis: illustrating the effect of the data variability
Power analysis was used to illustrate the effects of data variability (both biological and technical) on the automated imaging quantification. For a proof of concept, we chose two regions (one with a large ICC and the other with a low ICC), from the volumetric T1‐based analysis and from the DTI analysis. We calculated the sample size necessary to detect group differences at an alpha of 0.05 and a power of 0.8, using GPOWER (http://www.gpower.hhu.de/). The sample size that resulted was inversely proportional to the data variability, which was inversely proportional to the ICC.
4. RESULTS
4.1. Volumetric (T1‐based) test–retest reliability
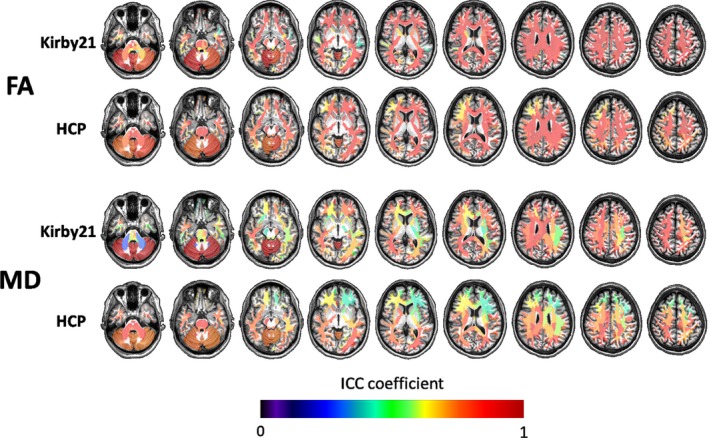
The global I2C2 coefficients for the MRICloud volumetric analysis were very high (1 indicating perfect agreement): HCP dataset: 0.989 (confidence interval, CI: 0.987–0.992) and 0.936 (CI: 0.870–0.998), Kirby21 dataset: 0.988 (CI: 0.982–0.991) and 0.997 (CI: 0.995–0.999), for the cerebral cortex and deep gray matter, respectively (Figure 1). The ROIs showed consistently high ICCs (Table 1, Figure 2), including those in the white matter, which we were able to obtain because MRICloud performs whole‐brain parcellation. Only a few small parcels, primarily in the brainstem, had ICCs below 0.9, and no region had an ICC below 0.8.
Figure 1.

I2C2 for the results of T1‐volumetric analysis, fractional anisotropy (FA), and mean diffusivity (MD) from DTI, and resting‐state fMRI, in two independent datasets (Kirby21 and HCP), using different platforms (MRICloud [MC], FreeSurfer [FS], Connectivity toolbox in SPM [CONN‐SPM])
Figure 2.

Color‐coded regional ICCs for the volumetric outputs of MRICloud (MC) and FreeSurfer (FS), in two independent datasets (Kirby21 and HCP), overlaid on a representative brain
Compared to MRICloud, the I2C2s for Kirby21 were slightly lower for the FreeSurfer results: 0.920 (CI: 0.871–0.951) for the cerebral cortex and 0.967 (CI: 0.933–0.988) for the deep gray matter. The regional ICCs were also lower, in general (Figure 2, bottom), with a few regions, particularly at the deep gray matter, showing an ICC of approximately 0.8.
The three‐dimensional PCA plot (Figure 3, top) for Kirby21 data shows that the measurement variability was higher for the results of FreeSurfer (average Euclidian distance between the test–retest pair 0.043 ± 0.025) compared to those from MRICloud (average Euclidian distance between the test–retest pair 0.016 ± 0.007 for Kirby21 and 0.016 ± 0.010 for HCP), while still lower than that of the anatomical variability in both cases. Similar results were obtained using the deep gray matter volumes (Figure 4, top). Again, the measurement variability for deep gray matter volumes was higher for the results of FreeSurfer (average Euclidian distance between the test–retest pair 0.042 ± 0.033) compared to those from MRICloud (average Euclidian distance between the test–retest pair 0.028 ± 0.017 and 0.028 ± 0.073 for Kirby21 and HCP respectively), while still lower than that of the anatomical variability in both cases.
Figure 3.
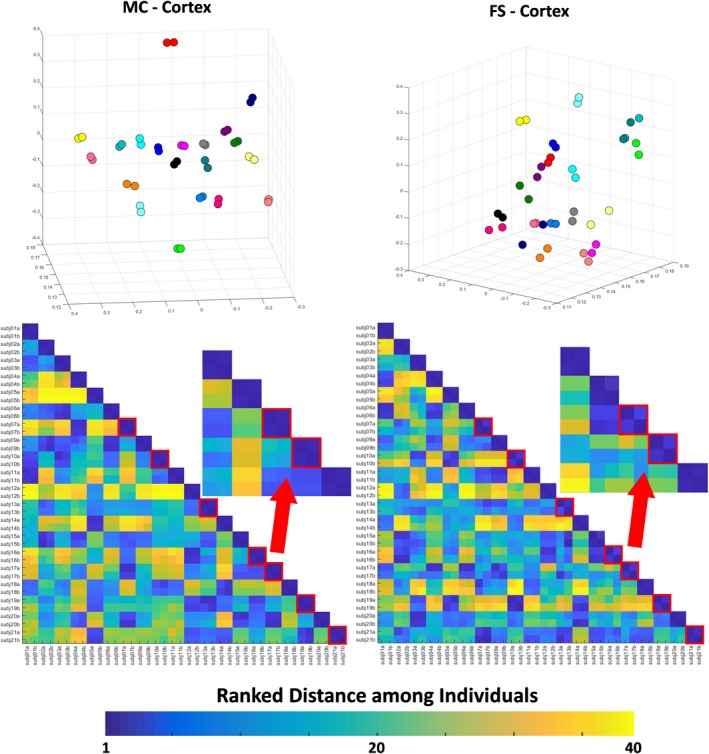
Top: 3D PCA plot created with the volumes of Kirby21 cortical areas, outputted by MRICloud (MC) and FreeSurfer (FS). Individuals are color‐coded, that is, the same color represents a “test–retest” pair. Bottom: matrix of ranked distance between individuals in the three‐dimensional PCA plot. If the variance in the measurement between scan sections was minimal, a test–retest pair was scored 1 (dark blue). Test–retest pairs that scored higher than 1 (i.e., the individual was closer to someone else rather than him/herself in the second scan) are framed in red
Figure 4.

Top: 3D PCA plot created with the volumes of the Kirby21 deep gray matter areas, outputted by MRICLoud (MC) and FreeSurfer (FS). Individuals are color‐coded; that is, the same color represents a “test–retest” pair. Bottom: matrix of ranked distance between individuals in the three‐dimensional PCA plot. If the variance in the measurement between scan sections was minimal, a test–retest pair was scored 1 (dark blue). Test–retest pairs that scored higher than 1 (i.e., the individual was closer to someone else rather than to him/herself in the second scan) are framed in red
This idea was reinforced by the ranked distance matrix (Figures 3 and 4, bottom). For the results of MRICloud, individuals in the test–retest pair were always the closest (ranked distance of 1) when using cortical volumes (Figure 3, bottom right), or almost always the closest (except by one case), when using the deep gray matter volumes (Figure 4, bottom right). There were 7 “misclassifications” (i.e., the closest individual in the first scan was not him/herself in the second scan) when using the volumetric results of FreeSurfer, both for the superficial and for the deep gray matter (Figures 3 and 4, bottom left).
There were no significant differences in regional volumes, as outputted by MRICloud, between the test and the retest sets. The average difference between the test and retest volumes was 1.76% for Kirby21, and 2.8% for HCP. The Dice indices between pairs (test–retest) of parcels were high 0.814 ± 0.141 for Kirby21 and 0.8 ± 0.097 for HCP.
4.2. DTI test–retest reliability
The global I2C2 coefficients for the MRICloud analysis of the fractional anisotropy (FA) and mean diffusivity (MD) were as follows: Kirby21: 0.836 (CI: 0.798–0.869) and 0.787 (CI: 0.735–0.851), respectively; HCP: 0.844 (CI: 0.751–0.892) and 0.733 (CI: 0.666–0.793), respectively (Figure 1). The regional ICCs (Table 2, Figure 5) were higher for FA than for MD. The FA ICCs were virtually higher than 0.8, while, for MD, a few regions scored below this level, particularly in the brainstem. In contrast to the volumetric analysis, there was more variation on the ICCs, with some areas scoring high (ICC > 0.9) and others low (ICC < 0.5).The cerebellar peduncles had the lowest ICCs.
Figure 5.
Color‐coded regional ICCs for the DTI outputs of MRICloud (FA, fractional anisotropy, MD, mean diffusivity) in two independent datasets (Kirby21 and HCP), overlaid on a representative brain
Although higher than in the volumetric analysis, the measurement variability for Kirby21 FA and MD (the distance between the rest–retest individuals, or dots with the same color in the PCA plots of Figure 6) was, on average, lower than the anatomical variability (the distance among different individuals). The measurement variability was higher for MD (average Euclidian distance between the test–retest pair 0.147 ± 0.079 and 0.119 ± 0.072 for Kirby21 and HCP, respectively) than for FA (average Euclidian distance between the test–retest pair 0.060 ± 0.039 and 0.057 ± 0.032 for Kirby21 and HCP, respectively). Again, the ranked distance matrices offered a different view of the same findings. Using the FA metrics, individuals in a test–retest pair were the closest (ranked distance of 1) in the majority of cases (Figure 6, bottom right), although there were 9 “misclassifications” (i.e., the closest individual in the first scan was not him/herself in the second scan). Using MD, individuals in the test–retest pair were often not the closest (Figure 6, bottom left, 19 “misclassifications”).
Figure 6.
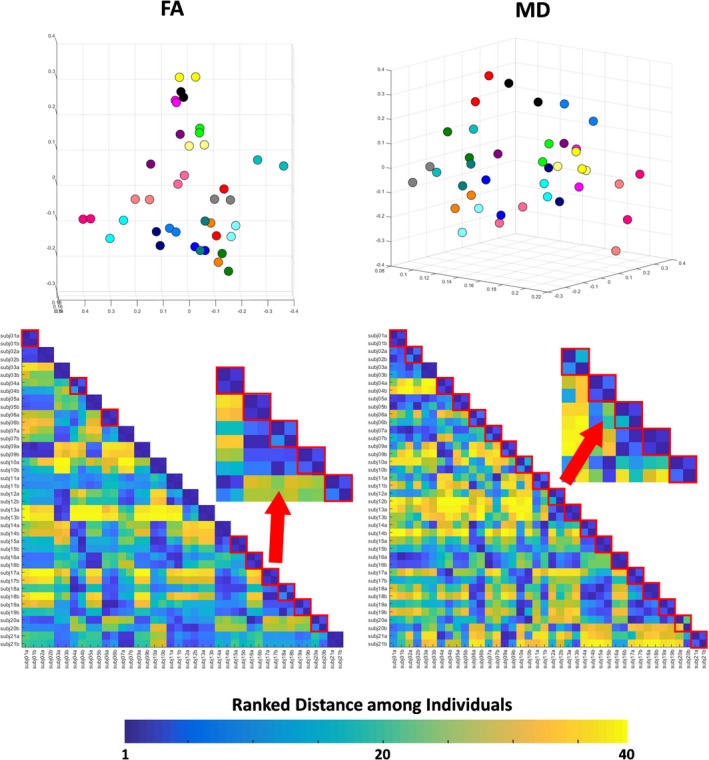
Top: 3D PCA plot created with the Kirby21 regional measures of fractional anisotropy (FA) and mean diffusivity (MD). Individuals were color‐coded; that is, the same color represents a “test–retest” pair. Bottom: matrix of ranked distance between individuals in the three‐dimensional PCA plot. If the variance in the measurement between scan sections was minimal, a test–retest pair scored 1 (dark blue). Test–retest pairs that scored higher than 1 (i.e., the individual was closer to someone else rather than to him/herself in the second scan) are framed in red
There was no significant difference in FA or MD between the test and the retest sets. The difference between the test and retest metrics was 0.64% for FA and 1.79% for MD, in Kirby21, and 0.5% for FA and 1.9% for MD, in HCP. The Dice indices between pairs (test–retest) of parcels were high (0.896 ± 0.05 and 0.838 ± 0.066 for Kirby21 and HCP, respectively).
4.3. rsfMRI test–retest reliability
The rsfMRI showed the lowest global I2C2 and regional ICCs among all the tested modalities. The global I2C2 for the MRICloud outputs (z‐transformed correlation among pairs of cortical seeds) was 0.437 (CI: 0.337–0.530) in HCP and 0.403 (CI: 0.309–0.507) in Kirby21. For the SPM CONN outputs, the I2C2 was 0.227 (CI: 0.164–0.293) in Kirby21 (Figure 1). The ICC for a given label was calculated as the mean of the ICCs for correlations between that given seed to each other seed (Table 3). The maximum ICC for a parcel using the MRICloud outputs did not exceed 0.6, with the majority of ICCs fluctuating around 0.4 (Figure 7). For the SPM CONN processing, the maximum ICC did not exceed 0.5, with the majority of ICCs fluctuating around 0.25.
Figure 7.
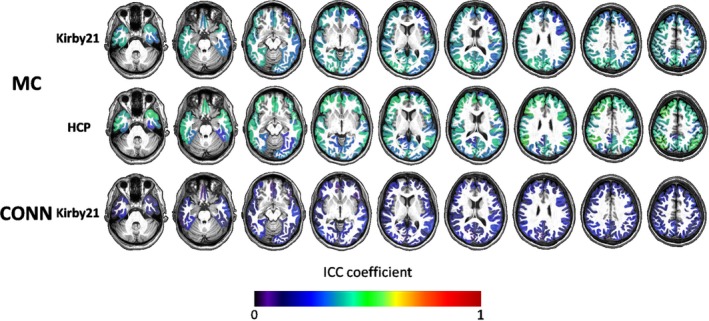
Color‐coded regional mean ICCs for the resting‐state fMRI outputs of MRICloud (MC) and CONN‐SPM, in two independent datasets (Kirby21 and HCP), overlaid on a representative brain, overlaid on a representative brain
The measurement variability, or the distance among test–retest pairs (same color dots) in the PCA plots created with the pairwise z‐rsfMRI correlations (Figure 8, top), was lower, on average, than the anatomical/functional variability, or the distance among different individuals, although the variability was seemingly higher than that obtained for volumes or DTI metrics.The ranked distance among Kirby21 individuals (Figure 8, bottom) showed predominantly “misclassifications” (the closest individual in the first scan was not him/herself in the second scan): 15 for MRICloud, 15 for CONN‐SPM. The individual variability was still lower for MRICloud (average Euclidian distance between the test–retest pair 0.163 ± 0.093 and 0.134 ± 0.090 for Kirby21 and HCP, respectively) compared to CONN‐SPM (average distance between the test–retest pair 0.175 ± 0.131).
Figure 8.

Top: 3D PCA plot created with z‐transformed correlations between the Kirby21 fMRI time courses of a pair of seeds, outputted by MRICloud (MC) and SPM CONN. Individuals were color‐coded, that is, the same color represents a “test–retest” pair. Bottom: matrix of ranked distance between individuals in the three‐dimensional PCA plot. If the variance in the measurement between scan sections was minimal, a test–retest pair scored 1 (dark blue). Test–retest pairs that scored higher than 1 (i.e., the individual was closer to someone else rather than to him/herself in the second scan) are framed in red
There were no significant differences in the outputs of MRICloud between the test and the retest sets.
4.4. Power
The power analysis illustrated the effects of data variability on the automated imaging quantification. For proof of concept, we chose regions with the highest and the lowest test–retest reliability, as measured by ICCs. The power analysis (Table 4) showed that the volumetric data were very stable, meaning that there is a small effect size among scan sets and that thousands of subjects would be needed to detect differences between them. The results are even more drastic for regions with a high ICC (e.g., precentral gyrus > globus pallidus). For the DTI analysis, here represented by the fractional anisotropy, the results were the same for highly reproducible areas (e.g., projection fibers at the pons level), namely, a small effect size between examinations, and a large sample needed to detect differences between them. However, as the range of ICCs was wider compared to volumes in areas with low ICCs (e.g., inferior cerebellar peduncle), the effect size between scans was relatively high (0.69) and less than 100 patients would be needed to detect differences between the scan sets. As this uses a test–retest design, these differences are technical, rather than biological.
Table 4.
Power analysis illustrated for regions with high and low ICCs in the T1‐volumetric analysis and DTI quantification performed with MRICloud
| T1‐based volumes | Fractional anisotropy (FA) – DTI | |
|---|---|---|
| High ICC area |
Precentral (ICC = 0.99) d = 0.04/n = 20,260 |
Projection fibers at pons level (ICC = 0.89) d = 0.1/n = 3,234 |
| Low ICC area |
Globus pallidus (ICC = 0.92) d = 0.06/n = 8,072 |
Inferior cerebellar peduncle (ICC = 0.43) d = 0.69/n = 70 |
Abbreviations: DTI, diffusion tensor images; ICC, intraclass correlation coefficients.
5. DISCUSSION
We test–retested an automated web‐based tool (MRICloud) that performs segmentation and quantification of multimodality MRI (volume from T1‐WIs and FA, and MD from DTI and rsfMRI seed‐by‐seed synchrony). The reproducibility rivaled, or was slightly superior, to that from other well‐established methods (FreeSurfer, SPM CONN). As discussed in detail below, the reproducibility was (a) globally very high for T1‐volumetric analysis; (b) high for DTI analysis, but regionally more variable than for T1‐volumetric analysis; and (c) globally low for rsfMRI. To shed light on the reproducibility of postprocessing and quantification tools for MRI is essential, particularly when, by their nature (automated, user‐friendly), these tools are used for processing data on a large scale.
5.1. Reproducibility of volumetric quantification
The I2C2 and the regional ICCs were high for the volumetric analysis (vast majority > 0.9, while perfect agreement is 1), reflecting the high stability of the volumetric data and suggesting that subtle differences appointed by them are reliable (Wonderlick et al., 2009). Although we observed a tendency of small areas to have lower ICCs than large areas, the small variation of ICCs prevented the determination of a significant relationship between the ROI volume and the respective reproducibility of its volume measures. We found reproducibility similar to that in previous studies for data processed with FreeSurfer (Morey et al., 2010; Wonderlick et al., 2009) using different scanners, inclusion criteria, scan–rescan intervals, and software versions, indicating that the stability of T1‐based volumetric analysis overcomes all these factors.
Both MRICloud and FreeSurfer had extremely high ICCs for volumetric analysis (0.98 vs. 0.92), which indicates very high reproducibility, suggesting both methods perform adequately in anatomically normal data. Nevertheless, understanding the source of ICCs variability can lead to improvements in data postprocessing by identifying factors (such as the parcellation scheme, mapping algorithm or set of atlases) that may impact reproducibility. For instance, MRICloud uses diffeomorphic mapping (LDDMM) and multiple atlases, with a large range of anatomical variability. This makes the method effective on both normal brains and brains with a large range of nonlocalized deformations (“atrophy‐like”), while methods that assume a stable, healthy pattern may perform worse on these scenarios {Oishi, 2009 #1831}. This is illustrated in Figure 9, where MRICloud outputted a qualitatively reasonable segmentation for an individual with marked brain atrophy, due to hereditary spastic paraplegia type 11.
Figure 9.
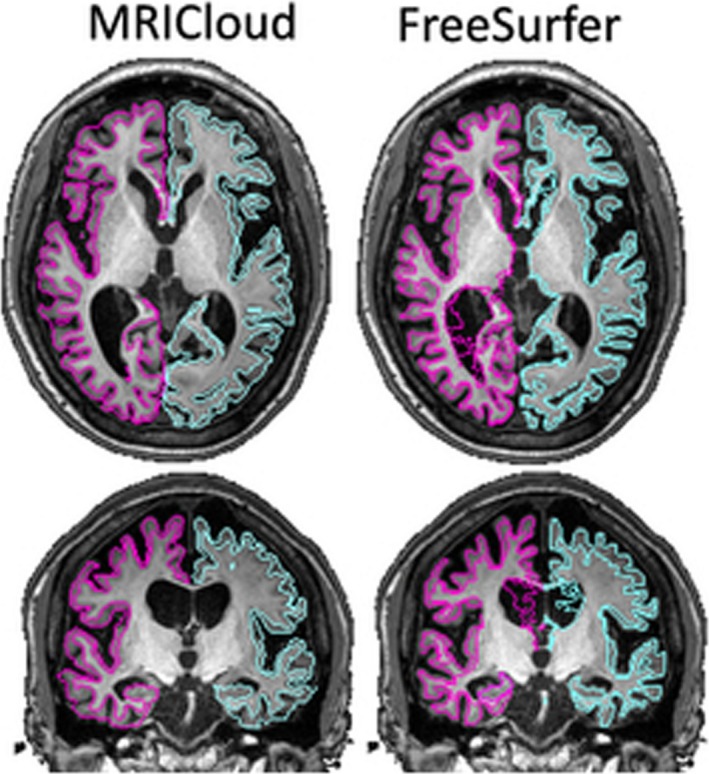
Segmentation of cortex and white matter outputted from MRICloud (left) and FreeSurfer (right) of a brain with large degree of atrophy
5.2. Reproducibility of DTI results
The I2C2s for DTI‐derived data, processed with MRICloud, were high, while lower than those from the volumetric analysis. Although most of the previous studies looked at DTI reliability on different scans and/or from multiple centers (Deprez et al., 2018; Fox et al., 2012; Jovicich et al., 2014), a few previous studies that addressed test–retest reproducibility (Huang et al., 2012; Shou et al., 2013; Zhang et al., 2019) found results comparable to ours. DTI‐derived metrics are calculated from multiple images and, thus, are inherently more noisy and affected by coregistration errors and other types of stability‐related issues (Morey et al., 2010). In addition, DTI is highly prone to voxel‐level motion of the subject, which would lead to various types of intensity‐modulating artifacts (Alexander, Lee, Wu, & Field, 2006; Ni, Kavcic, Zhu, Ekholm, & Zhong, 2006). Finally, a long retest interval may introduce technical and biological effects in the test retest analysis, which may partially explain the slightly lower DTI reproducibility we found for HCP, compared to Kirby21.
Regionally, we found more variation in the DTI ICCs than in the volumetric ICCs. Again, small parcels, which are more susceptible to noise and partial volume effects (Deprez et al., 2018; Vollmar et al., 2010), and parcels in the extremes of the sample (e.g., brainstem, extreme frontal and occipital areas), where the mapping is more challenging, tended to have lower ICCs. In addition, labels with a clearly predominant direction of fibers (high FA) tended to have high ICC, which was corroborated by the observed higher reducibility for an anisotropic phantom compared to human subjects (Morey et al., 2010). This has to be taken in account when planning or interpreting the results of clinical studies. Since DTI measures experience large variability, their sensitivity to detect biological effects may be low. For instance, our power analysis revealed that, while the scan session has a very small effect size in the volumetric analysis (and thousands of subjects would be needed to detect volumetric differences), the effect size of different sessions is much higher for FA, and less than hundred subjects would be needed to detect a significant difference between scan sessions for the same individuals, in areas of low ICC. Therefore, group differences in DTI metrics must be carefully evaluated depending on effect size, location, and related technical conditions.
Despite the lower reproducibility of DTI compared to T1 volumetric data analysis, the regional ICCs were, in general, high, and the measurement variance was still lower than that of the population variance (the distance between rest–retest pairs was lower than the distance among difference subjects, as demonstrated in Figure 6), revealing that MRICloud is a reasonably stable tool.
5.3. Reproducibility of rsfMRI results
The I2C2s for rsfMRI data, processed with MRICloud, were lower than those for volumetric and DTI data; the averaged ICCs for the regional correlations among seeds fluctuated around 0.4. Although there are a few reports of higher ICCs, the majority of previous studies that addressed the reproducibility of rsfMRI across individuals are in agreement with our findings (Andellini, Cannata, Gazzellini, Bernardi, & Napolitano, 2015; Deprez et al., 2018; Huang et al., 2012; Shou et al., 2013). As for the DTI data, but on larger scale, the (well‐known) rsfMRI low reproducibility is attributed not only to the postprocessing (which is extremely variable in methodology), but also to the actual nature of the sequence (Birn et al., 2013; Noble et al., 2017; Patriat et al., 2013). For instance, here we found reproducibility slightly superior for HCP data than for Kirby21. HCP has more frames per run and higher resolution that Kirby21, which may have contributed to the observed difference. Multiple technical factors (magnetic fields, sequence artifacts, motion) and biological conditions (physical and mental states, even in healthy individuals) contribute to data variability, some with a biologically relevant effect, and others as just noise (Airan et al., 2016; Kelly, Biswal, Craddock, Castellanos, & Milham, 2012). To isolate and quantify the contribution of each of these factors is one of the biggest challenges in the field and is not within the scope of this study.
We found that the reproducibility of the outputs of MRICloud is comparable, and slightly higher, to that obtained using SPM CONN. As the parcellation scheme applied in both methods is the same, as well as most of the postprocessing steps (slice‐time correction, coregistration, motion correction, outlier rejection, nuisance correction, etc.), the differences in the reproducibility are likely attributable to methodological differences in the image mapping. Likewise in the T1‐volumetric analysis, while this seems to have low influence in anatomical normal data, the differences in mapping may affect anatomically abnormal data differently and the indices of reliability may present a great variation, both absolutely and comparatively, among methods.
6. CONCLUSION
We tested–retested the reproducibility of MRICloud, a free, automated method for multimodal MRI segmentation and quantification, on two public, independent datasets. The reproducibility was extremely high for T1‐volumetric analysis, high for DTI (however, regionally variable), and low for resting‐state fMRI. The reproducibility for T1‐volumetric analysis and rsfMRI slightly over performed that of widely used software. The knowledge about the global reproducibility of each modality pipeline, as well as the regional reproducibility for each label, is essential for both study planning and data interpretation and is in line with the efforts to increase reproducibility and transparence in science.
CONFLICT OF INTEREST
None declared.
Supporting information
ACKNOWLEDGMENTS
The authors would like to thank Dr. Martin Lindquist for his statistical advice. This project was supported by FAPESP (2107/13102‐7, 2013/07559‐3), by the National Institute of Neurological Disorders and Stroke (R01 NS084957), and by the National Center for Research Resources and the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health (P41 EB015909). Data were provided [in part] by the Human Connectome Project, WU‐Minn Consortium (principal investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
Rezende TJR, Campos BM, Hsu J, et al. Test–retest reproducibility of a multi‐atlas automated segmentation tool on multimodality brain MRI. Brain Behav. 2019;9:e01363 10.1002/brb3.1363
DATA AVAILABILITY STATEMENT
The data analyzed in this study are publicly available as Tables [Link], [Link], [Link].
REFERENCES
- Airan, R. D. , Vogelstein, J. T. , Pillai, J. J. , Caffo, B. , Pekar, J. J. , & Sair, H. I. (2016). Factors affecting characterization and localization of interindividual differences in functional connectivity using MRI. Human Brain Mapping, 37, 1986–1997. 10.1002/hbm.23150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander, A. L. , Lee, J. E. , Wu, Y. C. , & Field, A. S. (2006). Comparison of diffusion tensor imaging measurements at 3.0 T versus 1.5 T with and without parallel imaging. Neuroimaging Clinics of North America, 16, 299–309. [DOI] [PubMed] [Google Scholar]
- Andellini, M. , Cannata, V. , Gazzellini, S. , Bernardi, B. , & Napolitano, A. (2015). Test‐retest reliability of graph metrics of resting state MRI functional brain networks: A review. Journal of Neuroscience Methods, 253, 183–192. 10.1016/j.jneumeth.2015.05.020 [DOI] [PubMed] [Google Scholar]
- Avants, B. B. , Tustison, N. J. , Song, G. , Cook, P. A. , Klein, A. , & Gee, J. C. (2011). A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage, 54, 2033–2044. 10.1016/j.neuroimage.2010.09.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behzadi, Y. , Restom, K. , Liau, J. , & Liu, T. T. (2007). A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. NeuroImage, 37, 90–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn, R. M. , Molloy, E. K. , Patriat, R. , Parker, T. , Meier, T. B. , Kirk, G. R. , … Prabhakaran, V. (2013). The effect of scan length on the reliability of resting‐state fMRI connectivity estimates. NeuroImage, 83, 550–558. 10.1016/j.neuroimage.2013.05.099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceritoglu, C. , Oishi, K. , Li, X. , Chou, M. C. , Younes, L. , Albert, M. , … Mori, S. (2009). Multi‐contrast large deformation diffeomorphic metric mapping for diffusion tensor imaging. NeuroImage, 47, 618–627. 10.1016/j.neuroimage.2009.04.057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deprez, S. , de Ruiter, M. B. , Bogaert, S. , Peeters, R. , Belderbos, J. , De Ruysscher, D. , … Achten, E. (2018). Multi‐center reproducibility of structural, diffusion tensor, and resting state functional magnetic resonance imaging measures. Neuroradiology, 60, 617–634. 10.1007/s00234-018-2017-1 [DOI] [PubMed] [Google Scholar]
- Faria, A. V. , Joel, S. E. , Zhang, Y. , Oishi, K. , van Zjil, P. C. , Miller, M. I. , … Mori, S. (2012). Atlas-based analysis of resting-state functional connectivity: Evaluation for reproducibility and multi-modal anatomy-function correlation studies. NeuroImage, 61, 613–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faria, A. V. , Liang, Z. , Miller, M. I. , & Mori, S. (2017). Brain MRI pattern recognition translated to clinical scenarios. Frontiers in Neuroscience, 11, 578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn, E. S. , Shen, X. , Scheinost, D. , Rosenberg, M. D. , Huang, J. , Chun, M. M. , … Constable, R. T. (2015). Functional connectome fingerprinting: Identifying individuals using patterns of brain connectivity. Nature Neuroscience, 18, 1664–1671. 10.1038/nn.4135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl, B. (2012). FreeSurfer. NeuroImage, 62, 774–781. 10.1016/j.neuroimage.2012.01.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl, B. , & Dale, A. M. (2000). Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences of the USA, 97, 11050–11055. 10.1073/pnas.200033797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl, B. , Salat, D. H. , Busa, E. , Albert, M. , Dieterich, M. , Haselgrove, C. , … Dale, A. M. (2002). Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron, 33, 341–355. 10.1016/S0896-6273(02)00569-X [DOI] [PubMed] [Google Scholar]
- Fox, R. J. , Sakaie, K. , Lee, J. C. , Debbins, J. P. , Liu, Y. , Arnold, D. L. , … Fisher, E. (2012). A validation study of multicenter diffusion tensor imaging: Reliability of fractional anisotropy and diffusivity values. AJNR American Journal of Neuroradiology, 33, 695–700. 10.3174/ajnr.A2844 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han, X. , Jovicich, J. , Salat, D. , van der Kouwe, A. , Quinn, B. , Czanner, S. , … Fischl, B. (2006). Reliability of MRI‐derived measurements of human cerebral cortical thickness: The effects of field strength, scanner upgrade and manufacturer. NeuroImage, 32, 180–194. 10.1016/j.neuroimage.2006.02.051 [DOI] [PubMed] [Google Scholar]
- Huang, L. , Wang, X. , Baliki, M. N. , Wang, L. , Apkarian, A. V. , & Parrish, T. B. (2012). Reproducibility of structural, resting‐state BOLD and DTI data between identical scanners. PLoS ONE, 7, e47684 10.1371/journal.pone.0047684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson, M. , Beckmann, C. F. , Behrens, T. E. , Woolrich, M. W. , & Smith, S. M. (2012). FSL. NeuroImage, 62, 782–790. 10.1016/j.neuroimage.2011.09.015 [DOI] [PubMed] [Google Scholar]
- Jovicich, J. , Czanner, S. , Han, X. , Salat, D. , van der Kouwe, A. , Quinn, B. , … Fischl, B. (2009). MRI‐derived measurements of human subcortical, ventricular and intracranial brain volumes: Reliability effects of scan sessions, acquisition sequences, data analyses, scanner upgrade, scanner vendors and field strengths. NeuroImage, 46, 177–192. 10.1016/j.neuroimage.2009.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jovicich, J. , Marizzoni, M. , Bosch, B. , Bartres‐Faz, D. , Arnold, J. , Benninghoff, J. , … Frisoni, G. B. (2014). Multisite longitudinal reliability of tract‐based spatial statistics in diffusion tensor imaging of healthy elderly subjects. NeuroImage, 101, 390–403. 10.1016/j.neuroimage.2014.06.075 [DOI] [PubMed] [Google Scholar]
- Kelly, C. , Biswal, B. B. , Craddock, R. C. , Castellanos, F. X. , & Milham, M. P. (2012). Characterizing variation in the functional connectome: Promise and pitfalls. Trends in Cognitive Sciences, 16, 181–188. 10.1016/j.tics.2012.02.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landman, B. A. , Huang, A. J. , Gifford, A. , Vikram, D. S. , Lim, I. A. , Farrell, J. A. , … van Zijl, P. C. (2011). Multi-parametric neuroimaging reproducibility: A 3-T resource study. NeuroImage, 54, 2854–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang, Z. , He, X. , Ceritoglu, C. , Tang, X. , Li, Y. , Kutten, K. S. , … Faria, A. V. (2015). Evaluation of cross‐protocol stability of a fully automated brain multi‐atlas parcellation tool. PLoS ONE, 10, e0133533 10.1371/journal.pone.0133533 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, J. , Liao, X. , Xia, M. , & He, Y. (2018). Chronnectome fingerprinting: Identifying individuals and predicting higher cognitive functions using dynamic brain connectivity patterns. Human Brain Mapping, 39, 902–915. 10.1002/hbm.23890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mars, R. B. , Sotiropoulos, S. N. , Passingham, R. E. , Sallet, J. , Verhagen, L. , Khrapitchev, A. A. , … Jbabdi, S. (2018). Whole brain comparative anatomy using connectivity blueprints. eLife, 7, e35237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller, M. I. , Faria, A. V. , Oishi, K. , & Mori, S. (2013). High-throughput neuro-imaging informatics. Frontiers in Neuroinformatics, 7, 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morey, R. A. , Selgrade, E. S. , Wagner, H. R. 2nd , Huettel, S. A. , Wang, L. , & McCarthy, G. (2010). Scan‐rescan reliability of subcortical brain volumes derived from automated segmentation. Human Brain Mapping, 31, 1751–1762. 10.1002/hbm.20973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori, S. , Oishi, K. , Faria, A. V. , & Miller, M. I. (2013). Atlas-based neuroinformatics via MRI: Harnessing information from past clinical cases and quantitative image analysis for patient care. Annual Review of Biomedical Engineering, 15, 71–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori, S. , Wu, D. , Ceritoglu, C. , Li, Y. , Kolasny, A. , Valliant, M. A. , … Miller, M. I. (2016). MRICloud: delivering high‐throughput MRI neuroinformatics as cloud‐based software as a service. Computing in Science & Engineering, 18, 15. [Google Scholar]
- Ni, H. , Kavcic, V. , Zhu, T. , Ekholm, S. , & Zhong, J. (2006). Effects of number of diffusion gradient directions on derived diffusion tensor imaging indices in human brain. AJNR American Journal of Neuroradiology, 27, 1776–1781. [PMC free article] [PubMed] [Google Scholar]
- Noble, S. , Spann, M. N. , Tokoglu, F. , Shen, X. , Constable, R. T. , & Scheinost, D. (2017). Influences on the test‐retest reliability of functional connectivity MRI and its relationship with behavioral utility. Cerebral Cortex, 27, 5415–5429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oishi, K. , Faria, A. , Jiang, H. , Li, X. , Akhter, K. , Zhang, J. , … Mori, S. (2009). Atlas‐based whole brain white matter analysis using large deformation diffeomorphic metric mapping: Application to normal elderly and Alzheimer's disease participants. NeuroImage, 46, 486–499. 10.1016/j.neuroimage.2009.01.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oishi, K. , Zilles, K. , Amunts, K. , Faria, A. , Jiang, H. , Li, X. , … Mori, S. (2008). Human brain white matter atlas: Identification and assignment of common anatomical structures in superficial white matter. NeuroImage, 43, 447–457. 10.1016/j.neuroimage.2008.07.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patriat, R. , Molloy, E. K. , Meier, T. B. , Kirk, G. R. , Nair, V. A. , Meyerand, M. E. , … Birn, R. M. (2013). The effect of resting condition on resting‐state fMRI reliability and consistency: A comparison between resting with eyes open, closed, and fixated. NeuroImage, 78, 463–473. 10.1016/j.neuroimage.2013.04.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny, W. , Friston, K. , Ashburner, J. , Kiebel, S. , & Nichols, T. (2007). Statistical parametric mapping (Friston K., Ashburner J., Kiebel S., Nichols T., & Penny W., Eds.). ISBN 9780123725608. Amsterdam and Boston: Elsevier and Academic Press; 10.1016/B978-012372560-8/50000-0 [DOI] [Google Scholar]
- Shou, H. , Eloyan, A. , Lee, S. , Zipunnikov, V. , Crainiceanu, A. N. , Nebel, N. B. , … Crainiceanu, C. M. (2013). Quantifying the reliability of image replication studies: The image intraclass correlation coefficient (I2C2). Cognitive, Affective, & Behavioural Neuroscience, 13, 714–724. 10.3758/s13415-013-0196-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrout, P. E. , & Fleiss, J. L. (1979). Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin, 86, 420–428. 10.1037/0033-2909.86.2.420 [DOI] [PubMed] [Google Scholar]
- Tae, W. S. , Kim, S. S. , Lee, K. U. , Nam, E. C. , & Kim, K. W. (2008). Validation of hippocampal volumes measured using a manual method and two automated methods (FreeSurfer and IBASPM) in chronic major depressive disorder. Neuroradiology, 50, 569–581. [DOI] [PubMed] [Google Scholar]
- Tang, X. , Crocetti, D. , Kutten, K. , Ceritoglu, C. , Albert, M. S. , Mori, S. , … Miller, M. I. (2015). Segmentation of brain magnetic resonance images based on multi‐atlas likelihood fusion: Testing using data with a broad range of anatomical and photometric profiles. Frontiers in Neuroscience, 9, 61 10.3389/fnins.2015.00061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang, X. , Oishi, K. , Faria, A. V. , Hillis, A. E. , Albert, M. S. , Mori, S. , & Miller, M. I. (2013). Bayesian parameter estimation and segmentation in the multi‐atlas random orbit model. PLoS ONE, 8, e65591 10.1371/journal.pone.0065591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang, X. , Yoshida, S. , Hsu, J. , Huisman, T. A. , Faria, A. V. , Oishi, K. , … Mori, S. (2014). Multi‐contrast multi‐atlas parcellation of diffusion tensor imaging of the human brain. PLoS ONE, 9, e96985 10.1371/journal.pone.0096985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tustison, N. J. , Cook, P. A. , Klein, A. , Song, G. , Das, S. R. , Duda, J. T. , … Avants, B. B. (2014). Large‐scale evaluation of ANTs and FreeSurfer cortical thickness measurements. NeuroImage, 99, 166–179. 10.1016/j.neuroimage.2014.05.044 [DOI] [PubMed] [Google Scholar]
- Van Essen, D. C. , Smith, S. M. , Barch, D. M. , Behrens, T. E. , Yacoub, E. , & Ugurbil, K. (2013). The WU‐Minn human connectome project: An overview. NeuroImage, 80, 62–79. 10.1016/j.neuroimage.2013.05.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vollmar, C. , O'Muircheartaigh, J. , Barker, G. J. , Symms, M. R. , Thompson, P. , Kumari, V. , … Koepp, M. J. (2010). Identical, but not the same: Intra‐site and inter‐site reproducibility of fractional anisotropy measures on two 3.0T scanners. NeuroImage, 51, 1384–1394. 10.1016/j.neuroimage.2010.03.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, H. , & Yushkevich, P. A. (2013). Multi‐atlas segmentation with joint label fusion and corrective learning‐an open source implementation. Frontiers in Neuroinformatics, 7, 27 10.3389/fninf.2013.00027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wonderlick, J. S. , Ziegler, D. A. , Hosseini-Varnamkhasti, P. , Locascio, J. J. , Bakkour, A. , van der Kouwe, A. , … Dickerson, B. C. (2009). Reliability of MRI-derived cortical and subcortical morphometric measures: Effects of pulse sequence, voxel geometry, and parallel imaging. NeuroImage, 44, 1324–1333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, D. , Ma, T. , Ceritoglu, C. , Li, Y. , Chotiyanonta, J. , Hou, Z. , … Mori, S. (2016). Resource atlases for multi‐atlas brain segmentations with multiple ontology levels based on T1‐weighted MRI. NeuroImage, 125, 120–130. 10.1016/j.neuroimage.2015.10.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye, C. , Ma, T. , Wu, D. , Ceritoglu, C. , Miller, M. I. , & Mori, S. (2018). Atlas pre‐selection strategies to enhance the efficiency and accuracy of multi‐atlas brain segmentation tools. PLoS ONE, 13, e0200294 10.1371/journal.pone.0200294 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, F. , Wu, Y. , Norton, I. , Rathi, Y. , Golby, A. J. , & O'Donnell, L. J. (2019). Test‐retest reproducibility of white matter parcellation using diffusion MRI tractography fiber clustering. Human Brain Mapping. 10.1002/hbm.24579 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data analyzed in this study are publicly available as Tables [Link], [Link], [Link].


