Assessing the effects of quantitative host resistance on the life-history traits of sporulating parasites with growing lesions

Abstract

Assessing life-history traits of parasites on resistant hosts is crucial in evolutionary ecology. In the particular case of sporulating pathogens with growing lesions, phenotyping is difficult because one needs to disentangle properly pathogen spread from sporulation. By considering Phytophthora infestans on potato, we use mathematical modelling to tackle this issue and refine the assessment of pathogen response to quantitative host resistance. We elaborate a parsimonious leaf-scale model by convolving a lesion growth model and a sporulation function, after a latency period. This model is fitted to data obtained on two isolates inoculated on three cultivars with contrasted resistance level. Our results confirm a significant host–pathogen interaction on the various estimated traits, and a reduction of both pathogen spread and spore production, induced by host resistance. Most interestingly, we highlight that quantitative resistance also changes the sporulation function, the mode of which is significantly time-lagged. This alteration of the infectious period distribution on resistant hosts may have strong impacts on the dynamics of parasite populations, and should be considered when assessing the durability of disease control tactics based on plant resistance management. This inter-disciplinary work also supports the relevance of mechanistic models for analysing phenotypic data of plant–pathogen interactions.

1. Introduction

The use of resistant cultivars in agricultural systems remains the best alternative to pesticides for mitigating the impact of diseases on commercial crops. However, as plant pathogen populations generally evolve and adapt rapidly, they often overcome resistances of cultivated hosts after a few growing seasons. Therefore, the optimal management of disease-resistant host plants that maximizes both the efficacy and the durability of the control is still a challenging question in plant disease epidemiology [1–5]. Pathogen populations that break down major genes that confer host immunity (i.e. qualitative resistance), quantitative or partial resistance, which reduces the level of disease, have gained interest among plant geneticists and pathologists during the last decade to improve the durability of resistance [6–10]. Nevertheless, while the mechanisms of pathogen adaptation to qualitative resistance are now well established, the case of quantitative resistance is relatively less well understood [11–14].

When it is present, quantitative host resistance to disease can occur alone or in combination with qualitative resistance. It generally reduces the fitness [15] of the target pathogens by altering one or several stages of their life cycles [12,16,17]. In filamentous plant pathogens, quantitative resistance applies not only to spore germination and infection but also to within-host growth and spore production [18]. Thus, the experimental measurement of quantitative traits, sometimes referred to as aggressiveness or pathogenicity components, is central to the study of interactions between resistant hosts and pathogens, and also to correlate the genetic background of both the host and the pathogen with their phenotypic traits (i.e. quantitative trait loci) [14,19]. Most empirical work consists of (i) inoculating organs, typically leaflets, under controlled conditions, (ii) monitoring the development of the lesion(s) caused by the pathogen and finally (iii) estimating various life-history traits such as latency period, sporulation rate and lesion size from lesion scale phenotyic data. However, in cases where the pathogen colonizes host tissues and induces a growing lesion, the estimation of various key traits, e.g. the latency period or sporulation dynamics, can actually be difficult. Indeed, to accurately assess those pathosystems, one needs to consider the age structure of the lesion to disentangle pathogen spread from the sporulation dynamics of infected host sites [20,21]. It is recognized that the use of mathematical epidemiological models in combination with empirical disease data offers a means of improving our understanding of the processes involved in the spatio-temporal development of pathogens [22,23] and assessing the effects of disease resistance [24]. Although mechanistic models could thus be useful to tackle sporulating parasites with growing lesions, they have been seldom considered by theoreticians, and rarely fitted against experimental data to infer pathogen traits in plant pathology [20,21,25], even when pathogen spread is negligible.

In this study, we consider the oomycete Phytophthora infestans (Mont.) de Bary as an example sporulating parasite with growing lesions. Phytophthora infestans, the causal agent of late blight of potato (Solanum tuberosum L.), played a substantial role in the Irish famine in the 1840s, and remains one of the most destructive plant diseases, causing important economic losses of potato crops worldwide each year [26]. The idea of breeding potatoes with resistance to P. infestans emerged after the Irish famine [27,28] and is still central to limit the damage due to late blight [29]. However, the explosive demography of P. infestans, due to the combination of a short generation time and a very high multiplication rate, associated with its ability to alternate between asexual and sexual cycles, still challenge its durable control based on host resistance [30].

We begin by developing a parsimonious mechanistic model that describes the within-host growth dynamics of a sporulating pathogen. Then, this leaf-scale model is fitted to phenotypic destructive data obtained on two isolates of P. infestans inoculated on three potato cultivars with contrasted levels of quantitative resistance. We show that it enables the disentanglement of the growth and sporulation processes and the estimation of key life-history traits (i.e. lesion growth rate, latent period, spore production by surface unit and the dynamics of spore emission). Afterwards, the comparison of isolates and cultivars allows us to provide new insights into the effects of quantitative host resistance on pathogen growth and sporulation. We finish by discussing our work, its limits and its application to the study of plant–pathogen interactions with a resistant host.

2. Material and methods

(a). Experimentation

(i). Biological material

Two aggressive isolates of P. infestans, originally collected in the north of France, were chosen from our collection: BP3 (mating type A1, origin Wavrin: 0°34′27″ N 2°56′2″ E) which was known to produce a large number of spores and BP6 (mating type A2, origin Gavrelle: 50°19′48″ N 2°53′13″ E) with a lower level of sporulation. These isolates were tested on three potato cultivars with contrasting levels of quantitative resistance, maintained at the Inra Station of Ploudaniel (UE RGCO, France), and tested in our laboratory: Bintje, which is a reference cultivar susceptible to P. infestans, Désirée, which mostly mitigates sporulation, and Möwe, which reduces both lesion growth and spore production [31].

(ii). Inoculations

For each of the six isolate–cultivar pairs, host leaflets were inoculated according to a standard biotest protocol developed in our laboratory [31]. Maintaining isolates on agar media can alter the pathogenicity of P. infestans, which can be restored after a re-infection of host tissues. Thus, for each isolate, the inoculum was produced separately on seven-week-old leaves of the reference cultivar Bintje inoculated with sporangia previously collected on three- to four-week-old colonies by washing the Petri dishes with 5 ml deionized sterile water. The inoculations were performed by placing a 20 μl droplet containing about 1000 sporangia at the centre of each leaflet. Then, leaflets were placed on the lids of inverted Petri dishes containing water agar, to maintain saturating moisture, and kept in clear plastic boxes stored in a climate chamber regulated at 18°C (days) and 15°C (night) with 16 h of daylight. Six days later, sporangia produced on the inoculated leaves were collected by washing the symptomatic leaves in 10 ml deionized sterile water, before adjusting the concentration of the obtained suspension to 5 × 10⁴ sporangia ml⁻¹. Afterwards, these suspensions were used to inoculate each isolate onto around 100 leaflets of each cultivar (table 2), using the protocol described above.

Table 2.

Estimated parameters of lesion and sporulation models. Estimates correspond to the mean of the posterior distributions. For each parameter, the standard deviation (s.d.), the first quartile (q-25%) and the third quartile (q-75%) are given in parenthesis as (s.d., q-25%–q-75%). Parameter n in the last row indicates the number of inoculated leaflets used for destructive sampling.

parameter	units	BP3			BP6
		Bintje	Möwe	Désirée	Bintje	Möwe	Désirée
t0	hours	68.8	64.1	55.9	68.7	68.7	41.4
		(1.2, 68.3–69.7)	(4.5, 61.6–67.5)	(3.9, 53.3–58.6)	(1.1, 68.1–69.6)	(1.1, 68.2–69.7)	(3.7, 38.8–44.0)
t1	hours	72.4	83.9	68.2	88.7	121.4	79.3
		(2.0, 70.8–73.5)	(8.5, 77.2–90.8)	(6.4, 63.5–72.5)	(4.5, 85.8–91.7)	(11.6, 114.1–129.1)	(5.2, 75.2–82.8)
δ = t0 − t1	hours	−3.6	−19.8	−12.3	−20.0	−52.7	−37.9
ρ	mm h−1	0.26	0.17	0.24	0.30	0.23	0.19
		(0.005, 0.254–0.263)	(0.008, 0.169–0.179)	(0.013, 0.234–0.253)	(0.006, 0.294–0.303)	(0.005, 0.223–0.229)	(0.009, 0.184–0.196)
S	spores mm−2	367	322	193	238	186	152
		(13, 358–377)	(18, 311–333)	(13, 184–202)	(10, 232–245)	(16, 175–197)	(9, 146–158)
μ	hours	3.6	13.4	14.6	6.7	14.5	10.3
		(2.6, 1.6–5.0)	(10.9, 5.4–18.4)	(7.8, 8.2–20.3)	(3.9, 3.7–9.4)	(7.9, 8.4–19.8)	(4.0, 7.2–12.5)
n	samples	127	99	104	139	104	125

(iii). Measurements

In order to capture the dynamics of both lesion growth and sporulation, we used a destructive sampling of several inoculated leaflet replicates (about 10) with times of observation empirically tuned for each isolate–cultivar pair to match their respective lesion development speed. At each time (since inoculation) of observation $\mathcal{T}$ and for each individual leaflet, we used a sliding caliper to measure the minor and major radii of both the host-leaflet (${\mathcal{R}}_1<{\mathcal{R}}_2$, respectively) and the lesion induced by the pathogen (${\mathcal{L}}_1<{\mathcal{L}}_2$, respectively). It is important to note that the visible measured lesion was an area including both the necrotic zone and a surrounding zone corresponding to spore-producing structures, that is commonly distinguishable under optimal conditions for P. infestans. Thereafter, sporangia were collected by washing each leaflet in a 10 ml Isoton (Saline buffer; Beckman Coulter, Villepinte, France) and the total number of sporangia present, at this time, on the lesion $\mathcal{S}$ was assessed with a Coulter Z2 counter (Beckman Coulter with lower and upper thresholds of 10 μm and 20 μm, respectively).

(iv). Lesion growth model

We make the assumption of an ellipse-shaped leaflet that seems to be reasonable in the particular case of this pathosystem. This hypothesis was verified before model development by comparing the surface predicted by the ellipse equation against the surface obtained through the manual segmentation of images performed with the ImageJ software. Despite the presence of some outliers, the linear relationship (slope of 1.04, R² = 0.98) conformed to our assumption. We did not detect any statistical effect of the cultivar on the slope with an ANCOVA (figure 1). Letting R₁ < R₂ be the minor and major radii of the leaf, its surface L is given by L = πR₁R₂. In this simple leaf-scale epidemiological model, we assume that the lesion starts from the centre of the leaflet and expands as a circle until reaching an edge, afterwards it expands as an ellipse up to completely recovering the surface of the leaf (figure 2). If we call r₁(t) < r₂(t), respectively, the minor and the major radii of the lesion at time t, the surface of the lesion ℓ at time t follows ℓ(t) = πr₁(t)r₂(t). We consider that the symptomatic lesion appears after a fixed delay t₀ ≥ 0 which corresponds to the incubation period (i.e. the delay between inoculation and disease symptom) (figures 2 and 3a,b). Tip growing filamentous pathogens often show a constant radial growth rate in a homogeneous medium [32,33]. Let ρ be the radial growth rate of the parasite, and assume ρ is maximal and constant until reaching the leaflet edges: i.e. for i = 1, 2 and t ≥ t₀ r_i(t) = min (ρ(t − t₀), R_i). The lesion surface is described as

$$\ell (t)=\pi min(\rho (t-t_0),R_1)min(\rho (t-t_0),R_2),$$ 2.1

for all t ≥ t₀, and ℓ(t) = 0 for all t < t₀.

Figure 1.

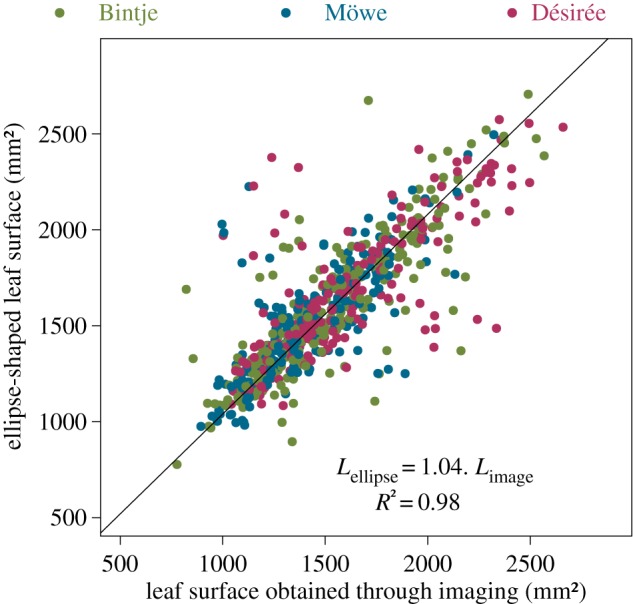
Ellipse-shaped assumption for potato leaflets: relationship between the leaf surface of potato leaves obtained through manual annotation of images versus the surface calculated with the ellipse-shaped assumption and the measured radii ($L=\pi {\mathcal{R}}_1{\mathcal{R}}_2$). (Online version in colour.)

Figure 2.

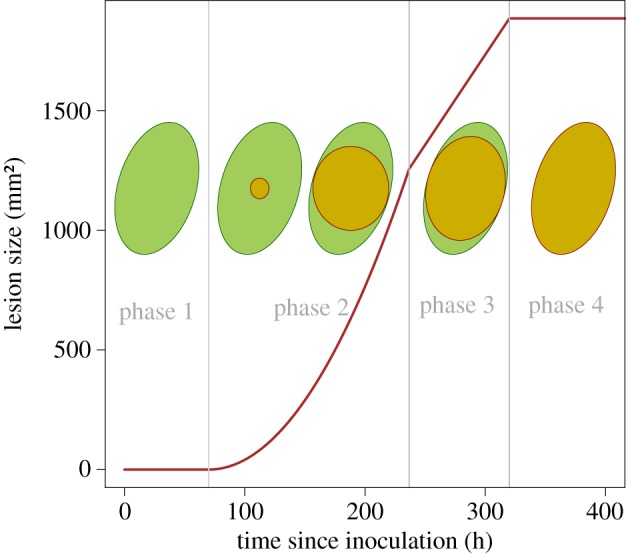
Lesion growth model: schematic lesion growth on an ellipse-shaped host leaf with the corresponding temporal dynamics. (Online version in colour.)

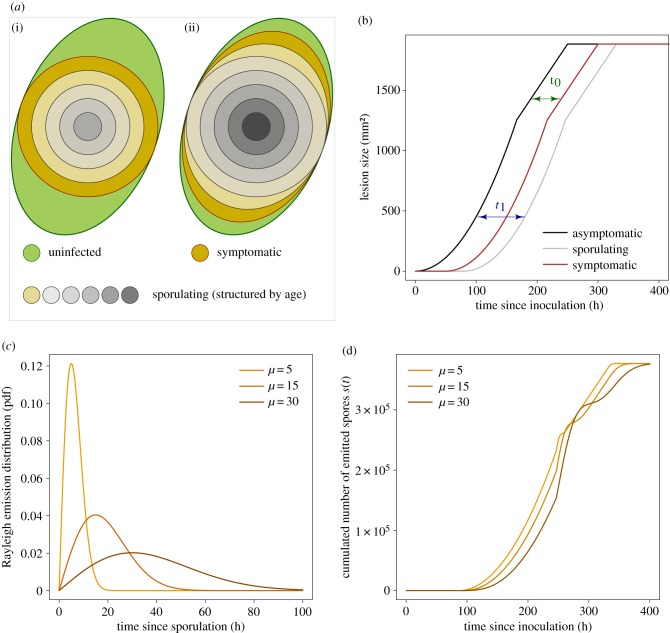
As illustrated in figure 2, the dynamics of the symptomatic lesion on the ellipse-shaped leaflet is characterized by four phases. After the incubation period t₀ during which no symptom is visible (phase 1), the symptomatic lesion increases quadratically until it reaches the minor radius of the host leaflet R₁ (phase 2). Thereafter, the lesion size grows linearly until the major leaf radius (phase 3) after which it saturates at the leaflet size L = πR₁R₂ (phase 4).

(v). Sporulation model

Let us partition the host leaflet into small surfaces (or host spatial units), and call σ(a) a continuous-time emission (or sporulation) function giving the distribution of spores (sporangia here) released by a spatial host unit according to its age since infection a. In the case of a growing lesion, to scale-up the sporulation dynamics from small host units to the lesion level, one needs to consider the inherent age structure of infected (and infectious) host tissues (figure 3a) [21]. Then, the total number of spores produced at time t at the lesion level can be obtained through the following convolution product:

$$s(t)={\int }_0^t{\ell }^{\mathrm{\prime }}(t-a)\sigma \hspace{0.17em}(a)\hspace{0.17em}\text{d}a,$$ 2.2

where ℓ′(t) describes the development of an infectious lesion over time, either symptomatic or asymptomatic.

Figure 3.

Sporulation model: (a) schematic illustration of the age-structuring of the lesion for two successive times corresponding to phase 3 (i) and phase 4 (ii) of the dynamics; (b) representation of the lags between the dynamics of asymptomatic (black), symptomatic (red) and sporulating (grey) lesions induced by respectively the incubation t₀ and the latency t₁ periods; (c) probability density function of the Rayleigh distribution describing spore emission; and (d) the corresponding dynamics of the cumulated number of spores produced by the lesion s(t) obtained through the convolution model. In consistency with our results, panels (a,b) show an illustrative instance where the latency period is higher than the incubation period (i.e. the sporulating area is inside the symptomatic one). The dynamics presented here were obtained using t₀ = 60, t₁ = 80, ρ = 0.12, R₁ = 20, R₂ = 30 and S = 200. (Online version in colour.)

Let t₁ be the latency period, i.e. the delay between host infection and sporulation, and let us recall that t₀ is the incubation period, i.e. the delay between host infection and the onset of disease symptoms [34]. We assume that these two periods are fixed, i.e. distributed according to a Dirac, and distinct from each other: t₁ − t₀ ≠ 0. Taking our lesion growth model (2.1), the two lags related to t₁ and t₀ (figure 3a,b), and a generic emission function σ(a), equation (2.2) becomes

$$s(t)={\int }_0^t\ell (t+t_0-t_1-a)\sigma (a)\hspace{0.17em}\mathrm{d}a.$$ 2.3

Several sporulation functions have already been proposed and discussed in plant disease epidemiology [24,35–37]. Here, we opt for a Rayleigh distributed sporulation that has an asymmetric probability density function with a distinct mode (figure 3c). The use of this specific case allowed us to get an analytical solution of the convolution product (2.3), and therefore, to simplify calculations (see electronic supplementary material, Math_Stat). Calling S the sporulation capacity of an infinitesimal host unit, i.e. the total amount of spores produced per infectious host unit, the sporulation function follows:

$$\sigma \hspace{0.17em}(a)=S\times \frac{a}{{\mu }^2}\exp (-\frac{a^2}{2{\mu }^2}).$$ 2.4

where (a/μ²) exp ( − a²/2μ²) is the probability density function of the Rayleigh distribution with parameter μ that corresponds to the mode.

(b). Model fitting and statistical analyses

For the six isolate–cultivar pairs, the lesion growth model (2.1) and the sporulation model (2.3) were sequentially fitted to empirical data. We first estimated the incubation period t₀ and the lesion growth rate ρ from independent measurements i of the symptomatic lesion surface ${\mathcal{L}}^i=(\pi {\mathcal{L}}_1^i{\mathcal{L}}_2^i)$ for a range of times since inoculation ${\mathcal{T}}^i$ (table 1). Afterwards, we inferred the latency period t₁, the sporulation capacity S, and the mode of the sporulation function μ from destructive spore counting data ${\mathcal{S}}^i$, knowing the estimates of both the incubation period and the lesion growth rate. The variability in potato leaflets’ size (figure 1) was taken into account by letting the minor and major leaf radii be the measured ones: $R_1^i={\mathcal{R}}_1^i$ and $R_2^i={\mathcal{R}}_2^i$, respectively.

Table 1.

Parameters with their definitions and units.

parameter	definition	units
lesion model ℓ(t)
t0	incubation period	hours
ρ	lesion growth rate	mm h−1
R1	minor leaf radius	mm
R2	major leaf radius	mm
sporulation model s(t)
t1	latency period	hours
S	spore production by infectious host unit	spores mm−2
μ	mode of the sporulation function σ	hours
observations $\mathcal{O}$
$\mathcal{T}$	time of observation	hours
${\mathcal{R}}_1$	minor leaf radius	mm
${\mathcal{R}}_2$	major leaf radius	mm
${\mathcal{L}}_1$	minor lesion radius	mm
${\mathcal{L}}_2$	major lesion radius	mm
$\mathcal{S}$	total number of spores	spores

The two models were fitted to data by considering Gaussian likelihood functions (i.e. normally distributed errors). Parameter estimation was performed via a Bayesian Markov chain Monte Carlo sampling with non-informative prior distributions and an Adaptive Metropolis algorithm that is available in the FME package [38]. The adequacy of the models to the data were assessed visually by looking at the raw residuals and by considering the residual sum of squares (RSS) as a measure of the goodness-of-fit. We performed a goodness-of-fit test using the distribution of the RSS in least-squares estimation: $\text{RSS}/{\sigma }_r^{\hspace{0.17em}2}\sim {\chi }_{n-k}^2$, where σ_r² is the residual variance, n is the number of data points and k is the number of parameters.

Finally, the effects of pathogen isolate {BP3, BP6} and host genotype {Bintje, Möwe, Désirée} on the parameters of models (2.1) and (2.3) were assessed through F-tests and pairwise comparisons (see electronic supplementary material, Math_Stat for details).

The implementation of the models and the statistical analyses were performed using the R free software environment [39].

3. Results

The empirical destructive sampling strategy allowed us to fit the two models that both captured the essential patterns of data. The goodness-of-fit tests supported the null hypothesis for all cases (p-values ≥0.39), giving evidence of a good fit for both models (electronic supplementary material, table S1). The visual assessment of lesion growth model adequacy suggested a good, and similar, homoscedasticity of raw residuals for the six isolate–cultivar combinations (electronic supplementary material, figure S1). For the sporulation model, it pointed out a higher heteroscedasticity in some combinations, e.g. Bintje—BP3 or Möwe—BP3 (electronic supplementary material, figure S2). This increasing variability in the number of spores produced by a lesion can be explained by the inherent variability of the biological processes [17] but could have been also partially induced by some measurement error.

The values of parameter estimates were consistent with previous studies [31,40,41]. Among the tested isolate–cultivar cases, the time to symptom appearance after inoculation t₀ ranged from 41.4 to 68.8 h, while the latency period t₁ ranged between 68.2 and 121.4 h (table 2). The related time lag between the onset of disease and sporulation δ = t₀ − t₁ varied between −3.6 and −52.7 h (table 2), showing that symptoms occurred before spores release, as illustrated in figure 3a,b. Finally, the lesion radial growth rate ρ, the amount of spores produced by infectious host unit S and the mode of the sporulation curve μ were estimated to vary between 0.17 and 0.30 mm h⁻¹, 152 and 367 spores mm⁻², and 3.6 and 14.6 h (after t₁), respectively (table 2).

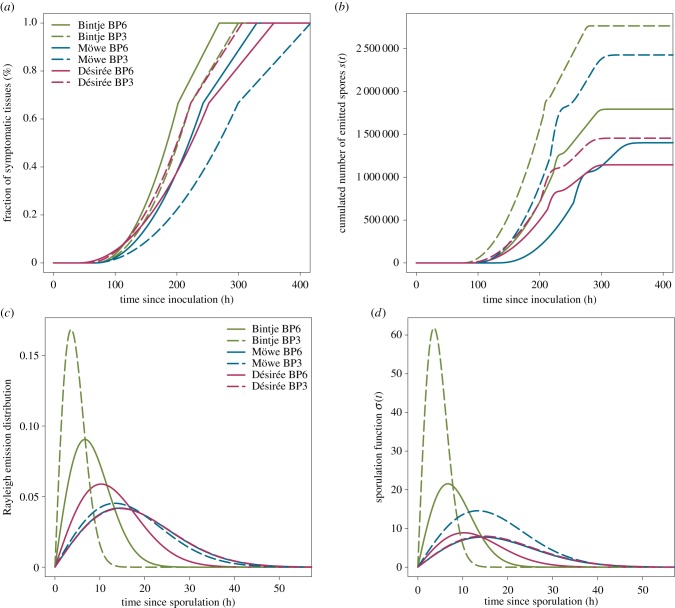
Our results confirmed a significant isolate–cultivar interaction for the quantitative traits of P. infestans considered in the study [31,40] (figure 4; electronic supplementary material, tables S2–4). Regarding the lesion growth model, our study confirms that quantitative resistance of the considered potato cultivars significantly reduces the rate at which the pathogen colonizes host tissues ρ. Isolate BP6 was faster than BP3 on the susceptible reference cultivar Bintje (table 2 and figure 4a). Although the cultivar Désirée had a stronger effect on pathogen colonization than Möwe for BP6 (ρ = 0.19 and 0.23 mm.h⁻¹, respectively), it was the opposite for isolate BP3 (ρ = 0.24 and 0.17 mm.h⁻¹, respectively).

Figure 4.

Fitted models for the six isolate–cultivar cases considered in the study. (a) The fitted growth of the lesion ℓ(t); (b) the fitted dynamics of the cumulated number of emitted spores s(t) on an ellipse-shaped host leaflet with minor (R₁) and major radii (R₂) of 40 and 60 mm, respectively; (c) the fitted emission probability density function; and (d) the sporulation function σ(t). In (d), the sporulation curves of BP6 on Möwe (blue solid line), and BP3 on Désirée (maroon dashed line) overlap. (Online version in colour.)

Perhaps surprisingly, the fitting of the models suggested that quantitative resistance tends to decrease the incubation period t₀ (table 2). In comparison with Bintje, t₀ exhibited a small reduction for BP3 in Möwe and a higher decrease on Désirée with the two isolates (table 2), even though the difference between Bintje and Désirée was non-significant for BP6 (electronic supplementary material, table S4). As parameter t₀ actually aggregates the delay between host leaflet exposure to particulate inoculum (sporangia) and infection as well as the true incubation period, it is difficult to identify here which process has been actually affected by quantitative resistance. Nevertheless, according to previous studies that have shown that infection efficiency can be higher in some partially resistant cultivars than in Bintje [42], we could speculate that some resistant potato cultivars like Désirée might be more susceptible to infections by external inoculum (asexual spores here) than the reference cultivar Bintje.

The estimates of the latency period t₁ on the resistant cultivar Möwe were in agreement with previous findings [31,40] and confirmed the putative increase of the latency induced by quantitative resistance in this cultivar (table 2). Nevertheless, the estimated decrease of the latency on the cultivar Désirée (electronic supplementary material, table S2) and the non-significant differences in t₁ between Möwe and Désirée for the two isolates (electronic supplementary material, tables S3 and S4) showed that the results on the latency should be interpreted with care. Clement et al. [31] also demonstrated that the latency period of P. infestans may not differ significantly on Bintje and Désirée, but found a significant difference in t₁ between Möwe and Bintje. In addition, looking at the lag between the incubation and the latency δ = t₀ − t₁ our results interestingly suggest that quantitative resistance may increase the delay between symptom appearance and spore release (table 2).

Finally, by fitting our sporulation model, we confirmed that quantitative resistance reduces significantly the number of (asexual) spores produced by an infectious host spatial unit S (electronic supplementary material, tables S2–S4). As expected, isolate BP3 had a higher sporulation (367, 322 and 193 spores mm⁻² on Bintje, Möwe and Désirée, respectively) than BP6 (238, 186 and 152 spores mm⁻² on Bintje, Möwe and Désirée, respectively) (table 2). Most interestingly, we found that quantitative resistance can modify significantly the dynamics of spore emission (figure 4d). Indeed, on the two resistant cultivars Möwe and Désirée, the mode of the emission function was delayed and the variance of the distribution was increased (figure 4c). Besides the reduction in spore production, it demonstrates that quantitative host resistance may also slow down and make more variable the timing of spore emission. On Bintje, contrary to isolate BP6 for which μ was estimated to 6.7 h, BP3 had a very narrow distribution with a mode at only 3.6 h, indicating a quasi-instantaneous release of spores after latency. While the strong difference in the distribution of spore emission between the reference susceptible Bintje and the two resistant cultivars were significant for both BP3 (μ = 13.4 and 14.6 h for Möwe and Désirée, respectively) and BP6 (μ = 14.5 and 10.3 h for Möwe and Désirée, respectively), we did not find significant differences in μ between Möwe and Désirée (figure 4c and table 2; electronic supplementary material, tables S3 and S4).

4. Discussion

Identifying and quantifying the components of pathogen aggressiveness and disease resistance requires numerous careful, and sometimes laborious, experimental measurements. Nevertheless, this step is a keystone for understanding the adaptation of pathogen populations to quantitative host resistance [16,17,43,44], the coevolution of plants and their pathogens in natural systems [11,14,45], or to identify the genetic structures of quantitative resistance and aggressiveness [19]. In this study, we have addressed the particular case of sporulating pathogens with growing lesions, for which the accurate estimation of some key life-history traits is difficult from common lesion-scale phenotypic data.

We considered P. infestans on potato as an example pathosystem with an inter-disciplinary approach to tackle this issue and refine the assessment of quantitative host resistance on life-history traits. By combining a parsimonious model that describes the key monocyclic periods of the sporulating pathogen on a host leaflet, with phenotypic data obtained on two French isolates inoculated and a reference susceptible potato cultivar and two resistant ones, we were able to (i) capture the essential patterns of both lesion size and cumulated spores data, (ii) deconvolve pathogen spread and spore emission, (iii) provide estimates of key life-history traits of the pathogen and (iv) identify the effects of quantitative resistance on the monocyclic periods of P. infestans. Our results were consistent with previous works on this cultivated pathosystem [31,40]. They confirm a significant isolate–cultivar interaction (electronic supplementary material, tables S2–S4), and support already known effects of quantitative disease resistance, i.e. the decrease of both the pathogen growth rate and the sporulation capacity (table 2 and figure 4), observed on several pathosystems [17,44].

Moreover, by fitting the lesion growth (2.1) and the sporulation (2.3) models to the data we found that the incubation period t₀ was always shorter than the latency period t₁ (i.e. δ = t₀ − t₁ < 0) (table 2), and pointed out that quantitative resistance tends to increase the time-lag between these two periods. P. infestans is a near-obligate hemibiotrophic pathogen that has both biotrophic and necrotrophic phases during its asexual cycle [30]. Although one would expect the symptomatic lesion to match with the necrotic area, in our experiments that were conducted under optimal conditions for pathogen development, the visible lesion was rather an area including both the necrotic zone and a surrounding whitish elliptical ring, corresponding to spore-producing structures. Therefore, we cannot correlate the observed increase in the delay between incubation and latency periods (i.e. δ) on resistant hosts with any biotrophy-necrotrophy switch. But, we speculate that this feeds the hypothesis of an increase in the latency period (i.e. time to spore release) due to quantitative resistance, though it was not possible to unequivocally identify it here. For future investigations, it would then be interesting to distinguish between the symptomatic and necrotic phases during host colonization to assess how such resistant cultivars might impact the hemibiotrophic behaviour of P. infestans [46].

Most interestingly, combining modelling and experimentation allowed us to show that quantitative resistance also impacts the distribution of the infectious period, i.e. the temporal spore emission function [24,36], by moving its mode back and extending its variance (figure 4c). It means that, besides the limitation of the sporulation capacity, quantitative host resistance may also lag the peak of spore emission and make more variable the temporal production of spores. The effects of residence time distributional models, which describe the time spent by hosts in infectious and pathology compartments, on epidemics have been addressed by numerous studies that have demonstrated that changes in these distributions can produce significant modifications of epidemic behaviour [34,47]. For plant pathogens, several distributional models have been proposed and discussed for the infectious-sporulating period with non-growing lesions [35–37], but the change in this distribution caused by host resistance remains unknown. New studies on more potato cultivars and other isolates of P. infestans, as well as on other pathosytems, would be necessary to evaluate to what extent this phenomenon is generic or specific. However, it may be worth including this phenomenon into theoretical models or frameworks developed in evolutionary ecology, to assess its influence on the timing of pathogen evolution [6,12], the coevolution of hosts and parasites in natural systems [14], and the management of plant resistances [4,8].

The use of mechanistic models for analysing empirical data is recognized to be insightful for our understanding of epidemics [22,24]. For instance, it enables one to test and select models, and the underlying hypotheses, and to quantify the main processes from observations [23]. Surprisingly, while a large amount of data is collected by biologists at the lesion scale, the use of mechanistic models for analysing these data is still seldom considered in phytopathology. In the case of pathogens with growing lesions, one needs to take into account the age-structure of the infected host tissues to scale up the dynamics of sporulation at the symptom level, for instance, by using a convolution product or a Leslie matrix [20,21]. Then, the identification of the life cycle periods of the pathogen for a small host unit from observation at a higher level becomes non-trivial (figure 3), and actually, difficult to capture accurately without using some advanced modelling. Our models are quite generic and can be used to estimate life-history traits of several sporulating pathogens with growing lesions. The R code attached to the manuscript enables one to fit the models against temporal data and may help non-modellers to apply the framework on their specific datasets. As long as the temporal data cover the dynamics of both lesion spread and sporulation, the implemented Bayesian procedure should provide estimates of the parameters, even with fewer replicates than we had. Furthermore, the implemented estimation procedure is relatively fast (e.g. about respectively 1 and 3 min for fitting models (1) and (3) with 100 000 MCMC iterations on a Intel^® Xeon^® E5 with 32 Go of RAM) and, from a computational time point of view, its application to large datasets may be reasonable.

Of course, this study has some limits that need to be discussed. To begin with, it is based on experiments led under controlled conditions, and it is essential to question the transfer of these results to the field. As in the particular case of the late blight of potato, it has been shown that laboratory tests give similar results for the ranking of resistant cultivars [42], we could speculate that our results may qualitatively apply to field conditions. Then, as we aimed at comparing the behaviour of two isolates, we inoculated leaflets with asexual spores of P. infestans, a partially clonal heterothallic oomycete that can also produce sexual spores when the two mating types meet. It would be interesting to run similar experiments using sexual spores and use our models to investigate the impact of host resistance on the sexual reproduction of the pathogen and assess whether it confirms previous results [31]. Moreover, albeit our models fitted the data reasonably well we made strong assumptions, which could be relaxed for further investigations. First, for the sake of simplicity and to keep the possibility of finding an analytical solution to the convolution product we put severe constraints on the distributions of both the latency and the infectious periods, which were assumed to respectively follow a Dirac and a Rayleigh distribution. Generally, the distributional analysis of empirical epidemic data shows that the time spent by a host unit in the infectious status is better described by asymmetric distributions with a distinct mode such as gamma, Weibull or lognormal distributions [34]. Therefore, considering such distributional models may provide a better description of the latency t₁ and the incubation t₀ periods, and contribute to decrease the discrepancy between the model and the data (electronic supplementary material, figures S1 and S2). On the other hand, this would increase the mathematical complexity of the model [36,48] and would require the use of advanced numerical methods for implementation and simulation. Second, to describe the spread of the pathogen, we assumed (i) an ellipse-shaped leaf, (ii) that inoculation was always done at the centre of the leaflet, and, (iii) considered a constant radial growth of the pathogen with a saturation at leaflet edges. Considering a spatial model and the explicit shapes of leaves may provide a finer description of the host–pathogen interaction. Further studies could rely on recent advances in image-based phenotyping of plant diseases to automatically extract leaves features (e.g. shapes, veins structures) and segment lesions [49]. Then, combining spatial process-based models with image data appears as an interesting means to (i) improve our understanding of pathogen spread at the lesion level, (ii) identify physiological responses of host tissues, such as ontogenetic and disease-induced changes in the susceptibility that are known to occur in several pathosystems [46,50], and (iii) introduce the leaf vein structure that can be crucial to predict the spatial expansion of some pathogens. Although such approaches are widely used for the study of human lesions or tumours [51], they remain unusual for plant diseases.

To finish with, mathematical modelling offers a means to improve plant disease phenotyping by allowing a finer quantification of traits. Thus, it would be relevant to promote model-based phenotyping, especially for assessing the genetic architecture of traits, either for the plant or the pathogen. However, generating data for modelling purposes in genetic studies can increase the already substantial experimental cost. This experimental bottleneck might be partially overcome by using methods from the Optimal Design of Experiments [52,53]. This field of statistics provides methods for designing experiments (e.g. size of the experiment, times of observation, number of replicates) that optimize the information on the processes for parameter estimation or model selection. In this study, the experiment was rather designed based on our knowledge on the timescale of pathogen development, and our experimental constraints. While this empirical space-filling design allowed us to fit the models, it would be interesting to improve our modelling framework by defining optimal experimental strategies that enable the proper estimation of life-history traits with the minimal number of lesion-scale data [54].

Data accessibility

Data and an R scripts for model fitting are available from the Dryad digital Repository: https://doi.org/10.5061/dryad.g108557 [55].

Competing interests

We declare we have no competing interests.

Funding

This study was partly funded by the Plant Health and Environment Division of the Institut National de la Recherche Agronomique (INRA), and by the European Union's Horizon 2020 research and innovation programme through the Organic-Plus project (grant agreement 774340).