Resolution characterization of a silicon-based, photon-counting computed tomography prototype capable of patient scanning

Abstract.

Photon-counting detectors are expected to bring a range of improvements to patient imaging with x-ray computed tomography (CT). One is higher spatial resolution. We demonstrate the resolution obtained using a commercial CT scanner where the original energy-integrating detector has been replaced by a single-slice, silicon-based, photon-counting detector. This prototype constitutes the first full-field-of-view silicon-based CT scanner capable of patient scanning. First, the pixel response function and focal spot profile are measured and, combining the two, the system modulation transfer function is calculated. Second, the prototype is used to scan a resolution phantom and a skull phantom. The resolution images are compared to images from a state-of-the-art CT scanner. The comparison shows that for the prototype $19\mathrm{lp}/\mathrm{cm}$ are detectable with the same clarity as $14\mathrm{lp}/\mathrm{cm}$ on the reference scanner at equal dose and reconstruction grid, with more line pairs visible with increasing dose and decreasing image pixel size. The high spatial resolution remains evident in the anatomy of the skull phantom and is comparable to that of other photon-counting CT prototypes present in the literature. We conclude that the deep silicon-based detector used in our study could provide improved spatial resolution in patient imaging without increasing the x-ray dose.

1. Introduction

The introduction of energy-resolved, photon-counting detectors is expected to constitute the next big development in computed tomography (CT).¹ The anticipation is that such CT systems will provide higher spatial resolution, improved signal-to-noise ratio through optimal energy weighting,² material-selective imaging through material basis decomposition,^3,4 elimination of certain imaging artifacts (e.g., beam hardening), and the possibility to lower the patient dose in low-dose imaging tasks.^5,6 Despite extensive research with the aim to develop the necessary technology, photon-counting CT suitable for patient scanning is currently limited to a handful of prototype systems used for proof-of-principle patient imaging.^7–12

Research into photon-counting CT has been focused mainly on two detector materials, namely cadmium (zinc) telluride (CdTe) and silicon. In addition to the common challenges of photon-counting detectors, either material has its own characteristics and challenges, and which detector material will be long-time preferable based on performance, reliability, and cost is still an open question.

A common challenge for photon-counting detectors is the high count rate in CT applications, which can lead to pulse pile-up, where two (or more) incident photons arrive at a detector pixel within the same dead time. This causes the photons to be counted as one, resulting in both a loss of counts and a degradation of the recorded energy spectrum. To reduce the amount of pileup, pixels can be made smaller to decrease the probability of simultaneous photon arrivals. However, this increases the probability of charge sharing, where a single photon interaction is registered in two (or more) adjacent pixels. This results in double counting of photons and as well as a skewing of the spectrum toward lower energies.¹³ Although anticoincidence logic in the readout electronics can be used to reduce the impact of charge sharing (and K-fluorescence),^14,15 it tends to perform poorly under high count rates.¹⁶

Other challenges for photon-counting detectors, causing double counting and degraded spatial and energy resolution, are Compton interactions and K-fluorescence.^13,17–20 Detectors based on CdTe have a low probability of Compton interactions but a high probability of K-fluorescence, whereas the opposite is true for silicon. In K-fluorescence, part of the deposited energy from an x-ray interaction is emitted as a secondary photon and reabsorbed up to a few hundred micrometers away. Similarly, a Compton-scattered photon deposits only a small fraction of its energy at the site of interaction, whereas the energy in the scattered photon either escapes the detector or is reabsorbed several millimeters away.²¹ As long as the energy of the primary interaction is above the minimum energy threshold, however, the photon will still be counted and contribute signal to the image, albeit in a lower energy bin.

Compound semiconductor detectors, such as CdTe, further have a high probability of charge trapping and charge carrier recombination due to impurities in the detector material, leading to degraded spectral information.¹³ At high photon fluxes, low hole mobility can also lead to polarization, which can cause a complete breakdown of the sensor.²² Silicon, on the other hand, has a low probability of charge trapping and recombination due to the high crystal purity. Furthermore, the charge carrier mobility is high for both electrons and holes, minimizing the risk of polarization and preventing energy blur due to slow charge collection. This makes it possible to combine high count-rate capability with high energy resolution, and energy resolutions in the range of 3.5 to 5.4 keV full-width at half-maximum (FWHM) or 1.6 to 2.3 keV root mean square (RMS) has been reported for a silicon strip detector for CT.^23,24 Even though CdTe sensors can achieve resolutions below 1 keV when connected to slower readout electronics,^20,25,26 typical energy resolution values reported for high-flux CdTe detectors are 6 to 10 keV FWHM (2.5 to 4.2 keV RMS).^27,28

For dose efficiency reasons, the depth of a photon-counting detector is determined by its material. Full absorption requires a few millimeters of CdTe but 60 mm of silicon, increasing the requirements on alignment for a silicon-based detector and preventing placing the electrodes at the top and bottom of the detector.

Of the limited number of photon-counting CT systems capable of patient scanning described in the literature, all use CdTe-based detectors.^7,29,30 In this paper, we describe the resolution characterization of a CT scanner using a deep, silicon-based, photon-counting detector, which, to the best of our knowledge, is the first such prototype system capable of patient scanning. The system is based on a commercial CT gantry where the original detector has been replaced by several edge-on, silicon strip detectors developed specifically for CT applications.^24,31,32 The edge-on design alleviates several of the challenges mentioned above. First, charge sharing cannot occur between silicon strips, effectively limiting the charge sharing to a single detector dimension (instead of two). Second, the silicon strips are interfolded with tungsten sheets, which minimizes the probability that a Compton scattered x-ray will interact elsewhere in the detector and cause a double count. Third, the use of depth segments reduces the count rate per channel proportional to the number of segments, effectively decoupling pile-up from pixel size and enabling handling of the high count rates encountered in CT applications.^24,33 Fourth, the strips can be kept at around 0.5-mm thickness, resulting in very fast charge collection and low diffusion of charge carriers. In addition to the detector, the original x-ray tube has been replaced by a modified tube with smaller focal spot in the prototype system. The combination of smaller pixel size offered by the silicon strip detector and the small focal spot results in a system with significantly higher spatial resolution than current state-of-the-art scanners found in clinical use.

Similar studies have been carried out for existing photon-counting CT prototypes. These have demonstrated not only the ability to produce images with higher spatial resolution, as expected from the smaller pixel size, but also the clinical value of such images.^{10,12,34–37} Higher spatial resolution is expected to improve the diagnostic quality in several CT applications, including imaging of the temporal bone, lung nodule characterization, visualization of calcified plaques, and imaging of bone fractures in trauma patients.⁶ Here, we aim to demonstrate that deep silicon-based, photon-counting detectors offer similar benefits in terms of image resolution and thus that silicon may constitute a viable alternative for future photon-counting CT detectors.

2. Methods

2.1. System Description

The photon-counting prototype system used here is based on a commercial Lightspeed VCT scanner (GE Healthcare, Chicago, Illinois). The original energy-integrating detector has been replaced by a new detector housing, equipped with eight-energy-bin silicon strip detectors, described in detail elsewhere,²⁴ placed side by side in the imaging plane. This results in a single-slice, full-field-of-view CT scanner with 0.19-mm in-plane pixel size measured at the isocenter. The original x-ray tube has further been replaced by a modified version, where the height of the filament was changed to reduce the focal spot size, giving a nominal in-plane focal spot of 0.4 according to IEC60336/1993. In the current work, the lowest energy threshold for each detector strip was selected as low as possible such that for the majority of pixels, no noise counts were typically recorded over a frame time with the x-ray tube switched off. The remaining energy threshold was then chosen so that at low count rate and with 6-cm polyethylene (PE) attenuation, an equal number of counts were registered in each energy bin. Below, bins 1 to 3 are referred to as low energy bins, bins 4 to 6 as medium energy bins, and bins 7 and 8 as high energy bins.

A well-known method for increasing the in-plane sampling in CT systems is the quarter pixel offset, i.e., letting the center of the central detector pixel be offset laterally by 0.25 pixels from the center line (drawn from the focal spot through the isocenter). Ideally, this ensures that conjugate rays from projections 180 deg apart are offset by exactly half a pixel, effectively increasing the spatial sampling by a factor of two. However, due to the small pixel size and mechanical limitations, it was not possible to achieve and maintain a center pixel offset to this accuracy in the presented system. Therefore, although interlacing of conjugate rays was used when resampling and interpolating the sinogram, the resulting increase in the radial sampling is expected to be lower than for the ideal case.

The detector was run at $300\mu \mathrm{s}$ projection time, giving 3333 projections per revolution. After reading out the raw data from the detector, all data handling was performed in Matlab (Mathworks, Natick, Massachusetts). Before image reconstruction, flat fielding was performed in the projection domain using calibration data obtained with a step wedge phantom of varying PE thicknesses in the range of 0 to 40 cm. For each individual detector channel, the sum of photon counts over all energy bins was mapped to PE thickness and stored in a look-up table. This map was subsequently applied to the measured photon count sinogram (where all energy bins had been summed) to generate a PE thickness sinogram, employing logarithmic interpolation between the measured points. (For the pixel response and focal spot measurements, naïve flat fielding was obtained by normalizing the response of each pixel with its corresponding response in the absence of a knife edge or tungsten wire.) Finally, after transforming the fan-beam sinogram into a parallel-beam geometry (interlacing conjugate rays and resampling on a finer grid), Matlab’s built-in function for filtered back projection (FBP), iradon, was used for image reconstruction. The pixel size of the reconstructed images was varied for different imaging tasks, as indicated in Sec. 3.

2.2. Pixel Response and Focal Spot Measurement

The in-plane pixel response was characterized by keeping the x-ray tube stationary and placing a knife edge across the row of pixels as close to the detector as possible, about 80 mm from the proximal silicon edge. The method was adapted from the literature, but since the presented system consists of a single slice only, oversampling could not be achieved by placing the knife edge diagonally across the row of pixels.^38,39 Instead, a stepper motor was used to scan the knife edge across several pixels in steps of $48\mu \mathrm{m}$ (corresponding roughly to eight times oversampling) with submicrometer precision. The obtained scan profiles from multiple pixels were then combined into a single, oversampled edge spread function. By fitting measurements from several pixels and enforcing geometric consistency, the uncertainty in the distance from the knife edge to the detector (estimated to be a few millimeters) could further be prevented from directly affecting the measurement result. To reduce the effect of measurement noise, spline smoothing was applied, after which the pixel response was obtained through direct differentiation. The proximity of the knife edge to the detector ensured a large magnification of the pixels and the estimated widening of the pixel response due to the finite focal spot size was estimated to less than 1%. Therefore, deconvolving the measured pixel response with the focal spot profile would have negligible effect on the result and was omitted.

The in-plane focal spot profile was characterized using two methods. First, in order to get an accurate measurement near the center of the detector, a knife edge scan was performed in the same way as for the pixel response. This time, the knife edge was placed as close to the x-ray tube window as possible, about 200 mm from the nominal focal spot position, and scanned across several pixels using $9\mu \mathrm{m}$ steps between projections (corresponding roughly to eight times oversampling at the detector). As for the pixel response, the measurements were combined, smoothed, and the focal spot profile was then obtained through differentiation. The magnification of the focal spot at the detector plane resulted in an estimated widening of the focal spot due to the finite pixel size by less than 3%, which was deemed negligible.

Second, to measure the how the in-plane focal spot width varies with distance from the central line, simpler but coarser wire measurements were performed.³⁹ The focal spot profiles at off-center positions were measured by keeping the x-ray tube stationary and introducing several $100\text{-}\mu \mathrm{m}$ tungsten wires placed close to the x-ray tube window with different lateral offsets from the center line. The focal spot profiles were obtained directly from these projections after normalization and smoothing to remove noise. As before, omitting deconvolution with the pixel response function and the projected wire cross section was justified by the negligible effect on the spot profile due to the thin wires and large magnification of the focal spot.

The pixel response and focal spot profile at the isocenter, obtained from edge scan measurements, were Fourier transformed to obtain the corresponding MTFs. These were then multiplied to obtain the in-plane system MTF at the isocenter.

2.3. Imaging

Tomographic images were acquired using the medium bowtie filter, a tube current of 200 mA, a tube voltage of 120 kVp, and a fixed rotation speed of $1\text{revolution}/\mathrm{s}$. The tube current was chosen to achieve a clinically relevant patient dose at the limited rotation speed of $1\text{revolution}/\mathrm{s}$ of the prototype system. At the given tube current and for the imaging tasks described below, the number of counts directly behind the objects imaged is up to a few hundred per projection and pixel. This count rate should be close to the linear regime of the detector and little effect of pileup is therefore expected behind the object. (At the object edges, however, count rates can be much higher for some projections; this is handled by the flat fielding and logarithmic interpolation described above.)

For the FBP reconstruction, a Hamming filter with cutoff at 2.0 times the native Nyquist frequency of the detector (i.e., assuming ideal quarter pixel offset) was used, independently of the reconstructed pixel size. In order to investigate the effect of noise on the perception performance (i.e., the ability to distinguish small features) and to perform approximate dose-matching, images were reconstructed using projections from between one and four revolutions.

For dose matching purposes, the CT dose index (CTDI) in free air was calculated. In our prototype, a wider-than-usual margin for the collimation had to be applied to compensate for the lack of focal spot tracking in the collimator. To enable fair comparison and representative dose, the overbeaming was compensated for in the CTDI calculation by only including the part of the dose aimed at the detector (treating the single slice as if it were one of infinitely many in the $z$-direction). (The same compensation was done for the state-of-the-art system used for comparison.) This was achieved by first measuring the beam profile in the $z$-direction at the isocenter by continuously translating a small solid-state detector (LoniMover with CT Dose Profiler, RTI, Mölndal, Sweden) through the beam. The geometric efficiency was then calculated as the fraction of the radiation that was within the nominal collimation width of the single detector slice. The measured CTDI for the full beam (Piranha with DCT10, RTI, Mölndal, Sweden) was then multiplied by this value for an effective CTDI of 55 mGy per revolution.

In the first imaging task, the spatial resolution in reconstructed images was assessed using the high-resolution module CTP714 of a Catphan 700 CT phantom (The Phantom Laboratory, Greenwich, New York). The module contains sets of aluminum line pairs in a matrix of urethane, with spatial frequency of between 1 and $30\mathrm{lp}/\mathrm{cm}$. Images from the prototype system acquired according to above were compared to axial images of the same phantom obtained on a clinical state-of-the-art scanner with 0.62-mm in-plane pixel size measured at the isocenter. These were obtained from an axial scan of a single revolution using the smallest focal spot at 270-mA tube current, 120-kVp tube voltage, $1\text{-}\text{revolution}/\mathrm{s}$, and 40-mm nominal collimation. The reference images were reconstructed using the highest-resolution mode and kernel available on the scanner, with the adaptive iterative reconstruction switched off in order to give a fair comparison. The tube current was chosen to match the photon flux at the isocenter for the two systems (given the different source-to-isocenter distance and x-ray tubes), as verified by measurement of the CTDI in free air using a 100-mm pencil ionization chamber (Piranha with DCT10, RTI, Mölndal, Sweden). Based on manufacturer documentation, the overbeaming for the state-of-the-art scanner was taken to be 10% at 40-mm collimation, which was compensated for in the CTDI calculation. The CTDI corrected for overbeaming was found to be 3% lower for the prototype system compared to the state-of-the-art system at the given tube currents.

In the second imaging task, an anthropomorphic skull phantom was used to demonstrate the spatial resolution in a situation more closely related to those encountered clinically. The phantom consists of a cranium enclosed in a thin-walled plastic tube filled with deionized water. The parameters used for sinogram acquisition and image reconstruction for the prototype system were identical to those used for the resolution phantom.

In addition, a point-spread function (PSF) phantom consisting of a 16-cm-diameter disk of PE with a $100\text{-}\mu \mathrm{m}$ tungsten wire running axially through the center was imaged on the prototype system. From the reconstructed image, a patch of $41\times 41\text{pixels}$, centered on the wire and corresponding roughly to nine times the FWHM of the PSF, was extracted. The average PSF was obtained by averaging (in order to reduce noise) four line spread functions, two horizontal, and two vertical, going through the center of the patch. Finally, the MTF was obtained by taking the Fourier transform of the averaged PSF. Since the FWHM of the averaged PSF in the image was about seven times the width of the tungsten wire, it was deemed that no oversampling or compensation for the wire thickness was necessary.

3. Results

3.1. Pixel Response and Focal Spot Measurement

The results from the edge scan measurements of the in-plane detector pixel response and focal spot profile are shown in Fig. 1. The FWHMs were calculated to be 0.21 and 0.22 mm for the pixel and focal spot, respectively, in good agreement with what is expected from the system specifications. The focal spot profile shows two horns, as expected from the spiral shape of the filament.⁴⁰ In addition, two side lobes, likely a result of over-focusing electrons from the filament edges, are visible and account for roughly 20% of the total output.

Fig. 1.

(a) In-plane pixel response and (b) focal spot profile along the center line measured using edge scan and shown at the isocenter.

An interesting feature of the pixel response of energy-resolved detectors, previously predicted analytically and in simulations,^41–44 becomes apparent in Fig. 2(a), where the in-plane pixel response curve from Fig. 1 has been decomposed according to photon energy. Due to charge sharing between adjacent pixels and the resulting categorization of a single high-energy photon as multiple low-energy photons, the pixel response for low-energy bins is widened and has pronounced horns close to the pixel boundary. For high-energy bins, the opposite is true; fewer high-energy photons are registered close to the pixel boundary due to their deposited energy being shared between pixels. No similar effect is seen between the energy bins in the focal spot profile measurement, shown in Fig. 2(b), where all curves have similar FWHM (despite slight individual shifts induced by the curve fitting and large amounts of noise on the left-hand side where the knife edge shadow results in poor statistics). This indicates that the horns and lobes in the focal spot profile share a similar energy spectrum as the rest of the profile.

Fig. 2.

(a) In-plane pixel response and (b) focal spot profile for different energy bins measured using an edge scan and shown at isocenter.

Figure 3 shows the results from the wire-based focal spot profile measurement for different perpendicular distances to the center line at the isocenter depth. There is a seemingly linear widening of the focal spot profile with lateral distance from the isocenter, as expected from rectangular illumination of an anode disk with beveled edge. Although the profiles are less well resolved than those in Fig. 1, the wire and edge scan measurements agree both in shape and FWHM.

Fig. 3.

Focal spot profiles at (a) different distances perpendicular to the center line at the isocenter depth and (b) corresponding calculated focal spot FWHM values measured using tungsten wires.

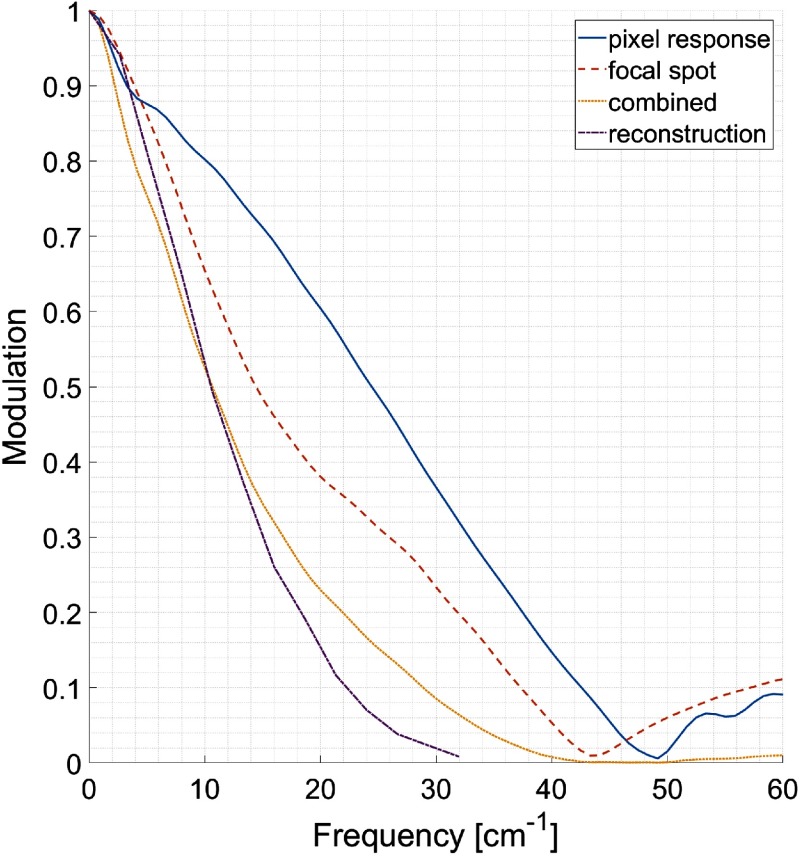
The isocenter MTFs for the pixel response, the focal spot profile and the combined system (obtained by multiplying the former two), are shown in Fig. 4. The combined system MTF intersects 50%, 10%, and 2% modulation at 10.7, 28.9, and $37.4{\mathrm{cm}}^{-1}$, respectively. In addition, the MTF calculated from the reconstruction of the tungsten wire phantom, using one revolution of sinogram data and 0.16-mm pixel size [identical to Figs. 6(b)–6(d)], is shown. The intersects for the reconstructed MTF at 50%, 10%, and 2% are 10.5, 22.3, and $29.9{\mathrm{cm}}^{-1}$, respectively.

Fig. 4.

MTFs from edge scans corresponding to pixel response, focal spot profile and their product projected at the isocenter. In addition, the MTF as measured from the PSF of the reconstructed image of a wire is shown.

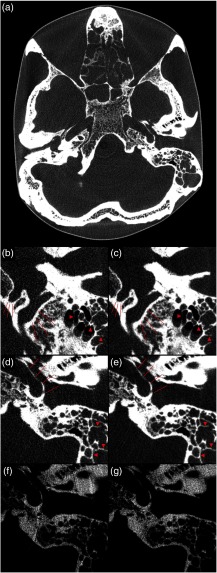
Fig. 6.

Photon-counting CT images of the anthropomorphic skull phantom at clinical photon fluxes. (a) A reconstruction with 190-mm field-of-view and 0.19-mm pixel size whereas the remaining panels show detailed views with 0.16-mm pixel size. (b) and (d) Reconstructed from one revolution, corresponding to native slice thickness; (c) and (e) reconstructed from two revolutions, mimicking the number of photons per slice of a conventional CT detector. Arrow heads indicate septations in mastoid cells and lines indicate delineation of the hypoglossal canal, the sigmoidal sinus and the carotid canal. (f) and (g) The same detail as (d) and (e), reconstructed from two revolutions using only the low and high energy bins, respectively.

3.2. Imaging

Figure 5 shows the results from the line pair imaging, both on the prototype system and on the reference state-of-the-art scanner. The higher resolution of the prototype system becomes evident when comparing the detectability of line pairs in Figs. 5(a) and 5(b) with that of Figs. 5(e) and 5(f); with the prototype system lines up to $19\mathrm{lp}/\mathrm{cm}$ are detectable, whereas with the state-of-the-art system individual lines are detectable up to $14\mathrm{lp}/\mathrm{cm}$. Reducing the image pixel size, modulation is detectable up to around $22\mathrm{lp}/\mathrm{cm}$ for the prototype system as seen in Fig. 5(c). Further, the perception performance in Figs. 5(c) and 5(d) is limited by statistical noise; doubling the number of photons allows detection of lines at even higher spatial frequencies, as seen in Figs. 5(g) and 5(h).

Fig. 5.

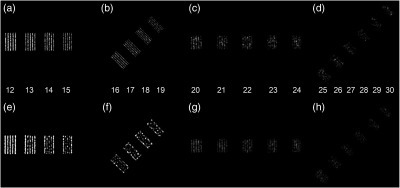
Catphan 714 line pair images. (a)–(d) 12 to $30\mathrm{lp}/\mathrm{cm}$ on the prototype system, reconstructed from two revolutions. (e) and (f) 12 to $19\mathrm{lp}/\mathrm{cm}$ on the state-of-the-art system, dose matched to (a)–(d). (g) and (h) 20 to $30\mathrm{lp}/\mathrm{cm}$ on the prototype scanner reconstructed at twice the dose of (a)–(d). (a), (b), (e), and (f) Reconstructed with 0.098-mm pixel size; (c), (d), (g), and (h) reconstructed with 0.059-mm pixel size.

Finally, the results of the skull phantom imaging are shown in Fig. 6. Figure 6(a) shows a full reconstruction on a $1024\times 1024\text{-}\text{pixel}$ matrix at clinical CDTI and native slice resolution (e.g., about half that of a conventional CT scanner, and thus about half the number of photons). Figures 6(b) and 6(d) show reconstructions with a smaller field of view of the same data, with markers highlighting the fine details visible. For comparison, Figs. 6(c) and 6(e) show the same views reconstructed from two revolutions, mimicking the number of photons expected if using the same slice thickness as a conventional CT scanner. This shows the noise level that would be expected with the presented detector if maintaining the same slice thickness as a conventional scanner by summing two adjacent slices. Figures 6(f) and 6(g) show details reconstructed using only low and high energy bins, respectively, in order to show the effect of the narrower pixel response function for high energy bins (seen in Fig. 2) on a reconstructed image. Although care should be taken when interpreting these panels, given that the noise structure and amount of ring artifacts differ, the high-energy-bin image is perceived as somewhat sharper and more detailed.

4. Discussion

The above results demonstrate the feasibility of employing previously presented edge-on, silicon-based detectors in a full-field-of-view CT system under clinical imaging conditions. This confirms that the developed detector is capable of handling the fast acquisition times and high photon fluxes necessary for patient scanning. Further, the resolution agrees well with what we have previously seen in single-sensor tabletop experiments, showing that multiple sensors can be tiled into a full-field-of-view detector while maintaining resolution performance.

Looking at Fig. 4, it is evident that the resolution of the system is due both to the smaller detector pixels and the focal spot; a smaller focal spot alone would not have resulted in a considerable improvement in a state-of-the-art system for which the pixel MTF decays twice as fast as in our prototype. Although this is an intrinsic feature of smaller pixel size (with the same resolution benefit expected regardless of the detector type), achieving the same results with an energy integrating detector would be difficult for two reasons. First, the relative area taken up by the reflective layers between individual scintillator crystals in an energy integrating detector increases with smaller pixels, resulting in an expected lower dose efficiency and thereby more noise. Second, in an energy integrating detector there is no ability to discriminate and filter out electronic noise using a low-energy threshold, as is done in a photon-counting detector, which is also expected to increase the relative noise level if moving toward smaller pixel size.

The dip at low frequencies seen for the pixel MTF in Fig. 4 likely stems from the wide but low-intensity (a few percent of maximum) shoulders in the pixel response function seen in Fig. 1. These are not an artifact but rather attributed to scatter in the detector. However, due to the small absolute magnitude the shoulders, their effect on the MTF becomes sensitive to measurement noise and normalization. Therefore, the dip at low frequencies may be exaggerated in the edge measurement, as suggested by the higher values of the MTF obtained from the reconstructed image compared to the combined system MTF at frequencies below $10{\mathrm{cm}}^{-1}$. The MTF shape is consistent with the expected effect of secondary interactions of Compton scattered photons, namely, to superimpose an image blurred by a wide kernel on top of the image of primary interactions. This preserves the largest image features, i.e., the spatial frequencies close to zero, while suppressing contrast for medium-sized and small features.

The effect of charge sharing is less readily visible from the pixel MTF in Fig. 4, but its existence can be inferred from the energy-dependence of the in-plane pixel response. The horns visible in the low-energy-bin PSF in Fig. 2 shows that photons interacting near the boundary between two pixels are registered as two low-energy photons, one in each of the two pixels, rather than as a single high-energy photon. This effect has previously been predicted in simulations of charge sharing in photon-counting detectors.^41–44 An interesting consequence of charge sharing is that the resolution becomes dependent on the energy threshold, as the broadening of the PSF takes place in the low-energy bins whereas the PSF in the high energy bins is narrowed by the relocation of counts to lower energy bins.⁴⁵ In theory, this would allow tuning the resolution of the system by adjusting the lower threshold or by weighting of the energy bins. However, this would come with a large penalty in dose efficiency or noise, as seen in the reconstruction from high-energy bins only in Fig. 6.

The steeper slope in the focal spot MTF before $20{\mathrm{cm}}^{-1}$ seen in Fig. 4 can be attributed to the pronounced side lobes of the focal spot profile in Fig. 1. However, the focal spot MTF suggests that the side lobes, perhaps surprisingly, do not affect the expected system resolution noticeably. Still, the number of line pairs visible in Fig. 5 is lower than what would be expected from the combined system MTF but is in reasonable agreement with the MTF obtained from the reconstructed tungsten wire. The lower MTF of the reconstructed images is likely due to four causes: the lack of ideal quarter pixel offset (as mentioned in Sec. 2), artifacts due to the naïve detector calibration and preprocessing (seen in Fig. 6 and discussed below), the limit set by the photon statistics (as mentioned under Sec. 3), and the interpolation applied in the reconstruction. Since the former two are areas where improvements are possible, it is expected that the overall detectability could be further increased.

Based on Fig. 6, it is clear that the presented prototype is capable of high-resolution imaging of the skull without increasing the x-ray dose to the patient compared to current protocols. In particular, the sharp bone septa of the ethmoidal sinuses and mastoid cells and the clear delineations of foramina, emphasized in the magnified panels, are expected to be of interest to ear–nose–throat and neuroradiologists. It should be stressed that the resolution benefit presented here is expected also when using the silicon sensors for spectral imaging since the spectrally separated data are acquired simultaneously using multiple energy bins in each pixel. In dual-kVp systems (dual source and kVp-switching) on the other hand, the spectral data are acquired separated in time and space, and the spectral reconstruction has to combine the data from the separate measurements. This results in a spatial blur of the image and current clinical dual-kVp systems generally only offer soft reconstruction kernels for spectral images.

The clinical benefit of high-resolution, photon-counting CT of the skull has been previously established in the literature by imaging formalin-fixed cadaveric temporal bones on a prototype scanner.³⁷ The images presented above show a comparable level of detail to those presented in the temporal bone study, at a comparable patient dose (55 mGy versus 61 mGy CTDI). This qualitative assessment is supported by the values of the reconstructed MTF presented above, compared to the mentioned temporal bone study at 50%, 10%, and 2% modulation: 10.5 versus 11.2, 22.3 versus 18.4, and 29.9 versus $21.1{\mathrm{cm}}^{-1}$, respectively. Therefore, we argue that the same clinical benefit could be achieved with a CT system mounted with the silicon-based detector used here.

Figure 6 also reveals beam hardening and ring artifacts in the images from the prototype system, both of which are mainly due to the naïve calibration and flat fielding of the prototype detector used here. In particular, beam hardening artifacts can be removed by employing a proper material calibration before reconstruction and performing basis material decomposition on the measured data.³ In this procedure, the object composition is approximated as a linear combination of two or three basis materials, and the projected amount of each basis material along each projection line is inferred based on the spectral information from the detector. This allows reconstructing monoenergetic images free from beam hardening artifacts.³ Further, the images from the prototype system in Fig. 6 do not benefit from the extensive pre- and postprocessing applied in a commercial reconstruction software, which likely further contributes to the visibility of artifacts.

It is sometimes claimed that decreasing the pixel size has the drawback of increasing image noise. It is true that the reconstructed image resolution must be increased in order to take advantage of the improved spatial resolution enabled by smaller detector pixels, and this leads to a higher noise variance in the reconstructed image. However, if the detector pixel size is decreased while other performance parameters are kept equal, the result is that more information becomes available to the reconstruction algorithm, and the resolution of the reconstructed image can be adapted to the imaging task under consideration. In fact, decreasing the detector pixel size allows reducing the image noise level if the reconstructed image resolution is kept constant.⁴⁶ For many realistic detector designs, however, there is a decrease in dose efficiency and energy resolution with decreased pixel size since smaller pixels suffer more from charge sharing and K-fluorescence, as discussed previously.

5. Conclusion

We have performed the first quantitative evaluation of the spatial resolution performance of a photon-counting prototype CT scanner employing a full-field-of-view silicon-based detector. The presented system offers higher spatial resolution than a current clinical state-of-the-art scanner, on par with that of the photon-counting CT prototype systems capable of patient scanning present in the literature. The high spatial resolution is visible in images of an anthropomorphic skull phantom acquired at clinical CTDI and at native slice thickness, which is about half that of a conventional CT system. Given the clinically relevant scan settings and the full field-of-view, we argue that the resolution benefit would remain when scanning live patients in a clinical setting. Further taking into account the discussed benefits of deep silicon-based, edge-on detectors (absence of K-fluorescence and polarization and less sensitivity to pileup and charge sharing), we view these as potential candidates for future photon-counting CT systems.

Biography

Biographies of the authors are not available.

Disclosures

JdS, FG, BC, MP, MS, and MD are shareholders and/or have other financial interests in Prismatic Sensors AB developing silicon-based, photon-counting CT detectors. MP is a visiting researcher with GE Research, New York, USA.