The Role of Humidity in Associations of High Temperature with Mortality: A Multicountry, Multicity Study

Abstract

Background:

There is strong experimental evidence that physiologic stress from high temperatures is greater if humidity is higher. However, heat indices developed to allow for this have not consistently predicted mortality better than dry-bulb temperature.

Objectives:

We aimed to clarify the potential contribution of humidity an addition to temperature in predicting daily mortality in summer by using a large multicountry dataset.

Methods:

In 445 cities in 24 countries, we fit a time-series regression model for summer mortality with a distributed lag nonlinear model (DLNM) for temperature (up to lag 3) and supplemented this with a range of terms for relative humidity (RH) and its interaction with temperature. City-specific associations were summarized using meta-analytic techniques.

Results:

Adding a linear term for RH to the temperature term improved fit slightly, with an increase of 23% in RH (the 99th percentile anomaly) associated with a 1.1% [95% confidence interval (CI): 0.8, 1.3] decrease in mortality. Allowing curvature in the RH term or adding terms for interaction of RH with temperature did not improve the model fit. The humidity-related decreased risk was made up of a positive coefficient at lag 0 outweighed by negative coefficients at lags of 1–3 d. Key results were broadly robust to small model changes and replacing RH with absolute measures of humidity. Replacing temperature with apparent temperature, a metric combining humidity and temperature, reduced goodness of fit slightly.

Discussion:

The absence of a positive association of humidity with mortality in summer in this large multinational study is counter to expectations from physiologic studies, though consistent with previous epidemiologic studies finding little evidence for improved prediction by heat indices. The result that there was a small negative average association of humidity with mortality should be interpreted cautiously; the lag structure has unclear interpretation and suggests the need for future work to clarify. https://doi.org/10.1289/EHP5430

Introduction

There is strong experimental physiologic evidence that the stress put on the human organism by high air temperatures is higher, by many measures, if humidity is higher, in particular because heat loss by evaporation is reduced in a more humid environment (Davis et al. 2016; Hanna and Tait 2015; McGregor and Vanos 2017). Various heat indices have been developed to allow for this (Anderson et al. 2013; Davis et al. 2016; Hanna and Tait 2015; McGregor and Vanos 2017; Steadman 1979) and, in particular, used in heat warning systems (Hajat et al. 2010). These thermal comfort variables were not developed to predict mortality, but, following a prima facie argument that they might do so better than dry-bulb temperature, some epidemiologists have used them in mortality studies. Of studies comparing a heat index with dry-bulb temperature as predictors of mortality, some found evidence that the index predicted better [e.g., Zhang et al. (2014)], but others found no consistent improvement of fit (Ragettli et al. 2017; Rodopoulou et al. 2015; Vaneckova et al. 2011), particularly the largest such study, comprised of 107 U.S. cities (Barnett et al. 2010).

The heat indices imply a prespecified form for a combination of risks from humidity and heat. Some daily mortality studies focusing on temperature have included humidity as a separate additional predictor, but usually they viewed it as a confounder, so very few reported the nature of any temperature-adjusted humidity–mortality association. The largest such study, using year-round monthly data from U.S. counties over 30 y (Barreca 2012), found a reverse J-shaped impact of specific humidity (SH), thus indicating slightly positive impacts at the highest levels, which would generally have occurred in summer. A daily year-round mortality study of 11 cities in Zhejiang Province, China, also found increased mortality at high relative humidity (RH) at cold temperatures but little impact of RH at high temperatures (Zeng et al. 2017). A daily summer-only study in three Swedish cities (Rocklöv and Forsberg 2010) found an adverse impact of high RH, particularly at high temperatures, in Stockholm but not the other cities. A daily study of Valencia, Spain, reported the presence of a nonsignificant inverse association of RH with mortality in summer, but gave no further details (Ballester et al. 1997). One other daily study of three European cities found models adding RH separately to temperature fit better [by Akaike information criterion (AIC)] than those incorporating it as apparent temperature, but did not report the nature of the temperature-adjusted RH–mortality association (Rodopoulou et al. 2015). In summary, those few studies reporting the joint temperature and humidity association with mortality do not present a consistent pattern of the residual impact of humidity.

We aimed to clarify the potential contribution of humidity an addition to temperature in predicting daily mortality in summer by use of a large multicountry dataset.

Methods

The data comprised daily counts of deaths (all ages, either all or all natural causes), mean temperatures, and RH from 445 locations from 23 countries across all continents except Africa, with total durations of 5–41 y (between 1972 and 2015) for each location (summarized in Table 1; sources and further details given in Tables S1–S3). These data were assembled through the Multi-Country Multi-City (MCC) Collaborative Research Network (http://mccstudy.lshtm.ac.uk/), described in several previous publications (Armstrong et al. 2017; Gasparrini et al. 2015a, 2015b, 2016, 2017; Guo et al. 2014, 2016, 2017, 2018; Lee et al. 2018; Vicedo-Cabrera et al. 2018). All analyses on the combined data set were carried out in London by the first author.

Table 1.

Distribution of key variables by country.

Country	$N$	Period	Deaths (in thousands)	Distribution of temperature and RH: mean (minimum, maximum) of location means and of location SDs (for RH) across days
				Temperature mean	RH mean	RH SD
Argentina	3	2005–2015	206	23.6 (23.4, 23.6)	68.4 (67.5, 69.9)	11.9 (11.2, 13.1)
Australia	3	1988–2009	360	22.2 (20.1, 24.2)	69.0 (65.7, 70.7)	10.2 (8.5, 11.4)
Brazil	17	1997–2011	1,034	25.6 (20.8, 28.1)	78.0 (70.0, 87.5)	7.7 (5.1, 12.3)
Canada	21	1986–2009	778	17.1 (13.9, 21.0)	71.8 (62.8, 81.8)	10.8 (7.4, 13.8)
Chile	4	2004–2014	89	18.2 (15.5, 21.0)	67.9 (52.0, 74.4)	10.0 (8.2, 11.0)
China	13	1996–2008	250	24.8 (17.6, 28.4)	71.6 (60.1, 80.4)	11.4 (7.4, 15.6)
Czech Republic	4	1994–2015	225	17.3 (16.4, 18.5)	71.1 (67.1, 73.8)	11.6 (11.0, 12.2)
Estonia	5	1997–2015	46	15.5 (15.0, 15.9)	77.8 (77.7, 78.0)	9.5 (9.2, 9.8)
France	18	2000–2010	375	19.4 (16.6, 23.2)	70.1 (57.9, 78.4)	10.3 (8.8, 15.5)
Ireland	6	1984–2007	317	14.2 (13.7, 14.6)	82.2 (80.9, 84.0)	6.8 (5.7, 8.4)
Italy	12	1987–2010	245	23.2 (20.6, 24.9)	68.0 (58.9, 77.8)	11.3 (8.5, 15.5)
Japan	47	1972–2012	10,853	24.2 (19.4, 27.9)	75.2 (67.9, 82.0)	9.2 (6.7, 11.5)
Mexico	10	1998–2014	726	21.7 (14.8, 28.2)	64.6 (42.2, 75.2)	10.8 (7.3, 17.0)
Philippines	4	2006–2010	94	28.5 (28.1, 29.0)	81.5 (78.5, 82.8)	5.1 (3.2, 6.4)
South Korea	7	1992–2010	548	23.7 (23.0, 24.4)	74.4 (69.4, 78.3)	10.6 (9.7, 11.7)
Spain	50	1990–2014	865	22.3 (17.5, 26.9)	60.9 (42.5, 82.9)	11.1 (6.8, 15.9)
Sweden	3	1998–2005	52	16.1 (15.8, 16.3)	73.5 (70.5, 77.2)	9.3 (8.0, 11.1)
Switzerland	8	1995–2013	75	17.9 (15.8, 20.6)	71.7 (67.7, 75.2)	10.4 (9.0, 13.2)
Taiwan	3	1994–2007	246	28.4 (28.1, 28.6)	76.7 (74.4, 79.8)	7.2 (6.4, 8.2)
Thailand	60	1999–2008	540	28.3 (26.4, 29.6)	79.6 (72.5, 86.9)	5.2 (3.7, 7.5)
United Kingdom	10	1993–2006	2,286	15.8 (14.6, 17.5)	69.2 (60.9, 74.8)	11.0 (9.5, 12.2)
United States	135	1985–2006	6,657	23.4 (17.1, 33.2)	67.1 (21.5, 81.4)	10.0 (4.9, 15.4)
Vietnam	2	2009–2013	36	28.7 (28.4, 29.1)	75.5 (72.1, 78.8)	9.7 (5.2, 14.1)
All	445	1972–2015	26,901	23.1 (13.7, 33.2)	70.7 (21.5, 87.5)	9.4 (3.2, 17.0)

Note: N is the number of locations for which useable data was available. The minimum and maximum temperature and relative humidity (RH) are those for each country’s location summer means over all days available for that location, not the minimum and maximum of individual daily means. Daily meteorological data comprised means calculated from hourly data in all except four countries. The exceptions were: Czech Rep: 0700, 1400, and 2100 hours; Italy: every 6 hours; Thailand: minimum and maximum; United Kingdom: hourly for temperature, and 0900 and 1500 hours for RH. For more information including sources, see Table S1. SD, standard deviation.

We focused primarily on mean RH because that was the daily measure of humidity most commonly available. However, there are strong advocates of absolute measures of humidity as most relevant for health (Davis et al. 2016; McGregor and Vanos 2017), in particular because of the strong dependence of RH on temperature, giving rise, for example, to large diurnal variation.

Thus, to allow investigation of whether using an absolute measure of humidity gave different results, we also estimated two measures of absolute humidity: dewpoint and SH. Calculation of these measures from RH and temperature followed standard formulae using the R packages weathermetrics and humidity (version 3.5.0; R Development Core Team), as illustrated in the R code in the supplemental material. Although it was not our intention to provide a comprehensive investigation of heat indices, we also computed apparent temperature (a popular combined temperature and humidity metric, also computed using the weathermetrics package) from temperature and dewpoint (Anderson et al. 2013).

For brevity, we use the term heat as a synonym for high temperature, although we acknowledge that this term is used differently in other contexts (McGregor and Vanos 2017). Because we were concerned with heat, we included only summer months in our analyses (June–September in the northern hemisphere and December–March in the southern hemisphere). Because we primarily sought to identify the contribution of humidity in addition to temperature in predicting mortality, we concentrated on models including both variables, but we also report preliminary analyses comparing the fit of models with just temperature, RH, and dewpoint individually to test our expectation that temperature would have the dominant effect. Statistical core models are described below, with core R code and data on which it can be demonstrated given in the supplemental material. The core models were modified in sensitivity analyses.

We proceeded with a standard two-stage approach, fitting distributed lag nonlinear models (DLNMs) for weather variables at each location and summarizing the distribution of these using multivariate meta-analyses (Armstrong 2006; Gasparrini et al. 2010). The base terms in the location-specific models were similar to those used in summer-only analyses of similar data (Gasparrini et al. 2015a). They comprised smooth functions of calendar year [2 degrees of freedom (df)/decade] for long-term trends and of day in year (4 df with interaction with year as a factor) for within-season variation.

In broad alignment with previous practice, temperature was modeled as a natural cubic spline of 4 df with knots at equal percentiles. Because previous publications indicated that the most adverse effects of heat would be apparent within 3 d (Guo et al. 2014) and exploratory analyses of humidity suggested a similar main lag range, our DLNMs were defined over lags 0–3. For transparency, which we judged important given the complex lag structures for humidity in preliminary analyses, we used a simple stratified (stepped) lag structure: 0, 1, and 2–3, rather than the more usual smooth spline.

For our preliminary analyses, we compared total qAIC (quasi-AIC, summed over all locations) for separate models, each with a single different weather variable: a) temperature, b) RH, c) dewpoint, and d) apparent temperature. All of these variables were included with the same DLNM structure as temperature described above to ensure like-for-like comparability of qAIC. Also for comparability of qAIC, all models were fitted using the same data sample (i.e., excluding days missing in any of the variables, included or not in that model).

To better focus our exploration of models with temperature and humidity, we first explored qAIC in models supplementing the DLNM for temperature with a range of functions for humidity. Because we found that models including dewpoint and temperature gave very similar results to those adding RH, we focused our main attention on RH because of its greater familiarity in public health discourse.

We also explored mutual effect modification of humidity and temperature (interaction). The representation of interactions between two variables with distributed lags is potentially complex, even when both have main linear associations with mortality (Muggeo 2007), and it becomes more so if nonlinearity of one or both associations is considered, as appears strongly indicated for temperature here. We thus made the following simplifying assumptions, which we found broadly supported in the exploratory analyses: a) no cross-lag interactions, i.e., humidity at a specific lag (such as l d) would modify the impact of temperature only at the same lag; and b) the main effect of humidity on mortality, to which interaction terms were added, was assumed linear. Within that framework, we considered that the interaction models in which the humidity coefficient depended on temperature: a) linearly; b) nonlinearly by dividing into temperature ranges with cut points at location-specific percentiles (33rd and 67th, then 50th and 80th, then 50th and 90th); and c) the same as b), but using global percentile cut points.

Associations estimated from the location-specific models were summarized and their heterogeneity explored using random-effects meta-analysis techniques (Gasparrini et al. 2012; Viechtbauer 2010) applied to the weather–mortality associations summed (cumulated) over all lags considered (Gasparrini and Armstrong 2013).

Results

The climates of the 445 locations were primarily temperate, although some were tropical (country summaries given in Table 1, with further variables and location summaries in Tables S1–S3). Mean summer RH was mostly between 60 and 80%. The standard deviation of day-to-day variation in RH, on which our estimate of RH-mortality association depended, was, on average, 9%, although smaller in tropical countries. Within locations, correlations of daily RH, dewpoint, and SH with temperature were, on average, $r=-0.39$, 0.59, and 0.59, respectively. Partial within-location correlations of RH with dewpoint and SH, controlling for temperature, were $r=0.99$ and 0.98 on average and in no country less than 0.97 (details in Table S2).

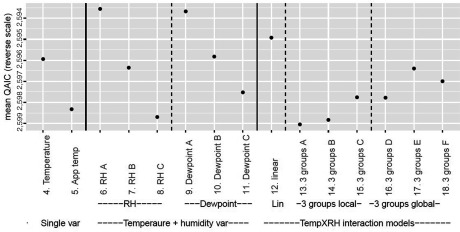
The goodness of fit, as indicated by qAIC (mean over all locations), is shown for all models that include temperature (models 4–18) in Figure 1, which has a reverse y-scale so that better-fitting models are highest (details and results for models 1 to 3 in Table S4). Models with just RH or dewpoint (models 2 and 3, not shown in figure) fit much less well than any of the models that included temperature, only marginally better than the model with no weather terms (model 1).

Figure 1.

Preliminary investigation of goodness of fit of alternative models for humidity. The y-axis shows the goodness of fit as measured by qAIC (quasi-Akaike’s information criterion), averaged over all 445 locations, in reverse order so that higher points better fit the model. All models from model number 6 include temperature [4-degrees of freedom (df) natural cubic spline] plus a range of humidity terms. Models 6–8 include RH (relative humidity) as linear (A), quadratic (B) and cubic (C) polynomials, and models 9–11 are the same for dewpoint. Models 12–18 include, in addition to a linear term for RH, a range of forms of interaction between temperature (temp) and linear RH: linear temperature (model 12); separate RH slopes for each of three groups of temperature with cut points defined by location-specific (models 13–15) and global (models 16–18) percentiles. Further detail is provided in Table S4.

Using mean apparent temperature (model 5) in place of simple temperature (model 4) slightly increased qAIC, indicating poorer predictive ability. Adding a linear RH term to the model including temperature slightly reduced qAIC, indicating better predictive ability (model 6); higher-order polynomial models had higher qAIC (models 7 and 8). We therefore focus most further analysis on linear models. Models for dewpoint (9–11) fit very similarly to those for RH of the same functional form, as did those for SH (not shown), as expected given the high partial correlation of these measures with RH noted above.

Variants of models allowing modification of the RH coefficient by temperature (interaction models) are shown as models 12–18 in Figure 1 (see legend for details of these models). None of these interaction models reduced qAIC if compared to the linear model without interaction (model 6). Interaction model 12, which assumes that the humidity coefficient changed linearly with temperature, came closest, indicating that the grouped temperature models gave no evidence against a linear–linear interaction. The model that fit separate RH coefficients for temperature bins divided at the 50th and 80th percentiles of pooled daily temperatures (22.6 and 25.2ºC) fit second best among the interaction models. We also considered more elaborate models (not shown), for example, those in which the modification of the humidity coefficient by temperature followed a spline curve, but these had markedly higher qAIC.

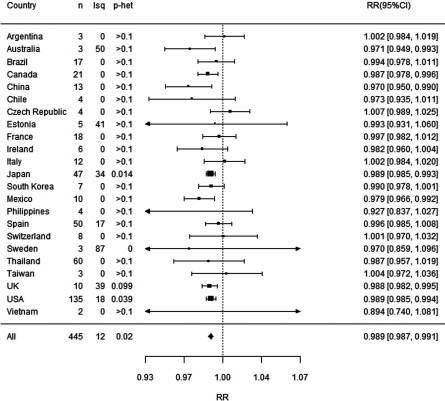
We therefore focus now on the model that fit best: the one that included a temperature spline and a linear term for RH (model 6). Figure 2 shows the average cumulative relative risk (RR) over lags 0–3 associated with high RH by country and overall for this model. The RR shown is for an increment in RH of 23.4%, which is the average of the 99th percentile of the RH deviations from the mean RH for the same day’s temperature. Overall mortality reduced slightly following days with higher humidity, with 99th percentile RH anomalies associated with $\text{RR}=0.989$ [95% confidence interval (CI): 0.987, 0.992]. There was no underlying variation beyond chance between countries [estimated percentage of variation across countries that is due to heterogeneity rather than chance $\left(I^2\right)=0$) and little between locations overall ($I^2=12\%$), although the latter was significant ($p=0.02$).

Figure 2.

Increment in mortality for high humidity, overall and by country. RH is included as a linear term with relative risk given per 23.4% increase, which is the 99th percentile of RH anomalies. All models are adjusted for seasonality, long-term time trends, day of the week, and temperature. For RH and temperature, lag is distributed over lags 0–3 as described in the text. Note: CI, confidence interval; Isq, $I^2$, estimated percentage of variation across studies that is due to true heterogeneity rather than chance; p-het, the p-value for Cochran’s test for heterogeneity between location; RH, relative humidity; RR, rate ratio.

To explore further whether this overall mean result might not pertain to some groups of locations apart from countries, we explored factors that might explain what variation there was in the RH–mortality association across locations within countries by use of meta-regression. However, in doing so, we found no association that could not easily be explained by chance [$p>0.1$ for location-wise summer mean temperature, RH, daily deaths as indicator of population size, or country gross domestic product (GDP)].

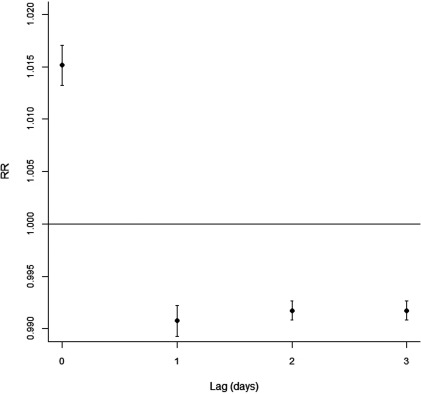
The lag structure of the RH–mortality association was different than anticipated, with positive lag 0 coefficient ($\text{RR}=1.015$) outweighed by negative lag 1 and 2–3 coefficients (with $\text{RR}=0.991$ and 0.992, respectively) (Figure 3).

Figure 3.

Lag structure of relative humidity (RH)–mortality association. The model is as described for Figure 2.

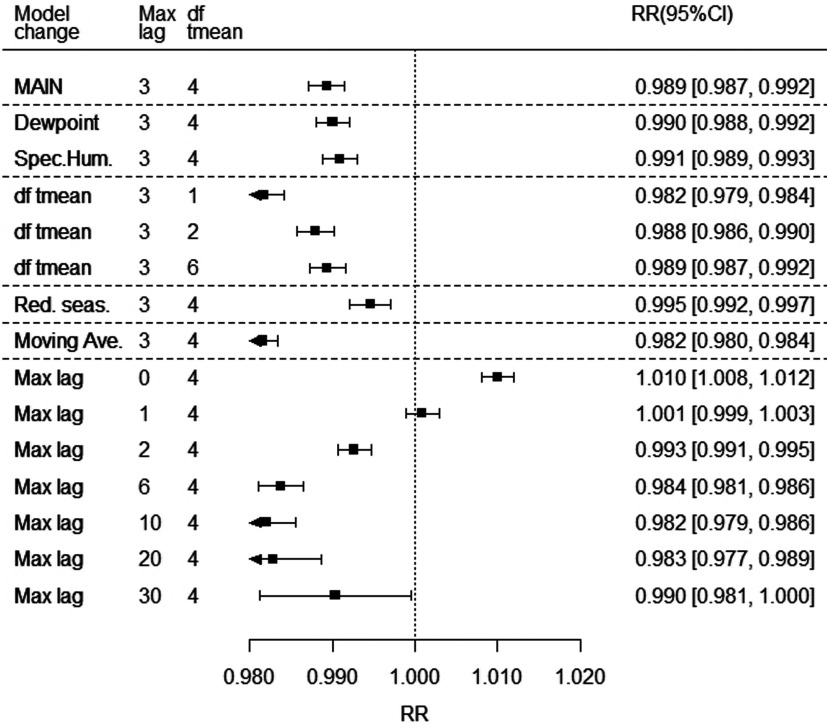
Figure 4 shows the sensitivity of the estimated overall mean cumulative RH–mortality coefficient from model 6 to several alternative model specifications. The only models giving substantially different coefficients were those considering only lag 0, for which RH showed a small positive association with mortality, and lags 0 and 1 (null association). These models had substantially poorer predictive ability by qAIC, however, than the main lag 0–3 model.

Figure 4.

Sensitivity of relative humidity (RH) coefficient estimate to model specification. The figure shows the meta-analytic mean of the coefficient of RH, expressed as rate ratio (RR) for an incement in relative humidity (RH) of 23.4%, which is the mean of 99th percentile anomalies (residual given temperature) over all 445 locations. The top row shows the value of the main model (as in Figure 2), and other rows modify this model as indicated: a) replacing RH with dewpoint and specific humidity, showing RR for the mean of their 99th percentile anomalies: 5.2°C and $3.6\mathrm{g}/\mathrm{kg}$; b) df tmean, modifying the flexibility of the temperature term; c) “Red.seas,” reducing seasonal control by omiting season by year interaction terms; d) “Moving ave.,” replacing the 3-lag-strata distributed lag nonlinear model (DLNM) by a single stratum, equivalent to using a moving average of humidity (and temperature) over lags 0–3; and e) “Max lag,” changing maximum lag of the model, with lags 6–30 with additional lag strata breaking at lags 4,7,14, and 21. Note: CI, confidence interval; df, degrees of freedom.

Figure 4 also shows that using absolute measures of humidity (SH or dewpoint) gave a very similar average rate ratio in a linear model to that for RH, if rate ratios were expressed for the average to 99th percentile anomaly, as with the RH. This was true also for the qAIC (Table S4), distribution of coefficients in the linear model, absence of evidence for modification by temperature, and lag pattern (Figure S1).

Although no model for modification of the humidity–mortality association (interaction) was significant, we mention estimated coefficients for the model in which linear RH coefficients were estimated for each of three temperature groups to demonstrate the extent to which our data may have missed some interaction due to lack of precision. The temperature groups were those that provided optimal fit, with cut points at 22.6 and 25.2°C, which were the global 50th and 80th percentiles. The coefficients varied little by temperature, with CIs that were quite narrow, even for the smaller highest temperature range. They were expressed in the same units as for the overall model and comprised low: 0.989 (95% CI: 0.987, 0.991), medium: 0.989 (95% CI: 0.986, 0.992), and high: 0.986 (95% CI: 0.982, 0.990) (also graphed in Figure S2).

The temperature–mortality associations (Figure S3 shows the meta-analytic average) were virtually identical to those without humidity, described elsewhere (Gasparrini et al. 2015a, 2015b). They varied substantially between (multivariate $I^2=72.8\%$) and within countries ($I^2=53.8\%$).

Discussion

On average, over a large sample of locations in over 23 countries, there was little association of humidity with mortality in summers after adjustment for the effect of temperature. The direction of the small association observed was for lower mortality when humidity was high, opposite to what would be expected if the experimentally well-established impacts of humidity on physiological heat stress translated to impacts on mortality in populations. This study does not identify why this is the case, but one may hypothesize that any adverse health effects from increased heat stress from humidity might be offset or outweighed by other causal pathways; for example, dehydration might be greater in low humidity, particularly from respiration (Sauer et al. 1984), and dehydration has several known adverse health impacts (Liu et al. 2015).

Of previous publications reporting humidity–mortality associations after allowing for temperature effects (reviewed briefly in the “Introduction”), only one other small study (Ballester et al. 1997) reported presence of a negative association in summer, but it did not give details. We also found the adverse impact of high RH reported for Stockholm (Rocklöv and Forsberg 2010) in our Stockholm data, one of a few locations with nonsignificant positive associations. Barreca (2012)’s finding of a small adverse impact of high SH on mortality in the United States contrasts somewhat with ours, including our U.S.-specific result. There were, however, several important differences in methods. In particular, units in the Barreca study were monthly rather than daily mortality, all-year data were used, and although a temperature effect was adjusted for, this was with a single curve assumed to apply across all the United States.

Correlations between temperature and humidity (all measures) were appreciable, but not so high that they prevented estimating mutually adjusted associations of each with mortality. However, we found high very partial correlation between absolute and relative measures of humidity given temperature and, consequently, very similar impacts on mortality (if comparing RRs at the same percentile anomalies in each measure) when temperature was also in the model, as Barreca (2012) also reported. The practical implication of this is that for the purpose of prediction of a health outcome in a regression model with humidity included as a linear term, the additional prediction allowed by adding humidity to temperature will not depend on whether an absolute or relative measure of humidity is used. This is reassuring given uncertainty as to which might be expected a priori as more relevant for health (Davis et al. 2016).

The lag structure of the association of RH with mortality is intriguing. Although a short lag-positive association followed by a longer lag-negative association is sometimes reasonably interpreted as suggestive of short-term mortality displacement (harvesting), we do not find this very plausible here. The negative association appears at lag 1, much earlier than similar patterns that have been seen for heat (Baccini et al. 2008; Hajat et al. 2005), and also, the cumulative negative association outweighing the positive does not fit well with a displacement hypothesis. Another possibility we investigated was that cross-lag correlations of humidity, especially relative, with temperature might play a part. However, after identifying that such cross-lag correlations were small (Table S5), we did not pursue this further.

A hypothesis we find more plausible, though speculation, is that the sharp change from positive to negative association between lags 0 and 1 reflects the impact of change in RH from lags 1 and 2–3 to lag 0. As noted in previous discussions of models for impact of changes in temperature from 1 d to the next, a model with linear impacts for, for example, lags 0 and 1 is algebraically equivalent to one with (linear) impacts of exposure at lag 0 and change in exposure between lags 1 and 0 (Vicedo-Cabrera et al. 2018). This extends to a model with three lag strata as here. In algebra:

$${\mathrm{\beta }}_0{x}_{\text{lag}0}+{\mathrm{\beta }}_1{x}_{\text{lag}1}+{\mathrm{\beta }}_2{x}_{\text{lags}2–3}={\mathrm{\beta }}_0^{\prime }{x}_{\text{lag}0}+{\mathrm{\beta }}_1^{\prime }(x_{\text{lag}0}-x_{\text{lag}1})+{\mathrm{\beta }}_2^{\prime }(x_{\text{lag}0}-x_{\text{lag}2–3}),\text{\hspace{0.17em} \hspace{1em} with \hspace{0.17em}}{\mathrm{\beta }}_0^{\prime }={\mathrm{\beta }}_0+{\mathrm{\beta }}_1+{\mathrm{\beta }}_2,\hspace{0.17em}{\mathrm{\beta }}_1^{\prime }=-{\mathrm{\beta }}_1,\hspace{0.17em}{\mathrm{\beta }}_2^{\prime }=-{\mathrm{\beta }}_2.$$

Thus, a positive coefficient at lag 0 nearly balancing negative coefficients at lags 1 and 2–3 as we found in our results can be interpreted as a near-null coefficient at lag 0, then a change in RH from lag 1 and 2–3 associated with a change in risk in the same direction as the RH change. This interpretation is widely known in life course epidemiology, for example, with opposing-sign coefficients for height at two points in time as predictors of a later health outcome, suggestive of high or low growth being the causal predictors (Cole 2007). Whatever the mechanism, in this time-series context, the impact of the opposite-signed lag-specific associations that we have observed will be approximately neutral on overall cumulative risk over a long period (a summer, for examples) apart from the small beneficial impact of high RH overall. This is because day-to-day increases in RH will be balanced by decreases unless there has been a sustained trend.

The strength of our study lies particularly in its large and geographically varied data set and well-tested methodology. We believe that this is easily the largest study addressing the acute impact of humidity on mortality. However, there are some limitations. Coverage of tropical climates and less developed economies was limited. Our approach would find acute but not chronic effects. Our results were for humidity in ambient air, and we cannot make conclusions from this about effects of humidity in indoor air on mortality. We considered only mortality, and only all-cause mortality; other adverse health events or specific causes of death might exhibit different patterns. It is also possible that our study may have missed particular conditions under which humidity may have had an association with mortality different from the average. The absence of evidence for variation in humidity coefficients across countries or by meta-regression according to broad climate or social indicators (mean temperature or RH; GDP) excludes obvious contenders but cannot exclude some unmeasured factor as being important. Residual confounding is always possible, though our models included those factors that are usually considered critical.

Although we do not draw firm conclusions from this study alone, our results suggest caution against assuming a substantial causal relationship between humidity and mortality in hot weather. Such assumptions are sometime made in designing heat watch warning systems or in projecting impacts on mortality of climate change.

In summary, contrary to widespread expectation, this large study found little association of humidity with mortality in the following few days after allowing for temperature impacts. This indicates that studies considering heat effects on mortality without considering humidity are unlikely to be misleading. The small association we found was of lower mortality following high-humidity days, but we suggest that this should be interpreted cautiously. The absence of evidence from our data for an adverse association of humidity with mortality suggests that public health policy cannot assume presence of such an impact from the physiologic evidence alone, in particular when implementing heat warning systems and estimating climate change impacts.