Abstract
The spinal neurons of the Xenopus embryo that participate in the swimming motor pattern possess two kinetically distinct sets of potassium currents: the fastIKf and sodium-dependentIKNa, which together constitute ∼80% of the outward current; and the slowIKs, which constitutes the remainder. To study their respective roles in cell excitability and the swimming pattern, we have characterized their pharmacological properties. Catechol selectively blocked the fast potassium currents (IC50, ∼10 μm). The block was voltage-dependent, with partial unblocking occurring at positive voltages. α-Dendrotoxin and dendrotoxin-I selectively blocked the slow potassium current. Catechol and the dendrotoxins had different effects on membrane excitability: catechol caused spike broadening but had little effect on repetitive firing, whereas both dendrotoxins markedly increased repetitive firing without affecting spike width. By applying these agents to the whole embryo, we tested the role of the fast and slow currents in motor pattern generation. Catechol had little effect on fictive swimming, suggesting that the fast K+ currents are not critical to circuit operation. However, dendrotoxin disrupted swimming early in the episode and increased the duration of ventral root bursts. The slow K+ current, which is a minor component of the total outward current, thus appears to play an important role in motor pattern generation.
Keywords: potassium channels, catechol, dendrotoxin, 4-aminopyridine, Xenopus, central pattern generator, neural model, repetitive firing
The pattern of neural output produced by a circuit of interconnected neurons depends on the biophysical properties of the constituent neurons, the pattern of synaptic interconnections, the transmitter–receptor systems of those synapses, and the neurohumoral environment. The roles of individual voltage- and ion-gated ion channels have been studied in shaping reflex responses (Byrne, 1979), and recently this analysis has been extended to more complex circuits (e.g., Golowasch and Marder, 1992; El Manira et al., 1994; Dale, 1995b; Nadim et al., 1995; Olsen et al., 1995;Tegner et al., 1997). These channels determine how the synaptic currents are integrated into a pattern of action potentials. They may also be targets for neuromodulators that alter the outputs of the neural circuit (Harris-Warrick et al., 1995a,b; Dale and Gilday, 1996;Nadim and Calabrese, 1997). Potassium channels, in particular, are very diverse and control aspects of membrane excitability such as the delay in spiking in response to sustained synaptic input, the frequency of action potentials, and the degree of accommodation within a burst (e.g., Connor, 1975; Byrne, 1980a,b; McCormick and Huguenard, 1992;Brew and Forsythe, 1995). Testing the roles of potassium currents experimentally requires selective pharmacological tools. However, because few potassium channel blockers are specific, appreciation of the roles of these channels may also depend on computer simulations that incorporate quantitative models of the circuit and the known conductances.
The Xenopus embryo is a preparation in which detailed understanding of how ion channels contribute to motor behavior is possible. The embryonic neurons that control swimming fire a single spike on each cycle. Discharge on either side of the body alternates, causing flexions that drive the animal forward. The spinal circuitry that generates swimming has been well characterized (Arshavsky et al., 1993; Roberts, 1990), and through voltage-clamp analysis of acutely dissociated neurons, quantitative kinetic descriptions of the principal voltage- and ion-dependent channels are available (Dale, 1991, 1993,1995a; Wall and Dale, 1995). Three potassium channels can play a role in the cycle by cycle pattern: the fast-activatingIKf, the slow-activatingIKs, and the sodium-dependent potassium current IKNa, which is kinetically similar to IKf. Through a physiologically based model of the swimming circuit, Dale (1995b) hypothesised that theIKf and IKs play distinct roles in producing the swimming motor pattern. The effects on swimming of nonspecific potassium channel blockers, such as tetraethylammonium and 3,4-diaminopyridine, give some support to these predictions (Wall and Dale, 1994).
We have identified pharmacological agents that selectively block the fast and slow potassium currents in Xenopus spinal neurons; catechol specifically inhibited IKf andIKNa in a voltage-dependent manner, whereas both dendrotoxin-I (DTX-I) and α-dendrotoxin (α-DTX) preferentially blocked the slow current. The effects of catechol and dendrotoxins on cell firing properties were very similar to the predictions of the model. Furthermore catechol, at doses that blocked up to 50% of the fast currents, had no effect on fictive swimming in the intact embryo, but the dendrotoxins significantly altered the motor pattern.
MATERIALS AND METHODS
Dissociation of spinal neurons. Spinal neurons of stage 37/38 Xenopus laevis (Nieuwkoop and Faber, 1956) embryos were dissociated as described previously (Dale, 1991) with slight modifications. Embryos were anesthetized in tricaine methane sulfonate (MS-222, 0.5 mg/ml; Sigma, St. Louis, MO), and, using sharpened tungsten needles, a section of spinal cord extending from the obex of the hindbrain to the level of the anus was removed. The cords from three embryos were incubated for at least 3 min in “normal” saline [in mm: 115 NaCl, 3 KCl, 1 MgCl2, 2 CaCl2, 2.4 NaHCO3, 10 HEPES (Sigma), 10 glucose, and 0.13 mg/ml DNase I (Boehringer Mannheim, Indianapolis, IN), pH 7.6]. The tissue was then incubated for 1 min with Pronase E (1.5 mg/ml, type XIV; Sigma) in “trituration” saline, which was the same as normal saline, except that NaCl was substituted by sodium methane sulfonate. The tissue was then washed in a low-divalent saline [in mm: 115 sodium methane sulfonate, 3 KCl, 2 EDTA (Sigma), 10 1,4-piperazinediethanesulfonic acid (PIPES; Sigma), and 10 glucose, pH 7.0] for 1 min and in a second solution (containing in mm: 115 sodium methane sulfonate, 3 KCl, 0.1 MgCl2, 0.1 CaCl2, 10 PIPES, 20 glucose, and 0.13 mg/ml DNase, pH 7.0). The cords were then gently triturated in trituration saline and DNase (4 mg/ml) to yield isolated cells. These were spread on polylysine-coated plastic culture dishes containing O2-saturated normal saline.
Cell identification. Neurons that had been acutely dissociated in this way retained much of their morphology and could be identified by the criteria of Dale (1991). The cells that make up the swimming central pattern generator (CPG) neurons fall into three classes: “commissural” cells (monopolar cells with pear-shaped somata and initial segments), monopolar cells with circular somata, and multipolar cells. Approximately 90% of cells in the commissural class are glycinergic commissural cells of the spinal circuit, and ∼70% of the monopolar class are also commissural interneurons. The remainder of these and the multipolar classes include mainly descending excitatory interneurons and motor neurons (Dale, 1991; Roberts and Clarke, 1982). Dorsolateral commissural cells are relatively rare in the spinal cord and were presumably included in the CPG class, although they are not part of the central pattern generator per se (Roberts and Sillar, 1990). Rohon Beard (RB) sensory neurons were identified by their large, circular somata containing a large nucleus and prominent nucleolus.
Patch recording in isolated cells. For making whole-cell patch recordings the normal solution bathing the cells was exchanged for a “control” recording medium that contained (in mm) 115 NaCl, 3 KCl, 1 MgCl2, 10 CaCl2, 2.4 NaHCO3, and 10 HEPES. The pH was adjusted to 7.4, and the osmolarity was ∼260 mOsm. The intracellular solution contained (in mm) 100 potassium methane sulfonate, 5 KCl, 6 MgCl2, 5 ATP (sodium salt), 2 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (Molecular Probes, Eugene, OR), and 20 HEPES. The pH was adjusted to 7.4 with KOH, and the osmolarity was adjusted to 240 mOsm, usually by increasing the volume by 10%. Both of these solutions were sterile-filtered before use. In the dendrotoxin experiments we found that the block was more reliable if the extracellular calcium was reduced to 5 mm and the osmolarity was adjusted with glucose. The Ag/AgCl2 ground electrode was separated from the bath by an agar bridge containing control saline. Drugs were applied through a nine-barrel microperfusion apparatus with the nozzle positioned within 150 μm of the cell. Adequate flow was judged by the movement of cells and debris within the field of the microscope when the flow was turned on and off. In voltage-clamp experiments all solutions contained 150 nm tetrodotoxin to block sodium channels and 100 μm CdCl2 to block calcium currents (both from Sigma), and in all experiments the holding potential was −50 mV. In some experiments the sodium-dependent potassium current was blocked by replacing the sodium in the control medium with equimolar N-methyl-d-glucamine (Sigma). To measure INa we modified the external saline by replacing half of the NaCl with TEA-Cl and adding 100 μm CdCl2 and 1 mm 4-aminopyridine (4-AP). The internal saline contained (in mm) 100 cesium methane sulfonate, 1 CaCl2, 10 EGTA, 20 HEPES, 5 ATP, and 6 MgCl2, pH 7.4.
Recordings were made with a List Biologic (Campbell, CA) L/M EPC7 patch-clamp amplifier with the stimulus input and data acquisition controlled by an IBM-compatible computer and a Data Translation DT2831 data acquisition board. When filled with intracellular recording saline the electrode resistance was 4–10 MΩ in the bath. After breaking through to whole-cell configuration the series conductance was ≥0.1 μS, and in voltage clamp the series resistance compensation was typically between 75 and 80%.
Patch recording in the intact spinal cord. Although many neurons fired repetitively in cell culture, we found that repetitive firing was more reliable when making patch recordingsin situ. In accordance with the United Kingdom Animals (Scientific Procedures) Act of 1986, embryos were anesthetized with MS-222, and their dorsal fins were slit open using fine tungsten needles. They were incubated in 0.077 mg/ml α-bungarotoxin (Sigma) for 20 min or until they stopped swimming in response to a tactile stimulus. The skin and muscles on the side and overlying the spinal cord were removed. The embryo was pinned with two tungsten needles through the notochord in a recording chamber that had a volume of 200 μl. A “blind” recording technique was used in which the recording electrode was positioned by course adjustment to just touch the spinal cord, and then it was slowly advanced into the cord to a depth of ∼20 μm. Swimming was initiated by dimming the lights. All recordings included in this study were from neurons that received a rhythmic synaptic drive and were active during swimming and therefore had a high probability of being part of the CPG (Arshavsky et al., 1993).
Drugs. DTX-I and α-DTX were obtained from Alomone Labs (Jerusalem, Israel). Stock solutions of 20 μm were made in control saline and kept refrigerated but used within 2 weeks. Catechol (1,2-benzenediol) and 4-aminopyridine were from Sigma. Catechol is light-sensitive, so refrigerated stock solutions (100 mm) were discarded after 1 week.
Fictive swimming. For convenience, in this paper fictive swimming recorded from the ventral roots of a paralyzed embryo will be referred to simply as “swimming.” The preparation for extracellular recording of ventral root activity was similar to that described forin situ patch recording, except that the embryo was spinalized at the level of the first or second postotic myotome. The embryo was held upright between two pairs of tungsten pins so that glass suction electrodes could be pressed against the intermyotomal clefts to make ventral root recordings. Swimming was started by a brief electrical stimulus to the skin of the tail. At least 3 min elapsed between the end of the last swim episode and the next stimulus. Data were recorded on a cassette tape for later analysis.
To measure burst duration and cycle period, episodes of swimming were acquired with a Data Translation DT31EZ board onto a computer disk. The ventral root records were rectified and integrated over a 2 msec interval. Cycle period was calculated from the midpoints of the ventral root bursts, and the duration of a burst was measured as the time between the first crossing above a threshold and the last crossing below the threshold per burst. Thirty cycles were also averaged, triggered from the leading edge of the burst. The area under the averaged record was a measure of the number of spikes contributing to the bursts.
Statistical analysis. Results are presented as mean ± SEM. In dose–response curves the error bars are 1 SD. Exponential curves were fitted to experimental data using the Simplex algorithm, and concentration–response curves were fitted by the Levenburg–Marquardt method of least squares fitting (Press et al., 1988). Tests of significance are described in Results.
RESULTS
Central pattern generator neurons and Rohon Beard neurons have different K+ currents
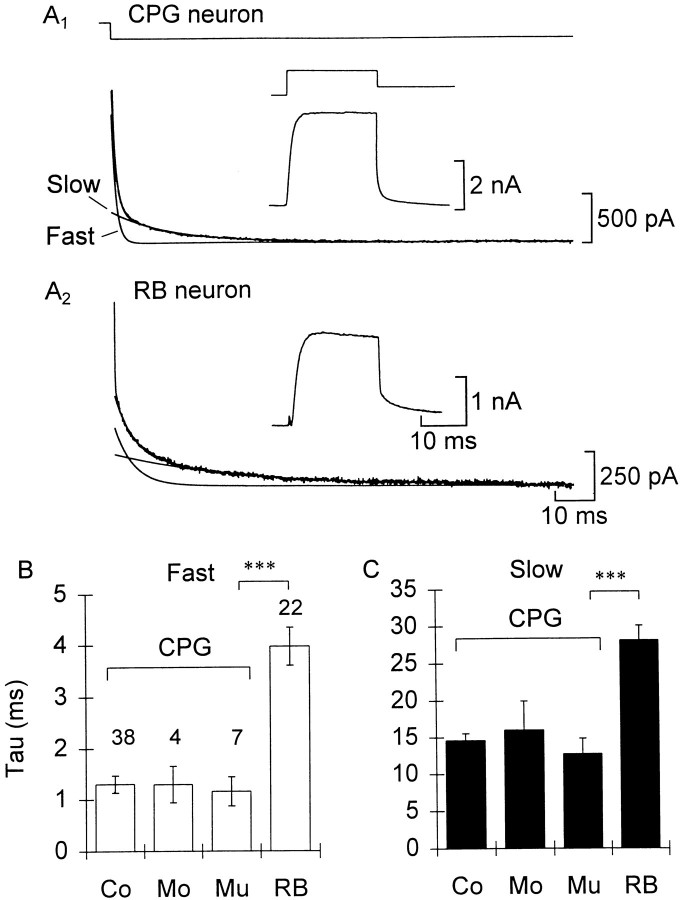
All of the cell types in this study possessed K+ currents that were not inactivated at a holding potential of −50 mV and that activated at potentials between −20 mV and +20 mV. The tail currents were well fitted by sum of two exponentials, indicating the presence of two kinetically distinct currents, but the activation phase of the current records proved difficult to fit reliably, because most cells displayed some K+ current inactivation. To measure the fast and slow components separately, we evoked tail currents by first stepping the cell from a −50 mV holding potential to +10 or +20 mV and then repolarizing the cell to −30 mV (Fig.1A).
Fig. 1.
The potassium currents of CPG neurons are faster than RB sensory neurons. A1, From a holding potential of −50 mV a CPG (commissural) neuron was depolarized to 10 mV for 20 msec and repolarized to −30 mV (traces are averages of 7 leak-subtracted sweeps). The inset shows the current during the step. The tail current (bottom left) was fitted by the equation I = 22 + 1320(exp(−t/0.9)) + 317(exp(−t/12.1)).Solid lines show the exponential fits of the fast, slow, and total currents. A2, Same asA1 for an RB neuron. The tail currentI = 119 + 321(exp(−t/3.8)) + 174(exp(−t/24.9)). B, C, Summary of fitted time constants for the fast and slow components, respectively, for the different cell types (Co, commissural;Mo, monopolar; Mu, multipolar). Error bars indicate 1 SEM in this and, unless otherwise specified, subsequent figures. The sample size for each class is indicated. Significance levels of comparisons in this and subsequent figures: *p < 0.05; **p < 0.01; ***p < 0.001.
The channel kinetics were similar across cell types that make up the central pattern generator for swimming but were slower in the Rohon Beard sensory neurons. We separated the time constants from fits of a sample of 71 cells according to cell morphology (Fig.1B,C; see Materials and Methods, Cell identification). An ANOVA including all cell types was highly significant (F(3,67) = 22.89 fast and 18.24 slow; p < 0.001 for both). In the planned comparison of time constants from the different (CPG) cell classes (Fig.1B,C, Co, Mo, Mu) there was no difference for either the fast components or IKs between the different morphological types (F(2,46) = 0.06 fast and 0.42 slow). However, when the CPG groups were pooled and compared with RB neurons, the RB neurons were significantly slower for both components (F(1,69) = 70.57 fast and 55.27 slow;p < 0.001 for both).
A second difference between the cell types is in the fraction of the total outward current carried by IKs. By extrapolating the curves fitted to the tail currents back to the moment of repolarization, the amplitudes of the fast (IKf and IKNa) and slow (IKs) components could be estimated. Using this protocol 22 ± 2% of the tail current wasIKs in CPG neurons compared with 40 ± 2% in RB cells (n = 49 CPG and 38 RB cells;p < 0.001). The similarity of the potassium currents across the CPG classes suggests that they are a homogeneous population and are quite distinct from the RB neurons. In addition, the pharmacological properties of RB K+ channels differed from those of CPG neurons (F. M. Kuenzi and N. Dale, unpublished results). Thus, we will not consider the RB neurons further in this paper. Only the properties of K+ currents in CPG neurons will be described.
Catechol specifically blocks the fast potassium currents
Catechol caused a rapid and reversible block of the K+ current at voltages lower than +20 mV. At voltages more positive than +20 mV the block partially reversed with a slow time course relative to channel opening.
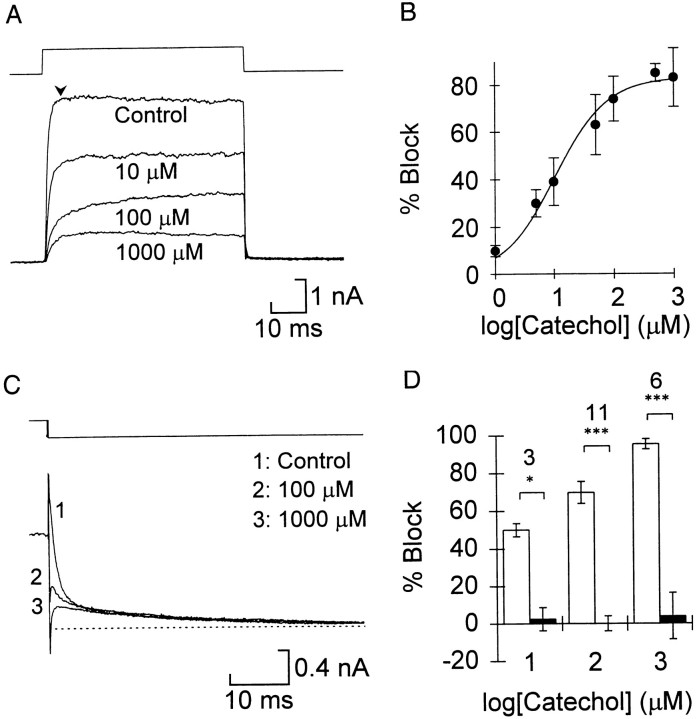
During test steps to +10 or +20 mV the greatest block of the total current occurred early in the voltage step (Fig.2A). The dose–response relationship for the percent block of the peak current early in the step (Fig. 2B, measured at the arrowheadin Fig. 2A) was well fitted by the Hill equation with an IC50 of 9.1 ± 1.9 μm and assuming a one-to-one binding (Hill coefficient = 1). When the Hill coefficient was allowed to vary, the best fit was 0.793 ± 0.162, which was not significantly different from 1, and the IC50was not significantly different from the result using the simpler equation. The maximum block was 85.0 ± 3.6%, which corresponds well with the relative amount of fast current in these cells. The activation of the current became slower between 10 and 100 μm, which again suggested that the slow component was resistant to catechol. The current appeared to reach equilibrium faster in 1 mm than in 100 μm, which may be attributable to voltage-dependent unblocking at the lower concentrations (see below).
Fig. 2.
Catechol selectively blocked the fast voltage-gated potassium currents. A, Effect of catechol on currents during the step recorded in control saline and the concentrations of catechol indicated. The voltage (top trace) was stepped from a holding potential of −50 mV to 20 mV. B, Summary of the concentration dependence of block for the current early in the pulse (measured at thearrowhead in A). Eachpoint represents the mean of 5–14 cells except that at 500 μm (n = 2). Error bars indicate 1 SD. The points are fitted by the Hill equation, (Imax −I)/Imax × 100 =A/(1 + (IC50/[Cat])h), where Imax is the peak current in control,I is the current at this time in different concentrations of catechol ([Cat]), IC50 is the concentration that reduces the current by 50%, and h is the Hill coefficient, here assumed to be 1. C, Catechol selectively blocks the fast tail current. The dotted line shows the steady-state current at −30 mV. Tail currents were measured as described in Figure 1. D, Summary of the catechol block of the fast (open bars) and slow (filled bars) tail currents. Sample size is indicated for each concentration. The significance level of the paired comparison between fast and slow is indicated (see legend of Fig.1).
We examined the tail currents to see whether catechol specifically blocked the fast component. Increasing the concentration of catechol to 100 and 1000 μm reduced the fast component but had little effect on the slow component (Fig. 2C,D). Paired comparisons of the percent block at each concentration of catechol showed that the fast component was blocked significantly more than the slow component at all concentrations. The dose response for the fast tail current was very similar to that of the total current (Fig. 2B). Again, the values in Figure 2D include partial unblocking during the test pulse (see Fig.3B).
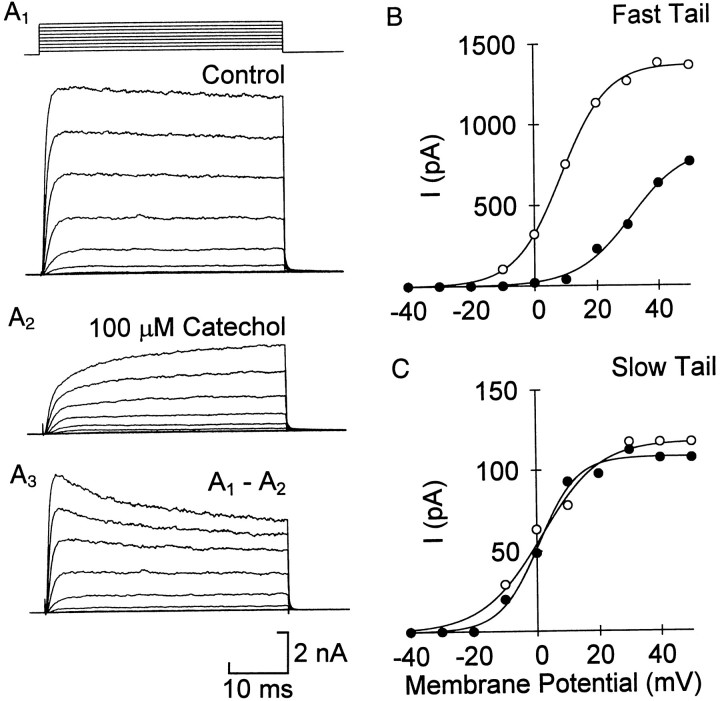
Fig. 3.
Voltage dependence of catechol- resistant and -sensitive current. Example of total current in control (A1) and 100 μm catechol (A2). A3, Difference currents, obtained by subtracting traces in A2from the corresponding ones in A1, show a decay in the catechol-sensitive current at positive voltages. Test voltages ranged from −40 to 40 mV in intervals of 10 mV. B, C, The catechol block of the fast currents partially reverses at positive voltages. The activation of the fast and slow currents was measured from the tail currents of a representative cell. B, In 100 μm catechol (filled circles) the activation of the fast current was shifted positive compared with control (open circles), whereas the shift of the slow current was small (C). The solid lines are the best fit of the equation: I= Imax/(1 + exp[(V − V½)/slope]) to the data. For the fast current the values for V½ and slope were 8.9 and −7.6 in control and 30.9 and −8.7 in catechol. The corresponding values for the slow current were 1.9 and −8.2 (control) and 0.6 and −6.8 (catechol).
The near total blockade of the fast component suggested that bothIKf and IKNa are sensitive to catechol. We tested this directly by applying catechol in the presence and absence of external sodium. Replacing sodium in the control medium with N-methyl-d-glucamine reduced the total current by 31 ± 3%. This was the percentage ofIKNa in these cells (Dale, 1993).N-Methyl-d-glucamine reduced the block by catechol by 23 ± 3% (n = 4), which is consistent with an equal block of IKf andIKNa.
In keeping with the effect on tail currents, the current that remained in 100 μm catechol activated with a slow time course across the physiological range of voltages (Fig.3A2). Difference currents obtained by subtracting the current in 100 μm catechol from the control current (Fig. 3A1) at each voltage step showed a fast-activating, partially inactivating current (Fig.3A3). At voltages of +20 mV and more, the current in catechol was greater than expected from the dose–response curve measured at lower voltages; it increased to ∼50% of control rather than 20–30% predicted from Figure 2. This suggested that the block was voltage-dependent.
We constructed voltage–activation curves from tail currents after long voltage pulses. The fast and slow components were estimated by extrapolating the fitted curves back to the end of the test pulse as before. These curves showed that catechol appeared to shift the activation of the fast current toward more positive voltages (Fig.3B). In six CPG cells the voltage for half-activation was 6.9 ± 1.6 mV in control and 26.4 ± 3.4 mV in 100 μm catechol (pairwise p < 0.01). In the four cells with a measurable slow component the voltage–activation curve was not shifted significantly (Fig. 3C).
Time dependence of catechol block
We explored the time and voltage dependence of catechol block further. The process of unblocking was studied by delivering a positive prepulse of varying duration and measuring the tail currents when the membrane was returned to −30 mV. In the example in Figure4A1 the control current reached its maximum within 3 msec. The fast component of the tail reached near maximum after 1 msec and decayed slightly with longer pulses (Fig. 4B). In 100 μm catechol, however, the fast component increased slowly over several milliseconds (Fig. 4A2,B). There was no change in the time course of fast deactivation in the tail current compared with control, so we interpret this slow “activation” of the fast component as an unblocking reaction; depolarization causes some of the blocked channels to become unblocked and pass current during the step, after which they close according to the normal channel kinetics. Note that unblocking was never complete; here it recovered to ∼50% block. We measured the time constant for unblocking in three cells to be 3.3 ± 0.4 msec in 100 μm catechol and at +20 mV. In contrast, the tail currents of IKs increased at the same rate in control and catechol, as would be expected from the insensitivity of IKs to catechol (τ = 6.3 ± 1.1 and 5.5 ± 0.8 msec in control and catechol, respectively;n = 3) (Fig. 4C).
Fig. 4.
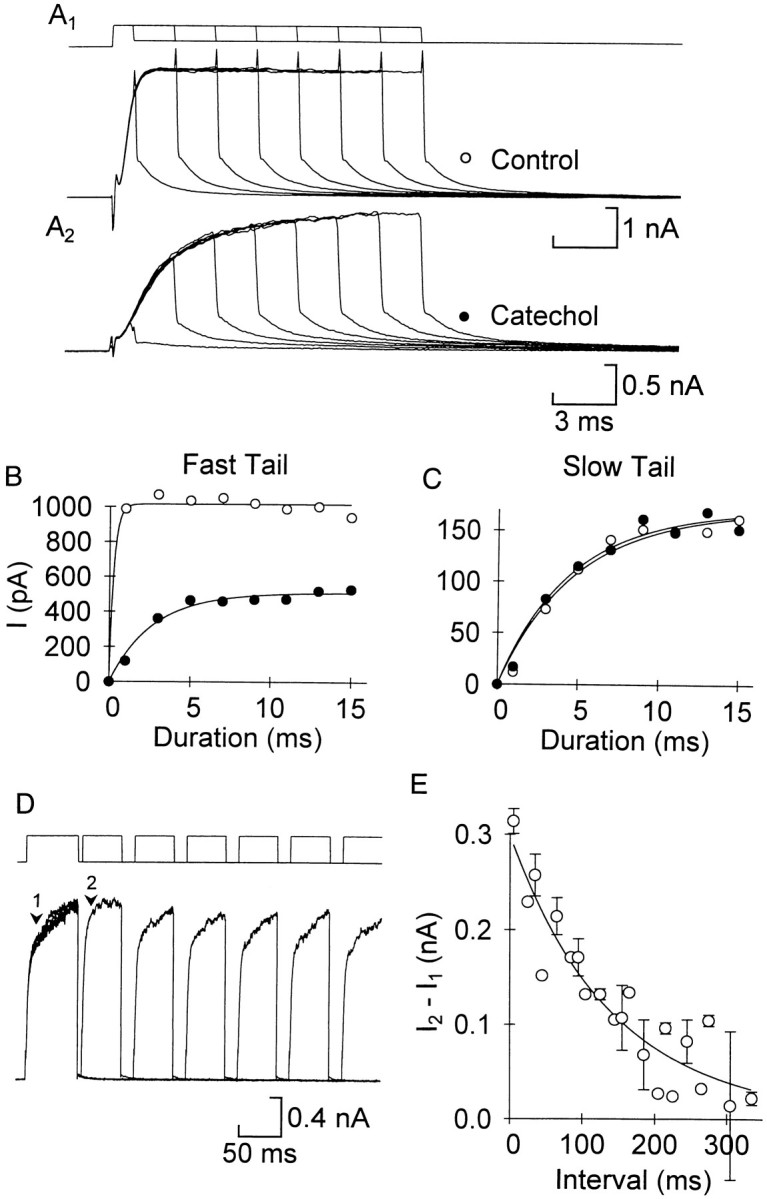
The fast current showed time-dependent unblocking and reblocking. A, The pulse length of a voltage step to 20 mV was increased from 1 to 15 msec in control (A1) and 100 μm catechol (A2). The tail current was fitted with a double exponential to measure the fast (B) and slow (C) components in the two conditions (symbols as in A). Pointswere fitted by the equation I =Imax[1 − exp(−(t/τ)]. For the fast current in this example τ = 0.3 msec in control (although there were not enough points for an accurate fit) and 2.7 msec in catechol, and for the slow current the corresponding values were 4.9 and 4.6 msec. D, Reblocking was measured with twin pulses to 20 mV separated by a variable interval at −50 mV. The example shows six pairs of pulses, with the first pulse of each aligned. In 100 μm catechol, the current during the first pulse activated slowly, but with a short latency the current during the second pulse activated more rapidly. With longer latencies between pulses the activation rate slowed. E, The amount of current that could be blocked was the difference in current between the second (I2) and first (I1) pulses measured 10 msec after the start of the pulse (arrows 2 and 1 inD, respectively). As the interval increased this difference decreased, and the block approached its steady-state level (n = 3 cells; the set of intervals was different for one cell). The fitted curve was (I1 −I2) = 0.003 + 0.296exp(−t/142 msec).
Returning the cell to a negative voltage reverses this process and favors the reblocking reaction. We therefore measured the time dependence of reblocking by using a twin-pulse protocol (Fig.4D). In the control, the activation of the current was the same in both pulses at all interpulse intervals, but in 100 μm catechol (Fig. 4D) the current during the second pulse activated much faster than the first at short interpulse intervals. As the interval increased the activation of the second pulse slowed and became more like the first, indicating a recovery of block. This recovery of block was examined in three cells by measuring the current 10 msec after the start of both pulses. The difference between the current during the first and second pulses at this point indicates the amount of unblocked current under these conditions (Fig. 4E). The points were well fitted by a single exponential, giving a time constant for reblocking of 141 ± 10.1 msec. Thus, IKf andIKNa undergo rapid, partial unblocking during the voltage step (Fig. 4B) followed by slow reblocking at the holding potential.
4-Aminopyridine preferentially blocks the fast current
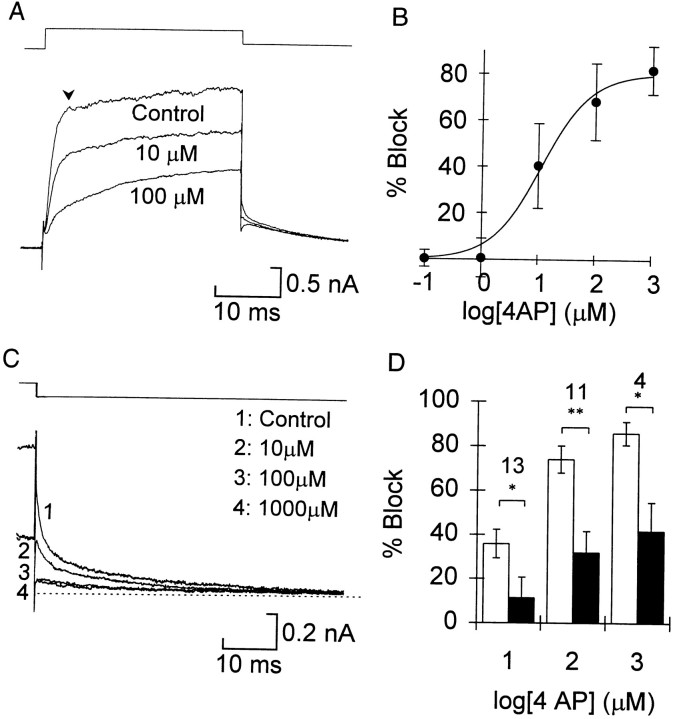
In many types of neuron 4-AP specifically blocks the transient potassium current IA; however, we found that in embryonic Xenopus spinal neurons it blocked the sustained currents at low concentrations. With repeated pulses the block developed slowly, requiring >20 sec to reach a steady state, and it was only partially reversible. Like catechol, 4-AP slowed the activation of the current during the step (Fig.5A). The concentration dependence of block for the current early in the pulse was also similar to that of the block by catechol (Fig. 5B). Assuming a single binding site, the data were well fitted by the Hill equation, with an IC50 of 15 ± 12 μm and maximum block of 82 ± 10%. There was a wide range of responses, with 100 μm causing near complete block (>80%) in some cells and <50% block in others.
Fig. 5.
4-Aminopyridine blocked both fast and slow potassium currents. A, During the voltage step the current during the beginning of the pulse is blocked more than the end.B, Concentration–response curve for the current early in the step (arrowhead in A). Error bars indicate 1 SD (n = 4–17 cells for each point).C, Tail currents at −30 mV show complete block of the fast and partial block of the slow component at ≥100 μm. The dotted line indicates the steady-state current.D, Summary of block of the fast (open bars) and slow (filled bars) tail currents in 13 cells. The sample size for each concentration is indicated. Asterisks are as in Figure 1.
Analysis of the tail currents showed that 4-AP preferentially blocked the fast component (Fig. 5C). In contrast to the effect of catechol, these concentrations also significantly reduced the slow component (p < 0.01 at 100 μm andp < 0.05 at 1 mm). Nevertheless, at every concentration the mean block of the fast component was greater than that of the slow component, and the pairwise differences in block were significant (Fig. 5D). The poor selectivity of 4-AP rendered it of limited value for functional studies, so it was not considered further.
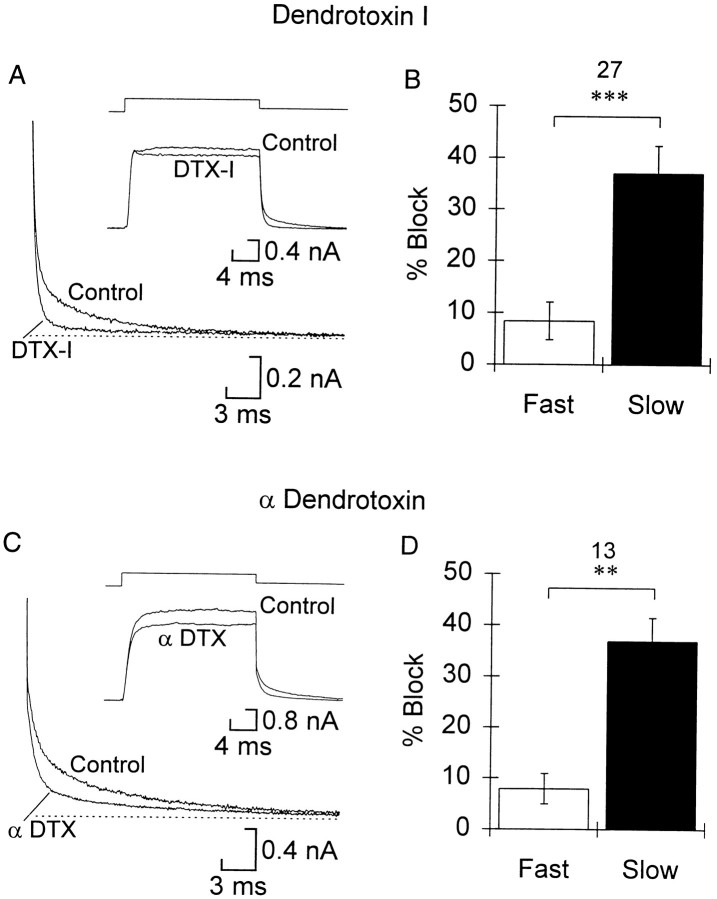
Dendrotoxin-I and α-Dendrotoxin specifically blockIKs
DTX-I blocked the slow component of tail currents by ∼40% at 0.5 μm (Fig.6A,B). The slow component was blocked more than the fast component in a pairwise comparison (Fig. 6B), although the fast component was reduced by a small, but significant, amount. There was no measurable increase in the block of IKs at the highest concentration tested, 4 μm, nor was the selectivity less. In keeping with the relative size of IKs, the current during the step was reduced by only 10–15%. α-DTX presented a similar picture in the concentration range of 0.5–2 μm (Fig. 6C,D). When tested, the block ofIKs was slowly and only partially reversible with washing.
Fig. 6.
Dendrotoxin-I and α-dendrotoxin block slow current selectively. A, C, Tail currents are shown at the bottom left in control and either dendrotoxin-I (A) or α-dendrotoxin (C). The dotted line shows the steady-state current. The insets show the current during the step in control and dendrotoxin as indicated. Traces are averages of three to four leak-subtracted sweeps. B, D, Summary of changes in the fast and slow tail currents caused by 500 nm DTX-I and 2 μm α-DTX, respectively (n as indicated, and asterisks are as in Fig. 1). Both toxins caused a significant block of both fast and slow components. Also, for both toxins the amount of block did not increase with concentrations >500 nm (data not shown).
Dendrotoxin causes a small reduction in the sodium current
DTX has been found to modulate INa as well as blocking Ik in some preparations (Li and McArdle, 1993; Schauf, 1987) but not in others (Halliwell et al., 1986). We found that 1 μm DTX-I reversibly reduced the peak sodium current (stepping from a holding potential of −50 to +10 mV) by 8.8 ± 1.7% (p < 0.01;n = 6). This was accompanied by a small but significant shift in the V½ for steady-state inactivation of −3.7 ± 0.6 mV (p < 0.01;n = 5), but there was no change in either the steepness of the voltage dependence or the time course of inactivation.
Catechol broadens the action potential
The specificity of catechol and DTX allowed us to test the control that the fast and slow potassium currents have over neuronal firing properties. Whole-cell recordings were made under current clamp to measure changes in action potential duration and repetitive firing. To study the repolarizing phase of the action potential, a brief outward current pulse was delivered to a cell to initiate an action potential near the end of the pulse (Fig.7A). We measured spike width as the time required for the voltage to return from the peak to one-third of the spike amplitude (resting potential to peak). In the control, spike width was 1.3 ± 0.1 msec; catechol increased this to 2.7 ± 0.6 msec at 100 μm (n = 10) and 4.1 ± 0.8 msec at 1 mm (n = 10; Fig. 7A). Both increases were significant at the 5% level. In a similar protocol and in repetitive firing studies (see below) the dendrotoxins caused no change in the spike width (mean width at 0 mV, 1.3 ± 0.1 and 1.2 ± 0.1 msec in control and 1 μm DTX, respectively; n = 5 (Fig.8A–C).
Fig. 7.
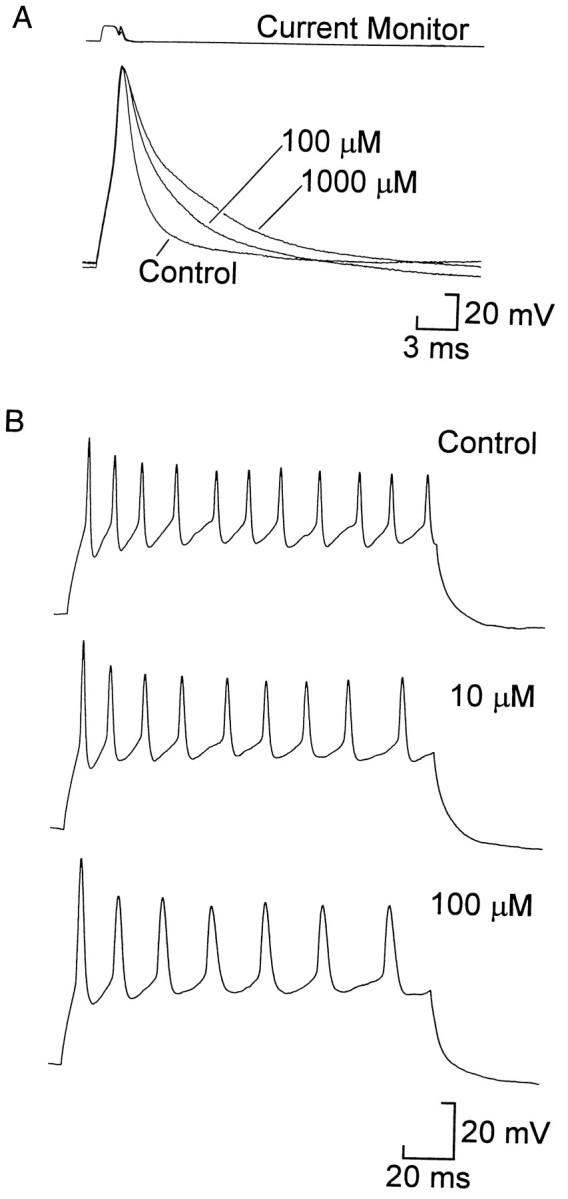
Catechol broadened spikes and slightly inhibited repetitive firing. A, In current-clamp recordings from a dissociated neuron a brief outward current pulse triggered a spike (bottom traces, voltage). One hundred micromolar and 1 mm catechol progressively slowed the repolarizing phase, broadening the spike compared with control. B, Repetitive firing of a cell that was depolarized by 80 pA to elicit a train of spikes in control saline. Ten micromolar and 100 μm catechol reduced the average frequency of firing and thus the number of spikes during the pulse. In this cell the initial frequency was also slightly reduced, but across all cells the change was not significant. Similar results were seen in cells that exhibited stronger accommodation.
Fig. 8.
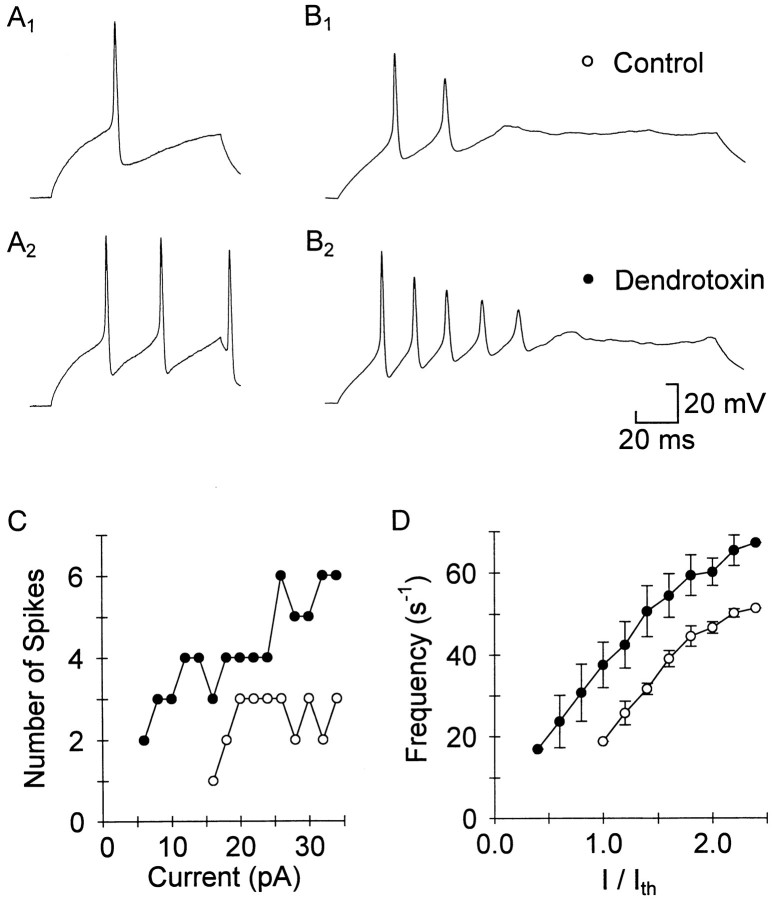
Dendrotoxin has little effect on spike width and increases repetitive firing. A, B, Current-clamp recordings from a dissociated cell (A) and a cell recorded in situ in control (A1,B1) and 1 μm DTX-I (A2, B2). After perfusing with 1 μm DTX-I the cells increased their firing, and the first spike was the same width as in control. C, A series of pulses of increasing magnitude were delivered to the cell inB to show changes in threshold and repetitive firing properties in DTX. DTX-I (filled circles) increased the number of spikes fired at each level of current.D, For three cells with similar thresholds the initial firing frequency (1/first interspike interval) is plotted against the current normalized to the control threshold current. At every current level the frequency in DTX (filled circles) was higher than in control (open circles).
Repetitive firing is slightly depressed by catechol but enhanced by dendrotoxins
Repetitive firing was examined by injecting a series of long outward current pulses of increasing amplitude, the highest of which was strong enough to activate multiple action potentials in most cells (Figs. 7B, 8B). In this study we found that the firing properties of cells ranged from those that had a graded response (number of spikes and frequency) to the amount of current injected to those that showed moderate or strong accommodation. Despite this variability in control conditions, the changes in firing caused by catechol and DTX were similar across cells. We considered changes in the total number of spikes and the threshold. Because the activity of cells during swimming suggested that the firing of the first two spikes was the most functionally relevant repetitive firing characteristic, we also measured the initial frequency (inverse of first interspike interval) at the current level that evoked at least two spikes in control. Both 10 and 100 μm reduced the total number of spikes during the train, but the change was only significant in 100 μm (p < 0.05; n = 7) (Fig. 7B). Catechol also lowered the threshold for firing spikes by 20 ± 8% at 10 μm(p < 0.05). The initial frequency, however, was not affected significantly by either concentration (n = 8 for 10 μm; n = 7 for 100 μm).
Dendrotoxins increased the repetitive firing capabilities of the cells. One micromolar DTX-I reduced the membrane accommodation, and neurons became capable of firing many more spikes in response to the same current injection (n = 10 of 12; Fig.8A,B). An example of the relationship between current injected and the number of spikes evoked is shown in Figure8C, and a similar trend was evident in five of six cells tested with graded steps. The threshold current decreased in 1 μm DTX-I to 57 ± 9% of control (p < 0.01; n = 6). In DTX the cells fired at higher frequencies at each current level. This is shown for three cells that had very similar thresholds (between 10 and 40 pA) in Figure 8D. At twice threshold current the frequency in control corresponded to an interspike interval of 20 ± 1 msec, which was significantly longer than the interspike interval in DTX-I (17 ± 1 msec; p < 0.05;n = 3). There were no noticeable differences between the effects of DTX-I and α-DTX or between isolated neurons and recordings made from the intact spinal cord, although in the intact cord repetitive firing was much more reliable in control, and the membrane potential was much more stable.
The swimming pattern generator is very sensitive to changes in the slow current
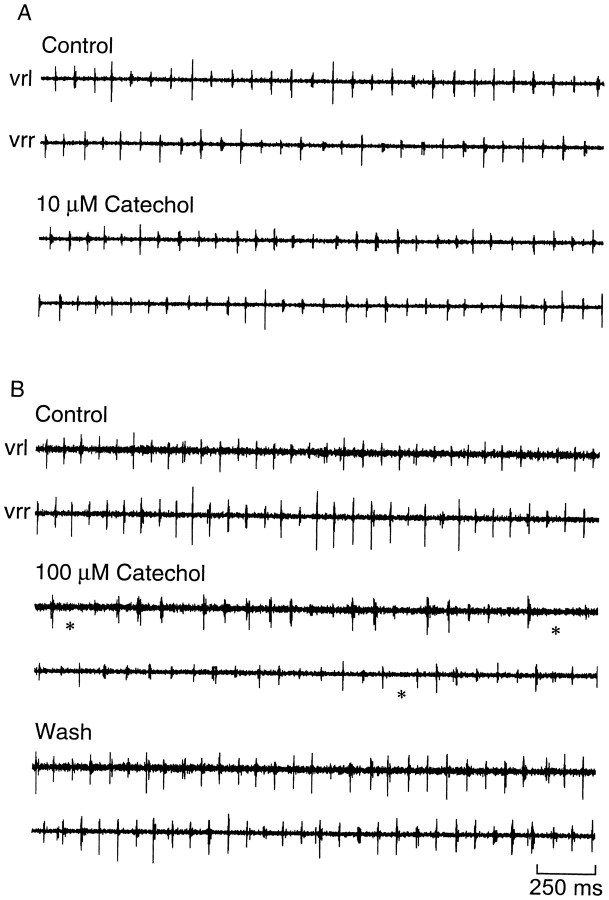
We tested whether catechol block of the fast K+currents could disrupt the basic pattern of swimming recorded in the ventral roots of the spinal cord. In control, the swimming pattern is characterized by brief bursts of activity that alternate on the two sides of the body; a burst on the right occurs midcycle of the burst on the left (Fig. 9A). The cycle period ranges from ∼50 msec at the beginning of an episode to ∼100 msec just before swimming stops. In the presence of 10 μmcatechol, the basic pattern (cycle period, burst duration, and alternation) was unchanged (Fig. 9A, Table1). After blocking at least 70% of the fast current with 100 μm, the embryo was surprisingly still capable of generating an alternating rhythm with a normal cycle period and burst duration. However, abnormalities were present, such as periods during which the ventral root discharge was missing on one side of the embryo (Fig. 9B). To examine the effects on burst duration more closely, the rectified and integrated extracellular record was averaged over 30 cycles in control (Fig.10, thick line) and in catechol (Fig. 10, thin line). Ten and 100 μmcatechol did not significantly change the number of spikes fired by motor neurons, as measured by the area under the curve (Fig. 10; change in area, −13 ± 12%, n = 4 in 10 μm; −7 ± 16%, n = 4 in 100 μm). The averaging also confirmed that the burst duration was also unchanged.
Fig. 9.
The swimming pattern is relatively insensitive to catechol. Records of ventral root activity on the two sides of the embryo (vrl, vrr, left and right ventral root records, respectively) show that 10 μm catechol (A), which is near the IC50 for block of the fast current, has little effect on swimming; 100 μm catechol (B) caused some abnormalities in the pattern, with discharge absent on some cycles (*). Segments illustrated are taken 8 sec from the electrical skin stimulus that initiated the swimming episode.
Table 1.
Effect of potassium channel blockers on the swimming pattern (mean change ± SEM)
| Blocker | n | Change in burst duration | Change in cycle period | Missing half-cycles | ||
|---|---|---|---|---|---|---|
| msec | % | msec | % | |||
| 10 μmCatechol | 4 | −1.2 ± 1.0 | −7 ± 6 | −3.7 ± 1.5 | −6 ± 3 | No |
| 100 μmCatechol | 5 | 0.9 ± 0.9 | 10 ± 10 | 5.0 ± 5.6 | 7 ± 8 | Yes |
| 100 nm α-DTX | 6 | 3.6 ± 1.0 | 44 ± 13* | −1.1 ± 3.0 | −1 ± 5 | No |
| 1 μm DTX-I | 7 | 6.4 ± 0.8 | 78 ± 13*** | 7.6 ± 3.3 | 11 ± 6 | No |
See text for measures under control conditions.
*,***, Significant changes as described in legend of Figure 1.
Fig. 10.
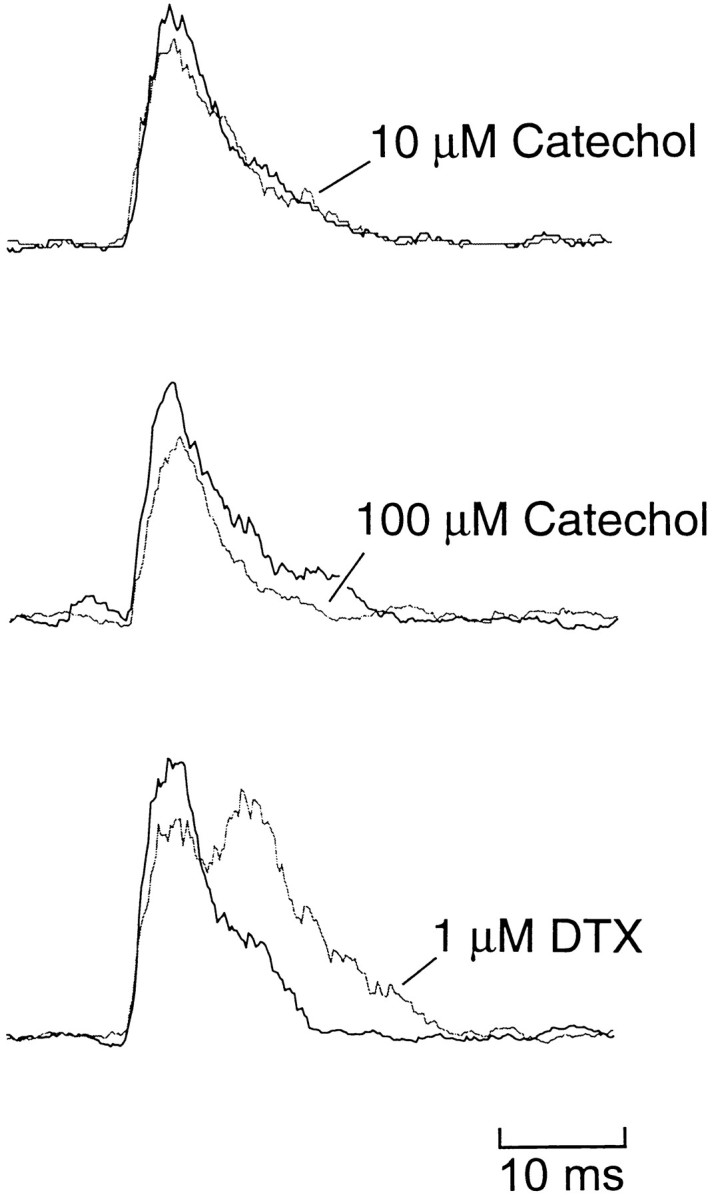
Catechol has no effect, but DTX increases the burst duration during swimming. Ventral root recordings were rectified, integrated (2 msec steps), and averaged over the first 30 cycles. In each panel the thick line is in control, and thethin line is in the treatment indicated. Although catechol had no consistent effect on burst shape, DTX increased burst duration and increased the burst intensity (area under the curves).
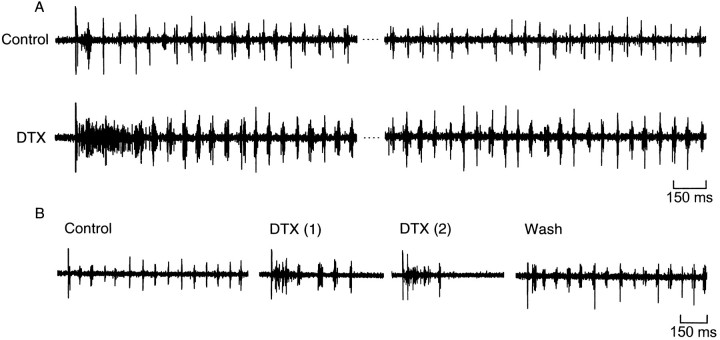
In contrast to the relative insensitivity of motor pattern generation to catechol, the spinal circuit was sensitive to both α-DTX and DTX-I. We found that these abolished the alternating pattern of ventral root bursts for up to several hundred milliseconds (Fig.11A). The skin stimulus evoked continuous and unpatterned activity on both sides, which was sometimes followed by a period of quiescence before swimming began. Once swimming had been established, the pattern of alternation was preserved, but the duration of the ventral root bursts increased from 9.4 msec in control to 16.2 msec in 1 μm DTX-I (Table 1). Importantly, the area under the averaged extracellular records increased by 89 ± 24% (p < 0.01;n = 7), indicating that more motor neuron spikes occurred during each cycle (Fig. 10; see Discussion). The effect of DTX on cycle period at both 100 nm and 1 μm was rather variable, but overall the mean change was not significant (Table1). In some cases (n = 2; Fig. 11B) the swimming pattern failed to occur after the initial burst of activity. In most preparations there was either full or partial reversal of the prolonged initial ventral root burst with washing (Fig.11B); however, the change in burst duration was irreversible.
Fig. 11.
Dendrotoxins disrupt the swimming pattern.A, Ventral root records from one side at the beginning and near the end of a swimming episode in control saline and α-DTX. α-DTX caused a prolonged burst of activity on both sides, followed by swimming in which the duration of the ventral root bursts increased.B, Example in which DTX increased burst duration and then abolished swimming activity. The initial burst was reversed during the wash, but the change in burst duration was not.
DISCUSSION
Pharmacological dissection of the fast and slow currents
Our results support the hypothesis that slow and fast potassium channels are distinct at the molecular level. In addition to having widely different opening and closing kinetics (Dale, 1995a), the fast and slow currents were blocked by different agents (catechol and dendrotoxins, respectively), and they were expressed in different proportions in nonsensory and Rohon Beard neurons. In light of thein situ hybridization results of Ribera and colleagues, it is possible that IKs is coded for (in part) by Kv1.1, and IKf is coded for by Kv2.2.IKs is more prominent in Rohon Beard neurons (Fig. 1), which co-localize with expression of a Kv1.1-like transcript (Ribera and Nguyen, 1993), whereas a Kv2.2 transcript is expressed most strongly ventrally (Burger and Ribera, 1996), butIKf is more prominent. Differences in the kinetics of the respective channels between the Rohon Beard and the other neurons could be attributable to other co-expressed α and β subunits in the native channels (Scott et al., 1994).
For pharmacological agents to be useful in studying how ion channels influence circuit operation, they must satisfy two criteria: specificity for blocking one or a restricted set of channels, and maintenance of block during circuit operation. Catechol and DTX appear to satisfy both of these criteria in the Xenopus embryo; catechol blocks the fast currents, whereas DTX blocks the slow currents. Although we have demonstrated specificity for these two types of current, some stage 37/38 Xenopus neurons possess a smallIA (F. M. Kuenzi and N. Dale, unpublished observations), and an “A” current is present in neurons grown in culture (Ribera and Spitzer, 1990). Catechol can blockIA in some preparations, but the IC50 values of 0.5–5 mm (Ito and Maeno, 1986;Erdélyi and Such, 1988; Kehl, 1991; Sah and McLachlan, 1992) are much higher than for block of the fast Xenopus currents. In the few Xenopus neurons tested, 100 μmcatechol blocked IA by 10–20% (Kuenzi and Dale, unpublished observations). Such a small block of a rare current may not be of functional significance at this stage of development. In addition to blocking IKs, the dendrotoxins also slightly blocked INa. However, this is unlikely to complicate our interpretation of the changes in cell firing or circuit operation, because block ofINa would tend to oppose the increases in excitability we observed.
The second criterion, that the block is maintained during circuit activity (swimming), depends on the level of depolarization during activity within the circuit. During swimming the membrane potential is tonically depolarized to approximately −30 mV, and cells fire a single spike (∼2 msec long and reaching +20 mV) per cycle (Roberts and Kahn, 1982; Dale, 1995b). Thus, although we found a voltage dependence to the catechol block, most of the time is spent in the voltage range in which unblocking is not a factor (Fig. 3B). During each action potential, however, some unblocking would occur, and the total block would decrease toward its equilibrium value of ∼70% at +20 mV (Figs.2D, 3B). With a cycle period of 70 msec (Kahn and Roberts, 1982a,b) and with the rates of unblocking (during a square pulse of half of the spike width) and reblocking given above, this equilibrium will be reached within the first 50 cycles. Because episodes tend to last a few minutes, the dose–response data of the fast tail current in Figure 2D is a good measure of the expected block for most of the episode. We did not see any changes in swimming early in the episode in 10 μm catechol but saw them throughout the episode in 100 μm, suggesting that the sensitivity of the circuit lies between 50 and 70% block ofIKf and IKNa. A similar argument holds for the DTX block, which has some voltage dependence (Werkman et al., 1992). The increase in burst duration occurred throughout the swimming episodes, so any unblocking was not functionally significant.
Kinetically distinct potassium currents play different roles in neural circuit function
The model of the Xenopus swimming circuit produced byDale (1995b) is based on the measured kinetics of the principal voltage and ligand gated channels in stage 37/38 neurons. It incorporated single-compartment neurons and a reduced representation of spinal circuitry. The model reproduced the basic pattern of neuron firing and the dependence of cycle period on reciprocal inhibition. It also predicted that IKf andIKs would have very different roles both in the control of membrane excitability and in circuit operation. In the model, reducing IKf by 50% or eliminating it caused spike broadening and a lowering of threshold. These effects (Dale, 1995b, his Fig. 2) are qualitatively very similar to the changes in spike shape and repetitive firing caused by catechol (Fig. 7). By contrast, the model predicted a different role forIKs. Reductions of IKs by 50% in the model had no effect on threshold or spike width but greatly increased the slope of the frequency–current relation. Like the model, applications of DTX to real neurons increased the amount and frequency of repetitive firing at all levels of current injection without broadening the spike. DTX also greatly lowered the threshold, an effect not seen in the model. Both IKf andIKs undergo slow inactivation with long depolarizing steps. This feature has not yet been included in the model. With long current injections of the type used in these experiments, the slow kinetics of IKs may be important for compensating for inactivation ofIKf. Weakening IKs with DTX may shift the balance of inward and outward currents late in a previously subthreshold pulse to allow spiking. Interestingly, injection of cesium either through sharp microelectrodes (Soffe, 1990) or patch electrodes containing low concentrations of cesium (Dale, 1991) also enhances repetitive firing without affecting spike width. The simplest explanation of these observations is that low concentrations of internal cesium preferentially blockIKs.
The model predicts that the swimming circuit is not very sensitive to changes in IKf but depends very strongly onIKs. Our results with catechol and DTX support this prediction; reducing the fast currents by 50% had no effect, whereas the block of IKs by DTX significantly altered the swimming pattern. In the model a 50% reduction ofIKs did not disrupt the alternation between the two sides, but it did cause cells to fire a pair rather than a single spike in each cycle. In real embryos after treatment with DTX the alternation of ventral root activity on the two sides during swimming was normal. However, the ventral root burst duration was greatly increased. This increase could occur either through motor neurons firing a second spike during the excitatory phase of the cycle or through desynchronization of the motorneuron firing. Our data support the first interpretation. DTX increased the area under the curve of the averaged ventral root bursts (Fig. 10C). Because there was no spike broadening, more motor neuron spikes must have occurred during each cycle. This eliminates simple desynchronization, unless recruitment from a large pool of previously silent motor neurons occurred to provide extra spikes. This is unlikely because intracellular recordings from ventral neurons (primarily motor neurons) suggest that most fire during every swimming cycle (Soffe, 1993). Also, recruitment of subthreshold CPG neurons (by application of glutamate) did not increase burst duration (Soffe, 1996). In contrast, dual spiking by motor neurons is consistent with the observed changes in ventral root activity; the increase in burst duration was ∼16 msec, which was very similar to the minimum interspike interval seen under current clamp (Fig. 8D), and in some experiments the averaged ventral root burst clearly showed a second hump (Fig.10C), as would be expected if cells were firing twin spikes rather than single ones. We therefore conclude that DTX, by inhibitingIKs, caused a fundamental change that allowed neurons to fire repetitively during swimming cycles rather than the single spike, which is characteristic of the embryonic pattern.
Taken together these results confirm the predictions from our earlier model and suggest that IKs is a “strategic” current in the Xenopus swimming circuit. It is small in comparison with other outward currents (20% of the total) yet plays an important role in the function of the circuit. As such, the slow current could be a key target for modulation of the whole circuit. In vertebrate neurons some delayed rectifier currents are controlled by neuromodulators (Rehm and Tempel, 1991; Hille, 1992; Grudt and Williams, 1993; Simmons and Chavkin, 1996). The Xenopuscircuit is also regulated by adenosine triphosphate, which inhibits the potassium currents (Dale and Gilday, 1996). The magnitude of this inhibition is within the range for a specific action onIKs, and it will be important to determine whether this is so.
Developmental changes in expression of IKs may also underlie changes in the swimming motor pattern that occur in the transition from embryo (stage 37/38) to larva (stage 41). During this period the pattern matures from the short bursts of ventral root activity in the embryo to much longer bursts in the larva (Sillar et al., 1991). The slow potassium current limits repetitive firing in the model, and the similarity between the DTX-induced bursts in the embryo and the 15–20 msec bursts in the larva suggests that downregulation ofIKs may indeed be a key step in the maturation of the motor pattern.
Footnotes
We thank the Biotechnology and Biological Sciences Research Council and the Royal Society for their generous support. We also thank Dr. William J. Heitler for his helpful comments on this manuscript.
Correspondence should be addressed to Nicholas Dale, Bute Medical Building, Westburn Lane, St. Andrews, Fife KY16 9TS, UK.
REFERENCES
- 1.Arshavsky YI, Orlovsky GN, Panchin YV, Roberts A, Soffe SR. Neuronal control of swimming locomotion: analysis of the pteropod mollusc Clione and embryos of the amphibian Xenopus. Trends Neurosci. 1993;16:227–232. doi: 10.1016/0166-2236(93)90161-e. [DOI] [PubMed] [Google Scholar]
- 2.Brew HM, Forsythe ID. Two voltage-dependent K+ conductances with complementary functions in postsynaptic integration at a central auditory synapse. J Neurosci. 1995;15:8011–8022. doi: 10.1523/JNEUROSCI.15-12-08011.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Burger C, Ribera AB. Xenopus spinal neurons express Kv2 potassium channel transcripts during embryonic development. J Neurosci. 1996;16:1412–1421. doi: 10.1523/JNEUROSCI.16-04-01412.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Byrne JH. Ionic currents and behavior. Trends Neurosci. 1979;2:268–270. [Google Scholar]
- 5.Byrne JH. Analysis of ionic conductance mechanisms in motor cells mediating inking behavior in Aplysia californica. J Neurophysiol. 1980a;43:630–650. doi: 10.1152/jn.1980.43.3.630. [DOI] [PubMed] [Google Scholar]
- 6.Byrne JH. Quantitative aspects of ionic conductance mechanisms contributing to firing pattern of motor cells mediating inking behavior in Aplysia californica. J Neurophysiol. 1980b;43:651–668. doi: 10.1152/jn.1980.43.3.651. [DOI] [PubMed] [Google Scholar]
- 7.Connor JA. Neural repetitive firing: a comparative study of membrane properties of crustacean walking leg axons. J Neurophysiol. 1975;38:922–932. doi: 10.1152/jn.1975.38.4.922. [DOI] [PubMed] [Google Scholar]
- 8.Dale N. The Isolation and identification of spinal neurons that control movement in the Xenopus embryo. Eur J Neurosci. 1991;3:1025–1035. doi: 10.1111/j.1460-9568.1991.tb00039.x. [DOI] [PubMed] [Google Scholar]
- 9.Dale N. A large, sustained Na+- and voltage-dependent K+ current in spinal neurons of the frog embryo. J Physiol (Lond) 1993;462:349–372. doi: 10.1113/jphysiol.1993.sp019559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dale N. Kinetic characterization of the voltage-gated currents possessed by Xenopus embryo spinal neurons. J Physiol (Lond) 1995a;489:473–488. doi: 10.1113/jphysiol.1995.sp021066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dale N. Experimentally-derived model for the locomotor pattern generator in the frog embryo. J Physiol (Lond) 1995b;489:489–510. doi: 10.1113/jphysiol.1995.sp021067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dale N, Gilday D. Regulation of rhythmic movements by purinergic neurotransmitters in frog embryos. Nature. 1996;383:259–263. doi: 10.1038/383259a0. [DOI] [PubMed] [Google Scholar]
- 13.El Manira A, Tegnér J, Grillner S. Calcium-dependent potassium channels play a critical role for burst termination in the locomotor network in lamprey. J Neurophysiol. 1994;72:1852–1861. doi: 10.1152/jn.1994.72.4.1852. [DOI] [PubMed] [Google Scholar]
- 14.Erdélyi L, Such G. The A-type potassium current—catechol-induced blockage in snail neurons. Neurosci Lett. 1988;92:46–51. doi: 10.1016/0304-3940(88)90740-9. [DOI] [PubMed] [Google Scholar]
- 15.Golowasch J, Marder E. Ionic currents of the lateral pyloric neuron of the stomatogastric ganglion of the crab. J Neurophysiol. 1992;67:318–331. doi: 10.1152/jn.1992.67.2.318. [DOI] [PubMed] [Google Scholar]
- 16.Grudt TJ, Williams JT. κ-opioid receptors also increase potassium conductance. Proc Natl Acad Sci USA. 1993;90:11429–11432. doi: 10.1073/pnas.90.23.11429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Halliwell JV, Othman IB, Pelchen-Matthews A, Dolly JO. Central action of dendrotoxin: selective reduction of a transient K conductance in hippocampus and binding to localized acceptors. Proc Natl Acad Sci USA. 1986;83:493–497. doi: 10.1073/pnas.83.2.493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Harris-Warrick RM, Coniglio LM, Barazangi N, Guckenheimer J, Gueron S. Dopamine modulation of transient potassium current evokes phase-shifts in a central pattern generator network. J Neurosci. 1995a;15:342–358. doi: 10.1523/JNEUROSCI.15-01-00342.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Harris-Warrick RM, Coniglio LM, Levini RM, Gueron S, Guckenheimer J. Dopamine modulation of 2 subthreshold currents produces phase-shifts in activity of an identified motoneuron. J Neurophysiol. 1995b;74:1404–1420. doi: 10.1152/jn.1995.74.4.1404. [DOI] [PubMed] [Google Scholar]
- 20.Hille B. Ionic channels of excitable membranes, Ed 2. Sinauer; Sunderland, MA: 1992. [Google Scholar]
- 21.Ito I, Maeno T. Catechol: a potent and specific inhibitor of the fast potassium channel in frog primary afferent neurones. J Physiol (Lond) 1986;373:115–127. doi: 10.1113/jphysiol.1986.sp016038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kahn JA, Roberts A. Experiments on the central pattern generator for swimming in amphibian embryos. Philos Trans R Soc Lond B Biol Sci. 1982a;296:229–243. doi: 10.1098/rstb.1982.0004. [DOI] [PubMed] [Google Scholar]
- 23.Kahn JA, Roberts A. The central nervous origin of the swimming motor pattern in embryos of Xenopus laevis. J Exp Biol. 1982b;99:185–196. doi: 10.1242/jeb.99.1.185. [DOI] [PubMed] [Google Scholar]
- 24.Kehl SJ. Catechol blocks the fast outward potassium current in melanotrophs of the rat pituitary. Neurosci Lett. 1991;125:136–138. doi: 10.1016/0304-3940(91)90010-q. [DOI] [PubMed] [Google Scholar]
- 25.Li XY, McArdle JJ. Dendrotoxin inhibits sodium and transient potassium currents in murine hippocampal neurons. Biophys J. 1993;64:A198. [Google Scholar]
- 26.McCormick DA, Huguenard JR. A model of the electrophysiological properties of thalamocortical relay neurons. J Neurophysiol. 1992;68:1384–1400. doi: 10.1152/jn.1992.68.4.1384. [DOI] [PubMed] [Google Scholar]
- 27.Nadim F, Calabrese RL. A slow outward current activated by FMRFamide in heart interneurons of the medicinal leech. J Neurosci. 1997;17:4461–4472. doi: 10.1523/JNEUROSCI.17-11-04461.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nadim F, Olsen ØH, De Schutter E, Calabrese RL. Modeling the leach heartbeat elemental oscillator I. Interactions of intrinsic and synaptic currents. J Comp Neurosci. 1995;2:215–235. doi: 10.1007/BF00961435. [DOI] [PubMed] [Google Scholar]
- 29.Nieuwkoop PD, Faber J. Normal tables of Xenopus laevis (Daudin). North-Holland; Amsterdam: 1956. [Google Scholar]
- 30.Olsen ØH, Nadim F, Calabrese RL. Modeling the leach heartbeat elemental oscillator II. Exploring the parameter space. J Comp Neurosci. 1995;2:237–257. doi: 10.1007/BF00961436. [DOI] [PubMed] [Google Scholar]
- 31.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical recipes in C, the art of scientific computing. Cambridge UP; New York: 1988. [Google Scholar]
- 32.Rehm H, Tempel BL. Voltage-gated K+ channels of the mammalian brain. FASEB J. 1991;5:164–170. doi: 10.1096/fasebj.5.2.2004663. [DOI] [PubMed] [Google Scholar]
- 33.Ribera AB, Nguyen DA. Primary sensory neurons express a shaker-like potassium channel gene. J Neurosci. 1993;13:4988–4996. doi: 10.1523/JNEUROSCI.13-11-04988.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ribera AB, Spitzer NC. Differentiation of IKA in amphibian spinal neurons. J Neurosci. 1990;10:1886–1891. doi: 10.1523/JNEUROSCI.10-06-01886.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Roberts A. How does a nervous system produce behaviour? A case study in neurobiology. Sci Prog. 1990;74:31–51. [PubMed] [Google Scholar]
- 36.Roberts A, Clarke JDW. The neuroanatomy of an amphibian embryo spinal cord. Philos Trans R Soc Lond B Biol Sci. 1982;296:195–212. doi: 10.1098/rstb.1982.0002. [DOI] [PubMed] [Google Scholar]
- 37.Roberts A, Kahn JA. Intracellular recordings from spinal neurons during “swimming” in paralysed amphibian embryos. Philos Trans R Soc Lond B Biol Sci. 1982;296:213–228. doi: 10.1098/rstb.1982.0003. [DOI] [PubMed] [Google Scholar]
- 38.Roberts A, Sillar KT. Characterization and function of spinal excitatory interneurones with commissural projections in Xenopus laevis embryos. Eur J Neurosci. 1990;2:1051–1062. doi: 10.1111/j.1460-9568.1990.tb00017.x. [DOI] [PubMed] [Google Scholar]
- 39.Sah P, McLachlan EM. Potassium currents contributing to action potential repolarization and the afterhyperpolarization in rat vagal motoneurons. J Neurophysiol. 1992;68:1834–1841. doi: 10.1152/jn.1992.68.5.1834. [DOI] [PubMed] [Google Scholar]
- 40.Schauf CL. Dendrotoxin blocks potassium channels and slows sodium inactivation in Myxicola giant axons. J Pharmacol Exp Ther. 1987;241:793–796. [PubMed] [Google Scholar]
- 41.Scott VES, Muniz ZM, Sewing S, Lichtinghagen R, Parcej DM, Pongs O, Dolly JO. Antibodies specific for distinct Kv subunits unveil a heterooligomeric basis for subtypes of α-dendrotoxin-sensitive K+ channels in bovine brain. Biochemistry. 1994;33:1617–1623. doi: 10.1021/bi00173a001. [DOI] [PubMed] [Google Scholar]
- 42.Sillar KT, Wedderburn JFS, Simmers AJ. The development of swimming rhythmicity in post-embryonic Xenopus laevis. Proc R Soc Lond B Biol Sci. 1991;246:147–153. doi: 10.1098/rspb.1991.0137. [DOI] [PubMed] [Google Scholar]
- 43.Simmons ML, Chavkin C. κ-Opioid receptor activation of a dendrotoxin-sensitive potassium channel mediates presynaptic inhibition of mossy fiber neurotransmitter release. Mol Pharmacol. 1996;50:80–85. [PubMed] [Google Scholar]
- 44.Soffe SR. Active and passive membrane properties of spinal cord neurons that are rhythmically active during swimming in Xenopus embryos. Eur J Neurosci. 1990;2:1–10. doi: 10.1111/j.1460-9568.1990.tb00376.x. [DOI] [PubMed] [Google Scholar]
- 45.Soffe SR. Two distinct rhythmic motor patterns are driven by common premotor and motor neurons in a simple vertebrate spinal cord. J Neurosci. 1993;13:4456–4469. doi: 10.1523/JNEUROSCI.13-10-04456.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Soffe SR. Motor patterns for two distinct rhythmic behaviors evoked by excitatory amino acid agonists in the Xenopus embryo spinal cord. J Neurophysiol. 1996;75:1815–1825. doi: 10.1152/jn.1996.75.5.1815. [DOI] [PubMed] [Google Scholar]
- 47.Tegner J, Hellgren-Kotaleski J, Lansner A, Grillner S. Low-voltage-activated calcium channels in the lamprey locomotor network: simulation and experiment. J Neurophysiol. 1997;77:1795–1812. doi: 10.1152/jn.1997.77.4.1795. [DOI] [PubMed] [Google Scholar]
- 48.Wall MJ, Dale N. A role for potassium currents in the generation of the swimming motor pattern of Xenopus embryos. J Neurophysiol. 1994;72:337–348. doi: 10.1152/jn.1994.72.1.337. [DOI] [PubMed] [Google Scholar]
- 49.Wall MJ, Dale N. A slowly activating Ca2+-dependent K+ current that plays a role in termination of swimming in Xenopus embryos. J Physiol (Lond) 1995;487:557–572. doi: 10.1113/jphysiol.1995.sp020900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Werkman TR, Kawamura T, Yokoyama S, Higashida H, Rogawski MA. Charybdotoxin, dendrotoxin and mast cell degranulating peptide block the voltage-activated K+ current of fibroblast cells stably transfected with NGK1 (Kv1.2) K+ channel complementary DNA. Neuroscience. 1992;50:935–946. doi: 10.1016/0306-4522(92)90216-o. [DOI] [PubMed] [Google Scholar]