Translation-Invariant Orientation Tuning in Visual “Complex” Cells Could Derive from Intradendritic Computations

Abstract

Hubel and Wiesel (1962) first distinguished “simple” from “complex” cells in visual cortex and proposed a processing hierarchy in which rows of LGN cells are pooled to drive oriented simple cell subunits, which are pooled in turn to drive complex cells. Although parsimonious and highly influential, the pure hierarchical model has since been challenged by results indicating that many complex cells receive excitatory monosynaptic input from LGN cells or do not depend on simple cell input. Alternative accounts of complex cell orientation tuning remain scant, however, and the function of monosynaptic LGN contacts onto complex cell dendrites remains unknown. We have used a biophysically detailed compartmental model to investigate whether nonlinear integration of LGN synaptic inputs within the dendrites of individual pyramidal cells could contribute to complex-cell receptive field structure. We show that an isolated cortical neuron with “active” dendrites, driven only by excitatory inputs from overlapping ON- and OFF-center LGN subfields, can produce clear phase-invariant orientation tuning—a hallmark response characteristic of a complex cell. The tuning is shown to depend critically both on the spatial arrangement of LGN synaptic contacts across the complex cell dendritic tree, established by a Hebbian developmental principle, and on the physiological efficacy of excitatory voltage-dependent dendritic ion channels. We conclude that unoriented LGN inputs to a complex cell could contribute in a significant way to its orientation tuning, acting in concert with oriented inputs to the same cell provided by simple cells or other complex cells. As such, our model provides a novel, experimentally testable hypothesis regarding the basis of orientation tuning in the complex cell population, and more generally underscores the potential importance of nonlinear intradendritic subunit processing in cortical neurophysiology.

The mechanisms underlying orientation tuning in visual cortical neurons are among the most studied in systems neuroscience. Under the original Hubel and Wiesel (1962) classification scheme, simple cell receptive fields (RFs) could be subdivided into separable, oriented ON and OFF subregions, with quasilinear spatial summation within a subregion and antagonism between subregions. Orientation tuning in simple cells is now widely considered to derive from a combination of influences, specifically a weak orientation bias in the input from LGN, modulated by feedback inhibition and excitation from other cortical neurons (Ferster et al., 1996; Vidyasagar et al., 1996; Somers et al., 1995; Krukowski et al., 1996). In contrast, complex cell receptive fields, with overlapping ON and OFF subfields, exhibit a number of fundamentally nonlinear behaviors that distinguish them from simple cells, including orientation tuning across a receptive field much wider than an optimal bar stimulus, responses to both light and dark bars at the same receptive field loci (Hubel and Wiesel, 1962), and antagonistic interactions between pairs of bars that are individually excitatory (Movshon et al., 1978).

The Hubel and Wiesel (1962) model and several subsequent models (Movshon et al., 1978; Pollen and Ronner, 1983; Heeger, 1992) have held that complex cell orientation tuning is achieved by pooling the outputs of a set of simple cell-like subunits with different positions and phases, allowing the complex cell to respond selectively to a particular stimulus orientation while generalizing over position and contrast polarity. This kind of subunit pooling is of relevance well beyond the primary visual cortex, because the construction of receptive fields that grow progressively more stimulus specific, and more spatially invariant, roughly characterizes the transformation of the visual code from level to level in the form-processing cortical stream and culminates in cells in the inferotemporal complex with elaborate form preferences maintained over very large receptive fields (Ito et al., 1995). The ubiquity of subunit pooling as a cortical computation, therefore, makes it essential to establish which biophysical mechanisms and cortical circuit properties contribute to it.

The idea that simple cells are the exclusive oriented subunits contributing to complex cell responses has been challenged repeatedly. Four types of evidence may be cited, including (1) evidence for direct LGN input to complex cells (Hoffmann and Stone, 1971; Toyama et al., 1973; Singer et al., 1975; LeVay and Gilbert, 1976; Bullier and Henry, 1979; Sillito, 1979; Ferster and Lindstrom, 1983; Henry et al., 1983), (2) reports of visual stimuli that drive complex cells but not simple cells [Movshon (1975), although see Wilson and Sherman (1976), Gilbert (1977); Hammond and MacKay (1975, 1977), Hoffman and von Seelen (1978),Burr et al. (1981), Poggio et al. (1985), although see Skottun et al. (1988, 1991), Hammond (1991)], (3) a lack of monosynaptic connections from simple to complex cells as revealed by cross-correlation analysis (Toyama et al., 1981; Ghose et al., 1994), (although see Alonso, 1996), and (4) persistence of complex cell responses when simple cells are silenced by pharmacological inactivation of appropriate LGN layers. (Malpeli et al., 1986; Mignard and Malpeli, 1991) (although see Alonso, 1996).

Although many questions remain, the experimental record is consistent with a scenario in which some complex cells both receive direct LGN input and may not depend on simple cell input. The existence of cells of this kind, however, requires an alternative source of oriented subunits, “tiling” the cells’ receptive fields and acting in parallel with those putatively provided by simple cells. One possibility is that a network of complex cells with excitatory and inhibitory couplings could manufacture phase-independent orientation tuning from raw, unoriented LGN inputs. A second possibility is that the subunit computation necessary for constructing a complex cell receptive field could be carried out within the dendritic tree of an individual complex cell.

Similar proposals have been made in other contexts. Building on the work of Barlow and Levick (1965), for example, Koch et al. (1982, 1986) used a compartmental model to show that the divisive, “veto”-like action of shunting inhibition distributed across a large number of dendritic subunits could underlie direction-selective responses. Dendritic subunit computations based on expansive nonlinear synaptic interactions have also been modeled (Rall and Segev, 1987;Shepherd and Brayton, 1987; Mel, 1992a,b, 1993). In a precursor to the present work, it was established in Mel (1992b, 1993) that a neocortical pyramidal cell driven by strong NMDA-type synaptic currents and/or containing dendritic Ca²⁺ or Na⁺ channels, can respond more strongly when synapses are activated in spatially clustered groups, in comparison with the same number of synapses activated diffusely about the dendritic arbor. Furthermore, the steady-state input–output function of an active, “cluster-sensitive,” dendritic tree was abstracted as a “big sum of little products,” where the particular set of product terms depended on the spatial arrangement of synaptic inputs across the dendritic tree. A close match to the mathematical expressions underlying quadratic “energy” models for complex cell orientation tuning (Pollen and Ronner, 1983; Ohzawa et al., 1990; Heeger, 1992) suggested that an intracellular basis for complex cell responses was possible. We set out to investigate this possibility here, using compartmental modeling techniques.

MATERIALS AND METHODS

Simulations of a pyramidal cell from cat visual cortex (morphology courtesy of Rodney Douglas and Kevan Martin, Institute for Neuroinformatics, ETH/University of Zurich) were carried out in NEURON (Hines, 1989). Because the morphometric data for the cell used in these experiments were derived from a large layer 5 pyramidal cell, we also used spatially restricted subsets of the cell’s dendritic tree in control experiments to emulate smaller cells with varying geometries.

Because the available anatomical data did not encode the locations and structural parameters of dendritic spines, a scheme proposed byStratford et al. (1989) was used to increment the length and diameter of each dendritic branch so that its area, input resistance, axial resistance, and effective electrotonic length mimicked those of a branch covered with spines at an assumed density of one spine per micrometer (Douglas and Martin, 1990; Larkman, 1991). Under this manipulation, the total dendritic branch length was increased from 17 to 20 mm.

Biophysical simulation parameters are summarized in Table1. The soma and dendritic membrane contained Hodgkin–Huxley-type (HH) voltage-dependent sodium and potassium channels. Following evidence for higher spike thresholds and decremental propagation in dendrites (Stuart and Sakmann, 1994), HH channel density was set to a uniform, fourfold lower value in the dendritic membrane relative to that of the cell body. Excitatory synapses from LGN cells included both NMDA and AMPA-type synaptic conductances. Because the cell was considered to be isolated from the cortical network, inhibitory input was not modeled. Cortical cell responses were reported as average spike rate recorded at the cell body over the 500 msec stimulus period, excluding the 50 msec initial transient (because few spikes occurred during this period in the isolated cell model).

Table 1.

Biophysical simulation parameters

Parameter	Value
Rm	10 kΩcm2
Ra	200 Ωcm
Cm	1.0 μF/cm2
Vrest	−70 mV
Compartments	615
Somatic $\overline{g}$Na,$\overline{g}$DR	0.20, 0.12 S/cm2
Dendritic $\overline{g}$Na,$\overline{g}$DR	0.05, 0.03 S/cm2
Input frequency	0–100 Hz
$\overline{g}$AMPA	0.105–1.15 nS
τAMPA (on, off)	0.5 msec, 3 msec
$\overline{g}$NMDA	0.105–1.15 nS
τNMDA (on, off)	0.5 msec, 50 msec
Esyn	0 mV

Details of HH channel implementation are given elsewhere (Mel, 1993); original HH channel implementation adapted from Bernander et al. (1991). So that local EPSP size was held approximately constant across the dendritic arbor, peak synaptic conductance at dendritic locationx was approximately scaled to the local input resistance (inversely), given by $\overline{g}$_syn (x) = c/R̃_in (x), wherec was a constant, and R̃_in(x) = max (R_in (x), 200mΩ). Input resistance R_in(x) was measured for a passive cell. Thus$\overline{g}$_syn was identical for all dendritic sites with input resistance below 200 mΩ and was given by the larger conductance value shown; roughly 50% of the tree fell within a factor of 2 of this value. Peak conductances at the finest distal tips were smaller by roughly a factor of 10 (smaller number shown). Somatic input resistance was near 24 mΩ. Both AMPA- and NMDA-type synaptic conductances were modeled using the kinetic scheme of Destexhe et al. (1994); synaptic activation and inactivation time constants are shown for each. NMODL files used in the NEURON simulations are available for public download at http://lnc.usc.edu.

A stimulus image consisted of a 64 × 64 pixel array containing a stationary light or dark bar (pixel value ±1 against a background of 0) or a sinusoidal grating (peak values ±0.15). Images were spatially convolved with a center surround filter whose effective center diameter and optimal bar width was 7 pixels (Fig.1). Non-zero filter outputs were treated as subthreshold LGN cell activation values: positive values were mapped onto a 64 × 64 array of ON-center cells, and negative values were mapped (as positive values) onto the corresponding array of OFF-center cells. Accordingly, only one cell type could be active at any given LGN site for a given stimulus. Activation values for each cell were then linearly scaled to yield a mean firing rate for a Poisson spike-generating process, such that LGN cell outputs ranged from 0 Hz (no stimulus) to 100 Hz (high-contrast optimal width bar through center of receptive field). Temporal modulation of LGN cell responses was not modeled in the present experiments.

Fig. 1.

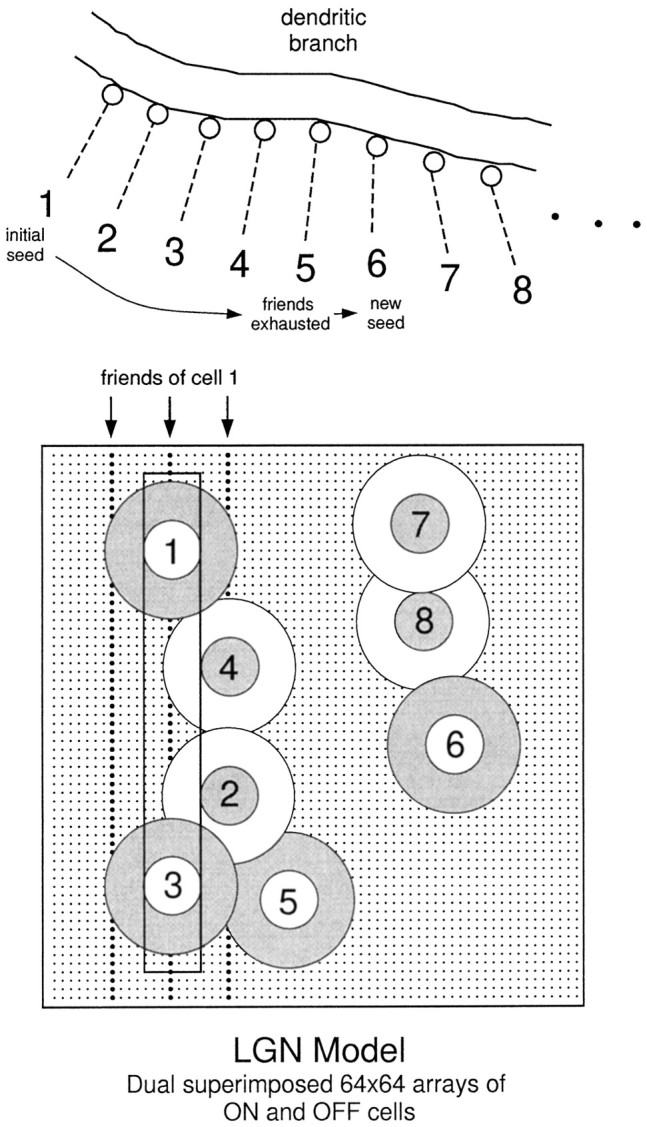
Connectivity from LGN cells onto cortical dendrites. The LGN model consisted of dual, superimposed 64 × 64 arrays of ON and OFF cells on a rectangular lattice. Receptive fields were represented by difference-of-Gaussian filters (center SD = 2, surround SD = 4; truncated to a size 16 × 16 with DC component subtracted away). RF center locations are indicated bysmall dots. An optimal width bar is shown passing through the center of two ON-center cells (1, 3) and through the ON-surrounds of two horizontally offset OFF-center cells (2, 4). For vertical orientation tuning, the three vertically aligned groups of 64 cells, with centers indicated by bolder dots, were designated as the “friends” of cell 1, i.e., they were maximally correlated with this cell for an ensemble of vertically oriented bars of optimal width. All ON-center cells in the same vertical group (e.g., 1, 3, etc.) had identical friends. Each OFF-center cell had friends organized in a precisely complementary arrangement. Given the random 1 in 8 subsampling from the LGN array to establish the connections onto any given complex cell, each designated LGN cell had on average 3 × 8 − 1 = 23 friends in the subsample. The available pool of designated LGN cell axons was spatially mapped onto the pyramidal cell dendrites by first randomly choosing a “seed” cell (1) and forming a connection at the first available dendritic site i, then randomly choosing one of its friends (2) for the next available dendritic sitei + 1, then randomly choosing a friend of the afferent at site i + 1 (3) for site i+ 2 (4), and so on, until either all of the friends of the cell at the current site were already deployed (occurred after5), in which case a new seed cell (6) was chosen at random to restart the sequence, or all cells had been chosen, indicating that all of the available LGN synapses had been mapped successfully onto the dendritic tree. Dendritic sites were mapped in depth-first order; in the standard complex cell run, LGN sites were separated by 20 μm.

Of the 8192 LGN neurons, one-eighth were chosen at random to form a single excitatory synapse onto the cortical cell’s dendritic tree. The assumption of ∼1000 excitatory synaptic inputs to the cell was based on reports that LGN inputs make up between 5 and 20% of the total synaptic contacts onto cells in the middle layers of cat primary visual cortex (LeVay and Gilbert, 1976; Peters and Payne, 1993), out of an assumed total of 10,000 synaptic contacts onto a relatively large cell such as we used in these simulations. Given the uncertainty in the precise numbers and distribution of LGN contacts on pyramidal cells in each layer, however, and to rule out major effects of cell size and dendritic morphology, we included control runs in which only 100 LGN synapses were activated, confined to either the apical or basal dendritic tree.

The activity pattern of one such random subset of 1024 LGN cells is shown in Figure 2A in response to vertical and oblique bars. The spatial arrangement of the synaptic contacts from these subsampled LGN cells onto the pyramidal cell dendrites was the crucial determinant of the cell’s nonlinear response selectivity. The arrangement was generated according to a pseudo-developmental rule that mimicked a balance of (1) random, activity-independent synapse formation and (2) activity-dependent synapse stabilization based on localized postsynaptic voltage signals (Shatz, 1990; Cline, 1991). As has been previously verified in simulation experiments, one outcome of learning rules of this type is that strongly correlated inputs are more likely to form synapses at nearby sites in the dendritic tree (Mel, 1992a). In the present context, ON and OFF cells whose activity was correlated with respect to an ensemble of vertically oriented light and dark bars were designated to form neighboring synaptic contacts (Fig. 1). Thus, the axodendritic contact of each ON-center cell in the LGN population was flanked at a distance of either 20 μm or 100 μm (in one control run) by connections from other ON-center cells in the same vertical strip and/or from OFF-center cells in horizontally offset vertical strips. A complementary arrangement held for OFF-center cells. This translation-invariant orientation bias in the microarrangement of dendritic input guaranteed that a vertically oriented stimulus activated more groups of neighboring synapses than did stimuli at nonoptimal orientations (Fig. 2B,C). We expected this orientation dependence to be functionally significant in light of previous work, which showed that synapses activated in a number of spatial clusters could produce significantly larger cell responses than the same number of synapses activated diffusely about the dendritic tree (Mel, 1992a,b, 1993). This expectation was borne out, as illustrated in Figure 2D.

Fig. 2.

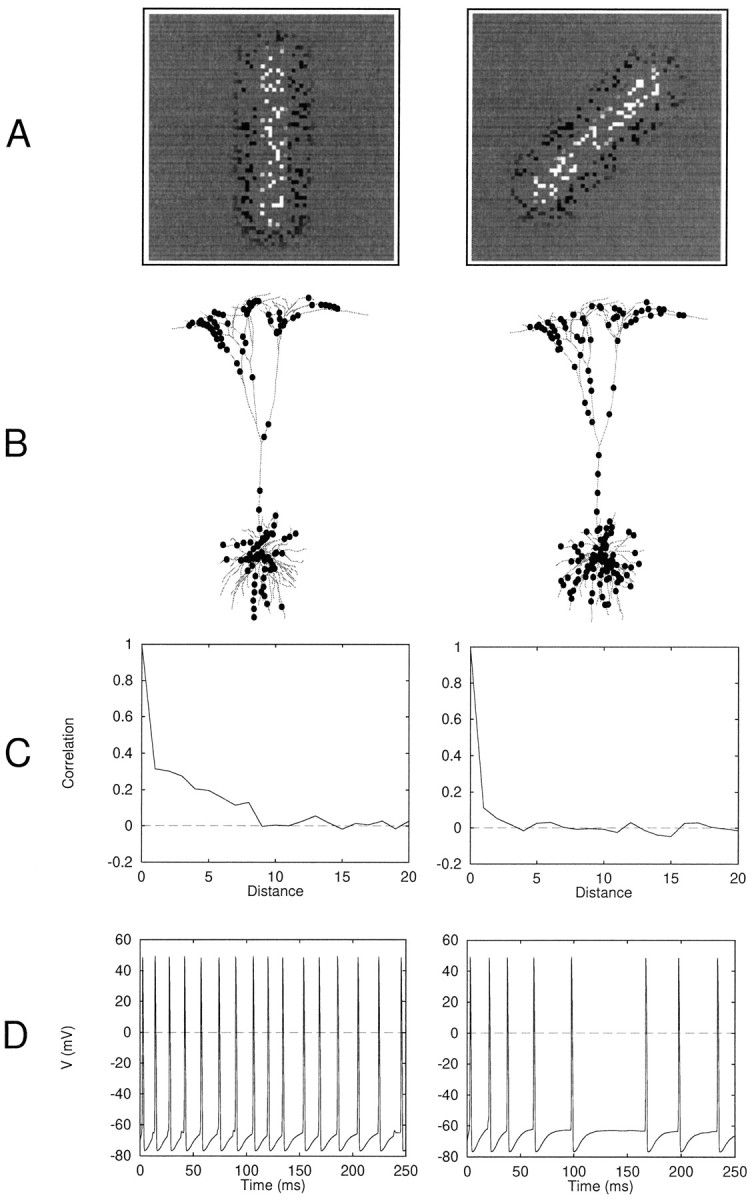
Mechanism underlying orientation tuning for a single neuron. A, Activity of 1024 randomly subsampled LGN cells in response to a vertical or oblique bar of optimal width.B, Distribution of ∼150 most active synapses on dendritic tree shows more clustery distribution for vertically oriented bar. In other cases, clustering was not easily visible by eye. C, Spatial correlation function for synaptic input to dendritic tree: plot shows Corr(x_i,x_j) against distance i −j measured in sites (20 μm spacing), wherex_i was the firing rate of the synapse at sitei. The correlation was measured in a linear array of site activity values before sites were mapped in depth-first order onto the dendritic tree at 20 μm intervals. For a vertically oriented bar, synaptic input is correlated to a distance of approximately eight sites (160 μm): an active (or inactive) synapse reliably predicts the same in its neighborhood of this size. In contrast, the correlation function for an oblique bar is close to a δ function, indicating minimal extent of spatial correlation. D, Corresponding records from cell body showing significantly larger response to vertical bar.

RESULTS

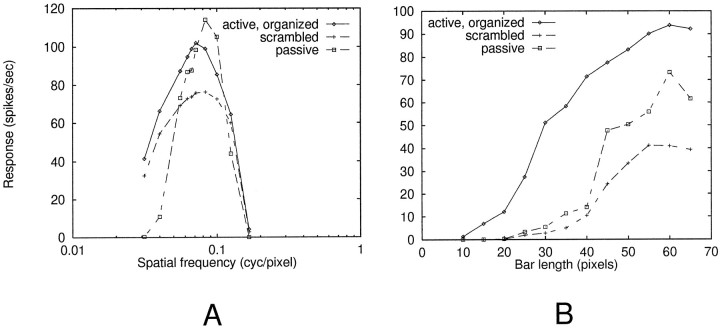
Average spatial-frequency tuning and bar length summation curves for model complex cells are shown in Figure3. Spatial-frequency tuning was largely inherited from the LGN cell model: the optimal grating wavelength (14 pixels) was twice the width of LGN receptive field centers. Curves are within normal ranges for complex cells, assuming a conversion of roughly 10 pixels per degree (Orban, 1984), although the comparison is weak because the isolated cell model used here lacks all intracortical (excitatory and inhibitory) influences that could act to shape its basic tuning curve. Because the general form of both spatial frequency and bar length curves were primarily related to total LGN output, i.e., did not depend on cooperative nonlinear synaptic interactions within cortical dendrites, qualitatively similar curves were obtained when LGN inputs to the cell were spatially scrambled or when all dendritic HH and NMDA channels were blocked, leaving an electrically passive dendritic tree (Fig. 3, dashed curves).

Fig. 3.

LGN-dependent response patterns. Each point is an average of 20–30 randomized runs. A, Spatial-frequency tuning. Cell responses (spikes per second) are plotted against spatial frequency of vertically oriented sinusoidal gratings applied to the entire receptive field. Three curves shown are for (1) active dendrites with spatially organized geniculocortical projection, (2) active dendrites but with spatially scrambled geniculocortical projection, and (3) passive dendrites with spatially organized geniculocortical projection. B, For length summation runs, a vertical bar of optimal width was presented at a range of lengths, centered in the receptive field. An increasing trend can be seen in all three cases (same conditions as in A).  

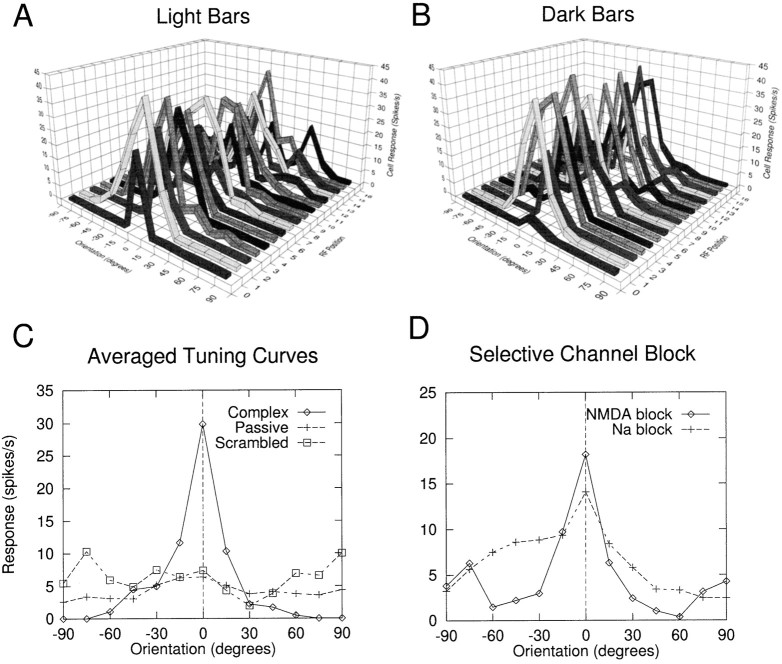
Orientation tuning curves for a complex cell are shown in Figure4A,B for light and dark bars at a range of receptive field locations. Half width at half maximum (HWHM) for this isolated cell was ∼15°; in the cat, complex cell HWHMs typically range from 20 to 30° (Orban, 1984). Tuning in this cell is roughly invariant to stimulus position and contrast polarity. This invariance was expected given that the statistics used to organize the LGN projection onto the cortical cell dendrites were both translationally invariant and symmetric with respect to ON and OFF cell types. Random departures from ideal tuning curves were attributable to (1) random subsampling of the LGN array, which led to fluctuations in total LGN drive to the cell at particular positions and orientations, and (2) randomness in the learning rule used to generate the spatial arrangement of LGN contacts onto the complex cell dendritic tree. That these effects were not systematic was revealed by the fact that averages over several complex cells (and RF positions) yielded smooth, peaked tuning curves. Tuning curves for sinusoidal gratings were essentially similar to those for bars (data not shown).

Fig. 4.

Complex cell orientation tuning. A,B, Orientation tuning curves are shown in response to optimal-width light and dark bars over a range of receptive field positions for a single complex cell. Tuning is roughly invariant to stimulus position and contrast polarity. C, Average of tuning curves at all positions for light and dark bars is shown for the cell in Aand B (Complex). Tuning was abolished when synapses onto this cell were spatially scrambled in the dendritic tree (Scrambled), or when all voltage-dependent channels (NMDA, dendritic HH) were blocked leaving an electrically passive cell (Passive). Somatic current injections were needed in these isolated cell cases to bring the response off the floor (0.3 nA inScrambled case, 1.2 nA in Passive case).D, Orientation tuning could be seen in complex cells that contained either of the two voltage-dependent mechanisms alone. Averaged tuning curves are shown for a cell in which NMDA channels were blocked, leaving only dendritic Na⁺ channels to support the nonlinear dendritic integration (diamonds). AMPA conductances were increased by a factor of 4 relative to values in Table 1 for this run. When dendritic HH channels were blocked instead, leaving the NMDA channels as the only source of voltage-dependent dendritic current, the cell remained orientation tuned, although individual tuning curves were broader and far noisier; an average tuning curve for five complex cells is shown in this case (+). Synaptic conductances were increased by a factor of 2 relative to Table 1 for this case, to compensate for the lack of Na⁺currents in the dendritic tree.

Separate tests were carried out in this cell to test the two crucial features of the model: the dependence on (1) a spatially organized axodendritic interface and (2) the presence of excitatory voltage-dependent membrane mechanisms in the dendrites. To confirm that orientation-tuning was mediated by spatially dependent intradendritic processing operations, the connectivity from LGN cells onto the dendritic tree was randomly scrambled for the cell from Figure4A,B, leading to a complete collapse of the cell’s tuning curve (Fig. 4C, Scrambled); the original averaged tuning curve is provided for comparison (Complex). Identical spike trains were delivered to each synapse in both the Complex and Scrambled conditions to maintain maximum experimental control. To confirm that active dendritic processing was responsible for the translation-invariant orientation tuning in this cell, all voltage-dependent dendritic channels were blocked (NMDA and dendritic HH), which again flattened the cell’s tuning curve (Fig.4C, Passive).

Orientation tuning could also be seen in complex cells that contained either of the two voltage-dependent mechanisms alone. Examples are shown for complex cells in which only Na⁺ channels or only NMDA channels were available to support the complex cell receptive field properties (Fig. 4D), confirming that a continuum of physiological configurations can support the needed dendritic subunit nonlinearity, involving NMDA channels and dendritic Na⁺ channels (and likely voltage-dependent Ca⁺ channels) in varying combinations. We easily generated examples in which selective NMDA-channel blockade led to suppression of cell responses, consistent with experiments involving NMDA blockade in visual cortex (Miller et al., 1989; Fox et al., 1989,1990; Fox et al., 1992), but in which complex-cell-like properties were maintained by dendritic Na⁺ channels. However, the degree of response suppression seen in tuned cells under NMDA block in our simulations could be controlled over a wide range by varying the initial (preblock) conductances of NMDA channels in the dendrites. The main lesson of this manipulation, therefore, was that complex-cell-like response did not require NMDA channel activation, assuming the presence in the dendrites of other excitatory voltage-dependent channels, even in cases where NMDA channels contributed strongly to the normal visually evoked responses of the cell.

In other experiments, we found that hyperpolarizing current injections to the soma were by themselves ineffective at eliminating orientation tuning in the subthreshold somatic voltage trace, because of inadequate space clamp within the pyramidal cell dendritic tree. This is consistent with the results of Schwindt and Crill (1997), who found that somatic hyperpolarization did not block dendritically generated action potentials.

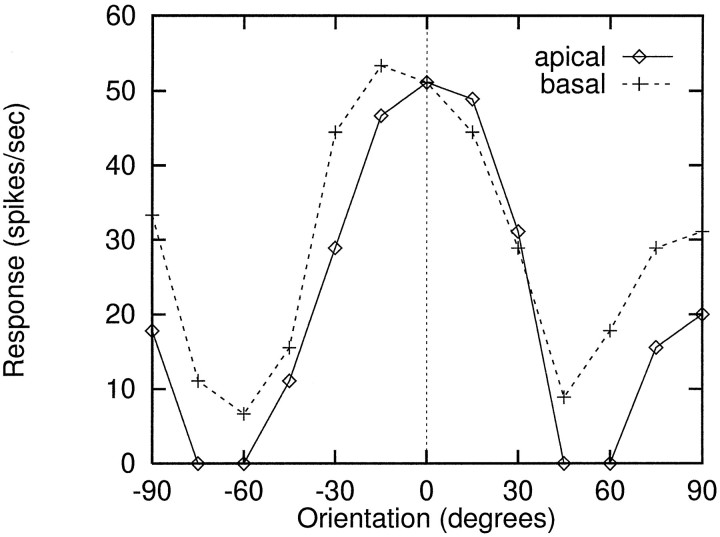
Having demonstrated that the full pyramidal cell dendritic tree could support the subunit computations underlying complex cell orientation tuning, control runs were carried out to assess the dependence of orientation tuning on gross dendritic morphology and synaptic activation density, because both of these factors could impact on the critical nonlinear interactions among synapses in the dendritic tree (Koch et al., 1982; Woolf et al., 1991). Runs were therefore carried out using only 100 excitatory inputs drawn from a 20 × 20 LGN receptive field, uniformly subsampled from dual ON and OFF layers as before. These 100 synaptic contacts were confined to either the apical or the basal dendritic tree, each of which accounted for approximately half of the total dendritic length.

Prominent orientation tuning persisted under these conditions; example tuning curves for an “apical” and a “basal” case are shown in Figure 5; curves are averaged over several RF positions. The bar stimulus used in these runs was a relatively squat 18 × 7 pixels, i.e., of optimal width but short enough to be completely contained within the cell’s 20 × 20 RF. In the absence of intracortical inhibition, this low aspect ratio tended to equalize the cell’s responses at 0 and 90°, explaining the significant elevation of the response curves at ±90°.

Fig. 5.

Replication of orientation tuning when LGN inputs were confined to either the apical or basal dendritic tree. Total branch length in each subtree was approximately half the 20 mm total length of the pyramidal cell dendritic tree. In these runs, 100 excitatory synapses from LGN were used to drive the cortical cell in lieu of the 1024 inputs used in the runs of Figure 4. Tuning was evaluated with a relatively short, wide bar (18 × 7). Curves shown are averages over several RF positions. Noticeable elevation of responses at 90° from optimal were evident as the horizontal top and bottom edges of the bar swung into vertical position at 90°. Biophysical parameters used here were as follows: HH conductances were double those of Table 1, and maximum peak synaptic conductances were$\overline{g}$_NMDA = 5 nS,$\overline{g}$_AMPA = 0.5 nS.

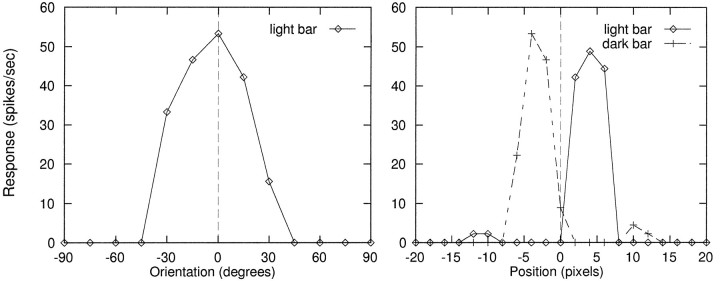
To verify that the presence of nonlinear voltage-dependent channels would not preclude a cortical cell from generating simplecell responses, we constructed a simple cell receptive field as follows. We drew ON and OFF inputs from adjacent, elongated, nonoverlapping subregions of the LGN array. The ON subregion consisted of all ON cells whose centers lay in five vertical columns of 20 cells ranging between +3 and +7 pixels to right of RF center, and the OFF subregion consisted of all OFF cells whose centers lay in five vertical columns of 20 cells in the range of −3 to −7 pixels to left of RF center. The separation between ON and OFF subgroups was chosen such that the centers of the centermost columns of ON and OFF cells just abutted each other. Single excitatory contacts from each of these 200 LGN cells were distributed at random across the full dendritic tree of the cortical cell (in contrast to the structured arrangement of LGN inputs to the model complex cell), with ON and OFF cells randomly intermixed. The cell’s orientation tuning is shown in Figure6A, measured using a light bar centered in the ON subregion. Clearly separable ON and OFF subregions were also mapped using light and dark vertical bars at a range of horizontal positions across the receptive field (Fig.6B).

Fig. 6.

Constructing a simple cell receptive field. Model cortical cell received 200 inputs drawn from elongated, nonoverlapping ON and OFF subregions of the LGN. Contacts were randomly intermixed in the dendrites. Left, Orientation tuning using a light bar centered in the ON subregion. Right, Map of ON and OFF subregions using vertical light and dark bars at a range of horizontal positions across the RF. Small ON and OFF sidelobes were caused by cell surrounds. Biophysical parameters used here were as follows: HH conductances were double those of Table 1, and maximum peak synaptic conductances were $\overline{g}$_NMDA = 4 nS,$\overline{g}$_AMPA = 0.4 nS.

DISCUSSION

An intracellular substrate for complex-cell orientation tuning

The results of Figure 4 indicate that an individual cortical pyramidal cell, driven exclusively by excitatory inputs from ON- and OFF-center LGN cells, is biophysically capable of producing robust orientation-tuned responses to both light and dark bars over a spatially extended receptive field—and in this important sense, of behaving like a complex cell. No systematic orientation bias existed in the LGN cell receptive fields themselves or in the spatial distribution of LGN cell receptive fields afferent to the cortical complex cell, so that total LGN cell activity—and hence mean input to the model complex cell—was equivalent at every bar position and orientation in these experiments. The significantly larger average responses to optimal orientations therefore could not be explained by an elevation in the total synaptic drive impinging on the cortical neuron. Moreover, individual synaptic efficacies were set quasiuniformly throughout the dendritic tree (Table 1 legend), ruling out any patterning of synaptic “weights” as a basis for these results.

Rather, the orientation effect could be explained in two steps: (1) optimally oriented stimuli typically drove synapses in a number of loose clusters scattered about the dendritic tree, whereas nonoptimal stimuli drove an equivalent number of synapses, but in a more diffuse spatial arrangement, and (2) these spatially concentrated domains of synaptic input were more effective at activating local intrinsic voltage-gated excitatory currents, which in turn led to larger postsynaptic responses.

Two key assumptions of the model

The intradendritic subunit computation at the heart of the present model depends on two main assumptions: (1) the dendritic tree must contain a sufficient set of voltage-dependent channels whose biophysics provide threshold-like behavior, hard or soft, and (2) the spatial arrangement of LGN synaptic contacts onto the complex cell dendrites must be manipulated to yield a pool of micro-oriented subunits scattered across the dendritic tree, each consisting of a loosely grouped cohort of ON and OFF cells co-consistent with an optimally oriented bar. The critical nature of these two assumptions is reflected in the observation that when the active dendritic channels included in our model (HH and NMDA) were suppressed together, or when the spatial arrangement of synaptic inputs was scrambled, complex cell response properties were abolished (Fig. 4C). In the following sections, we examine these key assumptions in greater detail.

Sensitivity to assumptions about dendritic channels

The generality of the present model depends critically on its sensitivity to the inventory and properties of voltage-dependent channels assumed to govern the dendritic tree’s electrical behavior. There is now solid evidence that the dendrites of neocortical pyramidal cells contain physiologically prominent concentrations of NMDA channels, which have been shown to contribute a large fraction of the excitatory synaptic drive in primary visual cortex (Miller et al., 1989; Fox et al., 1989, 1992), and voltage-dependent Na⁺ channels capable of generating full-blown dendritic action potentials (Amitai et al., 1993; Kim and Connors, 1993; Stuart and Sakmann, 1994; Schiller et al., 1995; Markram et al., 1997). However, the pattern of nonlinear synaptic integration under discussion here could reflect a highly specialized biophysical niche, unrelated to the normal operating conditions of pyramidal cells, arrived at by careful tuning of model parameters. Indeed, significant uncertainties remain regarding the biophysical parameters and spatial distribution of voltage-dependent channels throughout the dendritic tree, and the present model contains major simplifying assumptions in this regard. More importantly, other types of voltage-dependent channels are known to exist in these cells’ dendrites as well, including voltage-dependent calcium channels (Amitai et al., 1993;Reuveni et al., 1993; Markram et al., 1995), which could in principle complicate or disrupt the present story in unknown ways, and thereby frustrate our attempts to make general statements about the integrative behavior of “active” dendritic trees in visual cortex.

The specter of this unmodeled complexity is partly mitigated, however, by a result of the present study. In keeping with the results of previous work on the integrative properties of excitable dendritic trees (Mel, 1993), we found that the basic nonlinear spatial structure of a complex cell receptive field, which arose from a cell containing both NMDA and HH channels, could also be produced in a model cell whose dendrites contained only NMDA channels, or onlyHH channels, despite the radically different biophysics governing these two channel mechanisms. Thus, NMDA channels were not capable of producing regenerative currents and were in force only at the restricted loci of actively driven LGN synapses. Dendritic HH channels, in contrast, contained Na⁺ and K⁺components with different voltage sensitivities and kinetics, were capable of full regenerative signaling, and were in force across the entire dendritic tree. Given the profoundly different contributions of these two mechanisms to the postsynaptic voltage environment, it is striking that both mechanisms could effect the “same” nonlinear subunit computation (although not necessarily with comparable efficacy). We did not in the present study include voltage-dependent Ca²⁺ channels, although on the basis of the results of Mel (1992a, 1993), we would expect a qualitatively similar outcome, i.e., that Ca²⁺ channels are a sufficient, but not necessary, source of dendritic excitability to produce nonlinear receptive field subunits.

In more detailed examinations of the intradendritic signals generated by optimal visual stimuli, we noted qualitatively different patterns of synaptic integration for HH-only versus NMDA-only conditions. HH-only conditions involved frequent occurrences of actively propagated dendritic action potentials that could be initiated by a “cluster” of synaptic inputs in a distal dendritic region and propagated throughout the dendritic arbor, including the soma. In contrast, output spikes generated during NMDA-only conditions were caused by the combined (nonregenerative) EPSCs from widespread dendritic subunits driven by concentrated synaptic input. The kind of dendritic electrogenesis we see in the HH-only condition is on its face consistent with the results of Kim and Connors (1993), who inferred from intradendritically recorded voltage traces the existence of multiple independent sites of dendritic spike generation in response to distal synaptic inputs (also see Schwindt and Crill, 1997). However, the question as to the “normal” initiation and propagation patterns of dendritic spikes has yet to be settled satisfactorally (Stuart and Sakmann, 1994).

Required specificity of learned synaptic arrangements

Because the present model also depends critically on the spatial arrangement of LGN contacts onto the complex cell dendritic tree, it is important to assess the level of spatial precision required for the essential nonlinear synaptic interactions to take effect. At the experimental level, nothing is currently known about the spatial distribution of LGN contacts onto complex cell dendrites in relation to their ON and OFF receptive fields. However, we have observed that it is remarkably “easy” for a Hebbian learning rule to generate layouts of LGN connections that lead to orientation-tuned complex cell responses. One reason for this is that LGN (or other) contacts can interact cooperatively through shared voltage signals over considerable distances, making precise placement of contacts unnecessary. For example, in the simulations we report in which 1024 LGN inputs were modeled, the fixed distance between dendritic sites occupied by LGN inputs was 20 μm. This spacing allowed the LGN synapses to just span the total length of the dendritic tree at low density, under the assumption that the majority of contacts onto these cells derive from non-LGN sources. Because the orientation-related correlations among these LGN synapses were significant to a maximum distance of eight dendritic sites, or 160 μm (Fig. 2C), this suggests that the relevant nonlinear dendritic processing in these experiments was largely confined within a continuously sliding dendritic neighborhood of this approximate scale. In the experiments using only 100 LGN inputs onto half the dendritic tree, the LGN input site separation was a fixed 100 μm, such that only one or a few LGN synapses could occur on any given dendritic branch. Roughly speaking, the learning rule in this case needed only to ensure that each LGN afferent was anywhere within ∼100 μm in either direction of another LGN afferent with which it was correlated (i.e., vertically aligned).

The control runs of Figure 5 further demonstrate that pyramidal cell dendrites are extremely accommodating with respect to the intradendritic operations under study here. Using the identical developmental rule to micro-organize the geniculocortical interface in all cases, we showed that complex cell receptive fields could emanate from at least the two very different morphologies of the apical versus basal dendritic trees of pyramidal cells, in addition to the more typical cell morphology containing both. Furthermore, the demonstration of subunit-based orientation tuning when either 100 or 1024 LGN cells provided direct input to the cortical cell suggests that the relevant cooperative synaptic interactions can operate under a wide range of synaptic activation densities. These observations taken together suggest that any cell in the cortical column receiving even a modest number of direct LGN contacts onto either its apical or basal dendrites or both could have its response shaped in a functionally significant way by nonlinear intradendritic computations. Because LGN inputs to area 17 in cat terminate on the apical and basal dendrites of many pyramidal cells whose cell bodies reside outside layer 4, specifically onto the basal dendrites of cells near the layer 3-4 and 4-5 borders, emanating from LGN layers A and A1, and onto these cells’ apical tufts in layer 1 via the projection from LGN layer C (LeVay and Gilbert, 1976), many complex cells in primary visual cortex could be influenced by this type of mechanism.

LGN versus simple-cell subunit structure

It is worthwhile to consider the relatively subtle differences in the nonlinear receptive field structure afforded to a complex cell by simple-cell-like subunits versus center-surround LGN subunits. One important difference between these two cases is reflected in the geometry of nonlinear spatial antagonism expected within the complex cell’s receptive field, deriving from the geometry of the respective linear subunits (i.e., simple cells vs LGN cells).

In the case of simple cell subunits, two spots of light can interact antagonistically even when separated by the length of a simple cell’s long axis of orientation, giving rise to long-range suppressive nonlinear interactions in the complex cell. In a pure LGN-based complex cell model, on the other hand, two spots could interact antagonistically only within the more limited, circularly symmetric ON and OFF subregions of some given LGN subunit. Any longer-range antagonistic nonlinear interactions in a complex cell, such as are actually observed in second-order spatial kernels (Szulborski and Palmer, 1990; Gaska et al., 1994), therefore could not derive from LGN afferents alone. To explain such suppressive interactions, it is necessary to invoke larger linear subunits (e.g., simple cells) or some action of lateral inhibition within the cortical network.

One observation that could specifically signal a direct LGN contribution to a complex cell’s nonlinear receptive field structure would be whether the degree of nonlinear boosting between two spots of light varied significantly as the two spots were moved relative to each other, in and out of range of individual LGN receptive fields, although always remaining within the complex cell’s (and presumably simple cells’) more elongated receptive fields. White noise analysis has indicated that spatial modulation of nonlinear interactions in fact can occur on scales much smaller than the extent of a complex cell’s receptive field, traveling along the preferred orientation axis. For example, in a complex cell in cat V1 chosen to illustrate the nonlinear spatial interaction between pairs of light and dark spots [Szulborski and Palmer (1990), their Fig. 2], the peak nonlinear boost was seen when a second spot was illuminated within a fraction of a degree (on average) of the reference spot, for reference spots in four virtually nonoverlapping domains within a 6° diameter complex cell receptive field. Although the interpretation of these data is not entirely straightforward, this pattern of results could indicate a contribution from a subunit that is an order of magnitude smaller in spatial scale than the complex cell itself. The precise origin of these fine-spatial scale nonlinear boosting interactions, however, remains unknown.

Other avenues for experimental validation

Another approach to experimental validation of the present hypothesis involves intracellular suppression of the nonlinear membrane mechanisms underlying oriented subunit computations. Techniques could combine hyperpolarization with intracellular channel blockers, in analogy to the simulation experiments of Figure 4C,D. Under this type of manipulation, a complex cell that receives direct LGN inputs should show a partial or complete loss of orientation tuning as reflected in its output firing rate or subthreshold PSP. The degree of tuning suppression should grow with the relative effectiveness of the cell’s direct LGN drive, which could range from null to highly effective in different complex cells, and whose strength could be independently assessed.

The interpretation of results in such an experiment would be greatly facilitated if intracortical inputs could be selectively blocked, and LGN inputs to the cell are left functionally intact. This has been a technical objective of recent experiments involving the cooling of visual cortex (Ferster et al., 1996), which suppresses the firing of cortical cells and leaves afferent geniculocortical axonal transmission relatively unaffected. A serious complication of this type of technique, however, is that the intervention used to suppress cortical cell firing could interfere equally with active dendritic subunit processing. Thus, cooling, or alternatively application of GABA, could functionally inactivate the essential voltage-dependent dendritic ion channels that contribute to the cells’ orientation tuning. In such a case, any suppression of complex cell response tuning could be attributed to either the removal of input from external oriented subunits such as simple cells or to the loss of nonlinear intradendritic processing needed to compute the subunits locally, or both. Given the likely confounding effects of cortical response suppression methods in relation to the present hypothesis, other measures of LGN-derived orientation tuning could be attempted, such as the peak of the shortest latency EPSP. Observation of a phase-invariant orientation tuning curve in this measure, combined with a suppression of tuning under intracellular blockade of voltage-dependent channels, would constitute direct evidence for an intradendritic contribution to complex-cell orientation tuning.

Significance and limitations of the isolated complex-cell model

Although its central tenets remain to be experimentally validated, and despite various limitations, our dendritically based isolated complex-cell model provides the first detailed account, in answer to a longstanding puzzle, as to how direct LGN inputs to a complex cell could contribute nondestructively to the cell’s shift-invariant orientation tuning, in cooperation with oriented inputs provided by simple or other complex cells.

Its independence from the cortical circuit, however, also leads to one of the present model’s main weaknesses: it cannot easily generate clean experimental predictions regarding the behavior of complex cells as they normally exist within the cortical circuit. Thus, many important aspects of complex-cell physiology are inaccessible to our isolated-cell model in its present form, including, for example, all consequences of intracortical inhibition (e.g., sharpening of receptive field tuning, long-range paired-stimulus suppression effects, contrast gain control, etc.), or of the long-range excitatory connections that may contribute to extra-classical receptive field structure (Gilbert et al., 1996). Furthermore, our overly simplistic steady-state model of LGN responses has left many important questions of cortical receptive field dynamics outside the scope of our current model.

Finally, the present model raises questions, but provides no answers, regarding the intriguing relation between oriented receptive field subunits that could be computed within the postsynaptic dendritic milieu of an individual LGN-recipient complex cell and those computed by a presynaptic population of simple cells, where in principle both could mix within the dendrites of a single complex cell. In spite of its limitations, our model emphasizes the potential importance of intradendritic computation for visual neurophysiology and points to new experimental approaches relating to the role of the individual neuron in neocortical information processing.