Directional Tuning of Single Motor Units

Abstract

The directional activity of whole muscles has been shown to be broadly and often multimodally tuned, raising the question of how this tuning is subserved at the level of single motor units (SMUs). Previously defined rules of SMU activation would predict that units of the same muscle (or at least of the same neuromuscular compartment) are activated homogeneously with activity peaks in the same “best” direction(s). In the present study, the best directions of SMUs in human biceps (both heads) and deltoid (anterior, medial, and posterior portions) were determined by measuring the firing rate and threshold force of units for recruitment during isometric force ramps in many different directions. For all muscles studied, neighboring motor units could have significantly different best directions, suggesting that each muscle receives multiple directional commands. Furthermore, 17% of the units sampled clearly had a second-best direction, consistent with a convergence of different directional commands onto the same motoneuron. The best directions of the units changed gradually with location in the muscle. Best directions did not cluster into separate groups, thus, not supporting the existence of clearly distinguished neuromuscular compartments. Instead, the results reveal a more gradually distributed activation of the biceps and deltoid motoneuron pools. A model is proposed in which the central control mechanism optimizes the fulfillment of the continuously changing directional force requirements of a movement by gradually recruiting and derecruiting those units ideally suited for the production of the required force vector at any given time.

The complex task of coordinating the activation of the appropriate fibers in a given muscle appears, in many instances, to be fulfilled automatically. Assuming a “common drive” to all motoneurons (MNs) of each muscle (DeLuca and Erim, 1994; Iyer et al., 1994), recruitment order during an augmenting contraction may be determined by MN size alone (Henneman et al., 1965). Because of the orderly relation between the size of an MN and the mechanical and biochemical properties of its target muscle fibers (Burke, 1967), such size-ordered recruitment results in a smoothly graded force rise with minimal fatigue development. Thus, certain aspects of a motor act appear to be optimized requiring only the most parsimonious neural circuitry. Unfortunately, however, this elegant functional simplicity of the size principle/common drive concept is not without drawbacks. When applied to human arm movements it would predict rigidity within a system whose flexibility is, in fact, amazing. The directional aspects of everyday reaching movements are manifold, requiring a versatility that might make it necessary to allow for task-specific, differential activation of different subunits of the same muscle, resulting in deviations from a fixed recruitment order.

The results of several studies by Gielen, Denier van der Gon, and colleagues support the idea of task-dependent recruitment of the single motor units (SMUs) involved in elbow flexion–extension and pronation–supination. In the long head of biceps brachii,terHaar Romeny et al. (1984) found units activated differentially in supination, flexion, or a combination of the two in the lateral, medial, and central part of the muscle, respectively. In a study investigating SMU recruitment patterns in six human elbow muscles, van Zuylen et al. (1988) found evidence for the existence of subpopulations of SMUs in all but one of the muscles. One example of such differentiated input to SMUs of the same muscle may consist in a reciprocal inhibition between only parts of the MN pool of antagonistic muscles: Jongen et al. (1989) demonstrated that the relative activation of parts of the same muscle differed depending on whether the muscle was activated with or without the cocontraction of its antagonist.

One would thus predict that although the activity of whole muscles involved in a reaching task exhibits broad and often multimodal directional tuning (Buchanan et al., 1986; Flanders and Soechting, 1990), the SMUs of these muscles would be more narrowly tuned, with subpopulations of SMUs showing activity peaks for different directions. This has been confirmed by Theeuwen et al. (1994) for the bimodally tuned anterior deltoid (AD), a muscle whose two best directions closely corresponded to the activity peaks of two unimodally tuned subpopulations of SMUs. However, these investigators did not attempt to discern differences in the directional tuning of various SMUs within the same AD subpopulation or within other broadly tuned muscles. Thus, the issue of directional preferences and subpopulations of SMUs in proximal arm muscles requires further examination.

The present study examines the directional tuning properties of SMUs in human biceps brachii (long and short heads) and deltoid (anterior, medial, and posterior portions). We will present results indicating that the various SMUs within each portion of each muscle have different best directions. Directional preferences varied continuously with location in the muscle rather than clustering into distinct subpopulations located in the different heads or portions of the muscles. Furthermore, we found evidence for multiple directional preferences at a single location. This suggests that the activation of these muscles is more distributed than might be explained by their division into known anatomical compartments or discrete subpopulations of motor units.

MATERIALS AND METHODS

Subjects

Data were collected from a total of 203 units in four adult human subjects with no history of motor impairments. Subject A was a 6 ft 0 in (183 cm), 180 lb (81 kg) male; subject B was a 5 ft 9 in (175 cm), 130 lb (59 kg) female; subject C was a 5 ft 9 in (175 cm), 155 lb (70 kg) male; and subject D was a 5 ft 10 in (178 cm), 140 lb (64 kg) female. The protocol was approved by the Human Subjects Committee of the University of Minnesota, and all subjects gave their informed consent before participation in the study.

Experimental protocol

General. Subjects stood or sat with the upper arm vertical, the elbow flexed 90° (so that the forearm was horizontal and in a parasagittal plane), and the wrist neutral with regard to pronation–supination. The right wrist was strapped into a brace connected to a transducer measuring the forces exerted at the wrist (see Fig. 4a). Forces in various directions were produced by combinations of elbow flexion–extension and various moments about the rotational degrees of freedom of the shoulder. The brace rotated freely about the vertical axis of the transducer (∼2 cm proximal to the wrist flexion–extension axis) so that it was impossible to produce an isometric moment in this dimension.

Fig. 4.

Threshold force at recruitment and firing rate at steady state vary systematically with the direction of force at the wrist. a, Posture of the arm (side view) during the experiments. b, All unit recordings are aligned with force rise onset (marked by arrowhead below traces) and were recorded from one BI electrode during the same experiment. Three trials are shown for each direction; the presentation order was randomized during the experiment. As force direction changes from +1 to +3, and from 0 to −2, the force levels at recruitment become progressively higher, whereas firing rate at steady state decreases.c, Typical force trajectory with onset of force rise marked by the arrowhead. The vertical scale bar represents 20 N. d, Threshold force data plotted in y/x coordinates are fit by a line whose perpendicular (arrow) points in the best direction of the unit.

Two-dimensional experiments. In the first set of experiments, subjects produced ramp increases in isometric force in 20 different directions covering the sagittal plane (Fig.1a, Up–Back plane) and presented in random order while forces were recorded with a 2 df force sensor (Measurement Systems, Inc., Fairfield, CT). A cursor moving on an oscilloscope screen displayed the forces exerted at the wrist together with the 20 numbered targets representing force increases of equal magnitude in 20 different directions. The screen was aligned with the subject’s sagittal plane and placed so that the subjects could comfortably view the cursor movements during the trials. Before each trial the target number was announced. The subject then moved the cursor into the center target zone by exerting enough force to support the weight of the arm. When subjects indicated that they were ready, the trial was initiated with a frequency-ramped computer tone. The tone served as a cue for the subject to slowly and accurately acquire the target and hold the cursor in a steady state at the target for 2 sec. Data were acquired for 3.5 sec. For each unit, the magnitude of the target force was set somewhere between 8 and 20 N depending on the strength of the subject and/or the recruitment threshold of the unit to be studied.

Fig. 1.

a, Distribution of targets. First set of experiments: subjects produced isometric forces in 20 different directions covering the sagittal (Up–Back) plane. Second set: subjects produced forces in 54 different directions covering the sagittal (Up–Back), horizontal (Back–Out), and frontal (Up–Out) planes. b, Subject B, sagittal plane: 120 force traces (6 per direction) from four different experiments. Force traces stay close to the sagittal plane, especially those in the up and forward directions. c, Typical force trace (I), unit record (II), and unit raster (III). Threshold force is marked in force trace with a gray line. Close-up below unit trace shows consistent shape and amplitude of the potential of this unit.

Experiments were conducted in sets of ∼100 trials. None of the units recorded from was active over a range of >14 of the 20 directions. Each of the 20 directions was tested at least once for unit activity. After this, directions for which the unit had remained silent (except for the directions immediately bordering the activation range of the unit) were excluded from the experimental protocol. The remaining directions were tested five times each. To avoid fatigue, subjects were told to take breaks whenever they wished within a set, and intertrial intervals were kept between 3 and 10 sec.

Three-dimensional experiments. In a second series of experiments the set-up was expanded to include recordings during force ramps in the frontal and horizontal planes as well as the sagittal plane (Fig. 1a). Thus, subjects produced forces in 20 different directions in each of the three planes while forces and moments were recorded with a 6 df force–torque sensor (JR³ Inc., Woodland, CA). (Although the task required only the 3 linear df, recordings from the rotational degrees of freedom were used to cancel sensor cross-talk.) Two more oscilloscopes were added to the set-up to provide the subject visual feedback information concerning the forces in the frontal and horizontal planes. The screens were aligned with the frontal and horizontal planes and placed so they could be viewed comfortably by subjects during the experiments. Trials followed the same procedure as outlined above.

Experiments were conducted in sets of ∼120 trials divided into six blocks (two for each plane) of up to 20 different directions in each plane. Directions with no unit activity were gradually excluded from the protocol as described above. The remaining directions were tested two or three times each.

Using only a 2 df force transducer in the first set of experiments made it impossible for us to monitor whether subjects produced any forces out of the sagittal plane. However, we did test for this possibility at the start of the second experimental set in which a 6 df sensor was used. Figure 1b depicts 120 force traces to targets in the sagittal plane (six per direction) by subject B from four different experimental sessions. The figure shows little deviation from the sagittal plane, especially for the upward and forward directions [the directions for which biceps (BI) units are best activated]. Analogous to previous results, some directions show more intertrial variability than others (Buneo et al., 1995). It appears, however, that when instructed to do so, subjects are able to produce forces that are reasonably close to the sagittal plane.

Dynamic forces. At the end of two of the experiments in the second series, after the directional tuning data for various deltoid units had been acquired for slow ramp forces, subject D was asked to exert dynamic isometric pulses covering the range of directions in which the units were active. The subject acquired the target in the given direction rapidly and accurately before relaxing. Recordings during a total of 140 pulses were obtained (80 in the first experiment, 60 in the second experiment).

Data acquisition and processing

In the first set of experiments [the two-dimensional (2D) experiments], recordings were taken primarily from posterior deltoid (PD) and from BI. The border between posterior and medial deltoid and between medial and anterior deltoid cannot be discerned reliably on the skin surface. We initially sampled units from the posterior half of the whole deltoid muscle, thus including part of medial deltoid. In subject A we extended our sample to include units from almost the entire width of deltoid, thus including several units in anterior deltoid. In the second set of experiments [the three-dimensional (3D) experiments], we extended the sampling for all subjects across the entire deltoid muscle, including all of the posterior, medial, and anterior deltoid. We did not return to biceps to examine the 3D tuning, nor did we modify the apparatus to examine the recruitment of BI in pronation–supination.

Surface EMG was recorded with small bipolar electrodes placed on the belly of the muscle. The two electrodes were placed on a line running with the length of the muscle, ∼2 cm from each other. Surface EMG signals were amplified and bandpass filtered (10–5000 Hz). Both force and surface EMG data were digitized at 10 kHz. EMG levels at steady state were computed by averaging across a 200 msec segment of rectified EMG (Pellegrini and Flanders, 1996).

Single unit EMG was recorded with bipolar, Teflon-coated, fine-wire electrodes (∼25 μm bare diameter) inserted into the muscle with a 27 gauge hypodermic needle. The needle and wires were sterilized before the experiment, and the skin was rubbed clean with alcohol before insertion of the electrodes. Unit recordings were amplified, bandpass filtered (100–5000 Hz or 100–10,000 Hz), viewed on an oscilloscope, digitized (10 or 20 kHz), stored on magnetic disk, and backed up on magneto-optical disk. Over the course of an experimental series, recordings were made from 15–48 units per subject and muscle, such that the different recording locations covered the whole width of each muscle. The place of needle insertion was defined relative to anatomical landmarks and its location was marked on a “map” overlaid on the muscle using a transparency.

Data analysis

Unit identification. The activity of each unit was identified off-line and marked in the unit recording using a custom-written template-matching program. This program computed the Pearson correlation coefficient (r) between a template of the unit (selected from a trial with little noise) and the unit recording at every point of the trace. The value of rapproached 1.0 for the parts of the trace that closely corresponded to the template in shape and amplitude, whereas in our experience the maximum value of r between template and background noise was between 0.3 and 0.6. Each time the value exceeded a cut-off criterion (which depending on the background noise level was between 0.7 and 0.9), the program “recognized” this part of the record as the unit potential and marked it in a raster of the trace (Fig. 1c). Trials in which a unit started firing during the force ramp but quit completely at a later point were excluded from the analysis.

Relation between firing rate and recruitment threshold: the model. In the first series of experiments, whenever possible, threshold force for recruitment and firing rate at steady state were determined for each unit in each direction (it was not possible to measure firing frequency when the recruitment of additional units obscured the unit waveform). Firing frequency was graphed against direction in polar coordinates (Fig.2a). In such a polar plot, the direction of force at the wrist is given by the direction of the line connecting the origin to a data point (or to a point on the circle in Fig. 2a). The distance of the data point from the origin represents the firing frequency of the unit in this direction. Analogous to the analysis used by Flanders and Soechting (1990) for surface EMG activity, cosine functions with a threshold nonlinearity were fit to the frequency data according to the formula:

$$\text{Firing frequency}=c+a\ast \Vert F\Vert \ast cos({\phi }_0-\phi )$$ Equation 1

where c is a constant offset, a is a constant scaling the cosine function,  F  is force magnitude, φ₀ is the best direction of the unit defined as the center of the cosine peak, and φ is the current force direction.

Fig. 2.

Hypothetical, perfectly cosine-tuned unit with its best direction (arrows) straight up. a, Cosine-tuned firing frequency. In the right triangle, firing ratef is equal to the cosine of the angle φ.b, Inversely cosine-tuned threshold force. In the right triangle the threshold force t is equal to 1/cosφ.c, Relation between threshold force and firing frequency. Threshold force is minimal for directions in which firing frequency is maximal and vice versa. d, The fact that threshold data in 2D can be fit by a line is consistent with a model in which 3D threshold data fall on a plane, and the best direction of the unit is given by the direction of shortest (i.e., perpendicular) distance between the plane and the origin (straight up arrow).

Figure 2a depicts hypothetical unit activity that is perfectly cosine tuned with its best direction φ₀ being straight up. For forces in this direction, the unit fires at maximum frequency; as the force direction deviates from this best direction, firing frequency (the length of the dashed lines) decreases until the unit is silent at angles 90° away from φ₀.

Compared to the steady-state firing frequency, the level of threshold force should show the opposite relation to force direction: for its best direction φ₀, the unit should be recruited most readily, i.e., the force level at recruitment should be a minimum (Fig. 2, compare a,b). As force direction deviates from φ_0, the magnitude of threshold force (Fig.2b, the length of the dashed lines) should increase until for force directions ≥90° from φ_0, the unit is silent and threshold force is infinite. This relation of threshold force to force direction is fulfilled if threshold force data fall on a straight line when plotted in x, yforce coordinates. That this is, in fact, the case has been demonstrated by Theeuwen et al. (1994) using SMU threshold data from seven human shoulder and elbow muscles. In our model, threshold force (during the ramp) and firing frequency (at steady state) are thus inversely related. In the right triangles in Figure 2, a andb, firing frequency (f) is equal to the cosine of the angle φ between the best and the current force direction of the unit, whereas threshold force (t) is equal to 1.0 divided by the cosine of the same angle φ.

Based on the findings of Monster and Chan (1977), which show that SMUs are recruited at a characteristic frequency and increase their firing rate as force rises, we suggest the model outlined in Figure2c. According to this model, a unit starts firing at its characteristic recruitment frequency [here 7 impulses per second (ips)] when a threshold level of MN activation is reached. The horizontal parallel lines represent lines of constant activation level and, thus, of constant firing frequency. During a force ramp, activation level rises along the dashed lines with a slope depending on force direction. For forces in the best direction of the unit, the slope is maximal, and the force magnitude necessary to reach threshold activation is a minimum, whereas for other directions, the slope is lower and threshold force is higher. Beyond recruitment, activation level (and thus firing frequency) still rises with the same slope, and the final firing frequency reached for a given direction is given by a cosine function.

The fact that threshold data in 2D can be fit by a line is consistent with a model in which 3D threshold data fall on a plane (Fig.2d) and the best direction of the unit is given by the direction of the shortest (i.e., perpendicular) distance between the plane and the origin (Fig. 2d, straight-up arrow). Analogous to the circular fit to the polar coordinates of firing frequency in the 2D model, firing frequency in 3D would follow a sphere.

Relation between firing rate and recruitment threshold: fit to the data. We plotted 2D threshold data as the x andy components of the force at which a unit first was active during the ramp. We then found the best direction of each unit by fitting a regression line to the data. Only units whose threshold data could be well fit (p < 0.05) by a straight line were included in our final analysis.

In some cases the data were better fit by two lines with different slopes, indicating that the unit would be more appropriately described as having two best directions. To determine which of the data points belonged to each line, the data were grouped according to parameters found by a nonlinear least square estimation method in a standard statistical software package (Systat, Evanston, IL). The program fit the following model to the data:

$$Y=b_0+b_1\ast X+b_2\ast (X-Break)\ast [X>Break],$$ Equation 2

where [X > Break] returns 1.0 ifX > Break is true and 0.0 if it is false. Thus, Y was related to the X values below the break point with a slope of b₁. Above the break point, Y was then related to X with a slope of (b₁ + b₂).

Whereas this method worked well for BI data, for most bidirectional deltoid units threshold data for forces in the sagittal plane seemed to fall onto two parallel lines (see Fig. 9, unit 9.3). This created a discontinuous or multivalued function that could not be split according to the equation above. Therefore, these data sets were instead split by a 45° line with negative slope through the origin, which essentially divided the data points into those for upward–forward directions and those for downward–backward directions.

Fig. 9.

Threshold lines for units in deltoid. Best directions as found from the threshold line are marked byarrows. Units 1 and 2 had nearly opposite preferred directions. Units 3–5 showed more than one preferred direction. Action potential waveforms for units 3–5 are shown for trials in the different quadrants of activation.

The “likelihood-ratio test” for regression parameters was used to determine whether the fit of the model was significantly (p < 0.05) improved by adding a second line (Johnson and Wichern, 1982). If a two-line model could be fit to the threshold data of a unit, the frequency data were split up according to the same break point found in the threshold data, and the two groups were fit with separate cosine functions. Whether using a two-peak model was justified was again determined with the likelihood-ratio test.

Using the confidence limits on the regression coefficients, we tested (in 45 units) whether the best directions found with the cosine fit to the frequency data corresponded to those found with the linear regression analysis on the threshold data. Because we did not find a significant difference between these two measures of best direction in any of the units, we limited most of our analysis to the linear regression statistics of the threshold data. Employing the regression line fit to the threshold data made it possible to use standard linear regression statistics (t test on slopes) to test if the best directions of two units of the same muscle differed significantly (i.e., at the p < 0.05 level). Thus, most of the statistical testing was based on the linear parameters of 2D or 3D forces.

For the data obtained in the 3D experiments, threshold data were split into three groups according to the plane of the target force (Fig.1a), and each group was fit separately with 2D regression lines. In addition, data from trials in all three planes were combined in 3D and fit by a plane using multiple linear regression analysis (Fig. 2d). The best direction of a unit was then given by the line that was normal to the plane and passed through the origin of the 3D plot.

For units whose 2D plots indicated that they might have two preferred directions, the entire set of 3D threshold data were split into two groups. Data from trials with force ramps in the frontal and horizontal planes were split according to the break points found in each plane with the least-square estimation method described above. Data from trials in the sagittal plane were split by the line of intersection between the sagittal plane and the plane passing through the origin and the two break points found in the frontal and horizontal planes. The two groups of data were then fit with one plane each. Whether the two-plane model significantly improved the fit was determined with the likelihood-ratio test.

Cluster analysis. Cluster analyses (Systat, nonhierarchical K-means splitting method) were performed on the distribution of best directions of the biceps unit sample to divide the data into groups of units with similar best directions. After the data were broken into groups, group membership was examined to determine whether units with similar best directions were located in similar portions of the muscle.

RESULTS

The goal of the present study was to characterize how the directional activities of SMUs in one muscle combine to account for the observed directional pattern of whole muscle activation. Using surface EMG data, in Figure 3 we show the directional activity of some of the muscles examined in this study, BI (both heads) and PD, during isometric forces in the sagittal plane. BI was broadly tuned across the up–backward and up–forward directions. PD on the other hand, exhibited activity peaks in opposite directions, down–backward and up–forward, such that its activity was best fit by a double cosine function. By characterizing and comparing the directional activity of many SMUs in BI and deltoid we will show that the broad and/or bimodal tuning observed for these muscles arises because units within the same muscle have a range of significantly different preferred directions.

Fig. 3.

Directional activity tuning plots for whole muscles as measured with surface EMG. BI activity is broadly tuned and can be fit by a single cosine function. Data from PD can be best fit by two cosine functions with nearly opposite peaks (two circles with two arrows). Partially because of the sampling bias inherent in multiunit surface EMG, it is not clear exactly how these tuning curves correspond to the tuning of the individual motor units. All data are from subject B.

Threshold lines and recruitment reversal

Using data from a BI motor unit, Figure4 illustrates how threshold force at recruitment and firing rate at steady state vary systematically with the direction of force at the wrist. Directions of forces in the sagittal plane were denoted by positive and negative numbers (for forward and backward directions, as indicated in Fig. 4b) and will be referred to by these numbers in the following sections. All unit traces (three per force direction) were aligned with force onset (Fig. 4b,c, arrowheads); all were recorded during the same experiment. One unit could be easily distinguished from others by the large amplitude of its waveform. This unit started firing at a minimum force level for directions 0 and +1. As force direction moved forward from +1 to +3 and backward from 0 to −2, the force levels at recruitment became progressively higher, whereas firing rate at steady state generally decreased. Figure4d shows that the threshold force data plotted iny/x coordinates could be well fit by a line whose perpendicular (arrow) pointed in a direction closely corresponding to the direction in which threshold force was at a minimum (Fig. 4b, direction +1). The majority of BI and deltoid units examined in the 2D experiments exhibited this type of recruitment pattern, such that the threshold force data of 91% of the units could be fit by straight lines (p < 0.05).

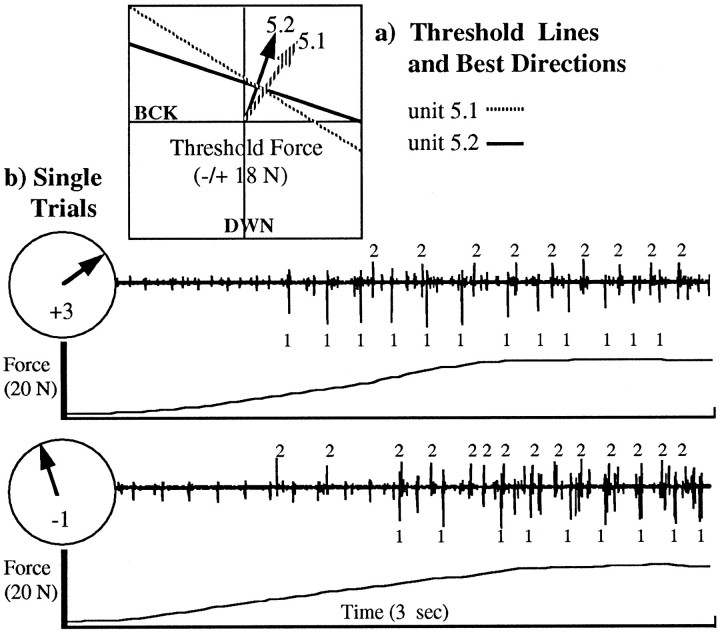
Significant differences in best direction were sometimes found between units recorded on the same electrode, in which case recruitment reversal could be observed across trials with different force directions. Figure 5a shows that the best directions for unit 5.1 (i.e., Fig. 5, unit 1) and unit 5.2 differed by 13°. The best directions were +31.9° (±5.7°) for unit 5.1, and +18.7° (±6.5°) for unit 5.2. Therefore, as shown in Figure 5b, the order of recruitment for these units changed with force direction, such that for the force ramp in direction 3 (closer to the best direction of unit 1), unit 1 was recruited before unit 2, whereas for the force ramp in direction −1 (closer to the best direction of unit 2), unit 2 was recruited first. Considering the series of 2D experiments (BI and deltoid), significant differences in best direction (t test on slopes, p < 0.05) were found in six pairs of units recorded on the same electrode and in nine pairs of units recorded on different electrodes but in the same experiment. These pairs of significantly different units found in BI are marked in Table 1. We can thus rule out the possibility that differences in best direction between units found in the 2D experiments are caused by day-to-day variability in the levels of force outside the sagittal plane, because these differences are also observed between unit recordings obtained under identical force conditions.

Fig. 5.

Recruitment reversal with force direction. Units 1 and 2 found on the same electrode had different preferred directions (arrows) as shown in a and were recruited in a different order depending on the force direction.b, For a force ramp in an up–forward direction, unit 1 was recruited before unit 2. For the force ramp in an up–backward direction, unit 2 was recruited before unit 1.

Table 1.

List of all biceps units, their best directions (degrees) as found from the threshold line and frequency cosine fit (where available), and their minimum threshold force magnitudes as found from the threshold line

Experiment	Electrode/unit	Threshold		Frequency
		Best direction (degrees)	Second best direction	Best direction	Second best direction	Threshold magnitude (newtons)
Subject A
1	I /1	16.1 (4.5)	107.6 (12.0)			13.3
	I /2	16.2 (4.0)	114.8 (11.8)			16.3
	I /3	26.4 (5.6)		28.7		22.1
2	II /1	19.4 (6.3)		not sig.		18.4
3	III /1a	36.4 (12.2)	−40 (12.6)	29.5	−45.4	22.6
	III /2a	26.3 (7.0)	−18.3 (4.8)	13.6	−18.5	22.3
4	III /2	30.5 (6.0)	−30.2 (10.4)	23.3	−26.6	23.7
	III /1*	29.7 (5.4)	−38 (11.4)	not sig.		15.0
	I /1a,*	18.7 (6.5)				16.6
	I /2a	31.9 (5.7)				15.4
5	I /1	8.6 (6.3)		8.1		19.1
6	II /1	20.7 (3.6)		17.6		21.3
7	III /1	38.7 (10.7)	−10.4 (6.2)			27.0
8	II /1	40.2 (7.2)		55.9		15.4
9	III /1	18.8 (9.3)				21.2
Subject B
1	I /1	−9.3 (8.9)	37.6 (4.8)	−19.1	64.6	22.5
2	I /1	21.1 (3.6)	−36.8 (3.8)	not sig.		12.5
3	I /1	23.65 (6.4)	−29.9 (12.6)	45.2	−23.7	19.8
4	I /1	−0.34 (6.8)	60.9 (40.1)	−15.6	46.6	15.6
5	I /1	21.2 (4.4)		29.9		11.4
6	I /1**	−7.1 (3.2)		−6.1		12.1
	III /1**	21.2 (6.4)		24.6		12.4
7	I /1**	−28.3 (17.5)	34.1 (21.0)	−26.5	31.5	20.6
	III /1**	23.7 (8.2)	−6.2 (6.0)	29.3	−21.2	16.2
8	II /1	16.44 (7.9)		31.9		14.9
9	I /1*	11.5 (4.1)		8.82		18.4
	III /1*	22.3 (2.4)		25.3		9.3
	III /2	48.1 (14.6)	−18.1 (11.9)	63.3	−19	22.0
10	II /1	23.1 (5.5)		38.6		13.2
11	III /1	31.6 (11.3)		54.9		11.3
12	II /1a	22.5 (1.7)		30.5		10.6
	II /2a	15.7 (3.7)		23.2		10.7
Subject C
1	I /1	17 (5.5)		0.7		26.0
2	I /1	8.5 (6.9)		16.8		12.6
3	II /1	12.3 (5.0)		not sig.		11.4
4	III /1	49 (12.2)		52.1		11.8
5	II /1	18.3 (5.6)		38.2		20.3
	III /1	18.6 (4.8)		18.6		14.4
6	II /1	20.88 (5.9)		28.3		11.2
	II /2	18.6 (4.5)		14.1		11.1
	III /1	31.4 (8.3)		24.3		11.2
7	I /1	25 (12.2)		26.5		12.1
8	I /1	35.9 (7.3)		48.7		21.1
9	III /1	12 (5.4)				12.9
	II /1	15.7 (3.4)				14.9
	II /2	13.5 (4.2)				13.2
10	I /1*	12.8 (6.4)				14.8
	III /1*	20.4 (4.1)				12.5
11	III /1	33.7 (3.0)		36		9.8
12	I /1	20.1 (7.5)				11.3
	I /2	25.1 (8.6)		39.6		11.8
13	II /1	34 (3.9)		39.8	−47.2	8.3
	III /1	31.5 (9.3)				14.5
14	III /1*	47.4 (16.0)	−31.5 (8.2)			24.5
	II /1*	26.8 (25.2)	−45.6 (4.7)			13.6

Values in parentheses denote SEs. Units with significantly different best directions from the same electrode (3 pairs) or in the same experiment (6 pairs) are marked with ^a and *, respectively. (** mark differences significant at the p< 0.01 level.) Correspondence between degrees and directions in the sagittal plane are as follows: Up, 0; down, 180; forward, 90; back, −90. Threshold magnitudes are in newtons.

Best directions of biceps motor units

Directional tuning of BI units

As mentioned in Materials and Methods, firing frequency and threshold data were never found to predict a significantly different best direction for a given unit. The best directions obtained from the threshold line fit were then compared among different SMUs in BI and were found to differ significantly. Figure6 shows three examples of units with obvious differences between their directional tuning curves. For unit 6.1, both firing rate and threshold data yielded a best direction that was up and slightly backward. However, unit 6.2 (found in BI of the same subject) exhibited activity whose best direction (up–forward) differed from that of unit 6.1 by 28° (t test,p < 0.001). Significant differences in best direction between units of BI were found in all subjects, and for unimodally tuned units, best directions covered a range of 32, 39, and 40° in subjects A, B, and C, respectively (Table 1).

Fig. 6.

Threshold lines and frequency data for units in biceps. Best directions as found from the threshold line or the cosine fit are marked by arrows. Units 1 and 2 had significantly different preferred directions. Unit 3 showed more than one preferred direction. Action potential waveforms for unit 3 are shown for trials in the two lobes of activation. All data are from subject B. Bimodally tuned activity was seen in 29% of the biceps units pooled across all subjects.

The directional tuning of the units 6.1 and 6.2 described above conformed to the predictions of the model suggested in Figure 2: threshold force and firing frequency varied as a simple function of force direction such that data were best fit by a single line and a single cosine peak. The slope of this line (and the angular location of the cosine peak), however, was significantly different for different units. It would appear from these findings that the broad (and possibly bimodal) tuning of the BI is accounted for by the combined activity of unimodally tuned SMUs with different best directions. Consider, however, the recruitment pattern of unit 6.3. The direction of lowest threshold force was up–forward. As force direction changed toward up–backward directions, threshold force initially increased, reached a (local) maximum for upward directions, but then decreased again and reached a second local minimum. Firing frequency varied in the reverse manner, reaching peaks for up–forward directions and up–backward directions, with a trough for forces directed upward. Threshold force data for this unit clearly could not be well fit by a single line, and a two-line model significantly improved the fit. A two-peak cosine function improved the fit to the frequency data significantly. It thus appears that this unit has two preferred directions: up–forward and up–backward. Such bimodally tuned BI units were found in all subjects (n = 16, 29%). The range of values representing the angular difference between first- and second-best directions was 45–98, 30–70, and 72–79° in subjects A, B, and C, respectively.

Correlation between directional tuning and recording location

Units were sampled from both the long and the short head of BI. These two parts of the muscle share a common tendon at the elbow but have different attachments at the shoulder joint and might, therefore, be expected to be activated differently for different force directions. This might be reflected in the best directions of their SMUs. Because we inserted most electrodes near the belly of biceps, the two heads could not be definitely distinguished for the midrange of electrode placements. We, therefore, report recording location (as marked for all subjects on the muscle map in Fig.7c) on a continuum from medial (toward the short head) to lateral (toward the long head).

Fig. 7.

Relation between the best direction of a unit and its location in BI. a, Best directions as found from the threshold line fit plotted against location in the muscle for each individual subject. The two preferred directions of a bidirectional unit are marked with a star for the best direction and an open circle for the second-best direction. Regressing only the best direction (for unimodally and bimodally tuned units) on location in the muscle yielded a significant correlation in subject B only. b, Pooling data from all subjects by normalizing recording location yielded a significant correlation between best direction and location (p < 0.005). This relation suggests that units located laterally and medially are best activated for upward and up–forward forces, respectively. (For simplicity, only the best direction is shown for each unit in the first plot. In the second plot, the second-best directions are included.)c, Map of biceps with recording sites in all subjects. Sites of electrode insertion for a particular subject are marked with a corresponding letter.

In Figure 7a the best direction as found from the threshold line fit is plotted against the location of the recording electrode for a given unit for each subject. The two preferred directions of a bidirectional unit are marked with a star for the best direction and an open circle for the second-best direction. Regressing only the best direction (for unimodally and bimodally tuned units) on location in the muscle yielded a significant correlation in subject B only. In the plot one can see a slight tendency for lateral (long head) units to be activated best for up and slightly backward directions, whereas medial (short head) units are activated for up and slightly forward directions. This slight trend can be seen in the two other subjects also but failed the tests for significance.

Normalizing location in the muscle and pooling data from all subjects yielded a significant correlation (p < 0.01) between best direction and location. For simplicity, the first plot in Figure 7b only includes best directions. In the second plot, the second-best direction of bidirectional units (open circles) is also included. In the first plot, one can see that, with a few exceptions, the first-best directions generally appeared to fall close to the line. In contrast, the second plot shows that the second-best directions were usually found at the extremes of the range. We conclude from the pooled data that there was a gradual location-dependent shift in first-best direction, and a wide range of first- and second-best directions (77° for best directions and 154° for first- and second-best directions).

Cluster analysis

If the BI MN pool receives only a limited number of different directional commands, the best directions of BI SMUs should cluster into a limited number of distinct groups. To test this hypothesis we performed a cluster analysis on the estimates of the best directions of the units. When data from all subjects were pooled, the distribution could be divided into three groups corresponding to up–backward, upward, and up–forward directions. Figure8a shows the histogram (with bar width of 18°, which was the angular separation between directions) of the best directions of the units for the pooled data. Superimposed in gray on the histogram is the more continuous distribution (bin widths of 1°) of best directions. Separations between groups are marked by the dashed lines. Visual examination of the histogram suggests, however, that the distribution can be characterized as having long tails rather than distinct peaks as would be expected from a distribution with several clusters. In the second plot of Figure 8a we, therefore, examined whether members of the three groups are restricted to certain locations in the muscle. Members of each group are marked with the number of the respective group. This plot shows that, in general, members of each group can be found anywhere in the muscle. There is a slight tendency for units in groups 2 and 3 to be found toward the long and short head, respectively. However, the separations are not as clear-cut as would be expected from a compartmentalized muscle.

Fig. 8.

Distribution of best directions of units in BI.Bars of histograms denote bins of 18°, the angular separation between experimental targets. Superimposed on one histogram is the “continuous” (bin width of 1°) distributions of best directions. a, Distribution of best directions as found from the threshold line. Data are pooled from all subjects and include only the best direction. Three clusters were found as marked in the histogram by horizontal, dashed lines. The second plot shows the distribution of units of each group in the muscle. Members of a group were not constrained to a specific area in BI. b, Distribution of best directions (pooled data) as found from the direction of minimum threshold force. Note the wider range of best directions when compared with that ofa.

The lack of consistent and convincing clustering might have arisen from an aspect of our analysis that might have introduced a central tendency into the distribution. Although the recruitment pattern of some units suggested the existence of a second preferred direction, a two-line model did not significantly improve the fit to the data (see, for example, unit 6.1). Thus, the unit would have been classified as unimodally tuned, and one threshold line would have been fit to all data points. The true best directions for such units might actually be at more extreme points in the range of best directions and might actually cluster into different groups. An estimate of best direction from the threshold data that would be resistant to this distortion toward a central value is the direction (i.e., one of the 20 directions used in the experiment) in which average threshold force is a minimum. Therefore, we repeated the cluster analysis with this more discrete estimate of the best directions of the units. A histogram of the pooled data is shown in Figure 8b. As expected, the range of best directions obtained with this method (144°) was substantially larger than the range obtained from the perpendicular directions to the regression lines. (The range was 108, 72, and 144° for subjects A, B, and C, respectively.) However, when splitting the distribution into 2, 3, or 4 groups by the means of cluster analysis, members of each group could be found anywhere in the muscle, thus, not providing evidence for a compartmentalized organization.

We also examined the combined distribution of first- and second-best directions (obtained from the threshold lines) and again found little evidence for compartmentalization. Thus, we conclude that the distribution of preferred directions is continuous over its wide range. Instead of clustering into distinct compartments, diverse directional inputs appear to be widely distributed across the width of the muscle.

Variations in threshold magnitude

It is possible that SMUs in BI are regionalized and/or differentially activated according to histochemical fiber type as shown for cat hindlimb muscle (Chanaud et al., 1991b). In this case (because histochemical fiber type is correlated with MN soma size and, therefore, with recruitment threshold; Burke, 1967) the force magnitude at recruitment would depend on the location of the unit in BI and/or on its best direction. We thus tested whether threshold magnitude varied systematically with the preferred direction of a unit or its location in BI. Of the six tests performed, the only significant correlation was obtained between threshold magnitude and location in subject A (p < 0.05), indicating that in this subject high- and low-threshold units tended to be found toward the short head and long head of BI, respectively. When data from all subjects were pooled by normalizing unit location, no significant relation was found between threshold magnitude and either best direction or location. Thus, the results do not support the hypothesis of compartmentalized fiber types in BI.

Best directions of deltoid motor units: 2D experiments

Considering only the sagittal plane, dramatic differences in preferred directions were found across the various units in deltoid. Unit 9.1 (Fig. 9) was best activated for down–backward forces. Unit 9.2, in contrast, was recruited best for up–forward force directions and, thus, had a best direction in the sagittal plane that differed by ∼180° from that of unit 9.1.

As in BI, we also found bimodally tuned units in deltoid. Their threshold plots for the sagittal plane were perhaps more striking than those of bidirectional units in BI, as the two areas of activation were generally opposite one another. An example is shown with unit 9.3, a bimodally tuned unit activated for forces both in the up–forward and down–backward directions. Recruitment thresholds were well fit by two nearly parallel lines indicating that the two best directions of this unit were nearly opposite each other. The matching shapes of the unit potentials shown for the two activation areas confirm that we were indeed recording from the same unit. Units with this activation pattern were found in all three subjects.

To exclude the possibility that units like unit 9.1 and 9.2 might have a second-best direction with a higher threshold force level than the level used in the experiment, we asked subjects at the end of the experiment to produce force ramps to a maximal force level in the up–forward (for unit 9.1) and down–backward directions (for unit 9.2). Because no activity of these units could be found during these maximal force ramps, the units were classified as unimodally tuned.

Rare units like unit 9.4 (found only in subject A) had two preferred directions, both within the range of the down–backward directions. Equally rare units like 9.5 (found only in subject D) were activated for up–forward and down–backward forces, much like unit 9.3, but had an additional area of activation in the down–forward directions. No line fits for this unit are shown in the figure because the assignment of the data points in the additional activation area would have been arbitrary: a third line could have been fit to all points in the lower right quadrant, or they could have been assigned partly to the line fits for the up–forward and back–down directions.

Because of the dramatic differences between best directions of units in deltoid we classified our sample into three main groups: units with best directions in the up–forward quadrant (e.g., unit 9.2, 22%,n = 16), units with best directions in the down–backward quadrant (e.g., unit 9.1, 56%, n = 41), and those bidirectional units with best directions in both of these two opposing quadrants (e.g., unit 9.3, 16%, n = 12). Units with two best directions within one quadrant (such as unit 9.4) and those that might have three best directions (unit 9.5) together constituted only 6% (n = 4) of the units examined.

The ranges of best directions within the two groups of unimodally tuned units were 57, 35, and 21° for the down–backward quadrant and 17, 27, and 21° for the up–forward quadrant for subjects A, B, and D, respectively. In the description of the 3D experiments below, we will explore whether units with similar best directions in the sagittal plane are necessarily similar when their activity tuning in 3D is considered.

Best directions of deltoid units in 3D

Although deltoid definitely contributes to shoulder flexion– extension, the primary mechanical action of most of its fibers is in abduction of the upper arm, i.e., in force directions outside the sagittal plane (Buneo et al., 1997). Describing the directional tuning of deltoid units only for forces within the sagittal plane therefore provides an incomplete understanding of unit activation. A threshold line in the sagittal plane lacks important information about the orientation of the 3D threshold plane (Fig.2d): for example, rotation of the threshold plane about any axis lying within the sagittal plane would not change the orientation of the threshold line in the sagittal plane. Therefore, units with threshold lines of similar orientation in the sagittal plane might, in fact, have very different preferred directions when their recruitment pattern in 3D is considered. Similarly, the two threshold planes of bidirectional units, such as unit 9.3, might be parallel yielding two best directions 180° apart, or they might have a line of intersection such that the two best directions differ by <180°. Thus, to complete the description of directional SMU activity in deltoid, we recorded from units during forces in directions uniformly covering all three planes (sagittal, horizontal, and frontal).

Unidirectional deltoid units

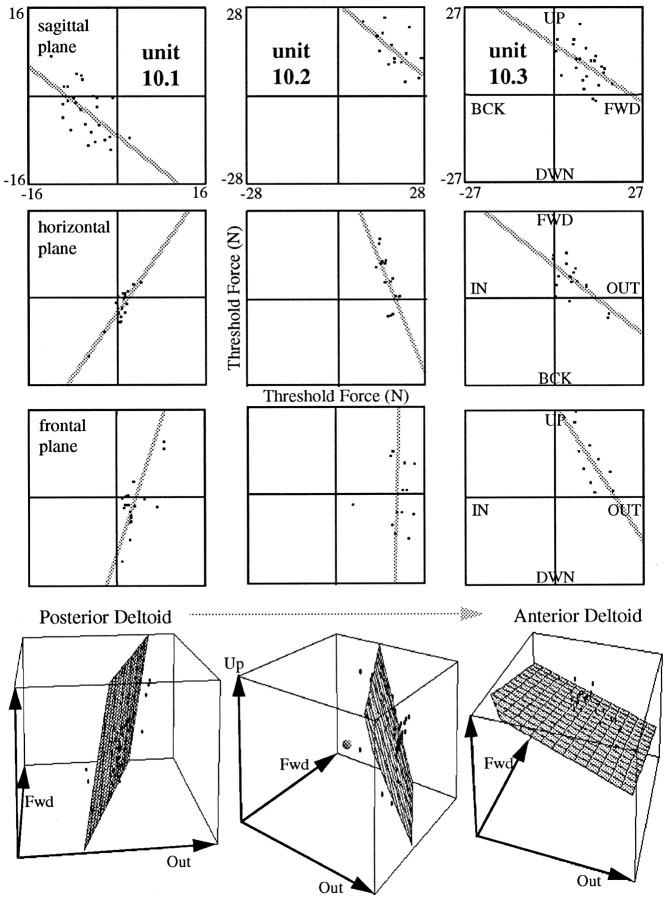
We found that the data from different deltoid units could be fit by planes with widely divergent orientations. Each of the three columns in Figure 10 represents threshold data for one deltoid unit. The top three rows depict the threshold lines for each of the three planes. These were derived only from trials with force ramps within the respective plane. The bottom row shows the 3D plane fit to data from all trials. In 57 of the 59 units examined in this set of experiments the plane fit to the threshold data was significant (p < 0.05). In 45 of these units the plane fit was significant at the p < 0.01 level. The values of the correlation coefficient r for thex, y, and z coordinates of the threshold force levels ranged from 0.40 to 0.95. These results illustrate that in consonance with the line fit to the 2D data, threshold data in 3D can be fit by a plane.

Fig. 10.

Threshold lines and planes for deltoid units 1 (most posterior) to 3 (most anterior). The top three rows show the threshold lines in each plane derived from trials with force ramps within the respective plane. For the plots in thebottom row, data from all trials were combined in 3D and fit by a plane. The origin of the plot is located at the center of the cube and is marked by the small sphere in the plot for unit 2. The equations for the plane fits are as follows: unit 1,z = −2196.3 + 7.4x − 2.8y; unit 2, z = 7628.3 − 3.4x − 1.9y; unit 3,z = 1245.6 − 0.4x− 0.3y, where x, y, andz have positive values for outward, forward, and upward, respectively. As location of the units changes from posterior to anterior, the best direction appears to “jump” from down–backward to up–forward in the sagittal plane; in the horizontal and frontal planes, however, it appears to gradually rotate counterclockwise from out–back to out–forward and from out–down to out–up. All data are from subject A.

In Figure 10, the threshold line for unit 10.1 in the sagittal plane was oriented much like that for unit 9.1, with a best direction in the down–backward direction. In the horizontal and frontal planes, the threshold line yielded a best direction of out–backward and out–downward, respectively. The orientation of the threshold plane in the bottom row illustrates that the 3D best direction of unit 10.1 was in the out–back–downward direction.

Unit 10.2 was found in a recording location 6.5 cm anterior to that of unit 10.1 (i.e., in the medial deltoid). Its best direction in the sagittal plane was in the up–forward direction, comparable to that of unit 9.2. Considering only the sagittal plane, one might thus conclude that the best directions for units 10.1 and 10.2 differed by 180°. The threshold lines for the horizontal and frontal planes, however, show that the best directions for unit 10.2 in these planes differed from those of unit 10.1 by only 60 and 15°, respectively. With respect to the lines for unit 10.1, the threshold lines for unit 10.2 were slightly rotated counterclockwise, such that the best direction was out–forward for the horizontal plane and straight outward for the frontal plane. Accordingly, the plane fit to the 3D data yielded a best direction for unit 10.2 that was oriented out–forward and slightly up.

Of the three units in Figure 10, unit 10.3 was found in the most anterior recording location. Considering only the sagittal plane, this unit appeared to have approximately the same best direction as unit 10.2; however, the threshold lines for the other two planes were rotated counterclockwise with respect to those of unit 10.2 (by 30 and 35° for the horizontal and frontal planes, respectively). The best directions for these planes are thus forward–out (with a greater forward component than that of unit 10.2) in the horizontal plane and out–up in the frontal plane. The orientation of the threshold plane in 3D confirms that the best direction of this unit is up–out–forward.

It follows from these results that the very large (or very small) differences found between the best directions of deltoid units for forces in the sagittal plane are deceptive. Units with apparently opposite best directions in the sagittal plane (such as units 10.1 and 10.2) might in fact have threshold planes that differ only relatively little in their orientations. Thus, in 3D space the difference between the best directions of units 10.1 and 10.2 was only 53°. On the other hand, units with approximately the same best direction in the sagittal plane might show significant differences between their best directions in 3D. Thus, the difference between the 3D orientation of the planes of units 10.2 and 10.3 was 48°, although their threshold lines in the sagittal plane differed by only 6°.

Bidirectional deltoid units

Analogous to the bimodal units described above for biceps (e.g., unit 6.3) we also found evidence for multiple directional inputs on deltoid SMUs (19%, n = 14 in the 2D experiment (Fig.9), 7%, n = 5 in the 3D experiments). The 3D recruitment data for a bidirectional deltoid unit are shown in Figure11. From the sagittal plane data, which are best fit by two approximately parallel threshold lines, one cannot discern whether the threshold planes in 3D would be parallel, yielding two best directions opposite to each other or whether the two planes would have a line of intersection. However, two parallel threshold planes would intersect all three experimental planes with two parallel lines, and the two-line fits to the horizontal and frontal plane data clearly show that this is not the case. The two lines in these plots are not parallel but instead intersect at an angle of 90° in the horizontal and 125° in the frontal plane. Accordingly, the two threshold planes fit to the 3D data have a line of intersection. The best directions for this unit are up–out–forward and down–out–backward and differ by 93° in 3D. None of the threshold data of bidirectional units found in the second set of experiments were fit by two parallel planes, meaning that all bidirectional units exhibited intersecting threshold planes. The differences between the two best directions of such units ranged from 58 to 96° in 3D space with an average value of 77°.

Fig. 11.

Threshold lines (top) and planes (bottom) for a deltoid unit with two preferred directions. The origin of the plot is located in the center of the polygon. From only the sagittal plane data, it might be assumed that the two threshold planes are parallel and the two best directions 180° apart. Data in the other two planes show, however, that the two threshold planes have a line of intersection.

The relation between location and best direction

In Figure 12, each deltoid SMU is represented by a unit vector radiating (from the origin) in the best direction of the unit. The color of the vector codes for the anterior–posterior location of the unit in the muscle. In general, as unit location changed from posterior (blue end of spectrum) to anterior (red end), best direction gradually changed from down–backward to up– forward. A similar pattern was found in all three subjects (Fig.12a). Regressing recording location on the x,y, z coordinate of the tip of the unit vector yielded significant correlations for subject A (p < 0.001, r = 0.79) and subject B (p < 0.05, r = 0.71) but a nonsignificant correlation for subject D (p = 0.066, r = 0.66). Because all subjects exhibited a qualitatively similar relation between best direction and location, we then pooled the data (Fig. 12b). Pooling data from all subjects by normalizing the unit location (across the width of each subject’s deltoid, see Fig.13b) yielded a highly significant relation between the 3D best direction and location (p < 0.001, r = 0.64). When regressing the 2D best directions for the horizontal and frontal planes on unit location, highly significant correlations (p < 0.001) were obtained for all three subjects in both planes, with r²-values ranging from 0.6 to 0.8 (plots not shown). Units located in the posterior part of the muscle were best activated for out–backward (horizontal plane) and out–downward (frontal plane) forces. As unit location changed to the more anterior part of the muscle, best directions gradually changed to the out–forward and out–upward directions, with no suggestion of discontinuity at posterior–medial or medial–anterior compartmental boundaries.

Fig. 12.

a, 3D best direction of each unit versus their locations in deltoid, for each subject. The best direction is given by the direction of the unit vector from the origin. The color of the vector codes for location. As location changes from posterior to anterior (and color changes from the blue to thered end of the spectrum), best direction changes from down–out–backward to up–out–forward. b, Pooled 3D best directions of all units versus their normalized locations in deltoid, for all subjects. Best directions are coded for location as ina.

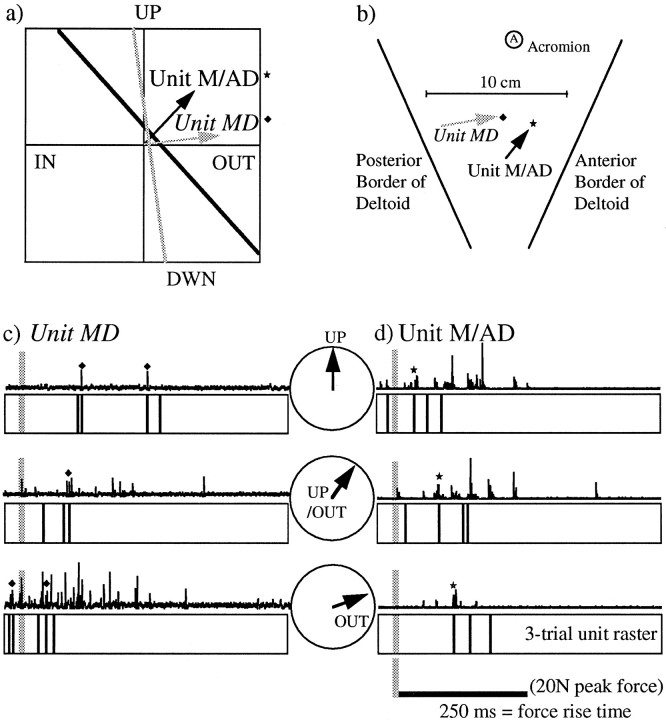
Fig. 13.

Dynamic pulses in the frontal plane; relative timing of two deltoid units with different best directions.a, Threshold lines of unitsM/AD (medial/anterior deltoid) andMD (medial deltoid) in the frontal plane.b, Locations of these units. Note that the more anterior unit has a best direction with a greater upward component than that of the more medial unit. c, MD rectified multiunit records for one trial and unit rasters for three trials in each direction (note that the unit potential could not always be recognized because of firing of other units). As the direction of the pulse changed from up to up–out, the bursts were earlier with respect to force onset (gray line). d, Simultaneously recorded EMG from M/AD exhibits the opposite temporal relation to force onset.

Extension to dynamic forces

The range of threshold magnitudes in our sample of BI and deltoid units extended from 0.2 to 28 N, and ∼50% of the units had threshold forces of >12 N. Thus, a substantial number of units in both muscles were recruited at relatively high force levels and could be assumed to contract quickly enough to be involved in the generation of fast-rising forces or movements. Moreover, as will be explained below, we found that units with threshold magnitudes as low as 2 N were involved in the generation of fast pulses of isometric force.

Figure 13 illustrates the results from an experiment in which subject D produced isometric pulses to different targets in the frontal plane. (This figure is also representative of the results of the second dynamic experiment.) Simultaneous recordings from two different electrodes are shown. The threshold lines and preferred directions (in the frontal plane) of two units found on the two different electrodes are shown in Figure 13a. The best direction of unit MD (found in the center of deltoid, Fig. 13b) was almost straight outward with only a slight upward component. On the other hand, unit M/AD (found in a recording location ∼3 cm anterior to unit MD) had an up–forward best direction.

Consider now the relative timing of the multiunit bursts on the two recording electrodes during dynamic pulses (with a 250 msec time to peak) in the three different directions (Fig.13c,d). As the direction of the pulse changed from upward (top lines) to up–out (bottom lines), the bursts in the two recordings reversed their order. For the upward direction (closer to best direction of unit M/AD), the burst in the recording at the more anterior site was earlier. For the outward direction (closer to best direction of unit MD), the burst in the recording at the more posterior site was earlier. Because we have ascertained that units M/AD and MD are involved in those bursts (as marked in the three-trial unit rasters), it appears that the recruitment order of these individual units also changed depending on the direction of the dynamic force.

DISCUSSION

We found that threshold data for 93% of our biceps and deltoid motor units could be fit with lines in 2D and/or planes in 3D, consistent with a model in which activation levels are tuned as a cosine function of force direction (Fig. 2) and in consonance with the well established idea that the descending inputs to spinal motoneuronal–interneuronal pools may have cosine-tuned activity (Georgopoulos et al., 1982, 1988; Fortier et al., 1993). Using the orientation of the line or plane as a measure of the best direction of a unit, we showed that SMUs of the same muscle were not activated homogeneously but instead different units had different best directions. The best directions of units changed continuously with their locations in the muscle and did not cluster into distinct groups. For deltoid, the gradual change in best directions may echo the gradual change in the mechanical actions of the muscle fibers (Buneo et al., 1996). As discussed below, the gradual change of best directions in biceps might be understood by considering that during the time course of a movement, biceps units may act in synergy with various deltoid units. Thus, the directional specificity of the recruitment order may act in conjunction with the phenomenon of size-ordered recruitment, to enable smooth and fatigue-resistant muscle contractions. But before developing these ideas, we will consider several technical issues that influence the interpretation of our data.

Technical issues

Using only a 2 df force transducer in the first set of experiments raised the concern that any significant differences between 2D best directions of different BI units might be caused by day-to-day variability in the levels of force outside the sagittal plane. This possibility was ruled out by the fact that unit recordings obtained under identical force conditions (on the same electrode and/or in the same recording session) yielded significantly different best directions (Fig. 5, Table 1). Moreover, we were often able to identify two different preferred directions for the same unit (Fig. 6, Table 1). This provides evidence for a wide range of different directional inputs to the BI MN pool.

Another caveat arose from cases in which the angular separation between the two putative best directions of a unit was not large enough, and a possibly bimodal unit was classified as unimodal. This would have introduced a bias toward a central value in the distribution of best directions. Despite this possible bias we found a wide range of different best directions (77° for BI units, Fig. 8a). When using a method that would be insensitive to this distortion toward a central value, the range of best directions of BI units increased to 144° (Fig. 8b). These findings support our main conclusion regarding the distributed activation of the MN pool.

A final issue concerns the validity of the results for anything other than isometric contractions. Our experimental paradigm seemed to favor the recruitment of low-threshold units primarily relevant in the production of static forces rather than movements. There is some indication that the CNS might employ different strategies in the control of the small SMUs principally subserving posture and the large units involved in movement (Ghez, 1979; Flanders and Herrmann, 1992). However, it has recently been reported that the same units are activated (albeit differently) for isometric forces and movements, thus supporting the idea that units in our sample are also involved in the generation of movements (van Bolhuis et al., 1997). Similarly, in the present study the same units active during slow ramps also fired during phasic EMG bursts (Fig. 13). Moreover, because subjects supported the weight of their arm at the beginning of each trial and because our analysis relied on the recruitment threshold of a unit, we excluded units that were active for postural support. Thus, at least for forces with an upward component (the preferred directions for BI and anterior deltoid units) our sample does not contain those units most likely to be involved in posture (Table 1). Furthermore, the wide range of threshold levels and the substantial number of units recruited only at relatively high forces would suggest that our conclusions also apply to those units involved in movement generation.

Neural substrate for bidirectional units

Although the majority of units in our sample exhibited tuning curves that were consistent with the unimodal cosine tuning reported for supraspinal inputs (Georgopoulos et al., 1988), 17% of the units examined were bimodally tuned. When considering the bidirectional units in BI and those found in deltoid in the 3D experiments, the angular differences between best and second-best directions ranged from 30 to 98°. The majority (75%) of these bimodally tuned units had best directions that were <90° apart. If the two activation lobes of bidirectional units were to subserve the activation of the muscle as an agonist and as an antagonist (working in conjunction with another muscle with the opposite mechanical action, see Flanders and Soechting, 1990), the two best directions might be expected to be opposite each other, i.e., 180° apart. Such an organization might help to stiffen the joint along the axis of the pulling direction of the muscle. The much smaller angular separation found here, on the other hand, might suggest that the second activation lobe of a bidirectional unit subserves an activation of part of the parent muscle in synergy with various other muscles or motor units in the system. The force vectors produced by such units might be necessary to balance the ones generated by other synergistic muscles during the production of a desired force (Flanders, 1993). Thus, the bidirectional units found here might constitute subpopulations that are activated in synergy with other units in the system. This idea is consistent with findings by Jongen et al. (1989) who report intramuscular differences in activation during cocontraction of other muscles.

If these bimodal SMUs receive input from only unimodally tuned neurons, the question arises as to how unimodal inputs can produce bimodal outputs. Summing two cosine functions always results in a third unimodal cosine function. Even when the two input functions have a threshold nonlinearity (see Materials and Methods section of this study and Flanders and Soechting, 1990) their addition results in a unimodal output function, unless the angular separation between the two input peaks is wide and/or the threshold is high. Thus, to reproduce the tuning pattern of bimodal units whose two best directions differ by <90° (the norm in our study), some kind of nonlinear interaction has to occur between the two unimodal inputs.

Using NEURON simulation software (Hines and Carnevale, 1997) we attempted to create the observed MN output solely from a specific pattern of convergence of unimodally tuned inputs at the dendritic arbor of the MN (Herrmann, 1998). Several combinations of inputs with different relative locations, weights, and preferred directions were simulated, but none of them resulted in the pattern of bimodal output observed experimentally. Thus, it seems that a solution at the level of the motoneurons would have to be a very specific one and that unimodal inputs do not tend to produce a bimodal output as a result of simple convergence patterns. An alternative model might contain a reciprocal inhibition between two unimodally tuned inputs. It is also possible that the bidirectional tuning of SMUs arises from bimodally tuned inputs.

Compartmentalization versus distributed innervation

It has been suggested that a muscle is organized into smaller submodules such that the elements controlled by the CNS are neuromuscular compartments rather than whole muscles (Windhorst et al., 1989; English et al., 1993). Such partitioned control might be functionally advantageous because individual muscles are nonuniform in their mechanical actions (Chanaud et al., 1991a; Carrasco and English, 1997) and/or their fiber type distribution (Chanaud et al., 1991b). The existence of neuromuscular compartments suggests the fractionation of the MN pool of a muscle into smaller, differently activated subpopulations. Presumably each subpopulation would then receive homogenous activation such that recruitment order within each compartment is determined by MN size (Windhorst et al., 1989). For cat hindlimb muscle, the fibers innervated by MNs of the same subpopulation have been found to be largely restricted to a distinct muscular territory (English and Letbetter, 1982).

According to these arguments we would have expected BI and deltoid units to fall into a limited number of groups, each group containing units with the same best direction and localized in a restricted muscle area. Instead we found a continuous distribution of best directions with no convincing evidence for clustering. When grouping BI units with similar best directions together, their anatomical territories overlapped widely and spanned the whole width of the muscle (Fig. 8). Thus, the MN pool of these muscles appears not to be compartmentalized but to instead receive a more continuously distributed innervation.Georgopoulos et al. (1988) have shown that the 3D best directions of motor cortical cells uniformly cover the 3D space and do not appear to cluster into distinct groups. Thus, the neural substrate to create a continuous, finely graded distribution of the best directions of SMUs is available at the supraspinal level.

A similar lack of compartmentalization has been found in a bitendoned finger extensor (Schieber et al., 1997). Although one might logically expect to find two distinct compartments in this muscle (one for each tendon), most units contribute to force on both tendons, with selectivity for either tendon ranging on a continuum. Analogously, BI has two distinct anatomical subdivisions with different attachments and moment arms at the shoulder (Wood et al., 1989), but the organization of its MN pool reveals more of a continuum. In deltoid, on the other hand, it seems apparent that the pulling directions of the SMUs change continually with location along the broad attachment of the muscle (Buneo et al., 1997), thus motivating the continuously changing directional innervation of different parts of the muscle. Accordingly, the best directions of deltoid SMUs varied continuously across a wide area of space (Fig. 12).

The correlation between best direction and recording location might also be related to the topography of the spinal MN pool as suggested byKernell (1989). A rostrocaudal topography has been described for MN pools of the two parts of deltoid muscle in the rat (Choi and Hoover, 1996). The considerable overlap found between these two pools may be consistent with our finding of continuous rather than compartmentalized preferred directions and multiple directional preferences for some units.

Implications for movement generation

Similar features of muscle activation are found in movements and dynamic isometric forces (Ghez and Gordon, 1987; Flanders et al., 1996;Pellegrini and Flanders, 1996). This suggests that similar control strategies are involved in these two tasks. In Figure 13 we show that the timing of the activity of a unit moved from an early to a progressively later point in the force pulse as the direction of the pulse moved away from the best direction of the unit. Given the parallels between the neural control of force pulses and movements, one can speculate that the relative timing of recruitment during a movement could potentially be predicted from the best directions of the units under static conditions and the directions of dynamic forces during movement.

As arm muscles change their mechanical actions with arm posture, the directional tuning of whole muscles generally changes in parallel with the new pulling directions of the muscles (Flanders and Soechting, 1990). Although it remains to be determined whether the best directions of the motor units change with posture (or if whole muscle tuning changes via recruitment of different units), this suggests that the central control mechanism takes limb configuration into account when issuing motor commands. Muscles with different mechanical actions are activated at different times during a reaching movement (Flanders et al., 1996). Thus, a factor determining the timing of the activation of a muscle might be the degree of correspondence between its pulling direction and the direction of force currently required. If differences in mechanical action exist across units within a muscle, the population of units optimally fit to produce a required force vector will change with limb position and force direction during a movement.

Based on this logic, we hypothesize that at different points in the movement, the various units are recruited according to their mechanical actions. The neuromuscular system could thereby gradually make use of the wide number of units available instead of activating a few discrete populations. This spatiotemporal recruitment rule would necessarily involve violations of the size principle (Henneman et al., 1965; see also DeLuca and Erim, 1994). However, reminiscent of the advantages of size-ordered recruitment, this strategy would minimize fatigue and increase efficiency because mainly those units ideally suited for the production of a required force vector would be active at any given time. Furthermore, because cosine-tuned units are active over a wide range of directions, the change in unit activation during a movement need not consist in the abrupt recruitment and derecruitment of distinct subpopulations but can instead proceed smoothly by gradual recruitment and derecruitment and differential modulation of the firing rates of different units. This smooth change in relative unit activity would agree with the postulate that in the execution of a motor act, the control mechanism strives to minimize abrupt changes in the motor commands (Dornay et al., 1996).