Short-Term Memory for Reaching to Visual Targets: Psychophysical Evidence for Body-Centered Reference Frames

Abstract

Pointing to a remembered visual target involves the transformation of visual information into an appropriate motor output, with a passage through short-term memory storage. In an attempt to identify the reference frames used to represent the target position during the memory period, we measured errors in pointing to remembered three-dimensional (3D) targets.

Subjects pointed after a fixed delay to remembered targets distributed within a 22 mm radius volume. Conditions varied in terms of lighting (dim light or total darkness), delay duration (0.5, 5.0, and 8.0 sec), effector hand (left or right), and workspace location. Pointing errors were quantified by 3D constant and variable errors and by a novel measure of local distortion in the mapping from target to endpoint positions.

The orientation of variable errors differed significantly between light and dark conditions. Increasing the memory delay in darkness evoked a reorientation of variable errors, whereas in the light, the viewer-centered variability changed only in magnitude. Local distortion measurements revealed an anisotropic contraction of endpoint positions toward an “average” response along an axis that points between the eyes and the effector arm. This local contraction was present in both lighting conditions. The magnitude of the contraction remained constant for the two memory delays in the light but increased significantly for the longer delays in darkness. These data argue for the separate storage of distance and direction information within short-term memory, in a reference frame tied to the eyes and the effector arm.

When reaching to a remembered target, how does the CNS specify the endpoint of the intended movement? It appears that the CNS does not specify all three spatial dimensions together. Instead, movement parameters are parcellated into distance and directional components (Rosenbaum, 1980; Georgopoulos, 1991;Flanders et al., 1992; Fu et al., 1993; Gordon et al., 1994), but the question remains regarding the origin to which the distance and direction are referred. Greater variability of final positions in the direction of movement versus along an orthogonal axis (Gordon et al., 1994; Desmurget et al., 1997; Messier and Kalaska, 1997), accumulation of errors for sequential movements (Bock and Eckmiller, 1986), and different central processing times for direction and extent (Rosenbaum, 1980) all suggest that the upcoming movement is planned in terms of the displacement from the initial posture. In other studies, however, viewer-centered (Soechting et al., 1990; McIntyre et al., 1997) or shoulder-centered (Soechting and Flanders, 1989a,b; Berkinblit et al., 1995) distributions of errors indicate an internal specification of the final intended position, as opposed to the movement direction and extent. Differences among these various findings might be explained by the likely dependence of the reference frame on both task requirements and available sensory cues (Desmurget et al., 1997; Lacquaniti, 1997;Messier and Kalaska, 1997).

Additional insight into the encoding schemes used by the CNS can be gained by imposing a controlled time delay between the target presentation and the movement. Using this paradigm, characteristics of internal storage mechanisms can be distinguished from effects of noise in the sensory input or motor output. Furthermore, the evolution of errors as the memory delay increases may reveal the reference frames inherent in the neural circuits that encode the remembered target position. With this in mind, we performed a series of psychophysical studies of errors made when pointing to remembered targets presented visually in three-dimensional (3D) space. We compared performance under two lighting conditions and three different memory delays. We developed 3D statistical tools used to identify sources of noise, bias, and local distortion in the transformation from target to pointing position. Using this approach we have characterized the acquisition, transformation, and memory storage of sensorimotor information for an arm-reaching task. We conclude that short-term memory mechanisms store distance and direction separately in an arm-centered reference frame, with a faster rate of decay for distance information in the dark. When vision of the hand is permitted, a viewer-centered memory of the target position can be used to reduce variability and distortions at the output.

MATERIALS AND METHODS

Analyses of constant and variable pointing errors have been used in the past to identify the sources of information that contribute to the internal representation of a memorized target position (Foley and Held, 1972; Prablanc et al., 1979;Poulton, 1981; Soechting and Flanders, 1989a; Darling and Miller, 1993;Berkinblit et al., 1995; Desmurget et al., 1997; McIntyre et al., 1997). Constant error refers to bias in the mean response for repeated trials to a given target, and variable errordescribes the variability of individual responses, as quantified by the variance or SD about the mean. Three-dimensional variable error is represented as a 3 × 3 covariance matrix, where the eigenvalues of this matrix describe the magnitude of the variability. In this paper we introduce a third measure of error, which we call the local distortion. Local distortion describes the mapping of spatial relationships between nearby points as data are processed through the sensorimotor pathways.

Constant error, variable error, and local distortion provide three complementary measures of the characteristics of a sensorimotor pathway. Specific workspace-related patterns in any one of these three measures can provide evidence for the internal structure of a sensorimotor process. In the following experiments we have used all three measures of pointing error to characterize the acquisition, transformation, and storage of sensorimotor information within the nervous system.

Experimental protocols

The experimental apparatus was identical to that described byMcIntyre et al. (1997). Subjects sat on a 45-cm-high straight-back chair facing a table measuring 150 cm wide × 54.5 cm deep at a height of 69 cm. To the opposite edge of the table was fixed an upright, flat backboard measuring 130 cm wide × 85 cm high. Subjects were seated ∼20 cm from the front edge of the table (75 cm from the backboard). A headrest helped the subject maintain a constant head position throughout the experiment, although the head was free to turn.

A red, 5-mm-diameter light-emitting diode (LED) was presented to the subject by a robot, in the region between the subject and the backboard. The subject placed the index finger of the hand (left or right, depending on the specific protocol) on one of two starting positions, located on the table top 10 cm from the front edge of the table and 20 cm to the right or left of the midline (depending on the experiment variant; see below). The starting position was an upraised bump (2.5-mm-radius hemisphere) on the table surface that could be located by touch.

At the beginning of a trial, a green fixation LED was illuminated, located on the surface of the backboard at the midline, 13 cm above the tabletop. One second later an audible attention signal sounded. After a random delay of 1.2–2.4 sec, the fixation light was extinguished, and the red target LED was lighted at the target position for a period of 1.4 sec, then extinguished, and quickly removed. After a memory delay that followed the extinction of the target LED (0.5, 5.0, or 8.0 sec, depending on the specific protocol described below), a second audible tone sounded, indicating that the subject should initiate the pointing movement. Subjects were instructed to place the tip of the index finger so as to touch the remembered location of the target LED and to attempt to maintain fixation of the remembered target position during the memory delay period. The subject had 2 sec to perform the movement and hold at the remembered target position.

Visual conditions

The board, the rod carrying the LED, and the top surface of the table were painted black. During target presentation, the room was dimly illuminated with indirect lighting coming from behind the backboard. Under these conditions, no discernible visual points could be seen directly behind the presented target. For a gaze fixated on the center of the backboard, the visual field was uniform over a range of ±40° horizontally and ±30° vertically. Robot motion occurred only with the LED turned off and thus could not be seen.

The actual pointing movements were performed under two different illuminations: dim light and total darkness. In the dim light condition, illumination was held constant as described above throughout the target presentation, memory delay, and pointing periods. The finger was dimly visible (0.0029 cd/m²) against the black background (0.0010 cd/m²). For trials conducted in total darkness, the dim room lights were extinguished at the same moment as the target LED and remained off during the memory delay and movement.

Positions and movements were measured by a three-dimensional infrared tracking system (Elite System, BTS, Milan, Italy). During the experiment, the movement was measured by means of a reflective marker attached to the fingertip (McIntyre et al., 1997). The marker position was sampled at a rate of 100 Hz. A second marker attached to the forehead 2 cm above the midpoint between the eyes was also tracked during each trial. To measure the actual location of each target position, the subjects performed a set of 10 control trials before starting the experiment in which they moved the index finger to touch the actual LED situated at each of the target positions.

The three-dimensional trajectory of the finger-tip marker was computed for each trial. We calculated the initial and final position of each movement as the mean position computed over the first and last 10 samples, respectively, of the 2 sec movement recording. A threshold based on the SD for these mean positions was used to reject trials in which the final endpoint position was not stable. Fewer than 2% of trials were rejected on this basis. A measured 0.16 mm average SD of the endpoint during the final hold period gives an estimate of the resolution of our measurements of the endpoint position, taking into account measurement noise and the stability of the finger at the endpoint. Variability of the starting position was <2.5 mm (SD) in all three directions, as noted previously (McIntyre et al., 1997).

Target configurations

Trials were performed in blocks of 60 or 90, with one block of trials lasting ∼15 min. Within a single block of trials, target locations were restricted to a relatively small volume in three-dimensional space. Three different regions of the workspace were measured in separate blocks, all located ∼10 cm above the shoulder (35 cm above the table): (1) the middle region, located 60 cm directly in front of the subject, (2) the left region, 60 cm in front of the subject and 38 cm to the left of the midline, and (3) the right region, 60 cm in front of the subject and 38 cm to the right. For a single workspace region, eight targets were distributed uniformly on the surface of a sphere of 22 mm radius, with a ninth target located at the center. This configuration is equivalent to points on the corners of a cube. The cube was tilted such that two opposite corners and the center formed a vertical line, and rotated to be symmetric across the midline. Subjects performed a total of 180 test trials to targets within a single condition and workspace region (20 trials per target).

Protocols

Two sets of experiments were performed: one to identify the effects of visual conditions and memory delay period on pointing errors to remembered targets, and the other to clarify the organization of pointing errors when the hand cannot be seen during the pointing task. All subjects were right-handed and were naive to the hypotheses being tested in these experiments.

Lighting and delay. To compare effects of lighting conditions and memory delay, subjects performed a set of pointing experiments using the right hand from the right starting position. Six subjects used the right hand to perform pointing movements in the dim light conditions, with a 0.5 sec memory delay (light–short), to all three workspaces regions (left, middle, and right, in separate blocks). Five of these six subjects repeated the experiment with pointing movements performed in total darkness after a 0.5 sec memory delay (dark–short). These same five subjects performed the pointing task in darkness after a 5.0 sec memory delay (dark–long). Two subjects performed the task in dim light with a 5.0 sec delay only (light–long) to the three workspace regions. In a separate experiment, six subjects pointed to targets in the middle workspace region, with two memory delays (0.5 and 8.0 sec) mixed within the same block of trials.

Effector arm and starting position. We tested for a center of rotation for observed effects in darkness by testing two different starting positions and both arms. Results from thedark–long protocol provided data for pointing with the right arm from the right side (right–right). Five subjects pointed in darkness after a 5.0 sec delay to the left, middle, and right workspace regions with the right arm, starting from the left position (right–left). Eight subjects performed the same protocol to the left and right workspace regions only using the left arm and starting from the left position (left–left).

Analysis

Constant error vectors, computed as the average error over all nine targets within a single workspace region, were calculated for each workspace region as described in McIntyre et al. (1997):

$$e=\frac{1}{n} \sum _{i=1}^9 \sum _{j=1}^{n^i} p_j^i-t^i,$$ Equation 1

where tⁱ is the 3D vector location of target i, p_j ⁱ is the final pointing position for trial j to target i, andnⁱ and n are the number of valid trials to target i, and the total number of valid trials to all nine targets, respectively. The 3D covariance estimated from data over all k = 9 targets is computed byMorrison (1990):

$$S=\frac{\sum _{i=1}^k \sum _{j=1}^{n^i} {\delta }_j^i({\delta }_j^i{)}^T}{n-k},$$ Equation 2

where the deviation δ_jⁱ =p_jⁱ −$\overline{p}$ⁱ for trial j to targeti is computed relative to the mean$\overline{p}$ⁱ of trials to targeti, not to the overall mean for all targets. The 3D covariance matrix S can be scaled to compute the matrix describing the 95% tolerance ellipsoid, based on the total number of trials n:

$$T_{0.95}=q \frac{(n+1)(n-k)}{n(n-q-k+1)} F_{0.05,q,n-q-k+1}S,$$ Equation 3

where q = 3 is the dimensionality of the Cartesian vector space and k = 9 is the number of targets.

Local distortion

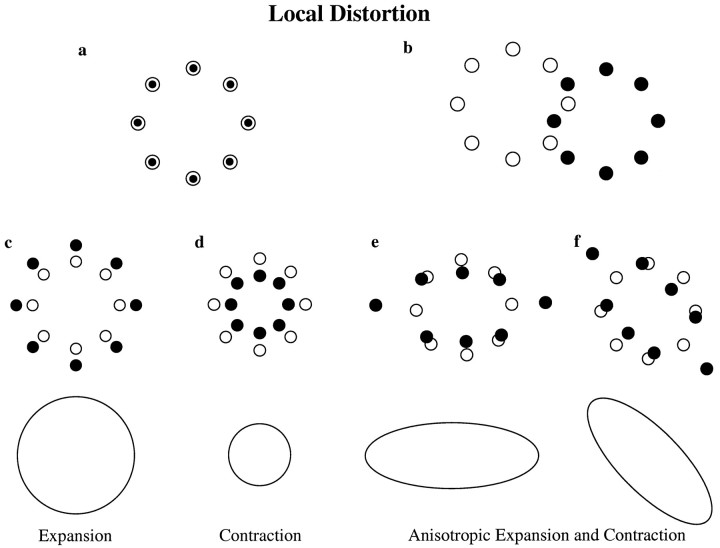
Consider a circular array of targets as shown in Figure1a (open circles). The mean position of repeated movements to each target creates an array of final pointing positions (filled circles). The measurement of local distortion refers to the fidelity with which the relative spatial organization of the targets is maintained in the configuration of final pointing positions. If the constant error in the mapping from target to endpoint position is approximately the same for all eight targets, the array of final pointing positions will be an undistorted replica of the target array, despite the overall displacement from the center (Fig.1b). On the other hand, differences in the mapping of individual targets can result in a distorted representation of the target array within the pattern of final pointing positions. This distortion can manifest itself as an expansion or contraction of the local space (Fig. 1c,d). The expansion or contraction may be unequal for different dimensions, resulting in an anisotropic distortion of the target array (Fig. 1e,f). The transformation from target to endpoint position might also include a rotation of the local space, or reflections through the center position, either alone or in combination with a local expansion or contraction (data not shown).

Fig. 1.

Definition of local distortion. a, When pointing accurately, the endpoint positions (•) reproduce the spatial organization of the target locations (○). b, Transformation from target to endpoint positions with a large constant error but no local distortion. c–f, Types of local distortion that can be introduced by a linear transformation, excluding rotations: local expansion (c), local contraction (d), anisotropic expansion, and contraction aligned with two different axes (e, f).

The transformation from target to final pointing position in general will be a nonlinear process in which the binocularly acquired target position is transformed into an appropriate joint posture. For a small area of the workspace, however, one would expect the transformation to be continuous and smooth. In this case, local distortions of the spatial organization of the targets can be approximated by a linear transformation from target to endpoint position. Such linear approximations can be represented by a transformation matrix, which in turn can be presented graphically as an oriented ellipse (ellipsoid in 3D). Note that rotations or mirror reflections within the local transformation are lost when the transformation is represented graphically in this manner. However, such reflections and rotations can be extracted from the local transformation estimate and represented separately (see below). Figures 1c–f shows the representation of each type of distortion as a two-dimensional ellipse.

We therefore wished to find the 3 × 3 transformation matrix that maps target positions (relative to the average target position) onto the corresponding endpoint positions (relative to the overall average endpoint position for all trials). We computed the estimated transformation matrix M as the local linear relationship that best describes the transformation between targets and endpoints using standard least-squares estimation.

The linear estimation of the local transformation may contain rotation or reflections as well as a local expansion and/or contraction. A reflection through the center position would mean, for example, that for a target located to the left of center, the subject consistently pointed to the right, and vice versa. Such reflections would be indicated by negative eigenvalues for the transformation matrixM. Because no such reflections were observed in the measured data, the overall local transformation can be represented as the cascade of two components: a symmetric matrix A, representing the local distortion, and a rotation matrixR:

$$M=RA.$$ Equation 4

The symmetric component A was computed from the eigenvectors and eigenvalues of the quantityM^TM as follows:

$$A=W\left[\begin{array}{ccc}\sqrt{{\lambda }_1}& 0& 0\\ 0& \sqrt{{\lambda }_2}& 0\\ 0& 0& \sqrt{{\lambda }_3}\end{array}\right]W^T,$$ Equation 5

where:

$$M^{T}M=W\left[\begin{array}{ccc}{\lambda }_1& 0& 0\\ 0& {\lambda }_2& 0\\ 0& 0& {\lambda }_3\end{array}\right]W^T,$$ Equation 6

and the columns of W are thus eigenvectors for the matrix M^TM. The orthogonal matrix R represents a rotation of θ degrees around a single axis ν_R. For A nonsingular, the matrixR is given by:

$$R={MA}^{-1}.$$ Equation 7

For a 3 × 3 rotation matrix R:

$$\theta ={cos}^{-1}\left(\frac{[trace(R)-1]}{2}\right),$$ Equation 8

$${\nu }_R=\frac{1}{2sin\theta }\left[\begin{array}{c}{R}_{\text{zy}}-R_{\text{yz}}\\ \hfill R_{\text{xz}}-R_{\text{zx}}\hfill \\ \hfill R_{\text{yx}}-R_{\text{xy}}\hfill \end{array}\right].$$ Equation 9

The symmetric local distortion matrix A can be plotted as an oriented 3D ellipsoid, where the major and minor axes indicate the directions of maximal and minimal expansion.

Ensemble averages

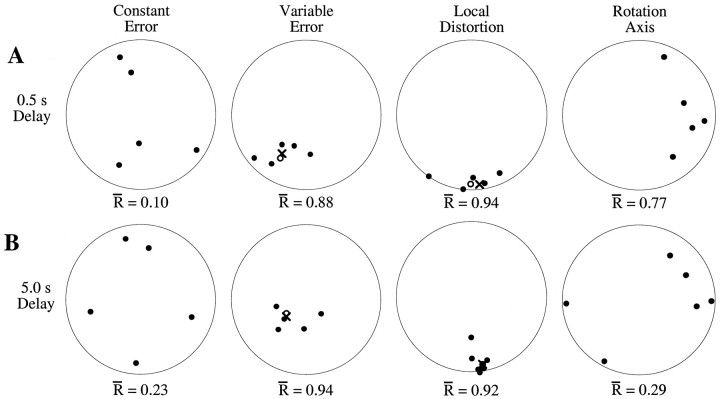
Directional data computed from the constant error vectors, the covariance matrices, and the transformation matrices varied between subjects. Two different methods were used to compute the average responses across subjects. In the first method, the average constant error vectors, covariance matrices, or transformation matrices were computed by pooling individual trial data from all subjects. The second method consisted of computing the direction vectors for each subject and type of measurement and then computing the spherical mean of these individual vectors (Mardia, 1972). Averages of directional data provide meaningful information only when the individual eigenvectors are clustered around a common direction. Clustering can be measured as the length of the average resultant vector $\overline{R}$ (Mardia, 1972). Figure 2 shows typical intersubject variability for the dark–short and dark–long pointing conditions. Distributions of constant error directions varied too widely in our experiment to allow for the computation of a preferred axis. Similarly, the variability of axes of rotation within the local transformation matrix did not indicate a preferred axis of rotation. On the other hand, the directions of maximum variation (first eigenvector of the covariance matrix) and distortion (third eigenvector of the local distortion matrix) did cluster significantly across subjects. The two methods of computing the ensemble averages produced very similar results for these two measures. In the Results section, 3D figures were generated from the average constant error vector, average variable error matrices, and average local distortion matrices, as computed by method 1. Statistical analyses of directional data were based on direction vectors computed for individual subjects.

Fig. 2.

Intersubject variability and the computation of ensemble averages. Each panel represents an equal-area projection of direction vectors into the horizontal plane, for trials to the mid-target region in the dark–short (A) and dark–long (B) conditions. Each filled circle represents the average response for a single subject for (1) the constant error, (2) variable error (first eigenvector indicating the direction of maximum variability), (3) local distortion (third eigenvector indicating the axis of maximum contraction), and (4) rotation axis within the local transformation. Points near the center of each panel represent upward pointing vectors, whereas points near the edge of the bounding circle indicate forward, backward, leftward, or rightward directions for the top, bottom, left, and right edges, respectively. Direction vectors are clustered for the variable error and local distortion vectors but not for the constant error directions or rotation axes. Open circles indicate the average of the individual direction vectors for the distributions showing significant clustering. The symbol X indicates the direction vector computed from the corresponding ensemble covariance or local transformation matrix.

RESULTS

Variable error

Clear differences emerged in the patterns of variable errors for movements in the light versus dark. Movements performed in the light produced axes of maximum variability (Fig.3, dark bars) that converge toward the head, indicating a viewer-centered reference frame for the endpoints of these movements. In contrast, variable error eigenvectors for movements in the dark do not converge toward a unique origin. Viewed from the side (Fig. 3B), the major eigenvectors in the dark tend to point upward, above the head, with a greater such tendency for movements performed after a long (5 sec) delay. Viewed from above (Fig. 3A), the major eigenvectors appear to be parallel for the short memory delay in the dark, whereas for the long delay, the vectors rotate from left to right around a body axis.

Fig. 3.

Average variable errors across subjects for two lighting conditions and two delays, viewed from above (A), from the right side (B), and perpendicular to the plane of movement (C). Ellipsoids represent the tolerance region containing 95% of responses (see Materials and Methods). Dark line segments indicate the direction of the major eigenvector computed for the tolerance ellipsoid. For movements in the dark, a pattern of major eigenvector rotations upward and away from the starting position emerges in the ensemble averages, in comparison to head-centered eigenvector directions seen in the light.

An interesting pattern for variable errors for long delays in the dark becomes apparent when the data are viewed from a direction orthogonal to the movement plane (the plane containing the centers of the three workspace regions and the hand starting position), as shown in Figure3C. Under these conditions, the direction of maximum variability changed for different workspace regions. The major eigenvector rotates more and more counterclockwise in this plane as one moves from the right to the left workspace regions. Such an effect was not readily discernible for movements performed with the lights on (McIntyre et al., 1997).

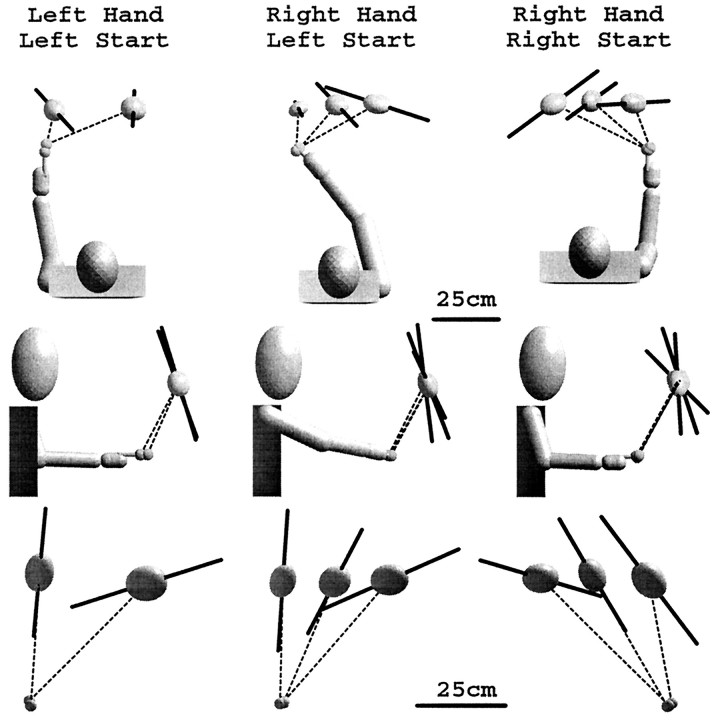
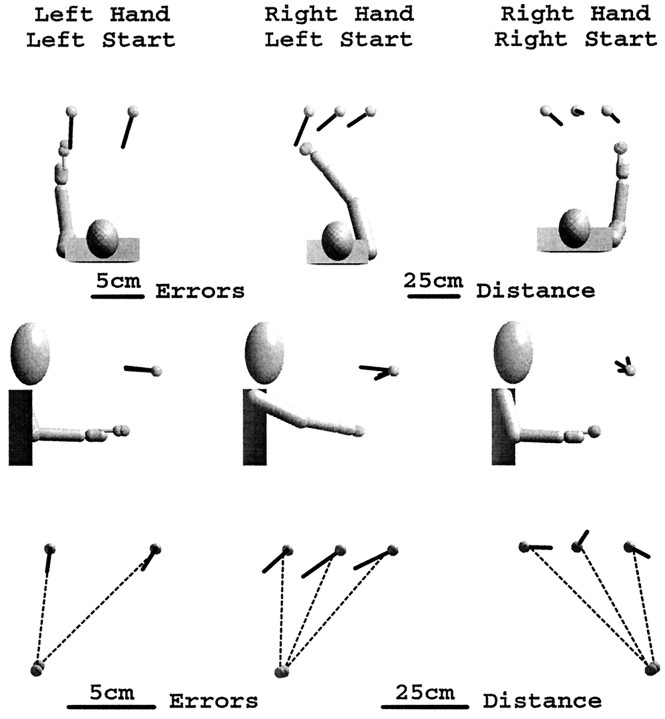
The bottom row of Figure 4 shows that for movements performed in the dark with a 5 sec delay, the direction of greatest variability was affected more by the starting position of the hand than by the choice of hand used to perform the task. In the plane of movement (Fig. 4, bottom row), the major eigenvector of the variable error ellipsoid tilts closer to the horizontal as the workspace region moves laterally away from the starting position. Furthermore, transferring the starting position across the midline for the same set of targets produced roughly a mirror image of the eigenvector rotation pattern (Fig. 4, center vs right column, bottom row). The effect of starting position on the orientation of the variable error within the movement plane was highly significant (F_(1,8) = 17.98, p< 0.0028). Changing the effector hand had little visible effect on the orientation of the major eigenvector (Fig. 4, left vscenter column), although the difference is statistically significant (F_(1,11) = 5.775, p< 0.035).

Fig. 4.

Variable errors for two different starting positions and two different effector hands, averaged across subjects, for pointing in the dark with a 5.0 sec delay. The orientation of the variable error ellipsoid is affected by the relative starting position of the hand but not by the hand used to perform the pointing. Note the change of scale for ellipsoids viewed in the plane of movement.

Changing the starting position can change the final configuration of an arm having redundant degrees of freedom when pointing to the same endpoint (Soechting et al., 1995). One must consider whether the observed changes in variable error tied to the starting position stem from different endpoint arm configurations rather than from different movement directions. The orientation of the plane containing the wrist, the elbow, and the shoulder provides a measure of the configuration of the arm for a given endpoint position. Soechting and colleagues found variations of the order of 10–15° for pointing with the same arm to a single target. However, a simple observation of the left and right arms held at the right target region shows a much larger (90°) difference between the planar orientations of the two arms. Yet, changing the effector arm had little influence on the orientation of the variable error. Thus, it seems that the starting-position effect is most likely related to the direction of movement, rather than to changes in arm configurations. Note, however, that although variable error was affected by the starting position, the axis of maximum variability did not align with the direction of the pointing movements. In fact, when viewed from the side (Fig. 3B), the major eigenvectors for movements in the dark are almost perpendicular to the direction of movement.

Constant error

As was seen for pointing in the light (McIntyre et al., 1997), subjects performing movements in the dark did not show a single pattern of constant errors for either short (0.5 sec) or long (5.0 sec) memory delays. Both overshoots and undershoots with respect to the subject’s body were observed. For the five subjects who performed the experiment under three conditions (light–short, dark–short, and dark–long), there was no significant effect on distance error (overshoot or undershoot) of either lighting conditions (p > 0.15) or memory delay (p > 0.50) as within-subjects factors. Final pointing positions were located both above and below the actual target position for both memory delay conditions. There was no strict correlation between errors performed by a given subject for the two different memory delays, and no clear pattern of constant error emerged for these subjects.

Nevertheless, constant errors did tend to be biased toward the body. When measured over all subjects, including subjects who used the left hand or the left starting position, a detectable bias in distance error emerges, changing from an average of +2.6 mm (overshoot) to −29.3 mm (undershoot) as a function of memory delay (comparison of mean overshoot for 0.5 and 5.0 sec delays; F_(1,30) = 9.13, p < 0.006). In Figure5, there appears to be an effect of hand starting position on the average constant errors shown, although the vectors do not align with the movement axis. No statistically significant effect of starting position (F_(1,8)= 2.051, p < 0.19), workspace region (F_(1,11), p < 0.91), or effector arm (F_(1,11) = 0.60, p< 0.46) was measured for constant error directions.

Fig. 5.

Constant errors for two different starting positions and two different effector hands, averaged across subjects, for pointing in the dark with a 5.0 sec memory delay. Dark bars indicate the direction and extent of the average constant error vector (magnified 5× for visibility), pointing away from the target position indicated by the small sphere. Note the change of scale for data viewed in the plane of movement.

Local distortions

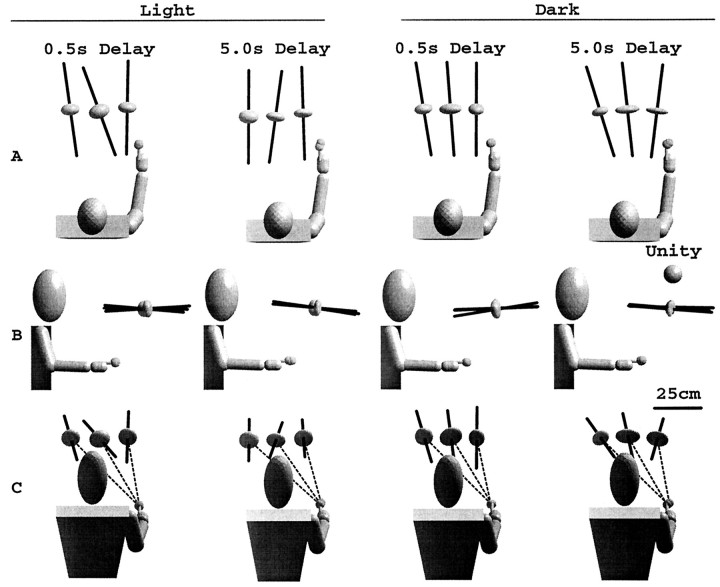
Measurements of the local distortion reveal the most consistent pattern of errors across subjects. Figure6 shows the average local distortion ellipsoids for the two lighting and two delay conditions. The eigenvectors corresponding to the smallest eigenvalue of the local distortion (Fig. 6, dark bars), indicating the axes of maximum contraction, point toward the subject for all workspace regions, intersecting the plane of the body at a height that varies between the level of the eyes and the shoulder. In Figure 6 this pattern of distortion is apparent for both memory delays and both lighting conditions.

Fig. 6.

Average local transformation ellipsoids for two lighting conditions and two delays. Ellipsoids indicate the local distortions induced by the sensorimotor transformation, as estimated by a linear approximation to the local transformation (see Materials and Methods). The unit sphere indicates the ellipsoid corresponding to an ideal, distortion-free local transformation. Dark barsindicate the direction of the third (minor) eigenvector, indicating the axis of maximum local contraction. Under all lighting conditions, axes of maximal contraction point toward the subject.

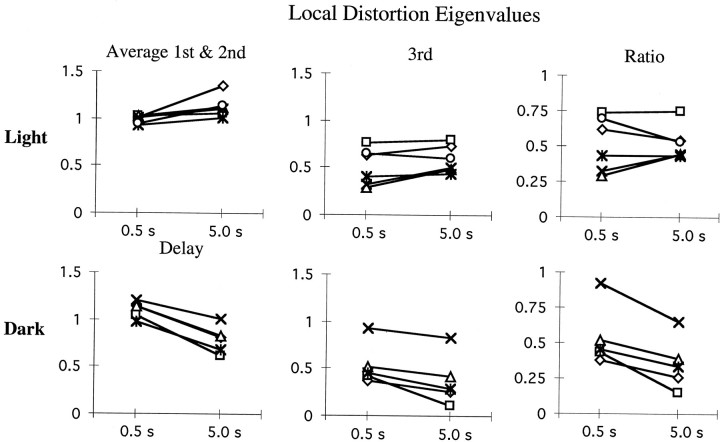
Although the orientations of the local distortions were similar for all conditions, lengthening the time delay had a differential effect on the magnitude of the distortion, depending on lighting conditions (Fig.7). Because the contraction was limited to a single axis (the first and second eigenvalues are approximately equal), the relative contraction along the axis is described by the ratio of the third (smallest) eigenvalue to the average of the other two. Both lighting conditions showed comparable levels of contraction for a 0.5 sec delay (0.58 and 0.60 for light and dark, respectively). However, although contraction increased only insignificantly to 0.50 in the light (F_(1,5) = 3.55, p > 0.1), contraction increased significantly (ratio decreases) to 0.36 in the dark (F_(1,4)=23.56, p < 0.0083). Note that for the statistical tests reported here, the two memory delays for trials performed in the light were mixed within the same block of trials, whereas in the dark, the two memory delays were tested in different blocks on different days. Nevertheless, two subjects who performed reaching movements in the light to targets with only a single 5.0 sec memory delay showed a contraction ratio of 0.54, on average. This confirms that the lack of contraction change in the light was independent of whether memory delays were tested separately or together within the same block of trials.

Fig. 7.

Eigenvalues of the local transformation estimate. Eigenvalues are unitless gains indicating spatial expansion or contraction in 3D target-to-endpoint mappings. Eigenvalues >1 indicate magnification of the local space along the corresponding eigenvector, whereas eigenvalues <1 indicate spatial contraction. First and second eigenvalues are averaged (left column) and compared with the third eigenvalue (center column) representing the amount of maximal contraction along the corresponding eigenvector. The right column shows the ratio of the third eigenvalue over the average of the first and second, indicating the amount of distortion introduced in the visuomotor transformation. Contraction is relatively constant in the light, whereas contraction increases with memory delay duration in the dark.

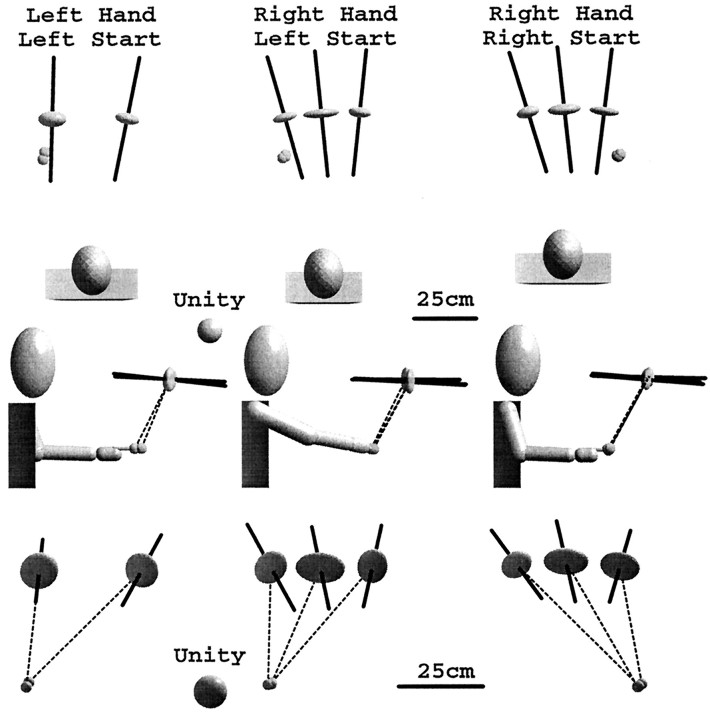
Figure 8 shows the effects of starting position and workspace region on the orientation of the local distortion for movements in the dark with a 5 sec delay. The azimuth of the axis of maximal contraction changes significantly between the left and right workspace regions (F_(1,8) = 12.582,p < 0.0075). Changing the starting position of the hand (right hand, left start vs right hand, right start) had little effect on the orientation of the transformation matrix when projected into the horizontal plane (F_(1,8) = 0.648,p < 0.442). No consistent pattern is apparent in the distortion when viewed in the movement plane (bottom row).

Fig. 8.

Effects of workspace region and movement starting position on estimates of the local transformation. Axes of maximum contraction are biased slightly toward the side of the effector hand, independent of the starting hand position.

The eigenvectors of maximum contraction did not point unambiguously toward the head/body midline or toward the shoulder. However, changing the effector hand did have a measurable effect on the orientation of the distortion matrix. The eigenvectors in Figure 8 are biased toward the left side for pointing with the left hand, and toward the right side for pointing with the right hand. Local distortion eigenvectors were biased to the right side for pointing with the right hand from either starting position. Changing the effector arm had a significant effect on local transformation azimuth (F_(1,11)= 5.46, p < 0.039). Minor axes of the distortion ellipsoids were generally tilted outward, away from the zero (straight-ahead direction) for both the left and right workspace regions. The tilt away from straight ahead for the ipsilateral side was 0.83± 6.43° (mean ± SE), which is not statistically different from zero at the p = 0.05 confidence level. In contrast, the tilt away from straight ahead for the contralateral side (−15.39°± 2.69°) was in fact statistically significant atp < 0.01. The amount of tilt away from zero is significantly greater for movements to the contralateral workspace region (F_(1,17) = 4.77, p < 0.043), consistent with a rotation of the distortion around an axis related to the effector arm.

In the current study, the observed contractions in measurements of local distortion were relatively independent of the observed constant errors. There was no correlation between the amount of undershoot and the magnitude of the local contraction (r = −0.047).

Rotations within the estimates of local transformations were in general relatively small over all workspace regions and starting hand locations in the dark. The median value of rotation was 10.3°, with 95% of all values falling between 3.6 and 28.8° (rotation magnitudes are not normally distributed). Because the axes of rotation varied widely between subjects, the mean amplitude of rotation is not meaningful. Because no obvious patterns emerged in the direction of the axes of rotation across different conditions, we will not discuss further rotations within the local transformations.

Transformed variable error

When viewed in the horizontal plane, variable errors were greater in distance from the subject for movements in the light, but greater in the lateral direction for movements in the dark (Fig. 3). This can be explained by the compression inherent in the local distortion (Fig. 6). If a distorted transformation compresses positions along a given axis, variables errors arising from noise before the distortion will also be compressed along the same axis. However, the measured local distortion was independent of the starting hand position. Therefore, the distortion of viewer-centered noise cannot explain the dependence of the direction of maximum variability on the starting hand position (Fig. 4). Thus, although some of the difference in variable errors observed for movement in the dark versus the light can be attributed to distortions introduced in the overall transformation, an additional source of noise is required to fully account for the dependence of variable error orientation on the starting point of the movement.

DISCUSSION

In these experiments we observed both nonisotropic variable errors and local distortions that were aligned in two different egocentric reference frames. The observed variable errors pointing toward the eyes might indicate a viewer-centered representation of the target position, but these errors might also arise from anisotropic sensitivity to noise in retinal or oculomotor signals mapped onto an otherwise uniform representation (McIntyre et al., 1997). However, the distortions of local spatial relationships along axes pointing between the head and shoulder cannot be explained by anisotropic sensitivity to noise, and thus more clearly indicate a transformation through a body-centered coordinate system.

In the dark, local contraction increased for longer delays along an axis that points between the head and the shoulder (hereafter referred to as the head/shoulder axis). This argues for a separation of target distance and direction within short-term memory. Note that although local contraction is apparent both in light and darkness, this distortion did not increase for longer memory delays in the light. Thus, additional information about the target position in a viewer-centered reference frame may be used to correct the final pointing position when vision of the fingertip is allowed.

Combined viewer-centered and arm-centered reference frames

Our measurements of local distortion point to an origin between the eyes and shoulder for movements in the dark. Soechting and Flanders and colleagues (Soechting et al., 1990; Flanders et al., 1992) have similarly identified an intermediate reference frame that is related to both the visual target and the effector arm. Simulations show how the cascading effects of two transformations, one centered at the eyes, the other centered at the shoulder, can predict the intermediate reference frame seen in the data (J. McIntyre, unpublished observations). The combination of two effects, each tied to a specific anatomical reference, provides a parsimonious description of the underlying phenomenon.

Although our methods for documenting distortions in 3D are novel, evidence for contractions along the sight-line has been reported previously for visual estimates of target distance. Foley (1980) found that the slope of perceived versus actual target distance is consistently less than unity for various different estimation tasks.Gogel (1969, 1973) proposed that the CNS computes target distance as a weighted sum of different inputs (stereodisparity, vergence, accommodation, etc.), including a “specific distance” toward which the estimate is biased in the absence of adequate sensory cues. Contractions of pointing positions may reflect the bias toward the specific distance postulated by Gogel. In three dimensions, however, there is a greater bias toward a specific distance than toward a “specific direction,” reinforcing the conclusion that the CNS parcellates the representation of target location into separate distance and directional components.

In the current experiment, local distortion was uncorrelated with the magnitude of constant errors. Thus, local distortion is not simply the product of a global underestimation of egocentric target distance, nor can the contraction be accounted for by a consistent underestimation in the mapping between a desired 3D displacement of the hand onto a corresponding change of joint angles. The magnitude of radial contraction was similar for movements directed to the same target, starting from the left or right, yet the change in elbow angle was quite different in these two cases. Local distortion is thus not the product of an inaccurate global transformation that is consistently present across subjects. One might argue that the CNS operates locally when transforming spatial information about nearby objects (Lacquaniti, 1997). In visual tasks, subjects produce large errors in estimates of absolute target distances but much better estimates of relative distances once a local reference frame is established (Gogel, 1961;Foley, 1980). Such local frames of reference could explain the conflicting results observed for measurements of constant errors in different experiments (Foley and Held, 1972; Soechting and Flanders, 1989a; Berkinblit et al., 1995; McIntyre et al., 1997). Measurements of distortion reported here indicate nonetheless that the reference frame for the local transformation is linked to the effector arm.

Local distortion increased with lengthening memory delays. The memory of the target position apparently decays toward an “average” central response. Bias toward an average response value can also be seen when subjects are forced to respond to a set of stimuli without sufficient time to adequately prepare the movement (Hening et al., 1988). In our experiment, the contraction toward the central value is greater along a head/shoulder-centered axis, arguing once again for an egocentric reference frame for the representation of the remembered target position.

A hand-centered reference frame?

Gordon et al. (1994) have argued that increased variability along the line of movement indicates an internal representation of the hand displacement in terms of direction and extent from the starting position. In the current study, ensemble averages of variable errors were affected by the starting point of the hand, although the axes of maximum variability did not align with the movement direction. The effects of starting position are most likely related to the direction of movement and not to differences in arm configuration, as demonstrated by the minimal change in variable errors induced by changing the effector arm. However, the effects of starting position were not seen in measurements of local distortion, nor can they be predicted by the distorted transformation of viewer-centered input noise. If information indeed passes serially through a hand-centered movement representation, our data indicate that the transformation into this hypothetical representation is undistorted.

Noise related to movement direction does not necessarily imply a serial passage of information into a hand-centered reference frame. Additive noise is also consistent with parallel, convergent processes. Noise related to movement direction might result from dynamic components of the motor command added to a static specification of final equilibrium position (Feldman, 1966a,b; Hogan, 1985; Bizzi et al., 1992; McIntyre and Bizzi, 1993; Shadmehr et al., 1993). An overestimation or underestimation of the required dynamic command could cause an overshoot or undershoot along the movement axis and would thus add variability in this direction. The effects of variability in a dynamic motor command would interact with the nonisotropic limb stiffness, viscosity, and inertia (Hogan, 1985; Shadmehr et al., 1993) and would not necessarily align precisely with the movement axis. Friction would increase the likelihood that dynamic overshoot or undershoot would persist in the steady-state final position, which might explain why movements against a constraining surface show higher levels of variability related to the movement direction (Desmurget et al., 1997).

A conceptual model

Our observations of 3D pointing errors lead us to propose the schematic description of the pointing task illustrated by Figure9. Retinal and extra-retinal cues combine to form a viewer-centered representation of the target location. This representation is transformed into a reference frame linked to the effector arm. Finally, noise related to the movement direction is added to the endpoint position, either by a distortion-free transformation through a representation of hand displacement (Fig. 9B) or by the parallel addition of dynamic components to the motor command (Fig. 9C). In either case, the increase of the head/shoulder-centered local contraction for greater delays indicates that memory storage of the intended endpoint is held within the viewer-centered and arm-centered representations and not in terms of a hand-centered displacement. When vision is permitted, the final fingertip location may be compared with stored visual information of the target position, reducing the local distortion at the output.

Fig. 9.

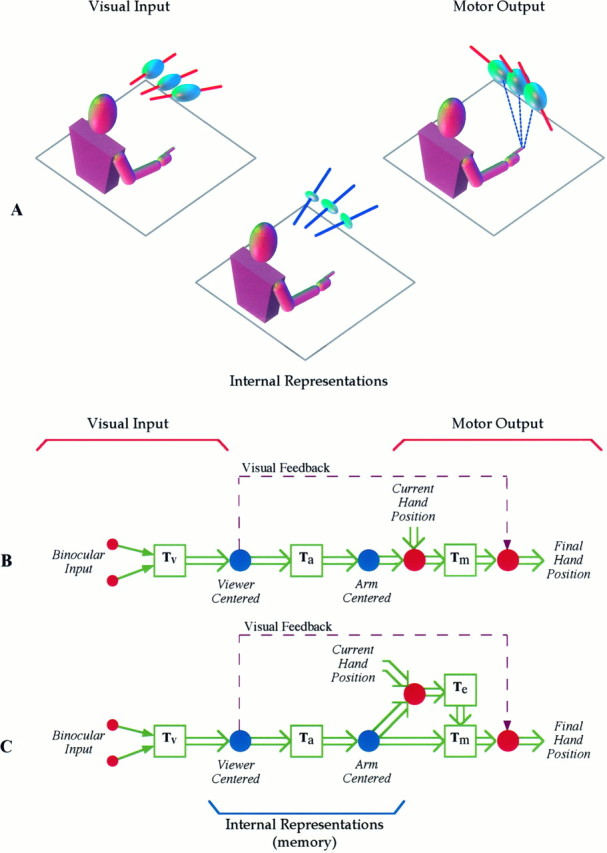
Summary of results regarding the sensorimotor chain for pointing to remembered targets. A, Viewer-centered visual inputs are passed through internal transformations that compress the target position along a body-centered axis as a function of memory delay and then transformed into a motor command. Ellipsoids marked with red bars indicate variable errors, for which the red bar indicates the direction of maximum variability. Ellipsoids marked with blue bars indicate estimates of local distortion, and the corresponding axis of maximum contraction. B, C, In the schematic diagrams of the sensorimotor processes used in pointing to remembered targets, circles depict data representations within a specific reference frame, whereas squaresindicate transformations between coordinate systems. Two models can capture the observed behavior. In both models, binocular visual inputs are transformed into a viewer-centered visual reference frame, with contraction of data along the sight line. Data are then transformed into a motor reference frame linked to the effector arm, with additional contraction along a shoulder-centered axis. InB the final output stage includes a distortionless transformation through a hand-centered reference frame. InC, a parallel, dynamic component is added to the remembered endpoint position to generate the final motor command. In both cases, if vision of the hand is permitted during the pointing movement, the observed final finger position is compared with the visual memory of the target to reduce errors at the output.

Neural substrates

The cascade combination of viewer-centered and arm-centered representations we have hypothesized here could be mediated by the combinatorial properties of cortical networks along the dorsal occipito-parieto-frontal stream (cf. Wise et al., 1997; Lacquaniti and Caminiti, 1998). In the monkey, gaze-position signals modulate the visual receptive fields in several of these areas. Retinal and extraretinal signals combine with arm position signals at early stages of the network, namely in superior parietal areas (areas 7m and V6A) of the mesial cortex (Ferraina et al., 1997a; Galletti et al., 1997;Lacquaniti and Caminiti, 1998). Cells in these areas discharge during instructed-delay tasks before and during arm movements to a visual target (Ferraina et al., 1997b). Area 7m is connected with area 5 in the superior parietal lobule, as well as with dorsal premotor cortex (PMd) and primary motor cortex (M1).

Many cells in these areas discharge in a manner correlated with the direction and extent of the upcoming movement (Georgopoulos et al., 1982; Kalaska et al., 1983; Schwartz et al., 1988; Fu et al., 1993). Other cells fire more consistently with respect to the intended movement endpoint (Hocherman and Wise, 1991; Lacquaniti et al., 1995). The anisotropic evolution of final pointing errors for different delays suggests that target memory could be implemented by egocentric endpoint-position neurons. Many neurons in dorsal area 5 are best tuned to either the azimuth, elevation, or distance of the endpoint relative to the body (Lacquaniti et al., 1995). Furthermore, the tuning curves of area 5 neurons that encode distance exhibit a body-centered contraction reminiscent of the radial contraction described here.

Cells that indicate the upcoming hand displacement are nevertheless active during memory delay periods (Smyrnis et al., 1992). We suggest that these cells may be involved in the computation of dynamic motor commands. The CNS might reasonably precompute and continually update the dynamic command, as evidenced by priming experiments (Rosenbaum, 1980). This update processing would be visible in the cell populations during the delay. In fact, neurons in motor and premotor areas that encode movement direction and extent appear also to be sensitive to dynamic parameters such as applied forces (Kalaska et al., 1989) and instantaneous speed (Schwartz, 1994), and many such neurons are modulated by changing limb configurations for the same hand displacement (Caminiti et al., 1991; Scott and Kalaska, 1997). Note that the population vector in M1 predicts the direction of dynamic force impulses but not static force biases (Georgopoulos et al., 1992).

Conclusions

Based on studies of psychophysics and cortical electrophysiology, different theories have recently emerged that argue for the representation of hand movements in terms of viewer-centered or arm-centered reference frames for the intended final position or in terms of a hand-centered representation of the impending displacement vector. In an analysis of 3D pointing errors to memorized targets, we found evidence that might support all three representations. However, we argue that short-term memory stores the endpoint position in a viewer-centered and/or shoulder-centered reference frame that differentiates between parameters of distance and direction.