Temporal and Spectral Sensitivity of Complex Auditory Neurons in the Nucleus HVc of Male Zebra Finches

Abstract

Complex vocalizations, such as human speech and birdsong, are characterized by their elaborate spectral and temporal structure. Because auditory neurons of the zebra finch forebrain nucleus HVc respond extremely selectively to a particular complex sound, the bird’s own song (BOS), we analyzed the spectral and temporal requirements of these neurons by measuring their responses to systematically degraded versions of the BOS. These synthetic songs were based exclusively on the set of amplitude envelopes obtained from a decomposition of the original sound into frequency bands and preserved the acoustical structure present in the original song with varying degrees of spectral versus temporal resolution, which depended on the width of the frequency bands. Although both excessive temporal or spectral degradation eliminated responses, HVc neurons responded well to degraded synthetic songs with time–frequency resolutions of ∼5 msec or 200 Hz. By comparing this neuronal time–frequency tuning with the time–frequency scales that best represented the acoustical structure in zebra finch song, we concluded that HVc neurons are more sensitive to temporal than to spectral cues. Furthermore, neuronal responses to synthetic songs were indistinguishable from those to the original BOS only when the amplitude envelopes of these songs were represented with 98% accuracy. That level of precision was equivalent to preserving the relative time-varying phase across frequency bands with resolutions finer than 2 msec. Spectral and temporal information are well known to be extracted by the peripheral auditory system, but this study demonstrates how precisely these cues must be preserved for the full response of high-level auditory neurons sensitive to learned vocalizations.

Temporal and spectral cues are critical for the identification of complex vocalizations such as speech, as shown in psychophysical experiments that use systematic degradations of the speech signal along these parameters (Liberman et al., 1967; Drullman, 1995; Drullman et al., 1995; Shannon et al., 1995). Moreover, temporal processing is thought to be critically involved in disorders of speech and language learning (Merzenich et al., 1996; Tallal et al., 1996). Very little is known, however, about the spectral and temporal sensitivity of the high-level central neurons that must mediate complex sound processing. In recent studies, researchers have described the response properties of neurons in the auditory cortex of cats and primates that are tuned to certain characteristics of natural sounds (Ohlemiller et al., 1994; Schreiner and Calhoun, 1994; Rauschecker et al., 1995; Wang et al., 1995). Birdsong provides a particularly useful model for studying the neural basis of complex vocalizations, however, because, like speech, song is a learned behavior and depends on auditory experience (Marler, 1970;Konishi, 1985). Moreover, song acquisition and production are mediated by a specialized set of forebrain sensorimotor areas unique to species that learn their vocalizations (Nottebohm et al., 1976; Kroodsma and Konishi, 1991). Electrophysiological experiments have shown that the brain areas for song contain some of the most complex auditory neurons known. These “song-selective” neurons respond more strongly to the sound of the bird’s own song (BOS) than to almost any other sounds, including simple stimuli such as pure tone or broadband noise bursts, and complex stimuli such as closely related songs of other individuals of the same species (conspecifics) (Margoliash, 1983, 1986; Margoliash and Fortune, 1992; Margoliash et al., 1994; Lewicki, 1996; Volman, 1996). These neurons are also sensitive to the temporal context of the sounds within the BOS, because both the BOS played in reverse and isolated sections of the BOS, which elicit strong responses in their natural context, are ineffective stimuli (Margoliash, 1983; Margoliash and Fortune, 1992; Lewicki and Arthur, 1996). Moreover, systematic modification of some of the parameters of white-crowned sparrow songs demonstrated the dependence of HVc neural responses on both spectral and temporal features of song (Margoliash, 1983, 1986). The highly selective auditory properties of these neurons and the fact that these features emerge during song learning suggest that these neurons play an important role in vocal learning and in the discrimination of adult vocalizations (Margoliash, 1983; Margoliash and Fortune, 1992; Volman, 1993; Doupe, 1997).

Although the general importance of spectral and temporal context for the response of HVc neurons was clear, in this study we developed a systematic and broadly applicable methodology, based on a time–frequency decomposition that is commonly used in speech analysis (Flanagan, 1980), to describe any song completely with a relatively simple set of parameters. This parametrization allowed us to define explicitly the spectral and temporal structure of these complex natural sounds. We then systematically modified the parameters in the decomposition to generate a series of synthetic versions of the BOS that preserved varying degrees of the temporal and spectral structure present in the original song. By comparing the response of HVc song-selective neurons to these synthetic songs with their response to the original BOS, we were able to characterize features of the temporal and spectral structure in the BOS that were essential for HVc neurons, and to quantify the sensitivity of the neuronal responses to the exact preservation of these features. This characterization also revealed the striking precision with which the temporal and spectral structure present in these learned vocalizations needs to be preserved from the auditory periphery to higher order auditory centers.

MATERIALS AND METHODS

Song selection and recording

Two to three days before the experiment, an adult male zebra finch was placed in a sound-attenuated chamber (Acoustic Systems, Austin, TX) to obtain clear audio recordings of its mature, crystallized song (this species usually sings only one song type as adults). An automatically triggered audio system was used to record ∼90 min of bird sounds, containing many samples of the song of the bird. The tape was scanned, and 10 loud, clear songs were digitized at 32 kHz and stored on a computer. Those songs were assessed further by calculating their spectrograms and by examining them visually. A representative version was then chosen from those 10 renditions and analyzed by a custom-made computer program to obtain a parametric representation based on the spectral and temporal components of the song (see below).

Zebra finch songs are organized into simple elements often called syllables. These syllables are in turn organized into a set sequence that is called a song phrase or motif. The motif is repeated multiple times in a song (Zann, 1996, pp 214–215). We chose songs that varied in length between 1.1 and 2.3 sec and consisted of two or three motifs. The length of the song is important because it has been reported that HVc neurons integrate over long periods of time and that the maximal responses are not necessarily found in the first motif (Margoliash and Fortune, 1992; Sutter and Margoliash, 1994).

Parametric representation of song

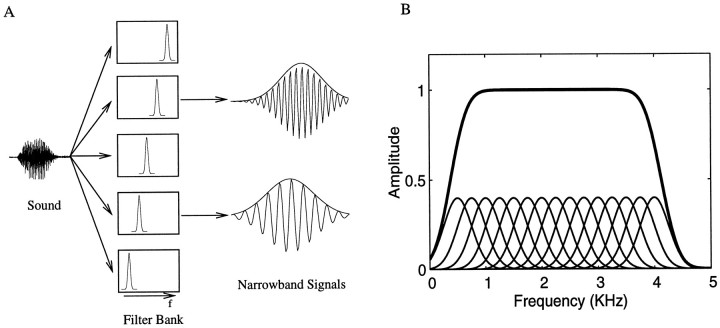
The analysis consisted of decomposing the original song into a set of narrowband signals by filtering the song through a bank of overlapping filters (Fig.1A). The narrowband signals could then be represented by two parameters, one that describes the amplitude envelope and one that describes the time-varying phase of the carrier frequency. The set of time-varying amplitude envelopes characterizes the time-varying power in each frequency band and therefore represents both the spectral and temporal structure of the song. The time-varying phase carries additional spectral and temporal information for each band, but as we will describe in detail in Synthetic songs, this information can become redundant with the information embedded in the joint consideration of the amplitude envelopes. In this section, we describe the mathematics involved in the original decomposition. The next section describes what aspects of the spectral and temporal structure are actually represented in the amplitude and phase components, how the two are related, and how we used variations of these parameters to generate songs with specific spectral and temporal properties.

Fig. 1.

A, Schematic showing the decomposition of a complex sound into a set of narrowband signals, each described by an amplitude envelope and a frequency-modulated carrier. The complex sound is the input to a filter bank composed of a set of adjoining, and in this case overlapping, filters that cover the frequency range of interest. The narrowband output signals of two of the filters in the bank is shown. The envelope that was obtained with the analytical signal is drawn. The carrier frequency is centered at the frequency corresponding to the peak of the filter and has slow frequency modulations that are not easily discernible in this figure.B, Overall filter transform (thick line) obtained from a set of overlapping Gaussian filters (thin lines), the center frequencies of which are separated by one bandwidth (1 SD). The overall filter transform is almost perfectly flat for a large frequency range. In this example, we used 15 Gaussian filters with a bandwidth of 500 Hz and center frequencies between 500 and 4000 Hz.

The decomposition of each narrowband signal into its amplitude and phase constituents was obtained using the analytical signal (Cohen, 1995). As will be emphasized below, this particular decomposition generates an amplitude envelope function that is identical to the one obtained by calculating the short time Fourier transform of the signal, just as is done when a spectrogram is generated. In addition, this operation generates the phase of the short time-window Fourier transform in a form that is continuous with time and that can be interpreted as an instantaneous frequency modulation. A detailed mathematical description of this parametric representation can be found in Flanagan (1980). The decomposition is briefly summarized here.

The original signal s(t) is first divided inton bandpassed component signalss_n(t). To be able to resynthesize the original signal from the bandpassed components, we must choose the filters in the filter banks so that the overall filter transform (obtained by summing the transforms from each filter) is flat over all frequencies occupied by s(t). In addition, the phase distortion of each filter must be insignificant. If these requirements are satisfied, we can recreate the original sound by summing all of the bandpassed signals:

$$s(t)=\sum _n s_n(t).$$

In our decomposition, we used Gaussian filters that were separated along the frequency axis by exactly 1 SD. It can be shown analytically (and verified numerically) that the deviations from a flat amplitude transform in that case are of the order of 1 in 10⁹(Fig. 1B). Enough filters were used to cover the frequency range from 500 to 8000 Hz. The filtering was performed digitally in the frequency domain, resulting in no phase distortions.

In the next step, to extract the instantaneous amplitude envelopeA_n(t) and the instantaneous phase θ(t) of each narrowband signal, we calculated the analytical signal of eachs_n(t):

$$s_n(t)=A_n(t)cos[\theta (t)].$$

The analytical signal decomposition ofs_n(t) guarantees that the frequency components of A_n(t) are all below those of cos[θ(t)] (Cohen, 1995). In particular, it can be shown that for a bandpassed signal of bandwidth ς_w, all of the frequency components of  A_n(t) ² are below ς_w (Flanagan, 1980). In general,A(t) is what one would intuitively call the amplitude envelope of the signal. For example, theA(t) calculated for a beat signal made of two pure tones with amplitudes A₁ andA₂, frequencies w₁and w₂, and absolute phases θ₁ and θ₂ is given by:  A(t) ² =A₁² +A₂² + 2A₁A₂cos[(w₁ −w₂)t + (θ₁ − θ₂)]. The calculation of A(t) for a complex signal is just the extension of this simple vector sum to include all frequency components of the signal. Finally, it can be shown that A_n(t) corresponds to the amplitude at the center frequency w_nof the Fourier transform of s(t) as seen by a window centered around t and with shape given by the inverse Fourier transform of the filter transform function expressed in the frequency domain. In other words,  A_n(t) ² is the running power at frequency w_n calculated with a window centered around t. The width and shape of the window is related to the shape and width of the frequency filter. This is exactly the value achieved when one calculates a spectrogram of a signal.

The part of the signal that is not described by the amplitude envelope (and therefore not shown explicitly in a spectrogram) is often called the fine structure of the signal and is given in the analytical signal by an instantaneous phase, θ(t). The instantaneous phase can in turn be expressed in terms of its derivative and an absolute phase. The derivative of the instantaneous phase is taken as the instantaneous frequency:

$$s_n(t)=A_n(t)cos\left[\underset{0}{\overset{t}{\int }} w(\tau )\text{d}\tau +{\theta }_n\right].$$

We further expressed the instantaneous frequency as a modulation around the center frequency of the bandw_n:

$$s_n(t)=A_n(t)cos\left[w_{n}t+\underset{0}{\overset{t}{\int }} w_{\text{FMn}}(\tau )\text{d}\tau +{\theta }_n\right].$$

In this final form,A_n(t) will be referred to as the amplitude modulation or AM component of the signal,w_FMn(t) is the frequency modulation or FM around the center frequencyw_n, and θ_n is the absolute phase.

Synthetic songs

Four synthetic song families were generated using systematic degradations of the parametric representation described above. Each family of songs preserved some aspect of the original signal. In the following description, the song families are organized approximately in terms of increasing similarity with the original signal. The first set of songs was generated by preserving only the AM components in the decomposition. This resulted in synthetic songs with amplitude envelopes similar to that in the original song. The second set of songs progressively restored the relative instantaneous phase across frequency bands, improving both the FM and AM quality of the synthetic song. The third and fourth set distorted the FM component by additive FM noise. This distortion was done in two ways, one that randomized (third set) and one that preserved (fourth set) the original relative phase. Finally, as a control, we also created the single synthetic song that preserved all of the original parameters. This song is referred to as Syn in Results. The Syn song is identical to the original song filtered by the combined filter transform function obtained from our filter bank.

Synthetic AM songs and the time–frequency scale. The first set of songs was generated by preserving the AM components obtained in the decomposition but by generating a new and random instantaneous phase for each bandpassed signal. The instantaneous phase was chosen to be random so that the new component bandpassed signals of song become effectively noise, band-limited to the same frequency band as the original bandpassed signal and modulated by the same amplitude envelope. The full degraded synthetic song is the sum of these narrowband signals. A family of such AM songs can be generated by increasing or decreasing the width of the filters in the filter bank used to extract the AM waveforms of the original song.

When the filter bandwidth is very wide, the entire song will fit in the band of a single filter, and the resulting AM song will be similar to white noise modulated by the overall amplitude envelope of the signal (see Figs. 2, 6, AM-1 panel). As one narrows the bandwidths of the filters, more filters are needed to cover the entire song, and the amplitude envelopes from each filter characterize the spectral structure more precisely. However, because of the time–frequency resolution trade-off, the amplitude envelopes in each band will now be limited to coarser time resolutions [A_n(t) is band-limited by the width of the filter]. Normally, when the full song is resynthesized by summing the signals in each band and by preserving all parameters, the fine temporal aspect of the overall song envelope is recovered because the phase in each band interacts with that in the other bands in a specific manner to recreate the overall temporal structure of the signal. However, by randomizing the phase, we eliminated this particular relationship between the phases in each band and affected the overall temporal structure. Because our phase is random, the overall time resolution is effectively the time resolution of the amplitude envelopes in each band. This time resolution is given by the inverse of the bandwidth of the filters. Just as the songs modified after filtering through wideband filters have good temporal but poor spectral resolution, songs created at the very narrowband filter extreme characterize the frequency content of the song well but have poor temporal resolution; the amplitude envelopes in each band are effectively flat, and the resulting song is a colored-noise signal with a flat amplitude and overall frequency spectrum identical to that of the original signal (see Fig. 6, AM-256 panel). At intermediate time–frequency resolutions, the synthetic AM signals can capture both the spectral and temporal structure of the original signal but always with a particular trade-off between time and frequency (see Fig. 6, intermediate panels). We subsequently denote the width of the filters used in generating an AM song as the time–frequency scale of the synthesized signal. The AM songs are labeled with “AM scale,” in which the scale is a number specifying the time scale in milliseconds.

Fig. 2.

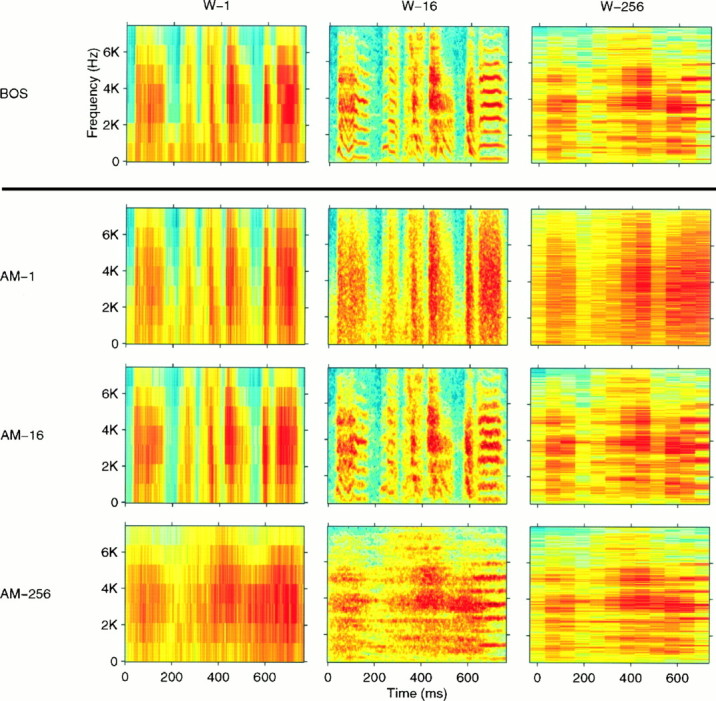
Wideband (W-1), middleband (W-16), and narrowband (W-256) spectrograms generated with different time windows for a representative section of a zebra finch song motif (BOS) and three synthetic AM songs derived from that particular song (AM-1, AM-16, andAM-256). The time windows used to generate the spectrograms had a Gaussian shape and a width of 1, 16, or 256 msec, respectively. The three AM songs were generated by preserving the AM waveforms of the frequency decomposition of the original BOS obtained with a bank of Gaussian-shaped frequency filters, as explained in Materials and Methods. The filters also had widths of 1, 16, or 256 msec expressed in the time domain (1 kHz, 62.5 Hz, or 3.9 Hz, respectively, in the frequency domain). Therefore, theW-1 (W-16 andW-256) spectrogram for the AM-1(AM-16 and AM-256) song approximately matches the W-1 (W-16 andW-256, respectively) spectrogram for theBOS. At other time–frequency scales, the spectrograms of the AM songs do not match that of the BOS, illustrating the information that is lost in the AM songs. TheAM-1 song preserves the fine temporal modulations but does not have the frequency resolution of the BOS. TheAM-256 has good frequency discrimination calculated at longer time scales (notice the finer frequency bands for the last harmonic stack in the song) but has smeared the temporal structure present in the BOS. The AM-16 shows good time–frequency compromise.

Fig. 6.

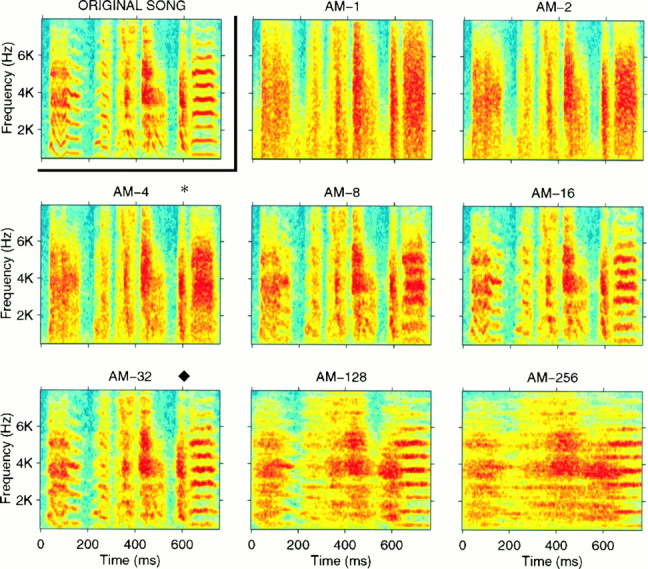
Spectrograms of a representative section of an original song and its corresponding degraded AM synthetic songs. The spectrograms of the AM-1 to AM-256 songs are shown. The songs generated with small time windows (1–4 msec) preserve the temporal modulations seen in the original song but have poor frequency resolution. For long time windows (such as 256 msec), the spectral resolution calculated at longer time scales is good, but the temporal structure present in the original signal is smeared. Thesymbols (*, ♦) indicate the time–frequency scale that gave the best neural response (*) and the best discrimination among songs (♦) (see Fig. 10 and the corresponding text). The samesymbols are also used below (see Figs. 7, 8). All spectrograms displayed in this figure were generated with 16 msec Gaussian windows.

The time–frequency scale trade-off of the AM songs is illustrated (see both Figs. 2, 6). These figures show spectrograms for synthetic AM songs generated with progressively narrower frequency filters. In Figure 2, we also show the spectrograms of the original signal calculated with the same windows that were used to obtain the AM songs. This allows for direct comparison between the amplitude envelope of the AM songs and those of the original song. In Figure 6, the full range of AM songs is displayed in spectrograms all calculated with the time–frequency scale that was best at representing the original song. These spectrograms illustrate how, as one goes from AM-1 to AM-256, spectral resolution is gained at the cost of temporal resolution.

In our experiments, we used a range of frequency filters by varying their width from 2 kHz to 2 Hz in logarithmic steps. The corresponding width of these filters in the time domain ranged from 0.5 to 512 msec. To cover the frequency range from 500 to 8000 Hz, the number of filters ranged from 4 for the 2-kHz-wide filters to 3840 for the 2-Hz-wide filters. For each time–frequency value describing the filter width, we generated a synthetic AM song.

Mathematically, the synthesis went as follows. TheA_n(t) in the synthesis was calculated from the original song, but thew_FMn(t) and θ_n were random. The randomw_FMn(t) was generated so that w_FM had a Gaussian distribution of zero mean and SD equal to the bandwidth of the filters in the filter bank, ς_w. In addition, we required thatw_FMn(t) be band-limited to frequencies below ς_w. These two requirements guarantee that the function:

$$cos\left[w_{n}t+\int w_{FMn}(\tau )\text{d}\tau +{\theta }_n\right]$$

is the analytical representation of a bandpassed signal centered at w_n, with bandwidth ς_w and unit amplitude (i.e., flat bandpassed noise). Finally, these unit amplitude signals from each frequency band were multiplied by the originalA_n(t) and were summed together. The result was a synthetic song with an amplitude envelope in each band similar to that in the original song but with significantly different fine structure.

The resulting synthetic songs have an amplitude envelope in each of their component bands similar to but not exactly the same as that in the original signal because, in the AM songs, the phase relationship between each band and its neighboring “overlapping” frequency bands was altered. Just as randomizing the phase altered the overall amplitude envelope in the AM songs, it will also alter the amplitude envelopes in each band when all the bands are summed together in the synthesis. In other words, in fully parameterized song, there exists redundant information in the time-varying amplitude envelopes and in the relative phase across overlapping frequency bands. One cannot therefore be scrambled without affecting the other. Under certain conditions (of enough overlap between the frequency bands), the amplitude envelopes can completely determine the value of the relative phase across frequency bands. In those cases, one can say that the spectrogram (i.e., the set of amplitude envelopes) is invertible in the sense that the original signal (except for an absolute phase) can be recovered solely from the set of amplitude envelopes. The relative instantaneous phase and therefore the exact representation of the amplitude envelopes will be restored in the family of synthetic songs described in the next section.

To estimate the degree of distortion of theA_n components of the AM synthetic songs, we calculated the normalized cross-correlation between theA_n of the original song and theA_n of the synthetic songs (see below for the definition of cross-correlation). We found that the average cross-correlation (± SEM) was 0.737 ± 0.003 (range, 0.634–0.798) for all 74 AM songs used in these experiments. Significantly for the interpretation of our results, this value was independent of the width of the filters used in generating the songs. Our AM synthetic songs can therefore be thought of as the typical signal that would be estimated in a inverting operation (done, e.g., by the high-level auditory areas) from a noisy representation of the complex sound by its amplitude envelopes (e.g., noisy neural encoding of these envelopes at the auditory periphery). The amount of noise is equal to ∼26% of the signal. The noise in the representation is more detrimental to temporal information when many frequency bands are used, because in those cases the temporal information is present in the fine differences in amplitude across bands. Similarly, the noise is more detrimental to spectral resolution when few frequency bands are used. To eliminate completely the noise in the amplitude envelopes, we had to restore the relative phase across bands perfectly. Therefore in our particular decomposition using overlapping Gaussian frequency bands, the amplitude envelopes can fully characterize the signal (except for an absolute phase that can shift the phase by the same amount in each band).

Note that any other mathematical representation of a signal in terms of sums of amplitude envelopes [including those used in Shannon et al. (1995)] is also affected by the fact that one cannot independently change time-varying spectral and temporal information. For example, decreasing the overlap between the filters would reduce the contamination in the amplitude envelope attributable to the interaction with the neighboring bands but would result in an increase in spectral fluctuations caused by a nonuniform sampling of the frequency range covered by the overall filter transform of the filter bank (as shown in Fig. 1B). Both errors in the synthesis could apparently be eliminated by using nonoverlapping boxcar filters, but in reality the amplitude envelope of a synthetic song made from such boxcar filters would only match the amplitude envelopes of the original song extracted with the exact same set of filters that was used to obtain the A_n(t) waveforms for the synthesis. The amplitude envelopes of the synthetic and the original song extracted with differently shaped filters or with filters of the same shape but shifted along the frequency axis would be different, again because of different interference terms. For example, for boxcar filters, the error would be the greatest for amplitudes extracted when the filters were shifted by exactly one-half the bandwidth. On the other hand, our formulation, using Gaussian overlapping filters, would result in similar errors for amplitude envelopes extracted with filters (of equivalent bandwidth) of any shape and centered at any arbitrary point along the frequency axis. This uniformity of representation of the amplitude envelopes is physiologically more realistic, just as the shape and the overlap of our overlapping Gaussian filters constitute a better model of the auditory periphery than does a set of nonoverlapping boxcar filters. These were important factors, because we wanted to analyze our results in light of the encoding occurring at the different stages of the auditory system. Finally, we wanted to use a formulation that was completely symmetric along the time and frequency dimensions, so that we could interchangeably quantify the scale of our AM synthetic song (given by the width of the filters) in the time domain or in the frequency domain. The choice of Gaussian filters separated by 1 SD was the result of all of these considerations.

Songs that preserve the relative instantaneous phase. In the second and third set of synthetic songs, we progressively restored the fine structure components of the signal that had been eliminated from the AM songs. Our starting point was the AM synthetic song generated for the time–frequency scale of 16 msec or 62.5 Hz (AM-16). This particular time–frequency scale was chosen both because AM songs generated at this scale elicited good responses from HVc neurons and because the amplitude waveforms calculated at this scale were the most informative for discriminating among zebra finch songs from different birds (see Results).

In the second set of synthetic songs, we progressively restored the instantaneous relative phase across adjoining frequency bands. In practice, we generated a set of songs with Gaussian noise added to the values of the instantaneous phase waveforms θ_n(t), obtained from the original song. This is different than the situation for the AM songs in which the instantaneous phase waveforms from the original song were ignored and new random instantaneous phase waveforms were generated. The amount of noise was specified to preserve the relative phase across adjoining frequency bands to within a given temporal resolution. The temporal resolution was implemented by allowing Gaussian deviations from the original relative phase at each time point. The value of the temporal resolution was varied by changing the width of the Gaussian noise. The width of the Gaussian was expressed in radians, which were translated into time units by dividing by (2π)62.5. The value of 62.5 Hz corresponds to the interval between the center of two adjoining frequency bands for the time–frequency scale of 16 msec.

Songs with temporal resolutions in the relative phase ranging from 10 to 0 msec were generated. Gradually restoring the relative instantaneous phase had two effects; it progressively restored the FM in each band and improved the quality of the AM component. The FM component is the derivative of the instantaneous phase, which is independent of the absolute phase and will therefore be preserved when the relative phase is preserved. The quality of the AM component also depends on the relative phase in order to obtain the same interference terms as those of the original song (see synthetic AM songs and the time–frequency scale). To indicate the accuracy of the representation of the AM component, we also calculated for each temporal resolution the cross-correlation value between the AM component of the synthetic songs and the one of the original song. The 0 msec temporal resolution resulted in a synthetic song that was similar to the original song except for an identical shift in absolute phase in all frequency bands. That particular synthetic song was called RAP for random absolute phase. The RAP song has the same AM and the same FM that the BOS has.

Songs that preserve various amounts of the FM component. For the third and fourth sets of songs, we added noise to the original FM component in each band. In addition, the fourth set preserved the relative phase exactly across all bands. To preserve the relative phase, we added the same FM noise to every frequency band. For the third set, independent frequency noise was added to the FM component in each band. We generated a set of songs by varying the SD of the FM Gaussian noise from 0 to 30 Hz. As in the previous set of songs, the FM noise was band-limited to frequencies below 62.5 Hz. Recall that an AM-16 song is generated with random Gaussian FM with 62.5 Hz SD; thus 30 Hz corresponds to approximately half that amount of noise. For the synthetic songs designed to preserve various amounts of FM, however, the noise was added to the FM components of the original song. The absolute phase was also random, one random shift for all absolute phases for the set that preserved the relative phase and an independent phase shift in each band for the set that did not preserve the relative phase. The randomness of the absolute phase is only significant in the 0 Hz case. The 0 Hz noise value corresponds to synthetic songs with the original FM. For the cases in which the relative phase was preserved (fourth set), the 0 Hz song was identical to the RAP song. For the cases in which we generated a different absolute phase in each band (third set), the 0 Hz song will be called RP for random phase.

Measure of song similarity based on the amplitude envelope

We estimated the degree of similarity between zebra finch songs from different birds or between our synthetic songs and the original song by calculating the normalized cross-correlation coefficient of their respective AM components:

$$C_A=\frac{{〈\sum _n A_{1n}(t)A_{2n}(t)〉}^2}{〈\sum _n A_{1n}(t{)}^2〉〈\sum _n A_{2n}(t{)}^2〉}.$$

The 〈〉 indicate averages over the length of the song. C_A was calculated for a range of time delays between the two signals, and the largest correlation was taken as the measure of song similarity. Because different songs could vary in duration, the time averages were performed only for the duration of the shortest song.

The correlation measures were repeated for a range of time–frequency scales to allow the study of the effect of time–frequency scale on the discriminability of songs based on their amplitude waveforms. We also performed this calculation on a syllable-by-syllable basis by comparing syllables from one song with syllables from the other songs. By looking only at syllables, we could separate the effect of the temporal scale given by the rhythmic succession of silences and syllables from the temporal scale of the sounds within a syllable. The syllable cross-correlation reported in this work was limited to the pair of syllables that were the most similar between the two songs. These particular pairs are presumably the most difficult to differentiate.

The syllable decomposition was done by a computer program that automatically divided the song into sections of sounds and silences based on the waveform profile of the overall power envelope calculated with an 8 msec hanning window. The peaks and troughs of this amplitude envelope that were a factor of 10 apart were used to define sections of silence and sections of sound in the song. The sections of sound could be separated by very short silences (one point or 4 msec) and vice-versa. The temporally discrete sections of sounds obtained with this algorithm are a particular implementation of what is usually defined somewhat subjectively as a syllable in the zebra finch song by human experts (Sutter and Margoliash, 1994; Zann, 1996, pp 214–215). Figure 3 shows the syllable decomposition obtained for one of the songs used in this work. Our algorithm efficiently divides the song into syllables, with the limitation that for syllables separated by longer periods of silence, the boundaries between sound and silence are not necessarily at the same threshold levels of sound intensity that would be used by a human expert. Because the measurement of the length of the syllables or of the interval between syllables was not part of our work, these differences are not important.

Fig. 3.

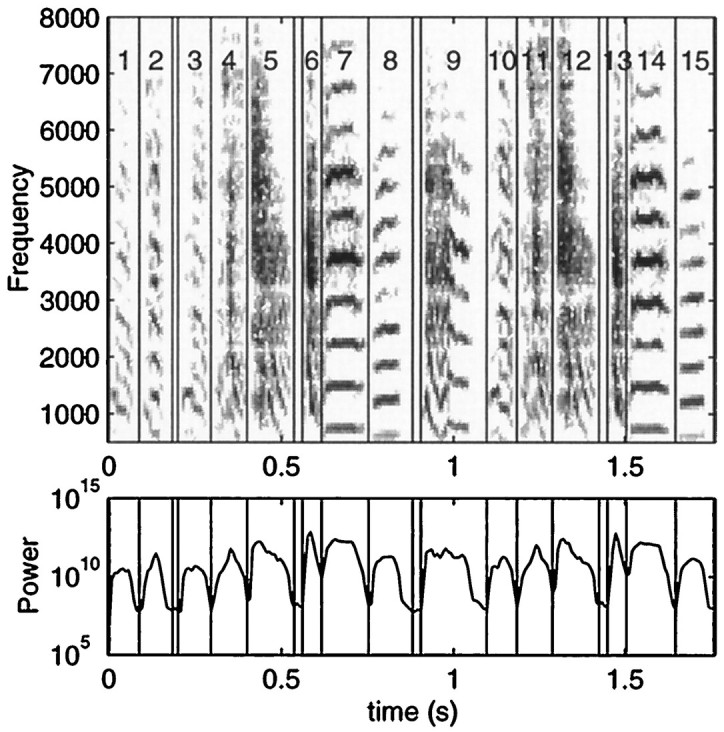
Spectrogram (top) and overall power envelope (bottom) of one of the representative songs used in these experiments. The vertical lines are the divisions obtained from a computer program that automatically divides the song into syllable-like elements based on the peaks and troughs of the overall power (see Materials and Methods). Syllables 9–14 were chosen for the color spectrograms (see Figs. 2, 6).

The cross-correlation analysis was performed for 16 songs from our zebra finch colony, including the songs from the seven birds used in this experiment. The songs belonged to birds from different families and had different temporal and spectral structure. This ensemble of songs was not necessarily representative of all song sounds that zebra finches can produce but was more than sufficient to characterize the time–frequency scale of zebra finch sounds, as evidenced by the small error bars that we obtained for the C_Ameasure.

Electrophysiology

All physiological recordings were done in anesthetized adult male zebra finches in acute experiments. Two days before the recording session, a small surgical procedure was performed to prepare the bird for the recording session. The bird was anesthetized with 20–30 μl of Equithesin intramuscularly (0.85 gm of chloral hydrate, 0.21 gm of pentobarbital, 0.42 gm of MgS0₄, 2.2 ml of 100% ethanol, and 8.6 ml of propylene glycol to a total volume of 20 ml with H₂0), and a small patch of skin on the head was removed to expose the skull. The top bony layer of the skull was removed around the dorsal part of the midsagittal sinus and in an area a few millimeters lateral of the sinus. A ink mark was made 2.4 mm lateral from the dorsal bifurcation point of the sinus to be used as a reference point for electrode penetration. Finally, a metallic stereotaxic pin was glued to the skull with dental cement.

For the recordings, the bird was slowly anesthetized with urethane (75 μl of a 20% solution administered in three doses over a 1.5 hr period) and immobilized with the stereotaxic pin. A very small patch of the lower layer of the skull and the dura was removed at the marked location exposing the brain. Extracellular electrodes were inserted through this opening at and around the location originally marked by the ink dot. The stimuli were presented inside a sound-attenuated chamber (Acoustic Systems) with a calibrated speaker 20 cm away from the bird. The volume of the speaker was adjusted to deliver peak levels of ∼85 dB. The rate-intensity function of HVc neurons quickly plateaus above threshold values. The 85 dB value was chosen so that the sound level of the song was in the range at which the rate-intensity function of the neurons is flat (Margoliash and Fortune, 1992). We did not investigate what effect low sound levels would have on our results. Data were collected when the base line activity and auditory responses were characteristic of the nucleus HVc. As reported in other studies both for zebra finches (Margoliash and Fortune, 1992) and for white-crowned sparrows (Margoliash, 1986), HVc responses, in both the urethane-anesthetized and the awake-restrained animal, are characterized by bursting spontaneous activity and by auditory responses that show a strong preference for the BOS in comparison with the responses to other complex auditory stimuli, such as the BOS played in reverse or the song of conspecifics. These characteristic properties can be used to distinguish the neural responses of HVc neurons proper from those of the neighboring neostriatal areas. Our experience is in complete agreement with this phenomenology. The exact location of the recording sites was also verified postmortem by finding the electrode tracks and lesion reference points in Nissl-stained sections of the brain of the bird [for detailed histological methods, see Doupe (1997)]. The data from this paper consist solely of recordings from within the nucleus HVc [for a detailed anatomical description of the HVc, see Fortune and Margoliash (1995)].

The data consisted of neural responses obtained in 77 distinct recording sites in seven birds. In any particular bird, the recording sites were at least 75 μm apart. This distance was sufficient to guarantee that the neural activity recorded from two successive sites originated from different units. A window discriminator was used to translate the neural activity at each recording site into spike arrival times of small clusters of one to five neurons. The single-cell spike arrival times were obtained when a stereotyped spike shape was easily selected with a window discriminator. The multiunit recordings consisted of spikes of various shapes that could easily be discriminated from the background activity with a window discriminator but not from each other. We assessed that responses from small clusters of two to five neurons were obtained in such recordings. Additional single units were isolated from the clusters of neurons using the spike-sorting algorithm of Lewicki (1994) and showed very similar results to the small clusters of neurons and to the single units isolated with a window discriminator but were not used in the analysis presented here.

Stimulus repertoire and presentation

Stimulus repertoire consisted of the BOS, all of the synthetic versions of the BOS, the BOS played in reverse, the BOS played in reverse order, two conspecific songs, and broadband noise bursts. In addition, in some experiments, we used pieces of songs to test for temporal combination-sensitive neurons. The BOS, the BOS played in reverse, the broadband noise bursts, and the conspecific songs were used both as search stimuli and to initially characterize the selectivity of the recording sites for the BOS. The synthetic stimuli were then presented in subgroups that consisted of most of the synthetic songs from one of the four families and the BOS. Ten interleaved trials were collected for all of the stimuli in the subgroup. The stimulus presentation order was randomized for each trial number. The interstimulus interval was between 7 and 8 sec. Two seconds of background activity was recorded before each stimulus, and between 4 and 5 sec was recorded after the stimulus. An additional time interval between 1 and 3 sec (uniform random distribution) was added between collections. When a single stimulus such as the BOS was presented with this interstimulus interval, no measurable adaptation in the responses was found.

In the analysis, the response to the synthetic songs was compared with the response to the BOS obtained during the same collection trials. This was a precaution used in case the response properties were not stationary during the long period of time that was required for the presentation of all synthetic stimuli. Because the set of collection trials was repeated for a subgroup of stimuli to assess stationarity, we obtained between 10 and 40 trials for each stimulus. However, 10 trials were used most of the time to be able to record the responses to the largest ensemble of synthetic stimuli at each recording site. This small number of trials was sufficient to characterize single recording sites in terms of their classic selectivity properties (i.e., BOS vs conspecific song) because the magnitude of the response is clearly different in those cases. For stimuli that gave similar responses (such as AM-16 vs AM-8), more trials would be required in particular cases to obtain significant differences for single recording sites (although some neurons showed statistically significant differences). Our conclusions for those stimuli are based on the population study.

Not all synthetic stimuli were presented at each recording site. The total number of recording sites for each stimulus is specified in each of the figure legends when the results are presented. Table1 summarizes the number of recording sites per bird and the number of sites where data were obtained for each of the four synthetic stimuli ensembles.

Table 1.

Distribution of recording sites per bird and per stimulus ensemble

Bird	# recording sites (selective)	AM songs	Relative phase	FM random phase	FM relative phase	Song duration (motifs)
Zfa_14	11  (9)	11  (9)	0	10  (9)	0	1.48/sec  (2)
Zfa_16	9  (7)	8  (6)	0	6  (5)	0	1.44/sec  (2)
Zfa_18	12  (10)	8  (8)	0	10  (8)	10  (8)	1.04/sec  (2)
Zfa_20	13  (8)	6  (5)	7  (6)	0	5  (5)	2.07/sec  (2)
Zfa_21	7  (6)	4  (3)	5  (5)	0	2  (2)	1.18/sec  (2)
Zfa_23	15  (14)	7  (6)	9  (9)	0	5  (5)	2.31/sec  (3)
Zfa_25	10  (9)	6  (5)	8  (7)	9  (8)	9  (8)	1.78/sec  (2)
Total	77  (63)	50  (42)	29  (27)	35  (30)	31  (28)

The table shows the number of recording sites inside the nucleus HVc from which data were acquired. The number inparenthesis is the number of recording sites that were selective for the BOS (d′ > 1 as explained in Materials and Methods and Results). The first column shows the distribution per bird. The second to fifth columns show the number of sites in which stimuli from each of the four families of synthetic songs were presented. The last column shows the length and the number of motifs for each song.

Neural response characterization

The neural response to any given stimulus was expressed as aZ score. The Z score is given by the difference between the firing rate during the stimulus and that during the background divided by the SD of this difference quantity:

$$Z=\frac{{\mu }_S-{\mu }_{BG}}{\sqrt{\text{Var}(S)+\text{Var}(BG)-2\text{Covar}(S,BG)}},$$

where μ_S is the mean response during the stimulus (S) and μ_BG is the mean response during the background (BG). The denominator is the equation for the SD of S − BG. The background was estimated by averaging the firing rate during the 2 sec period before the stimulus. For each unit, the Z score for the response to any stimulus was then compared with the Zscore for the response to the BOS by calculating the ratio of these two values. The Z score was in most cases larger for the BOS than for any other stimuli, so that the fraction of the BOSZ score is also an estimate of the response relative to the maximal response. The fractions for different units were then averaged to generate a result for the entire data set.

We also used the psychophysical measure d′ (Green and Swets, 1966) to estimate the strength of the selectivity of the recorded neurons. The selectivity of HVc neurons is determined by their response to the BOS in comparison with their response to conspecific songs or to the BOS played in reverse. We calculated the d′ to estimate the difference between such responses. The d′ value for the discriminability between stimuli i and j is calculated as:

$$d^{\prime }=\frac{2({\overline{R}}_i-{\overline{R}}_j)}{\sqrt{{\varsigma }_i^2+{\varsigma }_j^2}},$$

where R is the response to a given stimulus.$\overline{R}$ is the mean value of R, and ς is its SD. We took R to be S − BG. The d′ value for neuronal responses can be compared with psychophysical or behavioral responses in a forced-choice paradigm [see, for example,Delgutte (1996)]. For our purposes, d′ is the simplest measure of selectivity that takes into account not only the estimate of mean responses but also their variance.

RESULTS

Song selectivity

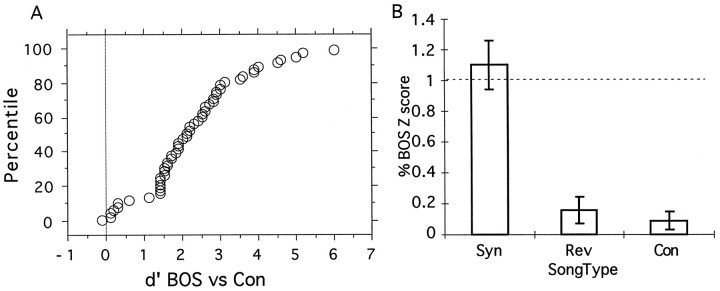
In this paper, we were interested in quantifying the selectivity seen in HVc neurons. Our goal was to find what aspects of the acoustical structure inherent to all songs are essential to obtain neural responses and to measure the sensitivity of the neurons to systematic degradation of the necessary structure. The first step in our analysis involved measuring the classic song selectivity of the auditory neurons recorded in the experiments. A rigorous quantification of the selectivity was needed to compare our responses with those found in previous work and to select a group of neurons from our data set that we determined to be highly song selective. The song selectivity in HVc neurons has been characterized by a much stronger mean response to the BOS than to songs from conspecifics or to the BOS played in reverse (Margoliash, 1986; Margoliash et al., 1994; Lewicki and Arthur, 1996;Volman, 1996). To also take into account the variance seen in the responses, we chose to quantify the degree of selectivity by calculating the psychophysical measure of discrimination d′(see Materials and Methods).

Figure 4A shows the cumulative probability distribution of the d′ measure for BOS versus conspecific song for all the recording sites in our data set. The mean d′ value is 2.3 with 86% of the recording sites showing a selectivity greater than d′ = 1.0. These values are not necessarily representative of all auditory neurons in HVc because we did not attempt to map the nucleus in a systematic manner. For certain recording sites, the responses to conspecific songs were missing, but we had data to characterize the selectivity of BOS versus BOS played in reverse. In either case, all neural recordings for which d′ was >1 were classified as song selective.

Fig. 4.

A, Cumulative probability distribution of the measure d′ from signal detection theory for the discriminability between the BOS and conspecific songs (Con), calculated from the neural responses obtained at 54 recording sites. B, Response, measured as a percent of the response to the BOS, for the synthetic song that preserved all of the parameters obtained in our decomposition (Syn), for the song played in reverse (Rev), and for conspecific songs (Con). The data are obtained fromn = 30 for Syn,n = 39 for Rev, andn = 47 for Con (nrefers to the number of recording sites). The error bars show 1 SEM.

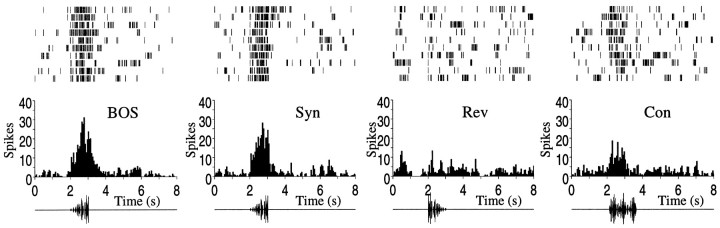
Figure 4B shows the mean relative Z score of all song-selective responses to conspecific songs and to the BOS played in reverse. The response to these stimuli was close to zero. Figure 4B also shows the mean response to the synthesized BOS in which all parameters in the decomposition have been preserved (Syn). As expected, the response to Syn is statistically indistinguishable from the response to the BOS because the two stimuli are identical except for the overall bandpass filtering from 500 to 8000 Hz. Figure 5 shows the peristimulus spike time histogram (PSTH) and the single-spike train records from a single-unit recording for these four stimuli.

Fig. 5.

Individual spike rasters and peristimulus time histograms (top) for the response of a particular single unit in the HVc to the BOS, Syn,Rev, and Con stimuli (see Fig. 4). Oscillograms (waveform representations of the sound pressure) of the stimuli are shown below each histogram. Thed′ for this particular single unit was 1.5. As shown in Figure 4, ∼75% of the recording sites showed greater selectivity than did this particular neuron, and this neuron, despite its evident selectivity, is among the less selective members of the population that was used for the studies involving the synthetic stimuli (d′ > 1).

Time–frequency scale tuning

To investigate the spectral and temporal requirements of the song-selective neurons, we first generated synthetic songs that, when decomposed into defined frequency bands, had amplitude envelopes similar to that of the BOS in each frequency band. However, the time-varying phase of the signal in each band (which can also be expressed as a frequency modulation and absolute phase) was set to be different from the one in the original BOS and was randomized. By varying the width (and correspondingly the number) of the frequency bands, we generated a set of AM songs with systematically varying degradations of temporal versus spectral resolution (see Materials and Methods for more details). Figure 6 shows the spectrograms for a set of such AM songs, illustrating the trade-off between synthetic songs that preserve the time structure of the original song (AM-1 to AM-16) and synthetic songs that preserve the spectral structure of the original song (AM-16 to AM-256). Based on visual inspection, the synthetic songs in the middle values of the time–frequency scale (AM-16 or AM-32) show a good compromise, achieving seemingly minimal temporal and spectral degradation. We will come back to this issue in the next section.

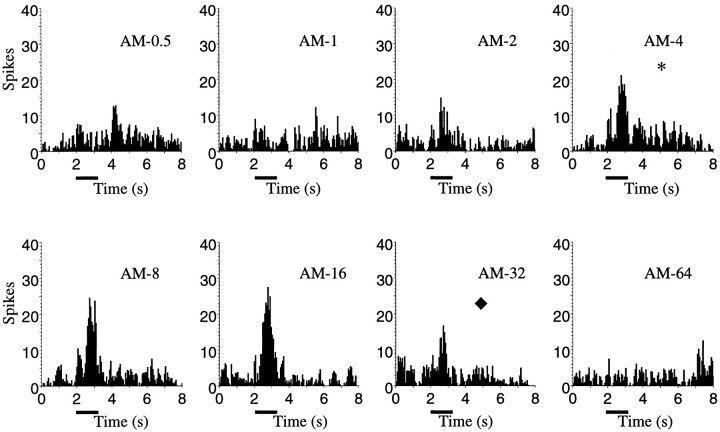
Figure 7 shows the PSTHs for a representative single unit obtained in response to eight AM songs generated with time windows ranging from 0.5 to 64 msec. The PSTHs in this figure can be compared with the ones obtained from the same unit in response to the original BOS and other songs shown in Figure 5. As the time window was increased, the responses of this particular neuron to the AM songs increased, peaked at ∼16 msec, and then decreased. The response to AM songs synthesized with time windows of <2 or >32 msec was indistinguishable from background activity. The maximal response obtained at 16 msec was slightly less than was the response to the BOS. Thus, this neuron showed good responses to synthetic songs based only on the amplitude envelopes, as long as these were obtained in a particular time–frequency range. This time–frequency scale included songs that, by visual inspection of the spectrograms of Figure 6, were good at representing both the spectral and temporal structure in song (AM-16 in Figs. 6, 7) but also included songs that showed substantial spectral degradation (AM-4 andAM-8 in Figs. 6, 7).

Fig. 7.

Peristimulus histograms for a single-unit recording in response to the set of AM songs spanning the range of time–frequency scales between 0.5 and 64 msec. The responses to AM songs generated with time windows of >64 msec were similar to those obtained at 64 msec. The stimuli started at t = 2 sec and lasted ∼1 sec. This single unit and song were from bird zfa_18. This neuron is the same as that of Figure 5. Thesymbols (*, ♦) indicate the time–frequency scale that gave the best neural response (*) and the best discrimination among songs (♦) (see Figs. 6, 8, 10).

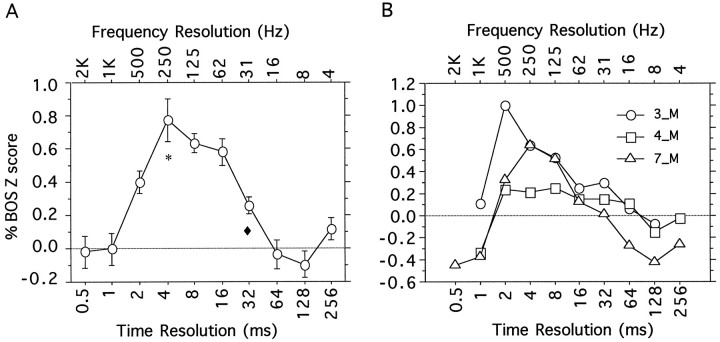
The mean relative Z score of all song-selective neuronal responses in our data set for the entire range of AM songs is shown in Figure 8A. All individual song-selective recording sites exhibited similar tuning, with responses that peaked at time–frequency scales between 2 and 16 msec. The exact location of the peak as well as the width of the tuning curve varied slightly across units, as exemplified in the three single-unit response traces shown in Figure 8B and in the example shown in Figure 7. This variability was present both in neuronal responses from the same bird (as shown here) or across birds.

Fig. 8.

A, Time–frequency tuning curve of HVc in response to AM song stimuli. The x-axis shows the time (bottom) or frequency (top) scale that was used to generate the AM song stimuli. The response is measured as a percent of the response to the BOS. The error bars show 1 SEM. The number of recording sites for each stimulus was n = 31 for t = 0.5 msec, n = 31 fort = 1.0 msec, n = 42 fort = 2.0 msec, n = 35 fort = 4.0 msec, n = 41 fort = 8.0 msec, n = 37 fort = 16 msec, n = 42 fort = 32 msec, n = 33 fort = 64 msec, n = 40 fort = 128 msec, and n = 25 fort = 256 msec. The symbols (*, ♦) indicate the time–frequency scale that gave the best neural response (*) and the best discrimination among songs (♦) (see Figs. 6, 7, 10).B, Time–frequency tuning curves for three different single units from an individual bird. The x- andy-axes are identical to those in A.

In all cases, the response at the extreme time–frequency scales was similar to or below background. The stimulus at the extreme time scale of 0.5 msec is similar to a broadband white noise stimulus modulated by the overall amplitude envelope of the BOS calculated with a 0.5 msec window. This stimulus is analogous to the noise stimulus defined inMargoliash and Fortune (1992). For that particular stimulus, our results are similar to theirs; they reported a weak response to noise syllables, and we found a weak or inhibitory response for the AM-0.5 synthetic song. At the other end of time–frequency scale, the synthetic song preserves the overall spectrum of the BOS, but because we randomized the phase of its frequency components, it has lost almost all of the original temporal modulations (Figs.2, 6); such a stimulus is often referred to as colored noise, as opposed to white noise that is characterized by a flat spectrum. As seen in Figure 8, this stimulus also elicited a weak or inhibitory response. The song played in reverse is another example of a synthetic stimulus that preserves the spectral quality of the song on the time scale of the song duration but distorts the temporal structure. In the song played in reverse, the temporal distortion is a very particular one, whereas the distortion from the random phase in the AM songs generates a systematically degraded version of the original temporal envelope (see Materials and Methods).

Neither AM song with a very precise temporal profile nor AM song with a highly precise spectral profile elicited a positive response, and in some cases these stimuli even inhibited the cells. However, as we moved from one time–frequency extreme to the other, the response to the AM synthetic songs traced a smooth tuning curve, reflecting a graded sensitivity to the temporal–spectral precision trade-off inherent in these synthetic AM songs. The responses were the largest for time–frequency scales between 4 and 16 msec. The mean response at the peak time–frequency scale of 4 msec was on average 77 ± 13% (± SEM) of the response to the BOS. Most individual neuronal responses also showed a response at the peak of their tuning that was high but still below that of the BOS; 83% of the recording sites hadZ scores below the value of their Z score to the BOS. A one-tail paired t test comparing the meanZ score obtained for the AM-4 songs and the meanZ score for the BOS shows that the mean for AM-4 is clearly below the mean for BOS (n = 34; t = −4.264; p = 0.0001).

In summary, HVc neurons show a strong response to synthetic songs that preserve only the amplitude envelopes of a filter bank decomposition of the original song, but only do so for a range of time–frequency scales between 4 and 16 msec (250–62 Hz). On visual inspection, it appears that some of the synthetic songs that gave the best neural responses were also the ones that were in some sense most like the original signal. On the other hand, we also found large responses to synthetic songs that apparently had large amounts of spectral degradation. In the next section, we will attempt to quantify these observations about how the different AM songs characterize the acoustical structure in the song and how this compares with neural responses. It is also true that even the responses for the optimal time–frequency scales were still below those of the original song, reflecting the fact that HVc song-selective neurons are sensitive to additional temporal and spectral structure of the original song that was not reflected in these AM songs (see Materials and Methods). The nature of the missing structure and the sensitivity of the neurons to the gradual restoration of this structure will be addressed in a subsequent section.

Relative preference for temporal cues

The next goal in our analysis was therefore to compare the time–frequency scale tuning of HVc neurons with the time–frequency scale that would best characterize the acoustical structure in song obtained in an independent manner. For instance, it is well known that a given sound is best represented in a spectrogram when this spectrogram is calculated at a particular time–frequency scale. For example, on visual inspection, the acoustical structure of the zebra finch song shown in Figure 2 seems best represented by the spectrogram calculated with a 16 msec window. Similarly, when we look at the spectrograms of the synthetic songs generated from amplitude envelopes of the BOS obtained from a range of time windows such as those shown in Figure 6, we can visually decide on a time window that seems to be the best at characterizing the structure present in the original song. In general, the optimal time window depends on the properties both of the acoustical signal and of the particular acoustical features that are of interest. Optimally, we would like to base our criteria for the “best representation” not necessarily on all the information that could be extracted from the spectrogram (or the set of amplitude envelopes), but on the aspects of that information that represent the behaviorally relevant bioacoustical structure of zebra finch song. To do so, one might want to evaluate the quality of AM songs generated at different time–frequency scales by testing the efficacy of the songs in eliciting the appropriate natural behaviors.

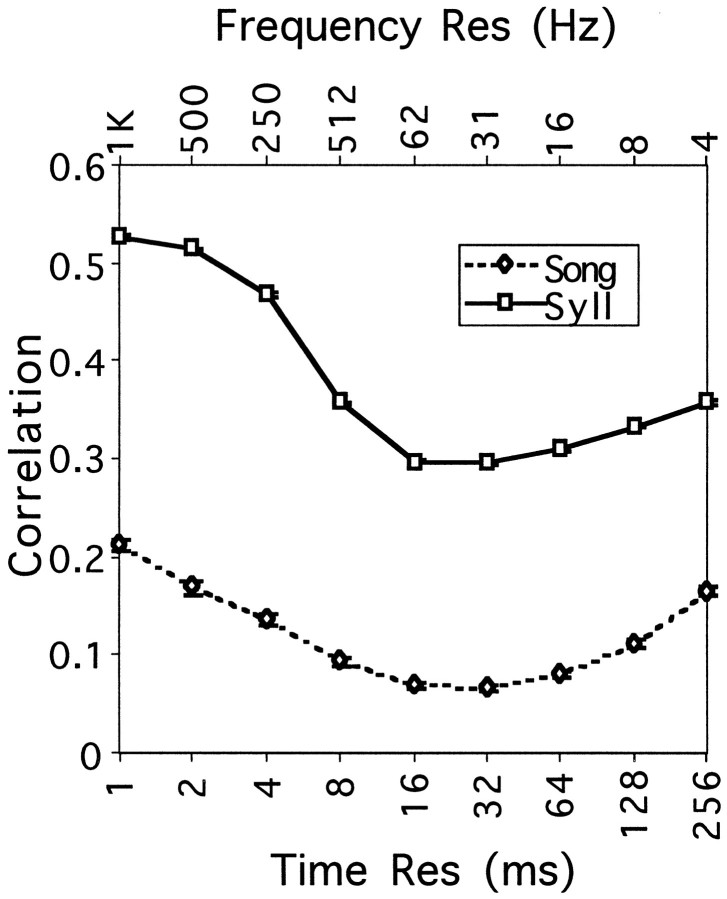
Short of this, we estimated the time window at which a simple measure of discrimination based on the spectrogram would give us the most information and enable us to distinguish songs from different zebra finches. Our measure of discrimination was based on the cross-correlation between the amplitude envelopes of the different songs (i.e., C_A). We calculated the pairwise correlations between 16 zebra finch songs from our colony (120 comparisons) and between the syllables in each of the songs that were the most similar (n = 2031). The correlations were calculated for a range of time scales from 1 to 256 msec and are shown in Figure 9.

Fig. 9.

Cross-correlation between amplitude envelopes calculated at different time–frequency scales for songs (Song) and syllables (Syll) from different birds. Sixteen different songs were used, resulting in 120 pairwise correlation measures for songs and over 2000 pairwise comparisons for syllables. Low values of cross-correlation indicate large differences between signals and therefore show the time–frequency scales that are best at discriminating among zebra finch songs. The error bars showing 1 SEM are smaller than the size of the markers.

The cross-correlation measure shows a tuning with a minimum at 32 msec. This minimum point corresponds to the time–frequency scale at which the amplitude envelopes of the two songs are the most different according to the cross-correlation measure (other measures based on higher order statistics might give slightly different answers). This quantitative measure matches our visual estimates of the “best” spectrograms in Figures 2 and 6. Note that, in contrast to the AM songs used in the physiology, in this calculation the amplitude envelopes are not distorted because new synthetic songs were not generated in the process. Moreover, the amplitude envelopes (or the spectrogram) obtained from the original decomposition using our overlapping filters completely characterize the original songs, except for an absolute phase. The same information about the identity of each song is therefore present in the amplitude envelopes at any time–frequency scale but in a different form. At particular (optimal) time–frequency scales, the temporal and spectral structure that is most useful in distinguishing between songs is encoded in large fluctuations in each of the envelopes. At other time–frequency scales, the same temporal and spectral structure can only be recovered by examining the joint small fluctuations in the envelopes from multiple bands (see Materials and Methods). This is the effect that we are quantifying with the measure of cross-correlation between amplitude envelopes. For the same reason, the noise added to the amplitude envelopes of the AM songs at those optimal time–frequency scales by randomizing the phase has the smallest effect in altering the time–frequency structure of the signal, as illustrated in Figures 2 and 6.

One might expect the time–frequency scale of individual syllables to be different from that of an entire song, because a large fraction of the temporal complexity of a full song is attributable to the more or less precise sequence of syllables and silences. In fact, the curves for song and syllable shown in Figure 9 peak at around the same point. The effect of the overall temporal pattern in the entire song is nevertheless reflected in the relatively larger width of the curve for discriminations based on the entire song, particularly at finer time resolutions; there the overall temporal pattern given by the sequence of syllables still allows one to discriminate across songs. In contrast, as the time resolution is made finer, all individual syllables begin to resemble each other, being described by a few Gaussian-shaped amplitude envelopes.

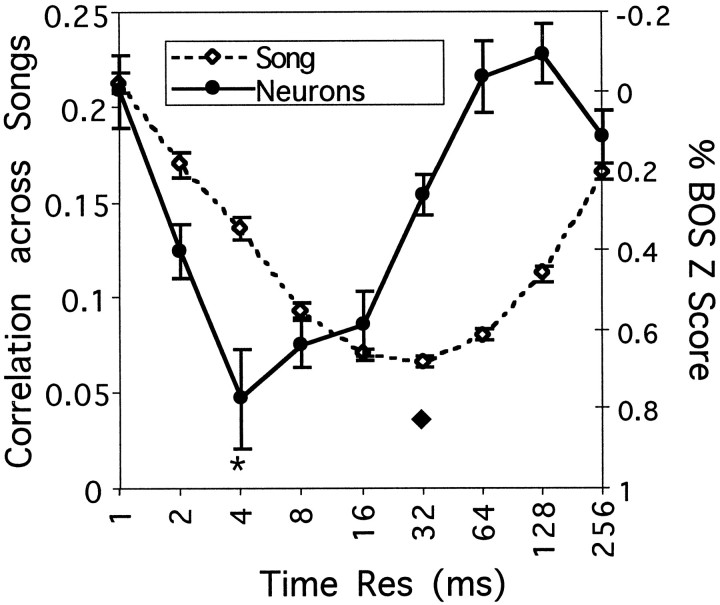
The time–frequency tuning of the correlation measure can now be compared with the time–frequency tuning of HVc neurons to the AM songs shown in Figure 8. The two curves are plotted together in Figure10 to facilitate the comparison. Thesymbols (*, ♦) in Figures 6-8 and 10 indicate the time-scales for the peak of the averaged neural responses (*) and for the peak of the average discrimination based on the cross-correlation measure (♦). The symbols are used to facilitate further the comparison between all of the figures, but note that the strength of the neural response at the 4 msec peak is not significantly different from those at 8 and 16 msec. However, it is clear that the two curves are shifted along the time–frequency axis. To test whether this shift was significant, we compared the distribution of peaks in neuronal responses with the distribution of minima in the cross-correlation values. The distribution of neural sites with peak responses at the different time scales was as follows: 4, 13, 16, and 8 sites at 2, 4, 8, and 16 msec, respectively (total = 41 neurons). The distribution of minima in the cross-correlation was 5, 42, 66, 6, and 1 song pairs at 8, 16, 32, 64, and 128 msec, respectively (total = 120). A Kolmogorov–Smirnov test (insensitive to the logarithmic scale) shows that these two distributions are different from each other with high statistical significance (p < 0.0001). The mean time–frequency value for neuronal peak is 7.7 msec, whereas the mean time–frequency value for minimum cross-correlation is 27.8 msec. A one-tail t test done both with and without a log transform shows that these two means are statistically different (p < 0.0001 in both cases). The difference is striking when one compares the spectrograms for the AM-4 song that elicited a maximal response in 13 of 41 recording sites with the spectrogram for the AM-32 song that elicited no peak responses and small average responses overall (Fig. 6).

Fig. 10.

Comparison of the cross-correlation measure for song similarity and of the response of HVc neurons as a function of the time–frequency scale. The data in Figures 8A and 9 are plotted together to facilitate the comparison. Note that theright y-axis for the neural response has been inverted and that the left y-axis for the cross-correlation among songs has been expanded. The symbols (*, ♦) indicate the time–frequency scale that gave the best neural response (*) and the best discrimination among songs (♦). The samesymbols are used in Figures 6-8.

Note, however, that the curves showing discriminability as a function of time–frequency scale (Figs. 9, 10) reflect the average time–frequency scale of the entire song and of all types of syllables. Individual syllables, or different parts of the entire song, might be best characterized at different time–frequency scales, and the neurons might be more tuned to such segments of songs. If so, we might expect that these segments of songs are best characterized by time resolutions finer than the average. Despite the significant shift toward finer temporal resolution of the neural responses, the large overlap between the two curves in Figure 10 also suggests that the spectral and temporal requirements of the neurons make them effective encoders of the specific acoustical structure present in the song.

Relative phase and fine tuning

To investigate further the absolute sensitivity of the neurons to the precise spectral–temporal quality of the BOS, we generated a second set of synthetic songs that preserved greater temporal–spectral information than did the AM songs. The AM songs deviate from the original BOS in two ways. Their amplitude envelopes calculated at any time scale are slightly different (C_A = 0.737 ± 0.003), and they have different fine structure, which is reflected by a different FM and a different and random absolute phase. In these experiments, we generated synthetic songs that had amplitude envelopes that were progressively closer to those of the BOS. We restored the quality of the amplitude envelopes by restoring the relative instantaneous phase across frequency bands with various degrees of precision. Restoring the relative phase will, at the same time, restore the FM. When the relative phase is preserved exactly, only a single absolute phase remains arbitrary and in these stimuli is random (RAP song). The other synthetic songs in this set are characterized by the precision with which the relative instantaneous phase is preserved, which can be expressed in time units (see Materials and Methods for details). The effect of preserving the relative phase on the representation of the amplitude envelopes was estimated by calculating C_A between the synthetic and the original BOS.

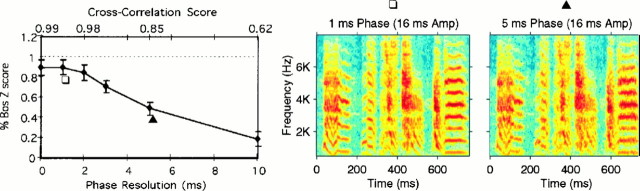
The average neuronal response of our data set to these stimuli is shown in Figure 11. The relative phase in the synthetic songs was progressively restored by decreasing the phase resolution toward zero (reading the curve on the graph fromright to left). As the relative phase was restored from being almost completely random at 10 msec to being exactly preserved at 0 msec, the response increased almost linearly, approaching 100% for phase resolution values finer than 2.0 msec. A paired t test was used to compare the differences in means between the Z scores obtained for the synthetic songs and the corresponding Z scores obtained for the BOS. For 95% confidence, the mean in the responses for phase resolutions finer than 2 msec is not statistically different from the mean in the responses for the BOS (p = 0.03, p = 0.06, and p = 0.14 for t = 2,t = 1, and t = 0 msec, respectively).

Fig. 11.

Left, Mean HVc response curve to the synthetic songs that preserved the instantaneous relative phase across frequency bands with different degrees of accuracy. Thebottom x-axis shows the resolution expressed as 1 SD of relative phase noise (in units of milliseconds) that was added to each band. The top x-axis shows the normalized cross-correlation between the amplitude envelope of the synthetic songs and that of the original song. The error bars show 1 SEM. The number of recording sites for each point was n = 43 fort = 0.0 msec, n = 25 fort = 1.0 msec, n = 25 fort = 2.0 msec, n = 23 fort = 3.0 msec, n = 27 fort = 5.0 msec, and n = 26 fort = 10 msec. Middle,Right, Spectrograms of sections of a typical synthetic song with 1 msec (middle) and 5 msec (right) relative phase precision. The song shown is the same as that in Figures 2 and 6. The symbols are used to indicate the corresponding points in the leftcurve.

At 2 msec phase resolution, there was high fidelity in the representation of the overlapping amplitude envelopes of the BOS, expressed by a C_A of 0.976 ± 0.002. This extreme sensitivity of the neurons is also evident in the spectrographic representations of the songs for 5 and 1 msec shown in Figure 11, which illustrate how subtle the differences between these songs are, although these stimuli elicit very different levels of response.

As an extension of these results, we found that the absolute phase has no detectable effect on the response of the neurons; the response to the RAP stimulus (the 0 msec point on the graph in Fig. 11,left) is statistically similar to the one obtained in response to the BOS.

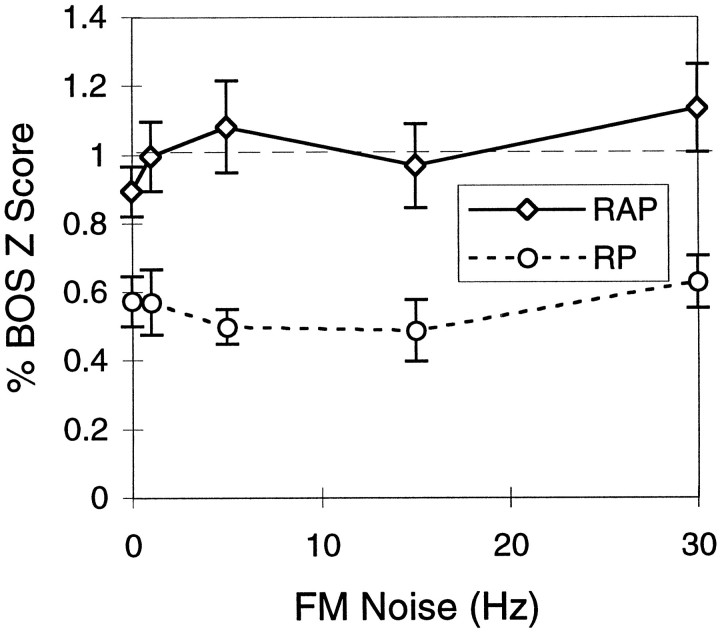
FM tuning

In this third series of neuronal experiments, we tested the effect on the response of the neurons of the preservation of various amounts of the original FM, independent of the restoration of the relative instantaneous phase. With a first set of synthetic FM songs, we examined the effect of perturbing the FM component while preserving the relative phase across frequency bands and therefore also preserving the high level of accuracy in the amplitude envelopes. To do so, we added the same FM noise to all frequency bands (see Materials and Methods). As shown in Figure 12 (solid curve), the response of the neurons is remarkably unaffected by the addition of correlated FM noise. We could not detect any significant differences in the response to the synthetic song and to the BOS for FM noise values up to 30 Hz. Note that the stimulus for 0 Hz noise is again the RAP song. Also note that none of these synthetic FM songs, irrespective of their FM noise, preserved the absolute phase of the original signal. Therefore, these data also constitute more evidence that these auditory neurons are not sensitive to the absolute phase of the signal.

Fig. 12.

Mean HVc response curves to synthetic songs that had various amounts of FM noise added to each frequency band. Thex-axis shows the amount of noise expressed as 1 SD of the additive Gaussian noise. The RAP stimuli were generated by adding the same FM noise to each band and therefore preserving the relative instantaneous phase (n = 43 for FM = 0,n = 22 for FM = 1, n = 23 for FM = 5, n = 23 for FM = 15, andn = 25 for FM = 30). The RP stimuli had different FM noise added in each band (n = 28 for FM = 0, n = 24 for FM = 1,n = 25 for FM = 5, n = 15 for FM = 15, and n = 26 for FM = 30). For both cases, the absolute phase was random. The error bars show 1 SEM.

The second question was whether restoring the FM in the AM songs without restoring the relative phase would improve the neural response. To answer this question, we effectively reduced the randomness of the FM by varying the amount of FM noise that was added to the actual FM profile of the song from a large amount (30 Hz) to zero (reading the graph from right to left). The relative phase across bands was not preserved because different FM noise and a different absolute phase were used for each frequency band (see Materials and Methods). As shown in Figure 12 (dotted curve), restoring the FM component had no effect on improving the response of the neurons; there were no changes in the response in going from the completely random FM of the AM songs to synthetic songs for which, in the synthesis, we used the actual FM from the BOS but ignored the relative phase (the RP song). Note that, here again, when the synthetic stimulus is generated by summing the signals from the complete set of overlapping frequency bands, the AM and FM components will be slightly distorted. However, the distortion in the AM component as measured with the cross-correlation decreased as the FM noise decreased. The C_A for the synthetic song generated with 0 Hz FM noise and random relative phase is 0.8 ± 0.02 compared with 0.7 ± 0.01 for the AM song at 16 msec. In this case, the slight improvement in the AM representation did not lead to an increase in the neural response.

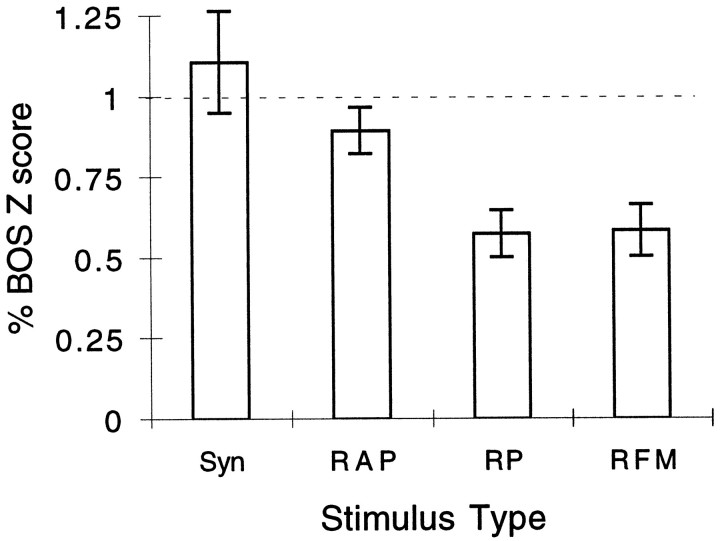
Because the FM variations described above had no effect on the neural response, we can summarize the effect of preserving various aspects of the instantaneous phase by looking at the responses to four stimuli. The AM-16 (called RFM) song yielded a response that was on average half of that of the BOS. A synthetic stimulus generated with the actual FM component but a random phase in each band (RP) yielded the same response as the AM-16 song. Restoring the relative phase but leaving an absolute phase random (RAP) yielded identical responses to the synthetic song that also preserved the absolute phase (Syn), and these responses were indistinguishable from the response to the original BOS. The mean responses to these four stimuli are shown in Figure13.

Fig. 13.

Summary response values for four synthetic songs that preserved various amounts of information embedded in the instantaneous phase. From right to left, the bars represent the average neural response to the following songs: RFM (random FM) is the AM song at 16 msec that has both random FM and absolute phase; RP song preserves the FM in each band but does not preserve the relative phase;RAP song has the correct FM and relative phase but random absolute phase; and Syn is the synthetic song in which all of the parameters are preserved. The error bars show 1 SEM. The number of recording sites for each stimulus wasn = 37 for RFM,n = 28 for RP, n= 43 for RAP, and n = 30 forSyn.

DISCUSSION

Using systematically perturbed versions of the optimal song stimulus, we studied the song-selective properties of HVc neurons by quantifying the sensitivity of the neurons to parameters that describe the spectral and temporal structure present in the BOS. Such quantitative investigations of the tuning of HVc neurons are necessary to understand the form and amount of information that must be preserved from the auditory periphery to this high-level brain area, to constrain the mechanisms that give rise to song-selectivity, and ultimately to begin to explore possible roles of these neurons in perceptual tasks.

Parametric representation of a song

In addition to the use of ethologically based stimuli such as conspecific songs, simple temporal or spectral manipulations of song, such as reversing its order and breaking it into its component syllables, originally determined the importance of both spectral and temporal cues for the response of HVc neurons (cf. McCasland and Konishi, 1981; Margoliash, 1983, 1986). Ultimately, however, greater understanding of these complex sensory neurons also requires more systematic decomposition of acoustic signals, including graded manipulation of different parameters of these signals to assess their importance. Margoliash first showed the importance and power of this approach in his original characterization of the properties of HVc neurons in the white-crowned sparrow (Margoliash, 1983, 1986). In that work he used a parametric representation for the relatively tonal white-crowned song that was based on a single time-varying amplitude envelope and instantaneous frequency. Using this representation, he manufactured synthetic songs that preserved the amplitude envelope of the original song but had different time-varying frequency profiles. He showed that the neurons were sensitive to the actual frequency profiles of the song because they had much weaker responses to synthetic songs that used a constant frequency profile or in which the frequency profile was randomized within sections of the songs. He also showed that progressively increasing the frequency of the synthetic song would also result in a smaller response.

Our approach to parameterizing the song was to use a time–frequency grid to represent the original song. We then developed a methodology that allowed us to quantify precisely the amount of spectral and temporal distortion of any synthetic stimulus relative to the BOS. Moreover, we used this approach to sample the spectral and temporal resolutions in a systematic manner. Similar approaches have also been used in studies of speech psychophysics but only to study restricted ranges of temporal and spectral distortions (cf. Drullman, 1995;Shannon et al., 1995).

Our parametric representation of song was based on a decomposition of the song into its constituent signals obtained through a bank of frequency filters. Each narrowband signal could then be fully described by a relatively simple and mathematically tractable set of parameters: the time-varying amplitude envelope, the center frequency of the carrier signal, the frequency modulation of this signal, and its absolute phase (the latter three parameters constituting the instantaneous phase). By summing the narrowband signals to recreate song while systematically preserving or altering these parameters, we could generate a variety of synthetic songs that preserved the amplitude envelope of the entire song with various degrees of precision and use these to test HVc neurons. When all of the parameters were preserved, the synthetic song (Syn) was virtually identical to the original signal and elicited responses from the song-selective HVc neurons that were indistinguishable from those obtained in response to the original BOS.

Amplitude envelopes and temporal–spectral scale tuning

The amplitude envelopes of the narrowband signals in the different overlapping frequency bands carry both temporal and spectral information. The scale at which the amplitude envelopes are extracted determines the efficiency with which either the spectral or temporal structure is represented, with a trade-off between efficient spectral and efficient temporal representation. We characterized the tuning of HVc neurons to this temporal–spectral scale by measuring the response to synthetic songs that had amplitude envelopes similar to those of the original song in their gross detail, but the fine structure of which had been degraded. The neurons were tuned to the time–frequency scale parameter, showing no responses at time–frequency scale extremes and relatively large responses for values of ∼5 msec or 200 Hz.

The fact that the time–frequency response curve is bell-shaped confirms previous experimental studies showing that HVc neurons are sensitive to both the spectral and temporal content of the song. The importance of the temporal structure of song was demonstrated either with coarse manipulations of the stimulus such as playing the song in reverse or in reverse order (Margoliash, 1986; Volman, 1993; Margoliash et al., 1994; Lewicki, 1996; Lewicki and Arthur, 1996) or with finer manipulations that examined the effect of increasing the time between syllables in the song (Margoliash, 1983; Margoliash and Fortune, 1992). Margoliash and colleagues further characterized the importance of the spectral quality both in the white-crowned sparrow (as described above) and in the zebra finch (Margoliash and Fortune, 1992). In the work here, our systematic analysis also shows the full range of time–frequency scales that are needed to get appropriate neural responses. Moreover, as discussed below, our method allowed us to evaluate the relative importance of temporal versus spectral cues and to measure the absolute spectral and temporal sensitivity of the neurons.

At the peak of the tuning curve, the response to the AM song approached the response to the original BOS, showing that, as long as it is extracted at an optimal time scale, the coarse detail in the amplitude envelopes alone can carry a large fraction of the significant structure embedded in song and required by song-selective neurons.

Time–frequency tuning of HVc neurons and speech psychophysics

The effectiveness of a set of amplitude envelopes in representing the structure in complex acoustical signals, as seen here in the neural responses, is also evident in psychophysical experiments in speech intelligibility (Drullman, 1995; Drullman et al., 1995; Shannon et al., 1995) and in the common use of spectrograms to represent pictorially the structure of both human speech and animal sounds. In both cases, however, one has to decide on a time–frequency scale at which to calculate the amplitude envelopes. In psychophysical experiments, the scale is often chosen by using filters with a one-fourth octave bandwidth because this value matches the measured critical band of audition in humans (Flanagan and Christensen, 1980; Drullman, 1995). Shannon and colleagues have also shown that speech comprehension increases rapidly as the number of frequency bands is increased from one very wide band to a small number of still relatively wide bands, emphasizing the relative importance of temporal structure over spectral structure in speech comprehension (Shannon et al., 1995). For one-fourth octave bandwidth, speech comprehension is excellent and robust to large noise distortions (Drullman, 1995). We have found a correlate of these human perceptual results in the response of song-selective neurons of the HVc; their response increased rapidly from none to significant when we increased the number of frequency bands (and simultaneously decreased their bandwidth), and neurons responded well to spectrally degraded sounds generated with wide bandwidths (50% of maximum response at 500 Hz).

Moreover, we found that additional spectral information from frequency bands finer than 500 Hz could further increase neural responses, but that this increase was limited when the cost of temporal degradation overran the improvement in spectral resolution. From our experience with these synthetic songs, we would expect that in speech studies as well, if the widths of the frequency bands used were decreased even further, speech comprehension would showed a tuned response, improving at first and then deteriorating. A full characterization of the time–frequency trade-off has not yet been done in a speech intelligibility experiment. The optimal time–frequency scale for other species (including other songbirds or humans) might also be different from the peak tuning that we measured for zebra finches, reflecting differences both in the natural properties of the relevant vocalizations and possibly in sound processing by the respective auditory systems.

Neural preference for temporal cues

We also began to examine the natural spectral and temporal properties of zebra finch vocalizations to compare them with the spectral and temporal tuning of neural responses. We did so by calculating a measure of discriminability among a set of unrelated zebra finch songs, using only the amplitude envelopes describing each song. By calculating this measure for amplitude envelopes extracted at a range of time–frequency scales, we found that, just as there was an optimal scale for neural responses, there was a time–frequency scale for amplitude envelope extraction that gave the best discrimination between songs. Although the range of good time–frequency scales for song overlapped with the range that gave the best neuronal responses, the neurons showed significantly more sensitivity to temporal structure relative to spectral structure than did the song discrimination. This confirms the impression from the neurophysiology that songs with striking amounts of spectral degradation but good preservation of temporal cues still elicited neural responses. As proposed byMargoliash (1983) and in a different form by Lewicki and Konishi (1995), one of the mechanisms leading to song selectivity could involve the temporal interaction of excitatory and inhibitory responses to individual song syllables. Such mechanisms would be dependent on the precise timing of a succession of syllables. Although it is clear from our results and those of others (see above) that the song recognition mechanism also involves detecting the characteristic spectral structure of the individual syllables, the data here suggest that, on average, precise timing plays a more important role than precise spectral recognition.

We also examined the spectral sensitivity of HVc neurons in a different way, by testing their responses to synthetic songs to which various degrees of frequency modulation noise had been added. We found that, despite the high sensitivity of HVc neurons to the accurate representation of the amplitude envelopes, their response was remarkably unaffected by the addition of FM noise values of up to 30 Hz, regardless of whether the relative phase was preserved or not. The insensitivity to FM noise may have a correlate in the variability seen in the production of individual songs or in the degradations of sound propagation in natural environments (Wiley and Richards, 1982). Note that these large FM perturbations will undoubtedly be encoded at the auditory periphery and therefore must be filtered out in the auditory processing leading to the HVc.

Absolute spectral and temporal requirements

The responses of HVc neurons to AM songs at the best time–frequency scale were large but still significantly less than was the response obtained from the presentation of the BOS. The amplitude envelopes of the synthetic AM songs, however, were not exactly identical to those of the original BOS, because only the gross detail in the amplitude waveform was preserved. The characterization of the fine structure in the amplitude envelope also requires preservation of the relative phase across adjoining frequency bands. The relative phase had to be restored with an accuracy finer than 2 msec to obtain neuronal responses to synthetic songs that were identical to those to the BOS. At this spectral–temporal resolution, the amplitude envelope is preserved with high fidelity, as shown by cross-correlations of >98%. Our measures quantitatively characterize the threshold of the temporal–spectral resolution that needs to be preserved at all levels of auditory processing, from the auditory periphery to the nucleus HVc. This high spectral and temporal resolution implies that HVc neurons are sensitive to information that must be extracted at the temporal scales with better than 2 msec precision, while at the same time integrating over long periods of time to achieve the measured spectral resolution. Moreover, these neurons have very context-dependent responses and actually integrate over much longer periods of time, on the order of several hundreds of milliseconds (Margoliash, 1983; Margoliash and Fortune, 1992; Lewicki and Arthur, 1996). It is remarkable that these long integration times coexist with the requirement for fine temporal precision described here.

Studies of high-level cortical areas that could be potentially involved in representing and distinguishing among complex natural sounds such as speech or animal calls have described single neurons that, despite showing preferences for complex characteristics of natural sounds, are still relatively broad in their tuning and correspondingly somewhat insensitive to their precise spectral and temporal structure (Langner et al., 1981; Rauschecker et al., 1995; Wang et al., 1995). In such areas, the precise acoustical structure is presumably represented in the joint responses of many neurons, which makes the determination of absolute spectral and temporal requirements difficult. In contrast, our systematic characterization of very specialized auditory neurons revealed the high degree of temporal–spectral information needed for neural recognition of complex vocalizations. This high neural sensitivity is reminiscent of high-order cortical neurons that are specialists at other specific auditory tasks: the phase delay neurons involved in sound localization (Brugge and Merzenich, 1973; Reale and Brugge, 1990) and the echo delay neurons involved in bat echolocation (Suga, 1988; Dear et al., 1993). It seems likely that, if highly specialized cortical auditory neurons involved in processing the identity of complex animal vocalizations were to be found, they might have similar spectral–temporal sensitivity to those found in song-selective neurons.

Representation of time-frequency structure at the periphery

The efficient representation of the acoustical structure in song by amplitude envelopes may reflect the fact that, to a first approximation, simple linear filters are responsible both for producing complex vocalizations and for the initial processing of acoustical information by the auditory periphery. The peripheral auditory system, acting in part as a filter bank, extracts and neurally encodes a set of amplitude envelopes (Ruggero, 1992). The tuned responses of the high-level HVc neurons indicate that there is a time–frequency scale at which the amplitude envelopes carry the most information about the structure of song. The critical bandwidth of zebra finches measured behaviorally and the Q values of auditory nerve fibers of other birds imply auditory filter widths of ∼500 Hz at 2 kHz (Sachs et al., 1980; Okanoya and Dooling, 1987). The approximate match between the time–frequency scale tuning of HVc neurons and that of the auditory filters suggests that song is efficiently represented in the encoding of the amplitude envelopes generated at the periphery. Moreover, the best scale for distinguishing different zebra finch songs can be thought of as the time–frequency scale of the motor vocal output. The similarity between this vocal output time scale, that of the auditory periphery, and that of HVc neurons may reflect a coevolution in the perceptual and motor structures of the songbird.

The absolute fine spectral and temporal requirements of HVc neurons that we measured suggest further predictions about the form and quality of the representation of complex acoustical signals at the auditory periphery. In particular, because auditory filters overlap, as did our analysis filters, our results raise the possibility that the actual fine structure encoded by the phase-locked response to the carrier frequency of auditory nerves is not necessary to represent the significant structure in the BOS; the relative phase needs to be preserved with a certain degree of accuracy, but this information is present in redundant form in the precise representation of the amplitude envelopes. On the other hand, enough temporal precision must be preserved to be able to encode these time-varying envelopes with 98% accuracy or with finer than 2 msec resolution (with 62 Hz bandwidth filters).

As a caveat, we want to emphasize that we only characterized theaverage time–frequency scale of the auditory signals and therefore of the HVc responses. To understand further the implications of the time–frequency scale tuning of HVc neurons for processing in the auditory periphery, a more detailed characterization of the song based on a more realistic model would be required. Such a model would take into account the fact that multiple time–frequency scales are involved in auditory processing. The bandwidth of peripheral auditory filters varies approximately logarithmically with center frequency, such that, on average, different time–frequency scales are used for different frequency ranges (Moore and Patterson, 1986). Also, a range of time–frequency scales can be encoded at each center frequency by combining information from different neurons or by combining the encoding of the fine temporal information with that of the amplitude envelope. Finally, mechanisms such as adaptation and amplitude compression can lead to time–frequency scales that vary in time. Models of auditory processing that take into account some of the complexity observed in the auditory system have been proposed elsewhere (Lyon and Shamma, 1996).

It would also be interesting to investigate the level of temporal precision in the response of auditory nerve fibers that actually needs to be preserved in order to reconstruct the amplitude envelope of a complex signal with the degree of accuracy shown here to be necessary. The 2 msec resolution required for central responses is much longer that the precision needed to phase lock to high-frequency carrier signals but might be greater than the precision with which the mean firing rates of the ensemble of auditory nerve fibers encode amplitude envelopes. If so, one would have definitive proof that precise phase-locking information present at the auditory periphery is used not only for binaural sound localization (Konishi et al., 1988; Yin and Chan, 1988) but also in the monaural processing of complex sounds.