Predicting the Consequences of Our Own Actions: The Role of Sensorimotor Context Estimation

Abstract

During self-generated movement it is postulated that an efference copy of the descending motor command, in conjunction with an internal model of both the motor system and environment, enables us to predict the consequences of our own actions (von Helmholtz, 1867; Sperry, 1950;von Holst, 1954; Wolpert, 1997). Such a prediction is evident in the precise anticipatory modulation of grip force seen when one hand pushes on an object gripped in the other hand (Johansson and Westling, 1984;Flanagan and Wing, 1993). Here we show that self-generation is not in itself sufficient for such a prediction. We used two robots to simulate virtual objects held in one hand and acted on by the other. Precise predictive grip force modulation of the restraining hand was highly dependent on the sensory feedback to the hand producing the load. The results show that predictive modulation requires not only that the movement is self-generated, but also that the efference copy and sensory feedback are consistent with a specific context; in this case, the manipulation of a single object. We propose a novel computational mechanism whereby the CNS uses multiple internal models, each corresponding to a different sensorimotor context, to estimate the probability that the motor system is acting within each context.

The ability to predict the consequences of our own actions using an internal model of both the motor system and the external world has emerged as an important theoretical concept in motor control (Kawato et al., 1987; Jordan and Rumelhart, 1992; Jordan, 1995; Wolpert et al., 1995; Miall and Wolpert, 1996; Wolpert, 1997). Such models are known as forward models because they capture the forward or causal relationship between actions, as signaled by efference copy (Sperry, 1950; von Holst, 1954; Jeannerod et al., 1979), and outcomes. Such forward models may play a fundamental role in coordinative behavior. For example, to prevent an object held in a precision grip from slipping, sufficient grip force must be generated to counteract the load force exerted by the object. Despite sensory feedback delays associated with the detection of load force by the fingertips (Johansson and Westling, 1984), under both discrete (Johansson and Westling, 1984; Flanagan and Wing, 1993) and continuous (Flanagan and Wing, 1993, 1995) self-generated movement and when pulling on fixed objects (Johansson et al., 1992b), grip force is modulated in parallel with load force. Conversely, when the motion of the object is generated externally, grip force lags behind load force (Cole and Abbs, 1988; Johansson et al., 1992b). This suggests that for self-produced movements the CNS may use the motor command, in conjunction with internal models of both the arm and the object, to anticipate the resulting load force and thereby adjust grip force appropriately (Flanagan and Wing, 1997).

To assess the generality of such a predictive mechanism, we have examined the relationship between grip and load force when a sinusoidal load is applied to an object held in a fixed location by the right hand. The first experiment was designed to test the hypothesis that predictive grip force modulation will be observed provided the load force is self-generated. We examined conditions in which the load force was generated by motion of either the right or left hand. When the left hand generated the motion, it did so either directly on the object or indirectly by causing a robot, under joystick control, to exert the force on the object. We also examined a condition in which the sinusoidal load force was externally generated by a robot. Precise predictive grip force modulation was seen when either the right or left hand generated the load force directly. However, when the left hand produced the load force indirectly, via the joystick, there was no prediction. A significant lag between grip and load force was seen, similar to when the load was generated externally.

To examine the reasons for this lack of prediction, a second experiment was performed in which we examined the conditions necessary for prediction when the left hand generated the load force on the right hand by acting through a virtual object. Using the virtual object, simulated by two robots, we could dissociate the forces acting on each hand. The force acting on the active left hand relative to the right hand was parametrically varied. This allowed us to test the hypothesis that to use the motion of the left hand to generate precise predictive grip force modulation in the right hand, the hands must act through a physically realizable object. At one level of the force feedback parameter, the force feedback to each hand was equal and opposite, thereby simulating a normal physical object between the hands. Precise prediction was seen under this condition but smoothly deteriorated as the force feedback deviated from that consistent with a real, rigid object held between the hands.

MATERIALS AND METHODS

A total of 14 right-handed subjects (age range, 21–30 years), who were naive to the issues involved in the research, gave their informed consent and participated in the study. Nine subjects (six male, three female) participated in the first experiment. Nine subjects (six male, three female) participated in the second experiment, including four of the subjects who had participated in the first experiment. The experiments were performed 1 month apart.

Apparatus. Subjects sat at a table and gripped a cylindrical object (radius, 1 cm; width, 4 cm) with the tips of their right thumb and index finger (Fig. 1). The forearm was supported on the table and stabilized using velcro straps. The hand was further stabilized by requiring subjects to grasp a vertically oriented aluminum rod (diameter, 2 cm) with their three ulnar fingers. The mass of the gripped object (50 gm) was centered midway between the two grip surfaces, which were covered with sandpaper (No. 240). A six-axis force transducer (Nano ATI) embedded within the object allowed the translational forces (and torques) to be recorded with an accuracy of 0.05 N, including cross-talk. The forces and torques were sampled at 250 Hz by a CED 1401plus data acquisition system. The data were stored for later analysis and were also used on-line during the experiments. Grip force was measured perpendicular to the plane of the grip surface and load force tangential to this plane.

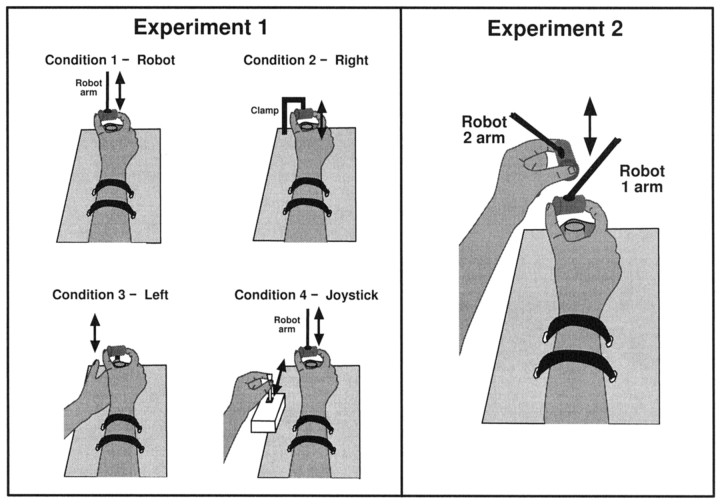
Fig. 1.

Schematic diagram of the apparatus used in each condition of Experiment 1 and in Experiment 2. Experiment 1: In all conditions subjects held a cylindrical object in their right hand. In condition 1 (Robot), the object was attached to the robot, which produced the load force on the object. In condition 2 (self-produced; right hand), subjects were required to pull down on the object, which was fixed in a clamp, to track the target load waveform. In condition 3 (self-produced; left hand), subjects were required to push the object upward from underneath with their left index finger to match the target load waveform. In condition 4 (self-produced; joystick), the object was attached to the robot and the forces produced by the robot were determined by the position of a joystick moved by the left hand. Experiment 2: An object attached to a second robotic device was held in the left hand. The motion of the left hand determined the load force on the object in the right hand. The relationship between the force acting on the left and right objects was parametrically varied between trials. See text for details.

Procedure. In all experiments the target and actual load force acting on the right hand were displayed to the subject as a continuous scrolling trace on an oscilloscope. The target load force acted as a guide to the subjects’ movements; the subject was instructed to produce a load force that corresponded to the frequency and amplitude of the sinusoidal target waveform. For clarity, the load force produced by the subject was displayed on the oscilloscope below the target waveform. Two horizontal lines indicated the desired load amplitude.

In conditions 1 and 4 of Experiment 1 and in Experiment 2 the object was attached at its midpoint to the end of a lightweight, robotic manipulator (Phantom Haptic Interface, Sensable Devices, Cambridge, MA). The robot could generate vertical forces up to 10 N.

Experiment 1. Subjects performed trials of 14 sec in which they were required to produce a load force that matched the target load force. The target load force was a sinusoid with offset of 3.5 N and amplitude of 3 N. The target load force, therefore, varied between 0.5 and 6.5 N, and always acted in an upward direction on the subjects’ right hand. In all conditions, subjects were instructed to hold onto the object with their right hand and maintain it in a constant position. For each trial the target frequency was fixed. Six different target frequencies equally spaced between 0.5 and 3.5 Hz were each repeated five times in pseudorandom order. To prevent the analysis of initial transients, 10 sec of data were recorded after the first 4 sec of each trial. Subjects practiced each condition until they could perform the task adequately. This took between 30 and 60 sec.

In condition 1 (externally produced; robot, Fig. 1), the object was attached to the robot, which was programmed to produce the target waveform. Subjects gripped the object with their right hand and were required to restrain the object, and the target and actual load force were displayed on the oscilloscope. In this condition the subject did not need to track the load force because this was generated automatically by the robot. In condition 2 (self-produced; right hand), subjects gripped the object, which was fixed in a clamp, with their right hand. They were required to pull down on the object to track the target load waveform so that the force acting on their right hand was in an upward direction. In condition 3 (self-produced; left hand), subjects were required to push the object upward from underneath with their left index finger to match the target load waveform. Subjects were specifically instructed to use their right hand to restrain the object only, and to avoid using it to push down on the object to match the target waveform. In condition 4 (selfproduced; joystick), the object was attached to the robot, and the forces produced by the robot were determined by the position of a low-friction joystick held in the left hand. The force generated by the robot was linearly related to the angular position of the joystick with a movement of 4° (4 mm) producing 1 N. Subjects were required to move the joystick in the sagittal plane to match the target waveform and were informed that movements of the joystick caused the force exerted on their right hand. The order of the conditions was counterbalanced between subjects.

Experiment 2: virtual objects. The object in the right hand was attached to the robot, and subjects held a second object in a precision grip with the thumb and index finger of their left hand. This object was held directly above the first and was attached to a second robotic device (Fig. 1). Subjects were required to move the object held in their left hand vertically to produce the load force on the object held in their right hand. The load force acting on the right hand was the same for all trials.

Vertical forces at time t into the trial were generated independently on both the right handF_t^r and the left handF_t^l. For all trials the relationship between movement of the left hand and the force generated on the right object was simulated, by the robot, as a stiff spring between the objects. The force was given by F_t^r =K (L_t − R_t −D), where L_t andR_t were the vertical positions of the left and right object, respectively, at time t, K was a fixed spring constant of 20 N cm⁻¹, and D was the initial vertical distance between the objects at the start of the trial. Hence, at the start of each trial there was no force acting on the right hand (as L₀ −R₀ − D = 0), and an upward movement of the left hand caused an upward force on the object in the right hand. The force acting on the left hand depended on a feedback gain parameter g, which could be varied between trials such that F_t^l = −gK(L_t − R_t −D). When g = 0, the left hand received no force feedback, whereas when g = 1, the force feedback to the left hand was equal and opposite to that exerted on the right. These conditions are similar, in terms of haptic feedback to the left hand, to conditions 4 (self-produced; joystick) and 3 (self-produced; left hand) of Experiment 1, respectively.

For each block of trials, the value of the feedback gain parameterg was fixed at one of seven values equally spaced between 0 and 1.5. Within each block, for gains of 0 and 1, six different target frequencies equally spaced between 0.5 and 3.5 Hz were used as in Experiment 1. For each of the other gain values (0.25, 0.5, 0.75, 1.25, and 1.5), three different target frequencies (1.1, 2.3, and 3.5 Hz) were used. Each frequency was presented for 10 sec and repeated five times in pseudorandom order; data were recorded after 2 sec in each trial. Subjects were told that load on the object held in their right hand was produced by the movements of their left hand. They were instructed to move the object in their left hand to match the target waveform whose amplitude was 2 N with offset 2.3 N. The load force therefore varied between 0.3 and 4.3 N and was always in an upward direction. Subjects practiced the task until they could perform it adequately. This took between 1 and 2 min.

Data analysis. Load and grip force were filtered using a Butterworth 5th order, zero phase lag, low-pass filter with a 10 Hz cut-off. To analyze the relationship between these two time series, cross-spectral analysis was performed using Welch’s averaged periodogram method (window width, 512 points with a 50% overlap; Matlab signal analysis toolbox).

Because the time series were predominantly sinusoidal, we calculated five measures at the dominant load frequency. To quantify amplitude relationships between the two signals, independent of the phase relationship, two measures were used. The baseline gain was taken as the ratio of the mean grip and load force ( grip/ load). The relative degree of modulation was quantified by the amplitude gaintaken as the ratio between the amplitude of the grip and load force modulation. To quantify the relative temporal relationships between the grip and load force series, three measures were made. The first two,phase and lag, quantify the temporal shift required to align the two series. Phase is expressed in degrees and was taken to lie between −270 and +90°, with negative values corresponding to grip lagging behind load. This split was chosen at a point where there were very few data points; based on all the data, only 0.9% lay within a 45° band of +90°. The lag represents the same shift in milliseconds (and should not be confused with phase lag that is used to measure phase delays in degrees), and again a negative value indicates grip lagging behind load. Finally, thecoherence of the two signals was used as a measure of the variability of the phase relationship between grip and load force. Coherence values always lie between 0 and 1. If the phase difference is constant over the entire trial, coherence is 1, whereas fluctuations in the phase difference results in coherence values lower than 1.

For each condition in Experiment 1 and for the g = 0 and g = 1 conditions of Experiment 2, the five measures were averaged across all trials and subjects, binned by frequency, and plotted with SE bars. Actual rather than target frequency of tracking was used when calculating statistics and plotting graphs.

In Experiment 1, average values across frequencies and linear regression as a function of load force frequency were used to test the influence of frequency and condition on the five measures. To test the influence of frequency on a particular measure and condition, separate linear regressions were performed for each of the nine subjects, and paired t tests were performed across the slope estimates. To compare the parameters between conditions, paired t tests, by subject, were performed on these parameters. To test the mean levels across all frequencies, paired t tests were performed for each subject mean within a condition and between conditions.

In Experiment 2, a repeated-measures ANOVA was performed on each measure as a function of the gain g (as categorical variables). A polynomial contrast was used to determine whether there were significant linear, quadratic, or higher order trends across the gains g. The highest order polynomial for which this was true was used to fit the ensemble data for individual and combined frequencies. For all plots for which a quadratic regression significantly fitted the data, the g value at which the quadratic peaked was calculated and t tests were performed to test whether this point differed significantly from 1 across the subjects. The value of the peak of the quadratic was also calculated.

RESULTS

After practice each subject was able to track the desired load waveform with reasonable accuracy and produced load forces that were predominately sinusoidal with narrow power spectra around their dominant frequency. The grip forces were also predominantly sinusoidal. In particular, the modulation was smooth and showed little evidence of catch-up responses, which have been reported to occur to unpredictable onsets of load force (Johansson et al., 1992b).

Experiment 1

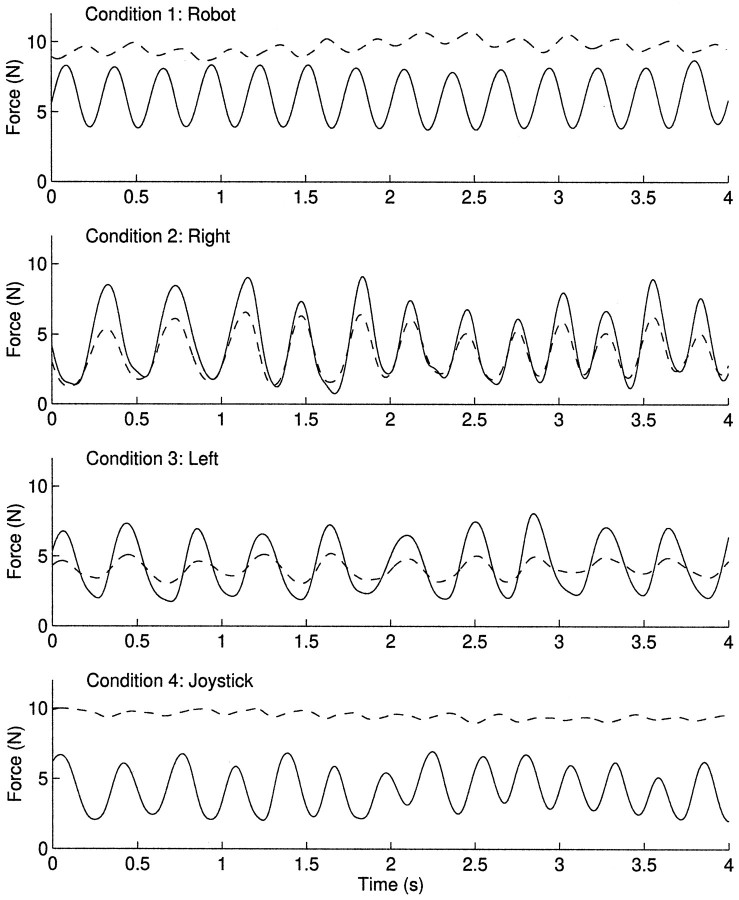
Typical raw data for the four conditions are shown in Figure2. These traces show that when the load force was generated externally by the robot, the mean grip force level was high, showed low modulation, and lagged behind the load force (Fig.2, Condition 1). In contrast, when the load force was self-generated by the right hand, the mean grip force level was lower, showed a large degree of modulation, and appeared in phase with the load force (Fig. 2, Condition 2). When the left hand was used to generate the load, a predictive modulation was seen similar to that in the right hand condition, but with a smaller amplitude of modulation (Fig. 2, Condition 3). However, when the left hand generated the load force indirectly through the joystick, the pattern of grip force modulation was similar to that of the externally generated condition (Fig. 2, Condition 4).

Fig. 2.

Typical example of grip force (dashed line) and load force (solid line) traces for the four conditions of Experiment 1 taken from a single subject tracking a frequency of 3.5 Hz. The data are taken from the same 4 sec time period in each trial and have been low pass-filtered.

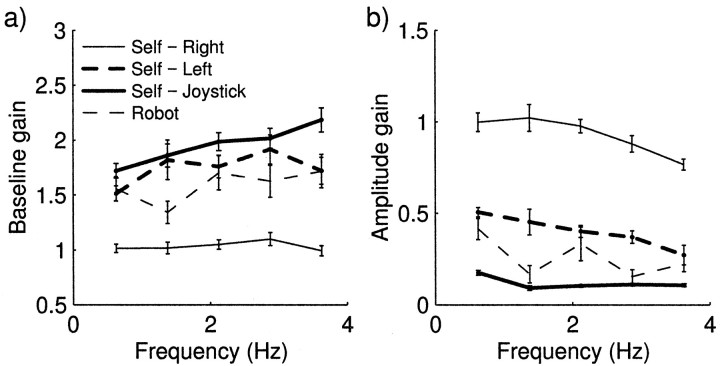
Analysis of the group data is shown in Figures3 and 4. In all conditions, subjects showed a grip force that modulated, to some extent, with load force. As expected, when the subjects generated the load force with their right hand they showed a large degree of grip force modulation (Fig. 3b), and this modulation showed a small significant (p < 0.01) average phase advance of +10.6 msec across the frequencies tested (Fig.4b). However, when the same load force was produced externally by the robot, the modulation was significantly smaller (p < 0.01) and showed a significant (p < 0.001) average phase lag of −100.4 msec.

Fig. 3.

Average baseline (a) and amplitude gain(b) of grip force modulation against frequency for the four conditions of Experiment 1.

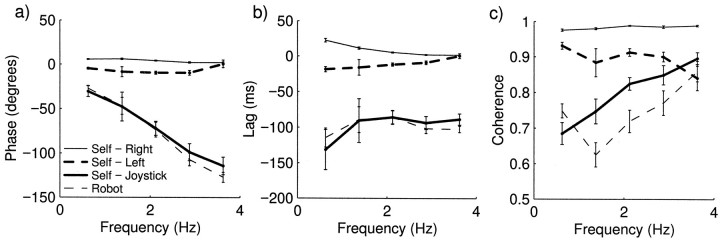
Fig. 4.

Average phase (a), lag (b), and coherence (c) between load force and grip force against frequency for the four conditions of Experiment 1.

When subjects used their left hand to generate the load force directly, there was a small average phase lag of −12 msec that was not significantly different from 0. However, when the left hand generated the same load force through the joystick-controlled robot, and subjects were explicitly informed of this relation, performance was markedly different. In this condition the baseline gain, amplitude gain, phase, and lag were not significantly different from these values in the externally generated condition. In particular, in the joystick condition, the grip force modulation had a significant phase lag of −104.2 msec with respect to load (p < 0.01).

Analysis of coherence (Fig. 4c) showed that it was significantly higher when the movements were self-generated by the right hand compared with the other three conditions (p < 0.01).

Experiment 2

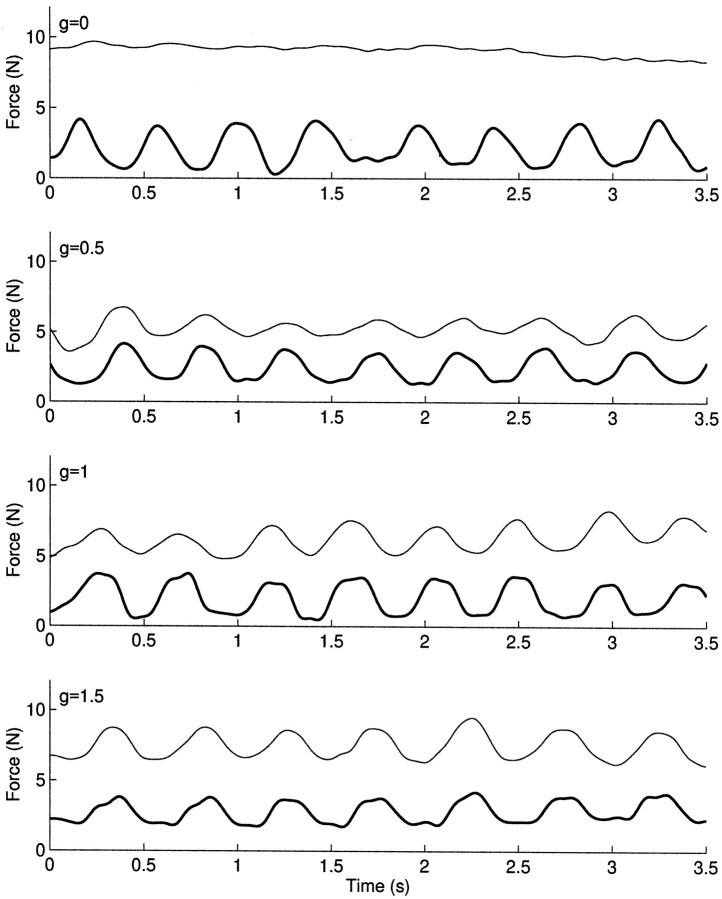
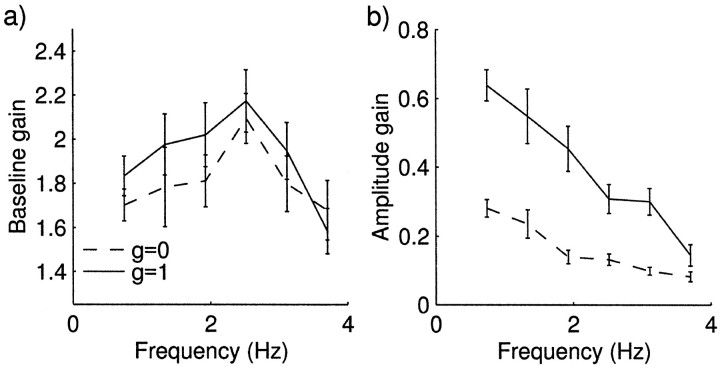
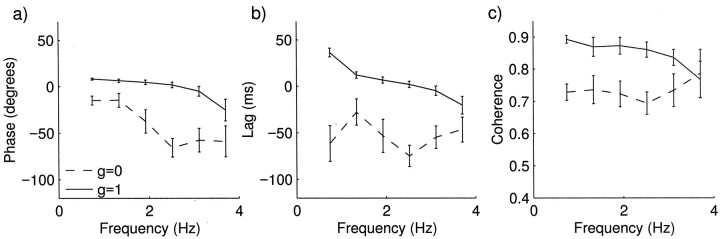
Typical raw data for four of the levels of feedback gains,g to the left hand, are shown in Figure5. This shows that modulation of grip force grip was small for g = 0 and increased as the feedback gain to the left hand increased. Analysis of the group data for feedback parameter g = 1 (solid lines) andg = 0 (dashed line) are shown in Figures6 and 7. At a value g = 1, the effect should be qualitatively similar to the left hand direct condition of Experiment 1 because the robots simulate a single object between the two hands. Correspondingly, when g = 0 the effect should be similar to left hand operating indirectly through the joystick. When the feedback gain parameter g was 1, the average phase advance was significantly higher (p < 0.01) at +11.4 msec compared with a lag of −57.7 msec when g = 0. The grip force modulation amplitude was significantly greater forg = 1 compared with g = 0 (p < 0.05) (Fig. 6b). Modulation of grip decreased in amplitude with increasing frequencies in both conditions (p < 0.05). Coherence (Fig.7c) was significantly higher when g = 1 compared with 0 (p < 0.01). Therefore the differences between the g = 0 and g = 1 conditions are qualitatively similar to the joystick and left-hand conditions of Experiment 1.

Fig. 5.

Typical example of grip force (thin line) and load force (thick line) traces for four feedback gains, g, of Experiment 2 taken from a single subject tracking a frequency of 2.3 Hz. The data are taken from the same time period in each trial and have been low pass-filtered.

Fig. 6.

Baseline gain (a) and amplitude gain(b) of grip force modulation against frequency at feedback gains 1 (solid lines) and 0 (dashed lines).

Fig. 7.

Phase, lag, and coherence at different frequencies at feedback gains 1 (solid lines) and 0 (dashed lines). Average phase (a), average lag (b), average coherence (c) between load force and grip force.

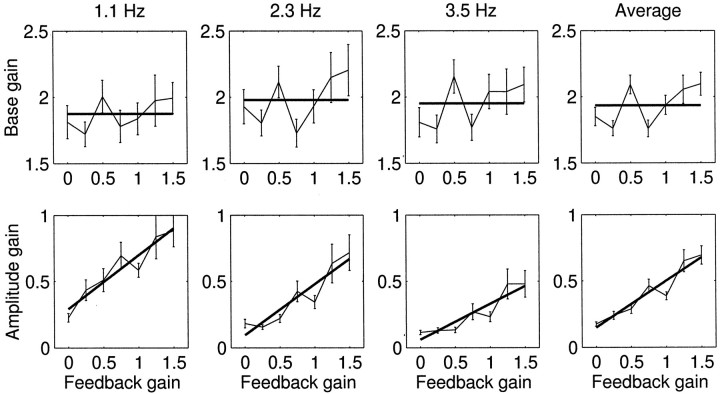
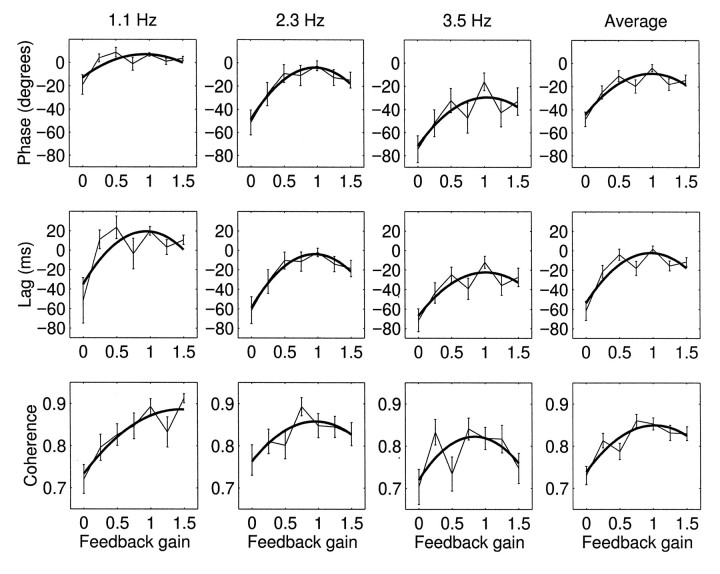
Figures 8 and9 compare the grip force responses to different frequency load forces applied to the object by the left hand via a second robot with different levels of force feedback gain (g varied between 0 and 1.5). The ANOVA performed on the measures as a function of gain showed that a significant difference between the seven levels of gain for lag (p < 0.01), phase (p < 0.05), coherence (p < 0.01), and amplitude gain (p < 0.05). There was no significant difference between the seven levels of gain for baseline gain (p = 0.67). A polynomial contrast on the gains showed a significant fit for the quadratic term for lag (p < 0.01), phase (p < 0.01), and coherence (p < 0.05), and for the linear term for amplitude gain (p < 0.05). A comparison of the extremal values of gain (g = 0 and g = 1.5) with g = 1 showed a significant difference for phase (p < 0.01 forg = 0; p < 0.05 for g= 1.5), lag (p < 0.01 for g = 0; p < 0.05 for g = 1.5), and coherence (p < 0.01 for g = 0;p < 0.05 for g = 1.5). For the combined frequencies, therefore, the highest significant term for the amplitude gain was linear, and for the phase, lag, and coherence it was quadratic. For baseline gain a linear fit was not significant.

Fig. 8.

Baseline gain and amplitude gain of grip force modulation at different frequencies with different force feedback coupling, g, between the robots held in each hand. Graphs show the baseline gain (solid line shows the mean) and the amplitude of grip force modulation (solid line shows linear regression fit) at different feedback gains at three different frequencies and the average over all six frequencies.

Fig. 9.

Phase, lag, and coherence at different frequencies with different force feedback coupling between the robots held in each hand. Graphs show phase, lag, and coherence at different feedback gains at three different frequencies and the average over all six frequencies. The solid line shows the quadratic fits to the data.

An analysis of the location of the maxima of the quadratic fits for lag and phase (Fig. 9) showed that they occurred at a feedback gain value not significantly different from 1 at each frequency. For lag this value was 1.10 ± 0.22 (SE) at 1.1 Hz, 0.92 ± 0.07 at 2.3 Hz, 0.87 ± 0.11 at 3.5 Hz, and on average (combining all six frequencies) 1.05 ± 0.09. The mean lag value at which the peaks occurred was −0.3 ± 12.0 msec. Therefore with feedback gains of less or more than one, grip significantly lagged behind load. Similarly, coherence significantly decreased at feedback gains of less or more than one. The mean location of the peak (combining frequencies) in coherence was at a feedback gain of 0.81 ± 0.06. As the feedback gain g increased, the amplitude of modulation increased significantly for the ensemble data (p< 0.05).

DISCUSSION

Although previous studies have demonstrated predictive modulation of grip force to self-generated load forces, we have shown that this self-generation in itself is not sufficient to produce precise predictive grip force modulation. Precise prediction was seen only when the left hand experienced force feedback that was equal and opposite to the force exerted on the right hand, a situation consistent with the presence of a real, rigid object between the hands. However, when the force feedback to the left hand was either greater or less than the force experienced by the right hand, grip lagged behind load force.

To prevent a gripped object from slipping during movement without maintaining an excess safety margin, grip force must change with load force. In line with previous findings (Johansson and Westling, 1984;Johansson et al., 1992b; Flanagan and Wing, 1995, 1997), we have demonstrated that when load force is generated by the hand holding the object, grip force is modulated in parallel with load force. Grip force anticipated load force even at frequencies as high as 3.5 Hz (Fig.4b), and as demonstrated by the high coherence (Fig.4c), the phase relationship showed minimal variability within each trial. The large amplitude and parallel nature of the grip force modulation allows a small safety margin to be achieved while preventing the object from slipping and may be important in economizing muscular effort (Johansson and Westling, 1984). However, when the load force was externally produced by the robot, the grip force modulation lagged ∼100 msec behind load force. This lag is similar to that seen in response to unpredictable load force perturbations (Cole and Abbs, 1988; Johansson et al., 1992a,b), showing that even for a repetitive sinusoid there is no predictive modulation. If in the presence of such a large delay the amplitude of modulation and the baseline force were similar to that in the self-produced condition, the object would slip. Therefore, when little grip force prediction is seen, there is a concomitant increase in the baseline grip force (Fig. 3a, Robot) and a reduction in grip force modulation amplitude (Fig.3b, Robot). In addition, the phase relationship, as indicated by the low coherence, is more variable in this externally produced condition compared with the self-generated condition. When the load force was generated by the left hand pushing directly on the object, grip force modulation was predictive but of a smaller amplitude than when the load force was generated by the right hand. This parallel modulation suggests that the motor command sent to the left hand can be used to produce precise predictive modulation by the right hand. The phase relationship was strikingly similar to the relationship when the right hand produced the load.

Previous studies have shown anticipatory responses to discrete events such as loading the limb by dropping a ball (Johansson and Westling, 1988; Lacquaniti et al., 1992) or unloading the limb using the opposite hand (Lum et al., 1992). For example, when subjects are required to remove an object held in one hand with the other, anticipatory deactivation of the forearm muscles occurs before the unloading, and therefore the position of the loaded hand remains unchanged (for review, see Massion, 1992). However, when the subjects were required to press a button that caused the load to be removed from their other hand, no anticipatory behavior was seen (Dufosse et al., 1985). These two conditions can be thought of as analogous to our self-produced left hand and joystick conditions. When the load force was indirectly generated by the left hand controlling the robot via a low-friction joystick, grip force lagged significantly behind load force by over 100 msec. This is comparable to the externally produced condition. Therefore, although the load force was self-generated by the left hand in both the direct and indirect (joystick) conditions, only the former elicited precise predictive grip force modulation. The present study extends this work by examining the reasons behind such a discrepancy in anticipatory responses.

Two possible reasons were hypothesized to account for the lack of precise prediction in our indirect (joystick) condition when compared with the direct action of the left hand on the object. The first was that the coordinate transformation between joystick action, which was both remote to the right hand and in the sagittal direction, prevented precise prediction. Alternatively, the difference in sensory feedback received by the left hand in the two conditions produced the differential results. In the direct condition, the left hand received force feedback that was equal and opposite to that experienced by the right hand, whereas in the joystick case the left hand received minimal force feedback. To investigate this issue we examined grip force modulation when the force feedback to the left hand was parametrically varied. This was achieved by simulating a virtual object between the two hands, whose properties did not necessarily conform to normal physical laws. The first hypothesis was rejected as precise prediction was not observed in the condition g = 0, although both hands acted in the same coordinate system. However, we found that the lag between load and grip force was minimal (0.3 msec) when the feedback gain to the left hand simulated a normal physical object (g = 1), and the lag increased in a systematic way as the virtual object deviated from normal physical laws, supporting the second hypothesis.

The present results can be interpreted within a new computational framework of multiple forward models. One problem the CNS must face when both hands are in contact with objects is determining whether the hands are manipulating a single object or are acting on separate objects and thereby select the appropriate control strategy. Only in the former case should the motor commands to each limb be used in a predictive manner to modulate the grip force of the other hand. For example, when holding a cup in one hand and a saucer in the other, there is no reason why one hand should take account of what the other is doing in terms of grip force modulation. However, if the cup and saucer were rigidly joined, then it would be desirable for each hand to take account of the other’s actions.

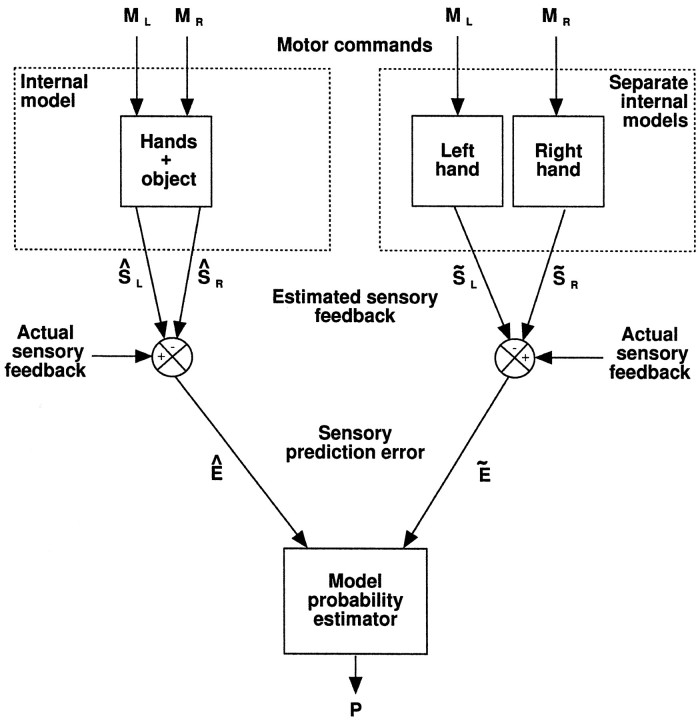
One computational solution to this problem is to use multiple internal forward models, each predicting the sensory consequences of acting within different sensorimotor contexts (Fig.10). For example, one internal model could capture the relation between the motor commands and subsequent sensory feedback when the hands manipulate a single object (Fig. 10,left) while another model captures the condition in which the hands act on separate objects (Fig. 10, right). Each forward model predicts the sensory consequences, based on its particular model of the context and the motor command, and these predictions are then compared with the actual sensory feedback. The errors in these predictions are then used to estimate the probability that each model captures the current behavior. In the present study, for example, when the feedback is equal and opposite to both hands (g = 1), the internal model of a single object between the hands would have a small error compared with the separate models. This would give rise to a high probability that the hands are manipulating a single object, thereby allowing the efference copy of the command to the left hand to modulate predictively, as was observed, the grip force in the right hand. As the sensory feedback deviates from the prediction of the model (g more than 1 org less than 1), the probability of this model capturing the behavior would fall, leading, as observed, to an increase in the lag between grip and load force. Our results therefore suggest that an internal model exists that captures the normal physical properties of an object and is used to determine the extent to which the two hands are manipulating this object. Although it is probably not possible to have a model for every context that we are likely to experience, we propose that by selectively combining the outputs of multiple simple forward models we could construct predictions suitable for many different contexts.

Fig. 10.

A model for determining the extent to which two hands are acting through a single object. For simplicity only two internal models are shown. On the left is an internal forward model that captures the relationship between the motor commands sent to the left (M_L) and right(M_R) hands and expected sensory feedback when the two hands act on a single object. On the right is shown the two internal forward models that capture the behavior when the hands are manipulating separate objects. Both models make predictions of the sensory feedback from both the left(S_L) and right(S_R) hands based on the motor commands. These predictions are then compared with the actual sensory feedback to produce the sensory prediction errors (E). The errors from each model, Ê and Ẽ, are then used to determine the probability P that each model captures the current behavior. This probability determines the extent to which the motor command to one hand can be used in predictive grip force modulation of the other hand.

The observed relationship between lag and feedback gain, g, constrains the way in which sensory prediction errors could be used to select between the internal models (Fig. 10). Our results rule out a model selector producing a hard classification in which grip force modulation corresponds to the hands acting on either a single object or separate objects. Such a relationship would have led to a binary distribution of the lags consistent either with predictive modulation (lag of zero) or no prediction (lag ≈ 100 msec). However, our results show that the lag was minimal when the feedback gain to the left hand was 1 and increased smoothly when the feedback gain was either greater or less than 1. Prediction is therefore graded by the similarity between the force feedback expected for a real, rigid object and the feedback actually received.

Burstedt et al. (1997) recently demonstrated that grip force is modulated in parallel with load force when subjects lifted an object between the index finger of their left and right hands, and cooperatively with another subject using the right index finger. Performance was similar in both these conditions and was comparable to that when subjects lifted the object between the thumb and index finger of their right hand. The authors suggest that this result demonstrates that the forward model can be adjusted to account for various situations. In our study we have shown that the context of the movement, as coded by the haptic feedback to each hand, critically modulates the nature of the grip force response.

Anticipatory grip force modulation has been shown to depend on several contextual cues such as object weight (Johansson and Westling, 1988), experience from previous lifts (Gordon et al., 1993), type of load (Flanagan and Wing, 1997), and friction of the object’s surface (Johansson and Westling, 1984). Knowledge of the mechanical properties of objects is probably also learned by handling and manipulating objects (Gordon et al., 1993), as is demonstrated by prediction improving throughout development (Eliasson et al., 1995), suggesting a continual refinement of the internal models. Our results support the hypothesis that predictive mechanisms rely on there being sensory feedback to the two hands that obey the physical laws encountered in normal objects.

In conclusion, the present results suggest that efference copy in itself is not sufficient to allow generalized prediction. Precise prediction is seen when the feedback to both hands is consistent with a single object and declines smoothly as the feedback becomes inconsistent with this context. We propose that multiple internal forward models can be used to estimate the context of the movement and thereby determine whether it is appropriate to use such a predictive mechanism.