Cognitive Channels Computing Action Distance and Direction

Abstract

Visually guided, goal-directed reaching requires encoding action distance and direction from attributes of visual landmarks. We identified a cognitive mechanism that seemingly performs visual motor extension before action initiation and replicated and extended previous results that identified a mechanism for visual motor mental rotation. We find that humans systematically delay action onset while newly planning increasingly distant arm movements beyond a visual landmark, consistent with an internal representation for visual motor extension. Onset times also changed systematically during concurrent mental rotation and visual motor extension computations required to process new directions and distances. Visual motor extension associated with reaching slowed when participants needed to plan action direction within the same time frame, whereas mental rotation efficiency was unaffected by concurrent needs to prepare action distance. In contrast to parallel direction and distance computations needed for direct aiming to a visual target, the planning of new directions and distances likely occurs at distinct times. When considered with previous findings, the current results suggest the existence of an intermediate component of motor preparation that engages a covert mechanism of cognitive motor planning.

Appearance of a visual landmark often triggers a temporally and spatially distributed cascade of preparatory neural and cognitive events leading to purposeful actions. For visually guided reaching, human observers compute a plan incorporating the location of the landmark into the distance and direction of an action. Evolving behavioral contexts, such as actual or predicted changes in the location of a visual landmark, often require rapid updates to action strategies (for example, Soechting and Lacquaniti, 1983; Port et al., 1997). Proper formulation of these decisions likely involves a precise spatiotemporal sequence of neural (Georgopoulos et al., 1986; Riehle and Requin, 1989; Lurito et al., 1991; Fu et al., 1993; Kurata, 1993; Riehle et al., 1994) and behavioral (Georgopoulos and Massey, 1987; Favilla et al., 1989, 1990;Bock and Arnold, 1992; Pellizzer and Georgopoulos, 1993) events, yielding coordinated actions to attain a goal with a defined spatial end point. Premovement processing also certainly involves encoding movement direction and distance.

Internal mechanisms likely compute intended action direction toward a new goal either during motor planning or perhaps in response to target shifts occurring during movement (Georgopoulos et al., 1981, 1989; Ashe et al., 1993), and ample evidence exists indicating that motor cortical areas in frontal and parietal lobes have neurons with the appropriate properties and large-scale mechanisms that could mediate direction encoding (Georgopoulos, 1991; Tagaris et al., 1996, 1997). However, direction encoding in the context of visually targeted movements or movements without visual targets cannot account completely for end-point planning and rapid action adjustments. Indeed, motor cortical networks that encode direction also encode other movement parameters such as distance, end point, velocity, and acceleration (Kalaska et al., 1989; Kalaska and Crammond, 1990; Fu et al., 1993, 1995; Ashe and Georgopoulos, 1994). Thus, a partner to direction planning, perhaps one that extends (or contracts) distances, likely operates in connection with direction planning to implement accurate reaching toward or referred to visual landmarks. Despite indications for neural and behavioral representations of action distance (for example, Favilla et al., 1989; Riehle and Requin, 1989; Soechting and Flanders, 1989; Fu et al., 1993), definitive evidence of a covert cognitive mechanism for distance computations similar to visual motor mental rotation remains elusive (but see Ghez et al., 1997). Previous work has shown that humans can mentally calculate environmental distances (Decety et al., 1989) and that cortical neurons encode performed distances (Fu et al., 1993, 1995). However, it remains somewhat unclear how humans may covertly calculate distances needed for accurate reaching before movement onset. Additionally, without detailed knowledge about such distance calculations, there remains uncertainty about possible relationships between the cognitive and neural representations for preparing action distance and direction from the time that visual landmarks appear until reaching begins. To complement mental rotation, we hypothesized that humans also use visual motor extension (or contraction) during action preparation to acquire a goal. Furthermore, we reasoned that visual motor extension operates cooperatively with mental rotation to compute action distance and direction in relation to visual landmarks, although these mechanisms might not necessarily operate within identical temporal intervals. To address these issues, we conducted several experiments designed to replicate earlier findings on visual motor mental rotation (Georgopoulos and Massey, 1987), to determine whether we could find evidence of visual motor extension, and to investigate potential interactions between visual motor mental rotation and visual motor extension.

Portions of this work have been reported in abstract form (Sanes and Bhat, 1994).

MATERIALS AND METHODS

Participants. Nineteen normal, right-handed, young human adults (aged 18–24 years) participated in these experiments. Participants had no previous knowledge about the design and goals of the study. All participants took part in the first two experiments, whereas only 10 out of 19 took part in the third experiment. Informed consent was obtained according to standard institutional guidelines. We provided modest monetary compensation for participation.

Apparatus. An electromagnetic stylus coupled to a Numonics (Montgomeryville, PA) model 2020-digitizing tablet measured arm reaching movements. The tablet had an embedded electromagnetic search coil and an active 60 × 60 cm measurement field. The stylus, resembling a fountain pen, was coupled to an interface that providedx and y coordinate pairs at 100 Hz with a nominal spatial accuracy of 0.1 mm. Participants sat directly in front of the table-mounted (parallel to the floor) tablet with a 19 inch monochrome computer monitor at a distance of ∼1 m. Participants grasped the stylus with the right hand and positioned the forearm in semipronation to allow for reaching movements made in response to visual stimuli appearing on the monitor. Movement of the stylus corresponded one-to-one with movement of a position-feedback cursor on the screen. Participants performed movements within a 30 × 30 cm work space centered in the midsagittal plane.

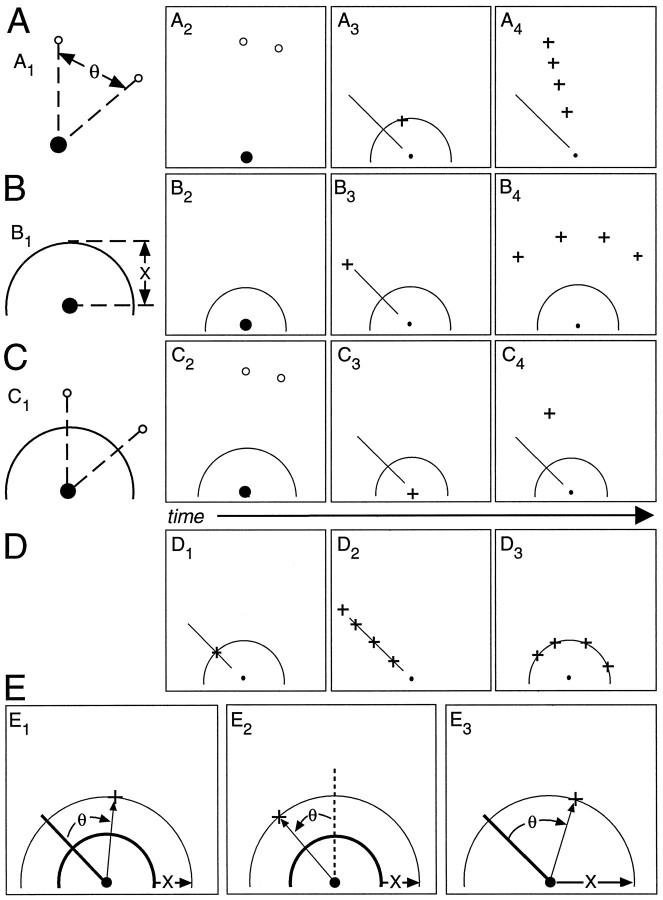
Procedures. Individual trials started with an initial orientation period, followed by a preparation period, a go-cue, and then reaction and movement periods. Stimuli indicating movement direction or distance or both appeared on the computer monitor. Participants moved their right hand in response to these stimuli, thereby causing simultaneous movement of the position cursor (small crosses in Fig.1) appearing on the computer monitor. Figure 1 illustrates visual stimuli for the different trial types. All trials began with the simultaneous appearance of a cross target indicating the starting position, or hold-zone (position of thesolid circle in Fig.1A₂,B₂,C₂), and the instruction for that trial (Fig.1A₁,A₂,B₁,B₂,C₁,C₂). The hold-zone target was centrally located near the bottom of the video screen, encompassed a circular area 10.2 mm in diameter, and becamesolid black (Fig.1A₂,B₂,C₂) when a participant aligned the position cursor with it. The instruction, as described below, provided information about the upcoming movement direction or distance. After 1.5 sec of successful alignment of the hand within the hold-zone, three events occurred simultaneously (Fig.1A₃,B₃, C₃,A₄,B₄); the instructional and the hold-zone stimuli each disappeared, a beep sounded as the go-cue, and a movement stimulus appeared (indicating either a movement direction, a movement distance, or both as required by each task). Participants had previous instructions to initiate movement only after determining the final end point for the movement and to move as quickly and as accurately as possible without path corrections. Participants were asked (and they complied in large part, as determined visually, after 10–50 training trials) to reach primarily by using their shoulder and elbow and not to use wrist or other body movements. Participants had 2.5 sec (3.5 sec for experiment 3) to initiate and to complete the appropriate movement. When the allotted time expired, all screen objects disappeared. The next trial began in 100 msec.

Fig. 1.

Methods for cognitive motor tasks.A, Rotation tasks. A₁, Instruction direction (θ) represented by angle formed by small annuli (open circles) relative to the hold-zone (solid circle). A₂, A direction instruction as it might appear on the video screen while a participant waits for a go-cue. A₃, Ideal reaching end point (cross) given a stimulus direction (avisible line extending from the hold-zone) and distance (a visible semicircle) in the constrained rotation task.A₄, Possible ideal responses in the unconstrained rotation task (crosses) given only the stimulus direction. B, Extension tasks.B₁, Instruction distance (X) represented by a semicirclecentered on the hold-zone. B₂, A distance instruction as it might appear while a participant waits for a go-cue. B₃, Ideal response for constrained task (cross) given the direction and distance stimuli. B₄, Possible ideal responses for unconstrained task (crosses) given only a stimulus direction. C, Combined task.C₁, Representation of instruction direction and distance. C₂, Appearance of a combined distance and direction instruction.C₃, Appearance of the go-cue stimuli.C₄, Ideal response. D, Baseline tasks, ideal responses (crosses).D₁, Constrained and combined tasks.D₂, Unconstrained rotation.D₃, Unconstrained extension. See text for task details. E, Depiction of kinematic measurement methods. θ and X refer to definitions of achieved direction and achieved distance, respectively, in the various tasks. See text for additional details.

Constrained rotation or extension. Two tasks comprised the “constrained” experiment (experiment 1), one instructed mental rotation and the other instructed presumed visual motor extension. For the rotation task, two annuli 1.35 mm in diameter appeared on the video monitor to instruct a movement direction (open circles in Fig.1A₁,A₂). These annuli appeared 187 mm from the hold-zone center, with one annulus appearing directly above the hold-zone stimulus and the other on the right half of the monitor. The angle formed between imagined vectors connecting each circle to the hold-zone center provided an instruction for upcoming movement direction. We used five instruction directions (20, 35, 50, 65, and 80°). For the extension task, the radius of a semicircle centered around the hold-zone provided an instruction for upcoming movement distance (Fig.1B₁,B₂). We used five instruction distances (25.5, 42.5, 59.5, 76.5, and 93.5 mm).

Movement stimuli were identical for both constrained tasks. Simultaneous with the occurrence of the auditory go-cue, a line (187 mm long, starting near the hold-zone and positioned on the left side of the monitor) that intersected a semicircle outline (centered around the hold-zone) appeared on the video monitor (Fig.1A₃,B₃). The line corresponded to one of five stimulus directions (−80, −65, −50, −35, and −20°) clockwise from a vertical vector extending from the hold-zone, whereas the radius of the semicircle corresponded to one of five stimulus distances from the center of the hold-zone (25.5, 42.5, 59.5, 76.5, and 93.5 mm). In separate runs, each of the 25 combinations of stimulus directions and distances was presented once for each instruction direction and each instruction distance.

For the rotation task, participants had previous instructions to reach clockwise away from the hold-zone by adding the instruction direction to the stimulus direction. Movement distance was constrained, by previous verbal instruction, to the stimulus distance (Fig.1A₃). For the constrained extension task, participants had previous instructions to reach away from the hold-zone and beyond the stimulus distance by adding the instruction distance to the stimulus distance. Movement direction was constrained, by previous verbal instruction, to the stimulus direction (Fig. 1B₃).

Unconstrained rotation or extension. Two tasks comprised the “unconstrained” experiment (experiment 2), one instructed mental rotation and the other instructed presumed visual motor extension. The five instruction directions and the five instruction distances were identical to those used for the constrained tasks, whereas movement stimuli and task requirements differed.

For the unconstrained rotation task, the movement stimulus was a vector indicating a direction. Each of the 20 stimulus directions (spaced evenly from −84° to −8°) was presented once for each instruction direction. As in the constrained rotation task, participants were instructed to reach clockwise away from the hold-zone by adding the instruction direction to the stimulus direction. Because no distance cue appeared on the screen, participants freely chose (that is, in an unconstrained manner) movement distance, with the provision that the movement remain within the work space (Fig.1A₄).

For the unconstrained extension task, the movement stimulus was a semicircle indicating a distance. Each of the 20 stimulus distances (spaced evenly from 27.2 to 59.5 mm) was presented once for each instruction distance. As in the previous extension task, participants reached away from the hold-zone to a distance that was the instruction distance beyond the stimulus distance. Because no directional cues appeared, the chosen movement direction was unconstrained, with no requirements (other than remaining in the work space) imposed (Fig.1B₄).

Combined rotation and extension. The final experiment (experiment 3) involved a single task combining instructions and task requirements from the constrained rotation and extension tasks (Fig. 1C). Using four directional (20, 35, 50, or 65°) and four distance (25.5, 42.5, 59.5, or 76.5 mm) instructions from experiment 1, we combined each direction cue with each distance cue (for a total of 16 combined instructions) to direct the magnitudes of mental rotation and visual motor extension (Fig.1C₁,C₂). Each of 25 movement stimuli (Fig. 1C₃), identical to those used for the constrained tasks, was presented once for each paired instruction. At the go-cue, participants were instructed to reach to an end point matching both the instruction direction clockwise from the stimulus direction and the instruction distance beyond the stimulus distance (Fig.1C₄).

Trial presentation orders. Participants performed the tasks in distinct sets of trials, separated either by 5–10 min rest periods or up to 2 d. All 19 participants performed experiments 1 and 2, with the order counterbalanced across participants, in the first two trial sets. Ten of the 19 participants performed experiment 3 in a third trial set.

Immediately before each trial set, participants learned and practiced the tasks (10–50 trials) until reaching became consistent in path, speed, and accuracy. Task performance began with a baseline block of trials using a null instruction stimulus (ideal responses illustrated in Fig. 1D). During the baseline task for the constrained and combined tasks, participants had instructions to target movements to the intersection of the direction vector and semicircular stimuli (Fig. 1D₁). During the baseline task for the unconstrained rotation task, participants had instructions to end movements at any point along one of 20 direction stimuli (Fig. 1D₂). During the baseline task for the unconstrained extension task, participants had instructions to end movements at any point along one of 20 distance stimuli (Fig. 1D₃). Participants then performed blocks of test trials with each block having a single instructional stimulus. Each instruction block was given once in a task (order randomized for each participant), and each block (including baseline blocks) had a single presentation of each go-cue stimulus (order randomized within each block). For the first two trial sets, blocks alternated between the rotation and extension tasks with the order counterbalanced across participants. For the third trial set, participants performed a baseline block after every four instruction blocks. Each baseline block of experiment 3 was preceded by a 2–5 min rest period.

Movement analysis. We used a computer display to inspect the time course of x and y coordinate pairs and the computed tangential hand velocity. Movement onset and the end of movement were marked with an electronic cursor using the hand speed record. By the use of an automatic routine, movement onset was marked when velocity increased to ∼1 cm/sec over the baseline hand velocity (typically averaging ≤0.1 cm/sec across participants). The end of movement was marked when hand speed decreased to (and remained for at least 200 msec) below a velocity of 0.5 cm/sec. Reaction time (RT) was calculated as the time elapsed between go-cue presentation and movement onset. Peak velocity was defined as the maximum tangential hand velocity occurring during the movement. To describe the spatial attributes at the end of movement, we used the same polar coordinate system used to describe the movement stimulus, with the origin at the center of the hold-zone and directions defined as clockwise angular deviations from a vertical vector. In this coordinate framework, movement direction and distance correspond to the direction and distance of the vector connecting the hold-zone to the movement end point. Compliance with the direction and distance instructions was determined by calculating an “achieved” direction and distance. To unify terminology across the various tasks, we used achieved direction or distance even for the unconstrained tasks that did not have explicit direction or distance instructions and for the baseline tasks for which commonly used terms such as constant error would have sufficed. For all tasks except for the unconstrained extension task, the achieved direction equaled the angular difference between the performed movement direction and the stimulus direction (see Fig.1A₃,B₃,C₃,D₁,D₂, for stimulus vectors,E₁,E₃, for an explicit illustration). For the unconstrained extension task, for which there was no movement direction stimulus, we defined achieved direction as the angular deviation from a vertical vector emanating from the hold-zone using the coordinate system described above (Fig.1E₂). For all tasks except for the unconstrained rotation task, the achieved distance equaled the difference between the total movement distance as referred to the hold-zone and the radius of the movement stimulus (Fig.1E₁,E₂). For the unconstrained rotation task, we defined the achieved distance as the distance between the movement end point and the hold-zone (Fig.1E₃).

The first three trials in each trial block (including baseline blocks) were excluded from further analysis to eliminate possible warm-up effects. Trials with movements not fully completed within an arbitrary allotted time of 2.5 sec for experiments 1 and 2 and 3.5 sec for experiment 3 were excluded. We rejected as outliers trials from the rotation and the combined tasks having achieved directions ≤10° or >100°, trials from the extension and combined tasks having achieved distances ≤10 mm or >150 mm, and trials from any task with RT ≤200 msec. The group means (±SEM) of participant percentages of rejected trials (after excluding warm-up trials) were 5.3 ± 1.3% for constrained rotation, 5.3 ± 2.1% for constrained extension, 4.2 ± 1.5% for unconstrained rotation, 3.0 ± 0.9% for unconstrained extension, and 1.3 ± 0.2% for the combined rotation and extension. The percentage of rejected trials did not differ between the constrained and unconstrained tasks (Friedman test, p > 0.05).

Statistical analysis. Statistical significance was defined as p ≤ 0.05, and significant statistical probabilities are reported to a maximum of 10⁻⁴ level of significance. Probability levels were “rounded” to 0.05, 0.025, 0.01, etc. Multiple regression methods were applied for major statistical analyses. We were interested in describing two aspects of the hypothesized mental calculations: movement accuracy (measured by the relation of the achieved direction to the instructed direction for rotation tasks or the achieved distance to the instructed distance for extension tasks) and movement initiation time (measured by the relation of RT to either the instruction or an achieved variable). An initial analysis of the data aimed to understand the nature of these relationships for each participant in each of the two constrained tasks to derive suitable regression models for statistical analysis.

We observed a linear dependence of the corresponding achieved variable (direction or distance) on the appropriate instruction (direction or distance) for each participant. We found considerable overlap in the raw achieved values among instructions and potential differences in the slope and intercept of the linear relation among participants. For these reasons, we initially modeled the mean achieved (per combination of participant and instruction) as a linear function of the instruction, controlling for differences among participants in the slope and intercept. Data from the constrained rotation and extension tasks were analyzed separately, and we started with:

$$\text{achieved variable}=a+b·\text{instruct}+\mathbf{\text{c}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}}\mathbf{+}\mathbf{\text{d}}\mathbf{ }\mathbf{·}\mathbf{ }\text{instruct}*\mathbf{\text{part}},$$

where the achieved variable corresponds to the achieved direction or distance, a and b are unknown coefficients, c and d are unknown sets of coefficients, “part” is a nominal term that labels each participant, and “instruct” equals the magnitude of the instruction for direction or distance depending on the task. Backward elimination of this model by iteratively using an F test to test for a significant difference between each model and the subsequent reduced model led to the exclusion of the “instruction * participant” interaction term for both constrained tasks and yielded the model of:

$$\text{achieved variable}=a+b·\text{instruct}+\mathbf{\text{c}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}}.$$

Estimates for the intercept and slope (coefficients aand b), the p value for the slope term (tested against the null hypothesis of a zero slope), and the fullR² statistic are reported for this reduced-regression model.

To compare movement accuracy between the constrained and unconstrained experiments, we analyzed data from both experiments, although separately for the rotation and extension tasks, with the model:

$$\text{achieved variable}=a+b·\text{instruct}+\mathbf{\text{c}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}}+d·\text{expt}+e·\text{instruct}*\text{expt}+\mathbf{\text{f}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}}*\text{expt},$$

where “expt” equals zero (assigned arbitrarily) for data obtained from the constrained experiment and equals one for data from the unconstrained experiment. d and c are unknown coefficients, and f is an unknown set of coefficients. We used Student’s t tests to evaluate potential differences between experiments in the intercept and slope (that is, against null hypotheses that coefficients d ande are zero). Data from the combined experiment were considered separately (see Results).

One major issue concerns comparing processing rates for mental rotation and visual motor extension under different task conditions. Previous findings (Georgopoulos and Massey, 1987) would suggest that a linear RT increase with the angular difference between the stimulus direction and the planned movement direction is consistent with a gradual mental rotation through imagined space. The inverse of the slope describing this relationship provides an estimate for the processing rate of the mental rotation. For example, because RT = a +b·angle, then the mental rotation rate equals 1/b. Analogous calculations might be used to estimate the processing rate for the hypothesized visual motor extension. That is, if RT = c + d·distance, then the visual motor extension rate equals 1/d. Of course, estimates of processing rates depend on how one defines the angular or distance difference (that is, whether we use the instruction or the achieved variable).

As seen in grouped accuracy relations, we also observed a linear change in initiation time (RT to instruction or achieved) in the constrained tasks when data from individual participants were grouped. However, when using the individual data, we observed what we term a “blocking effect”; that is, participants generally exhibited deviations from linearity in one or more of the five instruction blocks for each task. The blocking effect was often associated with either or both the block presentation order and the outlying movement speeds (measured by peak velocity, given the movement distance). Importantly, the blocking effect was more pronounced for the relationship between RT and instruction than for that between RT and the achieved variables. This approach provided a potential rationale for using the achieved data to analyze how humans plan movement distance and direction.

To test for a significant difference in the percentage of RT variance accounted for by a linear relationship to the instructions versus an achieved variable, we compared theR² statistic obtained for each participant for a linear regression of RT to the five instructions with that obtained for a linear regression of RT to the corresponding achieved variable. To equate the degrees of freedom between the comparisons, we binned the appropriate achieved variable into five approximately equal-sized intervals. For the constrained rotation task, the mean R² across the 19 participants equaled 0.62 ± 0.04 for a linear regression of RT to the instructed direction and 0.77 ± 0.05 for a linear regression of RT to the achieved direction. The fit accounted for by the achieved direction was greater for 16 out of 19 participants than was the fit accounted for by the instructed direction and differed significantly (n = 19; paired t = 3.82;p ≤ 0.005). For the constrained extension task, the mean R² across the 19 participants equaled 0.41 ± 0.06 for a linear regression of RT to the instructed distance and 0.55 ± 0.07 for a linear regression of RT to the achieved distance. The fit accounted for by the achieved distance was greater for 12 out of 19 participants than was the fit accounted for by the instructed distance and differed significantly (n = 19; paired t = 3.53;p ≤ 0.005). Based on these results, we decided to use the achieved data to estimate processing rates. Because binning the data may lead to arbitrary differences in estimated linear trends, we based subsequent analyses on the raw data. Because of the blocking effect described above, we decided not to analyze individual processing rates (in the first two experiments). For tasks of the constrained experiment, these considerations led us to the regression model of:

$$RT=a+b·\text{ach}+\mathbf{\text{c}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}},$$

where a and b are unknown coefficients,c is an unknown set of coefficients, “part” is a nominal term labeling each participant, and “ach” equals the magnitude of the achieved direction or distance. Estimates for the intercept and slope (coefficients a and b), thep value for the slope term (using a z test to compare the estimated slope with zero), and the fullR² are reported for the regression model above.

To compare RT data between the constrained and unconstrained experiments, we analyzed these data (separately for rotation and extension tasks) with the model:

$$RT=a+b·\text{ach}+\mathbf{\text{c}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}}+d·\text{expt}+e·\text{expt}*\text{ach}+\mathbf{\text{f}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}}*\text{expt},$$

where “expt” equals zero for data obtained from the constrained experiment and equals one for data from the unconstrained experiment. d and e are unknown coefficients and f is an unknown set of coefficients.z tests were used to test for differences between experiments in the intercept and slope (that is, against null hypotheses that coefficients d and e are zero). Data from the combined experiment were considered separately (see Results).

A final consideration in the statistical analysis of processing rates involves the non-normal distribution of RT, primarily related to an overabundance of long RTs. To attain an unbiased estimate of the processing rate corresponding to the average linear relationship of RT to achieved direction or distance, we applied biweight estimation with a tuning constant c = 4.685 (Mosteller and Tukey, 1977;Street et al., 1988). This regression approach is a robust method [for a discussion of robust regression, see Hamilton (1992)] that gradually diminishes the statistical influence of outlying values.

RESULTS

Constrained rotation and extension

Figure 2 illustrates hand paths and speeds obtained from a representative participant during the constrained visual motor rotation (Fig. 2A) and extension (Fig. 2B) tasks. As required by the instructions, this participant reached reasonably quickly (movement time, 439 ± 7 msec for constrained rotation) and with relatively straight-line paths (Fig. 2, insets above the velocity profiles). Consistent with fast-reaching movements aimed at a target decided before movement initiation (as instructed), velocity profiles were similarly bell-shaped for movements performed according to all instructions. The general absence of secondary changes in hand velocity indicated that participants generally complied with the request not to make corrective movements.

Fig. 2.

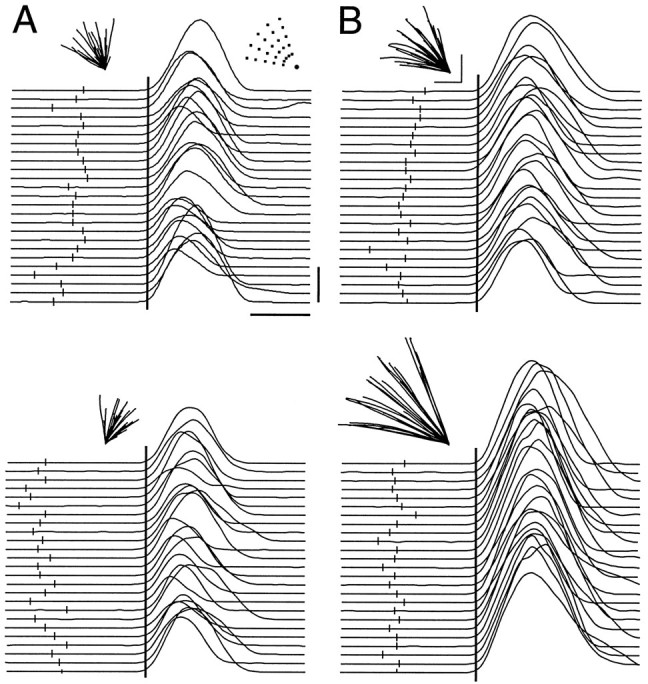
Movement kinematics from a representative participant in the constrained experiment. A, Rotation task. Hand paths (insets) and tangential velocity profiles (aligned at movement onset with tick marksindicating onset of go-cue) for accepted trials with instruction directions of 20° (top) and 80° (bottom). B, Extension task. Hand paths (insets) and velocity profiles for instruction distances of 25.5 mm (top) and 93.5 mm (bottom). The top right inset inA represents the 25 go-cue stimuli positioned relative to the location of the hold-zone. Calibration bars for path length correspond to 50 mm. Calibration bars for velocity profiles correspond to 250 msec (horizontal) and 20 cm/sec (vertical).

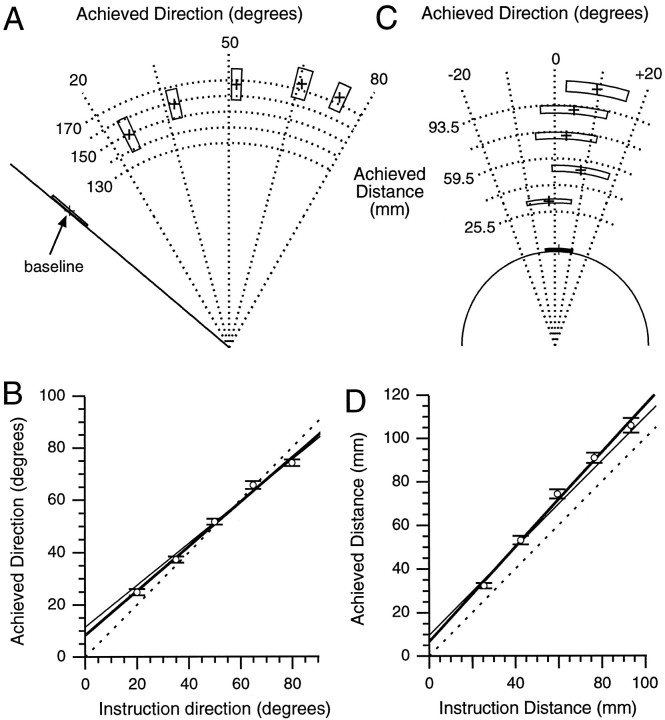
Figure 3A illustrates the grouped achieved directions and distances in the constrained rotation and extension tasks and the corresponding baseline task. For the baseline task, achieved direction (that is, angular deviation clockwise from the stimulus direction) approximated an ideal response when testing the hypothesis that achieved direction differed from zero (mean error, 0.5 ± 0.3°), although participants nevertheless slightly exceeded the visually instructed target by 1.8 ± 0.7 mm (signed rank = 55.0; p ≤ 0.05).

Fig. 3.

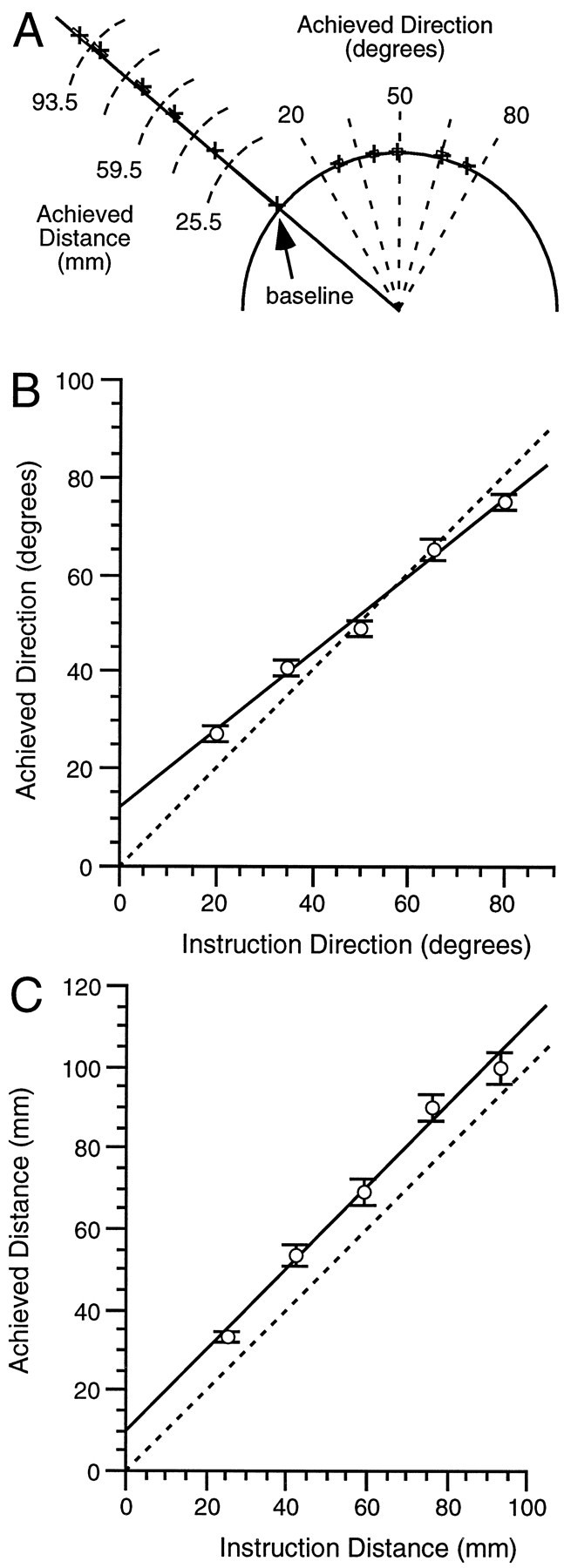
Reaching accuracy for the constrained tasks.A, All task conditions. Crosses indicate the group mean performance plotted in relation to a go-cue stimulus having a direction (line from origin) of −50° and 59.5 mm distance (semicircle around origin). The group mean was compiled from each participant’s mean achieved direction and distance for each instruction for the baseline, rotation, and extension tasks. The boxes indicate the SEM for each group mean direction and distance. The intersections of thedashed lines with the direction line and the distance semicircle indicate the ideal achieved distances and directions for each appropriate instruction.B, Rotation task. Each point indicates the mean of the participant’s mean responses of achieved versus instructed direction. Error bars indicate SEM in this and all subsequent figures. The solid line represents the calculated regression between achieved and instructed direction, whereas the dashed unity line represents perfect accuracy. C, Extension task. Symbols and features are analogous to the rotation task described inB.

For the constrained rotation task, the achieved direction increased linearly with the instruction direction (R² = 0.94; p ≤ 0.0001; Eq. 1; Fig. 3B). The estimated achieved direction for a 0° rotation instruction (intercept in Eq. 1) was 11.0 ± 1.9° more clockwise than was the achieved direction in the baseline task (signed rank = 93; p ≤ 0.001). For this rotation task, achieved distance was unaffected by instruction directions, and it did not differ from the distance achieved in the baseline task:

$${\text{Direction}}_{ACHIEVED}=11.5+0.8·{\text{Direction}}_{INSTRUCTED};$$ Equation 1

$${\text{Distance}}_{ACHIEVED}=9.6+1.0·{\text{Distance}}_{INSTRUCTED}.$$ Equation 2

For the constrained extension task, achieved distance increased linearly with the instruction distance (R² = 0.95; p ≤ 0.0001; Eq. 2; Fig. 3C). The estimated achieved distance for a 0° instruction (intercept in Eq. 2) was 7.8 ± 1.9 mm larger than was the achieved distance in the baseline task (signed rank = 76;p ≤ 0.001). For this extension task, achieved direction did not differ across instruction distances or from achieved direction in the baseline task.

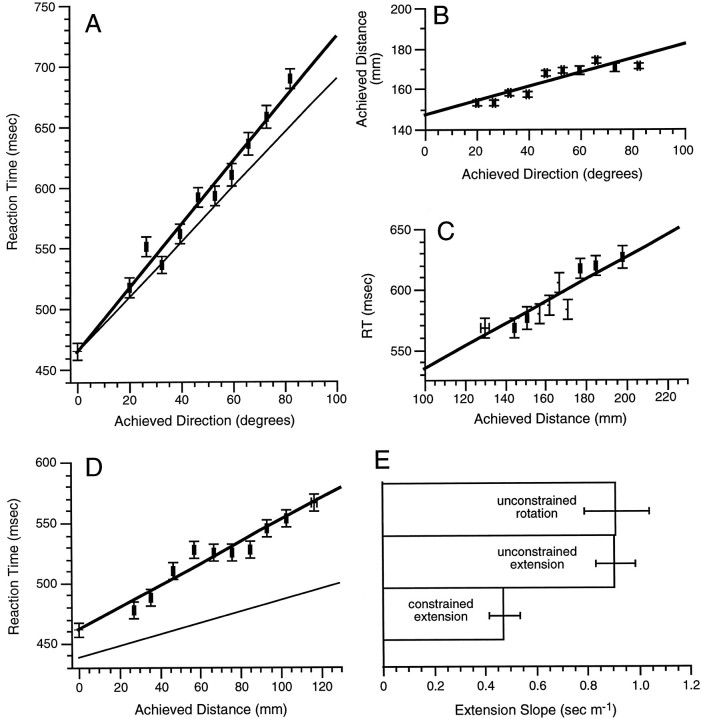
RT for the constrained baseline task was 425 ± 3 msec for the group. RT varied systematically and linearly with achieved direction in the constrained rotation task (R² = 0.79;p ≤ 0.0001; Eq. 3; Fig.4A, upper line). Estimated RT for an achieved direction of 0° (intercept in Eq. 3) was 41 ± 7 msec greater than was the baseline RT (z = 5.93; p ≤ 0.0001). The inverse of the slope of the function relating RT to achieved distance corresponds to a processing rate of 444° per sec (or 2.25 msec per degree) for a presumed gradual mental rotation of planned movement direction clockwise from the direction of the movement stimulus that occurs before movement initiation:

$$RT=466+2.25·{\text{Direction}}_{ACHIEVED}.$$ Equation 3

Fig. 4.

Reaction time for the constrained tasks.A, Mean normalized RT and mean achieved direction (or distance) for each of 10 “equally sized” bins of achieved direction (or distance) in the constrained rotation (or extension) task. Each fitted line corresponds to the regression through weighted raw data of the constrained rotation (or extension) task (see Materials and Methods). The estimated intercepts (at 0 mm for extension and 0° for rotation), as well as the mean RT for the constrained baseline task, are also illustrated. Data binning here and in other figures is used solely for illustrative convenience. All analyses were done with raw data (see Materials and Methods). B, Correlation between RT in the rotation and extension tasks. Additional details are in text.

RT varied systematically with the achieved distance in the constrained extension task (R² = 0.78;p ≤ 0.0001; Eq. 4; Fig. 4A,lower line). Estimated RT for an achieved distance of 0 mm (intercept in Eq. 4) was 12 ± 5 msec higher than was the baseline RT (z = 5.934; p ≤ 0.0001). The inverse of the slope corresponds to a processing rate of 2105 mm/sec (or 0.48 msec/mm) for a presumed gradual visual motor extension of planned movement distance beyond the distance of the movement stimulus occurring before movement initiation:

$$RT=437+0.48·{\text{Distance}}_{ACHIEVED}.$$ Equation 4

In addition to a linear increase in RT with the achieved direction or distance, RT also exhibited step increases during both the constrained rotation and extension tasks. Therefore, we examined whether these RT increases relative to the baseline RT were correlated across the 19 participants. For each 1 msec step RT change during the rotation task, we found a 0.43 ± 0.08 msec RT step during the extension task (R² = 0.64; p ≤ 0.0001; Fig. 4B).

We also assessed whether RT varied across stimulus direction or distance while participants performed the rotation or extension tasks. However, an ANOVA failed to reveal any statistically significant dependence of RT on stimulus characteristics. As an additional control, we considered the possibility that movement velocity may have changed concordantly with RT as participants needed to increase the magnitude of mental rotation or presumed visual motor extension. Although peak velocity scaled, as expected, to distance (modeled as a polynomial regressor per participant, R² = 0.95 for rotation; R² = 0.96 for extension), its scaling remained unaffected by changes in distance and direction instructions.

Unconstrained rotation and extension

The next two tasks assessed whether concurrent distance and direction processing occurring before movement initiation influenced either mental rotation or visual motor extension. For the constrained rotation or extension tasks, participants had previous instructions to prepare a single attribute of the upcoming movement, for example, direction in the constrained mental rotation task, whereas the go-cue stimulus provided additional information about the other attribute (Fig. 1). In the unconstrained versions of these tasks (see Materials and Methods), the stimuli and task requirements of the unconstrained and constrained tasks were essentially identical except that, during the unconstrained rotation task, participants freely chose movement distance (compare Fig. 1A₃ withA₄) and, during the unconstrained extension task, participants freely chose movement direction (compare Fig. 1B₃ withB₄). Thus, during the unconstrained rotation task, participants not only needed to rotate according to the explicit instructions, but they also needed to decide covertly how far to move. Analogously, during the unconstrained extension task, participants had an explicit extension instruction but needed to determine the movement direction covertly.

Figure 5 illustrates the spatial relationships between movement instructions and performed movements obtained during the unconstrained rotation (Fig.5A,B) and extension (Fig.5C,D) tasks. For the unconstrained rotation task, participants exhibited a linear response to rotation instructions (R² = 0.98; p ≤ 0.0001; Fig. 5B), and the observed relationship did not differ in the slope or the intercept from that obtained for the constrained rotation tasks (refer to Eq. 1). Across the group, participants reached 85.4 to 236.9 mm (range across participants) away from the hold-zone with a group mean of 164.6 ± 9.4 mm. Unexpectedly, the achieved distance increased monotonically with instruction direction (R² = 0.96; p ≤ 0.0001; this finding is not illustrated explicitly but can be inferred by comparing the lengths of vectors drawn from the origin of Fig.5A to each of the five mean end points). For the unconstrained extension task, participants moved a distance consistent with the instructions (R² = 0.97;p ≤ 0.0001; Fig. 5D), and the linear relationship between achieved and instructed distance did not differ in slope or intercept from that observed in the constrained extension task (refer to Eq. 2). Across participants in the unconstrained extension task and relative to a 0° vertical line from the hold-zone, achieved direction ranged from −66.6° to 41.4°, with a mean of 4.8 ± 7.6°. Despite this large range of movement directions, the average end-point direction did not differ among the five distance instructions (Fig. 5C).

Fig. 5.

Reaching accuracy in unconstrained tasks.A, Crosses represent movement end points for each instruction direction in the unconstrained rotation task (for additional details, see the legend for Fig. 3A).Dashed vertical orvertical-oblique lines that are drawn equidistant from the origin represent partial vectors on which “correct” end points could lie. B, Relationship between achieved and instructed direction in the unconstrained rotation task is shown. Symbols and features are described in Figure 3B except for the thin solid line that corresponds to the regression obtained from the constrained rotation task and the thick solid line that corresponds to the regression obtained from the unconstrained rotation task. C, Crosses represent movement end points for each instruction distance in the unconstrained extension task. Dashed semicircles partially represent the locations where correct end points could lie. D, Relationship between achieved and instructed distance in the unconstrained extension task is shown. Lines are described in B.

RT increased linearly with achieved direction during the unconstrained rotation task (R² = 0.78;p ≤ 0.0001; Eq. 5; Fig.6A). Neither the slope nor the intercept of the relationship between RT and achieved direction differed significantly from that found in the constrained rotation task, although the differences in slopes approached statistical significance (p = 0.06). Subsequent exploratory analyses suggested that the marginal increase in the RT slope for the unconstrained rotation task likely related to two confounding effects. First, achieved distance increased with achieved direction (Fig.6B), and second, RT covaried with achieved distance (0.92 ± 0.14 msec/mm; R² = 0.75;p ≤ 0.0001; Fig. 6C). When we accounted for these potential confounds by removing the expected RT increase for the achieved distance attained during each movement trial of the unconstrained rotation task, the slope of the relationship estimating RT in Eq. 5 became 2.26 msec per degree, identical to the corresponding slope estimate for the constrained rotation task (refer to Eq. 3). Thus, it seems that with appropriate corrections, the processing rate for mental rotation did not differ between the constrained and the unconstrained rotation tasks. Finally, there was no difference in RT obtained for the baseline tasks performed in conjunction with the constrained and unconstrained rotation tasks:

$$RT=465+2.61·{\text{Direction}}_{ACHIEVED};$$ Equation 5

$$RT=461+0.91·{\text{Distance}}_{ACHIEVED}.$$ Equation 6

Fig. 6.

Reaction time in the unconstrained tasks.A, Mean normalized RT and mean achieved direction for 10 bins of achieved direction in the unconstrained rotation task.Thinner lines here and in D illustrate that regression results from the constrained tasks. B, Mean normalized achieved movement distance and mean achieved direction for 10 bins of achieved direction in the unconstrained rotation task.C, Mean normalized RT and achieved movement distance for 10 bins of achieved movement distance in the unconstrained rotation task. D, Mean normalized RT and mean achieved distance for 10 bins of achieved distance in the unconstrained extension task.E, Comparison of the RT slopes for visual motor extension obtained from the constrained and unconstrained tasks.

RT increased linearly with achieved distance during performance of the unconstrained extension task (R² = 0.86;p ≤ 0.0001; Eq. 6; Fig. 6D). When comparing RT functions from the two extension tasks, we found a 23 ± 7.5 msec increase in the intercept (z = 3.05;p ≤ 0.005) and a 0.4 ± 0.1 msec/mm increase in slope (z = 4.24; p ≤ 0.0001) for the unconstrained extension task in comparison with the corresponding constrained task. The slope of the relationship between RT and achieved distance in the unconstrained extension corresponds to a processing rate of 1103 mm/sec, approximately one-half the rate inferred for constrained visual motor extension. Figure 6Eillustrates the visual motor extension slopes for the two extension tasks along with the extension slope corresponding to the covariance of RT and achieved distance during the unconstrained rotation task (Fig.6C). The baseline RT for the unconstrained extension task did not differ from that obtained for the constrained extension task.

Combined rotation and extension

For the combined task, unlike for previous tasks, participants were instructed to add both a direction and a distance to the movement stimulus appearing at the go-cue. Figure7A illustrates the group mean achieved directions and distances for each of the 16 instructions of the combined task. The separation of points, rotated and extended away from the stimulus, shows that participants were capable of following both direction and distance instructions. Figure 7, B andC, provides quantitative support for the ability of participants to process the spatial attributes of the instructions and stimuli concurrently and appropriately. For the combined task, as for the constrained tasks in which direction and distance processing occurred separately, the grouped achieved direction increased linearly with instruction direction (R² ≥ 0.97;p ≤ 0.0001; Fig. 7B), and the grouped achieved distance increased linearly with instruction distance (R² ≥ 0.97; p ≤ 0.0001; Fig. 7C).

Fig. 7.

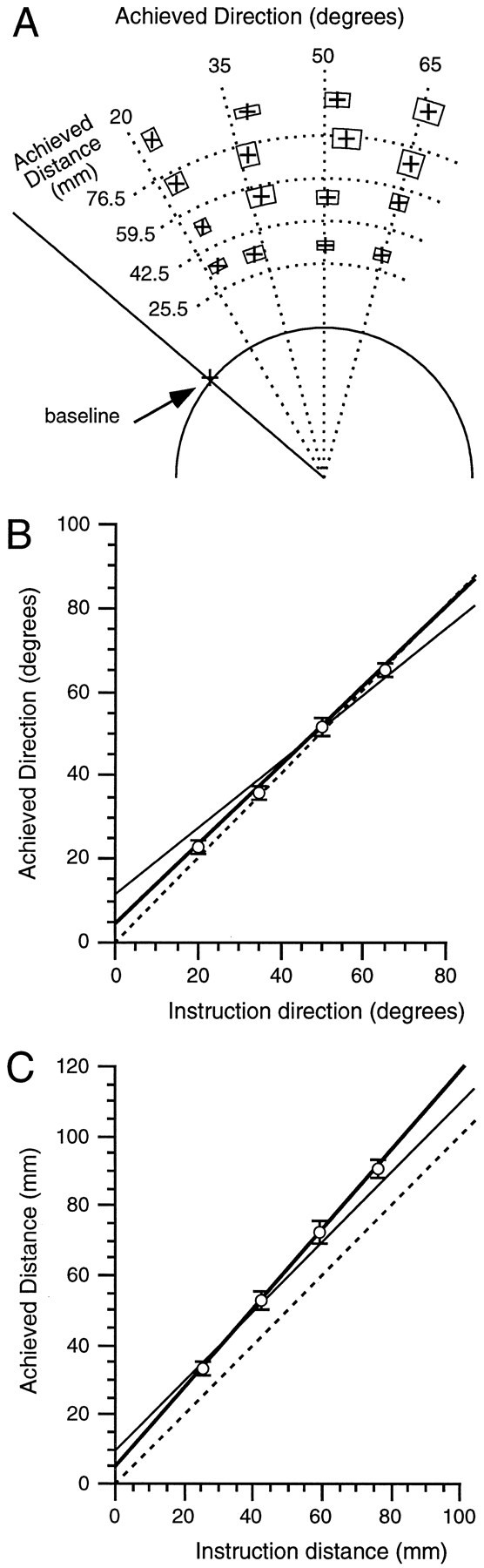
Reaching accuracy in the combined task.A, Achieved direction and distance for each combination of instructed direction and distance (details are in the legend for Fig. 3A). The intersections of the dotted lines represent the ideal achieved directions and distances for the 16 combinations of instructed direction and distance.B, Relationship between achieved and instructed direction (details are in the legend for Fig. 3B). C, Relationship between achieved and instructed distance (details are in the legend for Fig. 3C). Regression lines in B andC correspond to unity (dashed), constrained accuracy performance (thin), and combined performance (thick).

To assess whether the instruction direction and distance had independent or interacting effects on performance, we calculated for each participant the mean achieved direction, mean achieved distance, mean RT, and SD of RT separately for all 16 instructions. We then tested the following regression model for each performance variable:

$$\text{performance variable}=a+\mathbf{\text{b}}\mathbf{ }\mathbf{·}\mathbf{ }{\mathbf{\text{Direction}}}_{\mathbf{INSTRUCTION}}+\mathbf{\text{c}}\mathbf{ }\mathbf{·}\mathbf{ }{\mathbf{\text{Distance}}}_{\mathbf{INSTRUCTION}}+$$

$$\mathbf{\text{d}}\mathbf{ }\mathbf{·}\mathbf{ }{\mathbf{\text{Direction}}}_{\mathbf{INSTRUCTION}}*{\mathbf{\text{Distance}}}_{\mathbf{INSTRUCTION}}+\mathbf{\text{e}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}},$$

where a is an unknown coefficient,b–e are unknown sets of coefficients, “Direction_INSTRUCTION” is a nominal term labeling each instruction direction, “Distance_INSTRUCTION” is a nominal term labeling each instruction distance, and “part” is a nominal term labeling each participant. Instruction direction and distance were treated as nominal rather than continuous variables to avoid a priori specification of the type of interaction (that is,Direction_INSTRUCTION * Distance_INSTRUCTION). We found that the instruction direction affected the achieved direction [F_(3,135) = 845; p ≤ 0.0001], RT [F_(3,135)= 14.6; p ≤ 0.0001], and SD of RT [F_(3,135) = 2.79;p = 0.05] but not the achieved distance. The instruction distance affected the achieved distance [F_(3,135) = 513; p ≤ 0.0001], RT [F_(3,135) = 6.99; p = 0.0005], and SD of RT [F_(3,135) = 3.88;p = 0.01] but not the achieved direction. Significant differences across participants were observed for all four performance variables [F_(9,135) > 19; p ≤ 0.0001]. We did not observe a significant interaction between instruction direction and distance, which suggested independence of these two variables.

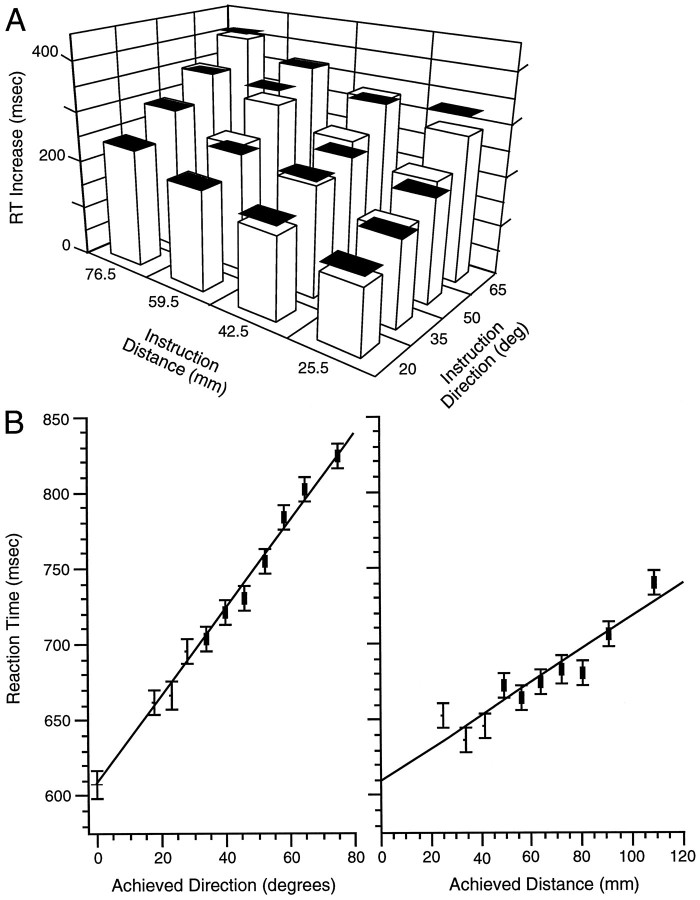
The results illustrated in Figure8A provide additional support for independent effects of instruction direction and distance on RT. As in the analysis just described, we examined mean RT (for each participant) separately for all 16 instructions. We then compared the observed data with the fitted data resulting from the following regression model:

$$RT=a+b·{\text{Direction}}_{INSTRUCTION}+c·{\text{Distance}}_{INSTRUCTION}+\mathbf{\text{d}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}},$$

where a–c are unknown coefficients, d is an unknown set of coefficients, “Direction_INSTRUCTION” is the magnitude of the instruction direction, “Distance_INSTRUCTION” is the magnitude of the instruction distance, and “part” is a nominal term labeling each participant. The strong correspondence between the observed and the fitted data indicates that instruction distance and direction had additive linear effects on RT (R² = 0.93; p ≤ 0.0001; Fig. 8A).

Fig. 8.

Reaction time in the combined task.A, Comparison of observed RT with an additive RT model. The horizontal black bars show the observed group mean RT obtained for each instruction combination. Each vertical white bar indicates the best-fitting expected mean RT when instruction direction and distance have independent linear effects on RT. The estimated intercept (that is, corresponding to mean RT for a zero instruction direction and distance) was subtracted from both the obtained and fitted means. B, Mean participant-normalized RT and mean achieved direction (left) or distance (right) for 10 bins of achieved direction (left) or distance (right) in the combined task. The fitted lines and the intercepts correspond to the regression of RT on both the achieved direction and achieved distance (see Results). For more detail on data representation, see the legend for Figure4A.

Finally, we used the achieved kinematic variables to determine processing rates for the presumed mental calculations in the combined task. Analogous to the method used to analyze processing rates for the constrained tasks (see Materials and Methods), analysis of the raw RT data used robust regression with the following model:

$$RT=a+b·{\text{Direction}}_{ACHIEVED}+c·{\text{Distance}}_{ACHIEVED}+\mathbf{\text{d}}\mathbf{ }\mathbf{·}\mathbf{ }\mathbf{\text{part}},$$

where a–c are unknown coefficients, d is an unknown set of coefficients, “Direction_ACHIEVED” is the magnitude of the achieved direction, “Distance_ACHIEVED” is the magnitude of the achieved distance, and “part” is a nominal term labeling each participant. This analysis indicated linear increases in RT with increases in both achieved direction and distance (R² = 0.81; p ≤ 0.0001; Fig. 8B; Eq. 7). The slopes of the RT function correspond to processing rates of 347° per sec for mental rotation and 921 mm per sec for visual motor extension. The intercept of the RT function for Equation 7 was 47 msec greater than was the baseline RT of 561 ± 3.2 (z = 4.75; p ≤ 0.0001):

$$RT=608+2.88·{\text{Direction}}_{ACHIEVED}+1.08·{\text{Distance}}_{ACHIEVED}.$$ Equation 7

Processing rates across tasks

Because mental rotation and visual motor extension appeared to operate independently during the combined task, we next examined whether the process of movement initiation varied across the three fundamental types of tasks. Although the baseline tasks were identical in the constrained and combined tasks, RT in the combined baseline task was 136 ± 4.3 msec higher than that for the constrained baseline tasks (z = 31.41; p ≤ 0.0001). Because we could not definitively determine why RT increased in the combined task over that observed in the other tasks, we could not make direct comparisons of processing rates obtained in the various tasks. Nevertheless, we considered two procedures to normalize observed data across experiments to compare processing rates for comparable cognitive operations.

We first considered the possibility that the general slowing of the baselines from the constrained to the combined tasks was reflected in the intercept and slopes of Equation 7. The ratio of the combined baseline RT to the constrained baseline RT was 1.32 ± 0.01. Dividing Equation 7 by this estimate normalized the relationship between RT, achieved direction, and achieved distance (Equation 8) for the combined tasks:

$$RT=460+2.18·{\text{Direction}}_{ACHIEVED}+0.82·{\text{Distance}}_{ACHIEVED}.$$ Equation 8

The intercept of this normalized function does not differ from that of the corresponding relationship in the constrained rotation task (see Eq. 3) but differs from that for the constrained extension task (z = 2.49; p ≤ 0.025; Eq. 4). The slopes obtained for achieved direction in the combined and constrained rotation tasks do not differ (see Eq. 3), whereas the slope for achieved distance in the combined task differs from that obtained in the constrained extension task (z = 3.52;p ≤ 0.0005; Eq. 4). Finally, the slope and intercept for the relationship between RT and achieved distance do not differ between the combined and unconstrained extension tasks (see Eq. 6). These results are consistent with the hypothesis that the combined task yielded an intercept and rotation processing rate comparable with that of mental rotation observed in both the constrained and unconstrained tasks. In contrast, these results indicate that the combined task yielded a processing rate for visual motor extension below that obtained in the constrained extension task but comparable with the rate obtained during the unconstrained extension task.

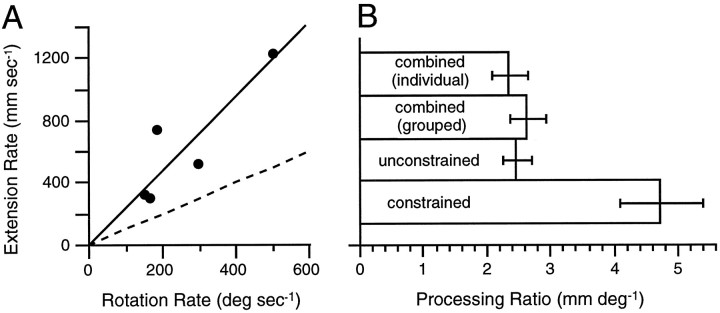
We also used an alternative and independent approach to compare the processing rates for visual motor extension among the three fundamental tasks to insure against possible idiosyncratic biases of the above-described normalizing procedure. Instead of normalizing the data with respect to baseline performance, we normalized all data to the observed processing rates for mental rotation. Validity of this approach rests on the contention that processing rates for visual motor extension and mental rotation have a consistent relationship within a given task. To examine this hypothesis, we analyzed individual processing rates in the combined task, that is, by including in the regression model interaction terms for each participant with the slopes for achieved direction and distance. All 10 participants taking part in the combined task showed a trend for increasing RT as achieved direction and distance each increased. For the 9 out of 10 participants with significant linear changes in RT for mental rotation (threshold ofp ≤ 0.05), the corresponding processing rates ranged from 150 to 1748° per sec. For the 6 out of 10 participants with significant linear RT changes with achieved distance (threshold ofp ≤ 0.05), processing rates ranged from 172 to 1231 mm per sec. Figure 9A illustrates the relationship between rotation and extension processing rates for the 5 out of 10 participants demonstrating both mental rotation and visual motor extension in the combined task. The fitted line corresponds to an extension–rotation processing ratio of 2.4 ± 0.3 mm per degree. As illustrated in Figure 9B, the estimated extension–rotation processing ratio corresponds to processing ratios estimated from the grouped RT results in the combined task (that is, from the slopes of Eq. 7) and the unconstrained task (that is, unconstrained slopes from Eqs. 5 and 6) but was significantly lower (z = 3.41; p ≤ 0.001) than the ratio of 4.8 ± 0.6 mm per degree for the constrained task (that is, estimated from the constrained slopes of Eqs. 3 and 4). The results support the hypothesis that the processing rate for visual motor extension was slowed for the combined and unconstrained tasks in comparison with constrained tasks.

Fig. 9.

Correlated processing rates for mental rotation and visual motor extension. A, Individual processing rates for both rotation and extension in the combined task (see Results for inclusion criteria). Initial regression through the five points yielded an insignificant intercept, and so the regression was fit through the origin. A dashed line is drawn through a relationship of unity. B, Comparison of the ratio of processing rates between rotation and extension obtained from all tasks.

DISCUSSION

The results provide support for the existence of a covert mechanism involved in movement distance encoding and the interaction of this mechanism with movement direction encoding. This distance mechanism has similarities to a previously described mechanism for visual motor mental rotation (Georgopoulos and Massey, 1987), and it likely engages neural circuits generally involved in visual motor transformations (Johnson et al., 1996). By requiring participants to process direction and distance information concurrently, we also found interactions between cognitive channels for visual motor mental rotation and visual motor extension. In its entirety, the current data set suggests that rotation precedes extension during premotor processing. Furthermore, the efficiency of visual motor extension apparently diminishes when volunteers choose a movement direction within the same time frame. The rotation and extension mechanisms do not seem related to extraneous variables such as movement speed or target location in visual motor space, as supported by the absence of statistically significant relationships between these variables and RT.

Previous studies investigating aspects of mental imagery have indicated distance processing somewhat analogous to the visual motor extension result described here. Visual mental imagery research suggests that RT increases systematically as participants “mentally zoom” in on a visual image or scan distances of such images (Kosslyn, 1975; Kosslyn et al., 1978). For visual motor tasks, the closest analogies to the current results could be those exemplified by Decety et al. (1989) in which RT increased as participants imagined walking greater distances. Our finding of visual motor extension likely differs from distance processing occurring during mental imagery in that the current participants likely mentally calculated a reaching distance in relation to an external target. In contrast, the cited mental imagery tasks engaging distance processing do not necessarily involve external targets (Decety et al., 1989) or the skeletal motor system (Kosslyn, 1975; Kosslyn et al., 1978). Additionally, we demonstrated that visual motor extension apparently occurs not only in response to external targets but also occurs when participants freely choose movement distance during a seemingly unrelated visual motor rotation task (see Fig. 6C,E). Thus, we believe that we have revealed and characterized a previously undocumented covert mental process by which humans add distances in the period immediately preceding movement.

Neuroanatomic substrates

Considerable attention has been devoted toward understanding how neural mechanisms code movement direction (Georgopoulos et al., 1982;Georgopoulos, 1990, 1994). It seems that neural populations in all major components of the CNS motor system participate in direction encoding (Georgopoulos et al., 1982; Fortier et al., 1989; Alexander and Crutcher, 1990; Caminiti et al., 1990a,b; Fu et al., 1993; Ferraina et al., 1997; Turner and Anderson, 1997). These findings collectively indicate that neurons in the motor system can have directional tuning and that spiking of individual neurons contributes toward forming a neuronal population vector that closely matches movement direction.

Another issue concerns whether neural mechanisms for distance and direction encoding exist within common structures and, if so, whether these mechanisms form the basis for kinematic neural representations (for example, Jaeger et al., 1993; Ashe and Georgopoulos, 1994;Lacquaniti et al., 1995). In this regard, Fu et al. (1993, 1995) have described neuronal activity in the premotor area (PMA) and primary motor cortex (MI) that covaries with both movement direction and distance. In analyzing spiking after a signal to begin movement, Fu et al. (1993, 1995) found that neural populations of PMA and MI apparently first encode direction and then distance, although the direction encoding occurred mostly before movement onset and distance encoding occurred mostly after movement onset. The current behavioral results indicating temporal ordering of direction and distance processing before movement onset indicate that the Fu et al. (1993, 1995) data do not directly relate to the current results. Somewhat more relevant are findings indicating modulation of neuronal activity in posterior parietal cortex, PMA, and basal ganglia during the explicit preparation of movement direction and distance (Riehle and Requin, 1989; Jaeger et al., 1993; Kurata, 1993; Lacquaniti et al., 1995; Turner and Anderson, 1997).

Although the data are not directly related to our findings using visual motor tasks, several investigators found activation in the frontal lobe, the parietal lobe, and the basal ganglia of humans during visual mental rotation tasks (Bonda et al., 1996; Cohen et al., 1996; Tagaris et al., 1996; Alivisatos and Petrides, 1997), tasks that have some commonality to those used here. Analysis of pathological cases also suggests the involvement of frontal and parietal lobes (e.g., Stein and Volpe, 1983; Triggs et al., 1994) and basal ganglia (for example,Pullman et al., 1988, 1990) in visual and visual motor spatial behavior, especially that involving direction and distance decisions. Taken together, the neuroimaging and lesion analysis findings indicate that the conclusions based on data obtained from humans are broadly consistent with those related to work with neuronal recordings in nonhuman primates. That is, there exists an interacting circuit encompassing structures in the parietal and frontal lobes (Wise et al., 1997), with likely involvement of the cortical-basal ganglia loops (Alexander et al., 1986), that coordinates the premotor processing required to mediate the transformation of visual coordinate information into appropriate signals for movement direction and distance.

Cognitive mechanisms

Not surprisingly, a likely conclusion of the current work is that intended movement direction and distance are primarily defined before response initiation. It also seems that explicit visual cues (as in the constrained tasks) mitigate certain needs for covert visual motor processing. That is, in the unconstrained rotation task when volunteers freely choose movement distance (Fig.1A₄), we found evidence of visual motor mental extension, even though participants had no explicit requirements to engage mechanisms for mental extension. Without one observing comparable RT changes in the constrained mental rotation task that may indicate mental extension, it appears that visual stimuli that simply indicate a reaching distance can suppress mental extension. It remains unclear how much one can generalize the finding that visual targets interfere with visual motor mental extension, although many have found that errors, especially for movement distance, increase in the absence of visual targets (for example, Soechting and Flanders, 1989).

Because the RT effects obtained in the combined task fit a stochastically independent, additive model (Fig. 8A), we believe that rotation and extension are processed serially (Sternberg, 1969). Such RT additivity clearly could not result from independent parallel processes specifying direction and distance. Although it is plausible for interacting parallel channels to mimic the additive mean RT responses we have observed (McClelland, 1979), the additivity of RT variability that we have additionally described is unlikely to result from this alternative processing scheme (Meyer et al., 1988). As such, the data from the combined task most likely result from serial processing of mental calculations for direction and distance.

The current results also indicate that movement direction and distance specification share neural processing resources (Favilla et al., 1989). The primary evidence of sharing of processing resources comes from the observations of slowed visual motor extension when volunteers internally generated movement direction, as in the unconstrained extension task, and when volunteers had explicit instructions to calculate mentally both direction and distance. Interestingly so, mental rotation rate was apparently not affected by either internal generation of movement distance or explicitly instructed visual motor extension.

On the basis of our finding suggesting that mental rotation and extension are processed serially, we believe that mental rotation precedes visual motor extension. As noted above, the rate of mental rotation remains unaffected by distance planning, whereas visual motor extension rates slow considerably when participants also planned direction. Assuming shared resources for movement direction and distance planning, either in a single structure, such as PMA (Riehle and Requin, 1989; Fu et al., 1995), or across a brain network including PMA, posterior parietal cortex, and basal ganglia (Jaeger et al., 1993;Wise et al., 1997), it is difficult to imagine how mental rotation would influence visual motor extension if it occurred after visual motor extension. Thus, by default, it would seem that mental rotation occurs before visual motor extension. However, we cannot definitively reject an alternative hypothesis that mental rotation, unlike extension, cannot be slowed even if preceded by distance planning. The current results could also be accounted for by the alternative hypothesis of unordered serial processing in which rotation and extension alternate in steps.

Our findings contribute to how humans use visual landmarks while making motor-related decisions before movement onset. A major unresolved issue concerns whether premotor action direction and distance computations operate serially or in parallel. To address this question, workers have examined temporal relationships between movement direction and distance processing with one of three main techniques: precueing (Goodman and Kelso, 1980; Rosenbaum, 1980; Bonnet et al., 1982; Larish and Frekany, 1985; Bock and Arnold, 1992), priming (Semjen, 1984; Larish and Frekany, 1985; Lepine et al., 1989), and timed responding (Hening et al., 1988; Favilla et al., 1989, 1990). The findings most relevant to ours come from Bock and Arnold (1992) and from Ghez and coworkers (Hening et al., 1988; Favilla et al., 1989, 1990; Ghez et al., 1997) because their tasks required continuous, rather than discrete, decisions about movement direction and distance. Using a precueing method, Bock and Arnold (1992) found that while participants prepare movements, they extract salient action direction and distance information from visual targets in a parallel, but noninteracting, manner. One might term this process sensory extraction, and Bock and Arnold (1992) argue that for this early stage of visual motor processing, direction and distance channels operate independently although within the same time frame. In contrast, motor specification of action direction and distance likely occurs via parallel but interacting channels (Hening et al., 1988; Favilla et al., 1989, 1990). We found that during cognitive planning of visually guided reaching, direction and distance computations occur serially and with stochastically independent processing rates. Further, these computations have limited capacity. An explanation for why the relationship between action direction and distance encoding varies during different aspects of action preparation may be related to the specific computations required for each distinct processing stage and the inputs to and imbedded circuits within brain structures mediating visual motor transformations.