Abstract
To obtain a quantitative characterization of voltage-activated calcium currents in respiratory neurons, we performed voltage-clamp recordings in the transverse brainstem slice of mice from neurons located within the ventral respiratory group. It is assumed that this medullary region contains the neuronal network responsible for generating the respiratory rhythm. This study represents one of the first attempts to analyze quantitatively the currents in respiratory neurons. The inward calcium currents of VRG neurons consisted of two components: a high voltage-activated (HVA) and a low voltage-activated (LVA) calcium current. The activation threshold of the HVA current was at −40 mV. It was fully activated (peak voltage) between −10 and 0 mV. The half-maximal activation (V50) was at −27.29 mV ± 1.15 (n = 24). The HVA current was inactivated completely at a holding potential of −35 mV and fully deinactivated at a holding potential of −65 mV (V50, −52.26 mV ± 0.27;n = 18). The threshold for the activation of the LVA current was at −65 mV. This current had its peak voltage between −50 and −40 mV (mean, V50 = −59.15 mV ± 0.21; n = 15). The LVA current was inactivated completely at a holding potential of −65 mV and deinactivated fully at a holding potential of −95 mV (mean,V50 = −82.40 mV ± 0.32;n = 38). These properties are consistent with other studies suggesting that the LVA current is a T-type current. The properties of these inward currents are discussed with respect to their role in generating Ca2+ potentials that may contribute to the generation of the mammalian respiratory rhythm.
Keywords: T-type calcium current, rhythm generation, brainstem, ventral respiratory group, medulla, breathing
There is increasing evidence that the neural network responsible for generating the rhythmic breathing movements in mammals is localized within the ventrolateral medulla (Smith et al., 1995; Richter et al., 1997; Rekling and Feldman, 1998). The neurons within this so-called ventral respiratory group (VRG) form excitatory and inhibitory synaptic interactions between each other and have specific membrane properties that are proposed to be critical for generating the respiratory rhythm (Richter et al., 1987, 1992; Funk and Feldman, 1995; Smith et al., 1995; Ramirez and Richter, 1996; Ramirez et al., 1997; Rekling and Feldman, 1998). Previous studies have shown that rhythmic postsynaptic activities and action potential discharges activate high and low voltage-activated (HVA and LVA) calcium currents (Richter et al., 1993; Champagnat and Richter, 1994; Pierrefiche et al., 1994). It therefore is assumed that such intrinsic membrane properties are involved in the generation and termination of rhythmic burst discharges (Pierrefiche et al., 1994). These in vivoexperiments are supported by in vitro studies that were performed in the neonatal brainstem–spinal cord preparation (Onimaru et al., 1996). Using current-clamp recordings, they have demonstrated qualitatively that rhythmic neurons have calcium currents that contribute to the generation of respiratory burst discharges (Onimaru et al., 1996). To better describe how such currents may contribute to rhythmic oscillations in VRG neurons, we found it necessary to perform a quantitative analysis. This is particularly important for computational models of respiratory rhythm generation, which at present have incorporated electrophysiological parameters obtained from other neuronal systems (Smith et al., 1995; Rybak et al., 1997). Here we present a quantitative analysis of the voltage-dependent activation and inactivation properties of low and high voltage-activated calcium currents in VRG neurons. With the use of the visually controlled whole-cell patch-clamp technique (Dodt and Ziegelgänsberger, 1990) VRG neurons were recorded in a spontaneously active transverse slice preparation.
This transverse slice preparation is a well established in vitro model for respiratory rhythm generation in neonatal rats (Smith et al., 1991) and neonatal and juvenile mice (Funk et al., 1994;Ramirez et al., 1996). The preparation contains the pre-Bötzinger complex (pBC), a subregion of the VRG that seems to be particularly important for generating the respiratory rhythm (Smith et al., 1991;Funk et al., 1993; Ramirez et al., 1998). The pBC projects to the hypoglossal (XII) nucleus. The XII nucleus and its peripheral projections in the XII nerve are rhythmically active in phase with inspiration (Withington-Wray et al., 1988). Here we used the XII nerve discharge to identify functionally a neuron within the ventrolateral medulla. The activity of a rhythmically active neuron was assumed to be “respiratory” in nature if its rhythmic synaptic input occurred in phase with XII burst discharge. A neuron that received no respiratory rhythmic synaptic input was called a “nonrhythmic” neuron. We characterized the voltage dependencies (activation and inactivation properties) of low and high voltage-activated calcium currents of rhythmic neurons as well as nonrhythmic neurons to determine whether rhythmic neurons are characterized by unique membrane properties.
MATERIALS AND METHODS
Preparation and solutions. The experiments were performed in the transverse medullary slice preparation obtained from 0- to 6-d-old neonatal mice (CD1 mice). The mice were anesthetized deeply with ether and decapitated at the C3/C4 spinal level. All steps to obtain functional slice preparations have been published elsewhere (Ramirez et al., 1996) and shall be summarized only briefly in this study. The brainstem was isolated in ice-cold artificial CSF (ACSF) containing (in mm): 128 NaCl, 3 KCl, 1.5 CaCl2, 1 MgSO4, 25 NaHCO3, 1 NaH2PO4, and 30 d-glucose equilibrated with carbogen (95% O2/5% CO2), pH 7.4. Secured in a vibratome with the rostral end up, thin slices were sectioned serially from rostral to caudal until the rostral boundary of the pBC was reached. This region was recognized by cytoarchitectonic landmarks such as inferior olive (IO), nucleus of the solitary tract (NTS), hypoglossal nucleus (XII), and nucleus ambiguus (NA), but there was no longer the facial nucleus (Fig.1A). Then a 650- to 700-μm-thick section was made caudal of this rostral boundary, and the resulting rhythmic slice was transferred immediately into a recording chamber. The preparationwas submerged with its rostral end up under a stream of ACSF (temperature, 29°C; flow rate, 16 ml/min) and stabilized for 10 min. The potassium concentration of the ACSF was raised over a period of another 15 min and maintained at 8 mm to keep the rhythmic activity regular for up to 13 hr.
Fig. 1.
Preparation and definition of rhythmic versus nonrhythmic neurons of the ventral respiratory group (VRG).A, Schematic representation of the transverse slice containing the pre-Bötzinger complex (pBC;gray area), a region in the VRG that is presumably the site for respiratory rhythm generation. The right panelshows a video image obtained from the VRG. The image contains neurons that were visualized with infrared Nomarski optics. The electrode tip is visible and points to the voltage-clamp recording shown inC. B, Extracellular recording obtained from the rhythmically active hypoglossal rootlet (XII,bottom trace) and its integrated signal (top trace). C, Burst activity in the integrated XII recording (top trace) corresponds to rhythmic inward currents in the whole-cell patch recording (bottom trace). A neuron with this property is defined as rhythmic (R). D, Burst activity in the integrated XII recording (top trace) is not correlated with synaptic activity in the intracellularly recorded VRG neuron (bottom trace). A neuron with this characteristic is defined as nonrhythmic (nR). IO, Inferior olive; NA, nucleus ambiguus; NTS, nucleus tractus solitarius; Sp5, spinal trigeminal nucleus;XII, hypoglossus motor nucleus; XII nerve, XII rootlet.
Recording and data analysis. The activity from the peripheral end of cut XII rootlets was recorded extracellularly with suction electrodes and integrated electronically with a leaky residual capacity circuit (Fig. 1B). Whole-cell patch recordings were obtained from the VRG. We assume that the recordings were obtained primarily from the pBC, a region that was identified by using anatomical landmarks clearly visible under a dissection microscope (Fig. 1A, inset). However, because the exact anatomical borders of the slice vary, we cannot exclude the possibility that some of our recordings also were obtained from VRG neurons that were localized more rostral to the pBC. Recordings were obtained with unpolished patch electrodes. These electrodes were manufactured from filamented borosilicate glass (Clark GC150F, Pangbourne, UK) and had a resistance of 3–5 MΩ when filled with a solution containing in concentration (in mm): 110 CsCl, 30 TEA-Cl, 1 CaCl2, 10 EGTA, 2 MgCl2, 4 Na2ATP, and 10 HEPES, pH 7.2.
VRG neurons were recorded with the conventional patch-clamp technique (Hamill et al., 1981) and were analyzed by using the software program pClamp 6.0 (Axon Instruments, Foster City, CA) and the patch-clamp amplifier (AxoPatch 1D), together with the digitizing interface (Digidata 1200A, Axon Instruments).
All quantitative data are given in mean ± SE, if not indicated otherwise. Significance was assessed with the Student’s ttest, and significance was assumed for values p < 0.05. This study is based on 48 whole-cell patch-clamp recordings from rhythmic (n = 19) and nonrhythmic (n = 29) neurons located in the ventrolateral medulla.
Because TTX was applied after a whole-cell configuration had been established, it was not possible to record more than one neuron from each slice preparation. VRG neurons located at least three to four cell layers (∼80–150 μm) caudal from the rostral surface of the slice were recorded under visual control (Fig. 1A). Neurons that were located directly at the slice surface were not analyzed, because they more likely were damaged during the preparation than neurons located deeper within the slice. VRG neurons were identified as rhythmic (R; Fig. 1C) if the intracellularly recorded rhythmic activity was in phase with the rhythmic activity recorded from the hypoglossal nerve (XII; Fig.1C) (for details, see Ramirez et al., 1996). Neurons without rhythmic synaptic input were declared as nonrhythmic neurons (nR; Fig. 1D). All rhythmic VRG neurons in this study received rhythmic synaptic inputs that were coincident with XII nerve discharge. Thus, as will be reviewed in Discussion, no preinspiratory neurons (Onimaru et al., 1996) nor type-1 and type-2 inspiratory neurons (Rekling et al., 1996) were considered in this study.
Current response traces were recorded with either off- or on-line leak subtraction (P/4 protocol), eliminating the linear leak current and residual capacity currents. The liquid junction potential was adjusted manually to zero immediately before the patch-clamp configuration was established. The serial resistance was always 80% compensated and regularly corrected throughout the experiments. The input resistance of all neurons was between 193 and 841 MΩ.
After establishing a whole-cell configuration (Hamill et al., 1981) and before commencing our measurements, we examined voltage-activated calcium currents every 90 sec for 5–10 min. During this time period no measurable rundown of the whole-cell calcium current amplitudes was observed in our recording conditions.
We have to emphasize that whole-cell voltage-clamp recordings from neurons embedded in a functional network are accompanied by difficult clamp control. This could lead to incorrect values for current amplitudes. Thus, recordings with obvious space-clamp problems (Armstrong and Gilly, 1992; White et al., 1995) were discarded. Poor space clamping was indicated by rebound spikes (rapid fast-inactivating inward currents, which were induced by steps from depolarizing test potentials to the former holding potential) or by an increase in the delay to onset of an inward current with increasing magnitude of test pulse. Steps to higher test potentials typically were associated with a reduction in delay to current onset. We also discarded neurons with insufficiently blocked K+ currents. This was evident in outward currents typically commencing at voltage steps to 10 mV.
To compare current densities, we calculated the area of the investigated neurons from the whole-cell capacity value (readings from the amplifier controls) obtained with 80% compensated serial resistance. We used 1 μF/cm2 for the value of specific capacitance (Hille, 1992) in our calculations.
Please note that the numbers of neurons that were evaluated quantitatively are not always consistent with the number of qualitative observations. In our computer analysis we were able to obtain average data only from those neurons that were examined with the identical experimental protocol. Because this was not always possible, most recordings were evaluated quantitatively for only a limited number of aspects.
All substances used in this study were obtained from Sigma (St. Louis, MO) except TTX, which was obtained from Alomone Labs (Jerusalem, Israel).
RESULTS
Pharmacological isolation of whole-cell voltage-activated calcium currents in VRG neurons
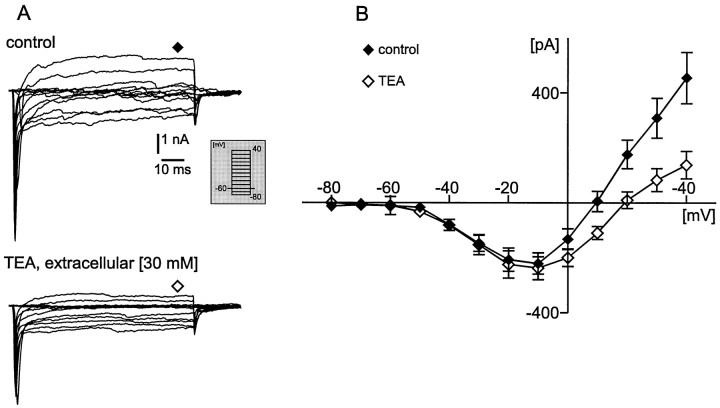
The voltage-activated potassium currents were blocked intracellularly with 110 mm CsCl and 30 mmtetraethylammonium (TEA) chloride. To test the effective intracellular block of voltage-activated potassium currents, we applied additional 30 mm TEA into the extracellular solution. Under these conditions the voltage-dependent currents (Fig.2A) were activated by depolarizing voltage steps from −80 to 40 mV (duration, 150 msec; step size, 10 mV) from a holding potential (Vh) of −60 mV (Fig. 2A, inset). The voltage steps were separated by an interval of 2 sec to avoid current inactivation. Note that, in the example shown in Figure 2A, sodium currents were not blocked (see next paragraph). Thus, the current amplitude was measured 75 msec after the onset of the test pulse (steady state, as indicated in Fig.2A, diamonds). The steady state also was measured in this case because the influence of possible unblocked potassium currents was larger at the steady-state value as compared with the peak value. However, even when the steady-state current amplitude was measured, the additional bath application of 30 mm TEA did not change the maximal steady-state inward current amplitude significantly (Vm −10, p = 0.508; Vm 0, p = 0.054), but it always reduced significantly the outward current amplitude at membrane potentials (Vm) from 10 to 40 mV (Vm 10, p = 0.004;Vm 20, p = 0.0003;Vm 30, p = 0.0001;Vm 40, p < 0.0001). An average of 25 neurons is shown in Figure 2B as a current–voltage relationship curve (control, filled diamonds; additional TEA, open diamonds). These experiments showed that the intracellular blockade of potassium currents with TEA and CsCl was sufficient for investigating the maximal inward current amplitude. This is particularly the case because we always quantified in the following experiments the peak current amplitude (as described in the next paragraph), which probably was affected less by unblocked outward currents as compared with the steady-state current amplitude (Figs.3-10). Thus, in the following experimental protocols we did not add extracellular TEA in order to save time associated with the solution exchange and to reduce the danger of losing the recording configuration.
Fig. 2.
A, Voltage-clamp current response traces from a holding potential of −60 mV to different test potentials (from −80 to 40 mV; see inset) obtained from a VRG neuron under control conditions [intracellular CsCl (110 mm) + TEA (30 mm); top panel] and after bath application of 30 mm tetraethylammonium (TEA) chloride (bottom panel). Possible remaining unblocked K+ currents were most obvious at the steady-state level. Therefore, current amplitudes were measured at the steady-state values (75 msec after onset of test pulse; seediamonds at top and bottom panels). B, Average current–voltage response curve from 25 VRG neurons. Filled diamonds represent current response under control conditions, and open diamonds correspond to current response after TEA application.
Fig. 3.
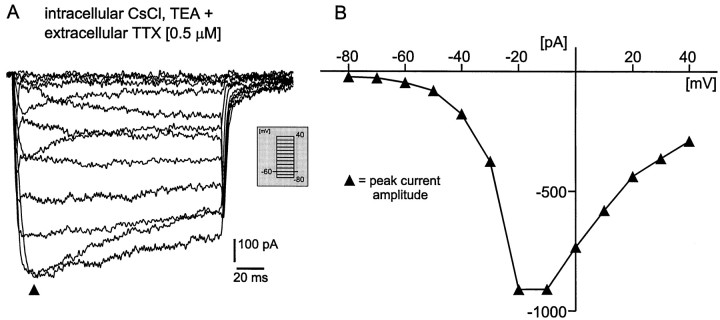
Voltage-clamp recordings from a VRG neuron after bath application of 0.5 μm TTX [intracellular solution contains CsCl (110 mm) and TEA (30 mm) to block potassium currents]. A, Current response traces from a holding potential (Vh) of −60 mV to different test potentials (see inset). B, Current–voltage response curve obtained from the current traces inA. Note that, in contrast to Figure 2, the current amplitude was measured at the peak response, as indicated inA (filled triangles).
Fig. 4.
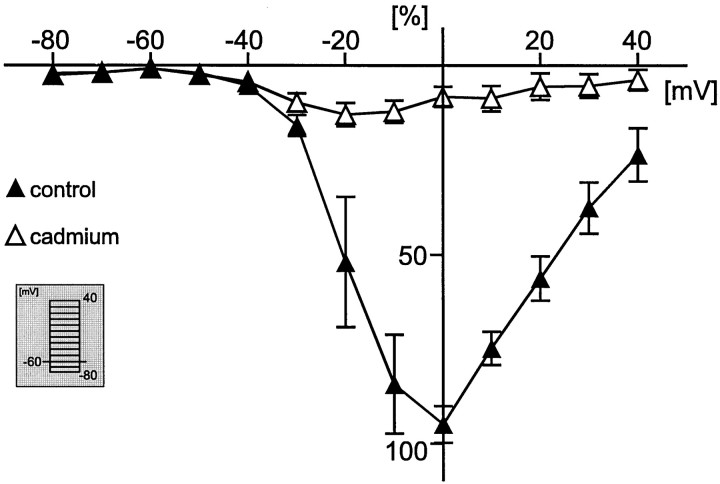
Normalized current–voltage curve (for calculations, see Results) from current response traces obtained by depolarizing steps from a holding potential (Vh) of −60 mV to different test potentials (see inset). The filled triangles represent the percentage peak current amplitude under control conditions (only voltage-activated sodium and potassium currents are blocked), and the open triangles indicate the percentage of peak current amplitude after bath application of 200 μm cadmium chloride.
Fig. 5.
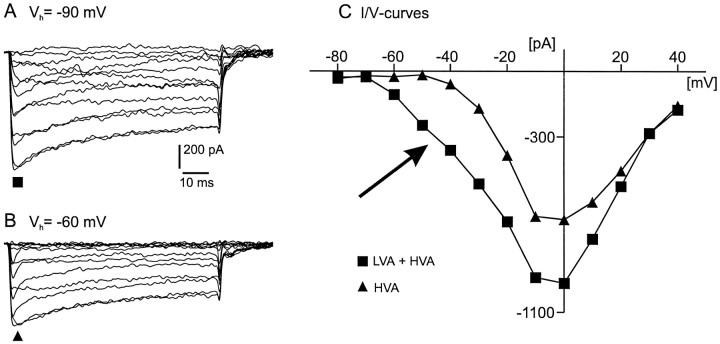
Calcium current response traces of a VRG neuron from different holding potentials. A, Current response traces obtained by steps from a holding potential of −90 mV to test potentials between −80 and 40 mV. B, Current response traces from a holding potential of −60 mV to the same test potentials as indicated for A. C, Current–voltage relation curve of the peak current amplitude from A(filled squares) and B(filled triangles). Filled triangles represent HVA calcium current, and filled squares indicate HVA plus LVA calcium currents.
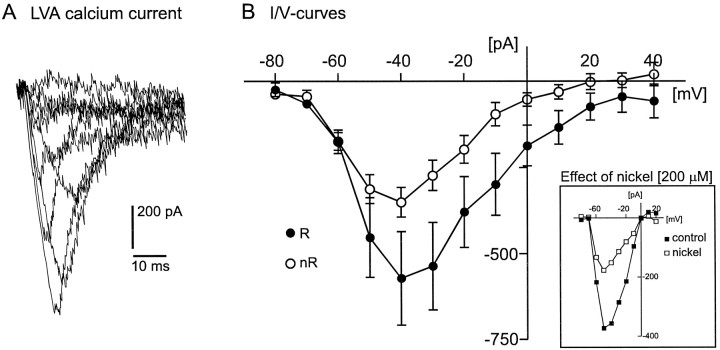
Fig. 6.
A, Example for LVA calcium current response traces (for protocol description, see Results).B, Comparison of the LVA peak current amplitude (current–voltage relationship curves) between rhythmic (R, filled circles; n = 12) and nonrhythmic (nR, open circles; n = 9) VRG neurons. Inset, Example (I–V curves) for a nickel-induced (200 μm) reduction of the LVA current amplitude (see Results).
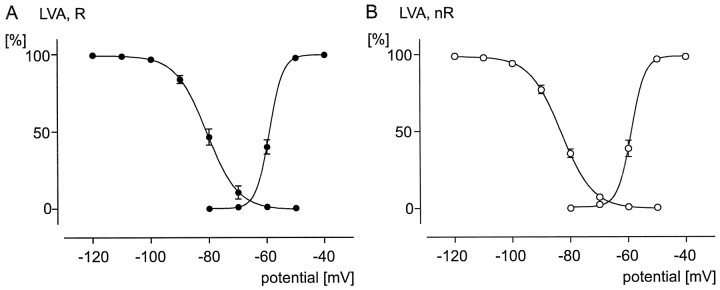
Fig. 7.
Comparison of voltage dependencies (activation and inactivation curves) of LVA calcium currents between rhythmic (R, filled circles) and nonrhythmic (nR, open circles) VRG neurons. All data points are normalized (see Results). A sigmoidal Boltzmann curve is fit through each data set (see Results). A, Voltage-dependent activation (data points on the right curve; n= 9) and inactivation (data points on theleft curve; n = 11) properties for the LVA calcium current in rhythmic neurons. B, Voltage-dependent activation (data points on theright curve; n = 6) and inactivation (data points on the left curve;n = 27) properties for the LVA calcium current in nonrhythmic neurons.
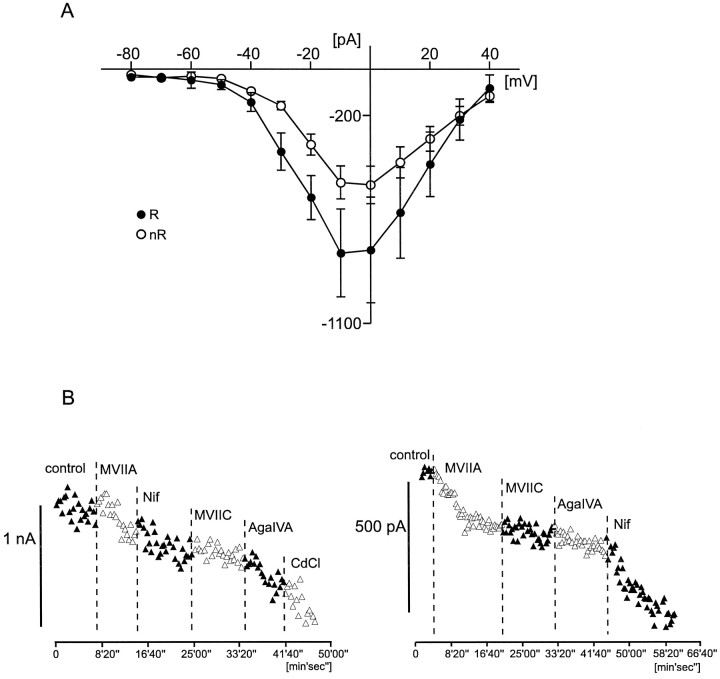
Fig. 8.
A, Comparison of the HVA calcium current amplitude (current–voltage relationship curves) between rhythmic (R, filled circles; n = 10) and nonrhythmic (nR, open circles; n= 21) VRG neurons. B, Two examples for a qualitative characterization of different subtypes of the HVA calcium current in VRG neurons (left figure, rhythmic;right figure, nonrhythmic). Current amplitude (for detailed protocol description, see Results) is plotted against time. Specific calcium channel blockers ω-conotoxin MVIIA (to block N-type calcium channels), ω-conotoxin MVIIC (to block Q-type calcium channels), ω-agatoxin IVA (to block P-type calcium channels), and nifedipine (to block L-type calcium channels) have been applied as indicated by the dotted lines. MVIIA, ω-Conotoxin MVIIA; MVIIC, ω-conotoxin MVIIC;AgaIVA, ω-agatoxin IVA; Nif, nifedipine; CdCl, cadmium chloride.
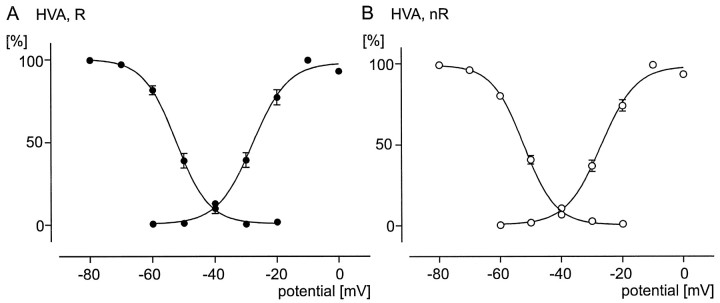
Fig. 9.
Comparison of voltage dependencies (activation and inactivation curves) of HVA calcium currents between rhythmic (R, filled circles) and nonrhythmic (nR, open circles) VRG neurons. All data points are normalized (see Results). A sigmoidal Boltzmann curve is fit through each data set (see Results). A, Voltage-dependent activation (data points on the right curve; n= 9) and inactivation (data points on theleft curve; n = 5) properties for the HVA calcium current in rhythmic neurons. B, Voltage-dependent activation (data points on theright curve; n = 15) and inactivation (data points on the leftcurve; n = 13) properties for the HVA calcium current in nonrhythmic neurons.
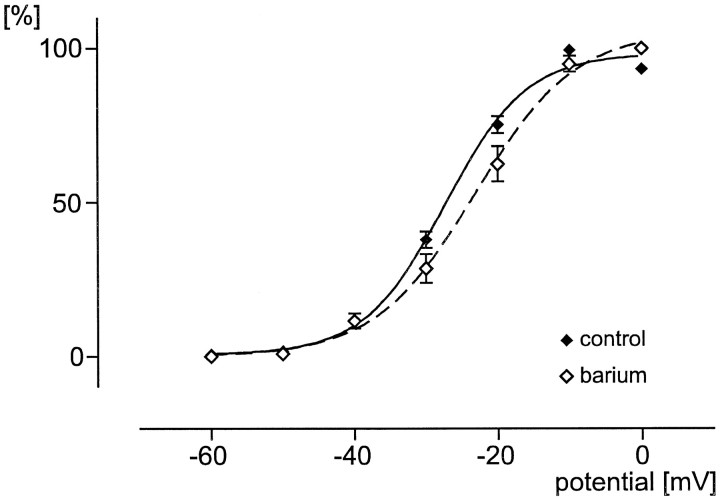
Fig. 10.
HVA voltage-dependent activation curves under control conditions (Ca2+ as charge carrier;filled diamonds) and after bath application of 5 mm barium chloride (open diamonds). The fit is a sigmoidal Boltzmann curve (control, solid line; barium, dotted line).
In addition, voltage-activated inward sodium currents were blocked by extracellular bath application of 0.5 μm tetrodotoxin (TTX). Using the same voltage protocol as described earlier, we activated voltage-dependent inward currents and measured the amplitudes at the peak response as indicated (filled triangles) in Figure 3A (I–V curve, Fig.3B). These currents appeared to be voltage-activated calcium currents, because 86.5% of the maximal peak current amplitude was blocked by extracellular 200 μm Cd2+(n = 10) [Fig. 4(normalized values, 0 ≅ 0%; maximum value, ≅ 100%), control (filled triangles) and cadmium (open triangles)].
Electrophysiological differentiation of whole-cell voltage-activated calcium currents in VRG neurons
When it was started from a holding potential of −90 mV, an additional component of the peak current (Fig.5A) was elicited by the same test voltage steps as described in Figure 3. This component was not evoked when the starting holding potential was −60 mV (Fig.5B). The difference between the currents elicited from the holding potentials of −60 and −90 mV is most evident in theI–V curve (Fig. 5C). In the following we will refer to the currents evoked from a holding potential of −60 mV as the HVA calcium currents (filled triangles). The additional currents evoked from a holding potential of −90 mV will be called the LVA calcium currents. In Figure 5C(filled squares) an arrow indicates the current containing both the LVA and HVA calcium currents (Carbone and Lux, 1984; Hille, 1992).
Isolation of the LVA calcium current and comparison between rhythmic and nonrhythmic VRG neurons
The current responses obtained by depolarizing voltage steps from a Vh of −60 mV were subtracted from the current responses obtained from a Vh of −90 mV to isolate the LVA calcium current from the HVA calcium current. This subtraction method frequently has been performed as a protocol to isolate the LVA calcium current (see Bean, 1985; Hille, 1992). The subtraction reveals an inactivating inward current (Fig.6A). The average peak voltage of the LVA calcium current was at −40 mV (Fig.6B). In all examined cases (n = 4) the LVA calcium current amplitude was reduced (>50%) in the presence of low nickel chloride concentrations (200 μm) as exemplified in Figure 6B (inset). The sensitivity to nickel was not quantified further.
We found that 79% of all investigated rhythmic neurons had a detectable LVA calcium current, whereas only 44% of the nonrhythmic neurons expressed a LVA calcium current. The average value of the detectable LVA calcium currents was larger for rhythmic (R;n = 12) (Vm −40, −572 ± 136 pA; Vm −50, −453 ± 116 pA) (Fig.6B, filled circles) than for nonrhythmic neurons (nR; n = 9) (Vm −40, −351 ± 43 pA; Vm −50, −312 ± 41 pA) (Fig. 6B, open circles). However, a significant difference between rhythmic and nonrhythmic neurons could not be observed (Vm −40, p = 0.644;Vm −50, p = 0.972).
The area for rhythmic neurons (n = 24) was 1854 ± 183 μm2. For nonrhythmic neurons (n = 25) the area was 1020 ± 114 μm2. The average area of the rhythmic neurons was significantly larger (p = 0.0014) than the area of the nonrhythmic neurons. The current density (pA/μm2) was calculated for LVA and HVA calcium currents. The calculated current density of LVA calcium currents for rhythmic neurons was 0.379 ± 0.074 pA/μm2(n = 10). For nonrhythmic neurons the current density was 0.414 ± 0.062 pA/μm2 (n= 8). The average current density value of rhythmic neurons was not significantly different (p = 0.729) from the value of nonrhythmic neurons.
Voltage-dependent activation and inactivation properties of the LVA calcium current
The activation properties were evaluated from the isolated LVA calcium currents (see above). The absolute peak current amplitudes were always normalized (0% ≅ minimum current amplitude; 100% ≅ maximum current amplitude), and all normalized data points obtained in that manner were distributed normally (p > 0.10). The average of all normalized values for each test potential was calculated and plotted against the respective test potentials as well as fit with a sigmoidal Boltzmann curve (I/Imax = 1/1 + exp(V50 − V/slope) (Fig.7). The half-maximal activation (V50, the membrane potential at which one-half of all involved channels are activated) obtained for rhythmic neurons (−59.05 ± 0.01 mV; n = 9) (Fig.7A, right curve) was not significantly different (p = 0.344) from the V50value (−58.91 ± 0.12 mV; n = 6) obtained for nonrhythmic neurons (Fig. 7B, right curve). Similarly, the slope (the slope factor describes the steepness of a curve) of activation was not significantly different (p = 0.067) between rhythmic (2.36 ± 0.02; Fig. 7A) and nonrhythmic neurons (2.40 ± 0.38; Fig. 7B).
The inactivation properties of the LVA calcium current were evaluated by using the following waveform protocol: different holding potentials incrementing in 10 mV steps from −120 to −60 mV were maintained for 2 sec before being stepped to a test potential of −50 mV (duration, 50 msec). This waveform protocol revealed the maximal peak amplitude of the LVA calcium current from different holding potentials. The measured peak amplitudes were normalized (see detailed description above), and all normalized data points were distributed normally (p > 0.10). The mean values were calculated and plotted against the respective holding potentials. A sigmoidal Boltzmann curve (I/Imax = 1/1 + exp(V − V50/slope) was fit through the data points (Fig. 7A,B). TheV50 value of inactivation obtained for rhythmic neurons (−80.72 ± 0.14 mV; n = 11) (Fig.7A, left curve) was not significantly different (p = 0.061) from the V50value (−83.09 ± 0.11 mV; n = 27) obtained for nonrhythmic neurons (Fig. 7B, left curve). Similarly, no significant difference (p = 0.584) between rhythmic (−5.31 ± 0.13 mV; Fig. 7A) and nonrhythmic neurons (−5.38 ± 0.09 mV; Fig. 7B) was found for the slope of inactivation.
Comparison between the HVA calcium current of rhythmic and nonrhythmic VRG neurons
To compare HVA calcium currents between rhythmic and nonrhythmic neurons, we obtained the current–voltage relationship of 31 neurons (10 rhythmic and 21 nonrhythmic neurons) by using the voltage protocol described in Materials and Methods. With 1.5 mm external Ca2+ as the charge carrier, the peak current amplitude for nonrhythmic neurons was −490 ± 71 pA at a test potential of −10 mV and −501 ± 81 pA at 0 mV (Fig.8A, open circles). For rhythmic neurons the peak current amplitude was −795 ± 189 pA at −10 mV and −782 ± 228 pA at 0 mV (Fig. 8A, filled circles). The HVA calcium current amplitude was not significantly different between rhythmic neurons and nonrhythmic neurons (Vm −10, p = 0.087;Vm 0, p = 0.145), but the values tended to be larger in rhythmic as compared with nonrhythmic neurons. The current density value of HVA calcium currents in rhythmic neurons was 0.437 ± 0.070 pA/μm2 (n= 14). For nonrhythmic neurons the current density was 0.558 ± 0.077 pA/μm2 (n = 17). The average current density values of the HVA calcium current for rhythmic and nonrhythmic neurons were not significantly different (p = 2.660).
Different subtypes of calcium currents contributed to the HVA currents. This is demonstrated by bath application of several specific HVA calcium channel blockers (Fig. 8B). The effect on HVA calcium peak current amplitudes was assessed by applying at every 20 sec a voltage step from −60 to −10 mV (duration, 150 msec). The HVA calcium current amplitudes were reduced after the application of ω-conotoxin MVIIA (0.5 μm), ω-conotoxin MVIIC (0.5 μm), ω-agatoxin IVA (200 nm), and nifedipine (4 μm), indicating the presence of several calcium current subtypes (N-, Q-, P-, and L-type, respectively) in both rhythmic and nonrhythmic neurons (Fig. 8B). However, the contribution of each of these subtypes varied between individual neurons; therefore, further quantification will be necessary to assess possible variations between functionally different neurons.
Voltage-dependent activation and inactivation properties of the HVA calcium current
To assess the activation properties of the HVA calcium currents, we increased the voltage in 10 mV steps from −60 to 0 mV from a holding potential of −60 mV. The measured peak amplitudes were normalized, and the mean values were calculated and plotted against the respective holding potentials (see detailed description above). A sigmoidal Boltzmann curve was obtained as described above (Fig.9A,B). The half-maximal activation of all examined rhythmic neurons (n = 9) wasV50 = −27.82 ± 1.13 mV, and the slope was 5.69 ± 1.10 (Fig. 9A, right curve). For nonrhythmic neurons (n = 15) the V50 value was −26.97 ± 1.13 mV, and the slope value was 5.70 ± 1.03 (Fig. 9B, right curve). The average voltage-dependent activation properties of rhythmic and nonrhythmic neurons were not statistically different (V50,p = 0.400; slope, p = 0.494).
The voltage-dependent inactivation properties were determined by using the following waveform protocol: the voltage was changed in 10 mV steps from −80 to −20 mV and maintained for 2 sec before being stepped to the test potential of −10 mV (duration, 50 msec). The measured peak amplitudes were normalized, and the mean values were calculated and plotted against the respective holding potentials. A sigmoidal Boltzmann curve was plotted as described above (Fig. 9A,B). The half-maximal inactivation for all investigated rhythmic neurons (n = 5) was V50 = −52.40 ± 0.27 mV, and the slope was −5.23 ± 0.25 (Fig. 9A, left curve). The inactivation properties for nonrhythmic neurons (n = 13) were V50 = −52.21 ± 0.42 mV, and the slope was −5.17 ± 0.38 (Fig. 9B, left curve). The average inactivation properties of nonrhythmic neurons were not significantly different from the properties of rhythmic neurons (V50, p = 0.973; slope, p = 0.833).
Effect of barium on the voltage-dependent activation of the HVA calcium current
We used Ca2+ as a charge carrier to assess the whole-cell calcium current that presumably will flow into the cell under normal conditions. However, this may lead to a calcium-dependent inactivation of the inward calcium current. To examine how this inactivation may affect the voltage-dependent activation properties, we added 5 mm barium chloride into the bath solution. As described above, no significant difference of the voltage dependencies between rhythmic and nonrhythmic neurons was observed. Thus, the data obtained for these two groups of neurons were pooled for this comparison. With Ca2+ ions as the charge carrier theV50 value for 24 neurons (9 rhythmic plus 15 nonrhythmic) was −27.29 ± 1.15 mV, and the slope was 5.70 ± 1.05 (Fig. 10, filled diamonds; fit, solid line); if barium ions were added (n = 6), the V50 value decreased to −23.12 ± 1.01 mV. The slope value increased significantly to 7.03 ± 0.95 (Fig. 10, open diamonds; fit, dotted line). The peak current amplitude increased by 85.4 ± 33.4%. However, at this relatively low concentration of barium (5 mm), which was added to the external 2 mmcalcium concentration, the increase was not significant (p = 0.1237). We also observed that the peak voltage tended to shift from −10 toward 0 mV. This shift was also not significant.
DISCUSSION
Calcium currents in rhythmic neurons
Low voltage- and high voltage-activated inward currents were characterized for rhythmic neurons located within the ventrolateral medulla of mice in the so-called VRG. We used the extracellularly recorded XII activity as a marker for inspiratory activity (Withington-Wray et al., 1988; Smith et al., 1990). All rhythmic neurons recorded in this study received rhythmic synaptic input coinciding with XII bursts (see Fig. 1). Those that received no rhythmic synaptic input were called nonrhythmic neurons. However, the identification of a nonrhythmic neuron is not unambiguous, because these neurons could be rhythmically active during other behaviors such as vomiting, mastication, or vocalization. Nonrhythmic neurons also could be respiratory neurons that are recruited only during more intense breathing conditions. Moreover, the presence of nonrhythmic neurons also could reflect an artifact of the in vitropreparation, because the slicing technique inevitably removed other portions of the respiratory network. It is well established that underin vivo conditions respiratory neurons are distributed widely within the VRG (Bianchi et al., 1995; Richter et al., 1997). Thus, the isolation of a portion of the VRG may lead to a loss of rhythmic input into some of the neurons. However, this possibility seems unlikely, because it would imply that some VRG neurons receive rhythmic input only from areas of the VRG that were not included in the slice.
In this study we did not investigate all known types of respiratory neurons. Our study focused only on those neurons that received phasic synaptic input coinciding with hypoglossus bursts. Thus, our conclusions cannot be extended to all known types of respiratory neurons.
Voltage dependencies of LVA and HVA calcium currents
The voltage-dependent activation and inactivation properties of calcium currents were similar in rhythmic neurons and nonrhythmic neurons. In the case of the LVA calcium current the voltage-dependent properties were also consistent with the values described for other central neurons. The half-maximal inactivation of −82 mV as described here was within the range seen elsewhere (−83 to −86 mV) (O’Dell and Alger, 1991; Swandulla et al., 1991; Huguenard et al., 1993; Dzhura et al., 1996; Beck et al., 1997; Mouginot et al., 1997) as was the threshold for activation at −65 mV (Hernandez-Cruz and Pape, 1989;Sayer et al., 1990; O’Dell and Alger, 1991; Huguenard et al., 1993;Viana et al., 1993; Dzhura et al., 1996; Beck et al., 1997; Mouginot et al., 1997). As was observed also in other studies, the electrophysiologically isolated LVA calcium current showed a more rapid decay than the HVA calcium currents (Fedulova et al., 1985; Bean, 1989;Hernandez-Cruz and Pape, 1989; Hess, 1990; Mynlieff and Beam, 1992;Huguenard et al., 1993; Viana et al., 1993; Wang et al., 1996; Beck et al., 1997; Mouginot et al., 1997).
The HVA calcium currents described in this study for rhythmic neurons had an activation threshold of −40 mV. This is also consistent with other studies (Sayer et al., 1990; Hay et al., 1996; Yu and Shinnick-Gallagher, 1997). The half-maximal inactivation potential described for amygdala neurons was −58 mV (Yu and Shinnick-Gallagher, 1997); in our study we obtained a value of −52 mV. However, it must be emphasized that in contrast to the LVA current there is greater variability in the half-maximal inactivation potential obtained for the HVA current in different preparations [intracardiac neurons, −33.7 mV (Joeng and Wurster, 1997); carotid body glomus cells, −38 to −47 mV (Silva and Lewis, 1995; Overholt and Prabhakar, 1997); olfactory bulb neurons, −67 mV (Wang et al., 1996); hippocampal pyramidal cells, −78 mV (Thompson and Wong, 1991)]. These differences could be attributable to the fact that different subtypes of HVA calcium currents (Fox et al., 1987) contribute to the whole-cell current in the different preparations. In this study we found qualitatively a great variability for the contribution of different subtypes. Thus, further studies will be necessary also to investigate quantitatively the known subtypes of HVA currents and their contribution to the discharge pattern of respiratory neurons.
The functional role of calcium currents in rhythmic respiratory neurons
The amplitude of the LVA calcium current, also known as T-type calcium current (Carbone and Lux, 1984, 1987; Fox et al., 1987; Tsien et al., 1988), previously was not determined quantitatively for neurons in the VRG. We observed that the T-type amplitude in rhythmic neurons was more variable and tended to be larger as compared with nonrhythmic neurons. The average current density of rhythmic and nonrhythmic neurons was almost similar; therefore, the larger average area of rhythmic neurons could be responsible for the difference in the T-type amplitudes in both groups.
However, most rhythmic neurons (79%) had a T-type calcium current, whereas it was expressed in only 47% of the nonrhythmic neurons. This finding is different from a previous in vitro study that suggested that only a minor proportion of respiratory neurons has T-type calcium currents (Onimaru et al., 1996). This discrepancy could be attributable to differences in the types of examined respiratory neurons. Our study included only neurons that commenced to discharge simultaneously with the hypoglossus burst, whereas the study of Onimaru et al. (1996) examined mostly the so-called preinspiratory neurons that discharge before the XII burst. Furthermore, the study by Onimaru et al. (1996) is based on current-clamp experiments in which the presence of a T-type calcium current was inferred from the ability to evoke a rebound spike.
The finding that rhythmic neurons more often express a T-type calcium current is interesting, because it is believed that the activation of the T-type calcium current plays an important role in triggering the onset of a respiratory cycle (Ramirez and Richter, 1996; Richter et al., 1997). The role of the T-type calcium currents in triggering a new rhythmic cycle also has been postulated in other rhythm-generating neuronal networks (Llinás and Yarom, 1981; Huguenard and McCormick, 1992; Huguenard and Prince, 1992; Huguenard, 1996).
However, as also discussed by Onimaru et al. (1996), it is unlikely that the T-type calcium current plays an important role in the initiation of a respiratory cycle under the in vitroconditions. Although the neurons receive massive synaptic glycinergic input during the interburst interval, the resting membrane potential of respiratory neurons under in vitro conditions is at a voltage range of approximately −55 mV (Onimaru et al., 1996). At this membrane potential most of the T-type calcium current is inactivated according to our study. However, this current may play an important role under in vivo conditions in which the membrane potentials are closer to −70 mV (Richter, 1983). During the interburst interval these in vivo neurons are hyperpolarized sufficiently to remove the inactivation of the T-type calcium current. This removal may prepare the T-type current for triggering the next respiratory cycle (Richter et al., 1993, 1997; Ramirez and Richter, 1996). In fact, under in vivo conditions some respiratory neurons are characterized by a rapid activity onset and a maximal peak frequency at the beginning of their active phase (Richter, 1983;Ramirez et al., 1997; Richter et al., 1997).
The functional role of the HVA calcium current in the different types of respiratory neurons remains unresolved. Given that the contribution of different subtypes was variable, it is conceivable that different neuron types have quantitatively different subtypes of currents that may contribute to the generation of bursting properties as well as synaptic transmission. To examine this possibility, we believe it will be necessary to identify quantitatively the different subtypes of HVA calcium currents in functionally identified neurons, as has been done in the lamprey swimming system (El Manira and Bussières, 1997).
It is agreed generally that the respiratory rhythm is generated by a combination of synaptic properties and voltage-dependent inward and outward currents (Bianchi et al., 1995; Smith et al., 1995; Ramirez and Richter, 1996; Richter et al., 1997; Rybak et al., 1997). However, all models proposed for respiratory rhythm generation are still qualitative and are based on membrane properties obtained from neurons in other brain areas. This study aimed at providing the first quantitative values for the calcium currents of rhythmic VRG neurons. This is an essential first step if we want to understand how the complex interplay between membrane and synaptic properties leads to the generation of rhythmic activity in the respiratory neuronal network.
Footnotes
This work was supported by an award to the University of Chicago’s Division of Biological Sciences under the Research Resources Program for Medical Schools of the Howard Hughes Medical Institute. The initial part of the study was supported by two operating grants from the Deutsche Forschungsgemeinschaft to J.M.R.
Correspondence should be addressed to Dr. Jan-Marino Ramirez, Department of Organismal Biology and Anatomy, The University of Chicago, 1027 East 57th Street, Chicago, IL 60637.
REFERENCES
- 1.Armstrong CM, Gilly WF. Access resistance and space clamp problems associated with whole-cell patch clamping. Methods Enzymol. 1992;207:100–122. doi: 10.1016/0076-6879(92)07007-b. [DOI] [PubMed] [Google Scholar]
- 2.Bean BP. Two kinds of calcium channels in canine atrial cells. Differences in kinetics, selectivity, and pharmacology. J Gen Physiol. 1985;86:1–30. doi: 10.1085/jgp.86.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bean BP. Classes of calcium channels in vertebrate cells. Annu Rev Physiol. 1989;51:367–384. doi: 10.1146/annurev.ph.51.030189.002055. [DOI] [PubMed] [Google Scholar]
- 4.Beck H, Steffens R, Heinemann U, Elger CE. Properties of voltage-activated Ca2+ currents in acutely isolated human hippocampal granule cells. J Neurophysiol. 1997;77:1526–1537. doi: 10.1152/jn.1997.77.3.1526. [DOI] [PubMed] [Google Scholar]
- 5.Bianchi AL, Denavit-Saubie M, Champagnat J. Central control of breathing in mammals: neuronal circuitry, membrane properties, and neurotransmitters. Physiol Rev. 1995;75:1–45. doi: 10.1152/physrev.1995.75.1.1. [DOI] [PubMed] [Google Scholar]
- 6.Carbone E, Lux HD. A low voltage-activated, fully inactivating Ca channel in vertebrate sensory neurons. Nature. 1984;310:501–502. doi: 10.1038/310501a0. [DOI] [PubMed] [Google Scholar]
- 7.Carbone E, Lux HD. Kinetics and selectivity of a low voltage-activated calcium current in chick and rat sensory neurons. J Physiol (Lond) 1987;386:547–570. doi: 10.1113/jphysiol.1987.sp016551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Champagnat J, Richter DW. The roles of potassium conductance in expiatory pattern generation in anaesthetized cats. J Physiol (Lond) 1994;479:127–138. doi: 10.1113/jphysiol.1994.sp020282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dodt HU, Ziegelgänsberger W. Visualizing unstained neurons in living brain slices by infrared DIC videomicroscopy. Brain Res. 1990;537:333–336. doi: 10.1016/0006-8993(90)90380-t. [DOI] [PubMed] [Google Scholar]
- 10.Dzhura IO, Naidenov VG, Lyubanova OP, Kostyuk PG, Shuba YM. Characterization of hypothalamic low voltage-activated calcium channels based on their functional expression in Xenopus oocytes. Neuroscience. 1996;70:729–738. doi: 10.1016/s0306-4522(96)83010-7. [DOI] [PubMed] [Google Scholar]
- 11.El Manira A, Bussières N. Calcium channel subtypes in lamprey sensory and motor neurons. J Neurophysiol. 1997;78((3):1334–1340. doi: 10.1152/jn.1997.78.3.1334. [DOI] [PubMed] [Google Scholar]
- 12.Fedulova SA, Kostyuk PG, Veselovsky NS. Two types of calcium channels in the somatic membrane of newborn rat dorsal root ganglion neurons. J Physiol (Lond) 1985;359:431–446. doi: 10.1113/jphysiol.1985.sp015594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fox AP, Nowycky MC, Tsien RW. Kinetic and pharmacological properties distinguishing three types of calcium currents in chick sensory neurons. J Physiol (Lond) 1987;394:149–172. doi: 10.1113/jphysiol.1987.sp016864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Funk GD, Feldman JL. Generation of respiratory rhythm and pattern in mammals: insights from developmental studies. Curr Opin Neurobiol. 1995;5:778–785. doi: 10.1016/0959-4388(95)80106-5. [DOI] [PubMed] [Google Scholar]
- 15.Funk GD, Smith JC, Feldman JL. Generation and transmission of respiratory oscillations in medullary slices: role of excitatory amino acids. J Neurophysiol. 1993;70:1497–1515. doi: 10.1152/jn.1993.70.4.1497. [DOI] [PubMed] [Google Scholar]
- 16.Funk GD, Smith JC, Feldman JL. Development of thyrotropin-releasing hormone and norepinephrine potentiation of inspiratory-related hypoglossal motoneuron discharge in neonatal and juvenile mice in vitro. J Neurophysiol. 1994;72:2538–2541. doi: 10.1152/jn.1994.72.5.2538. [DOI] [PubMed] [Google Scholar]
- 17.Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ. Improved patch-clamp techniques for high resolution current recording from cells and cell-free membrane patches. Pflügers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 18.Hay M, Hasser EM, Lindsley KA. Area postrema voltage-activated calcium currents. J Neurophysiol. 1996;75:133–141. doi: 10.1152/jn.1996.75.1.133. [DOI] [PubMed] [Google Scholar]
- 19.Hernandez-Cruz A, Pape HC. Identification of two calcium currents in acutely dissociated neurons from the rat lateral geniculate nucleus. J Neurophysiol. 1989;61:1270–1283. doi: 10.1152/jn.1989.61.6.1270. [DOI] [PubMed] [Google Scholar]
- 20.Hess P. Calcium channels in vertebrate cells. Annu Rev Neurosci. 1990;13:337–356. doi: 10.1146/annurev.ne.13.030190.002005. [DOI] [PubMed] [Google Scholar]
- 21.Hille B. Ionic channels of excitable membranes, pp 1–607. Sinauer; Sunderland, MA: 1992. [Google Scholar]
- 22.Huguenard JR. Low-threshold calcium currents in central nervous system neurons. Annu Rev Physiol. 1996;58:329–348. doi: 10.1146/annurev.ph.58.030196.001553. [DOI] [PubMed] [Google Scholar]
- 23.Huguenard JR, McCormick DA. Simulation of the currents involved in rhythmic oscillations in thalamic relay neurons. J Neurophysiol. 1992;68:1373–1383. doi: 10.1152/jn.1992.68.4.1373. [DOI] [PubMed] [Google Scholar]
- 24.Huguenard JR, Prince DA. A novel T-type current underlies prolonged Ca2+-dependent burst firing in GABAergic neurons of rat thalamic reticular nucleus. J Neurosci. 1992;12:3804–3817. doi: 10.1523/JNEUROSCI.12-10-03804.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Huguenard JR, Gutnick MJ, Prince DA. Transient Ca2+ currents in neurons isolated from rat lateral habenula. J Neurophysiol. 1993;70:158–166. doi: 10.1152/jn.1993.70.1.158. [DOI] [PubMed] [Google Scholar]
- 26.Joeng SW, Wurster RD. Calcium channel currents in acutely dissociated intracardiac neurons from adult rats. J Neurophysiol. 1997;77:1769–1778. doi: 10.1152/jn.1997.77.4.1769. [DOI] [PubMed] [Google Scholar]
- 27.Llinás R, Yarom Y. Properties and distribution of ionic conductances generating electroresponsiveness of mammalian inferior olivary neurons in vitro. J Physiol (Lond) 1981;315:569–584. doi: 10.1113/jphysiol.1981.sp013764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mouginot D, Bossu JL, Gähweiler BH. Low-threshold Ca2+ currents in dendritic recordings from Purkinje cells in rat cerebellar slice cultures. J Neurosci. 1997;17:160–170. doi: 10.1523/JNEUROSCI.17-01-00160.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mynlieff M, Beam KG. Characterization of voltage-dependent calcium currents in mouse motoneurons. J Neurophysiol. 1992;68:85–92. doi: 10.1152/jn.1992.68.1.85. [DOI] [PubMed] [Google Scholar]
- 30.O’Dell TJ, Alger BE. Single calcium channels in rat and guinea pig hippocampal neurons. J Physiol (Lond) 1991;426:739–767. doi: 10.1113/jphysiol.1991.sp018577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Onimaru H, Ballanyi K, Richter DW. Calcium-dependent responses in neurons of the isolated respiratory network of newborn rats. J Physiol (Lond) 1996;491:677–695. doi: 10.1113/jphysiol.1996.sp021249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Overholt JL, Prabhakar NR. Calcium current in rabbit carotid body glomus cells is conducted by multiple types of high voltage-activated calcium channels. J Neurophysiol. 1997;78:2467–2474. doi: 10.1152/jn.1997.78.5.2467. [DOI] [PubMed] [Google Scholar]
- 33.Pierrefiche O, Champagnat J, Richter DW. Calcium-dependent conductances control neurons involved in termination of inspiration in cats. Neurosci Lett. 1994;184:101–104. doi: 10.1016/0304-3940(94)11179-m. [DOI] [PubMed] [Google Scholar]
- 34.Ramirez JM, Richter DW. The neuronal mechanism of respiratory rhythm generation. Curr Opin Neurobiol. 1996;6:817–825. doi: 10.1016/s0959-4388(96)80033-x. [DOI] [PubMed] [Google Scholar]
- 35.Ramirez JM, Quellmalz UJA, Richter DW. Postnatal changes in the mammalian respiratory network as revealed by the transverse brainstem slice of mice. J Physiol (Lond) 1996;491:799–812. doi: 10.1113/jphysiol.1996.sp021258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ramirez JM, Telgkamp P, Elsen FP, Quellmalz UJA, Richter DW. Respiratory rhythm generation in mammals: synaptic and membrane properties. Respir Physiol. 1997;110:71–85. doi: 10.1016/s0034-5687(97)00074-1. [DOI] [PubMed] [Google Scholar]
- 37.Ramirez JM, Schwarzacher SW, Pierrefiche O, Olivera BM, Richter DW. Selective lesioning of the cat pre-Bötzinger complex in vivo eliminates breathing but not gasping. J Physiol (Lond) 1998;507:895–907. doi: 10.1111/j.1469-7793.1998.895bs.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rekling JC, Feldman JL. Pre-Bötzinger complex and pacemaker neurons: hypothesized site and kernel for respiratory rhythm generation. Annu Rev Physiol. 1998;60:385–405. doi: 10.1146/annurev.physiol.60.1.385. [DOI] [PubMed] [Google Scholar]
- 39.Rekling JC, Champagnat J, Denavit-Saubie M. Electroresponsive properties and membrane potential trajectories of three types of inspiratory neurons in the newborn mouse brainstem in vitro. J Neurophysiol. 1996;75:795–810. doi: 10.1152/jn.1996.75.2.795. [DOI] [PubMed] [Google Scholar]
- 40.Richter DW. Generation and maintenance of the respiratory rhythm. J Exp Biol. 1983;100:93–107. doi: 10.1242/jeb.100.1.93. [DOI] [PubMed] [Google Scholar]
- 41.Richter DW, Champagnat J, Mifflin SW. Membrane properties of medullary respiratory neurons of the cat. In: Sieck GC, Gandevia SC, Cameron WE, editors. Respiratory muscles and their neuromotor control. Liss; New York: 1987. pp. 9–15. [Google Scholar]
- 42.Richter DW, Ballanyi K, Schwarzacher S. Mechanisms of respiratory rhythm generation. Curr Opin Neurobiol. 1992;2:788–793. doi: 10.1016/0959-4388(92)90135-8. [DOI] [PubMed] [Google Scholar]
- 43.Richter DW, Champagnat J, Jacquin T, Benack AR. Calcium currents and calcium-dependent potassium currents in mammalian medullary respiratory neurons. J Physiol (Lond) 1993;470:23–33. doi: 10.1113/jphysiol.1993.sp019844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Richter DW, Ballanyi K, Ramirez JM. Respiratory rhythm generation. In: Miller AD, Bianchi AL, Bishop BP, editors. Neural control of the respiratory muscles. CRC; Boca Raton, FL: 1997. pp. 119–131. [Google Scholar]
- 45.Rybak IA, Paton JF, Schwaber JS. Modeling neural mechanisms for genesis of respiratory rhythm and pattern. I. Models of respiratory neurons. J Neurophysiol. 1997;77:1994–2006. doi: 10.1152/jn.1997.77.4.1994. [DOI] [PubMed] [Google Scholar]
- 46.Sayer RJ, Schwindt PC, Crill WE. High- and low-threshold calcium currents in neurons acutely isolated from rat sensorimotor cortex. Neurosci Lett. 1990;120:175–178. doi: 10.1016/0304-3940(90)90031-4. [DOI] [PubMed] [Google Scholar]
- 47.Silva MJMe, Lewis DL. L- and N-type Ca2+ channels in adult rat carotid body chemoreceptor type I cells. J Physiol (Lond) 1995;489:689–699. doi: 10.1113/jphysiol.1995.sp021083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Smith JC, Greer JJ, Liu G, Feldman JL. Neural mechanisms generating respiratory patterns in mammalian brainstem–spinal cord in vitro. I. Spatiotemporal patterns of motor and medullary neuron activity. J Neurophysiol. 1990;64:1149–1169. doi: 10.1152/jn.1990.64.4.1149. [DOI] [PubMed] [Google Scholar]
- 49.Smith JC, Ellenberger HH, Ballanyi K, Richter DW, Feldman JL. Pre-Bötzinger complex: a brainstem region that may generate respiratory rhythm in mammals. Science. 1991;254:726–729. doi: 10.1126/science.1683005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Smith JC, Funk GD, Johnson SM, Feldman JL. Cellular and synaptic mechanisms generating respiratory rhythm: insights from in vitro and computational studies. In: Trouth CO, Millis R, Kiwull-Schone H, Schlaefke M, editors. Ventral brainstem mechanisms and control of respiration and blood pressure. Dekker; New York: 1995. pp. 463–496. [Google Scholar]
- 51.Swandulla D, Carbone E, Lux H. Do calcium channel classifications account for neuronal calcium channel diversity? Trends Neurosci. 1991;14:46–51. doi: 10.1016/0166-2236(91)90018-p. [DOI] [PubMed] [Google Scholar]
- 52.Thompson SM, Wong RKS. Development of calcium current subtypes in isolated rat hippocampal pyramidal cells. J Physiol (Lond) 1991;439:671–689. doi: 10.1113/jphysiol.1991.sp018687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tsien RW, Lipscombe D, Madison DV, Bley KR, Fox AP. Multiple types of neuronal calcium channels and their selective modulation. Trends Neurosci. 1988;11:431–438. doi: 10.1016/0166-2236(88)90194-4. [DOI] [PubMed] [Google Scholar]
- 54.Viana F, Bayliss DA, Berger AJ. Calcium conductances and their role in the firing behavior of neonatal rat hypoglossal motoneurons. J Neurophysiol. 1993;69:2137–2149. doi: 10.1152/jn.1993.69.6.2137. [DOI] [PubMed] [Google Scholar]
- 55.Wang X, McKenzie JS, Kemm RE. Whole-cell calcium currents in acutely isolated olfactory bulb output neurons of the rat. J Neurophysiol. 1996;75:1138–1151. doi: 10.1152/jn.1996.75.3.1138. [DOI] [PubMed] [Google Scholar]
- 56.White JA, Sekar NS, Kay AR. Errors in persistent inward currents generated by space-clamp errors: a modeling study. J Neurophysiol. 1995;73:2369–2377. doi: 10.1152/jn.1995.73.6.2369. [DOI] [PubMed] [Google Scholar]
- 57.Withington-Wray DJ, Mifflin SW, Spyer KM. Intracellular analysis of respiratory-modulated hypoglossal motoneurons in the cat. Neuroscience. 1988;25:1041–1051. doi: 10.1016/0306-4522(88)90057-7. [DOI] [PubMed] [Google Scholar]
- 58.Yu B, Shinnick-Gallagher P. Dihydropyridine- and neurotoxin-sensitive and -insensitive calcium currents in acutely dissociated neurons of the rat central amygdala. J Neurophysiol. 1997;77:690–701. doi: 10.1152/jn.1997.77.2.690. [DOI] [PubMed] [Google Scholar]