A Model for Encoding Multiple Object Motions and Self-Motion in Area MST of Primate Visual Cortex

Abstract

Many cells in the dorsal part of the medial superior temporal (MST) region of visual cortex respond selectively to specific combinations of expansion/contraction, translation, and rotation motions. Previous investigators have suggested that these cells may respond selectively to the flow fields generated by self-motion of an observer. These patterns can also be generated by the relative motion between an observer and a particular object. We explored a neurally constrained model based on the hypothesis that neurons in MST partially segment the motion fields generated by several independently moving objects. Inputs to the model were generated from sequences of ray-traced images that simulated realistic motion situations, combining observer motion, eye movements, and independent object motions. The input representation was based on the response properties of neurons in the middle temporal area (MT), which provides the primary input to area MST. After applying an unsupervised optimization technique, the units became tuned to patterns signaling coherent motion, matching many of the known properties of MST cells. The results of this model are consistent with recent studies indicating that MST cells primarily encode information concerning the relative three-dimensional motion between objects and the observer.

Several areas of extrastriate visual cortex are well suited to the analysis of visual motion. Among these is the medial superior temporal area (MST) in the superior temporal sulcus of the macaque monkey visual cortex (Maunsell and van Essen, 1983a;Ungerleider and Desimone, 1986). MST receives its primary afferent inputs from the middle temporal area (MT), yet the response properties of neurons in MST are quite distinct from those of neurons in MT (Duffy and Wurtz, 1991a; Lagae et al., 1994). MST contains at least two major subdivisions (Saito et al., 1986; Komatsu and Wurtz, 1988), the lateroventral region (MSTI) and the dorsomedial region (MSTd).

Neurons in MSTI respond best to the motion of small spots of light. Electrical stimulation and chemical lesions of this region modify the maintenance of pursuit eye movements, suggesting that MSTI might contribute to the generation of these motion-dependent movements (Dürsteler and Wurtz, 1988; Komatsu and Wurtz, 1989). Cells in MSTd have large receptive fields and respond best to large-field motion. Some MSTd neurons are sensitive to simple translational (planar) motion, whereas many others respond to rotating or expanding/contracting visual stimuli (Saito et al., 1986; Sakata et al., 1986; Tanaka et al., 1986). Duffy and Wurtz (1991a) found that MSTd neurons respond not only to pure expansion/contraction, rotation, or translation, but often they respond to two or all three of these motions. Recently it has been found that many MSTd cells are preferentially tuned to specific intermediate motions, which combine these motion types (Graziano et al., 1994).

Combinations of these motions are generated as the animal moves through its environment, which suggests that area MSTd could be involved in optic flow analysis. When an observer moves through a static environment, a singularity in the flow field known as the focus of expansion may be used to determine the direction of heading (Gibson, 1950; Warren and Hannon, 1988; Heeger and Jepson, 1990; Hildreth, 1992). Previous computational models of MSTd (Perrone, 1992; Lappe and Rauschecker, 1993; Perrone and Stone, 1994) have shown how navigational information related to heading may be represented by these cells. These investigators propose that each MSTd cell represents a potential heading direction and responds to the aspects of the flow that are consistent with that direction.

In natural dynamic environments, however, MSTd cells are often faced with complex flow patterns that are produced by the combination of observer motion with other independently moving objects. These complex flow fields are not a single coherent pattern, but instead are composed of multiple coherent patterns that may be mixed at some locations because of occlusion. The observation that coherent flows correspond to local subpatterns in flow fields suggests an important role for the regular patterns to which MSTd cells have been found to be selectively tuned. These patterns may effectively segment a complex flow field into coherent patches, where each such patch corresponds to the aspects of the flow arising from a single cause—the relative motion of the observer and some object or surface in the scene (Nakayama and Loomis, 1974).

Adoption of this view implies a new goal for MST: to encode, or account for, the ensemble of motion causes that generated the complex flow field. An MST cell that responds to a local subpattern accounts for a portion of the flow field, specifically the portion that arises from a single motion cause. In this manner, MST could be providing a representation suitable for segmenting motion signals from the moving objects. An analogous operation is thought to be essential for object recognition in cluttered scenes, where deciding which features belong together as part of the same object reduces the complexity of matching image features to object models. Here a scene containing multiple moving objects may be parsed by grouping the components of the flow field that arise because of the motion of a single object or part of an object.

Unlike previous models, a cell in the model represents a motion hypothesis of a scene element relative to the observer. This is a more general purpose representation that could be useful not only in robustly estimating heading detection but also in facilitating several other tasks thought to occur further along the motion processing stream, such as localizing objects and parsing scenes containing multiple moving objects.

In this paper, we describe a computational model based on the hypothesis that neurons in MST signal those aspects of the flow that arise from a common underlying cause. We designed the model to match some basic aspects of the relevant areas of visual cortex and made a restricted set of computational assumptions. We then used an optimization method to compute the parameters of the model and compared the responses of units in the resulting model with the responses of MST neurons to the same visual stimuli. Our goal was first to demonstrate that a model based on the hypothesis of motion segmentation and constructed according to relevant aspects of the visual system could account for response properties of MST neurons, and second to show how these response properties could be extracted from the statistics of natural flow images, on the basis of inputs received from neurons in area MT.

The architecture of the model and the visual stimuli that we used to optimize it are described in Materials and Methods. In Results, we show that this model was able to capture several known properties of information processing in MST as tested with visual stimuli that have been used in physiological experiments. Finally, some of the specific and general implications of the model are presented in Discussion.

MATERIALS AND METHODS

The visual input to the system was a computer-generated movie containing some combination of observer motion, eye movements, and one to four objects undergoing independent three-dimensional (3-D) motion. An optical flow algorithm was then applied to yield local motion estimates that approximated the type of representation that may occur in area MT. The network consisted of three layers. The responses of units in the first layer, based on the response properties of neurons in area MT, served as input to the second layer, which was meant to represent area MST. The second layer had the same connectivity pattern to the output layer, which might be identified with the feedback connections back to area MT (see Discussion). The weights on all connections were determined by an optimization algorithm that attempted to force the network to recreate the input pattern on the output units. The optimization procedure was unsupervised insofar as the model received no information about the motions of objects in the movie from an external teacher. We discuss the inputs, the network, and the unsupervised optimization algorithm in more detail below.

Stimuli. The flow field input to the network was derived from a movie that was produced using a computer graphics program. The various movies were intended to simulate various natural motion situations. Sample situations included one in which all motion was caused by the observer’s movement, and the camera was pointed in the motion direction. Another situation that produced a qualitatively different flow field was when the motion was again solely caused by observer motion, but the camera was not pointed in that direction—it was either pointing in a fixed other direction or fixed on a stationary object in the scene, and hence rotating. Other situations included independent motion of some of the objects in the environment. Each movie was a sequence of images that simulated one of these situations.

The images were created using a flexible ray-tracing program (Persistence of Vision Ray Tracer, which is publically available on the Internet at http://www.povray.org), which allowed the simulation of many different objects, backgrounds, observer/camera motions, and lighting effects. We used a database of six objects (a block of Swiss cheese, a snail, a panther, a fish, a ball, and a teapot) and three different backgrounds. A movie was generated by random selection of one to four of the objects located in 3-D space (x, y, z) and a background. To simulate one of the motion situations, a random selection of motion parameters followed: (1) the observer’s motion along (x, z) gave the velocity of walking; (2) the camera could rotate and point at different locations in (x, y), allowing the simulation of either a fixed gaze direction or the tracking of an object during motion; or (3) each object could undergo independent 3-D motion.

We used the same stochastic algorithm to generate both the training and testing stimuli. First, a background and initial observer/camera position were chosen. Then the camera motion was selected from the following distribution: with probability 1/3 the camera was stationary; in the remaining 2/3, the total shift in the sequence in the x direction was chosen from a Gaussian distribution centered at 0 with SD of 6° of visual angle (10% change in field of view), whereas the z direction had a maximum shift of 30% of the field of view. An additional bias was added so that the camera motion in z was forward twice as often as backward. Then from one to four of the set of six objects was chosen to be present in the image. The position and motion of each object were chosen not to exceed a maximum shift of 10° of visual angle. These were also chosen to ensure that the object would always be visible, which was determined by computing the initial and final position of the center of the object (based on both its own and the camera motion) and testing that it lay within the field of view. An object was chosen to move in the scene with a probability of 1/5, which allowed for many images to contain independent object motion. Finally, the camera direction was chosen so that the following three conditions were equiprobable: the camera direction corresponded to the motion direction; it corresponded to a different fixed direction; and it remained fixed on one of the stationary objects in the scene. In general, these parameters were chosen to provide a rich training (and testing) set of possible inputs to the system.

To summarize, the ranges of stimulus parameters are as follows. Each is expressed with respect to the first and last frames of each 15 frame movie: (1) field of view, 60° horizontal × 45° vertical; (2) composition, one of three different backgrounds and up to four objects per movie; (3) object position, anywhere within the visual field, but each object could occupy up to no more than 20% and no less than 1% of the field; (4) independent object translation, up to 10° of visual angle; (5) camera translation, the typical simulated translation was within a range of 6° to the left and right of straight ahead; and (6) camera rotation, maximum of 5° of visual angle.

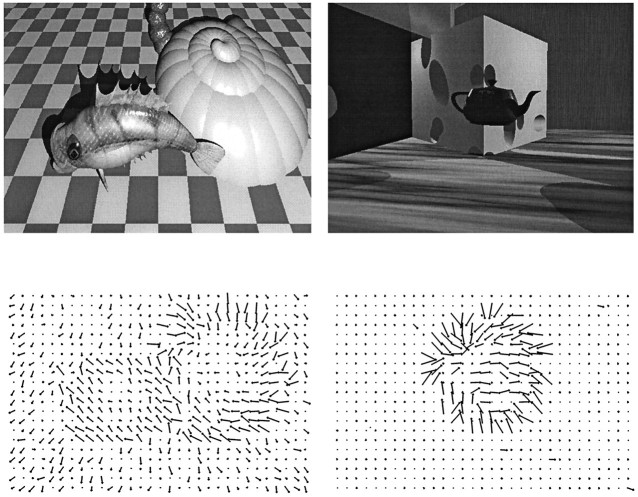
Once all of these parameters were determined, a computer program took them as inputs and created a script to make the movie. A sequence of 15 images was produced by specifying initial 3-D positions of the camera and each object in the image and then updating the pose of the camera and each object based on these motion parameters. The script contained this description of the contents of an image and called a set of stored graphics routines supplied in the ray-tracing package to render each image. The script also used a library contained in the package that included descriptions of the six objects and the three backgrounds. Creating each movie required ∼2 min of central processing unit (CPU) time on a DEC Alpha 300 MHz/21164A computer. Figure1 shows three images selected from a movie generated in this manner.

Fig. 1.

Example of flow-field input to the system.Top, Three images from a movie. In this movie, the observer was moving into the scene while maintaining gaze on the fish. The panther was moving independently. Bottom, The corresponding flow field represented by a 21 × 31 array of flow-field vectors. Note that the flow field contained coherent subpatterns that described the independent relative motion of different objects.

Optical flow. Many neurons in area MT are directionally selective and have a tuning curve with 30–60° width around the preferred direction of motion (Albright, 1984, 1992; Maunsell and van Essen, 1983b; Rodman and Albright, 1989). Rather than model all of the details in the neural circuits that might be responsible for achieving these directionally tuned responses in area MT, we instead used a simpler system to compute the local flow field from movies and then converted the resulting local velocity vectors into responses in a population of velocity-tuned units. This was used to generate a large number of flow fields, which would have been prohibitively slow using more detailed models of the response properties of cells in MT (Nowlan and Sejnowski, 1995).

The optical flow technique that was used to extract a single flow field from each synthetic image sequence was Nagel’s (1987) flow algorithm, which is a gradient-based scheme. This algorithm performs spatiotemporal smoothing on the set of images and then uses a multiresolution second-order derivative technique, in combination with an oriented smoothness relaxation scheme, to produce the flow field. We selected this algorithm because it has a relatively sophisticated smoothness assumption that prevents smoothing over discontinuities, which are especially important for segmentation, but the trade-off is that the resulting flow field is often sparse. Note that the flow field is noisy (as can be seen in Figure 1), and in many cases it is difficult to associate the elements in the flow field directly with the objects, particularly for nearby or occluding objects.

Input representation. The input to the model was intended to capture relevant tuning properties of MT neurons in terms of their velocity selectivity. The network input was a 21 × 31 array of optical flow vectors, where each vector was represented by a set of neurons that shared the same receptive field position but were tuned to different velocities (Maunsell and van Essen, 1983b). At each location there was a pool of eight units. Each unit was tuned to a particular velocity, and the activity of the unit was a Gaussian function based on the difference between its preferred velocity and the computed velocity at that position. The variance of the Gaussian produced a directional tuning half-width of 45° for each unit. Four of the units were tuned to a “fast” speed and the other half were tuned to a “slow” speed, and they evenly divided the space of preferred directions (Figure 2). We found that these two speeds sufficed in the network, because the motions in the movie were restricted to a speed range within one order of magnitude (between 0 and 10° of visual angle). The model would not require a qualitative change to extend it to a wider range of speeds.

Fig. 2.

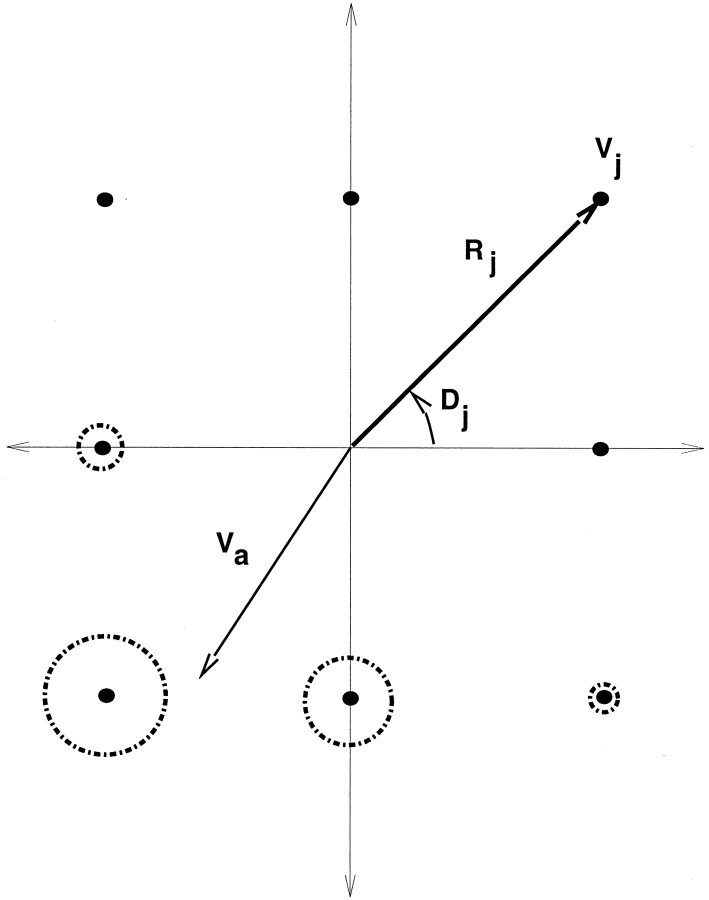
Distributed representation of velocity. Each location in the input layer of the network contains a pool of eight units, where each unit j is tuned to a different velocityV_j, denoted in the figure by a speedR_j and a direction D_j. The locations of the eight points denote the direction and speed of motion that produce maximum response from the corresponding unit. The actual velocity vector V_a at an image location (as determined by the flow algorithm) is uniquely encoded by the activities of the pool. The activity of each unit decreases with distance from the actual velocity to the center of the unit as exp(−‖‖V_i −V_a‖‖/2ς²), where ς/2 is the tuning half-width of the input unit. The width of the circles around each unit in the figure shows the activity of that unit for the particular V_a shown.

Two speeds and eight different directions also sufficed because the receptive fields of the units overlapped, as shown in Figure3. The activity pattern of the pool at a position thus acted as a population code for the local velocity. Several units in a given pool participate in coding the local velocity, which allows for a high degree of accuracy in the representation. [Each model MT unit is tuned to a particular velocity, but not a particular velocity gradient. Recent studies have revealed that many MT neurons are selective to velocity gradients (Treue and Andersen, 1996), which may be attributable in part to the nonuniform antagonistic surrounds of their receptive fields (Xiao et al., 1997). This velocity gradient sensitivity could play an important role in motion representation in MST.] A physiologically plausible network model that yields as its output a population encoding like the one we used here has been proposed by Wang et al. (1989). Such a model can be thought of as a preprocessing stage to our network, modeling the pathway from the retina to area MT.

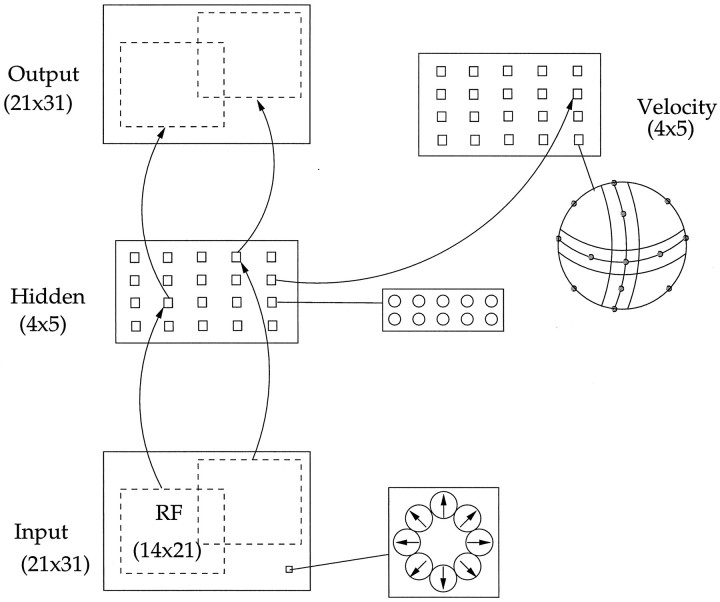
Fig. 3.

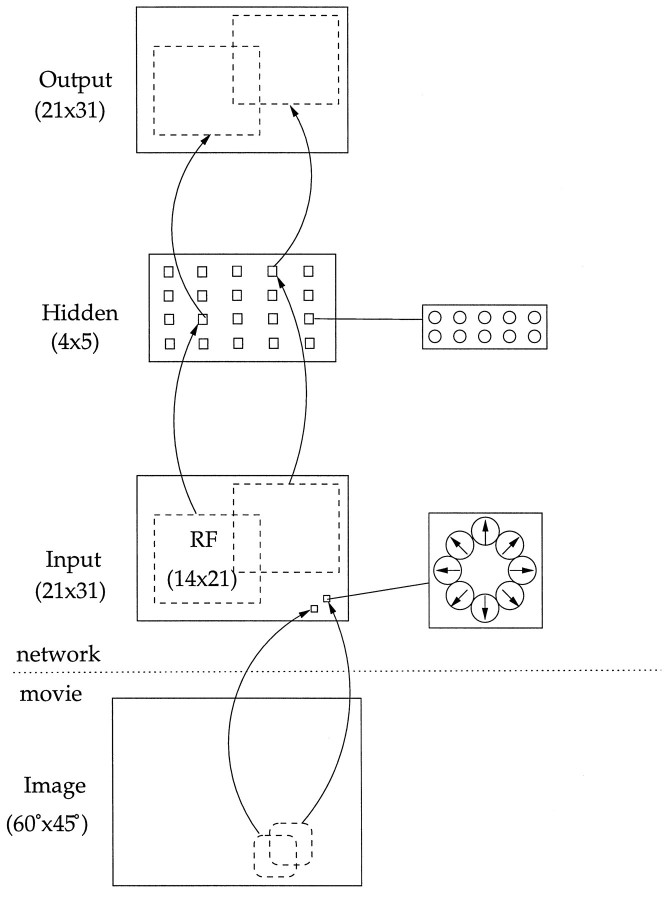
Architecture of the network model of area MST. The network input is intended to model area MT: each location in a 21 × 31 array contains a pool of eight units tuned to different motion directions and speeds. The middle layer in the network is intended to model area MST. Each unit in this layer has a receptive field that contains a 14 × 21 patch of input unit locations. There were 20 different centers of these receptive fields and 10 hidden layer units with different receptive field properties at each location in the hidden layer. The output layer of the network is a copy of the input layer, and a hidden unit is connected to each output unit that corresponds to an input unit in its receptive field. The goal of the network is to reproduce the input pattern on the output layer through the compressed representation in the hidden layer.

The activity of an individual unit in the input layer is then a number between 0 and 1 that describes the degree to which the local velocity matches its preferred velocity. We interpret this value as representing the probability that that unit will respond to a given motion sequence.

Model architecture. Although this population encoding in the input layer was intended to model the responses of cells in area MT to a motion sequence, the architecture of the model was designed to reflect some basic aspects of MT and MST cells, such as their receptive field sizes. The receptive field of each model MT unit was determined by the degree of spatial smoothing and subsampling in the flow algorithm. We set these so that each pool of input units in the model was sensitive to a 10° range in the visual field, which approximately matched the receptive field sensitivity of parafoveal MT neurons (Gattass and Gross, 1981; Maunsell and Newsome, 1987). Note that this means that the receptive fields of the input units overlap significantly.

The connectivity between the input layer and hidden layer of the network was based on the receptive field properties of MST cells. These receptive fields have always been reported to be large, but the exact size has been controversial. We based our receptive fields on the recent studies of Lagae et al. (1994), who found that most MSTd receptive fields included the fovea, and the sensitive part of the receptive field averaged 25–30° and was relatively independent of eccentricity. Our input images covered approximately a 60 × 45° portion of the visual field. We therefore evenly placed the centers of the receptive fields of the second layer cell to tile the image, such that the receptive field of each cell included approximately one-third of the image, and different receptive fields covered a different portion of the image. There were a total of 20 different receptive field centers, and 10 hidden layer units shared each retinal region; each of these 200 hidden units received input from a 14 × 21 unit patch in the input layer in a retinotopically organized fashion (Figure3).

The output layer had the same number of units as the input layer. The connections between the hidden layer and output layer mirrored the input-to-hidden connections; a hidden unit connected to each output unit that corresponded to an input unit within its receptive field. These connections might correspond to the feedback connections from MST neurons to MT neurons in their receptive field. The initial weights on all connections were random, and we used an optimization algorithm to determine the final weight values. After optimization of the connection strengths in the model, the feedback connections were not needed to compute the responses of units in the middle layer representing area MST.

Optimization of the MST model. We used a novel optimization algorithm to discover conditions under which the model would develop MST-like response properties in the second layer of the network using an unsupervised procedure, where no target response was provided for these units. The optimization algorithm we used created receptive field properties in the hidden units that efficiently represented the types of flow patterns that were characteristic of independently moving objects. We then tested the response properties of the hidden units and compared them with the properties found in MST neurons; similarity in their responses would suggest that MST neurons might be involved in analyzing the relative motion between objects and the observer. Furthermore, extracting these response properties using an unsupervised procedure would suggest that they can be derived from the statistics of natural flow images, based on inputs received from neurons in area MT, without the need for external feedback.

An earlier model (Sereno and Sereno, 1991; Zhang et al., 1993) showed how unsupervised Hebbian synapses can yield weight patterns resembling the combinations of motion components that neurons in area MST prefer, and a recent model (Wang, 1995) demonstrated similar results for a competitive optimization rule; the inputs to these models were simple linear combinations of these motion patterns. The flow patterns that we used were much more realistic than those used in these previous studies. For example, full-field expansion patterns used previously occur only when moving toward large flat walls, and full-field rotation in the frontoparallel plane almost never occurs in natural environments. We found that a Hebbian mechanism and a simple competitive mechanism each failed to find the underlying structure—the coherent motion patterns—for the more complicated, realistic inputs described above (see Results). Because these standard unsupervised methods failed to achieve the desired selectivity in the MST units, we used a different form of unsupervised optimization, a multiple cause model (described below).

The network we used for unsupervised optimization was an autoencoder, in which the network is optimized to reconstruct the input on its output units. The goal is to find a good representation on the middle, or hidden, layer for input patterns randomly drawn from some particular distribution. Unsupervised optimization methods attempt to extract the representations of the underlying causes of the inputs. Zemel (1993)showed that traditional unsupervised techniques, such as principal components analysis (PCA), contain implicit assumptions about the form of these underlying causes; these different assumptions can be incorporated explicitly into the network architecture, activations, and cost function, and the resulting network tends to learn representations that conform to these assumptions.

Multiple-cause model. Two assumptions were made about the causes that generated the visual scene on the basis of previous knowledge of the underlying statistical structure in the flow fields. First, the input movie was assumed to be generated by several independent causes, each of which corresponded to the relative motion of the observer and one object, or a part thereof. Second, we assumed that the value of a single output dimension, here the response of an MT cell, could always be specified as coming from just one cause; that is, local flow was generally the result of the relative motion of the observer and the nearest object along that line of sight. This assumption is simply an application of the basic notion of occlusion to the flow-field domain.

These two assumptions were incorporated as two modifications to a standard autoencoder. We first briefly describe a standard autoencoder and then the modifications. An autoencoder typically consists of three layers: input, hidden, and output. The units in the hidden and output layer are sigmoid units. That is, the activity of hidden unit i is:

$$p_{\text{i}}=\varsigma \left(\sum _{\text{j}}{t}_{\text{j}}{w}_{\text{ij}}\right),$$ Equation 1

where ς( a ) = (1 + exp(− a ))⁻¹ and t_j is the activity of input unit j . The goal of optimizing the weights in the autoencoder is to make the activity of each output unit match the activity of its matching input unit on the set of training examples.

The activity of a unit in this type of network can be interpreted as a stochastic binary variable, where on a given input the activity of the unit is a continuous value between 0 and 1 that represents the probability that that unit will respond to that input pattern. In this probabilistic formulation each unit i has an underlying binary value s_i, and its activity p_i = p(s_i = 1) can be seen as the average over many samples from the probability distribution. This expected activity is computed in the sigmoid function by assuming that the binary activities of the presynaptic units can be summarized by their expected values; this is called amean-field type of approximation. Under this probabilistic interpretation of the network, the appropriate cost function to optimize the weights is the cross-entropy measure:

$$C_{\text{j}}=\sum _{\text{j}}\left[t_{\text{j}}log\left(\frac{t_{\text{j}}}{p_{\text{j}}}\right)+(1-t_{\text{j}})log\left(\frac{1-t_j}{1-p_{\text{j}}}\right)\right],$$ Equation 2

where p_j is the value of output unit j and t_j the value of the corresponding input unit.

The first modification to this standard autoencoder was to use an activation function for the output units that encouraged the causes to compete to account for the activity of an input unit and also allowed multiple causes to be present in each image (Dayan and Zemel, 1995). Whereas the standard sigmoidal activation function allows many partially active units to contribute to the activity of a unit, this new activation is derived from the assumption above, where the hidden units compete to find the single cause for the velocity in a local image patch. Rather than using the sigmoid function to estimate the expected activity of an output unit based on the expected activities of the hidden units, here instead the stochastic activity of an output unit j was given by:

$$p_{\text{j}}=\frac{\sum _i{s}_{\text{i}}{w}_{\text{ji}}}{1+\sum _{\text{i}}{s}_{\text{i}}{w}_{\text{ji}}},$$ Equation 3

where s_i is the binary output of hidden unit i , sampled from the standard sigmoidal function of its net input, and w_ji is the weight from hidden unit i to output j . In this formulation the weight w_ji represents the odds that cause i seeks to generate output j:

$$w_{\text{ji}}=\frac{p(s_{\text{j}}=1\Vert s_{\text{i}}=1)}{1-p(s_{\text{j}}=1\Vert s_{\text{i}}=1)}.$$

Note that the weights are constrained to be positive.

This new activation function resembles the traditional sigmoid in that only information local to a given unit is required to compute its activity; however, this new activation function models a form of competitive interaction between the afferent signals to a cell, whereas the net input to a standard sigmoid unit is modeled as a simple linear summation. This activation function was derived from a probabilistic formulation of the image formation process (Dayan and Zemel, 1995).

The second modification involved adding a second penalty term to the objective function used to optimize the network parameters. The first term in the objective was the standard cross-entropy cost, computed for each output unit (see Eq. 2). The second cost term implemented our assumption that only a few causes would account for an input example. This cost was the cross-entropy between the expected and actual activity distributions of each hidden unit, which encouraged the activity of the unit to match its expected activity b across the set of images on which the network parameters (weights) are optimized:

$$C_{\text{i}}=\sum _{\text{i}}\left[p_{\text{i}}log\left(\frac{p_{\text{i}}}{b}\right)+(1-p_{\text{i}})log\left(\frac{1-p_{\text{i}}}{1-b}\right)\right].$$ Equation 4

The parameter b provides a computational mechanism for the notion of unit selectivity: a low value of b indicates that a unit is highly selective, in that it responds to a small fraction of the input patterns. A cost is then incurred for activating a unit, but this is offset by the first cost term (Eq. 2), which forces the active units to generate the appropriate inputs.

A small value of b encourages the network to form a sparse distributed representation of an input pattern in the model MST units. In a sparse distributed representation, the number of cells that represent a particular input is low relative to the size of the population, and each cell has a roughly equal and low probability of responding across the set of inputs [see Fig. 1 in Field (1994) for an illustration]. This type of representation is related to a factorial representation (Barlow, 1961), which captures and removes the redundant aspects of the input. A sparse distributed representation has been hypothesized previously for a number of other brain structures, including inferotemporal cortex (Tanaka et al., 1991; Rolls and Tovee, 1995), the hippocampus (Heit et al., 1988), and motor cortex (Georgopoulos et al., 1986). In our model, we set the value of b according to the results reported in Lagae et al. (1994), in which an average MST cell was found to be active on ∼10% of the different motion types they tested. [If we assume that each of the four motion types examined by Lagae et al. (1994) occur equally often in each of the 22 directions they tested, then their results on the proportion of MST cells with directionally selective responses to the different numbers of motion types leads to the conclusion that an average MST cell would be active on ∼10% of the inputs.]

The total objective function was then the sum of this hidden unit activity cost and the output cost. We optimized the weights in the network to minimize the summed cost:

$$E=C_{\text{i}}+C_{\text{j}}.$$ Equation 5

This could be accomplished by gradient descent. The resulting gradient for the hidden-to-output connections is a simple variation on the delta rule:

$$\frac{\partial E}{\partial w_{\text{ji}}}\propto \frac{1-p_{\text{j}}}{p_{\text{j}}}(t_{\text{j}}-p_{\text{j}})s_{\text{i}}.$$ Equation 6

We simulated the network using a mean-field type of approximation rather than a stochastic sampling procedure (Dayan and Zemel, 1995). In addition, we used backpropagation to speed up optimization. A biologically plausible learning rule (Hinton et al., 1995) could be applied if the network was run using a stochastic sampling procedure.

The important point here is that a model in which the weights are optimized with respect to a cost function and activation function that together embody our two assumptions will tend to form representations that conform to the assumptions. The network will thus attempt to find a minimal number of maximally independent causes that are capable of cooperating to describe a given flow field.

This optimization procedure was not intended to model the actual process of development or learning in cortex; instead, our goal was to determine whether a set of hidden units could perform the encoding task and to compare the properties of these units with the properties of neurons in area MST. Because the optimization procedure was unsupervised, it is more plausible that biologically realizable learning mechanisms could achieve the same response properties in cortical neurons.

Principal components and competitive optimization. To determine whether these two modifications to a standard unsupervised procedure are necessary to develop the desired response properties, we also tested two more standard procedures on this problem. These procedures could be examined within the same architectural framework, because the autoencoder is an architecture that accommodates various unsupervised procedures.

We first modified the procedure described above by using a linear activation for the hidden units and a sigmoidal activation at the outputs and removing the second cost term in the objective function. The resulting network computed a version of principal components analysis. PCA tends to produce distributed representations in which the hidden units in the model have maximum variance over the optimization set.

Our second standard unsupervised procedure performed competitive optimization. We implemented this procedure by modifying the multiple cause model to use the single cost term and a normalized exponential (“soft-maximum”) activation function in the hidden layer:

$$p_{\text{i}}=exp\left(\sum _{\text{j}}{t}_{\text{j}}{w}_{\text{ij}}\right)/\sum _{\text{k}}exp\left(\sum _{\text{j}}{t}_{\text{j}}{w}_{\text{kj}}\right),$$ Equation 7

where p_i is the probability that hidden unit i is active for a given input pattern, and k indexes the hidden units. The soft-maximum makes the hidden units compete to represent the input pattern: this function tends to enhance the probabilities of the most likely hidden units, which represent competing “causes.”

RESULTS

For each of the three unsupervised procedures described above, the optimization algorithm adjusted the parameters of the network to minimize the cost function. This cost function was computed over a set of 600 flow fields, each derived from a different motion sequence. We then tested the ability of these networks to generalize from the optimization set by presenting 50 flow fields from novel random motion sequences.

All of the networks were optimized using a conjugate gradient training algorithm, along with a line search. The weights were initially random, selected from a uniform distribution between 0.01 and 0.2. On average, 1150 epochs of training were required to reach a minimum of the cost function, where an epoch denotes a cycle through the entire training set. Training was stopped when the cost function could not be reduced; this was determined by the line search procedure. The total training time for the network required ∼15 min of CPU time on a DEC Alpha 300 MHz/21164A computer.

There are many final states for the network that are approximately equivalent: the weights of any two units within a pool of model MST units could be swapped without affecting the performance measures described below. We thus trained a family of networks, each with its own random set of initial weights. Each network was trained separately, and the final cost function associated with the network provided a metric to compare the different networks. Most of the trained networks were approximately equal on the basis of this metric; a few (∼5%), however, ended up in a local minimum, as is standard for any numerical optimization procedure operating on a complicated search space. The three training procedures (multiple-cause, PCA, and competitive) required a roughly similar number of epochs and similar computational expense per epoch. Although for each procedure we report the results for the network that had the lowest cost value at the end of training, we found that the variation across different trained networks for a given procedure was minimal.

We further examined the robustness of the system by testing it on noisy versions of the test set, as well as on two additional test sets. We defined three different noisy test sets, with independent Gaussian noise levels of 3, 5, and 10% added to the activity levels of the input units on each of the 50 examples in the test set. A separate test set of 20 examples contained particularly difficult situations for a motion segmentation network: nearby objects and objects moving with similar velocities. Each of these sequences contained two moving objects; in half of them the objects were within 5° of each other and their velocities was chosen randomly as above, whereas in the other half they were within 10° of each other and their motions were in the same direction. Figure 4 shows two of the flow fields from this test set. Finally, we devised atransparency test set for the system. The flow algorithm was not able to produce multiple flows at a location, so we simulated 10 transparency flows by adding the flows generated by two objects moving in opposite directions through a local image region. Note that the distributed nature of our input representation allowed multiple motions to be represented at a location.

Fig. 4.

Two flow fields in the nearby object motion test set. Left, The camera is translating obliquely into the scene while two objects move independently of each other and the camera. Right, The camera is stationary while one small moving object passes in front of a larger object moving in a different direction. A simple regional thresholding technique would fail to group the overlapping components of the flow field into the separate object motions in both instances.

We first describe how principal components and competitive optimization perform on these test sets and then examine the performance of the multiple cause model. The results of these different procedures were compared on two criteria: how well they can reconstruct the inputs and how closely the response properties of the units in the network resemble the selectivity of neurons found in area MST. We then explored the response properties of the multiple cause model in more detail, using a set of flow stimuli that have been used in physiological experiments. Finally, we examined the degree to which the model MST units developed in each of these procedures contained the information necessary to extract the true velocities in the scene.

Standard unsupervised procedures

Our first test of the different networks concerned their ability to reconstruct the inputs in the test flows. We measured the reconstruction ability of a network by averaging the cross-entropy cost ( C_j; see Eq. 2) across the set of 50 test flows; this measure has a minimum value of 0, which occurs when the activity of each output unit exactly matches the activity of its corresponding input unit.

The PCA network was able to model the inputs fairly well. The mean C_j was 23.5 bits (SEM = 1.69), which compared favorably to an average of 18.92 (1.28) bits on the optimization set. The competitive optimization network, on the other hand, was not able to reconstruct the inputs; for the optimization set, C_j = 43.12 (2.19) bits, whereas for the test set, C_j = 62.91 (2.83) bits. The problem was that the inputs contained multiple independent causes, which violated the assumption of the competitive model that there was only one cause.

We also examined these networks on the other test sets. In both networks, noise had a limited effect on the reconstructions. The average cross-entropy of the PCA network on the 3, 5, and 10% levels of noise was 26.13, 27.41, and 30.19 bits, whereas for the competitive network it was 65.42, 69.96, and 75.33 bits, respectively. Both networks had difficulty with the nearby motion sequences. The PCA network had an average cross-entropy of 92.3 bits, whereas the competitive network averaged 104.12 bits. Finally, on the transparent test flows, neither network could accurately reconstruct the inputs, with the averages being 102.18 and 106.89 bits.

We also explored the selectivity of the hidden units in these two networks. In neither the PCA nor the competitive network did the individual hidden units have response properties resembling those of MST neurons. Many hidden units were partially active for each motion sequence, which meant that none were selective to particular flow patterns. This observation was reflected in the weight vector fields, which did not resemble any coherent pattern. These results motivated us to introduce the multiple-cause model described above.

Representations and generalization in the multiple-cause model

We tested the generalization ability of our model using the same test set of 50 flow fields from novel motion sequences. The network using the activation function and objective function described above was able to successfully reconstruct these fields using only a few active hidden units. The average cross-entropy was slightly better than that of the PCA network on both the optimization set [ C_j = 15.23 (1.09) vs C_j 18.92 (1.28) bits for the PCA network] and the test flows [ C_j = 18.38 (2.03) bits vs C_j = 23.5 (1.69)].

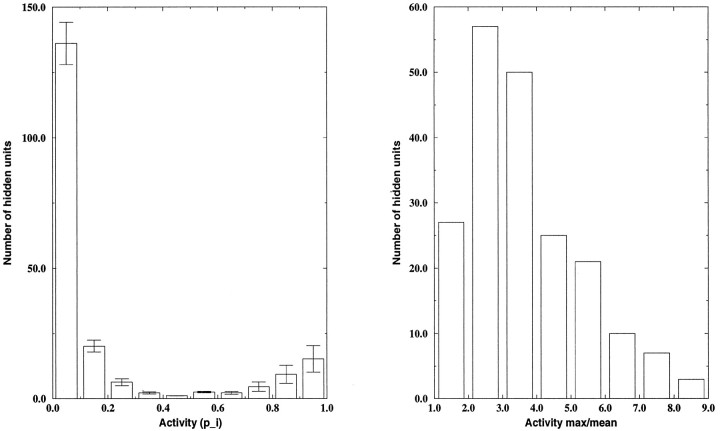
The network also succeeded in forming representations of these test flows that were sparse and distributed, in that a few hidden units were active for each test flow. This is reflected in the histogram of activity levels ( p_i) of the hidden units on each flow. Figure 5 (left panel) shows that most of the 200 hidden units were inactive for a given input, whereas a few were active ( p_i ≈ 1.0).

Fig. 5.

Hidden unit activities form a sparse and distributed representation of each test flow. Left panel, Only a few hidden units were highly active. Each bar in this histogram represents the number of hidden units (averaged over the 50 test flows) having an activity level (p_i) within the range indicated.Right panel, Hidden units are highly selective. Eachbar in this histogram represents the number of hidden units (averaged over the 50 test flows) having a ratio of maximum to mean activity (p_max/$\overline{p}$) within the range indicated.

More importantly, the hidden units were selective, because each unit was active on only a few examples. This selectivity was reflected in (and attributed to) the weight patterns of the hidden units. In many cases, these weight patterns resembled the types of coherent flows that have been observed (see Fig. 6 for some examples). These weight patterns are examples of the “direction mosaic” hypothesis (Duffy and Wurtz, 1991b) for MST receptive field mechanisms.

Fig. 6.

Three examples of weight patterns for hidden units after optimization of the multiple-cause model. These weights illustrate how the receptive fields of the MST neurons are constructed from MT inputs. The selectivities of many of the hidden units in the model may be predicted from their weight patterns.

Selectivity was quantified by comparing the maximum activity of each hidden unit ( p_max) to its mean ( $\overline{p}$) across the 50 test flows; selective units will have a high ratio as shown in Figure 5 (right panel).

Most hidden units had selectivities that were >2. Both of these measures, along with the low cross-entropy on the test flows, indicate that the model was able to encode the underlying structure of compound flow fields.

It is important to note here that the nature of the representations in the optimized network was not built in, but rather is an emergent property of the system. The activation and optimization functions in the multiple cause model encouraged but did not ensure the emergence of sparse distributed representations. Thus we had to check that this was a property of the final system and that it generalized; that is, the system formed sparse distributed representations when novel flow fields were presented as input.

The nature of the representations is determined partly by network parameters, such as the number of hidden units. We found that decreasing the number of hidden units in this model can lead to non-sparse solutions. For example, when we ran the same optimization procedure with only three hidden units per region rather than 10, on average over half of the hidden units had an activity level greater than 0.6 for the test set, which is not a sparse representation. This is a direct result of the trade-off between the two terms in the objective function (Eq. 5): reconstruction error ( C_j) vs sparseness ( C_i). With fewer hidden units each unit must play a role in a greater percentage of input patterns, which leads to a more distributed representation.

Selectivity of unit responses

The reconstruction ability and sparse distributed nature of the multiple-cause network demonstrates that this procedure is capable of developing representations that satisfy the dual assumptions in this optimization procedure. Additional tests are required to determine how these representations compare with the encoding of motion in MST neurons.

In networks derived from the multiple-cause model, many hidden units had weight patterns resembling the types of coherent flows to which MST neurons respond. Analysis of the hidden unit weight patterns also revealed a similarity to a recent neurophysiological finding. Duffy and Wurtz (1995) showed that the response of many MSTd neurons changes as the center of motion is shifted to different parts of their receptive fields, and the peak response often occurs when the motion is not centered in the receptive field. In the model, the center of the preferred flow patterns of many units did not correspond to their receptive field centers (Figure 6), which means that their peak response would also occur off center.

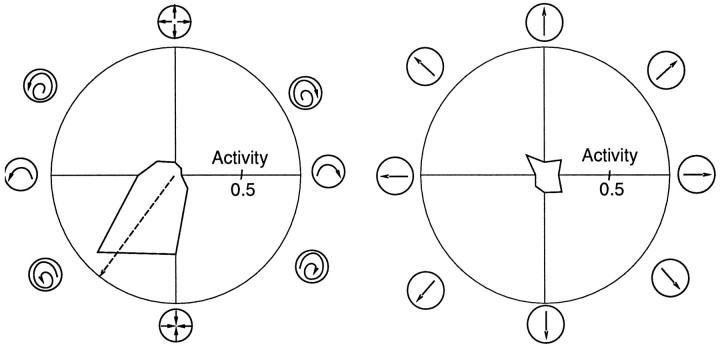
To quantify the hidden unit selectivity, we analyzed the individual hidden unit responses in more detail. We examined the selectivity of individual hidden units to particular motion types by presenting various coherent flow patterns in the receptive field of the unit. These motion stimuli were similar to those used in the experiments ofGraziano et al. (1994). Two groups of these stimuli were used. The first contained spiral flows, which combined expansion/contraction with rotation, whereas the second set contained translation flows. The speed was held equal for all stimuli, and the pitch of the motion was systematically varied. Figure 7 shows examples of spiral stimuli. The space of possible spiral stimuli of constant speed can be represented as a circle, where the radius describes the speed; a position along the circle specifies a particular spiral flow with a certain amount of clockwise/counterclockwise rotation and expansion/contraction.

Fig. 7.

Three sample stimuli from the space of spiral stimuli. These stimuli resemble the flow fields that arise from the moving random dot stimuli used in neurobiology experiments. The speed was the same for all three stimuli here: contraction, contraction/clockwise spiral, and clockwise rotation.

Eight stimuli were presented, evenly placed around the circle, from each of the two classes to each MST unit in the model. Figure8 shows the result for one unit, which was typical in preferring a particular combination of the motion stimuli. A wrapped normal function was fit to the tuning curve of each unit to assess its selectivity. [The wrapped normal is a version of a Gaussian distribution suited to a circular range (Fisher et al., 1987). Its form is:p(x)=[2πς²]^−1/2Σ^∞_a=−∞exp [−(x−μ−2aπ)²/2ς²]]. We found that 71% of the units (all with p_max > 0.9) were selective: their tuning half-width (ς/2) was <30°. We estimated the fit of the wrapped normal using the standard correlation coefficient r , where r → 1.0 as the fit improves. The selective units generally had smooth tuning curves and good wrapped-normal fits, with $\overline{r}$ = 0.92.

Fig. 8.

The response selectivity of an individual model MST unit to various motion types. In these polar plots, the angle represents the pitch of motion, and the radius represents the response of the unit. Eight directions were sampled in two continuous spaces, one for spiral motion (rotation–expansion/contraction) and the other for translation.

To make a quantitative comparison between the preferred direction distribution in the model and the data, we calculated the direction of best response using the wrapped-normal fit for each of the 142 selective units. Figure 9 shows the result: 87 of the 142 units preferred a direction in the spiral space, whereas the remaining units preferred a translation direction.

Fig. 9.

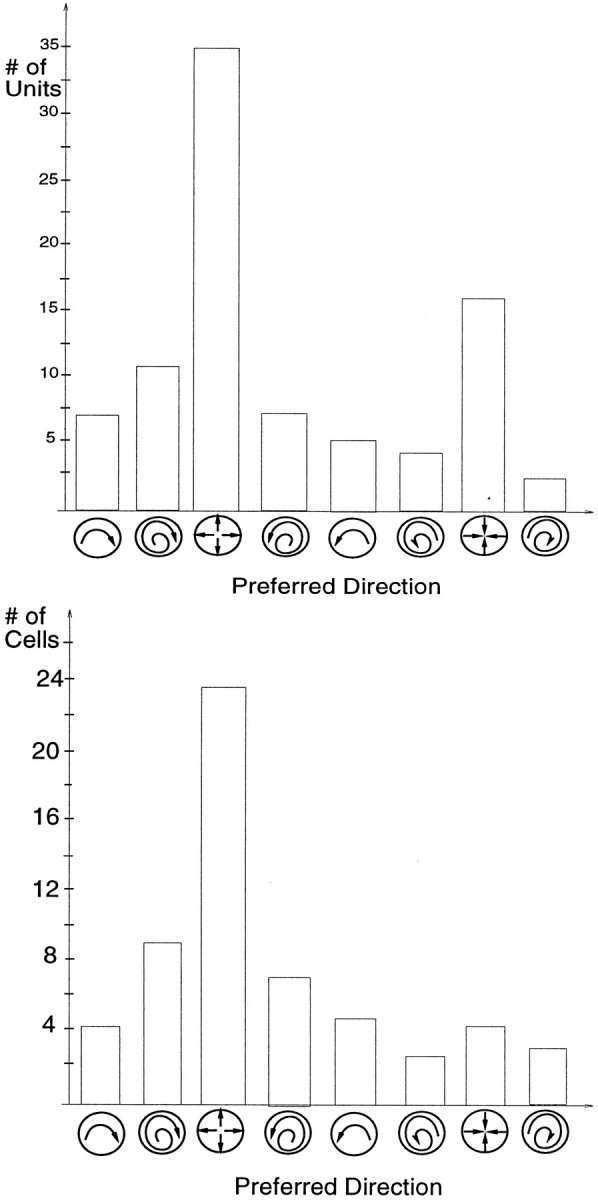
Preferred directions for the spiral selective units in the model, and for the selective cells in the Graziano et al. (1994) study. The height of each bar in a histogram represents the number of units or cells having a preferred direction within 45° of a particular motion type. Top, Of the 142 selective model units, 87 preferred a direction in the spiral space.Bottom, The direction of preferred responses for the 57 cells with smooth tuning curves and good Gaussian fits in the Graziano et al. (1994) study.

In the model, the overall distribution of preferred directions is a function of the statistics of the motion behaviors in the flows used to optimize the network. For example, the velocity distribution for the camera motion in the movie-generating program had a bias for forward motion. This bias was reflected in the distribution of preferred directions: of the 87 units that preferred a direction in the spiral space, 35 of them were tuned to expansion. This strong expansion bias matches the bias found by Tanaka and Saito (1989) and Graziano et al. (1994). [Note however that other studies (Orban et al., 1995) have not found MST cells to be selective to spiral flows but instead suggest that their selectivity corresponds to the different components such as rotation and expansion/contraction. This distinction is not important in our work. We analyzed the spiral selectivities of the units in the model to make quantitative relations between the model and data, and could also analyze the selectivity with respect to the underlying motion components.] Overall, in the Graziano et al. study, the distribution for preferred directions was expansion (42%), spiral [35% (expanding spiral 28%, contracting spiral 7%)], rotation (16%), and contraction (7%). In the model, the distribution was expansion (40%); spiral [28% (expanding spiral 21%, contracting spiral 7%)], rotation (14%), and contraction (18%).

One parameter that plays an important role in the properties of the model is the value of b , the expected activity of a model MST unit. Although the value of 0.1 was chosen to roughly match the data of Lagae et al. (1994), we found that the results are not affected much by small changes in this parameter. Larger changes, however, lead to quite different results. For example, when b = 0.2, the hidden units become less selective, and more are active for each flow input. In this case, the number of selective cells shrinks to 53%. Conversely, when b is decreased, the units become more selective: 82% of the hidden units are selective when b = 0.05. The trade-off for this increase in selectivity is an increase in the reconstruction error, as C_j = 21.57 (1.89) bits for this value of b , as opposed to C_j = 18.38 (2.03) when b = 0.1 [and C_j= 16.95 (2.11) when b = 0.2]. Thus the value of b = 0.1 represents a compromise between hidden unit selectivity and reconstruction error.

Position invariance of unit responses

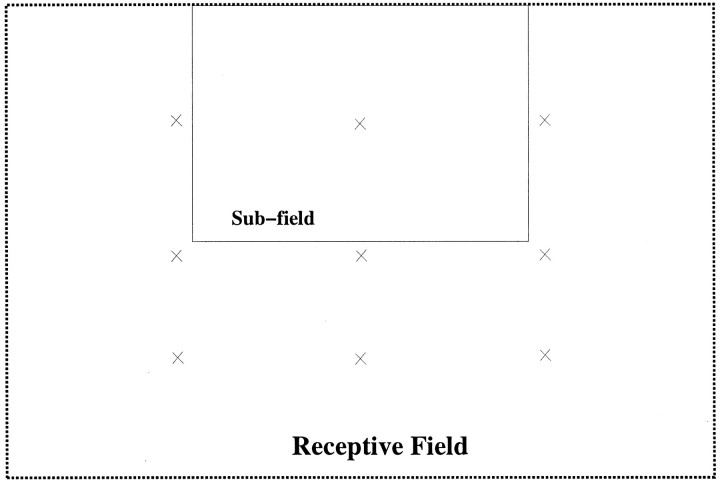
Several studies have reported that some dorsal MST neurons maintain their preference for a motion pattern regardless of the location of the velocity flow center within the receptive fields (Duffy and Wurtz, 1991b; Graziano et al., 1994). We tested the position invariance of each model MST unit in our network by shrinking the flow stimuli from the class of motion types preferred by that cell to one fourth of their original size and placing them in nine different positions within the receptive field of the unit (Fig.10).

Fig. 10.

Subfield test for response selectivity. Flow-field stimuli such as those shown in Figure 7 were shrunken and placed in nine different positions within the receptive field of each unit. Each X marks a center of one of the nine stimuli, and the size of the subfield occupied by the shrunken stimulus is indicated by the rectangle within the receptive field.

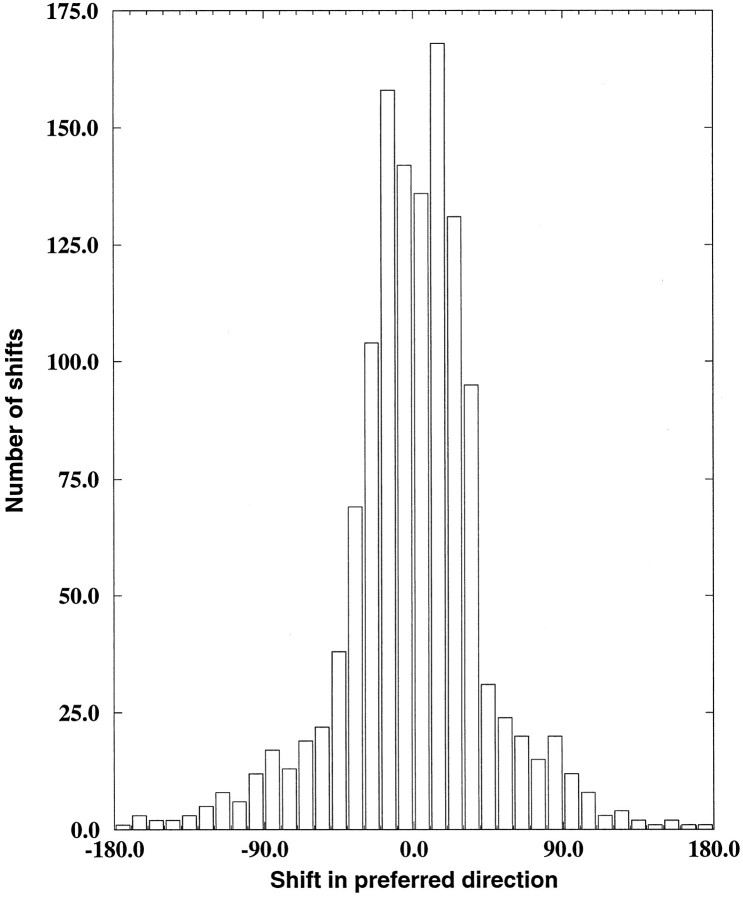
We measured the position invariance of each model MST unit by finding its preferred direction in each of these nine different positions and computing the difference between each of these preferred directions and the original preferred direction for that unit. The nine shifts per cell computed in this manner were then combined to yield an overall shift in preferred direction between the original whole-field stimuli and the smaller subfield stimuli, as shown in Figure11. We would expect that position-invariant units would have negligible shifts in preferred directions across the different positions. The results shown in Figure11 bear out this prediction, because the peak around a shift of 0° indicates that most responses were relatively position-invariant. Note that a random selection of preferred directions would lead to a uniform distribution in this graph. Therefore most of the selective units retained their preferences in these experiments. Using a similar measure, Graziano et al. (1994) found an average shift in preferred direction of 10.7°, whereas the average in the model was 14.3°.

Fig. 11.

Subfields preserve response selectivity. Shift in preferred direction between each of nine different placements of subfield stimuli and the whole-field preferred direction for the 142 selective hidden units.

In performing this position invariance test, we discovered another interesting property of the network: 41 of the 58 model MST units that were not selective for a particular motion type on the full field test were selective when the stimuli were reduced in size; that is, these units responded preferentially to particular flows at specific positions in their receptive fields. We assessed these preferences by fitting a wrapped normal to their tuning curves in positions in which they had a significant response ( p_max > 0.75). For each of these 41 locally selective units, we found that their tuning half-width (ς/2) was <45°, and the fit was good, with $\overline{r}$ = 0.87.

This local flow specificity is a natural consequence of modeling not only observer motion but also independent object motion; the motion of small or distant objects can produce a small patch of coherent flow, as can be seen in Figure 1. As a result, many of the subpatterns in the flow inputs do not occupy the entire receptive field of a unit, so some of the hidden units become selective to a motion type within a subregion of their receptive fields (see Fig. 6 for an example). The responses of these locally selective units resemble the response properties of MSTI cells, in that they respond best to motion within a smaller region of the visual field.

Segmentation based on MST representations

The match between the response properties of MST neurons and the hidden units of the multiple-cause network demonstrates that this model can account for a range of experimental data concerning MST neurons. A further hypothesis in our model is that the nature of the representation in MST subserves a number of important behaviors, such as independent velocity judgements and heading detection. Here we describe experiments designed to determine whether the hidden units of the model contained sufficient information to at least coarsely segment images into the underlying moving objects.

In our formulation, the actual segmentation of a complex image sequence into component object motion is not hypothesized to take place in MST but rather is facilitated by representations in MST. We therefore evaluated the segmentation ability of the network by adding a layer of units that obtained their input from the hidden unit representations described above. We designed each unit in this new layer to respond maximally to its preferred velocity within a local image region, and its activity falls off smoothly with increasing difference between the true velocity and its preferred velocity. So the pattern of activity across the set of velocity units can represent a wide variety of velocities. We then compared the peaks in this distributed representation to the actual motions in the image to see whether the model had accurately segmented the image into the independent velocities.

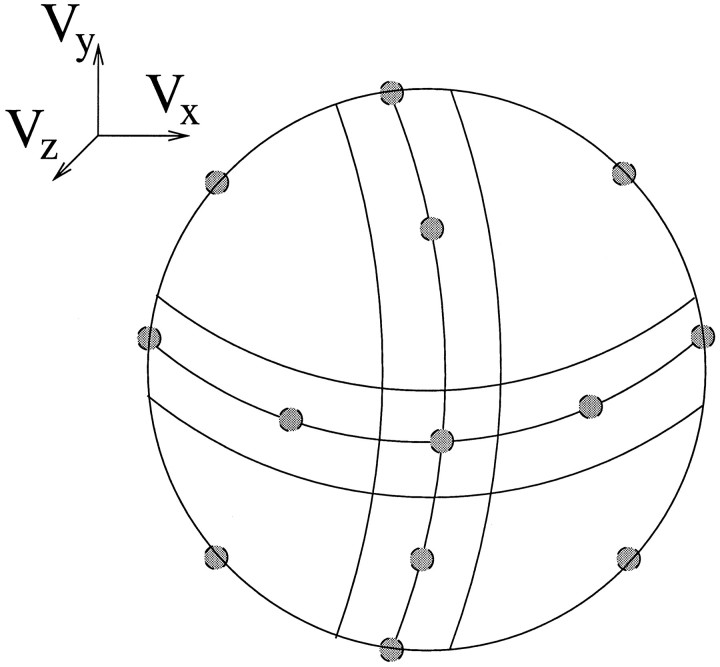
The units in this velocity extraction layer were designed to represent the 3-D translational component of motion in a local image region. Each unit within a local pool of velocity units had a preferred direction of 3-D motion, and the 18 units in a pool were laid out in a regular pattern on the unit circle (Fig. 12). The exact 3-D motion parameters depend on the depth of elements in the scene, so without knowing the layout of the scene the system can only determine velocity up to a scale factor. Each velocity unit therefore represented a unit vector in the direction of 3-D translation.

Fig. 12.

A pool of velocity units represented the 3-D translational component of motion in a local image region. The 18 units in a pool formed a coarse-coded representation of local velocity. Each unit had a unique preferred 3-D velocity, and this set of preferred velocities had an orderly configuration on the unit circle. Twelve of the 18 units are shown on the unit hemisphere in this diagram.

There were 20 pools of local velocity units in the velocity layer, dividing the image into a 4 × 5 grid of overlapping regions in the same manner as the MST layer. The full network architecture including this velocity layer is shown in Figure13. The units in a given region had receptive fields in the image identical to those of the corresponding MST units. Each pool of velocity units received inputs from its corresponding model MST units. Note that although the pools each obtained information from separate but overlapping patches of the 2-D image, they each encode the particular 3-D motions in that portion of the image.

Fig. 13.

Architecture of network including the velocity extraction layer, shown on the right. This layer was arranged in a 4 × 5 grid of pools, each containing 18 units.

The velocity units were sigmoid units (Eq. 1). The weights of these 360 velocity units were optimized using the same set of 600 images used to optimize the autoencoder, with an additional set of 200 images generated in the same manner. The target output for each velocity unit was computed as a Gaussian function based on the difference between its preferred velocity and the true image velocities within its receptive field. These true velocities were known because of the method of generating the motion sequences. If the image of an independently moving object was within the receptive field of a pool for the majority of the images in a movie, then the velocity of that object was a target for the pool. The target velocity was expressed as velocity relative to the camera motion, because this is the information available in the flow field. The 3-D translational component of camera motion was a target for all pools.

Note that this distributed representation of local velocity permitted multiple velocities to be represented within a single region. Multiple velocities would be recoverable to the extent that multiple activation peaks could be distinguished in the pattern of activation of a pool. Also, the aim of this module was not to localize a particular motion within a specific image region. Instead the goal was to match every velocity in the image, including that of the camera, by at least one pool, and to represent no spurious velocities.

After training the system on the 800 flow fields, we evaluated its performance on the different training sets. Extracting the underlying values from a population code is a difficult computational problem when the number of values being represented is unknown. We used a form of template matching (Lehky and Sejnowski, 1990; Wilson and McNanghton, 1993) to read out motion parameters from the velocity layer representation. We tessellated the unit sphere into 500 bins, where each bin corresponded to a single direction of 3-D motion. Then the target activation pattern for that bin was computed by the same method used to set target activation values for training the weights. An error measure for the bin was computed by comparing the actual activation to the target activity levels using the cross-entropy error measure (Eq.2), and the velocities with error below some chosen thresholdT were retained. A resolution limit was then imposed to eliminate aliasing (multiple instances of a single velocity), because only the velocity with the minimum error within a 3 × 3 velocity neighborhood was retained. This thresholding method lost some of the information in the representation but provided a simple performance measure by allowing us to match the list of true and extracted velocities. An extracted velocity within a fixed distance of a true velocity (∼5° error) in an image was considered a match. The sum of false positives (spurious extracted velocity) and misses (unmatched true velocity) was then computed; the threshold T was optimized to minimize this sum. This count estimated the number of segmentation errors in the system.

Using this method, the true 3-D translational component of observer/camera motion was matched in all 50 test cases in the standard test set. The network formed a redundant representation of this velocity, because typically several pools in a single image matched it (Fig. 14). For the independently moving objects, the network made seven errors across the 50 flows; it was error-free on 47 of these examples. Most of the errors occurred in movies in which the rotational component of the camera motion was significant, which typically produces error in the extraction of the translational component of object motion. In addition, although the method did not explicitly penalize redundant representations of velocities, <8% of the independently moving object velocities in the test set had multiple matches.

Fig. 14.

The output of the velocity module on the two test movies from Figure 4 is shown below the respective flow field. Each velocity unit is plotted within its local pool as a vector pointing in its preferred 3-D direction, with a magnitude proportional to its activity. A histogramming technique was used to extract local velocity from this coarse-coded representation. These two examples demonstrate that several pools may represent the same underlying velocity and that a single pool can represent two velocities when the relevant region in the flow field contains a motion border.

Adding noise to these test flows did not have much effect on the segmentation performance. Additional noise at the 3, 5, and 10% levels increased the total number of errors by 0, 1, and 3, demonstrating a reasonable degree of robustness. On the nearby motion test set, both motions were extracted correctly from the velocity layer on 17 of the 20 flows. In the other cases, the motions were either too close and/or too similar for the network to extract both velocities. Finally, in the transparency test set, the network successfully extracted the two motions in 8 of the 10 test cases.

For the sake of comparison, we ran the same tests on the PCA and competitive networks (reoptimizing the weights and threshold for the velocity layer for both cases). As could be predicted from its inability to reconstruct the input, the competitive network segmented poorly. It had 32 errors on the 50 test flows and correctly segmented only 4 of the 20 nearby motions and 2 of the 10 transparency cases. The PCA network performed better: it committed 21 errors on the test flows, but correctly segmented only 7 of the 20 nearby motions and 5 of the 10 transparent examples. The substantial performance advantage of the multiple-cause network, particularly on the more difficult test cases, suggests that the underlying assumptions in this model enable the optimized hidden unit representations to contain information required to at least coarsely segment the input into the independent motions.

Heading detection based on MST representations

A function that is widely believed to be subserved by MST neurons is heading detection. To examine the ability of the network to encode sufficient information to accurately determine heading from the complex flow fields, we implemented a very simple mechanism for heading detection.

The underlying assumption in this computation is that when the observer is moving, most of the flow is caused by self-motion. So an underlying velocity that is common to multiple image patches, thereby accounting for most of the motion in the scene, is likely to correspond to the motion of the observer. In our network, we computed this by identifying the single velocity value extracted in multiple pools of the velocity network described above.

This heading velocity h was computed by combining across all velocity pools j to determine the number of instances of each velocity i , and then choosing the predominant velocity:

$$h=\text{arg} \underset{\text{i}=1}{\overset{50}{max}}\left[\sum _{\text{j}=1}^{20}{v}_{\text{ij}}\right].$$ Equation 8

As in the velocity determination scheme, heading detection was considered correct if the extracted velocity had an error of <5% of the true velocity.

This method produced the correct heading velocity in 45 of the 50 test cases. On the multiple motion test set, it was correct in 16 of the 20 cases, and it correctly assessed heading in 7 of the 10 transparent test cases. Analysis of the error cases revealed that most errors were caused by the independent motion of a large object, which could overwhelm the camera motion signal. Thus the camera motion was the second largest velocity signal in 8 of the 12 error cases.

DISCUSSION

The network model of visual processing in areas MT and MST presented here was capable of efficiently representing components of the optical flow field for various visual scenes. This was accomplished through the cooperative activity of several MST processing units, each of which accounted for a portion of the visual field indicative of coherent motion. This novel approach, which has produced an alternative interpretation for what the responses of MST neurons are encoding, has two primary advantages. First, it has been successful on more realistic inputs than the previous optimization models (Sereno and Sereno, 1991;Zhang et al., 1993; Wang, 1995), and it has demonstrated that the neurophysiologically determined MSTd response properties are consistent with the statistics of complex motion images. Second, this approach expands the potential role for the information represented in MST to include other aspects of optic flow field analysis and other behaviors in addition to heading detection. In addition, the model is consistent with the anatomy and physiology of areas MT and MST.

Biological comparisons

Some version of the optimization algorithm could be implemented biologically because it is unsupervised, and only local information available to each neuron is used. The unsupervised procedure has two cost terms. The first term involved a comparison between the ongoing activity rate of an individual MST unit and its stimulated rate: this error signal can be computed by a single neuron or small population of neurons. The second term compared the actual firing rate of an MT unit to its predicted rate of firing. This predicted firing rate could plausibly be computed using feedback connections within local circuits in area MST. Although we have assumed that learning takes place in only one layer of processing, learning could take place in a hierarchy of layers, for which unsupervised algorithms have recently been proposed (Hinton et al., 1995).

Many of the hidden units in the model have receptive fields that prefer coherent flow fields and resemble the responses observed in area MST neurons. Several other properties are consistent with this identification. For example, many of the model MST units are selective to a particular type of flow pattern, and the distribution of these preferred flows corresponds to the distribution found by Graziano et al. (1994). Also, many of the motion selectivities of the model MST units were unaffected by placing the stimulus in different locations within the receptive field, which matches the results of Duffy and Wurtz (1991b), Graziano et al., (1994), and others.

Another property of the model that is consistent with MST neurophysiology (Duffy and Wurtz, 1995) is the fact that the preferred center of motion field of many of the hidden units are not in the center of the receptive field. Finally, the general architecture of the model also fits recent psychophysical evidence for two stages of processing of complex flow fields in human vision (Morrone et al., 1995). The results of this study suggest that the first stage consists of local motion mechanisms, whereas the second stage integrates motion signals along complex trajectories involving circular and radial motion.

One way that our simulation results diverge from the neurophysiological findings on MSTd is the presence of units that are selective to a particular motion type at specific locations within their receptive field. These units would then be very useful in resolving the aforementioned ambiguity caused by the position-invariance property of the other units. This local selectivity suggests that these units may more closely resemble the response properties of cells that have been described in MSTI, the lateral portion of MST. Hence, although we have concentrated on comparisons with data from MSTd, our model suggests a more unified perspective on MST, including the lateral portion as well as the dorsal part.

Our model thus leads to a testable prediction concerning these cells: within their smaller receptive fields, they should exhibit selectivities to particular flow patterns similar to those found in MSTd cells in the full-field flow selectivity experiments. This is an original prediction of our model.

Segmentation

One of the most important functions of the visual system is that of segregating the continuous input stream into discrete objects and events. Our model of motion processing in area MST implicitly provides such segregation on the basis of independent causes; that is, the optimization procedure was chosen so that a hidden unit would respond in a selective fashion to the flow pattern caused by the relative motion of an object and the observer, within the receptive field. We then showed that hidden unit responses developed via this optimization procedure provided information that allowed at least a coarse segmentation of the flow field into independent motions.

The overall hypothesis behind this model is that a coarse, rapid, feedforward segmentation may be facilitated by representations in area MST, which could then aid a more detailed, iterative segregation and grouping procedure. This iterative procedure may fill in and refine the initial segmentation. This hypothesis mirrors the underlying strategy of an earlier model of area MT (Nowlan and Sejnowski, 1994, 1995), where a set of model MT units attempted to find regions of an image that contained the most reliable information for particular velocity hypotheses. However, the implementation of this computation was different in that model. In the MT model, some units computed local velocity estimates, whereas a separate set of units explicitly determined the reliability of different estimates; these selection units then acted to suppress activity in regions that contained ambiguous or unreliable information. Here estimation and selection are integrated into a single feedforward system.

Many previous computational studies have proposed methods of segmenting optic flow patterns into independent motions (Adiv, 1985; MacLean et al., 1994). Many of these approaches operate by attempting to group flow elements into objects so that the recovered motion is consistent with some assumed motion constraints, such as rigidity and smoothness. These algorithms face a standard cyclic dilemma: segmentation must be performed to check motion constraints, but the constraints need to be checked to segment (Ullman, 1981). Our model suggests that a convenient computational strategy, one that also may be used in biological systems, is to use common local flow patterns to rapidly determine a coarse segmentation. Thus, the model described here is not so much an alternative to these earlier models but instead can be seen as providing a good initial guess for the segmentation.

MST and heading detection

Our model is consistent with previous computational models of MSTd (Perrone, 1992; Lappe and Rauschecker, 1993; Perrone and Stone, 1994), which have shown how navigational information related to heading may be encoded by these cells. Like these earlier models, each MST unit in our model responds to the aspects of the flow that are consistent with a particular relative motion between the observer and the environment. In situations in which the flow field is caused by a single relative motion between the environment and the observer, the responses of the MST units can be pooled directly to determine heading. Unlike these earlier approaches, however, in which this single-cause assumption was built into the construction and processing of a model, in our model the units were optimized in situations in which the flow field contained the motion of multiple independent objects.

The simple heading detection mechanism that we implemented showed that the MST-like representation in the hidden layer of the network contained sufficient information to at least coarsely determine heading in a various noisy flow fields containing multiple motions. Most of the errors were attributable to erroneous identification of heading with the independent motion of a large object. The other errors were when the scene contained insufficient depth variation, a problem shared by any method that attempts to determine heading solely based on retinal image information (Longuet–Higgins and Prazdny, 1980; Rieger and Lawton, 1985). Note that the approach to heading determination in this module is similar to that of Hildreth (1992), in that first the 3-D motion of portions of the scene are computed, and then heading is identified by combining similar 3-D motion estimates.

Our model makes different experimental predictions than does a model in which MST responses are directly consistent with heading. The distinction can be viewed in terms of the pattern-selectiveand component-selective motion dichotomy used to characterize the response of MT cells to plaid stimuli (Movshon et al., 1986). The key experiment entails recording from a MSTd neuron while the monkey views a compound flow stimulus caused by two different motions. A single-cause model that posits a purely heading-based response would predict that MSTd will respond in a pattern-selective manner: a neuron selective to a motion involving some combination of the two true motions will be active. On the other hand, our model predicts that a number of MSTd cells will respond in a pattern-selective manner: a neuron selective to one or the other underlying motion will be active. These different predictions arise from alternative underlying statistical justifications. A single-cause model involves a competition based on the assumption that only one alternative is correct, whereas the multiple-cause model involves separate competitions for each input. The multiple cause model can have a multitude of fully active hidden units, whereas in the single-cause models, as the activity of one unit increases the activation of a second unit necessarily decreases, preventing a full representation of multiple motions.

Limitations and extensions

The current model does not examine some important issues that are consequences of the underlying hypothesis.

(1) We have added other modules to demonstrate that the representations in the model MST units contain information that is required to compute heading and to perceive multiple moving items in a scene, and these representations may therefore be useful in determining the locations and boundaries of these items. Adding these new modules effectively pushes the locus of heading determination further downstream, possibly into posterior parietal cortex. This formulation is consistent with the recent results of Beusmans (1994), who found that scene structure and other factors besides optic flow played important roles in the ability of human subjects to accurately perceive heading. Also, the direct projections to posterior parietal cortex from MST may allow moving objects to be localized, whereas the projections to inferotemporal cortex could allow the boundary information to be used in object identification. Further research is required to explore how projections from MST to these other areas may subserve these functions.

(2) Additional modules are required to test other predictions of our model. One prediction is that MST may be an important area in which to look for neural correlates to the perception of some types of motion transparency. For example, Duffy and Wurtz (1993) found that human observers were accurate in locating the focus of expansion of flow fields that combined planar and radial flow, but made systematic errors when the two were transparent. These errors were consistent with the identification of one of the overlapping flows as being caused by an eye movement. Our model could account for these findings by adding a module that determined the focus of expansion based on the representation formed in the model MST units, analogous to the manner in which heading is extracted from these representations. This module would make different judgments in the two cases, because one set of hidden units would represent the combined flow field, but two separate sets of hidden units would represent the transparent flow pair. The recent results of Duffy and Wurtz (1997) provide preliminary corroboration for this prediction; they found that MST neurons with strong directional responses preserved their selectivities when their preferred motion was overlapped with a transparent motion stimulus.

An additional prediction is that MST responses may shift in a way that corresponds to perceptual shifts concerning the number of objects that a subject will judge to be present in a scene. For example, Stoner and Albright (1992) showed that altering the luminance of the intersection between two overlapping gratings forming a plaid stimulus affected the perception of the motion as being coherent or two separate components, and they showed that some MT cell responses were correlated with this judgment. We predict that for more complex motion patterns to which MST has been shown to be more selective than MT, the neural correlates for such a determination of the number of objects may be found in MST rather than MT.

(3) Extraretinal signals are not included in the model, but they clearly play a role in MST responses. For example, eye position modulates the responses of many MST cells (Bradley et al., 1996). Studies have also shown that >90% of MSTd cells are sensitive to the disparity of the visual stimulus (Roy et al., 1992); for some MSTd cells the preferred direction of stimulus motion reversed as the disparity (relative to the plane of fixation) of the stimulus changed sign. Our model can be considered as accounting for the subpopulation of MST cells that are not affected by these other cues (Erickson and Thier, 1991). In both of these examples, adding this information to the model input should improve the representational power in the MST units. For instance, disparity sensitivity provides an additional criterion for making segmentation decisions, because image components at similar depths may be grouped. Adding disparity information and eye position to the network input would allow the hidden units to respond to particular combinations of these cues, and the resulting responses could convey additional information concerning object location.

Maunsell (1995) and Treue and Maunsell (1996) have recently reported that the responses of neurons in areas MT and MST can be modulated by attention, so that top-down influences need to be included as well as the bottom-up processing that we have modeled. Including an extraretinal signal in the network would also tie the model more closely to animal behavior in an active perception framework (Ballard, 1991).

Conclusion

We suggest that the motion of objects relative to an observer are represented in area MST by a sparse distributed population code, which would include observer self-motion as a special case. This representation can be viewed as a partial segmentation of the scene into independent moving objects that could then be used for various tasks such as eye tracking, reaching, and throwing. The results reported here also suggest that these representations could be formed during development through unsupervised learning mechanisms. The predictions of the model can be tested by studying the responses of neurons in area MST to multiple moving objects.