Task-Dependent Viscoelasticity of Human Multijoint Arm and Its Spatial Characteristics for Interaction with Environments

Abstract

Human arm viscoelasticity is important in stabilizing posture, movement, and in interacting with objects. Viscoelastic spatial characteristics are usually indexed by the size, shape, and orientation of a hand stiffness ellipse. It is well known that arm posture is a dominant factor in determining the properties of the stiffness ellipse. However, it is still unclear how much joint stiffness can change under different conditions, and the effects of that change on the spatial characteristics of hand stiffness are poorly examined. To investigate the dexterous control mechanisms of the human arm, we studied the controllability and spatial characteristics of viscoelastic properties of human multijoint arm during different cocontractions and force interactions in various directions and amplitudes in a horizontal plane. We found that different cocontraction ratios between shoulder and elbow joints can produce changes in the shape and orientation of the stiffness ellipse, especially at proximal hand positions. During force regulation tasks we found that shoulder and elbow single-joint stiffness was each roughly proportional to the torque of its own joint, and cross-joint stiffness was correlated with elbow torque. Similar tendencies were also found in the viscosity–torque relationships. As a result of the joint stiffness changes, the orientation and shape of the stiffness ellipses varied during force regulation tasks as well. Based on these observations, we consider why we can change the ellipse characteristics especially in the proximal posture. The present results suggest that humans control directional characteristics of hand stiffness by changing joint stiffness to achieve various interactions with objects.

In all manipulation tasks such as door opening, cup holding, or ball hitting, the force exerted by the hand on an object is governed by motions and mechanical impedances of the hand and the object. Thus, to succeed in performing tasks stably and smoothly, not only the kinematics relationships between the hand and object, but also the hand impedance (viscoelastic properties) should be regulated by the CNS.

The spatial variation of the spring-like property of the two-joint arm is frequently depicted as an ellipse. It was reported that hand stiffness magnitude (ellipse size) can be altered by cocontraction during posture maintenance but that altering the shape and orientation of the ellipse requires a change in posture (Mussa-Ivaldi et al., 1985;Flash and Mussa-Ivaldi, 1990; Dolan et al., 1993; Tsuji et al., 1995). This suggests that some mechanism imposes a constraint in coordinating multiple muscle activation such that the geometrical characteristics of the hand stiffness does not change. This mechanism is quite intriguing from the viewpoint of control strategy; it may offer some advantage by reducing the computational complexity in the planning movements and their interactions with objects (Flash, 1987; Bizzi et al., 1992).

In interactions or in preparation for interaction with various environments, however, flexibility in coordinating multiple muscle activation seems necessary. This could result in the modification of the geometrical characteristics of hand stiffness. In fact, recent studies have demonstrated changes in those geometrical characteristics during the preparation phase of catching tasks (Lacquaniti et al., 1993) and during movements under an external constraint (Gomi and Kawato, 1996, 1997). Although many attempts have been made to quantify human single-joint dynamics as summarized in Kearney and Hunter (1990),Lacquaniti et al. (1993), and Latash and Zatsiorsky (1993), it is not possible to infer from these the coordination between multiple components of joint stiffness or the effects of cross-joint stiffness (off-diagonal components of the joint stiffness matrix that governs the interaction between shoulder and elbow joints) in multijoint control. To explore the mechanisms of multijoint viscoelastic regulation by the CNS, we need to examine the general behavior of multijoint viscoelasticity based on detailed observations made under various conditions. To characterize the coordination of viscoelasticity and to find invariant factors in the control of the multijoint neuromusculoskeletal system, which may lead to constraints on the computational models of limb control, we investigate the changes in human arm viscoelasticity on a horizontal plane during various cocontraction and force regulation tasks. From these observations, we examine the controllability of stiffness at the hand position. Additionally, for force regulation tasks, we characterize torque stiffness and torque–viscosity relationships of the shoulder and elbow single-joint and cross-joint components and describe certain invariances. A part of this work has been reported in Gomi and Osu (1996a,b), and the analyses of electromyogram (EMG) stiffness relationship were presented elsewhere (Osu and Gomi, 1996, 1997).

MATERIALS AND METHODS

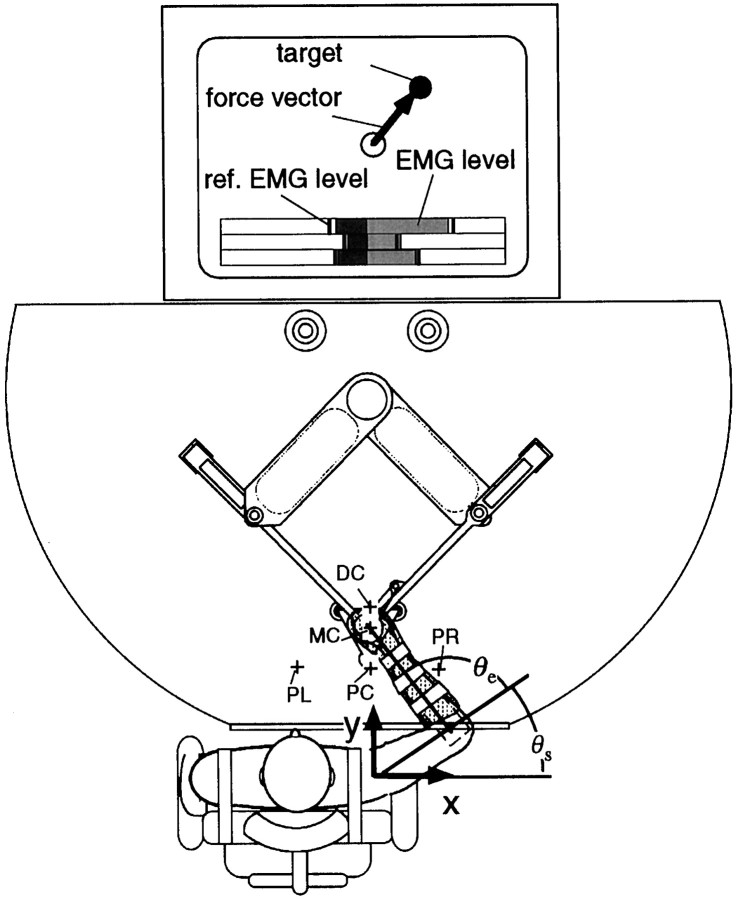
Experiment. Four subjects, ranging in age from 23 to 34 years (subjects A, B: male, right-handed; C: female, ambidextrous; D: female, right-handed) participated in this study. The subject was restrained by straps in a chair in front of the Parallel Link Drive Air-Magnet Floating Manipulandum (PFM) (Fig.1). The handle position of the PFM was controlled by a high-gain position servo. The subject’s hand position (handle center) was kinematically derived from joint positions of the PFM as measured by the position encoder (409,600 pulses per revolution). The force exerted on the hand by the PFM (i.e., an external interaction force) was measured by a force sensor (resolution, 0.006 kg) between the handle and the PFM links. Position and force data were sampled at 500/sec. The right forearm was placed in a molded plastic cuff (0.47 kg) tightly coupled to the handle, and supported against gravity by a horizontal beam (0.4 kg). The external interaction force vector between the subject’s hand and the handle and a force target were displayed on a computer monitor placed in front of the subject and behind the PFM; the subject was assisted in keeping the external force constant during the experiments by viewing the monitor. Additionally, rectified and filtered surface EMG [cut-off frequency, 25 Hz (low), 1500 Hz (high); moving average, 500 msec] of six muscles [shoulder monoarticular muscles, pectoralis major (flexor) and posterior deltoid (extensor); elbow monoarticular muscles, brachioradialis (flexor) and lateral head of triceps brachii (extensor); biarticular muscles, biceps brachii (flexor) and long head of triceps brachii (extensor)] were also displayed in a bar graph with an arbitrary scale (Fig. 1). Reference EMG markers, representing desired EMG values for each task were established just before each experimental set and displayed as well. The subject was asked to keep his or her muscle activities constant at the reference markers throughout each experimental set.

Fig. 1.

The PFM system and the experimental setup for measuring human arm mechanical impedance. The x-axis indicates the rightward direction, and the y-axis indicates the frontal direction away from the body. The origin for both axes is the shoulder position. The force vector in the horizontal plane was displayed on the computer monitor. To maintain the muscle activation level throughout each experimental set, the EMG (rectified and averaged) levels of six muscles were shown by a bar graph.

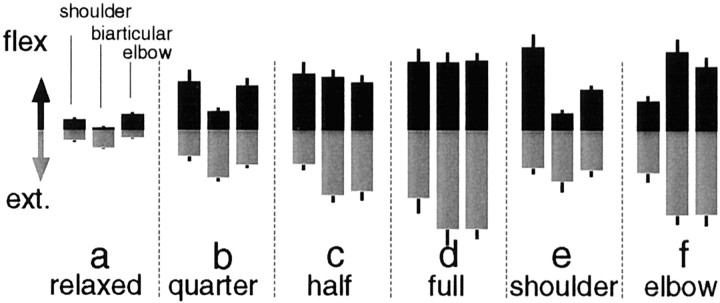
For posture maintenance tasks, an experimental set consisted of asking the subject to position the arm to one of five hand positions and maintain a specified condition of muscle cocontraction, using the EMG bar graphs on the monitor. The six cocontraction conditions were (1) without cocontraction, (2) with quarter cocontraction, (3) with half cocontraction, (4) with full cocontraction, (5) with cocontraction only in the shoulder, or (6) with cocontraction only in the elbow. The subject was instructed to cocontract but not push the handle in any direction (which could be determined from the monitor) or voluntarily react to the perturbations.

To estimate impedance parameters (stiffness and viscosity), the hand was slightly pushed and pulled back in eight randomized directions within a brief period (6–8 mm, 0.3 sec) [eight directions (±x, ±y, ±x±y, ±x∓y) * three times in each task]. There were >3 sec (with arbitrary intermission) between perturbations. During perturbation, all visual feedbacks (i.e., the current force vector and EMG bar graph) were frozen on the monitor.

For force regulation tasks, the subject was instructed to push the handle and keep a specified force vector (5, 10, 15, or 20 N) constant on the computer monitor without cocontraction. The required forces were in 8 directions for 5 N and in 16 directions for other cases. The subjects were also asked not to change the EMG levels and not to impose any rotational force to the handle while perturbations were applied.

In both kind of tasks, a small circle was displayed on the monitor as the target force, and the subject was asked to hold the head of the force arrow on the circle. These tasks were performed at three to five hand positions: proximal center (PC, [x, y] = [0.0, 0.35] m), middle center (MC, [0.0, 0.45] m), distal center (DC, [0.2, 0.55] m), proximal left (PL, [−0.2, 0.35] m), and proximal right (PR, [0.2, 0.35] m) (Fig. 1). The error between target and realized force was 0.28 ± 0.10 N (mean ± SD) for all experiments. The details of requested tasks for each subject are shown in Table1.

Table 1.

Requested tasks for each subject

Subject	Posture maintenance tasks	5 N (8 directions)	Force regulation task
	(a–f)		10 N (16 directions)	15 N (16 directions)	20 N (16 directions)
A	PC, MC, DC, PL, PR	PC, MC	PC, MC, DC, PL, PR	PC, MC	PC
B	PC, MC, DC	PC	PC, MC, DC	PC	PC
C	PC, MC, DC	PC	PC, DC, PL, PR	PC
D	PC, MC, DC	PC	PC, MC, DC	PC

Data analysis. The details of arm impedance estimation method have been explained in Gomi and Kawato (1995, 1996, 1997). Briefly, upper arm and forearm dynamics in the horizontal plane can be generally modeled according to the following second-order nonlinear differential equation:

$$\mathbf{I}(\mathbf{\text{q}})\ddot{\mathbf{\text{q}}}+\mathbf{H}(\dot{\mathbf{\text{q}}},\mathbf{\text{q}})={\mathbf{\tau }}_{\text{in}}(\dot{\mathbf{\text{q}}},\mathbf{\text{q}},\mathbf{\text{u}})+{\mathbf{\tau }}_{\text{ext}}$$ Equation 1

Here, q, q˙, andq̈ are joint angular position (q = [θ_s,θ_e]^T;θ_s: shoulder angle, θ_e: elbow angle), velocity, and acceleration vector, respectively. In the present experiment, the joint angle qwas obtained from the handle position by using the kinematics relationship, and the joint angular velocityq˙ and its accelerationq̈ were obtained by three and five point numerical differentiation (without delay) of q. τ_in denotes the torque generated by muscles, andτ_ext denotes the torque vector transmitted to the arm by the manipulandum (i.e., external torque) at shoulder and elbow joints, which was derived from the force measured by the force sensor (τ_ext = J^TF_ext). Here,J is a Jacobian matrix of human arm kinematics. Iand H and denote the inertial matrix (2 × 2) and Coriolis centrifugal force vector, respectively.

The torque, τ_in, generated by the muscles because of their length tension and velocity tension properties (i.e., muscle viscoelasticity) is assumed to be a function of angular position, velocity, and motor command, u, from the CNS. Assuming the motor command, u, does not change during or after the perturbation, the following variational equation can be derived:

$$\mathbf{I}\delta \ddot{\mathbf{\text{q}}}+\frac{\partial \mathbf{H}}{\partial \dot{\mathbf{\text{q}}}}\delta \dot{\mathbf{\text{q}}}+\left(\frac{\partial \mathbf{I}\ddot{\mathbf{\text{q}}}}{\partial \mathbf{\text{q}}}+\frac{\partial \mathbf{H}}{\partial \mathbf{\text{q}}}\right)\delta \mathbf{\text{q}}=\frac{\partial {\mathbf{\tau }}_{\text{in}}}{\partial \dot{\mathbf{\text{q}}}}\delta \dot{\mathbf{\text{q}}}+\frac{\partial {\mathbf{\tau }}_{\text{in}}}{\partial q}\delta \mathbf{\text{q}}+\delta {\mathbf{\tau }}_{\text{ext}}.$$ Equation 2

Here, δq, δq˙, δq̈, δτ_ext are variational components of corresponding signals caused by perturbation. Position and velocity coefficients are defined as viscosity and stiffness matrix (2 × 2) as D and R such that:

$$-\frac{\partial {\mathbf{\tau }}_{\text{in}}}{\partial \dot{q}}\equiv \mathbf{D}=\left[\begin{array}{cc}{D}_{\text{ss}}& D_{\text{se}}\\ D_{\text{es}}& D_{\text{ee}}\end{array}\right],-\frac{\partial {\mathbf{\tau }}_{\text{in}}}{\partial q}\equiv \mathbf{R}=\left[\begin{array}{cc}{R}_{\text{ss}}& R_{\text{se}}\\ R_{\text{es}}& R_{\text{ee}}\end{array}\right].$$ Equation 3

The subscripts “ss” of D andR represent a shoulder single-joint effect. Similarly, “se” and “es” denote cross-joint effects, and “ee” denotes an elbow single-joint effect. Equation2 can be globally linearized with respect to all unknown parameters including arm-dynamics parameters (i.e., structural dependent parameters in I and H) (Gomi and Kawato, 1995, 1996, 1997); thus, stiffness R and viscosityD can be uniquely estimated by the linear regression method. Moreover, to avoid the estimation errors caused by insufficient richness of frequency components from the perturbation (i.e., nonpersistent excitation), the arm-dynamics parameters were pre-estimated and fixed in all estimations for each subject (Gomi and Kawato, 1995, 1996, 1997). Note that the estimations of parametersR and D are only slightly affected by using pre-estimated arm-dynamics parameters as shown in Appendix A.

In Figure 2a we show two examples of perturbed joint angle shifts and the reconstructed variational torques at the shoulder and elbow joints during a force regulation task (10 N x-direction at the proximal hand position). Note that regression was performed on the time series for data for all eight directions at once, using the average of the three trials for each direction. The top two graphs represent the observed joint angle shifts caused by the perturbations in two opposite directions (distinguished by thick and thin lines). The second row of graphs represent the corresponding variational torque (including inertial torque) at the shoulder and elbow joints. The variational components were extracted by a subtraction method (Gomi and Kawato, 1995, 1997). The third row of graphs shows the variational torque (solid lines) ascribed to the stiffness and viscosity (i.e.,Dδq˙ +Rδq) and those patterns (dashed lines) reconstructed by using estimated parameters. The reconstructed patterns were well fitted with observed ones. Similarly, the variational torques for all perturbations in eight directions were well reconstructed (coefficient of determination (CD) = 0.92). The good reconstruction of variational torque patterns for all experiments (CD = 0.93 ± 0.03, mean ± SD) indicates our model adequately represents musculoskeletal dynamics. The bottom graphs represent torque components decomposed into (dotted lines) and (dash-dot lines) from the reconstructed torque shown in the second row. Position and velocity components in the shoulder and elbow torque were excited variously by applying perturbations in eight directions, thus the errors of estimated parameters were small.

Fig. 2.

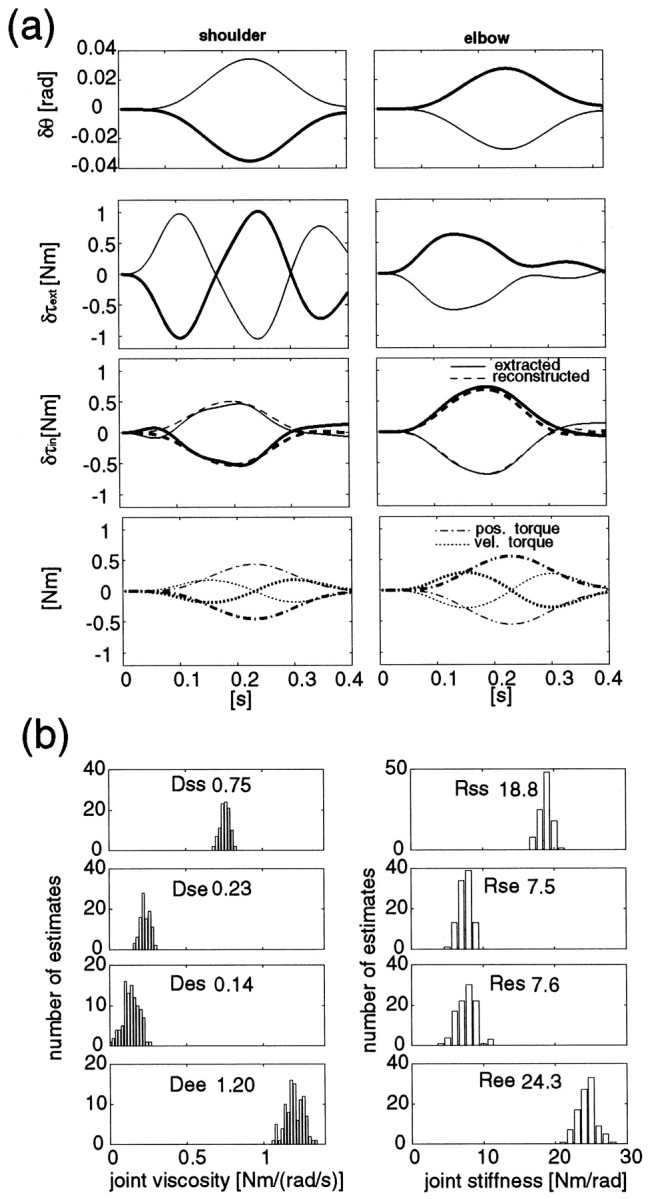
a, Positional shifts and variational torques at the shoulder and elbow joints caused by perturbations in opposite directions (thick andthin lines for each perturbation) during a force regulation task (subject B, 10 N, x-direction). Fromtop to bottom, δθ, δτ_ext,Dδq˙ +Rδq (solid line, observed;dashed line, reconstructed), and bothDδq˙ (dotted lines) and Rδq(dash-dot lines) at the shoulder (left graphs) and elbow (right graphs) are shown. b, The estimated distribution functions of viscosity and stiffness parameters obtained by random sampling (100 times) from experimental data (see Materials and Methods). The number attached in each graph is the mean value of the estimates for each parameter.

To estimate variances of these parameters ascribed to trial fluctuations, a data resampling method, the bootstrap method (Shao and Tu, 1995), was used. This method enabled us to predict variances of estimates from a small number of data sets. Note that, because of the high modeling performances shown above and the sufficient excitation of perturbations, the variances of estimates caused by modeling error (mean confidence interval of stiffness: 0.43 Nm/rad for four subjects) were smaller than those caused by trial fluctuations (mean SD of stiffness by the resampling method: 0.93 Nm/rad for four subjects). The processing procedure in our analysis was as follows. As noted in the experimental protocol, each perturbation was applied three times. From these three responses (each response consists of q,q˙, q̈,τ_ext), we randomly selected three responses with admitting repeated combination (e.g., [1,1,2], [1,2,2]… ), then made an ensemble response for the corresponding perturbation. There are ten possible combinations in making an ensemble response. By using ensemble responses perturbed in the eight directions (one data set), one parameter set (viscosity and stiffness parameters) was estimated at once. From 10⁸ possible combinations of data sets, we repeatedly (100 times) and randomly selected data sets, then estimated parameters for each data set. Figure 2b shows an example of the distribution functions of the 100 estimates for each parameter. From these distributions, we can estimate the variances caused by trial fluctuation as well as the mean of the parameter estimates. SDs of these distributions are presented as error bars on the joint stiffness graphs shown in the Results section.

From the estimated joint stiffness matrix R, the hand stiffness matrix in Cartesian coordinates,

$$\mathbf{K}\left(=-\frac{\partial {\mathbf{F}}_{\text{in}}}{\partial \mathbf{\text{x}}}=\left[\begin{array}{c}{K}_{\text{xx}}\\ \hfill K_{\text{xy}}\hfill \end{array}\begin{array}{c}{K}_{\text{yx}}\\ \hfill K_{\text{yy}}\hfill \end{array}\right]\right),$$

which characterizes arm elastic properties at one hand position, can be obtained using the following equation from the virtual work principle.

$$\mathbf{K}=({\mathbf{J}}^T{)}^{-1}\left(\mathbf{R}+\frac{\partial {\mathbf{J}}^T}{\partial \mathbf{\text{q}}}{\mathbf{F}}_{\text{in}}\right){\mathbf{J}}^{-1}.$$ Equation 4

Here, F_in (= (J^T)⁻¹ τ_in) denotes the force generated by the arm in Cartesian coordinates, and J denotes the Jacobian matrix of kinematics transformation. Note thatF_in is equal to the external interaction force under static conditions and is almost zero in the posture maintenance tasks.

From this hand stiffness matrix K, a stiffness ellipse can be drawn to represent the direction and magnitude of elastic, resisting forces to a unit-length position perturbations in any direction. The major axis of the ellipse represents the maximum resisting force, which indicates the greatest stiffness. Conversely, the minor axis represents the minimum resisting force, indicating the least stiffness. To summarize the hand stiffness ellipse for each task, we use the major axis direction ϕ_e (or its relative angle to the shoulder–hand direction: ϕ_e–ϕ_h; Fig.3), its shape eccentricity s(ratio of the major and minor axis length), and size A of the stiffness ellipse as represented in Equations 5-7 (for which the symmetry of the stiffness matrix is not required). Note that, in the case of symmetrical stiffness (i.e., same values ofK_xy and K_yx), these equations yield the same values as the methods used in Mussa-Ivaldi et al. (1985).

$${\varphi }_e={tan}^{-1}(U_{max\_y}/U_{max\_x})0\le {\varphi }_e<\pi$$ Equation 5

$$s={\alpha }_{min}/{\alpha }_{max},\text{where} {\alpha }_{max}=({\lambda }_{max}({\mathbf{K}}^T\mathbf{K}){)}^{1/2},{\alpha }_{min}=({\lambda }_{min}({\mathbf{K}}^T\mathbf{K}){)}^{1/2}.$$ Equation 6

$$A=\pi {\alpha }_{max}{\alpha }_{min}.$$ Equation 7

Here, U_{max_x} and U_{max_y} are the x and y components of the maximum resisting force vector for unit displacements, which can be obtained by the singular value decomposition of stiffness matrix K (i.e.,K =U · S · V^T). This is because first and second columns of matrix

$$\mathbf{U}\left(=\left[\begin{array}{c}{U}_{max\_x}\\ \hfill U_{max\_y}\hfill \end{array}\begin{array}{c}{U}_{min\_x}\\ \hfill U_{min\_y}\hfill \end{array}\right]\right)$$

represent the major and minor axis directions of the ellipse.

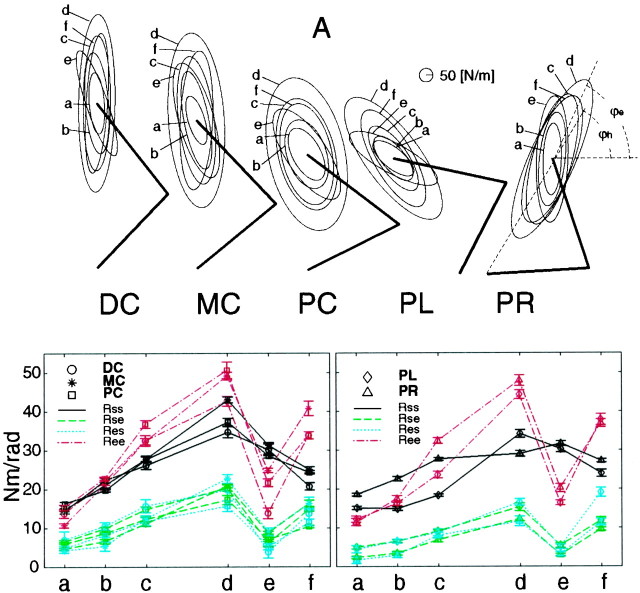
Fig. 3.

Stiffness ellipses (top figures) and corresponding joint stiffness values (bottom figures) of subject A during posture maintenance tasks (a–f) in five different postures (DC, distal center; MC, middle center;PC, proximal center; PL, proximal left;PR, proximal right). Each ellipse represents the stiffness during the requested task indexed by a roman character: (a) without cocontraction, (b) with quarter cocontraction, (c) half cocontraction, (d) full cocontraction, (e) cocontraction only in the shoulder, and (f) cocontraction only in the elbow. The thick line represents the arm configuration in each posture. The bottom graphsrepresent the stiffness values (R_ss,solid black line; R_se,dashed green line; R_es,dotted blue line; R_ee,dash-dot red line) during each task (a–f) at the hand positions [theleft graph is for DC (circle), MC (star), and PC (square); the right graph is for PL (diamond) and PR (triangle)]. The error bars represent the SD of estimates.

RESULTS

Stiffness change under different contraction conditions during posture maintenance tasks

As mentioned in the introductory remarks, earlier studies (Mussa-Ivaldi et al., 1985; Flash and Mussa-Ivaldi, 1990) found that the geometric characteristics of stiffness during posture maintenance, with or without cocontraction, were predominantly dependent on posture. We found however that the application of external force greatly alters the joint stiffness ratios as shown later. This raises the question of whether we can change joint stiffness ratios during posture maintenance without applying external forces. Figure 3 shows the stiffness ellipses (top figures) and corresponding joint stiffness (bottom two graphs) of subject A during the six posture-maintenance tasks.

In different tasks, the orientation and shape were altered as shown in the top figures in Figure 3. In task e (shoulder cocontraction) in all five postures, the orientations of the ellipses were rotated counterclockwise compared with those in other tasks, and the shoulder stiffness (R_ss) values were higher than the elbow stiffness (R_ee) values (bottom two graphs in Fig. 3).

On the other hand, in task f, the orientations of ellipses, ϕ_e, were similar to or smaller than those in taskd, and the elbow joint stiffness values were higher than the shoulder values in all five postures. Cross-joint stiffness values also increased in this task, whereas cross-joint stiffness values did not increase in task e. This tendency was consistent with an increase in cross-joint stiffness in accordance with the elbow joint stiffness increases seen during the force regulation tasks described later.

As shown in the bottom graphs in Figure 3, in tasksa–d in the distal center,b–d in the middle-center, anda–d in the proximal center postures, the elbow joint stiffness values (R_ee) were higher than, or similar to, shoulder joint stiffness (R_ss), although the ratios between the shoulder and elbow stiffness were not specified. This tendency was frequently observed in the other three subjects as well. On the other hand, in tasks a andb in the proximal left posture and in task a in the proximal right posture, the shoulder joint stiffness values (R_ss) were higher than the elbow joint stiffness (R_ee). This may be caused by increases in shoulder flexor or extensor muscle activation to hold a left or right posture. By increasing the cocontraction level (tasks cand d), however, the elbow joint stiffness (R_ee) exceeded the shoulder joint stiffness (R_ss).

To confirm muscle activation patterns, Figure4 shows, as an example, the EMG levels when subject A performed each task in the middle-center posture. As stiffness increased according to the task (Fig.3a–d), the EMG levels of both the flexor and the extensor muscles increased. In task e (shoulder cocontraction task), the EMG of the shoulder flexor muscle increased remarkably, whereas that of the shoulder extensor muscle did not increase much. Some extensor muscles whose EMGs were not observed may generate counter torque against the shoulder flexor muscle so as not to generate a net torque at the shoulder joint. In task f, the EMG levels of the elbow joint muscles increased in accordance with the requested elbow cocontraction condition, and the EMG levels of the biarticular muscles also increased, which was consistent with the stiffness observation shown above. Overall, EMG levels were roughly proportional to the joint stiffness values.

Fig. 4.

The magnitudes of rectified and averaged surface electromyograms (EMG level) from six muscles (shoulder monoarticular flexor and extensor muscles, biarticular flexor and extensor muscles, and elbow monoarticular flexor and extensor muscles) of subject A during posture maintenance tasks (a–f) in the middle center posture. The EMG levels were normalized in these tasks by the maximum EMG level for each individual muscle. The EMG levels of flexor muscles are depicted as black bars in the top portion of each graph, and the EMG levels of extensor muscles are depicted as gray bars in the bottom portion of each graph. Error bar on each bar graph represents SD of 24 trials of the corresponding EMG level.

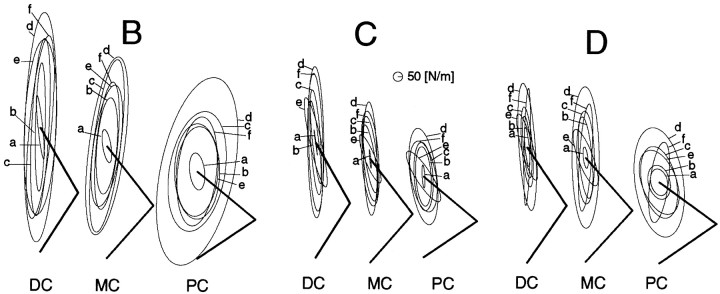
For the other three subjects, these five tasks were performed only in three postures (DC, MC, PC). Figure 5shows the stiffness ellipses during these tasks. The ellipses of subject B had the following two features of orientation unlike the other subjects: (1) most of the ellipses (except those for taska rotated clockwise compared with the shoulder–hand direction in each posture (Fig. 5), and (2) the ellipses in taske in each posture rotated less counterclockwise than those of subjects A, C, and D. The reason for the first feature is that the ratio of the cross-joint stiffness against the shoulder single-joint stiffness (R_cj/R_ss) in each condition was higher than that of the other subjects as explained in the Discussion. The second feature seems to be caused by differences in this individual’s skill. In particular, although the shoulder cocontraction was requested in task e, the elbow joint stiffness values at the middle and proximal hand positions of subject B were higher than the corresponding shoulder joint stiffness. This was not observed with subjects A, C, and D.

Fig. 5.

Stiffness ellipses of subjects B,C, and D during posture maintenance tasks in three postures (DC, MC,PC). See Figure 3 caption for notation.

In task f at the proximal hand position, the ellipse rotated greatly for subject D unlike the other subjects. In this task, the elbow joint stiffness of subject D was several times higher than the shoulder joint stiffness (R_ee/R_ss= 2.61), and the cross-joint stiffness was almost the same as the shoulder joint stiffness (R_cj/R_ss = 0.87), whereas the cross-joint stiffness ratio against the shoulder joint stiffness (R_cj/R_ss) in tasks a–e ranged from 0.45 to 0.66. The relationship between the stiffness ratio and the ellipse orientation and shape, and postural effect on these characteristics will be described in the Discussion in detail.

As observed above, in addition to the posture-dependent changes in orientation and shape of the ellipse (Mussa-Ivaldi et al., 1985; Flash and Mussa-Ivaldi, 1990; Tsuji et al., 1995), our results show that it is possible to change the stiffness ellipse characteristics by regulating joint stiffness ratios according to different task requirements, even during posture maintenance.

Joint stiffness change during force regulation tasks

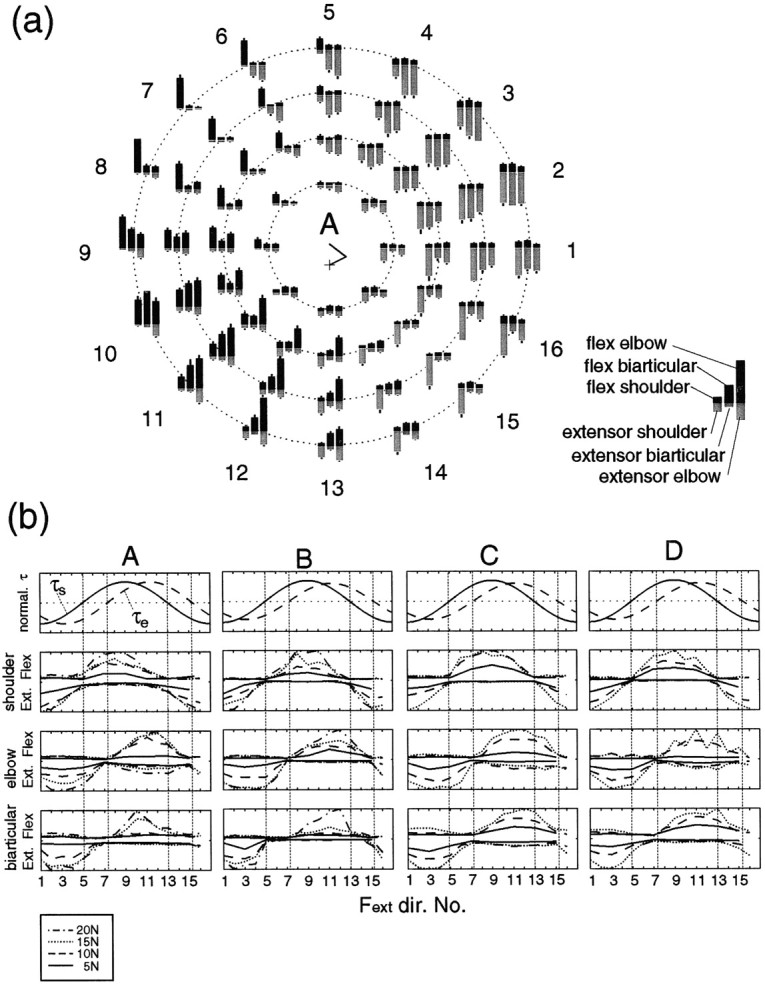
Figure 6a shows estimated joint stiffness values of subject A during force regulation tasks (5 N in eight directions, 10, 15, 20 N in 16 directions) without cocontraction at the proximal center hand position. Each bar graph, which represents R_ss,R_se, R_es, andR_ee, is aligned in a polar manner from the center to the outside according to the force directions and magnitudes. In all force directions, each stiffness component increased monotonically as force magnitude increased. However, each stiffness component greatly changed according to the force direction, resulting in a change in ratios between the stiffness components. Shoulder single-joint stiffness, R_ss, was higher in directions 1, 2, 8, 9, 10, and 16 compared with the other directions. Elbow single-joint stiffness, R_ee, increased in directions 2–4 and 9–12. Cross-joint stiffness,R_se and R_es, were almost the same in each condition as previously studied (Mussa-Ivaldi et al., 1985; Flash and Mussa-Ivaldi, 1990; Dolan et al., 1993; Tsuji et al., 1995) and covaried with the force directions.

Fig. 6.

a, Joint stiffness values (R_ss, R_se,R_es, R_ee) during force regulation tasks without cocontraction (instruction) at a proximal hand position (subject A). The stick picture in the center of the a shows the arm configuration (+ denotes shoulder position). Bar graphs were aligned in a polar manner according to force directions and magnitude (Fig. 10,arrows). The eight bar graph sets placed in the innermost circle represent the stiffness values during force regulation tasks at 5 N in the eight directions. Similarly, 16 bar graphs placed on the second, third, and fourth circular positions from center to outside represent those during force regulation tasks at 10, 15, and 20 N in each direction, respectively. The error bar on each bar represents SD of the corresponding estimate. b, Changes in joint torque and joint stiffness values according to the force directions of all four subjects. In the top row,solid and dashed lines represent shoulder and elbow normalized joint torque, respectively. In the second to fourth rows, lines represent each stiffness component (R_ss, shoulder; R_ee, elbow; R_cj = (R_se +R_es)/2, cross-joint) during force regulation tasks with 5 (solid line), 10 (dashed line), 15 (dotted line), and 20 N (dash-dot line). The numbers on the abscissa denote the force directions applied to the handle (see also Fig. 10a).

The directional dependent changes in stiffness at the proximal center hand position for all subjects can be seen more clearly in Figure6b. The first row of Figure 6b shows the normalized shoulder and elbow joint torques during these tasks. The shoulder single-joint stiffness shown in the second row of Figure6b was lowest in directions 5 and 13 where the shoulder joint torque was zero and covaried with the absolute value of the shoulder joint torque. Similarly, elbow joint stiffness was lowest in the directions where the elbow joint torque was zero and covaried with the absolute value of the elbow joint torque. The coupling of stiffness and torque was also observed at the other hand positions as shown later. The fourth row of Figure 6b shows the averaged cross-joint stiffness (R_cj = (R_se + R_es)/2). In subjects A, B, and D, cross-joint stiffness covaried with elbow joint torque rather than shoulder joint torque. In subject C, cross-joint stiffness stayed low in the directions 5–7 and 13–15. This may be because, in those directions, the shoulder torque and elbow torque are produced in opposite directions; thus, the biarticular muscles cannot contribute effectively to both joints. In those directions of subjects A, B, and D, torque generated by biarticular muscle may be canceled by the antagonist shoulder muscles.

To examine the muscle activities during these tasks, Figure7a shows the rectified and averaged EMG magnitudes (arbitrarily normalized) of six muscles of subject A. The EMG values of three flexion muscles (shoulder monoarticular, biarticular, and elbow monoarticular) are depicted in the top portion of each bar graph, and those of three extension muscles are depicted in the bottom portion. Roughly, extension muscles were activated to produce forces in directions 1–4, and 16, and flexion muscles were activated to produce forces in directions 8–12.

Fig. 7.

a, The magnitudes of rectified and averaged surface electromyograms (EMG level) from six muscles (shoulder monoarticular flexor and extensor muscles, biarticular flexor and extensor muscles, and elbow monoarticular flexor and extensor muscles) during force regulation tasks in 16 directions without cocontraction (instructed) at the proximal hand position (subject A). The magnitudes of EMG were normalized by the maximum EMG value for each muscle within these tasks. The EMG results of flexor muscles are depicted as theblack bars in the top portion of each graph, and the EMG results of extensor muscles are depicted as thegray bars in the bottom portion of each graph. Error bar on each bar graphrepresents SD of 24 trials of the corresponding EMG level. The manner of graph arrangement is the same as in Figure 6a.b, Changes in joint torque and EMG levels of six muscles for all four subjects according to force direction. The top row shows the normalized torque. The second rowshows the normalized EMG levels of the shoulder monoarticular flexor (upper side) and extensor (lower side) muscles. Thethird and fourth rows show the normalized EMG levels of the elbow monoarticular and the biarticular muscles, respectively, in the same manner as the second row.

Figure 7b shows the EMG values of the four subjects. The EMG values of the reciprocally activated flexor and extensor monoarticular muscles (Fig. 7b, second andthird rows) covaried with the torque of their respective joint (Fig. 7b, first row). In the elbow monoarticular muscles, however, the EMG of the antagonist muscles slightly increased in accordance with increases of the agonist muscles (coactivation) (see graphs of subjects A, C, and D).

As for the biarticular muscle (Fig. 7b, fourth row), its EMG roughly covaried with the elbow torque as observed in the cross-joint stiffness case (Fig. 6b,fourth row). This is consistent with the results of covariation between flexor biarticular (biceps) and elbow monoarticular muscle (brachioradialis) activations (Wadman et al., 1980; Flanders and Soeching, 1990). However, some discrepancies are also found; the extensor biarticular muscle (long head of triceps) exhibited strong coactivation shown in (Flanders and Soeching, 1990), but this was not seen here. This may be ascribed to posture differences (horizontal vs vertical planes) and experimental protocol (we required subject to keep generating force without cocontraction). The shoulder joint effects on the activation of biarticular muscles found in (Flanders and Soeching, 1990) can be observed in some of the present results: peak-activation of the flexor biarticular muscle was shifted to the peak of shoulder torque from the peak of elbow torque (Fig. 7b, subject A), and biarticular muscle activation was silent for generating torques in different directions at shoulder and elbow (Fig. 7b, directions 6 and 14 of subject B). Note that, because the EMG merely represents the partial activities of all muscles (or motor units) effective in generating force, measured EMG may be insufficient to explain the observed stiffness.

The covariation between stiffness and torque shown in Figure 6 was also observed at different hand positions. Figure8 depicts the relationships between the joint torque and the joint stiffness components during force regulation tasks without cocontraction at the all hand positions (see Materials and Methods) for each subject. The correlation coefficient between the absolute torque and stiffness is indicated in the top left corner of each graph. Single-joint stiffness values (R_ssand R_ee) strongly correlate to the absolute values of the corresponding joint torque (τ_s and τ_e). This phenomenon is consistent with the observations in single-joint studies (Agarwal and Gottlieb, 1977; Hunter and Kearney, 1982; Gottlieb and Agarwal, 1988; Kearney and Hunter, 1990). On the other hand, cross-joint stiffness values, R_seand R_es, correlate to the absolute value of elbow joint torque, but not to shoulder joint torque, especially in subjects A, B, and D. Considering the covariation between the EMG of biarticular muscle and the elbow joint torque mentioned above, this suggests that the biarticular muscles mainly contribute to generating torque at the elbow joint.

Fig. 8.

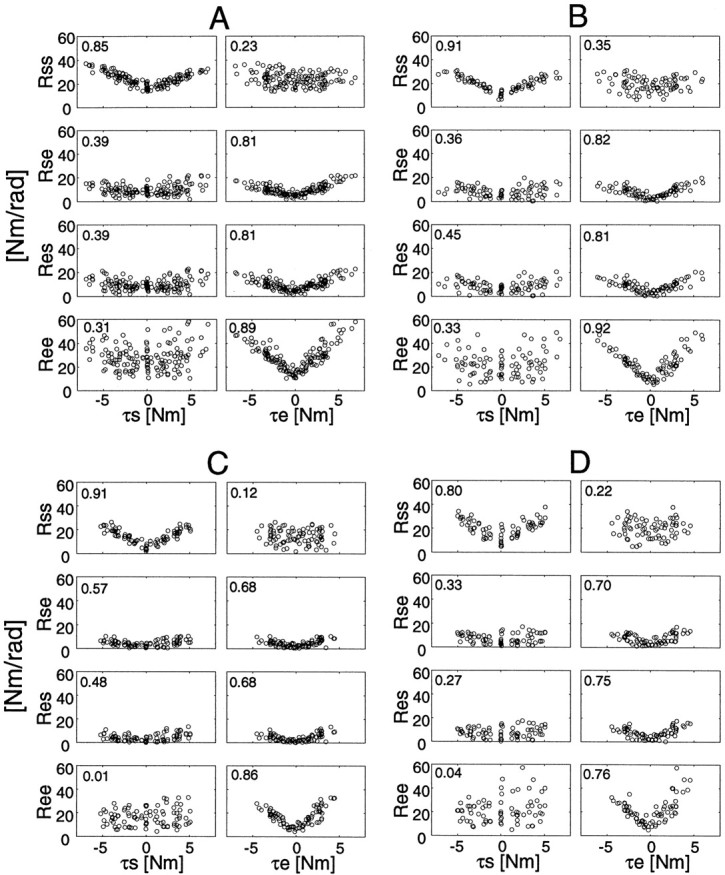
Joint torque and joint stiffness relationships during all force regulation tasks without cocontraction at the all hand positions. Each correlation coefficient between absolute torque and stiffness is placed in the top left corner of each graph.

To examine the relationships in detail, we summarize the slopes and intercepts of regression lines between stiffness and torque (absolute torque or positive/negative torque) in Table2. The slopes of the regression lines between elbow single-joint stiffness (R_ee) and elbow torque (τ_e) were greater (statistically significant,p < 0.005 for all subjects) than those between shoulder single-joint stiffness (R_ss) and shoulder torque (τ_s) for all four subjects. This may be because, as seen in the EMG graphs (Fig. 7b), small cocontractions occurred at the elbow monoarticular muscles. Additionally, the slopes of the regression lines in the positive and negative directions were slightly different from each other. This difference in slope may be caused by the asymmetrical contractions when producing positive/negative (flexor/extensor) torque by different combinations of multiple muscles, and differences in muscle-inherent characteristics, moment-arms, and reflex effects.

Table 2.

Torque–stiffness relationships [slopes, intercepts, and those 95% confidence intevals (CI) of Fig. 7] during force regulation tasks without cocontraction

Subject	Absolute		−		+
	Slope ± CI	Intercept ± CI	Slope ± CI	Intercept ± CI	Slope ± CI	Intercept ± CI
(a) τs vs Rss
A	2.57  ± 0.26	16.67  ± 0.89	−2.71  ± 0.34	17.87  ± 1.18	2.39  ± 0.28	15.61  ± 0.94
B	2.86  ± 0.27	11.11  ± 0.94	−3.23  ± 0.38	10.57  ± 1.36	2.54  ± 0.36	11.50  ± 1.21
C	3.60  ± 0.35	5.13  ± 1.05	−3.75  ± 0.53	4.93  ± 1.58	3.45  ± 0.49	5.32  ± 1.45
D	3.71  ± 0.66	10.29  ± 2.02	−4.41  ± 0.83	7.91  ± 2.53	3.08  ± 1.02	12.44  ± 3.09
Mean	3.18	10.80	−3.53	10.32	2.86	11.22
(b) τe vs Rse
A	2.16  ± 0.26	4.72  ± 0.77	−1.73  ± 0.34	4.84  ± 1.02	2.57  ± 0.31	4.63  ± 0.93
B	2.40  ± 0.36	2.49  ± 1.00	−1.94  ± 0.56	3.53  ± 1.54	2.89  ± 0.42	1.33  ± 1.18
C	1.59  ± 0.36	1.51  ± 0.83	−1.38  ± 0.46	1.44  ± 1.06	1.80  ± 0.55	1.58  ± 1.26
D	2.46  ± 0.60	2.58  ± 1.37	−2.15  ± 0.78	2.70  ± 1.78	2.76  ± 0.92	2.47  ± 2.14
Mean	2.15	2.83	−1.80	3.13	2.51	2.50
(c) τe vs Res
A	2.33  ± 0.28	4.16  ± 0.85	−2.08  ± 0.41	4.10  ± 1.24	2.58  ± 0.36	4.23  ± 1.08
B	2.41  ± 0.38	3.01  ± 1.05	−2.12  ± 0.58	3.76  ± 1.59	2.73  ± 0.50	2.19  ± 1.39
C	1.81  ± 0.42	0.89  ± 0.95	−1.48  ± 0.46	0.88  ± 1.05	2.16  ± 0.66	0.88  ± 1.50
D	2.82  ± 0.58	1.98  ± 1.35	−2.35  ± 0.78	2.31  ± 1.79	3.28  ± 0.85	1.66  ± 1.98
Mean	2.34	2.51	−2.01	2.76	2.69	2.24
(d) τe vs Ree
A	5.89  ± 0.49	13.44  ± 1.48	−5.27  ± 0.54	13.54  ± 1.63	6.48  ± 0.76	13.38  ± 2.27
B	6.38  ± 0.59	7.89  ± 1.62	−5.94  ± 0.51	8.82  ± 1.41	6.85  ± 1.09	6.87  ± 3.04
C	5.48  ± 0.70	5.68  ± 1.61	−5.02  ± 0.65	5.21  ± 1.47	5.94  ± 1.18	6.15  ± 2.70
D	6.95  ± 1.42	7.68  ± 3.26	−5.83  ± 1.06	6.81  ± 2.41	8.01  ± 2.36	8.72  ± 5.48
Mean	6.18	8.67	−5.52	8.60	6.82	8.78

Joint viscosity change during force regulation tasks

Figure 9 shows the viscosity–torque relationships of the four subjects during the force regulation tasks without cocontraction in all postures. As with the stiffness cases shown above, the correlation coefficients between the absolute torque at each joint and the corresponding single-joint viscosities are greater than other correlation coefficients. These correlation values, however, are lower than those in the stiffness cases (compare Figs. 8and 9), indicating a less linear relationship between viscosity and torque.

Fig. 9.

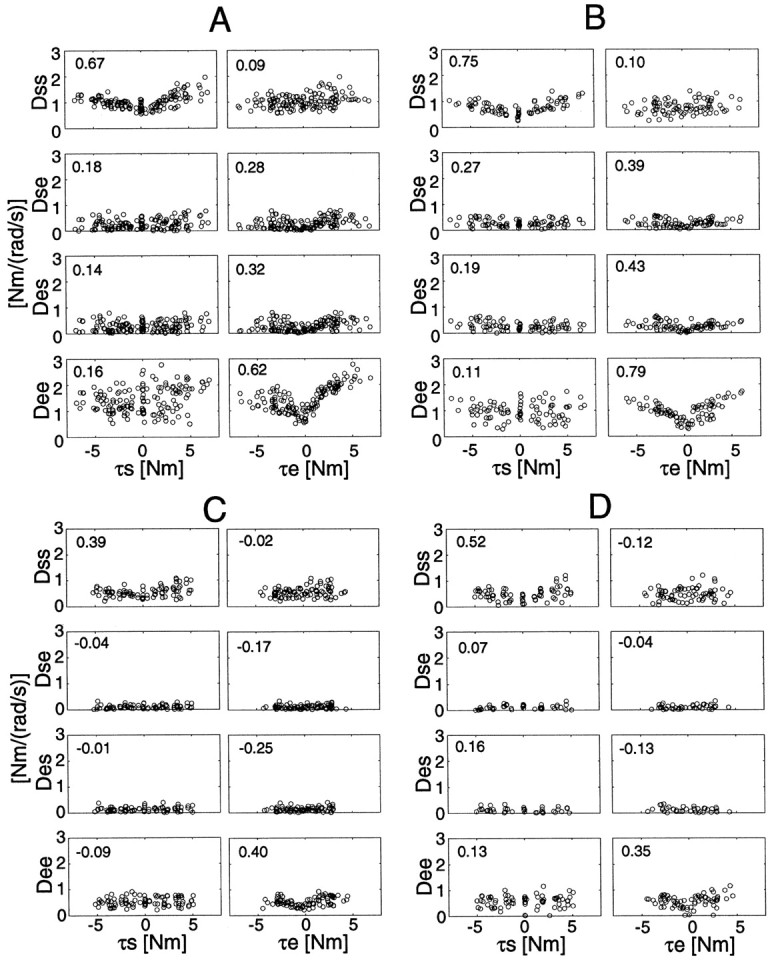
Joint torque and joint viscosity relationships during all force regulation tasks without cocontraction at the all hand positions. Each correlation coefficient between absolute torque and viscosity is placed in the top left corner in each graph.

Table 3 summarizes the slopes and intercepts of the regression lines between viscosity and torque for subjects A and B. From Figure 9 and Table 3, we can find the following trends: (1) the slopes of viscosity change against the torque at the elbow joint were greater than those at the shoulder joint in subjects A and B, and (2) the trends of viscosity changes in positive and negative directions were asymmetrical (especially at the elbow joint in subject A). These phenomena may be caused by differences in cocontraction, moment-arm, muscle-inherent properties, or reflex effects as mentioned in the stiffness case. Additionally, joint mechanical viscosity (or friction-like properties) dependent on joint torque could be a potential factor in each single-joint component.

Table 3.

Torque–viscosity relationships [slopes, intercepts, and those 95% confidence intervals (CI) of Fig. 8] during force regulation tasks without cocontraction

Subject	Absolute		−		+
	Slope ± CI	Intercept ± CI	Slope ± CI	Intercept ± CI	Slope ± CI	Intercept ± CI
(a) τs vs Dss
A	0.09  ± 0.02	0.77  ± 0.06	−0.06  ± 0.02	0.81  ± 0.06	0.12  ± 0.03	0.72  ± 0.09
B	0.10  ± 0.02	0.49  ± 0.06	−0.09  ± 0.03	0.47  ± 0.09	0.11  ± 0.02	0.50  ± 0.08
Mean	0.10	0.63	−0.08	0.64	0.12	0.61
(b) τe vs Dse
A	0.03  ± 0.02	0.17  ± 0.06	−0.02  ± 0.03	0.14  ± 0.08	0.05  ± 0.03	0.20  ± 0.08
B	0.04  ± 0.02	0.18  ± 0.05	−0.03  ± 0.03	0.19  ± 0.08	0.04  ± 0.02	0.16  ± 0.06
Mean	0.04	0.18	−0.03	0.17	0.05	0.18
(c) τe vs Des
A	0.04  ± 0.02	0.19  ± 0.06	−0.02  ± 0.03	0.17  ± 0.09	0.05  ± 0.02	0.20  ± 0.07
B	0.04  ± 0.02	0.16  ± 0.06	−0.04  ± 0.03	0.20  ± 0.09	0.05  ± 0.02	0.12  ± 0.06
Mean	0.04	0.18	−0.03	0.19	0.05	0.16
(d) τe vs Dee
A	0.19  ± 0.04	0.97  ± 0.12	−0.12  ± 0.04	0.89  ± 0.12	0.27  ± 0.03	1.05  ± 0.10
B	0.18  ± 0.03	0.55  ± 0.08	−0.15  ± 0.03	0.59  ± 0.08	0.21  ± 0.05	0.51  ± 0.14
Mean	0.19	0.76	−0.14	0.74	0.24	0.78

Relationships between joint stiffness and viscosity

Several studies (Agarwal and Gottlieb, 1977; Lacquaniti et al., 1982; Kusumoto et al., 1994) have shown that viscosity also increases as the muscle activity increases. This is consistent with our multijoint experiment, in which both stiffness and viscosity simultaneously increased as the torque increased as shown above. In detail, it can be also found that the viscosity–stiffness ratios (D/R) are slightly different among different components and different torque directions even for the same subject. Especially at the proximal hand position, the viscosity–stiffness ratio of the elbow joint component (0.031, averaged for subjects A and B) was twice that of the cross-joint component (0.016, averaged for subjects A and B). On the other hand, at the distal hand position, the viscosity–stiffness ratio of the cross-joint components (0.043, subjects A and B) increased and approached those of the elbow joint components (0.049, subjects A and B). Additionally, it seems that not only the slopes of the cross-joint components but also those of the single-joint components were altered in different postures as observed in Tsuji et al. (1995)(the viscosity–stiffness ratios in the distal and proximal postures differed by a factor of 2.4 in their experiment). These mechanical impedance changes may be caused by the difference in muscle-inherent properties, reflex effects, and/or the differences in joint mechanical viscosity.

In previous studies on the relationships between joint stiffness and its viscosity (Lacquaniti et al., 1982; Kearney and Hunter, 1990), the experimental data suggest that the damping ratio was constant regardless of cocontraction. This indicates a linear relationship between square root stiffness and viscosity. Additionally, it was reported (Dolan et al, 1993) that the modeling of multijoint arm impedance by “multiple-constant damping ratio” was better than modeling by “multiple-constant scaling” in which stiffness is linearly proportional to viscosity. As shown in some cases of Figure 9, the rate of the viscosity increase gradually fell as torque increased, whereas the stiffness increased linearly with torque (Fig. 8). Although this fact supports the constant damping ratio hypothesis (Lacquaniti et al., 1982; Dolan et al., 1993), it is difficult to claim strong evidence for the constant damping ratio under the multijoint conditions because of the large variance which may be partially caused by task-dependent changes in reflex activity.

Spatial characteristics of hand stiffness depending on force direction

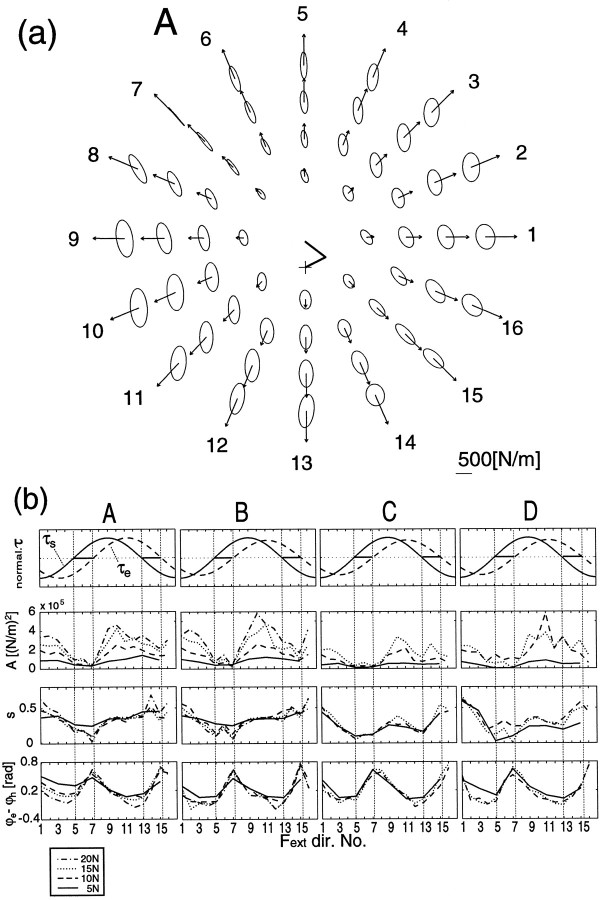
Because the joint stiffness changes according to the joint torque magnitudes, it is to be expected that the orientation and shape of the stiffness ellipse should vary for different force directions as it did in the different cocontraction tasks shown earlier. Figure10a shows the stiffness ellipses of subject A during force regulation tasks in the proximal center posture. The ellipses were aligned in the order of the force directions and magnitudes (see figure legend). Figure 10bsummarizes the ellipse characteristics, size (A), shape eccentricity (s), and ellipse orientation relative to the hand-shoulder direction (ϕ_e–ϕ_h) of the four subjects during all force regulation tasks. The ellipse enlarged isomorphically according to the force magnitude in each force direction (Fig. 10a and second top graphs of 10b), but the ellipse orientations and shapes changed with force directions. Note that, as shown in the third row in Figure 10b, ellipse shapes for opposite force directions (e.g., direction 5 vs 13, 6 vs 14, and 7 vs 15) differed from each other. This difference is mainly ascribed to the distortion by external forces (Eq. 4) as examined inGomi and Osu (1996d) and McIntyre et al. (1996).

Fig. 10.

a, Stiffness ellipses during force regulation tasks without cocontraction at the proximal center hand position (subject A). Each ellipse represents the spatial characteristics of the elastic property of the arm at the corresponding hand position. All ellipses are aligned in a polar manner according to the force directions and magnitudes requested in each task. The ellipses placed in the innermost circle represent the hand stiffness during force regulation tasks at 5 N in eight directions. Similarly, 16 ellipses placed in the second, third, and fourth circle positions represent those during force regulation tasks at 10, 15, and 20 N in each direction, respectively. The arrow on each ellipse denotes the force magnitude and direction. The stick picture in the center of the polar graphs shows the arm configuration of each subject.b, The characteristics of the stiffness ellipses (sizeA, shape s, and orientation ϕ_e–ϕ_h) of all subjects during force regulation tasks without cocontraction at the proximal center hand position. Thetop graphs represent the normalized torque at the shoulder and elbow. In the second, third, and fourth graphs, solid,dashed, dotted, anddash-dot lines denote each index (see ordinate label) during force regulation tasks at 5, 10, 15, 20 N, respectively. The force regulation tasks at 20 N were not applied to subjects C and D. The numbers on the abscissa denote the force directions applied to the handle.

In directions 7 and 15, the ellipse orientations were rotated counterclockwise compared with those in other directions (Fig.10b, bottom row). In these directions, the elbow stiffness did not increase (Fig. 6) because of the small elbow joint torque. This is similar to the condition in the shoulder contraction task during posture maintenance in which the ellipse orientations were also rotated counterclockwise (Fig. 3, see the ellipses for task e).

We also found another remarkable feature of the variation of stiffness ellipse for different force direction in different postures. The variations of orientation (ϕ_e–ϕ_h) and shape (s) were smaller in the distal posture (variation range of orientation, 0.34 ± 0.03 [rad]; shape, 0.21 ± 0.04 for four subjects) than in the proximal posture (orientation, 0.75 ± 0.12 [rad]; shape, 0.45 ± 0.04). In other words, controllability of stiffness ellipse was larger in the proximal posture than in the distal posture, which may be important for flexible manipulation. We will further examine this mechanism in the Discussion.

DISCUSSION

Condition-dependent viscoelasticity

Let us now compare the present results with previous observations that reported elbow and shoulder stiffness during posture maintenance at zero external force. Note that the intercepts of the stiffness–torque regression lines summarized in Table 2 correspond to the stiffness during posture maintenance without cocontraction. The intercepts of elbow single-joint stiffness (R_ee) against the elbow torque observed in the present study (7.7–13.4 Nm/rad) were close to the estimates for single-joint posture maintenance under relaxed conditions observed in several studies such as Lacquaniti et al. (1982) (15.0 Nm/rad in mean by weak and medium springs; 12.7 Nm/rad in mean by random perturbation), MacKay et al. (1986) (∼18 Nm/rad by a small perturbation), and Bennett et al. (1992) (14–17 Nm/rad by random perturbation). The stiffness values during multijoint posture maintenance measured by Mussa-Ivaldi et al. (1985) ([R_ss, R_cj,R_ee] = [25.7, 10.3, 28.9] in mean from Table1) and by Flash et al. (1990) ([22.1, 9.3, 23.2] in mean from Table1) were greater than those observed here ([10.8, 2.7, 8.7] in mean from Table 2 of this paper). As compared all results, some of our estimates were close to theirs. Similar experiments by Tsuji et al. (1995) (mean values [R_ss,R_cj, R_ee] = [8.3, 3.1, 7.5] for four postures in four subjects) have shown that an increase in the handle-gripping force leads to cocontraction, which increases stiffness. Because our experimental setup is similar to that of Tsuji et al. (1995), our results are comparable to their results. These results suggest that the discrepancies in stiffness in different studies may be caused by the differences in individuals, experimental setups, and instructions.

As in the stiffness case, the intercept of the viscosity–torque regression lines summarized in Table 3 can be compared with the viscosity during relaxed posture maintenance of previous studies. The mean values of intercepts in Table 3 ([D_ss,D_cj, D_ee] = [0.63, 0.18, 0.76] Nm/(rad/sec), where D_cj= (D_se + D_es)/2) are comparable with the results found by Lacquaniti et al. (1982) (the elbow single-joint viscosity (D_ee) = 0.31 Nm/(rad/sec) in mean for spring perturbations) and by Tsuji et al. (1995) (mean values [D_ss,D_cj, D_ee] = [0.71, 0.21 0.43] Nm/(rad/sec) for four postures of four subjects from Table 3 in their report). The small discrepancies between the reports may be caused by the differences in the individual subjects as mentioned in the stiffness case.

However, for the viscosity, the different properties of the perturbations cannot be ignored in quantifying viscosity components as shown in Lacquaniti et al. (1982) [D_ee = 1.28 Nm/(rad/sec)] in mean for random perturbations). Viscoelastic properties not only are altered by muscle activation levels, but also are affected by gains and delays in reflex feedback loops and by the nonlinearity of muscles and tendons. Transient EMG changes during perturbations were frequently observed in our analysis (Osu and Gomi, 1997), and, thus, reflexes may have contributed to viscoelasticity. However, in the present study, we cannot directly quantify the effects of reflexes on measured stiffness and viscosity because of the complex mechanisms of the neuromusculoskeletal system. To further understand the characteristics of neuromusculoskeletal system, it is essential to quantify the mechanical characteristics in a variety of tasks to reveal both the reflex contributions and the muscle dynamics.

Arm posture affects the controllability of orientation and shape of stiffness ellipse

Hand stiffness (or compliance) is important in ensuring stability when interacting with objects, thus, manipulation flexibility is dependent to how much we can control stiffness characteristics at the hand. McIntyre et al. (1996) showed that stability of the arm during pushing force control is achieved by increasing joint stiffness as torque increased. Based on the several experiments in which stiffness ellipse orientations were shown to be roughly directed to the shoulder at any arm postures, we expected that the CNS would keep a constant ratio between shoulder and double-joint stiffness (Flash, 1987; Flash and Mussa-Ivaldi, 1990; Gurevich, 1993; Flash and Gurevich, 1997). From the analyses shown above, however, it appears that joint stiffness ratios can be altered by different cocontraction and/or different force directions. This results in changes of the geometric characteristics of hand stiffness.

To avoid misinterpretation of these experimental results, it is important to quantify the effect of the change in the ratio of joint stiffnesses on the stiffness-ellipse characteristics. Because multiple factors (stiffness ratios in R and Jacobian of arm kinematics J) affect hand stiffness characteristics (Eq. 4), it may be difficult to realize how much we can change these characteristics in different postures. To examine the postural effect on the controllability of ellipse orientation, Figure11a-1,b-1depicts theoretical variations in the orientation of the stiffness ellipse (ϕ_e–ϕ_h) according to changes in the joint stiffness ratios (R_ee/R_ss,R_cj/R_ss) at the distal and proximal postures (hand position:[x, y] = (a) [0.0,0.5], (b) [0.0, 0.35] m; upper arm, 0.31 m, forearm, 0.35 m). The surfaces were obtained from Equations 4 and 5 by changing joint stiffness ratio in R (0.3 <R_ee/R_ss < 2.5, 0.1 < R_cj/R_ss < 1.0;R_cj, averaged value ofR_se and R_es) withF_in = 0. The ellipse orientations derived from stiffness ratios experimentally obtained in all tasks of subject A were represented on the both surfaces of distal and proximal postures as open circles. Because the effects of external force on the ellipse characteristics were much smaller than those of joint stiffness variation in our tasks (Gomi and Osu, 1996d), they are not considered in this figure. Because of the limited variation of the actual stiffness ratios empirically obtained (Fig. 11, open circles), the variable range of orientation is affected by the shape of the surface characterized by the arm configuration. Indeed, as compared a-1 withb-1 in Figure 11, the surface is flatter within the actual range of stiffness ratios in the distal posture than in the proximal posture. As a result of this surface change, ellipse orientation in the distal posture does not change much from altering joint stiffness ratios. For example, for the two joint stiffness ratios (1) and (2) indicated on the bottom axes plane of a-1 andb-1, the difference in the ellipse orientation at the distal posture is twice smaller than that at the proximal posture as shown in the middle of Figure 11. Additionally, the surface figures clearly show that the negative rotation of ellipse (ϕ_e–ϕ_h < 0) is achieved when there is a large ratio of double-joint stiffness to shoulder stiffness. Hence, double-joint stiffness is important in altering stiffness characteristics.

Fig. 11.

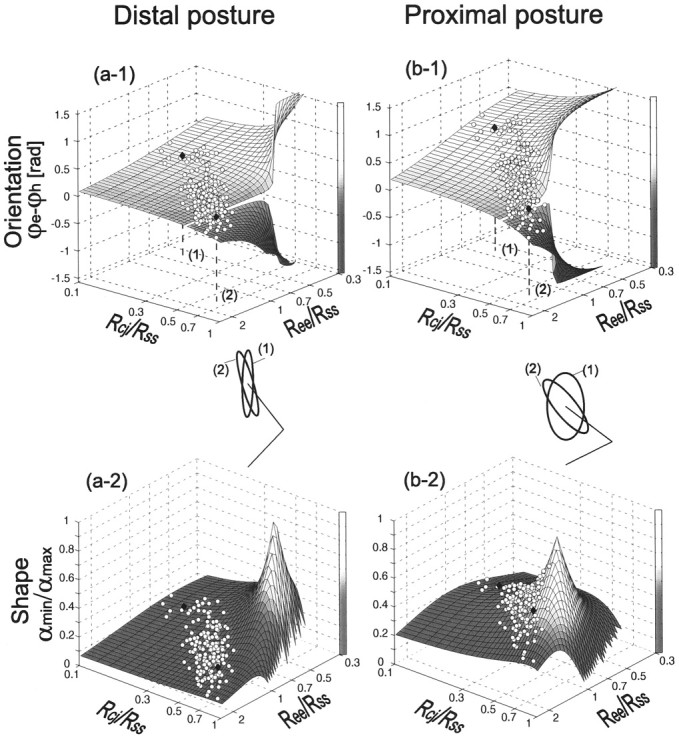
The theoretical (surface) and experimental (open circles) variations of orientation (ϕ_e–ϕ_h; top graphs) and shape (s; bottom graphs) of the stiffness ellipse at a distal ([x, y] = [0.0, 0.5]m; left graphs) and proximal ([0.0, 0.35]m; right graphs) postures according to the change in stiffness ratios (R_ee/R_se,R_cj/R_ss). In thetop graphs, the surface representing theoretical variation of orientation split away at 0 rad, indicating that the major axis of ellipse is in the hand–shoulder direction. Experimental data points (open circles) on the surfaces were derived from Equations 5 and 6 with the stiffness ratios of subject A, realized in all tasks. The ellipses for two sets of stiffness ratios (indicated on the bottom axes plane of top figures) are depicted for distal and proximal postures. Each ellipse size is normalized by the major axis of the ellipse. Their orientations and shapes are indicated by filled diamonds on the corresponding surfaces.

Similarly, the theoretical variations in ellipse shape according to changes in the joint stiffness ratios at the two postures are depicted as surfaces in a-2 and b-2of Figure 11. These surfaces were obtained from Equations 4 and 6 withF_in = 0. The vertical height of surfaces at each stiffness ratio represents the shape of the ellipse indexed bys (Eq. 6). Note that the ellipse comes close to a circle when the shape index approaches to one. The shape of ellipse (height of surface) changes little within the range of stiffness ratios experimentally obtained (marked by open circles) for the distal posture (a-2) but changes a lot at the proximal posture (b-2). In other words, in the proximal posture, ellipse shape is also sensitive to the actual variation in joint stiffness. This can be also known from the differences in the shape of ellipse placed at the middle of Figure11.

Because of these posture-dependent sensitivities, the controllability (or flexibility) of hand stiffness characteristics (orientation and shape of stiffness ellipse) may be an important factor in determining a preferable posture for an intended task. The experimental results support the idea that, for the various kinds of task requirements in manipulation, a human can change not only the size, but also the orientation and shape of the stiffness ellipse by regulating the joint stiffness ratios (Hogan, 1985).

Task-dependent coordination of multiple muscle regulation

This study has revealed that elbow single-joint stiffness and cross-joint stiffness change according to the elbow torque during force regulation tasks. EMG activities also indicated that the activations both of elbow monoarticular and of biarticular muscles covaried with elbow torque. This behavior is consistent with the idea of “synergistic muscle regulation mechanism”. A study of the recruitment threshold of motor units (van Zuylen et al., 1988), which showed ∼40% relative contribution of the biceps in the elbow flexion isometric contraction, provides evidence of a cooperative mechanism between the elbow monoarticular muscles and the biarticular muscles.

However, this cooperative mechanism in biarticular and monoarticular muscles is eliminated in some cases. In the isometric multijoint force regulation tasks, it was shown in Gomi and Osu (1996a) that the relative contribution of the cross-joint stiffness to the elbow torque varies with the ratio of elbow/shoulder torque. Especially, when the torque at the elbow opposes that at the shoulder, it may be that the elbow joint torque is produced only by the elbow monoarticular muscles (Gomi and Osu, 1996a,c). This suggests that the relative contribution of a biarticular muscles is greatly dependent on the total behavior of all joints.

On the other hand, during the isometric force regulation tasks, activation of the elbow monoarticular muscle varied with the activation in the biarticular muscle, although the monoarticular muscle contributes little to joint torque production in some force directions (Gomi and Osu, 1996a). This invariance could imply an unavoidable mechanism inherent in muscle coordination. However, during voluntary movements in some directions, it has been observed that the biarticular muscle was activated without the activation of the synergist elbow monoarticular muscle (Karst and Hasan, 1991). Additionally, even in the single-joint movements, it has been observed (Tax et al., 1989; van Groeningen and Erkelens, 1994) that the recruitment threshold of the biarticular muscle was changed from that in static force regulation. These results contradict an inescapable synergistic mechanisms, but rather imply that the objective tasks (including dynamic aspects) may be fully considered in coordinating multiple muscle activations. The redundancy of multiple muscle regulation may be partly solved by the prewired synergistic mechanisms such as intermuscle reflexes (Miyasaka et al., 1995; Naito et al., 1996) and synergistic connections in descending pathways (Shinoda et al., 1979; Fetz and Cheney, 1980). In addition to such basic mechanisms, the CNS may supervise and regulate these behaviors and directly and/or indirectly control temporal and spatial muscle activation patterns according to the task demands and environmental conditions. We will clarify the task and environment-dependent rules of multijoint musculoskeletal dynamics in the next stage to further investigate the computational mechanisms of arm control.

In our analyses, the arm-dynamics parameters (including the cuff and handle) were pre-estimated from all data sets as in the procedure in Gomi and Kawato (1995, 1996, 1997). Because arm-dynamics parameters are used to calculate the left side of Equation 2, the errors in the pre-estimated arm-dynamics parameters could cause estimation errors in viscosity D and stiffness R. By using a simulation, we will examine these estimation error variances. First, a data set was generated by the computer simulation of a static stiffness experiment using the arm-dynamics parameters of subject B, a particular parameter set of D and R, and perturbations similar to those in the experiment. The parameters used are as follows: arm-dynamics parameters: [Z1, Z2,Z3] = [0.327, 0.109, 0.106] Nm/(rad/sec²); viscosity parameters: [D_ss, D_se,D_es, D_ee] = [0.80, 0.30, 0.30, 0.70] Nm/(rad/sec); and stiffness parameters: [R_ss, R_se,R_es, R_ee] = [11, 3, 3, 9] Nm/rad.

To check the estimation error of viscosity and stiffness caused by errors in the arm-dynamics parameters, we repeatedly (100 times) estimated viscosity and stiffness by using Equation 2 with arm-dynamics parameters that were randomly selected between 0.320 and 0.336 forZ1, 0.081 and 0.140 for Z2, and 0.100 and 0.112 for Z3. These lower and upper limits were 25 and 75% bounds of the distributions of the estimated arm-dynamics parameters from all the empirical data sets (68 sets) of subject B. As a result, the maximum estimation error of viscosity and stiffness parameters were [0.037, 0.023, 0.020, 0.018] Nm/(rad/sec) and [1.76, 2.97, 1.08, 1.74] Nm/rad, respectively. These maximum errors are relatively small compared with the variations of stiffness and viscosity shown in Figures 8 and 9, thus indicating that viscosity and stiffness parameters can be reliably estimated by our method.