Linearity of Cortical Receptive Fields Measured with Natural Sounds

Abstract

How do cortical neurons represent the acoustic environment? This question is often addressed by probing with simple stimuli such as clicks or tone pips. Such stimuli have the advantage of yielding easily interpreted answers, but have the disadvantage that they may fail to uncover complex or higher-order neuronal response properties. Here, we adopt an alternative approach, probing neuronal responses with complex acoustic stimuli, including animal vocalizations. We used in vivo whole-cell methods in the rat auditory cortex to record subthreshold membrane potential fluctuations elicited by these stimuli. Most neurons responded robustly and reliably to the complex stimuli in our ensemble. Using regularization techniques, we estimated the linear component, the spectrotemporal receptive field (STRF), of the transformation from the sound (as represented by its time-varying spectrogram) to the membrane potential of the neuron. We find that the STRF has a rich dynamical structure, including excitatory regions positioned in general accord with the prediction of the classical tuning curve. However, whereas the STRF successfully predicts the responses to some of the natural stimuli, it surprisingly fails completely to predict the responses to others; on average, only 11% of the response power could be predicted by the STRF. Therefore, most of the response of the neuron cannot be predicted by the linear component, although the response is deterministically related to the stimulus. Analysis of the systematic errors of the STRF model shows that this failure cannot be attributed to simple nonlinearities such as adaptation to mean intensity, rectification, or saturation. Rather, the highly nonlinear response properties of auditory cortical neurons must be attributable to nonlinear interactions between sound frequencies and time-varying properties of the neural encoder.

Introduction

Although it is widely agreed that the primary visual cortex decomposes images into components such as oriented edges (Hubel and Wiesel, 1962), the corresponding decomposition of acoustic stimuli in the primary auditory cortex remains uncertain. The spectrotemporal receptive field (STRF) has recently attracted increased interest as a candidate framework for characterizing the function of auditory cortical neurons (Kowalski et al., 1996a,b; deCharms et al., 1998; Blake and Merzenich, 2002; Miller et al., 2002; Rutkowski et al., 2002; Linden et al., 2003). Part of the appeal of the STRF rests in its conceptual simplicity; like its successful visual counterpart, the spatiotemporal receptive field, it offers a straightforward linear description of the behavior of a neuron.

The cortical STRF has been estimated using a variety of stimulus ensembles, including dynamic ripples (Kowalski et al., 1996a; Klein et al., 2000; Miller et al., 2002), random chord stimuli (deCharms et al., 1998; Rutkowski et al., 2002; Linden et al., 2003), and random tone pips (Blake and Merzenich, 2002). However, the ultimate test of any model of sensory function rests in the ability of the model to predict responses to natural stimuli. It remains, at present, an open question how well the STRF can explain the behavior of the auditory cortex under natural conditions, in which an organism encounters highly complex, dynamically changing stimuli. Although natural stimuli have long been used to probe cortical responses (Wollberg and Newman, 1972; Sovijärvi, 1975; Creutzfeldt et al., 1980; Nelken et al., 1999) and have been widely used in other preparations to compute STRFs (Eggermont et al., 1983; Yeshurun et al., 1989; Theunissen et al., 2001), they have only rarely been used to test the STRF on cortical neurons (Rotman et al., 2001; Machens et al., 2003).

Here, we estimate the STRF defined by subthreshold membrane potentials using in vivo whole-cell recording. Whereas the output of cortical neurons is digital, consisting of a series of zeros (inactivity) punctuated by the occasional one (a spike), the subthreshold membrane potential is analog, because it can in principle assume any value within some range given by the various ionic driving forces. Hence, the membrane potential provides a much richer source of information about the response of the neuron and permits insight into the computations performed by the total synaptic input to a neuron. It should be noted that whole-cell recording also has a different sampling bias from conventional extracellular recording; instead of recording from active neurons with large action potentials (i.e., those that are most easily isolated on the electrode), whole-cell recording selects for neurons solely on the basis of the experimenter's ability to form a gigaohm seal.

Using these novel methods, we analyzed the response properties of single neurons in the primary auditory cortex (region A1) of rats. In particular, we focused on two questions: (1) what kind of STRFs do we obtain using subthreshold responses recorded in whole-cell mode? (2) how well do these STRFs predict the responses of cortical neurons to natural sounds?

Materials and Methods

Surgery. Sprague Dawley rats (postnatal day 17–20) were anesthetized with ketamine (60 mg/kg) and medetomidine (0.48 mg/kg) in strict accordance with the National Institutes of Health guidelines as approved by the Cold Spring Harbor Laboratory Animal Care and Use Committee. After the animal was deeply anesthetized, it was placed in a custom naso-orbital restraint, which left the ears free and clear. Local anesthetic was applied to the scalp, a cisternal drain was performed, and a small craniotomy and durotomy were performed above the left auditory cortex. The cortex was covered with physiological buffer containing (in mm): 127 NaCl, 25 Na₂CO₃, 1.25 NaH₂PO₄, 2.5 KCl, 1 MgCl₂, mixed with 1.5% agar. Temperature was monitored rectally and maintained at 37°C using a feedback controlled blanket. Depth of anesthesia was monitored throughout the experiment, and supplemental anesthesia was provided when required.

Whole-cell recordings. We used standard blind whole-cell patch-clamp recording techniques modified from brain slice recordings (Stevens and Zador, 1998). Membrane potential was sampled at 4 kHz in current-clamp (I = 0) mode using an Axopatch 200 b amplifier (Axon Instruments, Union City, CA) with no on-line series resistance compensation. Electrodes were pulled from filamented, thin-walled, borosilicate glass (outer diameter, 1.5 mm; inner diameter, 1.17 mm; World Precision Instruments, Sarasota, FL) on a vertical two-stage puller. Internal solution contained (in mm): 140 K-gluconate, 10 HEPES, 2 MgCl₂, 0.05 CaCl₂, 4 MgATP, 0.4 NaGTP, 10 Na₂ Phosphocreatine, 10 BAPTA, 5 N-ethyl bromide quaternary salt (QX-314; an intracellular sodium channel blocker for blocking action potentials), 0.1 Alexa-594 (a fluorescent dye), pH 7.25, diluted to 290 mOsm. Mean series resistance was 82.9 ± 16.5 MΩ, and mean resting membrane potential was –70.0 ± 8.8 mV (n = 22). Resistance to bath was 3–5 MΩ before seal formation.

Recordings were made from primary auditory cortex (A1) as determined by the tonotopic gradient and “V-shaped” frequency–amplitude tuning properties of cells and local field potentials. We recorded from the superficial layers (subpial depth range, 203–526 μm, as determined from micromanipulator travel). One cell was recovered histologically, which was verified to be a layer 2/3 pyramidal cell. Altogether, we recorded from 22 cells. Some neurons (n = 3) responded so rarely that they did not allow the computation of the linear response component (see Fig. 1).

Figure 1.

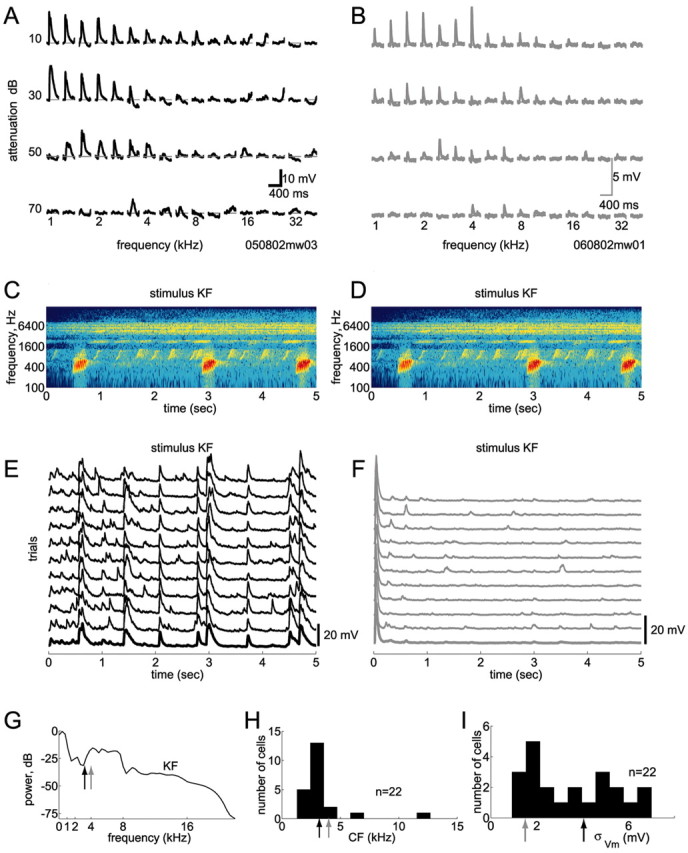
Responsive and unresponsive cells. We used in vivo whole-cell methods to record subthreshold responses of single neurons in auditory cortex A1. Action potentials were blocked pharmacologically. A, B, Responses of two cells to conventional pure-tone stimuli. Evoked membrane potentials are shown for an array of frequencies and intensities (the loudest tones are on the top row). Both cells exhibited robust responses to pure tones, with typical V-shaped tuning, and had similar characteristic frequencies (CFs) of 3.2 kHz (A) and 4 kHz (B). C, D, Spectrogram of a 5 sec segment of the call of a Knudsen's Frog (stimulus KF). E, F, Responses of these two cells to this sound were strikingly different. In E, this stimulus evoked robust and reliable responses, whereas in F, after a transient onset response, the cell was completely unresponsive. The cell in F was similarly unresponsive to all six natural stimuli tested (data not shown). G, This stimulus contained power at the CFs of both cells (arrows show CFs; colors match traces in A, B, E, and F). In fact, stimulus power was greater at the CF of the unresponsive cell. H, Most cells in our sample had CFs of 1–5 kHz. Arrows show CFs of the two cells in A, B, E, and F. I, Responsiveness to natural stimuli varied across cells. Here, responsiveness is quantified by the SD of the membrane potential evoked by natural stimuli (note that nonstimulus-evoked activity also contributes to this measure). Arrows show the different responsiveness of the two cells in E and F.

Stimulus presentation. Pure tone stimuli (frequencies, 1–40 kHz in one-third octave increments; attenuations, 10–70 dB in 20 dB increments) were sampled at 97.656 kHz and had a duration of either 25 msec with 5 msec 10–90% cosine-squared ramp, or 70 msec with 20 msec ramp, and were delivered in a pseudorandom sequence at a rate of 1–2 Hz.

All natural sounds were taken from commercially available audio compact discs (CDs), originally sampled at 44.1 kHz and resampled at 97.656 kHz for stimulus presentation. Sound sections of animal vocalizations were selected from The Diversity of Animal Sounds and Sounds of Neotropical Rainforest Mammals (Cornell Laboratory of Ornithology, Ithaca, NY). A variety of sound sections of environmental noises were taken from the CD series Great Smoky Mountains National Park (Cornell Laboratory of Ornithology) and Spectacular Sound Effects (Madacy Records, Montreal, Canada). The beginning sequence of Purple Haze (Jimi Hendrix) was taken from audio CD. Although the majority of the sound sections lasted for 7.5–15 sec, some were considerably shorter (for example, 1 sec for the sound of a closing door), whereas some lasted longer if they were deemed to have sufficient complexity (for example, up to 31 sec for Jimi Hendrix). A 20 msec cosine-squared ramp was applied at the onset and termination of some (but not all) sound segments (see below). The peak amplitude of each segment was normalized to the ±10 V range of the speaker driver.

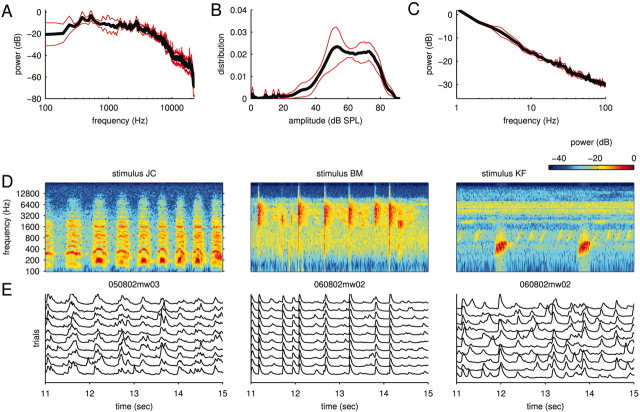
Altogether, our ensemble of natural stimuli consisted of 122 different sounds. The stimuli covered all frequencies from 0 to 22 kHz and ranged from narrow-band stimuli (such as cricket calls) to broad-band stimuli (such as a gurgling creek). Figure 2 A (black line) shows the average power spectrum of the natural stimuli tested on the cells in this study. Note that only a subset of the natural stimuli was tested on any particular cell so that the power spectra usually differed from cell to cell. This subset was chosen so that significant power fell into the range of frequencies covered by the tuning curve of a neuron. The red lines in Figure 2 A indicate the spread (measured as the SD) of these power spectra. The distribution of sound intensities (defined here as the square root of the power measured in short time bins; Δt = 1 msec) of the natural stimuli is displayed in Figure 2 B. The power spectrum of the amplitude modulations is shown in Figure 2C.

Figure 2.

Natural stimuli and responses. Most of the stimuli used in this study were animal communication signals and environmental noises. A, Power spectrum of natural sounds. The sets of natural sounds tested on different cells usually varied slightly. The figure shows the mean (black line) of the power spectra of these different ensembles as well as their SD (red lines). B, Distribution of sound intensities (modulation amplitudes; same format as in A). The small peaks on the left correspond to moments of relative silence in the stimuli. C, Power spectrum of the modulation amplitudes (same format as in A). D, Spectrograms of three short stimulus sections. The spectrograms illustrate some of the diversity and complexity of the natural signals used in this study. E, Subthreshold membrane potential responses. The traces show highly reliable stimulus-locked activity to 10 repetitions of the corresponding stimuli as well as some spontaneous events. The level of spontaneous activity was stimulus dependent; note the very low level in the central panel.

All stimuli were delivered at 97.656 kHz using a System 3 Stimulus Presentation Workstation with an ED1 electrostatic speaker (Tucker-Davis Technologies, Alachua, FL). Sounds were presented free-field in a double-walled sound booth with the speaker located 8 cm lateral to, and facing, the contralateral ear. The speaker had a maximum intensity (at 10 V command voltage) of 92 dB sound pressure level (SPL), and its frequency response was flat from 1 to 22 kHz to within an SD of 3.7 dB. Sound levels were measured with a type 7012 one-half inch ACO Pacific microphone (ACO Pacific, Belmont, CA) positioned where the contralateral ear would be (but without the animal present).

In a first set of experiments (n = 10), a fixed subset of natural sounds was used and repeated up to 20 times. These experiments allowed us to assess response reliability. In a second set of experiments (n = 12), as many natural sounds as possible were presented, each once or twice only. For these stimuli, a 20 msec cosine-squared ramp was applied at the onset and termination of each segment. Some of the natural stimuli are referred to in the Results and figures. The abbreviations used are as follows: jaguar (Panthera onca) mating call (JC), Bowhead whale (Balaena mysticetus) (BC), Knudsen's frog (Leptodactylus knudseni) (KF), and bearded manakin (Manacus manacus) (BM).

Data analysis. All data analysis was performed in MATLAB (Math-Works, Natick, MA). Responses to conventional pure tone stimuli were assessed by constructing frequency-intensity profiles, in which the evoked membrane potential for each frequency and intensity was averaged across trials (see Fig. 1 A, B). Frequency tuning curves at a given intensity were constructed using the peaks of these mean evoked responses (see Fig. 7 E, F). Best frequency (BF) was defined as the frequency which evoked the maximal mean membrane potential at a given intensity, whereas characteristic frequency (CF) was defined as the frequency at which a response could be evoked at the lowest possible intensity.

Figure 7.

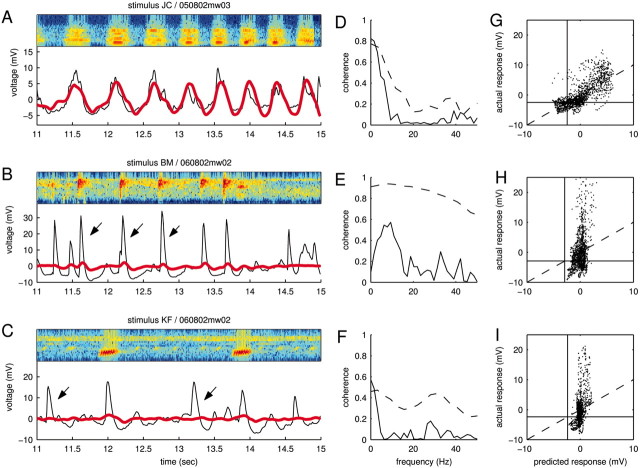
Prediction success and failures. A–C, Spectrogram, measured and predicted responses for the same data as shown in Figure 2. In A, the prediction (red) captures the gross features of the mean response (black) but not the fine details. In B, the STRF rightly predicts the occurrence of most PSPs but markedly fails to predict their overall size (arrows). In C, the STRF not only underestimates the size of PSPs but, at times, completely fails to predict their overall occurrence (arrows), hinting at more complicated nonlinearities. D–F, Coherence between measured and predicted responses (solid lines), corresponding to the data shown in A–C, respectively. The coherence functions underpin the observation that the STRF succeeds at best in capturing slower temporal components. For comparison, the dashed lines replot the coherence between a single trial and the mean (compare Fig. 3B), which provide an upper bound. G–I, Calibration plot (same data as in A–C, respectively). Plotting the predicted versus the actual response reveals any static, systematic errors inherent to the linear model. The black lines show the baselines of the actual responses. Although the plot in G suggests an overall linear relationship between actual and measured responses, the plots in H and I demonstrate the presence of nonlinearities. The vertical alignment of the clouds of dots indicate failures of the STRF to predict PSPs or strong underestimation of the PSP amplitude.

The responses to natural stimuli were analyzed by means of the STRF. As a first step of the data analysis, all natural stimuli were transformed into the time–frequency domain using the short-term Fourier transform, which is often simply termed the spectrogram (Cohen, 1995; Klein et al., 2000). This transform serves as a rough approximation of the cochlear transform and considerably simplifies the subsequent analysis of auditory computation. Use of the short-term Fourier transform also facilitates comparison with other studies in the field. At any particular time, t, and frequency, f, the spectrogram is given by the energy density spectrum of the sound pressure wave, s(t):

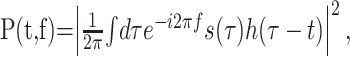(1)

where h(·) is a window function (Cohen, 1995). In our analysis, we used the Hamming window function (Press et al., 1992).

The numerical analysis requires a discretization of both time and frequency. To account for properties of the cochlea, we used a logarithmic discretization of the frequency axis. Within a reasonable and computationally feasible range (time window and discretization, Δt = 5–25 msec; frequency discretization, Δx = 1–5 frequencies/octave), several choices were used independently of each other, essentially yielding the same results. In the analysis presented in the figures, we used a time window of Δt = 10 msec and a frequency discretization of Δx = 3 frequencies/octave. Because the response traces have almost no power on time scales below Δt = 10 msec (or frequencies >100 Hz) (cf. Fig. 3B), stimulus power on these shorter time scales cannot influence the response in a linear manner.

Figure 3.

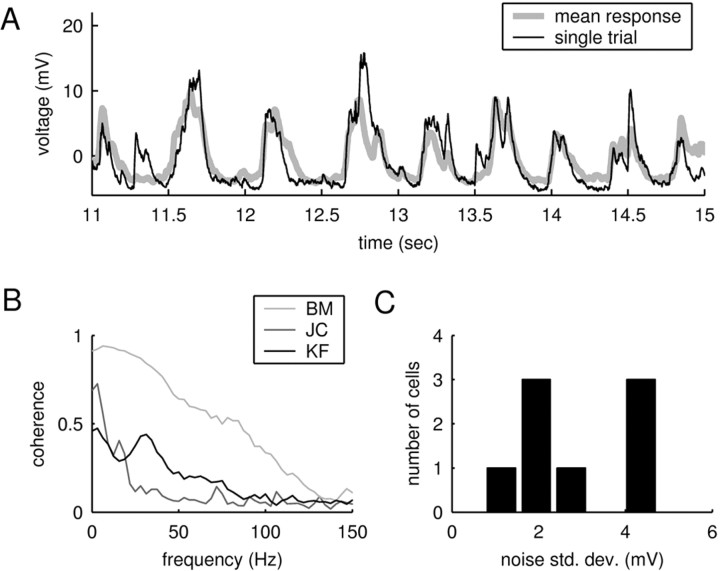
Reliability of responses. A, Mean response compared with a single trial for a natural stimulus (same data as in Fig. 2 D, E, left panel). The overall correspondence between the two traces shows that the amount of spontaneous activity is relatively small. B, Average coherence functions between the mean response and a single trial for the data shown in Figure 2, D and E. The curves demonstrate that the average level of background activity depends on the stimulus. C, Noise level for different cells. The noise level was quantified as the average deviation of the single response trials from the mean response. Although the noise level differed between cells and stimuli, it was always small compared with the size of the PSPs, which typically ranged between 10 and 30 mV.

Given equally spaced time steps, t_i, with i = 1... M and logarithmically spaced frequency steps, f_l, with l = 1... L, we computed the discretized spectrogram, S(t_i, f_l), as:

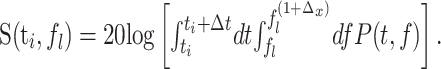(2)

To estimate the response, the stimulus spectrogram S(t_i, f_l) was filtered linearly with the spectrotemporal receptive field H(–t_k, f_l) of the neuron:

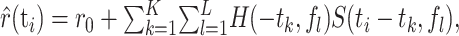(3)

where r₀ is a constant offset. (We use a negative time index in the STRF, –t_k, for formal equivalence with the conventions of the reverse correlation approach.) Assuming a finite memory of the system, the STRF has a finite temporal extent, as indicated by the indices k = 1... K. Note that the response is usually taken to be the average firing rate (Eggermont, 1993; Klein et al., 2000; Theunissen et al., 2000), whereas here, the response is given by the subthreshold voltage trace.

To estimate the STRF, we used linear regression techniques that generalize the more widely used reverse correlation methods to arbitrary stimulus ensembles (Klein et al., 2000). To illustrate this approach, it is helpful to simplify the notation. We write r̂_i = r̂(t_i) and re-order indices such that a_j = H(–t_k, f_l) and s_ji = S(t_i – t_k, f_l) with j = (l – 1) · K + k. Furthermore, without loss of generality, we center both response and stimulus to have zero mean, 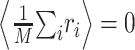and 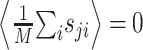for all j, where angular brackets denote averaging over trials. Note that we distinguish the estimated response, r̂_i, from the measured response, r_i, by a hat. It follows that r₀ = 0 so that the model (Eq. 3) simplifies to:

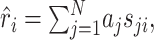(4)

where N = KL. By definition, the STRF is now given by the parameters a_j, which can be fitted by minimizing the mean square error between the estimated response, r̂_i, and the measured response, r_i:

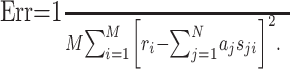(5)

This is the problem solved by multidimensional linear regression. In terms of the stimulus–response cross-covariance, 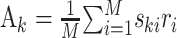and the stimulus–stimulus autocovariance 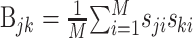, the solution is given by:

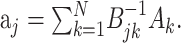(6)

The negative power denotes the matrix inverse. In the neurophysiological jargon, A_k is usually referred to as the reverse correlation function and B_jk as the autocorrelation of the stimulus. “White” stimuli are often defined as stimuli with autocovariance matrix proportional to the identity matrix. In these cases, the reverse correlation function equals the STRF.

For natural stimuli, use of the autocovariance matrix is crucial to divide out the stimulus correlations (Eq. 6) (Theunissen et al., 2001). However, additional complications may arise from undersampling if the number of stimulus–response pairs is too small to obtain an adequate estimate of all coefficients of the STRF. Mathematically, this problem is reflected in an autocovariance matrix that has many eigenvalues close to zero. The inversion of this matrix therefore results in a very noisy estimate of the STRF, corresponding to strong overfitting of the poorly sampled dimensions and poor predictive power of the model.

To address this issue, we used a regularization approach, which places constraints on the parameter values (Hastie et al., 2001). We used two types of constraints. The first penalizes strong deviations of the parameters from zero; this is the same constraint used in ridge regression (Hastie et al., 2001). The second penalizes strong deviations between neighboring parameters and therefore enforces smoothness of the STRF. Consequently, the parameters a_j are obtained by minimizing the following error function:

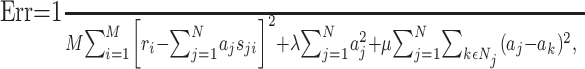(7)

where N_j denotes the set of indices describing the neighbors of j. In the toy example shown in Figure 4 A, the set is given by N₇ = {2,6,8,12}. The parameters μ and λ determine the strength of the constraints. For notational simplification, we write:

(8)

where the constraints are now absorbed in the matrix elements:

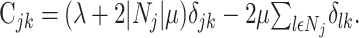(9)

Here, δ_lk denotes the Kronecker δ with δ_lk = 1, if l = k and δ_lk = 0; otherwise, |N_j| denotes the number of elements in the set N_j. The minimization of Equation 8 with respect to a_j now results in:

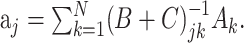(10)

In the case C_jk = λδ_jk, this solution reduces to ridge regression (Hastie et al., 2001), and in the case C_jk = 0 to “naive” regression (Eq. 6).

Figure 4.

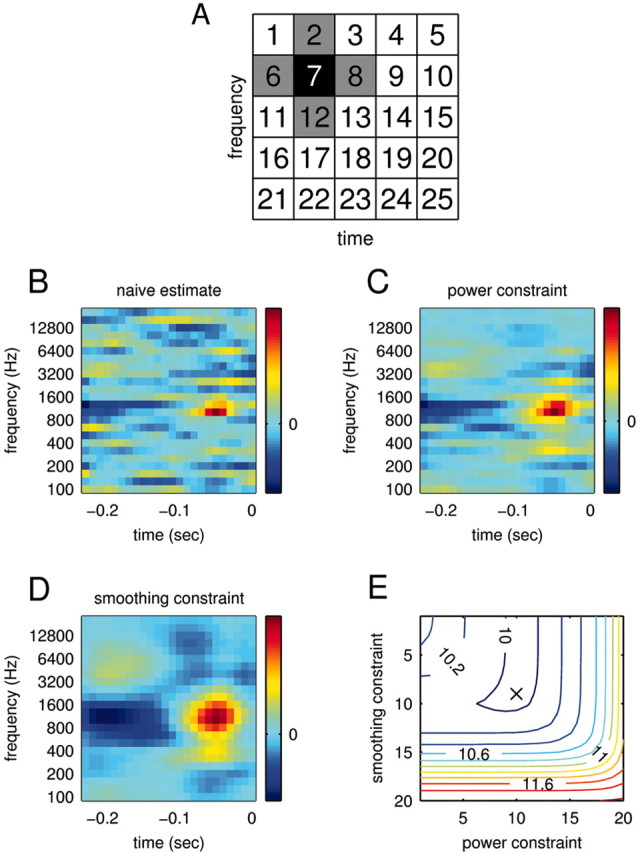
STRF estimation. To estimate a relationship between stimulus and response, we computed the STRFs of the recorded neurons. To circumvent estimation problems deriving from the usage of natural stimuli, we subjected the STRF estimation to a smoothing and power constraint. A, Range of smoothing constraints. The smoothing constraint enforces that the values of neighboring bins do not deviate too strongly. The neighbors of bin 7, for example, are shown in gray. B, Naive estimate of the STRF via linear regression. An estimate without any constraints achieves a mean square error ϵ = 5.6 mV² between actual and predicted response on the data used for the STRF estimation (training) and an error ϵ = 10.69 mV² on new data (prediction). The large difference indicates strong overfitting, which is also visible in the noisy structure of the STRF. C, Optimal estimate of the STRF subject to a power constraint. Here, the power constraint was chosen to minimize the prediction error. Indeed, whereas the training error increases (ϵ = 6.95 mV²), the prediction error is now considerably lower (ϵ = 9.97 mV²). D, Optimal estimate of the STRF subject to smoothing constraint. Both training error (ϵ = 7.08 mV²) and prediction error (ϵ = 10.01 mV²) are similar to those for the power constraint. E, Prediction error for different combinations of smoothing and power constraints. For this cell, combining the two types of constraints does not significantly enhance the prediction success. The absolute minimum (ϵ = 9.97 mV²) is denoted by the black cross. The STRFs inside the trough (blue contours) are therefore equally valid estimates; showing the “extremes” in C and D allows an assessment of the robustness of the estimates.

Thus far, the method leaves the two constraint parameters μ and λ undetermined. When the data are split into training and prediction sets, the STRF can be estimated on the training set for fixed values of the constraint parameters. This STRF can in turn be used to estimate the responses in the prediction set. Repeating this procedure for different constraint parameters, we find the values, μ and λ, that minimize the mean square error between the estimated and actual responses of the prediction set (see Fig. 4 B–E). Given data for natural stimuli (n), we used n – 1 stimuli for the training set and the remaining data for the prediction set. To avoid overfitting of the constraint parameters on a specific prediction set, this procedure was repeated on permutations of prediction and training sets; in the end, the average constraint parameters were selected for final evaluation of STRFs and prediction errors.

Static nonlinearities. Simple nonlinearities such as rectification or saturation can easily corrupt the predictions of the linear model. The occurrence of such static nonlinearities can be visualized in a calibration plot in which the actual response, r_i, is plotted against the estimated response r̂_i (see Fig. 8 A, B). A static nonlinearity is present when the average of the actual response, conditioned on the estimated response, deviates from the identity line (see Fig. 8 A, B, gray lines). Formally, a static nonlinearity can be quantified as a function g(·) that acts on the output of the linear model (Eq. 4) to form a new estimate:

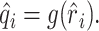(11)

To fit the nonlinear function g(·) to the calibration plot, the axis of the linearly estimated responses, r̂_i, was divided into equally spaced bins. The actual responses, r_i, corresponding to a specific bin were averaged and yielded the function value q̂ = g(r̂) for all estimated responses, r̂, falling into the same bin. To obtain a nonragged estimate of g(·), the function values over neighboring bins were smoothed with a Gaussian kernel.

Figure 8.

Static nonlinearities and adaptation to mean intensity. A, B, Fits of static nonlinearities to the calibration plots. Shown are scatter plots of the estimated response and the actual response (training data). The dashed lines denote the identity line, and the gray lines show fits of the static nonlinearities (see Materials and Methods). The fitted function in A deviates from the identity line within the cloud of dots, showing weak rectification. In comparison, the cell in B closely adheres to the identity line within the cloud of dots, demonstrating that this cell does not feature any static nonlinearities. C, D, Training and prediction success of the linear and nonlinear models. To assess the importance of static nonlinearities, these were incorporated into the model (see Materials and Methods). For all (n = 19) cells, the plots show the average training (C) and prediction (D) success as well as the SE. Accordingly, static nonlinearities lead to small increases in the training and prediction success in some of the cells. However, they fail to explain the dramatic shortcomings of the linear model. E, Scatter plot of the training success for different stimuli versus the respective SD in mean intensity (measured in T = 2 sec time windows). No systematic dependency is visible, demonstrating that the training success of the linear STRF model is independent of variations in the mean intensity of the stimuli for this time window. F, Correlation coefficients for different time windows (T). The arrow shows the correlationforT = 2 sec; all time windows show only a small correlation (<0.1). Because adaptation to mean intensity can only be a strong effect when the mean intensity changes strongly, the figure demonstrates that the training success is not significantly influenced by adaptation to mean intensity.

Note that this approach does not formally yield the optimal estimate of both the STRF and the static nonlinearities, because the use of natural stimuli leads to a bias of the STRF estimation in a linear–nonlinear cascade even in the absence of regularization (Paninski, 2003). Because using the regression method on different stimulus subsets yielded very similar STRFs, the influence of this bias is presumably only small.

Analysis of prediction errors. The utility of the STRF is ultimately determined by its ability to correctly estimate the response. A natural measure for the quality of these estimates is the mean square error between estimated and measured response, 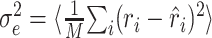, where the angular brackets denote trial averaging. In the nonlinear case (Eq. 11), the linear estimate r̂_i was replaced by the nonlinear estimate q̂_i. However, even for a perfect fit, this error will not be zero, because the actual response is contaminated by a certain amount of noise (Sahani and Linden, 2003a). Hence, the best we can do is to reach this level of noise. Assuming a simple additive model of response and noise, the residual noise component can be estimated as:

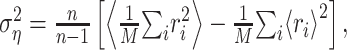(12)

where n is the number of trials. Given the response power 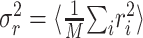, a natural measure of the relative success of the STRF model is given by (Sahani and Linden, 2003a):

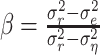(13)

which generally varies between 0% (when the mean square error 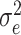equals the response variance) and 100% (when the mean square error reaches the residual noise 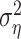). On the training set, the relative success might also exceed 100% in the case of overfitting. For the same reason, the relative prediction success can fall below 0%.

In cases where only one trial was available (n = 6 cells), the noise component could not be computed from the data. To compare estimates of the training and prediction success in these cells, we set the noise component 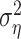in the one-trial experiments to a conservative 50% of the response power; this fraction corresponds to the relative noise level measured in the least reliable cells.

To uncover temporal structure of the error function, we resolved the error in the frequency domain using the coherence function defined as (Brockwell and Davis, 1991):

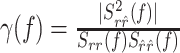(14)

where S_rr̂(f) is the Fourier transform of the cross-correlation between r_i and r̂_i (also termed the cross-spectrum), and S_rr(f), S_r̂r̂(f) are the power spectra of measured and estimated responses, respectively. The coherence takes values between zero (no correlation between measured and estimated response at a certain frequency) and one (perfect correlation).

Results

In this study, we sought to characterize cortical neurons on the basis of their responses to natural sounds. In particular, we tested the ability of a linear model to account for the stimulus–response relationship. Our analysis consisted of the following steps. First, we quantified responsiveness and response reliability. Second, we computed the linear component of the stimulus–response relationship (the STRF). Finally, we quantified the ability of this linear component to approximate the actual responses of auditory cortical neurons and characterized the successes and failures of this linear predictor.

Tuning curves and responsiveness

We recorded intracellularly from single neurons in primary auditory cortex of rats using the whole-cell patch-clamp recording technique in vivo. We prevented action potentials pharmacologically using the intracellular sodium channel blocker QX-314 (see Materials and Methods) so that recordings consisted only of fluctuations in the subthreshold membrane potential, the total synaptic input to the cell, before thresholding by the spike-generating mechanism. We emphasize that the absence of spikes implies that any nonlinearities in the stimulus–response relationship cannot be attributed to the effect of spike threshold in the neuron under study.

Although most neurons featured strong subthreshold membrane potential fluctuations, a few neurons were essentially unresponsive to natural stimuli, except for transient onset responses to any sound. Surprisingly, these same cells generated robust and reliable responses to conventional pure tone stimuli presented at 1–2 Hz. Figure 1 compares the responses of two cells to pure tones and to an animal vocalization. Although both cells showed robust responses to pure tones (Fig. 1A,B) with similar frequency and intensity tuning, one cell (Fig. 1E) responded strongly to the natural sound, whereas the other cell (Fig. 1F) did not. The natural stimulus shown in this example contained power at the preferred frequencies of both cells (Fig. 1G). Thus, neither the tuning of the cells nor the spectral structure of the stimulus can easily explain the striking difference in responsiveness of these two cells. Altogether, we found a continuum of responsiveness across cells, as measured by the square root of the average power in the responses (Fig. 1I). Note that this measure takes into account both stimulus-locked and stimulus-independent activity.

Although the existence of such unresponsive neurons is intriguing, establishing the causes underlying this unresponsiveness is beyond the scope of this study. Because the absence of stimulus-locked fluctuations in membrane potential in unresponsive neurons precluded the estimation of reliable STRFs using natural sounds, such neurons (n = 3) were excluded from our analysis and are not included in the results below.

Natural stimuli

The natural sounds used in our study were primarily animal communication calls and environmental sounds that lasted for 7.5–15 sec. We selected this ensemble of sounds for its spectral and temporal complexity and diversity. To the extent that these sounds, taken from commercially available audio CDs, are representative of the acoustic environment of humans, they are also representative for rats, which share the same habitat as humans. Although the hearing range of rats extends to higher frequencies than that of humans, we chose to record only from neurons that responded to frequencies within the human range (and therefore within the range of our stimulus ensemble) (compare Figs. 1H and 2A).

The overall ensemble consisted of 122 different sound segments, of which only a subset was tested on any particular cell. This subset was chosen to match approximately the frequency tuning of the cells. Figure 2A shows the average power spectrum of these stimulus subsets, demonstrating that ample power fell into the frequency range covered by most of the cells (compare with Fig. 1H).

The stimulus ensemble exhibited properties typical of natural sounds and in accordance with previous observations (Attias and Schreiner, 1997). The distribution of modulation amplitudes or sound intensities (Fig. 2B), measured as the root-mean-square of the sound pressure wave over 1 msec intervals, demonstrates the large dynamic range of the natural sounds. The presence of long-range correlations can be inferred from the power-law behavior of the spectrum of the modulation amplitudes (Fig. 2C). Accordingly, the natural sounds are nonstationary (i.e., their statistical properties, such as mean intensity, fluctuate over time). These properties distinguish natural sounds from conventional artificial stimuli, which are either deterministic stimuli (such as moving ripple stimuli) or stationary random stimuli (such as random chord stimuli). The spectrograms of three example sections of natural sounds used in this study are shown in Figure 2D.

Response reliability

Responsive neurons typically showed a combination of both spontaneous and stimulus-locked voltage fluctuations in response to natural stimuli (Figs. 1E, 2E). Both spontaneous and stimulus-locked responses are presumably attributable to the synchronous arrival of many postsynaptic potentials (PSPs) (Wehr and Zador, 2003). If spikes had not been blocked pharmacologically, the larger PSPs would likely have triggered spikes. With, at most, two to three large PSPs per second, the activity of these neurons is temporally sparse.

Neurons sometimes showed striking trial-to-trial reliability, consistent with the high trial-to-trial reliability of spike count reported previously (DeWeese et al., 2003). This is particularly evident in the central panel of Figure 2E, in which the responses to repeated presentations of the same stimulus are nearly identical. Reliability was stimulus dependent; the same neuron was less reliable for a different stimulus (Fig. 2E, right panel).

To quantify the amount of stimulus-locked activity, we compared a single response trace with the average over the remaining trials. A sample comparison (Fig. 3A; same data as in Fig. 2D,E, left panel) shows that the deviations of a single trial from the average primarily involved the fine structure of the voltage fluctuations. To quantify this observation, we computed the coherence function between the single and average traces. The coherence measures the frequency-resolved correlation of two time series (see Materials and Methods) and ranges from zero (absence of stimulus-locked activity) to one (when all traces feature the same stimulus-locked excursion in membrane potential). The average coherence functions corresponding to the three examples in Figure 2, D and E, are shown in Figure 3B. These functions demonstrate the typical range of stimulus-independent background activity observed in the experiments. All cells feature reliable activity for lower frequencies (<40 Hz). However, when presented with the right stimulus, the coherence increased dramatically; the light gray curve (BM) shows the coherence corresponding to the central panel in Figure 2, D and E.

Response reliability also differed from cell to cell. Figure 3C displays the average magnitude of the stimulus-independent activity. To compute this quantity, the variance of the response about its mean was averaged over time (see Materials and Methods). In all cases, the average magnitude of the noise (1–5 mV) is small compared with the magnitude of the PSPs (10–30 mV), emphasizing the overall reliability of the responses.

Spectrotemporal receptive fields

In the next step, we characterized the linear component of the stimulus–response relationship. This task is considerably simplified when the stimulus is represented by a spectrogram (Cohen, 1995; Klein et al., 2000) (see Materials and Methods) as in Figure 1, C and D, and Figure 2D. The spectrogram provides a rough approximation of the first stage of auditory processing, when the sound pressure wave is transformed into spike trains in the cochlea. Using the spectrogram representation of the stimulus, we then analyzed the linear component of the response (i.e., the spectrotemporal receptive field).

The STRF has often been estimated using the reverse-correlation method (Eggermont, 1993; deCharms et al., 1998) on the basis of well defined random stimuli. However, natural stimuli feature correlations in both the temporal and spectral domains. Linear regression generalizes this approach to arbitrary stimulus ensembles by dividing the reverse-correlation solution (technically the cross-covariance between the stimuli and the response) by the autocovariance of the stimulus (Eq. 6) (Theunissen et al., 2001).

Additional complications may arise from undersampling (i.e., if the number of stimulus-response pairs is too small to obtain an adequate estimate of all coefficients of the STRF). To avoid overfitting along the undersampled directions, we developed a regularization procedure, which incorporated power and smoothness constraints on the STRF parameters (see Materials and Methods for details). This method is similar in spirit to principal component regression (Theunissen et al., 2001) but has the advantage that it generalizes readily to nonlinear models.

In general, either the power or the smoothing constraint was sufficient, with little predictive power gained by combining them. We therefore used STRFs obtained with only one of these constraints (smoothing) for response prediction. However, the trade-offs between these constraints permitted us to assess the robustness of the STRF estimates; STRFs computed from the same set of data with different constraints are shown in Figure 4, C and D. We found that major features of the STRFs, such as the approximate positions of the excitatory and inhibitory peaks, were generally independent of the precise constraints used. Minor characteristics, such as the relative widths of these peaks, were however more sensitive to the precise details of the regularization. We emphasize that because the fine structure of the STRF was not necessarily robust, care must be taken to avoid overinterpreting the details of the STRF structure.

STRFs typically featured an arrangement of both inhibitory and excitatory fields, as shown by a few examples in Figure 5A–D. The excitatory (red) and inhibitory (dark blue) fields indicate times and frequencies at which stimulus energy leads to an increase or decrease in the response of the neuron, respectively. Because an inhibitory field usually preceded an excitatory field, the STRF often predicted strong responses to stimulus onsets within a specific frequency range, as was in fact observed. Excitatory regions usually extended ∼1–3 octaves and 50–100 msec.

Figure 5.

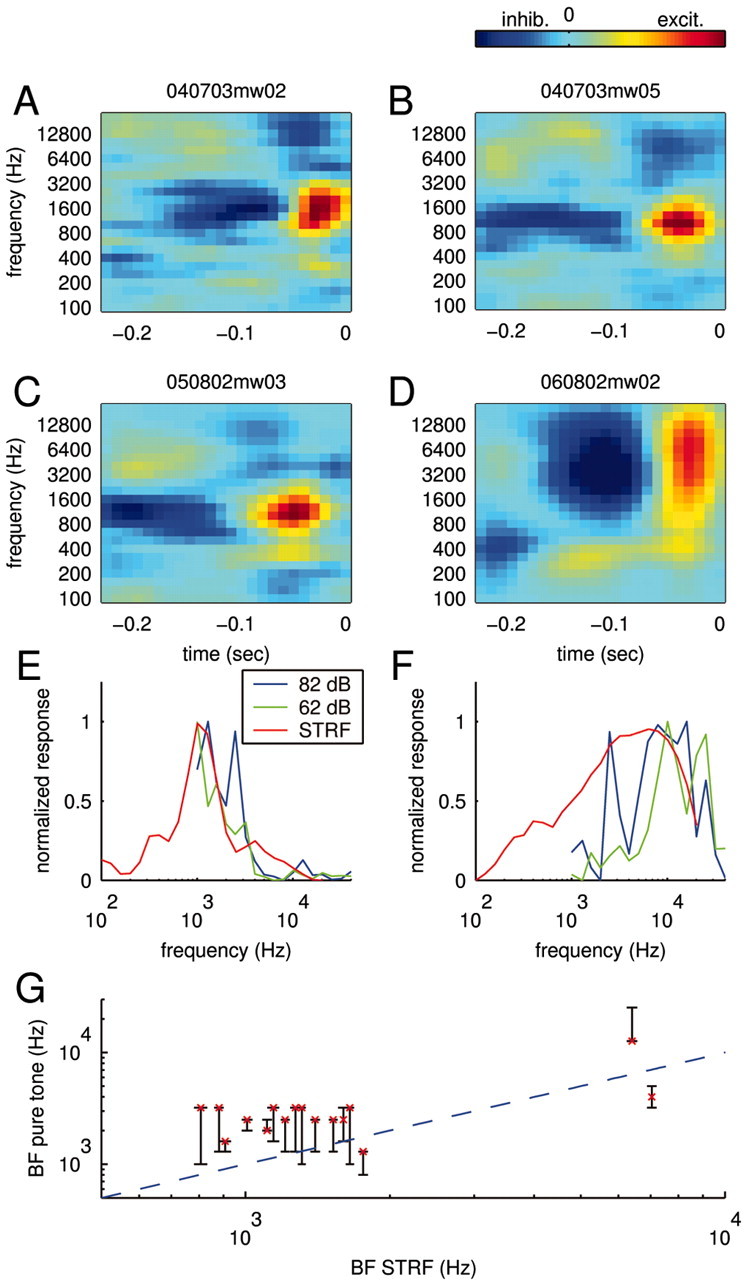
STRFs and tuning curves. A–D, STRFs for four different neurons obtained using smoothing constraints. The STRFs feature both negative (inhibitory) and positive (excitatory) contributions to the response displayed by dark blue and yellow–red, respectively. All STRFs show a sequence of inhibitory and excitatory fields; this characteristic predicts positive responses to sound onsets. E, F, Tuning curves. The STRFs predict a specific frequency tuning shown as solid red lines for the STRFs in C (panel E) and D (panel F). Overall, this prediction is in accord with the frequency sensitivity measured with pure tones. For comparison, two tuning curves recorded at 82 dB SPL (blue) and 62 dB SPL (green) are displayed. G, Comparison of best frequencies as measured by the tuning curve and the STRF. The conventional tuning curve exhibits a range of best frequencies at different intensities displayed as black bars. The characteristic frequency (best frequency at the lowest intensity) of the cells is shown as a red cross. Overall, the best frequencies predicted by the STRF (abscissa) are in good agreement with those measured with pure tones (ordinate). Some cells with incomplete tuning curves were excluded.

Although qualitatively similar STRFs have been reported for spiking neurons in similar preparations (deCharms et al., 1998; Klein et al., 2000; Miller et al., 2002; Linden et al., 2003), our STRFs appear to be more extended both temporally and spectrally. This is consistent with previous observations that subthreshold tuning curves to pure tones are broader than the corresponding suprathreshold tuning curves (DeWeese and Zador, 2000; Ojima and Murakami, 2002).

Within the reliability of our estimates, most cells had STRFs (such as those shown in Fig. 5A–D) that were fully separable (Depireux et al., 2001). That is, these STRFs can be rewritten in the form H(t, f) = Θ2(t)Φ(f), where the functions Θ2(t) and Φ(f) now completely describe the time and frequency components.

The STRFs derived from natural stimuli were generally consistent with the frequency sensitivity of the neuron as measured with short pure tones (see Materials and Methods). The frequency sensitivity of the STRF can be obtained by predicting the response to different pure tone pips and plotting the peak response values for every frequency (a comparison of the derived and measured curves is shown in Figure 5E,F). Although the overall frequency sensitivity is captured by the STRF, the curves nevertheless differ in their details. These differences may arise in part from a fundamental limitation of all linear models, which require that tuning curves obtained at different intensities may differ only in magnitude and not in form; no linear model can account for an amplitude-dependent shift in best frequency. Comparison of the pure tone tuning curves measured at 62 versus 82 dB SPL (Fig. 5E,F, green and blue curves) shows that their forms differ. Note the shifts in the best frequency and the appearance of a second peak in the 82 dB responses, which might be caused by a simple threshold effect. Such intensity dependence is effectively averaged in the STRF model. Nevertheless, across the population, the best frequencies derived from the STRFs were in rough agreement with those measured by pure tones (Fig. 5G).

Stimulus dependence of training success

Although the linear component of the input–output function of most neurons showed well defined structure, the analysis presented thus far does not indicate how strong this linear component is (i.e., how much of the stimulus-locked response we can capture using the, purely linear, STRF alone). We assessed the potential limitations of the linear STRF by testing it on the same set of data used in its training. To compare different natural stimuli, we restricted the analysis to 15 sec-long stimulus sections (most of which were individual stimuli) and their respective responses. The relative training success was quantified as the percentage of the stimulus-locked response variance captured by the STRF (see Materials and Methods). This procedure yields an upper bound for the quality of any linear model.

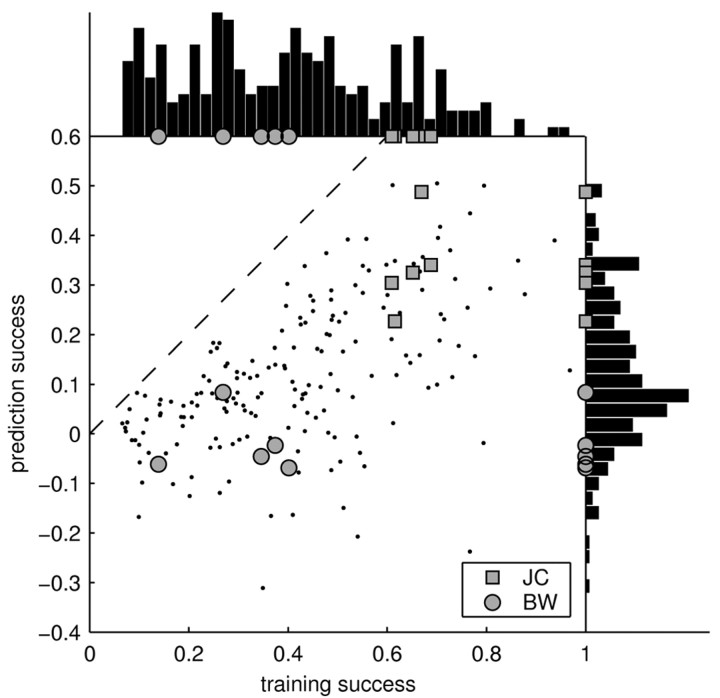
As indicated in Figure 6 (histogram at top), training success varied considerably across cells and stimuli. Some recordings led to a good training success, whereas some recordings fared considerably worse (as low as 7%). The latter is particularly surprising, because it shows that the linear model can fail completely. These failures cannot be trivially attributed to differences in the amount of stimulus-locked activity, because our measure of the training success explicitly corrects for these differences (see Materials and Methods). Interestingly, the variability in the performance of the STRF can be partially explained by a systematic stimulus dependence of the training success. Some stimuli, such as jaguar mating call JC (Fig. 6, squares), always lead to a high training success, whereas others, such as BW (Fig. 6, circles), are consistently worse. Because stimuli were normalized to peak intensity, their mean sound intensity varied. However, this did not account for the stimulus dependence of the training success, which showed only a weak correlation with mean sound intensity (correlation coefficient, r = –0.1).

Figure 6.

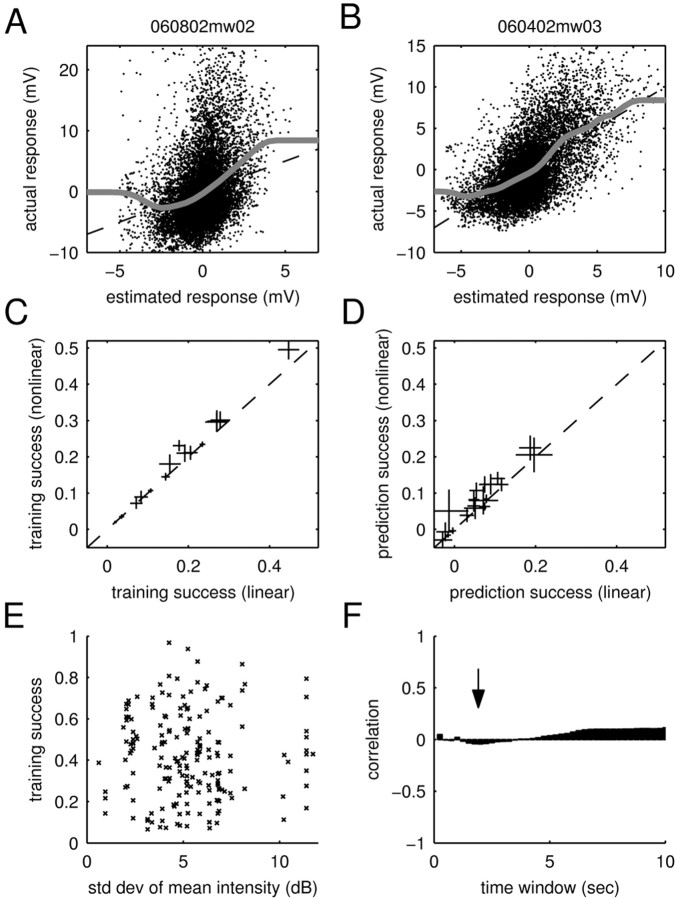
Summary of training and prediction success. Each point in the main panel represents the success of the STRF model in estimating the response to an individual stimulus (15 sec). For the training success (x-axis), the same individual stimulus was used for both estimating and testing the STRF. For the prediction success (y-axis), the STRF was tested on the individual stimulus but trained on all others. To permit the individual points on the graph to be resolved, only a subset of the stimuli (n = 10; chosen randomly for each neuron) is shown. Although the prediction success provides a lower bound on the capability of the model to estimate the response, the training success yields an upper bound. Surprisingly, some of the stimuli are consistently better than others across neurons [compare JC (squares) and BW (circles)]. Hence, the STRF is able to capture a significant part of the response to some stimuli, yet it fails to predict the response to others. The distribution of training and prediction success is displayed as a histogram on the top and the right, respectively. Averaged over all stimuli and cells, the training success was 39%, and the prediction success was 11%. Hence, the responses of cortical neurons to natural stimuli are dominated by nonlinearities.

Although we used regularization, the training success is artificially boosted because of some overfitting. In particular, certain stimuli might lend themselves to stronger overfitting and lead to a systematically higher training success than other stimuli. To clarify these issues, we also investigated how well the STRF can predict the responses to stimuli not included in its estimation. Given an individual stimulus and its respective responses, the STRF was estimated on the remaining data, and its prediction on the individual stimulus was evaluated. This procedure yields the relative prediction success, which is compared against the relative training success in Figure 6. The relative prediction success provides a lower bound on the performance of the STRF model. As demonstrated by Figure 6, the differences between individual stimuli are retained for the relative prediction success. Hence, there is a systematic relationship between the type of stimulus used and the success of the linear STRF model.

Altogether, the relative success of the linear STRF model is bounded between 11% (the average relative prediction success) and 39% (the average relative training success). The “true” relative success of the linear model must lie within these bounds.

Qualitative characterization of the failures

The widespread failure of the linear model to predict responses for many but not all complex stimuli indicates a high but stimulus-dependent degree of nonlinearity. By comparing the predicted and actual responses, we can characterize the different failure modes of the STRF model.

Three sample predictions are shown in Figure 7, A–C, for the same data as in Figures 2, D and E, and 3, A and B. Although the predicted trace (red line) in Figure 7A accounts for the approximate times at which PSPs occur, it does not capture their precise shape. This observation can be quantified by spectrally resolving the prediction success. For that purpose, we again use the coherence function as a measure of the correlation at each frequency (in this case, between actual and predicted response) (Fig. 7D, solid line). Clearly, this particular STRF does not predict any response fluctuations faster than ≈10 Hz. As a comparison, recall that the response is reliable up to at least 20 Hz (Fig. 7D, dashed line).

Figure 7B shows a natural stimulus that elicited a highly reliable response that the STRF predicted only poorly. The example uses the same data as in Figure 2, D and E (central panel). Although the STRF predicts the timing of the PSPs, it underestimates their amplitudes (Fig. 7B, arrows).

As demonstrated by Figure 7C, the linear model can sometimes fail completely in predicting PSPs. The arrows point to PSPs that occurred reliably in the actual response but were not predicted by the STRF. Such failures lead to a correspondingly weak coherence (Fig. 7F) and a small prediction success (in this case, 8%).

The inability of the STRF to predict the correct size of the PSPs and its occasional failure to predict the occurrence of PSPs can be visualized in a calibration plot in which the actual response is plotted against the predicted response (Fig. 7G–I). In Figure 7G, most dots cluster around the identity line, suggesting an overall match between actual and predicted response. In Figure 7, H and I, however, most of the dots fall clearly above the identity line, corresponding to underestimated PSP amplitudes or PSPs that were missed by the STRF.

Ruling out trivial nonlinearities

Although the failure to predict PSPs suggests the existence of complex nonlinearities, the incorrect size of predicted PSPs could be caused by more trivial nonlinearities such as rectification or saturation. For instance, neurons in A1 often respond to the offset of sounds (OFF-response) (He, 2001; Tai and Zador, 2002). Because many of the STRFs predict strong responses to the onset of stimulus features (ON-response), they also predict strong negative responses at termination. If the actual response of the cell is just the opposite (i.e., a strong excitatory response at the termination of the stimulus), then the cell acts as a rectifier. Rectification, as well as saturation and thresholding, can be readily incorporated into the model as a static nonlinearity acting on the output of the STRF model.

To investigate whether such static nonlinearities could account for the underestimation of PSP amplitudes, we explicitly included them in our model (see Materials and Methods). For that purpose, a nonlinear function was fitted to the calibration plot (Fig. 8A,B) and used to enhance the estimation of the responses. A few cells exhibited signs of some rectification, as would occur in the presence of OFF-responses (Fig. 8A). However, most cells featured a mostly linear relationship between estimated and actual response (Fig. 8B). Accordingly, the overall effect of the static nonlinearities on training and prediction success was only minor. As demonstrated by Figure 8, C and D, explicit inclusion of the static nonlinear functions in the response estimation increases the average training or prediction success up to 5% only. Static nonlinearities could therefore not account for the dramatic failure of the linear model.

Another possible explanation of the shortcomings of the STRF relates to adaptation. Previous tests of linearity in cortical neurons have assumed that the neurons are in an adapted state (Kowalski et al., 1996b). Natural sounds are nonstationary stimuli, meaning that their statistics (such as mean intensity) fluctuate over time. These continuous changes in mean intensity might therefore prevent the neuron from settling into an adapted state. Correspondingly, this might erode the estimates of the STRF and be responsible for systematic differences between stimuli. To see whether this is the case, we plotted the training success of different stimuli against the variations in the mean intensity of the respective stimuli (shown in Fig. 8E when sound intensity is measured in time windows of T = 2 sec). We found essentially no correlation between the ability of the STRF to estimate responses (training success) and the fluctuations in mean intensity of the stimuli. Moreover, this was true across a wide range of time scales (Fig. 8F). Hence, adaptation to mean intensity is only a negligible factor in the failure of the STRF to predict the responses to natural stimuli.

The failure of the STRF model must therefore be attributed to other forms of nonlinearities. These might include more sophisticated models of adaptation to sound intensity, adaptation to other stimulus parameters such as auditory contrast (Barbour and Wang, 2003), spectrotemporal interactions between ON- and OFF-responses (Tai and Zador, 2001), or other cellular and synaptic nonlinearities such as synaptic depression (Markram and Tsodyks, 1996; Abbott et al., 1997).

Discussion

We used whole-cell patch-clamp methods in vivo to record subthreshold membrane potential fluctuations elicited by natural sounds. In the majority of cells, subthreshold responses were sufficiently rich and robust to permit a reliable estimation of the linear predictor of the response of the neuron, the STRF. The present study represents the first analysis of subthreshold responses elicited by natural stimuli in vivo.

Major response properties, such as frequency tuning, were similar, whether assessed by pure sine tones or complex sounds. However, the STRFs estimated from complex sounds provided a more complete picture of the dynamics of the neuron, so that it was possible to compare the predicted and experimentally measured responses with complex stimuli.

Prediction success depended strongly on the particular sounds used in the experiment (Fig. 6). On average, only ∼11% of the response power could be predicted by the STRF, indicating that neuronal responses were highly nonlinear. Neither static nonlinearities nor adaptation to the mean intensity could account for the failure of the STRF model. Hence, the nonlinearities must be attributable to second-order interactions or adaptation to other stimulus parameters. The presence of these strong nonlinearities should also caution the reader against overinterpreting the STRF, because nonlinearities in responses will create artifactual structure in the linear STRF.

Our observations are in accord with recent work on neurons in the auditory forebrain of zebrafinches (Theunissen et al., 2000), in which neurons show a high degree of feature selectivity in response to natural stimuli. In contrast, previous work in the auditory cortex has suggested that the responses of cortical neurons to ripple stimuli can be well predicted by the linear STRF (Kowalski et al., 1996b; Klein et al., 2000; Schnupp et al., 2001). However, our results have shown that the success of the STRF depends strongly on the type of stimulus used (Fig. 6). Ripple stimuli (and combinations thereof) could therefore fall into the class of stimuli for which responses can be well predicted by a linear model. It will be interesting to investigate whether the STRF model also provides good predictions in this system when more complex stimuli are used.

A recent study (Sahani and Linden, 2003a) confirms the importance of nonlinearities in the rat auditory cortex. Using random chord stimuli, they showed that ∼19% of the stimulus-locked response power could be predicted by the linear STRF model. This result is close to the 11% obtained in our study. Note, however, that the linear model can fail completely if certain natural stimuli are used. The use of stationary random stimuli versus nonstationary natural stimuli might again explain the differences in these findings.

The concept of the STRF, derived and evolved from the second-order Volterra kernel, has long been used as a tool in auditory research (Eggermont, 1993). Unfortunately, this history has led to various definitions of the STRF. In our definition, the STRF constitutes a linear transform between the spectrogram of the stimulus and the response. Thus, this definition is similar in spirit to the work of Kowalski et al. (1996b) and deCharms et al. (1998). Recent work has also fitted a second-order Volterra series to the responses of neurons in the auditory cortex of anesthetized cats (Rotman et al., 2001). Although natural stimuli were used in the estimation and a second-order kernel acting on the sound pressure wave is formally equivalent to the linear STRF model acting on the spectrogram, there are important differences from our work. Rotman and colleagues used very short snippets of natural stimuli (132 msec length) to estimate correspondingly short kernels (6 msec length for prediction). In comparison, we used 7.5–15 sec-long stimuli and STRFs that were 250 msec long. These important differences render direct comparison difficult.

The estimation of STRFs from natural stimuli presents a statistical challenge, because these stimuli fill the high-dimensional stimulus space in an irregular manner. Conventionally, researchers have sought to reduce the dimensionality of the problem. One possibility is to expand the STRF or second-order Volterra kernel in a small number of basis functions (Yeshurun et al., 1989). Another possibility is to restrict the stimulus to basis functions derived from the principal components of the natural stimuli (Theunissen et al., 2001). In the statistical literature, the latter is sometimes referred to as principal component regression (Hastie et al., 2001).

Here, we used a more general approach on the basis of regularization techniques that constrain the model parameters without any previous dimensionality reduction. The regularization methods used here perform approximately as well as principal components regression (Hastie et al., 2001). However, regularization methods provide a strong conceptual advantage: they allow a straightforward generalization to nonlinear models. Regularization techniques have also been used recently to compute STRFs of simple cells in V1 from natural stimuli (Smyth et al., 2003). Other developments seek to solve the estimation problems using evidence optimization (Sahani and Linden, 2003b) or by fitting the best linear stimulus subspace (as opposed to the best linear model) to the neurons (Paninski, 2003; Sharpee et al., 2003).

In the end, however, we believe that the most urgent problem concerns the quantitative characterization of the observed nonlinearities. Explaining these nonlinearities represents an exciting challenge for future research.