Prism Adaptation of Reaching Movements: Specificity for the Velocity of Reaching

Abstract

Accurate reaching toward a visual target is disturbed after the visual field is displaced by prisms but recovers with practice. When the prisms are removed, subjects misreach in the direction opposite to the prism displacement (aftereffect). The present study demonstrated that the severity of the aftereffect depends on the velocity of the movements during and after the visual displacement. Trained subjects were required to reach with one of four movement durations (<300, ∼800, ∼2000, and ∼5000 msec) from a fixed starting point to a target that appeared at a random location on a tangent screen (400 mm away). The size of the aftereffect was largest when the movement after the removal was performed with the same duration as that performed with the prisms. It became smaller as the difference in velocity became larger. When the contralateral arm was used after visual displacement, the aftereffect was never significant. Because the adaptation does not generalize across velocities or to the other arm, we infer that the underlying changes occur at a later stage in the transformation from visual input to motor output, in which not only the direction but also the time-dependent parameters of movements, such as velocity, acceleration or force, are represented.

Accurate reaching toward a visual target is disturbed when the visual field is displaced by prisms (prism exposure) but recovers with practice (prism adaptation; for review, see Harris, 1965; Welch, 1986). After the prisms are removed, errors in the direction opposite to the prism displacement are observed (aftereffect). We previously reported that the subject’s adaptation to the prism displacement depends critically on the availability of visual information within 50 msec after the completion of the reaching movement (Kitazawa et al., 1995b). Those results strongly suggest that internal information regarding the generated movement, which is essential for the adaptation, decays within a brief period of time after the movement. A question is thereby derived: What kind of information on the movement was used for the adaptation? In the present study, we examined whether the velocity of the reaching movement is a factor in the behavioral adaptation.

A reaching movement defines a vector in space that can be described by its direction and amplitude (Georgopoulos, 1995). Of the two parameters, the direction of movement alone is sufficient to accomplish the prism adaptation, because the subject can adapt to the visual displacement by changing only the direction of the movement. The direction of movement during reaching has been reported to be represented in various cortical areas (Georgopoulos et al., 1982;Kalaska et al., 1992) (for review, see Georgopoulos, 1995) and in the cerebellum (Fortier et al., 1989). However, in addition to the direction of movement, various parameters that are influenced by movement duration, such as velocity, acceleration, and force, have been reported to be represented in the cerebral cortex (Humphrey et al., 1970; Hamada, 1981; Flament and Hore, 1988; Schwartz, 1993; Ashe and Georgopoulos, 1994) and in the cerebellum (Thach, 1978; Mano and Yamamoto, 1980; Van Kan et al., 1993). The present study investigates whether these time-dependent parameters of the reaching movement contribute to prism adaptation.

Previous studies have reported incomplete generalization of prism adaptation across different tasks in which the parameters of movement varied (for review, see Welch, 1986). Baily (1972) demonstrated that the adaptation acquired with a pointing task that required slow, horizontal, oscillatory arm movements around the shoulder joints with decreasing amplitudes did not transfer completely to rapid, straight, reaching movements. Freedman et al. (1965) showed that the adaptation of pointing movements in the horizontal plane transferred incompletely to movements in the sagittal plane. Recently, Martin et al. (1996)reported that the prism adaptation acquired with the overhand throwing of clay balls did not transfer to underhand throwing. In each of these studies the subjects were required to make movements that differed not only in time-dependent parameters but also in the direction or the shape of hand trajectories. Thus, it is not clear whether the incomplete transfer resulted from differences in the direction or the time-dependent parameters of movement.

To determine whether the time-dependent parameters of movement are involved in prism adaptation, we studied the specificity of the adaptation for the speed of movement during the acquisition period. If the adaptation is derived solely from time-independent parameters, such as the direction of movement, the adaptation acquired with a fast-reaching movement would transfer completely to a different slow-reaching movement, provided that the two movements involve the same vectorial displacement of hand in space. The present study reports that the transfer of prism adaptation between reaching tasks with different speeds, but identical displacement, is incomplete and that the amount of transfer decreases as the difference in speed increases. We also studied the transfer of adaptation between the subject’s two arms to determine where the velocity-specific adaptation occurred in the transformation from visual input to motor output. Our data indicate that the adaptation scarcely generalizes across the arms.

A preliminary account of this study has appeared elsewhere (Kitazawa et al., 1995a).

MATERIALS AND METHODS

Subjects. Ten male subjects (age 20–33, right-handed) participated in the experiments. All subjects had normal or corrected-to-normal visual acuity and had no significant neurological history. All except the two authors (S.K., T.K.) were unaware of the purpose of the experiments and were paid for their participation.

Apparatus and task procedures. The apparatus and task procedures were performed as described previously (Kitazawa et al., 1995b). Subjects were required to reach toward a target on a tangent screen. Vision of the target and the moving arm was blocked by shutters and then allowed again when the subject’s index finger touched the screen. When wedge prisms were used, the screen was displaced so the subject viewed the target in the same straight-ahead direction. After the initial reaches with the prisms, when the shutters opened, the subject would notice that his hand was no longer near the target, although the target had appeared in the same place.

The subject was seated facing a tangent 14 inch CRT screen, 400 mm from the eyes, with his head restrained by a chin rest and a head band. The subject wore a pair of spectacles with liquid crystal shutters (PLATO spectacles, Translucent Technology, Toronto, Canada) and viewed through opaque tubes that restricted his view of the screen (Fig.1D). A trial was initiated (Fig.1D, 0: Start) by three successive mid-tone beeps of 800 msec duration while the subject pressed a button (Button, Fig. 1D) with his right index finger. The button was positioned 300 mm below and 100 mm ahead of the subject’s eyes in the midsagittal plane. These mid-tone beeps were followed by a single high-tone beep, at which time a target (a cross, 10 mm wide) appeared at a random place in a square area (40 mm × 40 mm) on the screen. The subject was required to release the button (2, Fig.1D) within 200 msec of the appearance of the target and to touch the screen within one of four time periods (<300, ∼800, ∼2000, or ∼5000 msec). The strict requirement for reaction time (Kitazawa et al., 1995b) was imposed to inhibit the subjects from making “conscious correction” (Welch, 1986) during the process of prism adaptation. Vision of the hand and the arm was blocked at the release of the button by the shutters. The shutters were opened again on touching the screen (3, Fig. 1D) to allow the subject to see the target and the final position of the hand for 100 msec. Subjects were required to hold the final position until a low-tone beep instructed the subject to return his hand to the starting position. Intertrial intervals were kept constant, ∼15 sec, by adjusting the holding period from 7–12 sec, depending on the duration of achieved movement.

Fig. 1.

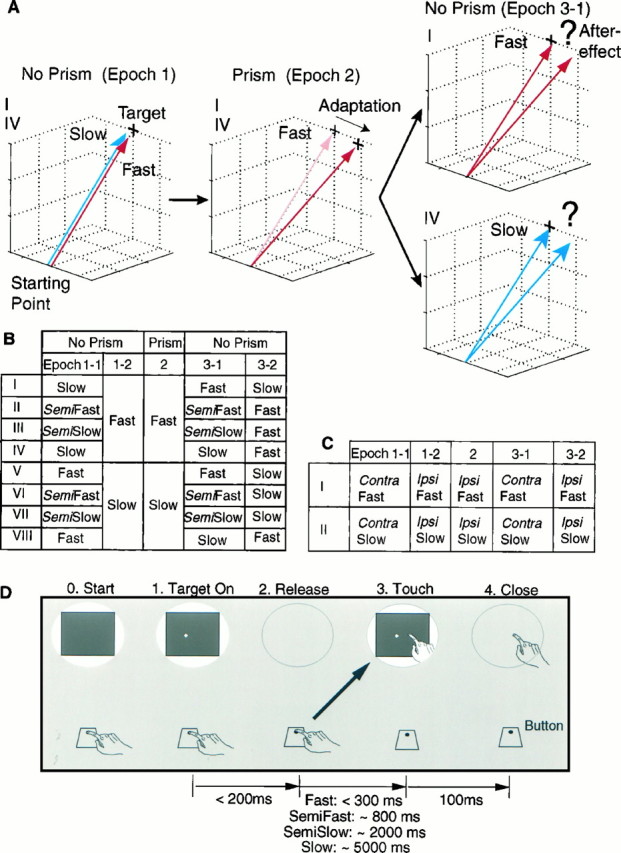
Design of experiments. A, General concept, taking conditions I and IV in B as examples. The subject is required to make slow (blue arrow) and fast (red arrow) reaching movements to a target without prisms inEpoch 1. Then the visual field is displaced to theleft by prisms in Epoch 2, during which the subject is required to make the fast reaching movements. The subject initially reaches to the position of the virtual image of the target (gray cross) but, after practice, reaches to the position of the real target (solid cross, Adaptation). InEpoch 3-1, when the prisms are removed, the subject is required to execute the fast reaching movements in one condition (I) and the slow reaching movements in another (IV). B, Eight conditions (I–VIII) of four reaching movements (Fast, Semifast, Semislow, and Slow) that required movement durations of <300, ∼800, ∼2000, and ∼5000 msec, respectively. One experiment consisted of 90 trials: 15, 15, 30, 15, and 15 trials for Epoch 1-1, 1-2, 2, 3-1, and 3-2, respectively. In Epoch 2, the visual field was displaced to the left or to the right by 15-diopter wedge prisms. The prisms were removed for the last Epochs (No Prism). C, Intermanual transfer of adaptation acquired with fast (I) and slow (II) reaching movements of the ipsilateral arm (Ipsi) to the contralateral arm (Contra). D, Time sequence of one trial. Each column schematically shows the status of the visual field (oval shape) and the position of the hand relative to the button and the screen. Shutters opened at 0(Start), when the subject pressed the button. A target appeared after beeps at a random location in a square area (40 mm × 40 mm) on the screen (1, Target On). Vision was blocked from 2 (Release) to 3(Touch) and allowed again for 100 msec immediately after the touch.

The reaction time and movement duration were measured with a time resolution of 1 msec by computer (NEC, PC9801RA). The researcher monitored these values and informed the subject of the values whenever he failed to react within 200 msec or failed to complete the movement within the required period. The required time periods were (1) less than 300 msec for the fast, (2) 720–880 msec for the semifast, (3) 1800–2200 msec for the semislow, and (4) 4500–5500 msec for the slow reaching tasks. The touch position was recorded using a transparent sheet of touch sensor (NPC-2000, Nihon Binary, Tokyo, Japan) (sampling frequency 100 Hz, accuracy 2 mm) that tightly covered the surface of the screen and was connected to a computer. These measured variables and target locations were stored for off-line analysis.

Although the subjects were instructed to reach as precisely as possible with a required movement duration, there were no particular requirements for the shape or temporal pattern of the hand movements. Thus, they were free to use trajectories that were comfortable for them. In later experiments, the trajectory of the hand during the task movements was monitored at a sampling frequency of 120 Hz by placing a reflective marker (half-sphere of 5 mm radius, 0.1 g) on the nail of the subject’s index finger (MacReflex 4 camera system, Qualisys, Sweden; spatial accuracy 1 mm). These position data were stored on another computer (Macintosh Quadra 630) and analyzed off-line by MATLAB on a workstation (Sun, Sparc Station 5) to yield three-dimensional trajectories and velocity profiles of the movements. Velocity components were smoothed by the moving average method with a window width of 42 msec for the fast and semifast reaching tasks and of 125 msec for the slow and semislow reaching tasks.

Training. The subjects were trained beforehand until they became familiar with the task procedure and had little difficulty in generating the task movement within each of the four required time periods. Subjects performed at least 30 movements for each time period. In these training trials, subjects were informed of the duration of their movements after each trial. No prisms were used during the training sessions.

General design of experiments. One experiment consisted of 90 trials evenly divided into three epochs of 30. The subject performed the reaching task without prisms for the first 30 trials (Epoch 1). For the next 30 trials (Epoch 2), the visual field was displaced to the right or to the left by base-left or base-right prisms (15 diopters) positioned inside the opaque tubes through which the subject viewed the screen. The distance between the screen and the eyes was 400 mm; therefore, the prisms produced an apparent visual displacement of 60 mm. The CRT screen was displaced around the vertical axis that passed through the midpoint of the subject’s eyes to compensate for the visual displacement of the screen caused by the prisms. This procedure (Kitazawa et al., 1995b) kept the location of the visual image of the screen in Epoch 2 nearly identical to that in Epoch 1. Hence, the subject was not forced to gaze into a particular direction even when the prisms were used. This procedure was used to avoid prolonged asymmetric positioning of the eyes, possibly resulting in a shift of eye position after the prisms were removed (Paap and Ebenholtz, 1976) (for review, see Welch, 1986). For the last 30 trials (Epoch 3), the screen was returned to the same position as in Epoch 1, and the subject performed the reaching task without prisms. Interepoch intervals were ∼1 min, during which time the subjects waited for the ready instruction with their vision blocked by the liquid crystal shutters. One experiment required ∼25 min to complete.

Velocity specificity of adaptation. Figure1B shows eight experimental conditions (I–VIII), in which four speeds of movement (fast, semifast, semislow, and slow, as defined above) were permuted to five blocks of trials. The five blocks consisted of the first 15 trials of Epoch 1 (Epoch 1-1), the second 15 trials of Epoch 1 (Epoch 1-2), Epoch 2, the first 15 trials of Epoch 3 (Epoch 3-1), and the second 15 trials of Epoch 3 (Epoch 3-2). Conditions I–IV were designed to determine whether the prism adaptation acquired with the fast reaching task is transferred to the other tasks, and conditions V–VIII whether the prism adaptation acquired with the slow reaching task is transferred to the others. Figure 1A schematically represents the rationale of the experiments, using conditions I and IV as an example. In both conditions, the subjects were required to make slow (blue arrow) or fast (red arrow) reaching movements without prisms in Epoch 1 and to make fast reaching movements in Epoch 2 with prisms. The prisms were removed in Epoch 3-1, and the subject was required to make the 15 fast movements under condition I or the 15 slow movements under condition IV. Errors in the initial trials (Epoch 3-1) under condition I reflect the amount of adaptation acquired with fast reaching movements during visual displacement (Epoch 2) and serve as a control to test the transfer of adaptation from the fast reaching movement. If the size of the initial errors in Epoch 3-1 under condition IV is the same as that under condition I, the transfer from the fast reaching task to the slow reaching task is judged as complete; if smaller, it is judged as incomplete.

The subject further was required to make 15 reaching movements with the other velocity (Epoch 3-2). The size of the initial errors in Epoch 3-2 under condition IV reflects the residual component of adaptation acquired with the fast reaching task after readaptation in Epoch 3-1 with the slow reaching task.

In the design of this experiment, there were 16 alternative permutations with two directions of displacement (right or left) and eight velocity conditions (Fig. 1B, I–VIII). In the initial run of experiments, eight permutations, consisting of two directions and the four velocity conditions I, IV, V and VIII, were chosen to test the transfer of adaptation between the fast and slow reaching tasks. Condition I was designed to be identical to condition IV during Epoch 1 and 2, as was condition V to condition VIII. Ten subjects participated in this initial run, and the eight permutations were randomly ordered for each subject. The first permutation for each subject also was calculated as the ninth permutation to examine the reproducibility of the experiments. Ninety such experiments were performed. Data were averaged from the first and the ninth experiments for each subject, because in all but three of the 90 trials no significant difference existed in the data of these two experiments (trials 72, 73 and 86, two-tailed paired t test; 10 pairs for each trial). In the second run, four permutations, consisting of two directions and the two velocity conditions II and III, were chosen to test the transfer of adaptation from the fast to the semifast and from the fast to the semislow reaching tasks. In the third run, the other four permutations (two directions × VI and VII) were chosen to test the transfer from the slow to the semifast and from the slow to the semislow reaching tasks. The same ten subjects from the first run participated in the second and the third runs. All subjects completed four experiments in each run, covering the four conditions in a random order. Thus, 40 experiments were performed in each of the second and the third runs. Each subject completed the designated experiments once or twice a day, allowing 1–3 months for each run. In total, 170 experiments were performed.

Intermanual transfer of adaptation. To determine whether the neural systems in which the adaptation occurred control bilateral arm movements or unilateral arm movement, we examined intermanual transfer of the adaptation. Eight subjects were trained further to make fast or slow reaching tasks with their left arm. In one condition (Fig. 1C, I), the subject was required to make the fast reaching movements with his contralateral and ipsilateral arms in Epoch 1-1 and 1-2 without prisms, with his ipsilateral arm in Epoch 2 with prisms, and then again with his contralateral and ipsilateral arms in Epoch 3-1 and 3-2 without prisms. This condition was designed to test intermanual transfer of the fast reaching task. The other condition (Fig. 1C, II) was designed to test intermanual transfer of the slow reaching movements. For some experiments, the left arm served as the ipsilateral arm, and for others the right arm so served. Base-right or base-left prisms were used to displace the visual field in Epoch 2. Thus, there were eight alternative conditions consisting of two directions of displacement, two velocities of movement (fast and slow), and two permutations of arm allocation. Four subjects completed eight experiments to cover the eight conditions in randomized order. The other four subjects completed four experiments in which only the right arm served as the ipsilateral arm. Forty-eight experiments were performed.

RESULTS

Movement profiles

Figure 2 shows sample trajectories of the hand (Fig. 2A–D) and its tangential velocities (Fig.2E,F) from one subject during the four reaching tasks involving fast, semifast, semislow, and slow movements. Trajectories were almost similar at all speeds, although the side view of the trajectories of fast movements (Fig. 2B, red) were slightly sigmoidal, whereas the others were nearly linear. These characteristics remained fairly consistent among all subjects throughout the experiments, although the direction of movements in Epochs 2 (Fig. 2D) and 3 (not shown) differed from that in Epoch 1 (Fig. 2A–C) because of the adaptation to visual displacement.

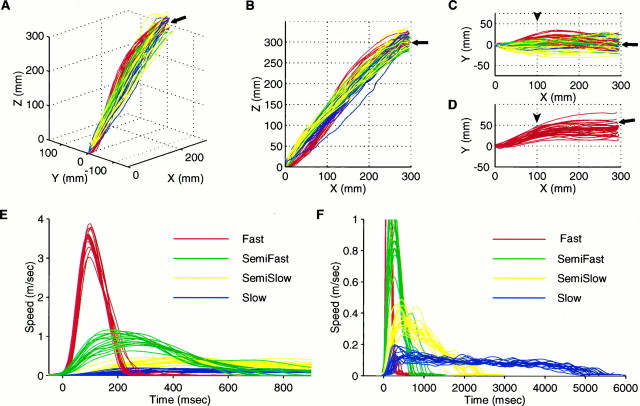
Fig. 2.

Trajectories (A–D) and tangential velocity profiles (E, F) of the hand (tip of the index finger) during the four task movements. Red, green, yellow, and blue traces show data for the fast, semifast, semislow, and slow reaching tasks, respectively. All data were obtained from subject TY. A–C, Three-dimensional display (A), lateral view (B), and top view (C) of the hand trajectories in Epoch 1. Fifteen traces for each of the four types of movements are superimposed. Starting point (origin) is located on the sagittal midplane (Y = 0) of the subject, and the center of the screen (fitted arrows) is positioned 300 mm ahead of (x-axis) and 300 mm above (z-axis) the starting point. A target appears at a random location in a square area (40 mm × 40 mm), which is covered by the terminal points of the trajectories. Note the overlap of trajectories drawn with different colors. D, Top view of the hand trajectories in Epoch 2. Thirty traces of the fast movements are superimposed. Note that the center of the screen (filled arrow) is displaced to compensate for the visual displacement of the screen caused by the prisms. E, F, Tangential velocity profiles of the hand during the task movements shown inA–C. Profiles are aligned at the release of the button. Note the difference of scales in E and F.

In contrast, the temporal profiles of tangential speed during the four types of movement were clearly different. The fast reaching movements (Fig. 2E, red) had bell-shaped profiles with peak velocities of 3–4 m/sec. The velocity profiles of the semifast, semislow, and slow movements had peaks of 0.5–1 m/sec (Fig.2E, green), 0.2–0.4 m/sec (Fig. 2F, yellow), and 0.1–0.2 m/sec (Fig. 2F, blue), respectively. The shapes of the velocity profiles depended on the desired movement duration and remained almost consistent throughout the epochs and experiments, as well as among the subjects.

Subjects could switch immediately from one type of movement to another when required, as shown in Figures 3, 4, 5, by the instantaneous change in movement durations (open squares) at the beginning of each Epoch. Subjects could react within the required 200 msec in most trials (86, 129, and 158 msec for the 25, 50, and 75 percentile;n = 19,620), as shown in Figures 4 and 5(filled squares).

Fig. 3.

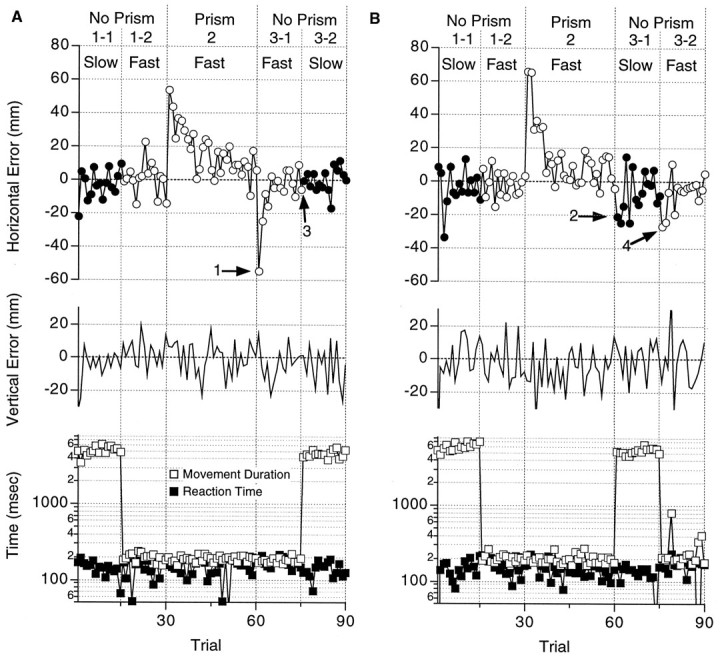
Errors in two experiments (subject TY, base-left prisms) testing the transfer of adaptation from the fast to the slow reaching movements. A, Data under condition I from Figure1B. Open and filled circles in thetop panel show the horizontal errors relative to the target in the fast and the slow reaching task, respectively. Horizontal errors (ordinate) were measured in the direction of visual displacement in Epoch 2 and plotted against the trial sequence (abscissa). Vertical errors are shown in the middle panel with upward errors in the positive direction. Reaction times (filled squares) and movement durations (open squares) are plotted (ordinate, log scale) against trial sequence in the bottom panel. Vertical dotted linesshow the borders between Epoch 1-1, 1-2, 2, 3-1, and3-2. Required task movements (fast or slow) and the existence or absence of prisms (prism or no prism) are shown above.B, Data under condition IV from Figure 1B. Axes and symbols are the same as in A. Note the difference between the horizontal errors in Epoch 3 of B (arrows 2 and 4) and A (arrows 1and 3).

Fig. 4.

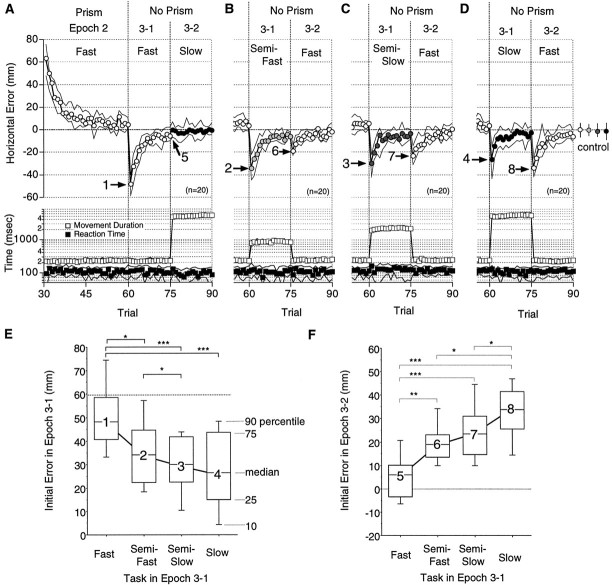
Velocity specificity of prism adaptation with fast reaching. A–D, Circles in the top panel show the median horizontal errors (n = 20) for 10 subjects under conditions I (A), II (B), III (C), and IV (D) from Figure 1B. Open, light-shaded, dark-shaded, and filled circles show errors from trials in the Fast, Semifast, Semislow, and Slowreaching tasks, respectively. The median horizontal errors for the four tasks in Epoch 1 (control) are indicated by circles at theright-hand side. Error bars indicate 25 and 75 percentiles. The median movement duration (open squares) and reaction time (filled squares) are shown in the bottom panel. The medians (symbols) lie between the 25 and 50 percentiles shown by solid lines. Note that most of the 25 and 75 percentiles of the movement duration (open squares) are hidden under the symbols. Data in Epochs 2 and 3 are shown inA, whereas only those in Epoch 3 are shown inB–D. Other notations are the same as in Figure 3. E, F, Distributions of the initial errors in Epoch 3-1 (E) and Epoch 3-2 (F) shown, respectively, for the required task movement in Epoch 3-1. Note that in F errors in the last trial of Epoch 3-1 are shown for the fast reaching task (5). Each box plot shows the 10, 25, 50, 75, and 90 percentiles of distribution. Numbers on the box plots correspond to arrows 1–8 in A–D. Note the decrease from 1 to 4 and the increase from 5 to 8. The medians were 48, 34, 30, and 26 mm for 1–4, and 6, 19, 23, and 34 mm for 5–8, respectively. Significant differences are indicated bybrackets with asterisks (*p < 0.05; **p < 0.01; ***p < 0.001; Wilcoxon signed rank test).

Fig. 5.

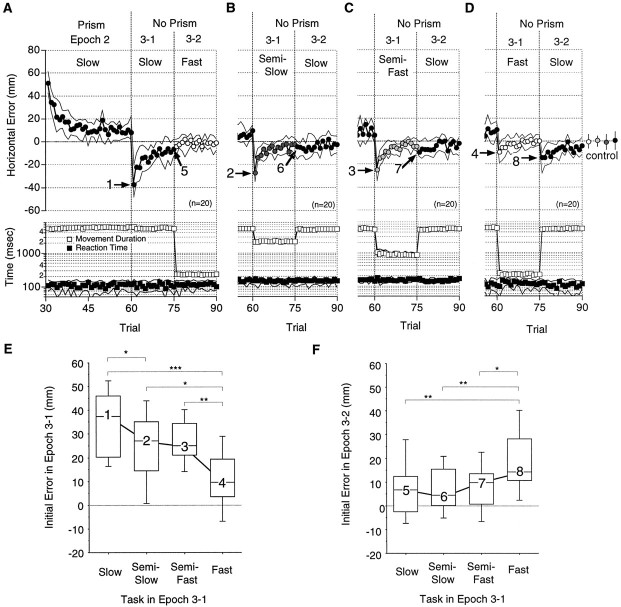
Velocity specificity of prism adaptation with slow reaching. A–D, Median horizontal errors (circles), movement durations (open squares), and reaction times (filled squares) under conditions VIII (A), VII (B), VI (C), and V (D) from Figure 1B. E, F, Distributions of the initial errors in Epoch 3-1 (E) and Epoch 3-2 (F) shown, respectively, for the required task movement in Epoch 3-1. Note that in F errors in the last trial of Epoch 3-1 are shown for the slow reaching task (5).Numbers correspond to arrows 1–8 inA–D. The medians were 37, 27, 25, and 9.5 mm for1–4 and 6.7, 4.5, 9.7, and 14 mm for 5–8, respectively. Other notations are the same as in Figure 4.

Specificity of adaptation for speed of reaching: fast movements

Figure 3A shows a typical pattern of errors in one experiment under condition I from Figure1B. In the first Epoch (Trials 1–30, No Prism), horizontal errors in reaching were distributed around the zero point when the subject made slow (Epoch 1-1, filled circles; −2.9 ± 8.7 mm, mean ± SD) or fast (Epoch 1-2, open circles; 0.6 ± 9.5 mm) reaching movements. The position of touch correlated well with the position of the target that appeared at a random location in a 40 mm × 40 mm area around the center of the screen: correlation coefficients were 0.72 (n = 15; p < 0.01) for the horizontal direction and 0.67 (n = 15; p < 0.01) for the vertical direction in the fast and 0.81 (n = 15; p < 0.001) and 0.65 (n = 15;p < 0.01), respectively, in the slow reaching tasks. This indicates that the reaching movement was generated in response to the location of the visual target.

The subject made fast reaching movements in Epoch 2 with the prisms in place. In the initial trial (trial 31, Fig. 3A), the subject misreached 52 mm to the right, which was nearly equal to the extent of the visual displacement (60 mm). In the example shown, the visual field was displaced to the right by base-left prisms (15 diopter), and the CRT screen was displaced to the left by 60 mm to compensate for the displacement of the visual field (see Materials and Methods for details). The horizontal errors decreased in an exponential manner with the number of trials performed. If we compare the trajectories of fast reaching movements in Epoch 1 (Fig. 2C, red traces) with those in Epoch 2 (Fig. 2D), it is apparent that the trajectory had already changed when the hand passed a frontal plane 100 mm away from the starting point (arrowheads). This suggests that even the initial 100 msec of the movement was changed because of the adaptation, because the movement durations of fast movements were ∼200 msec for this subject (Fig. 3A, open squares).

In Epoch 3-1, the prisms were removed and the subject was required to make a fast reaching movement, as in Epoch 2. The subject strayed as far as 50 mm in the opposite direction in the initial trial (arrow 1, Fig. 3A); the error decreased with the number of trials performed (arrow 3). Then the subject was required to make slow reaching movements in Epoch 3-2 (Trials 76–90,filled circles). Horizontal errors were distributed about the zero point as in Epoch 1-1.

Vertical errors were not affected during the experiment (Fig. 3A, Vertical Error) and will not be mentioned further.

Figure 3B shows the results from another experiment in which the same subject made reaching movements under condition IV from Figure1B. In this experiment, conditions in Epoch 1 and 2 were exactly the same as those in the experiment shown in Figure3A (the control experiment). The subject was exposed to visual displacement with fast reaching movements, as in the control experiment, and the errors changed in a similar manner as in the control experiment during Epoch 1 and 2. A difference occurred in Epoch 3, however, when the subject was required first to reach slowly in Epoch 3-1 and then to reach rapidly in Epoch 3-2. The error in the initial trial of Epoch 3-1 (arrow 2, Fig. 3B) was only 20 mm, almost one-half of the corresponding error in the control experiment with fast reaching movements (arrow 1, Fig.3A). This smaller error decreased in the 15 successive trials, but when the subject was required to make fast movements again in Epoch 3-2, an error of 27 mm recurred (arrow 4, Fig.3B).

Data thus obtained from 10 subjects are summarized in Figure4, which shows the patterns of errors obtained under conditions I (Fig. 4A) and IV (Fig.4D). Errors during exposure to visual displacement (Epoch 2, Prism) showed similar changes in both of these conditions: the median errors (open circles) decreased exponentially from 60 mm (Trial 31) and almost returned to the control level by the last trials (Trials 55–60) of Epoch 2. When the subjects made fast reaching movements in Epoch 3-1, as during the period of visual displacement, the median of the errors was 48 mm (arrow 1, Fig. 4A). In contrast, the median of the errors was one-half as large when the subjects were required to make slow reaching movements (26 mm; arrow 4, Fig.4D). This smaller aftereffect nearly disappeared after the 15 trials of slow reaching movements (Fig. 4D, filled circles). The error recurred, however, in Epoch 3-2, when fast reaching movements again were required in the initial trial of Epoch 3-2 (arrow 8, Fig. 4D).

We also examined the transfer of adaptation from the fast to the semifast (condition II, Fig. 1B) and from the fast to the semislow (condition III) reaching tasks. Figure 4B shows the errors in Epoch 3 under condition II, when the subjects were required to make semifast reaching movements (∼800 msec duration) after the adaptation was acquired with the fast reaching movements. The initial median error in Epoch 3-1 (arrow 2, Fig. 4B) was less than that under condition I (arrow 1, Fig. 4A). The error recurred in Epoch 3-2, when the subjects again made fast reaching movements (arrow 6, Fig. 4B).

Figure 4C similarly shows the errors in Epoch 3 under condition III, when the subjects were required to make semislow reaching movements (∼2000 msec duration) after adaptation with the fast reaching movements. The initial median errors in Epoch 3-1 (arrow 3) and Epoch 3-2 (arrow 7) fall between the corresponding errors under conditions II (Fig.4B) and IV (Fig. 4D).

Figure 4E summarizes the dependence of the initial errors in Epoch 3-1 on movement duration after exposure to visual displacement with fast reaching movements. The figure shows that (1) the initial error was largest (median, 48 mm) when the subject was required to make the same fast reaching movement as during visual displacement, (2) the error decreased considerably (median, 71% of the maximum) when the movement was semifast, and (3) the errors decreased more gradually thereafter with the semi-slow (63%) and slow (54%) movements. The decreases in the initial errors were significant between the fast and semifast (p = 0.011), the semifast and semislow (p = 0.04), the fast and semi-slow (p = 0.0004), and between the fast and slow (p = 0.0007) reaching movements. The Wilcoxon signed rank tests (a nonparametric equivalent of the two-tailed paired t test) were used to compare the initial errors. Each test used 20 pairs: the initial errors in Epoch 3-1 obtained from a subject after a given direction of visual displacement in Epoch 2 were paired for each test (Kitazawa et al., 1995b). The same test is used in the following evaluations, unless described otherwise.

Figure 4F shows the initial errors in Epoch 3-2 when the subjects were required to make fast reaching movements after making 15 semifast, semislow, or slow reaching movements in Epoch 3-1. As a control, we used the error of the last fast reaching movement in Epoch 3-1 under condition I that was obtained after 14 fast reaching movements (arrow 5, Fig. 4A). The median control error was 6.0 mm (5, Fig. 4F), but larger errors were observed in Epoch 3-2 after the slower movements were required in Epoch 3-1: 19 mm for semifast (6), 23 mm for semislow (7), and 34 mm for slow (8) reaching movements. The differences in the errors were significant between the fast and semifast (p = 0.0019), the fast and semislow (p = 0.0009), the fast and slow (p = 0.0002), the semifast and slow (p = 0.02), and between the semislow and slow (p = 0.038) reaching movements. These results suggest that the adaptation acquired with fast reaching movements did not generalize completely to the slower reaching movements. It is possible, however, that the size of the aftereffect also depends on the velocity of movement itself. As such, the transfer of adaptation from the slow reaching tasks was studied as well.

Specificity of adaptation for speed of reaching: slow movements

Figure 5A–D shows the patterns of errors in Epochs 2 and 3 when the subject was required to make slow reaching movements during Epoch 2 (conditionsV–VIII, Fig. 1B). Errors in Epoch 2 decreased in an almost exponential manner from ∼60 mm to near the control level in 30 trials (Fig. 5A). In Epoch 3-1, after the prisms were removed, errors were observed in the direction opposite to prism displacement. The largest initial error (median, 37 mm) among the four conditions was observed when the same slow reaching movements were required as during the exposure to visual displacement (arrow 1, Fig. 5A). The median initial errors decreased as the velocity of Epoch 3-1 increased: 27 mm with semislow (arrow 2, Fig. 5B), 25 mm with semifast (arrow 3, Fig. 5C), and 9.5 mm with fast (arrow 4, Fig. 5D) reaching movements. Figure5E summarizes the decrease in initial errors in Epoch 3-1. The differences were significant between the slow and semislow (p = 0.028), the slow and fast (p = 0.0001), the semislow and fast (p = 0.044), and between the semifast and fast (p = 0.0051) reaching movements. These initial errors in Epoch 3-1 decreased in succeeding trials (Fig.5A–D, Trials 61–75).

Errors recurred in Epoch 3-2 when slow reaching tasks again were required after semifast (arrow 7, Fig. 5C) or fast (arrow 8, Fig. 5D) reaching movements, although errors did not recur after semislow reaching movements (arrow 6, Fig. 5B). Figure 5F reveals a tendency for the initial errors in Epoch 3-2 to increase as the required movement in Epoch 3-1 became faster: 4.5 mm for semislow (6), 9.7 mm for semifast (7), and 14 mm for fast (8) reaching movements. The differences in errors were significant between the slow and fast (p = 0.0067), the semislow and fast (p = 0.009), and between the semifast and fast (p = 0.021) reaching movements.

The size of the aftereffects in Epoch 3-1 decreased as the difference in velocity increased, not only when the adaptation was acquired with fast reaching movements (Fig. 4E) but also when the adaptation was acquired with slow reaching movements (Fig. 5E). The size of the aftereffects was larger, however, when the adaptation was acquired with fast reaching movements (Fig.4E) than when acquired with slow reaching movements (Fig. 5E). An ANOVA indicated that both the difference of velocity between Epochs 2 and 3-1 (df = 3, F = 15.6; p = 0.0001) and the velocity of movement during Epoch 2 (df = 1, F = 20.9; p = 0.0001) significantly affected the size of the aftereffects in Epoch 3-1. Similarly, the size of the aftereffects in Epoch 3-2 (Figs.4F, 5F) also depended on both the difference of velocity (df = 3, F = 23.2;p = 0.0001) and the speed of movement in Epoch 2 (df = 1, F = 24.7; p = 0.0001). These analyses show that, in general, the fast movements produced greater aftereffects than the slow movements. Differences in the delay of visual feedback might partially explain the variation observed in the aftereffects: visual feedback on the error for the slow movements was much more delayed than that for the fast movements, when the timing of feedback was measured from the onset of the movement. This longer interval between the onset of movements and visual feedback might have decreased the size of aftereffects produced by the slow movements, because an additional delay of 50 msec in the visual feedback has been reported to decrease the size of aftereffects (Kitazawa et al., 1995b).

Manual specificity of adaptation

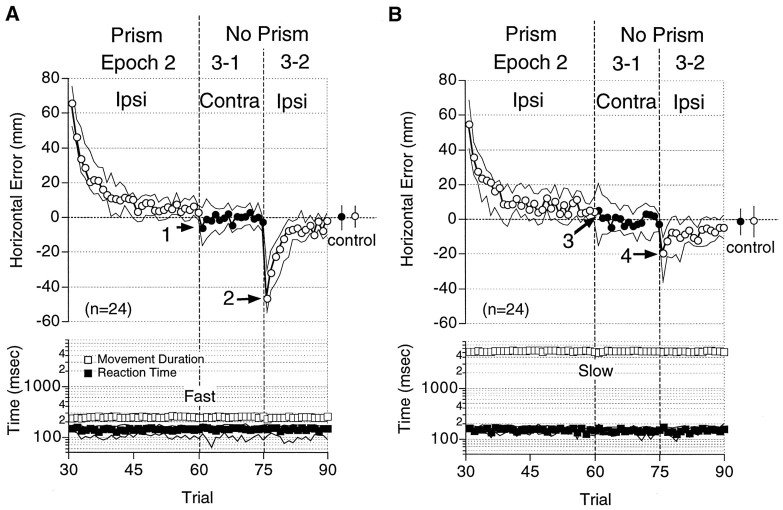
Next, we investigated whether the adaptation generalizes across the arms. In one condition (Fig. 1C, I), the subject was required to make fast reaching movements first with one arm (Contra) and then with the other (Ipsi). Then the subject was required to continue to use the same (ipsilateral) arm when the visual field was displaced by prisms in Epoch 2. The errors exponentially decreased with the number of trials performed (Epoch 2, Fig. 6A), similar to that seen in the previous experiments with the fast reaching tasks (Epoch 2, Fig. 4A). The prisms were removed, and the subject was required to use his other (contralateral) arm (Epoch 3-1, Fig. 6A). The median initial error was as small as 6.3 mm (arrow 1, Fig. 6A) and was not significantly different from that of the control levels in Epoch 1 (p = 0.065, Wilcoxon signed rank test;n = 24). In contrast, the median error of 47 mm recurred in Epoch 3-2 (arrow 2, Fig. 6A), when the subject again was required to use his ipsilateral arm.

Fig. 6.

Lack of intermanual transfer of adaptation acquired with fast (A) and slow (B) reaching. Median horizontal errors (circles), movement durations (open squares), and reaction times (filled squares) are plotted against the trial sequence. Openand filled circles indicate the data from the ipsilateral (Ipsi) and the contralateral (Contra) arms, respectively. Mean errors in Epoch 1 (control) are shown to the right (circles) with error bars (25 and 75 percentiles). Only the data in Epochs 2 and 3 are shown. These figures show combined data from experiments in which the right (n = 16) and the left (n = 8) arms were used during the exposure to visual displacement. Note the larger initial errors in Epoch 3-2 (arrows 2, 4) than in Epoch 3-1 (arrows 1, 3). Other notations are the same as in Figure 4.

Figure 6B shows the results from experiments in which the subject was required to make slow reaching movements (Fig.1C, II). In these experiments as well, the size of the aftereffect displayed by the contralateral arm (−5.2 mm,arrow 3) was not significantly different from that of the control level (p = 0.21, Wilcoxon signed rank test; n = 24), and a significant error appeared again in Epoch 3-2 (20 mm, arrow 4) when the ipsilateral arm was used. These results indicate that the adaptation, whether acquired with fast or slow reaching movements, showed almost no transfer from one arm to the other. Likewise, no significant transfer was observed when the data (n = 24) were analyzed separately to examine the transfer from the right to left (n = 16) and from the left to right (n= 8) arms.

DISCUSSION

In the present study we investigated whether prism adaptation acquired with reaching movements of a certain duration transferred to reaching movements of equal amplitude and direction, but of different duration. We measured the reaching errors observed after exposure to visual displacement and found these errors, or aftereffects, to decrease as the difference increased between movement duration during and after exposure. This was observed whether the adaptation was acquired during fast or slow reaching movements. That the adaptation was velocity-specific, even for slow reaching movements, excluded the possibility that the size of the aftereffect depended merely on the velocity of the ongoing movement. Furthermore, even after recovering from misreaching with a different velocity of movement, the subject misreached again when required to make the same velocity of movement as during the prism displacement trials. These results indicate that the adaptation did not depend solely on the direction of the movements but also on the time-dependent parameters of the movements.

Other researchers also have studied various task movements during and after exposure to visual displacement (Freedman et al., 1965;Baily, 1972; Martin et al., 1996) (for review, see Welch, 1986).Freedman et al. (1965) employed transverse and sagittal pointing movements. Baily (1972) studied rapid, straight pointing movements and slow pointing movements characterized by the extension of the elbow joint, followed by transverse oscillation of the extended arm around the shoulder. Incomplete generalization of the effects of exposure was found in both studies: from the transverse to the sagittal pointing movement (Freedman et al., 1965) and from the slow transverse oscillatory movement to the fast straight movement (Baily, 1972). These results were in accord with the present investigation, because the tasks studied had different time-dependent parameters of movement as well as different directions of movement. In both of the previous studies, however, visual displacement during the sagittal pointing movement (Freedman et al., 1965) and the rapid, straight pointing movement (Baily, 1972) produced aftereffects with the other tasks that were as large as those with the same task movement. These results seemingly contradict the present results. Each of the earlier studies used two tasks: one was executed in the sagittal direction and involved movements around multiple joints, whereas the other involved only one free movement around the shoulder joint, at least in the later half of the movement. Considering these differences in the degrees of free movement, the results suggest that perhaps the effects of visual displacement on arm movements involving more degrees of freedom (sagittal movement) generalize more completely to those having fewer degrees of freedom (transverse movement) than vice versa. Martin et al. (1996) examined prism adaptation acquired with underhand and overhand throwing of clay balls, both of which involved movements with multiple degrees of freedom around arm joints and which differed in directions as well as in time-dependent parameters. The investigators found the adaptation to be specific to the type of throw (underhand or overhand), which is in accord with the results of the present study. The present study, in contrast to the previous ones (Freedman et al., 1965; Baily, 1972; Martin et al., 1996), used movements of different durations but involved equivalent vectorial displacement of the hand in space. As such, we are the first to report that at least a part of prism adaptation is specific to the velocity of movement.

According to Welch et al. (1974), the aftereffects of prism adaptation are composed of three components: a visual shift, a proprioceptive shift, and a change in visuo-motor translation. In the following discussion, we attribute each component to respective changes of three different transformations (arrows 1–3, Fig.7) that lie between visual input and motor output and hypothesize which of the three components was responsible for the velocity specificity. Previously, we reported (Kitazawa et al., 1995b) that a small amount of correction, in proportion to the error made in the present trial, is added to each transformation after every trial and that the updated transformations influence the movement made in the next trial. It should be noted that sources of error signals for correcting the transformations could include signals from somatosensory as well as visual afferents.

Fig. 7.

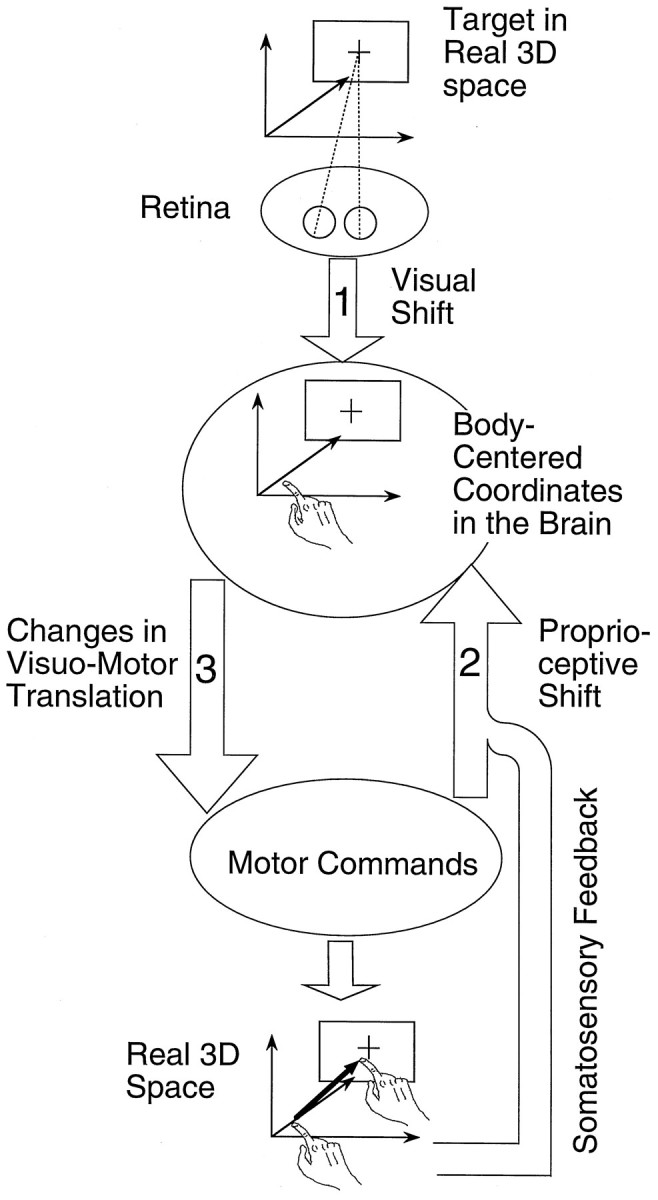
Three sites for prism adaptation in the transformations from visual input to motor output mediating target reaching. Optical images of the target on the retina are assumed to be mapped onto body-centered coordinates in the brain (arrow 1). This process is postulated to be used for the control of bilateral arm movements. The target location represented in the body-centered coordinates is translated into motor commands (arrow 3). Somatosensory signals from the arms and the efference copy of the motor commands are used for the estimation of hand position in the body-centered coordinates (arrow 2). Changes in the three transformations (arrows 1, 2, and3) correspond to the concepts of a Visual Shift, a Proprioceptive Shift, and Changes in Visuo-Motor Translation, respectively. See Discussion for details.

No change in visual coordinates

The first component (visual shift) is a change in visual coordinates: a change in the mapping of visual images on the retina into body-centered coordinates (arrow 1, Fig. 7). The existence of a visual shift has been demonstrated, for example, by requiring the subject to align a movable spot in the subjective straight-ahead position (Welch et al., 1974). Because this initial mapping from the visual images to body-centered coordinates should be shared by reaching movements of different velocities, the velocity specificity of the movements in the present study could not be produced by a visual shift. In addition, it is clear that a visual shift did not occur under our conditions because the adaptation in our experiments was specific for the arm used. Thus, the adaptation must have occurred during later stages in which the synaptic networks related to the unilateral limb could be altered independently of those related to the other limb.

The absence of visual shift apparently contradicts previous studies in which the visual shift was preferentially observed when the resultant hand position was shown to the subject at the end of the reaching movement, as in the present study (Uhlarik and Canon, 1971) (for review, see Welch, 1986). Ebenholtz and colleagues (Paap and Ebenholtz, 1976), however, have argued that the visual shift is associated with the shift in gaze in the direction of displacement of the visual field. They have provided convincing evidence that prolonged asymmetric positioning of the eyes leads to a tendency to maintain this ocular position even after attempting to relax the eye (for review, seeWelch, 1986). In the present study, the screen was repositioned so as to compensate for visual displacement; therefore, no asymmetric positioning of the eyes was required. The absence of a visual shift in the present study is, thus, in good accord with the arguments of Paap and Ebenholtz (1976).

Proprioceptive shift?

The second component (proprioceptive shift) is a change in the “felt” hand position (for review, see Welch, 1986) in body-centered coordinates. The existence of a proprioceptive shift has been demonstrated, for example, by requiring a blindfolded subject to point to the subjective straight-ahead direction with his arm (Welch et al., 1974). We define this component as a change in a forward model (Wolpert et al., 1995) that yields an estimate of hand position when it receives the efference copy of motor commands and the signals from sensory afferents, as illustrated in Figure 7 (arrow 2).

It should be noted that this forward model (arrow 2) is not necessarily involved in feed-forward control of the movement, because the arrow is directed upward, whereas in visuo-motor translation (arrow 3) it is directed downward. A proprioceptive shift is most likely to alter the in-flight corrections of movements that use the efference copy of motor commands and the signals from somatosensory afferents.

Because a visual shift was absent in the present study, a proprioceptive shift might have occurred in the adaptation; in particular, with the slow reaching movements in which the subject had ample time to make the felt hand position coincide with the memorized target location. That the transfer was incomplete, even from the slow (5 sec) to the semislow (2 sec) reaching tasks in which the subject also had enough time to allow for correction suggests that the estimation depended on the movement duration. It is reasonable to hypothesize that both the afferent and the efferent signals used for estimating hand position (Wolpert et al., 1995) vary with movement velocity; hence, it seems likely that a change in the estimated hand position (proprioceptive shift) would depend on movement velocity as well. Thus, the velocity specificity of the adaptation acquired with the slow reaching task might have been caused by a proprioceptive shift.

The velocity specificity of the adaptation acquired with the fast reaching task might have been caused partly by a proprioceptive shift as well. However, the adaptive change of the fast movements was already apparent in the initial 100 msec of the movement (Fig.2C,D). If we assume 100 msec is the time required for proprioceptive feedback to be effective (for review, see Jeannerod, 1988), the changes of movement in the initial 100 msec of the fast movement cannot be explained by the proprioceptive shift. Hence, we must look for a mechanism other than a proprioceptive shift to explain the adaptation acquired with the fast movements.

Rescaling visuo-motor translation

The third component, a learned visuo-motor response (Welch et al., 1974), is thought to have a more subtle affect on adaptation than the visual shift and the proprioceptive shift (Welch, 1986). Here, we define the third component as a change in translating the spatial position of the target represented in the body-centered coordinate into an appropriate motor command (arrow 3, in Fig. 7). We postulate that changes occur during this translation, especially with fast reaching, because a visual shift was absent and a proprioceptive shift could not have explained all effects observed with the fast movements. Using two major models of visuo-motor translation, the equilibrium-point hypothesis (Hogan, 1984; Bizzi et al., 1991) and another that involves stepwise translation from kinematics to dynamics (Kawato et al., 1987; Soechting and Terzuolo, 1990; Kalaska et al., 1992), we describe how the visuo-motor component significantly induces velocity specificity.

In the equilibrium-point hypothesis (Hogan, 1984; Bizzi et al., 1991), the translation from visual input to a motor command is achieved by sending an “equilibrium-point trajectory” to the periphery as a motor command. The equilibrium-point trajectory is a time series of equilibrium points, each of which would be realized if the motor command at some instant were maintained indefinitely. Flash (1987)assumed that each point in an equilibrium-point trajectory approximately matches a point in the realized trajectory. Under this assumption, a series of equilibrium points that successfully produced an adaptive movement at one speed should yield a similar shape of trajectory at another speed. Thus, changes in visuo-motor transformation could not be velocity-specific so long as each equilibrium point is realized in all speeds of movement.

Others, however, have suggested that equilibrium point trajectories could deviate considerably from the realized trajectories (Hogan, 1984; Latash and Gottlieb, 1992). Gomi and Kawato (1996)recently have shown that equilibrium-point trajectories do deviate from the realized trajectories in experiments involving human subjects. Furthermore, in a simulation study, Katayama and Kawato (1993)suggested that equilibrium-point trajectories differ in shape when the speeds of movement are different. It is plausible that the adaptation acquired with a movement with a given shape of equilibrium-point trajectory would not transfer well to another movement that has a different shape of equilibrium-point trajectory. Hence, the equilibrium-point hypothesis, as long as it predicts different shapes of equilibrium-point trajectories for different velocities of movements, would explain why the adaptation was specific for the velocity of movement.

Another set of models assumes that visuo-motor translation involves a sequence of steps proceeding from the more general aspects of movement kinematics to the more specific details of the causative dynamics (Kawato et al., 1987; Soechting and Terzuolo, 1990; Kalaska et al., 1992). At the level of movement kinematics in visuo-motor translation, often it is assumed that hand trajectories represented in the visual coordinates are translated into proprioceptive coordinates as muscle lengths and joint angles (Kawato et al., 1987; Soechting and Terzuolo, 1990; Kalaska et al., 1992). Under this assumption, recalibration of the proprioceptive coordinates relative to the visual coordinates is achieved by changes at the level of movement kinematics in visuo-motor translation.

Cell discharges correlated with the velocity or acceleration of hand positions or joint angles have been reported in the motor cortex (Humphrey et al., 1970; Hamada, 1981; Flament and Hore, 1988; Schwartz, 1993; Ashe and Georgopoulos, 1994), area 5 (Ashe and Georgopoulos, 1994), the cerebellum (Thach, 1978; Mano and Yamamoto, 1980; Van Kan et al., 1993), and the red nucleus (Gibson et al., 1985; Miller and Houk, 1995). It is likely that these areas are involved in the changes at the level of movement kinematics in visuo-motor translation. It is reasonable to postulate that the distribution of activity among these populations of cells varies with the speed of movement and that the changes underlying the adaptation observed in the present study are stored by these different populations of neurons. Thus, changes at the level of movement kinematics in visuo-motor translation, or the recalibration of the proprioceptive coordinates relative to the visual coordinates, may have caused the velocity specificity of the observed adaptation.

The velocity-specific adaptation also may have been caused by changes at the level of movement dynamics in the visuo-motor translation, because the dynamics of arm movement are influenced by kinematic parameters of the movement, such as velocity and acceleration. It also has been reported that other parameters of movement dynamics, such as forces and muscle activation, are represented in the motor cortex (Humphrey et al., 1970; Cheney and Fetz, 1980) and the red nucleus (Miller and Houk, 1995).

Further studies, both behavioral and neurophysiological, are required to elucidate the levels in the assumed model of motor control and the regions of the brain that are responsible for velocity-specific adaptation. The present study has revealed that the simple, traditional paradigm of prism adaptation, which merely involves static displacement of the visual field, can produce changes in the part of the brain that contributes to the generation of the dynamic signals for motor control without altering the static visual coordinates.