Postural Dependence of Muscle Actions: Implications for Neural Control

Abstract

The neural control of reaching entails the specification of a precise pattern of muscle activation distributed across the many muscles of the arm. Musculoskeletal geometry limits the possible solutions to this problem. Insight into the nature of this constraint was obtained by quantifying the postural variation in the mechanical actions of six human shoulder muscles. Estimates of muscle mechanical actions were obtained by electrically stimulating muscles to the point of contraction and recording the resulting forces and torques with a six-degree-of-freedom force–torque transducer. In a given experiment, data were obtained for up to 29 different arm postures. The mechanical actions of each muscle varied systematically with arm posture, regardless of the frame of reference used to define these actions. The nature of this dependence suggests that a relatively simple strategy can be used by the nervous system to account for the changing mechanical actions of arm muscles.

At first glance, the processes underlying the production of reaching movements appear dauntingly complex. The problems are typified by the concept of kinetic redundancy: because the number of force-generating elements of the arm exceeds the number of mechanical degrees of freedom, it is not clear how the motor system apportions activity among the various muscles during the performance of a particular motor task. Nevertheless, reaching movements tend to be performed in a relatively stereotypic manner, both with regard to their kinematics and, to a lesser extent, their muscle activation patterns (Morasso, 1981; Soechting and Lacquaniti, 1981; Atkeson and Hollerbach, 1985; Karst and Hasan, 1991; Buneo et al., 1994). Therefore, there seem to be constraints limiting the number of ways in which a particular reaching movement will be produced, and a great deal of research in motor control is aimed at elucidating the nature of these constraints. Constraints may be imposed as the result of the optimization of some neural or mechanical cost function associated with the production of movement. These types of constraints (e.g., minimum energy) have been given the most attention in the literature (cf. Hogan and Flash, 1987;Uno et al., 1989; Soechting et al., 1995). Other constraints may arise from the musculoskeletal anatomy. Muscles have mechanical actions about more than one axis. In addition, single-joint muscles can act to accelerate joints they do not span, and biarticular muscles even can act to accelerate a joint in a direction opposite to its anatomical classification (Zajac, 1993). Thus, muscle mechanical actions constrain, in a complicated way, the possible patterns of muscle activation that will be used to produce a particular movement.

Implicit in the above scenario is the idea that the motor system possesses an internal representation, or model, of the mechanical action of each muscle that it draws on in producing a particular movement. Information about muscle mechanical actions would be critical not only for the specification of the spatial and temporal aspects of the muscle activation pattern but also at earlier stages of movement planning. To plan a reaching movement to a particular target, the motor system must have some sense of the starting location of the hand or, alternatively, the initial arm configuration (Bizzi et al., 1984;Hogan, 1985; Flanders et al., 1992). Because one of the potential sources of this information is contained within muscles in the form of muscle spindles (McCloskey, 1978), the directions along which muscles change their length (and exert their forces) are likely to be important factors in representing the location of the hand, or arm posture in general. The complexity of muscle mechanical actions, therefore, has implications for the particular form of this representation. A critical question in this regard is whether the nervous system needs to account for muscle mechanical actions that change with arm posture, and if so, how is this accomplished?

Most existing data regarding muscle mechanical actions were obtained via gross anatomical dissection. In these methods, the origin and insertion of a muscle are measured, and assumptions are made about the center of joint rotation and the line of action to obtain an estimate of the mechanical action of that muscle (An et al., 1984; Zajac, 1993). These estimates are problematic in several respects. Because the experiments are performed postmortem, data are obtained from muscles that are not in a realistic state of tension. In addition, estimates typically are obtained with the joints in a single configuration and do not generalize well to other configurations (Soechting and Flanders, 1997). Last, even in cases in which measurements at multiple configurations are obtained, one is forced to arbitrarily represent both the line of action of the muscle (as straight or curved) and the center of rotation of the joint (as fixed or moving).

In the present paper we report estimates of the mechanical actions of six single-joint human shoulder muscles, obtained using an approach similar to the one used successfully by Lan and Crago (1992) and Lawrence and colleagues (1993) to characterize the mechanical actions of the hindlimb muscles of the cat. We found that the mechanical action of each muscle changed substantially with arm posture when this action was defined either in the frame of reference of the insertion (the upper arm) or the frame of reference of the origin (generally the trunk). This variation was not random, however; it depended on one or more of the arm angles defining arm posture in both frames of reference. The results demonstrate that a relatively simple model can account for the dependence of muscle mechanical actions on arm posture.

MATERIALS AND METHODS

General. Data were obtained from three adult human subjects. Subject A was a 5 ft, 9 in (175 cm), 130 lb (59 kg) female; Subject B was a 6 ft, 0 in (183 cm), 190 lb (86 kg) male; and Subject C was a 5 ft, 10 in (178 cm), 143 lb (65 kg) female. Informed consent was obtained from all subjects before their participation in this study. In addition, all experimental procedures were approved by the Institutional Review Board of the University of Minnesota.

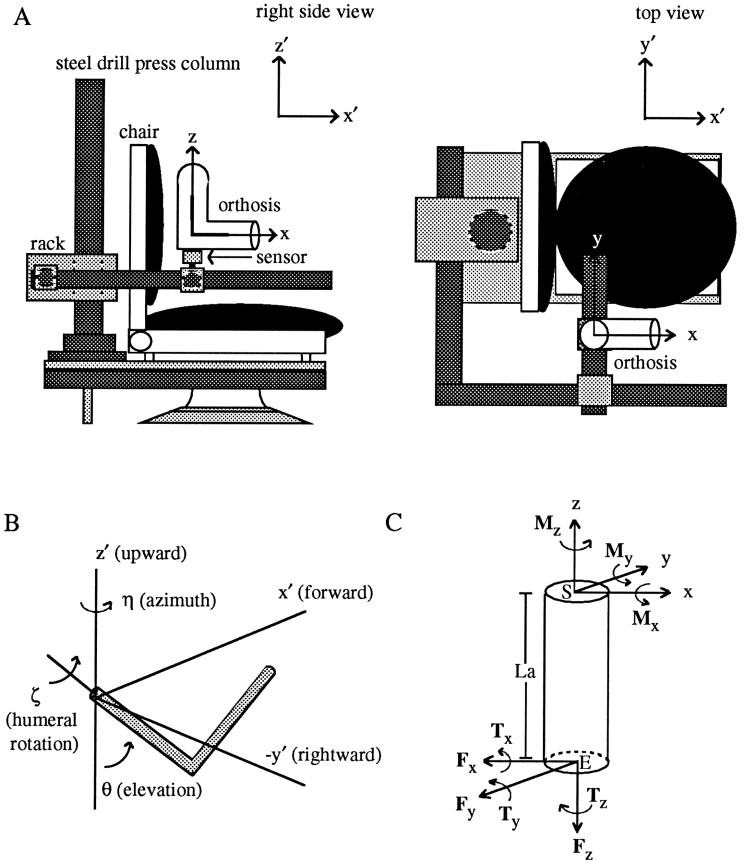
Subjects sat in a modified dental chair that was coupled to a rigid stereotaxic frame through a 1-cm-thick steel plate with stabilizing runners (Fig. 1A). The main pieces of the frame consisted of a 7-cm-diameter steel drill press column with a rack and several segments of 4- to 6-cm-diameter steel pipe. The frame allowed the six-degree-of-freedom force–torque sensor (JR3, Woodland, CA) to be positioned anywhere within a large portion of the three-dimensional workspace of the right arm. The sensor had a maximum load rating of 15 lbs [66.72 N (Newtons)] for the forces and 45 in-lbs [5.08 N-m (Newton-meters)] for the torques with 12-bit resolution. The sensor was coupled to the frame at one end and to a prefabricated, hinged, upper extremity orthosis at the other. The location of the sensor with respect to the orthosis is indicated in Figure 1A. In this figure, the upper arm portion of the orthosis is oriented vertically and the forearm portion horizontally. When the arm was in the orthosis, the sensor was located just distal to the elbow joint. (The precise alignment of the sensor with respect to the upper arm and forearm is described below under Coordinate Systems). The orthosis served to secure the sensor to the arm; this was facilitated by inflating air bladders lining its molded plastic segments. On average, the upper arm portion of the orthosis extended from just distal to the deltoid tuberosity of the humerus to just proximal to the elbow joint. The forearm segment began just distal to the elbow joint and ended just distal to the wrist. These two segments were connected by a steel hinge joint that was locked during all experiments at 90° of elbow flexion; elbow angle was not varied in these experiments.

Fig. 1.

Experimental apparatus (A), angles defining arm posture (B), and a free-body diagram of the forces and torques exerted on the upper arm (C).A, A six-degree-of-freedom force–torque sensor was rigidly coupled to an upper extremity orthosis at one end and a stereotaxic frame at the other. Two coordinate frames are illustrated: an x, y, z, frame that was fixed to the arm/sensor, and an x′, y′,z′ frame (inset) that was fixed in space. In this posture, the axes of the two frames were parallel. Thez- and x-axes were aligned with the long axes of the upper arm and forearm segments of the orthosis, respectively; the y-axis was orthogonal to the plane containing these two axes. B, Three angles were used to define upper arm posture: η, a rotation about the verticalz′-axis; θ, a rotation in a vertical plane passing through the upper arm (measured relative to the verticalz′-axis), and ζ, a rotation about the long axis of the humerus. C, A cylinder representing the upper arm is depicted along with the forces (F_x,F_y, F_z) and torques (T_x, T_y,T_z) recorded at the transducer and the corresponding torques at the shoulder (M_x,M_y, M_z). The shoulder, elbow, and length of the upper arm are labeledS, E, and La, respectively.

The following shoulder muscles of the right arm were examined in this study: anterior deltoid (AD), middle deltoid (MD), posterior deltoid (PD), latissimus dorsi (LaD), clavicular head of pectoralis major (CPec), and the upper portion of the sternocostal head of pectoralis major (SPec). Muscle contractions were elicited with a commercially available dual-channel neuromuscular electrical stimulation unit (Empi, St. Paul, MN). Bipolar, circular (3 cm diameter) surface electrodes were used to deliver the stimulation. The best position for the active electrode (cathode) was determined by moving this electrode to various points on the muscle belly and looking for the largest contraction for a given stimulus. The inactive electrode (anode) was placed ∼4 cm away from the cathode on the muscle belly. The unit was programmed to produce an asymmetrical biphasic waveform with a fixed pulse width of 300 μsec at a stimulation frequency of 50 Hz. The peak current was chosen to achieve a tetanic contraction (determined by visual inspection and palpation) while maintaining subject comfort and typically ranged from 15–20 mA. The unit was preprogrammed to follow a trapezoidal modulation of current: a 1 sec ramp up to peak current, followed by a 1 sec hold, followed by a 0.5 sec ramp down to 0 current. Stimulation was controlled by means of a hand switch that accompanied the stimulator. The stimulus was not painful, and subjects were instructed to relax and to not intervene intentionally in response to the stimulus. Five trials of stimulation were delivered at each arm posture, with an intertrial delay period of ∼30 sec to minimize fatigue. In each experiment, up to 29 postures of the upper arm were examined. (Throughout all experiments, motion of the scapula was not restricted.)

Data acquisition and processing. Muscle contractions resulted in the production of forces and torques that were transduced by foil strain gauges within the sensor into millivolt analog signals. These signals were sent to a signal conditioning board that accompanied the sensor and then digitized at 100 Hz. A complete trial produced a 5-sec-long record consisting of ∼1 sec of baseline before stimulation, 2.5 sec of data during stimulation, and 1.5 sec of poststimulation baseline. In addition to the six channels of force–torque data, a single channel carrying signals indicating the depression and release of the hand switch controlling the stimulator also was sent to the microcomputer. This signal was used to align the force and torque traces obtained from the repeated trials of stimulation at each arm posture (see Data Analysis below). Arm posture was derived from the recorded location of spherical reflective markers (placed on the orthosis at the approximate positions of the shoulder, elbow, and wrist), using a video-based, three-dimensional motion analysis system (VP110, Motion Analysis).

Coordinate systems. Because the transducer moved with the arm/orthosis during changes in arm posture, forces and torques applied to the transducer initially were defined in an arm-fixed frame of reference. In this coordinate system, the z-axis of the transducer was always aligned with the long axis of the upper arm. Thex-axis was oriented parallel to the long axis of the forearm. The y-axis was then defined as being perpendicular to the plane containing the upper arm and forearm. These axes are indicated on the orthosis in Figure 1A. Forces applied in the anterior (x) direction were defined as positive, as were forces applied in the medial (y) and superior (z) directions. By definition, torques about these positively directed axes were also positive.

When the upper arm was oriented vertically and the forearm horizontally within a parasagittal plane passing through the shoulder (as in Fig.1A), the axes of the transducer were parallel to the axes used to define upper arm posture (Fig. 1B). These latter axes were fixed in space and are labeled in Figure1A,B as x′, y′, andz′. When viewed from behind the right shoulder,x′ pointed in the forward direction, y′ pointed leftward, and z′ pointed upward. Arm posture was defined by three angles, depicted in Figure 1B. Upper arm azimuth (η) was defined as a rotation about the z′-axis. Upper arm elevation (θ) was defined as a rotation in a vertical plane passing through the upper arm and was measured relative to the verticalz′-axis. A third rotation about the long axis of the humerus defined humeral rotation (ζ).

Upper arm azimuth and elevation were computed from the measured location of the elbow relative to the shoulder by using the following relations:

$$tan(\eta )=(e_{{\text{y}}^{\prime }}/e_{{\text{x}}^{\prime }})(\eta =\text{upper arm azimuth})$$ Equation 1

$$tan(\theta )=(e_{{\text{x}}^{\prime }{\text{y}}^{\prime }}/-e_{{\text{z}}^{\prime }})(\theta =\text{upper arm elevation}),$$

in which e is a vector from the shoulder to the elbow, the subscripts x′, y′, andz′ represent Cartesian components, and the subscriptx′y′ represents a projection onto the horizontal plane. Humeral rotation was calculated by first computing the normalp to the plane of the arm from the cross product of the vector connecting the shoulder to the elbow with the vector connecting the elbow to the wrist (w):

$$p_{{\text{x}}^{\prime }}=e_{{\text{y}}^{\prime }}{w}_{{\text{z}}^{\prime }}-e_{{\text{z}}^{\prime }}{w}_{{\text{y}}^{\prime }}$$

$$p_{{\text{y}}^{\prime }}=e_{{\text{z}}^{\prime }}{w}_{{\text{x}}^{\prime }}-e_{{\text{x}}^{\prime }}{w}_{{\text{z}}^{\prime }}$$ Equation 2

$$p_{{\text{z}}^{\prime }}=e_{{\text{x}}^{\prime }}{w}_{{\text{y}}^{\prime }}-e_{{\text{y}}^{\prime }}{w}_{{\text{x}}^{\prime }}$$

If ν is defined to be the angle that pmakes with the horizontal plane, then humeral rotation can be calculated from the following relation:

$$sin(\zeta )=sin(\nu )/sin(\theta )(\zeta =\text{humeral rotation}).$$ Equation 3

Upper arm azimuth was 0° when the shoulder and elbow were in the parasagittal plane passing through the shoulder and was positive when the elbow moved left relative to the shoulder. Upper arm elevation was 0° when the upper arm was oriented vertically with the elbow down and was positive when the elbow moved forward relative to the shoulder. Humeral rotation was 0° when the wrist was in a vertical plane passing through the shoulder and was positive when the arm was rotated internally. The 29 postures examined in an experiment typically covered a range of ∼80° of azimuth and elevation and 120° of humeral rotation.

Data analysis. The following procedure was used to calculate the muscle torques acting at the shoulder. First, cross-coupling between channels of the force–torque sensor was removed numerically by means of a calibration matrix. Then the average value during the baseline period was subtracted from each force and torque trace. Repeated trials of stimulation at each arm posture were aligned at stimulation onset and averaged over the 2 sec corresponding to the stimulation ramp and hold periods. Torques at the shoulder were calculated from these force and torque traces with the following relations, in accord with the demands of static equilibrium:

$$M_{\text{x}}=T_{\text{x}}+{LaF}_{\text{y}}$$

$$M_{\text{y}}=T_{\text{y}}-{LaF}_{\text{x}}$$ Equation 4

$$M_{\text{z}} =T_{\text{z}},$$

in which La is the length of the upper arm,T_x, T_y, andT_z are the torques recorded at the transducer,F_x and F_y are forces recorded at the transducer, and M_x,M_y, and M_z are the corresponding muscle torques at the shoulder. These quantities are indicated on a free-body diagram in Figure 1C. Torques about the positive M_x, M_y, andM_z-axes are referred to throughout this manuscript as shoulder adduction (ADD), extension (EXT), and internal rotation (IR) torques, respectively. Torques about the corresponding negative axes are referred to as shoulder abduction (ABD), flexion (FLEX), and external rotation (ER) torques, respectively.

Figure 2A depicts the calculation of shoulder muscle torques graphically. The left and center plots show 1.5 sec of force and torque traces generated during stimulation of MD at a single arm posture. Data from five consecutive trials are depicted in each plot. The data are aligned at stimulation onset. In this example, only the forces changed substantially during the stimulation period. The F_x and F_y traces began to rise above baseline ∼0.5 sec after the onset of stimulation and then continued to rise monotonically and plateau after ∼1.1 sec (see below). Thus, the time course of force modulation followed the time course of current modulation; after an initial delay, forces ramped from a baseline value to a steady-state value over an ∼1 sec interval. It also can be seen in this example that both the sign and magnitude of the force and torque traces were consistent over consecutive trials obtained at the same arm posture. With regard to these findings, the data presented in this figure are representative of the data presented throughout this manuscript. The force and torque traces shown in the left and center plots were averaged (data not shown) and combined by using Equation 4 to yield the traces on the right, representing the components of torque at the shoulder with respect to an arm-fixed frame of reference. A complete set of these components for a particular arm posture will be referred to as a data set.

Fig. 2.

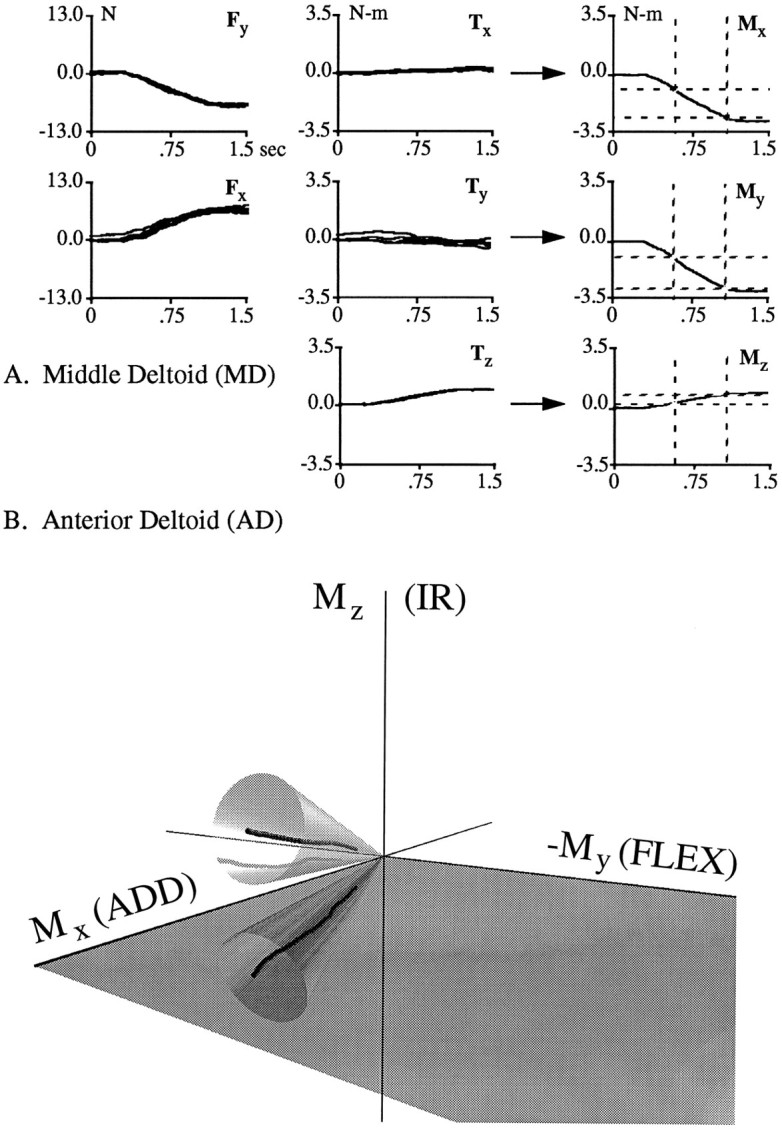
Graphical representation of the calculation of shoulder torques and the method used to evaluate the constancy of torque direction. A, The left andcenter plots show 1.5 sec of force (F_x, F_y) and torque (T_x, T_y,T_z) traces recorded at the transducer during the stimulation of MD at a single arm posture. Data from five consecutive trials aligned at stimulation onset are shown. These traces were averaged and combined using Equation 4 (see Materials and Methods) to obtain the traces on the right, representing the components of torque at the shoulder (M_x, M_y,M_z) in an arm-fixed frame of reference. Force units are Newtons (N), and torque units are Newton-meters (N-m). B, A three-dimensional torque trace obtained from AD during the ramp period of stimulation. The SD of the torque direction during this period had to be within the bounds of the 10° cone depicted here to be included in subsequent analyses.

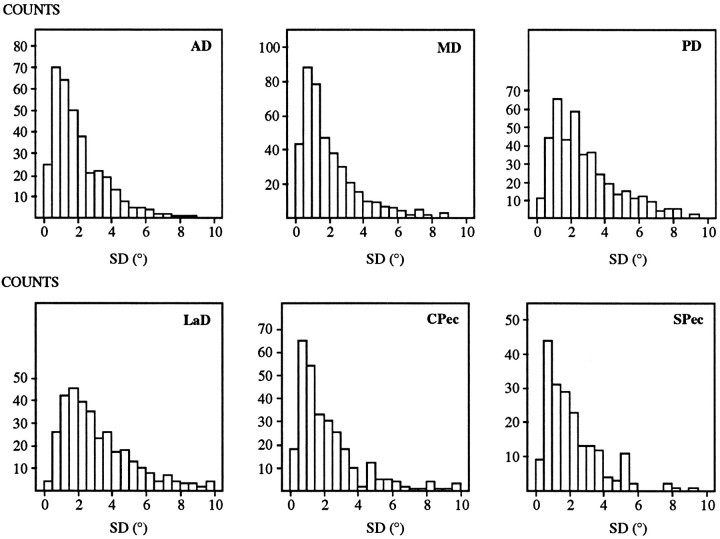
Each data set was evaluated to assess the extent to which torque direction changed during the ramp period of stimulation. The period of evaluation extended from 33% of the torque magnitude at steady state until the acquisition of steady state (steady state was chosen to be at 100 msec past the end of the stimulation ramp; 33% of this value was chosen to exceed baseline fluctuations in torque direction). This period is indicated in the shoulder torque traces of Figure2A by the dashed rectangles. If the SD of the three angles representing torque direction were <10° during this period, then the torque direction was judged to be constant. Data sets with torque directions that were not constant during the ramp period were excluded from further analyses (∼5% of the data sets).

This elimination process is depicted graphically in Figure2B. In this three-dimensional plot, a single torque trace resulting from the stimulation of AD is shown. This trace was obtained by plotting the three components of shoulder torque against each other for the evaluation period described above. Each point in the trace represents the value of torque at a particular instant during this period. The relative amount of shoulder flexion and adduction at each instant can be ascertained from the reflection of the trace onto the M_x/M_y plane. The relative amount of internal rotation is indicated by the height of each point above this plane. In this arm posture AD acted primarily to adduct and internally rotate the upper arm. Also depicted is a 10° cone centered on the mean torque direction of this trace. The SD of the torque direction during the ramp period of stimulation had to be within the bounds of this cone for the direction to be judged constant.

The SD of torque direction was generally much less than 10° for those data sets that were retained. For example, for the trace indicated in Figure 2B, the SDs of the M_x,M_y, and M_z components of torque direction were 1.03, 1.57, and 0.75°, respectively. Figure3 shows histograms of the SDs for all the retained data sets. A separate histogram for each muscle is shown. Each histogram was constructed by grouping the SDs of the three components of torque direction from each data set. For all muscles, the vast majority of these SDs were <5°. In fact, the median SD ranged from 1.43° (for MD) to 2.59° (for LaD). Thus, our stimulation protocol produced minimal changes in torque direction as current intensity increased during the ramp.

Fig. 3.

SD (in degrees) of the angles defining torque direction for each of the six muscles. Data from all retained data sets are shown.

Because torque direction was nearly constant during the ramp period of stimulation, each data set was reduced to a single point representing the instantaneous torque direction at steady state. This was accomplished by modeling each component of torque as a linear function of time during the ramp and evaluating this model for the time corresponding to steady state. In Results, the three components of torque at steady state are plotted against each other in separate two-dimensional plots; data are represented as vectors emanating from the center of each plot (see Fig. 4). These two-dimensional vectors can be thought of as projections of the three-dimensional torque vector. The torque direction can be inferred on these plots by applying the right-hand rule: if the thumb points along a particular vector (originating at the center), the fingers curl in the direction of the torque, which is also the direction the arm would rotate in response to this applied torque.

Fig. 4.

Shoulder torque vectors resulting from the stimulation of AD. Data were obtained from Subject A in one experimental session. Three separate views are shown, obtained by plotting the individual components of shoulder torque (M_x, M_y,M_y) against each other. Each vector is an average of five stimulations at a single arm posture. Data from 28 different arm postures are shown. Torques are defined in an arm-fixed frame of reference; units are Newton-meters (N-m).

During subsequent analysis we transformed these torque data from an arm-fixed frame of reference to a body-fixed (or trunk-fixed) frame of reference. This was accomplished by multiplying the muscle torques at the shoulder with the rotation matrix for each posture. Thus,

$$\left\{\begin{array}{c}{M}_{\text{x},\text{b}}\\ M_{\text{y},\text{b}}\\ M_{\text{z},\text{b}}\end{array}\right\}=[\begin{array}{ccc}C\zeta C\theta C\eta -S\zeta S\eta & -S\zeta C\theta C\eta -C\zeta S\eta & -S\theta C\eta \\ C\zeta C\theta S\eta +S\zeta C\eta & -S\zeta C\theta S\eta +C\zeta C\eta & -S\theta S\eta \\ C\zeta S\theta & -S\zeta S\theta & \hspace{0.5em}C\theta \end{array}]\left\{\begin{array}{c}{M}_{\text{x}}\\ M_{\text{y}}\\ M_{\text{z}}\end{array}\right\},(5)$$

in which C and S are shorthand for cosine and sine, respectively, and M_x,b,M_y,b, and M_z,b represent the components of muscle torque at the shoulder with respect to a body-fixed frame of reference. For this analysis, we retained our previous convention for naming the torques: (e.g., adduction torque for torques about the M_x,b-axis, etc.).

Multiple regression analysis. The dependence of muscle torque direction on arm posture was examined quantitatively by means of a multiple regression analysis. For this analysis, data from all subjects and experiments were grouped together (the rationale for doing so appears in Results). Rather than fit three normalized components of torque, we chose to represent torque direction with two angles. α is the angle that the projection of the three-dimensional torque vector onto the M_x/M_y plane makes with the −M_x-axis. β is the angle that the three-dimensional torque vector makes with theM_x/M_y plane. Stated mathematically (for the arm-fixed frame of reference),

$$tan(\alpha )=(M_{\text{y}}/-M_{\text{x}})$$ Equation 6

$$tan(\beta )=(M_{\text{z}}/M_{\text{xy}})[M_{\text{xy}}=(M_{\text{x}}^2+M_{\text{y}}^2{)}^{1/2}].$$

The angle α provides a direct indication of the relative amounts of flexion–extension and abduction–adduction, whereas β gives an indication of the degree of internal–external rotation.

Each angle originally was fit to a four-term model containing only linear functions of ζ, θ, and η, as well as a 20-term model containing linear, quadratic, and cubic polynomial terms. For example, for the linear model of β,

$$\beta =a_0+a_1\zeta +a_2\theta +a_3\eta +\epsilon ,$$ Equation 7

in which a₀ represents a constant,a₁–a₃ represent the coefficients of the various terms in the model, and ε represents the error (i.e., the difference between the actual value of β and the value predicted by the model). For all models, the parameters of the individual basis functions were determined by singular value decomposition (Press et al., 1992). We also computed similar models using only those terms that provided a significant contribution to the overall fit. Here the relevant terms were arrived at using a stepwise regression procedure, by which terms are added iteratively to the model and each term is tested for its contribution to the overall fit by means of a partial F test (Draper and Smith, 1981). The significance level for this procedure was chosen to be 95%. For all models, a summary measure of goodness-of-fit was reported as the value of r², defined as

$$r^2={SS}_{\text{m}}/{SS}_{\text{t}},$$ Equation 8

in which SS_m is the sum of squares of the model (i.e., the variation in the data that is explained by the model) and SS_t is the total sum of squares (the total variation in the data). The r² value represents the proportion of variance in the data that can be accounted for by the model.

RESULTS

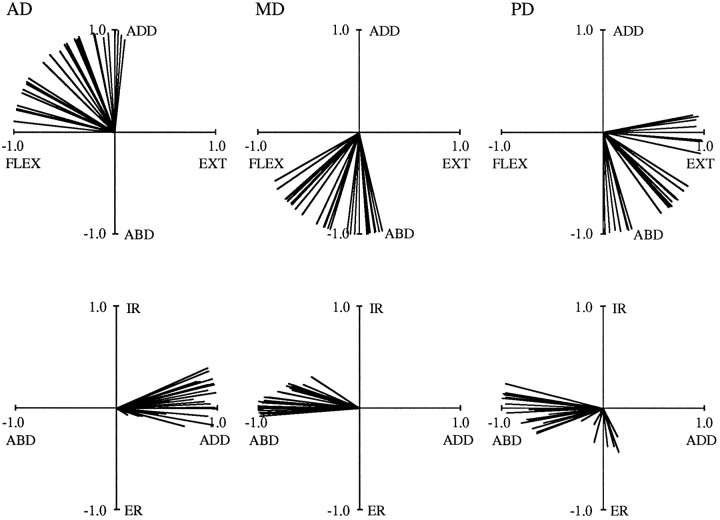
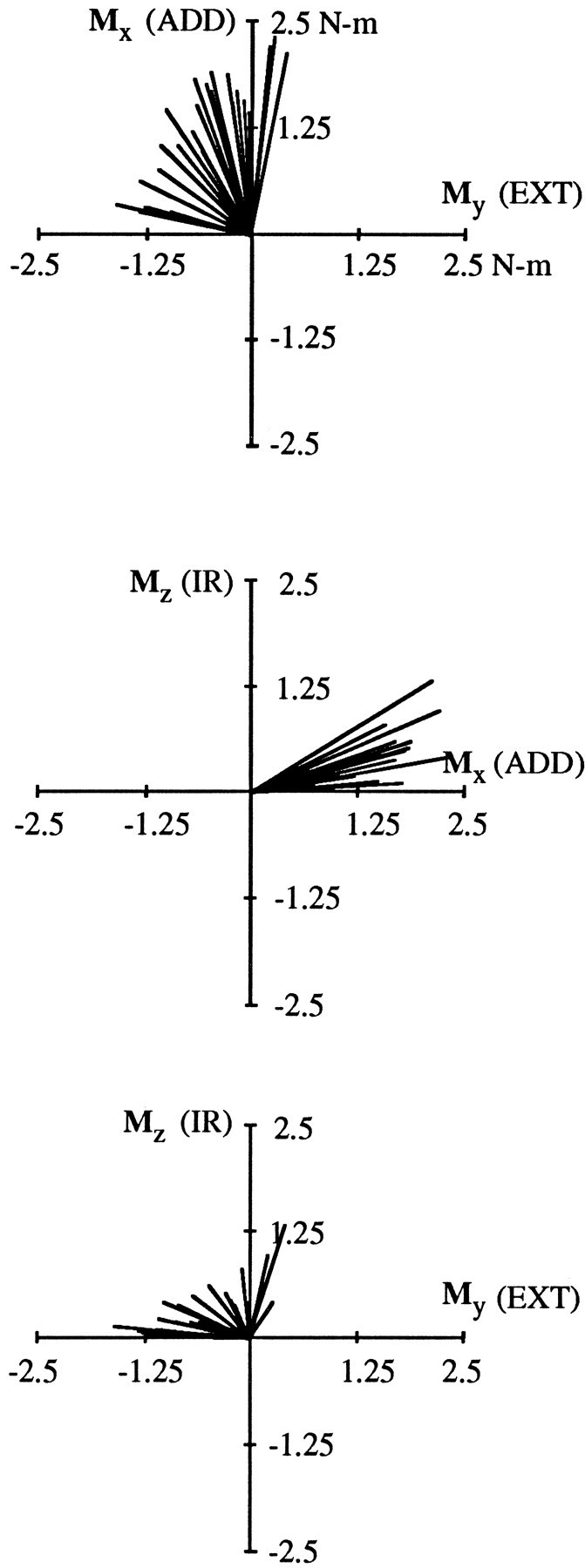
The results demonstrate the systematic manner in which the action of each of the six muscles changed with arm posture. Within each experimental session, both the magnitude and direction of shoulder muscle torques resulting from electrical stimulation varied with changes in arm posture. Figure 4 depicts data from AD of Subject A, obtained in one experimental session. Data are plotted in a vector format; the components of torque at the end of a stimulation ramp are plotted against each other and represented as vectors emanating from the center of each plot (see Materials and Methods for details). Each vector represents a single data set, i.e., an average of five stimulations at a single arm posture. Data from 28 different arm postures are shown, covering a range of 73° of azimuth, 78° of elevation, and 110° of humeral rotation. Magnitude variations across postures are apparent from the different lengths of the individual vectors. Torque direction variations (i.e., the relative amounts of flexion, adduction, and internal rotation) are evident from the wide range of vector orientations in each of the three plots of this figure. For most of the arm postures examined in this experiment, AD produced a combination of adduction, flexion, and internal rotation torques. These actions are generally consistent with previous investigations of this muscle (Basmajian and Deluca, 1985; Wood et al., 1989). For some arm postures, AD acted almost as a pure shoulder adductor, as indicated in the top plot of the figure by those vectors that are oriented nearly parallel to the M_x-axis. In other arm postures, AD acted primarily as a shoulder flexor; these vectors are oriented close to the −M_y-axis. For the remaining postures, the action of AD was between that of a flexor and an adductor. The range of α [the angle in theM_x/M_y plane, relative to the −M_x (ABD)-axis] provides an indication of the extent to which flexion and adduction torques varied. In this experiment, α ranged from 102 to 191°, with a mean of 147° and a SD of 29°.

For some of the arm postures depicted in Figure 4, AD produced substantial internal rotation torques, whereas for other postures these torques were negligible. The variation in the M_zcomponent of torque perhaps is best appreciated in the middle plot of Figure 4. Some vectors are oriented parallel or nearly parallel to theM_x-axis, indicating little or no component of humeral rotation for those arm postures. However, AD produced substantial internal rotation torques in other postures, as indicated by those vectors oriented at larger angles relative to theM_x-axis. The range of β (the angle relative to the M_x/M_y plane) gives an indication of the extent to which internal rotation torques varied. In this experiment, β ranged from 0 to 30°, with a mean of 11° and a SD of 8°. The ranges of α and β observed in this experiment were typical for AD. Comparable results were obtained for other muscles (see below).

As mentioned above, torque magnitude varied with arm posture within an experimental session. For example, for the data presented in Figure 4, torque magnitude varied from 0.97 N-m to 2.54 N-m, with a mean of 1.64 N-m and a SD of 0.39 N-m. Variations in torque magnitude were observed for all the muscles examined in this study, although the extent of this variation differed for different muscles. Because the focus of this manuscript is on the postural variation in the directions of exerted torques, there is no further description of torque magnitude variations. So that variations in torque direction may be visualized independently of torque magnitude variations, subsequent plots depict vector components that have been normalized by torque magnitude.

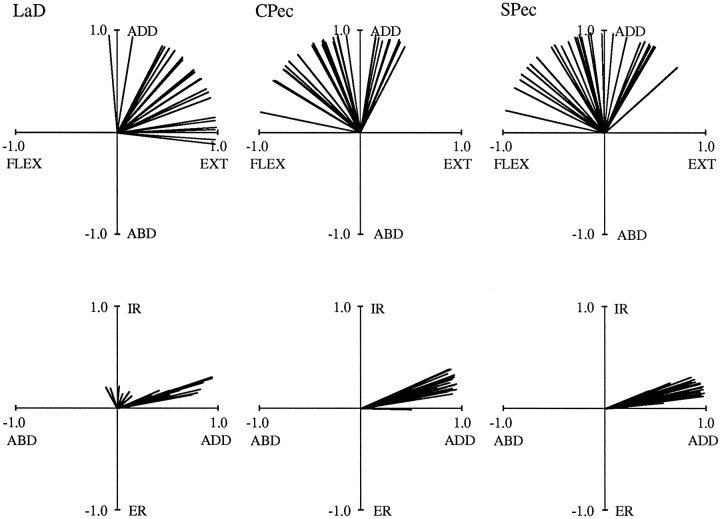
Torque directions varied with arm posture for all of the muscles examined in this study. Figures 5 and 6depict muscle torque vectors for all six muscles. In these and subsequent vector plots, only the top two views pictured in Figure 4are shown, and all vectors are of unit magnitude. The data illustrated were obtained from Subject C in three separate experiments. In Figure5, 29 postures are shown for both AD and MD, covering a range of 67° of azimuth, 70° of elevation, and 130° of humeral rotation. For PD, 28 postures are illustrated, covering a comparable range of 66, 72, and 117°. Torque directions varied for all three of these muscles, but these variations were limited to discrete regions of the vector space. This can be seen in the top plots of this figure, where vectors span a range of 90° for AD, 74° for MD, and 99° for PD. Similar degrees of variation were observed for the other muscles. In Figure 6, data for LaD (21 postures), CPec (29 postures), and SPec (28 postures) are shown. These postures varied to an extent similar to that described above. In the top plots of Figure 6, vectors vary over 101° for LaD, 107° for CPec, and 125° for SPec. For all muscles, internal and external rotation torques generally showed less variation. This can be appreciated from the bottom plots of Figures 5 and 6. For the experiments corresponding to these two figures, the range of β was as little as 12° (for LaD) and reached a maximum of only 40° (for PD).

Fig. 5.

Normalized shoulder torque vectors forAD, MD, and PD. The data in each plot were obtained from Subject C in one experimental session. Data are plotted in the same format as those in the top two panels of Figure 4.

Fig. 6.

Normalized shoulder torque vectors forLaD, CPec, and SPec. The data in each plot were obtained from Subject C in one experimental session. Date are plotted in the same format as in Figure 5.

Although torque direction varied, the “average” torque directions resulting from electrical stimulation generally agreed with previous descriptions of the actions of these muscles (Basmajian and Deluca, 1985; Wood et al., 1989). For instance, the top plots of Figure 5demonstrate that AD tended to produce combinations of flexion and adduction torques (as shown in Fig. 4 for Subject A), whereas MD acted as either a flexor or extensor (depending on the posture) and an abductor. Posterior deltoid (PD) produced combinations of extension and abduction torques that were approximately antagonistic to those of AD. With regard to internal and external rotation torques, the bottom plots of Figure 5 demonstrate that AD and MD acted as internal rotators in ∼70% of the postures. In contrast, PD acted primarily as an external rotator, producing internal rotation torques in only 30% of the postures. For the other muscles, the top plots of Figure 6 show that LaD acted primarily as an extensor and adductor, whereas the two heads of pectoralis produced adduction torques in combination with either flexion or extension torques. All three of the muscles in Figure 6 were internal rotators in all postures.

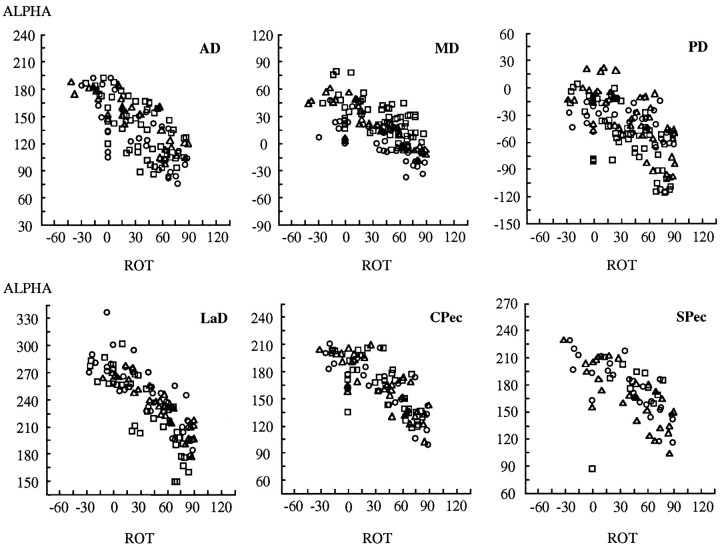
Muscle torque directions depended systematically on the angles defining arm posture. For example, Figure 7 depicts plots of α versus humeral rotation for all six muscles, and Figure8 depicts plots of β versus humeral rotation. The values on the abscissa range from −60° of external rotation to 120° of internal rotation. In both figures, data from all experiments and all subjects are presented, the symbols (□,○,▵) denoting the three subjects. Figure 7 reveals a strong dependence of α on humeral rotation, as indicated by the slopes of the relations between α and this arm angle. For all muscles, α (the angle in theM_x/M_y plane) decreased with increasing values of humeral rotation, and, for most muscles, the slope of this relation was approximately −1. Thus, there was an inverse relation between the angle of the torque vector in theM_x/M_y plane and the posture of the humerus in terms of rotation around its long axis (the M_z-axis; as seen in Fig.2B). This implies that a nearly complete counter-rotation of muscle mechanical actions accompanies postural changes in humeral rotation.

Fig. 7.

Dependence of torque direction (ALPHA) on humeral rotation [ROT(ζ)] for each of the six muscles. α is the angle in theM_x/M_yplane relative to the −M_x (ABD)-axis. Negative values of humeral rotation indicate external rotation; positive values indicate internal rotation. Each symbolrepresents a different subject.

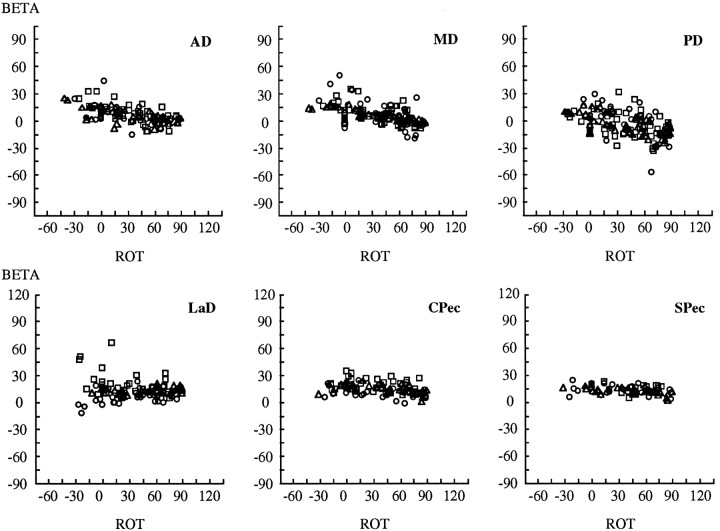
Fig. 8.

Dependence of torque direction (BETA) on humeral rotation [ROT (ζ)] for each of the six muscles. β is the angle relative to theM_x/M_yplane. Negative values of humeral rotation indicate external rotation; positive values indicate internal rotation. Each symbolrepresents a different subject.

Whereas the torque angle α exhibits a simple compensatory trend with humeral rotation, the second angle describing torque direction (β) exhibits very little dependence on this parameter of arm posture. Figure 8 shows the trends with humeral rotation for β: internal–external rotation torques varied in a weak but consistent manner with humeral rotation. In the figure, the three heads of deltoid show the strongest dependence. The two heads of pectoralis show similar but weak trends, and LaD exhibits considerable variability.

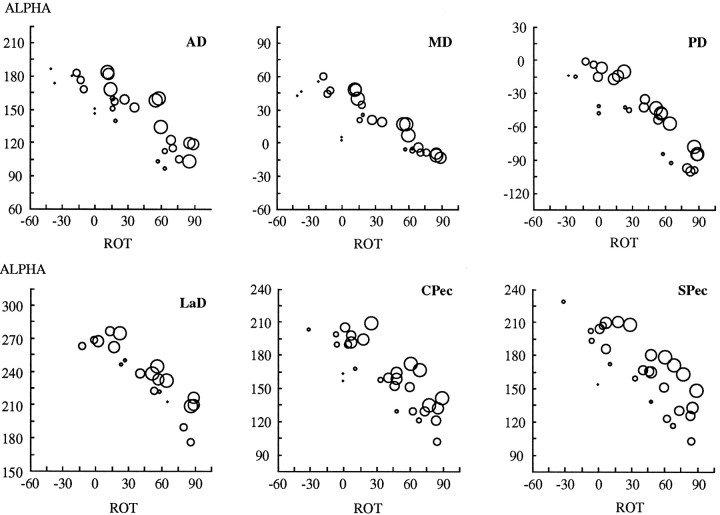
Torque direction also depends on the other two arm angles (elevation and especially azimuth), and this dependence accounts for much of the scatter of the data points in Figures 7 and 8. In Figure9, we show plots of α versus humeral rotation for the data presented in Figures 5 and 6 (Subject C). In each plot, an individual circle represents data from a single arm posture, the diameters of the individual circles being proportional to the values of azimuth at each posture. As shown in Figure 7, the value of α depends strongly on humeral rotation. However, Figure 9 demonstrates that α also depends on azimuth. A tendency for α to increase with decreasing arm azimuth (larger circles) is indicated in each plot by the changing diameter of the circles along a direction that is perpendicular to the main trend in the data. The trend perhaps is best appreciated in the plots for AD and SPec. Thus, Figure 9 reveals that torque direction (α) depends systematically on at least two of the angles defining arm posture.

Fig. 9.

Dependence of torque direction (ALPHA) on humeral rotation [ROT (ζ)] and upper arm azimuth (η) for each of the six muscles. Data are the same as those presented in the top plots of Figures 5and 6 (Subject C). α is the angle in theM_x/M_yplane, relative to the −M_x (ABD)-axis. Negative values of humeral rotation indicate external rotation; positive values indicate internal rotation. The diameters of the individual circles are proportional to values of upper arm azimuth, with the largest circles corresponding to the most lateral elbow locations.

These trends and others are evident in the results of the multiple regression analysis, presented in Table 1. As described in Materials and Methods, both α and β were fit to linear and cubic polynomial models of the parameters of upper arm posture (η, θ, and ζ). In general, quadratic and cubic terms contributed minimally to the overall fit of the data; this can be seen by comparing the r² values of the linear and cubic models (last two columns). As a result, we present regression coefficients only for the linear models. Nonsignificant terms (at the 95% level) are indicated by asterisks. In general, the linear models accounted for a substantial proportion of the variance, as indicated by the r² values. For α, humeral rotation (ζ) was the strongest predictor, as suggested by Figure 7. As discussed above, for most of the muscles the slope of the relation between α and ζ was close to −1, the only exception being MD. However, as suggested by Figure 9, upper arm azimuth (η) was also a strong predictor of α for most muscles, with a slope that ranged from −0.35 to −0.80. For a few muscles, θ provided a small but significant contribution to the fit of α. Not surprisingly, β showed less of a dependence on arm posture. In fact, for LaD, β could be fit only by a constant for both the linear and cubic models. For the deltoids, β depended mainly on ζ and η, whereas for the two heads of pectoralis β depended weakly on both ζ and θ.

Table 1.

Multiple regression analysis (arm-fixed frame of reference)

Muscle	Constant		η		θ		ζ		r2(linear)	r2(cubic)
α
AD	143.45	(2.59)	−0.80	(0.07)	*		−0.95	(0.05)	0.76	0.76
MD	19.85	(3.17)	−0.35	(0.07)	0.24	(0.07)	−0.62	(0.05)	0.55	0.60
PD	−38.77	(3.40)	−0.70	(0.09)	*		−0.83	(0.06)	0.57	0.59
LaD	269.62	(4.79)	−0.40	(0.08)	−0.26	(0.08)	−0.96	(0.06)	0.76	0.79
CPec	171.50	(2.84)	−0.65	(0.06)	0.01	(0.06)	−0.93	(0.04)	0.85	0.88
SPec	167.80	(6.11)	−0.80	(0.11)	0.27	(0.12)	−0.98	(0.08)	0.70	0.77
β
AD	13.94	(1.53)	−0.07	(0.03)	−0.12	(0.03)	−0.18	(0.02)	0.45	0.55
MD	1.79	(1.36)	−0.28	(0.03)	0.16	(0.03)	−0.31	(0.02)	0.62	0.64
PD	−9.62	(1.78)	−0.44	(0.04)	0.10	(0.04)	−0.39	(0.03)	0.65	0.65
LaD	12.26		*		*		*		0.00	0.00
CPec	21.49		*		−0.14	(0.03)	−0.05	(0.02)	0.31	0.38
SPec	19.32		*		−0.15	(0.02)	−0.03	(0.01)	0.42	0.43

Constants and parameter coefficients (±1 SD) from the multiple linear regression of the angles defining torque direction (α, β) on the angles defining arm posture (η, θ, ζ). Values for the constants are in degrees. Nonsignificant coefficients (p > 0.05) are indicated by asterisks.

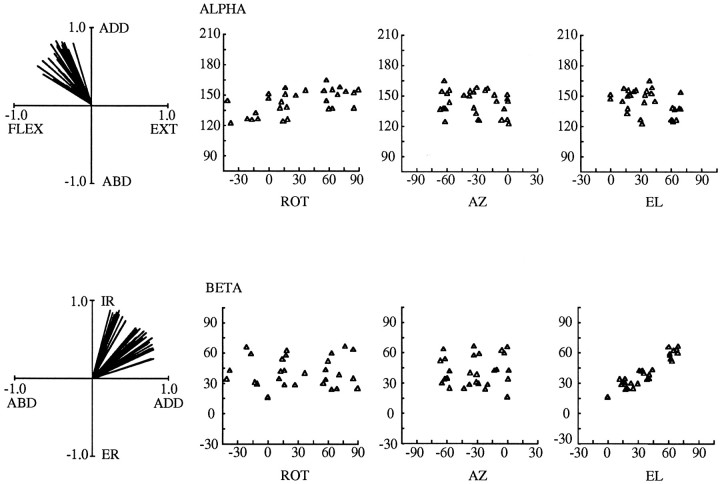
A dependence of muscle torque direction on arm posture also was evident when torque vectors were analyzed in a body-fixed frame of reference. In previous plots all data were represented in an arm-fixed frame of reference. The observed variation in muscle torque direction could have been a consequence of this chosen frame of reference; in another frame of reference torque directions could appear relatively constant across arm postures. To explore this possibility, we transformed the data from all experiments into a body-fixed frame of reference by multiplying each data set with the rotation matrix for that posture (Eq. 5). The results of this analysis are presented in Figure 10 for the AD of Subject C and can be compared with the data for the arm-fixed frame of reference shown in Figure 5. On the left are the two standard views of the torque vectors, now in a body-fixed frame of reference. It can be seen that there is still a substantial degree of variability in the orientations of the torque vectors. Although the variability in the abduction–adduction/flexion–extension plane is less than in Figure 5, the variability in internal–external rotation is greater (internal–external rotation now corresponds to a torque about a fixed vertical z-axis rather than about a moving humeral axis). To the right of these vector plots are scatterplots of α and β versus each of the arm angles defining arm posture. In contrast to the arm-fixed frame of reference, no clear trends exist between α or β and humeral rotation; these trends disappear in a body-fixed frame of reference. In fact, a strong relation seems to exist only between β and upper arm elevation (θ) in this frame of reference.

Fig. 10.

Dependence of torque direction (ALPHA and BETA) on the angles defining arm posture (ROT (ζ), AZ (η),EL (θ)) for the body-fixed frame of reference. Data from the AD of Subject C are shown; these are the same data that appear (in the arm-fixed frame of reference) in the extreme left plots of Figure 5. For the scatterplots, α is the angle in the M_x′/M_y′plane, relative to the -M_x′(ABD)-axis, and β is the angle relative to theM_x′/M_y′ plane. Negative values of humeral rotation indicate external rotation; positive values indicate internal rotation.

The results of a multiple regression analysis of the dependence of muscle torque direction on arm posture for the body-fixed frame of reference are depicted in Table 2. Here again, quadratic and linear terms did not improve the fit of the data substantially; therefore, only linear regression coefficients are shown. For β, the linear models accounted for a substantial proportion of the variance, with the exception of LaD. Upper arm elevation (θ) was the strongest predictor (again with the exception of LaD), and trends with upper arm azimuth (η) were consistently present. Trends with humeral rotation (ζ) were secondary, weak, or absent. For α, the results of the regression analysis were much less consistent. For AD and PD, α did not depend at all on the angles defining arm posture, and for the other muscles the results were highly variable. Only MD exhibited torque directions with a significant dependence on humeral rotation.

Table 2.

Multiple regression analysis (body-fixed frame of reference)

Muscle	Constant		η		θ		ζ		r2(linear)	r2(cubic)
α
AD	136.00	(1.88)	*		*		*		0.00	0.09
MD	21.00	(2.92)	0.82	(0.07)	0.30	(0.06)	0.51	(0.05)	0.61	0.67
PD	−44.48	(2.90)	*		*		*		0.00	0.27
LaD	269.48	(2.94)	0.65	(0.06)	*		*		0.48	0.51
CPec	160.09	(4.18)	0.16	(0.07)	0.56	(0.08)	*		0.35	0.43
SPec	155.14	(5.27)	*		0.76	(0.13)	*		0.35	0.43
β
AD	13.37	(1.78)	−0.12	(0.04)	0.74	(0.04)	−0.18	(0.03)	0.78	0.82
MD	−4.23	(1.88)	−0.25	(0.04)	−0.30	(0.04)	−0.11	(0.03)	0.40	0.48
PD	−9.43	(2.34)	−0.30	(0.05)	−0.67	(0.05)	−0.33	(0.03)	0.74	0.76
LaD	23.40	(3.66)	0.27	(0.06)	−0.15	(0.06)	*		0.20	0.26
CPec	26.51	(1.69)	0.11	(0.03)	0.70	(0.03)	−0.08	(0.02)	0.83	0.88
SPec	29.69	(2.15)	0.24	(0.03)	0.51	(0.04)	*		0.77	0.85

Constants and parameter coefficients (±1 SD) from the multiple linear regression of the angles defining torque direction (α, β) on the angles defining arm posture (η, θ, ζ). Values for the constants are in degrees. Nonsignificant coefficients (p > 0.05) are indicated by asterisks.

In summary, the mechanical actions of all six muscles varied substantially with arm posture when these actions were defined either in the frame of reference of the insertions of these muscles (the upper arm) or the frame of reference of their origins (the body or trunk). These variations were not random but depended strongly on arm posture. For both frames of reference, the dependence on arm posture could be described mathematically by a four-term model containing only linear functions of the angles defining arm posture. In the arm-fixed frame of reference, torque direction varied strongly with humeral rotation and, to a lesser extent, upper arm azimuth. In the body-fixed frame of reference, torque direction instead varied most strongly with upper arm elevation.

Although the dependence of muscle torque direction on arm posture was mathematically simple in both frames of reference, the three-dimensional nature of the torque vectors and the large number of postures used may make it difficult to get an intuitive feel for the main trends in the data. To assist the reader in this respect, in Figure 11 we present three-dimensional plots of the predicted torque direction vectors for AD and SPec in the body-fixed frame of reference. These vectors originate at the right shoulders of the depicted “mannequins” and are colored according to upper arm elevation (yellow vectors, 15°; orange, 45°; red, 75°). The direction in which the arm would rotate in response to an applied torque can be ascertained by applying the right-hand rule to these vectors (see Data Analysis). The top panel demonstrates that when the upper arm is nearly vertical (yellow vectors), contraction of AD will cause the humerus to move forward, upward, and inward (toward the midline of the body). When the arm is oriented more horizontally (redvectors), AD will rotate the humerus inward in a plane close to the horizontal plane. This postural change in the action of AD reflects the dependence of β on upper arm elevation (θ; see Table 2).

Fig. 11.

Predicted torque direction vectors for anterior deltoid (AD, top) and the sternocostal head of pectoralis major (SPec, bottom), viewed in the body-fixed frame of reference. Vectors from 28 different arm postures are shown, representing three values each of upper arm azimuth, elevation, and humeral rotation and one additional posture. For the 27 postures, η ranged from −15 to −75°, θ ranged from 15 to 75°, and ζ ranged from −15 to 75°. Also included in each panel is a vector representing upper arm vertical (the 28th vector). Vectors are colored for upper arm elevation (θ), withyellow vectors representing 0 or 15°,orange representing 45°, and redrepresenting 75°. All vectors originate at the right shoulder of a mannequin, and the mannequins faceforward. The M_x′-axis also points forward, the−M_y′-axis points to the leftof the page (the mannequins’ right), and theM_z′-axis points upward.

The effects of upper arm elevation, azimuth, and humeral rotation on the action of SPec are shown in the bottom panel of Figure 11. With regard to the effects of elevation, this muscle acts to move the humerus primarily upward and inward (toward the midline of the body) when the upper arm is oriented more vertically (yellow vectors) and downward and inward when the arm is oriented more horizontally (red vectors). The illustrated change in action corresponds to a strong dependence of both α and β on upper arm elevation (θ; see Table 2). The effects of azimuth on β are also identifiable in the figure: within each set of colored vectors (yellow, orange, orred) three clusters with different orientations are apparent. Each cluster corresponds to a different value of azimuth (−15, −45, and −75°), and the vertical separation of the clusters reflects the tendency for β to decrease as the arm moves toward the midline of the body. The vectors cluster into groups of three because there are three values of humeral rotation (−15, 30, and 75°) at each value of elevation and azimuth. Thus, it becomes apparent that humeral rotation had virtually no effect on the orientation of these vectors when viewed in the body-fixed frame of reference.

DISCUSSION

In this paper we describe the mechanical actions of six superficial shoulder muscles across a range of arm postures. Estimates of muscle mechanical actions were obtained by electrically stimulating muscles to the point of contraction and simultaneously measuring the resulting forces and moments with a six-degree-of-freedom force–torque transducer. Muscle mechanical actions, as indicated by the direction of exerted torques, varied systematically with arm posture. In this Discussion, we first will focus on issues related to the methodology used in this study. We then will discuss our results in relation to previous descriptions of the mechanical actions of these muscles. Last, we will discuss the implications of these results in relation to neural representations of posture and movement.

“Spillover” activation

As stated in the introductory remarks, we adapted the techniques of Lan and Crago (1992) and Lawrence and colleagues (1993) to characterize muscle mechanical actions across a range of arm postures. In addition to using multiaxis force sensors, these investigators used direct stimulation of nerve trunks in conjunction with selective denervations and tenotomies to ensure isolated activation of specific muscles. Because these latter techniques obviously could not be applied to human subjects, we instead delivered our electrical stimulation through surface electrodes. We chose surface electrodes over intramuscular ones because the latter allow activation of only a small number of muscle fibers. The disadvantage of surface stimulation is that one can never be entirely sure that stimulation has been confined to the muscle of interest. To minimize the possibility of including data in which spillover activation of other muscles had occurred, we instructed subjects to relax completely and then quantitatively evaluated the torque direction during the ramp period of stimulation (see Materials and Methods and Fig. 2). We reasoned that if stimulation were confined to a relatively homogenous group of muscle fibers, then torque direction should remain nearly constant during the ramp period of current increase. In other words, torque direction should be independent of both stimulation intensity and time during the ramp. As demonstrated in Figure 3, for those data sets that were analyzed fully in this study, torque direction was nearly constant during the ramp: the SDs of torque direction were typically <5° during this period. We conclude therefore that, although some spillover and/or reflex activation of additional muscles may have occurred, this activation was minimal and did not significantly contaminate our estimates of torque direction.

Compartmentalization

It is well known that some human arm muscles contain subpopulations of motor units that are recruited differentially, depending on task requirements (ter Harr Romeny et al., 1982, 1984; van Zuylen et al., 1988) (see also Pratt and Loeb, 1991). Little information is currently available, however, regarding the presence of such “compartmentalization” for the muscles examined in this study (Herrmann and Flanders, 1996). We therefore made no attempt to activate portions of particular muscles differentially, except in the most gross anatomical sense (the two heads of pectoralis, for example). The available data suggest that compartmentalization is a general phenomenon of muscles crossing the elbow joint (van Zuylen et al., 1988). If such a phenomenon were to be demonstrated for the muscles examined in this study, it would be of interest to repeat our experiments using intramuscular electrodes to determine whether fibers belonging to particular compartments have distinct mechanical actions and to determine if and how these actions vary across arm postures.

Comparisons with previous estimates

In general, the mechanical actions resulting from electrical stimulation agreed with estimates derived from EMG (for review, seeBasmajian and Deluca, 1985) and anatomical studies (Wood et al., 1989;Yamaguchi et al., 1995). With regard to the latter, several groups of investigators have developed geometrical models of the musculature of the human arm (Poppen and Walker, 1978; Högfors et al., 1987;Wood et al., 1989; Bassett et al., 1990; Van Der Helm and Veenbaas, 1991; Van Der Helm et al., 1992). For example, Wood et al. (1989) have published predictions of the mechanical actions of several muscles on the basis of data provided for a single arm posture (upper arm approximately vertical). We compared these data with data obtained in the present study for a similar arm posture. With regard to flexion–extension and abduction–adduction torques the only consistent discrepancies involved MD (which Wood et al. predicted should extend the upper arm, but which in the present study produced flexion torques) and PD (which these authors predicted should adduct, but which produced abduction torques in the present study). The mechanical actions of all of the other muscles agreed with at least one of the predictions of Wood et al. for this arm posture (these authors arrived at slightly different predictions depending on whether a particular muscle line of action was modeled as straight or curved). More consistent discrepancies were found with respect to the internal and external rotation torques. None of the muscles examined in the present study was predicted by Wood et al. to produce significant torques about the humeral axis. In the present study, only MD could be considered consistent with this viewpoint. All of the other muscles produced substantial humeral rotation torques.

As stated in the introductory remarks, a limitation of anatomical data in general is that they typically are obtained in a single arm posture. Attempts to estimate muscle mechanical actions in other postures on the basis of these data have suffered from a lack of information about how muscle lines of action and moment arms vary with arm posture (Soechting and Flanders, 1997). Several investigators have attempted to overcome such difficulties by incorporating these anatomical data into computer models that account for how muscles should wrap around the contours of the body. These models theoretically also can generate predictions of the forces and torques exerted by these muscles over a full range of humeral motions (Van Der Helm, 1994a,b; Yamaguchi et al., 1995). We have performed a comparison between the data obtained in the present study and the predictions of the model of Yamaguchi et al., which is based on data adapted from Wood et al. (1989). For some muscles (e.g., CPec and SPec) there was a good correspondence between the predictions of the model of Yamaguchi et al. (1995) and the predictions of the present study. However, other muscles exhibited substantial differences (e.g., AD, with respect to abduction–adduction torques). Nevertheless, simple models in which muscles are represented by three straight segments can account for the data presented here, provided the via points defining the intersections of these segments are located appropriately (Buneo et al., 1996).

Implications for representations of posture and movement

Muscle mechanical actions are undoubtedly a factor in the specification of the spatial and temporal aspects of muscle activation patterns. The influence of varying mechanical actions on muscle activity was highlighted by Hasan and Enoka (1985), who demonstrated that the pattern of activity in elbow muscles during certain elbow flexion tasks depends on the initial and final postures of the arm. Although mechanical actions strongly influence muscle selection, knowledge of muscle mechanical actions and how they vary with arm posture does not in itself reveal the strategies by which the nervous system specifies a given pattern of activation. This is partly because muscle activation patterns during movement are constrained by a variety of factors, including task demands (e.g., speed and accuracy, smoothness requirements) as well as other biomechanical realities (e.g., force/length and force/velocity relations of muscle). However, even under isometric conditions, the force direction for which a muscle is maximally active generally does not coincide with the direction in which a muscle would be expected to produce the most force, based on its mechanical action (Flanders and Soechting, 1990). This is to be expected because muscle actions add vectorially; therefore, both the magnitude and direction of torque produced by all of the muscles involved in a particular motor act must be known to understand the pattern of activation in any individual muscle (Pellionisz and Llinás, 1980; Soechting and Flanders, 1991).

What do the data from the present study add to this discussion? The extensive variation of muscle mechanical actions with arm posture initially appears to impose another level of complexity on the transformation from muscle forces to movement. However, a simplification has been provided in that the mechanical actions of these six muscles vary in a similar, linear manner with arm posture (see Figs. 7, 8, 9, 10, Tables 1, 2). When the actions of these muscles were viewed in an arm-fixed frame of reference, virtually the entire range of flexion–extension and abduction–adduction torques was covered by just four muscles (AD, MD, PD, LaD) examined over a large, but incomplete, range of arm postures. The fact that all of the muscles exhibited a similar dependence on arm posture indicates that the entire pattern of muscle mechanical actions rotates with respect to the arm during changes in arm posture, which, at least theoretically, provides a relatively simple means to adapt the activation pattern to the changing mechanical actions of muscle. Stated in terms of the scenario presented in the introductory remarks, the present data imply that the motor system must, indeed, account for changing muscle mechanical actions in an internal model. This process, however, need not be associated with an undue computational burden.

Of course in planning muscle activations for the entire reaching movement, other factors besides the changing pattern of mechanical actions would need to be incorporated into the internal model. In addition to the force/velocity and force/length characteristics mentioned above, these factors may include mechanical coupling between the shoulder and elbow joints. The internal model also may incorporate information about the inertial and viscoelastic properties of the arm; the spatial dimensions of these properties (e.g., the “inertial ellipse”) appear to rotate in a regular manner with changes in arm posture (Mussa-Ivaldi et al., 1985). However, despite the additional complexities that arise when the arm is accelerated, the results of the present study provide a clear and testable hypothesis regarding the frame of reference of reach-related neuronal activity: if cortical activity is in the frame of reference of the muscles, then postural changes in activity should reflect the geometric trends revealed by our data (see Table 2) .

The concept of frames of reference has proven useful in understanding the activity of both individual neurons and populations of neurons under a variety of circumstances (for review, see Simpson and Graf, 1985; Soechting and Flanders, 1992). However, despite the utility of the concept, few direct attempts have been made to determine the frame of reference for reach-related activity (Georgopoulos, 1995). For instance, although it is well known that the activities of many cells in motor cortex are tuned to the direction of reaching movements, a critical question remains unresolved: what is the directional reference for this activity? To state the two extremes: directionally tuned activity could be fixed to the arm or fixed in space. Alternatively, the directional tuning of this activity could be fixed in space, but the amplitude could be modulated with changes in arm posture (in the same way that visual receptive fields may be retinotopic, whereas cortical activity levels vary with eye position; cf. Andersen et al., 1985). Another alternative is that this activity could be neither fixed entirely in space nor to the arm (Caminiti et al., 1990). This final alternative might suggest that cortical activity was in the frame of reference of the muscles, because muscle mechanical actions are neither entirely fixed in space nor entirely fixed to the arm (see Tables 1 and 2).

As stated in the introductory remarks, information about the directions along which muscles change their length and exert their forces should be important to the nervous system for constructing a representation of arm posture for the planning of arm movement. Psychophysical experiments suggest that the orientations of the upper arm and forearm are represented as the angle of elevation with respect to vertical and the angle of azimuth with respect to a sagittal plane (Soechting and Ross, 1984). More recently, Lacquaniti et al. (1995) have demonstrated that variations in the activities of neurons in parietal area 5 during the maintenance of various static arm postures can be described quite well in a body-fixed frame of reference, the coordinates of which include the azimuth, elevation, and distance of the hand with respect to the shoulder (elbow angle). In the present study, when muscle torque directions were described in a body-fixed frame of reference, these directions were related almost exclusively to shoulder elevation and/or azimuth; in most cases torque direction did not depend on the third dimension of shoulder posture (humeral rotation). This reduction in degrees of freedom lends the postural representation of muscle actions the same dimensionality as the psychophysical and neuronal representations of arm posture: in each case information about body-fixed elevation and azimuth would need to be combined with information about the plane of the arm and the elbow angle. If defined in a body-fixed frame of reference, the action of elbow muscles would be altered drastically by humeral rotation; therefore, it may be more parsimonious to define elbow flexion–extension in an arm-fixed frame of reference. Nevertheless, the consolidation of shoulder muscle actions into body-fixed elevation and azimuthal components may prove to provide a simplification in the mapping between joint postures and joint torques.