Mosaics of Islet-1-Expressing Amacrine Cells Assembled by Short-Range Cellular Interactions

Abstract

The nervous system has a modular architecture with neurons of the same type commonly organized in nonrandom arrays or mosaics. Modularity is essential to parallel processing of sensory information and has provided a key element for brain evolution, but we still know very little of the way neuronal mosaics form during development. Here we have identified the immature elements of two retinal mosaics, the choline acetyltransferase (ChAT) amacrine cells, by their early expression of the homeodomain protein Islet-1, and we show that spatial ordering is an intrinsic property of the two Islet-1 mosaics, dynamically maintained while new elements are inserted into the mosaics. Migrating Islet-1 cells do not show this spatial ordering, indicating that they must move tangentially as they enter the mosaic, under the action of local mechanisms. Clonal territory analysis in X-inactivation transgenic mice confirms the lateral displacement of ChAT amacrine cells away from their clonal columns of origin, and mathematical models show how short-range cellular interactions can guide the assemblage of these mosaics via a simple biological rule.

The retina is one of the best examples of modular organization in neural circuitry. The five main types of retinal neurons are organized into three cell layers. Photoreceptors occupy the outer nuclear layer, bipolar, horizontal, and amacrine cells the inner nuclear layer (INL), and ganglion cells and displaced amacrine cells the ganglion cell layer (GCL). Each principal class of retinal neurons can be divided further into subtypes, which differ in morphology and connectivity as well as biochemical and physiological properties (for review, see Ramon y Cajal, 1892; Rodieck, 1973; Dowling, 1987; Wässle and Boycott, 1991). Within each layer, neurons of the same type are commonly spaced in an orderly manner, forming planar arrays that uniformly tile the retina. Such arrays are known as neuronal mosaics (Wässle and Riemann, 1978) because they bring to mind the regular arrangement of the tesserae of a mosaic.

Although the orderly organization of retinal cells is known to be fundamental to the parallel processing of visual information in the retina, little is known of the way neuronal mosaics form during development. Postmitotic retinal neurons migrate to their final positions from the proliferative neuroepithelium, but known markers for retinal mosaics are expressed only after the cells have attained a regular spatial arrangement (Wässle and Riemann, 1978; Mitrofanis et al., 1988; Vaney, 1990; Casini and Brecha, 1991; Wikler and Rakic, 1991; Hutsler and Chalupa, 1995; Scheibe et al., 1995), making it difficult to understand how such regularity comes about.

Here we report that the transcription factor Islet-1 is an early marker for cholinergic amacrine cells. Islet-1, a member of the LIM homeodomain family known to be involved in vertebrate and invertebrate development (Thor et al., 1991; Ericson et al., 1992; Tsuchida et al., 1994), is detected early in the developing retina and provides a unique opportunity to monitor the assembly of the cholinergic mosaics, comprising two arrays of amacrine cells of great importance for both the visual function (Masland and Tauchi, 1986) and the development of the visual system (Feller et al., 1996).

MATERIALS AND METHODS

Surgical procedures and tissue preparation.Long–Evans hooded rats were bred in the laboratory colony. Embryos of known gestational ages were obtained from animals allowed to mate for 12 hr. The morning after mating was designed as E0. To obtain fetal retinas, pregnant rats were anesthetized with Ketalar (ketamine chlorohydrate; Parke Davis Italia) (50 mg/kg body weight, i.m.) at chosen gestational ages, and their fetuses were dissected out. In some experiments, pregnant animals at 17 d of gestation were injected with 5-bromo-2′-deoxyuridine (BrdU) 2 hr before fixation to label proliferating cells. Animals were killed by decapitation, and their eyes were removed and fixed by immersion in 4% paraformaldehyde in 0.1m sodium phosphate buffer. Retinas were routinely dissected and mounted flat. When necessary, fixed eyes were cryoprotected in 20% sucrose in phosphate buffer overnight, embedded in Tissue Freezing medium (Jung), frozen with liquid nitrogen, and sectioned with a cryostat in 10-μm-thick radial sections.

To determine whether the cholinergic amacrine cells are among the cell types that have recently been shown to disperse tangentially from their clonal columns of origin (Reese et al., 1995), we immunostained whole-mounted adult retinas taken from X-inactivation transgenic mice (Tan et al., 1993) in which 50% of all retinal clones were labeled with the lacZ reporter gene product β-galactosidase. Mice were perfused with physiological saline followed by 4% paraformaldehyde in phosphate buffer. Retinae were dissected whole and then processed for X-gal histochemistry to yield the blue β-galactosidase reaction product, followed by immunohistochemistry using a mouse monoclonal antibody to ChAT (Boehringer Mannheim, Mannheim, Germany).

To distinguish Islet-1⁺ amacrine cells from Islet-1⁺ ganglion cells in the GCL, the optic nerve was transected at birth, which causes ganglion cell degeneration within 48 hr (Perry et al., 1983); alternatively, ganglion cells were retrogradely labeled by injecting 10 μl of a 4% solution of Fluorogold (Fluorochrome, Inc.) in saline in the superior colliculus on postnatal day (P) 0 (for the injection procedure, see Perry et al., 1983). Because it takes at least 36 hr for satisfactory labeling with Fluorogold, we did not analyze the GCL before P1.5.

Immunohistochemistry. 4D5 monoclonal antibody to Islet-1 (1:100), A8 rabbit antiserum against Islet-1 (1:5000; both kindly provided by Dr. T. Jessell, Columbia University), polyclonal anti-ChAT (1:100; Chemicon, Temecula, CA), and monoclonal anti-BrdU antibody (1:75; Boehringer Mannheim) were used. For retinal whole-mount immunohistochemistry, a standard protocol was used, with 4 d incubation in primary antibody and 2 d in secondary antibody (Casini and Brecha, 1991). This was followed by 1 d in avidin–biotin–peroxidase complex (Vector Laboratories, Burlingame, CA) and a subsequent DAB reaction when biotinylated secondary antibodies were used. To determine the correspondence between Islet-1 mosaics and the cholinergic mosaics, Islet-1/ChAT double-labeling experiments were performed by incubating retinas simultaneously in both primary antibodies (the monoclonal 4D5 anti-Islet-1 and the polyclonal anti-ChAT), followed by incubation in both secondary antibodies [biotinylated rat-absorbed anti-mouse IgG (Vector) and fluoresceinated anti-goat IgG (Sigma, St. Louis, MO)] and a final incubation in Extra-Avidin TRITC (Sigma). To define whether Islet-1 cells were all postmitotic, Islet-1/BrdU double-labeling experiments were first performed by immunohistochemistry for Islet-1 [A8 followed by biotinylated goat anti-rabbit and fluoresceinated Avidin (both from Vector)] and then for BrdU as described elsewhere (Galli-Resta and Ensini, 1996).

Data acquisition. Retinae were drawn before and after histological treatment and analyzed only if they had undergone minimal (<5%) shrinkage. Six retinas and 10–20 sampling fields (250 × 160 μm²) per retina, taken at three different eccentricities, were analyzed for each age. Cell positioning data and retinal size were acquired by means of an Image Analyzer (Imaging, Ontario, Quebec, Canada) connected to a Zeiss Axiophot microscope. The total number of labeled cells in a retina was determined by multiplying the retinal area, and the average density of labeled cells was determined in the sampling fields. A Leica TCSNT Confocal Microscope was used to determine colocalization for ChAT/Islet-1 and to analyze potential BrdU/Islet-1 double-labeling in retinal cross sections.

Data analysis. The analysis of the spatial organization of the two Islet-1 mosaics was performed by determining the classic distribution of nearest neighbor distances (Wässle and Riemann, 1978), as well as by studying the tiling of the plane associated with the mosaics. To achieve this, we computed the Voronoi (or Dirichlet) domains associated with the mosaic, which define for each cell the domain containing all of the points in the plane that are closer to that cell than to any other cell in the mosaic. The Delaunay segments, which link cells of adjacent Voronoi domains, were also computed for each mosaic (for more details, see Grumnbaum and Shephard, 1989). Although the distribution of nearest neighboring distances is a good indicator of mosaic regularity (Cook, 1996), it does not fully characterize the two-dimensional structure of an array of cells that we studied by means of the Voronoi domains and Delaunay segments associated with the mosaic cells. Voronoi domains, Delaunay segments, and nearest neighbor distances were computed by a modification of the scientific software described elsewhere (Fortune, 1987), available at the http://netlib.att.com/netlib/voronoi/sweep2.Z. In the computation, Voronoi domains intersecting the sampling frame and nearest neighbor distances of cells closer to the frame than to any cells in the sample were discarded. To analyze mosaic development during the phase of new cell addition, we also computed the expected distributions if newly added cells were randomly positioned within the preexisting mosaic. These distributions were generated in two steps. To model retinal expansion, we first performed an isotropic expansion of the mosaic fields obtained on E21.5 by a factor corresponding to the ratio between the P4 and the E21.5 retinal areas; then as many cells as those that reach the mosaic between E21.5 and P4 [that is, 30% more cells (see Results)] were randomly added to the INL mosaic with the constraint that cells could not physically overlap (i.e., the minimal distance, ordmin, was equal to one cell diameter on P4, which was 5 μm). For the GCL, mosaic fields obtained on P1.5 were expanded isotropically by the ratio between P4 and P1.5 retinal areas, and as many cells as those reaching the mosaic in this interval were randomly added [that is, 20% more cells (see Results)]. For the quantitative analysis of data we used χ² tests for comparison of two sets of data, deriving variances from the experimental data (which had a Gaussian distribution within each histogram bin). For this analysis, adjacent bins were pooled together when necessary to avoid cases with fewer than five events.

Analysis of transgenic retinae. Double-labeled transgenic whole mounts were scanned using a 100× oil immersion objective, and blue (transgene-expressing, or transgene⁺) ChAT⁺ double-labeled cells in the GCL and INL were counted. Each of these double-labeled cells was identified as being positioned within a blue (transgene⁺) or a white (transgene−) column. The latter provide an unambiguous index of the frequency of such cells outside of their clonal territories of origin (Reese et al., 1995), given that all retinal cells descend from multipotent progenitors (Turner et al., 1990). The physical separation of these latter, double-labeled cells situated in transgene-negative columns from the nearest transgene-positive columns was also determined, providing an estimate for the extent of tangential dispersion by these cells (for an equivalent treatment for horizontal cells, see Reese et al., 1995). To compute the number of cells that actually moves tangentially in the transgenic retinae, the percentage of ChAT⁺/transgene⁺(double-labeled) cells situated in transgene-negative columns was determined in two such retinae. Because a tangentially dispersing cell has an equal probability of moving into a blue or a white column in these X-inactivation transgenic retinae, the above percentages have been doubled to derive an estimate of the actual frequency of tangential dispersion (Reese et al., 1995).

Mathematical simulation. Distributions with a lower limit for intercellular distances were generated by randomly positioning one cell at a time in the sampling field, determining its distance from its closest neighbor and eliminating it whenever it was closer to its nearest neighbor than this selected minimal distance. This process was continued as described above, until the simulated distribution reached the same cell density as that of the real mosaic. Such a distribution corresponds to the distribution of spheres of diameter equal to the chosen minimal intercellular distance. Best simulations were obtained if the minimal distance was allowed to vary within a limited range, which corresponds to a more realistic biological constraint, in which minimal distance varies slightly around a mean value. In this case each cell generated in the simulation was left in place if its distance from its nearest neighbor was higher than a variable value drawn from a Gaussian distribution of given mean and width. To compare simulated and real mosaics, we also used Fourier transforms, which would reveal any hidden geometrical pattern. Fast Fourier transforms (FFTs) were generated by applying the FFT algorithm (Brigham, 1974) to each distribution of cells in the 256 × 160 pixel²(1 pixel = 1 μm) frame extracted from each sampling field. For the sake of simplicity each cell was represented as a 1-pixel dot, because this does not affect the relevant portion of the Fourier spectrum.

RESULTS

Islet-1 is expressed by amacrine cells forming two mosaics

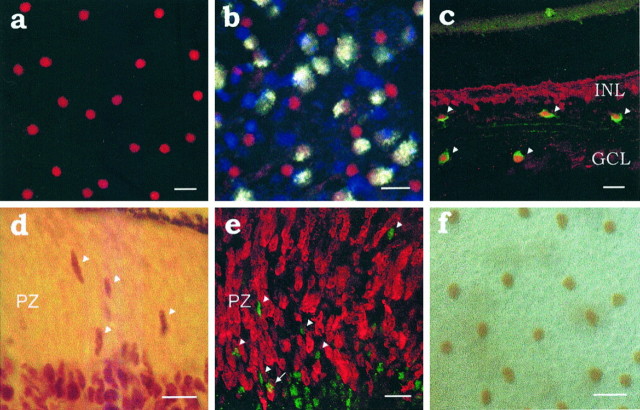
We have found that two mosaics of amacrine cells of the rat retina express the transcription factor Islet-1. One mosaic occupies the inner part of the INL (Fig. 1a), whereas the other is found in the GCL (Fig. 1b), where some ganglion cells also express Islet-1 (Thor et al., 1991). An example is illustrated in Figure 1b, where Islet-1 cells are red and ganglion cells are light yellow, having been retrogradely labeled with Fluorogold. The location of these Islet-1 mosaics, their cell densities, and soma size distributions suggested that they could correspond to the mosaics of cholinergic amacrine cells. This was confirmed by double-labeling experiments in the adult retina using antibodies to both Islet-1 and ChAT (Fig. 1c).

Fig. 1.

a, Islet-1 mosaic in the inner nuclear layer (INL) of a flat-mounted adult rat retina. Scale bar, 20 μm. b, Islet-1⁺(red) cells in the ganglion cell layer (GCL) of the same retina as in a. Ganglion cells, retrogradely labeled with Fluorogold (light yellow), in some cases reveal Islet-1 labeling. Blue patches are salt precipitates that fluoresce when viewed with the filter used for Fluorogold. Scale bar, 20 μm. c, Islet-1⁺ mosaics correspond to the mosaics of cholinergic amacrine cells, as demonstrated by double-immunofluorescence studies in adult rat retina. The figure shows a confocal image of a radial retinal section (perpendicular to the plane in a and b).Arrowheads point to the amacrine cells that are double-labeled for ChAT (green) and Islet-1 (red). All cholinergic amacrine cells are Islet-1⁺ immunoreactive amacrine cells and vice versa. Bipolar cells are also Islet-1⁺ in the adult retina but can easily be distinguished from other Islet-1⁺ cells by their different position in the retina. The retina illustrated has no ganglion cells; these had all been selectively removed by optic nerve section at birth. Scale bar, 20 μm. d, Expression of Islet-1 in the embryonic retina. On E17, Islet-1 (brown) was expressed by cells that were still in the proliferative zone (PZ), as well as by cells that had already migrated to the vitreal side of the retina (bottom), where different layers cannot yet be distinguished at this age. Scale bar, 10 μm. e, Islet-1⁺ cells are all postmitotic. Two hours after BrdU injection, no Islet-1⁺ cell (green, arrowheads) is labeled with BrdU (red), which had been incorporated by proliferating cells. Superimposition of eight optical sections was obtained with a confocal microscope across an overall depth of 10 μm in an E17 retinal section. The only apparent double-labeled cell (arrow) is due to the partial physical superimposition of two cells. PZ is the proliferative zone. Scale bar, 10 μm. f, Islet-1⁺ mosaic in the INL on E21.5. Note the similarity to the adult mosaic. Scale bar, 10 μm. Nomarski optics.

Islet-1 belongs to the family of LIM homeodomain proteins involved in cell fate determination in many different systems (Thor et al., 1991;Ericson et al., 1992; Tsuchida et al., 1994). This led to the expectation that Islet-1 expression could be found early enough in development to provide a tool to study the assembly of the two cholinergic mosaics. Indeed, Islet-1⁺ cells were found both in the proliferative zone and in the region of postmitotic cells lining the vitreal margin of the embryonic retina (Fig.1d). They were all postmitotic, as determined by the absence of any cell that was double-labeled for both Islet-1 and BrdU in the retinae of embryos injected with BrdU to label proliferating cells (Fig. 1e).

Immature Islet-1 mosaics have the same regularity of their adult form and preserve it throughout the time new cells are added

When the the inner portion of the INL became distinguishable within the region of postmitotic cells, it initially contained irregularly spaced Islet-1⁺ cells, comprising both the future INL mosaic cells and many Islet-1⁺ cells migrating toward the GCL (not shown). The mosaic of Islet-1⁺ cells in the INL was first identified 1 d before birth (E21.5) (Fig. 1f), long before any cholinergic marker is detectable (Mitrofanis et al., 1988). It contained two thirds of the cells found in the adult mosaic, but already showed an even intercellular spacing, with a regularity (expressed as the ratio of the mean nearest neighbor distance to its SD) (Wässle and Riemann, 1978) of 4.1 ± 0.2. This value is identical to that found in the adult by us (4.3 ± 0.4) as well as by others (4.4) (Voigt, 1986).

Between E21 and P4 the retina expands, and ∼30% more Islet-1⁺ cells enter the INL mosaic, which contains 24,300 ± 1000 cells on E21.5 and 32,000 ± 1800 on P4, when the adult complement of cells is reached. To monitor how the entry of new cells affected mosaic order, we have studied the tiling of the plane generated by the mosaics throughout this period, as well as the classic distribution of nearest neighboring distances (Wässle and Riemann, 1978). To this purpose, we have examined the distribution of the Voronoi domains, determined by associating to each mosaic cell the domain containing all of the points in the plane that are closer to the cell than to any other cell of the mosaic, and the distribution of Delaunay segments that are segments linking cells of adjacent Voronoi domains (Grumnbaum and Shephard, 1989).

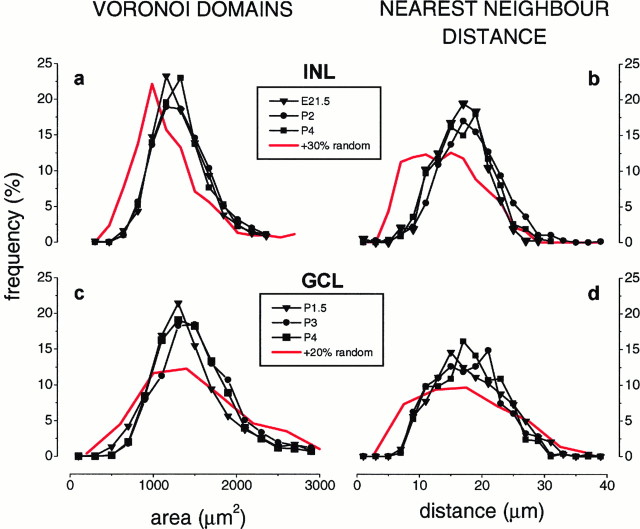
Throughout the period of new cell addition, the statistical distributions of Voronoi domains, nearest neighbor distances, and Delaunay segments associated with the Islet-1 mosaic in the INL remained unchanged, indicating that the mosaic preserved its spatial organization during the period of retinal expansion and Islet-1⁺ cell addition. These results are illustrated in Figure2a,b for the Voronoi domains and the nearest neighbor distance. The red lines in Figure2a,b show the expected final distributions if cells entering the mosaic between E21.5 and P4 were randomly positioned.

Fig. 2.

Islet-1 mosaics preserve their spatial organization while new cells are added. a, Voronoi domains and (b) nearest neighbor distances of the INL mosaic on E21.5 (triangles), P2 (circles), and P4 (squares). No change with time is observed in the normalized histograms, although ∼30% more cells enter the mosaic between E21.5 and P4. When experimental variation is considered (not shown), the P4 distribution represents a fit for the E21.5 distribution, with p > 0.99 for the nearest neighbor distance and p > 0.95 for the Voronoi distribution, as determined by χ² test.Red lines represent the distributions expected if the newly arrived cells were randomly added to the E21.5 mosaic. The difference between the P4 mosaic and the expected distribution in the case of random addition is statistically significant (χ² test; p < 0.001). No change with time was also observed in the distribution of Delaunay segments (not shown). c, Normalized histograms of Voronoi domains and (d) nearest neighbor distances for the GCL mosaic of Islet-1⁺ cells. P1.5 (triangles), P3 (circles), and P4 (squares). Approximately 20% more cells are added to the Islet-1 mosaic of the GCL between P1.5 and P4 (24,000 ± 2000 on P1.5; 29,000 ± 1300 on P4), but the two distributions remain more regular than the expected distribution (red lines) if the 20% additional cells were randomly inserted in the GCL mosaic between P1.5 and P4. Although the mean of the distributions obtained for the random addition of cells (red lines) is the same as that for the real data in the case of Voronoi areas, the SD is larger, and the difference between the real and simulated distribution is statistically significant (p< 0.00001, as determined by χ² analysis). Note that the two Islet-1 mosaics have the same minimal Voronoi area (compare a and c) and the same minimal intercellular spacing (compare b and d), although the regularity of the GCL mosaic is lower than that of the INL.

The second mosaic of Islet-1⁺ amacrine cells, located in the GCL, was studied from P1.5 onward. To be able to distinguish Islet-1⁺ amacrine cells from Islet-1⁺ ganglion cells in the GCL, we either severed the optic nerve at birth, which causes ganglion cell degeneration within 48 hr (Perry et al., 1983), or injected retrograde tracers in the superior colliculus. On P1.5 the Islet-1 mosaic of the GCL contained ∼80% of the cells found in the adult, but already showed a regularity of 2.9 ± 0.3, as is found in the adult mosaic (Voigt, 1986). After P1.5, 20% more cells were added to the GCL mosaic, producing the adult complement by P4. While new cells were being added, the Voronoi domain (Fig. 2c), the Delaunay segment (not shown), and the nearest neighbor distance (Fig.2d) distributions associated with the GCL mosaic remained largely unchanged, indicating that the GCL mosaic preserved its spatial organization. The expected distributions, if these newly arriving cells were randomly positioned, are illustrated for comparison by the red lines in Figure 2c,d.

In conclusion, immature Islet-1 mosaics had the same regularity of their adult forms and preserved it throughout the period of new cell addition, indicating the existence of an active control of regular cell positioning. In this respect, it is interesting to consider that the distributions associated with the two Islet-1 mosaics did not vary with eccentricity at the ages tested (not shown), and that both mosaics displayed the same minimal Voronoi area (compare a andc) and the same minimal intercellular spacing (compareb and d), although the regularity of the GCL mosaic was always lower than that of the INL.

Spatial ordering is not achieved at the time of terminal mitosis

To understand whether mosaic regularity reflects a spatial order that cells possess before reaching the mosaic layer, we analyzed the spacing between neighboring Islet-1⁺ cells before entry into the mosaic. This analysis required that a single population of migrating Islet-1 amacrine cells could be identified selectively, which was impossible in the proliferative zone where one could not discriminate between cells destined to enter separate mosaics. We therefore studied cells migrating through the inner plexiform layer (IPL) toward the GCL (Fig.3a), to examine only the population of Islet-1⁺ amacrine cells destined for the GCL. As mentioned before, some ganglion cells are also Islet-1⁺; however, several studies have documented the later migration of amacrine cells with respect to synchronously born ganglion cells, so that after P0 only amacrine cells are still migrating through the IPL in the central retina (Perry et al., 1983;Reese and Colello, 1992; Galli-Resta and Ensini, 1996). Thus nearest neighbor analysis was conducted after P0 in radial sections by sampling only these central retinal regions.

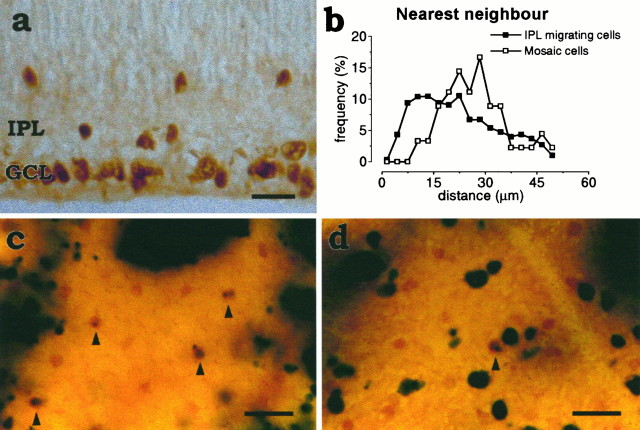
Fig. 3.

a, Islet-1⁺cells crossing the IPL have no minimal intercellular spacing. Cross section of a P1 retina. The spacing between Islet-1⁺amacrine cells migrating through the inner plexiform layer (IPL) was studied after P0 in the central retina, where the migration of ganglion cells that also express Islet-1 has ceased by this time. Scale bar, 10 μm. b, Lack of regular intercellular spacing between Islet-1 cells that are still outside the GCL mosaic. Normalized histogram of nearest neighbor distances between Islet-1⁺ cells in the IPL (filled squares) in P2 retinal sections. The histogram shows that the only limit to the spacing between Islet-1⁺ cells migrating through the IPL is the diameter of the cell, simply reflecting the fact that two cells cannot occupy the same physical space. The nearest neighbor distribution in the INL derived from the same sections (open circles) is shown as a comparison, because the minimal spacing is the same in both Islet-1 mosaics. As should be expected, the normalized distributions of nearest neighbor distances computed in sections and flat-mounted retina have the same minimal spacing but different tails, because the nearest neighbor in sections can be farther away (but, of course, never closer) than the real nearest neighbor in the mosaic. Counts were made in 30 randomly selected P2 sections from two retinae (n = 2).c, Retinal whole mount from an X-inactivation transgenic mouse showing a portion of the INL. Arrowheads point to four mosaic cells (brown; ChAT-immunoreactive) that are transgene-positive (blue) but are displaced in transgene-negative columns. These cells must be derived from neighboring transgene-positive clones. d, A portion of the ganglion cell layer showing one transgene-positive mosaic cell (arrowhead) and several transgene-positive ganglion cells (the largest cells in the field) in a transgene-negative column. These cells must have moved tangentially away from their clone of origin. Scale bar, 20 μm.

We have found that neighboring Islet-1⁺ cells crossing the IPL could frequently be found side by side in the central retina, as illustrated in Figure 3a. Consequently, the distribution of nearest neighboring distances for Islet-1⁺ cells crossing the IPL lacked the minimal intercellular distance characteristic of the elements of the mosaics (Fig. 3b). This indicates that Islet-1⁺amacrine cells attain their characteristic spacing only once they enter the mosaic layers.

Clonal territory analysis in X-inactivation transgenic mice reveals lateral movement of mosaic cells

We know from previous studies that certain types of retinal neurons become displaced tangentially from their clonal columns of origin, and it has been suggested that this tangential dispersion contributes to the formation of orderly retinal mosaics (Reese et al., 1995). To investigate whether ChAT amacrine cells are included in these populations of tangentially dispersing cells, we analyzed these two ChAT mosaics in X-inactivation transgenic mice, where lateral movement of cells could be revealed. Hemizygous female mice, which have thelacZ reporter gene integrated on one of the two X chromosomes, randomly inactivate one of the two X chromosomes before the formation of the optic vesicle, and their retinae in adulthood therefore express the lacZ product β-galactosidase in the clones of only 50% of the population of retinal progenitors. Previous studies have shown that most of the cells in these clones are aligned in radial columns, but a minority of retinal cell types were displaced tangentially from those radial columns (Reese et al., 1995). We found here that tangentially displaced cells include the ChAT-immunoreactive amacrine cells situated in the INL and GCL (Fig. 3c,d). Such transgene-positive cells situated in transgene-negative columns indicate a tangential dispersion from their clonal column of origin (Tan et al., 1993; Reese et al., 1995). In the case of ChAT amacrine cells, 70% of the cells in the INL and 90% of the cells in the GCL are dispersed tangentially, remaining within 30 μm of their clonal column of origin. Thus, short distance lateral displacement is the likely means by which cells attain positions compatible with mosaic regularity.

Short-range cellular interactions are sufficient to generate the Islet-1 mosaics

How cells “know” whether a given position is compatible with mosaic regularity remains unknown, but mathematical analysis provides some important clues. We have found that Islet-1⁺mosaics are indistinguishable from random distributions of the same density where neighboring cells could not be closer than a fixed minimal distance of 15 ± 2 μm.

The experimental distributions of Voronoi domains and Delaunay segments associated with the simulated distributions were the same as those associated with the real mosaic, as shown qualitatively in Figure4a–c, where the Voronoi domains associated with the real mosaic (Fig. 4a) are shown together with those associated with the simulated distribution (Fig. 4b), and for comparison are shown with those of a pure random distribution (Fig. 4c). In further support of this model, the FFTs, which would reveal any hidden geometrical patterns, were the same for the experimental and the simulated mosaics within a 10% error (Fig.4d–f).

Fig. 4.

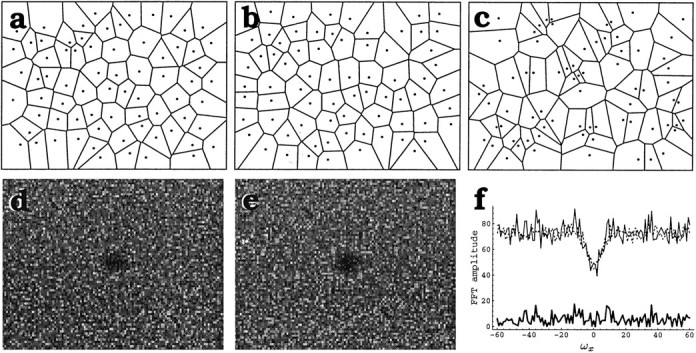
Islet-1 mosaics are indistinguishable from random distributions generated by imposing a minimal distance of 15 ± 2 μm between neighboring cells. a, A field of the INL Islet-1 mosaic is illustrated (dots represent cells) together with the tiling of the plane that it generates (Voronoi domains). b, Tiling of the plane arising from a random distribution of cells (random_dmin) that was generated, imposing a lower limit (dmin = 15 ± 2 μm) to the distance between neighboring cells. Cell density is identical to that of the Islet-1⁺ mosaic shown in a. c, Tiling generated by a random distribution of cells at the same cell density as ina. d, e, Fast Fourier Transform (FFT) of the Islet-1 mosaic (d) and the random_dmindistribution (e). FFTs are represented as amplitude maps and illustrated in the intervals ω_x ∈ (−60,60 μm⁻¹), ω_y ∈ (−40,40 μm⁻¹). The center of the figure is the center of the coordinates. In both cases the phase distributions are random. The FFTs of the real and simulated mosaic are nearly identical, which is also illustrated in f(top), where a horizontal section throughd (continuous line) and e(dotted line) at the midline are shown.Bottom, Difference between the amplitude of the two FFTs at the section level, illustrating that the two FFTs differ by no more than 10%.

These results indicate that short-range cellular interactions that prevent cells from getting closer than 15 ± 2 μm to one another are sufficient to generate the regularity of Islet-1 mosaics.

DISCUSSION

We have shown that two mosaics of amacrine cells express the transcription factor Islet-1 before their assembly is complete. As soon as Islet-1 mosaics can be identified, they show the same regularity of their adult form, and preserve it throughout the time new cells are added. Migrating Islet-1⁺ cells do not show this spatial ordering, indicating that they must move tangentially as they enter the mosaic, under the action of local mechanisms. Clonal territory analysis in X-inactivation transgenic mice confirms the lateral displacement of these cells away from their clonal columns of origin, and mathematical models show that a local rule forcing cells to stay at a minimal distance of 15 ± 2 μm from one another is sufficient to assemble Islet-1 mosaics.

Islet-1 is expressed by the elements of two mosaics of amacrine cells before mosaic assembly is complete

A number of previous studies have analyzed the development of retinal mosaics, but all relied on markers that are expressed by cells only after they have entered their mosaics, making it difficult to understand how regularity comes about (Wässle and Riemann, 1978;Mitrofanis et al., 1988; Vaney, 1990; Casini and Brecha, 1991; Wikler and Rakic, 1991; Hutsler and Chalupa, 1995; Scheibe et al., 1995). Here we could follow the assembly of two mosaics of amacrine cells that express the transcription factor Islet-1 early in development, because Islet-1 expression appears in postmitotic cells before they migrate to their final position.

Islet-1⁺ amacrine cells in the adult retina express ChAT immunoreactivity, but the appearance of orderly arrays of Islet-1⁺ amacrine cells precedes by more than 2 weeks the first detectable immunoreactivity for ChAT in the rat retina (Mitrofanis et al., 1988). An incomplete but regular mosaic of Islet-1 amacrine cells was first observed in the INL on E21.5, 1 d after the last mosaic cells were generated (Reese and Colello, 1992). According to the present estimates for the rate of cell migration (100 μm/d) (Jacobson, 1991), these newly generated cells should take at least 2 d to reach the INL. Thus, the growth of the mosaic after E21.5 reflects the migration of new cells into the mosaic layer, rather than the simple appearance of Islet-1 expression in cells that were already in the mosaic layer. Direct studies of the migration of BrdU-labeled cells in the retina confirm that cells born on E20, like the last generated mosaic cells, cannot reach the mosaic layers within 1.5 d (L. Galli-Resta, unpublished results). Indeed, migrating Islet-1⁺ cells were seen in the proliferative zone below the INL for several days after the INL mosaic was first analyzed (not shown).

Regularity is an intrinsic property of Islet-1 mosaics, dynamically preserved while new elements are added into the mosaics

Mathematical analyses show that both Islet-1 mosaics have an intrinsic regularity, which is the same found in the mature mosaics and is preserved throughout the time new cells are added. This was determined by monitoring mosaic regularity by means of the classic method of nearest neighbor distance, as well as by analyzing the tiling of the plane associated with the mosaics, described by the Voronoi domains, which assign to each cell the region of the plane containing the points closer to that cell than to any other cell of the mosaic. Although Voronoi domains are a pure geometrical abstraction, their biological significance should not be underrated. The Voronoi domain is the field the cell controls if all mosaic cells secrete some factor, and it is also the minimal region over which the dendritic tree of the cell should extend to ensure a complete tiling of the plane by the mosaic of dendritic fields. Thus, the constancy of the Voronoi domains associated with Islet-1 mosaics during development reveals the constancy of the biological interactions that underlie mosaic formation.

Clonal boundary analysis in X-inactivation transgenic mice reveals that lateral displacement is the likely means by which mosaic regularity is established

New Islet-1⁺ cells are not regularly spaced before their entry into the mosaic, indicating that an orderly spacing of Islet-1⁺ amacrine cells is not established at the time of terminal division or at the time of commitment to the Islet-1⁺ status. Indeed, because the genesis of mosaic cells destined to occupy the same retinal region occurs over several days (Reese and Colello, 1992) while the retina expands, it is difficult to imagine that all new cells could migrate to a position compatible with mosaic regularity only by radial migration, especially those cells that have to be woven into regions where other mosaic cells are already present. Analysis in X-inactivation transgenic mice, in which tangential cell displacement can be detected, shows that nearly all ChAT amacrine cells undergo tangential migration, that is, movement parallel to the plane of the mosaics. Thus, although we do not exclude that death of misplaced cells also contributes to the maintenance of mosaic regularity, lateral movement parallel to the mosaic layer is the likely means by which cells acquire appropriate positioning in the mosaics. This interpretation is strengthened by the observation that only cells that establish orderly arrays in the mature retina show tangential displacement in X-inactivation transgenic retinae (Reese et al., 1995).

Short-range interactions are sufficient to assemble the Islet-1 mosaic

The central biological question of how cells “know” where to go remains unsolved; however, the absence of order between Islet-1⁺ cells before their entry in the mosaics suggests that local mechanisms account for the appropriate positioning of the mosaic cells. By mathematical modeling we have shown that simulated distributions of cells that are constrained only by a minimal intercellular distance of 15 ± 2 μm are indistinguishable from the real Islet-1 mosaics. These correspond to random distributions of spheres of diameter 15 ± 2 μm. Because Islet-1⁺ cell bodies are only ∼4 μm in diameter at the ages studied (Fig. 1f), this model suggests a mechanism by which cells can exclude other cells in their layer from a minimal circular area of ∼π((15 ± 2)/2)²μm² around them. Whether this is achieved by contact inhibition between developing dendritic trees or by other means remains to be determined; mathematical modeling indicates only that this type of local mechanism can generate the mosaics, not that it actually does so.

Random distributions with a lower limit for intercellular distance may seem poor modular structures, but they offer considerable advantages. They can be generated entirely by local interactions, require a minimal building rule, are extremely tolerant to assembling errors, and can ensure a uniform sampling of space, a fundamental requirement for the formation of modular circuits. Furthermore, their regularity is not considerably altered by the random elimination of a limited number of cells (as could be the case with cell death), and their extent can easily be increased by the addition of new elements, a mechanism largely exploited in evolution (Rakic, 1995). All of these considerations suggest that a short-range mechanism like contact inhibition might be the biological rule accounting for Islet-1 mosaic formation, a possibility currently being explored.