Regulation of Neuroblast Cell-Cycle Kinetics Plays a Crucial Role in the Generation of Unique Features of Neocortical Areas

Abstract

Cortical neurons are generated in the germinal zones lining the ventricles before migrating predominantly radially. To investigate regional differences in the cell-cycle kinetics of neuroblasts, pulse [³H]-thymidine injections were made throughout corticogenesis, and labeled neuron counts were compared in areas 3, 6, 17, and 18a in the adult mouse. The relationship between height in the cortex and intensity of autoradiographic signal distinguishes first generation and subsequent generations of neurons. This provides the mitotic history of defined sets of neurons and is a powerful tool for analyzing areal differences in cell-cycle kinetics. The infragranular laminar labeling indices of different generations show significant differences in areas 3 and 6. The labeling index of first generation neurons shows that the rate of neuron production is higher in area 3 than in area 6. This increased generation rate in area 3 was accompanied by two major changes. First, computation of the labeling index of the subsequent generation neurons (which reflects percentages of precursors in S-phase at the moment of the pulse) indicates a shorter cell cycle in area 3. Second, the total population of labeled neurons contains a higher proportion of first generation neurons in area 3, implying a higher leaving fraction in this area. Computer simulations of these areal differences of cell-cycle kinetics generate neuron numbers that are in close agreement with published data. Altogether these findings reveal an early regionalization of the ventricular zone that serves to generate unique features of future cortical areas.

Use of [³H]-thymidine as an S-phase marker makes it possible to determine the timing of the final round of mitosis of cortical neurons (Angevine and Sidman, 1961; Rakic, 1976; Caviness, 1982; Luskin and Shatz, 1985; Miller, 1985). In the mouse, this shows that the frontoparietal areas 3, 4, and 6 have marked interareal differences in the timetables of layer formation (Polleux et al., 1997). The aim of the present study is to determine whether precursors of future cortical areas also differ in their cell-cycle kinetics as has been shown in the generation of monkey areas 17 and 18 (Dehay et al., 1993). If this were to be the case, then a spatial mosaic of proliferative programs could be a fundamental feature in the generation of cortical areas (Rakic, 1988).

To investigate the proliferative behavior of neuronal precursors, we injected an S-phase marker at different fetal stages and examined the intensity of autoradiographic labeling and the distribution of the cohorts of labeled neurons in the adult cortex (Schultze et al., 1974;Brückner et al., 1976). This makes it possible to describe the mitotic history of precisely defined neuronal populations (Sidman, 1970). This cannot be achieved by S-phase marker studies in the ventricular zone (Fujita, 1960; Waechter and Jaensch, 1972; Schmahl, 1983; Takahashi et al., 1995, 1996), because such studies will be measuring the proliferative behavior of a heterogeneous population of precursors that includes a significant amount of proliferating radial glial cells (Misson et al., 1988a,b; Johnston and van der Kooy, 1989;Gressens et al., 1992; Soriano et al., 1995).

[³H]-thymidine pulse labeling of cortical precursors leads to an inside-first outside-last pattern of laminar histogenesis in the adult cortex (Angevine and Sidman, 1961). Each division after the pulse reduces label in daughter cells so that quantification of grain counts indicates the successive generations in the adult cortex (Smart and Smart, 1977, 1982). We have developed an analytical procedure for identifying labeling threshold criteria that (1) shows that there is a halving of label at each division and (2) makes it possible to distinguish each of the first five generations. The relative percentages of first (FG) and subsequent generation (SG) neurons provide a powerful tool for analyzing cell-cycle kinetics of neuronal precursors. By comparing percentages of labeled neurons we eliminate the possibility that developmental cell death contributes to observed areal differences, because labeled and unlabeled neurons share common rates of cell death. The percentage of FG neurons defines a generation index that enables us to quantify rates of neuron production (Rakic, 1973; Carter-Dawson and LaVail, 1979; Mustari et al., 1979;Reznikov, 1990; Valverde et al., 1995; Polleux et al., 1997). This shows that area 3 is characterized by a higher rate of neuron production than area 6 during the generation of infragranular layers. Proportions of SG neurons enable us to analyze the cell-cycle parameters that underlie this increased generation rate in area 3. This shows that it is the consequence of (1) a shorter cell-cycle duration and (2) more frequent differentiative divisions.

Computer simulations of cortical neurogenesis using the areal differences in cell-cycle parameters found in the present study generate realistic neuron numbers characterizing frontal and parietal areas. These results suggest that regionalization of proliferative programs in the ventricular zone serves to generate unique features of cortical areas such as cytoarchitecture.

MATERIALS AND METHODS

Histology and autoradiographic procedure. Ten timed-pregnant BALB/C mice received a single intraperitoneal injection of [methyl-³H]-thymidine (Amersham, Braunschweig, Germany) (specific activity: 25 Ci/mmol, dose-injected, 5 mCi/gm body weight) at different gestational ages [from embryonic day (E) 11.5 to E19.5]. All females were put in the presence of males overnight, and the day when a vaginal plug was found was designated E1. All [³H]-thymidine injections were performed between 12:00 and 2:00 P.M. to overcome problems linked to circadian variations of proliferative activity (Miller, 1992). Pups were delivered and were killed at adulthood by a lethal injection (intraperitoneal) of sodium pentobarbital. Animals were perfused transcardially with a pH 7.4 saline solution [0.9% in 0.1 m phosphate buffer (PB) with 1 g/l Procaine] followed by a solution of 4% paraformaldehyde in 0.1m PB.

The brains were removed, post-fixed in the same solution for 2 d, rinsed in running tap water overnight, dehydrated by immersion in graded ethanol solutions (70–100%), and cleared in toluene. The brains were embedded in paraffin, cut serially (10 μm), and mounted on glass slides with a 5% albumin–gelatin mixture. One in six sections were dewaxed, rehydrated, air-dried, and dipped in autoradiographic Ilford K2 emulsion (45% in distilled water at 40°C). Sections were stored in a desiccating box for an exposure period of 6–8 weeks (4°C), developed with Ilford PQ Universal (10%, 19°C, 6 min), and fixed with Ilford Ilfospeed (20%, 20°C, 5 min). The sections were rinsed, air-dried, and counterstained with Cresyl violet (0.1%, 7–8 min).

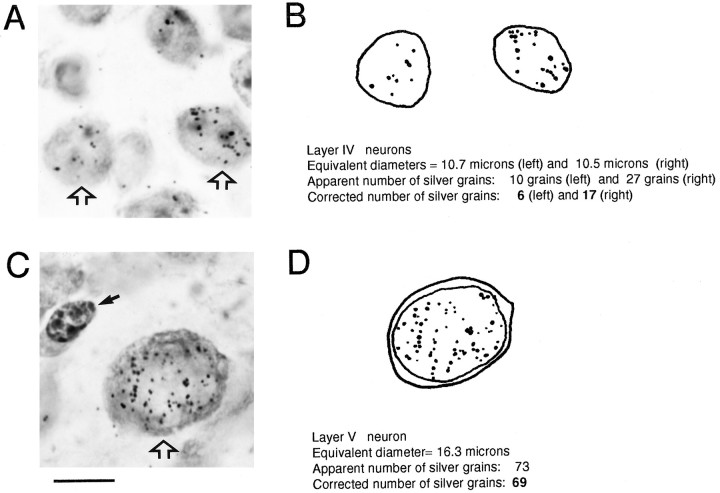
Quantification of autoradiographic signal. Exposure time was adjusted to ensure optimal blackening levels, which minimizes the problem of fused grains (Dörmer, 1967; Rogers, 1967; Dörmer and Brinkmann, 1968; Dörmer and Möller, 1968; Sidman, 1970). This is illustrated for individual neurons in different layers of parietal area 3 after injection on E14.5 (Fig.1). The background level has been estimated by calculating the density of silver grains in extracellular space and in all cases was inferior to one grain per 400 μm² (i.e., much lower than one silver grain per mean neuronal profile surface ∼250 μm²). In the present study, we consider neurons that present two or more silver grains over the nucleus as being labeled.

Fig. 1.

Autoradiographic signal on neurons in parietal area 3 in layer IV (A, B) and layer V (C, D) after injection on E14.5. A–C, High-power photomicrographs of labeled neurons showing different autoradiographic intensities. B–D, Outlines of the cell body and nuclear profiles showing individual silver grains detected by visual inspection at different focal depths. Note the low level of autoradiographic background. Small solid arrow in C: glial cell; open arrows: neurons of interest. Scale bar, 10 μm.

Detailed plots of different categories of labeled cells were made by means of a light microscope (Dialux 20, Leitz, Wetzlar, Germany) coupled to an interactive system of plotting (Microvid, Leitz), piloted by Histovid software (BIOCOM). Radial strips (500 μm wide) of cytoarchitectonically identified neocortical areas (Polleux et al., 1997) were drawn with a final magnification of 157 using an image projected on a VGA BARCO screen (CD 233) captured by a CCD COHU camera. The maximal number of silver grains per nucleus profile was estimated for each brain. Grains were counted over nuclear profile with a 50× oil objective and a final magnification of 3140. Grain counts were corrected for apparent diameter using the Appleton correction (Appleton et al., 1969). This correction is required, because in the case of two nuclei presenting different diameters and containing the same amount of labeled tritium, the number of silver grains overlying the small nucleus is artificially higher than for the large nucleus. This is because a section of constant thickness will represent a larger proportion of the total volume of a small nucleus than it does in a large nucleus (Appleton et al., 1969). The correction can be defined as:

$$N_{\text{corr}}=N_{\text{obs}}\times \frac{D_{\text{obs}}}{D_{\text{Nmax}}}$$

where N_corr is the corrected number of silver grains and N_obs is the observed number of silver grains. D_obs andD_Nmax are the equivalent diameters of the observed nucleus and the nucleus presenting the maximal labeling intensity, respectively (Appleton et al., 1969; Clark et al., 1990). Figure 1 illustrates the important variations of the apparent diameter of nuclei in different layers and points to the need to correct raw counts of numbers of silver grains for the diameter to estimate the labeling intensity characterizing each nucleus. Although the maximal number of silver grains varies between litters (range, 34–81), this number is remarkably constant within a given litter (maximum range, 4%). Neurons were distinguished from glial and endothelial cells using the criteria described by Heumann and Leuba (1983) (see Fig. 1).

Quantification of proportions and radial distributions of different categories of labeled neurons. Numbers of neurons showing heavy (FG neurons, >50% maximum labeling) and weak (SG neurons, <50% maximum labeling) labeling were counted in each layer in all four areas on two nonadjacent sections in two to three animals. Proportions of FG neurons were estimated with respect to the total number of labeled and unlabeled neurons (T) plotted in 500-μm-wide strips of cytoarchitectonically identified areas (Polleux et al., 1997). The labeling index (SG/T) and the generation profiles (ratios of number of first, second, third, and fourth generation neurons) were calculated in 200-μm-wide strips.

Except for generation profiles (see below), areal comparisons are performed between homologous layers and therefore concern cell populations of comparable dimensions (Beaulieu, 1993) so that counts did not have to be corrected for splitting errors. One possible source of error is the estimation of the population of unlabeled cells attributable to incomplete Nissl staining. In the present study, staining procedure and section thickness ensured optimal staining (Cooper et al., 1988).

The distance of the labeled nucleus from the white matter/gray matter limit was expressed as a percentage value of the cortical height and used to quantify the radial distribution of different categories of labeled neurons. We have used a box (or whisker) plot analysis (Tukey, 1977) to quantify the radial distribution of categories of neurons showing different intensities of labeling. This representation uses five different centile values [10th, 25th, 50th (the median), 75th, and 90th centiles]. Each box plot was prepared from the cumulative labeling over four to eight sections. For a given variable, if the 90th centile equals 87, it means that only 10% of the measured values are superior to 87. A nonparametric Kolmogorov–Smirnov test was used to compare pairs of distributions (i.e., for comparisons made between the adjacent categories of labeled cells as illustrated in Figs.2 and 3 or between first generation vs second, second generation vs third, etc., see Fig. 3).

Fig. 2.

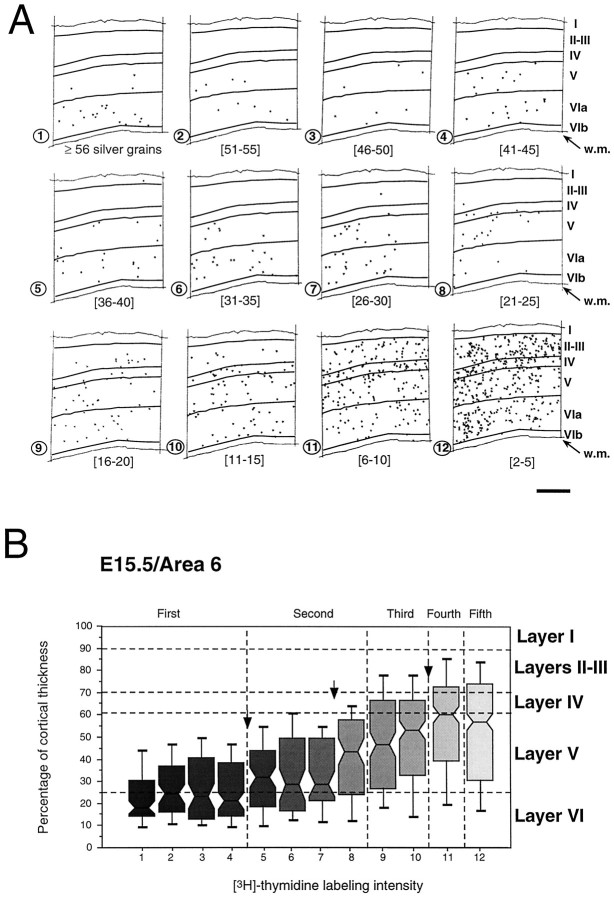
Influence of intensity of neuron labeling in area 6 on radial location after an injection of [³H]-thymidine at E15.5. A, Each panel shows the radial distribution of a category of labeled neurons defined by the numbers of silver grains per nucleus. B, Box plots of intracortical depth of different categories of labeled neurons. Each numbered group corresponds to a panel inA. This analysis has been performed on 1377 labeled neurons in six nonadjacent sections taken from two different mice from the same litter. For each box plot the top andbottom thick lines indicate, respectively, the 90th and the 10th centiles. Horizontal lines composing each box represent the 75th (bottom), 50th (median), and 25th (top) centiles. Scale bar, 300 μm. Arrows indicate statistically significant (p < 0.05) thresholds revealed by a Kolmogorov–Smirnov nonparametric test of adjacent distributions.Vertical dashed line: 50%, 25%, 12.5%, and 6.25% of maximum labeling.

Fig. 3.

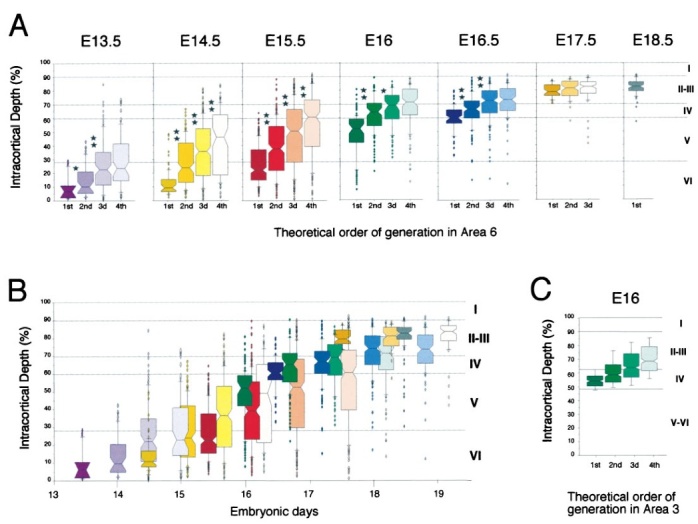
Radial location of separate generations after a single [³H]-thymidine pulse injection.A, Laminar location of the first four generations of neurons in area 6. Dots overlying each histogram indicate the radial position of individual neurons that form the 10% tails of each distribution. Stars indicate the statistical significance of the comparisons of adjacent distributions (Kolmogorov–Smirnov nonparametric test: *p < 0.05; **p < 0.01). B, Published cell-cycle duration indicates theoretical birthdate of each generation shown in A and is used to rank individual generations in chronological order. C, Radial deployment of successive generations in area 3 after injection of [³H]-thymidine on E16.

The determination of FG/T was based on the quantification of the autoradiographic labeling intensity of >150,000 neurons in areas 3 and 6 and 130,000 neurons in areas 17 and 18a. SG/T ratios were based on the quantification of the autoradiographic labeling of 88,000 neurons in areas 3 and 6 and 60,000 neurons in areas 17 and 18a. Generation profiles and leaving fraction (LF) were based on 6000 neurons in areas 3 and 6 and 3000 neurons in areas 17 and 18a. Statistical analysis was performed using Statview 4.02 software. Most of the parameters described in this study consisted of proportions of neurons, and the statistical significance of the results was examined by means of a χ² analysis. Variability in proportions from each section for a given injection (inner group comparisons) was tested and failed to show any statistical significance.

We have elaborated a mathematical model of cortical neurogenesis that has been programmed as an interface using Matlab software (version 4.2C.1; Mathworks Products). This compartmental model [see (Quastler and Sherman, 1959; Godfrey, 1983)] is used to simulate the dynamics of neuron production during cortical neurogenesis. The model consists essentially of ordinary differential equations (ODE) in which time is the independent variable. Matlab provides functions for the numerical solutions of ODE. These functions use automatic stepsize Runge–Kutta–Fehlberg integration methods.

RESULTS

Identification of successive generations within the cohort of neurons labeled by a single pulse makes it possible to define rates of neuron production and to monitor those changes in cell-cycle parameters that influence the rate of neuron production.

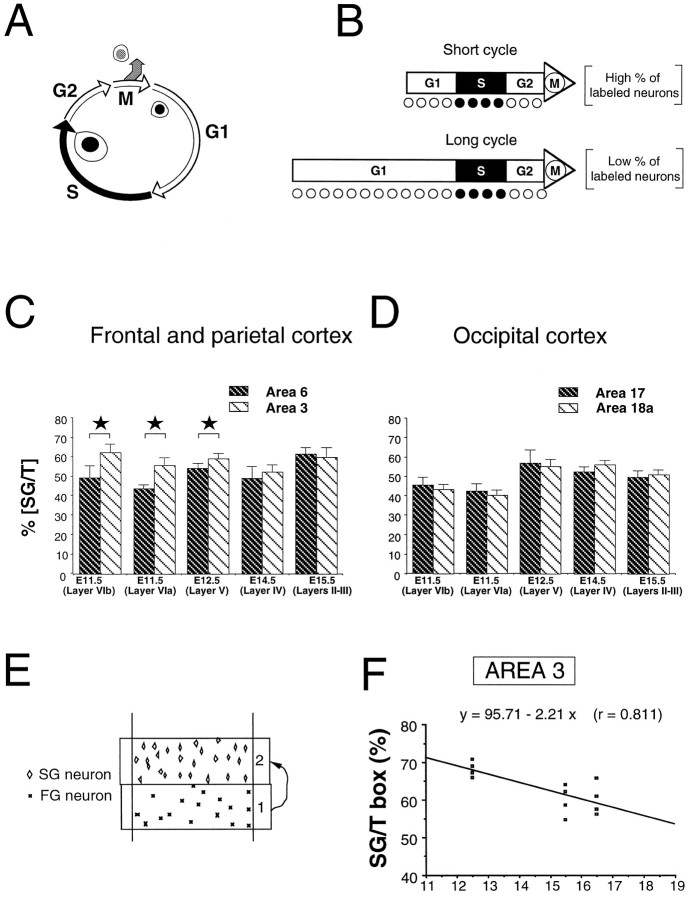
First is the mode of division. The two daughter cells resulting from mitosis either can remain proliferative (proliferative division) or one or both can quit the cell cycle (differentiative division) (Fig.6A). The higher the frequency of differentiative divisions, the higher the leaving fraction (LF) (Rakic, 1977; 1988;Miller, 1988; Takahashi et al., 1996). In the present study, we detect areal differences in LF by detecting differences in the ratio of FG to SG neurons (Rakic and Sidman, 1968; Miller, 1988).

Fig. 6.

Changes in the labeling index and duration of the cell cycle. A, Different phases of the cell cycle.B, Incidence of changes in the length of the cell cycle on labeling index. S-phase has been shown to remain fairly constant throughout cortical neurogenesis so that an S-phase marker will label a high proportion of precursor cells when the cell cycle is short and a low percentage when it is high. C, Labeling index (SG/T) in the cortical layer immediately above FG neurons in areas 3 and 6.D, Labeling index (SG/T) in cortical layer immediately above FG neurons in areas 17 and 18a. E, SG/T in a restricted zone immediately above the FG neurons. F, SG/T values obtained in area 3 at E12.5, E15.5, and E16.5 using the approach illustrated in E. Individual points indicate values obtained on four nonadjacent sections taken from two animals at each age of injection. At E15.5 and E16.5, there is a significant decrease in SG/T compared with E12.5 in area 3 as shown by the negative slope of the regression line. This is compatible with the developmental decrease of labeling indices found at these stages in the ventricular zone (see text). Statistical analysis: *p < 0.05, according to a χ² analysis.

Second is the duration of the cell cycle (Tc). S-phase is relatively invariant during cortical neurogenesis, and variations in the Tc are mostly attributable to G1 modification (Kaufmann, 1968; Waechter and Jaensch, 1972; Hoshino et al., 1973; Schultze et al., 1974; Korr, 1980; Schmahl, 1983; Miller and Kuhn, 1995; Reznikov and van der Kooy, 1995; Takahashi et al., 1995). Variations in theTc lead to a variation of the percentage of precursors in S-phase so that after a pulse, short Tc values result in high labeling indices and long Tc values result in low labeling indices (Fujita, 1967; Waechter and Jaensch, 1972) (Fig.6B). In the present study we can detect variations inTc by monitoring changes in the labeling index of SG neurons (Schultze et al., 1974; Brückner et al., 1976).

Relationship of intensity of autoradiographic labeling and order of generation

In the present study we need to reliably determine the threshold between FG and SG neurons. By identifying each of the first five generations of labeled neurons after a pulse of [³H]-thymidine, we are able to show that there is actually a halving principle at each round of mitosis.

The cohort of labeled neurons that quit the cell cycle during the first round of mitosis after the [³H]-thymidine pulse will show maximum levels of labeling (FG neurons). The cohort of labeled precursors that continue to cycle reduce their radioactivity at each subsequent round of division (Hughes et al., 1958; Appleton et al., 1969; Korr, 1980) and give rise to successively weaker labeled neurons (SG neurons).

Theoretically therefore, the intensity of autoradiographic signal could provide an indication of the order of generation after a pulse injection (Bisconte and Marty, 1975b). A number of artifacts, however, are liable to blur this distinction. (1) Precursors at the beginning or end of S-phase at the moment of the pulse have a reduced uptake of the labeled nucleotide (Fig. 13). This will result in a contingent of FG neurons being weakly labeled (Bisconte and Marty, 1974, 1975a; Gray et al., 1981; Clausen et al., 1985; Naito et al., 1987). (2) Death of precursors leads to a liberation of [³H]-thymidine metabolites that could be available for secondary uptake and labeling (Feinendegen, 1967; Sidman, 1970; Korr, 1980; Reznikov and van der Kooy, 1995). (3) There are FG neurons with high [³H]-thymidine uptake that are artifactually lightly labeled because the nucleus is too deep in the section, thereby reducing the effective interaction of the radioactive particles with the surface emulsion layer (Rogers, 1967; Sidman, 1970). Because the combined influence of these factors is to artificially increase the proportion of lightly labeled neurons, we need to examine to what extent the intensity of labeling effectively distinguishes successive generations of labeled neurons after a single pulse of [³H]-thymidine. This involves investigating the correlation between labeling intensity and the radial position of labeled neurons in order to establish threshold criteria that optimally distinguish successive generations of labeled neurons.

Fig. 13.

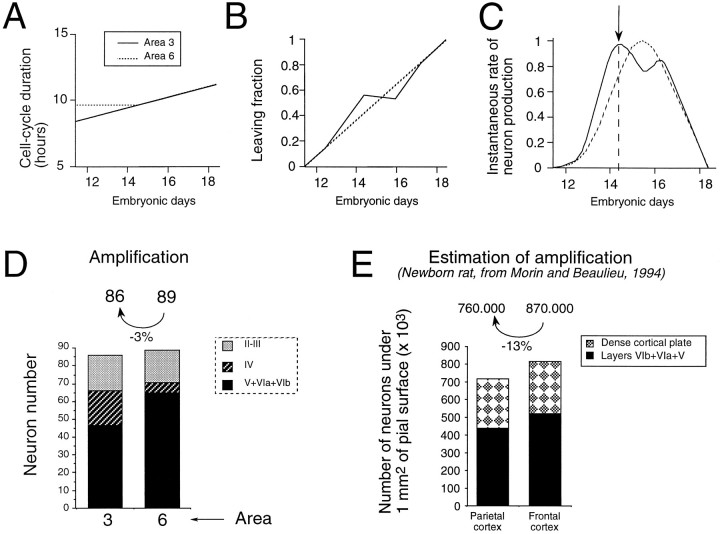
Simulations of the consequences of (1) cell-cycle parameters Tc and LF and (2) timetable of layer production on the dynamics of neuron production in areas 6 and 3. Changes during development in areas 3 and 6 of (A) Tc, (B) LF, and (C) dynamics of neuron production (i.e., the instantaneous rate of neuron production generated by the parameters in A and B). D, The timetable of laminar production in areas 3 and 6 (see ) and the dynamics of neuron production generate (1) the amplification (number above each histogram), i.e., the number of neurons in each area produced by one initial precursor, and (2) within each area the proportion of neurons in each layer. This simulation shows that although amplification in both areas is comparable, the proportion of neurons allocated to each layer is very different in the two areas. E, Number of neurons under 1 mm² of pial surface in frontal and parietal cortex of the newborn rat (Morin and Beaulieu, 1994). The simulated values show a relatively good fit with the published experimental values (see text).

Pulse injections of [³H]-thymidine at successive embryonic ages result in a staggered distribution of FG neurons going from layer VI to layer II (Fig. 4) (Angevine and Sidman, 1961; Rakic, 1976; Smart and Smart, 1977; Luskin and Shatz, 1985; Bayer and Altman, 1991). The inside-first outside-last gradient of corticogenesis means that the date of birth of a neuron determines its radial position in the cortex so that the later the birthdate, the higher the neuron in the cortex.

Fig. 4.

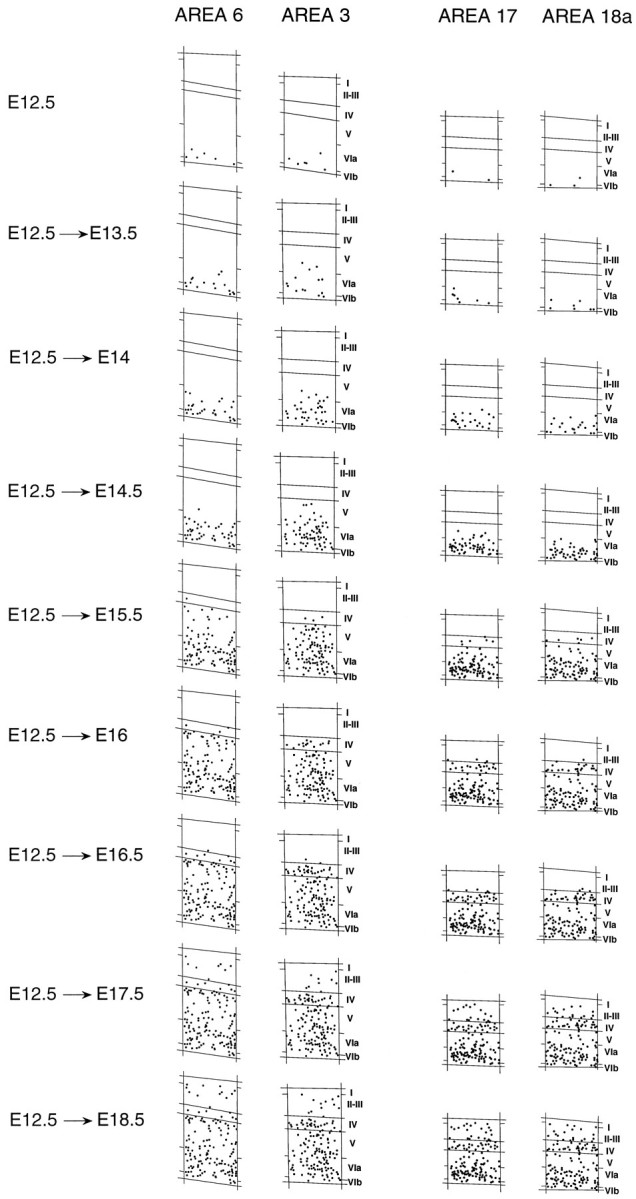
Distribution of FG neurons in frontoparietal and occipital cortex after injections on embryonic dates spanning the entire mouse corticogenesis. Each panel represents the FG neurons on one section after injection on the embryonic day indicated, plus the FG neurons from preceding injections.

For a single injection, we observe a strict relationship between the radial location of a neuron and the intensity of its autoradiographic labeling: heavily labeled FG neurons show a restricted radial distribution and lie at a lower level in the cortex than weakly labeled SG neurons, which have a more extended distribution (Smart and Smart, 1977, 1982). Within the SG population, the lighter the labeling, the higher the neuron is in the cortex.

The labeling thresholds that effectively allow the radial separation of different categories of labeled neurons correspond to the optimal values for distinguishing rank of generation. This exhaustive analysis of the relation of labeling density and radial location has been performed for seven pulse injections at different stages of corticogenesis.

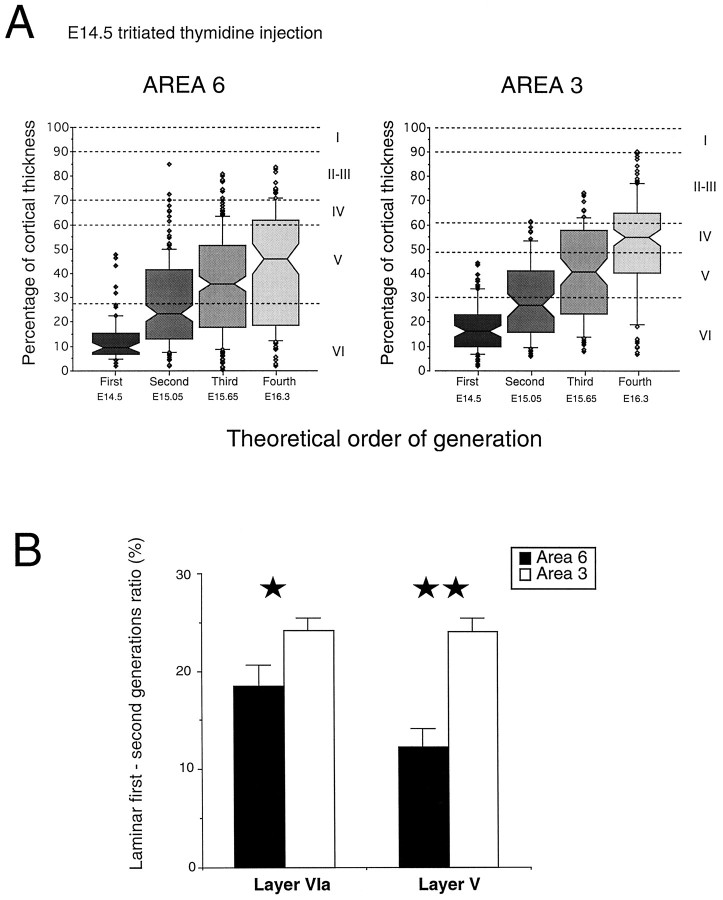
Figure 2A shows the distribution of autoradiographic labeling after an injection at E15.5, when neuroblasts destined for layer VIa are undergoing their final mitosis in the ventricular zone. In this figure, each panel shows the distribution of a single category of labeling taken from one section. This injection returned a maximum count of 81 grains per cell. The heaviest labeled neurons (≥56 grains, panel 1) are largely located in layer VIa, with only three labeled neurons in layer V. There is a steady increase in the numbers of labeled layer V neurons in the lighter labeling categories (panels4–6). Categories with labeling intensities <25 grains per neuron show increasing numbers of labeled neurons, first in layer IV (panels 7–8) and then in supragranular layers II–III (panels 9–12).

The radial location and dispersion of each category of labeling is revealed by a box plot analysis (see Materials and Methods). The box plots (Fig. 2B) show changes in the median height and the other centile values as percentages of the radial thickness of the cortex. As labeling intensity drops, the radial dispersion increases, and median height is displaced from the top of layer VIa to the top of layer V.

The box plot analysis of the E15.5 injections (Fig.2B) shows that the first four groups have similar radial locations. Between groups 4 and 5 there is a major and significant (p < 0.05; Kolmogorov–Smirnov) outward shift in radial location. This corresponds to a shift at the 50% level and defines the threshold that distinguishes FG and SG neurons. This was a common finding for all seven injections investigated in this way: neurons with >50% of the maximum labeling share a restricted deep radial distribution. At the 50% threshold there is an abrupt shift in the mean radial location, which confirms that FG neurons contain 50% or more of maximum labeling.

The presence of the first threshold at the 50% level suggests that the intensity of label is halved at each division. This should lead to a second threshold at the 25%. However, in the labeling pattern shown in Figure 2B, the second shift occurs at the 32% level, indicated by an arrow between groups 7 and 8, and not at the predicted 25% levels (dashed line). One possibility is that group 8 (21–25 grains) contains a mixed population of second and third generation neurons. To determine whether there was a mixed population of two generations in group 8, we examined the radial distribution of labeled neurons in this group to see whether neurons with 21–23 and 24–25 grain counts constitute two subpopulations with different median locations. This was not found to be the case in either the E15.5 or the E16 injection. This result suggests that there is an uncertainty in the threshold criteria that concerns 28% at E15.5 and 32% at E16 of the neurons classified as second generation. A third threshold occurred at the 12.5% level, as the halving principle would predict. This was found to be the case in six of seven injections. The forth threshold was found at the predicted 6.25% level in five of seven injections.

The reproducibility of the 50, 12.5, and 6.25% threshold levels in the seven injections analyzed suggests that at each round of mitosis there is a halving of the autoradiographic signal. We have compared the distribution of thresholds with what would be obtained by chance using a bootstrap analysis (Efron and Tibshirani, 1993) programmed with Matlab (version 4.2C.1). This showed that the observed distribution is significantly different from that obtained by chance (p < 10⁻⁴); therefore, we have retained the 25% threshold in all cases.

The fifth generation in the E13.5–E16 injections showed a significant outward shift in radial location but showed a wide radial distribution, which undoubtedly reflects that this lightest category includes many artifactually lightly labeled first to fourth generation neurons. Therefore we have not used this category for comparison of generation profiles (see below), although we have used this category for calculating SG/T (see below).

These results show that using 50, 25, 12.5, and 6.25% of maximum labeling gives an acceptable segregation of the first five generations. The reliability of the analysis can be estimated by comparing the radial positions for different generations obtained for the range of injections that have been analyzed, and the results in area 6 for the first four generations are summarized in Figure 3A. On E13.5, E14.5, E15.5, E16, and E16.5 there is a radial separation for the successive generations after each injection. Except for the third and fourth injection at E13.5 and cohorts that leave the ventricular zone after E18.5, the radial separations were statistically significant (Fig. 3A). Overall, the radial deployment of successive generations is progressively restricted during corticogenesis so that injections at E17.5 and E18.5 return successive generations that are very tightly grouped. The last round of mitosis during neurogenesis of the mouse cortex is on E19.3 (Polleux et al., 1997), so that the E17.5 injection generates three successive generations and the E18.5 only one generation.

To compare the radial locations of generations labeled by different injections, we have used published Tc values to calculate the theoretical embryonic age at which each of the four generations labeled by an injection quit the cell cycle (Fig. 3B). This analysis shows that there is an appropriate intermeshing of generations from separate injections resulting in a smooth progression of the median height, so that cohorts that are labeled by different injections within 6–12 hr return median values that are not separated by >16–22% of the thickness of the cortex.

Areal differences in rates of neuron production–FG/T

Originally the ratio FG/T (where T equals the total number of neurons) was defined by Rakic (1973) as a generation rate and subsequently has been used by a number of authors to accurately define the onset and duration of the formation of a layer as well as to reflect the rate of layer production (Carter-Dawson and LaVail, 1979;Mustari et al., 1979; Reznikov, 1990; Valverde et al., 1995; Polleux et al., 1997). Because cell death will equally influence labeled and unlabeled cells, this measure is immune to regional variations of cell death.

A cortical layer is generated over the time period during which its neurons undergo their final mitosis in the ventricular zone. Injections given at closely spaced intervals throughout the generation period will lead first to an increase and then to a decrease of FG/T neurons in the cortical layer under consideration.

The onset of corticogenesis occurs simultaneously at E12.5 across the cortex in occipital and frontoparietal areas and terminates in all areas shortly after E18.5 (Fig. 4). Up to and including E14.5, all labeled neurons are confined to infragranular layers. Onset of layer IV production is at E15.5, and at this age there are noticeably more labeled neurons in this layer in area 3, 17, and 18a than in area 6.

Cumulative numbers of FG neurons per layer generated between the onset of corticogenesis and successively later stages are shown in Figure 4. The number of FG neurons in a layer cumulated over all ages which contribute to that layer is taken as 100%, so that the increment from each injection gives a measure of the proportion of that layer which is generated at the moment of the pulse. These cumulative measures provide a temporal description of the rate of generation (LaVail et al., 1991). However, areal differences of cumulative FG curves alone would be influenced by cell death should the rate of cell death be different in the homologous layers compared in the two areas. The problem of differential cell death can be overcome by dividing the cumulative FG measure by T, because larger amounts of cell death in one of the areas will influence similarly FG and T (Fig.5).

Fig. 5.

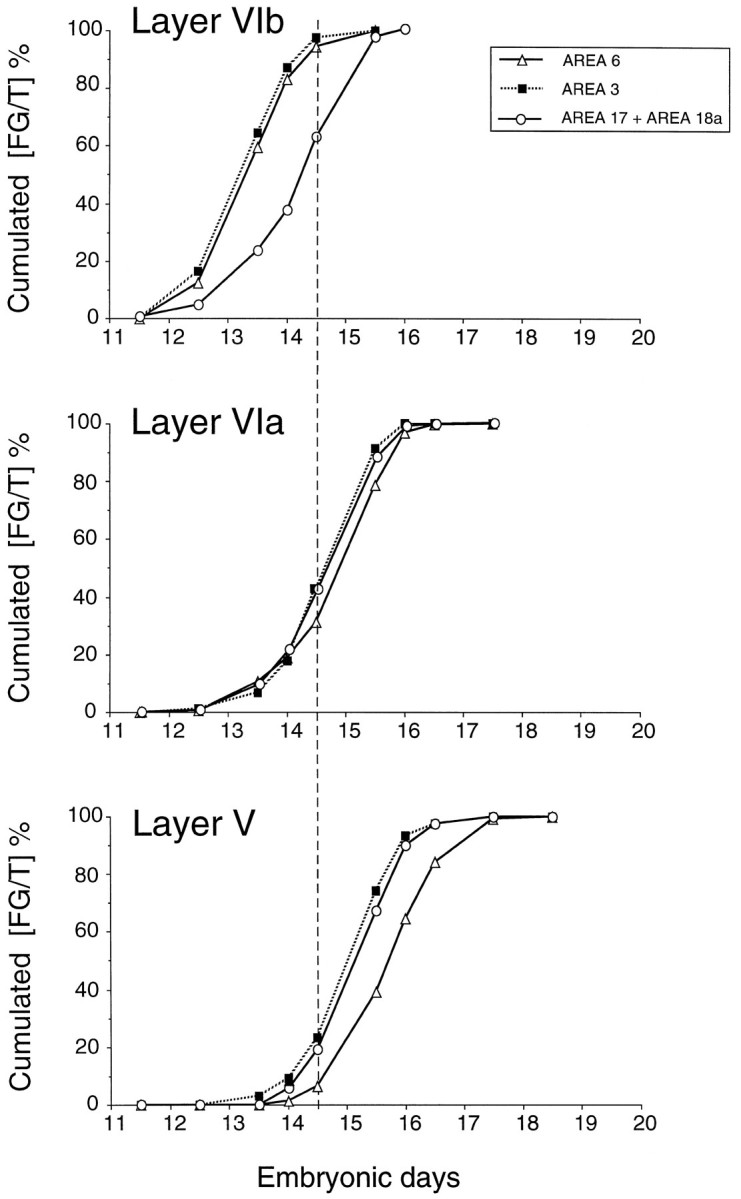
Cumulative laminar generation curves (FG/T). Thevertical dotted line indicates age limit (E14.5) before which FG neurons are limited to infragranular layers and where differences between generation curves reflect areal differences in the rate of neuron production (see text). At E14.5, the cumulative FG/T ratios in both layers VIa and V are significantly different in areas 3 and 6 (χ² analysis; Table 1).

Cumulative FG/T values were identical for the generation of supragranular layers of areas 3 and 6 as well as for all layers of areas 17 and 18a (Table 1).

Table 1.

Summary of numerical data and statistical analysis obtained for the cumulative FG/T ratio

	Area 6	Area 3	χ2analysis	Area 17	Area 18a	χ2analysis
			E14.5–area 6 vs area 3			E14.5–area 17 vs area 18a
Layer VIb	E11.5–E14.5	E11.5–E14.5	0.444 (n.s.)	E11.5–E15.5	E11.5–E15.5	1.523 (n.s.)
	59/1597 (22; 10)	39/1214 (22; 10)		103/2583 (48; 12)	100/2522 (48; 12)
Layer VIa	E11.5–E16.5	E11.5–E16.5	24.128 (p < 0.0001)	E11.5–E16.5	E11.5–E16.5	1.322 (n.s.)
	242/11636 (34; 16)	248/10274(34; 16)		299/9152 (56; 14)	312/9684(56; 14)
Layer V	E11.5–E16.5	E11.5–E14.5	68.192 (p < 0.0001)	E11.5–E16.5	E11.5–E16.5	0.875 (n.s.)
	123/10452 (34; 16)	158/8425(34; 16)		99/7684 (56; 14)	98/7751 (56; 14)
Layer IV	E11.5–E17.5	E11.5–E17.5		E11.5–E17.5	E11.5–E17.5
	18/3709 (38; 18)	77/6481 (38; 18)		160/9938 (62; 16)	175/10360 (62; 16)
Layers II–III	E11.5–E19.5	E11.5–E19.5		E11.5–E19.5	E11.5–E19.5
	45/13043 (46; 22)	51/11841 (46; 22)		152/20717 (78; 20)	151/20650 (78; 20)

In the columns titled by area, the time period of cumulation of the FG/T ratio is first indicated, followed by the numbers of FG and T neurons examined (bolded). Between the parentheses are indicated, respectively, the number of sections examined and the corresponding number of animals. Columns 4 and 7 indicate the results of a χ² analysis comparing the FG/T cumulated proportions up to E14.5 between areas 6 and 3 (column 4) and areas 17 and 18a (column 7). In each case, the χ² value is provided followed by the level of significance (between parentheses). No χ² value is indicated when ratios of cumulated FG/T in both areas equal zero on E14.5. n.s., Not significant.

Throughout the generation of layer VIb, identical values of cumulative FG/T are returned for the anterior areas 3 and 6 (Fig. 5). In layer VIb, starting from similar and minimal values, the rate of increase is significantly faster in frontoparietal areas than in occipital areas. The dynamics of production of layers VIa and V show a dramatic change. In both layers, occipital cortex (areas 17 and 18a) returns values that superimpose on those of area 3, whereas the rate of neuron production in area 6 is significantly lower than that of areas 3, 17, and 18a (Table 1).

Recruitment, the extent to which the neuron output for a given age is dedicated to one or more layers, will influence the curves in Figure 5. Up to and including E14.5, all FG neurons in all five areas are committed to the infragranular compartment (layers VIb, VIa, and V). This result is important because it enables us to eliminate compensatory recruitment as a factor generating FG/T differences in areas 3 and 6 during the generation of layers VIa and V. Instead, the steeper slopes of FG/T in area 3 compared with area 6 during the generation of layers VIa and V reflect increased rates of neuron generation. This finding is highly significant because it indicates that neighboring regions of the ventricular zone generating separate cortical areas display marked differences in the rate of neuron production during the production of infragranular layers.

Labeling index (SG/T) and changes in Tc

The fraction of the precursor population that is labeled by a [³H]-thymidine pulse is determined byTc (Fujita, 1967; Waechter and Jaensch, 1972) (Fig.6A,B). Assuming a predominantly homogeneous distribution of Tc, the subpopulation of precursors labeled by a pulse is determined randomly by the phase of the cell cycle at the time of injection, and the two populations of precursors (labeled and unlabeled) will have identical cycling behavior. All of the progeny of the precursors that incorporate [³H]-thymidine will be labeled, provided the number of successive divisions is insufficient to lead to a significant loss of signal (Bisconte and Marty, 1975a). Once postmitotic neuroblasts have migrated to the cortex, it is theoretically possible to compare the proportions of labeled and unlabeled cells. Proportions of labeled cells will reflect the proportion of the precursors that were in S-phase at the moment of injection, which in turn reflectsTc (Schultze et al., 1974; Brückner et al., 1976). However, one needs to define a neuronal population that is entirely generated after the injection to be sure that all the unlabeled cortical neurons are the progeny of those precursors present at the moment of the injection (and that were not in S-phase) and not cells that underwent their final division before the injection. This is ensured by counting SG neurons in the cortical layer immediately above the layer containing FG neurons. In this way, we are assured that all the neurons of the layer in which neurons are being counted (SG neurons and unlabeled neurons) underwent their final mitosis subsequent to the [³H]-thymidine pulse. The labeled precursors will therefore undergo a variable number of divisions before quitting the cycle, and their progeny will correspond to the SG neurons in the cortical layer examined. Under these conditions, the proportion of SG/T truly reflects the proportion of precursors in S-phase at the moment of the pulse (Schultze et al., 1974; Brückner et al., 1976). For these reasons we refer to SG/T as the labeling index, and differences in the labeling index in two homologous layers will largely reflect changes of Tc in the two founder populations. Cell death will influence SG and T similarly and therefore will not contribute to areal differences in this value.

Within frontoparietal areas, significant differences (p < 0.05 according to a χ²analysis) were observed in the laminar labeling indices of layers VIb, VIa, and V (Fig. 6C). This contrasts with the labeling indices in homologous layers in areas 17 and 18a, which were identical (Fig. 6D).

The SG/T ratios shown in Figure 6C,D fail to show a significant decrease during corticogenesis. This contradicts studies showing that during corticogenesis there is a decrease in the labeling index in the ventricular zone that is thought to reflect an increase inTc during development (Kaufmann, 1968; Waechter and Jaensch, 1972; Hoshino et al., 1973; Schmahl, 1983; Takahashi et al., 1995). This discrepancy could be attributable to a differential loss of signal, which could be more pronounced in the case of early injections, because they are followed by a large number of cell cycles, and could be relatively minor in the case of late injections, which are followed by a smaller number of cell cycles (Bisconte and Marty, 1975a).

To overcome this problem and to be able to compare changes of cell-cycle parameters during the generation of early and late generated layers, we developed an alternative procedure for estimating SG. Instead of measuring SG in the full thickness of a layer as in Figure6C,D, we have defined a restricted cortical volume for counting SG neurons immediately above the location of FG neurons. The height of this compartment was made equal to the radial width of cortex in which FG neurons are observed and is somewhat thinner than a layer (Fig. 6E). This analysis of labeling index for early and late stages of corticogenesis has been performed in area 3 (Fig.6F). At E12.5 the labeling index calculated in this way is 73%, which is significantly higher than the 59% calculated over the full width of layer V (Fig. 6C). At E15.5 the labeling index shows a drop to 62% and is close to the 61% value found at this age when the calculation is made throughout the full thickness of layers II–III.

To conclude, the use of a restricted box for calculating the SG/T ratio shows that there is a significant decrease in Tc from E11.5 to E18.5, in agreement with previous authors (Kaufmann, 1968; Waechter and Jaensch, 1972; Hoshino et al., 1973; Schmahl, 1983; Takahashi et al., 1995).

Proportions of FG and SG neurons (generation profiles) and areal differences in LF

At early stages of neuron production, a majority of divisions are proliferative and lead to an increase in the precursor pool. As corticogenesis proceeds, there is a steady increase in the proportion of differentiative divisions leading to an increase in the LF and a gradual exhaustion of the precursor pool (Rakic and Sidman, 1968;Rakic, 1977; Miller, 1988; Takahashi et al., 1996). At any given moment of corticogenesis, the neuron output from the ventricular zone will be determined by (1) the density of precursors in the ventricular zone, (2) Tc, and (3) LF. We have shown above that areal histogenesis is influenced by regional variations in Tc. In this section, we shall explore the possible contribution of LF to areal differences in histogenesis.

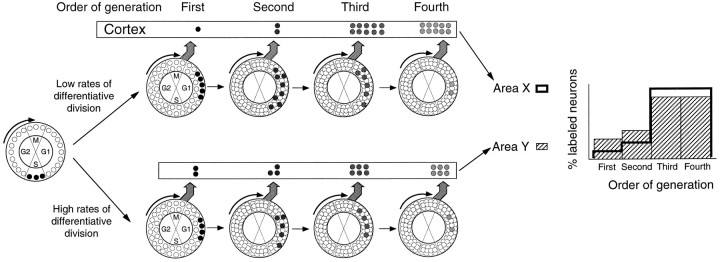
Theoretically, regions that are generated by pools of precursors exhibiting different proportions of differentiative and proliferative divisions are expected to show different proportions of first, second, third, and fourth generations as shown in Figure7. In this figure, the top row simulates the consequences of high rates of proliferative division (low LF), whereas the bottom row explores the consequences of high rates of differentiative division (high LF). When proliferative divisions predominate, few first and second generation neurons are generated, whereas there are large numbers of third and fourth generation neurons. The converse is true for high rates of differentiative divisions. In this way, differences in the generation profiles (Fig. 7) are to be expected when there are significant differences in LF.

Fig. 7.

Influence of the exit behavior of precursors cells on proportions of successive generations (generation profiles). After differentiative divisions one or both daughter cells quit the cell cycle and lead to high proportions of heavily labeled FG neurons (bottom pathway). After proliferative divisions, daughter cells remain in the cell cycle, and this leads to low numbers of FG neurons. During early stages of corticogenesis, when the proliferative pool is increasing, the percentage of differentiative divisions is low (top pathway). At later stages, high rates of differentiative divisions (bottom pathway) lead to a steady decline in the precursor pool. Ventricular regions characterized by high rates of differentiative division (i.e., high LF) lead to large numbers of heavily labeled FG neurons immediately after the pulse and low numbers of SG neurons. Thus, differences in the ratio between FG and SG neurons reflect the differences in the rate of differentiative divisions.

Figure 8 examines the generation profiles in frontoparietal cortex and occipital cortex. In both frontoparietal and occipital regions, as corticogenesis proceeds there is a steady increase in the ratio of FG neurons with respect to all other generations. This reflects the known increase in LF (Rakic and Sidman, 1968; Rakic, 1977; Miller, 1988; Takahashi et al., 1996).

Fig. 8.

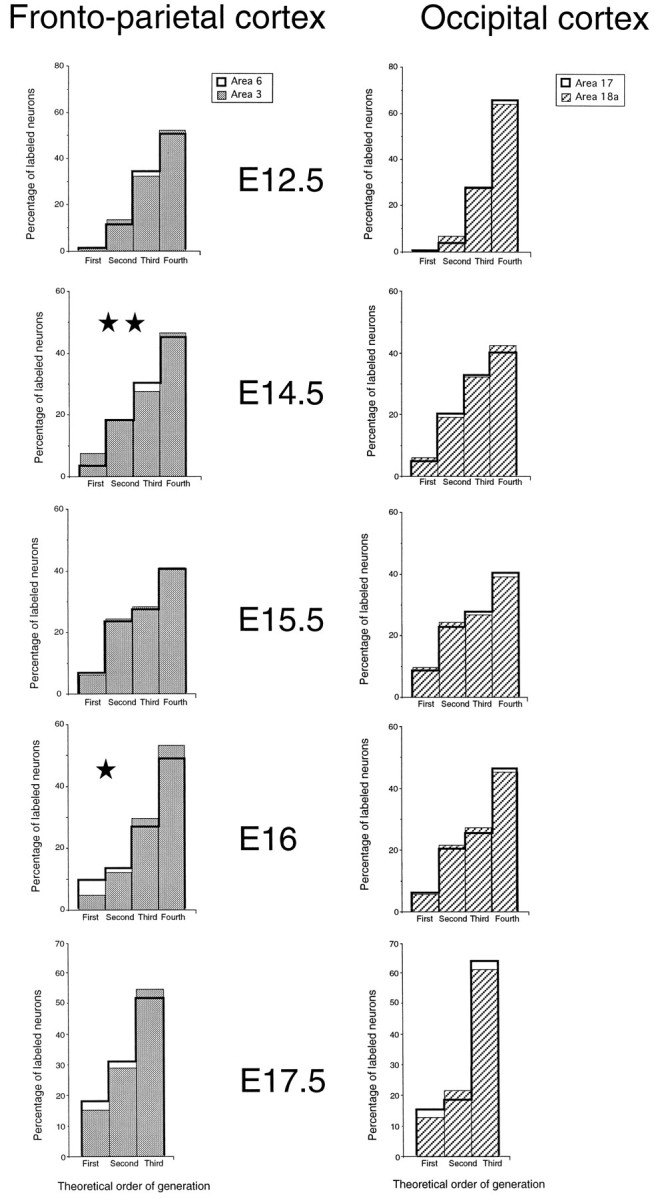
Generation profiles for areas 3 and 6 (left) and 17 and 18a (right). Statistical analysis: *p < 0.05; **p < 0.01, according to a χ²analysis.

In areas 3 and 6 there were significant differences in the generation profiles resulting from injections on E14.5 and E16. At E14.5, during the major phase of production of layers V and VIa, there is a significant increase in the proportion of FG neurons in area 3 compared with area 6 that is consistent with a transient relative increase of LF in area 3 during the production of infragranular layers. At E16, area 3 shows a decrease in the proportion of FG neurons that could reflect a reduction in LF during the production of layer IV (however, see counter arguments below).

In occipital cortex there were only small, nonsignificant differences in the generation profiles of areas 17 and 18a, suggesting that the mode of cell division is similar in the adjacent ventricular zones generating these two cortical areas. The changes in the proportions of FG neurons in areas 17 and 18a are similar to those found in area 3. As in area 3, there is a transient reduction of FG neurons at E16, suggesting that this might be a common feature in the generation of granular cortex. At E17.5, generation profiles are similar in all four areas so that altogether these results show similar modes of division at the onset and termination of corticogenesis.

One possibility that needs to be examined is whether differential cell death in cortical layers could lead to a selective decrease in one or several of the four generations and thereby bias the generation profiles. In areas 3 and 6, the injection on E14.5 labels FG neurons that are destined for layer VIa and second to fourth generations that in both areas are destined for layers VIa and V in area 6 and layers VIa–IV in area 3 (Fig. 9A). Hence, differential cell death could contribute to the differences in the generation profiles. It is possible to overcome this objection by considering only the first two generations (FG and second generation), which have very similar laminar distributions in the two areas. This makes it possible to compare the ratios of the first two generations for both areas separately within layers VIa and V. These ratios are significantly different in these two areas, as shown in Figure9B.

Fig. 9.

A, Box plot analysis of the radial deployment of successive generations in areas 3 and 6 after injection of [³H]-thymidine on E14.5 (area 3: 599 neurons obtained in three sections in two animals; area 6: 776 neurons, four sections, two animals). B, Ratio of the number of FG and second generation neurons within layer VIa and layer V in areas 6 and 3. Conventions as in Figure 2.

In contrast to the E14.5 injection, the E16 injection leads to a different laminar deployment of the first two generations in areas 3 and 6, because the FG in area 6 is in layer V and in area 3 it is in layer IV (Fig. 3A,C). If higher rates of cell death were to occur in layer IV of area 3 than in layer IV of area 6, then this could lead to the observed drop in the proportion of FG neurons in layer IV of area 3 and at least theoretically could create the areal differences in the generation profiles observed after the E16 injection.

Generation profiles shown in Figure 8 could be very sensitive to small errors in the estimation of the values for each generation. Hence, although one can feel confident that there are no differences in the profiles between areas 17 and 18a, could it be that the differences in the profiles for areas 3 and 6 are in some way the consequence of an error in the estimation of successive generations? To examine this issue, we have defined a LF index as the percentage of silver grains contained in the FG population with respect to the total number of grains in the overall population of FG and SG neurons (Fig.10). This LF index has the advantage of relying uniquely on the FG/SG threshold, which is extremely robust as we have shown above . Figure 10 shows that at early stages of corticogenesis, rates of differentiative divisions are minimal, a large fraction of the injected [³H]-thymidine is incorporated in precursors that undergo proliferative division, and the LF index tends to zero. As corticogenesis proceeds, LF indices increase to maximal values in the final stages (Miller, 1988).

Fig. 10.

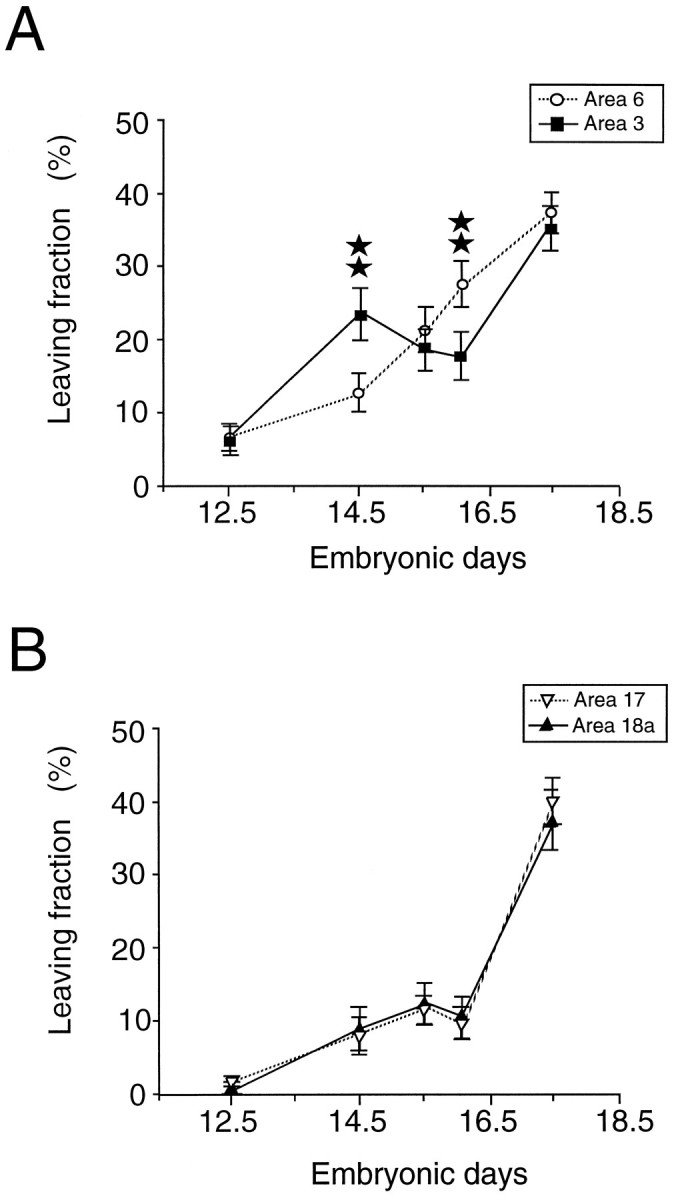
Comparison of LF characterizing neurogenesis of areas 3 and 6 (A) and of areas 17 and 18a (B). The LF has been estimated by the proportion of silver grains contained in the FG neurons expressed as a percentage of the number of silver grains contained in all labeled neurons.Stars refer to statistically significant differences (p < 0.05), according to a χ² analysis.

LF indices for areas 3 and 6 are shown in Figure 10Aand for areas 17 and 18a in Figure 10B. This analysis confirms that at E14.5, LF in area 3 is higher than in area 6 (p < 0.05; χ² analysis). The converse is true at E16: no difference is found between areas 17 and 18a. This analysis permits comparison between anterior and posterior regions. It shows that at E12.5, LF is higher in areas 3 and 6 compared with areas 17 and 18a, and this would be compatible with the higher generation rate in the anterior cortex as reflected by the higher FG/T values at this age (see “Areal differences in rates of neuron production—FG/T”).

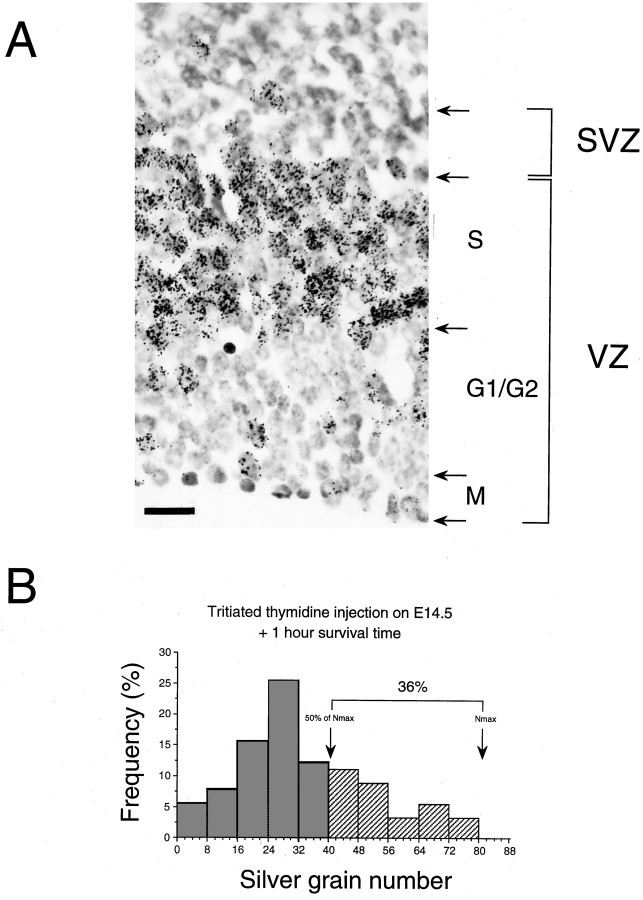
At the final stages of corticogenesis LF tends to 100%, so that theoretically one would predict that all labeled neurons would be FG neurons. In Figure 10 only 37–39% of the label is contained in the FG neurons at E17.5. To confirm that this is not the consequence of an error in the estimation of the FG population we have looked at the distribution of silver grains in labeled precursors in the ventricular zone 1 hr after a [³H]-thymidine pulse at E14.5 (Fig. 11). Labeled precursors in S-phase showed a range of numbers of silver grains with a maximum of 80 grains per cell. Only 36% of the labeled precursors contained >50% of the maximum labeling. This result suggests that the 50% maximum labeling threshold, which we have used to distinguish FG neurons in the cortex, will lead to an underestimation and that the maximum observed value of 37–39% LF index in the cortex is close to the 36% value observed in the ventricular zone.

Fig. 11.

[³H]-thymidine labeling in the ventricular zone of presumptive somatosensory motor cortex after injection at E14.5 with a survival time of 1 hr. A, Microphotograph of labeling in the S-phase zone. B, Grain distribution in labeled precursors (300 labeled precursors from three nonadjacent sections). G1/G2, G1/G2 zone of the ventricular zone (VZ); M, M-phase zone;S, S-phase zone; SVZ, subventricular zone. Scale bar, 30 μm.

Cell-cycle parameters are constant throughout single cortical areas

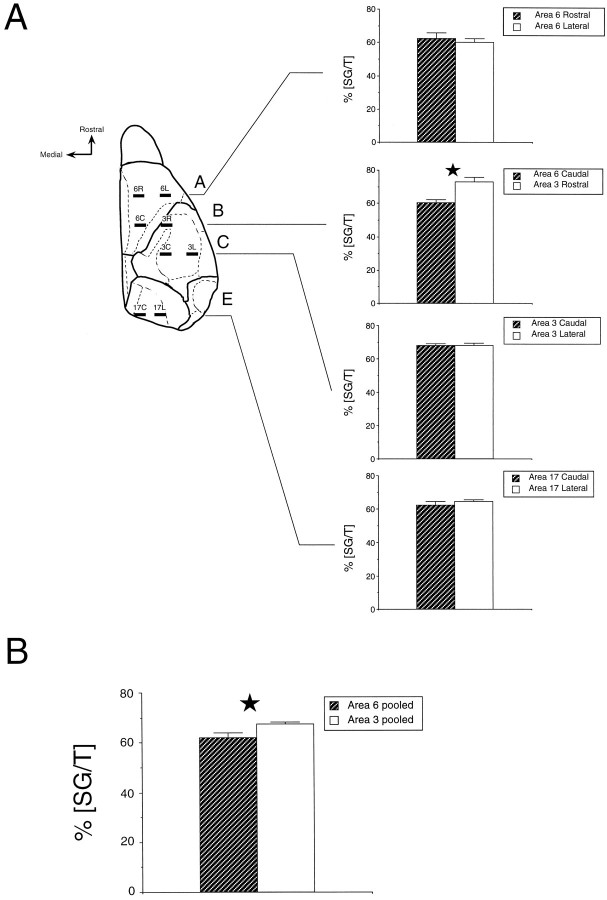
To directly investigate this issue we have measured SG/T after a pulse at E12.5 at maximally separated points within each area (Fig.12A). This shows that lateromedial separations within areas 6, 3, and 17 all return identical values for SG/T measured in layer VIa. This contrasts with the values in areas 3 and 6 that show a significant difference of 13%. Within area 6 there is a 3% variation and within area 3, a 5% variation. Nevertheless, when values from the three sites in each area are pooled, comparison of areas 3 and 6 continues to reveal a significant difference (Fig. 12B).

Fig. 12.

Comparison of laminar labeling index (SG/T) within and between areas. SG/T was measured in layer VIa after a pulse at E12.5. A, Percentages were measured with constant lateromedial separations at four rostrocaudal positions. Measurements at rostrocaudal positions within areas failed to show significant differences, whereas there was a significant 13% difference between areas 3 and 6. B, Differences between areas 3 and 6 remain significant after pooling the values from all three locations within each area. Statistical analysis: *p < 0.05, according to a χ² analysis.

Simulations of proliferation program predict the dynamics of neuron production characterizing areas 6 and 3

We have developed a mathematical model to simulate the roles ofTc, LF, and the timetable of laminae production in corticogenesis (see ).

The labeling index reflects the proportion of precursors in S-phase (Fig. 6B) so that SG/T equalsTs/Tc, where Ts is the duration of S-phase. Ts is considered invariant and equals ∼6 hr throughout corticogenesis (Hoshino et al., 1973; Schmahl, 1983;Takahashi et al., 1995). This means that labeling indices allow one to calculate theoretical Tc values. These values measured in both the cortex and the ventricular zones suggest that during corticogenesis there is a linear increase in Tc duration (Hoshino et al., 1973; Schultze et al., 1974; Brückner et al., 1976; Schultze and Korr, 1981; Schmahl, 1983; Takahashi et al., 1995). The SG/T values obtained in area 3 from E12.5 to E16.5 (Fig.6F) give the Tc curve shown in Figure13A. At E11.5 and E12.5, area 6 precursors showed 22% and 10%, respectively, higherTc values compared with area 3 precursors. No significant difference was found on E14.5 (Fig. 6C).

The developmental change in LF is derived from the LF index (Fig.10A). Because the maximum LF index that can be measured in the cortex is 40% of the true value because of the labeling profile in the ventricular zone, it is first necessary to normalize to 100% (Fig. 13C). During neurogenesis there is a progressive increase in the LF (Rakic and Sidman, 1968; Rakic, 1977;Miller, 1988; Takahashi et al., 1996). LF values for area 6 at different stages show a reasonably linear progression, as reported elsewhere (Rakic and Sidman, 1968; Miller, 1988; Takahashi et al., 1996). Compared with area 6, area 3 shows a significant increase at E14.5 followed by a decrease at E16 (Fig. 10).

The simulation using the theoretical Tc and LF curves (Fig. 13A,B) generate profiles of neuron production in areas 3 and 6 (Fig. 13C). When neuron output is restricted to either supra- or infragranular layers so that compensatory recruitment can be discounted, then and only then can the theoretical curves be compared with experimentally measured generation rates (FG/T).

The simulation curves show a rate of neuron production that is higher in area 3 than in area 6 during the formation of infragranular layers (Fig. 13C). The maximal difference is found on E14.5 (Fig.13C, dashed vertical line), which is when maximal differences of the generation index FG/T are found between areas 6 and 3. Up to E14.5, compensatory recruitment can be discounted, and therefore areal differences in FG/T correspond unambiguously to higher rates of neuron production in area 3 (Fig. 5). This shows that the theoretical increased rate of neuron production in area 3 predicted by the model during the production of infragranular layers agrees closely with our experimental findings. According to this simulation, neuron production in area 6 transiently exceeds that of area 3 between E15.5 and E16.5. However, because FG neurons at this stage span infra- and supragranular layers, we would not be able to experimentally detect this brief increased output of area 6.

There is good correspondence between experimental and simulated values during the final third of corticogenesis. After E16.5, simulated rates of neuron generation in areas 3 and 6 are identical. This finding is in agreement with the experimental findings, which show that FG/T values in areas 3 and 6 are identical at this age (Polleux et al., 1997). Given that the entire neuron output of the ventricular zone is dedicated to supragranular layers after E16.5, this means that compensatory recruitment is null, and under these conditions the experimental results show that rates of neuron production in the two areas are identical.

We have applied the timetables of laminar production characterizing corticogenesis of areas 6 and 3 (see ) to the simulation of neuron output. This enabled us to estimate the proportion of neurons allocated to each layer (Fig. 13D). There is no experimental data available concerning numbers of neurons in granular and supragranular layers before the onset of cell death, but it is interesting that the simulated proportions are reasonably similar to those reported in adult areas 6 and 3 (Beaulieu, 1993; Skoglund et al., 1996).

Neuron numbers in areas 3 and 6 in newborn rat have been investigated in stereological studies (Morin and Beaulieu, 1994). At birth the neocortex is not fully formed and consists of an infragranular compartment and a dense cortical plate, which subsequently differentiates into layers IV, II, and III. Although these authors could not therefore describe the proportions of neurons for each individual layer, they could determine the total number of neurons per radial unit as well as the proportions of neurons in infragranular layers. This showed that just after the end of cortical neurogenesis, the full thickness of area 6 contains 13% more neurons than does area 3, whereas the simulation predicts 3% more neurons in this area (Fig.13D,E). Areal differences between the numbers of neurons in infragranular layers predicted by the model was within 10% of the experimental values.

To conclude, the simulation of LF and Tc generates profiles of neuron production for areas 3 and 6 that display areal differences that closely correspond to those found experimentally. The addition of the timetable of layer production generates numbers of neurons both in the full thickness of cortex and in infragranular layers that are within 10% of those found experimentally.

DISCUSSION

In the present study we have compared proportions of different categories of labeled neurons after injections of [³H]-thymidine during corticogenesis. Significant differences were found between the two frontoparietal areas during the generation of infragranular layers. The differences in FG/T between areas 3 and 6 show that area 3 is characterized by higher rates of neuron production during the early stages of corticogenesis. Further analysis of SG/T and the FG/SG ratios indicates that the higher rates of neuron production are achieved by shorter Tc and higher LF. Modelization of these areal differences in cell-cycle kinetics generates realistic areal differences in numbers of neurons, suggesting that proliferative programs play a significant role in the generation of cortical architectures. These results have important consequences for theories of specification of cortical areas (Rakic, 1988; O’Leary, 1989).

The ventricular zone contains a heterogeneous population of multipotential precursors generating radial glial cells, neuronal precursors, and glial precursors (Rakic, 1972; Misson et al., 1988a,b;Johnston and van der Kooy, 1989; Gressens et al., 1992; Grove et al., 1993; Luskin et al., 1993; Williams and Price, 1995). Studies of the cell-cycle kinetics based on percentages of labeled precursors observed in the ventricular and subventricular zones will therefore be describing a range of proliferative behaviors (Fujita, 1967; Kaufmann, 1968; Waechter and Jaensch, 1972; Hoshino et al., 1973; Schmahl, 1983;Takahashi et al., 1995, 1996). A central requirement of the present study is to selectively determine the proliferative behavior of the limited population of precursors that at a given fetal stage are generating cortical neurons. The only available technique that can adequately achieve this aim is the examination of labeling in the adult. This is possible because the fetal [³H]-thymidine pulse labels all precursors in S-phase, and the two populations of precursors (labeled and unlabeled) will continue to proliferate and will subsequently maintain proportions of labeled cells within the differentiated progeny in the adult. This provides a description of the mitotic history of clearly defined neuronal populations in the cortex, making it possible to compare the proliferative behavior of neurons in homologous layers in different areas (Schultze et al., 1974; Rakic, 1976; Korr, 1980; Schultze and Korr, 1981; Miller, 1988). We need to determine how results obtained in the cortex might be expected to be influenced by cell death and migration as well as by quantification of labeling. Last we shall compare our results with quantitative studies both at the level of the cortex and in the ventricular zones.

Cell death

Cell death is known to occur in the developing neocortex, affecting neuronal precursors in the germinal zones as well as postmitotic neuroblasts in the cortical plate (Korr, 1980; Finlay and Slattery, 1983; Heumann and Leuba, 1983; Ferrer et al., 1990, 1994;Acklin and van der Kooy, 1993; Reznikov and van der Kooy, 1995;Spreafico et al., 1995; Blaschke et al., 1996). The SG/T and FG/T ratios in a radially restricted layer cannot be artifactually affected by cell death, because this phenomenon will equally affect labeled and unlabeled cells.

Radial versus tangential migration

Numerous studies have demonstrated that during cortical development there is radial as well as tangential migration (Rakic, 1972; 1988; O’Rourke et al., 1992, 1995). The mosaic expression of a reporter gene in transgenic mice generates strong radial bands (Tan and Breen, 1993; Soriano et al., 1995; Tan et al., 1995) and has enabledRakic (1995) to estimate the maximum contribution of tangential migration as being no more than 10%. Tangential migration would be expected to blur areal differences in kinetics of the cell cycle, suggesting that areal differences in the present report may be, in fact, an underestimation.

Underestimation of the proportion of FG neurons and overestimation of SG neurons.

This is principally attributable to (1) labeled progeny of precursors not being fully in S-phase at the moment of the pulse (Fig.13) and (2) FG neurons that are too deep in the section to effectively label the emulsion (Rogers, 1967; Sidman, 1970). In the present study laminar proportions of FG and SG neurons are compared between areas so that artifactual variation in (1) and (2) will be similar in both areas and will not contribute significantly to the measured differences.

The laminar SG/T ratio is measured before the appearance of any FG neurons in the layer examined, i.e., before the onset of production of the layer under consideration. Thus for this ratio, none of the SG neurons can be artifactually lightly labeled FG neurons.

Comparison with previous findings

Generation profiles and LF index

The only reported numerical value of LF at E15 is 36% (Takahashi et al., 1994, 1996). This value was obtained in the ventricular zone generating mouse sensorimotor cortex corresponding to both area 6 and area 3. In the present study, we obtained a mean LF value of 44% on E15, which is significantly higher than the 36% reported by Takahashi et al. (1994, 1996). This is exactly what one would predict. The LF values obtained in the ventricular zone are calculated for a total population of precursors, including 30% proliferating radial glial cells and precursors of supragranular layers (Misson et al., 1988a;Krushel et al., 1993; Williams and Price, 1995). The LF in the present study describes the exiting behavior within the pool of neuronal precursors that exit within five generations after the pulse.

Labeling indices (SG/T) and cell-cycle duration

In the present study SG/T showed a decrease in value between E12.5 and E16.5, indicating a progressive slowing down of the cell cycle during development as reported by a number of studies looking at labeling in the cortex (Schultze et al., 1974; Brückner et al., 1976; Korr, 1980; Schultze and Korr, 1981). Labeling index values measured in the ventricular zone over the same period also show a developmental decrease [34–27%, Takahashi et al., (1996); 55–42%,Schmahl (1983)].

The only factor that could influence the labeling index in the cortex is loss of signal caused by an excessive number of divisions (Bisconte and Marty, 1975b). If this were a problem one would predict that labeling indices obtained in the cortex would be lower than those obtained in the ventricular zones. A review of the literature shows that this is not the case. The labeling indices values of 73% at E12.5 and 60% at E16.5 agree with those reported by others in the cortex (Schultze et al., 1974; Brückner et al., 1976). Globally these values in the cortex are marginally higher than those reported in the ventricular zone (Fujita, 1963; Kaufmann, 1968; Waechter and Jaensch, 1972; Hoshino et al., 1973; Schmahl, 1983; Takahashi et al., 1995).

To conclude, comparison of labeling indices obtained in the cortex are relatively immune to major classes of artifacts (Schultze et al., 1974;Korr, 1980; Schultze and Korr, 1981). Measurements in the ventricular zone describe the LF and Tc for the overall population of precursors generating distinct but poorly defined regions of the cortex. This contrasts with measurement made in the cortex. These investigations provide more accurate data for restricted neuronal populations than do observations in the ventricular zone (Schultze et al., 1974; Korr, 1980; Schultze and Korr, 1981).

Cell cycle heterogeneity

The radial locations of successive generations shown in Figure 3suggest heterogeneity of Tc in the ventricular zone (Cai et al., 1997). For example, the third generation for the E13.5 injection shows a small number of neurons in layers III and IV. At this stage, the average Tc value is ∼12 hr in the mouse (Hoshino et al., 1973; Schmahl, 1983; Takahashi et al., 1995), so that these neurons supposedly underwent their last round of division at E14.5 (Fig. 3B). The highest number of FG neurons resulting from an injection at E14.5, however, are located in the upper part of layer V; none are found in layers III and IV. What is the generation status of layers III and IV neurons in the third generation on E13.5? One possibility is that those third generation neurons that are abnormally high in the cortex actually quit the ventricular zone later than expected because their Tc was longer than the average value at the moment of injection. FG neurons are not found at the bottom of layer III before injections on E16. Therefore the most superficial neurons of the third generation of the E13.5 injection have undergone three cell cycles during the 60 hr period (i.e., E13.5–E16) after the injection, suggesting a cell cycle on the order of 20 hr. This is considerably longer than the 12 hr for the average value at this age. Of the 11 instances in which this phenomenon could occur, it was observed in seven, and it specifically concerned 2.4% of the total number of labeled neurons.

Regionalization of cell-cycle parameters and areal specification

In the present study, we show that during production of infragranular layers there are important areal differences inTc and LF. These areal differences are relatively abrupt and closely linked to areal borders. They are considerably more pronounced than are the rather gentle neurogenic gradients that can be detected across large stretches of cortex (Smart and Smart, 1982; Bayer and Altman, 1991; Polleux et al., 1997).

Although all of the areas examined initiate and complete corticogenesis simultaneously, there are important areal differences in the timetable of layer production (Polleux et al., 1997). The simulation of these results (LF and Tc) shows that regional differences of the proliferative program generate important variations of laminar neuron number comparable to those observed just after the end of neurogenesis (Morin and Beaulieu, 1994). This suggests that the proliferative program plays a major role in regulating proportions of neurons allocated to each layer, whereas as suggested by Finlay, the final number of neurons per radial column is adjusted by cell death (Finlay and Slattery, 1983).

The present results show differences within sensorimotor areas as well as between sensorimotor and visual areas. The apparent absence of differences between areas 17 and 18a could be attributable to the visual areas having truly identical kinetics. This would suggest that these two areas may have identical laminar neuron numbers at birth. Alternatively, these two areas may exhibit cell-cycle differences that are too subtle to be detected in our experiments.

Cell-cycle dependent mechanisms have been implicated in the specification of allocortex (Eagleson et al., 1997). McConnell and colleagues have shown that cell–cell signaling during the final division specifies laminar fate in the neocortex (McConnell and Kaznowski, 1991; Frantz and McConnell, 1996; Bohner et al., 1997). Laminar fate restriction determines the timetable of layer production, which we have shown is area specific, thereby linking the specification of cortical areas and layers (Polleux et al., 1997). Here we show that regulation of the parameters of the cell cycle along with the signaling that McConnell and colleagues have shown specifies the recruitment to a particular layer play important roles in the generation of unique features of neocortical areas and are a consistent feature across mammalian orders (Dehay et al., 1993). The role of the cell cycle in the specification of cortical areas provides further evidence of an inter-relationship between CNS pattern formation and cell-cycle regulation (Oppenheim et al., 1989; Ross, 1996).

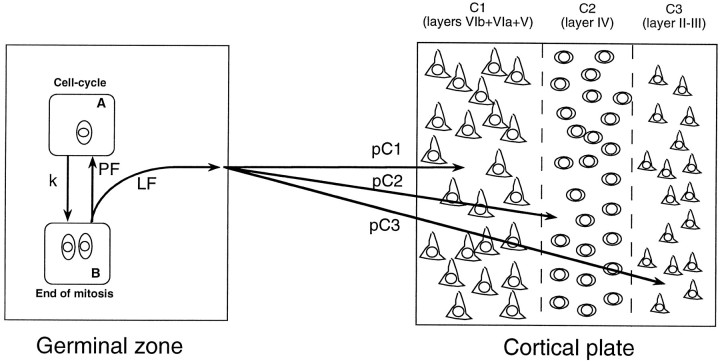
The model of cortical neurogenesis we have elaborated is a deterministic, compartmentalized model. The use of compartments represents a powerful tool to simulate transitions of cells from one state to another as a function of time (Quastler and Sherman, 1959;Godfrey, 1983). In the ventricular zone, we distinguished two compartments to simulate progression of precursors through the cell cycle (Fig. 14). The first compartment A represents cycling precursors in phases G1, S, or G2, and the second compartment B represents precursors in M phase when they have to either leave the cell cycle (defining the leaving fraction, LF) or continue to progress through the cell cycle (proliferative fraction,PF = 1 − LF). The transition from compartment A to B is proportional to the duration of the cell cycle (Tc), and the number of divisions per unit of time (D) is defined as:

$$D=\frac{\text{dN}}{\text{dt}}=k\times N$$ Equation 1

where N represents the number of precursors at the instant t and where k corresponds to division constant, i.e., the probability for a precursor to divide per unit of time.

Fig. 14.

Schematic view of the compartments used in our model of cortical neurogenesis. In the germinal zone (left) compartment A represents the pool of precursors progressing through the cell cycle. CompartmentB represents precursors at the end of mitosis when they either have to leave the cell cycle and become postmitotic (LF) or remain in the cell cycle and return to compartment B (PF). Transition from compartment A to B is proportional to the probability for a precursor to undergo mitosis per unit of time and thus is inversely proportional to the duration of cell cycle (Tc) (see ). Postmitotic neurons leaving the ventricular zone end their migration in the cortical plate in one of three different laminar compartments (C1, C2, or C3) according to probabilities (pC1, pC2, orpC3) that have been determined previously (Table 2) (Polleux et al., 1997).

Equation 1 can also be expressed as:

$$D=D_0\times e^{\text{kt}}=k\times N_0\times e^{\text{kt}}$$ Equation 2

where D₀ and N₀represent, respectively, the value of D and N at time 0.

Tc can be defined as the time required for a precursor to go from one mitotic phase to another but can also be described as the time needed for a precursor to give rise to two daughter cells (doubling time). According to the second definition, Tc is equivalent to the period required for the proliferative activity to be doubled. Thus, according to Equation 2 we can write:

$$\frac{A}{A_0}=\frac{2}{1}=e^{\text{k}\times \text{Tc}}$$ Equation 3

From this we can extract the value of the constantk:

$$k=\frac{ln2}{\text{Tc}}$$ Equation 4

By definition, postmitotic neurons that constitute the LF cannot reenter the cell cycle and instead migrate to one of the three laminar compartments that constitute the neocortex: compartment C1 (infragranular compartment including layers VIb, VIa, and V), compartment C2 (layer IV), and compartment C3 (layers II–III). The probability (pC₁,pC₂, pC₃, respectively) for a neuron to end up in a given laminar compartment is a function of time, which is defined on the basis of our own experimental measures of the timetable of laminar production (Table2). At any given momentpC₁ + pC₂ +pC₃ = 1.

Table 2.

Evolution of the laminar probabilities characterizing areas 6 and 3 neurogenesis

Embryonic days of tritiated thymidine injection	Laminar probabilities (%)
	Infragranular		Layer IV		Supragranular
	Area 6	Area 3	Area 6	Area 3	Area 6	Area 3
E12.5	100	100
E13.5	100	100
E14	100	100
E14.5	100	100
E15.5	100	95		5
E16	88.9	22.6	11.1	73.6		3.8
E16.5	64.5	7.3	32.3	78.1	3.2	14.6
E17.5					100	100
E18.5					100	100

This parameter is defined as the probability for a neuron born on a given embryonic day in one of three radial compartments: (1) infragranular compartment (layers VIb + VIa + V), (2) layer IV, and (3) supragranular compartment (layers II and III). For experimental measures, see Polleux et al. (1997).

From these considerations, we obtained the following ODE:

Transition from compartment A to B:

$$\frac{{\text{dN}}_A}{\text{dt}}=[PF\times N_B]-[k\times N_A]=[(1-LF)\times N_B]-[k\times N_A]$$ Equation 5

Transition from compartment B to A:

$$\frac{{\text{dN}}_B}{\text{dt}}=[2\times k\times N_B]-N_A$$ Equation 6

Transition from compartment B to Cx (which represent C1, C2, or C3):

$$\frac{{\text{dC}}_{\text{x}}}{\text{dt}}=LF\times N_B\times {\text{pC}}_{\text{x}}$$ Equation 7

Our simulations always start with an initial number of precursors in the ventricular zone compartment A (N_A), which equals 1, a number of precursors in compartment B (N_B), and a number of postmitotic neurons in compartments Cx (N_Cx), which both equal 0.