Abstract
Optimal choices benefit from previous learning. However, it is not clear how previously learned stimuli influence behavior to novel but similar stimuli. One possibility is to generalize based on the similarity between learned and current stimuli. Here, we use neuroscientific methods and a novel computational model to inform the question of how stimulus generalization is implemented in the human brain. Behavioral responses during an intradimensional discrimination task showed similarity-dependent generalization. Moreover, a peak shift occurred, i.e., the peak of the behavioral generalization gradient was displaced from the rewarded conditioned stimulus in the direction away from the unrewarded conditioned stimulus. To account for the behavioral responses, we designed a similarity-based reinforcement learning model wherein prediction errors generalize across similar stimuli and update their value. We show that this model predicts a similarity-dependent neural generalization gradient in the striatum as well as changes in responding during extinction. Moreover, across subjects, the width of generalization was negatively correlated with functional connectivity between the striatum and the hippocampus. This result suggests that hippocampus–striatal connections contribute to stimulus-specific value updating by controlling the width of generalization. In summary, our results shed light onto the neurobiology of a fundamental, similarity-dependent learning principle that allows learning the value of stimuli that have never been encountered.
Introduction
A shiny object on the floor easily compels us to pick it up. Such behavior is caused by a representation of predicted reward: glitter is associated with gold. According to reinforcement learning (RL) theory, reward predictions of different stimuli need to be learned by experience. However, animals and humans approach stimuli that have never been paired with reward but are perceptually similar to a previously rewarded stimulus. This ability, named stimulus generalization (Guttman and Kalish, 1956), is a key process underlying adaptive behavior because it relieves the learning system from the requirement of strict stimulus identity. For decades, experimental psychology has studied stimulus generalization (Ghirlanda and Enquist, 2003; Pearce et al., 2008) and neuroscientific attempts to capture how the brain generalizes from past experience have focused on acquired equivalence, inference, and categorization (Shohamy and Wagner, 2008; Seger and Miller, 2010; Chumbley et al., 2012; Wimmer et al., 2012). However, the neurobiological mechanisms underlying stimulus generalization have remained unclear.
Stimulus generalization is usually examined by pairing a stimulus with reward [rewarded conditioned stimulus (CS+)] and pairing another stimulus with no reward [unrewarded conditioned stimulus (CS−)]. Importantly, the sensory features of the CS+ and the CS− differ only in one continuous dimension (orientation, wavelength, etc.). Behavioral generalization gradients are then revealed during a test phase in extinction in which the animal is presented with a set of stimuli that also vary along that dimension (Hanson, 1959). Although the test stimuli have never been paired with reward, animals respond to test stimuli that are similar to the CS+. A key finding in these experiments is the peak shift (Purtle, 1973; Wisniewski et al., 2009; Derenne, 2010): the peak of the generalization gradient is displaced from the CS+, in the direction away from the CS−, thereby enhancing the subjective difference between CS+ and CS−.
RL theory provides a powerful framework for the study of learning processes (Sutton and Barto, 1998). The teaching signals in RL models are reward prediction errors (PEs) that update the reward predictions of sensory stimuli. However, standard RL models fail to account for stimulus generalization because they do not consider the similarity between stimuli. Here we propose a similarity-based RL model wherein stimulus generalization is implemented by PEs that update not only the value of the currently presented stimulus but also of other, similar stimuli that have not been presented. We use an intradimensional discrimination task in combination with fMRI and examine behavioral and neural generalization gradients during the test phase in extinction. We apply our similarity-based RL model to the behavioral and neural data to test whether it accounts for stimulus generalization on both levels. Given previous reports of PE responses in the ventral striatum (O'Doherty et al., 2003), we hypothesized that model-generated PEs correlate with activity in the striatum. Moreover, the striatum is closely connected to the hippocampus (Grace et al., 2007), and both systems interact during other generalization-like inference phenomena (Wimmer et al., 2012). Accordingly, we hypothesized that interactions between the striatum and the hippocampus mediate similarity-dependent stimulus generalization.
Materials and Methods
Subjects.
Twenty-three healthy subjects (10 females, 21.52 ± 0.43 years old, mean ± SEM) with normal or corrected-to-normal vision were included in the experiment. The study was approved by the local ethics review board of the University of Zurich, and subjects provided informed consent to participate.
Experimental design and stimuli.
Subjects learned the association between oriented Gabor patches (39° and 51°; Fig. 1C) and reward or no reward (0 and 30 points, respectively) using a classical conditioning procedure (see below). Each point was converted to 0.01 Swiss Francs (CHF) and paid to the subjects in addition to a 30 CHF show-up fee at the end of the experiment. After learning, subjects performed test sessions (in extinction) while fMRI data were acquired. In each trial of the test phase (see below), 1 of 15 oriented Gabor patches (17°, 21°, 25°, 29°, 33°, 37°, 41°, 45°, 49°, 53°, 57°, 61°, 65°, 69°, and 73°; Fig. 1C) was presented and no outcome was shown. In total, subjects performed eight test sessions during fMRI acquisition. Before each test session, the conditioning procedure was repeated to refresh stimulus–outcome associations (Fig. 1D).
Figure 1.
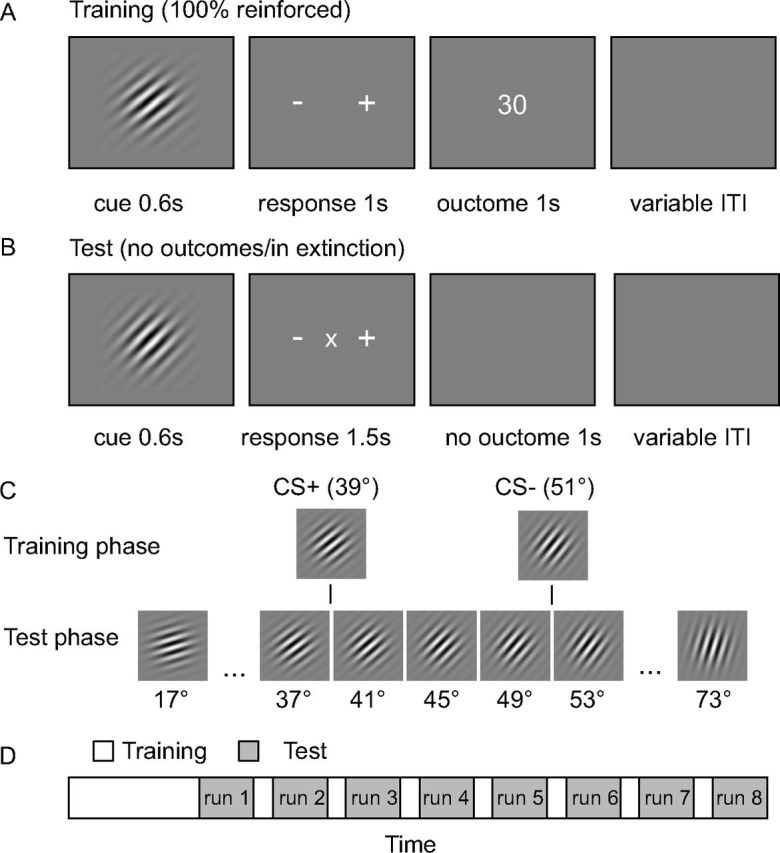
Experimental design and stimuli. A, Classical conditioning procedure. During each conditioning trial, one orientation (CS+ or CS−) was shown for 600 ms. Subjects had to indicate whether the current orientation will be rewarded (+) or not (−) using a button press. After the response, the outcome was presented (30 or 0 points for CS+ and CS−, respectively). B, Test phase in extinction. In each trial, subjects were presented with 1 of 15 different test orientations and had to indicate whether the current orientation was the one previously associated with reward (+), no reward (−), or neither of them (×). The mapping between buttons and +/−/× was randomized in each trial. Importantly, the test was performed in extinction, and thus, no outcomes were provided. C, Stimuli used during training and test phases. Please note that the CS+ and CS− were not shown during the test phase. D, In total, subjects performed eight test runs, and, after each scanning run, the training was repeated for 20 trials.
Conditioning procedure.
In each trial, subjects were presented with an oriented Gabor patch for 600 ms (Fig. 1A). Subjects had to indicate whether the current stimulus will lead to reward (+) or no reward (−) by pressing a button corresponding to the signs on a response mapping screen. Responses to both CS+ and CS− were required to ensure that fMRI results during the test session are not attributable to differential motor associations (excitation vs inhibition) of CS+ and CS−. The mapping between motor responses and +/− was randomized in each trial. When subjects pressed a button, the brightness of the signs on the screen slightly decreased to indicate that a response has been made. The screen disappeared after 1000 ms (maximum decision time) and was replaced by an outcome screen (1000 ms) indicating the amount of points they received (30 or 0). When subjects failed to respond within 1000 ms, “too slow” was presented instead of the outcome. The CS+ and CS− predicted the outcome with 100% contingency, and the outcome was independent of the correctness of the behavioral response. The association between orientation (39° and 51°) and reward was counterbalanced across subjects. The initial training phase consisted of 20 consecutive trials of CS+ and 20 consecutive trials of CS− (randomized across subjects), followed by 50 CS+ trials randomly intermixed with 50 CS− trials. The retraining sessions between the test sessions consisted of 20 trials with CS+ and CS− trials (10 each) randomly intermixed.
Test in extinction.
Each of the eight test sessions during fMRI acquisition consisted of 60 trials. In each trial, subjects saw 1 of 15 orientations for 600 ms (Fig. 1B,C), and each orientation was presented four times per session in pseudorandom order such that each orientation was presented once before orientations were repeated. Please note that the original CS+ and CS− were not shown during the test. Directly after the stimulus, subjects had to indicate whether the current orientation was the one that predicts reward (+), no reward (−), or neither of both (×), by pressing a button with the index, middle, or ring finger of their right hand, corresponding to the signs on a response mapping screen. The mapping between buttons (fingers) and +/−/× was randomized in each trial to dissociate signals related to motor preparation and execution from reward predictions. Again, when subjects pressed a button, the brightness of the signs on the screen slightly decreased to indicate that a response has been made and the screen disappeared after 1500 ms (maximum decision time). Importantly, the test was performed in extinction, i.e., no outcomes were shown for all orientations. This design ensured that subjects made motor responses to all stimuli and thus allowed us to observe reward PE responses to all orientations independent of potential confounds attributable to reward feedback, different visual stimulation, and different cognitive or motor demands. Trials were separated by a variable interval ranging from 1.9 to 11.9 s (1.9 s fix, plus a variable interval drawn from an exponential distribution with mean of 2 s, truncated at 10 s).
Similarity-based RL model.
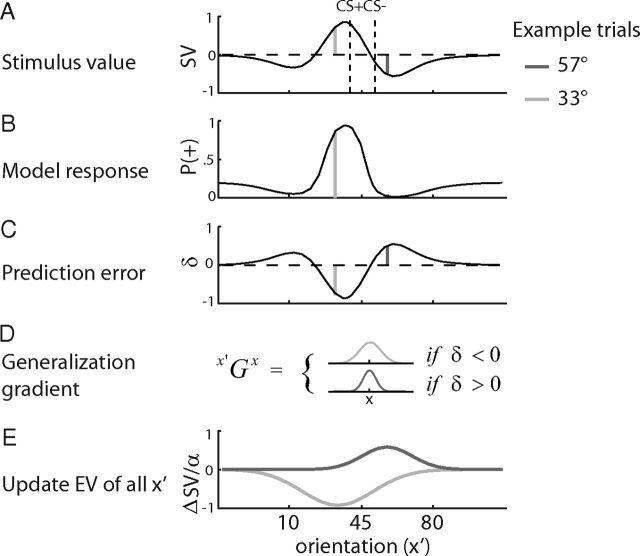
The values of all orientations x are stored in a stimulus value buffer SVx (Fig. 2). On trial t, the predicted reward is given by Vt = SVtx. Based on this value, the model makes a response (P) whether the current stimulus is a non-rewarded or rewarded stimulus (probability of a + response ranging from 0 to 1) given by , where a is the horizontal offset of the sigmoid function, and β is its slope. A PE δ is computed as the difference between actual reward received R (1 or 0 for received or omitted outcomes, respectively) and the predicted reward V according to δt = Rt − Vt. Importantly, δ is not only used to update the value of the current orientation x (SVtx) but also the values of all other stimuli x′ (SVtx′) in proportion to their similarity with x according to ΔSVx′ = δt × αphase × x′Gx, where αphase is a set of learning rates (separate learning rates for the training phase with feedback and testing phase in extinction). x′Gx is a subjective measure of the similarity between x′ and x that varies between 0 and 1 and is defined as x′Gx = , where σsign(δt) controls the width of generalization and is allowed to have different values for positive and negative PEs. x′Gx is scaled to a minimum and maximum of 0 and 1, respectively, such that x′Gx = 1 for x′ = x.
Figure 2.
A similarity-based RL model. A, Illustration of stimulus values as a function of orientation (1 subject, averaged over runs). Black line depicts the stimulus value of different orientations that have been learned by rewarding only the CS+ but not the CS− during conditioning. Bright and dark gray vertical lines depict example trials with different orientations during the test phase. B, Model responses (P, probability of + response) as a function of orientation. C, PEs (δ) for the two example trials during the test in extinction. D, The model allowed different widths of generalization for negative and positive PEs. E, Change of SV as a function of orientation. In this model, the stimulus value of all orientations is updated in each trial in proportion to the similarity between a given orientation and the current orientation.
The free parameters of this model (σneg, σpos, a, β, αtrain, and αtest) were individually fitted for each subject (using all data from initial conditioning, all test runs in extinction, as well as the conditioning sessions between scanning runs) by maximizing the log likelihood estimate, i.e., the logarithm of the product of the modeled probabilities of subjects' actual responses (coded as 1 for + and 0 for − or × responses, respectively). On average, this fitting procedure yielded the following set of parameters: σneg = 21.66 ± 1.68, σpos = 17.49 ± 1.54, β = 3.65 ± 0.23, a = 0.48 ± 0.03, αtrain = 0.85 ± 0.05, and αtest = 0.03 ± 0.01.
fMRI acquisition and preprocessing.
Functional imaging was performed on a Philips Achieva 3 T whole-body scanner equipped with an eight-channel head coil. During each of the eight test sessions, 177 T2*-weighted whole-brain EPI images (37 transversal slices acquired in ascending order) were acquired with a repetition time of 2000 ms. Imaging parameters were as follows: slice thickness, 3 mm; in-plane resolution, 2.75 × 2.75 mm; echo time, 30 ms; flip angle, 90°. Preprocessing was performed using SPM8 and consisted of slice-time correction, realignment, spatial normalization to the standard EPI template of the Montreal Neurological Institute, and spatial smoothing using a Gaussian kernel of 8 mm FWHM.
fMRI data analysis.
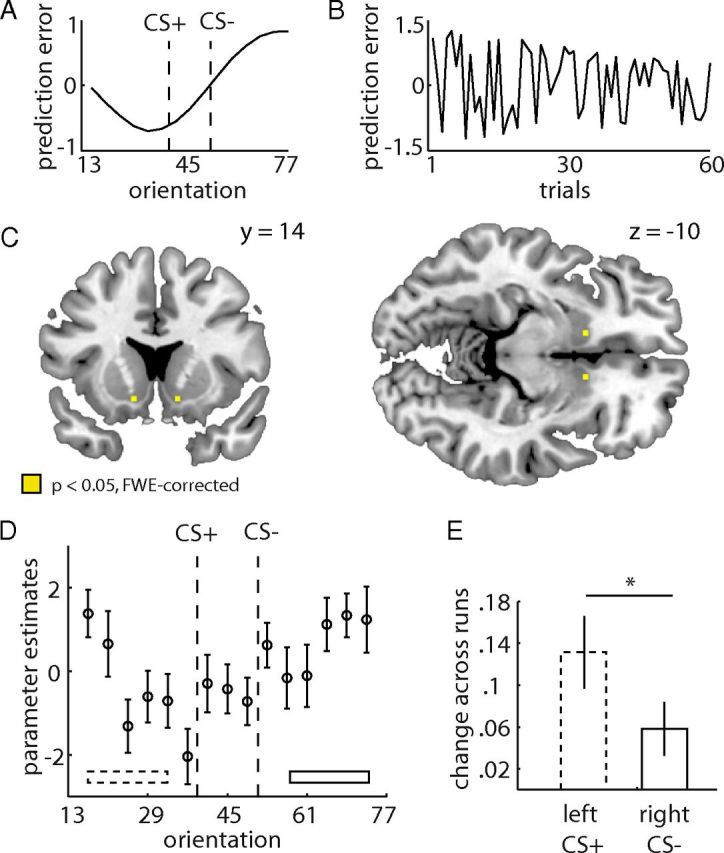
To identify brain regions correlating with PEs derived from the similarity-based RL model, we used a general linear model (GLM) with the following three regressors for each of the eight test sessions: (1) onset of expected time of outcome (offset of the response mapping screen), (2) a parametric regressor of stimulus orientation (z-standardized), and (3) a parametric regressor of PE (z-standardized). Because PEs are correlated with stimulus orientation, including orientation as a parametric regressor in the GLM controlled for a simple verbal rule (“angle x is proportional to the probability of reward”) and for signals related to the orientation rather than the PE per se. In a separate GLM, we also controlled for an alternative verbal rule (“angles larger than 45° lead to reward”), as implemented by a step function (x < 45° = −1 and x > 45° = 1). This GLM revealed very similar PE results in the striatum (FWE-corrected for the striatum) as the primary model. All regressors were convolved with a canonical hemodynamic response function (HRF) and together with the motion parameters from the realignment procedure regressed against the BOLD signal in each voxel. Voxelwise second-level t tests (that included σneg and σpos as covariates) were applied to the resulting parameter estimates of the PE regressor. To identify significant voxels, we used a threshold of p < 0.05, FWE corrected for multiple comparisons in the striatum [bilateral caudate and putamen of the Automated Anatomical Labeling (AAL) atlas].
The behavioral generalization gradient showed changes left of the CS+ (i.e., distal to the CS−) across consecutive runs (see Figs. 3B, 4D), which were also predicted by the similarity-based RL model (see Fig. 4C,D). To investigate whether striatal PE responses elicit similar changes across runs, we defined a functional region of interest (ROI) that is independent of any changes across runs (i.e., unbiased). Specifically, we estimated an additional single-subject GLM with 15 onset regressors, one for the outcome omission of each orientation. The single-subject parameter estimates per orientation (averaged across runs) were then applied to a second-level, one-way ANOVA with repeated measures and 15 levels (one for each orientation). We computed a contrast based on the average (mean corrected and multiplied by −1) behavioral generalization gradient [average P(+ response) across subjects and runs; Fig. 2A]. This contrast identified peak voxels in the bilateral ventral striatum [left (−12, 11, −11) and right (15, 14, −11)], around which the ROI was created from 9 mm spheres. Please note that the ROI is unbiased because it is not based on regions identified to correlate with model-derived PEs, which already incorporate changes between runs (accordingly, using the parametric PE contrast to define the ROI would result in a biased, i.e., non-independent, ROI). In other words, the resulting ROI is independent of between-run (within-orientation) PE effects but not of between-orientation PE effects. Importantly, because we used this ROI only to test for activity changes between runs (and within orientation), the ROI is independent with respect to the analysis that was performed on the data extracted from this ROI.
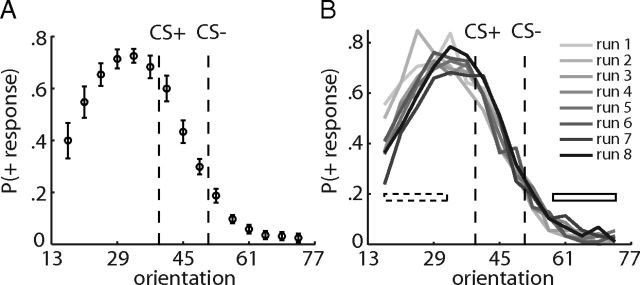
Figure 3.
Behavioral generalization gradient. A, The average proportion of + responses is plotted as a function of stimulus orientation. Error bars are SEM for n = 23 subjects. Responses were displaced from the CS+, in the direction away from the CS− (peak shift). B, Average + responses as a function of orientation and test run. Each gray shaded line represents data from one test run.
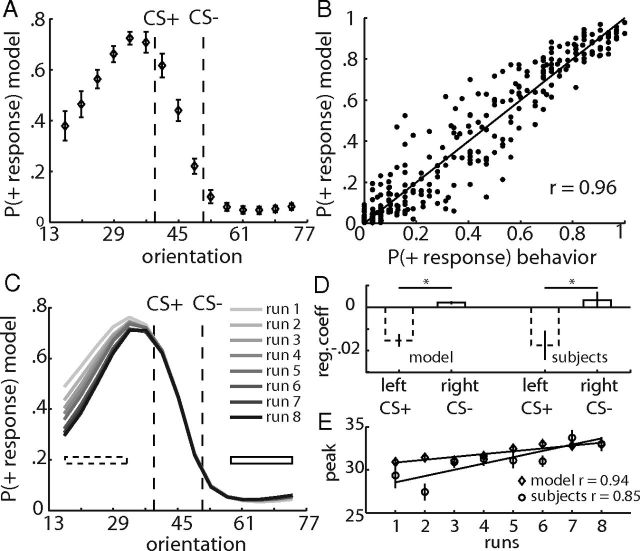
Figure 4.
Model behavior and comparison with subjects' behavior. A, Average model responses as a function of stimulus orientation. Error bars are SEM for n = 23 models. The model also reveals a peak shift away from the CS−. B, Scatter plot depicts relationship between the individual subject and model responses (1 point per orientation and subject). C, Average (across models) model responses as a function of orientation. Each gray shaded line represents data from one test run. D, Change of model (left) and subjects' responses (right) as a function of runs. Dotted bars depict change of responses across runs to orientations left of the CS+ (average across orientations indicated by dashed bar in C), and solid bars depict change of responses across runs to orientations right of the CS− (average across orientations indicated by solid bar in C). Changes across runs are regression coefficients from individual regressions of responses on run number. Error bars are SEM for n = 23. E, Change of peak shift across runs. The peaks of model (diamonds) and subjects' responses (circles) are plotted as a function of test runs. Error bars are SEM for n = 23.
Functional connectivity analysis.
We investigated PE-related differences in the functional connectivity between the striatum and the hippocampus by using a variant of the psycho-physiological interaction (PPI) model (Friston et al., 1997; Kahnt et al., 2009; Park et al., 2012). For each subject, the average time course was extracted from voxels in the striatum and multiplied with two indicator variables [one for high and one for low PEs (median split)] that were set to 1 for six volumes (12 s) after each onset of each trial and to 0 otherwise. These two regressors (psycho-physiological regressors for positive and negative PEs) were then included in a GLM along with two HRF-convolved onset regressors (psychological regressors for positive and negative PEs), the average time course in the striatum (physiological regressor), and the six head movement realignment parameters. The parameter estimates of the two psycho-physiological regressors reflect the correlation between activity in the striatum and activity in every other voxel during positive and negative PEs, respectively. In contrast to standard PPI models, the PPI term was then created on the single-subject level by computing the contrast between the parameter estimates of the two psycho-physiological regressors (positive vs negative PEs) (McLaren et al., 2012). For statistical inference, the resulting contrast images were applied to a second-level one-sample t test that included σneg and σpos as covariates. We searched for voxels in which functional connectivity (positive vs. negative PE) is significantly correlated with the difference between σpos and σneg by contrasting these two covariates. Significant correlations between σpos − σneg and functional connectivity (positive vs negative PE) were identified using a threshold of p < 0.05, FWE corrected for multiple comparisons in the bilateral hippocampus (AAL atlas).
Results
Behavioral generalization gradient
Although the test stimuli were never paired with reward, we found robust and differential + responses to the test stimuli. A one-way ANOVA with repeated measures revealed a significant main effect of orientation (F(14,308) = 53.78, p < 0.001). The average behavioral generalization gradient during the test phase is depicted in Figure 3A. In line with previous findings (Purtle, 1973; Wisniewski et al., 2009; Derenne, 2010), we found a strong peak shift, i.e., the peak of the generalization gradient was displaced from the CS+, in the direction away from the CS− (t test between responses left vs right of the CS+; t = 3.28, p < 0.01). Moreover, response times (RTs) were modulated by the orientation of the stimulus (one-way ANOVA with repeated measures, F(14,308) = 4.83, p < 0.001) and revealed a similar gradient as the behavioral responses (higher RT with higher probability of + responses).
Extended training and extinction during test trials have been shown to narrow the behavioral generalization gradient and reduce the peak shift (Terrace, 1966; Cheng et al., 1997). In line with this, we found that responses to orientations left of the CS+ (i.e., distal to the CS−) decreased with successive test runs (Fig. 3B). To quantify this decrease across runs, we averaged responses left of the CS+ (first five orientations) and regressed these responses against the run number (1–8) for each subject. As a control, this was also performed for responses right of the CS−, in which responses seemed to stay relatively constant across runs. This analysis revealed a significant negative slope for the responses left of the CS+ (t = −2.64, p < 0.05), which was significantly different from that of the responses right of the CS− (paired t test, t = −2.36, p < 0.05; Fig. 4D, right). Moreover, across runs, the peak of the behavioral generalization gradient seemed to shift back toward the CS+ (Fig. 3B). A one-way ANOVA with repeated measures on the peaks revealed a significant main effect of run (F(7,147) = 3.49, p < 0.05; Fig. 4E) and, importantly, a significant linear trend across runs (F(1,21) = 5.48, p < 0.05), demonstrating that the peak of responding shifts toward the CS+ across time.
A similarity-based RL model
To account for the observed behavioral generalization gradients, we designed a similarity-based RL model (Rescorla and Wagner, 1972). In this model, learning does not only occur for the stimulus that is present in a trial but also for stimuli that are similar to the current stimulus (Fig. 2; see Materials and Methods). The crucial difference to standard RL models is that the PE is used to update not only the value of the current stimulus x but also the values of all other stimuli x′ in proportion to their similarity to the current stimulus. This mechanism allows generalization because stimuli can acquire or lose reward value even though they have never been paired with reward or non-reward, respectively. Moreover, positive (outcome better than expected) and negative (outcome worse than expected) PEs can arise from one and the same outcome (i.e., nothing), depending on the relative similarity of the presented stimulus with the CS+ or the CS−.
For each subject, model parameters were fitted separately on a trial-by-trial basis, including all trials from initial training, test runs, and interim training sessions (see Materials and Methods). Importantly, positive PEs and negative PEs are assumed to lead to different widths of generalization. This was implemented by allowing separate model parameters for the width of generalization from positive (σpos) and negative (σneg) PEs. To test whether different widths for positive and negative PEs are necessary, we compared this model with a simpler model in which both widths were set to be identical (σpos = σneg). A formal model comparison (accounting for the number of free parameters) revealed that the model with separate widths for positive and negative PEs explained subjects' behavior significantly better than the simpler model (likelihood ratio test, χ2 = 727.98, p < 0.001). Strikingly, across subjects, the widths of generalization gradients for negative and positive PEs (σneg and σpos, respectively) differed significantly (t = 2.10, p < 0.05), with wider generalization for negative than positive PEs (mean ± SEM, σneg = 21.66 ± 1.68, σpos = 17.49 ± 1.54). This suggests that subjects tend to generalize more in the face of negative outcomes (Schechtman et al., 2010). Moreover, the widths of generalization gradients were not significantly correlated (r = 0.24, p = 0.27), indicating that generalization from negative and positive PEs represent independent processes. For completeness, we also compared our model with a standard RL model without generalization (i.e., x′Gx = 1 if x′ = x, and 0 otherwise). This model learns only the value of the CS+ and CS− during training, whereas the values of all test stimuli remain 0. Accordingly, as can be expected, the similarity-based RL model explained behavior significantly better than the standard RL model (likelihood ratio test, χ2 = 5572.3, p < 0.001).
Comparison of the model and behavioral data
In the following analyses, we compare the behavior of the model with the behavior of the subjects to assess how well the model characterizes subjects' responses during the test trials in extinction. The individually estimated model parameters and the individual sequences of stimuli and responses were used to simulate trialwise + responses [P(+ response)] for each subject. Notably, because the test stimuli were never paired with reward, the standard RL model predicts indifferent null responses to all test stimuli. However, the responses of our similarity-based model revealed a generalization gradient (Fig. 4A) as well as a peak shift (t test between behavioral responses left vs right of the CS+; t = 6.27, p < 0.001), very similar to subjects' actual responses. Indeed, across orientations and subjects, we found a significant correlation (r = 0.96, p < 0.001) between the responses of the model and the responses of the subjects (Fig. 4B).
To investigate whether the model predicts changes in responding across runs, we plotted the model responses for each test run separately. Like the behavioral responses, the predicted responses for orientations left of the CS+ decreased with successive test runs (Fig. 4C). Regressing these individual model responses against the run number (1–8) revealed a significant negative slope for the responses left of the CS+ (t = −5.37, p < 0.001), which was significantly different from that of the responses right of the CS− (paired t test, t = −5.33, p < 0.001; Fig. 4D, left). Across subjects, the regression coefficients from the model responses left of the CS+ were significantly correlated with the regression coefficients from subjects' actual responses (r = 0.87, p < 0.001). Similarly to subjects' actual behavior, we found that the peak of model responses shifted toward the CS+ across runs (Fig. 4E; main effect in ANOVA, F(7,147) = 3.51, p < 0.05; linear trend, F(1,21) = 6.88, p < 0.05). Indeed, the run-wise peaks of the models and the subjects were significantly correlated across subjects and runs (r = 0.76, p < 0.001). Together, these analyses indicate that our similarity-based RL model closely accounts for the observed behavioral generalization gradients.
PEs in the striatum during test in extinction
In our model, the reward PE forms a teaching signal that drives learning and stimulus generalization. To control for obvious signal differences induced by differential feedback during the outcome phase, we focus on the fMRI data during the test phase and identify brain regions that track the similarity-dependent PE derived from our model. Importantly, in the test phase, stimuli were shown in extinction, that is, without any outcome (blank screen). Thus, trial-by-trial differences in activity cannot be explained by different physical stimuli or different reward outcomes but must purely depend on internal representations of PE.
We generated trial-by-trial PEs using our similarity-based RL model. Because none of the test stimuli were ever paired with reward, the standard RL model does not predict any differential PE responses to the test stimuli. Thus, the test session in extinction is the ideal situation to test the predictions of our model. PEs result from violated reward predictions, and negative PEs can be expected at orientations in which reward predictions [i.e., P(+response)] are high (for the PEs of a single subject as a function of orientation; Fig. 5A). Moreover, the PEs during extinction decrease the value of the stimuli, leading to smaller PEs across time (for the PEs of a single subject as a function of trial number, see Fig. 5B). Thus, model-derived PEs vary across both orientation and trials in extinction.
Figure 5.
PEs during the test phase in extinction. A, Model-derived PEs from a single subject as a function of orientation. Note that the most negative PEs occur left of the CS+, in which subjects showed highest P(+ responses). B, PEs of a single subject as a function of trials within a run. Note that PEs decrease over time (i.e., during extinction). C, Activity in the ventral striatum correlates significantly with similarity-dependent PEs derived from the model. Activity is thresholded at p < 0.05 FWE corrected for the bilateral striatum. D, Average responses to the omission of outcomes (mean corrected) are plotted as a function of stimulus orientation. Error bars are SEM for n = 23 subjects. E, Change in striatal responses (independent ROI) to omitted outcomes across runs. Dotted bar depicts change of responses to orientations left of the CS+ (average across orientations indicated by dashed bar in B), and solid bar depicts change of responses to orientations right of the CS− (average across orientations indicated by solid bar in B). Changes across runs are regression coefficients from individual regressions of striatal responses on run number. Error bars are SEM for n = 23 subjects.
To identify regions in which activity correlates with PEs, we regressed the trial-by-trial vector of signed similarity-dependent PE against the BOLD signal in each voxel during the time of the expected outcome (offset of the response mapping screen; see Materials and Methods). Previous research on associative learning without generalization has revealed PE responses in the human striatum (O'Doherty et al., 2003; Tobler et al., 2006; Kahnt et al., 2009). In line with these findings, PE signals were significantly related to the activity in the bilateral ventral striatum [left, (−12, 14, −11), t = 4.74; right, (12, 17, −8), t = 4.70; p < 0.05, FWE corrected; Fig. 5C]. We observed no significant voxels outside the striatum (p < 0.05, FWE whole-brain corrected). To illustrate the neural responses to the different orientations, we extracted the response amplitudes during outcome omission for each orientation. Signal decreases to omitted outcomes differed as a function of stimulus orientation and showed a similar response profile (including the peak shift) as the behavioral generalization gradient (Fig. 5D; please note that this plot is purely illustrative because voxels that correlate with similarity-dependent PE were selected for signal extraction). These data suggest that striatal PE responses generalize in proportion to the similarity between novel and learned stimuli. That is, activity in the striatum represents a neural generalization gradient that mirrors the behavioral generalization gradient. To rule out that these PE responses are simply driven by differences in RT (or task difficulty reflected in RT), we estimated an additional GLM that also included a regressor of trial-by-trial RT. This GLM revealed very similar PE results in the ventral striatum [left, (−12, 8, −8), t = 4.23; right, (15, 20, −8); t = 4.78, p < 0.05, FWE corrected for the striatum], indicating that PE responses are robust to changes in RT.
Both the observed behavior and our similarity-based RL model indicate that the value of orientations left of the CS+ decreases across test runs. According to the model, this should be accompanied by increasing (less negative) PE responses to these orientations across runs. To test this prediction on the neural level, we used an unbiased ROI from a contrast that is independent of changes in PEs across runs (see Materials and Methods). As in the behavioral analysis, we regressed the individual responses in this ROI to orientations left of the CS+ (average of the first five orientations) against the run number (1–8) for each subject. To control for unspecific changes across runs, we performed the same analysis for responses right of the CS− (average of the last five orientations). We found a significant positive slope for BOLD responses left of the CS+ (t = 3.79, p < 0.01), which was significantly higher than the slope for responses right of the CS− (paired t test, t = 2.51, p < 0.05; Fig. 5E). These analyses further corroborate the notion that responses in the striatum reflect signals corresponding to PEs in our similarity-based RL model.
Hippocampal–striatal connectivity predicts generalization
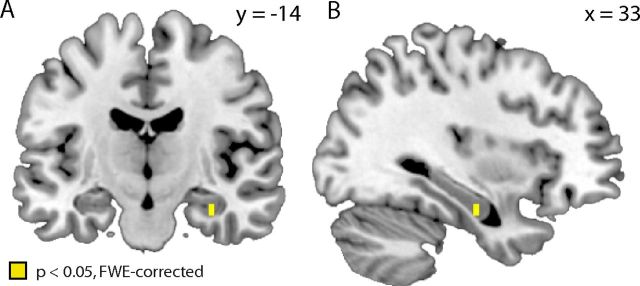
In a next step, we tested the idea that interactions between the striatum and the hippocampus are related to basic similarity-dependent stimulus generalization effects. The analyses above have shown that subjects generalized differentially from positive and negative PEs. We reasoned that, if the connectivity between the hippocampus and the striatum mediates generalization, the width of generalizing from positive versus negative PEs (σpos − σneg) should be correlated with the strength of hippocampal–striatal connectivity during positive versus negative PEs (see Materials and Methods). In line with our hypothesis, we found a significant correlation in the right anterior hippocampus [(33, −13, −23), t = 5.18, p < 0.05, FWE corrected; Fig. 6]. In these voxels, functional connectivity with the striatum (during positive vs negative PE) was negatively correlated with the strength of generalizing from positive versus negative PEs. This negative correlation suggests that subjects with weak hippocampal–striatal connectivity tend to update a wide range of stimuli, leading to wide generalization gradients. Conversely, subjects with strong hippocampal–striatal connectivity tend to update stimulus values more discriminatively, leading to narrow generalization gradients. In line with the finding that generalization gradients were significantly wider for negative versus positive PEs, across subjects, stronger hippocampal–striatal connectivity was found for positive versus negative PEs (t = 2.09, p < 0.05). We observed no significant voxels outside the hippocampus (p < 0.05, FWE whole-brain corrected).
Figure 6.
Hippocampal–striatal connectivity predicts width of generalization. Coronal (A) and sagittal (B) slices depicting the significant negative correlation between functional connectivity in positive versus negative PEs trials and the width of generalization from positive versus negative PEs (σpos − σneg). Correlation is thresholded at p < 0.05 FWE corrected for the bilateral hippocampus.
Finally, we tested whether not only hippocampal–striatal connectivity but also PE-related activity in the hippocampus is related to the width of generalizing from positive versus negative PEs (σpos − σneg). We did not find any significant correlation in the hippocampus cluster identified above (r = 0.06, p = 0.77) or any other voxel in the hippocampus, even at an uncorrected threshold of p < 0.001. However, a whole-brain analysis revealed a significant (p < 0.05, FWE whole-brain corrected) negative correlation between the width of generalizing from positive versus negative PEs and PE-related activity in the left DLPFC [BA 9, (−51, 14, 43), t = 7.70]. This finding suggests that the lower the PE-related activity in the DLPFC, the more subjects tend to generalize from positive versus negative PEs.
Discussion
Stimulus generalization relieves individuals from having to learn the reward value of each and every stimulus before these stimuli can be used to guide choices. Conversely, generalizing too widely is maladaptive because no discriminative predictions about reward (or punishment) can be acquired. Despite its importance for adaptive behavior, the computational implementation of stimulus generalization as well as its underlying neural mechanisms have remained unclear. Here we have shown that a novel, similarity-based RL model accounts for both behavioral and neural generalization gradients. We observed PE responses in the ventral striatum to stimuli that have never been paired with reward. Thus, these PE responses rely purely on value representations that have been generalized from the previously rewarded CS+. Moreover, functional connectivity between the ventral striatum and the hippocampus predicted individual differences in the width of generalization.
A number of connectionist models have been developed that also explain generalization effects (Pearce, 1994; Saksida, 1999; Ghirlanda and Enquist, 2003; Guillette et al., 2010; Wisniewski et al., 2012). For instance, a modified perceptron model can account for dynamic changes in generalization gradients over the course of training (Wisniewski et al., 2012). In contrast to using a neural network model, here we took an RL approach to generalization. RL is rooted in animal learning theory (Sutton and Barto, 1998), and the computational variables of RL models (such as the PE) reflect neural processes critical for learning (Schultz et al., 1997; Waelti et al., 2001; Montague et al., 2004), providing a direct link to brain functioning. Because these signals are well documented, a similarity-based modification of RL models is relatively straightforward, and the biological implementation can be easily understood. In our model, the PE is not only used to update the value of the current stimulus but also the value of similar stimuli that have not been presented. This provides a computational mechanism for a fundamental, similarity-dependent learning principle that allows individuals to learn the value of stimuli that have not been paired with reward.
Our model predicted the behavioral generalization gradient, including the observed peak shift and changes in responding across test sessions. Also, similarity-dependent PE signals derived from our model were found to correlate with activity in the striatum. Specifically, PE responses in the ventral striatum were not symmetrically distributed around the CS+ but were displaced from the CS+ in the direction away from the CS−, closely mirroring the behavioral generalization gradient. Moreover, striatal PE responses followed the changes across subsequent test sessions that occurred also in the behavior and were predicted by the model. Given that PEs are teaching signals of the model, these findings suggest that the ventral striatum is the core region for similarity-dependent value updating. The present results thus extend those of previous studies showing PE-related activity in the striatum across a wide range of learning tasks not involving similarity-dependent generalization (O'Doherty et al., 2003; Tobler et al., 2006; Kahnt et al., 2009, 2011; Burke et al., 2010; Park et al., 2010; Daw et al., 2011; Li et al., 2011). Together, our similarity-based RL model provides a powerful account for stimulus generalization. It can be used to make novel and testable predictions about behavioral and neural effects of stimulus generalization in more complex environments, such as situations involving multiple dimensions or complex patterning (Pearce et al., 2008).
Subjects generalized differently based on positive and negative PEs. Specifically, wider generalization gradients were found for negative compared with positive PEs. Such wider generalization for negative than positive events is consistent with previous behavioral studies of generalization (Schechtman et al., 2010) and has potential implications for models of anxiety disorders and posttraumatic behavior. Additional analyses on the neurobiological origin of the width of generalization revealed that individual differences in this parameter are mediated by the functional connectivity between the striatum and the hippocampus. Specifically, the width of generalization was negatively correlated with the strength of hippocampal–striatal connectivity. In other words, subjects with stronger connectivity showed more discriminative value updating, whereas subjects with weaker connectivity generalized more widely. Thus, by regulating the width of generalization, the connection between the hippocampus and the striatum implements an essential mechanism for discriminative value updating. Previous research on hippocampal–striatal interactions is in line with this idea. The hippocampus sends excitatory projections to the ventral striatum (Kelley and Domesick, 1982), and stimulation of the hippocampus causes striatal neurons to enter a depolarized state (O'Donnell and Grace, 1995). By extension, projections from the hippocampus to the ventral striatum can gate dopaminergic activity in the midbrain (Grace et al., 2007), suggesting that dopamine may control the width of generalization. Indeed, administration of chlorpromazine, an effective D2 dopamine receptor blocker, affects generalization gradients in pigeons (Lyons et al., 1973).
Traditionally, declarative memory processes in the medial temporal lobe (Eichenbaum, 2000; Norman and O'Reilly, 2003; Squire and Wixted, 2011) and RL processes in the striatum (Montague et al., 2004; Frank and Claus, 2006; Samejima and Doya, 2007; Daw et al., 2011) have been conceptualized to work rather independently from each other. Our findings concur with reports of interactions between both systems (Poldrack et al., 2001), specifically in mediating generalization phenomena such as transitive inference or acquired equivalence (Frank et al., 2006; Shohamy and Wagner, 2008; Moustafa et al., 2010; Wimmer et al., 2012). Unlike stimulus generalization tasks, in which sensory similarity builds the basis for generalization, in acquired equivalence tasks, physically different stimuli acquire relational similarity through their association with the same stimulus or outcome. Interestingly, an integrated computational model of basal ganglia and hippocampus function predicts specific performance alterations on such tasks in different neurological and psychiatric disorders involving damage in both regions (Moustafa et al., 2010). Moreover, connectivity between the striatum and the hippocampus correlates with the degree to which subjects acquire and use relational similarity information in a reward-based acquired equivalence task (Wimmer et al., 2012). Our results extend these findings to basic stimulus generalization in which sensory rather than relational similarity builds the basis for generalization. In particular, by showing that functional connectivity between the striatum and the hippocampus mediates basic similarity-based generalization, our data suggest that interactions between the two systems might be more profound than previously thought.
In theory, a behavioral generalization gradient as observed in our study may occur because of a failure to discriminate between cues (as a result of noise or because of the imprecision of the perceptual system) rather than similarity-dependent updating of reward predictions. Specifically, stimulus generalization (including the peak shift) could also result from forming finer tuning curves for CS+ and CS− by actively delineating a boundary between them. However, in our data, the widths of the generalization gradients for negative and positive PEs were uncorrelated and differed significantly, indicating that generalization from negative and positive PEs represent independent processes. This suggests that similarity-based generalization does not simply reflect a failure to perceptually discriminate the different orientations, because this would have resulted in correlated and statistically indistinguishable widths of generalization gradients for positive and negative PEs. Furthermore, our PE results in the striatum could have been driven by responses to easy versus difficult stimuli (i.e., stimuli farther away from 45° are easier to perceptually discriminate and therefore cause higher striatal activity). However, controlling for trial-by-trial RTs (which should reflect difficulty) did not change the PE results, indicating that difficulty is a very unlikely explanation for our PE findings. Moreover, BOLD responses left of the CS+ (but not right of the CS−) changed across runs, which was predicted by our similarity-based RL model but is hard to explain in terms of difficulty.
Our experiment was explicitly designed to investigate similarity-dependent PEs. This came at the cost of not being able to investigate anticipatory value signals. However, future research should specifically aim at identifying brain regions correlating with anticipatory value signals to provide complementary evidence for the neural basis of similarity-based learning.
In summary, we have shown behavioral and neural reward responses to stimuli that have never been paired with reward. Our proposed model provides a computational mechanism for this fundamental learning principle, which leads to learning in stimuli that have never been experienced. This mechanism is highly adaptive because it allows individuals to behave successfully in novel but similar situations. Our results suggest that functional connections between the hippocampus and the ventral striatum are involved in stimulus generalization by regulating the width of generalization, possibly by exerting control over dopamine transmission. This indicates that stimulus generalization depends on the dynamic interplay between brain regions associated with RL and declarative memory processes.
Footnotes
This work was supported by Swiss National Science Foundation Grant PP00P1_128574 and the Swiss National Centre of Competence in Research in Affective Sciences. We thank the Neuroscience Center Zurich and the Zurich Center for Integrative Human Physiology.
References
- Burke CJ, Tobler PN, Baddeley M, Schultz W. Neural mechanisms of observational learning. Proc Natl Acad Sci U S A. 2010;107:14431–14436. doi: 10.1073/pnas.1003111107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng K, Spetch ML, Johnston M. Spatial peak shift and generalization in pigeons. J Exp Psychol Anim Behav Process. 1997;23:469–481. [Google Scholar]
- Chumbley JR, Flandin G, Bach DR, Daunizeau J, Fehr E, Dolan RJ, Friston KJ. Learning and generalization under ambiguity: an fMRI study. PLoS Comput Biol. 2012;8:e1002346. doi: 10.1371/journal.pcbi.1002346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw ND, Gershman SJ, Seymour B, Dayan P, Dolan RJ. Model-based influences on humans' choices and striatal prediction errors. Neuron. 2011;69:1204–1215. doi: 10.1016/j.neuron.2011.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derenne A. Shifts in postdiscrimination gradients within a stimulus dimension based on bilateral facial symmetry. J Exp Anal Behav. 2010;93:485–494. doi: 10.1901/jeab.2010.93-485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichenbaum H. A cortical-hippocampal system for declarative memory. Nat Rev Neurosci. 2000;1:41–50. doi: 10.1038/35036213. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Claus ED. Anatomy of a decision: striato-orbitofrontal interactions in reinforcement learning, decision making, and reversal. Psychol Rev. 2006;113:300–326. doi: 10.1037/0033-295X.113.2.300. [DOI] [PubMed] [Google Scholar]
- Frank MJ, O'Reilly RC, Curran T. When memory fails, intuition reigns: midazolam enhances implicit inference in humans. Psychol Sci. 2006;17:700–707. doi: 10.1111/j.1467-9280.2006.01769.x. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Buechel C, Fink GR, Morris J, Rolls E, Dolan RJ. Psychophysiological and modulatory interactions in neuroimaging. Neuroimage. 1997;6:218–229. doi: 10.1006/nimg.1997.0291. [DOI] [PubMed] [Google Scholar]
- Ghirlanda S, Enquist M. A century of generalization. Anim Behav. 2003;66:15–36. [Google Scholar]
- Grace AA, Floresco SB, Goto Y, Lodge DJ. Regulation of firing of dopaminergic neurons and control of goal-directed behaviors. Trends Neurosci. 2007;30:220–227. doi: 10.1016/j.tins.2007.03.003. [DOI] [PubMed] [Google Scholar]
- Guillette LM, Farrell TM, Hoeschele M, Nickerson CM, Dawson MR, Sturdy CB. Mechanisms of call note-type perception in black-capped chickadees (Poecile atricapillus): peak shift in a note-type continuum. J Comp Psychol. 2010;124:109–115. doi: 10.1037/a0017741. [DOI] [PubMed] [Google Scholar]
- Guttman N, Kalish H. Discriminability and stimulus generalization. J Exp Psychol. 1956;51:79–88. doi: 10.1037/h0046219. [DOI] [PubMed] [Google Scholar]
- Hanson HM. Effects of discrimination training on stimulus generalization. J Exp Psychol. 1959;58:321–334. doi: 10.1037/h0042606. [DOI] [PubMed] [Google Scholar]
- Kahnt T, Park SQ, Cohen MX, Beck A, Heinz A, Wrase J. Dorsal striatal-midbrain connectivity in humans predicts how reinforcements are used to guide decisions. J Cogn Neurosci. 2009;21:1332–1345. doi: 10.1162/jocn.2009.21092. [DOI] [PubMed] [Google Scholar]
- Kahnt T, Grueschow M, Speck O, Haynes JD. Perceptual learning and decision-making in human medial frontal cortex. Neuron. 2011;70:549–559. doi: 10.1016/j.neuron.2011.02.054. [DOI] [PubMed] [Google Scholar]
- Kelley AE, Domesick VB. The distribution of the projection from the hippocampal formation to the nucleus accumbens in the rat: an anterograde- and retrograde-horseradish peroxidase study. Neuroscience. 1982;7:2321–2335. doi: 10.1016/0306-4522(82)90198-1. [DOI] [PubMed] [Google Scholar]
- Li J, Schiller D, Schoenbaum G, Phelps EA, Daw ND. Differential roles of human striatum and amygdala in associative learning. Nat Neurosci. 2011;14:1250–1252. doi: 10.1038/nn.2904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons J, Klipec WD, Steinsul G. Effect of chlorpromazine on discrimination performance and peak shift. J Comp Physiol Psychol. 1973;1:121–124. [Google Scholar]
- McLaren DG, Ries ML, Xu G, Johnson SC. A generalized form of context-dependent psychophysiological interactions (gPPI): a comparison to standard approaches. Neuroimage. 2012;61:1277–1286. doi: 10.1016/j.neuroimage.2012.03.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montague PR, Hyman SE, Cohen JD. Computational roles for dopamine in behavioural control. Nature. 2004;431:760–767. doi: 10.1038/nature03015. [DOI] [PubMed] [Google Scholar]
- Moustafa AA, Keri S, Herzallah MM, Myers CE, Gluck MA. A neural model of hippocampal-striatal interactions in associative learning and transfer generalization in various neurological and psychiatric patients. Brain Cogn. 2010;74:132–144. doi: 10.1016/j.bandc.2010.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman KA, O'Reilly RC. Modeling hippocampal and neocortical contributions to recognition memory: a complementary-learning-systems approach. Psychol Rev. 2003;110:611–646. doi: 10.1037/0033-295X.110.4.611. [DOI] [PubMed] [Google Scholar]
- O'Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ. Temporal difference models and reward-related learning in the human brain. Neuron. 2003;38:329–337. doi: 10.1016/s0896-6273(03)00169-7. [DOI] [PubMed] [Google Scholar]
- O'Donnell P, Grace AA. Synaptic interactions among excitatory afferents to nucleus accumbens neurons: hippocampal gating of prefrontal cortical input. J Neurosci. 1995;15:3622–3639. doi: 10.1523/JNEUROSCI.15-05-03622.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park SQ, Kahnt T, Beck A, Cohen MX, Dolan RJ, Wrase J, Heinz A. Prefrontal cortex fails to learn from reward prediction errors in alcohol dependence. J Neurosci. 2010;30:7749–7753. doi: 10.1523/JNEUROSCI.5587-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park SQ, Kahnt T, Talmi D, Rieskamp J, Dolan RJ, Heekeren HR. Adaptive coding of reward prediction errors is gated by striatal coupling. Proc Natl Acad Sci U S A. 2012;109:4285–4289. doi: 10.1073/pnas.1119969109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce JM. Similarity and discrimination: a selective review and a connectionist model. Psychol Rev. 1994;101:587–607. doi: 10.1037/0033-295x.101.4.587. [DOI] [PubMed] [Google Scholar]
- Pearce JM, Esber GR, George DN, Haselgrove M. The nature of discrimination learning in pigeons. Learn Behav. 2008;36:188–199. doi: 10.3758/lb.36.3.188. [DOI] [PubMed] [Google Scholar]
- Poldrack RA, Clark J, Paré-Blagoev EJ, Shohamy D, Creso Moyano J, Myers C, Gluck MA. Interactive memory systems in the human brain. Nature. 2001;414:546–550. doi: 10.1038/35107080. [DOI] [PubMed] [Google Scholar]
- Purtle RB. Peak shift: review. Psychol Bull. 1973;80:408–421. [Google Scholar]
- Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical conditioning II: current research and theory. New York: Appleton Century Crofts; 1972. [Google Scholar]
- Saksida LM. Effects of similarity and experience on discrimination learning: a nonassociative connectionist model of perceptual learning. J Exp Psychol Anim Behav Process. 1999;25:308–323. [PubMed] [Google Scholar]
- Samejima K, Doya K. Multiple representations of belief states and action values in corticobasal ganglia loops. Ann N Y Acad Sci. 2007;1104:213–228. doi: 10.1196/annals.1390.024. [DOI] [PubMed] [Google Scholar]
- Schechtman E, Laufer O, Paz R. Negative valence widens generalization of learning. J Neurosci. 2010;30:10460–10464. doi: 10.1523/JNEUROSCI.2377-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275:1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Seger CA, Miller EK. Category learning in the brain. Annu Rev Neurosci. 2010;33:203–219. doi: 10.1146/annurev.neuro.051508.135546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shohamy D, Wagner AD. Integrating memories in the human brain: hippocampal-midbrain encoding of overlapping events. Neuron. 2008;60:378–389. doi: 10.1016/j.neuron.2008.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Squire LR, Wixted JT. The cognitive neuroscience of human memory since H.M. Annu Rev Neurosci. 2011;34:259–288. doi: 10.1146/annurev-neuro-061010-113720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton R, Barto A. Reinforcement learning: an introduction. Cambridge, MA: Massachusetts Institute of Technology; 1998. [Google Scholar]
- Terrace HS. Behavioral contrast and peak shift: effects of extended discrimination training. J Exp Anal Behav. 1966;9:613–617. doi: 10.1901/jeab.1966.9-613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobler PN, O'Doherty JP, Dolan RJ, Schultz W. Human neural learning depends on reward prediction errors in the blocking paradigm. J Neurophysiol. 2006;95:301–310. doi: 10.1152/jn.00762.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waelti P, Dickinson A, Schultz W. Dopamine responses comply with basic assumptions of formal learning theory. Nature. 2001;412:43–48. doi: 10.1038/35083500. [DOI] [PubMed] [Google Scholar]
- Wimmer GE, Daw ND, Shohamy D. Generalization of value in reinforcement learning by humans. Eur J Neurosci. 2012;35:1092–1104. doi: 10.1111/j.1460-9568.2012.08017.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wisniewski MG, Church BA, Mercado E., 3rd Learning-related shifts in generalization gradients for complex sounds. Learn Behav. 2009;37:325–335. doi: 10.3758/LB.37.4.325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wisniewski MG, Radell ML, Guillette LM, Sturdy CB, Mercado E., 3rd Predicting shifts in generalization gradients with perceptrons. Learn Behav. 2012;40:128–144. doi: 10.3758/s13420-011-0050-6. [DOI] [PubMed] [Google Scholar]