Temporal phosphate gradients reveal diverse acclimation responses in phytoplankton phosphate uptake

Abstract

Phytoplankton face environmental nutrient variations that occur in the dynamic upper layers of the ocean. Phytoplankton cells are able to rapidly acclimate to nutrient fluctuations by adjusting their nutrient-uptake system and metabolism. Disentangling these acclimation responses is a critical step in bridging the gap between phytoplankton cellular physiology and community ecology. Here, we analyzed the dynamics of phosphate (P) uptake acclimation responses along different P temporal gradients by using batch cultures of the diatom Phaeodactylum tricornutum. We employed a multidisciplinary approach that combined nutrient-uptake bioassays, transcriptomic analysis, and mathematical models. Our results indicated that cells increase their maximum nutrient-uptake rate (V_max) both in response to P pulses and strong phosphorus limitation. The upregulation of three genes coding for different P transporters in cells experiencing low intracellular phosphorus levels supported some of the observed V_max variations. In addition, our mathematical model reproduced the empirical V_max patterns by including two types of P transporters upregulated at medium-high environmental and low intracellular phosphorus levels, respectively. Our results highlight the existence of a sequence of acclimation stages along the phosphate continuum that can be understood as a succession of acclimation responses. We provide a novel conceptual framework that can contribute to integrating and understanding the dynamics and wide diversity of acclimation responses developed by phytoplankton.

Introduction

Phytoplankton play a key role in global biogeochemical cycles, being responsible for ~40% of the global primary production and fueling oceanic food webs [1–3]. Phytoplankton grow in the euphotic layers of aquatic environments, where concentrations of inorganic nutrients fluctuate widely. Such fluctuations affect phytoplankton community composition by favoring species and ecotypes with eco-physiological traits best suited to exploit available nutrients [4]. Nutrient changes also trigger responses at the cellular level, as phytoplankton modify their eco-physiological traits, including those related to nutrient uptake [5–7]. Due to the short time required for these individual level acclimation changes to occur, these responses can be relevant for exploiting a variety of conditions along the nutrient continuum, from oligotrophic environments to sharp and/or short-lived nutrient pulses [5, 6, 8–10]. In spite of their importance, acclimation dynamics along nutrient spatiotemporal gradients are still poorly understood.

The study of phytoplankton nutrient-uptake acclimation responses associated with changes in nutrient levels has been traditionally based on the variations of the maximum nutrient-uptake rate (V_max) and the half saturation constant for nutrient uptake (K) measured from nutrient-uptake bioassays [6, 11, 12]. V_max and K are the parameters of the Michaelis-Menten equation, commonly employed to describe nutrient-uptake rate as a function of the external nutrient concentration [13, 14], and are linked to key eco-physiological traits [15, 16]: V_max determines the potential of the cell to take up nutrients and is related to the number of nutrient-uptake sites present in the cell membrane [5, 17]. K and the ratio between V_max and K [18] indicate the efficiency of the process and define the ability of the cell to exploit oligotrophic environments (for constant V_max, the lower the K the higher the nutrient uptake). Existing literature has reported, however, contradictory relationships between V_max and the limiting nutrient concentration.

Most empirical studies show a higher V_max in cultures where nutrients are depleted, enabling the cells to improve nutrient intake abilities [6, 11, 12, 19]. In contrast to these observations, some investigations reported a higher V_max at high nutrient levels, suggesting that cells could take advantage of the often brief high nutrient concentrations [5, 20]. Regarding variations in K, these have been linked to the existence of different types of nutrient transporters, each of which can display different nutrient-uptake rates and regulation mechanisms [20–23]. Transporters have consequently been divided in high and low-affinity groups attending to their half saturation constant [23]. Recent transcriptomic analyses confirmed the existence of different transporters for the same nutrient, with likely different V_max and K values and regulation mechanisms [24–28]. Such transporter diversity might contribute to the aforementioned variation in V_max patterns.

Despite their potential relevance for the understanding of phytoplankton acclimation, there is a lack of empirical work combining V_max and K measurements with transcriptomic analysis for identifying the mechanisms underlying V_max and K variations along the nutrient spatiotemporal gradient. Furthermore, most V_max studies have been addressed using steady state cultures, i.e., chemostats, or batch cultures sampled at unique time shots (but see ref. [17]), which has limited the comprehension of the dynamics of the acclimation process and the development of mechanistic mathematical models. Indeed, no existing theoretical framework integrates the wide diversity of acclimation patterns occurring along the spatiotemporal nutrient gradient. Theories considering acclimation responses typically focus on the negative relationship between V_max and nutrient concentrations, mostly using phenomenological expressions [7, 15, 29].

Here, we aim to fill this gap by (i) understanding mechanistically the dynamics of phytoplankton phosphate uptake acclimation along temporal gradients of phosphate (hereafter P), and (ii) providing a theoretical framework able to integrate the wide diversity of nutrient-uptake acclimation responses and consider the temporal dimension of the acclimation process. To this end, we followed a multidisciplinary approach combining P uptake bioassays, transcriptomic analysis, and mathematical models [30]. We monitored for the first time the dynamics (i.e., behavior through several consecutive time points) of V_max and K for phosphate along different P gradients by using batch cultures of the diatom Phaeodactylum tricornutum supplied with different pulses of P. We also measured the expression of genes coding for P transporters and proteins involved in phosphorus metabolism. Finally, we developed a mechanistic model that integrates the specific temporal patterns of acclimation observed in our experiments in a continuous moving picture [30]. Building on previous work [31], we considered two kinds of nutrient transporters operating in parallel [32]. The combination of our empirical and theoretical results revealed a sequence of acclimation responses along the temporal nutrient gradients that includes both positive and negative V_max-nutrient relationships. Our results provide a novel ecological framework that can contribute to understanding and constraining the dynamics and wide diversity of nutrient-uptake acclimation responses displayed by phytoplankton.

Material and methods

Phytoplankton cultures and experimental design

Strain 1052/1A (isolated off Plymouth, UK) of the diatom P. tricornutum was obtained from the culture collection of the Scottish Association of Marine Sciences (SAMS). P. tricornutum is an emerging model species in molecular biology. It mainly grows in coastal waters from tropical and temperate latitudes, including estuaries and areas affected by tidal mixing. Some of these environments show strong and sharp nutrient variations [33–35]. This makes P. tricornutum a good candidate for the present study. We inoculated 10 flasks with 5 × 10⁴ cells mL⁻¹ and F/2 medium (200 mL) with a reduced concentration of P (3 µM instead of the 36.2 µM from F/2) to ensure phosphorus limitation. Based on Zhang et al. [8], we also added a mix of antibiotics containing penicillin (1.00 gL⁻¹), kanamycin (0.50 gL⁻¹), and neomycin (0.25 gL⁻¹) to prevent the growth of bacteria. We used a light intensity of 20 µmol m⁻² s⁻¹. Temperature was set at 20 °C and shaking at 140 rpm.

Five days after starting the cultures, we collected different aliquots from one of the ten flasks (see Fig. S1 for a schematic diagram of the experimental design). These aliquots were employed for measuring V_max, K, intracellular phosphorus content (i.e., quota, Q), and expression of genes related to phosphorus metabolism (see below). One day later (day 6), when cells were in a transition to a stationary phase (i.e., phosphorus limited but not totally starved; Fig. S2), we added nutrient pulses (F/2 medium with different levels of P) to the nine remaining flasks: three flasks were supplied with no P (reference treatment, P_ref), three with 3 µM P (low P pulse treatment, P_low), and three with 15 µM P (high P pulse treatment, P_high). One flask from each treatment was sampled and measurements performed 3.5, 28, and 100 h after adding the corresponding pulse of nutrients, so that we obtained a time series for the three different P addition levels (Fig. S1). The whole experiment was carried out three times with 1 week in between to generate three replicates (Fig. S1). In order to keep the metabolic state of the cells as similar as possible among the three replicates, the cells inoculated to each experiment came from cultures sequentially initiated (also with one week in between). We alternated the time at which each P pulse was added among experimental replicates to prevent a spurious association between P pulse and uptake traits due to the effect of the cell dial cycle. For similar reasons, we used continuous (i.e., 24 h) illumination.

Phosphate uptake bioassays

We estimated V_max and effective K (K_eff) by performing P-uptake bioassays based on Lomas et al. [10]. We incubated solutions (10 mL) containing 7500 cells mL⁻¹, 0.20 µCi of H₃³³PO₄, and different amounts of non-radioactive H₃PO₄ (from 0.1 to 7 µM) for 20 min, so that each solution contained a different concentration of non-radioactive H₃PO₄ (see SI for further details). Samples were filtered and the radioactivity in the filters was measured using a scintillation counter. The rate of P-uptake rate (V, fmol cell^-1 d^-1) was then estimated from the measured radioactivity and the P concentration during incubations (Eq. [S2]). We fitted the Michaelis-Menten function (Eq. [S1]) to P-uptake observations using R software to obtain the curve (Fig. S3) and its associated parameters, V_max and K_eff. We repeated this process with the different cultures (i.e., flasks) to estimate V_max and K_eff in each P pulse treatment 24 h before and 3.5, 28, and 100 h after P pulses (Fig. S1).

Intracellular phosphorus measurement

The culture aliquots (25 mL) were filtered through a 47 mm pre-combusted glass fiber filter with 1.2 µm of pore size. The filters were then washed with salt water and an oxalate solution to remove any P adsorbed to the cells [36]. Subsequently, we digested the organic phosphorus in the filters by using concentrated nitric acid (see SI). Filters washed with salt water and oxalate solution were used as a negative control (blank). The phosphorus quota (fmol cell⁻¹) was estimated from the P concentration in the digested solution (Eq. [S3]), which was measured using a flow injection autoanalyzer.

Gene expression analysis: RNA extraction and quantitative real-time PCR analysis (qRT-PCR)

RNA extraction was performed on a 150 mL cell culture aliquot that was centrifuged at 4000 × g for 15 min. The supernatant was removed and the cells (pellet) were stored in −80 °C. Total RNA was extracted using the RNAeasy plant mini kit (Qiagen) and cDNA was synthesized from 250 ng of RNA using the QuantiTect reverse transcription kit (Qiagen). Quantitative RT-PCR was performed to analyze the expression of the following genes: HISTONE 4 (H4) (ref. [37]), Na/P co-transporters 47666 (Na/Pi 47666) and 47667 (Na/Pi 47667), P transporter 39515 (Pi 39515), Alkaline phosphatase 49678 (AP 49678), and Carbamoyl phosphate synthetase 1583 (CPS 1583) (ref. [28]; see SI for further details). Normalization of the quantitative real-time PCR data was calculated by geometric averaging of the internal reference gene H4 (refs. [38, 39]).

Statistical analyses

Uptake traits, quota, and cell abundance

The effect of P pulses (P_ref, P_low, and P_high) on the temporal dynamics of V_max, K_eff, V_max:K_eff, Q, and N was tested with analysis of variance (ANOVA) on a linear mixed effects model including P pulse and time as fixed factors and experiment as a random factor (each experiment constitutes a separate set of measurements; see SI for a detailed description of the model). Data were fourth-root transformed to approximate to homoscedasticity and normality assumptions (Fig. S4; ref. [40]). The occurrence of differences in the response variables among the three P temporal gradients corresponding to the three nutrient pulses would be reflected by a significant effect of the factor P pulse or an interaction between the factors P pulse and Time. Models were fitted by employing the nlme R package [41, 42]. To test for statistical differences between specific levels of fixed factors, we conducted pairwise comparisons using the emmeans R package [43] and correcting p-values according to the Benjamini and Hochberg [44] procedure (see SI for further details).

Gene expression

The relative expression of each gene (%) was estimated by using P_ref 3.5 h after the pulse as a reference. Since we were only able to extract RNA from two experiments, we focused on whether the response presented the same trend across different P pulses and time points.

Mathematical model for phosphate uptake acclimation

Our mechanistic eco-physiological model describing acclimation responses uses a modified Droop model [14] to represent the link between the specific growth rate (µ, d⁻¹) and the intracellular content or quota (fmol cell⁻¹) of the limiting nutrient, in our case phosphorus:

$$\mu \left(Q,N\right)={\mu }_{\infty }\left(1-\frac{Q_{\min }}{Q}\right)-\alpha N^2,$$ 1

where µ_∞ is the growth rate for infinite Q, Q_min is the minimum quota required for growth (i.e., Q when µ = 0), and N is the abundance of cells (cells L⁻¹). Differently from the usual Droop equation, we included a αN² term representing generically density-dependent effects such as mutual shading or the release of secondary metabolites to the medium that may occur, ultimately impacting growth at the cellular level ([45, 46]; see SI for further details). The temporal dynamics of the population abundance are given by:

$$\frac{dN}{dt}=\mu \left(Q,N\right)N,$$ 2

where we have considered any source of mortality negligible. The change with time of Q, in turn, depends on the balance between phosphate uptake rate (V) and cell division (note that cell division leads to a distribution of the cell’s phosphorus content):

$$\frac{dQ}{dt}=V-\mu \left(Q,N\right)Q.$$ 3

V (fmol cell^-1 d^-1) is represented as a function of the external P concentration (µmol L^-1) by using a modified version of the Michaelis-Menten´s equation that considers the potential effect that the simultaneous operation of several types of transporters may have on the uptake of the focal nutrient. Thus, V is estimated by adding the uptake associated with all transporter types for P [32]:

$$V=\sum _{i=1}^j{V}_{\max ,i}\frac{P}{P+K_{\mathrm{eff},i}},$$ 4

where j is the number of different transporter types, and V_max,i and K_eff,i are the maximum uptake rate and effective half saturation constant linked to transporter type i (see SI).

We considered two types of P transporters (j = 2): transporter₁ and transporter₂, which represent high-affinity (low K) and low-affinity (high K) transporters, respectively (see SI and ref. [23]). The effective V_max measured in the uptake bioassays effectively includes the transporter-specific V_max,i, in turn linked to the abundance (per cell) of each type of transporter i (n_i) (see SI for further details).

Because the focal acclimation response here is the cell´s ability to regulate the number of transporters of each type as nutrient availability changes, we represented explicitly the dynamics of the abundance of each type of transporter as a balance between the synthesis and decrease in number due to cell division. Based on Lomas et al. [10], transporter₁ is upregulated at low intracellular P levels, which facilitates survival in oligotrophic environments:

$$\frac{d{n}_1\left(t\right)}{dt}={\nu }_{1}H\left(c_H-\sum _{i=1}^j{A}_{rel,i}\left(t\right)\right)F\left(\frac{c_{F,a}{Q}_{\min }-Q\left(t\right)}{c_{F,a}{Q}_{\min }-Q_{\min }}\right)-n_1\left(t\right)\mu \left(Q,N\right),$$ 5

where v₁ is the maximum synthesis rate of transporter₁ (transporters d⁻¹). F is a sigmoid function representing the expression of transporter:

$$F\left(\frac{c_{F,a}{Q}_{\min }-Q\left(t\right)}{c_{F,a}{Q}_{\min }-Q_{\min }}\right)=\frac{1}{1+e^{-c_{F,b}\left(\frac{c_{F,a}{Q}_{\min }-Q\left(t\right)}{c_{F,a}{Q}_{\min }-Q_{\min }}\right)}},$$ 6

The expression of transporter₁ is maximum when Q = Q_min and minimum when Q » Q_min. Note that we replaced the maximum quota (Q_max) from the Lomas et al. [10] function with c_F,a Q_min ≤ Q_max, which effectively allowed us to calibrate with our experimental data the value of Q at which high-affinity transporters become upregulated. This modification of the F function implied that, as in the case of the growth rate, the gene expression variations of high-affinity transporters mainly occurred at low Q values. Both c_F,a and c_F,b control the shape of the function. Finally, H is a Heaviside function that limits the synthesis of transporters when the proportion of the cell surface occupied by transporters (A_rel) surpasses a certain threshold (c_H): H = 0 if ${\sum }_{i=1}^j{A}_{rel,i}\left(t\right)>c_H$, or H = 1 if ${\sum }_{i=1}^j{A}_{rel,i}\left(t\right)<c_H$, where ${\sum }_{i=1}^j{A}_{rel,i}\left(t\right)={\sum }_{i=1}^j{n}_i\left(t\right)\frac{r_{s,i}^2}{r_c^2}$). Thus, high and low-affinity transporters compete for the cell surface (see SI for further details).

On the other hand, transporter₂ is upregulated at high environmental P levels, enabling the cell to take advantage of P pulses:

$$\frac{d{n}_2\left(t\right)}{dt}=v_{2}H\left(c_H-{\sum }_{i=1}^j{A}_{rel,i}\left(t\right)\right)H\left(\frac{V_2\left(t\right)}{V_{\max ,2}\left(t\right)}-g_H\right)-n_2\left(t\right)\mu \left(Q,N\right),$$ 7

where v₂ is the maximum synthesis rate of transporter₂. We represent the expression of transporter₂ as a switch, using a Heaviside function that stops the synthesis of transporters when the ratio V₂/V_max,2, the fraction of occupied transporters [31], falls below a threshold g_H (see SI for further details). This formulation implies that transporter₂ has both transporter and signaling functions and is therefore considered a transceptor [47]. We assumed that both type of transporters can operate simultaneously. Nonetheless, the model could be modified to take into account the potential occurrence of feedback mechanisms preventing the simultaneous operation of high and low-affinity transporters [47].

Finally, the temporal dynamics of the P concentration in the medium, affected by the pulse of P when t = 6 days, is provided by:

$$\frac{dP}{dt}=-V\left(t\right)N\left(t\right),$$ 8

The specific values assigned to each parameter and the initial conditions were based on the experimental results and design (see SI text and Table S1). Simulations including only transporter₁ or transporter₂ were also run to compare the V_max predictions with those obtained when both transporters were considered.

Results

Observed dynamics of uptake traits

Phosphorus-limited cultures of P. tricronutum were supplied with different levels of P pulses (0, 3, and 15 µM P; named P_ref, P_low, and P_high, respectively). Measuring phosphate uptake traits at three time points following P pulses enabled us to track the dynamics of the acclimation process. The temporal behavior of V_max, obtained from P-uptake curves, differed depending on the pulse of P (Fig. 1a). This was confirmed by the significant interaction between P pulse and Time (ANOVA, p < 0.01; Table S2). V_max in P_ref was similar along the whole experiment (pairwise contrasts, p > 0.10; Table S3). On the contrary, V_max showed a V-shape pattern in P_low and a sharp decrease without a subsequent recover in P_high (Fig. 1a). Specifically, V_max was higher in P_high than in P_ref 3.5 h after the nutrient pulse (pairwise contrast, p < 0.05). However, V_max notably decreased between 3.5 and 28 h after the pulse of nutrients in P_low and, more markedly, in P_high (pairwise contrasts, p < 0.01). One hundred hours after the nutrient pulse, V_max in P_low recovered the baseline levels observed in P_ref (pairwise contrast, p > 0.30) but remained low in P_high (pairwise contrast, p < 0.01).

Fig. 1.

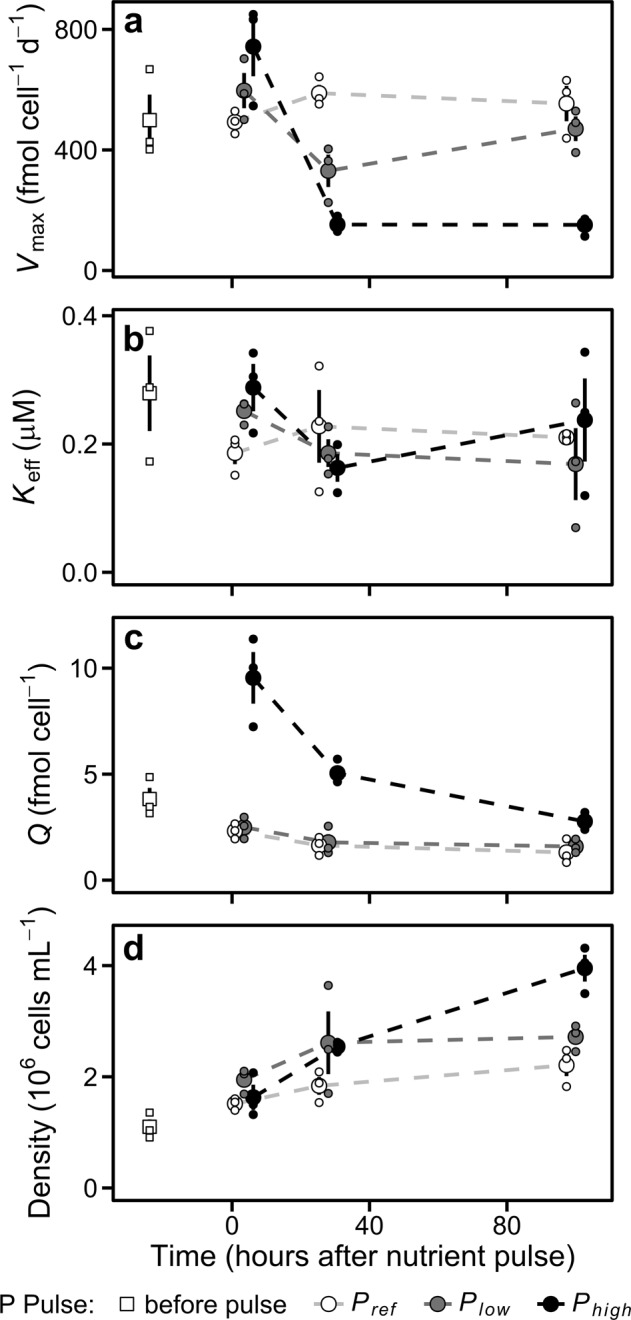
Dynamics of the population and cellular traits measured in the different P pulse treatments. a Maximum phosphorus uptake rate (V_max). b Effective half saturation constant for phosphorus (K_eff). c Phosphorus quota. d Cell density. Big dots represent mean values. Small dots are the observations from the three experiments. Error bars show standard error estimated from untransformed data. Dashed lines join mean values. The horizontal position of the dots is slightly adjusted to avoid overlapping

The dynamics of K_eff are shown in Fig. 1b. We did not observe a significant effect of P pulse on K_eff (ANOVA, p > 0.14; Table S2), but we found a marginally significant effect of P pulse 3.5 h after the nutrient pulses (ANOVA, n = 9, p < 0.10). As a result of the effect of P pulse on the dynamics of V_max, the V_max:K_eff ratio temporal behavior was also affected (Fig. S5; Table S2).

The addition of P also affected the dynamics of intracellular phosphorus quota (Fig. 1c). We found a significant interaction between P pulse and Time (ANOVA, p < 0.05; Table S2). 3.5 h after the nutrient pulse Q was higher in P_high than in P_ref (Fig. 1c; pairwise contrast, p < 0.01; Table S3). Differences in Q among P pulse treatments decreased with time and were related to changes in V_max (Figs. 1c and S6). Finally, the P pulses also altered population growth, as revealed by the significant effect of P pulse on population abundances (Fig. 1d; ANOVA, p < 0.01; Table S2). One hundred hours after the nutrient pulse, cell concentrations were higher in P_high than in P_ref (Fig.1d; pairwise contrast, p < 0.05; Table S3). This higher growth in P_high contributed to the marked quota decrease observed from 3.5 to 100 h (Fig. 1c).

Modelled dynamics of uptake traits

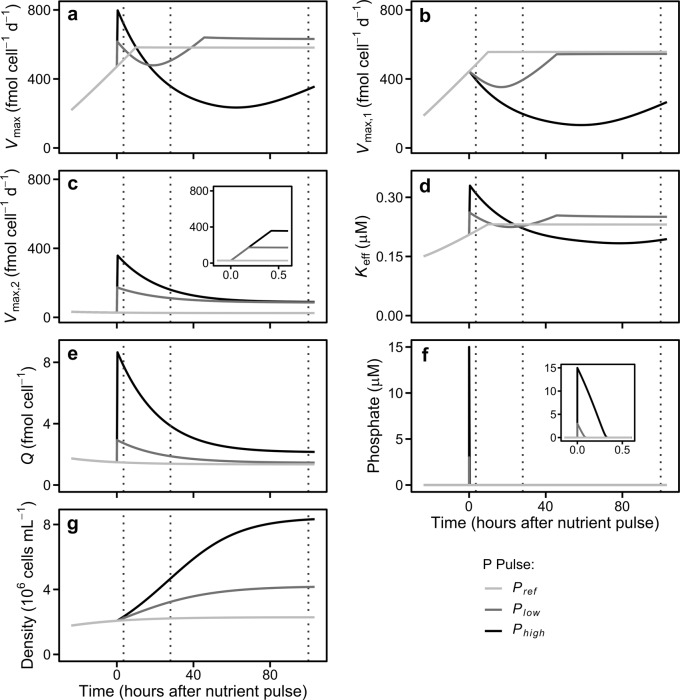
The temporal behavior of V_max predicted by our model with two types of nutrient transporters and different regulation mechanisms matched the patterns observed empirically. The magnitude of the P pulses affected the in silico V_max dynamics (Fig. 2a). The upregulation of transporter₂ led to a peak in the simulated V_max just after the pulse of P in both P_low and P_high (Fig. 2c). The V_max peak in P_high was higher than in P_low because the environmental P concentrations remained for a longer time period above the threshold level (g_H) that keeps low-affinity transporter upregulated (Fig. 2c, f). A high growth rate (Fig. 2g), which reduced the amount of transporters per cell, and the downregulation of high and low-affinity transporters lead to a subsequent V_max decrease (Fig. 2b, c). Both the high growth rate and the downregulation of high-affinity transporters were promoted by the high phosphorus quota (Fig. 2e; Eq. (6)), whereas the downregulation of low-affinity transporters was caused by the low environmental P levels (Fig. 2f; Eq. (7)). This V_max decrease did not occur in P_ref, where Q was close to Q_min and V_max,1 rose up to the threshold set by the maximum cell surface area occupied by P transporters, being the system close to a stationary phase by the end of the simulation (Fig. 2; Eq. (5)).

Fig. 2.

Dynamics of cellular and population traits predicted by the model in nutrient regimes analogous to those occurring in cultures. a Maximum phosphorus uptake rate (V_max). b Maximum phosphorus uptake rate for transporter₁. c Maximum phosphorus uptake rate for transporter₂ (V_max,2); the inset shows a zoom of the V_max,2 just when the pulses occur (note the different x-axis scale). d Effective half saturation constant for phosphorus (K_eff). e Phosphorus quota. f Extracellular phosphate concentration; the inset shows a zoom when the pulses occur (note the different x-axis scale). g Cell density. To facilitate comparison with empirical results, vertical dotted lines indicate the times when measurements were taken during the experiments

The decrease in V_max in P_low transitioned to an increase within the first 24 h after the P pulse. This V_max recovery was promoted by the upregulation of transporter₁ as a consequence of the reduction of Q, and stopped a few hours later when V_max,1 reached the limit set by the maximum cell surface area occupied by uptake sites (Fig. 2a, b, e; Eq. (6)). On the other hand, the long-lasting V_max and V_max,1 decreases in P_high ceased at late stages of the simulation as cell depleted P reserves. Interestingly, the simulations carried out using a version of our model with just transporter₁ or transporter₂ were not able to qualitative reproduce all the V_max patterns: a model including only transporter₁ did not capture the rise in V_max just after P pulses (Fig. S7a), whereas a model with only transporter₂ failed to reproduce the recovering in V_max observed in P_low 100 h after P pulse (Fig. S7b).

The K_eff peaks observed in P_low and P_high after the pulse of P (Fig. 2d) were fostered by the upregulation of low-affinity transporters, which show a high K, and the increases in diffusion limitation ultimately caused by V_max raises (see Eq. [S5]). The subsequent K_eff decrease and rebound found in both P_low and P_high is explained by variations in diffusion limitation, ultimately resulting from variations in V_max (Fig. 2a, d; see Eq. [S5]). As a result of the effects of the pulses of P on V_max and K_eff the temporal dynamics of the V_max:K_eff ratio were also affected (Fig. S8).

Gene expression

In our experiments, all the genes analyzed related to phosphorus metabolism (AP 49678, CPS 1583), including the three genes coding for P transporters (Na/Pi 47666, Na/Pi 47667, and Pi 39515), were downregulated in both P_low and P_high just after the P pulse (Figs. 3 and S9). The stronger gene downregulation in P_high was associated with a higher phosphorus quota, which supports the role assigned to the intracellular P content in the regulation of transporter₁ (see F function in methods). Indeed, the decrease in the expression of Na/Pi 47666, Na/Pi 47667, and Pi 39515 transporters within the first 28 h supports the reduction of V_max empirically observed and V_max,1 predicted by our model (Figs. 1a and 2b). Furthermore, the expression of these transporters in P_ref showed a similar temporal behavior to that reported for V_max and V_max,1. The downregulation of P transporters in P_low and P_high ceased 100 h after P pulses, when the three P added treatments showed similar expression values (Fig. 3a–c).

Fig. 3.

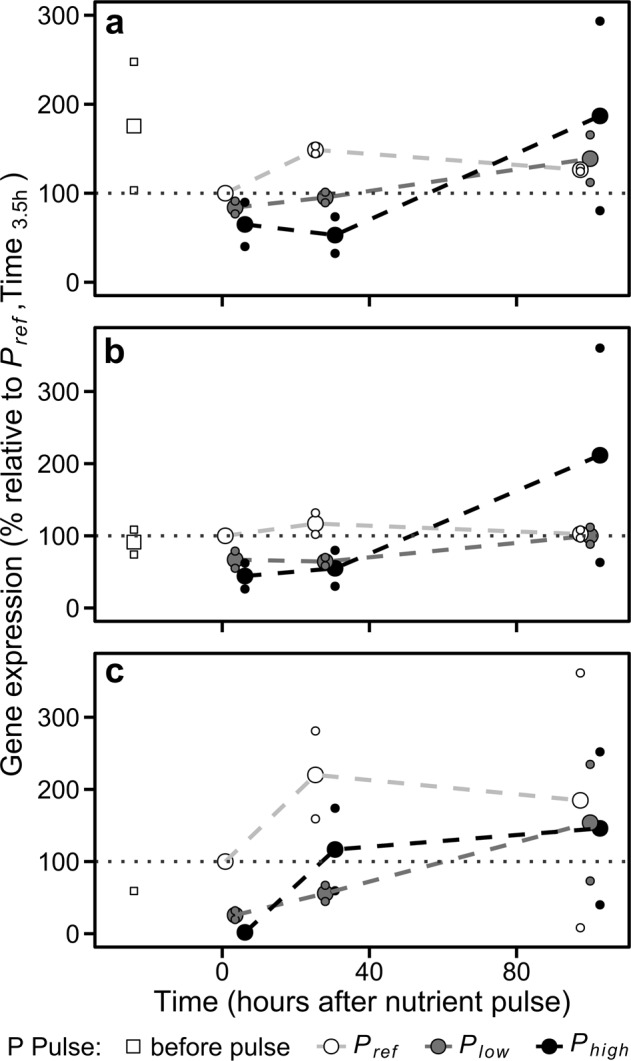
Gene expression patterns in the different levels of phosphate addition. a Na/Pi 47666. b Na/Pi 47667. c Pi 39515. Big dots represent mean values. Small dots are the observations from experiments 2 and 3. Dashed lines join mean values. Grey dotted lines point out the reference level (i.e., 100%). The horizontal position of the dots is slightly adjusted to avoid overlapping

Discussion

We addressed the dynamics of phosphate uptake traits in different P temporal gradients resulting from pulses of different magnitudes. Our results revealed two opposite V_max-nutrient trends along the nutrient temporal gradient: in both P_high and P_low we observed an increase in V_max just after the P pulse, followed by a decrease observed 28 h after the P pulse. In the case of P_low, V_max eventually recovered the values observed before the pulse. These changes in V_max were accompanied by changes in Q, and the expression of genes involved in P uptake and metabolism. Variations in V_max associated with different nutrient conditions have been previously described and modelled, especially those V_max increases occurring under oligotrophic conditions [6, 7, 10, 29]. However, to the best of our knowledge, none of these previous studies reported different V_max-nutrient patterns along a nutrient continuum and the transition of V_max between opposite trends, nor provided a mechanistic theoretical framework broad enough to integrate the observed diversity of phytoplankton nutrient-uptake acclimation responses.

The key feature that allows our mathematical model to reproduce the empirical V_max dynamics is the inclusion of two types of P transporters with different regulation mechanisms: the synthesis of transporter₁ (high-affinity) and transporter₂ (low-affinity) depended on intracellular phosphorus quota and V₂/V_max,2, respectively. The regulation proposed for transporter₁ was supported empirically by the upregulation at low phosphorus levels of the three genes coding for P transporters (Fig. 3), and has been widely reported for high-affinity transporters [17, 23, 25, 48]. On the other hand, none of the genes analyzed showed a regulation similar to transporter₂. The regulation of transporters right after P pulses in phosphorus-limited phytoplankton cultures has been less analyzed. Nonetheless, Feng et al. [49], in a proteomic analysis in P. tricornutum observed higher levels of a permease involved in P uptake in phosphorus-replete than in phosphorus-limited conditions. Moreover, a higher activity of low-affinity transporters at high P concentrations, regulated after transcription, has been reported in yeast [47, 50, 51]. Other possibilities (e.g., high-affinity transporters upregulated at high nutrient levels) previously observed in diatoms for other nutrients like nitrate [52] might occur as well for phoshorus. The existence of transporters with different regulations and kinetics is in agreement with previous works that reported variations in K_eff for species like Cosmarium abbreviatum ([21–23], but see also ref. [19]), and the identification of up to 24 putative P transporter genes (including mitochondrial carrier proteins) in P. tricornutum upregulated at different phosphorus conditions [28]. More than two types of transporters may be present in the cell surface indeed [47], leading to a finer regulation of the P uptake and a greater capacity to exploit phosphate gradients. Our model provides a simplified version of this transporter diversity, in which transporter₁ and transporter₂ can represent clusters of P uptake proteins upregulated at different phosphorus levels.

The empirical V_max patterns and the model parameterization required to reproduce such patterns suggest differences in the cellular responses to phosphorus limitation and nutrient pulses. For example, the maximum synthesis rate for low-affinity transporters required to reproduce V_max peaks after P pulses was notably higher than that for high-affinity transporters to reproduce V_max increases at low P levels (unless K₂ > 3.3 µM was used). Analogously, we included different function types (i.e., step vs continuous) to describe the dynamics of both transporters (Eq. (5) and Eq. (7)). The expression of high-affinity transporters occurs at low quotas [23], usually reached after a progressive nutrient depletion; cells with a finer control on the expression of these transporters would make a better use of their internal phosphorus resources and, therefore, would be positively selected. On the contrary, in the case of low-affinity transporters, which mainly take advantage of high environmental P concentrations, quick responses might be selected for instead: the cells that respond faster will store more nutrients before they are again depleted, with the efficient use of resources being secondary. Indeed, alternative mechanisms faster than transporter synthesis (e.g., activity regulation of existing uptake sites) have been described in yeast for low-affinity transporters [47, 50]. These ideas about the different velocities and type of responses to phosphorus limitation and pulses somewhat resemble the findings reported by Menge et al. [53], who theoretically predicted that cells showing slow and sensitive plastic responses (i.e., a tortoise-like strategy) prevail in stable environments, whereas cells with fast plastic responses (i.e., a hare-like strategy) prevail in environments showing a higher variability (below certain limits). Interestingly, our results highlight the possibility for the same cell to develop the two strategies, alternating between them thanks to the different regulation of the two types of transporters.

The theoretical model, by considering the temporal dimension and potential mechanisms of the acclimation process, enabled the integration of the snapshots provided by our empirical measurements in a moving picture and broad conceptual framework [30, 31]. In light of our simulations, run under the conditions defined by our experimental design, the V_max and acclimation stage of phosphorus-limited P. tricornutum cells can be predicted from environmental and intracellular phosphorus levels, which mainly reflect the present and past nutrient history of the cell, respectively (Fig. S10; refs. [14, 54]). We can indeed classify P. tricornutum´s uptake acclimation responses along these environmental and intracellular nutrient gradients in four scenarios that can occur sequentially (Fig. 4): (1) low environmental and intracellular phosphorus levels, (2) high environmental P concentration and low Q, (3) low environmental P concentration and high Q, and (4) high environmental and intracellular phosphorus levels (although we did not observe the latter case during our experiments). The scenarios with both environmental and intracellular phosphorus at high or low levels represent homeostasis (i.e., intracellular phosphorus levels matching environmental concentrations) and could lead to stationary dynamics if conditions are prolonged in time. On the contrary, the other two scenarios represent transient situations resulting from environmental nutrient fluctuations and the lag in the cellular physiology. The V_max trends and gene expression patterns observed in our experiments and replicated by our model can therefore be understood as a kind of succession of acclimation responses (Fig. 4; see below for a description of each acclimation stage). Along this succession, the lag in the cell response may lead to a mismatch between gene expression and nutrient-uptake traits, as it occurred during our experiments (e.g., P_high at 100 h after the P pulse) and it has been suggested for Prochlorococcus sp. [17].

Fig. 4.

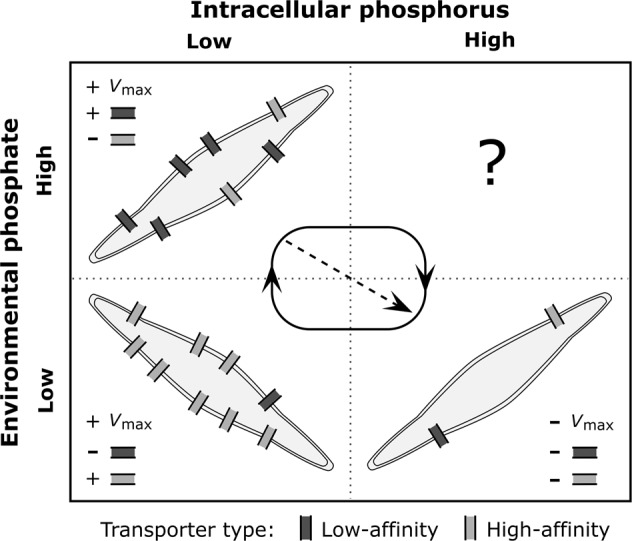
Schematic figure representing the stages of phosphate uptake acclimation in P. tricornutum under different nutrient scenarios along the nutrient spatiotemporal gradient. Black arrows indicate the dominant direction of the acclimation succession. The dashed arrow shows the alternative acclimation succession pathway observed in our experiments. The plus sign indicates an increase in trait value or transporter number, whereas minus sign shows a decrease in trait value or transporter number

The scenario of high environmental and low intracellular phosphorus levels was observed in P_low and P_high immediately after P pulses. It was characterized by an increase in V_max which, according to our model, occurred due to the upregulation of low-affinity transporters (Figs. 2 and 4). The positive relationship between V_max, nutrient transporters, and nutrient levels has been linked to a maximization of the phytoplankton capacity to exploit usually scarce resources [5]. Nevertheless, to the best of our knowledge, our model is the first theoretical effort that mechanistically reproduces the increase in V_max under these conditions. The increase in Q led to the scenario of low environmental and medium-high intracellular phosphorus levels, which was observed in P_high after pulse depletion. Here, V_max reached minimum values due to the downregulation of the synthesis of both transporter types (Figs. 1a, 2a and 4). This suggests a cost for the synthesis of transporters and maybe a potential trade-off with other cell functions: cells invest in nutrient transporters only when it provides an increase in nutrient uptake or cell growth is strongly nutrient limited, otherwise cells invest their resources on growth or the uptake of other nutrients [53, 55]. Finally, growth caused the draw-down of environmental and intracellular phosphorus levels observed in P_ref, and P_low and P_high 100 h after P pulses. In this scenario we found an increase in V_max promoted by the upregulation of high-affinity transporters (Figs. 2 and 4). This V_max increase and transport upregulation has been reported in nutrient limited cultures and natural populations of phytoplankton [6, 9, 10, 17, 24, 28]. Such V_max responses can be limited by extreme cellular quota conditions occurring at homeostatic scenarios and systems in a stationary phase. V_max can decrease due to a negative feedback of the internal phosphorus pool on P uptake or the synthesis of transporters when Q is close to Q_max [12]. Also, Krumhardt et al. [9] reported a marked decrease in V_max in phosphorus-starved (Q close to Q_min) cultures of Prochlorococcus sp., not observed for P. tricornutum in the present study.

It is plausible that a similar succession of acclimation responses occurs in natural phytoplankton populations experiencing some degree of phosphorus deficiency and environmental variability. Nonetheless, the succession we described could be restricted to those species and ecotypes with both high and low-affinity transporters, as some acclimation strategies might be absent in organisms with just one transporter type. Species and ecotypes with both high and low-affinity transporters would be encountered more often in environments showing high nutrient variations [25], as is the case in the coastal waters inhabited by P. triconutum. Indeed, Scanlan et al. [25], in an analysis of several strains of Prochlorococcus and Synechococcus, reported that the only strain with genes coding for potentially both high and low-affinity transporter proteins likely inhabited an estuarine environment, whereas the strains from oligotrophic and less variable waters lacked genes coding for low-affinity transporters.

Based on the comparison of the acclimation responses in the three P pulse treatments, we suggest that the acclimation succession experienced by a specific cell type would depend on the environment. The amplitude of the acclimation succession (i.e., the V_max range in the present context) would tend to decrease from ecosystems (and seasons) with marked temporal nutrient gradients to ecosystems with narrow gradients (Figs. 2 and S10). In addition, the dominant (i.e., most frequent) acclimation stage would change between ecosystems. For example, higher V_max values and the expression of high-affinity transporters as in P_ref would dominate in oligotrophic ecosystems. In this regard, Lomas et al. [10] reported that picocyanobacteria in the Sargasso Sea usually show higher V_max values in summer (strong phosphorus limitation) than in winter. On the contrary, the expression of low-affinity transporters could dominate in eutrophic environments [56]. Other factors like temperature and the availability of non-limiting nutrients might also affect acclimation responses; for instance, temperature may influence the synthesis of transporter proteins [57]. As a result, the succession of acclimation responses occurring at the organismal level might influence the fitness of the cells, the community composition and, therefore, interact with the ecological succession occurring at the community level at wider temporal scales [4, 58].

Final remarks

Although maybe intrinsic to the concept of acclimation, the idea of a temporal sequence of cellular responses might not have been stressed enough in the literature on nutrient-uptake acclimation. We believe that understanding acclimation as a succession of responses along the nutrient spatiotemporal gradient offers a novel framework that may contribute to integrating the diverse responses developed by phytoplankton.

Future studies analyzing the dynamics along nutrient spatiotemporal gradients of the traits involved in nutrient uptake in different phytoplankton groups, as well as the expression of genes coding for nutrient transporters, are key to disentangling the diversity of responses and underlying regulation pathways. Sequenced species like Synechococcus sp., Micromonas sp. or Emiliana huxleyi are good candidates. Empirical results could inform mechanistic theoretical models similar to the one proposed here, which could be indeed modified to include alternative or additional regulation mechanisms and transporters, and accommodated to other nutrients or resources. These multidisciplinary studies would chart a way forward to assess the ecological importance of acclimation and bridge the gap between cellular physiology, community ecology, and evolution.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Supplementary information

The online version of this article (10.1038/s41396-019-0473-1) contains supplementary material, which is available to authorized users.