Target Interception: Hand–Eye Coordination and Strategies

Abstract

This study was designed to define the characteristics of eye–hand coordination in a task requiring the interception of a moving target. It also assessed the extent to which the motion of the target was predicted and the strategies subjects used to determine when to initiate target interception. Target trajectories were constructed from sums of sines in the horizontal and vertical dimensions. Subjects intercepted these trajectories by moving their index finger along the surface of a display monitor. They were free to initiate the interception at any time, and on successful interception, the target disappeared. Although they were not explicitly instructed to do so, subjects tracked target motion with normal, high-gain smooth-pursuit eye movements right up until the target was intercepted. However, the probability of catch-up saccades was substantially depressed shortly after the onset of manual interception. The initial direction of the finger movement anticipated the motion of the target by ∼150 ms. For any given trajectory, subjects tended to initiate interception at predictable times that depended on the characteristics of the target trajectories [i.e., when the curvature (or angular velocity) of the target was small and when the target was moving toward the finger]. The relative weighting of various parameters that influenced the decision to initiate interception varied from subject to subject and was not accounted for by a model based on the short-range predictability of target motion.

Introduction

We interact with countless moving objects each day (e.g., when we catch a ball, retrieve luggage from a carousel, or celebrate by exchanging “high fives”). Even when the environment is stable, we may be in motion relative to it (e.g., when we grasp the handle of a door while approaching it). However, with some exceptions (Flanders et al., 1999; Daghestani et al., 2000; Pigeon et al., 2003; Zago et al., 2004), in a laboratory setting, subjects standing still typically reach toward stationary targets. Here, we describe the results of a study in which subjects intercepted targets moving along quasi-unpredictable trajectories in two dimensions, and we focus on two aspects of the behavior: the patterns of coordination between eye and hand movements and the strategies that determine when the interception movement is initiated and the direction of the initial motion of the hand.

When subjects view a target moving against a stationary background, they almost automatically follow the target with smooth-pursuit eye movements (Lisberger et al., 1987). However, when subjects reach to a stationary target, it has been reported that gaze is anchored on the target (Neggers and Beckering, 2000, 2001) and, under some conditions, may anticipate the hand motion to the target (Johansson et al., 2001). Evidence for predictive, saccadic eye movements was also found in a task in which subjects had to learn coordinated hand movements to control a cursor motion on the screen (Sailer et al., 2005). These authors found that, initially, subjects tracked the cursor with their eyes, but as they learned the task, eye movements changed to a predictive mode. Furthermore, neural recordings from posterior parietal cortex suggest that the spatial goal of an arm movement is encoded in an eye-fixed (retinocentric) frame of reference (Batista et al., 1999; Buneo et al., 2002). Such an encoding would appear to be simplified if gaze were stable. Based on these considerations, one might expect a predictive saccadic eye movement around the time of the interceptive hand movement, providing a target for the hand. However, we will report the contrary: pursuit was maintained until the target was successfully intercepted, and, in fact, saccades tended to be suppressed during the target interception.

In previous studies of interception, subjects either had to intercept the target at a specified location (Port et al., 1997, 2001; Tresilian and Lonergan, 2002; Merchant et al., 2003) or after command (i.e., in a reaction-time task) (van Donkelaar et al., 1992; Smeets and Brenner, 1995; de Lussanet et al., 2004). In the present experiments, subjects were free to initiate the hand movement at a time of their choosing. One might expect that subjects would adopt a strategy that would maximize their chance of success (Ernst and Banks, 2002; Körding and Wolpert, 2006). Specifically, because successful interception requires the prediction of target motion, one might expect subjects to initiate target interception at a time at which uncertainty in the future target motion was low, and hence the uncertainty in the required direction and amplitude of the finger movement was minimal. We did find that subjects initiated target interception at predictable times. However, a model in which interception is initiated when the uncertainty in predicting target motion is small did not account well for the data.

Materials and Methods

Subjects and experimental overview

Nine subjects participated in the experiments. Eight of the nine subjects used the right hand (one was ambidextrous); six were females, and three were males. All had no history of neurological disorders and had normal vision corrected to 20/20. The procedures were approved by the University of Minnesota Institutional Review Board, and all subjects provided informed consent.

They watched a small cyan circular target (0.6° diameter) that moved on the screen of a touch-sensitive 20 inch computer monitor (Diamond Scan 20 M; refresh rate of 60 Hz, and a resolution of 640 × 480 pixels; Mitsubishi Imaging Products, Irvine, CA). Room lighting was dimmed to improve contrast. In the main experiment (involving seven subjects), subjects were asked to intercept the target as it smoothly traversed a two-dimensional path on the screen by moving their extended index finger along the surface of the screen to the location of the target. In an additional control experiment (involving five subjects, including three who had previously performed the main experiment), subjects were instructed to visually track the same target motions, without manual interception.

Stimuli

The target motion was periodic and constructed using sinusoids (fundamental and the second or third harmonic in x and y):

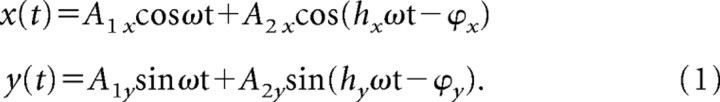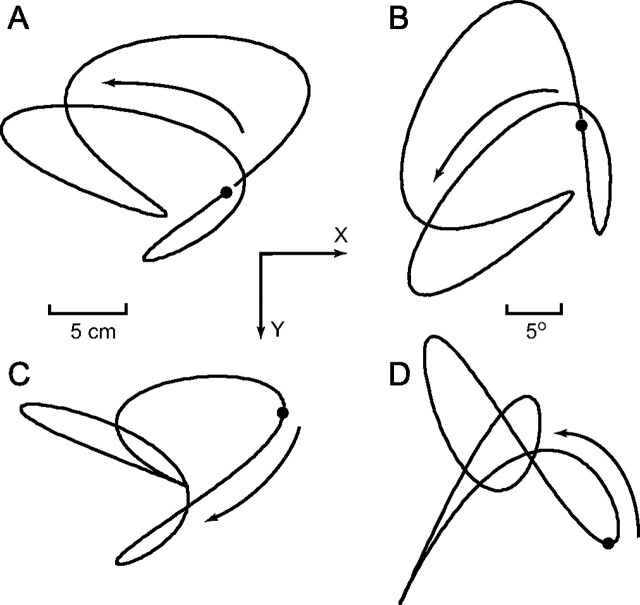
There were three possible target paths, which are shown in Figures 1A, C, and D. Furthermore, the parameters used to generate each of these curves are listed in Table 1. Each of these paths was presented in six orientations, obtained by rotating the curves in increments of 60°. For example, the trajectory in Figure 1B was obtained by rotating the one in Figure 1A by 60°. The initial target position is indicated with a small black circle, and the direction of target motion is shown with the arrow. The trajectories had a period of 4.5 s.

Figure 1.

Target path trajectories showing relative size and direction of target motion. The black dot shows the initial position of the target, and the arrow shows the direction of target motion. The screen was oriented vertically; thus, the x-direction was horizontal, and the y-direction was vertical. All three paths are shown in A, C, and D. B shows the same path as in A, rotated through 60°.

Table 1.

Target trajectory parameters

Trajectory	A1x (cm)	A2x (cm)	Harmx	Phasex (°)	A1y (cm)	A2y (cm)	Harmy	Phasey (°)
1	5.40	5.40	3	−95	2.70	5.40	2	−25
2	4.32	4.32	3	0	2.70	4.32	2	50
3	2.70	5.40	2	35	4.32	4.86	3	260

Harm, Harmonic.

Hand interception task

Subjects were seated at a comfortable reaching distance from the screen, with the head stabilized by a chinrest. Eye movements were recorded with a head-mounted eye-tracking system to monitor gaze location on the screen, and finger location was recorded from the touchscreen monitor (see below). Subject wore a knit glove on the pointing hand to allow for smoother movements when sliding the finger along the screen.

Before the start of each trial, the target appeared at the starting location of the trajectory, and a red box appeared in the middle at the bottom of the screen. The latter denoted the starting location of the finger. None of the target trajectories passed through this initial finger location. Each trial began when the subject touched the computer monitor; at this time, the target began to move along one of the predefined trajectories. The subjects were to intercept the target by moving their index finger along the surface of the screen. Interception was successful when the finger was within 20 pixels (1 cm) of the center of the target. The target then immediately disappeared from view, but data recording continued for another 200 ms. The subjects were told that the target would move for almost 10 s (two cycles) and that they could move to intercept it at any time. (After the first cycle, the color of the target changed from cyan to yellow. However, in most instances, subjects began to move before the first cycle was completed.) They were asked to intercept the target by means of a smooth finger movement (i.e., to intercept it on the first try). If they did not succeed, they were to continue to follow the target until they intercepted it. The pointing finger was required to maintain contact with the screen at all times. There were no instructions concerning eye movements, and they were afforded two to three practice trials to familiarize themselves with the experimental protocol.

There were 18 conditions (three paths by six orientations) and 10 repeats for a total of 180 trials for each subject. The trajectories were presented in a pseudorandom order. The subjects were interviewed after the experimental session; none of the subjects realized that there were only three paths. Some subjects were unaware that there were consistent patterns in the target motion, and other subjects estimated that there were eight or more paths.

Eye tracking task

Five subjects, including three (2, 4, and 6, who first completed the interception experiment), volunteered for a second, control experiment in which they were asked to visually track the target throughout its entire trajectory. The same 18 trajectories were used in these experiments, following the same protocol as in the interception experiment, except that the target only completed slightly more than one cycle (5 s) rather than two. Each condition was repeated 10 times for a total of 180 trials. These data permitted an assessment of the effect of finger movement on visual tracking.

Data collection and analysis

Eye movements.

The subjects were fitted with an eye-tracking system using head-mounted infrared cameras (EyeLink System; SensoMotoric Instruments, Boston, MA). The system has three cameras, all with a collection rate of 250 Hz. Two cameras recorded eye motion in the head, whereas the third monitored head position in space. The eye-tracking system was calibrated with a nine-point grid at the beginning of each experimental session and any time the head-mounted cameras were moved. A drift compensation was performed with a fixation point before each trial.

Eye position data were analyzed with specialized off-line software. The x and y data were first filtered with a double-sided exponential filter (time constant, 4 ms) and then differentiated. In most experiments, eye position records from the two eyes were averaged to reduce noise. Saccades were identified from the velocity data, using a threshold detection algorithm. Pursuit velocity was obtained by interpolating the data using a cubic spline (Barnes, 1982; Mrotek et al., 2006).

Pursuit gain was obtained on a trial-by-trial basis. We first computed the average pursuit eye velocity (v_e) over 40 ms, in overlapping bins at intervals of 20 ms. This was done to increase the signal-to-noise ratio in the recordings and was essentially equivalent to low-pass filtering the eye velocity signal with a frequency cutoff of 25 Hz. Pursuit gain was then computed from the component of eye velocity in the direction of target velocity (v_t) at a time delay τ:

We also computed the direction cosine at time t to characterize the extent to which pursuit velocity was aligned with the target velocity:

Data from individual trials were aligned on the time of initiation of the finger movement and averaged, and the direction cosine was z-transformed before averaging. All 180 trials from each experiment were included in the average. The results from the interception experiments were then compared with those from the control experiments. For the control experiments, we computed the gain and direction cosine in the same manner, but we aligned the trials using the time of initiation from the corresponding trial in an interception experiment. We used three values for the time delay τ: 0, 50, and 100 ms. The results for the three time delays were virtually identical.

We also computed the extent to which gaze position (p_e) lagged the position of the target (p_t), by minimizing the error function f(τ):

where v_e is the eye speed. The first term represents the distance between gaze and target position, and the second term was included to minimize the likelihood of spurious values at times when the target reversed direction. Time delays of ±200 ms were explored, at intervals of 16.7 ms (the frame rate of the display). As was done for the computation of pursuit gain, data from individual trials were aligned on the time of finger movement initiation and averaged.

Finger movements.

Finger position was measured using a touch-sensitive monitor (Elo TouchSystems, Menlo Park, CA) with a spatial resolution of better than 0.01 cm at the center of pressure of the finger and a temporal resolution of 100 Hz. The monitor was calibrated with a 5 × 5 grid of targets. Hand motion data were also analyzed with off-line custom software. Hand speed was computed by numerically differentiating the x- and y-finger position data after double-sided exponential filtering (time constant, 10 ms). Peak velocity was computed, and the initiation of finger movement was defined as the time speed first exceeded 5% of the maximum.

Results

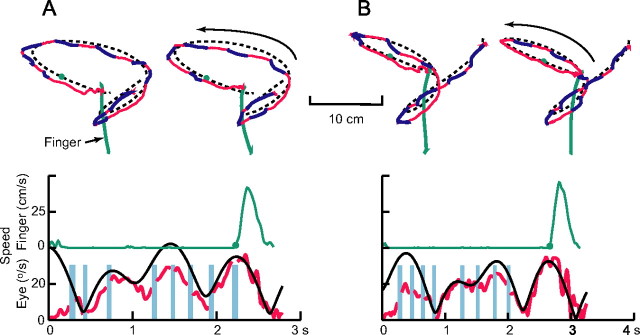
Results for four representative trials from one subject are shown in Figure 2, illustrating the main findings that will be reported in more detail subsequently. The results are for 2 of the 18 trajectories used in the experiments (compare Fig. 2A with Fig. 1A and Fig. 2B with Fig. 1C), as denoted by the dashed black curves. The plots end 200 ms after the target was intercepted. The solid red and blue traces depict the motion of the eyes, and saccades are represented in dark blue. The subject was engaged in smooth pursuit throughout the trial. This can also be appreciated in the plot of eye speed (red trace) as a function of time in the plots in the bottom row. Target speed is shown for comparison by the solid black curve. (These plots correspond to the second of the two trials in the top row in each panel.) The modulation in pursuit speed follows the modulation in target speed, with pursuit gain slightly <1. Saccades, denoted by the thin cyan bands interrupting the eye speed plots, are absent after the hand begins to move.

Figure 2.

Representative trials for two different target trajectories. Top, The target trajectory is shown with the black dashed line, and the arrows denote the direction of the target motion. The red and dark blue traces depict eye motion, with red denoting smooth pursuit and dark blue segments indicating saccades. The finger motion is represented with a green line, and the green circle indicates the target position at the time finger motion began. The interception always began at the bottom center of the screen and, in all of these cases, required an upward movement to reach the target. The traces end 200 ms after the time of successful target interception. Bottom, Variations in hand and gaze speed over time. Smooth-pursuit speed is shown with the red trace, and the solid black line shows target speed for comparison. The thin cyan vertical bars depict the time and duration of saccades. All trials shown are for one subject (1) and path 1, 0° orientation (A) and path 2, 0° orientation (B). In each case, the plot in the bottom panel corresponds to trial on the right in the top panels.

The finger path is shown in green in the plots in the top row, and the target location at the onset of finger motion is denoted with a filled green circle. Note that the initial direction of the finger movement anticipates the target motion and that the hand paths are fairly straight and direct. In these trials, the speed profile showed a single peak and a bell-shaped profile. The time at which this subject initiated the interception movement was highly consistent for the two trials for each of the target trajectories. Furthermore, there were consistent features in the motion of the target at the time of hand movement initiation: the target was traveling down toward the initial finger location and along a relatively straight path.

On average, subjects were successful in intercepting the target with a single movement 73% of the time (range, 58–83% for individual subjects). In the remaining trials, the speed of finger movement showed two or more distinct peaks (Lee et al., 1997) and often sharp changes in direction. Most subjects did not initiate the interception right away and visually tracked the target motion for some time before moving the finger to intercept the target. Five of seven subjects initiated target interception an average of 1.71 ± 1.02 s after target motion onset (i.e., approximately one-third of the way through the first cycle), with a range of 0.70 ± 0.26 to 2.45 ± 0.76 s. Only occasionally (<6% of trials) did they wait until the second cycle of the target motion to initiate target interception. The remaining two subjects (one male and one female) began to move the finger immediately or very shortly after the target began to move (0.07 ± 0.10 and 0.38 ± 0.33 s). These two subjects were also less successful than were the others in intercepting the target on the first try, with success rates of 58 and 68%. Rather than anticipating target motion (as illustrated in Fig. 2), they tended to move to the present location of the target, often requiring large subsequent corrections to catch up to the new target location. Below, we focus our analysis on the five subjects who used a more successful strategy. Furthermore, although subjects succeeded in ultimately intercepting the target on every trial, we will denote a “successful trial” as one in which the subject intercepted the target on the first attempt (Fig. 2).

General characteristics of finger motion

On successful trials, the average amplitude of finger movement was 12.34 cm, and the average movement time was 350 ms (ranging from 227 ± 50 to 462 ± 47 ms for the five subjects). As expected (Tresilian and Lonergan, 2002), hand speed increased with the amplitude of the motion (r values ranging from 0.487 to 0.872). Typically, the path to intercept the target was curved, with an average maximum deviation from a straight path of 0.94 ± 0.76 cm. The direction of the curvature depended on the direction of target motion such that the path of the finger curved in the direction of the target motion (see second trial in Fig. 2A and both trials in Fig. 2B). This observation suggests that subjects initially underestimated the distance the target would traverse during the finger movement. In agreement with this interpretation, the amount by which the finger path deviated from its initial direction (to the left or right) was significantly related to the distance that the target moved to the left (or right) during the last half of the hand movement (r = 0.488).

The angle at which subjects intercepted the target, defined as the angle between target velocity and finger velocity at the time of interception, was not distributed uniformly for individual subjects. Two subjects tended to intercept the target close to head on (150–180°), whereas another subject tended to pursue the target from behind (0–30°). However, overall the distribution of interception angles did not differ statistically from uniformity (ANOVA on data binned in 15° intervals).

Hand–eye coordination

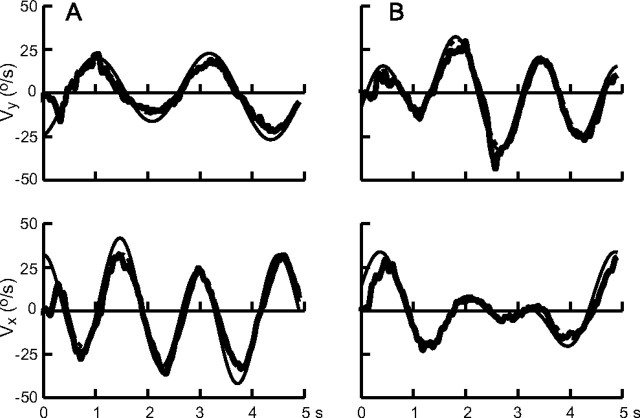
During the interception task, subjects visually tracked the target with a combination of pursuit and saccades. To assess the influence of hand movement on visual tracking, we used a control task in which subjects were specifically instructed to only track the target with their eyes. For this control experiment, we used three subjects that had first completed the interception experiment and two subjects who were naive to the task. Representative results of smooth-pursuit velocities for two target trajectories are shown in Figure 3, A (path 1 at the 180° orientation) and B (path 2 at the 120° orientation). The thick solid traces show the x- and y-components of pursuit velocity, obtained by averaging the 10 trials for each condition after removing saccades by interpolation. The thinner solid lines show target velocity for comparison, and the thinner dashed line depicts the result of fitting pursuit velocity with a sum of sines (the fundamental and the first two harmonics). The illustration shows that the tracking performance was good and that the Fourier analysis gave an excellent fit to the data (<3% variance not accounted for) (Table 2).

Figure 3.

Variations in smooth-pursuit velocity during visual tracking. The two panels in A and B show vertical velocity (v_y; top) and horizontal velocity (v_x; bottom). The thick black line depicts averaged smooth-pursuit velocity, and target velocity is indicated with the thin solid line. The dashed line shows the best fit of a sum of sinusoids to the smooth-pursuit velocity. The results are for two subjects who participated in the control experiment: A, subject 6, path 1, and 180° orientation; B, subject 4, path 2, and 120° orientation.

Table 2.

Pursuit gain

Frequency (Hz)	x gain	x delay (ms)	x VNAF	y gain	y delay (ms)	y VNAF
0.222	0.80 ± 0.10	−74 ± 78	0.018 ± 0.004	0.67 ± 0.13	−59 ± 73	0.035 ± 0.014
0.444	0.86 ± 0.06	13 ± 21		0.75 ± 0.11	8 ± 20
0.667	0.92 ± 0.07	50 ± 6		0.83 ± 0.11	42 ± 7

VNAF, Variance not accounted for.

The analysis showed that pursuit gain increased with frequency (ranging from 0.73 at 0.22 Hz to 0.88 at 0.67 Hz), as did the time delay, reversing from lead (−66 ms) at 0.22 Hz to a lag (46 ms) at 0.67 Hz. These trends were significant (ANOVA; gain: F_(2,24) = 5.59, p = 0.01; lag: F_(2,24) = 16.04, p < 0.001). Pursuit gain in the vertical direction was smaller than the gain for horizontal pursuit (F_(1,24) = 9.44; p = 0.005). These observations are consistent with previous reports of tracking performance in humans and in non-human primates (Collewijn and Tamminga, 1984; Barnes et al., 1987; Barnes and Ruddock, 1989; Kettner et al., 1996).

The gain of smooth pursuit did not change as subjects moved their finger to intercept the target, but the probability of saccades decreased substantially shortly after the onset of finger motion. As a consequence, the eyes progressively lagged behind the target during the interception. This is illustrated in Figure 4, which shows representative data from one subject who participated in both experiments, in separate sessions. The results for the interception task are shown in black, and the results for purely visual tracking are shown in red. Data from the control trials were averaged and aligned on the time of initiation of finger motion for the corresponding trial in the interception task (see Materials and Methods). Note that in both experiments, pursuit gain was ∼0.75 throughout the interval of 1 s before to 0.5 s after the onset of finger motion. Furthermore, in both experiments the direction cosine (second panel from top) was close to one throughout this interval, indicating that pursuit velocity was in the same direction as target velocity. These results were obtained using a time delay of 50 ms, but the results did not depend crucially on the value of the time delay in the range of 0–100 ms.

Figure 4.

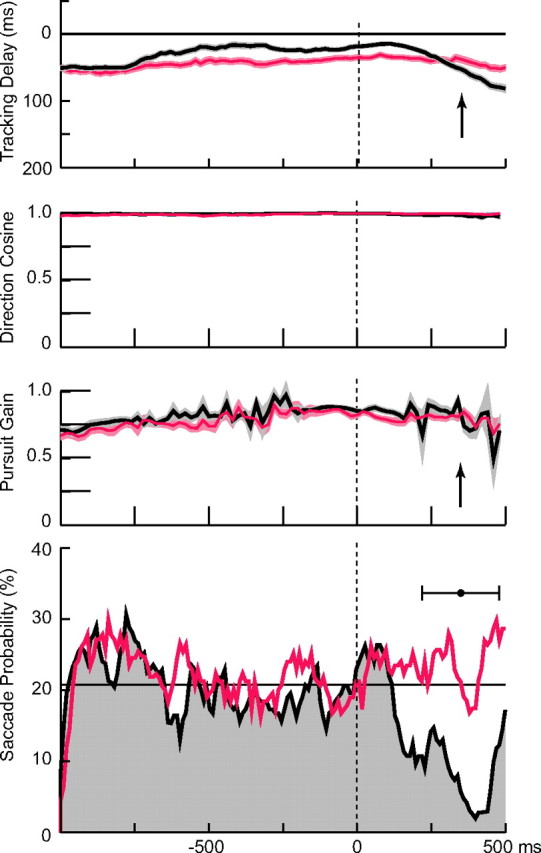
Variations in saccade probability and pursuit gain during target interception. The black traces (from top to bottom) show (1) the time delay between target and gaze position; (2) the direction cosine, defined as the cosine of the angle between direction of pursuit and the direction of target velocity; (3) pursuit gain; and (4) the saccade probability. The shaded area in the top three curves encompasses ±1 SEM, and the traces are averages over all 180 trials for this subject, aligned on the time of initiation of finger movement. Trials were excluded from the average after the time of target interception, when the target disappeared. The filled black circle in the bottom panel shows the average interception time (±1 SD), which is also indicated by the arrows in other panels. The horizontal line in the bottom panel denotes the average saccade probability in the 1 s interval preceding the onset of finger motion. The red lines show for comparison data obtained in the control experiment from the same subject (6) in which the target was only tracked visually. These data were averaged by aligning them on the times of interception onset for corresponding trials in the interception task.

In the control task, the probability of the occurrence of a saccade was also relatively constant (Fig. 4, bottom, red trace). On average, saccades occurred ∼22% of the time. In the interception experiment before the onset of the finger movement, saccade probability was comparable to that in the control trials (21% on average). However, ∼110 ms after the onset of finger movement, the saccade probability began to decrease dramatically, reaching a minimum of 1.8% 400 ms after the onset of interception. The results from the other subjects were comparable. In the interception experiment, the saccade probability reached minima ranging from 1.1 to 3.9% in the five subjects, at times ranging from 300 to 480 ms after the onset of finger movement. To the contrary, saccade probability in the control task was consistently larger, the minimum in the same time interval averaging 14.6% with a range of 6.2–20.0%.

Because pursuit gain was less than unity and because saccades tended to be suppressed, gaze position began to lag the target position by progressively greater amounts after the onset of the interception movement (Fig. 4, top, black trace). Approximately 1 s before the onset of interception, gaze lagged the target by ∼50 ms. This lag actually decreased to ∼20 ms, 500 ms before the onset of interception, and remained at that value until it began to increase ∼150 ms after the onset of interception. At +500 ms (after onset of interception movement), gaze lagged the target by 80 ms.

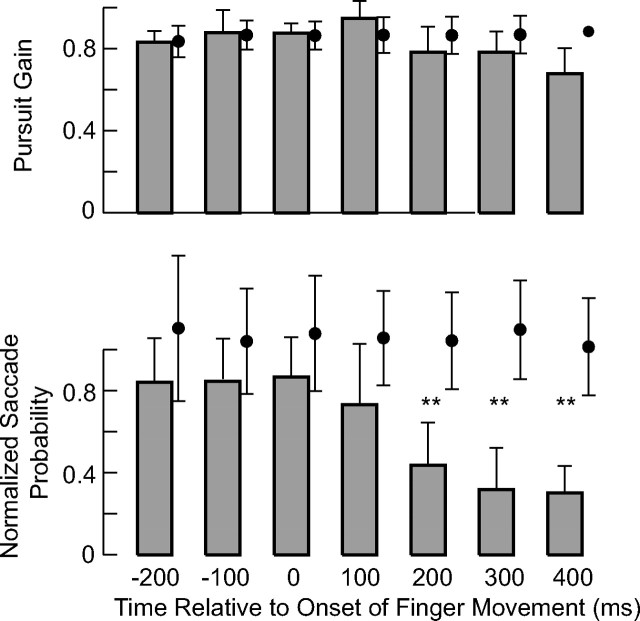
A statistical analysis of the data for all five subjects confirmed the conclusions drawn from the results illustrated in Figure 4. The histograms in Figure 5 present summary data at 100 ms intervals for pursuit gain and for saccade probability in the interception task. The average probability of a saccade in a 1 s interval before the onset of finger movement (ranging from 15 to 23%) was used to normalize the saccade probability for each subject. The filled circle to the side of each bar shows the control data, obtained by aligning trials from the five control experiments on the onset of finger movements for each subject. An ANOVA for pursuit gain showed that the gain did not vary in the control condition. During the interception task, pursuit gain after time 0 did not differ from the gains at previous times. However, the gain at +100 ms was significantly greater than the pursuit gain at +400 ms (F_(6,27) = 3.78; p < 0.01; post hoc test with Bonferroni correction). Moreover, a paired t test comparison between pursuit gain in the two experimental conditions at each of the time points showed no significant differences.

Figure 5.

Variations in saccade probability and pursuit gain during the interception task. The bars show means (±1 SD) for five subjects in the interception experiment, and corresponding values for the control experiment are shown to the side by filled black circles. Saccade probability was normalized for each subject using the average value over the 1 s interval preceding the onset of finger movement. **p < 0.01, significant differences in the values between the interception and control tasks.

On the contrary, the probability of making a saccade was significantly reduced in the interception task in the interval from 200 to 400 ms after interception onset (paired t test; t > 5.82; p < 0.001), and an ANOVA showed that the normalized saccade probability varied with time in the interception task (F_(6,27) = 6.89; p < 0.001), but not during the control task (F_(6,163) = 0.35; p = 0.9). Subjects tended to miss the target on the first try more often (30% of trials) when there was a saccade than when there was not (19% of trials). However, there were no differences in minimum finger position error at end of the first finger movement when we sorted trials according to the presence or absence of a saccade and according to success (trials with one finger motion: t₍₆₈₆₎ = 0.351, p = 0.726; trials with more than one finger motion: t₍₁₆₉₎ = 0.101, p = 0.919).

Factors triggering the onset of finger movement

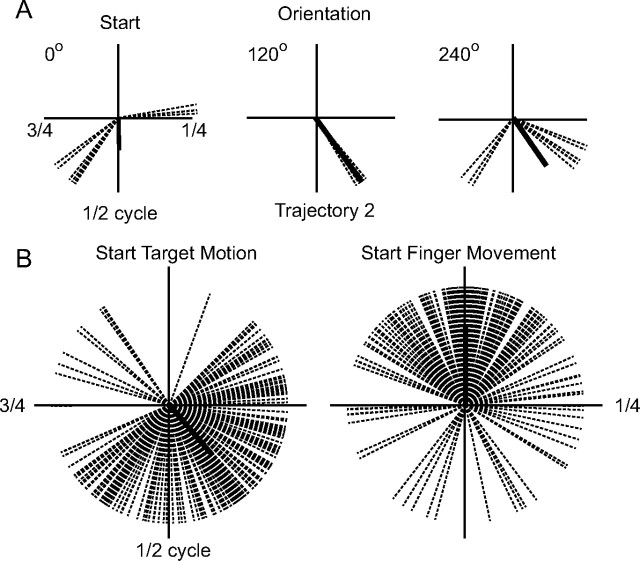
Although the subjects had a long interval (9 s) in which they could have initiated the movement to intercept the target, they did so at a time that was highly consistent for a particular path and orientation. This was already suggested by the illustrative trials shown in Figure 2. Figure 6 documents this observation in more detail, using the results for another subject (6). The plots in this illustration depict the time of onset of finger motion in polar form, the time from the onset of target motion progressing clockwise for one full period (4.5 s) of target motion. Each dashed line denotes the time of onset for one trial, with trials grouped according to path (Fig. 1C) and orientation (ranging from 0 to 240°) in Figure 6A. The bold line shows the vector average for each condition, the length of which provides a measure of the circular SD (Batschelet, 1981). When the trajectory was oriented at 120°, the subject consistently began to move when the target had traversed 40% of the cycle (i.e., 1.80 ± 0.03 s after the onset of the target motion). In the other two examples in Figure 6A, the times of target initiation clustered around two times; for example, at 0° orientation, interception was initiated either when the target traversed 23% of the cycle (four trials) or 61% of the cycle (six trials). Figure 6B demonstrates that the dispersion of the time of initiation was smaller when the start time for each trial was plotted relative to the mean start time for that trajectory (right; SD, 46.3°) than when the times were aligned on the start of target motion (left; SD, 54.3°). This difference was significant (ANOVA; F_(17,162) = 3.57; p < 0.01). This was true for all five subjects; F values ranged from 3.42 to 7.54.

Figure 6.

Variations in the time of interception for individual trials. Each dashed line in the polar plots denotes the time in the periodic motion of the target at which finger movement was initiated in one trial (time progressing in a clockwise direction). The thick black line represents the circular average of the data; its length representing the consistency of the distribution. Results for all trials performed by the subject are depicted. A, Data for one subject (6) and three orientations (0, 120, and 240°) of path 2. B, All of the data from this subject, centered on the start of target motion (left) or on the average time of initiation of finger motion for each path and orientation.

Note that in Figure 6, the time at which interception was initiated did not depend purely on intrinsic characteristics of the target trajectory, such as its speed, curvature or angular velocity, because these parameters, at a given time, are the same for all orientations. Clearly, it also did not depend merely on the amount of time elapsed since the onset of target motion (Fig. 6B). Thus, this result suggests that the direction of the motion of the target also influenced the time at which target interception was initiated. An examination of the data in Figure 2 suggests there was a tendency to initiate the finger movement when the target was traveling in a fairly straight line (low curvature and angular velocity) and when it was moving toward the bottom of the screen and toward the initial finger position.

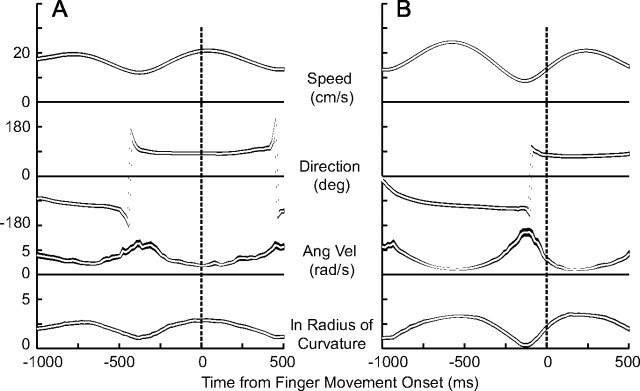
We first assessed this suggestion by aligning all of the trials for a particular subject on the time at which target interception was initiated to determine the average target motion around this time. Figure 7 shows the results of this analysis for two subjects for several target motion parameters: speed, direction, angular velocity, and radius of curvature. There are similarities and differences in the results for these two subjects, and the results in Figure 7A are more representative of the behavior of the other three subjects. All subjects preferred to begin to move when the target was traveling toward the bottom of the screen, the averages ranging from 55 to 100°. (In this plot, 0° represents target motion to the right, and 90° represents target motion straight down.) However, there was a wide distribution in the target directions for individual trials, and circular SDs ranged from 44 to 70°.

Figure 7.

Variations in target motion parameters around the time of initiation of the interception of the target. The traces from top to bottom show the average target speed, its direction of motion, angular velocity, and logarithm of the radius of curvature of the target. For direction, 0° is to the right, and 90° is down. The ln of the radius of curvature is shown because this parameter varies over a much larger range than do the other variables. The shaded areas for each trace encompass ±1 SEM. All trials from one subject were aligned on the onset of finger movement before averaging. A, Data from subject 1. B, Data from subject 4.

On average, interception was initiated when target speed was close to maximal (Fig. 7A) or when the target was accelerating (Fig. 7B) and when angular velocity was small and the radius of curvature of the target motion was large, the latter two implying that target motion was close to straight. This was true for the other three subjects as well. These three parameters are not independent because the speed is equal to the product of the radius of curvature ρ and the angular velocity ω (v = ρ ω). For pure harmonic motion, speed and radius of curvature are related through the “2/3 power law” (v = K ρ^1/3) (Lacquaniti et al., 1983; Soechting and Terzuolo, 1986). In the present experiments, the trajectories were constructed from sums of sines, thus the power law relationship does not hold exactly. Nevertheless, the three parameters v, ln ρ, and ω were significantly correlated, with |r| values ranging from 0.63 to 0.78. However, the three parameters were not correlated with target direction (|r| < 0.09). Thus, the results in Figure 7 indicate that at least two target motion parameters influenced the decision to initiate target interception.

To more precisely determine the relative importance of various target motion parameters in triggering target interception, we first computed the probability distribution of their values at the onset of finger motion and compared these distributions to the ones obtained had subjects begun to intercept the target at random times throughout the cycle (Fig. 8). A quantitative measure of the extent to which these two distributions differ can be obtained from the receiver operating characteristic (ROC), which is a plot of one cumulative probability distribution versus the other (cf. Britten et al., 1992), the area between this curve and a 45° line (the no-discrimination line) representing the dissimilarity. The results for some of the parameters tested are shown in Figures 8. Those in Figure 8B are from the same subject as in Figure 7B, whereas the results in Figure 8A are from a more representative subject. Summary results for the ROC for all parameters and all five subjects are presented in Table 3.

Figure 8.

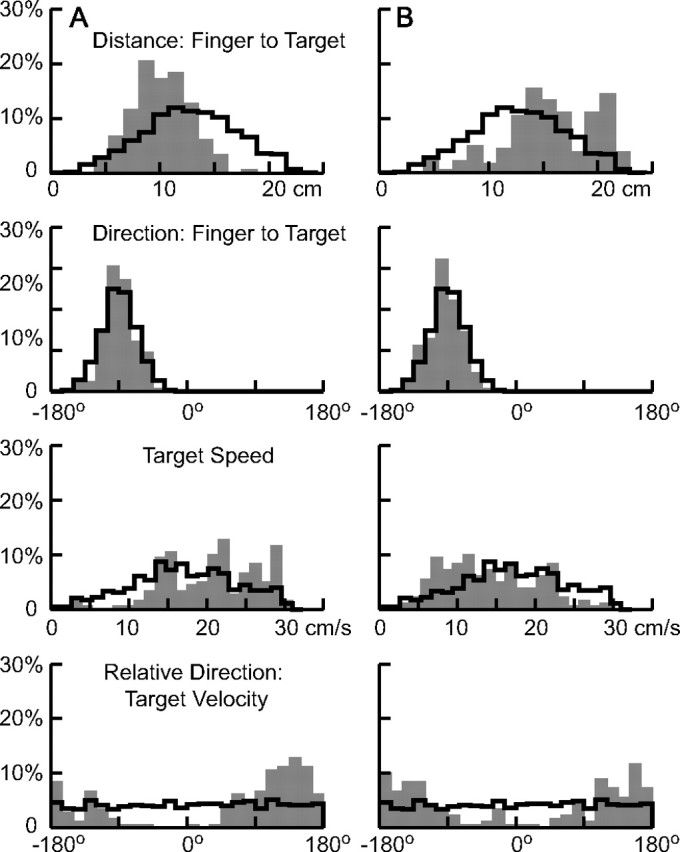
Distribution of target parameters at the time of initiation of interception. The shaded histograms in the top two panels show the probability distribution of the distance of the target from the finger and the direction from the finger to the target (−90° is straight up). The thick black line shows, for comparison, the distribution of these values had the interception been initiated at random times throughout the cycle. The bottom two panels show the distributions in the speed of the target and the direction of its motion relative to the direction from the finger to the target (0° indicates the target is moving directly away from the finger; at 180°, it is moving toward the target). A, B, Results from two subjects (A, 6; B, 4; the same as shown in Fig. 7B). All trials from each subject were included in these plots.

Table 3.

ROC area for various target motion parameters

Subject	Distance	Direction	Speed	RadCurv	AngVel	VelDir	RelVDir	Time
1	8.02	4.36	15.62	13.94	12.94	21.23	22.38	6.15
3	15.13	8.30	6.95	4.83	4.70	12.70	15.91	24.08
4	18.93	5.67	14.20	2.22	6.72	12.38	15.80	13.33
6	19.77	2.73	15.95	15.92	14.91	13.53	18.89	13.03
7	3.52	4.55	6.25	4.67	3.77	5.16	11.40	35.47

RadCurv, Radius of curvature; AngVel, angular velocity.

In Figure 8, the gray bars depict the distribution of target motion parameters at the onset of the finger movement across all trials, and the random distribution is outlined in the thick black line. We computed these distributions for two parameters related to target position: (1) the distance from the finger to the target (first row); and (2) the direction from the finger to the target (−90° is straight up; second row). We also computed them for three parameters related to target motion: (1) the speed of the target; (2) its direction of motion in screen coordinates (VelDir; data not shown); and (3) its direction of motion relative to the direction from finger to target (RelVDir; bottom row; 180° represents the target moving directly toward the finger). Finally, we assessed two geometric parameters describing the motion of the target: (1) the logarithm of the radius of curvature and (2) the angular velocity.

The direction from the finger to the target (Fig. 8, second row) had little influence on when interception was initiated. This was true for all five subjects, and the area under the ROC was small (Table 3). The distance from the finger to the target did influence the time of initiation, but in a manner that was different for different subjects. Subject 6 tended to initiate interception when the target was closer to the finger (Fig. 8A, top), as did two other subjects. However, one other subject (4) (Fig. 8B) preferred to move when the target was farther from the finger, and this factor had little influence on the last subject's decision.

The speed (Fig. 8, third row) and direction of the target had an appreciable influence on when interception was initiated, consistent with the results shown in Figure 7. Subject 6 (Fig. 8A) had a tendency to initiate interception when the target was moving faster, as did two other subjects, but subject 4 (Fig. 8B) showed the opposite tendency. All five subjects tended to initiate the interception when the target was traveling in a downward direction. The clustering of target velocity direction was even more accentuated when this direction was measured relative to the direction from the finger to the location of the target (RelVDir) (Fig. 8, bottom row). Note that for both subjects, the distributions of RelVDir are centered ∼180°. This was the case for the other three subjects as well. In all five subjects, the area under the ROC was greater for RelVDir than it was for VelDir (target velocity in screen coordinates) (Table 3).

The angular velocity of the target and the radius of curvature also influenced the time when interception was initiated, with ROC areas for these two parameters generally comparable but slightly smaller than those for speed (Table 3). Because angular velocity and radius of curvature are not independent of speed (see above), it was not possible to assess whether more than one of these variables actually entered into the decision.

An examination of the ROC areas for the various parameters in Table 3 indicates that for all subjects more than one parameter entered into the decision, in a strategy that varied from subject to subject. The ROC area for RelVDir was large for all subjects, and four of the five subjects gave considerable weight to the speed of the target and/or its distance from the finger. Two subjects (3 and 7) tended to initiate movements at a relatively consistent time. To more precisely determine the relative influence of various parameters, we computed relative weightings of the target motion parameters and time (Table 4). We included five independent parameters: two parameters for position (distance and direction) and two parameters for target motion (speed and RelVDir) and time. We computed the relative weighting for each parameter by normalizing the ROC areas in Table 3 such that the sum of their squares was unity. As noted before, each subject had a different set of weightings; however, there were some consistencies. All subjects had a relatively high weighting for the relative velocity direction (RelVDir), indicating that the subjects were more likely to begin the movement when the target was traveling toward the hand. In two subjects (3 and 7), the time that the target had moved was a major contributor to the decision, whereas two other subjects (4 and 6) gave the strongest weighting to the distance of the target from the finger.

Table 4.

Relative weighting of various target motion parameters

Subject	Overall weighting	Distance	Direction	Speed	Relative velocity direction	Time
1	29.43	0.27	0.15	0.53	0.76	0.21
3	34.34	0.44	0.24	0.20	0.46	0.70
4	31.93	0.59	0.18	0.44	0.49	0.42
6	34.34	0.58	0.08	0.46	0.55	0.38
7	38.21	0.09	0.12	0.16	0.30	0.93

Predicting target motion

In the examples shown in Figure 2, the finger initially moved in anticipation of the motion of the target. This was a general finding, and the average difference between the direction from the finger to the target and the initial direction of finger movement was 15°. The amount by which the finger motion anticipated the location of the target varied considerably from trial to trial, with SDs of ∼70% of the mean. If this variation depended on target parameters, it would suggest that subjects did not merely use a default strategy, advancing the direction of motion by a fixed amount, but that they actually predicted the motion of the target in some detail.

We tested this idea more precisely, using several models to predict target motion. In all instances, we used the average direction for the first 100 ms of finger movement and compared this direction with the direction to the predicted location of the target extrapolated according to several different assumptions. Specifically, in some models, we used the average target motion over 100 ms ending 50 ms before the onset of finger motion (Fig. 9, prediction interval). In other models, we used the motion of the target at one fixed time to make the prediction. The direction of the initial finger motion was compared with two predictions of extrapolated target motion, linear and curvilinear (Fig. 9). For the linear extrapolation, we assumed the target continued to move in the same direction at a constant speed. For the curvilinear extrapolation, we assumed the target continued to move at the same speed and angular velocity along a circular arc. For each of the models, we tested the extent to which target motion extrapolated for intervals up to 400 ms could predict the direction of initial finger motion.

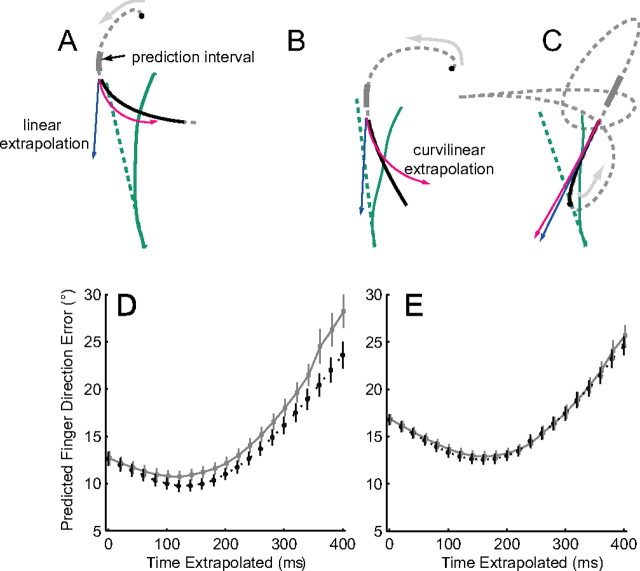
Figure 9.

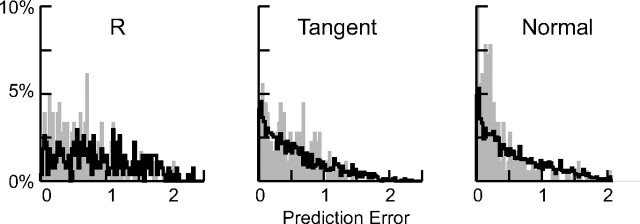
Target motion prediction used to define initial direction of finger motion. A–C, The traces in the top row show three exemplary trials for one subject (3). The target trajectory up to the time of interception is shown in the dashed gray lines, with the arrows showing the direction of movement and the black circles indicating the target start position. Target motion was extrapolated using average motion during the prediction interval, indicated by the thick gray lines. The solid black line shows the target motion throughout the finger movement. The blue and red lines indicate the extrapolated target trajectory using the linear prediction (blue) or the curvilinear prediction (red). The finger motion is shown in green (solid trace), and the direction of the initial finger motion is indicated by the dashed green line. Note that, in some instances, curvilinear extrapolation was more consistent with the initial direction of finger motion (A), whereas in other instances, the results were more consistent with a linear extrapolation (B). The bottom row shows the error between the actual initial finger direction and the direction predicted by the extrapolating target motion for times ranging from 0 to 400 ms after the onset of interception. Errors are shown for curvilinear (black line) and linear (gray line) extrapolations (average ± 1 SEM). D, Data for subject 3. E, Data for all five subjects.

Three example trials are shown in Figure 9A–C. The trajectory is shown for all trials; the path is the same, and each trial is at a different orientation (0, 240, 300°). The initial position of the target is shown with the filled black circle, and the gray arrow depicts the direction of target motion. The thick gray line shows the location of the target during the prediction interval, and the black line shows the motion of the target for the time that the finger moved. The green trace at the bottom of each panel shows the finger motion, whereas the dashed green line shows the initial direction of the finger motion predicted for 400 ms. The predicted target trajectory using the linear extrapolation (blue) and the curvilinear extrapolation (red) are also shown. In Figure 9A, the initial direction in finger motion is more in accord with the curvilinear prediction, whereas in Figure 9B, the linear prediction provides a better match. However, most commonly for all subjects, both extrapolations predicted similar target trajectories (Fig. 9C).

To determine how far in advance target motion was extrapolated, we computed the difference between the initial finger direction and the direction to the predicted target locations at 20 ms intervals beginning at the onset of interception. Figure 9D shows this unsigned error for all trials for one subject and both methods of extrapolation (gray, linear; black, curvilinear). For this subject, the minimum occurred for motion that was extrapolated for 120 ms beyond the onset of finger motion (Fig. 9D). The minimum error for the linear extrapolation (10.7°) was slightly larger than that for the curvilinear extrapolation (9.7°). The average error (for all subjects) was the lowest for both extrapolations at 160 ms (Fig. 9E), with a range of 120–400 for the five subjects.

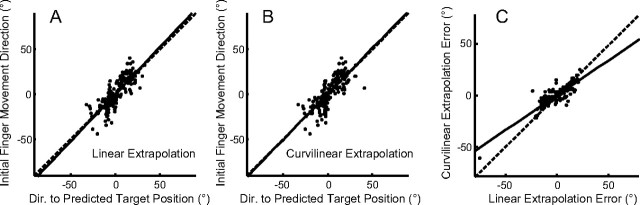
Both methods of extrapolation were able to account well for the initial direction of finger motion, as shown in Figure 10, A (r² = 0.688 for linear extrapolation) and B (r² = 0.631 for the curvilinear extrapolation). Data for the other subjects show similar results (linear r² = 0.361–0.688; curvilinear r² = 0.335–0.644). Across all subjects, we found that the curvilinear extrapolation gave a slightly better fit to the data than the linear extrapolation. Comparing the error magnitude of the curvilinear extrapolation to that of the linear extrapolation (Fig. 10C), we found that the errors of the two models were highly correlated but that the error of the curvilinear extrapolation model was slightly less. For all subjects and all trials, the absolute curvilinear prediction error was less than the absolute linear prediction error (11.02 vs 13.19°; t₍₈₉₉₎ = 13.508; p < 0.001).

Figure 10.

The direction to the predicted target position (extrapolated for 160 ms) compared with the initial finger motion direction. Both directions were measured relative to the direction from finger to the target at the end of the prediction interval. A, B, Results (for subject 1) are shown for the linear extrapolation (A) and for the curvilinear extrapolation (B). C, A comparison of the extent to which the two models account for the data; extrapolation error was defined as the difference between actual initial finger direction and its predicted direction. Results for all trials performed by the subject are depicted. In all graphs, the thick black line shows the line of best fit of a regression on the data.

In the analysis described in Figures 9 and 10, we assumed that target motion was extrapolated based on average motion parameters (velocity and angular velocity) in a 100 ms interval. However, the conclusions of this analysis did not depend critically on this assumption, because we obtained essentially the same results when we assumed that motion was extrapolated based on the values at one instant in time. Using the velocity of the target 50 ms before the onset of finger motion, we found that four of the five subjects moved their finger in a direction that anticipated the motion of the target by 134–200 ms. (The extrapolation interval for the fifth subject was longer at 350–450 ms). This model also gave a good fit to the data, with r² values for the regression between predicted and actual direction of finger motion averaging 0.682 (linear prediction) and 0.650 (curvilinear prediction). However, under this assumption, the absolute linear prediction error (9.55°) was slightly less than the one for the curvilinear extrapolation (10.53°).

Thus, it appears that the subjects predicted the motion of the trajectory using a simple model. Presumably because they initiated the interception at times when the trajectory of the target did not change much (i.e., a large radius of curvature and small angular velocity) (Fig. 7), the several models we tested gave essentially similar results. Most subjects extrapolated the motion of the target by ∼150 ms.

Kalman filtering is an iterative process that provides an optimal means for estimating and predicting the state of a dynamical system (Welch and Bishop, 2003). At each iteration, the best estimate of the state (in this instance, target motion) is obtained by a weighted combination of a prediction and of measured values, the relative weighting depending on the uncertainties in both estimates. Wolpert et al. (1995) have described results of behavioral experiments that suggest that such a mechanism is used in motor planning, and Wu et al. (2006) have implemented such a scheme in decoding motor cortical signals to control a prosthetic arm. Regardless of whether or not this algorithm is used in interception, it seems reasonable to assume that one stage in any predictive process would involve an assessment of the prediction error, by comparing predicted and sensed target locations. If such a comparison is made in real time, subjects might base their decision to initiate target interception on the results of such a comparison, initiating the interception when the prediction error was small. The results in Figure 7 are in qualitative accord with this notion, because subjects tended to initiate interception when the target was moving along a relatively straight path.

We tested this notion more precisely, invoking two models to predict target motion. In the first model, at each time step, target location was extrapolated using the linear and angular velocity of the target (curvilinear extrapolation). In the second model, we used the statistical properties of the trajectories (i.e., the covariance matrix between successive time steps) to extrapolate the motion (Wu et al., 2006). Both models gave very similar results, and we will consider only the first one. Figure 11 shows that indeed the quality of the predicted motion is not uniform throughout the trajectory. The shaded ellipses [at 50 ms intervals along one trajectory (Fig. 1A)] represent the error in predicting the location of the target (extrapolation error). The results are in accord with qualitative expectations: along the straight portions of the target trajectory, the uncertainty is almost zero, but in areas of greater curvature, the uncertainty is quite large.

Figure 11.

The results of a prediction algorithm for one target trajectory (0) and one orientation (0°). The target trajectory is shown with the black line. The algorithm we used calculated the position of the target 50 ms in the future using the current speed and direction and angular velocity of the target motion. The extent to which this prediction differed from the actual location of the target is denoted by the size and orientations of the shaded ellipses.

We then tested the possibility that the subjects monitored the error in prediction algorithm to guide movement onset (Fig. 12). We used the experimentally obtained times for the onset of interception and computed the extrapolation error 50 ms before finger movement onset. We computed the size of the ellipse (Fig. 12, left, R) and the cross section of the ellipse along the direction from the finger to the target and in the normal direction (Fig. 12, middle and right). The thick black lines represent the results if the subject were to initiate finger movement at random times, whereas the gray shading shows the distribution of the extrapolation errors at the times the subject actually began the interception. From these distributions, we computed the area under the ROC. The ROC curves using the combined data for all subjects did not differ substantially from a random distribution. Even the results for the subject illustrated in Figure 12, which showed the largest deviation from a random distribution, provide only modest support for the hypothesis. For this subject (1), the area under the ROC curve was largest for the extrapolation in the normal direction (9.54), but this value was substantially smaller than the ROC areas for the several target motion parameters (Table 3). Thus, it appears that subjects did not base their decision to initiate target interception on a formal assessment of the error in predicting target motion. However, this result does not rule out that their performance was optimal according to other criteria.

Figure 12.

The distribution of extrapolation errors at the time interception was initiated for one subject (1). The gray shading shows the results of the subject's performance, and the thick black trace shows the results had the onset of interception been randomly distributed. The first column shows the overall size of the error (r = x × y); the next two columns show the size of the error in the direction tangent from a line drawn from the target to the finger and in the direction normal to this line. Of the five subjects, the data show the largest deviation from randomness.

Discussion

In these experiments, subjects were asked to catch a target that moved along one of several two-dimensional trajectories using a single finger movement. These conditions are more naturalistic than some experimental protocols because the subjects intercepted a target moving quasi-unpredictably and initiated the movement under their own volition. In our analysis, we focused on the pattern of coordination of eye and hand movements in this task, the extent to which the motion of the target was predicted, and the factors that entered into the decision to initiate interception.

Hand–eye coordination

Although there was no instruction to do so, subjects used smooth-pursuit eye movements to track the target up to the time of interception, with no reduction in pursuit gain. Thus, our subjects used a strategy similar to that described for skilled batsmen in cricket (Land and McLeod, 2000) and in baseball (Bahill and LaRitz, 1984). These authors have reported that highly skilled batsmen track the pitched ball with a combination of eye and head movements for as long as possible. Also, in agreement with previous reports, the pursuit gain was greater in the horizontal direction compared with the vertical direction (Kettner et al., 1996; Leung and Kettner, 1997). However, in our experiment, pursuit gain increased with higher sinusoidal frequencies, whereas previously gain had been shown to decrease with frequency (Leung and Kettner, 1997). However, those authors explored a much larger range of frequencies, and within the range that we used, their results show only small variations in gain. Importantly, we could discern no differences in the characteristics of smooth pursuit when we changed the task from intercepting the target to merely tracking it visually (Fig. 4).

In contrast, saccades tended to be suppressed during the finger movement. This was an unexpected finding because, for a stationary target, the target is typically foveated before the hand movement (Johansson et al., 2001; Crawford et al., 2004) or a saccade is made coincident with the hand movement (Gribble et al., 2002). It has also been reported that gaze is anchored on the target of a reaching movement even when the task requires a reorientation of gaze (Neggers and Bekkering, 2000, 2001). Furthermore, recordings from posterior parietal cortex indicate that the motor error for a hand movement to a stationary target (i.e., the direction of the intended movement) is encoded in a retinocentric frame of reference (Batista et al., 1999; Buneo et al., 2002). At subsequent stages (e.g., motor cortex), this representation is remapped into a body-centered frame of reference. If an eye-centered frame of reference was also used to represent the goal of reaching to a moving target, as in our task, it would seem that this representation and the subsequent remapping would be simpler if the direction of gaze did not change continuously, as it does during smooth pursuit.

Thus, our results indicate the importance of the information provided by the smooth-pursuit system regarding the target motion parameters. During saccades, visual information is suppressed (Campbell and Wurtz 1978). Thus, although the suppression of saccades during the hand movement led to an increase in the position error between the eye and the target (Fig. 4), it also allowed for continued visual monitoring of the speed and direction of the target motion and facilitated visually mediated corrections to the hand movement in a reactive manner (Merchant and Georgopoulos, 2006).

The subjects' gaze typically lagged behind the target by ∼50–100 ms, in a similar range as reported previously (Mrotek et al., 2006). A frequency analysis of smooth pursuit when subjects merely tracked the target also gave time delays of ≤50 ms (Table 2). Because these values are less than the latency for the initiation of smooth pursuit (∼100 ms), our observations indicate a predictive element in its control (Mrotek and Soechting, 2007).

Predicting target motion

The initial direction of finger motion also anticipated the trajectory of the target (Fig. 2), further supporting the involvement of predictive mechanisms in this task. Using several different assumptions to predict target motion, we found that the finger tended to be directed to a location ∼150–200 ms in advance of the target. Note that subjects typically required a substantially longer time (350 ms) to actually reach the target. In fact, the finger often followed a slightly curved path and curved in the direction of target motion during the last half of the finger movement. Although we did not examine this phenomenon in detail, it suggests the existence of on-line visually mediated corrections of finger movements during the interception.

The finding that the range of target motion prediction did not extend over the full amount of time required to reach the target suggests a limitation (150–200 ms) in the temporal extent of predictive mechanisms. Recent observations by Ariff et al. (2002) are in accord with this suggestion. These authors studied eye movements as subjects tracked the motion of their unseen hand and found that the saccadic goals anticipated hand location by a similar amount. Monkeys making hand movements to trace the outline of a template also made anticipatory saccades to the location of their unseen hand, anticipating its location by 50–100 ms (Reina and Schwartz, 2003).

In our models, we always assumed that the velocity of the target (i.e., its speed and direction) was used to predict future locations. We also considered the possibility that its angular velocity (i.e., the rate of change in direction) might be used in prediction, but we did not include changes in speed in these models. Thus, we incorporated the normal component of target acceleration (a_n = vω; v, speed; ω, angular velocity) but not the tangential component of acceleration (a_t = dv/dt).

Our choice was motivated by previous behavioral observations as well as by the response characteristics of neurons in MT, the primary cortical area for transducing visual motion. For example, subjects were able to estimate the new direction of a target after an abrupt change in direction after viewing the new direction for only 50 ms (Mrotek et al., 2004). Furthermore, when subjects tracked a target that underwent curvilinear motion, and transiently disappeared behind an occlusion, pursuit eye movements continued to change direction while the target was occluded (Mrotek and Soechting, 2007). These results indicate predictive mechanisms can incorporate information about angular velocity. To the contrary, smooth pursuit is much less sensitive to linear acceleration (Krauzlis and Lisberger, 1994; Soechting et al., 2005). Furthermore, information about changes in speed is only encoded weakly in the signal of neurons in MT (Lisberger and Movshon, 1999). Subjects are able to accurately time their hand movement to catch a falling ball (Zago et al., 2004), but it has been suggested that this ability results from an internal model of gravitational motion rather than a visually mediated sensing of target acceleration.

Deciding to intercept the target

In our experiments, subjects were free to initiate the movement to intercept the target throughout a long interval. Nevertheless, for any particular target trajectory, the time of initiation was remarkably consistent (Fig. 6), and this time was linked to several parameters defining the trajectory of the target (Fig. 8). Most subjects initiated the finger motion at a time when the target was moving at a relatively high speed, but along a fairly straight trajectory. The distance from the finger to the target (not too near and not too far) and the direction of motion of the target (toward the finger) also entered into the decision (Tables 3, 4). These findings make intuitive sense. For example, it is easier to predict the future location of the target when its trajectory is curving little (Fig. 10). Moving to a target located near the center of the screen, rather than close to the finger, would provide ample time for correction. Furthermore, for a target moving toward the finger in a straight line, there is little uncertainty in choosing the proper direction of finger movement. Because the time of interception did not have to be controlled (the finger could be moving when it intercepted the target), hitting the target head on would appear to maximize the chance of success.

These qualitative observations suggested to us that subjects might implement a strategy that optimized their chance of intercepting the target based on an evaluation of the uncertainty in predicting target motions. The assumption that movements are controlled in an optimal manner is a common one (cf. Todorov and Jordan, 2002; Körding and Wolpert, 2006; Bays and Wolpert, 2007), and there is evidence in support of this hypothesis. For example, Ernst and Banks (2002) have shown that subjects assign relative weights to visual and haptic information based on the uncertainty in each of the two measures in a manner optimal for decoding the stimulus. An optimal predictive mechanism also appears to be evoked when subjects are required to estimate the unseen motion of their hand (Wolpert et al., 1995). Applying this hypothesis to the present situation, one might expect subjects to initiate the movement to intercept the target when the uncertainty in future target locations was small. We tested the predictions of such a model. We reasoned that at each point in time, there would be a comparison of predicted target location, based on an extrapolation of previous target motion, with the currently sensed location of the target in a process akin to Kalman filtering (Welch and Bishop, 2003). If so, finger movements would be initiated when the prediction differed little from the actual target location. However, the evidence for such a process was not compelling (Fig. 12). The distribution of the errors in predicting target motion at movement initiation did not differ substantially from those had subjects initiated interception at random. Thus, it appears that although subjects did base their decision to intercept the target on the values of several target motion parameters, this process did not involve a formal model of the predictability of target motion that led to an optimal solution. However, the possibility remains open that the strategy adopted by the subjects, incorporating preferred locations, speeds, and direction and presumably based on life-long experience with intercepting moving targets, may be optimal according to other criteria.