Nonlinear Spatial Integration in the Receptive Field Surround of Retinal Ganglion Cells

Abstract

Throughout different sensory systems, individual neurons integrate incoming signals over their receptive fields. The characteristics of this signal integration are crucial determinants for the neurons' functions. For ganglion cells in the vertebrate retina, receptive fields are characterized by the well-known center-surround structure and, although several studies have addressed spatial integration in the receptive field center, little is known about how visual signals are integrated in the surround. Therefore, we set out here to characterize signal integration and to identify relevant nonlinearities in the receptive field surround of ganglion cells in the isolated salamander retina by recording spiking activity with extracellular electrodes under visual stimulation of the center and surround. To quantify nonlinearities of spatial integration independently of subsequent nonlinearities of spike generation, we applied the technique of iso-response measurements as follows: using closed-loop experiments, we searched for different stimulus patterns in the surround that all reduced the center-evoked spiking activity by the same amount. The identified iso-response stimuli revealed strongly nonlinear spatial integration in the receptive field surrounds of all recorded cells. Furthermore, cell types that had been shown previously to have different nonlinearities in receptive field centers showed similar surround nonlinearities but differed systematically in the adaptive characteristics of the surround. Finally, we found that there is an optimal spatial scale of surround suppression; suppression was most effective when surround stimulation was organized into subregions of several hundred micrometers in diameter, indicating that the surround is composed of subunits that have strong center-surround organization themselves.

Introduction

Individual neurons typically combine multiple input signals to form their output. This signal integration is a key factor of neuronal function; neurons that sum their inputs linearly show very different response characteristics compared with neurons with strongly nonlinear integration. Retinal ganglion cells, for example, combine spatially distributed visual signals through their receptive fields, which are organized in the well-known center-surround structure (Barlow, 1953; Kuffler, 1953). Beginning with the distinction of linearly integrating X cells and nonlinearly integrating Y cells (Enroth-Cugell and Robson, 1966), the question of how ganglion cells integrate signals over their receptive fields has received considerable attention (Hochstein and Shapley, 1976; Victor and Shapley, 1979a, 1979b; Enroth-Cugell and Freeman, 1987) and is considered crucial for endowing different types of ganglion cells with different functions (Gollisch and Meister, 2010; Schwartz and Rieke, 2011; Gollisch, 2013; Leonardo and Meister, 2013). Studies of spatial integration in the receptive field center have suggested that nonlinearities arise from presynaptic bipolar cells, which act as nonlinear subunits (Enroth-Cugell and Robson, 1966; Hochstein and Shapley, 1976; Victor and Shapley, 1979a; Demb et al., 2001; Bölinger and Gollisch, 2012; Schwartz et al., 2012).

Less is known, however, about how signals are integrated in the receptive field surround. Classical models treat the center-surround receptive field as a linear spatial filter, as in the difference-of-Gaussians model (Schade, 1956; Rodieck, 1965) or in the linear–nonlinear model (Chichilnisky, 2001), which can explain the role of the surround in local contrast enhancement and redundancy reduction (Srinivasan et al., 1982; Atick and Redlich, 1993; Dan et al., 1996; Tokutake and Freed, 2008; but see Pitkow and Meister, 2012). However, nonlinear mechanisms beyond the receptive field center also exist, as demonstrated by the suppressive effects of moving gratings in the periphery or other stimuli that do not active a linear surround (Werblin, 1972; Schwartz, 1973; Shapley and Victor, 1979; Enroth-Cugell and Jakiela, 1980; Frishman and Linsenmeier, 1982; Passaglia et al., 2001; Solomon et al., 2006; Passaglia et al., 2009). Furthermore, nonlinear signal integration in the surround is involved in specific retinal functions, such as the distinction between local and global motion signals (Olveczky et al., 2003; Baccus et al., 2008) or the gating of center signals through motion in the surround (Roska and Werblin, 2003; Geffen et al., 2007).

Therefore, we sought here to assess quantitatively the spatial integration in the receptive field surround of salamander ganglion cells. In particular, we investigated whether this integration is linear or nonlinear and how it compares with the spatial integration characteristics in the center of different ganglion cell types. To this purpose, we apply the technique of iso-response measurements (Gollisch and Herz, 2012) as follows: using closed-loop control of visual stimuli, we identify different stimulus patterns in the surround that lead to the same amount of suppression of the center-evoked ganglion cell response. Iso-response measurements previously revealed two types of nonlinear spatial integration in receptive field centers (Bölinger and Gollisch, 2012). We now show that these are accompanied by distinct types of nonlinear stimulus integration in the surround.

Materials and Methods

Electrophysiology and visual stimulation.

Retinas were isolated from the eyecups of axolotl salamanders (Ambystoma mexicanum; pigmented wild-type) of either sex and spiking activity of retinal ganglion cells was recorded with a 60-channel multielectrode array (10 μm electrode diameter, 100 μm spacing, 25 kHz sampling rate; Multichannel Systems) as described previously (Bölinger and Gollisch, 2012). During the recordings, retinas were superfused with oxygenated Ringer's solution at room temperature (20–22°C). All experimental procedures were performed in accordance with the institutional guidelines of the University Medical Center Göttingen.

Visual stimuli were displayed with a gamma-corrected white OLED display (600 × 800 pixels; eMagin), demagnified to 7.5 × 7.5 μm per pixel, and projected onto the photoreceptor layer of the retina through a telecentric lens (Edmund Optics). All stimuli were presented on a background light intensity of 2.6 mW/m² in the photopic range. The stated contrast values refer to percent Weber contrast, 100*(I_stimulus − I_background)/I_background.

Online spike sorting and closed-loop measurements.

For data acquisition, online spike sorting, and data analysis, we used custom-made software, written in C++ and applying the Qt framework for graphical interaction. To analyze the spatial integration characteristics of a single cell, we selected one channel of the multielectrode array with sufficiently good spike signals for online analysis. For this channel, online spike sorting was performed through template matching. To create templates, a full-field Gaussian flicker or binary checkerboard stimulus was applied to the retina for 2–3 min and then a threshold was determined (typically 5 SDs of the noise level on that channel, but occasionally adjusted slightly as appropriate) to detect local peaks of sufficient size in the voltage trace. For each detected peak, the sequence of the surrounding 64 sample points was collected, with peaks aligned at the 24^th sample point (corresponding to a time interval between 0.9 ms before and 1.6 ms after the peak). To separate spikes from different ganglion cells, we performed principal-component analysis on these voltage sequences and then applied K-means clustering in the space of the first three principal components. The number of clusters was determined according to visual inspection of the separation of data points in the 3D space and of the superposed voltage sequences from each cluster. When good separation between clusters was observed, a template for each cluster was calculated as the average over all voltage sequences in the cluster. One of the thus identified ganglion cells, typically the one with the largest peak amplitude among all the templates, was selected for further in-depth analysis. This entire procedure of online template generation typically took a few minutes, after which recordings were resumed.

In subsequent measurements, peaks in the voltage trace were detected with the same threshold as before and were assigned to one of the clusters by identifying the minimal Euclidean distance between the corresponding voltage sequence and each of the templates. The timings of the detected spikes were then saved to disk and also used for immediate online analysis. The amplitude of spikes was visually observed by the experimenter during further measurements. When there was a noticeable change in the amplitude, templates were recomputed and used for further online analysis. To check the quality of online spike sorting, a histogram of the interspike intervals (ISIs) of the recorded cells was inspected for all iso-response measurements. Refractory period violations were defined as ISIs of <2 ms. None of the analyzed cells (n = 42) showed violations for >0.7% of ISIs and the majority of the cells (28 of 42 cells) had no violations at all.

Receptive field estimation.

We determined the size and position of the receptive field center and surround using closed-loop measurements in a manner similar to that used in a previous study (Bölinger and Gollisch, 2012), with some modifications. First, we determined the center location of the receptive field as the intersection of two orthogonal midlines of the receptive field. For each midline, an initial estimate of the position was obtained by stimulating the retina with dark and bright edges that moved successively in 1 of 2 opposing directions (single repeat, 1 s duration). From the relative response strength to the dark and bright edges, the recorded ganglion cell was identified as either an On or an Off type; only Off-type cells, which represent the vast majority in the amphibian retina (Burkhardt et al., 1998; Segev et al., 2006; Marre et al., 2012), were used for further analysis. The initial estimate of the midline was then calculated based on the difference in first spike timing for the two motion directions of the dark edges.

Next, the location of each midline was refined as follows. We applied brief stimulation with dark contrast separately on either side of the midline estimate (typically −20% contrast, 330 ms stimulus duration, with 3–5 s intervals between individual stimuli) and computed the difference in spike count. To obtain the final midline location, we used a modified search algorithm from stochastic root finding (Wu, 1986) to determine the location with zero spike count difference. The algorithm comprised two phases. In the first phase, the position of the midline estimate was successively shifted until both positive and negative differences in spike count were observed. The size of each shift was chosen randomly as 75, 150, 225, or 300 μm and the direction was determined based on the sign of the observed spike count differences. In the subsequent second phase, linear regression on the spike count difference versus the midline estimate was performed after each stimulus set. This was used to update the estimated location of the midline position as the position that should yield zero spike count difference according to the regression model. The updated prediction was applied as the midline estimate for the next iteration. The evolution of the estimated midline position was visually monitored and the search was terminated when no more changes in the estimate were observed.

Next, the size of the receptive field center was determined from responses to flashed dark spots around the identified receptive field midpoint. Spots of different sizes, ranging from 37.5 to 1500 μm radius, were presented for 330 ms with 3 s interval typically at −20% contrast in randomized order to determine the radius that yielded the maximal response. Based on these measurements, we chose a spot size for stimulating the center region and an annulus size around the spot for stimulating the surround region. Both the spot and annulus were centered on the identified midpoint of the receptive field.

To minimize the influence of the transition region between center and surround, where excitatory and inhibitory signals mix with similar strength, we enforced a gap between the radius of the center spot and the inner radius of the surround annulus. The radius of the center spot was typically selected to be somewhat smaller than the spot radius of the maximal response, in particular when the response curve had a flat, plateau-like region around its maximum, which suggests a region of similar strength of excitatory and inhibitory effects. For the surround annulus, the inner and outer radii were selected in the following way. We first chose the outer radius by the spot size that yielded no further decrease in response. The inner radius of the annulus was then determined through additional measurements, for which annuli with the selected outer radius and varying inner radius were presented without an accompanying center stimulus. From these measurements, the inner radius of the annulus was chosen as the minimal inner radius for which no spikes were elicited. This means that the selected surround annulus alone did not provide substantial excitatory signals. The identified inner radius always turned out to be larger than the spot size of maximal response. The resulting gap between the center spot and the surround annulus was in the range of 75–525 μm.

Iso-response measurements.

We measured iso-response stimuli for combinations of surround contrast and for pure center stimulation for the sake of comparison. For iso-response measurements in the center, the stimulus region over the receptive field center was divided into two halves and different combinations of contrast in the two halves were used for stimulation, as described previously (Bölinger and Gollisch, 2012). To ensure symmetric division of the receptive field center, each of the two compartments was stimulated separately three to five times with a fixed negative contrast and their average responses (spike counts) were compared. When the difference was more than one spike, the bisecting line was rotated and the measurements were repeated until the response difference was smaller than one spike.

For iso-response measurements in the receptive field surround, the center region was stimulated with fixed negative contrast and the surround region was divided into two halves and stimulated with different combinations of contrast. The negative contrast value for the center ranged from −70% to −20%. The value was chosen so that the elicited spike count was large enough for the response not to be completely suppressed by stimulation of the surround. The angle of the bisecting line of the surround was again adjusted until stimulation of each of the two surround compartments, together with the center, resulted in a response difference of less than one spike.

For both types of iso-response measurements, individual stimuli corresponded to points in a 2D stimulus space, given by the two contrast values, S₁ and S₂, in the two halves of the investigated receptive field region. The aim of the iso-response measurements was to identify iso-response curves in this space, which were defined as the sets of those stimuli that led to the same, predefined response by the recorded ganglion cell. Here, we assessed the response as the number of spikes elicited by the stimulus, counted from stimulus onset to 25 ms after stimulus offset, thus avoiding spikes that might be elicited by the offset. We typically aimed at successively measuring several iso-response curves with different target responses, corresponding to different overall levels of contrast of the stimulus components. To select a suited target response, N_target, we first chose a contrast level from the range of −20% to −80% and then determined N_target as the average spike count that was obtained by applying the chosen contrast to the two stimulus components individually.

To measure individual iso-response stimuli for an iso-response curve, we performed a series of line searches along different radial directions in the stimulus space spanned by S₁ and S₂. For each search direction, the radius $r=\sqrt{S_1^2+S_2^2}$ of consecutive measurements was adjusted according to the previously encountered responses to find the radius r₀ that yielded the target spike count N_target. This corresponds to changing the two contrast values in the two investigated receptive field regions while keeping their ratio constant. Individual stimuli were presented as contrast steps for 330 ms, with 5–10 s interstimulus intervals.

The line search was performed in a manner similar to the search for the location of the receptive field center. Again, the search consisted of two phases. In the first phase, starting from an initial value chosen as explained after the description of the search algorithm, the radius r was adjusted until spike counts both below and above the target had been observed. Therefore, depending on the previous response, r was increased or decreased as appropriate to increase or decrease the response. The size of the change of r was chosen randomly as 2%, 4%, 6%, or 8% contrast.

In the second phase, a new estimate of r₀ was obtained after each stimulus presentation by fitting a straight line to the set of applied radii r and observed spike counts N as follows:

using the fitting parameters r₀ and b. To determine when the line search should be stopped, we monitored the change in the estimate of r₀. Specifically, we chose as a convergence criterion that the absolute deviation of the new estimate from the previous four estimates be <1.5% contrast on average. The last estimate of r₀ then provided a data point for the iso-response curve and plotted error bars correspond to one SD of the fitted parameter r₀. When the convergence criterion was not reached after 25 iterations from the beginning of phase 1, the search was abandoned and no data point was obtained for this search direction.

The first line search was always performed along a search direction that corresponded to stimulating only one of the two stimulus components. Here, the initial value for r was simply the same contrast level as was applied for determining the target spike count. For subsequent searches, the new direction was chosen as a neighboring direction of the previous search, separated by an angle of 10 degrees. The initial value for the search was then given by the radius r₀ that had been identified for the previous search direction.

We classified cells into two previously described types (Bölinger and Gollisch, 2012) based on visual inspection of the shape of the measured iso-response curves for the receptive field center. One type is characterized by a circular arc in the lower left quadrant of the stimulus space. The other type is characterized by a notch along the lower left diagonal. For the large majority of cells (40 of 42 cells), this classification was unambiguous. The two cells that could not clearly be classified into one of the two types were excluded from further analysis.

Analysis of iso-response curve shapes.

We assessed the shape of the iso-response curve in two ways, analogous to a previous study (Bölinger and Gollisch, 2012). To quantify the degree of the convexity of an iso-response curve, we calculated a form factor as the ratio of the observed radius r_observed of the curve along the lower left diagonal to the linear prediction r_linear that was obtained from the two intersections r_x and r_y of the iso-response curve with the x and y-axis, respectively. Concretely, r_observed was calculated as the average of the radii for the two closest measured data points as follows:

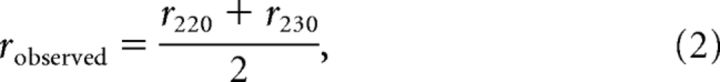where r₂₂₀ and r₂₃₀ are the measured radii of the curve at 220° and 230° in the stimulus space, respectively. r_linear was calculated as follows:

where r_x and r_y are the radii of the iso-response stimuli for each of the two stimulus components in isolation. The form factor was then obtained as r_observed/r_linear.

We frequently measured multiple iso-response curves in either the center or the surround of a single ganglion cell using different target spike counts. This allowed us to analyze the dependence of the form factor F on the overall contrast level C in a quantitative fashion. The overall contrast level was defined as the average contrast required for reaching the target response when only one of the two stimulus components was used; that is, C = (r_x + r_y)/2. We then computed the relative changes of form factor per contrast for individual cells as the ratio δF/δC, where δF is the difference of two measured form factors and δC is the corresponding difference of contrast levels. When more than two iso-response curves had been measured, we computed this relative change for all pairs of form factor measurements with neighboring contrast values.

To evaluate the degree of rectification, we calculated the average slope of each iso-response curve using linear regression in the region of the stimulus space where one contrast value was negative and the other was positive. As detailed in Bölinger and Gollisch (2012), the slope was defined so that perfect rectification (i.e., iso-response curve parallel to the x-axis and y-axis, respectively) and linear integration (i.e., iso-response curve parallel to the upper left or lower right diagonal) corresponded to values of zero and unity, respectively.

Estimation of the subunit nonlinearity.

To obtain a descriptive model of how the two stimulus components are combined by the ganglion cell, we fitted a subunit model to the iso-response curves. The model assumes that the integrated effect of the two stimulus components S₁ and S₂ is given by a weighted sum of N(S₁) and N(S₂), where N(S_i) is the subunit nonlinearity, parameterized as a sigmoidal function (Hill equation) as follows:

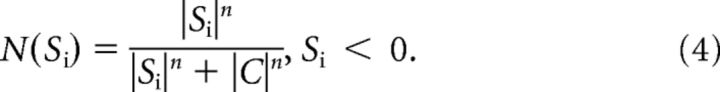For this analysis, we focused measurements on the lower left quadrant of stimulus space (“Off-Off quadrant” where both contrast values S₁ and S₂ are negative). We often measured multiple curves from a single ganglion cell and the parameters were determined to simultaneously fit multiple curves. The j^th iso-response curve intersecting with x-axes and y-axes at (S_x,j, 0) and (0, S_y,j) can be represented as follows:

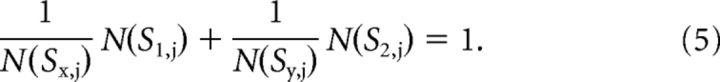The parameters n, C, S_x,j, and S_y,j were optimized according to a least-squares criterion using the Nelder-Mead simplex algorithm (using a built-in function, fminsearch, in MATLAB) and taking into account all iso-response curves measured for a given cell. In this calculation, residuals were obtained as the differences between the experimentally determined radii $r=\sqrt{S_{1,\text{j}}^2+S_{2,\text{j}}^2}$ and the corresponding model predictions for each angle in stimulus space for which an iso-response stimulus had been measured. The predicted radius was obtained by numerically solving Equation 5 for S_1,j and S_2,j.

To quantify the degree of saturation of the determined subunit nonlinearity, we calculated the ratio of the value of the subunit nonlinearity N(S) at S = −50% contrast to that at S = −100%. This ratio, denoted as N(−50)/N(−100), ranges from zero to unity and a larger value indicates a higher degree of saturation. This was used to assess population differences in saturation between center and surround and between the different cell types.

Results

Assessing spatial stimulus integration with iso-response curves

Retinal ganglion cells are well known for their center-surround receptive field structure. Visual stimulation of the surround antagonizes stimulation of the center region. In most natural situations, however, the surround is not homogeneously stimulated, but contains regions with different illumination, the combined effect of which depends on how these different surround signals are integrated. In the present study, we therefore investigated how the surround region of ganglion cell receptive fields in the salamander retina combines different stimulus components. We focused on Off-type ganglion cells, which form the vast majority of ganglion cells in the salamander (Burkhardt et al., 1998; Segev et al., 2006; Marre et al., 2012).

The basic stimulus layout we used for studying this question is illustrated in Figure 1A. The receptive field center was stimulated with a fixed contrast C to set a basic activation level of the ganglion cell, upon which the surround stimulus could act in a suppressive fashion. The stimulus region of the surround was subdivided into two halves, which were stimulated at the same time as the center region with contrast values of S₁ and S₂, respectively. We then investigated the way in which S₁ and S₂ are combined to determine the total effect of the surround.

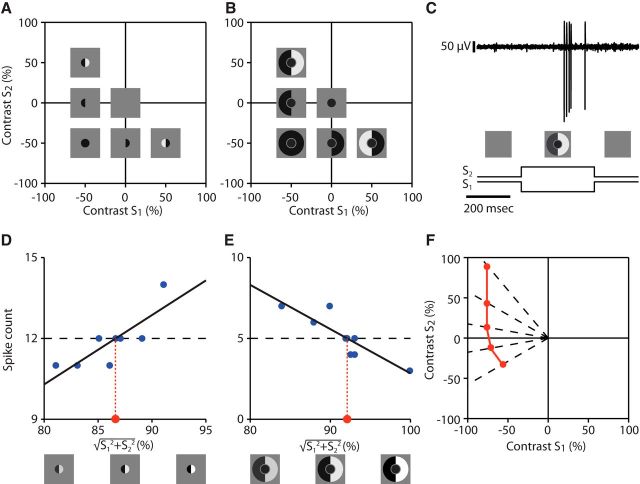
Figure 1.

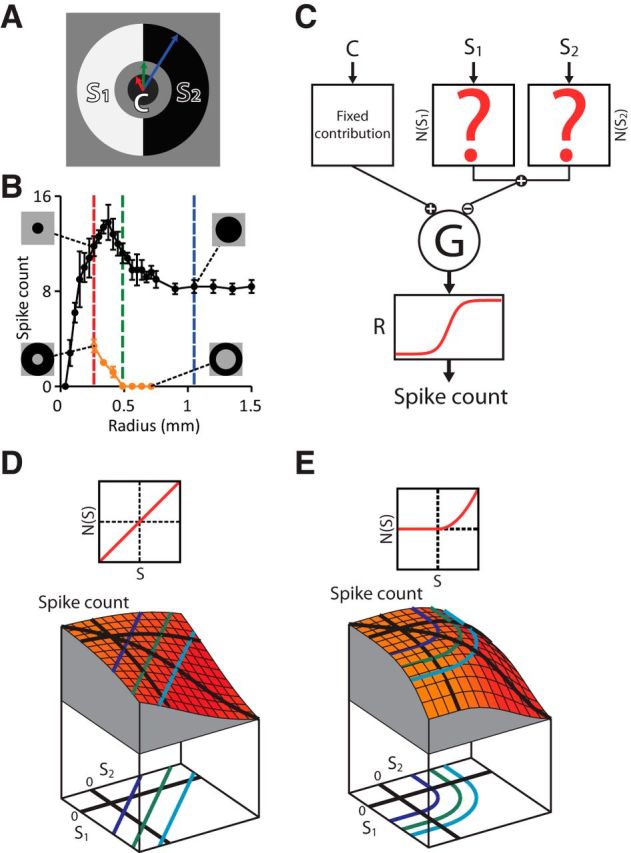
Strategy of iso-response measurements for characterizing stimulus integration in the receptive field surround. A, Stimulus structure to study surround integration. The receptive field surround is divided into two regions and stimulated with two contrast values, S₁ and S₂, whereas the receptive field center is stimulated with a fixed contrast value, C. Note that there is a gap between the center and surround to avoid the region where excitatory and inhibitory effects have similar strength. B, Example for assessing the size of the receptive field center and surround of a recorded ganglion cell. The responses to spot stimuli with different radius (black curve) were used to determine the radius of the center spot (red dashed line) and the outer radius of the surround annulus (blue dashed line). The responses to annuli with different inner radius (orange curve) were used to determine the inner radius of the surround annulus (green dashed line). C, Subunit model consisting of an input unit for the receptive field center and two subunits for the surround. We consider a fixed input C to the center and vary the inputs to the surround subunits, S₁ and S₂. These two inputs are first transformed and then integrated to yield N(S₁) + N(S₂). This signal is combined with the center signal and fed into an output nonlinearity R, which determines the model's output spike count. D, Simulated stimulus-response relation for the subunit model with linear integration. Top, Shape of the subunit transformation N(·), which here is simply the identity. Bottom, Stimulus–response plot with iso-response curves projected below. The shape of iso-response curves (straight lines) reflects the linear integration of the surround subunits. E, Same as D, but each surround subunit transforms its input with a threshold-quadratic nonlinearity (top), which corresponds to the summation of squared positive inputs. Therefore, iso-response curves (bottom) have two straight segments parallel to the axes, reflecting the threshold operation, and a circular arc in the center region, reflecting the quadratic summation.

To investigate this question experimentally, we first needed to determine the appropriate regions for placing the center and surround stimuli for a given ganglion cell. We identified the receptive field center location and size for each cell using online analysis of the extracellularly recorded spikes (see Materials and Methods). The size of the stimulus regions for the center and surround was chosen according to responses to dark spots and annuli centered on the receptive field (Fig. 1B). A classical way to determine the border between center and surround is to use the spot size where the ganglion cell response is maximal. Here, however, we chose the center stimulus region to be slightly smaller and the inner radius of the surround annulus to be slightly larger to minimize the effect of the transition region between the receptive field center and surround, where activating and suppressive effects are approximately equally strong. Specifically, the inner radius of the surround annulus was chosen so that the annulus alone generated no spikes (Fig. 1B, orange data points). The region between the center spot and surround annulus was kept constant at background intensity and the outer radius of the surround annulus was determined by the spot size where no further reduction in the spike count was observed.

With this stimulus layout, we then aimed at determining how the surround signals S₁ and S₂ were combined by the ganglion cell. To illustrate the challenge and the approach for assessing stimulus integration in the receptive field surround, let us consider a simple model (Fig. 1C) of how a ganglion cell may respond to the stimulus layout of Figure 1A. In the model, we assume that the surround signals S₁ and S₂ are transformed by some function N(·), which allows for nonlinear effects of surround activation. Subsequently, the combined surround signal N(S₁) + N(S₂) is subtracted from the fixed center activation. The shape of the function N(·) determines how the surround components S₁ and S₂ are integrated. If N(·) is simply linear (Fig. 1D, top), the total suppressive signal is just the sum of the two surround components, whereas nonlinear transformations such as a threshold-quadratic transformation (Fig. 1E, top) lead to a different combination of S₁ and S₂.

The difficulty in assessing experimentally whether individual stimulus components in the surround contribute linearly or through some specific kind of nonlinearity lies in the fact that processing by the ganglion cell itself imposes another nonlinearity on the integrated signal, which we call the output nonlinearity (Fig. 1C, function R). The challenge is to separate this output nonlinearity, which may comprise the spiking threshold, response saturation, or transformation induced by voltage-dependent ionic currents, from nonlinearities that occur before signal integration and therefore affect how signals are combined (see also McFarland et al., 2013). Our approach was to determine iso-response stimuli, which are defined as different combinations of the stimulus components S₁ and S₂ that yield the same, predefined neuronal response (Gollisch et al., 2002; Bölinger and Gollisch, 2012; Horwitz and Hass, 2012). The iso-response stimuli trace out iso-response curves in stimulus space with shapes that do not depend on the output nonlinearity of the ganglion cell and therefore provide characteristic signatures of nonlinearities that affect stimulus integration (Gollisch and Herz, 2012). For the models of Figure 1, for example, linear integration is reflected by iso-response curves in the shape of straight lines (Fig. 1D, bottom), whereas the threshold-quadratic transformation of surround signals corresponds to iso-response curves with circular and straight segments (Fig. 1E, bottom).

Note that the iso-response curves measure specifically how signals are integrated within the surround; the curves do not depend on how the combined surround signal finally links to the center signal. In the model of Figure 1, we have assumed a subtractive effect of the surround for concreteness, but a different center-surround interaction; for example, divisive, as also considered for retinal ganglion cells (Merwine et al., 1995; Zaghloul et al., 2007), would be equivalent when considering iso-response curves of stimulus integration in the surround.

Experimentally determining iso-response curves

To measure an iso-response curve during an experiment, rather than measuring neuronal responses to predefined stimuli, we needed to find a set of stimuli that led to a predefined response. To this end, we extended the closed-loop measurement system used previously to measure stimulus integration in the receptive field center (Bölinger and Gollisch, 2012). This online analysis system enabled us to automatically detect spikes from individual ganglion cells and adaptively update stimulus parameters depending on responses to previous stimuli so that we could quickly tune a stimulus to the desired response with little interaction required from the experimenter.

After determining the receptive field center and surround for a recorded ganglion cell as explained in the preceding section, we performed iso-response measurements for the receptive field center and for the surround. For iso-response measurements in the receptive field center, the center was divided into two halves and stimuli were defined by the two corresponding contrast values, S₁ and S₂ (Fig. 2A). These measurements were primarily used to identify the type of center integration as described previously (Bölinger and Gollisch, 2012). For iso-response measurements in the surround, the center was always stimulated with the same, fixed contrast (see Materials and Methods), whereas the surround region was now divided into two halves and stimuli were defined by the corresponding contrast values, S₁ and S₂ (Fig. 2B). All stimuli in these measurements were briefly flashed on a gray background and ganglion cells typically responded with a brief burst of spikes (Fig. 2C), which were identified by online spike sorting (see Materials and Methods). The brief flashes are particularly suited for our closed-loop approach because they allow a rapid and reliable assessment of the obtained response and therefore a speedy tuning of stimulus parameters toward the target response.

Figure 2.

Identification of iso-response curves. A, Stimulus space for assessing spatial integration in the receptive field center. The space is spanned by the contrast values S₁ and S₂, which are displayed in the two halves of the receptive field center. B, Stimulus space for assessing spatial integration in the receptive field surround. The space is spanned by the contrast values S₁ and S₂, which are displayed in the two halves of the receptive field surround, whereas the center is stimulated with fixed contrast. C, Sample voltage trace for a single stimulus presentation (top) and corresponding time course of the stimulus (bottom). D, Sample data displaying a single line search in the receptive field center for a target spike count of 12 spikes. The overall contrast level was varied with a fixed ratio of S₁ to S₂, corresponding to varying the radius $\sqrt{S_1^2+S_2^2}$ along a fixed radial direction in the stimulus space shown in A. Linear regression (black line) was used to determine the required contrast (red dot) for reaching the target spike count. E, Same as D, but for a line search in the receptive field surround corresponding to the stimulus space shown in B. Note that, here, the spike count decreases as the overall contrast level increases. F, Schematic illustration of the buildup of an iso-response curve (red line) through successively identified stimuli (red dots) along different radial directions (dashed lines) that yield the same target spike count.

For both types of iso-response measurements, we selected a fixed spike count as the target response and then performed multiple line searches along different radial directions of the stimulus space spanned by S₁ and S₂. The individual searches made use of the fact that, apart from noise, spike counts showed a monotonic dependence on radius along each search direction, either increasing or decreasing depending on whether measurements were taken for the center (Fig. 2D) or surround (Fig. 2E), respectively. The radial distance of the iso-response stimulus was then determined from a linear fit of nearby data points and the search proceeded to the next radial search direction (Fig. 2F).

Distinct nonlinear integration characteristics in the receptive field center and surround

Figure 3 shows examples of measured iso-response curves from both the receptive field center and surround. As in a previous study (Bölinger and Gollisch, 2012), we observed two distinct types of iso-response curves for the receptive field center and we accordingly classified cells into two types. The first type (Fig. 3A–C, left) had convex iso-response curves in the center, with an approximately circular segment in the lower left quadrant of stimulus space (“Off-Off quadrant”). In the regions where only one half of the receptive field center was stimulated with positive contrast (“On-Off quadrants”), the curves run approximately parallel to the axes. These characteristics of the iso-response curves indicate that positive contrast components do not affect the response and are truncated by a threshold operation. Conversely, negative contrast components combine in a quadratic fashion, which gives rise to the circular part of the iso-response curve. In total, these cells are characterized by a nonlinear, threshold-quadratic transformation of center signals before integration by the ganglion cell (Bölinger and Gollisch, 2012), so we will therefore subsequently refer to this type as “quadratic cells.”

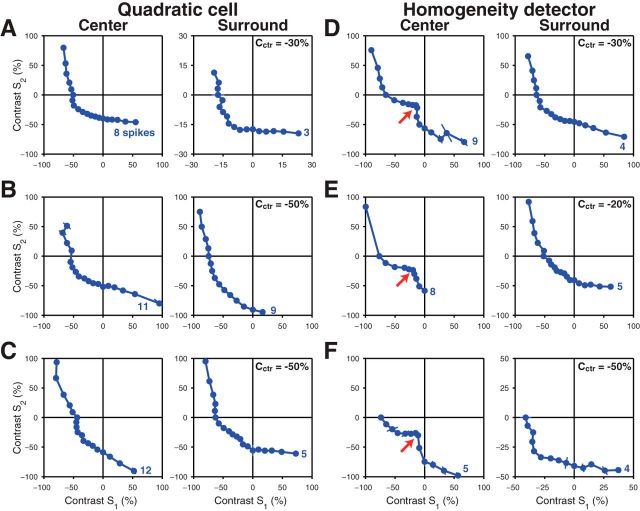
Figure 3.

Measured iso-response curves for different retinal ganglion cells. A–C, Examples from three different quadratic cells for measurements in the receptive field center (left) and surround (right). The applied target spike count is denoted next to each curve. For the iso-response curves measured in the surround, the fixed contrast C_ctr used for stimulating the center is also denoted in the plots. D–F, Examples of iso-response curves from three different homogeneity detectors, displayed in the same way as in A–C. Here, the arrows point to the characteristic notch along the lower left diagonal in the iso-response curves.

The second type of center iso-response curves (Fig. 3D–F, left) is characterized by a notch along the lower left diagonal (red arrows), giving the curves a distinctive nonconvex shape. The notch corresponds to the fact that particularly little contrast was required to reach the target spike count when both halves of the receptive field were stimulated with similar contrast. This particular sensitivity for homogeneous stimulation of the receptive field center had been shown to result from a local inhibition-mediated gain control circuit and has provided these cells with the label “homogeneity detectors” (Bölinger and Gollisch, 2012).

To determine whether similar types of nonlinear spatial integration exist in the receptive field surround of these two cell types, we measured iso-response curves for surround stimulation. For both cell types, we found that these surround iso-response curves deviated strongly from linearity (Fig. 3A–F, right), showing that stimulus integration in the receptive field surround of salamander ganglion cells is also generally nonlinear. For the quadratic cells (Fig. 3A–C), the curves had an approximately similar shape as the center iso-response curves, indicating that a similar type of nonlinearity governs stimulus integration in both center and surround. In particular, the segments parallel to the axes in the On-Off quadrants correspond to truncation of positive contrast signals.

Conversely, the surround iso-response curves of homogeneity detectors (Fig. 3D–F) differed strongly in shape from the corresponding center iso-response curves and were more similar to those of quadratic cells. This suggests that the gain control mechanism that conveys sensitivity to spatially homogeneous stimulation in the receptive field center is not active in the surround. As in the other cases, the segments in the On-Off quadrants approximately run parallel to the axis, suggesting truncation of positive contrast signals.

To quantify the degree of truncation of positive contrast signals, we calculated the slopes of iso-response curves in the On-Off quadrants (Bölinger and Gollisch, 2012). The slope values were defined in such a way (see Materials and Methods) that zero corresponds to complete rectification of positive contrast signals (iso-response curves parallel to the axes) and unity corresponds to linear integration of positive and negative contrast signals (iso-response curves running parallel to the upper left to lower right diagonal). For quadratic cells, the average slope values were 0.29 ± 0.16 (mean ± SD, n = 25 curves) for the center and −0.02 ± 0.16 (n = 28) for the surround; for homogeneity detectors, the values were 0.33 ± 0.11 (n = 20) for the center and 0.24 ± 0.16 (n = 19) for the surround. In all cases, the slope values were significantly smaller than unity (p < 10⁻⁶ in all cases, t test), which is consistent with the qualitative observation of strong rectification seen in the examples. Among the four groups, the slopes for the surround of the quadratic cell were significantly smaller than for the other cases (p < 10⁻⁶, unpaired t test), indicating that rectification is particularly strong in the surround of quadratic cells.

Dependence of iso-response curves on target spike count reveals differences in surround integration between cell types

To determine whether the observed nonlinear characteristics of stimulus integration in center and surround depend on the overall level of stimulus contrast, we aimed at measuring multiple iso-response curves with different target spike counts for individual cells. For center iso-response curves of quadratic cells, in agreement with previous results (Bölinger and Gollisch, 2012), we observed that the shape was largely independent of the target response; for higher target spike count, larger contrast values were required and the iso-response curve correspondingly shifted outwards, but otherwise retained its shape (Fig. 4A, left).

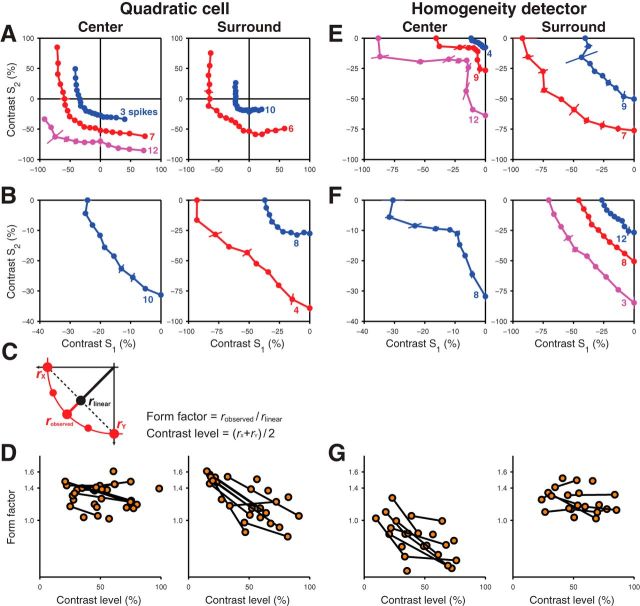
Figure 4.

Dependence of the shape of iso-response curves on the overall contrast level. A, B, Examples with multiple measured iso-response curves for two different quadratic cells showing measurements in the receptive field center (left) and surround (right). Note that, in B, searches were restricted to the lower left quadrant of stimulus space. C, Definition of the form factor based on the measurements of an iso-response curve (red) and the linear interpolation of the curve's intersection with the axes (dashed black line). Along the lower left diagonal, the radii of the iso-response curve and of the linear interpolation are denoted as r_observed and r_linear, respectively. Their ratio defines the form factor, whereas the overall contrast level was represented by the average contrast of the curve's intersection with the axes, r_x and r_y. D, Dependence of form factors on contrast level for quadratic cells measured for the receptive field center (left) and surround (right). Data points obtained from the same cell are connected by black lines. Ticks on the vertical axes denote values corresponding to linear, quadratic and cubic integration (1.0, $\sqrt{2}$ ≈ 1.4 and 2^2/3 ≈ 1.6, respectively). E, F, Examples with multiple measured iso-response curves for two different homogeneity detectors with searches restricted to the lower left quadrant of stimulus space. G, Form factors for homogeneity detectors plotted against the overall contrast level.

For the iso-response curves of surround integration in these cells, however, we found that the exact shape of the iso-response curve in the Off-Off quadrant depended systematically on the target spike count (Fig. 4A,B, right). Higher spike count required smaller surround contrast and, correspondingly, a smaller radius of the iso-response curve, as expected. In addition, however, the surround iso-response curve for higher spike count was more strongly curved, whereas the iso-response curve for lower spike count, which required larger contrast values, was nearly linear in the region of the Off-Off quadrant.

To quantify the observed dependence of the shape of the iso-response curve on target spike count, we characterized the iso-response curve in the Off-Off quadrant by computing a form factor (Bölinger and Gollisch, 2012). This form factor was defined as the ratio of the radius of the experimentally observed curve along the lower left diagonal to that of the linear prediction that is obtained by linearly connecting the two intersections of the curve with the axes (Fig. 4C and Materials and Methods). For a linear iso-response curve, this value should be close to unity, whereas a circular curve or one resulting from a cubic nonlinearity yield values of $\sqrt{2}$ (≈1.4) or 2^2/3 (≈1.6), respectively. We then analyzed how the form factor depended on the overall contrast level that was required to reach the target response. We defined the contrast level as the average radius of the iso-response curve along the two axes; that is, as the average contrast required for reaching the target response when only one of the two stimulus components was used.

The form factor confirmed that for both cell types and both center and surround, stimulus integration differed systematically from the linear case. For quadratic cells, the form factors of center iso-response curves were typically near the value of 1.4 (Fig. 4D, left), corresponding to a nearly circular shape in the Off-Off quadrant, consistent with a quadratic nonlinearity. Furthermore, the form factor appeared to be independent of the contrast rage for which the iso-response curve was measured. Conversely, for surround iso-response curves, the form factor showed a clear dependence on the contrast level, dropping from values of ∼1.5 to near unity as the contrast level increased (Fig. 4D, right).

Iso-response curves of homogeneity detectors showed a different dependence on target spike count. For these cells, the shapes of center iso-response curves depended strongly on the response level, as described previously (Bölinger and Gollisch, 2012), with a more pronounced notch at higher target spike count (Fig. 4E, left). Iso-response curves of the receptive field surround, however, showed the expected change in radius for different target spike counts, but little alteration in overall shape (Fig. 4E,F, right).

Assessment of form factors again corroborated this observation. For center iso-response curves of homogeneity detectors, the form factor declined with increasing contrast level (Fig. 4G, left) and, for high enough contrast level, form factors were typically much smaller than unity, corresponding to the nonconvex shape of the iso-response curves. Form factors of surround iso-response curves of these cells, however, stayed consistently above unity and showed no obvious dependence on the contrast range (Fig. 4G, right), unlike for the surround of quadratic cells.

To analyze the dependence of the form factor (F) on the contrast level (C) in a more quantitative fashion, we computed the relative changes of form factor per contrast (δF/δC) for individual cells if multiple iso-response measurements in either center or surround were available (see Materials and Methods). This analysis amounts to collecting the slopes of all the connecting lines in Figure 4, D and G. We then tested statistically whether these slope values differed from zero for either center or surround of either cell type and whether there was a significant difference between cell types or between center and surround. For quadratic cells, the slope values in the center did not deviate significantly from zero (p > 0.1; signed-rank test), but those in the surround did (p < 0.01). Conversely, homogeneity detectors showed the opposite, with the slopes in the center deviating from zero (p < 0.005), but not for the surround (p > 0.9). For both cell types, the slope values differed significantly between the center and surround (p < 0.005 in both cases, rank-sum test). Furthermore, the slope values in the surround depended more strongly on contrast for quadratic cells than for homogeneity detectors (p < 0.005, rank-sum test). These results corroborate the observation that the shapes of iso-response curves in the surround show a strong dependence on contrast for quadratic cells, but not for homogeneity detectors.

Extraction of subunit nonlinearities from iso-response curves

A standard framework for describing nonlinear stimulus integration in the retina is provided by subunit models (Hochstein and Shapley, 1976; Victor and Shapley, 1979a; Enroth-Cugell and Freeman, 1987; Cox and Rowe, 1996; Demb et al., 1999; Meister and Berry, 1999; Gollisch and Meister, 2010, see also Fig. 1). In these models, the integrated signal results from a summation of nonlinearly transformed local signals. For stimulus integration in the receptive field center of quadratic cells, for example, a threshold-quadratic subunit nonlinearity provides a good description of the iso-response curves (Bölinger and Gollisch, 2012), but such a polynomial nonlinearity cannot capture the dependence of the iso-response curve's shape on the contrast level in the surround of quadratic cells. To determine whether an alternative subunit model can capture the iso-response curves in the surround, we used a parameterized sigmoidal function as a subunit nonlinearity (Equation 4 in Materials and Methods). We determined the parameters of the subunit nonlinearity by fitting the iso-response curves predicted from the nonlinearity to those measured in an experiment. For optimizing the parameters of the nonlinearity, all iso-response curves measured with different target spike counts in the surround of a single cell were simultaneously taken into account to obtain a single subunit nonlinearity for the surround of this cell. For comparison, subunit nonlinearities for the receptive field center were determined in the same fashion.

The fits showed that the measured surround iso-response curves are indeed consistent with the subunit model (Fig. 5B,C). For quadratic cells, extracted subunit nonlinearities of the surround exhibited strong saturation (Fig. 5B, insets), showing that a saturating subunit nonlinearity may underlie the observed change in shape of the iso-response curves. In contrast, for homogeneity detectors, no or very little saturation was observed (Fig. 5C, insets), showing that a polynomial model without saturation is sufficient for describing surround integration by these cells, similar to the center integration of quadratic cells (Fig. 5A). The nonconvex center iso-response curves of homogeneity detectors were generally not well fitted by such a subunit model (data not shown). They are thought to obtain their shape through a different type of mechanism (Bölinger and Gollisch, 2012) and were therefore not analyzed further through the subunit model.

Figure 5.

Extraction of subunit nonlinearities by fitting iso-response curves with a subunit model. A–C, Three examples are shown for the quadratic cell centers (A), quadratic cell surrounds (B), and homogeneity detector surrounds (C). Each panel shows multiple iso-response curves measured in the lower left quadrant of stimulus space (colored dots) together with model-derived iso-response curves (solid black lines) obtained by optimizing the subunit nonlinearity, N(S), shown by the orange line in the inset. The dashed lines in the insets represent parts of the subunit nonlinearities outside of the contrast range that was covered by the identified iso-response stimuli. D, Analysis of the saturation of the extracted subunit nonlinearities. For each subunit nonlinearity N(S), we calculated the saturation ratio N(−50)/N(−100) and compared the distributions of saturation ratios for the center and surround of quadratic cells and for the surround of homogeneity detectors. The box plots depict the median, the 25^th and 75^th percentiles, and the total range of the saturation ratio for each distribution.

To compare the degree of saturation in the extracted subunit nonlinearities across the population of recorded cells, we calculated a saturation ratio from the subunit nonlinearity by comparing its value at −50% contrast with its value at −100% contrast, N(−50)/N(−100). This saturation ratio is small for a nonsaturating nonlinearity, but approaches unity in the case of strong saturation because N(−50) and N(−100) would then both be close to the saturation level. The distributions of the obtained saturation ratios are shown in Figure 5D. For quadratic cell surrounds, the saturation ratio was 0.68 ± 0.17 (mean ± SD, n = 9 cells), which was significantly larger than both the value for the center of the same cell type (0.37 ± 0.18, n = 7, p < 0.01, rank-sum test) and the value for the surround of homogeneity detectors (0.38 ± 0.15, n = 7, p < 0.005). This confirmed the observation of particularly strong saturation in the surround of quadratic cells.

Differences in adaptation characteristics can explain the different behaviors of iso-response curves in the surround

The above results have shown that quadratic cells and homogeneity detectors differ, not only in how they integrate stimuli in their receptive field centers, but also in their surrounds, though in a more subtle way. Quadratic cells show a systematic dependence of surround iso-response curves on the contrast level, corresponding to a saturating subunit nonlinearity, whereas homogeneity detectors display a more constant shape in their surround iso-response curves and no saturation in their subunit nonlinearities. A possible mechanism for such saturation is a rapid adaptation process in the receptive field surround. This could be mediated, for example, by synaptic depression, which is prominent at the synaptic terminals of bipolar cells (Burrone and Lagnado, 2000; Singer and Diamond, 2006) and has been implicated in various adaptation effects (Manookin and Demb, 2006; Beaudoin et al., 2007; Gollisch and Meister, 2010; Jarsky et al., 2011; Ozuysal and Baccus, 2012; Chen et al., 2013; Garvert and Gollisch, 2013). Although synaptic depression has a rapid onset and can thereby lead to response saturation even for a brief activation, its recovery is notably slower with time scales typically on the order of several seconds (Manookin and Demb, 2006; Singer and Diamond, 2006; Li et al., 2007). We therefore expect that the adaptation effects in the surround last for some time and can be revealed by their effects on subsequent responses.

Therefore, we set out to determine whether there is a difference in the surround adaptation characteristics between quadratic cells and homogeneity detectors by measuring the effect of a preceding stimulus in the surround. To do so, we recorded responses to a stimulus that activated center and surround simultaneously. This stimulus was either presented in isolation (control condition) or it was preceded by a stimulus that activated the surround half a second earlier (prestimulus condition), as shown in Figure 6A. The half-second interval was chosen to be long enough so that potential immediate effects of surround activation on the ganglion cell, such as inhibitory rebound (Mitra and Miller, 2007), have already decayed, whereas adaptation effects of the surround should still persist.

Figure 6.

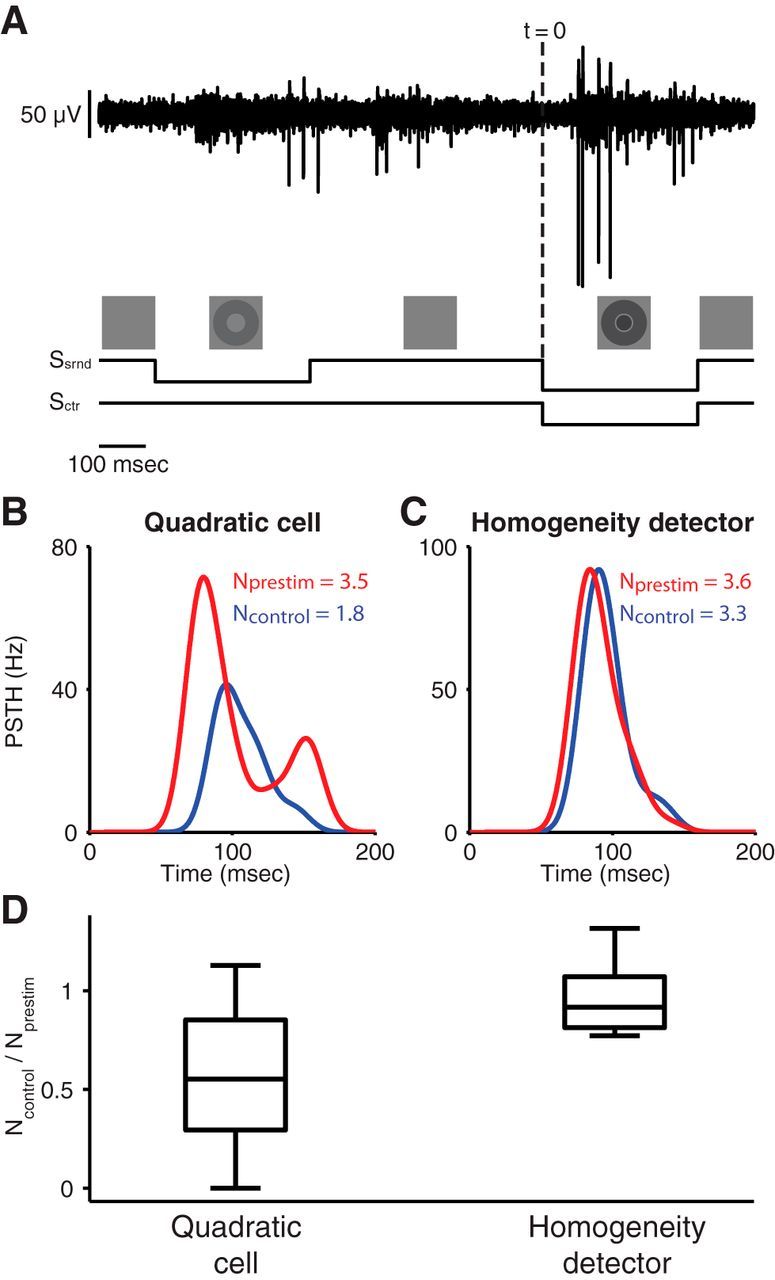
Test for surround adaptation by applying a prestimulus to the surround. A, Sample voltage trace (top) and stimulus layout (bottom). A test stimulus consisted of a center and a surround component (−50% and −70% contrast, respectively). In the prestimulus condition, this was preceded by a sole stimulation of the surround (−40% contrast), which terminated 500 ms before the onset of the test stimulus. In the control condition, only the test stimulus was presented. B, Sample peristimulus time histograms (PSTH) obtained from a quadratic cell for the prestimulus (red) and control (blue) conditions. Time 0 corresponds to the onset of the test stimulus (dashed line in A). The average spike counts for the two conditions, N_prestim and N_control, are denoted in the plot. C, Sample PSTH obtained from a homogeneity detector for the prestimulus (red) and control (blue) conditions. D, Comparison of the effects of the prestimulus on spike counts for quadratic cells and homogeneity detectors. For each recorded cell, the spike count ratio N_control/N_prestim was calculated and the box plots depict the median, the 25^th and 75^th percentiles, and the total range of these spike count ratios for the two distinguished cell types.

For quadratic cells, we found that the preceding stimulus in the surround indeed strongly enhanced the elicited response (Fig. 6B), indicating that the surround was less effective following the adaptation induced by the preceding stimulus. For homogeneity detectors, on the other hand, we did not observe such an adaptation effect of the surround; the preceding surround stimulus only had a small effect on the elicited response (Fig. 6C).

To quantify this effect, we calculated the spike count ratio of the control condition to the prestimulus condition. For cells with no adaptation in the surround, this ratio should be close to unity, whereas surround adaptation will produce values smaller than unity because the adaptation enhances the response in the prestimulus condition. We found that the spike count ratio was significantly smaller for quadratic cells than for homogeneity detectors (quadratic cells: 0.57 ± 0.38, mean ± SD, n = 12; homogeneity detectors: 0.97 ± 0.20, n = 6; p < 0.05, rank-sum test). This suggests that the receptive field surround of quadratic cells has indeed substantially stronger adaptation effects than that of homogeneity detectors.

Spatial scale of stimulus integration in the surround

So far, our stimulus components in the surround have covered large areas that should span many of the subunits that form the basis of nonlinear stimulus integration in the surround. Varying the size of the stimulus components can reveal the relevant spatial scale for nonlinear signal integration, which should provide information about where in the retinal circuitry the nonlinearities may occur (Gollisch and Herz, 2012). For the receptive field center, for example, a transition from nonlinear to linear stimulus integration occurs approximately over the receptive field size of bipolar cells (Bölinger and Gollisch, 2012). We therefore performed iso-response measurements with a modified spatial arrangement of the stimulus components in the surround. We spatially interleaved the components by arranging them in a checkerboard pattern and varied the size of the checkerboard squares.

As shown by an example in Figure 7A, we found that, indeed, the iso-response curve became linear when the squares were sufficiently small, indicating that spatial stimulus integration is linear over small spatial scales, as in the receptive field center (Bölinger and Gollisch, 2012). Surprisingly, however, the change in the shape of the iso-response curve with changing spatial scale was nonmonotonic; there was an intermediate regime for which the iso-response curves were even more strongly bent (Fig. 7A, green curve) compared with the control condition, where the surround region was just divided into two halves.

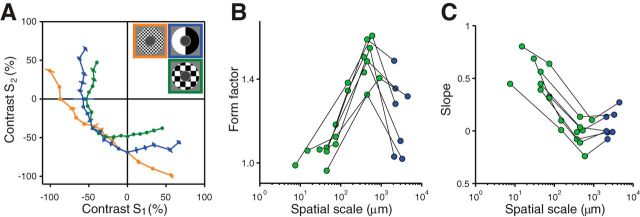
Figure 7.

Effect of spatial scale on iso-response curves in the receptive field surround. A, Iso-response curves for the standard stimulus layout (blue) and for two checkerboard arrangements of the two stimulus components with edge lengths of 600 μm (green) and 7.5 μm (orange). Target spike count was five spikes. Note that, for all three conditions, stimuli are identical along the lower left diagonal (S₁ = S₂). Correspondingly, the three iso-response curves meet on this diagonal. B, Dependence of iso-response curve convexity on spatial scale. Form factors, which denote the degree of curvature of measured iso-response curves in the Off-Off quadrant of stimulus space, were plotted against the spatial scale of the stimulus layout, that is, the edge length of the applied checkerboard pattern. Black lines connect data points obtained from the same cell. Green data points represent iso-response curves measured with checkerboard arrangement; blue points correspond to the standard stimulus layout. C, Dependence of rectification on spatial scale. We fitted the two ends of the iso-response curves with straight lines separately and calculated their average slope as a measure of rectification. Values of zero and unity correspond to perfect half-wave rectification and to absence of rectification, respectively. As in B, the values are plotted against the applied spatial stimulus scale and measurements from the same cell are connected with black lines. Green and blue data points represent data from the checkerboard and from the standard stimulus layout, respectively.

To quantify this dependence of iso-response curve shape on spatial scale, we again calculated the form factor for the curves (Fig. 7B). For small spatial scales below ∼100 μm, form factors generally tended toward unity, corresponding to linear integration. At an intermediate scale of several hundred micrometers, however, a maximum in the form factors was observed, corresponding to more strongly bent iso-response curves and therefore more pronounced nonlinear integration characteristics. To further characterize the shapes of the iso-response curves, we also quantified the amount of rectification in the On-Off quadrants by again computing the average slope of the iso-response curves (Fig. 7C). For spatial scales of about 100 μm or larger, the slope values were close to zero, indicating strong rectification of positive contrast signals, whereas smaller spatial scales gave larger slope values and correspondingly less rectification.

The nonmonotonic change of the iso-response curves means that there is an intermediate spatial scale for which surround activation is most effective in suppressing the response. At this scale, the iso-response curve is most strongly bent, such as the green curve in Figure 7A, so that the target spike count is reached with smaller contrast values in the surround compared with other stimulus layouts. To study this nonmonotonic behavior with finer spatial resolution, we again used a checkerboard layout in the surround, but now kept every second checkerboard square at the background light intensity. These patterns were presented with fixed negative contrast, but varying size of the checkerboard squares, while the center was activated simultaneously with a homogeneous fixed-contrast signal (Fig. 8, bottom row). Note that the total area of stimulation in the surround was always the same, half of the entire surround region; only the spatial distribution of the stimulus in the surround region was changed.

Figure 8.

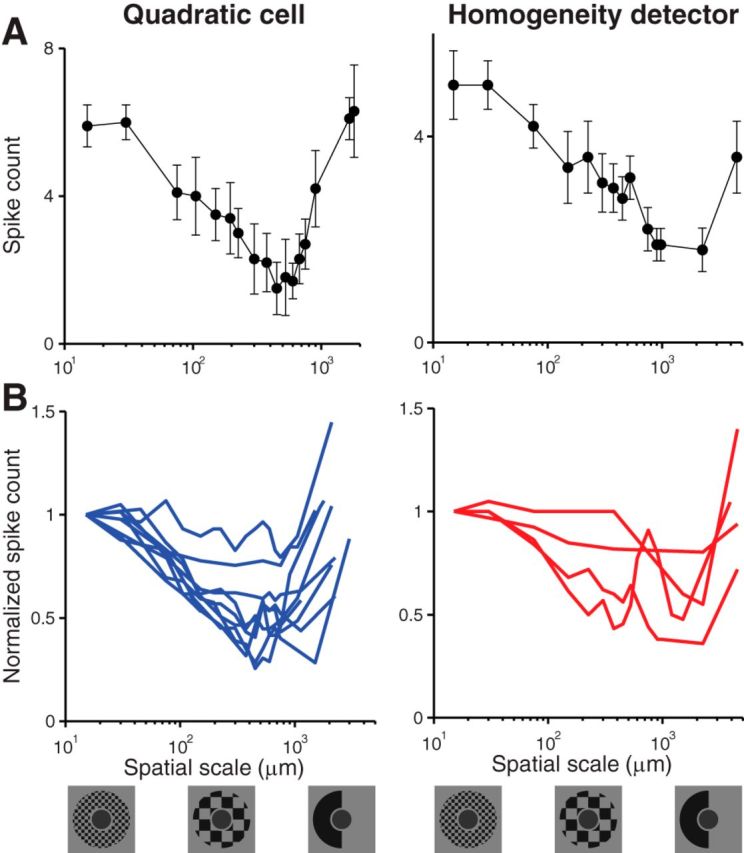
Effect of spatial scale on the strength of surround suppression. Stimuli consisting of a center spot and a checkerboard arrangement in the surround, using only half of the squares, were presented with different spatial scales (bottom row). Contrast in the surround was fixed at −70%. For the center, a fixed contrast level was chosen for each cell in the range from −70% to −30%, depending on the cell's sensitivity. A, Examples from a quadratic cell (left) and a homogeneity detector (right). Spike counts were plotted against the spatial scale of the stimulus pattern in the receptive field surround. B, Overview of measurements from all recorded quadratic cells (left) and homogeneity detectors (right). Spike counts were normalized for each cell by the value obtained for the smallest spatial scale.

For both quadratic cells (Fig. 8, left column) and homogeneity detectors (Fig. 8, right column), we found a nonmonotonic dependence of the spike count on spatial scale. Typically, we observed that a minimal spike count was reached for spatial scales around several hundred micrometers, with the location of observed minima ranging from 300 to 2300 μm. At these spatial scales, the activation of the surround appears to be most effective. This indicates that some of the cells that mediate surround suppression have themselves center-surround receptive field organization. The optimal spatial scale of surround activation then matches the size of receptive field centers of these cells, thus strongly activating the center regions of a subset of these cells while avoiding concomitant activation of their surrounds.

Discussion

In this study, we investigated how visual stimuli are spatially integrated in the receptive field surround of Off-type ganglion cells in the salamander retina. We based our investigations on closed-loop experiments designed to identify iso-response stimuli rapidly, similar to previous applications in different sensory systems (Gollisch et al., 2002; Gollisch and Herz, 2005; Bölinger and Gollisch, 2012; Horwitz and Hass, 2012). Our main findings were as follows: (1) all recorded ganglion cells showed strongly nonlinear stimulus integration in the surround, (2) the integration characteristics in the surround were overall more similar across cell types than integration characteristics in the center, (3) different cell types showed systematic differences in the adaptation characteristics of the surround, and (4) surround suppression depended on the spatial scale of the stimulus and was most effective for stimulus structures spanning several hundred micrometers on the retina.

Interpretation of iso-response measurements

Interpretations of measured iso-response curves were guided by a modeling framework in which different stimulus components in the surround are individually transformed and then summed without direct interactions (Fig. 1C). Indeed, we found that, for our standard stimulus layout (Fig. 1A), we could describe the shapes of iso-response curves through such a model using a simple form of the nonlinear transformation (Fig. 5).

However, measurements with different spatial layouts, probing finer spatial scales, suggested that signals from different stimulus components could interact, presumably because individual subunits in the surround themselves display center-surround organization. Stimulation of the subunit center by one stimulus component and its surround by the other component then results in interactions before the subunit output. For our standard stimulus layout, the effect of this interaction is presumably small, because the large size of the stimulus components mitigates the relative contribution of the border area where interactions would be strongest. Note that, although such an interaction of stimulus components may influence the exact shapes of the extracted subunit nonlinearities (Fig. 5), it does not affect the finding that different cell types have systematic differences in surround integration. Furthermore, our interpretation of saturating nonlinearities in the surround of quadratic cells is further supported by the observed adaptation characteristics in the surround (Fig. 6).

Possible mechanisms for nonlinearities

A prominent nonlinear feature observed in both the receptive field center and surround was the thresholding of positive contrast signals (Figs. 3, 4). For excitatory signals in the receptive field center, a likely source for this nonlinearity is the synaptic transmission from bipolar to ganglion cells (Demb et al., 2001; Baccus et al., 2008; Molnar et al., 2009; Werblin, 2010; Schwartz et al., 2012; Chang and He, 2014), potentially with contributions from spike-like amplification in the bipolar cell terminals (Baden et al., 2013). Analogously, thresholding in the receptive field surround could originate in the synaptic transmission between bipolar and amacrine cells. This has been suggested for the surround of mammalian Y-type ganglion cells based on the suppressive effect of peripheral moving gratings (Zaghloul et al., 2007). For specific bipolar–amacrine connections, such rectification has indeed been observed (Jarsky et al., 2011).

In addition to thresholding, both center and surround typically displayed an expansive (approximately quadratic) nonlinearity for preferred contrast signals (Figs. 3, 4). Although spatial integration in bipolar cells appears to be linear (Baccus et al., 2008; Borghuis et al., 2013), synaptic transmission at bipolar cell terminals can produce such an expansive nonlinearity (Demb et al., 2001; Jarsky et al., 2011; Borghuis et al., 2013). For surround inhibition, an additional nonlinearity may arise from the extra transmission stage represented by amacrine cell synpases, regardless of whether these act primarily on bipolar cell terminals or directly on ganglion cells (Flores-Herr et al., 2001; Ichinose and Lukasiewicz, 2005; Zaghloul et al., 2007). With this additional potential source for nonlinear signal transmission in the surround pathway, one may expect the surround to show stronger nonlinear effects than the center. Indeed, some of our data point in this direction. For the surround of quadratic cells, rectification was stronger and form factors reached higher values than for the center.

Conversely, for homogeneity detectors, nonlinear effects in the surround appeared to be less pronounced than for quadratic cells and rather resembled the effects observed in the center of quadratic cells. This suggests that at least one of the signal transmission stages in the surround of homogeneity detectors is closer to linear. Indeed, some amacrine cells in the salamander retina respond nearly linearly to light flashes (Manu and Baccus, 2011).

Adaptation in the surround

The surrounds of quadratic cells and homogeneity detectors also differed in their adaptation characteristics, which may reflect the previously observed diversity of adaptation strength in different amacrine cell types of the salamander retina (Baccus and Meister, 2002). Furthermore, this may be connected to the recent observation that some ganglion cells show sensitization to increases in visual contrast (Kastner and Baccus, 2011). This sensitization appears to originate from synaptic depression in amacrine cells (Nikolaev et al., 2013), whereas classical adaptive characteristics mostly result from a decrease in excitatory input (Manookin and Demb, 2006; Beaudoin et al., 2007). Moreover, some ganglion cells in the salamander retina were characterized by adaptation for stimuli in the innermost region of the receptive field center but sensitization for stimuli in the rest of the center, whereas other cells showed sensitization throughout the receptive field center (Kastner and Baccus, 2013). It is conceivable that the diversity in the strength of surround adaptation observed in our recordings (Fig. 6D) contributes to the diversity of adaptation and sensitization in ganglion cells.

Spatial scale in surround suppression

A surprisingly strong influence on the effectiveness of surround stimuli was exerted by their spatial scale. At some intermediate scale of typically several hundred micrometers, the nonlinear effects of spatial integration peaked (Fig. 7A,B) and surround stimuli became maximally effective in suppressing the ganglion cell's response (Fig. 8). Interestingly, a strong dependence of inhibitory signals on the spatial stimulus layout was also observed in On-type parasol cells of the primate retina (Cafaro and Rieke, 2013).

The nonmonotonic dependence of surround suppression on spatial scale contrasts with previous findings for the receptive field center, where the dependence on spatial scale was monotonic (Bölinger and Gollisch, 2012). A likely explanation for an optimal spatial scale is that some of the neurons mediating surround suppression themselves have a center-surround structure. Stimuli with a spatial scale that matches the size of the receptive field centers are then particularly efficient because they can elicit strong activation in some of these neurons without large contributions from their surround regions.

Receptive fields of bipolar cells, which range from ∼50 to 150 μm in diameter (Wu et al., 2000; Baccus et al., 2008), appear too small for mediating the optimal spatial scale of surround stimulation. Instead, a good candidate mechanism seems to be serial connections between amacrine cells (Roska et al., 1998; Eggers and Lukasiewicz, 2010). Amacrine cells display extreme diversity in morphology (Masland, 2012a, 2012b). In the salamander, receptive field sizes of amacrine cells range from 100 to 2000 μm (Yang et al., 1991; Baccus et al., 2008; Zhang and Wu, 2010; de Vries et al., 2011), consistent with the observed optimal stimulus scales (300–2300 μm) in our experiments.

Potential contributions from the outer plexiform layer

In addition to the amacrine cell mechanisms considered so far, horizontal cells in the outer plexiform layer also contribute to the inhibitory surround by inhibiting cones and bipolar cells (Thoreson and Mangel, 2012). Because of electrical coupling between horizontal cells (Naka and Rushton, 1967; Kaneko, 1971; Bloomfield and Miller, 1982), their receptive fields can be fairly large, ranging from 500 to 1600 μm in the salamander retina (Lasansky and Vallerga, 1975; Zhang et al., 2006). However, the contributions to surround suppression that we observed in this study were characterized by strong nonlinearities, whereas signal processing in the outer plexiform layer appears largely linear. Both cones and horizontal cells have fairly linear response properties (Shapley, 2009) and horizontal cells show linear spatial integration (Tranchina et al., 1981; Baccus et al., 2008). Furthermore, bipolar cells, the output neurons of the outer retina, also display linear spatial integration (Baccus et al., 2008; Borghuis et al., 2013). It therefore seems unlikely that the outer plexiform layer contributes substantially to the nonlinear spatial integration properties observed here.

Future directions

The goal of this study was to describe the spatial stimulus integration characteristics of the receptive field surround in salamander retinal ganglion cells and to identify relevant nonlinear signal transformations. To extend this toward more detailed mechanistic investigations, combinations with other techniques will likely be required. An interesting avenue may be to combine the iso-response approach with intracellular recordings in ganglion cells to investigate directly the nonlinearities in the inhibition arriving at the ganglion cells. Similarly, a combination with recently developed optical techniques such as calcium imaging of retinal circuitry (Euler et al., 2002; Dreosti et al., 2011) could be used to study more directly the contributions of different elements to the nonlinearities observed in ganglion cell receptive fields.