Abstract
We theoretically investigate the mechanism of ferroelectric switching via interlayer shear in 3R MoS2 using first principles and lattice dynamics calculations. First principle calculations show the prominent anharmonic coupling of the infrared inactive interlayer shear and the infrared active phonons. The nonlinear coupling terms generates an effective anharmonic force which drives the interlayer shear mode and lowers the ferroelectric switching barrier depending on the amplitude and polarization of infrared mode. Lattice dynamics simulations show that the interlayer shear mode can be coherently excited to the switching threshold by a train of infrared pulses polarized along the zigzag axis of MoS2. The results of this study indicate the possibility of ultrafast ferroelectricity in stacked two-dimensional materials from the control of stacking sequence.
Subject terms: Atomistic models, Nanoscale materials
Introduction
Ferroelectric two-dimensional (2D) materials are of great importance in realizing non-volatile devices with extreme feature size1,2, and possibly with unforeseen functionalities from the unique properties of 2D materials3,4. However, studies on the 2D ferroelectrics are yet an emerging field. Only a few materials such as SnTe5, α-In2Se36 have been experimentally shown to work in agreement with theories7–9. Transition metal dichalcogenide (TMDC) is another major 2D materials class showing versatile electronic phases ranging from semiconducting or metallic phase to that with topological characteristics10–12. Nonetheless, the ferroelectricity of the TMDC is very scarce due to the underlying symmetry of single layer in stable phase, which is either non-polar or centrosymmetric, precluding the electric polarization; i.e. 2H (), 1T () and distorted 1T (P2/m) phases11. While theory showed ferroelectric instability of single layer 1T MoS213, its realization in the experiment is challenging because MoS2 is stable in semiconducting 2H phase rather than metallic 1T structure14.
The ferroelectricity is likely to appear in stacked TMDC rather than in single layer form. It was recently shown that the horizontal mirror symmetry of individual layers is broken by the stacking in 3R structure (P3m1 for finite layers and R3m for bulk), hence the vertical electric polarization manifests itself in accordance with the global polar symmetry15. The direction of polarization depends on the stacking sequence, hence is reversed by the interlayer translation between the AB and AC stackings15,16 as shown in Fig. 1a. The possibility of ferroelectric switching in the 3R structure via the interlayer translation has not been explored to date. Meanwhile, the multilayer distorted 1T WTe2 showed switching of the polarization17,18 and the topological phase12 in the recent experiments, probably via the interlayer translation. The stability of the 3R structure MoS2 is comparable to that of the 2H structure and can be selectively synthesized among competing polytypes19. It is hence a viable candidate for 2D ferroelectrics in which the fascinating phenomena such as high electron mobility16 and valleytronics15,19 can be explored altogether.
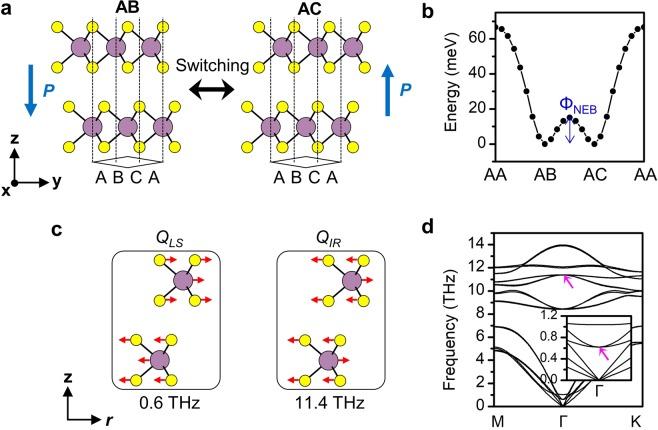
Figure 1.
(a) Stacking-dependent spontaneous polarization of bilayer 3R MoS2. (b) Energy of the bilayer structure depending on the stacking sequence. ΦNEB is the ferroelectric switching barrier calculated from the NEB method. (c) Displacement patterns of the interlayer shear mode (QLS) and the infrared mode (QIR) mode along the in-plane polarization direction r. (d) Phonon dispersion of the bilayer 3R MoS2.The zone-center QLS mode at 0.6 THz and QIR mode at 11.4 THz are denoted by arrows.
The interlayer translation universally manifests as Raman active low-frequency lattice vibrations in layered 2D crystals due to the weak van der Waals bonds (vdW) between layers20–22. Therefore, the ferroelectric switching using an optical field based on ionic Raman scattering is considerably appealing23–25. A particular mechanism, called nonlinear phononics, relies on the anharmonic phonon coupling between infrared active and targeted secondary vibrational modes, which displaces the crystal toward the reversal of polarization upon the irradiation of intense terahertz pulse26,27. The ionic Raman scattering is distinguished from the conventional Raman scattering which has been used to detect structural characteristics of 2D materials such as stacking structures28 and local bonding chemistry29. The use of pulse with the mid-infrared frequency within short duration allows the exploration of an extremely intense light field (peak electric field reaching ~600 MVcm−1) without the material damage30–32. The optical ferroelectric switching is a rapidly growing topic, which will enable the ultrafast and nondestructive way to achieve coherent switching26,27,33–35.
In this work, we theoretically show the possibility of the ferroelectric switching of the bilayer 3R MoS2 using the intense light pulse through the anharmonic phonon coupling. Density functional theory (DFT) calculations demonstrate that a large amplitude vibration of infrared mode can effectively lower the ferroelectric switching barrier, and induce an unidirectional anharmonic force on the interlayer shear mode along the switching direction. This effect depends on the polarization angle of the incident light pulse with respect to the crystallographic axis of MoS2 according to the selection rule. Lattice dynamics simulations indicate the possibility of dynamical ferroelectric switching through the coherent amplification of the interlayer shear mode and the lowering of the energy barrier under the repetitive pulses within a few picoseconds.
Results
Electric polarization and switching in bilayer 3R MoS2
The bilayer 3R MoS2 has the polar point group symmetry of C3v with the polar axis along the z-axis. The 3R structure can be constructed by either AB or AC stacking sequence, which develops the spontaneous electric polarization in the opposite direction of each other as shown in Fig. 1a. The magnitude of electric polarization of the bilayer structure was calculated from the Berry phase method as P = 0.24 μCcm−2, in agreement with previous reports15,16. Figure 1b shows the total energy of the bilayer structure (primitive cell consisting of 6 atoms) depending on the stacking sequence calculated from the nudged elastic band (NEB) method. Both the AB and AC stackings are stable and energetically degenerate structures. The AC stacking is obtained from the AB stacking by sliding the upper B layer along the +y direction by 1.82 Å. The interlayer translation over the weak vdW interaction results in the modest energy barrier ΦNEB = 15.0 meV.
The optical switching mechanism was investigated based on the nonlinear phononics23,24. The bilayer 3R MoS2 has 18 zone-center phonon modes which are decomposed into Γ = 6A1 + 6E representations. The singly degenerate A1 mode involves out-of-plane motion of atoms, while the doubly degenerate E mode involves in-plane motion of atoms. Figure 1c shows two kinds of E modes relevant to the nonlinear phononics mechanism. The low-frequency mode (ΩLS = 0.6 THz in phonon dispersion in Fig. 1d) referred to as the interlayer shear mode (denoted by QLS) involves the relative motion between adjacent layers along the in-plane polarization axis r. Therefore, the QLS mode is related to the AB ↔ AC stacking change. The infrared activity of the v-th mode is proportional to the square of mode effective charge 36. Due to the almost rigid relative ionic motion, the QLS mode does not produce net dipole moment as the calculated effective charge = 0.00 eμ−1/2 (where e is the electronic charge and μ is the atomic mass unit). The vanishing infrared activity indicates that it is almost impossible to directly excite the QLS mode with large amplitude to induce the stacking change. Nonetheless, the anharmonic coupling of QLS mode with other infrared active modes can provide an alternative route to control this mode, and the consequent ferroelectric switching. Among the other in-plane modes, only the high-frequency mode (denoted by QIR) at ΩIR = 11.4 THz shows finite effective charge = 0.23 eμ−1/2, and is the solely infrared active mode under vertical incidence of light.
The normal-mode coordinate Qv of v-th mode is related to the atomic displacement vector , where mi is the atomic mass of i-th atom and is the normalized eigenvector of the dynamical matrix. The orthogonal basis sets were chosen to represent the degenerate QLS and QIR modes as {QLSx, QLSy} and {QIRx, QIRy}, respectively. They correspond to the linear polarization along the zigzag (x-axis) and armchair (y-axis) axes shown in the top view of the AB stacking of the 3R MoS2 in Fig. 2a. The AB stacking deformed by the positive amplitude of QLSy = +16.29 Å (atomic displacement of the each of the adjacent layers in the opposite direction by 0.91 Å) corresponds to the AC stacking. Meanwhile, the deformation by the negative amplitude of the QLSy = −16.29 Å changes the AB stacking into the unstable AA stacking. The positive amplitude of QLS along three crystallographically equivalent directions, r1 (+y direction), r2 and r3 directions (−120° and +120° from the +y direction), equally change the AB stacking into AC stacking as shown in Fig. 2a.
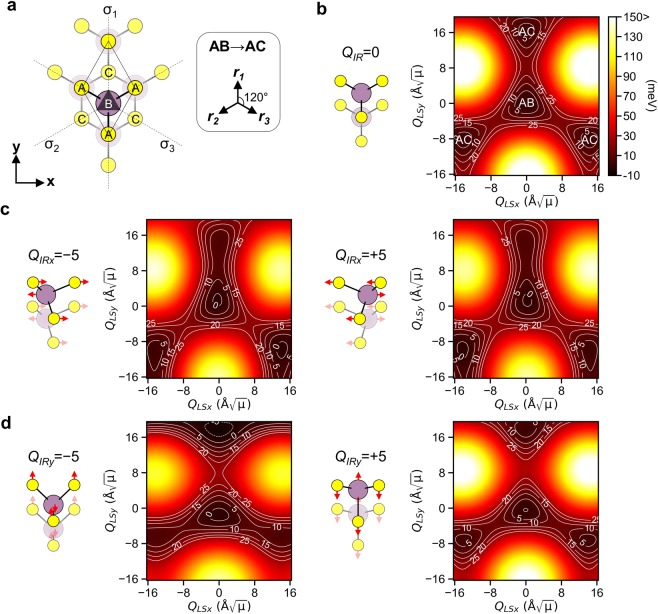
Figure 2.
(a) Top view of the AB stacked 3R MoS2 showing the C3v symmetry. In the AB stacking, the S atoms in the upper layer are on the top of the Mo atoms in the lower layer (bottom layer is depicted as dimmed). The x- and y- axis corresponds to the zigzag and armchair axis of MoS2, respectively. The AB stacking changes to the AC stacking under the deformation induced by the positive amplitude of QLS along the three equivalent directions r1, r2 and r3. (b) Potential energy surface V(QIR, QLSx, QLSy) on the (QLSx, QLSy) coordinates for QIR = 0 Å (μ is atomic mass unit). The AB stacking corresponds to the origin (0, 0). Polarization-dependent modulation of the potential energy landscape at (c) QIRx = ±5 Å and (d) QIRy = ±5 Å via anharmonic coupling.
The possibility of the ferroelectric switching hinges on how much the QLS mode can be amplified along the desired direction for the AB ↔ AC stacking change by the coupling with QIR. Here, the anharmonic coupling property was investigated from the potential energy surfaces as a function of normal-mode coordinates. The potential energy surfaces V(QIR, QLSx, QLSy) for each QIRx and QIRy were calculated using DFT on 21 × 21 × 23 points with steps of 0.82 Å for QIR and 1.63 Å for QLS modes. The energy surface was then fitted to the polynomial function as
| 1 |
where QIR is either QIRx or QIRy, and clmn is the anharmonic coefficient, and , denote the l, m and n powers of the normal-mode coordinates, respectively. Using this expression, we analyze the effect of the irradiating light pulse with the linear polarization along the x- or y-axis, thus exciting QIRx or QIRy mode, respectively. Note that the normal-modes in the cartesian basis are classified into the odd parity modes (QLSx and QIRx) and even parity modes (QLSy and QIRy) under the mirror symmetry σ1 shown in Fig. 2a. The mirror parity imposes the polarization-dependent selection rule on coupling such that clmn is nonzero only for l + m = even (m = even). The terms were included up to 15th power terms (l + m + n = 15) in the polynomial function, which fits the DFT potential energy surface accurately. The representative coupling terms are displayed in Table 1.
Table 1.
The anharmonic coefficient clmn for coupling terms for each QIRx and QIRy mode. The values are shown up to 5th power coupling terms in unit of meVÅ−(l+m+n)μ−(l+m+n)/2.
| l | m | n | Q IRx | Q IRy | l | m | n | Q IRx | Q IRy |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | −5.64 × 10−2 | −5.71 × 10−2 | 1 | 3 | 0 | 1.07 × 10−3 | |
| 0 | 0 | 4 | −2.48 × 10−3 | −2.29 × 10−3 | 1 | 3 | 1 | 1.15 × 10−4 | |
| 0 | 0 | 5 | 1.22 × 10−4 | 1.22 × 10−4 | 1 | 4 | 0 | −1.01 × 10−3 | |
| 0 | 2 | 0 | 7.93 × 10−1 | 7.90 × 10−1 | 2 | 0 | 0 | 2.66 × 10−2 | 2.62 × 10−2 |
| 0 | 2 | 1 | 1.70 × 10−1 | 1.71 × 10−1 | 2 | 0 | 1 | −6.64 × 10−2 | 1.03 × 10−1 |
| 0 | 2 | 2 | −4.92 × 10−3 | −4.79 × 10−3 | 2 | 0 | 2 | −3.28 × 10−3 | −6.17 × 10−4 |
| 0 | 2 | 3 | −2.85 × 10−4 | −2.88 × 10−4 | 2 | 0 | 3 | 5.91 × 10−4 | −5.58 × 10−5 |
| 0 | 4 | 0 | −2.38 × 10−3 | −2.30 × 10−3 | 2 | 2 | 0 | 3.98 × 10−4 | −6.14 × 10−3 |
| 0 | 4 | 1 | −3.76 × 10−4 | −4.00 × 10−4 | 2 | 2 | 1 | 1.30 × 10−4 | −1.13 × 10−3 |
| 1 | 0 | 1 | 1.81 × 10−2 | 3 | 0 | 0 | −5.66 | ||
| 1 | 0 | 2 | 5.43 × 10−2 | 3 | 0 | 1 | −1.5710−2 | ||
| 1 | 0 | 3 | 2.36 × 10−3 | 3 | 0 | 2 | −5.75 × 10−3 | ||
| 1 | 0 | 4 | −5.05 × 10−4 | 3 | 1 | 0 | 8.91 × 10−3 | ||
| 1 | 1 | 0 | −1.05 × 10−2 | 3 | 1 | 1 | 1.66 × 10−4 | ||
| 1 | 1 | 1 | −1.69 × 10−2 | 3 | 2 | 0 | −8.40 × 10−3 | ||
| 1 | 1 | 2 | 1.32 × 10−3 | 4 | 0 | 0 | −1.81 | −3.01 × 10−1 | |
| 1 | 1 | 3 | 1.47 × 10−4 | 4 | 0 | 1 | −2.41 × 10−3 | −1.31 × 10−2 | |
| 1 | 2 | 0 | 6.29 × 10−2 | 5 | 0 | 0 | 3.18 × 10−1 | ||
| 1 | 2 | 1 | 6.97 × 10−4 | ||||||
| 1 | 2 | 2 | −5.94 × 10−4 |
Figure 2b shows the potential energy surface V(QIR, QLSx, QLSy) represented on (QLSx, QLSy) coordinates when the amplitude of QIR is zero. The energy contour shows the directional dependence inherited from the C3v symmetry. The energy barriers for the AB → AC change along the equivalent r1, r2 and r3 directions in this potential energy surface are the same as Φ0 = 17.3 meV. The difference between Φ0 and ΦNEB for the AB → AC stacking change is because the deformation by the in-plane QLS mode does not include any out-of-plane relaxation, while the NEB path includes the relaxation from the slight increase (~1.6%) of the interlayer distance, reducing the barrier. It is worth to note that the Φ0 rather than the ΦNEB is relevant to the ultrafast switching in the picosecond time scale, while the latter is relevant to the conventional switching in a longer time scale.
The anharmonic coupling effect can be seen from the modulation of the potential energy landscape under the large QIR amplitude. Figure 2c,d show the potential energy landscapes when the amplitude of QIR was set to ±5.00 Å along the x- and y-axis, respectively. This amplitude corresponds to the displacement of Mo atoms by ~0.23 Å and that of S atoms by ~0.34 Å in opposite direction along the polarization axis. Due to the deformation, the C3v symmetry of the potential surface on the (QLSx, QLSy) coordinates was broken, and the energy barriers along the three equivalent directions became different. Under the negative amplitude of QIRx = −5.00 Å, the energy barrier along the r1 direction decreased to 8.6 meV, but that along the other directions increased to 19.4 meV (r2 direction) and 21.3 meV (r3 direction), respectively. The energy landscape for the positive amplitude QIRx = +5.00 Å is essentially the same with that for negative amplitude, except for the fact that the energy contour is flipped with respect to the mirror σ1. For both signs of QIRx, the coordinate of the potential energy minimum is slightly shifted along the r1 direction from the origin (QLSx = QLSy = 0 Å).
By contrast, the amplitude of QIRy largely increases the energy barrier along the r1 direction (31.7 meV at QIRy = −5.00 Å, and 23.8 meV at QIRy = +5.00 Å). This is accompanied by a slight shift of the potential minimum along the −r1 (−y) direction. The energy landscape is symmetric with respect to the mirror plane σ1, and the energy barrier along the r2 and r3 directions are reduced (13.4 meV at QIRy = −5.00 Å, and 10.1 meV at QIRy = +5.00 Å). The change in energy barriers and the shift of the potential minimum indicate that the coupling of QLS and QIR modes exerts an anharmonic force on the QLS mode.
Dynamics of coupled normal-modes under light pulse
The dynamical behavior of the normal-modes was investigated under light pulse with a specific polarization direction. Since the motion of the QIR mode is much faster than that of the QLS, the QLS modes experience the effective potential asserted by the rapidly oscillating QIR mode; i.e., time-averaged potential energy surface depending on QIR(t). The dynamics of the nonlinearly coupled modes were simulated by the following coupled equations of motion,
| 2 |
where γIR and γLS are the damping coefficients for each mode, and F(t) is the optical driving force on the QIR mode. We used Gaussian pulse , where E0 is the amplitude of the electric field, σ is the duration of the pulse and Ω is the frequency.
Figure 3 shows the evolution of potential energy curve on the QLS coordinate along the AB → AC switching directions when the QIR mode is resonantly pumped by a pulse with Ω = ΩIR, E0 = 34 MVcm−1 and σ = 100 fs. Such high intensity of the pulse is required to achieve the large amplitude of QIR (~5 Å) in MoS2, in order to explore the strong anharmonic coupling effect. The pulse intensity used in this study is comparable to the that used in the experiment on the high harmonic generation of the single layer MoS232. The energy curve (bold black line) corresponds to the static case (QIRx = 0 Å), where the energy of the AC stacking is slightly higher than that of the AB stacking because the layer-shearing by the QLS mode is not perfectly rigid.
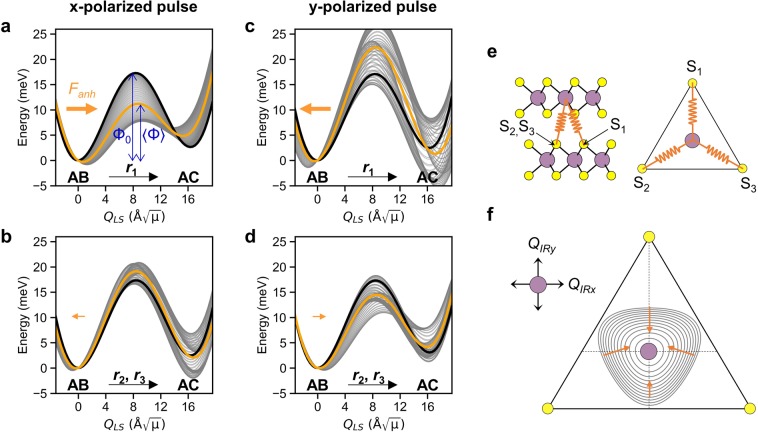
Figure 3.
Evolution of potential energy curve on the QLS coordinate along the ferroelectric switching directions under (a,b) x-polarized and (c,d) y-polarized pulse. Rapidly oscillating QIRx under pulse modulates the potential energy curve (grey lines) with respect to the static case at QIR = 0 Å (bold black line). The effective potential energy experienced by the QLS is the time-average of the potential energy curves (orange line). 〈Φ〉 is the effective energy barrier under the pulse while Φ0 is pristine energy barrier. Direction and relative magnitude of the effective anharmonic force Fanh on QLS are depicted by the orange arrow. (e) Effective interlayer interaction between the Mo and S sublattices induced by QIR. (f) Contour plot of the interaction energy indicates the direction and relative magnitude of the anharmonic force depending on the polarization direction of QIR.
The pulse polarized along the x-axis induces the oscillation of the QIRx mode with the amplitude between ± 5.35 Å by which the potential curve changes (grey line). The time-averaged potential energy (orange line) results in the effective barrier 〈Φ〉 = 11.5 meV along the r1 direction (Fig. 3a), which is a significant reduction from the 17.3 meV for the static case. The coordinate of the potential minimum was shifted by 0.72 Å along the r1 direction, and the energy of the AC stacking slightly increased compared to the static case. Meanwhile, a slight increase of the barrier to 19.2 meV along the r2 and r3 directions was observed (Fig. 3b). In contrast, the QIRy mode under the y-polarized pulse shows asymmetric vibration between −4.69 Å and +5.43 Å in the anharmonic potential due to the lack of the mirror plane perpendicular to the y-axis. This results in an increase of the effective barrier along the r1 direction to 22.5 meV, and the shift of the potential minimum by 0.36 Å along the −r1 direction (Fig. 3c). On the other hand, the effective energy barrier along the r2 and r3 directions diminishes to 14.4 meV (Fig. 3d).
The polarization-dependent modulation of the effective potential energy can be explained by the characteristics of the anharmonic coupling terms. The overall trend is captured by the coupling terms in the form of with even l, which impart an unidirectional anharmonic force on QLSy by . The sign of the coefficient of a quadratic-linear term determines the sign of Fanh. The calculated Fanh by the QIRx has a positive value of 0.92 meVÅ−1μ−1/2, hence unidirectionally drives the QLSy along the +y (r1) direction (as indicated by the orange arrow in Fig. 3a). The Fanh decreases the effective energy barrier along the r1 direction by 33%, but increases the energy barrier by 9% along the r2 and r3 directions (according to the factor ). Compared to QIRx, the Fanh from QIRy is in the opposite direction with a slightly smaller magnitude (−0.87 meVÅ−1μ−1/2). This explains the increase in the energy barrier along the r1 direction by 30% and the decreases along the r2 and r3 directions by 16%.
The polarization-dependent direction of Fanh has a geometrical origin related to the Mo and S sublattices, which are displaced by the QIR in the opposite direction (Fig. 1c). The motion of QIR modulates the interlayer interaction, which is approximated by the springs connecting the Mo and the S atoms (S1, S2, S3) in the adjacent layers as illustrated in Fig. 3e. The associated interaction energy is , where k is spring constant and is the change in distances between the Mo and S atoms. The contour plot of the interaction energy in Fig. 3f exhibits an anisotropy arising from the triangular geometry of the atomic arrangement. Particularly, the gradient of contour (orange arrow) indicates the force component along the +y direction when the Mo sublattice oscillates along the x-axis with respect to the S sublattice. On the contrary, the x-component of the force is canceled upon the rapid motion of QIRx. This simple picture explains the Fanh along the +y direction, and agrees with the selection rule (l + m = even) for coupling. In contrast, the QIRy motion induces net forces along the −y direction due to the imbalance of the force (see the length of orange arrows).
Neither QIRx nor QIRy imparts such an unidirectional force on QLSx since the relevant coupling terms (the with even l) are absent due to the odd parity of QLSx. It prohibits the excitation of the interlayer shear along the r2 and r3 directions. Although the y-polarized light pulse lowers the energy barrier along the r2 and r3 directions, it cannot induce the ferroelectric switching along these directions. Therefore, the most effective way to realize the ferroelectric switching is to use the x-polarized light pulse which induces both the interlayer shear motion and energy barrier lowering along the r1 direction for the ferroelectric switching to occur.
Next, we analyze the dynamics of ferroelectric switching based on the QIRx-QLSy coupling under the x-polarized pulse. First, we considered a case neglecting the damping of normal modes to simply show the essential consequences of the QIRx-QLSy coupling on the dynamics of QLSy mode. Figure 4a,b show the motions of QIRx and QLSy modes at 0 K and 300 K, respectively, without damping under the x-polarized pulse with E0 = 34 MVcm−1 and σ = 100 fs. The initial vibration amplitudes were set as the mean-square-displacement according to the Bose-Einstein distribution at each temperature. The initial vibration of QLS was assumed to be aligned to the y-axis by setting the initial coordinate as QLSx = 0 Å. This results in the initial amplitudes of QIRx = 0.21 Å and QLSy = 0.91 Å at 0 K, while QIRx = 0.28 Å and QLSy = 5.70 Å at 300 K, respectively.
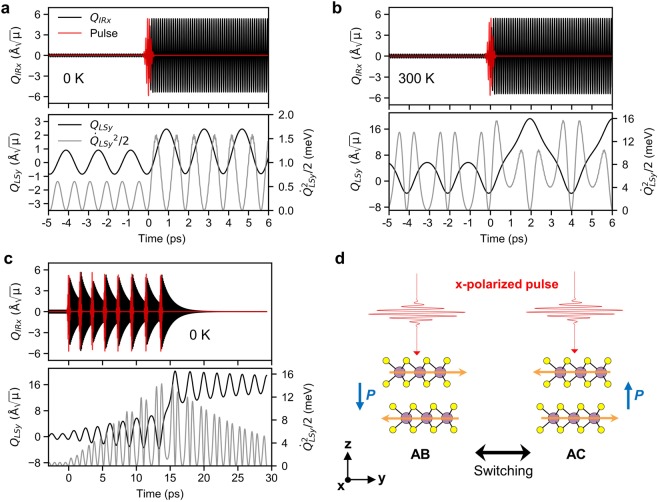
Figure 4.
Dynamics of the normal-modes under the x-polarized pulse (a,b) without and (c) with damping. (a) Amplification of the QLSy mode through the anharmonic force by the pulse at 0 K. (b) At 300 K, the QLSy has sufficient kinetic energy to overcome the effective energy barrier (〈Φ〉 = 11.5 meV at |QIRx| = 5.35 Å) after the pumping, and oscillates back and forth between AB (QLSy = 0 Å) and AC (QLSy = 16.29 Å) stackings. (c) In the presence of damping, the QLSy mode at 0 K overcomes the energy barrier after eight sequential pulses. The AB stacking changes to the AC stacking and does not return due to the dissipation of kinetic energy. (d) Schematics of ferroelectric switching through the QIRx-QLSy coupling. The orange arrows indicates the directions of interlayer shear induced by the x-polarized pulse, which are opposite in the AB and AC stackings.
In Fig. 4a, the QIRx and QLSy modes oscillate with the harmonic frequencies before the arrival of the pulse at 0 ps. The initial kinetic energy of QLSy mode was = 0.6 meV. When QIRx was pumped, QLSy started to oscillate with larger amplitude with respect to the shifted minimum at QLSy = 0.87 Å (in good agreement with aforementioned 0.72 Å shift in the effective potential minimum). The pumping does not affect the motion of QLSx (the value remains as ~0 Å) as there are no forcing terms on it. The kinetic energy of QLSy mode was increased to 1.6 meV by the anharmonic energy flow from the pumped QIRx mode. It is noted that the pulse and QLSy should be in-phase because the anharmonic force is unidirectional. The vibration of QLSy is restricted in a small region because the kinetic energy is still smaller than the effective barrier of 〈Φ〉 = 11.5 meV under the oscillating QIRx. In contrast, the oscillatory curve of QLSy mode at 300 K in Fig. 4b shows slight modulations in shape and frequency by the onset of anharmonicity of QLSy. The kinetic energy of QLSy mode was 13.4 meV which is yet below the static energy barrier Φ0 = 17.3 meV, but higher than the effective barrier 〈Φ〉 = 11.5 meV under the pulse. When QIRx mode was pumped, QLSy mode jumped over the barrier and oscillated with colossal amplitude between −3.79 Å and +19.19 Å. The vibration corresponds to the repetitive interconversion between AB and AC stackings, due to the absence of damping.
Secondly, a more realistic model that includes the damping of the normal modes was considered. The damping coefficients of γIR and γLS were taken as 2% of the harmonic frequencies, which are similar to the experimental values21. In Fig. 4c, the QIRx and QIRy modes initially oscillate with small amplitudes at 0 K until the arrival of the first pulse at 0 ps (damping is turned on at 0 ps). The eight sequencial pulses are applied to substantially amplify the QLSy mode from the zero-point vibration at 0 K. The time interval between the subsequent pulses is gradually increased by ~4% from the 1/ΩLS ~ 1.6 ps for the phase matching between the pulse and QLSy mode, considering the increase in the period of QLS mode due to anharmonicity. Upon each cycle of pulse irradiation, the QLSy mode is coherently amplified by gaining kinetic energy. After the eight pulses are irradiated, the QLSy mode has sufficient kinetic energy and jump over the effective barrier which is reduced by the QIRx mode. Once the initial AB stacking sequence changes to the AC stacking, it maintains the AC stacking due to the dissipation of the kinetic energies of the vibrations. This corresponds to the AB → AC ferroelectric switching. The opposite switching operation, AC → AB, can be performed by the same optical input as illustrated in Fig. 4d. The direction of Fanh on QLSy mode in the AC stacking is reversed (−r1 direction) with respect to that (r1 direction) in the AB stacking. The optical parameters of pulses (e.g. E0 and σ) used in this study might be optimized further for more efficient switching, for instance, via pulse shaping techniques37.
Conclusion
In summary, the polarization switching mechanism of the bilayer 3R MoS2 whose direction of the polarization is reversed by the change of the stacking sequence was investigated. The ferroelectric switching was achieved by driving the interlayer shear mode through the anharmonic energy flow from the optically pumped infrared mode. Remarkably, due to the selection rule from the crystal symmetry of MoS2, the degenerate interlayer shear mode can only be driven along its armchair axis whether the infrared mode is pumped along the zigzag or armchair axis. However, the optical pulse should be polarized along the zigzag axis for successful switching since the direction of anharmonic force is aligned with the switching direction. The coherent light pulses can amplify the interlayer shear mode substantially and unidirectionally, displacing the stacking sequence into the opposite polarization. The scheme for optical modulation of the stacking structure can be applied to other 2D materials exhibiting the interlayer shear mode to explore various stacking-dependent properties in a dynamical manner.
Methods
The density functional theory calculations were performed using Vienna Ab-initio Simulation Package (VASP)38,39. The projector-augmented wave (PAW) method40 and a cut-off energy of 500 eV were used with the valence electron configurations of Mo[4s24p65s24d4] and S[3s23p4], respectively. The generalized gradient approximation41 with Grimme’s D3 scheme42 was used to describe the van der Waals interaction. The bilayer structure was simulated by the supercell containing ~40 Å of vacuum layer to avoid the artificial interaction between periodic images. The structures were fully relaxed using 24 × 24 × 1 k-mesh until the residual forces on the atoms were less than 0.001 eVÅ−1. Spontaneous polarization was calculated using Berry phase method43. The phonon calculation was performed using PHONOPY code44 using 3 × 3 × 1 supercell and 8 × 8 × 1 k-mesh.
Acknowledgements
This work was supported by the Future Semiconductor Device Technology Development Program (10048490) funded by MOTIE (Ministry of Trade, Industry, & Energy), KSRC (Korea Semiconductor Research Consortium), and the Institutional Research Program of KIST (Korea Institute of Science and Technology) (2E29390). J.P. was partly supported by NRF-2013H1A2A1034588-Fostering Core Leaders of the Future Basic Science Program/Global Ph.D. Fellowship Program funded by NRF (National Research Foundation of Korea).
Author contributions
J.P. conceived the initial idea and performed all the calculations and analyses. I.W.Y. and G.H. helped all the calculations and discussed the technical contexts. C.S.H. helped prepare the manuscript from the viewpoint of the experimentalist. J.-H.C. arranged and supervised all the calculations and took charge of the manuscript preparation. All the authors reviewed the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Scott JF. Applications of Modern Ferroelectrics. Science. 2007;315:954–959. doi: 10.1126/science.1129564. [DOI] [PubMed] [Google Scholar]
- 2.Jeong DS, et al. Emerging memories: resistive switching mechanisms and current status. Reports Prog. Phys. 2012;75:076502. doi: 10.1088/0034-4885/75/7/076502. [DOI] [PubMed] [Google Scholar]
- 3.Wu M, Jena P. The rise of two-dimensional van der Waals ferroelectrics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018;8:e1365. doi: 10.1002/wcms.1365. [DOI] [Google Scholar]
- 4.Cui C, Xue F, Hu W-J, Li L-J. Two-dimensional materials with piezoelectric and ferroelectric functionalities. npj 2D Mater. Appl. 2018;2:18. doi: 10.1038/s41699-018-0063-5. [DOI] [Google Scholar]
- 5.Chang K, et al. Discovery of robust in-plane ferroelectricity in atomic-thick SnTe. Science. 2016;353:274–278. doi: 10.1126/science.aad8609. [DOI] [PubMed] [Google Scholar]
- 6.Cui C, et al. Intercorrelated In-Plane and Out-of-Plane Ferroelectricity in Ultrathin Two-Dimensional Layered Semiconductor In2Se3. Nano Lett. 2018;18:1253–1258. doi: 10.1021/acs.nanolett.7b04852. [DOI] [PubMed] [Google Scholar]
- 7.Ding W, et al. Prediction of intrinsic two-dimensional ferroelectrics in In2Se3 and other III2-VI3 van der Waals materials. Nat. Commun. 2017;8:14956. doi: 10.1038/ncomms14956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wan W, Liu C, Xiao W, Yao Y. Promising ferroelectricity in 2D group IV tellurides: a first-principles study. Appl. Phys. Lett. 2017;111:132904. doi: 10.1063/1.4996171. [DOI] [Google Scholar]
- 9.Fei R, Kang W, Yang L. Ferroelectricity and Phase Transitions in Monolayer Group-IV Monochalcogenides. Phys. Rev. Lett. 2016;117:097601. doi: 10.1103/PhysRevLett.117.097601. [DOI] [PubMed] [Google Scholar]
- 10.Manzeli S, Ovchinnikov D, Pasquier D, Yazyev OV, Kis A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017;2:17033. doi: 10.1038/natrevmats.2017.33. [DOI] [Google Scholar]
- 11.Qian X, Liu J, Fu L, Li J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science. 2014;346:1344–1347. doi: 10.1126/science.1256815. [DOI] [PubMed] [Google Scholar]
- 12.Sie EJ, et al. An ultrafast symmetry switch in a Weyl semimetal. Nature. 2019;565:61–66. doi: 10.1038/s41586-018-0809-4. [DOI] [PubMed] [Google Scholar]
- 13.Shirodkar SN, Waghmare UV. Emergence of Ferroelectricity at a Metal-Semiconductor Transition in a 1T Monolayer of MoS2. Phys. Rev. Lett. 2014;112:157601. doi: 10.1103/PhysRevLett.112.157601. [DOI] [PubMed] [Google Scholar]
- 14.Singh A, Shirodkar SN, Waghmare UV. 1H and 1T polymorphs, structural transitions and anomalous properties of (Mo,W)(S,Se)2 monolayers: first-principles analysis. 2D Mater. 2015;2:035013. doi: 10.1088/2053-1583/2/3/035013. [DOI] [Google Scholar]
- 15.Park J, et al. Optical control of the layer degree of freedom through Wannier–Stark states in polar 3R MoS2. J. Phys. Condens. Matter. 2019;31:315502. doi: 10.1088/1361-648X/ab1d0f. [DOI] [PubMed] [Google Scholar]
- 16.Li L, Wu M. Binary Compound Bilayer and Multilayer with Vertical Polarizations: Two-Dimensional Ferroelectrics, Multiferroics, and Nanogenerators. ACS Nano. 2017;11:6382–6388. doi: 10.1021/acsnano.7b02756. [DOI] [PubMed] [Google Scholar]
- 17.Fei Z, et al. Ferroelectric switching of a two-dimensional metal. Nature. 2018;560:336–339. doi: 10.1038/s41586-018-0336-3. [DOI] [PubMed] [Google Scholar]
- 18.Yang Q, Wu M, Li J. Origin of Two-Dimensional Vertical Ferroelectricity in WTe2 Bilayer and Multilayer. J. Phys. Chem. Lett. 2018;9:7160–7164. doi: 10.1021/acs.jpclett.8b03654. [DOI] [PubMed] [Google Scholar]
- 19.Suzuki R, et al. Valley-dependent spin polarization in bulk MoS2 with broken inversion symmetry. Nat. Nanotechnol. 2014;9:611–617. doi: 10.1038/nnano.2014.148. [DOI] [PubMed] [Google Scholar]
- 20.Tan PH, et al. The shear mode of multilayer graphene. Nat. Mater. 2012;11:294–300. doi: 10.1038/nmat3245. [DOI] [PubMed] [Google Scholar]
- 21.Zhang X, et al. Raman spectroscopy of shear and layer breathing modes in multilayer MoS2. Phys. Rev. B. 2013;87:115413. doi: 10.1103/PhysRevB.87.115413. [DOI] [Google Scholar]
- 22.Zhang X, et al. Phonon and Raman scattering of two-dimensional transition metal dichalcogenides from monolayer, multilayer to bulk material. Chem. Soc. Rev. 2015;44:2757–2785. doi: 10.1039/C4CS00282B. [DOI] [PubMed] [Google Scholar]
- 23.Först M, et al. Nonlinear phononics as an ultrafast route to lattice control. Nat. Phys. 2011;7:854–856. doi: 10.1038/nphys2055. [DOI] [Google Scholar]
- 24.Subedi A, Cavalleri A, Georges A. Theory of nonlinear phononics for coherent light control of solids. Phys. Rev. B. 2014;89:220301. doi: 10.1103/PhysRevB.89.220301. [DOI] [Google Scholar]
- 25.Juraschek DM, Maehrlein SF. Sum-frequency ionic Raman scattering. Phys. Rev. B. 2018;97:174302. doi: 10.1103/PhysRevB.97.174302. [DOI] [Google Scholar]
- 26.Subedi A. Proposal for ultrafast switching of ferroelectrics using midinfrared pulses. Phys. Rev. B. 2015;92:214303. doi: 10.1103/PhysRevB.92.214303. [DOI] [Google Scholar]
- 27.Mankowsky R, von Hoegen A, Först M, Cavalleri A. Ultrafast Reversal of the Ferroelectric Polarization. Phys. Rev. Lett. 2017;118:197601. doi: 10.1103/PhysRevLett.118.197601. [DOI] [PubMed] [Google Scholar]
- 28.Guo Z, et al. From Black Phosphorus to Phosphorene: Basic Solvent Exfoliation, Evolution of Raman Scattering, and Applications to Ultrafast Photonics. Adv. Funct. Mater. 2015;25:6996–7002. doi: 10.1002/adfm.201502902. [DOI] [Google Scholar]
- 29.Guo Z, et al. Metal-Ion-Modified Black Phosphorus with Enhanced Stability and Transistor Performance. Adv. Mater. 2017;29:1703811. doi: 10.1002/adma.201703811. [DOI] [PubMed] [Google Scholar]
- 30.Ghimire S, et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 2011;7:138–141. doi: 10.1038/nphys1847. [DOI] [Google Scholar]
- 31.You YS, et al. High-harmonic generation in amorphous solids. Nat. Commun. 2017;8:724. doi: 10.1038/s41467-017-00989-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu H, et al. High-harmonic generation from an atomically thin semiconductor. Nat. Phys. 2017;13:262–265. doi: 10.1038/nphys3946. [DOI] [Google Scholar]
- 33.Qi T, Shin Y-H, Yeh K-L, Nelson KA, Rappe AM. Collective Coherent Control: Synchronization of Polarization in Ferroelectric PbTiO3 by Shaped THz Fields. Phys. Rev. Lett. 2009;102:247603. doi: 10.1103/PhysRevLett.102.247603. [DOI] [PubMed] [Google Scholar]
- 34.Chen F, et al. Ultrafast terahertz-field-driven ionic response in ferroelectric BaTiO3. Phys. Rev. B. 2016;94:180104. doi: 10.1103/PhysRevB.94.180104. [DOI] [Google Scholar]
- 35.Juraschek DM, Fechner M, Spaldin NA. Ultrafast Structure Switching through Nonlinear Phononics. Phys. Rev. Lett. 2017;118:054101. doi: 10.1103/PhysRevLett.118.054101. [DOI] [PubMed] [Google Scholar]
- 36.Gonze X, Lee C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B. 1997;55:10355–10368. doi: 10.1103/PhysRevB.55.10355. [DOI] [Google Scholar]
- 37.Itin AP, Katsnelson MI. Efficient excitation of nonlinear phonons via chirped pulses: Induced structural phase transitions. Phys. Rev. B. 2018;97:184304. doi: 10.1103/PhysRevB.97.184304. [DOI] [Google Scholar]
- 38.Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996;6:15–50. doi: 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- 39.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- 40.Blöchl PE. Projector augmented-wave method. Phys. Rev. B. 1994;50:17953–17979. doi: 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- 41.Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 42.Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 43.King-Smith RD, Vanderbilt D. Theory of polarization of crystalline solids. Phys. Rev. B. 1993;47:1651–1654. doi: 10.1103/PhysRevB.47.1651. [DOI] [PubMed] [Google Scholar]
- 44.Togo A, Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 2015;108:1–5. doi: 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]